土力学-第四章地基的沉降计算3
合集下载
《土力学》 第四章土的压缩性
第四章土的压缩性与地基沉降计算
Soil compressibility and calculation of foundation deformation
学习基本要求
内 容
学时A（36学时制）
学时B（54学时制）
室内压缩试验与压缩性指标
1.5
1.5
现场载荷试验与指标
0.5
0.5
第四章土的压缩性与地基沉降计算
学习目标
单击此处添加文本具体内容，简明扼要的阐述您的观点。根据需要可酌情增减文字，以便观者准确的理解您传达的思想。
学习基本要求
单击此处添加文本具体内容，简明扼要的阐述您的观点。根据需要可酌情增减文字，以便观者准确的理解您传达的思想。
参考学习进度
单击此处添加文本具体内容，简明扼要的阐述您的观点。根据需要可酌情增减文字，以便观者准确的理解您传达的思想。
轴向应变
主应力差
室内三轴试验
§4土的压缩性与地基沉降计算
§4.2 一维压缩性及其指标
一、e – p 曲线
0
100
200
300
400
0.6
0.7
0.8
0.9
1.0
压缩系数，kPa-1，MPa-1
1
e0
侧限压缩模量,kPa ,MPa 侧限变形模量
固体颗粒
孔隙
体积压缩系数， kPa-1 ，MPa-1
P(kPa)
Kiss
第四章土的压缩性与地基沉降计算
Soil compressibility and calculation of foundation deformation 由于沉降相互影响，两栋相邻的建筑物上部接触
第四章土的压缩性与地基沉降计算
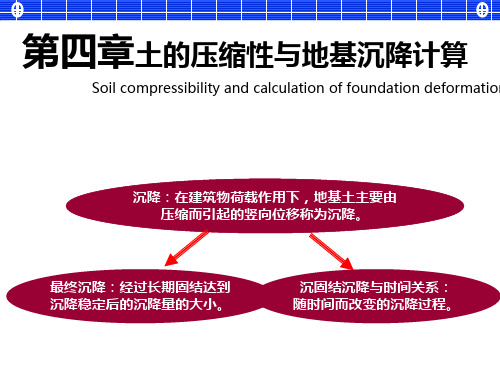
Soil compressibility and calculation of foundation deformation
学习基本要求
内 容
学时A（36学时制）
学时B（54学时制）
室内压缩试验与压缩性指标
1.5
1.5
现场载荷试验与指标
0.5
0.5
第四章土的压缩性与地基沉降计算
学习目标
单击此处添加文本具体内容，简明扼要的阐述您的观点。根据需要可酌情增减文字，以便观者准确的理解您传达的思想。
学习基本要求
单击此处添加文本具体内容，简明扼要的阐述您的观点。根据需要可酌情增减文字，以便观者准确的理解您传达的思想。
参考学习进度
单击此处添加文本具体内容，简明扼要的阐述您的观点。根据需要可酌情增减文字，以便观者准确的理解您传达的思想。
轴向应变
主应力差
室内三轴试验
§4土的压缩性与地基沉降计算
§4.2 一维压缩性及其指标
一、e – p 曲线
0
100
200
300
400
0.6
0.7
0.8
0.9
1.0
压缩系数，kPa-1，MPa-1
1
e0
侧限压缩模量,kPa ,MPa 侧限变形模量
固体颗粒
孔隙
体积压缩系数， kPa-1 ，MPa-1
P(kPa)
Kiss
第四章土的压缩性与地基沉降计算
Soil compressibility and calculation of foundation deformation 由于沉降相互影响，两栋相邻的建筑物上部接触
第四章土的压缩性与地基沉降计算
土力学第四章土的变形性质及地基沉降计算【优秀完整版】可编辑全文
s
VV1e0
Vs 1
压缩前
VV2 e
Vs 1
压缩后
H0 Hi H0si 1e0 1ei 1ei
si
e0 ei 1 e0
H0
ei
e0
si H0
1e0
e0
ds10w1
压力p与相应的稳定孔隙比的关系曲线称为压缩曲线。
a图：压力与加荷历时 关系。
b图：各级压力下，试 样孔隙比随时间的变化 过程。
(1) 压缩系数
P1——一般指地基某深度处土中竖向自重应力； P2——地基某深度处自重应力与附加应力之和； e1——相应于p1作用下压缩稳定后土的孔隙比； e2——相应于p2作用下压缩稳定后土的孔隙比；
ataα nΔee1e2 Δp p2p1
用单位压力增量 所引起的孔隙比的改 变，即压缩曲线的割 线坡度表征土的压缩 性的高低。
原始压缩曲线是由直线或折线组成，通过Cc或Ce两个压缩性指标即可计算，使用方便。
分层总和法计算地基的最终沉降量
1 Mpa-1
属低压缩性土。
1、土的压缩性：地基土在压力作用下体积减小的特性。
由e~p或e~lgp曲线求得
土体在无侧向变形条件下，竖直应力与竖向应变之比。
该式称为一维固结微分方程，
OCR>1 超固结状态
在整个固结过程中，土的渗透系数、压缩系数视为常数。
土层的平均固结度是时间因数Tv的单值函数，它与所加的附加应力的大小无关，但与土层中附加应力的分布形态有关。
分层总和法计算地基的最终沉降量
我国《建筑地基基础设计规范》规定
变形模量与压缩模量之间的关系
压缩模量Es：土在完全侧限条件下，竖向正应力与相应 的变形稳定情况下的竖向应变的比值。
土力学第四章、土的最终沉降量
工程设计中，我们不但需要预估建筑物基础可能产生 的最终沉降量，而且需要预估建筑物基础达到某一沉降量 所需的时间，亦即需要知道沉降与时间的变化过程。目前 均以饱和土体一维固结理论为研究基础。
一维固结力学模型
一维固结又称单向固结。土体在荷载作用 下土中水的渗流和土体的变形仅发生在一个方 向的固结问题。严格的一维固结问题只发生在 室内有侧限的固结试验中，实际工程中并不存 在。然而，当土层厚度比较均匀，其压缩土层 厚度相对于均布外荷作用面较小时，可近似为 一维固结问题。
使得上式与实测值之间的关系差 距较大。根据统计资料，E0值可 能是βEs值的几倍，一般说来， 土愈坚硬则倍数愈大，而软土的
E0值和βEs值比较接近。
4.2 地基最终沉降量计算
地基最终沉降量的计算方法主要有以 下几种方法：
1、 分层总和法 2、 规范法 3、 理论公式计算法
4.2.1 分层总和法
地基的最终沉 降量，通常采用 分层总和法进行 计算，即在地基 沉降计算深度范 围内划分为若干 层，计算各分层 的压缩量，然后 求其总和。
平均附加应力系数的物理
意义：分层总和法中地基附
加应力按均质地基计算，即 地基土的压缩模量Es不随深 度而变化。从基底至地基任 意深度Z范围内的压缩量为：
z
s'
dz
1
0
Es
0zzdzEAs
4.2.2 规范法分层总和法
附加应力面积：
z
z
Azdz p0dz
0
0
深度 z 范围内 的竖向平均附 加应力系数
土体变形机理非常复杂，土体不是 理想的弹塑性体，而是具有弹性、粘性 、塑性的自然历史的产物。
4.1.3 土的载荷试验及变形模量
通过载荷试验可测定地基变形模量，地 基承载力以及研究土的湿陷性等。
一维固结力学模型
一维固结又称单向固结。土体在荷载作用 下土中水的渗流和土体的变形仅发生在一个方 向的固结问题。严格的一维固结问题只发生在 室内有侧限的固结试验中，实际工程中并不存 在。然而，当土层厚度比较均匀，其压缩土层 厚度相对于均布外荷作用面较小时，可近似为 一维固结问题。
使得上式与实测值之间的关系差 距较大。根据统计资料，E0值可 能是βEs值的几倍，一般说来， 土愈坚硬则倍数愈大，而软土的
E0值和βEs值比较接近。
4.2 地基最终沉降量计算
地基最终沉降量的计算方法主要有以 下几种方法：
1、 分层总和法 2、 规范法 3、 理论公式计算法
4.2.1 分层总和法
地基的最终沉 降量，通常采用 分层总和法进行 计算，即在地基 沉降计算深度范 围内划分为若干 层，计算各分层 的压缩量，然后 求其总和。
平均附加应力系数的物理
意义：分层总和法中地基附
加应力按均质地基计算，即 地基土的压缩模量Es不随深 度而变化。从基底至地基任 意深度Z范围内的压缩量为：
z
s'
dz
1
0
Es
0zzdzEAs
4.2.2 规范法分层总和法
附加应力面积：
z
z
Azdz p0dz
0
0
深度 z 范围内 的竖向平均附 加应力系数
土体变形机理非常复杂，土体不是 理想的弹塑性体，而是具有弹性、粘性 、塑性的自然历史的产物。
4.1.3 土的载荷试验及变形模量
通过载荷试验可测定地基变形模量，地 基承载力以及研究土的湿陷性等。
土力学 第4章 土的压缩性与地基沉降计算
变形测量 固结容器
百分表
加压上盖
透水石
环刀 压缩
容器
加
压
试样
护环
支架
设 备
《土力学》 第4章 土的压缩性与地基沉降计算
（2）利用受压前后土粒体积不变和土样截面面积不变两个
条件，可求土样压缩稳定后孔隙比ei
受压前
:VS
(1
e 0
)
H
0
A
受压后:VS (1 e1) H1A
Vs
H 0
A
《土力学》 第4章 土的压缩性与地基沉降计算
土的固结状态对土的压缩性的影响：
在压力p作用下的地基沉降值si： 正常固结土为s1； 超固结土为s2； 欠固结土为s3。
则有：s2＜s1＜s3
《土力学》 第4章 土的压缩性与地基沉降计算
pc卡萨格兰德法
① 在e–lgp坐标上绘出试样
的室内压缩曲线； ② 找出压缩曲线上曲率最
Cc
lg
e1 p2
e2 lg
p1
e1 e2 lg p2
p1
一般认为：
cc＜0.2时， 为低压缩性土； cc=0.2～0.4时，属中压缩性土； cc＞0.4时， 属高压缩性土。
图5-6 由e-lgp曲线确定压缩系数cc
《土力学》
第4章 土的压缩性与ຫໍສະໝຸດ 基沉降计算（5）土的回弹与再压缩曲线
H1
A
1e 1e
0
1
受压前后Vs，A不变
H0 H1 H0 s1 1 e0 1 e1 1 e1
e1
e0
s1 H0
1
e0
式中 e0 为土的初始孔隙比，可由土的三个基本实验指标求得，即
土力学第四章(压缩)讲解
第四章：土的压缩及沉降计算名词解释1、压缩系数：土体在侧限条件下孔隙比减少量与竖向压应力增量的比值。
2、压缩指数：在压力较大部分,e-lgp关系接近直线,其斜率称为土的压缩指数。
3、压缩模量：土在侧限条件下竖向压应力与竖向总应变的比值，或称为侧限模量。
4、变形模量：土在无侧限条件下竖向压应力与竖向总应变的比值。
5、体积压缩系数：在单位压应力作用下单位体积的变化量。
6、超固结比：先期固结压力pc与现时的土压力p0的比值。
7、前期固结压力：指土层在历史上曾经受过的最大有效固结压力。
8、最终沉降量：地基变形稳定后基础底面的沉降量。
9、固结：土体在压力作用下，压缩量随时间增长的过程。
10、固结度：在某一固结压力作用下，经过一定时间土体发生固结的程度。
简答1、为什么可以用孔隙比的变化来表示土的压缩性？答：土体压缩的实质是孔隙体积减小的结果，土粒体积保持不变；而孔隙比反映了孔隙的体积和土粒的体积比，因此可以用孔隙比的变化来表示土的压缩性。
2、地基土变形的两个最显著的特征是什么？答：体积变形是由于正应力引起的，只能使土体产生压密，孔隙体积减小，但不会使土体产生破坏；形状变形是由剪应力引起的，在剪应力作用下土颗粒间产生移动，使土体产生剪切破坏。
3、工程中常用的压缩系数和模量是什么？如何判定土的压缩性？答：压缩系数和压缩模量都是变量，为比较土的压缩性高低，工程中常用的压缩系数和压缩模量是压力在100-200kPa下的值。
a v＜0.1MPa-1低压缩性土，0.1MPa-1≤a v＜0.5MPa-1中压缩性土，a v≥0.5MPa-1高压缩性土；Es＜4MPa高压缩性土，4MPa≤Es＜15MPa中压缩性土，Es≥15MPa低压缩性土；4、自重应力在任何情况下都不会引起地基沉降吗？为什么？答：对于正常固结土和超固结土来说，自重应力不会引起地基沉降了，但对于欠固结土（新沉积的土或刚填筑的土）来说，由于现有的固结应力大于先期固结应力，自重应力也会引起地基沉降。
土力学第四章
施加σ1－σ3时 排水
不排水 不排水
量测 体变 孔隙水压力 孔隙水压力
4.1 土的变形特性试验方法
4.1.2 常规三轴压缩试验
z
1
1
Et
Ei
z
维持围压不变
割线变形模量
E sec
z z
切线模量
Et
d z d z
Et随应力增大而变小
v 123 泊松比3 1(1v)
SSi
4.3 地基沉降量
4.3.2 沉降计算的分层总和法
2、计算步骤 不考虑地基回弹的情形： •沉降量从原基底算起； •适用于基础底面积小，埋深浅，施工快。
考虑地基回弹的情形： •沉降量从回弹后的基底算起； •基础底面大，埋深大，施工期长。
4.3.2 沉降计算的分层总和法
2、计算步骤——不考虑回弹
⑤ 直线BC即为原位压缩曲线。
4.3 地基沉降量
Sd ：初始瞬时沉降
t
Sc：主固结沉降
S
Ss: 次固结沉降
SSdScSs
4.3 地基沉降量
4.3.1 一维压缩基本课题
p
H/2
H sz 2
H/2
σ sz
σz=p H
压缩前
侧限条件 压缩后
p1 sz
e1
p2 sz z
e2
1 2 1
4.1 土的变形特性试验方法
4.1.2 常规三轴压缩试验
z p 侧限压缩试验
常规三轴试验
z
E Es 1 2 2
1
4.1 土的变形特性试验方法
4.1.3 土的变形特点和本构关系
土的主要变形特征： 非线性 弹塑性 剪胀（缩）性 压硬性 时间效应
软土地基沉降计算
n
Ecs mE ps (1 m) Ess
式中，S1 —加固区的沉降量； pi —附加应力增量； hi —分层厚度； E ps —桩体压缩模量； E ss —桩间土压缩模量； m —复合地基置换率； n—分层总数。 A p 复合地基置换率： m 式中：A p —单桩面积； A A —桩周复合土体单元面积。
下卧层的沉降计算
下卧层的沉降量通常采用分层总和法 计算： n
S2
i 1 zi
式中，S1 —下卧层的沉降量； —第 i 层土的平均附加应力； E si —第 i 层土的压缩模量； hi —第 i 层土的厚度。 其附加荷载的计算有应力扩散法、 等效实体法和改进Geddes法。
zi
E si
s 1 /1 mn 1
pi —天然地基在荷载 p 作用下第 i 层 式中， 土上的附加应力增量； p —复合地基中第 i 层桩间土的附 加应力增量； u s —应力修正系数（反映桩间土分 担应力比例的系数）； n —桩土应力比； E si —第 i 层桩间土的压缩模量。
§3 桩基沉降计算
桩基的沉降是受多种复杂的因素影响而 产生的，它涉及到桩和地基所受到的应力和 弹塑性变形、地基的固结沉降、桩的型式和 布置、施工或地基条件的变化等多种因素。 除单桩的弹、塑性变形可以用桩的静载试验 方法准确确定以外，其它因素只能根据建筑 经验和部分研究成果综合确定。对于桩基内、 桩基下的应力分布以及桩基沉降的计算有各 种各样的假设，以下将介绍目前国内外常用 的计算方法并进行一些讨论。
（2）计算步骤 1）根据地层剖面图把地基分成薄层，每 薄层的厚度不超过0.4b，b为基础宽。如 有不同性质的土层（包括重度、压缩性 质有变化者），不论多薄，也要单独分 层。 2）计算各薄层分界面上的原存压力（土 自重压力），按下式计算：
Ecs mE ps (1 m) Ess
式中，S1 —加固区的沉降量； pi —附加应力增量； hi —分层厚度； E ps —桩体压缩模量； E ss —桩间土压缩模量； m —复合地基置换率； n—分层总数。 A p 复合地基置换率： m 式中：A p —单桩面积； A A —桩周复合土体单元面积。
下卧层的沉降计算
下卧层的沉降量通常采用分层总和法 计算： n
S2
i 1 zi
式中，S1 —下卧层的沉降量； —第 i 层土的平均附加应力； E si —第 i 层土的压缩模量； hi —第 i 层土的厚度。 其附加荷载的计算有应力扩散法、 等效实体法和改进Geddes法。
zi
E si
s 1 /1 mn 1
pi —天然地基在荷载 p 作用下第 i 层 式中， 土上的附加应力增量； p —复合地基中第 i 层桩间土的附 加应力增量； u s —应力修正系数（反映桩间土分 担应力比例的系数）； n —桩土应力比； E si —第 i 层桩间土的压缩模量。
§3 桩基沉降计算
桩基的沉降是受多种复杂的因素影响而 产生的，它涉及到桩和地基所受到的应力和 弹塑性变形、地基的固结沉降、桩的型式和 布置、施工或地基条件的变化等多种因素。 除单桩的弹、塑性变形可以用桩的静载试验 方法准确确定以外，其它因素只能根据建筑 经验和部分研究成果综合确定。对于桩基内、 桩基下的应力分布以及桩基沉降的计算有各 种各样的假设，以下将介绍目前国内外常用 的计算方法并进行一些讨论。
（2）计算步骤 1）根据地层剖面图把地基分成薄层，每 薄层的厚度不超过0.4b，b为基础宽。如 有不同性质的土层（包括重度、压缩性 质有变化者），不论多薄，也要单独分 层。 2）计算各薄层分界面上的原存压力（土 自重压力），按下式计算：
土力学-第四章-概述 土的压缩性测试方法 张丙印
t
s
s3
s2
s1
t
§4.2 土的压缩性测试方法 – 压缩试验
智者乐水 仁者乐山
压缩曲线及特点
• 侧限变形（压缩）模量：
加载：
Es
Δσ z Δεz
卸载和重加载：
Ee
Δσz Δεz
非线性 弹塑性
土的一般化的压缩曲线
z= p
1 Ee 1 Es
e
z
( e )
侧限压缩试验
18
§4.2 土的压缩性测试方法 – 三轴试验
常规三轴：
• 存在破坏应力
侧限压缩试验：
• 不存在破坏应力 • 存在体积压缩极限
z=p
侧限压 缩试验
常规三 轴试验
e
z
( e )
常规三轴与侧限压缩试验
22
§4.2 土的压缩性测试方法
智者乐水 仁者乐山
变形模量 Et 与侧限变形模量 Es间的关系
虎 εz
σz Et
νt Et
σx σy
克 定 律
墨西哥某宫殿
左部：1709年 右部：1622年 地基：20多米厚粘土
问题： 沉降2.2米，且左右 两部分存在明显的 沉降差。左侧建筑 物于1969年加固
智者乐水 仁者乐山
工程实例
6
§4.1 概述
智者乐水 仁者乐山
墨西哥城的一幢建筑， 可清晰地看见其发生的 沉降及不均匀沉降。该 地的土层为深厚的湖相 沉积层，土的天然含水 量高达 650 ％，液限 500% ，塑性指数 350 ， 孔隙比为 15 ，具有极 高的压缩性。
《土力学1》之第四章
土的压缩性与地基沉降计算
张丙印
清华大学土木水利学院 岩土工程研究所
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
z k p0
II. 荷载不是瞬时施加。 因此，不同的附加应力条件下，其固结度的公式也不同。
那么，怎么求解其他应力条件下的固结度呢？
叠加原理
U F U a Fa U b Fb
任意随深度而变的应力图形可以分解为若干个图形，则 总应力图形的固结度乘上其总应力面积，等于各分力应 力图形的固结度乘上各应力面积之和。
1 U (t ) 1 2 Hp
udz
0
并代入u的表达式
U (t ) 1 2
1 exp( M 2Tv ) U (Tv ) （U与Tv为一一对应关系） 2 m0 M
近似式
U (Tv ) 1
8
exp( 2
2
4
Tv ) (U (t ) 30%)
U(t)是Tv的单值 函数，Tv可反映 固结的程度
（2）有效应力逐渐增大，最终与总应力相等。 （3）变形随固结过程逐渐增大，最终达到稳定。
11
2、Terzaghi一维渗透固结数学模型
基本假定： 1. 土层是均质且完全饱和
2. 3. 4. 5. 6. 土颗粒与水不可压缩 水的渗出和土层压缩只沿竖向发生 渗流符合达西定律且渗透系数k保持不变 压缩系数av是常数 荷载均布,瞬时施加，总应力不随时间变化
de av du
dV
故孔隙体积变化与孔隙水压的关系为
1 ∂e dz 1 e ∂t
av u u dV dz mv dz 1 e t t
16
（3）由dQ=dV 建立固结方程
k 2u dQ dz 2 w z
由此得到固结方程
u dV mv dz t
∂ 2u ∂ u Cv 2 ∂z ∂t
06-12 11.5 10.5 13.7 12.5 11.1 13.8 12.4 11.0 13.6 13.3 9.5 15.0 12.5
6
二、太沙基一维渗透固结理论
渗透固结理论是针对土这种多孔多相松散介质,建立起 来的反映土体变形过程的基本理论。土力学的创始人 Terzaghi教授于20世纪20年代提出饱和土的一维渗透 固结理论。 物理模型 － 太沙基一维渗透固结模型
• 其一般解的形式为：
u( z, t ) (C1 cos Az C2 sin Az)e
A2Cvt
• 只要给出定解条件，求解渗透固结方程，可得出u(z,t)
19
1 Mz 2 u 2 p sin( ) exp( M TV ) M (2m 1) 2 H m0 M
m 0,1,2,3
1 ∂e dz 1 e ∂t
土粒高度，保持不变
15
• 建立孔隙比e与孔隙水压u的关系
de av d
de av d
由于在均匀满布荷载产生的附加应力（总应力）沿深度不变，即
( z, t ) ( z, t ) u( z, t ) p
由此得到
d du
p
砂
u
u
H
t
t 0
饱 和 粘 土
t 0
H
p
砂
z
粘土层顶面、底面处排水距离为0，故孔隙水压始终为0；中心位 置排水距离最大，故孔隙水压最大，有效应力最小。
21
• 单面排水时
p
砂
u
u
饱 和 粘 土
H
t
t 0
t 0
基 岩
p
z
粘土层底面处排水距离最大，故故孔隙水压最大，有效应力最小。
17
3、Terzaghi一维渗透固结方程的求解
（1）初始条件和边界条件
• 初始条件
砂
p
u ( z , t ) t 0 p
• 边界条件
饱 和 粘 土
H
双面排水时
H
u ( z, t ) z 0 0
u ( z, t ) z 2 H 0
单面排水时
H 为粘土厚度的一半
砂
u ( z, t ) z 0 0
•2. 满布荷载双面排水时，平均固结度的计算公式
2H
最终的沉降
s
ds
0
2H 0
2H
0
pmv dz 2mv pH
2H
2H
时刻t 的沉降 s (t ) 由此得到
ds mv dz ( p u )mv dz 0
0
2H
2H
2mv pH mv
udz
0
22
三、固结度的计算
（1）固结度 percent consolidation,degree of consolidation 饱和粘土固结完成的程度。可按：I. 土层中一点孔隙水压消散 或II. 整个土层固结变形完成的程度来衡量。
• 一点处的固结度 （按孔隙水压消散或有效应力转化程度）
p u u U ( z , t ) 1 p p
测 点 及 沉 降 值（m） 7 8 10 11 12 15 16 17 平均
00-12 10.6 9.7 12.8 11.7 10.6 13.0 11.6 10.3 12.7 12.5 9.0 14.1 11.7
01-12 10.8 9.9 13.0 11.9 10.7 13.2 11.8 10.5 12.9 12.7 9.1 14.3 11.9
t 0 0u p 0 p
二、太沙基一维渗透固结理论
• 固结过程中的孔隙水压、有效应力、沉降
应 力 或 沉 降 总应力p 有效应力
effective stress
位 移 孔隙水压u pore water pressure 时间
随着固结过程的进行：
（1）孔隙水压（超静水压）逐渐消散，最终至0。
I. 固结度U为U′在粘土层厚度内的平均值。
II. H↑→ Tv ↓→ U↓。H 相当于最大排水距离。
25
固结度Ut与时间因数Tv的关系图
26
• 排水固结法
通过减小排水距离，加快黏土层的固结速度。
堆载
袋 装 砂 井
砂 井
排水塑料板
芯 板 滤膜
27
3. 实际工程中地基固结度的计算 I. 附加应力沿深度不是均匀分布。 地基土中应力的分布是随深度变化的，不是均匀满布荷载。
数学模型 － 渗透固结微分方程
方程求解 － 理论解答
7
太沙基一维渗透固结模型的假设背景
实践背景：大面积均布荷载
饱和 压缩层 不透水 岩层 p
侧限状态的简化模型
p
σz=p
K0p
p K0p
不变形 的钢筒
处于侧限状态，渗流和土体的变形只沿竖向发生
一维渗透固结
8
1、Terzaghi一维渗透固结物理模型
p
o
M
H
z
u
Uz,t=0～1：表征一点超静孔压的消散程度
z
p
23
三、固结度的计算
1. 一层土土层平均固结度 土层某一时刻的沉降（压缩量）与最终沉降（压缩量）之比。
S (t ) U (t ) S
由最终沉降（压缩量）及固结度可预测任意时刻的沉降（压缩量）。
S (t ) U (t ) S
28
(1)双面排水时平均固结度的计算
基本情况A
透水 应力分布 透水
无论哪种情况，均按情况A计算 Cv Tv 2 t 压缩土层深度H取1/2值 H
UA 1 8
2H
2
exp(
2
4
Tv )
29
（2）单面排水时的固结度计算 压缩应力分布不同时
情况A
r a b
情况1 情况2 情况2
3
•实例
麻省理工（MIT ）校园10号建筑物及其沉降曲线 该建筑在1915年建成后的10年中，一直以较大的速率沉降，并引起相当 大的惊慌。Terzaghi于1925年首次到美国后，通过检查和分析，正确地预测出 其沉降速率将逐渐减小。
4
日本关西国际机场
• 1986年：开工 • 1990年：人工岛完成 • 1994年：机场运营 • 面积：546万m2
30
U1 2U A U B
也可根据Tv值查表4－14
四、有关沉降－时间的工程问题
1.
2. 3.
求某一时刻t的固结度与沉降量
求达到某一固结度所需要的时间 根据前一阶段测定的沉降－时间曲
土体的固结 物理模型
p
p
侧限条件 土骨架 孔隙水 排水顶面 渗透性大小
钢筒 弹簧 水体 带孔活塞 活塞小孔大小
9
1、Terzaghi一维渗透固结物理模型
• 固结模型和固结过程
p
孔隙水 孔 隙 土骨架
p
p
u
t 0 u p 0
u
t
u0 p
10
时间 超静水压 有效应力
4370m×1250m
• 填筑量：180×106m3 • 平均厚度：33m • 地基：15-21m厚粘土
世界第二大人工岛
5
问题：沉降大，且不均匀
设计预测沉降： 5.7－7.5 m 完工实际沉降： 8.1 m，5cm/月 (1990年) 预测主固结完成： 20年后 比设计超填： 3.0 m
日期 1 2 3 5
• 时间因数 time factor
TV
cV t H2
为无量纲数，称为时间因数，反映超静 孔压消散的程度也即固结的程度。
• H （最大渗透距离）的确定 （1）双面排水时，取粘土层厚度的一半。 （2）单面排水时，取粘效应力的分布及变化
• 双面排水时
u p
情况B