2019八年级期末压轴题合集

合集下载

八年级压轴题期末复习试卷复习练习(Word版含答案)

八年级压轴题期末复习试卷复习练习(Word 版含答案)一、压轴题1．如图，直线2y x m =-+交x 轴于点A ，直线122y x =+交x 轴于点B ，并且这两条直线相交于y 轴上一点C ，CD 平分ACB ∠交x 轴于点D ．（1）求ABC 的面积．（2）判断ABC 的形状，并说明理由．（3）点E 是直线BC 上一点，CDE △是直角三角形，求点E 的坐标．2．如图，直线l 1：y 1=﹣x +2与x 轴，y 轴分别交于A ，B 两点，点P （m ，3）为直线l 1上一点，另一直线l 2：y 2=12x +b 过点P ．（1）求点P 坐标和b 的值；（2）若点C 是直线l 2与x 轴的交点，动点Q 从点C 开始以每秒1个单位的速度向x 轴正方向移动．设点Q 的运动时间为t 秒．①请写出当点Q 在运动过程中，△APQ 的面积S 与t 的函数关系式； ②求出t 为多少时，△APQ 的面积小于3；③是否存在t 的值，使△APQ 为等腰三角形？若存在，请求出t 的值；若不存在，请说明理由．3．如图（1），AB ＝4cm ，AC ⊥AB ，BD ⊥AB ，AC ＝BD ＝3cm ．点 P 在线段 AB 上以 1/cm s 的速度由点 A 向点 B 运动，同时，点 Q 在线段 BD 上由点 B 向点 D 运动．它们运动的时间为 t （s ）．（1）若点 Q 的运动速度与点 P 的运动速度相等，当t ＝1 时，△ACP 与△BPQ 是否全等，请说明理由，并判断此时线段 PC 和线段 PQ 的位置关系；（2）如图（2），将图（1）中的“AC ⊥AB ，BD ⊥AB”为改“∠CAB ＝∠DBA ＝60°”，其他条件不变．设点 Q 的运动速度为x /cm s ，是否存在实数x ，使得△ACP 与△BPQ 全等？若存在，求出相应的x 、t 的值；若不存在，请说明理由．4．如图1．在△ABC中，∠ACB=90°，AC=BC=10，直线DE经过点C，过点A，B分别作AD⊥DE，BE⊥DE，垂足分别为点D和E，AD=8，BE=6．（1）①求证：△ADC≌△CEB；②求DE的长；（2）如图2，点M以3个单位长度/秒的速度从点C出发沿着边CA运动，到终点A，点N 以8个单位长度/秒的速度从点B出发沿着线BC—CA运动，到终点A．M，N两点同时出发，运动时间为t秒(t＞0)，当点N到达终点时，两点同时停止运动，过点M作PM⊥DE 于点P，过点N作QN⊥DE于点Q；①当点N在线段CA上时，用含有t的代数式表示线段CN的长度；②当t为何值时，点M与点N重合；③当△PCM与△QCN全等时，则t=．5．直角三角形ABC中，∠ACB=90°，直线l过点C．（1）当AC=BC时，如图①，分别过点A、B作AD⊥l于点D，BE⊥l于点E．求证：△ACD≌△CBE．（2）当AC=8，BC=6时，如图②，点B与点F关于直线l对称，连接BF，CF，动点M从点A出发，以每秒1个单位长度的速度沿AC边向终点C运动，同时动点N从点F出发，以每秒3个单位的速度沿F→C→B→C→F向终点F运动，点M、N到达相应的终点时停止运动，过点M作MD⊥l于点D，过点N作NE⊥l于点E，设运动时间为t秒．①CM=，当N在F→C路径上时，CN=．（用含t的代数式表示）②直接写出当△MDC与△CEN全等时t的值．6．如图，以直角△AOC 的直角顶点O 为原点，以OC ，OA 所在直线为x 轴和y 轴建立平面直角坐标系，点A （0，a ），C （b ，0）满足280a b b -++-=．（1）点A 的坐标为________；点C 的坐标为________．（2）已知坐标轴上有两动点P ，Q 同时出发，P 点从C 点出发沿x 轴负方向以每秒2个单位长度的速度匀速移动，Q 点从O 点出发沿y 轴正方向以每秒1个单位长度的速度匀速移动，点P 到达O 点整个运动随之结束．AC 的中点D 的坐标是（4，3），设运动时间为t 秒．问：是否存在这样的t ，使得△ODP 与△ODQ 的面积相等？若存在，请求出t 的值；若不存在，请说明理由．（3）在（2）的条件下，若∠DOC=∠DCO ，点G 是第二象限中一点，并且y 轴平分∠GOD ．点E 是线段OA 上一动点，连接接CE 交OD 于点H ，当点E 在线段OA 上运动的过程中，探究∠GOA ，∠OHC ，∠ACE 之间的数量关系，并证明你的结论（三角形的内角和为180°可以直接使用）．7．观察下列两个等式：5532321,44133+=⨯-+=⨯-，给出定义如下：我们称使等式1a b ab +=-成立的一对有理数,a b 为“白马有理数对”，记为(,)a b ，如：数对5(3,2),4,3⎛⎫⎪⎝⎭都是“白马有理数对”．（1）数对3(2,1),5,2⎛⎫- ⎪⎝⎭中是“白马有理数对”的是_________；（2）若(,3)a 是“白马有理数对”，求a 的值；（3）若(,)m n 是“白马有理数对”，则(,)n m --是“白马有理数对”吗？请说明理由．（4）请再写出一对符合条件的“白马有理数对”_________（注意：不能与题目中已有的“白马有理数对”重复） 8．阅读下面材料，完成(1)-(3)题．数学课上，老师出示了这样一道题：如图1，已知等腰△ABC 中，AB ＝AC ，AD 为BC 边上的中线，以AB 为边向AB 左侧作等边△ABE ，直线CE 与直线AD 交于点F ．请探究线段EF 、AF 、DF 之间的数量关系，并证明．同学们经过思考后，交流了自已的想法：小明：“通过观察和度量，发现∠DFC 的度数可以求出来．”小强：“通过观察和度量，发现线段DF 和CF 之间存在某种数量关系．” 小伟：“通过做辅助线构造全等三角形，就可以将问题解决．” ......老师：“若以AB 为边向AB 右侧作等边△ABE ，其它条件均不改变，请在图2中补全图形,探究线段EF 、AF 、DF 三者的数量关系，并证明你的结论．”（1）求∠DFC 的度数；（2）在图1中探究线段EF 、AF 、DF 之间的数量关系，并证明；（3）在图2中补全图形，探究线段EF 、AF 、DF 之间的数量关系，并证明．9．在等腰△ABC 与等腰△ADE 中，AB ＝AC ，AD ＝AE ，∠BAC ＝∠DAE ，且点D 、E 、C 三点在同一条直线上，连接BD ．（1）如图1，求证：△ADB ≌△AEC（2）如图2，当∠BAC ＝∠DAE ＝90°时，试猜想线段AD ，BD ，CD 之间的数量关系，并写出证明过程；（3）如图3，当∠BAC ＝∠DAE ＝120°时，请直接写出线段AD ，BD ，CD 之间的数量关系式为：（不写证明过程）10．如图，在边长为2的等边三角形ABC 中，D 点在边BC 上运动（不与B ，C 重合），点E 在边AB 的延长线上，点F 在边AC 的延长线上，AD DE DF ==．（1）若30AED ∠=︒，则ADB =∠______．（2）求证：BED CDF △≌△．（3）试说明点D 在BC 边上从点B 至点C 的运动过程中，BED 的周长l 是否发生变化？若不变，请求出l 的值，若变，请求出l 的取值范围．11．直角三角形ABC 中，90ACB ∠=︒，直线l 过点C ．（1）当AC BC =时，如图1，分别过点A 和B 作AD ⊥直线l 于点D ，BE ⊥直线l 于点E ，ACD 与CBE △是否全等，并说明理由；（2）当8AC cm =，6BC cm =时，如图2，点B 与点F 关于直线l 对称，连接BF CF 、，点M 是AC 上一点，点N 是CF 上一点，分别过点M N 、作MD ⊥直线l 于点D ，NE ⊥直线l 于点E ，点M 从A 点出发，以每秒1cm 的速度沿A C →路径运动，终点为C ，点N 从点F 出发，以每秒3cm 的速度沿F C B C F →→→→路径运动，终点为F ，点,M N 同时开始运动，各自达到相应的终点时停止运动，设运动时间为t 秒，当CMN △为等腰直角三角形时，求t 的值．12．在△ABC 中，∠BAC =45°，CD ⊥AB ，垂足为点D ，M 为线段DB 上一动点（不包括端点），点N 在直线AC 左上方且∠NCM =135°，CN =CM ，如图①．（1）求证：∠ACN =∠AMC ；（2）记△ANC 得面积为5，记△ABC 得面积为5．求证：12S AC S AB=；（3）延长线段AB 到点P ，使BP =BM ，如图②．探究线段AC 与线段DB 满足什么数量关系时对于满足条件的任意点M ，AN =CP 始终成立？（写出探究过程）【参考答案】***试卷处理标记，请不要删除一、压轴题1．（1）5；（2）直角三角形，理由见解析；（3）44,33E ⎛⎫- ⎪⎝⎭或82,33E ⎛⎫- ⎪⎝⎭【解析】【分析】（1）先求出直线122y x =+与x 轴的交点B 的坐标和与y 轴的交点C 的坐标，把点C 代入直线2y x m =-+，求出m 的值，再求它与x 轴的交点A 的坐标，ABC 的面积用AB 乘OC 除以2得到；（2）用勾股定理求出BC 的平方，AC 的平方，再根据AB 的平方，用勾股定理的逆定理证明ABC 是直角三角形；（3）先根据角平分线求出D 的坐标，再去分两种情况构造全等三角形，利用全等三角形的性质求出对应的边长，从而得到点E 的坐标．【详解】解：（1）令0x =，则10222y =⨯+=， ∴()0,2C ，令0y =，则1202x +=，解得4x =-， ∴()4,0B -，将()0,2C 代入2y x m =-+，得2m =， ∴22y x =-+，令0y =，则220x -+=，解得1x =， ∴1,0A ，∴5AB =，2OC =，∴152ABC S AB OC =⋅=△；（2）根据勾股定理，222224220BC BO OC =+=+=，22222125AC AO OC =+=+=，且22525AB ==，∴222AB BC AC =+，则ABC 是直角三角形；（3）∵CD 平分ACB ∠， ∴12AD AC BD BC ==， ∴1533AD AB ==， ∴23OD AD OA =-=， ∴2,03D ⎛⎫-⎪⎝⎭①如图，CED ∠是直角，过点E 作EN x ⊥轴于点N ，过点C 作CM EN ⊥于点M ，由（2）知，90ACB ∠=︒， ∵CD 平分ACB ∠， ∴45ECD ∠=︒，∴CDE △是等腰直角三角形， ∴CE DE =，∵90NED MEC ∠+∠=︒，90NED NDE ∠+∠=︒， ∴MEC NDE ∠=∠，在DNE △和EMC △中，NDE MEC DNE EMC DE EC ∠=∠⎧⎪∠=∠⎨⎪=⎩， ∴()DNE EMC AAS ≅，设DN EM x ==，EN CM y ==，根据图象列式：DO DN CM EN EM CO +=⎧⎨+=⎩，即232x y x y ⎧+=⎪⎨⎪+=⎩，解得2343x y ⎧=⎪⎪⎨⎪=⎪⎩，∴43EN CM ==， ∴44,33E ⎛⎫-⎪⎝⎭；②如图，CDE ∠是直角，过点E 作EG x ⊥轴于点G ，同理CDE △是等腰直角三角形，且可以证得()CDO DEG AAS ≅， ∴2DG CO ==，23EG DO ==， ∴28233GO GD DO =+=+=， ∴82,33E ⎛⎫- ⎪⎝⎭，综上：44,33E ⎛⎫- ⎪⎝⎭，82,33E ⎛⎫- ⎪⎝⎭．【点睛】本题考查一次函数综合，解题的关键是掌握一次函数解析式的求解，与坐标轴交点的求解，图象围成的三角形面积的求解，还涉及勾股定理、角平分线的性质、全等三角形等几何知识，需要运用数形结合的思想去求解． 2．（1）b=72；（2）①△APQ 的面积S 与t 的函数关系式为S=﹣32t +272或S=32t ﹣272；②7＜t ＜9或9＜t ＜11，③存在，当t 的值为3或9+2或9﹣2或6时，△APQ 为等腰三角形．【解析】分析：（1）把P (m ,3)的坐标代入直线1l 的解析式即可求得P 的坐标，然后根据待定系数法即可求得b ；（2）根据直线2l 的解析式得出C 的坐标，①根据题意得出9AQ t =-，然后根据12P S AQ y =⋅即可求得APQ 的面积S 与t 的函数关系式；②通过解不等式273322t -<或327 3.22t -<即可求得7<t <9或9<t <11.时，APQ 的面积小于3；③分三种情况：当PQ =PA 时,则()()()2222(71)032103,t -++-=++-当AQ =PA 时,则()()222(72)2103,t --=++-当PQ =AQ 时,则()222(71)03(72)t t -++-=--，即可求得．详解：解;(1)∵点P (m ,3)为直线l 1上一点， ∴3=−m +2，解得m =−1， ∴点P 的坐标为(−1,3)，把点P 的坐标代入212y x b =+ 得,()1312b =⨯-+，解得72b =； (2)∵72b =； ∴直线l 2的解析式为y =12x +72， ∴C 点的坐标为(−7,0)，①由直线11:2l y x =-+可知A (2,0)， ∴当Q 在A . C 之间时，AQ =2+7−t =9−t ，∴11273(9)32222S AQ yP t t =⋅=⨯-⨯=-；当Q 在A 的右边时，AQ =t −9，∴11327(9)32222S AQ yP t t ；=⋅=⨯-⨯=- 即△APQ 的面积S 与t 的函数关系式为27322S t =-或327.22S t =- ②∵S <3，∴273322t -<或3273.22t -< 解得7<t <9或9<t <11.③存在；设Q (t −7,0)，当PQ =PA 时,则()()()2222(71)032103,t -++-=++-∴22(6)3t -=,解得t =3或t =9(舍去)，当AQ =PA 时,则()()222(72)2103,t --=++- ∴2(9)18,t -=解得9t =+9t =- 当PQ =AQ 时,则()222(71)03(72)t t -++-=--，∴22(6)9(9)t t -+=-，解得t =6. 故当t 的值为3或9+9-6时，△APQ 为等腰三角形．点睛：属于一次函数综合题，考查了一次函数图象上点的坐标特征，待定系数法求函数解析式，等腰三角形的性质以及三角形的面积,分类讨论是解题的关键.3．（1）全等，垂直，理由详见解析；（2）存在，11t x =⎧⎨=⎩或232t x =⎧⎪⎨=⎪⎩【解析】【分析】（1）在t =1的条件下，找出条件判定△ACP 和△BPQ 全等，再根据全等三角形的性质和直角三角形的两个锐角互余的性质，可证∠CPQ= 90°，即可判断线段 PC 和线段 PQ 的位置关系;（2）本题主要在动点的条件下，分情况讨论，利用三角形全等时对应边相等的性质进行解答即可. 【详解】(1)当t=1时，AP= BQ=1, BP= AC=3, 又∠A=∠B= 90°，在△ACP 和△BPQ 中，{AP BQA B AC BP=∠=∠= ∴△ACP ≌△BPQ(SAS). ∴∠ACP=∠BPQ ,∴∠APC+∠BPQ=∠APC+∠ACP = 90*. ∴∠CPQ= 90°，即线段PC 与线段PQ 垂直； (2)①若△ACP ≌△BPQ ，则AC= BP ，AP= BQ ，34tt xt =-⎧⎨=⎩解得11t x =⎧⎨=⎩; ②若△ACP ≌△BQP ，则AC= BQ ，AP= BP ，34xt t t =⎧⎨=-⎩解得：232t x =⎧⎪⎨=⎪⎩ 综上所述,存在11t x =⎧⎨=⎩或232t x =⎧⎪⎨=⎪⎩使得△ACP 与△BPQ 全等. 【点睛】本题主要考查三角形全等与动点问题，熟练掌握三角形全等的性质与判定定理，是解决本题的关键.4．（1）①证明见解析；②DE =14；（2）①8t －10；②t =2；③t =10,211【解析】【分析】（1）①先证明∠DAC ＝∠ECB ，由AAS 即可得出△ADC ≌△CEB ；②由全等三角形的性质得出AD ＝CE ＝8，CD ＝BE ＝6，即可得出DE ＝CD ＋CE ＝14；（2）①当点N 在线段CA 上时，根据CN ＝CN−BC 即可得出答案；②点M 与点N 重合时，CM ＝CN ，即3t ＝8t−10，解得t ＝2即可；③分两种情况：当点N 在线段BC 上时，△PCM ≌△QNC ，则CM ＝CN ，得3t ＝10−8t ，解得t ＝1011；当点N 在线段CA 上时，△PCM ≌△QCN ，则3t ＝8t−10，解得t ＝2；即可得出答案．【详解】（1）①证明：∵AD ⊥DE ，BE ⊥DE ，∴∠ADC ＝∠CEB ＝90°，∵∠ACB ＝90°，∴∠DAC ＋∠DCA ＝∠DCA ＋∠BCE ＝90°，∴∠DAC ＝∠ECB ，在△ADC 和△CEB 中ADC CEB DAC ECB AC CB ∠∠∠∠⎧⎪⎨⎪⎩＝＝＝，∴△ADC ≌△CEB （AAS ）；②由①得：△ADC ≌△CEB ，∴AD ＝CE ＝8，CD ＝BE ＝6，∴DE ＝CD ＋CE ＝6＋8＝14；（2）解：①当点N 在线段CA 上时，如图3所示：CN＝CN−BC＝8t−10；②点M与点N重合时，CM＝CN，即3t＝8t−10，解得：t＝2，∴当t为2秒时，点M与点N重合；③分两种情况：当点N在线段BC上时，△PCM≌△QNC，∴CM＝CN，∴3t＝10−8t，解得：t＝10 11；当点N在线段CA上时，△PCM≌△QCN，点M与N重合，CM＝CN，则3t＝8t−10，解得：t＝2；综上所述，当△PCM与△QCN全等时，则t等于1011s或2s，故答案为：1011s或2s．【点睛】本题是三角形综合题目，考查了全等三角形的判定与性质、等腰直角三角形的性质、直角三角形的性质、分类讨论等知识；本题综合性强，熟练掌握全等三角形的判定与性质是解题的关键．5．（1）证明见解析；（2）①CM=8t-，CN=63t-；②t=3.5或5或6.5．【解析】【分析】（1）根据垂直的定义得到∠DAC=∠ECB，利用AAS定理证明△ACD≌△CBE；（2）①由折叠的性质可得出答案；②动点N沿F→C路径运动，点N沿C→B路径运动，点N沿B→C路径运动，点N沿C→F 路径运动四种情况，根据全等三角形的判定定理列式计算．【详解】（1）∵AD⊥直线l，BE⊥直线l，∴∠DAC+∠ACD=90°，∵∠ACB=90°，∴∠BCE+∠ACD=90°，∴∠DAC=∠ECB ，在△ACD 和△CBE 中，ADC CEB DAC ECB CA CB ∠∠⎧⎪∠∠⎨⎪⎩＝＝＝，∴△ACD ≌△CBE （AAS ）；（2）①由题意得，AM=t ，FN=3t ，则CM=8-t ，由折叠的性质可知，CF=CB=6，∴CN=6-3t ；故答案为：8-t ；6-3t ；②由折叠的性质可知，∠BCE=∠FCE ，∵∠MCD+∠CMD=90°，∠MCD+∠BCE=90°，∴∠NCE=∠CMD ，∴当CM=CN 时，△MDC 与△CEN 全等，当点N 沿F→C 路径运动时，8-t=6-3t ，解得，t=-1（不合题意），当点N 沿C→B 路径运动时，CN=3t-6，则8-t=3t-6，解得，t=3.5，当点N 沿B→C 路径运动时，由题意得，8-t=18-3t ，解得，t=5，当点N 沿C→F 路径运动时，由题意得，8-t=3t-18，解得，t=6.5，综上所述，当t=3.5秒或5秒或6.5秒时，△MDC 与△CEN 全等．【点睛】本题考查了折叠的性质，全等三角形的判定和性质，掌握全等三角形的判定定理和性质定理，灵活运用分情况讨论思想是解题的关键．6．（1）（0，6），（8，0）；（2）存在t=2.4时，使得△ODP 与△ODQ 的面积相等；（3）2∠GOA+∠ACE=∠OHC ，理由见解析．【解析】【分析】（1）根据算术平方根的非负性，绝对值的非负性即可求解；（2）根据运动速度得到OQ=t ，OP=8-2t ，根据△ODP 与△ODQ 的面积相等列方程求解即可；（3）由∠AOC=90°，y 轴平分∠GOD 证得OG ∥AC ，过点H 作HF ∥OG 交x 轴于F ，得到∠FHC=∠ACE ，∠FHO=∠GOD ，从而∠GOD+∠ACE=∠FHO+∠FHC ，即可证得2∠GOA+∠ACE=∠OHC.【详解】（180b-=，∴a-b+2=0，b-8=0，∴a=6，b=8，∴A（0，6），C（8，0）；故答案为：（0，6），（8，0）；（2）由（1）知，A（0，6），C（8，0），∴OA=6，OB=8，由运动知，OQ=t，PC=2t，∴OP=8-2t，∵D（4，3），∴114222ODQ DS OQ x t t=⨯=⨯=△，11823123 22ODP DS OP y t t=⨯=-⨯=-△（），∵△ODP与△ODQ的面积相等，∴2t=12-3t，∴t=2.4，∴存在t=2.4时，使得△ODP与△ODQ的面积相等；（3）2∠GOA+∠ACE=∠OHC，理由如下：∵x轴⊥y轴，∴∠AOC=∠DOC+∠AOD=90°，∴∠OAC+∠ACO=90°.又∵∠DOC=∠DCO，∴∠OAC=∠AOD.∵x轴平分∠GOD，∴∠GOA=∠AOD.∴∠GOA=∠OAC.∴OG∥AC，如图，过点H作HF∥OG交x轴于F，∴HF∥AC，∴∠FHC=∠ACE.∵OG∥FH，∴∠GOD=∠FHO，∴∠GOD+∠ACE=∠FHO+∠FHC，即∠GOD+∠ACE=∠OHC，∴2∠GOA+∠ACE=∠OHC．【点睛】此题考查算术平方根的非负性，绝对值的非负性，坐标系中的动点问题，平行线的判定及性质定理，是一道较为综合的题型.7．（1）35,2⎛⎫⎪⎝⎭；（2）2；（3）不是；（4）（6，75）【解析】【分析】（1）根据“白马有理数对”的定义，把数对3(2,1),5,2⎛⎫- ⎪⎝⎭分别代入1a b ab+=-计算即可判断；（2）根据“白马有理数对”的定义，构建方程即可解决问题；（3）根据“白马有理数对”的定义即可判断；（4）根据“白马有理数对”的定义即可解决问题．【详解】（1）∵-2+1=-1，而-2×1-1=-3，∴-2+1≠-3，∴（-2，1）不是“白马有理数对”，∵5+32=132，5×32-1=132，∴5+32=5×32-1，∴35,2⎛⎫⎪⎝⎭是“白马有理数对”，故答案为：3 5,2⎛⎫ ⎪⎝⎭；（2）若(,3)a是“白马有理数对”，则a+3=3a-1，解得：a=2，故答案为：2；（3）若(,)m n是“白马有理数对”，则m+n=mn-1，那么-n+（-m）=-（m+n）=-（mn-1）=-mn+1，∵-mn+1≠ mn-1∴（-n，-m）不是“白马有理数对”，故答案为：不是；（4）取m=6，则6+x=6x-1，∴x=75，∴（6，75）是“白马有理数对”，故答案为：（6，75）．【点睛】本题考查了“白马有理数对”的定义，有理数的加减运算，一次方程的列式求解，理解“白马有理数对”的定义是解题的关键．8．（1）60°；（2）EF=AF+FC，证明见解析；（3）AF=EF+2DF，证明见解析．【解析】【分析】（1）可设∠BAD＝∠CAD＝α，∠AEC＝∠ACE＝β，在△ACE中，根据三角形内角和可得2α＋60＋2β＝180°，从而有α＋β＝60°，即可得出∠DFC的度数；（2）在EC上截取EG＝CF，连接AG，证明△AEG≌△ACF，然后再证明△AFG为等边三角形，从而可得出EF＝EG＋GF＝AF＋FC；（3）在AF上截取AG＝EF，连接BG，BF，证明方法类似（2），先证明△ABG≌△EBF，再证明△BFG为等边三角形，最后可得出结论．【详解】解：（1）∵AB=AC，AD为BC边上的中线，∴可设∠BAD＝∠CAD＝α，又△ABE为等边三角形，∴AE=AB=AC，∠EAB=60°，∴可设∠AEC＝∠ACE＝β，在△ACE中，2α＋60°＋2β＝180°，∴α＋β＝60°，∴∠DFC=α＋β＝60°；（2）EF=AF+FC，证明如下：∵AB=AC，AD为BC边上的中线，∴AD⊥BC，∴∠FDC=90°，∵∠CFD＝60°，则∠DCF=30°，∴CF＝2DF，在EC上截取EG＝CF，连接AG，又AE=AC，∴∠AEG=∠ACF，∴△AEG≌△ACF（SAS）,∴∠EAG＝∠CAF，AG＝AF，又∠CAF=∠BAD，∴∠EAG=∠BAD，∴∠GAF＝∠BAD+∠BAG=∠EAG+∠BAG=∠60°，∴△AFG为等边三角形，∴EF＝EG＋GF＝AF＋FC，即EF=AF+FC；（3）补全图形如图所示，结论：AF=EF+2DF．证明如下：同（1）可设∠BAD＝∠CAD＝α，∠ACE＝∠AEC＝β，∴∠CAE＝180°－2β，∴∠BAE＝2α＋180°－2β＝60°，∴β－α＝60°，∴∠AFC=β－α＝60°，又△ABE为等边三角形，∴∠ABE=∠AFC=60°，∴由8字图可得：∠BAD＝∠BEF，在AF上截取AG＝EF，连接BG，BF，又AB=BE，∴△ABG≌△EBF（SAS），∴BG＝BF，又AF垂直平分BC，∴BF=CF，∴∠BFA=∠AFC=60°，∴△BFG为等边三角形，∴BG=BF，又BC⊥FG，∴FG=BF=2DF，∴AF＝AG＋GF＝BF＋EF＝2DF＋EF．【点睛】本题考查了全等三角形的判定和性质、等边三角形的性质、等腰三角形的性质等知识，解决问题的关键是常用辅助线构造全等三角形，属于中考常考题型．9．（1）见解析；（2）CD＝2AD+BD，理由见解析；（3）CD＝3AD+BD【解析】【分析】（1）由“SAS”可证△ADB≌△AEC；（2）由“SAS”可证△ADB≌△AEC，可得BD＝CE，由直角三角形的性质可得DE＝2AD，可得结论；（3）由△DAB≌△EAC，可知BD＝CE，由勾股定理可求DH＝3AD，由AD＝AE，AH⊥DE，推出DH＝HE，由CD＝DE+EC＝2DH+BD＝3AD+BD，即可解决问题；【详解】证明：（1）∵∠BAC＝∠DAE，∴∠BAD＝∠CAE，又∵AB＝AC，AD＝AE，∴△ADB≌△AEC（SAS）；（2）CD＝2AD+BD，理由如下：∵∠BAC＝∠DAE，∴∠BAD＝∠CAE，又∵AB＝AC，AD＝AE，∴△ADB≌△AEC（SAS）；∴BD＝CE，∵∠BAC＝90°，AD＝AE，∴DE＝2AD，∵CD＝DE+CE，∴CD＝2AD+BD；（3）作AH⊥CD于H．∵∠BAC＝∠DAE，∴∠BAD＝∠CAE，又∵AB＝AC，AD＝AE，∴△ADB≌△AEC（SAS）；∴BD＝CE，∵∠DAE＝120°，AD＝AE，∴∠ADH＝30°，∴AH ＝12AD ， ∴DH2AD ， ∵AD ＝AE ，AH ⊥DE ，∴DH ＝HE ，∴CD ＝DE +EC ＝2DH +BD+BD ，故答案为：CD+BD ．【点睛】本题是结合了全等三角形的性质与判定，勾股定理等知识的综合问题，熟练掌握知识点，有简入难，层层推进是解答关键.10．（1）90°；（2）证明见解析；（3）变化，24l +≤<．【解析】【分析】（1）由等边三角形的性质可得∠ABC=∠ACB=60°，由等腰三角形的性质可求DAE=∠DEA=30°，由三角形内角和定理可求解；（2）根据等腰三角形的性质，可证得∠CDF=∠DEA 和∠EDB=∠DFA ，由此可利用“ASA”证明全等；（3）根据全等三角形的性质可得l =2+AD ，根据AD 的取值范围即可得出l 的取值范围．【详解】解：（1）∵△ABC 是等边三角形，∴AB=AC=BC=2，∠ABC=∠ACB=60°，∵AD=DE∴∠DAE=∠DEA=30°，∴∠ADB=180°-∠BAD-∠ABD=90°，故答案为：90°；（2）∵AD=DE=DF ，∴∠DAE=∠DEA ，∠DAF=∠DFA ，∵∠DAE+∠DAF=∠BAC=60°，∴∠DEA+∠DFA=60°，∵∠ABC=∠DEA+∠EDB=60°，∴∠EDB=∠DFA ，∵∠ACB=∠DFA+∠CDF=60°，∴∠CDF=∠DEA ，在△BDE 和△CFD 中∵CDF DEA DE DF EDB DFA ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△BDE ≌△CFD （ASA ）（3）∵△BDE ≌△CFD ，∴BE=CD ，∴l =BD+BE+DE=BD+CD+AD=BC+AD=2+AD ，当D 点在C 或B 点时，AD=AC=AB=2,此时B 、D 、E 三点在同一条直线上不构成三角形，2+AD=4；当D 点在BC 的中点时，∵AB=AC ，∴BD=112BC =，AD ==此时22l AD =+=综上可知24l +≤<．【点睛】本题考查全等三角形的性质和判定，勾股定理，等边三角形的性质，等腰三角形的性质，三角形内角和定理．（1）掌握等腰三角形等边对等角是解决此问的关键；（2）中注意角之间的转换；（3）中注意临界点是否可取．11．（1）全等，理由见解析；（2）t=3.5秒或5秒【解析】【分析】（1）根据垂直的定义得到∠DAC=∠ECB ，利用AAS 定理证明△ACD ≌△CBE ；（2）分点F 沿C→B 路径运动和点F 沿B→C 路径运动两种情况，根据等腰三角形的定义列出算式，计算即可；【详解】解：（1）△ACD 与△CBE 全等．理由如下：∵AD ⊥直线l ，∴∠DAC+∠ACD=90°，∵∠ACB=90°，∴∠BCE+∠ACD=90°，∴∠DAC=∠ECB ，在△ACD 和△CBE 中，ADC CEB DAC ECB CA CB ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△ACD ≌△CBE （AAS ）；（2）由题意得，AM=t ，FN=3t ，则CM=8-t ，由折叠的性质可知，CF=CB=6，∴CN=6-3t，点N在BC上时，△CMN为等腰直角三角形，当点N沿C→B路径运动时，由题意得，8-t=3t-6，解得，t=3.5，当点N沿B→C路径运动时，由题意得，8-t=18-3t，解得，t=5，综上所述，当t=3.5秒或5秒时，△CMN为等腰直角三角形；【点睛】本题考查的是全等三角形的判定和性质，掌握全等三角形的判定定理和性质定理，灵活运用分情况讨论思想是解题的关键．12．（1）证明见解析；（2）证明见解析；（3）当AC=2BD时，对于满足条件的任意点N，AN=CP始终成立，证明见解析．【解析】【分析】（1）由三角形的内角和定理可求∠ACN=∠AMC=135°-∠ACM；（2）过点N作NE⊥AC于E，由“AAS”可证△NEC≌△CDM，可得NE=CD，由三角形面积公式可求解；（3）过点N作NE⊥AC于E，由“SAS”可证△NEA≌△CDP，可得AN=CP．【详解】（1）∵∠BAC=45°，∴∠AMC=180°﹣45°﹣∠ACM=135°﹣∠ACM．∵∠NCM=135°，∴∠ACN=135°﹣∠ACM，∴∠ACN=∠AMC；（2）过点N作NE⊥AC于E，∵∠CEN=∠CDM=90°，∠ACN=∠AMC，CM=CN，∴△NEC≌△CDM（AAS），∴NE=CD，CE=DM；∵S112=AC•NE，S212=AB•CD，∴12S ACS AB=；（3）当AC=2BD时，对于满足条件的任意点N，AN=CP始终成立，理由如下：过点N作NE⊥AC于E，由（2）可得NE=CD，CE=DM．∵AC=2BD，BP=BM，CE=DM，∴AC﹣CE=BD+BD﹣DM，∴AE=BD+BP=DP．∵NE=CD，∠NEA=∠CDP=90°，AE=DP，∴△NEA≌△CDP（SAS），∴AN=PC．【点睛】本题三角形综合题，考查了全等三角形的判定和性质，三角形内角和定理，三角形面积公式等知识，添加恰当辅助线构造全等三角形是本题的关键．。

八年级数学压轴题期末复习试卷复习练习(Word版含答案)

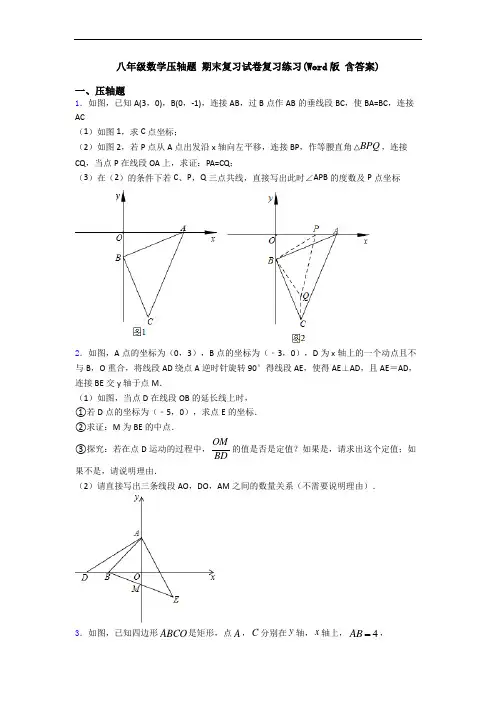
八年级数学压轴题期末复习试卷复习练习(Word版含答案)一、压轴题1．如图，已知A(3，0)，B(0，-1)，连接AB，过B点作AB的垂线段BC，使BA=BC，连接AC（1）如图1，求C点坐标；（2）如图2，若P点从A点出发沿x轴向左平移，连接BP，作等腰直角BPQ，连接CQ，当点P在线段OA上，求证：PA=CQ；（3）在（2）的条件下若C、P，Q三点共线，直接写出此时∠APB的度数及P点坐标2．如图，A点的坐标为（0，3），B点的坐标为（﹣3，0），D为x轴上的一个动点且不与B，O重合，将线段AD绕点A逆时针旋转90°得线段AE，使得AE⊥AD，且AE＝AD，连接BE交y轴于点M．（1）如图，当点D在线段OB的延长线上时，①若D点的坐标为（﹣5，0），求点E的坐标．②求证：M为BE的中点．③探究：若在点D运动的过程中，OMBD的值是否是定值？如果是，请求出这个定值；如果不是，请说明理由．（2）请直接写出三条线段AO，DO，AM之间的数量关系（不需要说明理由）．3．如图，已知四边形ABCO是矩形，点A，C分别在y轴，x轴上，4AB ，3BC =．（1）求直线AC 的解析式；（2）作直线AC 关于x 轴的对称直线，交y 轴于点D ，求直线CD 的解析式．并结合（1）的结论猜想并直接写出直线y kx b =+关于x 轴的对称直线的解析式；（3）若点P 是直线CD 上的一个动点，试探究点P 在运动过程中，||PA PB -是否存在最大值？若不存在，请说明理由；若存在，请求出||PA PB -的最大值及此时点P 的坐标．4．如图1．在△ABC 中，∠ACB =90°，AC =BC =10，直线DE 经过点C ，过点A ，B 分别作AD ⊥DE ，BE ⊥DE ，垂足分别为点D 和E ，AD =8，BE =6．（1）①求证：△ADC ≌△CEB ；②求DE 的长；（2）如图2，点M 以3个单位长度/秒的速度从点C 出发沿着边CA 运动，到终点A ，点N 以8个单位长度/秒的速度从点B 出发沿着线BC —CA 运动，到终点A ．M ，N 两点同时出发，运动时间为t 秒(t ＞0)，当点N 到达终点时，两点同时停止运动，过点M 作PM ⊥DE 于点P ，过点N 作QN ⊥DE 于点Q ；①当点N 在线段CA 上时，用含有t 的代数式表示线段CN 的长度；②当t 为何值时，点M 与点N 重合；③当△PCM 与△QCN 全等时，则t = ．5．在平面直角坐标系中点 A （m −3，3m +3），点 B （m ，m +4）和 D （0，−5），且点 B 在第二象限．（1）点 B 向平移单位，再向下平移（用含 m 的式子表达）单位可以与点 A 重合；（2）若点 B 向下移动 3 个单位，则移动后的点 B 和点 A 的纵坐标相等，且有点 C （m −2，0）．①则此时点 A 、B 、C 坐标分别为、、．②将线段 AB 沿 y 轴负方向平移 n 个单位，若平移后的线段 AB 与线段 CD 有公共点，求 n 的取值范围．③当 m <−1 式，连接 AD ，若线段 AD 沿直线 AB 方向平移得到线段 BE ，连接 DE 与直线y=−2 交于点 F ，则点 F 坐标为．（用含 m 的式子表达）6．如图，已知△ABC 中，AB=AC=10cm ，BC=8cm ，点D 为AB 的中点．如果点P 在线段BC 上以3cm/s 的速度由B 点向C 点运动，同时，点Q 在线段CA 上由C 点向A 点运动．（1）若点Q 的运动速度与点P 的运动速度相等，经过1s 后，BP= cm ，CQ= cm ．（2）若点Q 的运动速度与点P 的运动速度相等，经过1s 后，△BPD 与△CQP 是否全等，请说明理由；（3）若点Q 的运动速度与点P 的运动速度不相等，当点Q 的运动速度为多少时，能够使△BPD 与△CQP 全等？（4）若点Q 以（3）中的运动速度从点C 出发，点P 以原来的运动速度从点B 同时出发，都逆时针沿△ABC 三边运动，求经过多长时间点P 与点Q 第一次相遇？7．在平面直角坐标系中，点A 、B 在坐标轴上，其中()0,A a 、(),0B b 满足|21|280a b a b --+-=．（1）求A 、B 两点的坐标；（2）将线段AB 平移到CD ，点A 的对应点为()2,C t -，如图1所示，若三角形ABC 的面积为9，求点D 的坐标；（3）平移线段AB 到CD ，若点C 、D 也在坐标轴上，如图2所示．P 为线段AB 上的一动点（不与A 、B 重合），连接OP 、PE 平分OPB ∠，2BCE ECD ∠=∠．求证：3()BCD CEP OPE ∠=∠-∠．8．（1）填空①把一张长方形的纸片按如图①所示的方式折叠，EM ，FM 为折痕，折叠后的C 点落在1B M 或1B M 的延长线上，那么EMF ∠的度数是________；②把一张长方形的纸片按如图②所示的方式折叠，B 点与M 点重合，EM ，FM 为折痕，折叠后的C 点落在1A M 或1A M 的延长线上，那么EMF ∠的度数是_______．（2）解答：①把一张长方形的纸片按如图③所示的方式折叠，EM ，FM 为折痕，折叠后的C 点落在1B M 或1B M 的延长线上左侧，且80EMF ∠=︒，求11C MB ∠的度数； ②把一张长方形的纸片按如图④所示的方式折叠，B 点与M 点重合，EM ，FM 为折痕，折叠后的C 点落在1A M 或1A M 的延长线右侧，且60EMF ∠=︒，求11C MA ∠的度数．（3）探究：把一张四边形的纸片按如图⑤所示的方式折叠，EB ，FB 为折痕，设ABC α∠=︒，EBF β∠=︒，11A BC γ∠=︒，求α，β，γ之间的数量关系．9．如图1中的三种情况所示，对于平面内的点M ，点N ，点P ，如果将线段PM 绕点P 顺时针旋转90°能得到线段PN ，就称点N 是点M 关于点P 的“正矩点”．（1）在如图2所示的平面直角坐标系xOy 中，已知(3,1),(1,3),(1,3)S P Q ---，(2,4)M -．①在点P ，点Q 中，___________是点S 关于原点O 的“正矩点”；②在S ，P ，Q ，M 这四点中选择合适的三点，使得这三点满足：点_________是点___________关于点___________的“正矩点”，写出一种情况即可；（2）在平面直角坐标系xOy 中，直线3(0)y kx k =+<与x 轴交于点A ，与y 轴交于点B ，点A 关于点B 的“正矩点”记为点C ，坐标为(,)C C C x y ．①当点A 在x 轴的正半轴上且OA 小于3时，求点C 的横坐标C x 的值；②若点C 的纵坐标C y 满足12C y -<≤，直接写出相应的k 的取值范围．10．在等腰△ABC 与等腰△ADE 中，AB ＝AC ，AD ＝AE ，∠BAC ＝∠DAE ，且点D 、E 、C 三点在同一条直线上，连接BD ．（1）如图1，求证：△ADB ≌△AEC（2）如图2，当∠BAC ＝∠DAE ＝90°时，试猜想线段AD ，BD ，CD 之间的数量关系，并写出证明过程；（3）如图3，当∠BAC ＝∠DAE ＝120°时，请直接写出线段AD ，BD ，CD 之间的数量关系式为：（不写证明过程）11．如图，四边形ABCD 是直角梯形，AD ∥BC ，AB ⊥AD ，且AB ＝AD +BC ，E 是DC 的中点，连结BE 并延长交AD 的延长线于G ．（1）求证：DG ＝BC ；（2）F 是AB 边上的动点，当F 点在什么位置时，FD ∥BG ；说明理由．（3）在（2）的条件下，连结AE 交FD 于H ，FH 与HD 长度关系如何？说明理由．12．如图，直线l 1的表达式为：y=-3x+3，且直线l 1与x 轴交于点D ，直线l 2经过点A ，B ，直线l 1，l 2交于点C ．（1）求点D 的坐标；（2）求直线l 2的解析表达式；（3）求△ADC 的面积；（4）在直线l 2上存在异于点C 的另一点P ，使得△ADP 与△ADC 的面积相等，求点P 的坐标．【参考答案】***试卷处理标记，请不要删除一、压轴题1．（1）(1，-4)；（2）证明见解析；（3）()135,1,0APB P ︒∠= 【解析】【分析】（1）作CH ⊥y 轴于H ，证明△ABO ≌△BCH ，根据全等三角形的性质得到BH=OA=3，CH=OB=1，求出OH ，得到C 点坐标；（2）证明△PBA ≌△QBC ，根据全等三角形的性质得到PA=CQ ；（3）根据C 、P ，Q 三点共线，得到∠BQC=135°，根据全等三角形的性质得到∠BPA=∠BQC=135°，根据等腰三角形的性质求出OP ，得到P 点坐标．【详解】解：(1)作CH ⊥y 轴于H ，则∠BCH+∠CBH=90°，因为AB BC ⊥，所以.∠ABO+∠CBH=90°，所以∠ABO=∠BCH ，在△ABO 和△BCH 中，ABO BCH AOB BHC AB BC ∠=∠⎧⎪∠=∠⎨⎪=⎩ABO BCH ∴∆≅∆:BH=OA=3，CH=OB=1，:OH=OB+BH=4，所以C 点的坐标为（1，-4）；(2)因为∠PBQ=∠ABC=90°，,PBQ ABQ ABC ABQ PBA QBC ∴∠-=∠-∠∴∠=∠在△PBA 和△QBC 中，BP BQ PBA QBC BA BC =⎧⎪∠=∠⎨⎪=⎩PBA QBC ∴∆≅∆:.PA=CQ ；(3) ()135,1,0APB P ︒∠= BPQ ∆是等腰直角三角形，:所以∠BQP=45°，当C 、P ，Q 三点共线时，∠BQC=135°，由（2)可知，PBA QBC ∴∆≅∆；所以∠BPA=∠BQC=135°，所以∠OPB=45°，所以.OP=OB=1，所以P 点坐标为（1，0) ．【点睛】本题考查的是全等三角形的判定和性质、三角形的外角的性质，掌握全等三角形的判定定理和性质定理是解题的关键．2．（1）①E （3，﹣2）②见解析；③12OM BD =，理由见解析；（2）OD+OA ＝2AM 或OA ﹣OD ＝2AM【解析】【分析】（1）①过点E作EH⊥y轴于H．证明△DOA≌△AHE（AAS）可得结论．②证明△BOM≌△EHM（AAS）可得结论．③是定值，证明△BOM≌△EHM可得结论．（2）根据点D在点B左侧和右侧分类讨论，分别画出对应的图形，根据全等三角形的判定及性质即可分别求出结论．【详解】解：（1）①过点E作EH⊥y轴于H．∵A（0，3），B（﹣3，0），D（﹣5，0），∴OA＝OB＝3，OD＝5，∵∠AOD＝∠AHE＝∠DAE＝90°，∴∠DAO+∠EAH＝90°，∠EAH+∠AEH＝90°，∴∠DAO＝∠AEH，∴△DOA≌△AHE（AAS），∴AH＝OD＝5，EH＝OA＝3，∴OH＝AH﹣OA＝2，∴E（3，﹣2）．②∵EH⊥y轴，∴∠EHO＝∠BOH＝90°，∵∠BMO＝∠EMH，OB＝EH＝3，∴△BOM≌△EHM（AAS），∴BM＝EM．③结论：OMBD＝12．理由：∵△DOA≌△AHE，∴OD＝AH，∵OA＝OB，∴BD＝OH，∵△BOM≌△EHM，∴OM＝MH，∴OM＝12OH＝12BD．（2）结论：OA+OD＝2AM或OA﹣OD＝2AM．理由：当点D在点B左侧时，∵△BOM≌△EHM，△DOA≌△AHE∴OM=MH，OD=AH∴OH=2OM，OD－OB=AH－OA∴BD=OH∴BD＝2OM，∴OD﹣OA＝2（AM﹣AO），∴OD+OA＝2AM．当点D在点B右侧时，过点E作EH⊥y轴于点H∵∠AOD＝∠AHE＝∠DAE＝90°，∴∠DAO+∠EAH＝90°，∠EAH+∠AEH＝90°，∴∠DAO＝∠AEH，∵AD=AE∴△DOA≌△AHE（AAS），∴EH=AO=3=OB，OD=AH∴∠EHO＝∠BOH＝90°，∵∠BMO＝∠EMH，OB＝EH＝3，∴△BOM≌△EHM（AAS），∴OM＝MH∴OA＋OD= OA＋AH=OH=OM＋MH=2MH=2（AM＋AH）=2（AM＋OD）整理可得OA﹣OD＝2AM．综上：OA+OD＝2AM或OA﹣OD＝2AM．【点睛】此题考查的是全等三角形的判定及性质、旋转的性质和平面直角坐标系，掌握全等三角形的判定及性质、旋转的性质和点的坐标与线段长度的关系是解决此题的关键．3．（1）y =34-x +3；（2）y =34x -3，y =-kx -b ；（3）存在，4，(8，3) 【解析】【分析】（1）利用4AB =，3BC =，找出A 、C 两点的坐标，设直线解析式，利用待定系数法求出AC 的解析式；（2）由直线AC 关于x 轴的对称直线为CD 可知点D 的坐标，设直线解析式，利用待定系数法求出CD 的解析式，对比AC 的解析式进而写出直线y kx b =+关于x 轴的对称直线的解析式；（3）先判断||PA PB -存在最大值，在P 、A 、B 三点不共线时，P 点在运动过程中，与A 、B 两点组成三角形，两边之差小于第三边，得出结论在P 、A 、B 三点共线时，此时||PA PB -最大，y p = y A =3，求出P 点的纵坐标，最后根据点P 在直线CD 上，将P 点的纵坐标代入直线方程可得横坐标，从而求出P 点坐标．【详解】解：（1）在矩形ABCD 中，OC =AB =4，OA =BC =3，故A (0，3)，C (4，0)，设直线AC 的解析式为：y =kx +b (k ≠0，k 、b 为常数)，点A 、C 在直线AC 上，把A 、C 两点的坐标代入解析式可得：340b k b =⎧⎨+=⎩解得：343k b ⎧=-⎪⎨⎪=⎩，所以直线AC 的解析式为：y =34-x +3．（2）由直线AC 关于x 轴的对称直线为CD 可知：点D 的坐标为：(0，-3)，设直线CD 的解析式为：y =mx +n (m ≠0，m 、n 为常数)，点C 、D 在直线CD 上，把C 、D 两点的坐标带入解析式可得：-340n m n =⎧⎨+=⎩解得：343m n ⎧=⎪⎨⎪=-⎩，所以直线CD 的解析式为：y =34x -3，故猜想直线y kx b =+关于x 轴的对称直线的解析式为：y =-kx -b ．（3）点P 在运动过程中，||PA PB -存在最大值，由题意可知：如图，延长AB 与直线CD 交点即为点P ，此时||PA PB -最大，其他位置均有||PA PB -＜AB （P 点在运动过程中，与A 、B 两点组成任意三角形，两边之差小于第三边），此时，||PA PB -= AB =4，y p = y A =3，点P 在直线CD 上，将P 点的纵坐标代入直线方程可得：34x -3=3， x =8，故P 点坐标为(8，3)，||PA PB -的最大值为x p -x B =8-4=4．【点睛】本题主要考查利用待定系数法求解一次函数解析式及类比推理能力，掌握任意三角形两边之差小于第三边是解题的关键．4．（1）①证明见解析；②DE =14；（2）①8t －10；②t =2；③t =10,211【解析】【分析】（1）①先证明∠DAC ＝∠ECB ，由AAS 即可得出△ADC ≌△CEB ；②由全等三角形的性质得出AD ＝CE ＝8，CD ＝BE ＝6，即可得出DE ＝CD ＋CE ＝14；（2）①当点N 在线段CA 上时，根据CN ＝CN−BC 即可得出答案；②点M 与点N 重合时，CM ＝CN ，即3t ＝8t−10，解得t ＝2即可；③分两种情况：当点N 在线段BC 上时，△PCM ≌△QNC ，则CM ＝CN ，得3t ＝10−8t ，解得t ＝1011；当点N 在线段CA 上时，△PCM ≌△QCN ，则3t ＝8t−10，解得t ＝2；即可得出答案．【详解】（1）①证明：∵AD ⊥DE ，BE ⊥DE ，∴∠ADC ＝∠CEB ＝90°，∵∠ACB ＝90°，∴∠DAC ＋∠DCA ＝∠DCA ＋∠BCE ＝90°，∴∠DAC ＝∠ECB ，在△ADC和△CEB中ADC CEBDAC ECBAC CB∠∠∠∠⎧⎪⎨⎪⎩＝＝＝，∴△ADC≌△CEB（AAS）；②由①得：△ADC≌△CEB，∴AD＝CE＝8，CD＝BE＝6，∴DE＝CD＋CE＝6＋8＝14；（2）解：①当点N在线段CA上时，如图3所示：CN＝C N−BC＝8t−10；②点M与点N重合时，CM＝CN，即3t＝8t−10，解得：t＝2，∴当t为2秒时，点M与点N重合；③分两种情况：当点N在线段BC上时，△PCM≌△QNC，∴CM＝CN，∴3t＝10−8t，解得：t＝1011；当点N在线段CA上时，△PCM≌△QCN，点M与N重合，CM＝CN，则3t＝8t−10，解得：t＝2；综上所述，当△PCM与△QCN全等时，则t等于1011s或2s，故答案为：1011s或2s．【点睛】本题是三角形综合题目，考查了全等三角形的判定与性质、等腰直角三角形的性质、直角三角形的性质、分类讨论等知识；本题综合性强，熟练掌握全等三角形的判定与性质是解题的关键．5．（1）左；3；(1-2m)；（2）①（-4，0）；（-1，0）（-3，0）；②当平移后的线段AB与线段 CD 有公共点时，1913n ≤≤；③ F 9(,2)12m--．【解析】【分析】 (1)根据平面直角坐标系中点的平移计算方法即可得解(2)①根据B 点向下平移后，点B 和点A 的纵坐标相等得到等量关系，可求出m 的值，从而求出A 、B 、C 三点坐标；②过 C 作 CK 垂直 x 轴交 AB 于 K 点过 B 做 BM 垂直 x 轴于 M 点，设出K 点坐标，作 KH ⊥BM 与 H 点，表示出H 点坐标，然后利用面积关系ABM AKM BKM S S S ∆∆∆=+求出距离；当 B '在线段 CD 上时，BB '交 x 轴于 M 点，过 B '做 B 'E ⊥OD ，利用S △COD = S △OB'C + S △OB'D ，求出n 的值，从而求出n 的取值范围；③通过坐标平移法用m 表示出E 点的坐标，利用D 、E 两点坐标表示出直线DE 的函数关系式，令y=﹣2，求出x 的值即可求出F 点坐标．【详解】解：（1）根据平移规律可得：B 向左平移；m －（m －1）=3，所以平移3个单位；m+4－（3m+3）=1－2m ，所以再向下平移(1-2m )个单位；故答案为：左；3；(1-2m )（2）①点 B 向下移动 3 个单位得：B （m ，m+1）∵移动后的点 B 和点 A 的纵坐标相等∴m+1=3m+3∴m=﹣1∴A （-4,0）；B （-1,0）；C （-3,0）；②如图 1，过 C 作 CK 垂直 x 轴交 AB 于 K 点过 B 做 BM 垂直 x 轴于 M 点，设 K 点坐标为（-3，a ）M 点坐标为（-1,0）作 KH ⊥BM 与 H 点，H 点坐标为（-1，a ）AM=3,BM=3,KC=a,KH=2∵ABM AKM BKM S S S ∆∆∆=+ ∴222AM BM KC AM KH BM ⨯⨯⨯=+ ∴33323222a ⨯⨯⨯=+ 解得：1a =， ∴当线段 AB 向下平移 1 个单位时，线段 AB 和 CD 开始有交点，∴ n ≥ 1，当 B'在线段 CD 上时，如图 2BB'交 x 轴于 M 点，过 B'做 B'E⊥OD,B'M=n-3,B'E=1,OD=5,OC=3∵ S△COD = S△OB'C + S△OB'D∴'' 222 CO OD CO B M OD B E ⨯⨯⨯=+∴353(3)51 222n⨯⨯-⨯=+解得：193n=，综上所述，当平移后的线段 AB 与线段 CD 有公共点时，1913n≤≤．③∵A（m−3，3m+3）， B（m，m+4） D（0，−5）且AD 沿直线 AB 方向平移得到线段BE，∴E点横坐标为：3E点纵坐标为：﹣5+m+4－（3m+3）=﹣4－2m∴E（3，﹣4－2m），设DE：y=kx+b，把D（0，﹣5），E（3，﹣4－2m）代入y=kx+b∴3k+b=42mb=5⎧⎨⎩﹣－﹣∴1-2mk=3b=-5⎧⎪⎨⎪⎩，∴y=12mx53－－，把y=﹣2代入解析式得：﹣2=12mx53－－，x=912m－，∴F9(,2) 12m--．【点睛】本题考查平面直角坐标系中点的平移计算及一次函数解析式求法，解题关键在于理解掌握平面直角坐标系中点平移计算方法以及用待定系数法求函数解析式方法的应用．6．（1）BP=3cm，CQ=3cm；（2）全等，理由详见解析；（3）154；（4）经过803s点P与点Q第一次相遇．【解析】【分析】（1）速度和时间相乘可得BP、CQ的长；（2）利用SAS可证三角形全等；（3）三角形全等，则可得出BP=PC，CQ=BD，从而求出t的值；（4）第一次相遇，即点Q第一次追上点P，即点Q的运动的路程比点P运动的路程多10+10=20cm的长度．【详解】解：（1）BP=3×1=3㎝，CQ=3×1=3㎝（2）∵t=1s，点Q的运动速度与点P的运动速度相等∴BP=CQ=3×1=3cm，∵AB=10cm，点D为AB的中点，∴BD=5cm．又∵PC=BC﹣BP，BC=8cm，∴PC=8﹣3=5cm，∴PC=BD又∵AB=AC，∴∠B=∠C ，在△BPD 和△CQP 中，PC BD B C BP CQ =⎧⎪∠=∠⎨⎪=⎩∴△BPD ≌△CQP(SAS)（3）∵点Q 的运动速度与点P 的运动速度不相等，∴BP 与CQ 不是对应边，即BP≠CQ∴若△BPD ≌△CPQ ，且∠B=∠C ，则BP=PC=4cm ，CQ=BD=5cm ，∴点P ，点Q 运动的时间t=433BP =s ， ∴154Q CQ V t ==cm/s ；（4）设经过x 秒后点P 与点Q 第一次相遇．由题意，得154x=3x+2×10，解得80x=3 ∴经过803s 点P 与点Q 第一次相遇．【点睛】本题考查动点问题，解题关键还是全等的证明和利用，将动点问题视为定点问题来分析可简化思考过程．7．（1）A ，B 两点的坐标分别为()0,2，()3,0；（2）点D 的坐标是141,3⎛⎫-⎪⎝⎭；（3）证明见解析【解析】【分析】（1）根据非负数的性质得出二元一次方程组，求解即可；（2）过点B 作y 轴的平行线分别与过点A ，C 作x 轴的平行线交于点N ，点M ，过点C 作y 轴的平行线与过点A 作x 轴的平行线交于点T ，根据三角形ABC 的面积=长方形CMNT 的面积-（三角形ANB 的面积+三角形ATC 的面积+三角形CMB 的面积）列出方程，求解得出点C 的坐标，由平移的规律可得点D 的坐标；（3）过点E 作//EF CD ，交y 轴于点F ，过点O 作//OG AB ，交PE 于点G ，根据两直线平行，内错角相等与已知条件得出3BCD CEF ∠=∠，同样可证OGP OPE ∠=∠，由平移的性质与平行公理的推论可得FEP OGP ∠=∠，最后根据CEP CEF FEP ∠=∠+∠，通过等量代换进行证明．【详解】解：（1）21280a b a b --++-=，又∵|21|0a b --≥，280a b +-≥，|21|0a b ∴--=，280a b +-=，即210280a b a b --=⎧⎨+-=⎩，解方程组2128a b a b -=⎧⎨+=⎩得23a b =⎧⎨=⎩， A ∴，B 两点的坐标分别为()0,2，()3,0；（2）如图，过点B 作y 轴的平行线分别与过点A ，C 作x 轴的平行线交于点N ，点M ，过点C 作y 轴的平行线与过点A 作x 轴的平行线交于点T ，∴三角形ABC 的面积=长方形CMNT 的面积-（三角形ANB 的面积+三角形ATC 的面积+三角形CMB 的面积），根据题意得，11195(2||)232(2||)5||222t t t ⎡⎤=⨯+-⨯⨯+⨯⨯++⨯⨯⎢⎥⎣⎦，化简，得3||42t =，解得，83t =±，依题意得，0t <， 83t ∴=-，即点C 的坐标为82,3⎛⎫-- ⎪⎝⎭， ∴依题意可知，点C 的坐标是由点A 的坐标先向左平移2个单位长度，再向下平移143个单位长度得到的，从而可知，点D 的坐标是由点B 的坐标先向左平移2个单位长度，再向下平移143个单位长度得到的， ∴点D 的坐标是141,3⎛⎫- ⎪⎝⎭；（3）证明：过点E 作//EF CD ，交y 轴于点F ，如图所示，则ECD CEF ∠=∠，2BCE ECD ∠=∠，33BCD ECD CEF ∴∠=∠=∠，过点O 作//OG AB ，交PE 于点G ，如图所示，则OGP BPE ∠=∠，PE 平分OPB ∠，OPE BPE ∴∠=∠，OGP OPE ∴∠=∠，由平移得//CD AB ，//OG FE ∴，FEP OGP ∴∠=∠，FEP OPE ∴∠=∠，CEP CEF FEP ∠=∠+∠，CEP CEF OPE ∴∠=∠+∠，CEF CEP OPE ∴∠=∠-∠，3()BCD CEP OPE ∴∠=∠-∠．【点睛】本题综合性较强，考查非负数的性质，解二元一次方程组，平行线的性质，平移的性质，坐标与图形的性质，第（3）题巧作辅助线构造平行线是解题的关键．8．90︒，45︒；20︒，30︒；2a γβ+=，2a γβ-=.【解析】【分析】（1）①如图①知1112EMC BMC ∠=∠，1112C MF C MC ∠=∠得 ()1112EMF BMC C MC ∠=∠+∠可求出解. ②由图②知111111,22EBA ABC C BF C BC ∠=∠∠=∠得()1112EBF ABC C BC ∠=∠+∠可求出解.（2）①由图③折叠知11,CMF FMC BME EMB ∠=∠∠=∠，可推出11()BMC EMF EMF C MB ∠-∠-∠=∠，即可求出解.②由图④中折叠知11,CMF C MF ABE A BE ∠=∠∠=∠，可推出()112906090A MC ︒︒︒-+∠=，即可求出解.（3）如图⑤-1、⑤-2中分别由折叠可知，a ββγ-=-、a ββγ-=+，即可求得 2a γβ+=、2a γβ-=.【详解】解：（1）①如图①中，1112EMC BMC ∠=∠，1112C MF C MC ∠=∠， ()1111111800229EMF EMC C MF BMC C MC ︒︒∴∠=∠+∠=∠⨯=+∠=，故答案为90︒. ②如图②中，111111,22EBA ABC C BF C BC ∠=∠∠=∠， ()111111904522EBF EBC C BF ABC C BC ︒︒∴∠=∠+∠=∠+∠=⨯=，故答案为45︒.（2）①如图③中由折叠可知，11,CMF FMC BME EMB ∠=∠∠=∠，1111C MF EMB EMF C MB ∠+∠-∠=∠，11CMF BME EMF C MB ∴∠+∠-∠=∠，11()BMC EMF EMF C MB ∴∠-∠-∠=∠，111808020C MB ︒︒︒∴-=∠=；②如图④中根据折叠可知，11,CMF C MF ABE A BE ∠=∠∠=∠，112290CMF ABE A MC ︒∠+∠+∠=，112()90CMF ABE A MC ︒∴∠+∠+∠=，()1129090EMF AMC ︒︒∴-∠+∠=，()112906090AMC ︒︒︒∴-+∠=， 1130A MC ︒∴∠=；（3）如图⑤-1中，由折叠可知，a ββγ-=-，2a γβ∴+=；如图⑤-2中，由折叠可知，a ββγ-=+，2a γβ∴-=.【点睛】本题考查了图形的变换中折叠属全等变换，图形的角度及边长不变及一些角度的计算问题，突出考查学生的观察能力、思维能力以及动手操作能力，本题是代数、几何知识的综合运用典型题目.9．（1）①点P ；②见解析；（2）①点C 的横坐标C x 的值为-3；②334k -≤<-【解析】【分析】（1）①在点P ，点Q 中，点OS 绕点O 顺时针旋转90°能得到线段OP ，故S 关于点O 的“正矩点”为点P ；②利用新定义得点S 是点P 关于点M 的“正矩点”（答案不唯一）；（2）①利用新定义结合题意画出符合题意的图形，利用新定义的性质证明△BCF ≌△AOB ，则FC=OB 求得点C 的横坐标；②用含k 的代数式表示点C 纵坐标，代入不等式求解即可．【详解】解：（1）①在点P ，点Q 中，点OS 绕点O 顺时针旋转90°能得到线段OP ，故S 关于点O 的“正矩点”为点P ，故答案为点P ；②因为MP 绕M 点顺时针旋转90︒得MS ，所以点S 是点P 关于点M 的“正矩点”，同理还可以得点Q 是点P 关于点S 的“正矩点”．（任写一种情况就可以）（2）①符合题意的图形如图1所示，作CE ⊥x 轴于点E ，CF ⊥y 轴于点F ，可得 ∠BFC=∠AOB=90°．∵直线3(0)y kx k =+<与x 轴交于点A ，与y 轴交于点B ，∴点B 的坐标为3(0,3),(,0)B A k-在x 轴的正半轴上， ∵点A 关于点B 的“正矩点”为点(,)C C C x y ，∴∠ABC=90°，BC=BA ，∴∠1＋∠2=90°，∵∠AOB=90°，∴∠2＋∠3=90°，∴∠1=∠3．∴△BFC ≌△AOB ，∴3FC OB ==，可得OE ＝3．∵点A 在x 轴的正半轴上且3OA <，0C x ∴<， ∴点C 的横坐标C x 的值为－3．②因为△BFC ≌△AOB ，3(,0)A k-，A 在x 轴正半轴上，所以BF ＝OA ，所以OF ＝OB-OF ＝33k +点3(3,3)C k -+，如图2， -1＜C y ≤2，即：-1＜33k+ ≤2，则334k -≤<-．【点睛】本题考查的是一次函数综合运用，涉及到三角形全等、解不等式，新定义等，此类新定义题目，通常按照题设的顺序，逐次求解．10．（1）见解析；（2）CD 2AD +BD ，理由见解析；（3）CD 3+BD【解析】【分析】（1）由“SAS ”可证△ADB ≌△AEC ；（2）由“SAS ”可证△ADB ≌△AEC ，可得BD ＝CE ，由直角三角形的性质可得DE 2AD ，可得结论；（3）由△DAB ≌△EAC ，可知BD ＝CE ，由勾股定理可求DH ＝32AD ，由AD ＝AE ，AH ⊥DE ，推出DH ＝HE ，由CD ＝DE +EC ＝2DH +BD 3AD +BD ，即可解决问题；【详解】证明：（1）∵∠BAC ＝∠DAE ，∴∠BAD ＝∠CAE ，又∵AB ＝AC ，AD ＝AE ，∴△ADB≌△AEC（SAS）；（2）CD＝2AD+BD，理由如下：∵∠BAC＝∠DAE，∴∠BAD＝∠CAE，又∵AB＝AC，AD＝AE，∴△ADB≌△AEC（SAS）；∴BD＝CE，∵∠BAC＝90°，AD＝AE，∴DE＝2AD，∵CD＝DE+CE，∴CD＝2AD+BD；（3）作AH⊥CD于H．∵∠BAC＝∠DAE，∴∠BAD＝∠CAE，又∵AB＝AC，AD＝AE，∴△ADB≌△AEC（SAS）；∴BD＝CE，∵∠DAE＝120°，AD＝AE，∴∠ADH＝30°，∴AH＝12 AD，∴DH22AD AH3，∵AD＝AE，AH⊥DE，∴DH＝HE，∴CD＝DE+EC＝2DH+BD3+BD，故答案为：CD3+BD．【点睛】本题是结合了全等三角形的性质与判定，勾股定理等知识的综合问题，熟练掌握知识点，有简入难，层层推进是解答关键.11．（1）见解析；（2）当F运动到AF＝AD时，FD∥BG，理由见解析；（3）FH＝HD，理由见解析【解析】【分析】（1）证明△DEG≌△CEB（AAS）即可解决问题．（2）想办法证明∠AFD＝∠ABG＝45°可得结论．（3）结论：FH＝HD．利用等腰直角三角形的性质即可解决问题．【详解】（1）证明：∵AD∥BC，∴∠DGE＝∠CBE，∠GDE＝∠BCE，∵E是DC的中点，即DE＝CE，∴△DEG≌△CEB（AAS），∴DG＝BC；（2）解：当F运动到AF＝AD时，FD∥BG．理由：由（1）知DG＝BC，∵AB＝AD+BC，AF＝AD，∴BF＝BC＝DG，∴AB＝AG，∵∠BAG＝90°，∴∠AFD＝∠ABG＝45°，∴FD∥BG，故答案为：F运动到AF＝AD时，FD∥BG；（3）解：结论：FH＝HD．理由：由（1）知GE＝BE，又由（2）知△ABG为等腰直角三角形，所以AE⊥BG，∵FD∥BG，∴AE⊥FD，∵△AFD为等腰直角三角形，∴FH＝HD，故答案为：FH＝HD．【点睛】本题考查了全等三角形的判定和性质，平行线的判定，等腰直角三角形的性质，掌握三角形全等的判定和性质是解题的关键．12．（1）（1，0）；（2）362y x＝；（3）92；（4）（6，3）．【解析】【分析】（1）由题意已知l 1的解析式，令y=0求出x 的值即可；（2）根据题意设l 2的解析式为y=kx+b ，并由题意联立方程组求出k ，b 的值；（3）由题意联立方程组，求出交点C 的坐标，继而即可求出S △ADC ；（4）由题意根据△ADP 与△ADC 底边都是AD ，面积相等所以高相等，△ADC 高就是点C 到AD 的距离进行分析计算．【详解】解：（1）由y=-3x+3，令y=0，得-3x+3=0，∴x=1，∴D （1，0）；（2）设直线l 2的解析表达式为y=kx+b ，由图象知：x=4，y=0；x=3，y ＝32-，代入表达式y=kx+b ， ∴40332k b k b +⎧⎪⎨+-⎪⎩＝＝， ∴326k b ⎧⎪⎨⎪-⎩＝＝， ∴直线l 2的解析表达式为362y x -＝；（3）由33362y x y x ⎪-+-⎧⎪⎨⎩＝＝，解得23x y ⎧⎨⎩-＝＝， ∴C （2，-3），∵AD=3， ∴331922ADC S =⨯⨯-=；（4）△ADP 与△ADC 底边都是AD ，面积相等所以高相等，△ADC 高就是点C 到直线AD 的距离，即C 纵坐标的绝对值=|-3|=3，则P 到AD 距离=3，∴P 纵坐标的绝对值=3，点P 不是点C ，∴点P 纵坐标是3，∵y=1.5x-6，y=3，∴1.5x-6=3，解得x=6，所以P （6，3）．【点睛】本题考查的是一次函数图象的性质以及三角形面积的计算等有关知识，熟练掌握求一次函数解析式的方法以及一次函数图象的性质和三角形面积的计算公式是解题的关键.。

八年级数学压轴题期末复习试卷测试题(Word版含解析)

八年级数学压轴题期末复习试卷测试题（Word 版含解析）一、压轴题1．定义：在平面直角坐标系中，对于任意两点(),A a b ，(),B c d ，若点(),T x y 满足3a c x +=，3b d y +=那么称点T 是点A ，B 的融合点．例如：()1,8A -，()4,2B -，当点(),T x y 满足1413x -+==，()8223y +-==时，则点()1,2T 是点A ，B 的融合点．（1）已知点()1,5A -，()7,4B ，()2,3C ，请说明其中一个点是另外两个点的融合点．（2）如图，点()4,0D ，点(),25E t t +是直线l 上任意一点，点(),T x y 是点D ，E 的融合点．①试确定y 与x 的关系式；②在给定的坐标系xOy 中，画出①中的函数图象；③若直线ET 交x 轴于点H ．当DTH 为直角三角形时，直接写出点E 的坐标．2．在ABC 中，AB AC =，D 是直线BC 上一点（不与点B 、C 重合），以AD 为一边在AD 的右侧作ADE ，AD AE =，DAE BAC ∠=∠，连接CE .（1）如图，当 D 在线段BC 上时，求证：BD CE =.（2）如图，若点D 在线段CB 的延长线上，BCE α∠=，BAC β∠=.则α、β之间有怎样的数量关系？写出你的理由.（3）如图，当点D 在线段BC 上，90BAC ∠=︒，4BC =，求DCE S 最大值.3．在平面直角坐标系中点 A （m −3，3m +3），点 B （m ，m +4）和 D （0，−5），且点 B 在第二象限．（1）点B 向平移单位，再向下平移（用含m 的式子表达）单位可以与点A 重合；（2）若点B 向下移动 3 个单位，则移动后的点B 和点A 的纵坐标相等，且有点 C（m−2，0）．①则此时点A、B、C 坐标分别为、、．②将线段AB 沿y 轴负方向平移n 个单位，若平移后的线段AB 与线段CD 有公共点，求n 的取值范围．③当m<−1 式，连接AD，若线段AD 沿直线AB 方向平移得到线段BE，连接DE 与直线y=−2 交于点F，则点F 坐标为．（用含m 的式子表达）4．在等边△ABC的顶点A、C处各有一只蜗牛，它们同时出发，分别以每分钟1米的速度由A向B和由C向A爬行，其中一只蜗牛爬到终点时，另一只也停止运动，经过t分钟后，它们分别爬行到D、E处，请问：（1）如图1，在爬行过程中，CD和BE始终相等吗，请证明？（2）如果将原题中的“由A向B和由C向A爬行”，改为“沿着AB和CA的延长线爬行”，EB与CD交于点Q，其他条件不变，蜗牛爬行过程中∠CQE的大小保持不变，请利用图2说明：∠CQE=60°；（3）如果将原题中“由C向A爬行”改为“沿着BC的延长线爬行，连接DE交AC于F”，其他条件不变，如图3，则爬行过程中，证明：DF=EF5．在平面直角坐标系中，点A 、B 在坐标轴上，其中()0,A a 、(),0B b 满足|21|280a b a b --++-=．（1）求A 、B 两点的坐标；（2）将线段AB 平移到CD ，点A 的对应点为()2,C t -，如图1所示，若三角形ABC 的面积为9，求点D 的坐标；（3）平移线段AB 到CD ，若点C 、D 也在坐标轴上，如图2所示．P 为线段AB 上的一动点（不与A 、B 重合），连接OP 、PE 平分OPB ∠，2BCE ECD ∠=∠．求证：3()BCD CEP OPE ∠=∠-∠．6．如图所示，在平面直角坐标系xOy 中，已知点A 的坐标(3,2)-，过A 点作AB x ⊥轴，垂足为点B ，过点(2,0)C 作直线l x ⊥轴，点P 从点B 出发在x 轴上沿着轴的正方向运动．（1）当点P 运动到点O 处，过点P 作AP 的垂线交直线l 于点D ，证明AP DP =，并求此时点D 的坐标；（2）点Q是直线l上的动点，问是否存在点P，使得以P C Q、、为顶点的三角形和ABP∆全等，若存在求点P的坐标以及此时对应的点Q的坐标，若不存在，请说明理由．7．（阅读材科）小明同学发现这样一个规律：两个顶角相等的等腰三角形，如果具有公共的项角的顶点，并把它们的底角顶点连接起来则形成一组全等的三角形，小明把具有这个规律的图形称为“手拉手”图形．如图1，在“手拉手”图形中，小明发现若∠BAC=∠DAE，AB=AC，AD=AE，则△ABD≌△ACE．（材料理解）（1）在图1中证明小明的发现．（深入探究）（2）如图2，△ABC和△AED是等边三角形，连接BD，EC交于点O，连接AO，下列结论：①BD=EC；②∠BOC=60°；③∠AOE=60°；④EO=CO，其中正确的有．(将所有正确的序号填在横线上)．（延伸应用）（3）如图3，AB=BC，∠ABC=∠BDC=60°，试探究∠A与∠C的数量关系．8．已知在△ABC中，AB＝AC，射线BM、BN在∠ABC内部，分别交线段AC于点G、H．（1）如图1，若∠ABC＝60°，∠MBN＝30°，作AE⊥BN于点D，分别交BC、BM于点E、F．①求证：∠1＝∠2；②如图2，若BF＝2AF，连接CF，求证：BF⊥CF；（2）如图3，点E为BC上一点，AE交BM于点F，连接CF，若∠BFE＝∠BAC＝2∠CFE，求ABFACFSS的值．9．如图已知ABC中，,8B C AB AC∠=∠==厘米，6BC=厘来，点D为AB的中点．如果点P在线段BC上以每秒2厘米的速度由B点向C点运动，同时，点Q在线段CA上由C点向A点运动，设运动时间为t(秒)．（1）用含t 的代数式表示线段PC 的长度；（2）若点,P Q 的运动速度相等，经过1秒后，BPD △与CQP 是否全等，请说明理由；（3）若点,P Q 的运动速度不相等，当点Q 的运动速度为多少时，能够使BPD △与CQP 全等？（4）若点Q 以（3）中的运动速度从点C 出发，点v 以原来的运动速度从点B 同时出发，都顺时针沿三边运动，求经过多长时间，点P 与点Q 第一次在ABC 的哪条边上相遇？10．直角三角形ABC 中，90ACB ∠=︒，直线l 过点C ．（1）当AC BC =时，如图1，分别过点A 和B 作AD ⊥直线l 于点D ，BE ⊥直线l 于点E ，ACD 与CBE △是否全等，并说明理由；（2）当8AC cm =，6BC cm =时，如图2，点B 与点F 关于直线l 对称，连接BF CF 、，点M 是AC 上一点，点N 是CF 上一点，分别过点M N 、作MD ⊥直线l 于→路径运动，点D，NE⊥直线l于点E，点M从A点出发，以每秒1cm的速度沿A C→→→→路径运动，终终点为C，点N从点F出发，以每秒3cm的速度沿F C B C FM N同时开始运动，各自达到相应的终点时停止运动，设运动时间为t秒，点为F，点,△为等腰直角三角形时，求t的值．当CMN11．如图，直线l1的表达式为：y=-3x+3，且直线l1与x轴交于点D，直线l2经过点A，B，直线l1，l2交于点C．（1）求点D的坐标；（2）求直线l2的解析表达式；（3）求△ADC的面积；（4）在直线l2上存在异于点C的另一点P，使得△ADP与△ADC的面积相等，求点P的坐标．12．如图，在平面直角坐标系中，直线y＝2x+6与x轴交于点A，与y轴交于点B，过点B 的直线交x轴于点C，且AB＝BC．（1）求直线BC的解析式；（2）点P为线段AB上一点，点Q为线段BC延长线上一点，且AP＝CQ，设点Q横坐标为m，求点P的坐标（用含m的式子表示，不要求写出自变量m的取值范围）；（3）在（2）的条件下，点M在y轴负半轴上，且MP＝MQ，若∠BQM＝45°，求直线PQ 的解析式．【参考答案】***试卷处理标记，请不要删除一、压轴题1．（1）点C 是点A 、B 的融合点；（2）①2-1y x =；②见详解；③点E 的坐标为：（2，9）或（8，21）【解析】【分析】（1）根据融合点的定义3a c x +=，3b d y +=，即可求解；（2）①由题意得：分别得到x 与t 、y 与t 的关系，即可求解；②利用①的函数关系式解答；③分∠DTH ＝90°、∠TDH ＝90°、∠HTD ＝90°三种情况，分别求解即可．【详解】解：（1）x ＝-17233a c ++==，y ＝54333b d ++==，故点C 是点A 、B 的融合点；（2）①由题意得：x ＝433a c t ++=，y ＝2533b d t ++=，则3-4t x =，则()23-452-13x y x +==； ②令x ＝0，y ＝-1；令y ＝0，x ＝12，图象如下：③当∠THD ＝90°时，∵点E （t ，2t ＋5），点T （t ，2t−1），点D （4，0），且点T （x ，y ）是点D ，E 的融合点．∴t ＝13（t ＋4）， ∴t ＝2，∴点E （2，9）；当∠TDH ＝90°时，∵点E （t ，2t ＋5），点T （4，7），点D （4，0），且点T （x ，y ）是点D ，E 的融合点．∴4＝13（4＋t ） ∴t ＝8， ∴点E （8，21）；当∠HTD ＝90°时，由于EH 与x 轴不平行，故∠HTD 不可能为90°；故点E 的坐标为：（2，9）或（8，21）．【点睛】本题是一次函数综合运用题，涉及到直角三角形的运用，此类新定义题目，通常按照题设顺序，逐次求解．2．（1）见解析；（2）αβ=，理由见解析；（3）2【解析】【分析】（1）证明()ABD ACE SAS ≅△△，根据全等三角形的性质得到BD CE =；（2）同（1）先证明()ABD ACE SAS ≅△△，得到∠ACE=∠ABD ，结合等腰三角形的性质和外角和定理用不同的方法表示∠ACE ，得到α和β关系式；（3）同（1）先证明()ABD ACE SAS ≅△△，得到ABC ADCE S S ∆=四边形，那么DCE ADE ADCE S S S ∆∆=-四边形，当AD BC ⊥时，ADE S ∆最小，即DCE S ∆最大．【详解】解：（1）∵BAC DAE ∠=∠，∴BAC DAC DAE DAC ∠-∠=∠-∠，∴BAD CAE ∠=∠，在ABD △和ACE △中，AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩，∴()ABD ACE SAS ≅△△，∴BD CE =；（2）同（1）的方法得()ABD ACE SAS ≅△△，∴∠ACE=∠ABD ，∠BCE=α，∴∠ACE=∠ ACB+∠BCE=∠ACB+α，在ABC 中，∵AB= AC ，∠BAC=β，∴∠ACB=∠ABC =12(180°-β)= 90°-12β， ∴∠ABD= 180°-∠ABC= 90°+12β， ∴∠ACE=∠ACB +α= 90°-12β+α， ∵∠ACE=∠ABD = 90°+12β， ∴90°-12β+α= 90°+12β， ∴α = β；（3）如图，过A 做AH BC ⊥于点H ，∵AB AC =，90BAC ∠=︒，∴45ABC ∠=︒，122BH AH BC ===，同（1）的方法得，()ABD ACE SAS ≅△△，AEC ABD S S ∆∆∴=,AEC ADC ABD ADC S S S S ∆∆∆∆+=+，即142ABC ADCE S S BC AH ∆==⋅=四边形， ∴DCE ADE ADCE S S S ∆∆=-四边形，当ADE S ∆最小时，DCE S ∆最大，∴当AD BC ⊥2AD =，时最小，2122ADE S AD ∆==， 422DCE S ∆∴=-=最大．【点睛】本题考查全等三角形的性质和判定，等腰三角形的性质，三角形的外角和定理，解题的关键是抓住第一问中的那组全等三角形，后面的问题都是在这个基础上进行证明的．3．（1）左；3；(1-2m )；（2）①（-4，0）；（-1，0）（-3，0）； ②当平移后的线段 AB 与线段 CD 有公共点时，1913n ≤≤；③ F 9(,2)12m--．【解析】【分析】(1)根据平面直角坐标系中点的平移计算方法即可得解(2)①根据B 点向下平移后，点B 和点A 的纵坐标相等得到等量关系，可求出m 的值，从而求出A 、B 、C 三点坐标；②过 C 作 CK 垂直 x 轴交 AB 于 K 点过 B 做 BM 垂直 x 轴于 M 点，设出K 点坐标，作 KH ⊥BM 与 H 点，表示出H 点坐标，然后利用面积关系ABM AKM BKM S S S ∆∆∆=+求出距离；当 B '在线段 CD 上时，BB '交 x 轴于 M 点，过 B '做 B 'E ⊥OD ，利用S △COD = S △OB'C + S △OB'D ，求出n 的值，从而求出n 的取值范围；③通过坐标平移法用m 表示出E 点的坐标，利用D 、E 两点坐标表示出直线DE 的函数关系式，令y=﹣2，求出x 的值即可求出F 点坐标．【详解】解：（1）根据平移规律可得：B 向左平移；m －（m －1）=3，所以平移3个单位；m+4－（3m+3）=1－2m ，所以再向下平移(1-2m )个单位；故答案为：左；3；(1-2m )（2）①点 B 向下移动 3 个单位得：B （m ，m+1）∵移动后的点 B 和点 A 的纵坐标相等∴m+1=3m+3∴m=﹣1∴A （-4,0）；B （-1,0）；C （-3,0）；②如图 1，过 C 作 CK 垂直 x 轴交 AB 于 K 点过 B 做 BM 垂直 x 轴于 M 点，设 K 点坐标为（-3，a ）M 点坐标为（-1,0）作 KH ⊥BM 与 H 点，H 点坐标为（-1，a ）AM=3,BM=3,KC=a,KH=2∵ABM AKM BKM S S S ∆∆∆=+∴222AM BM KC AM KH BM ⨯⨯⨯=+ ∴33323222a ⨯⨯⨯=+ 解得：1a =，∴当线段 AB 向下平移 1 个单位时，线段 AB 和 CD 开始有交点，∴ n ≥ 1，当 B'在线段 CD 上时，如图 2BB'交 x 轴于 M 点，过 B'做 B'E ⊥OD,B'M=n-3,B'E=1,OD=5,OC=3∵ S △COD = S △OB'C + S △OB'D∴''222CO OD CO B M OD B E ⨯⨯⨯=+ ∴353(3)51222n ⨯⨯-⨯=+ 解得：193n =，综上所述，当平移后的线段 AB 与线段 CD 有公共点时，1913n ≤≤．③∵A（m−3，3m+3）， B（m，m+4） D（0，−5）且AD 沿直线 AB 方向平移得到线段BE，∴E点横坐标为：3E点纵坐标为：﹣5+m+4－（3m+3）=﹣4－2m∴E（3，﹣4－2m），设DE：y=kx+b，把D（0，﹣5），E（3，﹣4－2m）代入y=kx+b∴3k+b=42mb=5⎧⎨⎩﹣－﹣∴1-2mk=3b=-5⎧⎪⎨⎪⎩，∴y=12mx53－－，把y=﹣2代入解析式得：﹣2=12mx53－－，x=912m－，∴F9(,2) 12m--．【点睛】本题考查平面直角坐标系中点的平移计算及一次函数解析式求法，解题关键在于理解掌握平面直角坐标系中点平移计算方法以及用待定系数法求函数解析式方法的应用．4．（1)相等，证明见解析；（2)证明见解析；（3)证明见解析．【解析】【分析】（1）先证明△ACD≌△CBE，再由全等三角形的性质即可证得CD=BE；（2）先证明△BCD≌△ABE，得到∠BCD=∠ABE，求出∠DQB=∠BCQ+∠CBQ=∠ABE+∠CBQ=180°-∠ABC，∠CQE=180°-∠DQB，即可解答；（3）如图3，过点D作DG∥BC交AC于点G，根据等边三角形的三边相等，可以证得AD=DG=CE；进而证明△DGF和△ECF全等，最后根据全等三角形的性质即可证明．【详解】（1）解：CD和BE始终相等，理由如下：如图1，AB=BC=CA，两只蜗牛速度相同，且同时出发，∴CE=AD，∠A=∠BCE=60°在△ACD与△CBE中，AC=CB，∠A=∠BCE，AD=CE∴△ACD≌△CBE（SAS），∴CD=BE，即CD和BE始终相等；（2）证明：根据题意得：CE=AD，∵AB=AC，∴AE=BD，∴△ABC是等边三角形，∴AB=BC，∠BAC=∠ACB=60°，∵∠EAB+∠ABC=180°，∠DBC+∠ABC=180°，∴∠EAB=∠DBC ，在△BCD 和△ABE 中，BC=AB ，∠DBC=∠EAB ，BD=AE∴△BCD ≌△ABE （SAS ），∴∠BCD=∠ABE∴∠DQB=∠BCQ+∠CBQ=∠ABE+∠CBQ=180°-∠ABC=180°-60°=120°，∴∠CQE=180°-∠DQB=60°，即CQE=60°；（3）解：爬行过程中，DF 始终等于EF 是正确的，理由如下：如图，过点D 作DG ∥BC 交AC 于点G ，∴∠ADG=∠B=∠AGD=60°，∠GDF=∠E ，∴△ADG 为等边三角形，∴AD=DG=CE ，在△DGF 和△ECF 中，∠GFD=∠CFE ，∠GDF=∠E ，DG=EC∴△DGF ≌△EDF （AAS ），∴DF=EF.【点睛】本题主要考查了全等三角形的判定与性质和等边三角形的性质；题弄懂题中所给的信息，再根据所提供的思路寻找证明条件是解答本题的关键．5．（1）A ，B 两点的坐标分别为()0,2，()3,0；（2）点D 的坐标是141,3⎛⎫-⎪⎝⎭；（3）证明见解析【解析】【分析】（1）根据非负数的性质得出二元一次方程组，求解即可；（2）过点B 作y 轴的平行线分别与过点A ，C 作x 轴的平行线交于点N ，点M ，过点C 作y 轴的平行线与过点A 作x 轴的平行线交于点T ，根据三角形ABC 的面积=长方形CMNT 的面积-（三角形ANB 的面积+三角形ATC 的面积+三角形CMB 的面积）列出方程，求解得出点C 的坐标，由平移的规律可得点D 的坐标；（3）过点E 作//EF CD ，交y 轴于点F ，过点O 作//OG AB ，交PE 于点G ，根据两直线平行，内错角相等与已知条件得出3BCD CEF ∠=∠，同样可证OGP OPE ∠=∠，由平移的性质与平行公理的推论可得FEP OGP ∠=∠，最后根据CEP CEF FEP ∠=∠+∠，通过等量代换进行证明．【详解】解：（1）21280a b a b --++-=，又∵|21|0a b --≥，280a b +-≥，|21|0a b ∴--=，280a b +-=，即210280a b a b --=⎧⎨+-=⎩，解方程组2128a b a b -=⎧⎨+=⎩得23a b =⎧⎨=⎩， A ∴，B 两点的坐标分别为()0,2，()3,0；（2）如图，过点B 作y 轴的平行线分别与过点A ，C 作x 轴的平行线交于点N ，点M ，过点C 作y 轴的平行线与过点A 作x 轴的平行线交于点T ，∴三角形ABC 的面积=长方形CMNT 的面积-（三角形ANB 的面积+三角形ATC 的面积+三角形CMB 的面积），根据题意得，11195(2||)232(2||)5||222t t t ⎡⎤=⨯+-⨯⨯+⨯⨯++⨯⨯⎢⎥⎣⎦，化简，得3||42t =，解得，83t =±，依题意得，0t <， 83t ∴=-，即点C 的坐标为82,3⎛⎫-- ⎪⎝⎭， ∴依题意可知，点C 的坐标是由点A 的坐标先向左平移2个单位长度，再向下平移143个单位长度得到的，从而可知，点D 的坐标是由点B 的坐标先向左平移2个单位长度，再向下平移143个单位长度得到的， ∴点D 的坐标是141,3⎛⎫- ⎪⎝⎭；（3）证明：过点E 作//EF CD ，交y 轴于点F ，如图所示，则ECD CEF ∠=∠，2BCE ECD ∠=∠，33BCD ECD CEF ∴∠=∠=∠，过点O 作//OG AB ，交PE 于点G ，如图所示，则OGP BPE ∠=∠，PE 平分OPB ∠，OPE BPE ∴∠=∠，OGP OPE ∴∠=∠，由平移得//CD AB ，//OG FE ∴，FEP OGP ∴∠=∠，FEP OPE ∴∠=∠，CEP CEF FEP ∠=∠+∠，CEP CEF OPE ∴∠=∠+∠，CEF CEP OPE ∴∠=∠-∠，3()BCD CEP OPE ∴∠=∠-∠．【点睛】本题综合性较强，考查非负数的性质，解二元一次方程组，平行线的性质，平移的性质，坐标与图形的性质，第（3）题巧作辅助线构造平行线是解题的关键．6．（1）证明见解析；(2,3)D ；（2）存在，(0,0)P ，(2,3)Q 或(0,0)P ，(2,3)Q -或(4,0)P ，(2,7)Q 或(4,0)P ，(2,7)Q -或1(,0)2P -，(2,2)Q -或1(,0)2P -，(2,2)Q -．【解析】【分析】（1）通过全等三角形的判定定理ASA 证得△ABP ≌△PCD ，由全等三角形的对应边相等证得AP ＝DP ，DC ＝PB ＝3，易得点D 的坐标；（2）设P （a ，0），Q （2，b ）．需要分类讨论：①AB ＝PC ，BP ＝CQ ；②AB ＝CQ ，BP ＝PC ．结合两点间的距离公式列出方程组，通过解方程组求得a 、b 的值，得解．【详解】（1）AP PD ⊥90APB DPC ∴∠+∠=90A APB∴∠+∠=A DPC∴∠=∠在ABP∆和PCD∆中A DPCAB PCABP PCD∠=∠⎧⎪=⎨⎪∠=∠⎩()ABP PCD ASA∴∆≅∆AP DP∴=，3DC PB==(2,3)D∴（2）设(,0)P a，(2,)Q b①AB PC=，BP CQ=223aa b⎧-=⎪⎨+=⎪⎩，解得3ab=⎧⎨=±⎩或47ab=⎧⎨=±⎩(0,0)P∴，(2,3)Q或(0,0)P，(2,3)Q-或(4,0)P，(2,7)Q或(4,0)P，(2,7)Q-②AB CQ=，BP PC=，322a ab+=-⎧⎨=⎩，解得122ab⎧=⎪⎨⎪=±⎩1(,0)2P∴-，(2,2)Q-或1(,0)2P-，(2,2)Q-综上：(0,0)P，(2,3)Q或(0,0)P，(2,3)Q-或(4,0)P，(2,7)Q或(4,0)P，(2,7)Q-或1(,0)2P-，(2,2)Q-或1(,0)2P-，(2,2)Q-【点睛】考查了三角形综合题．涉及到了全等三角形的判定与性质，两点间的距离公式，一元一次绝对值方程组的解法等知识点．解答（2）题时，由于没有指明全等三角形的对应边（角），所以需要分类讨论，以防漏解．7．（1）证明见解析；（2）①②③；（3）∠A+∠C=180°．【解析】【分析】（1）利用等式的性质得出∠BAD=∠CAE，即可得出结论；（2）同（1）的方法判断出△ABD≌△ACE，得出BD=CE，再利用对顶角和三角形的内角和定理判断出∠BOC=60°，再判断出△BCF≌△ACO，得出∠AOC=120°，进而得出∠AOE=60°，再判断出BF＜CF，进而判断出∠OBC＞30°，即可得出结论；（3）先判断出△BDP是等边三角形，得出BD=BP，∠DBP=60°，进而判断出△ABD≌△CBP （SAS），即可得出结论．（1）证明：∵∠BAC=∠DAE，∴∠BAC+∠CAD=∠DAE+∠CAD，∴∠BAD=∠CAE，在△ABD和△ACE中，AB ACBAD CAEAD AE⎧⎪∠∠⎨⎪⎩＝＝＝，∴△ABD≌△ACE；（2）如图2，∵△ABC和△ADE是等边三角形，∴AB=AC，AD=AE，∠BAC=∠DAE=60°，∴∠BAD=∠CAE，在△ABD和△ACE中，AB ACBAD CAEAD AE⎧⎪∠∠⎨⎪⎩＝＝＝，∴△ABD≌△ACE，∴BD=CE，①正确，∠ADB=∠AEC，记AD与CE的交点为G，∵∠AGE=∠DGO，∴180°-∠ADB-∠DGO=180°-∠AEC-∠AGE，∴∠DOE=∠DAE=60°，∴∠BOC=60°，②正确，在OB上取一点F，使OF=OC，∴△OCF是等边三角形，∴CF=OC，∠OFC=∠OCF=60°=∠ACB，∴∠BCF=∠ACO，∵AB=AC，∴△BCF≌△ACO（SAS），∴∠AOC=∠BFC=180°-∠OFC=120°，∴∠AOE=180°-∠AOC=60°，③正确，连接AF，要使OC=OE，则有OC=12 CE，∵BD=CE，∴CF=OF=12 BD，∴OF=BF+OD，∴BF＜CF，∴∠OBC＞∠BCF，∵∠OBC+∠BCF=∠OFC=60°，∴∠OBC＞30°，而没办法判断∠OBC大于30度，所以，④不一定正确，即：正确的有①②③，故答案为①②③；（3）如图3，延长DC至P，使DP=DB，∵∠BDC=60°，∴△BDP是等边三角形，∴BD=BP，∠DBP=60°，∵∠BAC=60°=∠DBP，∴∠ABD=∠CBP，∵AB=CB，∴△ABD≌△CBP（SAS），∴∠BCP=∠A，∵∠BCD+∠BCP=180°，∴∠A+∠BCD=180°．【点睛】此题考查三角形综合题，等腰三角形的性质，等边三角形的性质，全等三角形的判定和性质，构造等边三角形是解题的关键．8．（1）①见解析；②见解析；（2）2【解析】【分析】（1）①只要证明∠2+∠BAF＝∠1+∠BAF＝60°即可解决问题；②只要证明△BFC≌△ADB，即可推出∠BFC＝∠ADB＝90°；（2）在BF上截取BK＝AF，连接AK．只要证明△ABK≌CAF，可得S△ABK＝S△AFC，再证明AF＝FK＝BK，可得S△ABK＝S△AFK，即可解决问题；【详解】（1）①证明：如图1中，∵AB＝AC，∠ABC＝60°∴△ABC是等边三角形，∴∠BAC＝60°，∵AD⊥BN，∴∠ADB＝90°，∵∠MBN＝30°，∠BFD＝60°＝∠1+∠BAF＝∠2+∠BAF，∴∠1＝∠2②证明：如图2中，在Rt△BFD中，∵∠FBD＝30°，∴BF＝2DF，∵BF＝2AF，∴BF＝AD，∵∠BAE＝∠FBC，AB＝BC，∴△BFC≌△ADB，∴∠BFC＝∠ADB＝90°，∴BF⊥CF（2）在BF 上截取BK ＝AF ，连接AK ．∵∠BFE ＝∠2+∠BAF ，∠CFE ＝∠4+∠1，∴∠CFB ＝∠2+∠4+∠BAC ，∵∠BFE ＝∠BAC ＝2∠EFC ，∴∠1+∠4＝∠2+∠4∴∠1＝∠2，∵AB ＝AC ，∴△ABK ≌CAF ，∴∠3＝∠4，S △ABK ＝S △AFC ，∵∠1+∠3＝∠2+∠3＝∠CFE ＝∠AKB ，∠BAC ＝2∠CEF ，∴∠KAF ＝∠1+∠3＝∠AKF ，∴AF ＝FK ＝BK ，∴S △ABK ＝S △AFK ，∴ABF AFCS 2S ∆∆=．【点睛】本题考查全等三角形的判定和性质、等边三角形的性质、等腰三角形的判定和性质、直角三角形30度角性质等知识，解题的关键是能够正确添加常用辅助线，构造全等三角形解决问题，属于中考压轴题．9．（1）6-2t ；（2）全等，理由见解析；（3）83；（4）经过24s 后，点P 与点Q 第一次在ABC 的BC 边上相遇【解析】【分析】（1）根据题意求出BP ，由PC=BC-BP ，即可求得；（2）根据时间和速度的关系分别求出两个三角形中，点运动轨迹的边长，由∠B=∠C ，利用SAS 判定BPD △和CQP 全等即可；（3）根据全等三角形的判定条件探求边之间的关系，得出BP=PC ，再根据路程=速度×时间公式，求点P 的运动时间，然后求点Q 的运动速度即得；（4）求出点P 、Q 的路程，根据三角形ABC 的三边长度，即可得出答案．【详解】（1）由题意知，BP=2t ，则PC=BC-BP=6-2t ，故答案为：6-2t ；（2）全等，理由如下：∵p Q V V =，t=1，∴BP=2=CQ ，∵AB=8cm ，点D 为AB 的中点，∴BD=4（cm ），又∵PC=BC-BP=6-2=4（cm ），在BPD △和CQP 中BD PC B C BP CQ =⎧⎪∠=∠⎨⎪=⎩∴BPD △≌CQP （SAS ）故答案为：全等．（3）∵p Q V V ≠，∴BP CQ ≠，又∵BPD △≌CPQ ，∠B=∠C ，∴BP=PC=3cm ，CQ=BD=4cm ，∴点,P Q 运动时间322BP t ==（s ）， ∴48332Q CQ V t===（cm/s ），故答案为：83；（4）设经过t 秒时，P 、Q 第一次相遇，∵2/p V cm s =，8/3Q V cm s =， ∴2t+8+8=83t ，解得：t=24此时点Q 走了824643⨯=（cm ），∵ABC 的周长为：8+8+6=22（cm ），∴6422220÷=，∴20-8-8=4（cm ），经过24s 后，点P 与点Q 第一次在ABC 的BC 边上相遇，故答案为：24s ，在 BC 边上相遇．【点睛】考查了全等三角形的判定和性质，路程，速度，时间的关系，全等三角形中的动点问题，动点的追及问题，熟记三角形性质和判定，熟练掌握全等的判定依据和动点的运动规律是解题的关键，注意动点中追及问题的方向．10．（1）全等，理由见解析；（2）t=3.5秒或5秒【解析】【分析】（1）根据垂直的定义得到∠DAC=∠ECB ，利用AAS 定理证明△ACD ≌△CBE ；（2）分点F 沿C→B 路径运动和点F 沿B→C 路径运动两种情况，根据等腰三角形的定义列出算式，计算即可；【详解】解：（1）△ACD 与△CBE 全等．理由如下：∵AD ⊥直线l ，∴∠DAC+∠ACD=90°，∵∠ACB=90°，∴∠BCE+∠ACD=90°，∴∠DAC=∠ECB ，在△ACD 和△CBE 中，ADC CEB DAC ECB CA CB ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△ACD ≌△CBE （AAS ）；（2）由题意得，AM=t ，FN=3t ，则CM=8-t ，由折叠的性质可知，CF=CB=6，∴CN=6-3t ，点N 在BC 上时，△CMN 为等腰直角三角形，当点N 沿C→B 路径运动时，由题意得，8-t=3t-6，解得，t=3.5，当点N 沿B→C 路径运动时，由题意得，8-t=18-3t ，解得，t=5，综上所述，当t=3.5秒或5秒时，△CMN 为等腰直角三角形；【点睛】本题考查的是全等三角形的判定和性质，掌握全等三角形的判定定理和性质定理，灵活运用分情况讨论思想是解题的关键．11．（1）（1，0）；（2）362y x -＝；（3）92；（4）（6，3）．【解析】【分析】（1）由题意已知l 1的解析式，令y=0求出x 的值即可；（2）根据题意设l 2的解析式为y=kx+b ，并由题意联立方程组求出k ，b 的值；（3）由题意联立方程组，求出交点C 的坐标，继而即可求出S △ADC ；（4）由题意根据△ADP 与△ADC 底边都是AD ，面积相等所以高相等，△ADC 高就是点C 到AD 的距离进行分析计算．【详解】解：（1）由y=-3x+3，令y=0，得-3x+3=0，∴x=1，∴D （1，0）；（2）设直线l 2的解析表达式为y=kx+b ，由图象知：x=4，y=0；x=3，y ＝32-，代入表达式y=kx+b ， ∴40332k b k b +⎧⎪⎨+-⎪⎩＝＝， ∴326k b ⎧⎪⎨⎪-⎩＝＝， ∴直线l 2的解析表达式为362y x -＝；（3）由33362y x y x ⎪-+-⎧⎪⎨⎩＝＝，解得23x y ⎧⎨⎩-＝＝， ∴C （2，-3），∵AD=3， ∴331922ADC S =⨯⨯-=；（4）△ADP 与△ADC 底边都是AD ，面积相等所以高相等，△ADC 高就是点C 到直线AD 的距离，即C 纵坐标的绝对值=|-3|=3，则P 到AD 距离=3，∴P 纵坐标的绝对值=3，点P 不是点C ，∴点P 纵坐标是3，∵y=1.5x-6，y=3，∴1.5x-6=3，解得x=6，所以P （6，3）．【点睛】本题考查的是一次函数图象的性质以及三角形面积的计算等有关知识，熟练掌握求一次函数解析式的方法以及一次函数图象的性质和三角形面积的计算公式是解题的关键.12．（1）y ＝﹣2x +6；（2）点P （m ﹣6，2m ﹣6）；（3）y ＝﹣x +32【解析】【分析】（1）先求出点A，点B坐标，由等腰三角形的性质可求点C坐标，由待定系数法可求直线BC的解析式；（2）证明△PGA≌△QHC（AAS），则PG＝HQ＝2m﹣6，故点P的纵坐标为：2m﹣6，而点P在直线AB上，即可求解；（3）由“SSS”可证△APM≌△CQM，△ABM≌△CBM，可得∠PAM＝∠MCQ，∠BQM＝∠APM＝45°，∠BAM＝∠BCM，由“AAS”可证△APE≌△MAO，可得AE＝OM，PE＝AO＝3，可求m的值，进而可得点P，点Q的坐标，即可求直线PQ的解析式．【详解】（1）∵直线y＝2x+6与x轴交于点A，与y轴交于点B，∴点B(0，6)，点A(﹣3，0)，∴AO＝3，BO＝6，∵AB＝BC，BO⊥AC，∴AO＝CO＝3，∴点C(3，0)，设直线BC解析式为：y＝kx+b，则036k bb=+⎧⎨=⎩，解得：26kb=-⎧⎨=⎩，∴直线BC解析式为：y＝﹣2x+6；（2）如图1，过点P作PG⊥AC于点G，过点Q作HQ⊥AC于点H，∵点Q横坐标为m，∴点Q(m，﹣2m+6)，∵AB＝CB，∴∠BAC＝∠BCA＝∠HCQ，又∵∠PGA＝∠QHC＝90°，AP＝CQ，∴△PGA≌△QHC（AAS），∴PG＝HQ＝2m﹣6，∴点P的纵坐标为：2m﹣6，∵直线AB的表达式为：y＝2x+6，∴2m﹣6＝2x+6，解得：x＝m﹣6，∴点P(m﹣6，2m﹣6)；（3）如图2，连接AM，CM，过点P作PE⊥AC于点E，∵AB＝BC，BO⊥AC，∴BO是AC的垂直平分线，∴AM＝CM，且AP＝CQ，PM＝MQ，∴△APM≌△CQM（SSS）∴∠PAM＝∠MCQ，∠BQM＝∠APM＝45°，∵AM＝CM，AB＝BC，BM＝BM，∴△ABM≌△CBM（SSS）∴∠BAM＝∠BCM，∴∠BCM＝∠MCQ，且∠BCM+∠MCQ＝180°，∴∠BCM＝∠MCQ＝∠PAM＝90°，且∠APM＝45°，∴∠APM＝∠AMP＝45°，∴AP＝AM，∵∠PAO+∠MAO＝90°，∠MAO+∠AMO＝90°，∴∠PAO＝∠AMO，且∠PEA＝∠AOM＝90°，AM＝AP，∴△APE≌△MAO（AAS）∴AE＝OM，PE＝AO＝3，∴2m﹣6＝3，∴m＝92，∴Q(92，﹣3)，P(﹣32，3)，设直线PQ的解析式为：y＝ax+c，∴932332a ca c⎧-=+⎪⎪⎨⎪=-+⎪⎩，解得：132ac=-⎧⎪⎨=⎪⎩，∴直线PQ的解析式为：y＝﹣x+32．【点睛】本题主要考查三角形全等的判定和性质定理，等腰直角三角形的性质定理以及一次函数的图象和性质，添加辅助线，构造全等三角形，是解题的关键．。

(2019秋)北师大版八年级上册期末压轴题系列专题练习(有答案)-(数学)-精编.doc

图3EDBA图2EDBA图1EDCBA北师大版八年级上册期末压轴题系列11、如图，已知：点D 是△ABC 的边BC 上一动点，且AB =AC ，DA =DE ，∠BAC =∠ADE =α. ⑴如图1，当α=60°时，∠BCE = ；⑵如图2，当α=90°时，试判断∠BCE 的度数是否发生改变，若变化，请指出其变化范围；若不变化，请求出其值，并给出证明；（图1）（图2）（图3）⑶如图3，当α=120°时，则∠BCE = ；2、如图1，在平面直角坐标系xoy 中，直线6y x =+与x 轴交于A ，与y 轴交于B ，BC ⊥AB 交x 轴于C 。

①求△ABC 的面积。

如图2，②D 为OA 延长线上一动点，以BD 为直角边做等腰直角三角形BDE ，连结EA .求直线EA 的解析式.③点E 是y 轴正半轴上一点，且∠OAE 是线段AO 上一动点，是判断是否存在这样的点M 、N ，使得OM +NM 其最小值，并加以说明.3. 如图，直线1l 与x 轴、y 轴分别交于A 、B 两点，直线2l 与直线1l 关于x 轴对称，已知直线1l的解析式为3y x =+，（1）求直线2l 的解析式；（2）过A 点在△ABC 的外部作一条直线3l ，过点B 作BE ⊥3l 于E,过点C 作CF ⊥3l 于F 分别，请画出图形并求证：BE ＋CF ＝EF（3）△ABC 沿y 轴向下平移，AB 边交x 轴于点P ，过P 点的直线与AC 边的延长线相交于点Q ，与y 轴相交与点M ，且BP ＝CQ ，在△ABC 平移的过程中，①OM 为定值；②MC 为定值。

在这两个结论中，有且只有一个是正确的，请找出正确的结论，并求出其值。

4. 如图①，直线AB 与x 轴负半轴、y 轴正半轴分别交于A 、B 两点.OA 、OB 的长度分别为a 和b ，且满足2220a ab b -+=. ⑴判断△AOB 的形状.CBAxy QM PCB Axy ①⑵如图②，正比例函数(0)y kx k =<的图象与直线AB 交于点Q ，过A 、B 两点分别作AM ⊥OQ 于M ，BN ⊥OQ 于N ，若AM=9，BN=4，求MN 的长.⑶如图③，E 为AB 上一动点，以AE 为斜边作等腰直角△ADE ，P 为BE 的中点，连结PD 、PO ，试问：线段PD 、PO 是否存在某种确定的数量关系和位置关系？写出你的结论并证明.5、如图，已知△ABC 和△ADC 是以AC 为公共底边的等腰三角形，E 、F 分别在AD 和CD 上，已知：∠ADC+∠ABC=180°，∠ABC=2∠EBF ；（1）求证：EF=AE+FC （2）若点E 、F 在直线AD 和BD 上，则是否有类似的结论？OQ NMyxBA②OPy xE DBA③EDCBAFEDCBAF6、操作：如图①，△ABC 是正三角形，△BDC 是顶角∠BDC=120°的等腰三角形，以D 为顶点作一个60°角，角两边分别交AB ，AC 边于M ，N 两点，连接MN ．（1）探究线段BM 、MN 、NC 之间的关系，并加以证明；（2）若点M 、N 分别是射线AB 、CA 上的点，其它条件不变，请你再探线段BM ，MN ，NC 之间的关系，在图④中画出图形，并说明理由．（3）求证：CN-BM=MN北师大版八年级上册期末压轴题5答案; 1、⑴如图1，当α=60°时，∠BCE =120°；⑵证明：如图，过D 作DF ⊥BC ，交CA 或延长线于F 。

北师大版八年级(上)期末数学压轴题系列专题练习(含答案)

图3EDBA图2EDCBA图1EDCBA2018-2019学年北师大版八年级数学（上）八年级数学期末试题北师大版八年级上册期末压轴题系列11、如图，已知：点D 是△ABC 的边BC 上一动点，且AB =AC ，DA =DE ，∠BAC =∠ADE =α.⑴如图1，当α=60°时，∠BCE = ；⑵如图2，当α=90°时，试判断∠BCE 的度数是否发生改变，若变化，请指出其变化范围；若不变化，请求出其值，并给出证明；（图1）（图2）（图3）⑶如图3，当α=120°时，则∠BCE = ；2、如图1，在平面直角坐标系xoy 中，直线6y x =+与x 轴交于A ，与y 轴交于B ，BC ⊥AB 交x 轴于C 。

①求△ABC 的面积。

如图2，②D 为OA 延长线上一动点，以BD 为直角边做等腰直角三角形BDE ，连结EA .求直线EA 的解析式.③点E 是y 轴正半轴上一点，且∠OAE =30°，上一动点，是判断是否存在这样的点M 、N ，使得OM +NM 的值最小，若存在，请写出其最小值，并加以说明.3. 如图，直线1l 与x 轴、y 轴分别交于A 、B 两点，直线2l 与直线1l 关于x 轴对称，已知直线1l 的解析式为3y x =+，（1）求直线2l 的解析式；（2）过A 点在△ABC 的外部作一条直线3l ，过点B 作BE ⊥3l 于E ,过点C 作CF ⊥3l 于F 分别，请画出图形并求证：BE ＋CF ＝EF（3）△ABC 沿y 轴向下平移，AB 边交x 轴于点P ，过P 点的直线与AC 边的延长线相交于点Q ，与y 轴相交与点M ，且BP ＝CQ ，在△ABC 平移的过程中，①OM 为定值；②MC 为定值。

在这两个结论中，有且只有一个是正确的，请找出正确的结论，并求出其值。

4. 如图①，直线AB 与x 轴负半轴、y 轴正半轴分别交于A 、B 两点.OA 、OB 的长度分别为a 和b ，且满足2220a ab b -+=.⑴判断△AOB 的形状.⑵如图②，正比例函数(0)y kx k =<的图象与直线AB 交于点Q ，过A 、B 两点分别作AM ⊥OQ 于M ，BN ⊥OQ 于N ，若AM =9，BN =4，求MN 的长.⑶如图③，E 为AB 上一动点，以AE 为斜边作等腰直角△ADE ，P 为BE 的中点，连结PD 、PO ，试问：线段PD 、PO 是否存在某种确定的数量关系和位置关系？写出你的结论并证明.①OQ NMyxBA②OPy xE DBA③5、如图，已知△ABC 和△ADC是以AC为公共底边的等腰三角形，E、F分别在AD和CD上，已知：∠ADC+∠ABC=180°，∠ABC=2∠EBF；（1）求证：EF=AE+FC（2）若点E、F在直线AD和BD上，则是否有类似的结论？6、操作：如图①，△ABC是正三角形，△BDC是顶角∠BDC=120°的等腰三角形，以D为顶点作一个60°角，角两边分别交AB，AC边于M，N两点，连接MN．（1）探究线段BM、MN、NC之间的关系，并加以证明；（2）若点M、N分别是射线AB、CA上的点，其它条件不变，请你再探线段BM，MN，NC之间的关系，在图④中画出图形，并说明理由．（3）求证：CN-BM=MN图①图②图③图④EDCBAF北师大版八年级上册期末压轴题5答案; 1、⑴如图1，当α=60°时，∠BCE =120°；⑵证明：如图，过D 作DF ⊥BC ，交CA 或延长线于F 。

2019-2020武汉市各区八年级上学期期末考试压轴题汇总

2019-2020年武汉市各区八年级上学期期末考试压轴题汇总1、（汉阳区第9题）如图，△ACB 和△ECD 都是等腰直角三角形，CA =CB =6，CE =CD ，△ACB 的顶点A 在△ECD 的斜边DE 上，若AE :AD =1:2，则两个三角形重叠的部分面积为（） A. 6 B. 9 C. 12 D. 14M =1+a a＋2、（汉阳区第10题）已知a ，b 为实数,且满足a ≠-1，b ≠-1，设1+b b ，N =11+a ＋11+b . ①若ab ＝1时，M =N ；②若ab>1时，M>N③若ab <1时， M <N ；④若a ＋b ＝0时，M ·N ≤0 则上述四个结论正确的有（）个A. 1B. 2C. 3D. 43、（汉阳区第16题）.如图，在△ABC 中，∠CAB ＝30°，∠ACB ＝90°，AC ＝3，D 为AB 的中点，E 为线段AC 上任意一点（不与端点重合），当E 点在线段AC 上运动时，则DE ＋21CE 的最小值为 .4、（汉阳区第23题）（本题10分）如图，在等边△ABC 中,点D ，E 分别是AC ，AB 上的动点，且AE ＝CD ，BD 交CE 于点P . （1）如图1，求证：∠BPC ＝120°；（2）点M 是边BC 的中点，连接P A ，PM .①如图2，若点A ，P ，M 三点共线，则AP 与PM 的数量关系是；②若点A ，P ，M 三点不共线，问①中的结论还成立么？若成立，请给出证明，若不成立，请说明理由.5、（汉阳区第24题）（本题12分）已知△ABC 中，如果过顶点B 的一条直线把这个三角形分割成两个三角形，其中一个为等腰三角形，另一个为直角三角形，则称这条直线为△ABC 的关于点B 的二分割线.例如：如图1，Rt △ABC 中,∠A ＝90°，∠C ＝20°，过顶点B 的一条直线BD 交AC 于点D ，若∠DBC ＝20°，显然直线BD 是△ABC 的关于点B 的二分割线.（1）在图2的△ABC中，∠C＝20°，∠ABC＝110°.请在图2中画出△ABC的关于点B的二分割线，且∠DBC的度数是；（2）已知∠C＝20°，在图3中画出不同于图1，图2的△ABC，所画△ABC同时满足：①∠C为最小角；②存在关于点B的二分割线，∠BAC的度数是；（3）已知∠C＝α，△ABC同时满足：①∠C为最小角；②存在关于点B的二分割线，请求出∠BAC的度数（用α表示）6、（洪山区第10题）如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点.若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为( )A.6B.8C.10D.127、（洪山区第16题）四边形ABCD中,∠BAD=125°,∠B=∠D=90°,在BC、CD上分别找一点M、N,当三角形AM周长最小时,∠MAN的度数为 .8、（洪山区第23题）(1)如图1,已知△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.求证:DE=BD+CE.(2)如图2,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC,求证:DE=BD+CE.(3)拓展与应用:如图3,D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC 平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,求证:△DEF为等边三角形.9、（洪山区第24题）已知△ABC 中,∠ACB =90°,(1)如图1,点B 与点D 关于直线AC 对称,连AD,点E 、F 分别是线段CD 、AB 上的点(点E 不与点D 、C 重合),且∠AEF=∠ABC,∠ABC=2∠CAE.求证:BF=DE.(2)如图2:若AC=BC,BD⊥AD,连DC,求证:∠ADC=45°.(3)如图3,若AC=BC,点D 在AB 的延长线上,以DC 为斜边作等腰直角△DCE,过直角顶点E 作EF⊥AC 于F,求证:点F 是AC 的中点.10、(黄陂区第10题) 如图,在Rt△ABC 中,∠A=90°,点D 在AB 边上,点E 在AC 边上,满足∠CDE=45°，∠AED=∠B,若DE=1,BC=7,则△CDE 的面积为（）(A) 2 (B) 3 (C) 4 (D) 511、(黄陂区第16题) 如图,在平面直角坐标系中,点A(4,0),将点A 绕平面内一点P 顺时针旋转60°至点B(1,m),若1≤m≤5,则符合条件的点P的路径长为ABCE D12、(黄陂区第23题) (本题10分)如图，等边△ABC 外有一点D ，连接DA,DB,DC ， (1)如图1，若∠DAB+∠DCB=180°，求证:BD 平分∠ADC； (2)如图2，若∠BDC=60°，求证:BDCD=AD; (3)如图3，延长AD 交BC 的延长线于点F ，以BF 为边向下作等边△BEF,若点D,C,在同一直线上,且∠ABD=a,直接写出∠CEF 的度数为(结(结果用含a 的式子表示).13、(黄陂区第24题) (本题12分)如图，在平面直角坐标系中,点A(0,a),B(b,0)，且a ，b 满足2a 2+2ab+b 2-8a+16=0，点P 为AB 上一个动点(不与A,B)重合)，连接OP. (1)直接写出a= ，b= ；(2)如图1，过点P 作OP 的垂线交过点A 平行于x 轴的直线于点C,若点P(-,n)，求点C 的坐标; (3)如图2，以OP 为斜边在OP 右侧作等腰Rt△OPD，PD=OD.连接BD,当点P 从 B 向A 运动过程中,△BOD 的面积是否发生变化,请判断并说明理由.14、（武昌区第10题）如图，∠BAC =90°,AB=AC=4√2,BE=√2,DE=2a,∠BDE=15°,点P 在线段AE上,PD=DE,△ADQ 是等边三角形,连PQ 交AC 于点F,则PF 的长为第10题图B15、（武昌区第16题）如图,△ABC中,∠ACB=60°,∠A=40°,CE⊥AB,CD 平分∠ACB,F 为AB 的中点，若AC=a,BD=b,则EF= (用含a,b 的式子表示).16、（武昌区第23题）(本题满分10分)已知等边△ABC 和等腰△CDE,CD=DE,∠CDE=120°.(1)如图1,点D 在BC 上,点E 在AB 上,P 是BE 的中点,连接AD,PD,则线段AD 与PD 之间的数量关系为 ; (2)如图2,点D 在△ABC 内部,点E 在△ABC 外部,P 是BE 的中点,连接AD,PD,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由；(3)如图3,若点D 在△ABC 内部,点E 和点B 重合,点P 在BC 下方,且PB+PC 为定值,当PD 最大时,∠BPC 的度数为 .17、（武昌区第24题）(本题满分12分)已知△ABC,AB=AC. (1)若∠BAC90°,作△BCE,点A 在△BCE 内.①如图1,延长CA 交BE 于点D,若∠EBC=75°,BD =2DE,则∠DCE 的度数为 ; ②如图2,DF 垂直平分BE,点A 在DF 上,AD AF= √3,求S △ABD : S △AFC 的值;(2)如图3,若∠BAC=120°,点E 在AC 边上,∠EBC=10°,点D 在BC 边上,连接DE,AD,∠CAD=40°,求∠BED 的度数.图1图2图3图1图2图3第16题图18、（东湖高新第10题）△ABC 中,∠C=2∠B=60°,AE 是中线,AD 是角平分线,AF 是高,则下列4个结论中正确是( )①S △ABE =S △ACE ②∠EAD=∠FAD=15° ③AE=BE=CE=AC ④S △A BD :S △ACD =BD:DC=AB:AC A. ①②③ B. ①②④ C. ①②③④ D. ②③④ 19、（东湖高新第16题）如图,等腰直角△ABC 中,AC=BC,∠ACB=90°,D 为BC 中点,AD=4,P 为AB 上一个动点,当P 点运动时,PC+PD 的最小值为20、（东湖高新第23题）(本题10分)(1)如图1,AB=AD,AE=AC,∠BAD=∠EAC,求证:BE=CD(2)如图2,△ACE 是等边三角形,P 为三角形外一点,∠APC=120°,求证:PA+PC=PE (3)如图3,若∠ACE=∠AEC=∠ADC=45°,∠ACD -∠AED=60°,DC=3,求DE 长21、（东湖高新第24题）(本题12分)如图,A(0,2),B(m,0)为x 轴上一个动点,AB=BC,∠ABC=90°， (1)如图1,当m=1,且A 、B 、C 按逆时针方向排列,求C 点坐标(2)如图2,若A 、B 、C 按顺时针方向排列,E(-2,0),连CE 交y 轴于F,求证:OE=OF(3)如图3,若D 、B 两点关于直线AC 的对称点,画出图形并用含m 的式子表示△OBD 的面积S △OBD图1图2图3x图1x图2x图3第10题图22、（硚口区第10题）如图,在Rt△ABC 中,∠ACB=90°,点D 在AB 上,连接CD,将△BCD 沿直线CD 翻折后,点B 恰好落在边AC 的E 点处,若CE:AE=5:3,S△ABC=20,则点D 到AC 的距离是（） A. 4013 B. 2013 C.4 D.323、（硚口区第16题）问题背景:如图1,点C 为线段AB 外一动点,且AB=AC=2,若BC=CD,∠BCD=60°,连接AD,求AD 的最大值.解决方法:以AC 为边作等边△ACE,连接BE,推出BE=AD,当点E 在BA 的延长线上时,线段AD 取得最大值4.问题解决:如图2,点C 为线段AB 外一动点,且AB=AC=2,若BC=CD,∠BCD=90°,连接AD,当AD 取得最大值时,∠ACD 的度数为 .24、（硚口区第23题）(本题10分)在等边△ABC 中,点E,F 分别在边AB,BC 上. (1)如图1,若AE=BF,以AC 为边作等边△ACD,AF 交CE 于点O,连接OD. 求证:①AF=CE;②OD 平分∠AOC(2)如图2,若AE=2CF,作∠BCP=∠AEC,CP 交AF 的延长线于点P,求证:CE=CP.图1EDCBA 图2CBDA图2图1CO DCABBAPE F EF25、（硚口区第24题）(本题12分)在Rt△ABC 中,AC=BC,∠ACB=90°,点D 是BC 上一点. (1)如图1,AD 平分∠BAC,求证:AB=AC+CD;(2)如图2,点E 在线段AD 上,且∠CED=45°,∠BED=30°,求证:BE=2AE;(3)如图3,CD=BD,过B 点作BM⊥AD 交AD 的延长线于点M,连接CM,过C 点作CN⊥CM 交AD 于N,求证:DN=3DM.26、（江夏区第16题）如图,△ABC 是等边三角形,点P 是AB 的中点,点M 在CB 的延长线上,点N 在AC 上且满足∠MPN=120°,已知△ABC 的周长为18,设t=2AC-CM-CN,若关于x 的方程2x+nx−2 = t 的解是正数,则n 的取值范围是 . 27、（江夏区第22题）(本题10分) 已知:等边△ABC 中.(1)如图1,点M 是BC 的中点,点N 在AB 边上,满足∠AMN=60°,求AN BN的值.(2)如图2,点M 在AB 边上(M 为非中点,不与A 、B 重合),点N 在CB 的延长线上且∠MNB=∠MCB,求证:AM=BN. (3)如图3,点P 为AC 边的中点,点E 在AB 的延长线上,点F 在BC 的延长线上,满足∠AEP=∠PFC,求BF−BE BC的值.图3图2图1第16题图28、（江夏区第24题）(本题12分)已知点A 在x 轴正半轴上,以OA 为边作等边△OAB,A(x,0),其中x是方程32−13x−1=226x−2的解.(1)求点A 的坐标.(2)如图1,点C 在y 轴正半轴上,以AC 为边在第一象限内作等边△ACD,连DB 并延长交y 轴于点E,求∠BEO 的度数.(3)如图2,若点F 为x 轴正半轴上一动点,点F 在点A 的右边,连FB,以FB 为边在第一象限内作等边△FBG,连GA 并延长交y 轴于点H,当点F 运动时,GH-AF 的值是否发生变化?若不变,求其值;若变化,求出其变化的范围.29、（青山区第16题）如图,在△ABC 中,AB=AC,点D 和点A 在直线BC 的同侧,BD=BC,∠BAC=82°,∠DBC=38°,连接AD 、CD,则∠ADB 的度数为。

八年级数学压轴题期末复习试卷测试卷附答案

八年级数学压轴题期末复习试卷测试卷附答案一、压轴题1．如图，以直角三角形AOC的直角顶点O为原点，以OC，OA所在直线为轴和轴建立平-+-=．面直角坐标系，点A（0，a），C（b，0）满足a6b80（1）a= ；b= ；直角三角形AOC的面积为．（2）已知坐标轴上有两动点P，Q同时出发，P点从C点出发以每秒2个单位长度的速度向点O匀速移动，Q点从O点出发以每秒1个单位长度的速度向点A匀速移动，点P到达O点整个运动随之结束．AC的中点D的坐标是（4，3），设运动时间为t秒．问：是否存在这样的t，使得△ODP与△ODQ的面积相等？若存在，请求出t的值；若不存在，请说明理由．（3）在（2）的条件下，若∠DOC=∠D CO，点G是第二象限中一点，并且y轴平分∠GOD．点E是线段OA上一动点，连接接CE交OD于点H，当点E在线段OA上运动的过程中，探究∠GOD，∠OHC，∠ACE之间的数量关系，并证明你的结论(三角形的内角和为180)．2．已知ABC是等腰直角三角形，∠C=90°，点M是AC的中点，延长BM至点D，使DM ＝BM，连接AD．（1）如图①，求证：DAM≌BCM；（2）已知点N是BC的中点，连接AN．①如图②，求证：ACN≌BCM；②如图③，延长NA至点E，使AE＝NA，连接，求证：BD⊥DE．3．如图，已知A(3，0)，B(0，-1)，连接AB，过B点作AB的垂线段BC，使BA=BC，连接AC（1）如图1，求C点坐标；（2）如图2，若P点从A点出发沿x轴向左平移，连接BP，作等腰直角BPQ，连接CQ，当点P在线段OA上，求证：PA=CQ；（3）在（2）的条件下若C、P，Q三点共线，直接写出此时∠APB的度数及P点坐标4．如图，在平面直角坐标系中，直线y＝﹣34x+m分别与x轴、y轴交于点B、A．其中B点坐标为（12，0），直线y＝38x与直线AB相交于点C．（1）求点A的坐标．（2）求△BOC的面积．（3）点D为直线AB上的一个动点，过点D作y轴的平行线DE，DE与直线OC交于点E （点D与点E不重合）．设点D的横坐标为t，线段DE长度为d．①求d与t的函数解析式（写出自变量的取值范围）．②当动点D在线段AC上运动时，以DE为边在DE的左侧作正方形DEPQ，若以点H（12，t）、G（1，t）为端点的线段与正方形DEPQ的边只有一个交点时，请直接写出t的取值范围．5．如图，在平面直角坐标系中，直线y＝2x＋4与x轴交于点A，与y轴交于点B，过点B 的另一条直线交x轴正半轴于点C，且OC＝3．图1 图2 （1）求直线BC 的解析式；（2）如图1，若M 为线段BC 上一点，且满足S △AMB ＝S △AOB ，请求出点M 的坐标；（3）如图2，设点F 为线段AB 中点，点G 为y 轴上一动点，连接FG ，以FG 为边向FG 右侧作正方形FGQP ，在G 点的运动过程中，当顶点Q 落在直线BC 上时，求点G 的坐标；6．在平面直角坐标系xOy 中，对于点(,)P a b 和点(,)Q a b '，给出如下定义：若1,(2),(2)b a b b a -≥⎧=<⎩'⎨当时当时，则称点Q 为点P 的限变点．例如:点(2,3)的限变点的坐标是(2,2)，点(2,5)--的限变点的坐标是(2,5)-，点(1,3)的限变点的坐标是(1,3)．（1）①点3,1)-的限变点的坐标是________；②如图1，在点(2,1)A -、(2,1)B 中有一个点是直线2y =上某一个点的限变点，这个点是________；（填“A ”或“B ”）（2）如图2，已知点(2,2)C --，点(2,2)D -，若点P 在射线OC 和OD 上，其限变点Q 的纵坐标b '的取值范围是b m '≥或b n '≤，其中m n >．令s m n =-，直接写出s 的值．（3）如图3，若点P 在线段EF 上，点(2,5)E --，点(,3)F k k -，其限变点Q 的纵坐标b '的取值范围是25b '-≤≤，直接写出k 的取值范围．7．(1)问题发现：如图1，△ACB 和△DCE 均为等边三角形，点A 、D 、E 在同一直线上，连接BE ．①请直接写出∠AEB 的度数为_____；②试猜想线段AD 与线段BE 有怎样的数量关系，并证明；(2)拓展探究：图2， △ACB 和△DCE 均为等腰三角形，∠ACB ＝∠DCE ＝90°，点A 、D 、E 在同－直线上， CM 为△DCE 中DE 边上的高，连接BE ，请判断∠AEB 的度数线段CM 、AE 、BE 之间的数量关系，并说明理由．8．如图所示，在平面直角坐标系xOy 中，已知点A 的坐标(3,2)-，过A 点作AB x ⊥轴，垂足为点B ，过点(2,0)C 作直线l x ⊥轴，点P 从点B 出发在x 轴上沿着轴的正方向运动．（1）当点P 运动到点O 处，过点P 作AP 的垂线交直线l 于点D ，证明AP DP =，并求此时点D 的坐标；（2）点Q 是直线l 上的动点，问是否存在点P ，使得以P C Q 、、为顶点的三角形和ABP ∆全等，若存在求点P 的坐标以及此时对应的点Q 的坐标，若不存在，请说明理由．9．（1）填空①把一张长方形的纸片按如图①所示的方式折叠，EM ，FM 为折痕，折叠后的C 点落在1B M 或1B M 的延长线上，那么EMF ∠的度数是________；②把一张长方形的纸片按如图②所示的方式折叠，B 点与M 点重合，EM ，FM 为折痕，折叠后的C 点落在1A M 或1A M 的延长线上，那么EMF ∠的度数是_______．（2）解答：①把一张长方形的纸片按如图③所示的方式折叠，EM ，FM 为折痕，折叠后的C 点落在1B M 或1B M 的延长线上左侧，且80EMF ∠=︒，求11C MB ∠的度数； ②把一张长方形的纸片按如图④所示的方式折叠，B 点与M 点重合，EM ，FM 为折痕，折叠后的C 点落在1A M 或1A M 的延长线右侧，且60EMF ∠=︒，求11C MA ∠的度数．（3）探究：把一张四边形的纸片按如图⑤所示的方式折叠，EB ，FB 为折痕，设ABC α∠=︒，EBF β∠=︒，11A BC γ∠=︒，求α，β，γ之间的数量关系．10．直角三角形ABC 中，90ACB ∠=︒，直线l 过点C ．（1）当AC BC =时，如图1，分别过点A 和B 作AD ⊥直线l 于点D ，BE ⊥直线l 于点E ，ACD 与CBE △是否全等，并说明理由；（2）当8AC cm =，6BC cm =时，如图2，点B 与点F 关于直线l 对称，连接BF CF 、，点M 是AC 上一点，点N 是CF 上一点，分别过点M N 、作MD ⊥直线l 于点D ，NE ⊥直线l 于点E ，点M 从A 点出发，以每秒1cm 的速度沿A C →路径运动，终点为C ，点N 从点F 出发，以每秒3cm 的速度沿F C B C F →→→→路径运动，终点为F ，点,M N 同时开始运动，各自达到相应的终点时停止运动，设运动时间为t 秒，当CMN △为等腰直角三角形时，求t 的值．11．如图，四边形ABCD 是直角梯形，AD ∥BC ，AB ⊥AD ，且AB ＝AD +BC ，E 是DC 的中点，连结BE 并延长交AD 的延长线于G ．（1）求证：DG＝BC；（2）F是AB边上的动点，当F点在什么位置时，FD∥BG；说明理由．（3）在（2）的条件下，连结AE交FD于H，FH与HD长度关系如何？说明理由．12．在等腰Rt△ABC中，AB＝AC，∠BAC＝90°（1）如图1，D，E是等腰Rt△ABC斜边BC上两动点，且∠DAE＝45°，将△ABE绕点A逆时针旋转90后，得到△AFC，连接DF①求证：△AED≌△AFD；②当BE＝3，CE＝7时，求DE的长；（2）如图2，点D是等腰Rt△ABC斜边BC所在直线上的一动点，连接AD，以点A为直角顶点作等腰Rt△ADE，当BD＝3，BC＝9时，求DE的长．【参考答案】***试卷处理标记，请不要删除一、压轴题t=时，使得△ODP与△ODQ的面积相等；（3）1．（1）6；8；24；（2）存在 2.4∠GOD+∠ACE=∠OHC，见解析【解析】【分析】（1）利用非负性即可求出a，b即可得出结论,即可求出△ABC的面积；（2）先表示出OQ，OP，利用那个面积相等，建立方程求解即可得出结论；（3）先判断出∠OAC=∠AOD，进而判断出OG∥AC，即可判断出∠FHC=∠ACE，同理∠FHO=∠GOD，即可得出结论．【详解】--=，解：(1) 解：（1）∵a6b80∴a-6=0，b-8=0，∴a=6，b=8， ∴A （0，6），C （8，0）；∴S △ABC=6×8÷2=24,故答案为（0，6），（8，0）； 6；8；24(2) ∵114222ODQ D S OQ x t t ∆=⋅=⋅⋅= 11(82)312322ODP D S OP y t t ∆=⋅=⋅-⋅=- 由2123t t =-时, 2.4t =∴存在 2.4t =时,使得△ODP 与△ODQ 的面积相等(3) ）∴2∠GOA+∠ACE=∠OHC ，理由如下：∵x 轴⊥y 轴，∴∠AOC=∠DOC+∠AOD=90°∴∠OAC+∠ACO=90°又∵∠DOC=∠DCO∴∠OAC=∠AOD∵y 轴平分∠GOD∴∠GOA=∠AOD∴∠GOA=∠OAC∴OG ∥AC ，如图，过点H 作HF ∥OG 交x 轴于F ，∴HF ∥AC∴∠FHC=∠ACE同理∠FHO=∠GOD ，∵OG ∥FH ，∴∠GOD=∠FHO ，∴∠GOD+∠ACE=∠FHO+∠FHC即∠GOD+∠ACE=∠OHC ，∴2∠GOA+∠ACE=∠OHC ．∴∠GOD+∠ACE=∠OHC ．【点睛】此题是三角形综合题，主要考查了非负性的性质，三角形的面积公式，角平分线的定义，平行线的性质，正确作出辅助线是解本题的关键．2．（1）见解析；（2）①见解析；②见解析【解析】【分析】（1）由点M 是AC 中点知AM=CM ，结合∠AMD=∠CMB 和DM=BM 即可得证；（2）①由点M，N分别是AC，BC的中点及AC=BC可得CM=CN，结合∠C=∠C和BC=AC 即可得证；②取AD中点F，连接EF，先证△EAF≌△ANC得∠NAC=∠AEF，∠C=∠AFE=90°，据此知∠AFE=∠DFE=90°，再证△AFE≌△DFE得∠EAD=∠EDA=∠ANC，从而由∠EDB=∠EDA+∠ADB=∠EAD+∠NAC=180°-∠DAM即可得证．【详解】解：（1）∵点M是AC中点，∴AM=CM，在△DAM和△BCM中，∵AM CMAMD CMBDM BM=⎧⎪∠=∠⎨⎪=⎩，∴△DAM≌△BCM（SAS）；（2）①∵点M是AC中点，点N是BC中点，∴CM=12AC，CN=12BC，∵△ABC是等腰直角三角形，∴AC=BC，∴CM=CN，在△BCM和△ACN中，∵CM CNC CBC AC=⎧⎪∠=∠⎨⎪=⎩，∴△BCM≌△ACN（SAS）；②证明：取AD中点F，连接EF，则AD=2AF，∵△BCM≌△ACN，∴AN=BM，∠CBM=∠CAN，∵△DAM≌△BCM，∴∠CBM=∠ADM，AD=BC=2CN，∴AF=CN，∴∠DAC=∠C=90°，∠ADM=∠CBM=∠NAC，由（1）知，△DAM≌△BCM，∴∠DBC=∠ADB ，∴AD ∥BC ，∴∠EAF=∠ANC ，在△EAF 和△ANC 中，AE AN EAF ANC AF NC =⎧⎪∠=∠⎨⎪=⎩，∴△EAF ≌△ANC （SAS ），∴∠NAC=∠AEF ，∠C=∠AFE=90°，∴∠AFE=∠DFE=90°，∵F 为AD 中点，∴AF=DF ，在△AFE 和△DFE 中，AF DF AFE DFE EF EF =⎧⎪∠=∠⎨⎪=⎩，∴△AFE ≌△DFE （SAS ），∴∠EAD=∠EDA=∠ANC ，∴∠EDB=∠EDA+∠ADB=∠EAD+∠NAC=180°-∠DAM=180°-90°=90°，∴BD ⊥DE ．【点睛】本题是三角形的综合问题，解题的关键是掌握中点的性质、等腰直角三角形的性质、全等三角形的判定与性质等知识点．3．（1）(1，-4)；（2）证明见解析；（3）()135,1,0APB P ︒∠= 【解析】【分析】（1）作CH ⊥y 轴于H ，证明△ABO ≌△BCH ，根据全等三角形的性质得到BH=OA=3，CH=OB=1，求出OH ，得到C 点坐标；（2）证明△PBA ≌△QBC ，根据全等三角形的性质得到PA=CQ ；（3）根据C 、P ，Q 三点共线，得到∠BQC=135°，根据全等三角形的性质得到∠BPA=∠BQC=135°，根据等腰三角形的性质求出OP ，得到P 点坐标．【详解】解：(1)作CH ⊥y 轴于H ，则∠BCH+∠CBH=90°，因为AB BC ⊥，所以.∠ABO+∠CBH=90°，所以∠ABO=∠BCH ，在△ABO 和△BCH 中，ABO BCH AOB BHC AB BC ∠=∠⎧⎪∠=∠⎨⎪=⎩ABO BCH ∴∆≅∆:BH=OA=3，CH=OB=1，:OH=OB+BH=4，所以C 点的坐标为（1，-4）；(2)因为∠PBQ=∠ABC=90°，,PBQ ABQ ABC ABQ PBA QBC ∴∠-=∠-∠∴∠=∠在△PBA 和△QBC 中，BP BQ PBA QBC BA BC =⎧⎪∠=∠⎨⎪=⎩PBA QBC ∴∆≅∆:.PA=CQ ；(3) ()135,1,0APB P ︒∠= BPQ ∆是等腰直角三角形，:所以∠BQP=45°，当C 、P ，Q 三点共线时，∠BQC=135°，由（2)可知，PBA QBC ∴∆≅∆；所以∠BPA=∠BQC=135°，所以∠OPB=45°，所以.OP=OB=1，所以P 点坐标为（1，0) ．【点睛】本题考查的是全等三角形的判定和性质、三角形的外角的性质，掌握全等三角形的判定定理和性质定理是解题的关键．4．（1）点A 坐标为（0，9）；（2）△BOC 的面积＝18；（3）①当t ＜8时，d ＝﹣98t+9，当t ＞8时，d ＝98t ﹣9；②12≤t≤1或7617≤t≤8017．【解析】【分析】（1）将点B 坐标代入解析式可求直线AB 解析式，即可求点A 坐标；（2）联立方程组可求点C 坐标，即可求解；（3）由题意列出不等式组，可求解．【详解】解：（1）∵直线y＝﹣34x+m与y轴交于点B（12，0），∴0＝﹣34×12+m，∴m＝9，∴直线AB的解析式为：y＝﹣34x+9，当x＝0时，y＝9，∴点A坐标为（0，9）；（2）由题意可得：38394y xy x⎧=⎪⎪⎨⎪=+⎪⎩，解得：83 xy=⎧⎨=⎩，∴点C（8，3），∴△BOC的面积＝12×12×3＝18；（3）①如图，∵点D的横坐标为t，∴点D（t，﹣34t+9），点E（t，38t），当t＜8时，d＝﹣34t+9﹣38t＝﹣98t+9，当t＞8时，d＝38t+34t﹣9＝98t﹣9；②∵以点H（12，t）、G（1，t）为端点的线段与正方形DEPQ的边只有一个交点，∴12≤t≤1或919829918t t t t ⎧-+≤-⎪⎪⎨⎪-+≥-⎪⎩， ∴12≤t≤1或7617≤t≤8017．【点睛】本题是一次函数综合题，考查了待定系数法求解析式，三角形的面积公式，不等式组的应用，灵活运用这些性质解决问题是本题的关键．5．（1）443y x =-+；（2）612(,)55M ；（3）23(0,)7G 或(0,-1)G 【解析】【分析】（1）求出点B ，C 坐标，再利用待定系数法即可解决问题；（2）结合图形，由S △AMB ＝S △AOB 分析出直线OM 平行于直线AB ，再利用两直线相交建立方程组求得交点M 的坐标；（3）分两种情形：①当n ＞2时，如图2-1中，点Q 落在BC 上时，过G 作直线平行于x 轴，过点F ，Q 作该直线的垂线，垂足分别为M ，N ．求出Q （n-2，n-1）．②当n ＜2时，如图2-2中，同法可得Q （2-n ，n+1），代入直线BC 的解析式解方程即可解决问题．【详解】解：（1）∵直线y=2x+4与x 轴交于点A ，与y 轴交于点B ，∴A （-2，0），B （0，4），，又∵OC=3，∴C （3，0），设直线BC 的解析式为y=kx+b ，将B 、C 的坐标代入得： 304k b b +=⎧⎨=⎩，解得：434k b ⎧=-⎪⎨⎪=⎩，∴直线BC 的解析式为443y x =-+；（2）连接OM ，∵S△AMB＝S△AOB，∴直线OM平行于直线AB，故设直线OM解析式为：2y x=,将直线OM的解析式与直线BC的解析式联立得方程组2443y xy x=⎧⎪⎨=-+⎪⎩，解得：65125xy⎧=⎪⎪⎨⎪=⎪⎩故点612(,)55M；（3）∵FA=FB，A（-2，0），B（0，4），∴F（-1，2），设G（0，n），①当n＞2时，如图2-1中，点Q落在BC上时，过G作直线平行于x轴，过点F，Q作该直线的垂线，垂足分别为M，N．∵四边形FGQP是正方形，易证△FMG≌△GNQ，∴MG=NQ=1，FM=GN=n-2，∴Q（n-2，n-1），∵点Q在直线443y x=-+上，∴41(2)43n n-=--+，∴23=7n , ∴23(0,)7G ． ②当n ＜2时，如图2-2中，同法可得Q （2-n ，n+1），∵点Q 在直线443y x =-+上， ∴4+1(2)43n n =--+， ∴n=-1， ∴(0,-1)G ．综上所述，满足条件的点G 坐标为23(0,)7G 或(0,-1)G 【点睛】本题属于一次函数综合题，考查了待定系数法，三角形的面积，全等三角形的判定和性质，正方形的性质等知识，解题的关键是学会用分类讨论的思想思考问题，学会添加常用辅助线，构造全等三角形解决问题，属于中考压轴题．6．（1）①()3,1；②B ；（2）3s =；（3）59k ≤≤．【解析】【分析】（1）利用限变点的定义直接解答即可；（2）先利用逆推原理求出限变点(2,1)A -、(2,1)B 对应的原来点坐标，然后把原来点坐标代入到2y =，满足解析式的就是答案；（3）先OC OD ，的关系式，再求出点P 的限变点Q 满足的关系式，然后根据图象求出m n ，的值，从而求出s 即可；（4）先求出线段EF 的关系式，再求出点P 的限变点Q 所满足的关系式，根据图像求解即可．【详解】解：（1）①∵32a =<，∴11b b ==-='，∴坐标为：()3,1，故答案为：()3,1； ②∵对于限变点来说，横坐标保持不变，∴限变点(2,1)A -对应的原来点的坐标为：()2,1-或()21--，，限变点(2,1)B 对应的原来点的坐标为：()2,2，∵()2,2满足2y =，∴这个点是B ，故答案为：B ；（2）∵点C 的坐标为(2,2)--，∴OC 的关系式为：()0y x x =≤，∵点D 的坐标为(2,2)-，∴OD 的关系式为：()0y x x =-≥，∴点P 满足的关系式为：()()00x x y x x ≤⎧⎪=⎨->⎪⎩， ∴点P 的限变点Q 的纵坐标满足的关系式为：当2x ≥时：1b x '=--，当02x <<时：b x x '=-=，当0x ≤时，b x x '==-，图像如下：通过图象可以得出：当2x ≥时，3b '≤-，∴3n =-，当2x <时，0b '≥，∴0m =，∴()033s m n =-=--=；（3）设线段EF 的关系式为：()022y ax c a x k k =+≠-≤≤>-，，，把(2,5)E --，(,3)F k k -代入得：253a c ka c k -+=-⎧⎨+=-⎩，解得：13a c =⎧⎨=-⎩， ∴线段EF 的关系式为()322y x x k k =--≤≤>-，， ∴线段EF 上的点P 的限变点Q 的纵坐标满足的关系式4(2)|3|3(22)x xb x x x -⎧'=⎨-=--<⎩，图象如下：当x ＝2时，b ′取最小值，b '＝2﹣4＝﹣2，当b '＝5时，x ﹣4＝5或﹣x +3＝5，解得：x ＝9或x ＝﹣2，当b ′＝1时，x ﹣4＝1，解得：x ＝5，∵ 25b '-≤≤，∴由图象可知，k 的取值范围时：59k ≤≤．【点睛】本题主要考查了一次函数的综合题，解答本题的关键是熟练掌握新定义“限变点”，解答此题还需要掌握一次函数的图象与性质以及最值的求解，此题有一定的难度．7．（1）①60°；②AD=BE.证明见解析；（2）∠AEB ＝90°；AE=2CM+BE ；理由见解析.【解析】【分析】（1）①由条件△ACB 和△DCE 均为等边三角形，易证△ACD ≌△BCE ，从而得到：AD=BE ，∠ADC=∠BEC ．由点A ，D ，E 在同一直线上可求出∠ADC ，从而可以求出∠AEB 的度数．②由△ACD ≌△BCE ，可得AD=BE ；（2）首先根据△ACB 和△DCE 均为等腰直角三角形，可得AC=BC ，CD=CE ，∠ACB=∠DCE=90°，据此判断出∠ACD=∠BCE ；然后根据全等三角形的判定方法，判断出△ACD ≌△BCE ，即可判断出BE=AD ，∠BEC=∠ADC ，进而判断出∠AEB 的度数为90°；根据DCE=90°，CD=CE ，CM ⊥DE ，可得CM=DM=EM ，所以DE=DM+EM=2CM ，据此判断出AE=BE+2CM ．【详解】（1）①∵∠ACB=∠DCE ，∠DCB=∠DCB ，∴∠ACD=∠BCE ，在△ACD 和△BCE 中，AC BC ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩, ∴△ACD ≌△BCE ，∴AD=BE ，∠CEB=∠ADC=180°−∠CDE=120°，∴∠AEB=∠CEB−∠CED=60°；②AD=BE.证明：∵△ACD ≌△BCE ，∴AD=BE ．（2）∠AEB ＝90°；AE=2CM+BE ；理由如下：∵△ACB 和△DCE 均为等腰直角三角形，∠ACB =∠DCE= 90°，∴AC = BC ， CD = CE ， ∠ACB =∠DCB =∠DCE －∠DCB ，即∠ACD = ∠BCE ，∴△ACD ≌△BCE ，∴AD = BE ，∠BEC = ∠ADC=135°．∴∠AEB =∠BEC －∠CED =135°－ 45°= 90°．在等腰直角△DCE 中，CM 为斜边DE 上的高，∴CM =DM= ME ，∴DE = 2CM ．∴AE = DE+AD=2CM+BE ．【点睛】本题考查了等边三角形的性质、等腰直角三角形的性质、三角形全等的判定与性质等知识，解题时需注意运用已有的知识和经验解决相似问题．8．（1）证明见解析；(2,3)D ；（2）存在，(0,0)P ，(2,3)Q 或(0,0)P ，(2,3)Q -或(4,0)P ，(2,7)Q 或(4,0)P ，(2,7)Q -或1(,0)2P -，(2,2)Q -或1(,0)2P -，(2,2)Q -．【解析】【分析】（1）通过全等三角形的判定定理ASA 证得△ABP ≌△PCD ，由全等三角形的对应边相等证得AP ＝DP ，DC ＝PB ＝3，易得点D 的坐标；（2）设P （a ，0），Q （2，b ）．需要分类讨论：①AB ＝PC ，BP ＝CQ ；②AB ＝CQ ，BP ＝PC ．结合两点间的距离公式列出方程组，通过解方程组求得a 、b 的值，得解．【详解】（1）AP PD ⊥90APB DPC ∴∠+∠=AB x ⊥轴90A APB ∴∠+∠=A DPC ∴∠=∠在ABP ∆和PCD ∆中A DPC AB PCABP PCD ∠=∠⎧⎪=⎨⎪∠=∠⎩()ABP PCD ASA ∴∆≅∆AP DP ∴=，3DC PB ==(2,3)D ∴（2）设(,0)P a ，(2,)Q b①AB PC =，BP CQ =223a a b ⎧-=⎪⎨+=⎪⎩，解得03a b =⎧⎨=±⎩或47a b =⎧⎨=±⎩ (0,0)P ∴，(2,3)Q 或(0,0)P ，(2,3)Q -或(4,0)P ，(2,7)Q 或(4,0)P ，(2,7)Q - ②AB CQ =，BP PC =，322a a b +=-⎧⎨=⎩，解得122a b ⎧=⎪⎨⎪=±⎩ 1(,0)2P ∴-，(2,2)Q -或1(,0)2P -，(2,2)Q - 综上：(0,0)P ，(2,3)Q 或(0,0)P ，(2,3)Q -或(4,0)P ，(2,7)Q 或(4,0)P ，(2,7)Q -或1(,0)2P -，(2,2)Q -或1(,0)2P -，(2,2)Q - 【点睛】考查了三角形综合题．涉及到了全等三角形的判定与性质，两点间的距离公式，一元一次绝对值方程组的解法等知识点．解答（2）题时，由于没有指明全等三角形的对应边（角），所以需要分类讨论，以防漏解．9．90︒，45︒；20︒，30︒；2a γβ+=，2a γβ-=.【解析】【分析】（1）①如图①知1112EMC BMC ∠=∠，1112C MF C MC ∠=∠得 ()1112EMF BMC C MC ∠=∠+∠可求出解.②由图②知111111,22EBA ABC C BF C BC ∠=∠∠=∠得()1112EBF ABC C BC ∠=∠+∠可求出解. （2）①由图③折叠知11,CMF FMC BME EMB ∠=∠∠=∠，可推出11()BMC EMF EMF C MB ∠-∠-∠=∠，即可求出解.②由图④中折叠知11,CMF C MF ABE A BE ∠=∠∠=∠，可推出()112906090AMC ︒︒︒-+∠=，即可求出解. （3）如图⑤-1、⑤-2中分别由折叠可知，a ββγ-=-、a ββγ-=+，即可求得 2a γβ+=、2a γβ-=.【详解】解：（1）①如图①中，1112EMC BMC ∠=∠，1112C MF C MC ∠=∠， ()1111111800229EMF EMC C MF BMC C MC ︒︒∴∠=∠+∠=∠⨯=+∠=，故答案为90︒. ②如图②中，111111,22EBA ABC C BF C BC ∠=∠∠=∠， ()111111904522EBF EBC C BF ABC C BC ︒︒∴∠=∠+∠=∠+∠=⨯=，故答案为45︒.（2）①如图③中由折叠可知，11,CMF FMC BME EMB ∠=∠∠=∠，1111C MF EMB EMF C MB ∠+∠-∠=∠，11CMF BME EMF C MB ∴∠+∠-∠=∠，11()BMC EMF EMF C MB ∴∠-∠-∠=∠，111808020C MB ︒︒︒∴-=∠=；②如图④中根据折叠可知，11,CMF C MF ABE A BE ∠=∠∠=∠，112290CMF ABE A MC ︒∠+∠+∠=，112()90CMF ABE A MC ︒∴∠+∠+∠=，()1129090EMF AMC ︒︒∴-∠+∠=，()112906090AMC ︒︒︒∴-+∠=， 1130A MC ︒∴∠=；（3）如图⑤-1中，由折叠可知，aββγ-=-，2aγβ∴+=；如图⑤-2中，由折叠可知，aββγ-=+，2aγβ∴-=.【点睛】本题考查了图形的变换中折叠属全等变换，图形的角度及边长不变及一些角度的计算问题，突出考查学生的观察能力、思维能力以及动手操作能力，本题是代数、几何知识的综合运用典型题目.10．（1）全等，理由见解析；（2）t=3.5秒或5秒【解析】【分析】（1）根据垂直的定义得到∠DAC=∠ECB，利用AAS定理证明△ACD≌△CBE；（2）分点F沿C→B路径运动和点F沿B→C路径运动两种情况，根据等腰三角形的定义列出算式，计算即可；【详解】解：（1）△ACD与△CBE全等．理由如下：∵AD⊥直线l，∴∠DAC+∠ACD=90°，∵∠ACB=90°，∴∠BCE+∠ACD=90°，∴∠DAC=∠ECB，在△ACD和△CBE中，ADC CEBDAC ECBCA CB∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△ACD≌△CBE（AAS）；（2）由题意得，AM=t，FN=3t，则CM=8-t，由折叠的性质可知，CF=CB=6，∴CN=6-3t，点N在BC上时，△CMN为等腰直角三角形，当点N沿C→B路径运动时，由题意得，8-t=3t-6，解得，t=3.5，当点N沿B→C路径运动时，由题意得，8-t=18-3t，解得，t=5，综上所述，当t=3.5秒或5秒时，△CMN为等腰直角三角形；【点睛】本题考查的是全等三角形的判定和性质，掌握全等三角形的判定定理和性质定理，灵活运用分情况讨论思想是解题的关键．11．（1）见解析；（2）当F运动到AF＝AD时，FD∥BG，理由见解析；（3）FH＝HD，理由见解析【解析】【分析】（1）证明△DEG≌△CEB（AAS）即可解决问题．（2）想办法证明∠AFD＝∠ABG＝45°可得结论．（3）结论：FH＝HD．利用等腰直角三角形的性质即可解决问题．【详解】（1）证明：∵AD∥BC，∴∠DGE＝∠CBE，∠GDE＝∠BCE，∵E是DC的中点，即DE＝CE，∴△DEG≌△CEB（AAS），∴DG＝BC；（2）解：当F运动到AF＝AD时，FD∥BG．理由：由（1）知DG＝BC，∵AB＝AD+BC，AF＝AD，∴BF＝BC＝DG，∴AB＝AG，∵∠BAG＝90°，∴∠AFD＝∠ABG＝45°，∴FD∥BG，故答案为：F运动到AF＝AD时，FD∥BG；（3）解：结论：FH＝HD．理由：由（1）知GE＝BE，又由（2）知△ABG为等腰直角三角形，所以AE⊥BG，∵FD∥BG，∴AE⊥FD，∵△AFD为等腰直角三角形，∴FH＝HD，故答案为：FH＝HD．【点睛】本题考查了全等三角形的判定和性质，平行线的判定，等腰直角三角形的性质，掌握三角形全等的判定和性质是解题的关键．12．（1）①见解析；②DE＝297；（2）DE的值为517【解析】【分析】（1）①先证明∠DAE＝∠DAF，结合DA＝DA，AE＝AF，即可证明；②如图1中，设DE＝x，则CD＝7﹣x．在Rt△DCF中，由DF2＝CD2+CF2，CF＝BE＝3，可得x2＝（7﹣x）2+32，解方程即可；（2）分两种情形：①当点E在线段BC上时，如图2中，连接BE．由△EAD≌△ADC，推出∠ABE＝∠C＝∠ABC＝45°，EB＝CD＝5，推出∠EBD＝90°，推出DE2＝BE2+BD2＝62+32＝45，即可解决问题；②当点D在CB的延长线上时，如图3中，同法可得DE2＝153．【详解】（1）①如图1中，∵将△ABE绕点A逆时针旋转90°后，得到△AFC，∴△BAE≌△CAF，∴AE＝AF，∠BAE＝∠CAF，∵∠BAC＝90°，∠EAD＝45°，∴∠CAD+∠BAE＝∠CAD+∠CAF＝45°，∴∠DAE＝∠DAF，∵DA＝DA，AE＝AF，∴△AED≌△AFD（SAS）；②如图1中，设DE＝x，则CD＝7﹣x．∵AB＝AC，∠BAC＝90°，∴∠B＝∠ACB＝45°，∵∠ABE＝∠ACF＝45°，∴∠DCF＝90°，∵△AED≌△AFD（SAS），∴DE＝DF＝x，∵在Rt△DCF中， DF2＝CD2+CF2，CF＝BE＝3，∴x2＝（7﹣x）2+32，∴x＝297，∴DE＝297；（2）∵BD＝3，BC＝9，∴分两种情况如下：①当点E在线段BC上时，如图2中，连接BE．∵∠BAC＝∠EAD＝90°，∴∠EAB＝∠DAC，∵AE＝AD，AB＝AC，∴△EAB≌△DAC（SAS），∴∠ABE＝∠C＝∠ABC＝45°，EB＝CD＝9-3=6，∴∠EBD＝90°，∴DE2＝BE2+BD2＝62+32＝45，∴DE＝35；②当点D在CB的延长线上时，如图3中，连接BE．同理可证△DBE是直角三角形，EB＝CD＝3+9=12，DB＝3，∴DE2＝EB2+BD2＝144+9＝153，∴DE＝317，综上所述，DE的值为35或317．【点睛】本题主要考查旋转变换的性质，三角形全等的判定和性质以及勾股定理，添加辅助线，构造旋转全等模型，是解题的关键．。

2018~2019学年度第一学期期末考试武汉市部分区八年级数学压轴题

学年度第一学期期末考试武汉市部分区八年级数学压轴题1.（硚口区）在平面直角坐标系中，已知A（-m,0），B（0,n），C（m,0）。

（1）如图1，若AC=AB，CM⊥AB于点M，MN∥y轴交AO于点N（-2,0），则m=__________。

（2）如图2，若m2-2mn+n2=0,∠ACB的平分线CD交AB于点D，过AC上一点E作EF∥CD，交AB于点F，AG是∆AEF的高，探究AG与EF的数量关系。

（3）如图3，在（1）的条件下，AC上一点H满足，直线MH交y轴于点Q，求点Q的坐标。

2．（东湖高新区）如图，在平面直角坐标系中，A（a,0），B（0,b），且|a+4|+ b2-8b+162=0。

（1）求a、b的值。

（2）如图1，C为y轴负半轴上一点，连接CA，过点C作CD⊥CA，使CD=CA，连接BD，求证：∠CBD=45°。

（3）如图2，若有一等腰Rt∆BMN，∠BMN=90°，连接AN，取AN中点P，连接PM、PO，试探究PM和PO的关系。

3.（江汉区）在平面直角坐标系中，点A （0,4），B （m,0）在坐标轴上，点C 与O 关于直线AB 对称，点D 在线段AB 上。

（1）如图1，若m=8，求AB 的长。

（2）如图2，若m=4，连接OD ，在y 轴上取一点E ，使OD=DE ，求证：CE= 。

（3）如图3，若m= ，在射线AO 上截取AF ，使AF=BD ，当CD+CF 的值最小时，请在图中画出点D 的位置，并直接写出这个最小值。

4.（江岸区）已知，平面直角坐标系中，A（0,4），B（b,0），（-4<b<0），将线段AB绕点A逆时针旋转90°得到线段AC，连接BC。

（1）如图1，直接写出点C的坐标：_______________________（用b表示）。

（2）如图2，取线段BC的中点D，在x轴取一点E使∠DEB=45°，作CF⊥x轴于点F。

2016-2019年八年级期末考压轴题专练(解答题)

2016-2019年八年级期末考压轴题专练（解答题）一．分式方程的应用（共1小题）1．（2016春•苏州期末）小明用12元买软面笔记本，小丽用21元买硬面笔记本．（1）已知每本硬面笔记本比软面笔记本贵1.2元，小明和小丽能买到相同数量的笔记本吗？（2）已知每本硬面笔记本比软面笔记本贵a元，是否存在正整数a，使得每本硬面笔记本、软面笔记本的价格都是正整数，并且小明和小丽能买到相同数量的笔记本？若存在，求出a的值；若不存在，请说明理由．二．一次函数综合题（共2小题）2．（2017春•姑苏区期末）如图，在平面直角坐标系中，一次函数y＝kx+6的图象分别与x 轴，y轴交于点A，B，点A的坐标为（﹣8，0）．（1）点B的坐标为；（2）在第二象限内是否存在点P，使得以P、O、A为顶点的三角形与△OAB相似？若存在，请求出所有符合条件的点P的坐标：若不存在，请说明理由．3．（2016春•张家港市期末）如图，直线l1：y＝﹣x+b分别与x轴、y轴交于A、B两点，与直线l2：y＝kx﹣6交于点C（4，2）．（1）点A坐标为（，），B为（，）；（2）在线段BC上有一点E，过点E作y轴的平行线交直线l2于点F，设点E的横坐标为m，当m为何值时，四边形OBEF是平行四边形；（3）若点P为x轴上一点，则在平面直角坐标系中是否存在一点Q，使得P、Q、A、B 四个点能构成一个菱形．若存在，求出所有符合条件的Q点坐标；若不存在，请说明理由．三．反比例函数系数k的几何意义（共1小题）4．（2019春•苏州期末）如图，点P为x轴负半轴上的一个点，过点P作x轴的垂线，交函数的图象于点A，交函数的图象于点B，过点B作x轴的平行线，交于点C，连接AC．（1）当点P的坐标为（﹣1，0）时，求△ABC的面积；（2）若AB＝BC，求点A的坐标；（3）连接OA和OC．当点P的坐标为（t，0）时，△OAC的面积是否随t的值的变化而变化？请说明理由．四．反比例函数与一次函数的交点问题（共3小题）5．（2019春•相城区期末）如图，在平面直角坐标系xOy，已知四边形DOBC是矩形，且D （0，6），B（8，0），若反比例函数y＝（x＞0）的图象经过线段OC的中点A，交DC于点E，交BC于点F．设直线EF的解析式为y＝k2x+b．（1）求反比例函数和直线EF的解析式；（2）求△OEF的面积：（3）请直接写出不等式k2x+b﹣＜0的解集．6．（2018•宁夏模拟）如图，在直角坐标系xOy中，一直线y＝2x+b经过点A（﹣1，0）与y轴正半轴交于B点，在x轴正半轴上有一点D，且OB＝OD，过D点作DC⊥x轴交直线y＝2x+b于C点，反比例函数y＝（x＞0）经过点C．（1）求b，k的值；（2）求△BDC的面积；（3）在反比例函数y＝（x＞0）的图象上找一点P（异于点C），使△BDP与△BDC 的面积相等，求出P点坐标．7．（2016•泰安）如图，在平面直角坐标系中，正方形OABC的顶点O与坐标原点重合，点C的坐标为（0，3），点A在x轴的负半轴上，点D、M分别在边AB、OA上，且AD＝2DB，AM＝2MO，一次函数y＝kx+b的图象过点D和M，反比例函数y＝的图象经过点D，与BC的交点为N．（1）求反比例函数和一次函数的表达式；（2）若点P在直线DM上，且使△OPM的面积与四边形OMNC的面积相等，求点P的坐标．五．反比例函数综合题（共16小题）8．（2019春•吴江区期末）直线MN与x轴、y轴分别交于点M、N，并且经过第二、三、四象限，与反比例函数y＝（k＜0）的图象交于点A、B，过A、B两点分别向x轴、y 轴作垂线，垂足为C、D、E、F，AD与BF交于G点．（1）比较大小：S矩形ACOD S矩形BEOF（填“＞，＝，＜”）．（2）求证：①AG•GE＝BF•BG；②AM＝BN；（3）若直线AB的解析式为y＝﹣2x﹣2，且AB＝3MN，则k的值为．9．（2019春•太仓市期末）如图，直线l的解析式为y＝﹣，与x轴，y轴分别交于A，B两点，双曲线y＝（x＞0）与直线l交于EF两点，点E的横坐标为1．（1）求k的值及F点的坐标；（2）连接OE，OF，求△EOF的面积；（3）若点P是EF下方双曲线上的动点（不与E、F重合），过点P作x轴，y轴的垂线，分别交直线l于点M，N，求BM•AN的值．10．（2019春•常熟市期末）如图，平面直角坐标系中，一次函数y＝kx﹣2的图象与反比例函数y＝（x＜0）的图象交于点B，与x轴，y轴交于点D，E，BC⊥x轴于C，BA⊥y 轴于A，＝，△ABE的面积为24．（1）点E的坐标是；（2）求一次函数和反比例函数的表达式；（3）以BC为边作菱形CBMN，顶点M在点B左侧的一次函数y＝kx﹣2的图象上，判断边MN与反比例函数y＝（x＜0）的图象是否有公共点．11．（2019春•相城区期末）如图，四边形OABC是矩形，点A的坐标为（0，6），点C的坐标为（4，0），点P从点A出发，沿AB以每秒2个单位长度的速度向点B出发，同时点Q从点B出发，沿BC以每秒3个单位长度的速度向点C运动，当点P与点B重合时，点P、Q同时停止运动．设运动时间为t秒．（1）当t＝1时，请直接写出△BPQ的面积为；（2）当△BPQ与△COQ相似时，求t的值；（3）当反比例函数的图象经过点P、Q两点时，①求k的值；②点M在x轴上，点N在反比例函数的图象上，若以点M、N、P、Q为顶点的四边形是平行四边形，请直接写出所有满足条件的M的坐标．12．（2018春•张家港市期末）已知点P（m，n）是反比例函数y＝（x＞0）的图象上的一动点，P A∥x轴，PB∥y轴，分别交反比例函数y＝（x＞0）的图象于点A，B，点C 是直线y＝2x上的一点．（1）点A的坐标为（，），点B的坐标为（，）；（用含m的代数式表示）（2）在点P运动的过程中，连接AB，证明：△P AB的面积是一个定值，并求出这个定值；（3）在点P运动的过程中，以点P，A，B，C为顶点的四边形能否为平行四边形？若能，求出此时m的值；若不能，请说明理由．13．（2018春•常熟市期末）如图，在平面直角坐标系中，直线y＝x，与反比例函数y＝在第一象限内的图象相交于点A（m，3）（1）求该反比例函数的表达式；（2）将直线y＝x沿y轴向上平移n个单位后与反比例函数在第一象限内的图象相交于点B，与y轴交于点C，若＝，连接AB，OB．①求n的值；②判断AB与OA的位置关系，并说明理由；（3）在（2）的条件下，在射线OA上有一点P（不与O重合），使△P AB∽△BAO，求点P的坐标．14．（2018秋•定兴县期末）如图，点A（1，4）、B（2，a）在函数y＝（x＞0）的图象上，直线AB与x轴相交于点C，AD⊥x轴于点D．（1）m＝；（2）求点C的坐标；（3）在x轴上是否存在点E，使以A、B、E为顶点的三角形与△ACD相似？若存在，求出点E的坐标；若不存在，说明理由．15．（2018春•相城区期末）如图，已知反比例函数的图象经过点A（﹣1，a），过点A 作AB⊥x轴，垂足为点B，△AOB的面积为．（1）求k的值；（2）若一次函数y＝mx+n图象经过点A和反比例函数图象上另一点，且与x轴交于M点，求AM的值；（3）在（2）的条件下，如果以线段AM为一边作等边△AMN，顶点N在另一个反比例函数上，则k'＝．16．（2018春•相城区期末）如图，在平面直角坐标系中，已知矩形OABC的顶点B（6，8），动点M，N同时从O点出发，点M沿射线OA方向以每秒1个单位的速度运动，点N沿线段OB方向以每秒0.6个单位的速度运动，当点N到达点B时，点M，N同时停止运动，连接MN，设运动时间为t（秒）．（1）求证△ONM～△OAB；（2）当点M是运动到点时，若双曲线的图象恰好过点N，试求k的值；（3）△MNB与△OAB能否相似？若能试求出所有t的值，若不能请说明理由．17．（2018春•高新区期末）如图，在平面直角坐标系中，直线y＝﹣2x+10与x轴、y轴分别交于A，B两点．（1）反比例函数y＝的图象与直线AB交于第一象限内的C，D两点（BD＜BC），当AD＝4DB时，求k1的值；（2）设线段AB的中点为P，过P作x轴的垂线，垂足为点M，交反比例函数y＝的图象于点Q，连接OP，OQ，当以P，O，Q为顶点的三角形与以O，B，P为顶点的三角形相似时，求k2的值．18．（2013•西宁）如图，正方形AOCB在平面直角坐标系xOy中，点O为原点，点B在反比例函数（x＞0）图象上，△BOC的面积为8．（1）求反比例函数的关系式；（2）若动点E从A开始沿AB向B以每秒1个单位的速度运动，同时动点F从B开始沿BC向C以每秒2个单位的速度运动，当其中一个动点到达端点时，另一个动点随之停止运动．若运动时间用t表示，△BEF的面积用S表示，求出S关于t的函数关系式，并求出当运动时间t取何值时，△BEF的面积最大？（3）当运动时间为秒时，在坐标轴上是否存在点P，使△PEF的周长最小？若存在，请求出点P的坐标；若不存在，请说明理由．19．（2017春•常熟市期末）如图，已知点A是反比例函数y＝（x＞0）的图象上的一个动点，经过点A的直线l交x轴负半轴于点B，交y轴正半轴于点C．过点C作y轴的垂线，交反比例函数的图象于点D．过点A作AE⊥x轴于点E，交CD于点F，连接DE．设点A的横坐标是a．（1）若BC＝2AC，求点D的坐标（用含a的代数式表示）；（2）若OC＝3，当四边形BCDE是平行四边形时，求a的值，并求出此时直线l对应的函数表达式．20．（2017春•工业园区期末）如图，等腰直角三角形ABC的直角顶点C在第一象限，顶点A、B分别在函数y＝﹣图象的两个分支上，且AB经过原点O，BC与x轴相交于点D，连接AD，已知AD平分四边形AODC的面积．（1）证明：BD＝2CD：（2）求点A的坐标．21．（2016春•常熟市期末）如图，点A是反比例函数y＝（x＞0）的图象上的一个动点，AC⊥x轴于点C；E是线段AC的中点，过点E作AC的垂线，与y轴和反比例函数的图象分别交于点B、D两点；连结AB、BC、CD、DA．设点A的横坐标为m．（1）求点D的坐标（用含有m的代数式表示）；（2）判断四边形ABCD的形状，并说明理由；（3）当m为何值时，四边形ABCD是正方形？并求出此时AD所在直线的解析式．22．（2016春•吴中区期末）已知点A（a，b）是反比例函数y＝（x＞0）图象上的动点，AB∥x轴，AC∥y轴，分别交反比例函数y＝（x＞0）的图象于点B、C，交坐标轴于D、E，且AC＝3CD，连接BC．（1）求k的值；（2）在点A运动过程中，设△ABC的面积为S，则S是否变化？若不变，请求出S的值；若改变，请写出S关于a的函数关系式；（3）探究：△ABC与以点O、D、E为顶点的三角形是否相似．23．（2016春•吴江区期末）如图，已知反比例函数y＝的图象经过点A（﹣1，a），过点A 作AB⊥x轴，垂足为点B，△AOB的面积为．（1）求a、k的值；（2）若一次函数y＝mx+n图象经过点A和反比例函数图象上另一点C（t，﹣），且与x轴交于M点，求AM的值；（3）在（2）的条件下，如果以线段AM为一边作等边△AMN，顶点N在一次数函数y ＝bx上，则b＝．六．三角形综合题（共1小题）24．（2019春•工业园区期末）如图，在△ABC中，∠C＝90°，AC＝9cm，BC＝12cm，在△DEF中，∠DFE＝90°，EF＝6cm，DF＝8cm．EF在BC上，保持△ABC不动，并将△DEF以1cm/s的速度向点C运动，移动开始前点F与点B重合，当点E与点C重合时，△DEF停止移动．边DE与AB相交于点G，连接FG，设移动时间为t（s）（1）△DEF从移动开始到停止，所用时间为s；（2）当DE平分AB时，求t的值；（3）当△GEF为等腰三角形时，求t的值．七．平行四边形的性质（共1小题）25．（2017•赤壁市一模）如图，在▱ABCD中，F是AD的中点，延长BC到点E，使CE＝BC，连接DE，CF．（1）求证：DE＝CF；（2）若AB＝4，AD＝6，∠B＝60°，求DE的长．八．四边形综合题（共15小题）26．（2019春•苏州期末）如图，矩形OABC的两条边OA、OC分别在y轴和x轴上，已知点B坐标为（4，﹣3）．把矩形OABC沿直线DE折叠，使点C落在点A处，直线DE与OC、AC、AB的交点分别为D、F、E．（1）线段AC＝；（2）求点D坐标及折痕DE的长；（3）若点P在x轴上，在平面内是否存在点Q，使以P、D、E、Q为顶点的四边形是菱形？若存在，则请求出点Q的坐标；若不存在，请说明理由．27．（2018春•张家港市期末）如图，长方形纸片ABCD中，AB＝8，将纸片折叠，折痕的一个端点F在边AD上，另一个端点G在边BC上，顶点B的对应点为E．（1）如图（1），当顶点B的对应点E落在边AD上时．①连接BF，试判断四边形BGEF是怎样的特殊四边形，并说明理由；②若BG＝10，求折痕FG的长；（2）如图（2），当顶点B的对应点E落在长方形内部，E到AD的距离为2，且BG＝10时，求AF的长．28．（2018春•苏州期末）如图1已知矩形ABCD，AB＞AD，点M为矩形中心（AC与BD 交点），现有两动点P、Q分别沿着A﹣B﹣C及A﹣D﹣C的方向同时出发匀速运动，速度都为每秒一个单位长度，当点P到达终点C时两动点都停止运动，连接PQ，在运动过程中，设运动时间为t（s），线段PQ长度为d个单位长度，d与t的函数关系如图2（1）AD＝AB＝．（2）t为多少时，线段PQ经过点M？并且求出此时∠APM的度数．（3）运动过程中，连接MQ和MP，求当∠PMQ为直角时的t值．29．（2019春•溧水区期末）如图，在△ABC中，∠ACB＝90°，AC＝30cm，BC＝40cm．点P从点A出发，以5cm/s的速度沿AC向终点C匀速移动．过点P作PQ⊥AB，垂足为点Q，以PQ为边作正方形PQMN，点M在AB边上，连接CN．设点P移动的时间为t（s）．（1）PQ＝；（用含t的代数式表示）（2）当点N分别满足下列条件时，求出相应的t的值；①点C，N，M在同一条直线上；②点N落在BC边上；（3）当△PCN为等腰三角形时，求t的值．30．（2018春•常熟市期末）如图，在△ABC中，∠ACB＝90°，AC＝4，BC＝3，点E、F 分别在AC，AB上，连接EF．（1）将△ABC沿EF折叠，使点A落在AB边上的点D处，如图1，若S四边形ECBD＝2S，求AE的长；△EDF（2）将△ABC沿EF折叠，使点A落在BC边上的点M处，如图2，若MF⊥CB．①求AE的长；②求四边形AEMF的面积；（3）若点E在射线AC上，点F在边AB上，点A关于EF所在直线的对称点为点P，问：是否存在以PF、CB为对边的平行四边形，若存在，求出AE的长；若不存在，请说明理由．31．（2020•安庆模拟）如图，在正方形ABCD中，对角线AC与BD相交于点O，点E是BC上的一个动点，连接DE，交AC于点F．（1）如图①，当＝时，求的值；（2）如图②当DE平分∠CDB时，求证：AF＝OA；（3）如图③，当点E是BC的中点时，过点F作FG⊥BC于点G，求证：CG＝BG．32．（2019•抚顺模拟）如图，AM是△ABC的中线，D是线段AM上一点（不与点A重合）．DE ∥AB交AC于点F，CE∥AM，连接AE．（1）如图1，当点D与M重合时，求证：四边形ABDE是平行四边形；（2）如图2，当点D不与M重合时，（1）中的结论还成立吗？请说明理由．（3）如图3，延长BD交AC于点H，若BH⊥AC，且BH＝AM，求∠CAM的度数．33．（2017春•常熟市期末）如图，在矩形ABCD中，AB＝6，BC＝8，点P从点C出发，沿CB向点B匀速运动，速度为每秒1个单位，过点P作PM⊥BC，交对角线BD于点M．点Q从点B出发，沿对角线BD向点D匀速运动，速度为每秒1个单位．P、Q两点同时出发，设它们的运动时间为t秒（0＜t＜8）．（1）当PQ⊥BD时，求出t的值；（2）连接AM，当PQ∥AM时，求出t的值；（3）试探究：当t为何值时，△PQM是等腰三角形？34．（2017春•张家港市期末）如图，在Rt△ABC中，∠B＝90°，AC＝60cm，∠A＝60°，点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动，同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D、E运动的时间是t秒（0＜t≤15）．过点D作DF⊥BC于点F，连接DE、EF．（1）DF＝，CF＝；（用含t的代数式表示）（2）若四边形AEFD为菱形，求t的值；（3）在运动过程中，四边形BEDF能否为正方形？若能，求出t的值；若不能，请说明理由．35．（2017春•张家港市期末）如图，▱ABCD的顶点A、B在x轴上，顶点D在y轴上，已知OA＝3，OB＝5，OD＝4．（1）▱ABCD的面积为；（2）如图1，点E是BC边上的一点，若△ABE的面积是▱ABCD的，求点E的坐标；（3）如图2，将△AOD绕点O顺时针旋转，旋转得△A1OD1，在整个旋转过程中，能否使以点O、A1、D1、B为顶点的四边形是平行四边形？若能，求点A1的坐标；若不能，请说明理由．36．（2016春•常熟市期末）如图，矩形ABCD中，AB＝3，AD＝4，E为对角线AC上的一个动点，连结DE，EF⊥DE交射线BC与点F，设AE为x．（1）当x取何值时，DE的值最小；（2）设CF＝y，当点F在线段BC上时，求y与x之间的函数关系式；（3）试探索：当x为何值时，△EFC为等腰三角形？37．（2016春•吴中区期末）如图1，在梯形ABCD中，AB∥CD，AD⊥AB，AB＝12，CD＝9，点M从点A出发，以每秒2个单位长度的速度向点B运动，同时，点N从点C出发，以每秒1个单位长度的速度向点D运动．其中一个动点到达终点时，另一个动点也随之停止运动．过点N作NP⊥AB于点P，连接BD交NP于点Q，连接MQ．设运动时间为t秒．（1）BM＝，BP＝；（用含t的代数式表示）（2）若t＝3，试判断四边形BNDP的形状；（3）如图2，将△BQM沿AB翻折，得△BKM．①是否存在某时刻t，使四边形BQMK为菱形，若存在，求出t的值，若不存在，请说明理由；②在①的条件下，要使四边形BQMK为正方形，则BD＝．38．（2016春•工业园区期末）如图，已知直线a∥b，a、b之间的距离为4cm．A、B是直线a上的两个定点，C、D是直线b上的两个动点（点C在点D的左侧），且AB＝CD＝10cm，连接AC、BD、BC，将△ABC沿BC翻折得△A1BC．（1）当A1、D两点重合时，AC＝cm；（2）当A1、D两点不重合时，①连接A1D，求证：A1D∥BC；②若以点A1、C、B、D为顶点的四边形是矩形，求AC的长．39．（2015•攀枝花）如图1，矩形ABCD的两条边在坐标轴上，点D与坐标原点O重合，且AD＝8，AB＝6．如图2，矩形ABCD沿OB方向以每秒1个单位长度的速度运动，同时点P从A点出发也以每秒1个单位长度的速度沿矩形ABCD的边AB经过点B向点C 运动，当点P到达点C时，矩形ABCD和点P同时停止运动，设点P的运动时间为t秒．（1）当t＝5时，请直接写出点D、点P的坐标；（2）当点P在线段AB或线段BC上运动时，求出△PBD的面积S关于t的函数关系式，并写出相应t的取值范围；（3）点P在线段AB或线段BC上运动时，作PE⊥x轴，垂足为点E，当△PEO与△BCD 相似时，求出相应的t值．40．（2016春•太仓市期末）如图，在△ABC中，BC＝10，AH⊥BC于点H，S△ABC＝25，点D为AB边上的任意一点（不与点A、B重合），过点D作DE∥BC，交AC于点E．交AH于点F，以DE为折线将△ADE翻折，所得的△A′DE与四边形BCED重叠部分的面积记为S（点A关于DE的对称点A′落在AH所在的直线上）．设DE＝x．（1）当x＝2时，重叠部分的面积S＝；（2）在（1）的条件下，若点D、A′、C在同一直线上时，求BH的长；（3）求S与x的函数关系式，并注明自变量x的取值范围．九．翻折变换（折叠问题）（共1小题）41．（2017春•工业园区期末）如图，在矩形ABCD纸片中，AB＝10cm，BC＝12cm．点P 在BC边上，将△P AB沿AP折叠，得△P AE，连接CE，DE．（1）当点E落在AD边上时，CE＝；（2）当点P是BC的中点时，求CE的长；（3）当△CDE分别满足下列条件时，求相应的PB的长：①DE＝CD；②DE＝CE．一十．相似三角形的判定与性质（共3小题）42．（2019春•吴江区期末）如图，在Rt△ABC中，∠C＝90°，且AC＝CD＝，又E，D为CB的三等分点．（1）证明：△ADE∽△BDA；（2）证明：∠ADC＝∠AEC+∠B；（3）若点P为线段AB上一动点，连接PE，则使得线段PE的长度为整数的点P的个数有几个？请说明理由．43．（2018•东营）（1）某学校“智慧方园”数学社团遇到这样一个题目：如图1，在△ABC中，点O在线段BC上，∠BAO＝30°，∠OAC＝75°，AO＝，BO：CO＝1：3，求AB的长．经过社团成员讨论发现，过点B作BD∥AC，交AO的延长线于点D，通过构造△ABD 就可以解决问题（如图2）．请回答：∠ADB＝°，AB＝．（2）请参考以上解决思路，解决问题：如图3，在四边形ABCD中，对角线AC与BD相交于点O，AC⊥AD，AO＝，∠ABC ＝∠ACB＝75°，BO：OD＝1：3，求DC的长．44．（2018春•苏州期末）如图，长度为5的动线段AB分别与坐标系横轴、纵轴的正半轴交于点A、点B，点O和点C关于AB对称，连接CA、CB，过点C作x轴的垂线段CD，交x轴于点D（1）移动点A，发现在某一时刻，△AOB和以点B、D、C为顶点的三角形相似，求这一时刻点C的坐标；（2）移动点A，当tan∠OAB＝时求点C的坐标．一十一．相似形综合题（共6小题）45．（2016春•苏州期末）如图，在平面直角坐标系中，△ABC是直角三角形，∠ACB＝90°，点A，C的坐标分别为A（﹣3，0），C（1，0），BC＝AC．（1）求过点A，B的直线的函数表达式；（2）在x轴上找一点D，连接DB，使得△ADB与△ABC相似（不包括全等），并求点D 的坐标；（3）在（2）的条件下，若P、Q分别是AB和AD上的动点，连接PQ，设AP＝DQ＝m，若△APQ与△ADB相似，求出m的值．46．（2019春•姑苏区期末）如图1，点O是正方形ABCD的中心，点E是AB边上一动点，在BC上截取CF＝BE，连接OE，OF．初步探究：在点E的运动过程中：（1）猜想线段OE与OF的关系，并说明理由．深入探究：（2）如图2，连接EF，过点O作EF的垂线交BC于点G．交AB的延长线于点I．延长OE交CB的延长线于点H．①直接写出∠EOG的度数．②若AB＝2，请探究BH•BI的值是否为定值，若是，请求出其值；反之，请说明理由47．（2019春•太仓市期末）如图，已知Rt△ABC中，∠C＝90°，AC＝6，BC＝8，点P以每秒1个单位的速度从A向C运动，同时点Q以每秒2个单位的速度从B向A方向运动，Q到达A点后，P点也停止运动，设点P，Q运动的时间为t秒．（1）求P点停止运动时，BP的长；（2）P，Q两点在运动过程中，点E是Q点关于直线AC的对称点，是否存在时间t，使四边形PQCE为菱形？若存在，求出此时t的值；若不存在，请说明理由．（3）P，Q两点在运动过程中，求使△APQ与△ABC相似的时间t的值．48．（2019春•常熟市期末）如图，矩形ABCD中，AD＝4cm，AB＝8cm，点P从点A出发在边AB上向点B匀速运动，同时点Q从点A出发在边AD上向点D匀速运动，速度都是1cm/s，运动时间是ts（0＜t＜4），PE⊥AB，交BD于点E，点Q关于PE的对称点是F，射线PF分别与BD，CD交于点M，N．（1）求∠BPN度数，并用含t的代数式表示PE的长；（2）当点F与点M重合时，如图②，求t的值；（3）探究：在点P，Q运动过程中，①的值是否是定值？若是，请求出这个值；若不是，请说明理由．②t为何值时，以点P，Q，E为顶点的三角形与△PMB相似？49．（2017春•昆山市期末）已知：如图，在平面直角坐标系中，△ABC是直角三角形，∠ACB＝90°，点A，C的坐标分别为A（﹣3，0），C（1，0），BC＝AC（1）求过点A，B的直线的函数表达式；（2）在x轴上找一点D，连接DB，使得△ADB与△ABC相似（不包括全等），并求点D 的坐标；（3）在（2）的条件下，如P，Q分别是AB和AD上的动点，连接PQ，设AP＝DQ＝m，问是否存在这样的m，使得△APQ与△ADB相似？如存在，请求出m的值；如不存在，请说明理由．50．（2016春•吴江区期末）已知点E、F分别是四边形ABCD边AB、AD上的点，且DE与CF相交于点G．（1）如图①，若AB∥CD，AB＝CD，∠A＝90°，且AD•DF＝AE•DC，求证：DE⊥CF：（2）如图②，若AB∥CD，AB＝CD，且∠A＝∠EGC时，求证：DE•CD＝CF•DA：（3）如图③，若BA＝BC＝3，DA＝DC＝4，设DE⊥CF，当∠BAD＝90°时，试判断是否为定值，并证明．2016-2019年八年级期末考压轴题专练（解答题）参考答案与试题解析一．分式方程的应用（共1小题）1．（2016春•苏州期末）小明用12元买软面笔记本，小丽用21元买硬面笔记本．（1）已知每本硬面笔记本比软面笔记本贵1.2元，小明和小丽能买到相同数量的笔记本吗？（2）已知每本硬面笔记本比软面笔记本贵a元，是否存在正整数a，使得每本硬面笔记本、软面笔记本的价格都是正整数，并且小明和小丽能买到相同数量的笔记本？若存在，求出a的值；若不存在，请说明理由．【分析】（1）设每本软面笔记本x元，则每本硬面笔记本（x+1.2）元，根据小明和小丽能买到相同数量的笔记本建立方程求出其解就可以得出结论；（2）设每本软面笔记本m元（1≤m≤12的整数），则每本硬面笔记本（m+a）元，根据小明和小丽能买到相同数量的笔记本建立方程就可以得出m与a的关系，就可以求出结论．【解答】解：（1））设每本软面笔记本x元，则每本硬面笔记本（x+1.2）元，由题意，得，解得：x＝1.6．此时＝7.5（不符合题意），所以，小明和小丽不能买到相同数量的笔记本；（2）设每本软面笔记本m元（1≤m≤12的整数），则每本硬面笔记本（m+a）元，由题意，得，解得：a＝m，∵a为正整数，∴m＝4，8，12．∴a＝3，6，9．当时，（不符合题意）∴a的值为3或9．【点评】本题考查了列分式方程解实际问题的运用，分式方程的解法的运用，二元一次不定方程的解法的运用，解答时求出根据两种笔记本购买的数量相等建立方程是关键．二．一次函数综合题（共2小题）2．（2017春•姑苏区期末）如图，在平面直角坐标系中，一次函数y＝kx+6的图象分别与x 轴，y轴交于点A，B，点A的坐标为（﹣8，0）．（1）点B的坐标为（0，6）；（2）在第二象限内是否存在点P，使得以P、O、A为顶点的三角形与△OAB相似？若存在，请求出所有符合条件的点P的坐标：若不存在，请说明理由．【分析】（1）令x＝0可得y＝6，由此可知B（0，6）；（2）如图，以OA、OB为边作矩形OAP3B，连接OP3，作OP1⊥AB于P1，作AP2⊥OP3于P2．易证△OAP1，△OAP2，△OAP3均与△AOB相似，易知P3（﹣8，6）．构建一次函数求出交点P1、P2的坐标，再由当△OAP4∽△BOA时，可得＝，推出OP4＝，由此可得P4的坐标；【解答】解：（1）令x＝0，得到y＝6，∴B（0，6）．故答案为（0，6）．（2）如图，以OA、OB为边作矩形OAP3B，连接OP3，作OP1⊥AB于P1，作AP2⊥OP3于P2．易证△OAP1，△OAP2，△OAP3均与△AOB相似，易知P3（﹣8，6）．∵直线AB的解析式为y＝x+6，∴直线OP1的解析式为y＝﹣x，由，解得，∴P1（﹣，），∵直线OP3的解析式为y＝﹣x，∴直线OP2的解析式为y＝x+，由，解得，∴P2（﹣，），当△OAP4∽△BOA时，可得＝，∴AP4＝，∴P4（﹣8，），综上所述，满足条件的点P的坐标为P1（﹣，），P2（﹣，），P3（﹣8，6），P4（﹣8，）．【点评】此题考查了一次函数综合题相似三角形的性质，坐标与图形性质，利用了分类讨论及数形结合的思想，解题的关键学会构建一次函数，利用方程组确定两个函数图象的交点坐标，属于中考常考题型．3．（2016春•张家港市期末）如图，直线l1：y＝﹣x+b分别与x轴、y轴交于A、B两点，与直线l2：y＝kx﹣6交于点C（4，2）．（1）点A坐标为（8，0），B为（0，4）；（2）在线段BC上有一点E，过点E作y轴的平行线交直线l2于点F，设点E的横坐标为m，当m为何值时，四边形OBEF是平行四边形；（3）若点P为x轴上一点，则在平面直角坐标系中是否存在一点Q，使得P、Q、A、B 四个点能构成一个菱形．若存在，求出所有符合条件的Q点坐标；若不存在，请说明理由．【分析】（1）由点C的坐标利用待定系数法即可求出直线l1的解析式，再分别令直线l1的解析式中x＝0、y＝0求出对应的y、x值，即可得出点A、B的坐标；（2）由点C的坐标利用待定系数法即可求出直线l2的解析式，结合点E的横坐标即可得出点E、F的坐标，再根据平行四边形的性质即可得出关于m的一元一次方程，解方程即可得出结论；（3）分AB为边和AB为对角线两种情况讨论．当AB为边时，根据菱形的性质找出点P 的坐标，结合A、B的坐标即可得出点Q的坐标；当AB为对角线时，根据三角形相似找出点P的坐标，再根据菱形对角线互相平分即可得出点Q的坐标．综上即可得出结论．【解答】解：（1）将点C（4，2）代入y＝﹣x+b中，得：2＝﹣2+b，解得：b＝4，∴直线l1为y＝﹣x+4．令y＝﹣x+4中x＝0，则y＝4，∴B（0，4）；令y＝﹣x+4中y＝0，则x＝8，∴A（8，0）．故答案为：8；0；0；4．（2）∵点C（4，2）是直线l2：y＝kx﹣6上的点，∴2＝4k﹣6，解得：k＝2，∴直线l2为y＝2x﹣6．∵点E的横坐标为m（0≤m≤4），∴E（m，﹣m+4），F（m，2m﹣6），∴EF＝﹣m+4﹣（2m﹣6）＝10﹣m．∵四边形OBEF是平行四边形，∴BO＝EF，即4＝10﹣m，解得：m＝．故当m＝时，四边形OBEF是平行四边形．（3）假设存在．以P、Q、A、B为顶点的菱形分两种情况：①以AB为边，如图1所示．∵点A（8，0），B（0，4），∴AB＝4．∵以P、Q、A、B为顶点的四边形为菱形，∴AP＝AB或BP＝BA．当AP＝AB时，点P（8﹣4，0）或（8+4，0）；当BP＝BA时，点P（﹣8，0）．当P（8﹣4，0）时，Q（8﹣4﹣8，0+4），即（﹣4，4）；当P（8+4，0）时，Q（8+4﹣8，0+4），即（4，4）；当P（﹣8，0）时，Q（﹣8+8﹣0，0+0﹣4），即（0，﹣4）．②以AB为对角线，对角线的交点为M，如图2所示．∵点A（8，0），B（0，4），∴M（4，2），AM＝AB＝2．∵PM⊥AB，∴∠PMA＝∠BOA＝90°，∴△AMP∽△AOB，∴，∴AP＝5，∴点P（8﹣5，0），即（3，0）．∵以P、Q、A、B为顶点的四边形为菱形，∴点Q（8+0﹣3，0+4﹣0），即（5，4）．综上可知：若点P为x轴上一点，则在平面直角坐标系中存在一点Q，使得P、Q、A、B四个点能构成一个菱形，此时Q点坐标为（﹣4，4）、（4，4）、（0，﹣4）或（5，4）．【点评】本题考查了待定系数法求函数解析式、平行四边形的性质以及菱形的性质，解题的关键是：（1）利用待定系数法求出直线解析式；（2）找出关于m的一元一次方程；（3）分AB为边或对角线考虑．本题属于中档题，难度不大，解决该题型题目时，充分利用平行四边形和菱形的性质是解题的关键．三．反比例函数系数k的几何意义（共1小题）4．（2019春•苏州期末）如图，点P为x轴负半轴上的一个点，过点P作x轴的垂线，交函。

2019-2020学年度北京市八年级上数学期末考试压轴题汇总

2019-2020学年度北京市八年级上数学期末考试压轴题汇总1.在直角三角形Rt△ABC中，∠C=90°，AC=BC。

在线段CB延长线上取一点P，以AP为直角边，点P为直角顶点，在射线CB上方作等腰直角三角形Rt△APD，过点D作DE⊥CB，垂足为点E。

1）请根据题意补全图形；2）证明AC=PE；3）连接DB，并延长交AC的延长线于点F，用等式表示线段CF与AC的数量关系，并证明。

2.在同一平面内，若点P与△ABC三个顶点中的任意两个顶点连接形成的三角形都是等腰三角形，则称点P是△___的巧妙点。

1）请用尺规作图求出△ABC的巧妙点P（保留作图痕迹）；2）在△ABC中，∠A=80°，AB=AC，用尺规作图求出所有巧妙点P（保留作图痕迹），并求出∠___的度数；3）等边三角形的巧妙点个数为12.3.定义：若一个三角形中，其中有一个内角是另外一个内角的一半，则这样的三角形叫做“半角三角形”。

例如，等腰直角三角形就是“半角三角形”。

在钝角三角形ABC中，BAC＞90，ACB=，ABC=。

过点A的直线l交BC边于点D，点E在直线l上，且BC=BE。

1）若AB=AC，点E在AD延长线上。

①当=30，请依据题意补全图1，并写出图中的一个“半角三角形”：△BDC；②如图2，若BAE=2，请判断图中是否存在“半角三角形”（△ABD除外），若存在，请写出图中的“半角三角形”，并证明；若不存在，请说明理由。

AABDCBCE图1图2l2）如图3，若AB＜AC，保持BEA的度数与（1）中②的结论相同，请直接写出BAE，，满足的数量关系：2=-，BAE=。

4.在直角三角形△ABC中，AB=AC，∠BAC=90°。

点D 是边BC上的动点，连接AD，点C关于直线AD的对称点为点E，射线BE与射线AD交于点F。

1）请根据题意补全图形；2）记DAC（45），求ABF的大小，即得到等式：sin⁡(∠ABF)=sin⁡(2α-∠ABC)。

2019-2020人教版数学八年级上册期末压轴题培优：全等三角形(含答案)

八年级上学期期末压轴题培优：全等三角形1．某中学八年级（5）班的学生到野外进行数学活动，为了测量一池塘两端A、B之间的距离，同学们设计了如下两种方案：方案1：如图（1），先在平地上取一个可以直接到达A、B的点C，连接AC并延长AC 至点D，连接BC并延长至点E，使DC＝AC，EC＝BC，最后量出DE的距离就是AB的长．方案2：如图（2），过点B作AB的垂线BF，在BF上取C、D两点，使BC＝CD，接着过D作BD的垂线DE，交AC的延长线于E，则测出DE的长即为AB间的距离问：（1）方案1是否可行？并说明理由；（2）方案2是否可行？并说明理由；（3）小明说：“在方案2中，并不一定需要BF⊥AB，DE⊥BF，将“BF⊥AB，DE⊥BF”换成条件AB∥DE也可以．”你认为小明的说法正确吗？如果正确的话，请你把小明所说的条件补上．解：（1）在△ABC和△DEC中，，∴△ABC≌△DEC（SAS），∴AB＝DE；（2）∵BF⊥AB，DE⊥BF，∴∠B＝∠BDE，在△ABC和△DEC中，，∴△ABC≌△DEC（ASA），∴AB＝DE；（3）只需AB∥DE即可，∵AB∥DE，∴∠B＝∠BDE，在△ABC和△DEC中，，∴△ABC≌△DEC（ASA），∴AB＝DE，故答案为：AB∥DE．2．小明用大小相同高度为2cm的10块小长方体垒了两堵与地面垂直的木墙AD，BE，当他将一个等腰直角三角板ABC如图垂直放入时，直角顶点C正好在水平线DE上，锐角顶点A和B分别与木墙的顶端重合，求两堵木墙之间的距离．解：由题意得：AC＝BC，∠ACB＝90°，AD⊥DE，BE⊥DE，∴∠ADC＝∠CEB＝90°，∴∠ACD+∠BCE＝90°，∠ACD+∠DAC＝90°，∴∠BCE＝∠DAC，在△ADC和△CEB中，，∴△ADC≌△CEB（AAS）；由题意得：AD＝EC＝6cm，DC＝BE＝14cm，∴DE＝DC+CE＝20（cm），答：两堵木墙之间的距离为20cm．3．某段河流的两岸是平行的，数学兴趣小组在老师带领下不用涉水过河就测得的宽度，他们是这样做的：①在河流的一条岸边B点，选对岸正对的一棵树A：②沿河岸直走20m有一树C．继续前行20m到达D处；③从D处沿河岸垂直的方向行走，当到达A树正好被C树遮挡住的E处停止行走；④测得DE的长为5米．（1）河的宽度是5米．（2）请你说明他们做法的正确性．证明：（1）由题意知，DE＝AB＝5米，即河的宽度是5米．故答案是：5．（2）如图，由题意知，在Rt△ABC和Rt△EDC中，∴Rt△ABC≌Rt△EDC（ASA）∴AB＝ED．即他们的做法是正确的．4．小明想知道一堵墙上点A的高度（AO⊥OD），但又没有直接测量的工具，于是设计了下面的方案，请你先补全方案，再说明理由．第一步：找一根长度大于OA的直杆，使直杆靠在墙上，且顶端与点A重合，记下直杆与地面的夹角∠ABO；第二步：使直杆顶端竖直缓慢下滑，直到∠OCD＝∠ABO．标记此时直杆的底端点D；第三步：测量OD的长度，即为点A的高度．说明理由：解：OCD，ABO，OD；理由：在△AOB与△DOC中，，∴△AOB≌△DOC（AAS），∴OA＝OD．故答案为：OCD，ABO，OD．5．如图，点C、E分别在直线AB、DF上，小华想知道∠ACE和∠DEC是否互补，但是他没有带量角器，只带了一副三角板，于是他想了这样一个办法：首先连结CF，再找出CF的中点O，然后连结EO并延长EO和直线AB相交于点B，经过测量，他发现EO＝BO，因此他得出结论：∠ACE和∠DEC互补，而且他还发现BC＝EF．小华的想法对吗？为什么？解：∵O是CF的中点，∴CO＝FO（中点的定义）在△COB和△FOE中，∴△COB≌△FOE（SAS）∴BC＝EF（对应边相等）∠BCO＝∠F（对应角相等）∴AB∥DF（内错角相等，两直线平行）∴∠ACE和∠DEC互补（两直线平行，同旁内角互补），6．如图，操场上有两根旗杆间相距12m，小强同学从B点沿BA走向A，一定时间后他到达M点，此时他测得CM和DM的夹角为90°，且CM＝DM，已知旗杆AC的高为3m，小强同学行走的速度为0.5m/s，则：（1）请你求出另一旗杆BD的高度；（2）小强从M点到达A点还需要多长时间？解：（1）∵CM和DM的夹角为90°，∴∠1+∠2＝90°，∵∠DBA＝90°，∴∠2+∠D＝90°，∴∠1＝∠D，在△CAM和△MBD中，，∴△CAM≌△MBD（AAS），∴AM＝DB，AC＝MB，∵AC＝3m，∴MB＝3m，∵AB＝12m，∴AM＝9m，∴DB＝9m；（2）9÷0.5＝18（s）．答：小强从M点到达A点还需要18秒．7．某段河流的两岸是平行的，数学兴趣小组在老师带领下不用涉水过河就测得河的宽度，他们是这样做的：①在河流的一条岸边B点，选对岸正对的一棵树A；②沿河岸直走20m有一树C，继续前行20m到达D处；③从D处沿河岸垂直的方向行走，当到达A树正好被C树遮挡住的E处停止行走；④测得DE的长为5米．求：（1）河的宽度是多少米？（2）请你证明他们做法的正确性．（1）解：河的宽度是5m；（2）证明：由作法知，BC＝DC，∠ABC＝∠EDC＝90°，在Rt△ABC和Rt△EDC中，，∴Rt△ABC≌Rt△EDC（ASA），∴AB＝E D，即他们的做法是正确的．8．某中学七年级同学到野外开展数学综合实践活动，在营地看到一池塘，同学们想知道池塘两端的距离．有一位同学设计了如下测量方案，设计方案：先在平地上取一个可直接到达A，B的点E（AB为池塘的两端），连接AE，BE，并分别延长AE至D，BE至C，使ED＝AE，EC＝BE．测出CD的长作为AB之间的距离．他的方案可行吗？请说明理由．若测得CD为10米，则池塘两端的距离是多少？解：在△AEB和△D EC中∴△AEB≌△DEC（SAS）；∴AB＝CD＝10米（全等三角形的对应边相等）．答；池塘两端的距离是10米．9．如图，一条河流MN旁边有两个村庄A，B，AD⊥MN于D．由于有山峰阻挡，村庄B 到河边MN的距离不能直接测量，河边恰好有一个地点C能到达A，B两个村庄，与A，B的连接夹角为90°，且与A，B的距离也相等，测量C，D的距离为150m，请求出村庄B到河边的距离．解：如图，过点B作BE⊥MN于点E，∵∠ADC＝∠ACB＝90°，∴∠A＝∠BCE（同角的余角相等）．在△ADC与△CEB中，．∴△ADC≌△CEB（AAS）．∴BE＝CD＝150m．即村庄B到河边的距离是150米．10．如图，小明站在乙楼BE前方的点C处，恰好看到甲、乙两楼楼顶上的点A和E重合为一点，若B、C相距30米，C、D相距60米，乙楼高BE为20米，小明身高忽略不计，则甲楼的高AD是多少米？解：∵AD⊥DC，EB⊥BC，∴AD∥BE，∴∠AEF＝∠C，∵B、C相距30米，C、D相距60米，∴EF＝DB＝BC＝30米，∵∠AFE＝∠EBC＝90°，∴△AEF≌△ECB（ASA），∴AF＝BE，∵DF＝BE，∴AD＝2BE＝2×20＝40（米）．答：甲楼的高AD是40米．11．茗茗用同种材料制成的金属框架如图所示，已知∠B＝∠E，AB＝DE，BF＝EC，其中△ABC的周长为24cm，CF＝3cm，则制成整个金属框架所需材料的长度为多少？解：∵BF＝EC，∴BF+FC＝CE+FC，即BC＝EF，∵在△ABC和△DEF中，∴△ABC≌△DEF（SAS），∴AC＝DF，∵△ABC的周长为24cm，CF＝3cm，∴制成整个金属框架所需这种材料的长度为24×2﹣3＝45cm．12．如图，某地在山区修建高速公路时需挖通一条隧道，为估计这条隧道的长度需测出这座山A、B间的距离，结合所学知识或方法，设计测量方案你能给出什么好的方法吗？解：选择一合适的地点O，连接AO、BO，测出AO和BO的长度，延长AO、BO至A′、B′，使OA′＝OA，OB′＝OB，连接A′B′，这样就构成两个三角形，在△AOB和△A′OB′中，，∴△AOB≌△A′OB′（SAS），∴AB＝A′B′．13．生活中处处有数学．（1）如图（1）所示，一扇窗户打开后，用窗钩AB将其固定，这里所运用的数学原理是三角形具有稳定性；（2）如图（2）所示，在新修的小区中，有一条“Z”字形绿色长廊ABCD，其中AB∥CD，在AB，BC，CD三段绿色长廊上各修一小凉亭E，M，F，且BE＝CF，点M是BC 的中点，在凉亭M与F之间有一池塘，不能直接到达，要想知道M与F之间的距离，只需要测出线段ME的长度，这样做合适吗？请说明理由．解：（1）如图1所示，一扇窗户打开后，用窗钩AB可将其固定，这里所运用的几何原理是：三角形的稳定性．故答案为：三角形具有稳定性；（2）合适，理由如下：∵AB∥CD，∴∠B＝∠C，∵点M是BC的中点，∴MB＝MC，在△MEB与△MCF中，∴△MEB≌△MFC（SAS），∴ME＝MF，∴想知道M与F之间的距离，只需要测出线段ME的长度．14．如图所示的A、B是两根呈南北方向排列的电线杆，A、B之间有一条小河，小刚想估测这两根电线杆之间的距离，于是小刚从A点开始向正西方向走了20步到达一棵大树C 处，接着又向前走了20步到达D处，然后他左转90°直行，当他看到电线杆B、大树C 和他自己现在所处的位置E恰在同一条直线上时，他从D位置走到E处恰好走了100步，利用上述数据，小刚测出了A、B两根电线杆之间的距离．（1）请你根据上述的测量方法在原图上画出示意图；（2）如果小刚一步大约60厘米，请你求A、B两根电线杆之间的距离．解：（1）根据题意画出图形，如图所示．（2）由题可知∠BAC＝∠EDC＝90°，60cm＝0.6m，AC＝20×0.6＝12m，DC＝20×0.6＝12m，DE＝100×0.6＝60m，∵点E、C、B在一条直线上，∴∠DCE＝∠ACB．∵∠BAC＝∠EDC＝90°，AC＝DC，∠DCE＝∠ACB，∴△ABC≌△DEC，∴AB＝DE．∵DE＝60m，∴AB＝60m，答：A、B两根电线杆之间的距离大约为60m．15．（1）如图1：在四边形ABC中，AB＝AD，∠BAD＝120°，∠B＝∠ADC＝90°．E，F 分别是BC，CD上的点．且∠EAF＝60°．探究图中线段BE，EF，FD之间的数量关系并证明．（提示：延长CD到G，使得DG＝BE）（2）如图2，若在四边形ABCD中，AB＝AD，∠B+∠D＝180°．E，F分别是BC，CD上的点，且∠EAF＝∠BAD，上述结论是否仍然成立，并说明理由；（3）如图3，在某次军事演习中，舰艇甲在指挥中心（O处）北偏西20°的A处，舰艇乙在指挥中心南偏东60°的B处，并且两舰艇到指挥中心的距离相等，接到行动指令后，舰艇甲向正东方向以60海里/小时的速度前进，舰艇乙沿北偏东50°的方向以80海里/小时的速度前进.1小时后，指挥中心观测到甲、乙两舰艇分别到达E，F处，且两舰艇之间的夹角为70°，试求此时两舰艇之间的距离．（可利用（2）的结论）解：（1）EF＝BE+DF；证明：如图1，延长FD到G，使DG＝BE，连接AG，在△ABE和△ADG中，，∴△ABE≌△ADG（SAS），∴AE＝AG，∠BAE＝∠DAG，∵∠EAF＝∠BAD，∴∠GAF＝∠DAG+∠DAF＝∠BAE+∠DAF＝∠BAD﹣∠EAF＝∠EAF，∴∠EAF＝∠GAF，在△AEF和△GAF中，，∴△AEF≌△GAF（SAS），∴EF＝FG，∵FG＝DG+DF＝BE+DF，∴EF＝BE+DF；（2）EF＝BE+DF仍然成立．证明：如图2，延长FD到G，使DG＝BE，连接AG，∵∠B+∠ADC＝180°，∠ADC+∠ADG＝180°，∴∠B＝∠ADG，在△ABE和△ADG中，，∴△ABE≌△ADG（SAS），∴AE＝AG，∠BAE＝∠DAG，∵∠EAF＝∠BAD，∴∠GAF＝∠DAG+∠DAF＝∠BAE+∠DAF＝∠BAD﹣∠EAF＝∠EAF，∴∠EAF＝∠GAF，在△AEF和△GAF中，，∴△AEF≌△GAF（SAS），∴EF＝FG，∵FG＝DG+DF＝BE+DF，∴EF＝BE+DF；（3）如图3，连接EF，延长AE、BF相交于点C，∵∠AOB＝20°+90°+（90°﹣60°）＝140°，∠EOF＝70°，∴∠EOF＝∠AOB，又∵OA＝OB，∠OAC+∠OBC＝（90°﹣20°）+（60°+50°）＝180°，∴符合探索延伸中的条件，∴结论EF＝AE+BF成立，即EF＝1×（60+80）＝140（海里）．答：此时两舰艇之间的距离是140海里．。

2019年上海市初二期末压轴题图文解析

2019年上海市各区初二期末压轴题图文解析目录例2019年上海市宝山区初二期末第24、25题/ 2例2019年上海市崇明区初二期末第24、25题/ 6例2019年上海市奉贤区初二期末第25、26题/ 10例2019年上海市虹口区初二期末第24、25题/ 14例2019年上海市黄浦区初二期末第25、26题/ 17例2019年上海市嘉定区初二期末第24、25题/ 20例2019年上海市金山区初二期末第24、25题/ 23例2019年上海市静安区初二期末第25、26题/26例2019年上海市闵行区初二期末第25、26题/ 29例2019年上海市浦东新区初二期末第24、26题/ 32例2019年上海市普陀区初二期末第25题/ 35例2019年上海市青浦区初二期末第24、25题/ 36例2019年上海市松江区初二期末第24、25题/ 39例2019年上海市杨浦区初二期末第25、26题/ 42例2019年上海市长宁区初二期末第24、25题/46例2019年上海市宝山区初二期末第18题/ 49例2019年上海市崇明区初二期末第18题/ 50例2019年上海市奉贤区初二期末第18题/ 51例2019年上海市虹口区初二期末第18题/ 52例2019年上海市黄浦区初二期末第18题/ 53例2019年上海市嘉定区初二期末第12题/ 54例2019年上海市金山区初二期末第18题/ 55例2019年上海市静安区初二期末第18题/ 56例2019年上海市闵行区初二期末第18题/ 57例2019年上海市浦东新区初二期末第18题/ 58例2019年上海市普陀区初二期末第18题/ 59例2019年上海市青浦区初二期末第18题/ 60例2019年上海市松江区初二期末第18题/ 61例2019年上海市杨浦区初二期末第18题/ 62例2019年上海市长宁区初二期末第18题/63例 2019年上海市宝山区初二下学期期末第24题观摩、学习是我们生活的一部分，而在观摩中与展览品保持一定的距离是一种文明的表现，某学校数学业余学习小组在平面直角坐标系xOy有关研讨中，将到线段PQ所在的直线的距离为3的直线，称为直线PQ的“观察线”，并称观察线上到P、Q两点的距离和最小的点L为线段PQ的“最佳观察点”．（1）如果P(1,3)、Q(4,3)，那么点A(1, 0)、B5(,23)2、C(3,3)中，处在直线PQ的“观察线”上的点是_______；（2）求直线33y x=的“观察线”的表达式；（3）若M(0,－1)，点N在第二象限，且MN＝6，当线段MN的一个“最佳观察点”在y轴正半轴上时，直接写出点N的坐标；并按逆时针方向联结M、N及其所有“最佳观察点”，直接写出联结所围成的多边形的周长和面积．图1动感体验打开几何画板文件名“18宝山24”，拖动点N在第二象限内的⊙M上运动，可以体验到，直线MN的两条“观察线”随点N的运动而变化．点击按钮“G是线段MN的最佳观察点”，可以体验到，此时四边形MGNG′是60°角的菱形．满分解答（1）如图2，由P(1,3)、Q(4,3)，可知直线PQ//x轴．与直线PQ间的距离等于3的直线有两条，分别是y＝0和y＝23．所以点A(1, 0)和点B5(,23)2处在直线PQ的“观察线”上．（2）直线l：33y x=与x轴正半轴的夹角为30°，与y轴正半轴的夹角为60°．如图3，设点E在y轴的正半轴上，设点E到直线l的距离EF＝3，那么EO＝2．过点E作直线l的平行线323y x=+，就是直线l的一条“观察线”．根据对称性，直线323y x=-也是直线l的一条“观察线”．图2 图3（3）第一步，证明线段PQ的“最佳观察点”在线段PQ的垂直平分线上．如图4，以直线PQ的“观察线”m为对称轴，作点P的对称点P′，联结P′Q与直线m 的交点L，就是线段PQ的“最佳观察点”．因为点L在线段P′P的垂直平分线上，所以LP′＝LP．所以∠1＝∠2．根据等角的余角相等，得∠3＝∠4．所以LP＝LQ．所以点L在线段PQ的垂直平分线上．图4第二步，求点N的坐标．如图5，作线段MN的垂直平分线，与y轴的正半轴交于点G，垂足为H，那么点G是线段MN的一个“最佳观察点”．在Rt△MHG中，MH＝3，GH＝3，由勾股定理，得MG＝23．所以∠HMG＝30°．作NK⊥y轴于K．在Rt△MNK中，∠NMK＝30°，MN＝6，所以NK＝3，MK＝33．所以OK＝MK－MO＝331-．所以N(3,331)--．第三步，求菱形MGNG′的面积和周长．如图6，因为菱形的边长MG＝23，所以菱形MGNG′的周长为83．因为Rt△MHG的面积为332，所以菱形MGNG′的面积为63．图5 图6例 2019年上海市宝山区初二下学期期末第25题如图1，在梯形ABCD 中，AD //BC ，AC ＝BC ＝4，∠D ＝90°，M 、N 分别是AB 、DC 的中点，过点B 作BE ⊥AC 交射线AD 于点E ，BE 与AC 交于点F ．（1）当∠ACB ＝30°时，求MN 的长；（2）设线段CD ＝x ，四边形ABCD 的面积为y ，求y 与x 的函数关系式及其定义域；（3）联结CE ，当CE ＝AB 时，求四边形ABCE 的面积．图1动感体验打开几何画板文件名“18宝山25”，拖动点D 运动，可以体验到，AD 随CD 的增大而减小．当CE ＝AB 时，四边形ABCE 是等腰梯形，△EBH 是等腰直角三角形．满分解答（1）如图2，因为AD //BC ，所以∠CAD ＝∠ACB ＝30°．在Rt △ACD 中，∠CAD ＝30°，AC ＝4，所以CD ＝2．由勾股定理，得23AD =．如图3，因为MN 是梯形ABCD 的中位线，所以MN ＝1()2AD BC +＝1(234)2+＝32+．图2 图3（2）如图4，在Rt △ACD 中， AC ＝4，CD ＝x ，由勾股定理，得216AD x =-．所以y ＝S 梯形ABCD ＝1()2AD BC CD +⋅＝21(164)2x x -+＝211622x x x -+．定义域是0＜x ＜4．图4（3）如图5，当CE＝AB时，四边形ABCE是等腰梯形．此时对角线BE＝AC＝4．【方法一】如图5，过点E作AC的平行线交BC的延长线于点H．所以四边形ACHE是平行四边形．所以AE＝CH．根据等底等高的三角形面积相等，得S△ABE＝S△ECH．所以S四边形ABCE＝S△EBH．因为BE⊥AC，所以BE⊥EH．所以△EBH是等腰直角三角形，S△EBH＝8．所以S四边形ABCE＝8．【方法二】如图6，因为BE⊥AC，所以S四边形ABCE＝S△ABC＋S△AEC＝1()2AC BF EF+＝12AC BE⋅＝1442⨯⨯＝8．图5 图6例 2019年上海市崇明区初二下学期期末第24题如图1，在平面直角坐标系中，过点A (3,0)-的两条直线分别交y 轴于B 、C 两点，且B 、C 两点的纵坐标分别是一元二次方程y 2－2y －3＝0的两个根．（1）求直线AC 与直线AB 的函数解析式；（2）求证：直线AC 与直线AB 互相垂直；（3）若点D 在直线AC 上，且DB ＝DC ，则直线BD 上是否存在点P ，使以A 、B 、P 三点为顶点的三角形是等腰三角形？若存在，请直接写出P 点的坐标；若不存在，请说明理由．图1动感体验打开几何画板文件名“18崇明24”，拖动点P 在直线BD 上运动，可以体验到△ABP 的顶点A 、P 可以落在对边的垂直平分线上，点B 可以两次落在对边的垂直平分线上．满分解答（1）解方程y 2－2y －3＝0，得y 1＝3，y 2＝－1．所以B (0, 3)，C (0, －1)．由A (3,0)-、C (0, －1)，得直线AC 的解析式为313y x =--．由A (3,0)-、B (0, 3)，得直线AB 的解析式为33y x =+．（2）如图2，在Rt △ABO 中，OA ＝3，OB ＝3，所以AB ＝23．在Rt △ACO 中，OA ＝3，OC ＝1，所以AC ＝2．在△ABC 中，AB ＝23，AC ＝2，BC ＝4，所以AB 2＋AC 2＝BC 2．由勾股定理逆定理，得△ABC 为直角三角形，∠BAC ＝90°．所以AC ⊥AB ．图2（3）由DB ＝DC ，可知点D 在线段BC 的垂直平分线上，所以y D ＝1．将y D ＝1代入313y x =--，得x D ＝－3D (－3, 1)．由B (0, 3)、D (－23, 1)，得直线BD 的解析式为333y x =+．设P (333x x +，)，已知A (3,0)-、B (0, 3)，所以AB 2＝223（）＝12， BP 2＝223()3x x +＝243x ，AP 2＝223(3)(3)3x x +++＝2443123x x ++． ①如图3，当AP 2＝AB 2时，2443123x x ++＝12．解得x 1＝0（与点B 重合，舍去），x 2＝－33，此时点P (－33,0)．②如图4，当BP 2＝BA 2时，243x ＝12．解得x 1＝3，x 2＝－3．此时点P (3，3＋3) 或 (－3，3－3)． ③如图5，当P A 2＝PB 2时，2443123x x ++＝243x ．解得x ＝－3．此时点P (－3, 2)．图3 图4 图5例 2019年上海市崇明区初二下学期期末第25题如图1，梯形ABCD 中，∠BCD ＝90°，AD ＝2，BC ＝4，CD ＝43，对角线AC 、BD 相交于点O ．点E 为BD 上一动点（不与点B 、D 重合）．联结AE 、CE ．设DE ＝x ，△AED 的面积为y ．（1）求y 关于x 的函数关系式，并写出定义域；（2）当AE ＝CE 时，求x 的值；（3）当x 取何值时，△AOD 与△EOC 面积相等？写出你的猜想，并证明你的结论．图1动感体验打开几何画板文件名“18崇明25”，在左图中，拖动点E 由D 向B 运动，可以体验到，y 随x 的增大而增大；在中间图形中，AE ＝CE ，可以体验到，AE 和CE 所在的两个直角三角形的斜边相等；在右图中，可以体验到，当△AOD 与△OEC 的面积相等时，点E 是线段OB 的一个四等分点．满分解答（1）如图2，在Rt △BCD 中，BC ＝4，CD ＝43，所以BD ＝8，∠BDC ＝30°．由△AED 和△ABD 是等高三角形，可得8AED ABD S ED x S BD ∆∆==．因为S △ABD ＝12AD CD ⋅＝12432⨯⨯=43，所以S △AED ＝32x ．定义域是0＜x ＜8．图2 图3 图4（2）如图3，在Rt △DEM 中，∠BDC ＝30°，DE ＝x ，所以EM ＝12x ，DM ＝32x ．如图4，作EN ⊥AD 于N ，作EM ⊥DC 于M ．在Rt △AEN 中，32NE DM x ==，NA ＝EM －AD ＝122x -，所以22231()(2)22AE x x =+-224x x =-+．在Rt △EMC 中，EM ＝12x ，MC ＝DC －DM ＝3432x -，所以22213()(43)22CE x x =+-21248x x =-+．因为AE ＝CE ，所以AE 2＝CE 2．所以224x x -+＝21248x x -+．解得x ＝225．（3）如图5，设G 、H 分别为OB 、OC 的中点，那么GH 为△OBC 的中位线．所以GH //BC //AD ，GH ＝12BC ＝2．所以∠ADO ＝∠HGO ，∠DAO ＝∠GHO ，AD ＝HG ．所以△AOD ≌△HOG ，所以S △AOD ＝S △HOG ．因为点H 是OC 中点，所以S △COG ＝2S △HOG ＝2S △AOD ．所以当点E 为OG 中点时，S △EOC ＝12S △COG ＝S △AOD ．因为GB ＝OG ＝OD ＝83，所以OB ＝163．因为OE ＝14OB ＝43，所以x ＝DE ＝OD ＋OE ＝8433+＝4．图5例 2019年上海市奉贤区初二下学期期末第25题如图1，一次函数y＝2x＋4的图像与x、y轴分别相交于点A、B，以AB为边作正方形ABCD（点D落在第四象限）．（1）求点A、B、D的坐标；（2）联结OC，设正方形的边CD与x轴相交于点E，点M在x轴上，如果△ADE与△COM全等，求点M的坐标．图1动感体验打开几何画板文件名“18奉贤25”，可以体验到，正方形ABCD的外接四边形PGHQ 也是正方形，四个直角三角形全等；点击屏幕左下角的按钮第（2）题，可以体验到，CM ⊥OC时，△ADE与△COM全等．满分解答（1）如图2，过点A、C作y轴的平行线，过点B、D作x轴的平行线，四条直线围成正方形PGHQ．由y＝2x＋4，得A(－2, 0)、B(0, 4)．因为四边形ABCD为正方形，所以AB＝AD，∠BAD＝90°．由同角的余角相等，得∠1＝∠2．所以△PBA≌△GAD．所以AG＝PB＝2，GD＝P A＝4．所以D(2,－2)．同理可得△PBA≌△GAD≌△HDC≌△QCB．所以CQ＝DH＝2，BQ＝CH＝4，所以C(4, 2)．图2 图3（2）第一步，找到△ADE与△COM全等时点M的位置．如图3，过点C作CL⊥x轴于L，过点D作DK⊥x轴于K．所以∠CLE＝∠DKA＝∠DKE＝90°．由A(－2, 0)、D(2,－2)、C(4, 2)，得OL＝AK＝4，CL＝DK＝2．所以△COL≌△DAK．所以CO＝DA，∠3＝∠4．过点C作CM⊥OC交x轴于点M．此时∠OCM＝∠ADE＝90°，△ADE≌△OCM．第二步，求点M的坐标．如图4，在△CLE和△DKE中，∠CLE＝∠DKE＝90°，CL＝DK＝2，∠CEL＝∠DEK，所以△CLE≌△DKE．所以KE＝LE．由D(2,－2)、C(4, 2)，可得KL＝2．所以KE＝LE＝1．所以AE＝AK＋KE＝4＋1＝5．所以OM＝AE＝5，M(5, 0)．图4例 2019年上海市奉贤区初二下学期期末第26题如图1，已知梯形ABCD 中，AD //BC ，∠ABC ＝90°，AB ＝3，BC ＝10，AD ＝5，M 是BC 边上的任意一点，联结DM ，联结AM ．（1）若AM 平分∠BMD ，求BM 的长；（2）如图2，过点A 作AE ⊥DM ，交DM 所在直线于点E ．①设BM ＝x ，AE ＝y ，求y 关于x 的函数关系式；②联结BE ，当△ABE 是以AE 为腰的等腰三角形时，请直接写出BM 的长．图1 图2动感体验打开几何画板文件名“18奉贤26”，拖动点M 在BC 上运动，可以体验到，y 随x 的增大先增大，后减小．观察左图，可以体验到，当AM 平分∠BMD 时，△AMD 是等腰三角形，存在两种情况．观察右图，可以体验到△ABE 的顶点E 可以落在对边的垂直平分线上，点A 可以落在对边的垂直平分线上两次．满分解答（1）如图3，过点D 作DN ⊥BC 于N ．所以DN ＝AB ＝3，BN ＝AD ＝5．因为AM 平分∠BMD ，所以∠1＝∠2．因为AD //BC ，所以∠1＝∠3．所以∠2＝∠3，DM ＝DA ＝5．在Rt △DNM 中，DM ＝5，DN ＝3，所以MN ＝4．如图3，当点M 在点N 左侧时，BM ＝BN －MN ＝5－4＝1；如图4，当点M 在点N 右侧时，BM ＝BN ＋MN ＝5＋4＝9．图3 图4（2）①如图5、图6，在Rt △DNM 中，DN ＝3，MN ＝|BN －BM |＝|5－x |，所以DM ＝22(5)3x -+＝21034x x -+．图4 图5因为S △AMD ＝12DM AE ⋅＝12AD DN ⋅，所以 21110345322x x -+=⨯⨯，所以2221515103410341034x xyx xx x-+==-+-+．②如图6，当EA＝EB时，点E在梯形ABCD的中位线上．所以DE＝EM．又因为AE⊥DM，所以AM＝AD＝5．在Rt△ABM中，AB＝3，AM＝5，所以BM＝4．图6如图7、图8，当AE＝AB时，在Rt△ABM和Rt△AEM中，AM＝AM，AB＝AE，所以Rt△ABM≌Rt△AEM．所以∠1＝∠2．由（1），可知当点M在点N左侧时，BM＝1；当点M在点N右侧时，BM＝9．图7 图8如图1，在平面直角坐标系xOy中，已知直线l与直线y＝2x平行，且直线l与x、y轴分别交于点A(－1, 0)、点B，点C(1, a)在直线l上．（1）求直线l的表达式以及点C的坐标；（2）点P在y轴正半轴上，点Q是坐标平面内一点，如果四边形P AQC为矩形，求点P、Q的坐标．图1动感体验打开几何画板文件名“18虹口24”，通过观察，可以体验到，四边形P AQC为矩形时点P的位置有两种情况，但是两种情况的矩形是同一个矩形．满分解答（1）设y＝2x＋b，代入点A(－1, 0)，得－2＋b＝0，解得b＝2．所以y＝2x＋2，B(0, 2)，C(1, 4)．（2）如图2，以AC为直径作圆与y轴的交点为点P1、P2．由A(－1, 0)、B(0, 2)、C(1, 4)，得AB＝BC＝5．因为四边形P AQC为矩形，所以BP＝BQ＝AB＝BC＝5．当点P在点B上方时，P1(0, 2＋5)，Q1(0, 2－5)；当点P在点B下方时，P2(0, 2－5)，Q2(0, 2＋5)．图2如图1，在等腰梯形ABCD 中，AD //BC ，∠B ＝60°，AD ＝2，BC ＝6，点E 为边CD 的中点，点F 为边BC 上的一动点（点F 不与点B 、C 重合），联结AE 、EF 和AF ，点P 、Q 分别为AE 、EF 的中点，设BF ＝x ，PQ ＝y ．（1）求AB 的长；（2）求y 关于x 的函数解析式，并写出定义域；（3）联结CQ ，当CQ //AE 时，求x 的值．图1 备用图动感体验打开几何画板文件名“18虹口25”，拖动点F 在BC 上运动，可以体验到，y 随x 的增大，先减小后增大．观察右图可以体验到，当CQ //AE 时，△ABF 和△CEF 为等边三角形．满分解答（1）如图2，过点A 作AH ⊥BC 于H ，过点D 作DG ⊥BC 于G ．所以四边形ADGH 为矩形，Rt △ABH ≌Rt △DCG ．在Rt △ABH 中，∠B ＝60°，BH ＝GC ＝2，所以AH ＝23，AB ＝4．图2 图3（2）如图3，在Rt △AHF 中，AH ＝23HF ＝|BF －BH |＝|x －2|，所以AF 22(23)(2)x +-2416x x -+在△AEF 中，点P 、Q 分别为AE 、EF 的中点，所以PQ//AF ，PQ ＝12AF ．所以y 214162x x -+．定义域是0＜x ＜6．（3）【方法一】如图4，延长AE ，交BC 延长线于点M ．因为点E 为边CD 中点，所以DE ＝CE ＝2．所以DE ＝AD ．所以∠1＝∠2＝30°．因为CM //AD ，所以∠4＝∠2．因为∠3＝∠1，所以∠3＝∠4＝30°．所以CE ＝CM ．如图5，过点M作MN//EF交QC延长线于N，所以∠5＝∠6．又因为CQ//EF，所以四边形QEMN为平行四边形．所以MN＝QE．因为QF＝QE，所以MN＝QF．在△CFQ和△CMN中，∠7＝∠8，∠5＝∠6，QF＝NM，所以△CFQ≌△CMN．所以CF＝CM．所以CF＝CE＝2．所以x＝BF＝BC－CF＝6－2＝4．图4 图5【方法二】如图6，因为点E为边CD中点，所以DE＝CE＝2．所以DE＝AD．所以∠1＝∠2＝30°．因为CQ//AE，所以∠1＝∠9＝30°．又因为∠BCD＝∠B＝60°，所以∠7＝30°，∠7＝∠9．如图7，延长CQ至C′，使得C′Q＝CQ．在△CFQ和△C′EQ中，QF＝QE，∠CQF＝∠C′QE，CQ＝C′Q，所以△CFQ≌△C′EQ．所以CF＝C′E，∠7＝∠10．所以∠9＝∠10，C′E＝CE．所以CF＝CE＝2．所以x＝BF＝BC－CF＝6－2＝4．图6 图7已知点P (1，m )、Q (n ，1)在反比例函数5y x =的图像上，直线y ＝kx ＋b 经过点P 、Q ，且与x 轴、y 轴的交点分别为A 、B 两点．（1）求 k 、b 的值；（2）O 为坐标原点，C 在直线y ＝kx ＋b 上且AB ＝AC ，点D 在坐标平面上，顺次联结点O 、B 、C 、D 得四边形OBCD ，满足BC //OD ，BO ＝CD ，求满足条件的D 点坐标．打开几何画板文件名“18黄浦25”，拖动点D 在直线OD 上运动，可以体验到，满足动感体验BC //OD ，BO ＝CD 的点D 存在两种情况，四边形OBCD 为等腰梯形或平行四边形．满分解答（1）由5y x=，得P (1，5)、Q (5，1)．将P (1，5)、Q (5，1)代入y ＝kx ＋b ，得5,51,k b k b +=⎧⎨+=⎩ 解得1,6.k b =-⎧⎨=⎩（2）由y ＝－x ＋6，得A (6，0)、B (0，6)，AB ＝62．设C (a ，－a ＋6)．因为AB ＝AC ，所以2262=(6)(6)a a -+-+．解得a 1＝12，a 2＝0(与点B 重合，舍去)．所以C (12, －6)．因为BC //OD ，所以OD 解析式为：y ＝－x ．设D (m , －m )．因为BO ＝CD ，所以226=(12)(6)m m -+-+．解得m 1＝6，m 2＝12．所以D (6,－6) 或 (12,－12)．当D (6,－6)时，四边形OBCD 为等腰梯形．当D (12,－12)时，四边形OBCD 为平行四边形．图1 图2如图1，已知正方形ABCD的边长为3，菱形EFGH的三个顶点E、G、H分别在正方形的边AB、CD、DA上，AH＝1，联结CF．（1）当DG＝1时，求证：菱形EFGH为正方形；（2）设DG＝x，△FCG的面积为y，写出y关于x的函数解析式，并指出x的取值范围；（3）当DG＝433时，求∠GHE的度数.图1 备用图动感体验打开几何画板文件名“18黄浦26”，拖动点G在DC上运动，可以体验到，△DGH与△NEF始终保持全等，△AHE与△MFG始终保持全等．满分解答（1）如图2，因为四边形ABCD是正方形，所以∠D＝∠A＝90°．因为四边形EFGH是菱形，所以HG＝EH．在Rt△DGH和Rt△AHE中，HG＝EH，DG＝AH＝1，所以Rt△DGH≌Rt△AHE．所以∠1＝∠2．因为∠2＋∠3＝90°，所以∠1＋∠3＝90°．所以∠GHE＝90°．所以菱形EFGH为正方形．图2 图3（2）如图3，过点F作DA的平行线，交DC延长线于M．所以FM⊥DC，∠M＝∠A＝90°．因为正方形ABCD和菱形EFGH，所以HE＝FG，DC//AB，GF//HE．所以∠MGF＝∠AEH．所以△HAE≌△FMG，MF＝AH＝1．所以y＝12GC MF⋅＝1(3)2x-，定义域为0≤x6．（3）过点G作GK⊥AB于K．在Rt△DGH中，DH＝2，DG＝433，所以HG＝224323⎛⎫+ ⎪⎪⎝⎭＝2213．在Rt△AHE中，AH＝1，HE＝HG＝2213，所以AE＝2222113⎛⎫-⎪⎪⎝⎭＝533．在Rt△GKE中，GK＝DA＝3，KE＝AE－DG＝533－433＝33，所以GE＝223221333⎛⎫+=⎪⎪⎝⎭．所以HE＝HG＝GE，△GHE是等边三角形．所以∠GHE＝60°．图4例 2019年上海市嘉定区初二下学期期末第24题如图1，在平面直角坐标系中，已知一次函数的图像经过点A (0，4)、B (2，0)．（1）求这个一次函数的解析式；（2）把直线AB 向下平移，若平移后的直线与x 轴、y 轴分别相交于点C 、D ，且AC ＝BC ，如果点E 在直线CD 上，四边形ABDE 是等腰梯形，求点E 的坐标．图1动感体验打开几何画板文件名“18嘉定24”，可以体验到，点C 在AB 中垂线上，四边形ABDE 是等腰梯形存在一种情况．满分解答（1）设y ＝kx ＋4，代入B (2，0)，得2k ＋4＝0，解得k ＝－2．所以y ＝－2x ＋4．（2）如图2，设C(a ，0)，已知A (0，4)，B (2，0)，AC ＝BC ，所以AC 2＝BC 2．所以22(4)= 2a a +--．解得a ＝－3．所以C (－3，0)．设CD 的解析式为y ＝－2x ＋b ，代入C (－3，0)，得6＋b ＝0．解得b ＝－6．所以y ＝－2x －6，D (0,－6)．因为四边形ABDE 是等腰梯形，可知AB //ED ．设E (m ，－2m －6)．【方法一】由腰AE ＝BD ，根据AE 2＝BD 2列方程．因为A (0，4)、B (2，0)、D (0,－6)，所以2222(210)=26m m +--+．解得m 1＝－6，m 2＝－2(此时ABDE 是平行四边形，舍去)．所以E (－6, 6)．【方法二】由对角线AD ＝BE ，根据AD 2＝BE 2列方程．因为A (0，4)、B (2，0)、D (0,－6)，所以222(2)(26)=10m m -+--．解得m 1＝－6，m 2＝2(此时点E 在点D 右侧，ABED 是平行四边形，舍去)．所以E (－6, 6)．【方法三】由HE ＝HD ，根据HE 2＝HD 2列方程．因为A (0，4)、B (2，0)、 D (0,－6)，所以H (1, 2)．所以22(1)(28)m m -+--＝2218+．解得m 1＝－6，m 2＝0(此时点E 与点D 重合，舍去)．所以E (－6, 6)．【方法四】由CA ＝CB ，根据CA 2＝CB 2列方程．因为E (m ,－2m －6)、 D (0,－6)，所以C (2m ,－m －6)．所以22()(10)2m m +--＝22(2)(6)2m m -+--．解得m ＝－6．所以E (－6, 6)．图2例 2019年上海市嘉定区初二下学期期末第25题如图1，在边长为2的正方形ABCD中，点P是对角线AC上的一个动点（与A、C不重合），过点P作PE⊥PB，PE交射线DC于点E，过点E作EF垂直直线AC，垂足为点F．（1）当点E在线段CD上时（如图1），求证：PB＝PE；（2）当点E在线段CD上时，在点P的运动过程中，PF的长度是否发生变化？若不变，试求出这个不变的值，若变化，试说明理由；（3）在点P的运动过程中，△PEC是否能成为等腰三角形？如果能，试求出AP的长，如果不能，试说明理由．图1 备用图动感体验打开几何画板文件名“18嘉定25”，拖动点P在AC上运动，观察左图可以体验到，△PBN与△PEM始终保持全等；观察中间图可以体验到，△BOP与△PFE始终保持全等；观察右图可以体验到，△PEC始终为钝角三角形，所以△PEC为等腰三角形存在一种情况．满分解答（1）如图2，过点P作PM⊥CD于M，PN⊥BC于N，得正方形PMCN．所以∠PME＝∠PNB＝∠NPM＝90°，PM＝PN．因为PE⊥PB，所以∠BPE＝90°．根据同角的余角相等，得∠1＝∠2．所以△PME≌△PNB．所以PB＝PE．（2）PF的长度不会发生变化．如图3，联结BD，得AC⊥BD，AC＝BD＝22．所以∠BOP＝90°．因为EF⊥AC，∠PFE＝90°．根据同角的余角相等，得∠3＝∠4．在△BOP和△PFE中，∠BOP＝∠PFE，∠3＝∠4，BP＝PE，所以△BOP≌△PFE．所以PF＝BO＝12BD＝2．图2 图3（3）△PEC能成为等腰三角形．①如图3，当点E在线段CD上时，△PEC为钝角三角形，所以只有当EC＝EP时，△PEC为等腰三角形．此时∠EPC＝∠ACD＝45°．如图4所示，点P与点A重合，不符合题意．②如图5，当点E在线段DC的延长线上时，△PEC为钝角三角形，所以只有当CP＝CE时，△PEC为等腰三角形．在△CPE中，∠PCE＝135°，所以∠E＝∠CPE＝22.5°．所以∠APB＝67.5°．在△ABP中，∠BAP＝45°，∠APB＝67.5°，所以∠ABP＝67.5°．所以AP＝AB＝2．图4 图5例 2019年上海市金山区初二下学期期末第24题如图1，在正方形ABCD中，AB＝4，点M是边BC的中点，点E是边AB上的一个动点，作EG⊥AM交AM于点G，EG的延长线交线段CD于点F．（1）如图1，当点E与点B重合时，求证：BM＝CF；（2）设BE＝x，梯形AEFD的面积是y，求y与x的函数解析式，并写出定义域．图1 备用图动感体验打开几何画板文件名“18金山24”，拖动点E在AB上运动，可以体验到，y随x的增大而减小．观察右图可以体验到△ABM和△EHF始终保持全等．满分解答（1）如图2，由正方形ABCD，得AB＝BC，∠ABC＝∠C＝90°．所以∠2＋∠3＝90°．因为EG⊥AM，所以∠EGA＝90°．所以∠1＋∠3＝90°．所以∠1＝∠2．在△ABM与△BCF中，∠1＝∠2，AB＝BC，∠ABC＝∠C，所以△ABM≌△BCF．所以BM＝CF．图2 图3（2）如图3，过点E作EH⊥DC于H，得矩形BCHE．所以EH＝BC＝AB，CH＝BE，∠EHF＝90°．由（1），得∠1＝∠2．在△ABM与△EHF中，∠1＝∠2，AB＝EH，∠B＝∠EHF，所以△ABM≌△EHF．所以HF＝BM＝2．因为BE＝x，所以AE＝4－x，DF＝DC―CH―HF＝2－x．所以11()(24)441222y DF AE AD x x x=+⋅=-+-⋅=-+，定义域是0≤x＜2．例 2019年上海金山初二下学期期末第25题如图1，已知直线AQ与x轴负半轴交于点A，与y轴正半轴交于点Q，∠QAO＝45°，直线AQ在y轴上的截距为2，直线BE：y＝－2x＋8与直线AQ交于点P．（1）求直线AQ的解析式；（2）在y轴正半轴上取一点F，当四边形BPFO是梯形时，求点F的坐标；（3）若点C在y轴负半轴上，点M在直线P A上，点N在直线PB上，是否存在以Q、C、M、N为顶点的四边形是菱形，若存在请求出点C的坐标；若不存在请说明理由．图1动感体验打开几何画板文件名“18金山25”，拖动点C在y轴负半轴上运动，可以体验到，菱形的顶点M、N分别落在直线P A和直线PB上存在两种情况．满分解答（1）如图2，在Rt△AOQ中，∠QAO＝45°，OQ＝2，所以AO＝2．所以A(－2, 0)．设y＝kx＋2，代入A(－2, 0)，得－2k＋2＝0，解得k＝1．所以AQ的解析式为y＝x＋2．（2）当四边形BPFO是梯形时，分两种情况讨论。

湖北省武汉市各区2019—2020学年度年八年级上学期数学压轴题汇编(无答案)

硚口区9．如图，在△ABC中，AD是它的角平分线，AB=9，AC=6，BC=10，则CD的长为B.3C.4.5D.6A10310．如图，在平面直角坐标系中，A点坐标为（8，0），点P从点O出发以1个单位长度秒的速度沿y轴正半轴方向运动，同时，点Q从点A出发以1个单位长度/秒的速度沿x轴负半轴方向运动，设点P、Q运动的时间为t（0<t<8）秒.以PQ为斜边，向第一象限内作等腰Rt△PBQ，连接OB.下列四个说法：①OP+OQ=8；②B点坐标为（4，4）；③四边形PBQO的面积为16；④PQ>OB.其中正确的说法个数有A.4B.3C.2D.115在等腰△AC中，AB=AC，AB边的垂直平分线MN与直线A（相交于点D，若∠DBC=42°，则∠BAC的大小为__________16.如图，牧人从A地出发，先到草地边MN的某处点C牧马，再到河边EF的某处点D饮马，然后回到B处，若从A到B走的是最短路径，CA与DB的延长线交于点H，设锐角∠1=a，则∠2的的大小为__________（用含a的式子表示）22（本题10分）已知CD∥AB，DE平分∠ADC（1）如图1，若∠B=90°，EB=EC，求证：AE平分∠DAB；（2）如图2，若AB+AD=CD，求证：EB=EC23.（本题10分）已知△ABC是等边三角形，点D是AC的中点，点E在射线BC上，点F在射线BA上，∠EDF=120（1）如图1，若点F与B点重合，求证：DB=DE；的值；（2）如图2，若点E在线段BC上，点F在线段BA上，求BE BFAC（3）如图3，若AF+CE=BD，直接写出∠EDC的度数为_________24.（本题1.分）在半面直角坐标系中，点A的坐标为（0，4）（1）如图1，若点B的坐标为（3，0），△ABC是等腰直角三角形，BA=BC，∠ABC=90°，求C点坐标；（2）如图2，若点E是AB的中点，求证：AB=2OE；（3）如图3，△ABC是等腰直角三角形，BA=BC，∠ABC=90°，△ACD是等边三角形，连接OD，若∠AOD=30°，求B点坐标江岸区9．已知△ABC 的内角平分线相交于点O ，三边的垂直平分线相交于点I ，直线OI 经过点A ．若∠BAC ＝40°，则∠ABC ＝（） A ．40°B ．50°C ．70°D ．80°10．如图，在△ABC 中，点D 是线段AB 的中点，DC ⊥BC ，作∠EAB ＝∠B ，DE ∥BC ，连接CE ．若52AE BC ，设△BCD 的面积为S ，则用S 表示△ACE 的面积正确的是（）A ．S 25B ．3SC ．4SD ．S 29 15．等腰三角形一腰上的高与另一腰的夹角为40°，则这个等腰三角形的底角为__________° 16．如图，已知点I 是△ABC 的角平分线的交点．若AB ＋BI ＝AC ，设∠BAC ＝α，则∠AIB ＝___________（用含α的式子表示）21．（本题8分）如图，Rt △ABC ≌Rt △CED （∠ACB ＝∠CDE ＝90°），点D 在BC 上，AB 与CE 相交于点F (1) 如图1，直接写出AB 与CE 的位置关系(2) 如图2，连接AD 交CE 于点G ，在BC 的延长线上截取CH ＝DB ，射线HG 交AB 于K ，求证：HK ＝BK22．（本题10分）如图，在△ABC 中，CE 为三角形的角平分线，AD ⊥CE 于点F 交BC 于点D(1) 若∠BAC ＝96°，∠B ＝28°，直接写出∠BAD ＝__________° (2) 若∠ACB ＝2∠B ① 求证：AB ＝2CF② 若EF ＝2，CF ＝5，直接写出CDBD＝__________23．（本题10分）如图1，AB＝AC，EF＝EG，△ABC≌△EFG，AD⊥BC于点D，EH⊥FG于点H(1) 直接写出AD、EH的数量关系：___________________(2) 将△EFG沿EH剪开，让点E和点C重合①按图2放置△EHG，将线段CD沿EH平移至HN，连接AN、GN，求证：AN⊥GN②按图3放置△EHG，B、C（E）、H三点共线，连接AG交EH于点M．若BD＝1，AD＝3，求CM的长度24．（本题12分）已知：如图，在平面直角坐标系中，A(a，0)、B(0，b)，且|a＋2|＋(b＋2a)2＝0，点P为x轴上一动点，连接BP，在第一象限内作BC⊥AB且BC＝AB(1) 求点A、B的坐标(2) 如图1，连接CP．当CP⊥BC时，作CD⊥BP于点D，求线段CD的长度(3) 如图2，在第一象限内作BQ⊥BP且BQ＝BP，连接PQ．设P(p，0)，直接写出S△PCQ＝_____24、在△ABC 中，AD 是高，AE 是角平分线，已知∠ACB = 700∠EAD = 15°,则∠A BC 的度数为。

八年级数学压轴题期末复习试卷复习练习(Word版含答案)

八年级数学压轴题期末复习试卷复习练习(Word 版含答案)一、压轴题1．如图，直线2y x m =-+交x 轴于点A ，直线122y x =+交x 轴于点B ，并且这两条直线相交于y 轴上一点C ，CD 平分ACB ∠交x 轴于点D ．（1）求ABC 的面积．（2）判断ABC 的形状，并说明理由．（3）点E 是直线BC 上一点，CDE △是直角三角形，求点E 的坐标．2．如图（1），AB ＝4cm ，AC ⊥AB ，BD ⊥AB ，AC ＝BD ＝3cm ．点 P 在线段 AB 上以 1/cm s 的速度由点 A 向点 B 运动，同时，点 Q 在线段 BD 上由点 B 向点 D 运动．它们运动的时间为 t （s ）．（1）若点 Q 的运动速度与点 P 的运动速度相等，当t ＝1 时，△ACP 与△BPQ 是否全等，请说明理由，并判断此时线段 PC 和线段 PQ 的位置关系；（2）如图（2），将图（1）中的“AC ⊥AB ，BD ⊥AB”为改“∠CAB ＝∠DBA ＝60°”，其他条件不变．设点 Q 的运动速度为x /cm s ，是否存在实数x ，使得△ACP 与△BPQ 全等？若存在，求出相应的x 、t 的值；若不存在，请说明理由．3．如图，在△ABC 中，AB =AC =18cm ，BC =10cm ，AD =2BD ．（1）如果点P 在线段BC 上以2cm /s 的速度由B 点向C 点运动，同时，点Q 在线段CA 上由C 点向A 点运动．①若点Q 的运动速度与点P 的运动速度相等，经过2s 后，△BPD 与△CQP 是否全等，请说明理由；②若点Q 的运动速度与点P 的运动速度不相等，当点Q 的运动速度为多少时，能够使△BPD 与△CQP 全等？（2）若点Q 以②中的运动速度从点C 出发，点P 以原来的运动速度从点B 同时出发，都逆时针沿△ABC三边运动，求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇？4．（1）在等边三角形ABC中，①如图①，D，E分别是边AC，AB上的点且AE=CD，BD与EC交于点F，则∠BFE的度数是度；②如图②，D，E分别是边AC，BA延长线上的点且AE=CD，BD与EC的延长线交于点F，此时∠BFE的度数是度；（2）如图③，在△ABC中，AC=BC，∠ACB是锐角，点O是AC边的垂直平分线与BC的交点，点D，E分别在AC，OA的延长线上，AE=CD，BD与EC的延长线交于点F，若∠ACB=α，求∠BFE的大小．（用含α的代数式表示）．5．如图，已知等腰△ABC 中，AB=AC，∠A＜90°，CD 是△ABC 的高，BE 是△ABC 的角平分线，CD 与BE 交于点P．当∠A 的大小变化时，△EPC 的形状也随之改变．（1）当∠A=44°时，求∠BPD 的度数；（2）设∠A=x°，∠EPC=y°，求变量y 与x 的关系式；（3）当△EPC 是等腰三角形时，请直接写出∠A 的度数．6．如图1．在△ABC 中，∠ACB =90°，AC =BC =10，直线DE 经过点C ，过点A ，B 分别作AD ⊥DE ，BE ⊥DE ，垂足分别为点D 和E ，AD =8，BE =6．（1）①求证：△ADC ≌△CEB ；②求DE 的长；（2）如图2，点M 以3个单位长度/秒的速度从点C 出发沿着边CA 运动，到终点A ，点N 以8个单位长度/秒的速度从点B 出发沿着线BC —CA 运动，到终点A ．M ，N 两点同时出发，运动时间为t 秒(t ＞0)，当点N 到达终点时，两点同时停止运动，过点M 作PM ⊥DE 于点P ，过点N 作QN ⊥DE 于点Q ；①当点N 在线段CA 上时，用含有t 的代数式表示线段CN 的长度； ②当t 为何值时，点M 与点N 重合； ③当△PCM 与△QCN 全等时，则t = ．7．如图，以直角△AOC 的直角顶点O 为原点，以OC ，OA 所在直线为x 轴和y 轴建立平面直角坐标系，点A （0，a ），C （b ，0）满足280a b b -++-=．（1）点A 的坐标为________；点C 的坐标为________．（2）已知坐标轴上有两动点P ，Q 同时出发，P 点从C 点出发沿x 轴负方向以每秒2个单位长度的速度匀速移动，Q 点从O 点出发沿y 轴正方向以每秒1个单位长度的速度匀速移动，点P 到达O 点整个运动随之结束．AC 的中点D 的坐标是（4，3），设运动时间为t 秒．问：是否存在这样的t ，使得△ODP 与△ODQ 的面积相等？若存在，请求出t 的值；若不存在，请说明理由．（3）在（2）的条件下，若∠DOC=∠DCO ，点G 是第二象限中一点，并且y 轴平分∠GOD ．点E 是线段OA 上一动点，连接接CE 交OD 于点H ，当点E 在线段OA 上运动的过程中，探究∠GOA ，∠OHC ，∠ACE 之间的数量关系，并证明你的结论（三角形的内角和为180°可以直接使用）．8．如图，A ，B 是直线y =x +4与坐标轴的交点，直线y =-2x +b 过点B ，与x 轴交于点C ．（1）求A ，B ，C 三点的坐标；（2）点D 是折线A —B —C 上一动点．①当点D 是AB 的中点时，在x 轴上找一点E ，使ED +EB 的和最小，用直尺和圆规画出点E 的位置（保留作图痕迹，不要求写作法和证明），并求E 点的坐标．②是否存在点D ，使△ACD 为直角三角形，若存在，直接写出D 点的坐标；若不存在，请说明理由9．如图1，在等边△ABC 中，E 、D 两点分别在边AB 、BC 上，BE =CD ，AD 、CE 相交于点F ．（1）求∠AFE 的度数；（2）过点A 作AH ⊥CE 于H ，求证：2FH +FD =CE ；（3）如图2，延长CE 至点P ，连接BP ，∠BPC =30°，且CF =29CP ，求PF AF的值．（提示：可以过点A 作∠KAF =60°，AK 交PC 于点K ，连接KB ）10．在ABC 中，AB AC =，D 是直线AB 上一点，E 在直线BC 上，且DE DC =．（1）如图1，当D 在AB 上，E 在CB 延长线上时，求证：EDB ACD ∠=∠；（2）如图2，当ABC 为等边三角形时，D 是BA 的延长线上一点，E 在BC 上时，作//EF AC ，求证：BE AD =；（3）在（2）的条件下，ABC ∠的平分线BF 交CD 于点F ，连AF ，过A 点作AH CD ⊥于点H ，当30EDC ∠=︒，6CF =时，求DH 的长度．11．在《经典几何图形的研究与变式》一课中，庞老师出示了一个问题：“如图1，等腰直角三角形的三个顶点分别落在三条等距的平行线1l ，2l ，3l 上，90BAC ∠=︒，且每两条平行线之间的距离为1，求AB 的长度”.在研究这道题的解法和变式的过程中，同学们提出了很多想法：（1）小明说：我只需要过B 、C 向1l 作垂线，就能利用全等三角形的知识求出AB 的长. （2）小林说：“我们可以改变ABC 的形状.如图2，AB AC =，120BAC ∠=︒，且每两条平行线之间的距离为1，求AB 的长.”（3）小谢说：“我们除了改变ABC 的形状，还能改变平行线之间的距离.如图3，等边三角形ABC 三个顶点分别落在三条平行线1l ，2l ，3l 上，且1l 与2l 之间的距离为1，2l 与3l 之间的距离为2，求AB 的长、”请你根据3位同学的提示，分别求出三种情况下AB 的长度.12．在Rt ABC 中，ACB =∠90°，30A ∠=︒，点D 是AB 的中点，连结CD ．（1）如图①，BC 与BD 之间的数量关系是_________，请写出理由；（2）如图②，若P 是线段CB 上一动点（点P 不与点B 、C 重合），连结DP ，将线段DP 绕点D 逆时针旋转60°，得到线段DF ，连结BF ，请猜想BF ，BP ，BD 三者之间的数量关系，并证明你的结论；（3）若点P 是线段CB 延长线上一动点，按照（2）中的作法，请在图③中补全图形，并直接写出BF ，BP ，BD 三者之间的数量关系．【参考答案】***试卷处理标记，请不要删除一、压轴题1．（1）5；（2）直角三角形，理由见解析；（3）44,33E ⎛⎫- ⎪⎝⎭或82,33E ⎛⎫- ⎪⎝⎭【解析】【分析】（1）先求出直线122y x =+与x 轴的交点B 的坐标和与y 轴的交点C 的坐标，把点C 代入直线2y x m =-+，求出m 的值，再求它与x 轴的交点A 的坐标，ABC 的面积用AB 乘OC 除以2得到；（2）用勾股定理求出BC 的平方，AC 的平方，再根据AB 的平方，用勾股定理的逆定理证明ABC 是直角三角形；（3）先根据角平分线求出D 的坐标，再去分两种情况构造全等三角形，利用全等三角形的性质求出对应的边长，从而得到点E 的坐标．【详解】解：（1）令0x =，则10222y =⨯+=， ∴()0,2C ，令0y =，则1202x +=，解得4x =-， ∴()4,0B -，将()0,2C 代入2y x m =-+，得2m =， ∴22y x =-+，令0y =，则220x -+=，解得1x =， ∴1,0A ，∴5AB =，2OC =，∴152ABC S AB OC =⋅=△；（2）根据勾股定理，222224220BC BO OC =+=+=，22222125AC AO OC =+=+=，且22525AB ==，∴222AB BC AC =+，则ABC 是直角三角形；（3）∵CD 平分ACB ∠， ∴12AD AC BD BC ==， ∴1533AD AB ==， ∴23OD AD OA =-=， ∴2,03D ⎛⎫-⎪⎝⎭①如图，CED ∠是直角，过点E 作EN x ⊥轴于点N ，过点C 作CM EN ⊥于点M ，由（2）知，90ACB ∠=︒， ∵CD 平分ACB ∠， ∴45ECD ∠=︒，∴CDE △是等腰直角三角形， ∴CE DE =，∵90NED MEC ∠+∠=︒，90NED NDE ∠+∠=︒， ∴MEC NDE ∠=∠，在DNE △和EMC △中，NDE MEC DNE EMC DE EC ∠=∠⎧⎪∠=∠⎨⎪=⎩， ∴()DNE EMC AAS ≅，设DN EM x ==，EN CM y ==，根据图象列式：DO DN CM EN EM CO +=⎧⎨+=⎩，即232x y x y ⎧+=⎪⎨⎪+=⎩，解得2343x y ⎧=⎪⎪⎨⎪=⎪⎩，∴43EN CM ==， ∴44,33E ⎛⎫-⎪⎝⎭；②如图，CDE ∠是直角，过点E 作EG x ⊥轴于点G ，同理CDE △是等腰直角三角形，且可以证得()CDO DEG AAS ≅， ∴2DG CO ==，23EG DO ==， ∴28233GO GD DO =+=+=， ∴82,33E ⎛⎫- ⎪⎝⎭，综上：44,33E ⎛⎫- ⎪⎝⎭，82,33E ⎛⎫- ⎪⎝⎭．【点睛】本题考查一次函数综合，解题的关键是掌握一次函数解析式的求解，与坐标轴交点的求解，图象围成的三角形面积的求解，还涉及勾股定理、角平分线的性质、全等三角形等几何知识，需要运用数形结合的思想去求解．2．（1）全等，垂直，理由详见解析；（2）存在，11t x =⎧⎨=⎩或232t x =⎧⎪⎨=⎪⎩【解析】【分析】（1）在t =1的条件下，找出条件判定△ACP 和△BPQ 全等，再根据全等三角形的性质和直角三角形的两个锐角互余的性质，可证∠CPQ= 90°，即可判断线段 PC 和线段 PQ 的位置（2）本题主要在动点的条件下，分情况讨论，利用三角形全等时对应边相等的性质进行解答即可. 【详解】(1)当t=1时，AP= BQ=1, BP= AC=3, 又∠A=∠B= 90°，在△ACP 和△BPQ 中，{AP BQ A B AC BP=∠=∠= ∴△ACP ≌△BPQ(SAS). ∴∠ACP=∠BPQ ,∴∠APC+∠BPQ=∠APC+∠ACP = 90*. ∴∠CPQ= 90°，即线段PC 与线段PQ 垂直； (2)①若△ACP ≌△BPQ ，则AC= BP ，AP= BQ ，34tt xt=-⎧⎨=⎩ 解得11t x =⎧⎨=⎩; ②若△ACP ≌△BQP ，则AC= BQ ，AP= BP ，34xtt t =⎧⎨=-⎩解得：232t x =⎧⎪⎨=⎪⎩综上所述,存在11t x =⎧⎨=⎩或232t x =⎧⎪⎨=⎪⎩使得△ACP 与△BPQ 全等.【点睛】本题主要考查三角形全等与动点问题，熟练掌握三角形全等的性质与判定定理，是解决本题的关键.3．（1）①△BPD 与△CQP 全等，理由见解析；②当点Q 的运动速度为125cm /s 时，能够使△BPD 与△CQP 全等；（2）经过90s 点P 与点Q 第一次相遇在线段AB 上相遇．【解析】（1）①由“SAS”可证△BPD ≌△CQP ；②由全等三角形的性质可得BP=PC=12BC=5cm ，BD=CQ=6cm ，可求解；（2）设经过x 秒，点P 与点Q 第一次相遇，列出方程可求解．【详解】解：（1）①△BPD 与△CQP 全等，理由如下：∵AB =AC =18cm ，AD =2BD ， ∴AD =12cm ，BD =6cm ，∠B =∠C ， ∵经过2s 后，BP =4cm ，CQ =4cm ， ∴BP =CQ ，CP =6cm =BD ，在△BPD 和△CQP 中，BD CP B C BP CQ =⎧⎪∠=∠⎨⎪=⎩， ∴△BPD ≌△CQP （SAS ），②∵点Q 的运动速度与点P 的运动速度不相等， ∴BP ≠CQ ，∵△BPD 与△CQP 全等，∠B =∠C ， ∴BP =PC =12BC =5cm ，BD =CQ =6cm ， ∴t =52， ∴点Q 的运动速度=612552=cm /s ，∴当点Q 的运动速度为125cm /s 时，能够使△BPD 与△CQP 全等；（2）设经过x 秒，点P 与点Q 第一次相遇，由题意可得：125x ﹣2x =36，解得：x =90，点P 沿△ABC 跑一圈需要181810232++=（s ） ∴90﹣23×3=21（s ），∴经过90s 点P 与点Q 第一次相遇在线段AB 上相遇．【点睛】本题考查了全等三角形的判定和性质，等腰三角形的性质，一元一次方程的应用，掌握全等三角形的判定是本题的关键．4．（1）①60°；②60°；（2）∠BFE =α．【解析】【分析】（1）①先证明△ACE≌△CBD得到∠ACE=∠CBD，再由三角形外角和定理可得∠BFE=∠CBD+∠BCF；②先证明△ACE≌△CBD得∠ACE=∠CBD=∠DCF，再由三角形外角和定理可得∠BFE=∠D+∠DCF=∠D+∠CBD=∠BCA；（2）证明△AEC≌△CDB得到∠E=∠D，则∠BFE=∠D+∠DCF=∠E+∠ECA=∠OAC=α．【详解】（1）如图①中，∵△ABC是等边三角形，∴AC=CB，∠A=∠BCD=60°，∵AE=CD，∴△ACE≌△CBD，∴∠ACE=∠CBD，∴∠BFE=∠CBD+∠BCF=∠ACE+∠BCF=∠BCA=60°．故答案为60．（2）如图②中，∵△ABC是等边三角形，∴AC=CB，∠A=∠BCD=60°，∴∠CAE=∠BCD=′120°∵AE=CD，∴△ACE≌△CBD，∴∠ACE=∠CBD=∠DCF，∴∠BFE=∠D+∠DCF=∠D+∠CBD=∠BCA=60°．故答案为60．（3）如图③中，∵点O 是AC 边的垂直平分线与BC 的交点，∴OC=OA ，∴∠EAC=∠DCB=α，∵AC=BC ，AE=CD ，∴△AEC ≌△CDB ，∴∠E=∠D ，∴∠BFE=∠D+∠DCF=∠E+∠ECA=∠OAC=α．【点睛】本题综合考查了三角形全等以及三角形外角和定理.5．（1）56°；（2）y=454x +；（3）36°或1807°. 【解析】【分析】（1）根据等边对等角求出等腰△ABC 的底角度数，再根据角平分线的定义得到∠ABE 的度数，再根据高的定义得到∠BDC=90°，从而可得∠BPD ；（2）按照（1）中计算过程，即可得到∠A 与∠EPC 的关系，即可得到结果；（3）分①若EP=EC ，②若PC=PE ，③若CP=CE ，三种情况，利用∠ABC+∠BCD=90°，以及y=454x +解出x 即可. 【详解】解：（1）∵AB=AC ，∠A=44°，∴∠ABC=∠ACB=（180-44）÷2=68°，∵CD ⊥AB ，∴∠BDC=90°，∵BE 平分∠ABC ，∴∠ABE=∠CBE=34°，∴∠BPD =90-34=56°；（2）∵∠A =x °，∴∠ABC=（180°-x°）÷2=（902x -）°，由（1）可得：∠ABP=12∠ABC=（454x -）°，∠BDC=90°， ∴∠EPC =y °=∠BPD=90°-（454x -）°=（454x +）°，即y 与 x 的关系式为y=454x +；（3）①若EP=EC ，则∠ECP=∠EPC=y ，而∠ABC=∠ACB=902x -，∠ABC+∠BCD=90°，则有：902x -+（902x --y ）=90°，又y=454x +， ∴902x -+902x --（454x +）=90°，解得：x=36°；②若PC=PE ，则∠PCE=∠PEC=（180-y ）÷2=902y -，由①得：∠ABC+∠BCD=90°， ∴902x -+[902x --（902y -）]=90，又y=454x +，解得：x=1807°； ③若CP=CE ，则∠EPC=∠PEC=y ，∠PCE=180-2y ，由①得：∠ABC+∠BCD=90°， ∴902x -+902x --（180-2y ）=90，又y=454x +，解得：x=0，不符合，综上：当△EPC 是等腰三角形时，∠A 的度数为36°或1807°. 【点睛】本题考查了等腰三角形的性质，二元一次方程组的应用，高与角平分线的定义，有一定难度，关键是找到角之间的等量关系.6．（1）①证明见解析；②DE =14；（2）①8t －10；②t =2；③t =10,211【解析】【分析】（1）①先证明∠DAC ＝∠ECB ，由AAS 即可得出△ADC ≌△CEB ；②由全等三角形的性质得出AD＝CE＝8，CD＝BE＝6，即可得出DE＝CD＋CE＝14；（2）①当点N在线段CA上时，根据CN＝CN−BC即可得出答案；②点M与点N重合时，CM＝CN，即3t＝8t−10，解得t＝2即可；③分两种情况：当点N在线段BC上时，△PCM≌△QNC，则CM＝CN，得3t＝10−8t，解得t＝1011；当点N在线段CA上时，△PCM≌△QCN，则3t＝8t−10，解得t＝2；即可得出答案．【详解】（1）①证明：∵AD⊥DE，BE⊥DE，∴∠ADC＝∠CEB＝90°，∵∠ACB＝90°，∴∠DAC＋∠DCA＝∠DCA＋∠BCE＝90°，∴∠DAC＝∠ECB，在△ADC和△CEB中ADC CEBDAC ECBAC CB∠∠∠∠⎧⎪⎨⎪⎩＝＝＝，∴△ADC≌△CEB（AAS）；②由①得：△ADC≌△CEB，∴AD＝CE＝8，CD＝BE＝6，∴DE＝CD＋CE＝6＋8＝14；（2）解：①当点N在线段CA上时，如图3所示：CN＝CN−BC＝8t−10；②点M与点N重合时，CM＝CN，即3t＝8t−10，解得：t＝2，∴当t为2秒时，点M与点N重合；③分两种情况：当点N在线段BC上时，△PCM≌△QNC，∴CM＝CN，∴3t＝10−8t，解得：t＝1011；当点N在线段CA上时，△PCM≌△QCN，点M与N重合，CM＝CN，则3t＝8t−10，解得：t＝2；综上所述，当△PCM与△QCN全等时，则t等于1011s或2s，故答案为：1011s或2s．【点睛】本题是三角形综合题目，考查了全等三角形的判定与性质、等腰直角三角形的性质、直角三角形的性质、分类讨论等知识；本题综合性强，熟练掌握全等三角形的判定与性质是解题的关键．7．（1）（0，6），（8，0）；（2）存在t=2.4时，使得△ODP与△ODQ的面积相等；（3）2∠GOA+∠ACE=∠OHC，理由见解析．【解析】【分析】（1）根据算术平方根的非负性，绝对值的非负性即可求解；（2）根据运动速度得到OQ=t，OP=8-2t，根据△ODP与△ODQ的面积相等列方程求解即可；（3）由∠AOC=90°，y轴平分∠GOD证得OG∥AC，过点H作HF∥OG交x轴于F，得到∠FHC=∠ACE，∠FHO=∠GOD，从而∠GOD+∠ACE=∠FHO+∠FHC，即可证得2∠GOA+∠ACE=∠OHC.【详解】（180b-=，∴a-b+2=0，b-8=0，∴a=6，b=8，∴A（0，6），C（8，0）；故答案为：（0，6），（8，0）；（2）由（1）知，A（0，6），C（8，0），∴OA=6，OB=8，由运动知，OQ=t，PC=2t，∴OP=8-2t，∵D（4，3），∴114222ODQ DS OQ x t t=⨯=⨯=△，11823123 22ODP DS OP y t t =⨯=-⨯=-△（），∵△ODP与△ODQ的面积相等，∴2t=12-3t，∴t=2.4，∴存在t=2.4时，使得△ODP与△ODQ的面积相等；（3）2∠GOA+∠ACE=∠OHC，理由如下：∵x轴⊥y轴，∴∠AOC=∠DOC+∠AOD=90°，∴∠OAC+∠ACO=90°.又∵∠DOC=∠DCO，∴∠OAC=∠AOD.∵x轴平分∠GOD，∴∠GOA=∠AOD.∴∠GOA=∠OAC.∴OG∥AC，如图，过点H作HF∥OG交x轴于F，∴HF∥AC，∴∠FHC=∠ACE.∵OG∥FH，∴∠GOD=∠FHO，∴∠GOD+∠ACE=∠FHO+∠FHC，即∠GOD+∠ACE=∠OHC，∴2∠GOA+∠ACE=∠OHC．【点睛】此题考查算术平方根的非负性，绝对值的非负性，坐标系中的动点问题，平行线的判定及性质定理，是一道较为综合的题型.8．（1）A(-4，0) ；B(0，4)；C(2，0)；（2）①点E的位置见解析，E（43，0）；②D点的坐标为（-1，3）或（45，125）【解析】【分析】（1）先利用一次函数图象上点的坐标特点求得点A、B的坐标；然后把B点坐标代入y=−2x＋b求出b的值，确定此函数解析式，然后再求C点坐标；（2）①根据轴对称—最短路径问题画出点E的位置，由待定系数法确定直线DB1的解析式为y=−3x−4，易得点E的坐标；②分两种情况：当点D在AB上时，当点D在BC上时．当点D在AB上时，由等腰直角三角形的性质求得D点的坐标为（−1，3）；当点D在BC上时，设AD交y轴于点F，证△AOF与△BOC全等，得OF=2，点F的坐标为（0，2），求得直线AD的解析式为122y x =+，与y=−2x ＋4组成方程组，求得交点D 的坐标为（45，125）．【详解】（1）在y=x +4中，令x =0，得y=4，令y =0，得x=-4，∴A(-4，0) ，B(0，4)把B(0，4)代入y=-2x+b ，得b =4，∴直线BC 为：y=-2x+4在y=-2x +4中，令y =0，得x=2，∴C 点的坐标为(2，0)；（2）①如图∵点D 是AB 的中点∴D （-2，2）点B 关于x 轴的对称点B 1的坐标为（0，-4），设直线DB 1的解析式为y kx b =+，把D （-2，2），B 1（0，-4）代入，得224k b b -+=⎧⎨=-⎩，解得k=-3，b=-4，∴该直线为：y=-3x-4，令y=0，得x=43-， ∴E 点的坐标为（43-，0）． ②存在，D 点的坐标为（-1，3）或（45，125）．当点D 在AB 上时，∵OA=OB=4，∴∠BAC=45°，∴△ACD 是以∠ADC 为直角的等腰直角三角形，∴点D的横坐标为4212，当x=-1时，y=x+4=3，∴D点的坐标为（-1，3）；当点D在BC上时，如图，设AD交y轴于点F．∵∠FAO＋∠AFO＝∠CBO＋∠BFD，∠AFO＝∠BFD，∴∠FAO=∠CBO，又∵AO=BO，∠AOF=∠BOC，∴△AOF≌△BOC（ASA）∴OF=OC=2，∴点F的坐标为（0，2），设直线AD的解析式为y mx n=+，将A（-4，0）与F（0，2）代入得402m nn-+=⎧⎨=⎩，解得1,22m n==，∴122y x=+，联立12224y xy x⎧=+⎪⎨⎪=-+⎩，解得：45125xy⎧=⎪⎪⎨⎪=⎪⎩，∴D的坐标为（45，125）．综上所述：D点的坐标为（-1，3）或（45，125）【点睛】本题是一次函数的综合题，难度适中，考查了利用待定系数法求一次函数的解析式、轴对称的最短路径问题、直角三角形问题，第（2）②题采用了分类讨论的思想，与三角形全等结合，解题的关键是灵活运用一次函数的图象与性质以及全等的知识．9．（1）∠AFE=60°；（2）见解析；（3）75【解析】【分析】（1）通过证明BCE CAD≌得到对应角相等，等量代换推导出60AFE∠=︒；（2）由（1）得到60AFE∠=︒，CE AD=则在Rt AHF△中利用30°所对的直角边等于斜边的一半，等量代换可得；（3）通过在PF上取一点K使得KF=AF，作辅助线证明ABK和ACF全等，利用对应边相等，等量代换得到比值.(通过将ACF顺时针旋转60°也是一种思路.)【详解】（1）解：如图1中．∵ABC为等边三角形，∴AC=BC，∠BAC=∠ABC=∠ACB=60°，在BCE和CAD中，60BE CDCBE ACDBC CA=⎧⎪∠=∠=︒⎨⎪=⎩，∴BCE CAD≌（SAS），∴∠BCE=∠DAC，∵∠BCE+∠ACE=60°，∴∠DAC+∠ACE=60°，∴∠AFE=60°．（2）证明：如图1中，∵AH⊥EC，∴∠AHF=90°，在Rt△AFH中，∵∠AFH=60°，∴∠FAH=30°，∴AF=2FH，∵EBC DCA≌，∴EC=AD，∵AD=AF+DF=2FH+DF，∴2FH+DF=EC．（3）解：在PF上取一点K使得KF=AF，连接AK、BK，∵∠AFK =60°，AF =KF ，∴△AFK 为等边三角形，∴∠KAF =60°，∴∠KAB =∠FAC ，在ABK 和ACF 中，AB AC KAB ACF AK AF =⎧⎪∠=∠⎨⎪=⎩，∴ ABK ACF ≌(SAS )，BK CF =∴∠AKB =∠AFC =120°，∴∠BKE =120°﹣60°=60°，∵∠BPC =30°，∴∠PBK =30°，∴29BK CF PK CP ===， ∴79PF CP CF CP =-=， ∵45()99AF KF CP CF PK CP CP CP ==-+=-= ∴779559CP PF AF CP == . 【点睛】掌握等边三角形、直角三角形的性质，及三角形全等的判定通过一定等量代换为本题的关键.10．（1）见解析；（2）见解析；（3）3【解析】【分析】（1）根据等腰三角形的性质和外角的性质即可得到结论；（2）过E 作EF ∥AC 交AB 于F ，根据已知条件得到△ABC 是等边三角形，推出△BEF 是等边三角形，得到BE=EF ，∠BFE=60°，根据全等三角形的性质即可得到结论；（3）连接AF ，证明△ABF ≌△CBF ，得AF=CF ，再证明DH=AH=12CF=3．【详解】解：（1）∵AB=AC ，∴∠ABC=∠ACB ，∵DE=DC ，∴∠E=∠DCE ，∴∠ABC-∠E=∠ACB-∠DCB ，即∠EDB=∠ACD ；（2）∵△ABC 是等边三角形，∴∠B=60°，∴△BEF 是等边三角形，∴BE=EF ，∠BFE=60°，∴∠DFE=120°，∴∠DFE=∠CAD ，在△DEF 与△CAD 中， EDF DCA DFE CAD DE CD ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△DEF ≌△CAD （AAS ），∴EF=AD ，∴AD=BE ；（3）连接AF ，如图3所示：∵DE=DC ，∠EDC=30°，∴∠DEC=∠DCE=75°，∴∠ACF=75°-60°=15°，∵BF 平分∠ABC ，∴∠ABF=∠CBF ，在△ABF 和△CBF 中，AB BCABF CBFBF BF=⎧⎪∠=∠⎨⎪=⎩，△ABF≌△CBF（SAS），∴AF=CF，∴∠FAC=∠ACF=15°，∴∠AFH=15°+15°=30°，∵AH⊥CD，∴AH=12AF=12CF=3，∵∠DEC=∠ABC+∠BDE，∴∠BDE=75°-60°=15°，∴∠ADH=15°+30°=45°，∴∠DAH=∠ADH=45°，∴DH=AH=3．【点睛】本题考查了全等三角形的判定与性质，等腰三角形和直角三角形的性质，三角形的外角的性质，等边三角形的判定和性质，证明三角形全等是解决问题的关键．11．（1522213221【解析】【分析】（1）分别过点B，C向l1作垂线，交l1于M，N两点，证明△ABM≌△CAN，得到AM=CN，AN=BM，即可得出AB；（2）分别过点B，C向l1作垂线，交l1于点P，Q两点，在l1上取M，N使∠AMB=∠CNA=120°，证明△AMB≌△CAN，得到CN=AM，再通过△PBM和△QCN算出PM和NQ的值，得到AP，最后在△APB中，利用勾股定理算出AB的长；（3）在l3上找M和N，使得∠BNC=∠AMC=60°，过B作l3的垂线，交l3于点P，过A作l3的垂线，交l3于点Q，证明△BCN≌△CAM，得到CN=AM，在△BPN和△AQM中利用勾股定理算出NP和AM，从而得到PC，结合BP算出BC的长，即为AB.【详解】解：（1）如图，分别过点B，C向l1作垂线，交l1于M，N两点，由题意可得：∠BAC=90°，∵∠NAC+∠MAB=90°，∠NAC+∠NCA=90°，∴∠MAB=∠NCA，在△ABM和△CAN中，===AMB CNAMAB NCAAB AC∠∠⎧⎪∠∠⎨⎪⎩，∴△ABM≌△CAN（AAS），∴AM=CN=2，AN=BM=1，∴AB=22251=+；（2）分别过点B，C向l1作垂线，交l1于P，Q两点，在l1上取M，N使∠AMB=∠CNA=120°，∵∠BAC=120°，∴∠MAB+∠NAC=60°，∵∠ABM+∠MAB=60°，∴∠ABM=∠NAC，在△AMB和△CNA中，===AMB CNAABM NACAB AC∠∠⎧⎪∠∠⎨⎪⎩，∴△AMB≌△CNA（AAS），∴CN=AM，∵∠AMB=∠ANC=120°，∴∠PMB=∠QNC=60°，∴PM=12BM，NQ=12NC，∵PB=1，CQ=2，设PM=a，NQ=b，∴2221=4a a+，2222=4b b+，解得：3=3a ，23=3b ， ∴CN=AM=222323⎛⎫+ ⎪ ⎪⎝⎭=43， ∴AB=22AP BP +=()22AM PM BP ++=221；（3）如图，在l 3上找M 和N ，使得∠BNC=∠AMC=60°，过B 作l 3的垂线，交于点P ，过A 作l 3的垂线，交于点Q ，∵△ABC 是等边三角形，∴BC=AC ，∠ACB=60°，∴∠BCN+∠ACM=120°，∵∠BCN+∠NBC=120°，∴∠NBC=∠ACM ，在△BCN 和△CAM 中，BNC CMA NBC MAC BC AC ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△BCN ≌△CAM （AAS ），∴CN=AM ，BN=CM ，∵∠PBN=90°-60°=30°，BP=2，∴BN=2NP ，在△BPN 中，222BP NP BN +=，即22224NP NP +=，解得：NP=33， ∵∠AMC=60°，AQ=3，∴∠MAQ=30°，∴AM=2QM ，在△AQM 中，222AQ QM AM +=，即22234QM QM +=，解得：QM=3，∴AM=23=CN ，∴PC=CN-NP=AM-NP=43，在△BPC 中，BP 2+CP 2=BC 2，即BC=22224322123BP CP ⎛⎫+=+= ⎪ ⎪⎝⎭， ∴AB=BC=2213.【点睛】本题考查了全等三角形的判定和性质，平行线之间的距离，等腰三角形的性质，等边三角形的性质以及勾股定理，解题的关键是利用平行线构造全等三角形，再利用全等三角形的性质以及勾股定理求解.12．（1）BC BD =，理由见解析；（2）BF BP BD +=，证明见解析；（3）BF BP BD +=．【解析】【分析】（1）利用含30的直角三角形的性质得出12BC AB =，即可得出结论；（2）同（1）的方法得出BC BD =进而得出BCD ∆是等边三角形，进而利用旋转全等模型易证DCP DBF ∆≅∆，得出CP BF =即可解答；（3）同（2）的方法得出结论．【详解】解：（1）90ACB ∠=︒，30A ∠=︒，60CBA ∴∠=︒，12BC AB =，点D 是AB 的中点，BC BD ∴=，故答案为：BC BD =；（2）BF BP BD +=，理由：90ACB∠=︒，30A∠=︒，60CBA∴∠=︒，12BC AB=，点D是AB的中点，BC BD∴=，DBC∴∆是等边三角形，60CDB∴∠=︒，DC DB=，线段DP绕点D逆时针旋转60︒，得到线段DF，60PDF∴∠=︒，DP DF=，CDB PDB PDF PDB∴∠-∠=∠-∠，CDP BDF∴∠=∠，在DCP∆和DBF∆中，DC DBCDP BDFDP DF=⎧⎪∠=∠⎨⎪=⎩，DCP DBF∴∆≅∆，CP BF∴=，CP BP BC+=，BF BP BC∴+=，BC BD=，BF BP BD∴+=；（3）如图③，BF BD BP=+，理由：90ACB∠=︒，30A∠=︒，60CBA∴∠=︒，12BC AB=，点D是AB的中点，BC BD∴=，DBC∴∆是等边三角形，60CDB∴∠=︒，DC DB=，线段DP绕点D逆时针旋转60︒，得到线段DF，60PDF∴∠=︒，DP DF=，CDB PDB PDF PDB∴∠+∠=∠+∠，CDP BDF ∴∠=∠，在DCP ∆和DBF ∆中，DC DB CDP BDF DP DF =⎧⎪∠=∠⎨⎪=⎩，DCP DBF ∴∆≅∆，CP BF ∴=，CP BC BP =+，BF BC BP ∴=+，BC BD =，BF BD BP ∴=+．【点睛】此题是三角形综合题，主要考查了含30的直角三角形的性质，等边三角形的判定，全等三角形的判定和性质，旋转的性质，解本题的关键是判断出DCP DBF ∆≅∆，是一道中等难度的中考常考题．。

郑州市2019-2020学年八年级下期期末压轴题精讲精练

图1图2图3F EDCBAGFEDCBAGGABCD E F 备用图ABCOOPEDCBA 专题郑州市2019-2020学年八年级下期期末压轴题精讲精练例1. (2013-2014郑州市)已知，在正方形ABCD 中，△BEF 是以BF 为斜边的等腰直角三角形，取DF 得中点G ，连接EG ，CG.⑴如图1，若△BEF 的斜边BF 在BC 边上，猜想EG 和CG 之间的数量关系，并证明； ⑵将图1中的△BEF 绕点B 顺时针旋转45°，如图2所示，则⑴中的结论是否仍成立？若成立，请给出证明；若不成立，请说明理由.⑶将图1中的△BEF 绕点B 顺时针旋转任意角度，如图3所示，则⑴中的结论是否仍成立？请直接写出结论.例2. (2014-2015郑州市)如图，已知在Rt △ABC 中，AB=BC ，∠ABC=90°，BO ⊥AC 于点O ，点P 、D 分别在AO 和BC 上，PB=PD ，DE ⊥AC 于点E. ⑴若PB 平分∠ABO ，其余条件不变．求证：AP=CD ．⑵若点P 是一个动点，点P 运动到OC 的中点P′时，满足题中条件的点D 也随之在直线BC 上运动到点D′，请直接写出CD′与AP′的数量关系．（不必写解答过程）例3. (2015-2016郑州市)在△ABC 中，AB=AC，∠A=30°，将线段BC绕点B逆时针旋转60°得到线段BD，再将线段BD平移到EF，使点E在AB上，点F在AC上．⑴如图1，直接写出∠ABD和∠CFE的度数；⑵在图1中，AE和CF有什么数量关系？请说明理由；⑶如图2，连接CE，判断△CEF的形状并加说明理由．例4. (2016-2017郑州市)在△ABC中，AC=BC，将△ABC绕点A顺时针方向旋转，得到△ADE，旋转角为α（0°＜α＜180°），点B的对应点为点D，点C的对应点为点E，连接BD．⑴如图，当α=60°时，△ABD是等边三角形吗？请说明理由；⑵在旋转过程中，过点D作DG垂直于直线AB，垂足为点G，连接CE，当∠DAG=∠ACB，∠C<90°，且线段DG与线段AE无公共点时，判断CE与AB的关系，并说明理由. (请在备用图中将图形补充完整)AB Ex 例5.( 2017-2018郑州市)如图，在平行四边形ABCD 中，∠B =90°，且AD =9cm ，AB =4cm ，延长BC 到点E ，使CE =3cm ，连接DE .若动点P 从A 点出发，以每秒2cm 的速度沿线段AD 向点D 运动;动点Q 从E 点出发以每秒3cm 的速度沿EB 向B 点运动，当点P 、Q 有一个到达指定位置时，动点P 、Q 同时停止运动，设点P 、Q 同时出发，并运动了t 秒，回答下列问题： (1)求DE 的长；(2)当t 为多少时，四边形PQED 成为平行四边形； (3)请直接写出使得△DQE 是等腰三角形时t 的值.例6. (2018-2019郑州市)如图，在平面直角坐标系中，直线y =kx +b 与x 轴、y 轴相交于A (6，0)、B (0，3)两点，动点C 在线段OA 上，将线段CB 绕着点C 顺时针旋转90°得到CD ，此时点D 恰好落在直线AB 上，过点D 作DE ⊥x 轴于点E . (1)求直线y =kx +b 的表达式及点D 的坐标；(2)若点P 在y 轴上，点Q 在直线AB 上，是否存在以C 、D 、P 、Q 为顶点的四边形是平行四边形？若存在，直接写出所有满足条件的Q 点坐标；若不存在，请说明理由.以上是郑州市2014-2020年八年级下册期末试卷压轴题真题，通过对前面的了解与分析，预测【2019-2020郑州市】八年级下册期末试卷压轴题应该延续以上题型，以几何变换综合题为压轴题，应引起同学们的重视.【预测1】已知O为直线MN上一点，OP⊥MN，在等腰Rt△ABO中，∠BAO=90°，AC ∥OP交OM于C，D为OB的中点，DE⊥DC交MN于E．⑴如图1，若点B在OP上，则①AC OE（填“＜”，“=”或“＞”）；②线段CA、CO、CD满足的等量关系式是；⑵将图1中的等腰Rt△ABO绕O点顺时针旋转α（0°＜α＜45°），如图2，那么⑴中的结论②是否成立？请说明理由；⑶将图1中的等腰Rt△ABO绕O点顺时针旋转α（45°＜α＜90°），请你在图3中画出图形，并直接写出线段CA、CO、CD满足的等量关系式．【预测2】如图1，在平面直角坐标系中，直线y=-1x+b与x轴、y轴相交于A、B两点，2动点C（m，0）在线段OA上，将线段CB绕着点C顺时针旋转90°得到CD，此时点D 恰好落在直线AB上，过点D作DE⊥x轴于点E．⑴求m和b的数量关系；⑵当m=1时，如图2，将△BCD沿x轴正方向平移得△B′C′D′，当直线B′C′经过点D时，求点B′的坐标及△BCD平移的距离；⑶在⑵的条件下，直线AB上是否存在一点P，以P、C、D为顶点的三角形是等腰直角三角形？若存在，写出满足条件的P点坐标；若不存在，请说明理由．【预测3】如图，在平面直角坐标系中，矩形OABC的顶点A在y轴的正半轴上，点C在x轴的正半轴上，线段OA，OC的长分别是m，n且满足(m−6)2+0，点D是线段OC上一点，将△AOD沿直线AD翻折，点O落在矩形对角线AC上的点E处．⑴求OA，OC的长；⑵求直线AD的解析式；⑶点M在直线DE上，在x轴的正半轴上是否存在点N，使以M、A、N、C为顶点的四边形是平行四边形？若存在，请直接写出点N的坐标；若不存在，请说明理由．。

(八年级下册数学)(期末压轴题汇编)

2019 年八年级下册数学期末压轴题汇编1. 如图，矩形 OABC的极点 A、C 分别在x、y的正半轴上，点 B 的坐标为 (3,4) 一次函数y 2x b 的图象与边OC 3AB分别交于点 D、 E，而且知足 OD= BE.点 M是线段 DE上的一个动点 .(1) 求 b 的值； (2)连结 OM，若三角形 ODM的面积与四边形OAEM的面积之比为1： 3，求点 M的坐标；(3) 设点 N 是x轴上方的平面内的一点，当四边形OM DN是菱形时，求点 N 的坐标；2. 如图，正方形ABCD中， P 为 BD上一动点，过点P 作 PQ⊥ AP交 CD边于点 Q，⑴求证： PA=PQ；⑵用等式表示222PB、PD、 AQ之间的数目关系，并证明；⑶点 P 从点 B 出发，沿 BD方向挪动，若挪动的路径长为2，则 AQ的中点 M挪动的路径为 ---------------；（直接写出答案）3.已知矩形 ABCD的一条边 AD=8，E 是 BC边上的一点，将矩形 ABCD沿折痕 AE折叠，使得极点 B 落在 CD边上的点 P 处，PC= 4（如图 1）；(1)求 AB的长；(2)擦去折痕 AE，连结 PB，设 M是线段 PA 的一个动点 ( 点 M与点 P 、 A 不重合 ).N 是 AB沿长线上的一个动点，而且知足PM=BN过.点 M作 MH PB，垂足为 H，连结 MN交 PB于点 F( 如图 2).①若 M是 PA 的中点，求MH的长；②试问当点M、N 在挪动过程中，线段FH的长度能否发生变化?若变化，说明原因，若不变，求出线段FH的长度；4. 如图，在四边形ABCD中， AD∥ BC，∠ B=90°， AD=6， BC=9，动点 P 从 D 点出发沿 DA以每秒 1 个单位的速度向 A 点运动，动点Q从 B 点出发沿BC以每秒 3 个单位的速度向C点运动．两点同时出发，当 Q点抵达 C点时，点 P 随之停止运动．设点 P 运动的时间为 t 秒；（ 1）求 t 的取值范围；（ 2）求 t 为什么值时， PQ与 CD相等？5. 已知：四边形ABCD是正方形， E 是 AB边上一点，连结DE，过点 D作 DF⊥ DE交 BC的延伸线于点F，连结 EF．（1）如图 1，求证：DE=DF；（2）若点D对于直线EF的对称点为H，连结CH，过点H作PH⊥CH交直线AB于点P；①在图 2 中依题意补全图形；②求证：E为AP的中点；2AM（ 3）如图 3，连结AC交EF于点M，求的值；AB AE6. 如图，在平面直角坐标系xOy中，直线l与x轴交于点A（ 4 ，0），与y轴的正半轴交于点B．点C在直线y x 1上，且 CA⊥ x 轴于点 A；（ 1）求点C的坐标；（ 2）若点D是OA的中点，点E是y轴上一个动点，当EC+ED最小时，求此时点E的坐标；（ 3）若点A 恰幸亏的垂直均分线上，点F在x轴上，且△是以AB为腰的等腰三角形，请直接写出全部知足条BC ABF件的点 F 的坐标；7. 把一个含45°角的直角三角板BEF和一个正方形ABCD摆放在一同，使三角板的直角极点和正方形的极点 B 重合，联络 DF，点 M， N分别为 DF， EF的中点，联络MA，MN．（ 1）如图 1，点E，F分别在正方形的边CB， AB上，请判断MA， MN的数目关系和地点关系，直接写出结论；（ 2）如图 2，点E，F分别在正方形的边CB， AB的延伸线上，其余条件不变，那么你在（1）中获得的两个结论还成立吗？若建立，请加以证明；若不建立，请说明原因；A DA DFMNB ME CB E CN图 1F图28 有一项工作，由甲、乙合作达成，工作一段时间后，甲改良了技术，提升了工作效率．设甲的工作量为y 甲（件），乙的工作量为y 乙（件），甲、乙合作达成的工作量为y（件），工作时间为x（时）， y 与 x 之间的部分函数图象如图①所示， y 乙与 x 之间的部分函数图象如图②所示；（ 1）分别求出甲 2 小时、 6 小时的工作量；（ 2）当 0≤ x≤6 时，在图②中画出 y 甲与 x 的函数图象，并求出 y 甲与 x 之间的函数关系式；（ 3）求工作几小时，甲、乙达成的工作量相等；（ 4）若 6 小时后，甲保持第 6 小时的工作效率，乙改良了技术，提升了工作效率，当x=8 时，甲、乙之间的工作量相差 30 件，求乙提升工作效率后均匀每小时做多少件；9. 如图，在平行四边形ABCD中，∠ BAD的均分线交直线BC于 E，交直线DC于点 F，以 CF为邻边作平行四边形ECFG；（1）如图 1，证明平行四边形 ECFG为菱形；（2）如图 2，若∠ ABC=90°， M是 EF 的中点，求∠ BDM的度数；（3）如图 3，若∠ ABC=120°，请直接写出∠ BDG的度数；。

2016-2019年八年级期末考压轴题专练(填空题)

2016-2019年八年级期末考压轴题专练（填空题）一．分式的加减法（共1小题）1．（2018春•相城区期末）观察下列的式子：＝1﹣，＝﹣，＝﹣……类比这种计算方法，可以求得+++…+＝．二．二次根式的化简求值（共1小题）2．（2018秋•临漳县期末）已知：x＝，y＝．那么+＝．三．一元二次方程的解（共1小题）3．（2014•襄阳）若正数a是一元二次方程x2﹣5x+m＝0的一个根，﹣a是一元二次方程x2+5x ﹣m＝0的一个根，则a的值是．四．解一元二次方程-公式法（共1小题）4．（2019春•太仓市期末）对任意的两实数a，b，用min（a，b）表示其中较小的数，如min（2，﹣4）＝﹣4，则方程x•min（2，2x﹣1）＝x+1的解是．五．一次函数综合题（共1小题）5．（2013•湖州）如图，已知点A是第一象限内横坐标为2的一个定点，AC⊥x轴于点M，交直线y＝﹣x于点N．若点P是线段ON上的一个动点，∠APB＝30°，BA⊥P A，则点P在线段ON上运动时，A点不变，B点随之运动．求当点P从点O运动到点N时，点B 运动的路径长是．六．反比例函数系数k的几何意义（共2小题）6．（2018春•常熟市期末）如图，在△ABC中，AB＝AC，底边BC在x轴正半轴上，点A 在第一象限，延长AB交y轴负半轴于点D，延长CA到点E，使AE＝AC，若双曲线y ＝（x＞0）经过点E，则△BCD的面积为．7．（2019春•常熟市期末）如图正方形OAPB的顶点A，B分别在x轴和y轴上，矩形OCQD 的顶点分别在边OA和y轴上，反比例函数y＝（x＞0）的图象经过P、Q两点．若四边形BDQE的面积为4，则Q的坐标为．七．反比例函数图象上点的坐标特征（共4小题）8．（2017春•工业园区期末）已知点O（0，0）、A（2，0）、B（0，1）．点P在函数y＝的图象上，过点P作PQ⊥x轴，垂足为点Q．若以点P、O、Q为顶点的三角形与△AOB 全等，则满足条件的点P共有个．9．（2017•启东市一模）如图，在平面直角坐标系中，点A（a，b）为第一象限内一点，且a＜b．连结OA，并以点A为旋转中心把OA逆时针转90°后得线段BA．若点A、B恰好都在同一反比例函数的图象上，则的值等于．10．（2018•张家界）如图，矩形ABCD的边AB与x轴平行，顶点A的坐标为（2，1），点B与点D都在反比例函数y＝（x＞0）的图象上，则矩形ABCD的周长为．11．（2019春•相城区期末）如图，在平面直角坐标系中，菱形OABC的边OA在x轴上，AC与OB交于点D（4，2），反比例函数的图象经过点D．若将菱形OABC向左平移n个单位，使点C落在该反比例函数图象上，则n的值为．八．反比例函数与一次函数的交点问题（共6小题）12．（2018•雨花区模拟）如图，正方形ABCD位于第一象限，边长为3，横坐标为1的点A 在直线y＝x上，正方形ABCD的边分别平行于x轴、y轴．若双曲线y＝与正方形ABCD 公共点，则k的取值范围是．13．（2016春•张家港市期末）如图，在平面直角坐标系中，反比例函数y1＝的图象与一次函数y2＝kx+b的图象交于A、B两点．若y1＜y2，则x的取值范围是．14．（2016春•常熟市期末）如图，已知反比例函数y＝与一次函数y＝x+1的图象交于点A（a，﹣1）、B（1，b），则不等式≥x+1的解集为．15．（2017春•姑苏区期末）如图，直线y＝2x与反比例函数y＝的图象交于点A（3，m），点B是线段OA的中点，点E（n，4）在反比例函数的图象上，点F在x轴上，若∠EAB ＝∠EBF＝∠AOF，则点F的横坐标为．16．（2012•丹徒区校级模拟）已知双曲线与直线y＝x﹣相交于点P（a，b），则．17．（2019春•吴江区期末）已知反比例函数y＝的图象与一次函数y＝k（x﹣3）+2（k＞0）的图象在第一象限交于点P，则点P的横坐标a的取值范围为．九．反比例函数综合题（共1小题）18．（2012•历城区模拟）如图，直线与双曲线（k＞0）在第一象限内的交点为R，与x轴的交点为P，与y轴的交点为Q；作RM⊥x轴于点M，若△OPQ与△PRM 的面积是4：1，则k等于．一十．全等三角形的判定与性质（共1小题）19．（2019春•工业园区期末）如图，四边形纸片ABCD中，∠A＝∠C＝90°，BC＝DC．若AB+AD＝8cm，则该纸片的面积为cm2．一十一．角平分线的性质（共1小题）20．（2013•南通二模）如图，已知正方形ABCD的边长为2，对角线AC、BD相交于点O，AE平分∠BAC交BD于点E，则BE的长为．一十二．直角三角形的性质（共1小题）21．（2016春•常熟市期末）如图，在平面直角坐标系中，点D为x轴上的一点，且点D坐标为（4，0），过点D的直线l⊥x轴，点A为直线l上的一动点，连结OA，OB⊥OA交直线l于点B，则的值为．一十三．三角形中位线定理（共1小题）22．（2014•花都区二模）如图，Rt△ABC中，∠ACB＝90°，∠ABC＝60°，BC＝2cm，D 为BC的中点，若动点E以1cm/s的速度从A点出发，沿着A→B→A的方向运动，设E 点的运动时间为t秒（0≤t≤8），连接DE，当△BDE是直角三角形时，t的值为．一十四．平行四边形的性质（共1小题）23．（2018春•常熟市期末）如图，在▱ABCD中，∠B＝60°，AB＝4，点H、G分别是边CD、BC上的动点．连接AH、HG，点E、F分别是AH、GH的中点，连接EF．则EF 的最小值为．一十五．菱形的性质（共1小题）24．（2019春•苏州期末）如图，在菱形ABCD中，∠ABC＝120°，AB＝6，点E在AC 上，以AD为对角线的所有平行四边形AEDF中，EF最小的值是．一十六．菱形的判定与性质（共1小题）25．（2018春•高新区期末）如图，在△ABC中，∠ABC＝90°，BD为AC的中线，过点C 作CE⊥BD于点E，过点A作BD的平行线，交CE的延长线于点F，在AF的延长线上截取FG＝BD，连接BG、DF．若AG＝13，CF＝6，则BG＝．一十七．正方形的性质（共4小题）26．（2016春•吴江区期末）如图，在边长为2的正方形ABCD中，点E是边AD中点，点F在边CD上，且FE⊥BE，设BD与EF交于点G，则△DEG的面积是．27．（2016春•工业园区期末）已知菱形ABCD中，AC＝6cm，BD＝4cm．若以BD为边作正方形BDEF，则AF＝cm．28．（2017春•常熟市期末）如图，正方形ABCD的两条对角线相交于点O．点E是OC的中点，连接DE，过点A作AF⊥DE于点F，交OD于点G．若正方形的边长为4，则DF＝．29．（2019春•苏州期末）如图，正方形ABCD的边长为5cm，E是AD边上一点，AE＝3cm．动点P由点D向点C运动，速度为2cm/s，EP的垂直平分线交AB于M，交CD于N．设运动时间为t秒，当PM∥BC时，t的值为．一十八．轴对称-最短路线问题（共2小题）30．（2018春•工业园区期末）如图，正方形ABCD与矩形EFGH在直线l的同侧，边AD，EH在直线l上，且AD＝5cm，EH＝4cm，EF＝3cm．保持正方形ABCD不动，将矩形EFGH沿直线l左右移动，连接BF，CG，则BF+CG的最小值为cm．31．（2019•陕西二模）如图，正方形ABCD中，AB＝8，点E、F分别在边AB、BC上，BE ＝BF＝2，点P是对角线AC上的一个动点，则PE+PF的最小值是．一十九．翻折变换（折叠问题）（共5小题）32．（2016春•太仓市期末）如图，△ABC中，∠B＝90°，AB＝6，BC＝8，将△ABC沿DE折叠，使点C落在AB边的C′处，并且C′D∥BC，则CD的长是．33．（2017春•张家港市期末）如图，在正方形ABCD中，E、F分别为BC、CD的中点，连接AE、BF，将△BCF沿BF对折，得到△BPF，延长FP交BA的延长线于点Q．给出下列结论：①AE＝BF；②AE⊥BF；③△BQF是等边三角形；④若正方形ABCD的边长为3，则线段AQ的长为其中，正确的结论有．（把你认为正确的结论的序号都填上）34．（2018春•工业园区期末）如图，在菱形ABCD中，AB＝3cm，∠A＝60°．点E，F分别在边AD，AB上，且DE＝1cm．将△AEF沿EF翻折，使点A落在对角线BD上的点A'处，则＝．35．（2017•武汉模拟）如图，菱形ABCD中，P为AB中点，∠A＝60°，折叠菱形ABCD，使点C落在DP所在的直线上，得到经过点D的折痕DE，则∠DEC的大小为°．36．（2019春•姑苏区期末）如图，正方形ABCD中，AB＝30，点E在边CD上，且CD＝3DE．将△ADE沿AE对折至△AFE，延长EF交边BC于点G．连接AG、CF．下列结论：①△ABG≌△AFG；②BG＝15；③△CFG是正三角形；④△FGC的面积为90．其中正确的是（填所有正确答案的序号）．二十．旋转的性质（共3小题）37．（2017春•工业园区期末）如图在四边形ABCD中，BC＝CD，∠BCD＝90°．若AB＝4cm，AD＝3cm，则对角线AC的最大值为cm．38．（2018春•苏州期末）如图，已知Rt△ABC中，两条直角边AB＝3，BC＝4，将Rt△ABC 绕直角顶点B旋转一定的角度得到Rt△DBE，并且点A在DE边上，则△BEC的面积＝．39．如图Rt△ABC中，∠ACB＝90°，D是斜边AB的中点，将△ABC绕点A按顺时针方向旋转，点C落在CD的延长线上的E处，点B落在F处，若AC＝4，BC＝2，则CE的长为．二十一．平行线分线段成比例（共1小题）40．（2019春•太仓市期末）如图，在△ABC中，AD是BC边上的中线，F是AD上一点，且AF：FD＝1：4，连结CF，并延长交AB于点E，则AE：EB＝．二十二．相似三角形的判定（共2小题）41．（2017•蜀山区校级模拟）如图，在△ABC中，∠C＝90°，BC＝16cm，AC＝12cm，点P从点B出发，沿BC以2cm/s的速度向点C移动，点Q从点C出发，以1cm/s的速度向点A移动，若点P、Q分别从点B、C同时出发，设运动时间为ts，当t＝时，△CPQ与△CBA相似．42．（2016春•虎丘区校级期末）如图，在四边形ABCD中，AD∥BC，∠ABC＝90°，AB ＝8，AD＝2，BC＝3，如果边AB上的点P，使得以P，A，D为顶点的三角形与P，B，C为顶点的三角形相似，这样的点P有个．二十三．相似三角形的判定与性质（共6小题）43．（2016春•苏州期末）如图所示，在△ABC中，BC＝4，E、F分别是AB、AC上的点，且EF∥BC，动点P在射线EF上，BP交CE于点D，∠CBP的平分线交CE于Q，当CQ＝CE时，EP+BP＝．44．（2017春•常熟市期末）如图，点F在平行四边形ABCD的边AB上，且AF：BF＝1：2，连接CF并延长，交DA的延长线于点E，若△AEF的面积为2，则平行四边形ABCD的面积为．45．（2018春•苏州期末）如图，在△ABC中，DE∥MN∥BC，且DE、MN把△ABC的面积三等分，那么DE：MN：BC＝．46．（2020•余干县模拟）如图，△ABC的面积为36cm2，边BC＝12cm，矩形DEFG的顶点D、G分别在AB、AC上，E，F在BC上，若EF＝2DE，则DG＝cm．47．（2019春•姑苏区期末）如图，在边长相同的小正方形网格中，点A、B、C、D都在这些小正方形的顶点上，AB，CD相交于点P，则△PBD与△P AC的面积比为．48．（2015•本溪模拟）如图，点M是△ABC内一点，过点M分别作直线平行于△ABC的各边，所形成的三个小三角形△1、△2、△3（图中阴影部分）的面积分别是1，4，9．则△ABC的面积是．二十四．相似三角形的应用（共1小题）49．（2018春•相城区期末）如图，一块直角三角形木板，一条直角边AC的长1.5m，面积为1.5m2．按图中要求加工成一个正方形桌面，则桌面的边长为m．二十五．位似变换（共1小题）50．（2016春•太仓市期末）将反比例函数y＝的图象以原点为位似中心，按相似比2：1放大得到的函数y＝的图象，则k的值为．2016-2019年八年级期末考压轴题专练（填空题）参考答案与试题解析一．分式的加减法（共1小题）1．（2018春•相城区期末）观察下列的式子：＝1﹣，＝﹣，＝﹣……类比这种计算方法，可以求得+++…+＝．【分析】根据＝×（﹣）裂项求和可得．【解答】解：原式＝×（﹣）+×（﹣）+×（﹣）+……+×（﹣）＝×（﹣+﹣+﹣+……+﹣）＝×（﹣）＝×＝，故答案为：．【点评】本题主要考查分式的加减运算，解题的关键是掌握＝×（﹣）和分式的加减运算法则．二．二次根式的化简求值（共1小题）2．（2018秋•临漳县期末）已知：x＝，y＝．那么+＝98．【分析】把x与y分母有理化得到结果，原式通分并利用同分母分式的加法法则计算即可得到结果．【解答】解：∵x＝＝5﹣2，y＝＝5+2，∴原式＝＝＝98，故答案为：98【点评】此题考查了二次根式的化简求值，以及分式的加减法，熟练掌握运算法则是解本题的关键．三．一元二次方程的解（共1小题）3．（2014•襄阳）若正数a是一元二次方程x2﹣5x+m＝0的一个根，﹣a是一元二次方程x2+5x ﹣m＝0的一个根，则a的值是5．【分析】把x＝a代入方程x2﹣5x+m＝0，得a2﹣5a+m＝0①，把x＝﹣a代入方程方程x2+5x﹣m＝0，得a2﹣5a﹣m＝0②，再将①+②，即可求出a的值．【解答】解：∵a是一元二次方程x2﹣5x+m＝0的一个根，﹣a是一元二次方程x2+5x﹣m＝0的一个根，∴a2﹣5a+m＝0①，a2﹣5a﹣m＝0②，①+②，得2（a2﹣5a）＝0，∵a＞0，∴a＝5．故答案为：5．【点评】本题主要考查的是一元二次方程的根即方程的解的定义：能使一元二次方程左右两边相等的未知数的值是一元二次方程的解．又因为只含有一个未知数的方程的解也叫做这个方程的根，所以，一元二次方程的解也称为一元二次方程的根．四．解一元二次方程-公式法（共1小题）4．（2019春•太仓市期末）对任意的两实数a，b，用min（a，b）表示其中较小的数，如min（2，﹣4）＝﹣4，则方程x•min（2，2x﹣1）＝x+1的解是x＝或x＝．【分析】分2＜2x﹣1和2x﹣1≤2两种情况，分别列出方程，解之可得．【解答】解：①若2＜2x﹣1，即x＞1.5时，x+1＝2x，解得x＝1（舍）；②若2x﹣1≤2，即x≤1.5时，x（2x﹣1）＝x+1，解得x＝或x＝，故答案为：x＝或x＝．【点评】本题主要考查解一元二次方程，解题的关键是根据定义列出关于x的方程，并准确求解．五．一次函数综合题（共1小题）5．（2013•湖州）如图，已知点A是第一象限内横坐标为2的一个定点，AC⊥x轴于点M，交直线y＝﹣x于点N．若点P是线段ON上的一个动点，∠APB＝30°，BA⊥P A，则点P在线段ON上运动时，A点不变，B点随之运动．求当点P从点O运动到点N时，点B 运动的路径长是．【分析】（1）首先，需要证明线段B0B n就是点B运动的路径（或轨迹），如答图②所示．利用相似三角形可以证明；（2）其次，如答图①所示，利用相似三角形△AB0B n∽△AON，求出线段B0B n的长度，即点B运动的路径长．【解答】解：由题意可知，OM＝，点N在直线y＝﹣x上，AC⊥x轴于点M，则△OMN为等腰直角三角形，ON＝OM＝×＝．如答图①所示，设动点P在O点（起点）时，点B的位置为B0，动点P在N点（终点）时，点B的位置为B n，连接B0B n∵AO⊥AB0，AN⊥AB n，∴∠OAC＝∠B0AB n，又∵AB0＝AO•tan30°，AB n＝AN•tan30°，∴AB0：AO＝AB n：AN＝tan30°（此处也可用30°角的Rt△三边长的关系来求得），∴△AB0B n∽△AON，且相似比为tan30°，∴B0B n＝ON•tan30°＝×＝．现在来证明线段B0B n就是点B运动的路径（或轨迹）．如答图②所示，当点P运动至ON上的任一点时，设其对应的点B为B i，连接AP，AB i，B0B i∵AO⊥AB0，AP⊥AB i，∴∠OAP＝∠B0AB i，又∵AB0＝AO•tan30°，AB i＝AP•tan30°，∴AB0：AO＝AB i：AP，∴△AB0B i∽△AOP，∴∠AB0B i＝∠AOP．又∵△AB0B n∽△AON，∴∠AB0B n＝∠AOP，∴∠AB0B i＝∠AB0B n，∴点B i在线段B0B n上，即线段B0B n就是点B运动的路径（或轨迹）．综上所述，点B运动的路径（或轨迹）是线段B0B n，其长度为．故答案为：．【点评】本题考查坐标平面内由相似关系确定的点的运动轨迹，难度很大．本题的要点有两个：首先，确定点B的运动路径是本题的核心，这要求考生有很好的空间想象能力和分析问题的能力；其次，由相似关系求出点B运动路径的长度，可以大幅简化计算，避免陷入坐标关系的复杂运算之中．六．反比例函数系数k的几何意义（共2小题）6．（2018春•常熟市期末）如图，在△ABC中，AB＝AC，底边BC在x轴正半轴上，点A 在第一象限，延长AB交y轴负半轴于点D，延长CA到点E，使AE＝AC，若双曲线y＝（x＞0）经过点E，则△BCD的面积为．【分析】连接BE，先根据题意证明BE⊥BC，进而判定△CBE∽△BOD，根据相似比得出BC×OD＝OB×BE的值即为|k|的值，再由三角形面积公式即可求解．【解答】解：如图，连接BE，∵等腰三角形ABC中，AB＝AC，∴∠ABC＝∠ACB，∵AE＝AC，∴AE＝AB，∴∠AEB＝∠ABE，又∵∠AEB+∠ABE+∠ABC+∠ACB＝180°，∴∠ABE+∠ABC＝90°，即BE⊥BC，∴∠CBE＝∠BOD＝90°，又∵∠ACB＝∠ABC＝∠OBD，∴△CBE∽△BOD，∴＝，即BC×OD＝OB×BE，又∵双曲线y＝（x＞0）的图象过点E，∴k＝OB×BE＝5，∴△BCD的面积为BC×OD＝．故答案为：．【点评】此题主要考查了反比例函数比例系数k的几何意义，解题时注意：过双曲线上任意一点引x轴、y轴垂线，所得矩形面积为|k|，体现了数形结合的思想．7．（2019春•常熟市期末）如图正方形OAPB的顶点A，B分别在x轴和y轴上，矩形OCQD 的顶点分别在边OA和y轴上，反比例函数y＝（x＞0）的图象经过P、Q两点．若四边形BDQE的面积为4，则Q的坐标为（3，）．【分析】根据反比例函数系数k的几何意义得出OA•OB＝OC•OD＝16，求得OA＝OB ＝4，四边形BDQE的面积为4，得出OC•OB＝12，从而求得Q点的横坐标为3，代入解析式求得纵坐标．【解答】解：由题意可知，OA•OB＝OC•OD＝16，∵四边形OAPB是正方形，∴OA＝OB＝4，∵四边形BDQE的面积为4，∴四边形OCEB的面积为12，∴OC•OB＝12，∴OC＝＝＝3，∴Q点的横坐标为3，把x＝3代入y＝（x＞0）得，y＝，∴Q（3，），故答案为（3，）．【点评】本题考查了反比例函数系数k的几何意义，正方形的性质，矩形的性质，反比例函数图象上点的坐标特征，根据面积求得OC的长是解题的关键．七．反比例函数图象上点的坐标特征（共4小题）8．（2017春•工业园区期末）已知点O（0，0）、A（2，0）、B（0，1）．点P在函数y＝的图象上，过点P作PQ⊥x轴，垂足为点Q．若以点P、O、Q为顶点的三角形与△AOB 全等，则满足条件的点P共有4个．【分析】根据全等三角形的判定，可得答案．【解答】解：当△OAB≌△QOP时，QO＝OA＝2，PQ＝0B＝1，P（2，1）或（﹣2，﹣1）；当△OAB≌△QPO时，QO＝OB＝1，PQ＝OA＝2P（1，2）或（﹣1，﹣2），故答案为：4．【点评】本题考查了全等三角形的判定与性质，利用全等三角形的判定与性质是解题关键，要分类讨论，以防遗漏．9．（2017•启东市一模）如图，在平面直角坐标系中，点A（a，b）为第一象限内一点，且a＜b．连结OA，并以点A为旋转中心把OA逆时针转90°后得线段BA．若点A、B恰好都在同一反比例函数的图象上，则的值等于．【分析】过A作AE⊥x轴，过B作BD⊥AE，利用同角的余角相等得到一对角相等，再由一对直角相等，且AO＝AB，利用AAS得出三角形AOE与三角形ABD全等，由确定三角形的对应边相等得到BD＝AE＝b，AD＝OE＝a，进而表示出ED及OE+BD的长，即可表示出B坐标；由A与B都在反比例图象上，得到A与B横纵坐标乘积相等，列出关系式，变形后即可求出的值．【解答】解：过A作AE⊥x轴，过B作BD⊥AE，∵∠OAB＝90°，∴∠OAE+∠BAD＝90°，∵∠AOE+∠OAE＝90°，∴∠BAD＝∠AOE，在△AOE和△BAD中，，∴△AOE≌△BAD（AAS），∴AE＝BD＝b，OE＝AD＝a，∴DE＝AE﹣AD＝b﹣a，OE+BD＝a+b，则B（a+b，b﹣a）；∵A与B都在反比例图象上，得到ab＝（a+b）（b﹣a），整理得：b2﹣a2＝ab，即（）2﹣﹣1＝0，∵△＝1+4＝5，∴＝，∵点A（a，b）为第一象限内一点，∴a＞0，b＞0，则＝．故答案为．【点评】此题属于反比例函数综合题，涉及的知识有：全等三角形的判定与性质，坐标与图形性质，等腰直角三角形的性质，以及一元二次方程的解法，熟练掌握反比例函数的性质是解本题的关键．10．（2018•张家界）如图，矩形ABCD的边AB与x轴平行，顶点A的坐标为（2，1），点B与点D都在反比例函数y＝（x＞0）的图象上，则矩形ABCD的周长为12．【分析】根据矩形的性质、结合点A的坐标得到点D的横坐标为2，点B的纵坐标为1，根据反比例函数解析式求出点D的坐标，点B的坐标，根据矩形的周长公式计算即可．【解答】解：∵四边形ABCD是矩形，点A的坐标为（2，1），∴点D的横坐标为2，点B的纵坐标为1，当x＝2时，y＝＝3，当y＝1时，x＝6，则AD＝3﹣1＝2，AB＝6﹣2＝4，则矩形ABCD的周长＝2×（2+4）＝12，故答案为：12．【点评】本题考查的是反比例函数图象上点的坐标特征、矩形的性质，掌握反比例函数图象上点的坐标特征是解题的关键．11．（2019春•相城区期末）如图，在平面直角坐标系中，菱形OABC的边OA在x轴上，AC与OB交于点D（4，2），反比例函数的图象经过点D．若将菱形OABC向左平移n个单位，使点C落在该反比例函数图象上，则n的值为1．【分析】要求n的值，求出CG即可，根据菱形OABC，AC与OB交于点D（4，2），可求出点B坐标和反比例函数的关系式，借助勾股定理可求菱形的边长，进而求出点C、G 的坐标，根据横坐标的变化得出平移距离．【解答】解：过点D、B分别作DE⊥x轴，BF⊥x轴，垂足为E、F，延长BC交反比例函数图象于点G，交y轴于点H，∵D（4，2）∴DE＝2，OE＝4，反比例函数的关系式为：y＝，∵OABC是菱形，∴OA＝AB＝BC＝CO，DO＝CD，又∵DE∥BF，∴＝＝＝，∴OF＝8，BF＝4，∴B（8，4），设菱形边长AB＝a，则AF＝8﹣a，在Rt△ABF中，由勾股定理得：a2＝（8﹣a）2+42，解得a＝5，∴CE＝BH﹣BC＝8﹣5＝3，∴C（3，4）把y＝4代入y＝得，x＝2，∴G（2，4）∴CG＝3﹣2＝1，即点C向左平移1个单位到点G．故答案为：1【点评】考查菱形的性质，相似三角形的性质，勾股定理以及反比例函数图象上点的坐标特征等知识，将坐标、线段长与图形的性质联系起来．八．反比例函数与一次函数的交点问题（共6小题）12．（2018•雨花区模拟）如图，正方形ABCD位于第一象限，边长为3，横坐标为1的点A 在直线y＝x上，正方形ABCD的边分别平行于x轴、y轴．若双曲线y＝与正方形ABCD 公共点，则k的取值范围是1≤k≤16．【分析】根据题意求出点A的坐标，根据正方形的性质求出点C的坐标，根据反比例函数图象上点的坐标特征解答即可．【解答】解：∵点A在直线y＝x上，横坐标为1，∴点A的坐标为（1，1），∵正方形ABCD的边长为3，∴点C的坐标为（4，4），当双曲线y＝经过点A时，k＝1×1＝1，当双曲线y＝经过点C时，k＝4×4＝16，∴双曲线y＝与正方形ABCD公共点，则k的取值范围是1≤k≤16，故答案为：1≤k≤16．【点评】本题考查的是反比例函数与一次函数的交点问题以及正方形的性质，掌握反比例函数图象上点的坐标特征、以及正方形的性质是解题的关键．13．（2016春•张家港市期末）如图，在平面直角坐标系中，反比例函数y1＝的图象与一次函数y2＝kx+b的图象交于A、B两点．若y1＜y2，则x的取值范围是x＜0或1＜x＜3．【分析】观察函数图象，当x＜0或1＜x＜3时，反比例函数图象都在一次函数图象下方．【解答】解：当x＜0或1＜x＜3时，y1＜y2．【点评】本题考查了反比例函数与一次函数的交点问题，也考查了观察函数图象的能力．14．（2016春•常熟市期末）如图，已知反比例函数y＝与一次函数y＝x+1的图象交于点A（a，﹣1）、B（1，b），则不等式≥x+1的解集为x≤﹣2或0＜x≤1．【分析】先根据函数解析式求得点A的横坐标，再根据函数图象进行判断，双曲线在直线的上方时x的取值范围即为不等式的解集．【解答】解：将A（a，﹣1）代入一次函数y＝x+1，得﹣1＝a+1，即a＝﹣2∴A（﹣2，﹣1）当≥x+1时，反比例函数值大于或等于一次函数值根据图象可得，当x≤﹣2或0＜x≤1时，双曲线在直线的上方∴不等式≥x+1的解集为x≤﹣2或0＜x≤1故答案为：x≤﹣2或0＜x≤1【点评】本题主要考查了反比例函数与一次函数的交点问题．解答此类试题的依据是：①函数图象的交点坐标满足函数解析式；②不等式的解集就是其所对应的函数图象上满足条件的所有点的横坐标的集合．15．（2017春•姑苏区期末）如图，直线y＝2x与反比例函数y＝的图象交于点A（3，m），点B是线段OA的中点，点E（n，4）在反比例函数的图象上，点F在x轴上，若∠EAB ＝∠EBF＝∠AOF，则点F的横坐标为．【分析】根据点A在直线y＝2x上可以求得点A的坐标，从而可以求得点B的坐标和k 的值，进而求得点E的坐标，然后根据三角形相似即可求得OF的长度，本题得以解决．【解答】解：∵直线y＝2x与反比例函数y＝的图象交于点A（3，m），∴m＝2×3＝6，∴点A（3，6），∴6＝，得k＝18，∵点B是线段OA的中点，点E（n，4）在反比例函数的图象上，∴点B（1.5，3），4＝，得n＝4.5，∴点E（4.5，4），∴AB＝，AE＝＝OB＝，∵∠EAB＝∠EBF＝∠AOF，∠ABE+∠EAB+∠AEB＝180°，∠ABE+∠EBF+∠OBF＝180°，∴∠AEB＝∠OBF，∵∠EAB＝∠BOF，∴△ABE∽△OFB，∴，即，解得，OF＝，即点F的横坐标是，故答案为：．【点评】本题考查反比例函数与一次函数的交点问题、三角形相似，解答本题的关键是明确题意，找出所求问题需要的条件，利用函数的思想和三角形相似的知识解答．16．（2012•丹徒区校级模拟）已知双曲线与直线y＝x﹣相交于点P（a，b），则﹣2．【分析】由两函数图象交于P点，将P坐标分别代入两函数解析式，得到ab与a﹣b的值，将所求式子通分并利用同分母分式的减法法则计算，把ab与a﹣b的值代入即可求出值．【解答】解：∵双曲线与直线y＝x﹣相交于点P（a，b），∴b＝，b＝a﹣2，∴ab＝1，a﹣b＝2，则﹣＝＝＝﹣2．故答案为：﹣2【点评】此题考查了反比例函数与一次函数的交点问题，利用了待定系数法，熟练掌握待定系数法是解本题的关键．17．（2019春•吴江区期末）已知反比例函数y＝的图象与一次函数y＝k（x﹣3）+2（k＞0）的图象在第一象限交于点P，则点P的横坐标a的取值范围为2＜a＜3．【分析】求出一次函数图象过点（3，2）根据k＞0得出直线向上倾斜，求出两函数图象的交点坐标是（2，2），即可得出答案．【解答】解：当x＝3时，y＝k（3﹣3）+2＝2，即一次函数过点（3，2），∵k＞0，∴一次函数的图象向上倾斜，当一次函数的图象垂直x轴时，即x＝3，当一次函数的图象垂直y轴时，即y＝2，即一次函数的图象和反比例函数y＝图象的交点坐标是（2，2），向上倾斜则在他们之间，∴2＜a＜3，故答案为：2＜a＜3．【点评】本题主要考查了反比例函数和一次函数的交点问题的应用，在解题时要根据函数图象解决问题，需从交点看起：图象在上方的对应的函数值大，反之就小．九．反比例函数综合题（共1小题）18．（2012•历城区模拟）如图，直线与双曲线（k＞0）在第一象限内的交点为R，与x轴的交点为P，与y轴的交点为Q；作RM⊥x轴于点M，若△OPQ与△PRM 的面积是4：1，则k等于．【分析】先求出Q的坐标为（0，﹣2），P点坐标为（，0），易证Rt△OQP∽Rt△MRP，根据三角形相似的性质得到＝＝，分别求出PM、RM，得到OM的长，从而确定R点坐标，然后代入（k＞0）求出k的值．【解答】解：对于y＝x﹣2，令x＝0，则y＝﹣2，∴Q的坐标为（0，﹣2），即OQ＝2；令y＝0，则x＝，∴P点坐标为（，0），即OP＝；∵Rt△OQP∽Rt△MRP，而△OPQ与△PRM的面积是4：1，∴＝＝，∴PM＝OP＝，RM＝OQ＝1，∴OM＝OP+PM＝，∴R点的坐标为（，1），∴k＝×1＝．故答案为．【点评】本题考查了解反比例函数的综合题．点在函数图象上，点的横纵坐标满足图象的解析式；三角形相似的性质：相似三角形面积的比等于相似比的平方，对应边的比相等．一十．全等三角形的判定与性质（共1小题）19．（2019春•工业园区期末）如图，四边形纸片ABCD中，∠A＝∠C＝90°，BC＝DC．若AB+AD＝8cm，则该纸片的面积为16cm2．【分析】过点C作CE⊥AD于点E，作CF⊥AB于点F，证明△DCE≌△BCF，可得CE ＝CF，则四边形AECF为正方形，可求出答案．【解答】解：过点C作CE⊥AD于点E，作CF⊥AB于点F，∴∠E＝∠CFB＝90°，∵∠A＝90°，∴四边形AECF为矩形，∴∠ECF＝90°，∵∠DCB＝90°，∴∠ECD＝∠FCB，∵BC＝DC，∴△DCE≌△BCF（AAS），∴CE＝CF，DE＝BF，∴四边形AECF为正方形，∴AE＝AF，∵AB+AD＝8cm，∴AE＝4cm，∵S△DEC＝S△BCF，∴该纸片的面积为正方形的面积＝42＝16cm2．故答案为：16．【点评】本题考查了全等三角形的判定与性质，正方形的判定与性质，正确作出辅助线是解题的关键．一十一．角平分线的性质（共1小题）20．（2013•南通二模）如图，已知正方形ABCD的边长为2，对角线AC、BD相交于点O，AE平分∠BAC交BD于点E，则BE的长为2﹣2．【分析】过E作EM⊥AB于M，根据正方形性质得出AO⊥BD，AO＝OB＝OC＝OD，由勾股定理得出2AO2＝22，求出AO＝OB＝，在Rt△BME中，由勾股定理得：2ME2＝BE2，求出即可．【解答】解：过E作EM⊥AB于M，∵四边形ABCD是正方形，∴AO⊥BD，AO＝OB＝OC＝OD，则由勾股定理得：2AO2＝22，AO＝OB＝，∵EM⊥AB，BO⊥AO，AE平分∠CAB，∴EM＝EO，由勾股定理得：AM＝AO＝，∵正方形ABCD，∴∠MBE＝45°＝∠MEB，∴BM＝ME＝OE，在Rt△BME中，由勾股定理得：2ME2＝BE2，即2（2﹣）2＝BE2，BE＝2﹣2，故答案为：2﹣2．【点评】本题考查了角平分线性质和正方形性质，勾股定理的应用，注意：角平分线上的点到线段两个端点的距离相等．一十二．直角三角形的性质（共1小题）21．（2016春•常熟市期末）如图，在平面直角坐标系中，点D为x轴上的一点，且点D坐标为（4，0），过点D的直线l⊥x轴，点A为直线l上的一动点，连结OA，OB⊥OA交直线l于点B，则的值为．【分析】先根据勾股定理得出OA2+OB2＝AB2，再用得出OD×AB＝OA×OB，最后通分所求式子再代换即可得出结论．【解答】解：∵OB⊥OA，∴∠AOB＝90°，∴OA2+OB2＝AB2，∵OD⊥AB，∴OD×AB＝OA×OB，∵点D坐标为（4，0），∴OD＝4，∴＝＝＝＝．故答案为：．【点评】此题是直角三角形的性质，主要考查了勾股定理，直角三角形的面积公式，分式的计算，利用面积和勾股定理得出OD×AB＝OA×OB和OA2+OB2＝AB2，是解本题的关键．一十三．三角形中位线定理（共1小题）22．（2014•花都区二模）如图，Rt△ABC中，∠ACB＝90°，∠ABC＝60°，BC＝2cm，D 为BC的中点，若动点E以1cm/s的速度从A点出发，沿着A→B→A的方向运动，设E 点的运动时间为t秒（0≤t≤8），连接DE，当△BDE是直角三角形时，t的值为2或6或3.5或4.5．【分析】先求出AB的长，再分①∠BDE＝90°时，DE是△ABC的中位线，然后求出AE的长度，再分点E在AB上和在BA上两种情况列出方程求解即可；②∠BED＝90°时，利用∠B的余弦列式求出BE，然后分点E在AB上和在BA上两种情况列出方程求解即可．【解答】解：∵∠ACB＝90°，∠ABC＝60°，BC＝2cm，∴AB＝BC÷cos60°＝2÷＝4，①∠BDE＝90°时，∵D为BC的中点，。

2016-2019年八年级期末考压轴题专练(选择题)

2016-2019年八年级期末考压轴题专练（选择题）一．二次根式的化简求值（共1小题）1．（2018春•相城区期末）已知，则的值为（）A．1B．C．D．二．动点问题的函数图象（共1小题）2．（2014•丰南区一模）如图1，在矩形ABCD中，动点P从点B出发，沿BC、CD、DA 运动至点A停止，设点P运动的路程为x，△ABP的面积为y，如果y关于x的函数图象如图2所示，则△ABC的面积是（）A．10B．16C．18D．20三．一次函数图象上点的坐标特征（共1小题）3．（2016春•太仓市期末）如图，直线l为正比例函数y＝x的图象，过点A（0，1）作y轴的垂线交直线l于点B，过点B作直线l的垂线交y轴于点A1；过点A1作y轴的垂线交直线l于点B1，过点B1作直线l的垂线交y轴于点A2；…；按此作法继续下去，则点B n的坐标是（）A．（×4n，4n）B．（×4n﹣1，4n﹣1）C．（×4n﹣1，4n）D．（×4n，4n﹣1）四．一次函数综合题（共1小题）4．（2009•鹤岗模拟）如果一次函数y＝﹣x+1的图象与x轴、y轴分别交于点A点、B点，点M在x轴上，并且使以点A、B、M为顶点的三角形是等腰三角形，那么这样的点M有（）A．3个B．4个C．5个D．7个五．反比例函数的性质（共1小题）5．（2009•宁波）反比例函数y＝在第一象限的图象如图所示，则k的值可能是（）A．1B．2C．3D．4六．反比例函数系数k的几何意义（共6小题）6．（2016春•张家港市期末）如图，点A、B在反比例函数y＝（k＞0，x＞0）的图象上，过点A、B作x轴的垂线，垂足分别为M，N，延长线段AB交x轴于点C，若OM＝MN ＝NC，S△BNC＝2，则k的值为（）A．4B．6C．8D．12 7．（2016•长春）如图，在平面直角坐标系中，点P（1，4）、Q（m，n）在函数y＝（x ＞0）的图象上，当m＞1时，过点P分别作x轴、y轴的垂线，垂足为点A，B；过点Q 分别作x轴、y轴的垂线，垂足为点C、D．QD交P A于点E，随着m的增大，四边形ACQE的面积（）A．减小B．增大C．先减小后增大D．先增大后减小8．（2019•港南区一模）如图，四边形AOBC和四边形CDEF都是正方形，边OA在x轴上，边OB在y轴上，点D在边CB上，反比例函数y＝在第二象限的图象经过点E，则正方形AOBC和正方形CDEF的面积之差为（）A．12B．10C．8D．69．（2019春•相城区期末）如图，已知点A在反比例函数y＝（x＞0）的图象上，作Rt△ABC，边BC在x轴上，点D为斜边AC的中点，连结DB并延长交y轴于点E，则△BCE 的面积为（）A．3B．C．D．610．（2019秋•乐亭县期末）如图，在平面直角坐标系中，点P在函数y＝（x＞0）的图象上从左向右运动，P A∥y轴，交函数y＝﹣（x＞0）的图象于点A，AB∥x轴交PO的延长线于点B，则△P AB的面积（）A．逐渐变大B．逐渐变小C．等于定值16D．等于定值2411．（2019春•姑苏区期末）如图，四边形OABC和四边形BDEF都是正方形，反比例函数y＝在第一象限的图象经过点E，若两正方形的面积差为12，则k的值为（）A．12B．6C．﹣12D．8七．反比例函数图象上点的坐标特征（共7小题）12．（2016春•常熟市期末）已知点P（a，b）是反比例函数图象上异于点（﹣2，﹣2）的一个动点，则的值为（）A．B．1C．D．4 13．（2017•河南模拟）如图所示，在Rt△AOB中，∠AOB＝90°，2OB＝3OA，点A在反比例函数y＝的图象上，若点B在反比例函数y＝的图象上，则k的值为（）A．3B．﹣3C．﹣D．﹣14．（2017春•常熟市期末）如图，已知点A是反比例函数y＝在第一象限图象上的一个动点，连接OA，以OA为长，OA为宽作矩形AOCB，且点C在第四象限，随着点A 的运动，点C也随之运动，但点C始终在反比例函数y＝的图象上，则k的值为（）A．﹣3B．3C．﹣D．315．（2019秋•大余县期末）在函数（k为常数）的图象上有三个点（﹣2，y1），（﹣1，y2），（，y3），函数值y1，y2，y3的大小为（）A．y1＞y2＞y3B．y2＞y1＞y3C．y2＞y3＞y1D．y3＞y1＞y2 16．（2018春•常熟市期末）如图，点A在反比例函数y＝﹣的图象上，点B在反比例函数y＝的图象上，AB∥x轴，连接OB，过点A作AC⊥x轴于点C，交OB于点D，若AC＝3DC，则k的值为（）A．﹣4B．﹣6C．﹣8D．﹣917．（2018春•工业园区期末）如图，等边△ABC的顶点A，B分别在函数y＝﹣图象的两个分支上，且AB经过原点O．当点A在函数y＝﹣的图象上移动时，顶点C始终在函数y＝的图象上移动，则k的值为（）A．8B．6C．D．218．（2019春•苏州期末）若点A（﹣2，y1）、B（﹣1，y2）、C（1，y3）都在反比例函数（k为常数）的图象上，则y1、y2、y3的大小关系为（）A．y1＜y2＜y3B．y1＜y3＜y2C．y2＜y1＜y3D．y3＜y2＜y1八．反比例函数综合题（共1小题）19．（2019•临河区二模）在平面直角坐标系xOy中，将一块含有45°角的直角三角板如图放置，直角顶点C的坐标为（1，0），顶点A的坐标（0，2），顶点B恰好落在第一象限的双曲线上，现将直角三角板沿x轴正方向平移，当顶点A恰好落在该双曲线上时停止运动，则此时点C的对应点C′的坐标为（）A．（，0）B．（2，0）C．（，0）D．（3，0）九．三角形的重心（共1小题）20．（2018春•工业园区期末）如图，△ABC的中线BE，CD相交于点O，若△DOE的面积为1cm2，则△ABC的面积为（）A．12B．8C．6D．4一十．平行四边形的性质（共3小题）21．（2018春•相城区期末）已知点A（4，0），B（0，﹣4），C（a，2a）及点D是一个平行四边形的四个顶点，则线段CD的长的最小值为（）A．B．C．D．22．（2019春•工业园区期末）如图，在△ABC中，AC＝4，BC＝3，AB＝5，D为AB上的动点，连接CD以AD、CD为边作平行四边形ADCE，则DE长的最小值为（）A．3B．4C．D．23．（2017•贵阳）如图，在▱ABCD中，对角线AC的垂直平分线分别交AD、BC于点E、F，连接CE，若△CED的周长为6，则▱ABCD的周长为（）A．6B．12C．18D．24一十一．菱形的性质（共1小题）24．（2020•市南区校级模拟）如图，在菱形ABCD中，∠A＝60°，AD＝8．P是AB边上的一点，E，F分别是DP，BP的中点，则线段EF的长为（）A．8B．2C．4D．2一十二．矩形的性质（共3小题）25．（2016春•张家港市期末）如图，矩形ABCD中，AB＝4，BC＝6，P是CD边上的中点，E是BC边上的一动点，M，N分别是AE、PE的中点，则随着点E的运动，线段MN长为（）A．B．4C．2D．不确定26．（2018春•张家港市期末）如图，矩形ABCD中，AB＝2，BC＝4，对角线AC的垂直平分线分别交AD、BC于点E、F，连接CE，则△DCE的面积为（）A．B．C．2D．1 27．（2018•邵阳县模拟）将矩形OABC如图放置，O为原点．若点A（﹣1，2），点B的纵坐标是，则点C的坐标是（）A．（4，2）B．（2，4）C．（，3）D．（3，）一十三．正方形的性质（共2小题）28．（2016春•常熟市期末）如图，在边长为的正方形ABCD中，E是边CD的中点，F 在BC边上，且∠EAF＝45°，连接EF，则BF的长为（）A．B．3C．D．4 29．（2016•徐州）如图是由三个边长分别为6、9、x的正方形所组成的图形，若直线AB将它分成面积相等的两部分，则x的值是（）A．1或9B．3或5C．4或6D．3或6一十四．轨迹（共3小题）30．（2016春•工业园区期末）如图，正方形纸片ABCD的边长为4cm，点M、N分别在边AB、CD上．将该纸片沿MN折叠，使点D落在边BC上，落点为E，MN与DE相交于点Q．随着点M的移动，点Q移动路线长度的最大值是（）A．4cm B．2cm C．cm D．1cm 31．（2017春•工业园区期末）如图，△ABC的面积为9，点P在△ABC的边上运动．作点P关于原点O的对称点Q，再以PQ为边作等边△PQM．当点P在△ABC的边上运动一周时，点M随之运动所形成的图形面积为（）A．3B．9C．27D．32．（2019春•姑苏区期末）如图，正方形纸片ABCD的边长为4cm，点M、N分别在边AB、CD上．将该纸片沿MN折叠，使点D落在边BC上，落点为E，MN与DE相交于点Q．随着点M的移动，点Q移动路线长度的最大值是（）A．2 cm B．4 cm C．cm D．1 cm一十五．轴对称-最短路线问题（共2小题）33．（2016春•吴江区期末）如图，已知线段AB＝12，点M、N是线段AB上的两点，且AM ＝BN＝2，点P是线段MN上的动点，分别以线段AP、BP为边在AB的同侧作正方形APDC、正方形PBFE，点G、H分别是CD、EF的中点，点O是GH的中点，当P点从M点到N点运动过程中，OM+OB的最小值是（）A．10B．12C．2D．1234．（2018春•杭州期末）如图，在菱形ABCD中，AB＝4，∠A＝120°，点P，Q，K分别为线段BC，CD，BD上的任意一点，则PK+QK的最小值为（）A．2B．2C．4D．2+2一十六．翻折变换（折叠问题）（共2小题）35．（2017•峄城区三模）如图，矩形ABCD中，E是AD的中点，将△ABE沿BE折叠后得到△GBE，延长BG交CD于F点，若CF＝2，FD＝4，则BC的长为（）A．6B．2C．4D．436．（2016春•虎丘区校级期末）如图，将△ABC沿着过AB中点D的直线折叠，使点A落在BC边上的A1处，称为第1次操作，折痕DE到BC的距离记为h1；还原纸片后，再将△ADE沿着过AD中点D1的直线折叠，使点A落在DE边上的A2处，称为第2次操作，折痕D1E1到BC的距离记为h2；按上述方法不断操作下去…，经过第5次操作后得到的折痕D4E4，到BC的距离记为h5；若h1＝1，则h5的值为（）A．B．C．D．一十七．旋转的性质（共1小题）37．（2019春•苏州期末）如图，在平行四边形ABCD中，AB＝26，AD＝6，将平行四边形ABCD绕点A旋转，当点D的对应点D'落在AB边上时，点C的对应点C'，恰好与点B、C在同一直线上，则此时△C'D'B的面积为（）A．240B．260C．320D．480一十八．平行线分线段成比例（共1小题）38．（2017春•工业园区期末）如图，l1∥l2∥l3，直线a、b与l1、l2、l3分别相交于点A、B、C和D、E、F．若＝，则等于（）A．B．C．D．一十九．相似三角形的性质（共1小题）39．（2018春•太仓市期末）如图，已知△ACD∽△ADB，AC＝4，AD＝2，则AB的长为（）A．1B．2C．3D．4二十．相似三角形的判定（共1小题）40．（2019春•吴江区期末）如图，已知点A（1，0），点B（b，0）（b＞1），点P是第一象限内的动点，且点P的纵坐标为，若△POA和△P AB相似，则符合条件的P点个数是（）A．0B．1C．2D．3二十一．相似三角形的判定与性质（共6小题）41．（2012•襄阳）如图，ABCD是正方形，G是BC上（除端点外）的任意一点，DE⊥AG 于点E，BF∥DE，交AG于点F．下列结论不一定成立的是（）A．△AED≌△BF A B．DE﹣BF＝EF C．△BGF∽△DAE D．DE﹣BG＝FG 42．（2016春•吴中区期末）如图，在矩形ABCD中，AB＝1，BC＝，M为BC中点，连接AM，过D作DE⊥AM于E，则DE的长度为（）A．1B．C．D．43．（2018春•常熟市期末）如图，在▱ABCD中，F是边AD上的一点，射线CF和BA的延长线交于点E，如果＝，那么的值是（）A．B．C．D．44．（2019春•相城区期末）如图，正方形ABCD中，M为BC上一点，ME⊥AM，ME交AD的延长线于点E，若AB＝12，BM＝5，则DE的长为（）A．B．18C．D．45．（2019春•常熟市期末）如图，四边形ABCD是正方形，以BC为底边向正方形外部作等腰直角三角形BCE，连接AE，分别交BD，BC于点F，G．则下列结论：①△ADF∽△GCE；②△AFB∽△ABE；③CG＝3BG；④AF＝EF，其中正确的有（）A．1个B．2个C．3个D．4个46．（2019春•太仓市期末）如图，在△ABC中，AB＝AC，∠A＝36°，BD平分∠ABC交AC于点D．若AC＝2，则AD的长是（）A．B．C．D．二十二．相似三角形的应用（共4小题）47．（2017春•相城区期末）如图，路灯灯柱OP的长为8米，身高1.6米的小明从距离灯的底部（点O20米的点A处，沿AO所在的直线行走14米到点B处时，人影的长度（）A．变长了1.5米B．变短了2.5米C．变长了3.5米D．变短了3.5米48．（2017春•姑苏区期末）如图，路灯灯柱OP的长为8米，身高1.6米的小明从距离灯的底部（点O）20米的点A处，沿AO所在的直线行走14米到达点B处，人影的长度（）A．变长了1.5米B．变短了2.5米C．变长了3.5米D．变短了3.5米49．（2006•深圳）如图，王华晚上由路灯A下的B处走到C处时，测得影子CD的长为1米，继续往前走3米到达E处时，测得影子EF的长为2米，已知王华的身高是1.5米，那么路灯A的高度AB等于（）A．4.5米B．6米C．7.2米D．8米50．（2019春•工业园区期末）如图，有一高度为8m的灯塔AB，在灯光下，身高为1.6m的小亮从距离灯塔底端4.8m的点C处，沿BC方向前进3.2m到达点D处，那么他的影长（）A．变长了0.8m B．变长了1.2m C．变短了0.8m D．变短了1.2m2016-2019年八年级期末考压轴题专练（选择题）参考答案与试题解析一．二次根式的化简求值（共1小题）1．（2018春•相城区期末）已知，则的值为（）A．1B．C．D．【分析】根据，可以求得a、b的值，从而可以求得所求式子的值，本题得以解决．【解答】解：∵，∴a﹣3＝0，2﹣b＝0，解得，a＝3，b＝2，∴＝＝＝，故选：D．【点评】本题考查二次根式的化简求值、非负数的性质，解答本题的关键是明确题意，求出a、b的值．二．动点问题的函数图象（共1小题）2．（2014•丰南区一模）如图1，在矩形ABCD中，动点P从点B出发，沿BC、CD、DA 运动至点A停止，设点P运动的路程为x，△ABP的面积为y，如果y关于x的函数图象如图2所示，则△ABC的面积是（）A．10B．16C．18D．20【分析】根据函数的图象、结合图形求出AB、BC的值，根据三角形的面积公式得出△ABC的面积．【解答】解：∵动点P从点B出发，沿BC、CD、DA运动至点A停止，而当点P运动到点C，D之间时，△ABP的面积不变，函数图象上横轴表示点P运动的路程，x＝4时，y开始不变，说明BC＝4，x＝9时，接着变化，说明CD＝9﹣4＝5，∴AB＝5，BC＝4，∴△ABC的面积是：×4×5＝10．故选：A．【点评】本题主要考查了动点问题的函数图象，在解题时要能根据函数的图象求出有关的线段的长度，从而得出三角形的面积是本题的关键．三．一次函数图象上点的坐标特征（共1小题）3．（2016春•太仓市期末）如图，直线l为正比例函数y＝x的图象，过点A（0，1）作y轴的垂线交直线l于点B，过点B作直线l的垂线交y轴于点A1；过点A1作y轴的垂线交直线l于点B1，过点B1作直线l的垂线交y轴于点A2；…；按此作法继续下去，则点B n的坐标是（）A．（×4n，4n）B．（×4n﹣1，4n﹣1）C．（×4n﹣1，4n）D．（×4n，4n﹣1）【分析】由直线l的解析式以及点A n、B n的找法，可列出部分A n的坐标，根据坐标的变化找出变化规律“A n（0，4n）”，再利用一次函数图象上点的坐标特征即可得出结论．【解答】解：∵直线l为正比例函数y＝x，点A（0，1），∴OA＝1，AB＝OA＝，AA1＝AB＝3，A1B1＝OA1＝4，A1A2＝A1B1＝12，∴A（0，1），A1（0，4），A2（0，16），…，∴A n（0，4n），∴B n（×4n，4n）．故选：A．【点评】本题考查了一次函数图象上点的坐标特征以及规律型中点的坐标变化，解题的关键是找出变化规律“A n（0，4n）”．本题属于中档题，难度不大，根据点的找法找出部分点A n的坐标，根据坐标的变化找出变化规律是关键．四．一次函数综合题（共1小题）4．（2009•鹤岗模拟）如果一次函数y＝﹣x+1的图象与x轴、y轴分别交于点A点、B点，点M在x轴上，并且使以点A、B、M为顶点的三角形是等腰三角形，那么这样的点M 有（）A．3个B．4个C．5个D．7个【分析】分别令一次函数y＝﹣x+1中x＝0和y＝0求出相应的y与x的值，得到A和B 的坐标，进而得到OA与OB的长，利用勾股定理求出AB的长，根据题意可分4种情况考虑，当BM＝BA时，由BO垂直于MA，根据三线合一得到O为MA的中点，由OA 得长得到OM的长，根据M为x轴负半轴的点写出此时M的坐标即可；当AB＝AM时，由AB的长，得到AM的长，进而由AM﹣OA得到OM的长，写出M的坐标即可；当MA＝MB时，此时M与原点O重合，写出M的坐标；当AB＝AM时，由AB的长得到AM的长，由OA+AM得到OM的长，写出M的坐标即可．【解答】解：一次函数y＝﹣x+1中令x＝0，解得y＝1；令y＝0，解得x＝1，∴A（1，0），B（0，1），即OA＝OB＝1，在直角三角形AOB中，根据勾股定理得：AB＝，分四种情况考虑，如图所示：当BM1＝BA时，由BO⊥AM1，根据三线合一得到O为M1A的中点，此时M1（﹣1，0）；当AB＝AM2时，由AB＝，得到OM2＝AM2﹣OA＝﹣1，此时M2（1﹣，0）；当BA＝AM3时，由AB＝，得到AM3＝，则OM3＝OA+AM3＝1+，此时M3（1+，0）；当M4A＝M4B时，此时M4与原点重合，此时M4（0，0）．综上，这样的M点有4个．故选：B．【点评】此题考查了等腰三角形的性质，勾股定理，以及一次函数与坐标轴的交点，利用了数形结合及分类讨论的思想，在分类讨论分情况解决数学问题时，必须认真审题，全面考虑，做到不重不漏，一次分类必须按同标准进行，分出的每一部分不需都是相互独立的．本题要求学生求出相应线段后，注意根据点在坐标轴上的位置选择合适的符号，进而写出坐标．五．反比例函数的性质（共1小题）5．（2009•宁波）反比例函数y＝在第一象限的图象如图所示，则k的值可能是（）A．1B．2C．3D．4【分析】根据图象，当x＝2时，函数值在1和2之间，代入解析式即可求解．【解答】解：如图，当x＝2时，y＝，∵1＜y＜2，∴1＜＜2，解得2＜k＜4，所以k＝3．故选：C．【点评】解答本题关键是要结合函数的图象，掌握反比例函数的性质．六．反比例函数系数k的几何意义（共6小题）6．（2016春•张家港市期末）如图，点A、B在反比例函数y＝（k＞0，x＞0）的图象上，过点A、B作x轴的垂线，垂足分别为M，N，延长线段AB交x轴于点C，若OM＝MN ＝NC，S△BNC＝2，则k的值为（）A．4B．6C．8D．12【分析】由BN∥AM可判断△CNB∽△CMA，根据相似的性质得S△CNB：S△CMA＝（）2＝，则S＝8，由于OM＝MN＝NC，根据三角形面积公式得到S△AOM＝S△AMC △CMA＝4，然后根据反比例函数k的几何意义得到S△AOM＝|k|＝4，再去绝对值易得k的值．【解答】解：∵BN∥AM，MN＝NC，∴△CNB∽△CMA，∴S△CNB：S△CMA＝（）2＝（）2＝，而S△BNC＝2，∴S△CMA＝8，∵OM＝MN＝NC，∴OM＝MC，∴S△AOM＝S△AMC＝4，∵S△AOM＝|k|，∴|k|＝4，∴k＝8．故选：C．【点评】本题主要考查了反比例函数的比例系数k的几何意义以及相似三角形的判定与性质．从反比例函数y＝（k≠0）图象上任意一点向x轴或y轴作垂线，这一点和垂足以及坐标原点所构成的三角形的面积是|k|，且保持不变．7．（2016•长春）如图，在平面直角坐标系中，点P（1，4）、Q（m，n）在函数y＝（x ＞0）的图象上，当m＞1时，过点P分别作x轴、y轴的垂线，垂足为点A，B；过点Q 分别作x轴、y轴的垂线，垂足为点C、D．QD交P A于点E，随着m的增大，四边形ACQE的面积（）A．减小B．增大C．先减小后增大D．先增大后减小【分析】首先利用m和n表示出AC和CQ的长，则四边形ACQE的面积即可利用m、n 表示，然后根据函数的性质判断．【解答】解：AC＝m﹣1，CQ＝n，则S四边形ACQE＝AC•CQ＝（m﹣1）n＝mn﹣n．∵P（1，4）、Q（m，n）在函数y＝（x＞0）的图象上，∴mn＝k＝4（常数）．∴S四边形ACQE＝AC•CQ＝4﹣n，∵当m＞1时，n随m的增大而减小，∴S四边形ACQE＝4﹣n随m的增大而增大．故选：B．【点评】本题考查了反比例函数的性质以及矩形的面积的计算，利用n表示出四边形ACQE的面积是关键．8．（2019•港南区一模）如图，四边形AOBC和四边形CDEF都是正方形，边OA在x轴上，边OB在y轴上，点D在边CB上，反比例函数y＝在第二象限的图象经过点E，则正方形AOBC和正方形CDEF的面积之差为（）A．12B．10C．8D．6【分析】设正方形AOBC的边长为a，正方形CDEF的边长为b，则E（b﹣a，a+b），再根据反比例函数图象上点的坐标特征得（a+b）•（b﹣a）＝8，因为S正方形AOBC＝a2，S正方＝b2，从而求得正方形AOBC和正方形CDEF的面积之差为8．形CDEF【解答】解：设正方形AOBC的边长为a，正方形CDEF的边长为b，则E（b﹣a，a+b），∴（a+b）•（b﹣a）＝﹣8，整理为a2﹣b2＝8，∵S正方形AOBC＝a2，S正方形CDEF＝b2，∴S正方形AOBC﹣S正方形CDEF＝8，故选：C．【点评】本题考查了反比例函数图象上点的坐标特征：反比例函数y＝（k为常数，k ≠0）的图象是双曲线，图象上的点（x，y）的横纵坐标的积是定值k，即xy＝|k|；也考查了正方形的性质．9．（2019春•相城区期末）如图，已知点A在反比例函数y＝（x＞0）的图象上，作Rt△ABC，边BC在x轴上，点D为斜边AC的中点，连结DB并延长交y轴于点E，则△BCE 的面积为（）A．3B．C．D．6【分析】先根据题意证明△BOE∽△CBA，根据相似比及面积公式得出EO×CB的值即为|k|的值，进而得BCE的面积．【解答】解：∵BD为Rt△ABC的斜边AC上的中线，∴BD＝DC，∠DBC＝∠ACB，又∠DBC＝∠EBO，∴∠EBO＝∠ACB，又∠BOE＝∠CBA＝90°，∴△BOE∽△CBA，∴，即BC×OE＝BO×AB．又∵点A在反比例函数y＝（x＞0）的图象上，∴BO×AB＝6，∴BC•EO＝6，∴．故选：A．【点评】本题考查反比例函数系数k的几何意义．反比例函数y＝中k的几何意义，即过双曲线上任意一点引x轴、y轴垂线，所得矩形面积为|k|，是经常考查的一个知识点；这里体现了数形结合的思想，做此类题一定要正确理解k的几何意义．10．（2019秋•乐亭县期末）如图，在平面直角坐标系中，点P在函数y＝（x＞0）的图象上从左向右运动，P A∥y轴，交函数y＝﹣（x＞0）的图象于点A，AB∥x轴交PO的延长线于点B，则△P AB的面积（）A．逐渐变大B．逐渐变小C．等于定值16D．等于定值24【分析】根据反比例函数k的几何意义得出S△POC＝×2＝1，S矩形ACOD＝6，即可得出＝，从而得出＝，通过证得△POC∽△PBA，得出＝（）2＝，即可得出S△P AB＝16S△POC＝16．【解答】解：由题意可知S△POC＝×2＝1，S矩形ACOD＝6，∵S△POC＝OC•PC，S矩形ACOD＝OC•AC，∴＝＝，∴＝，∴＝，∵AB∥x轴，∴△POC∽△PBA，∴＝（）2＝，∴S△P AB＝16S△POC＝16，∴△P AB的面积等于定值16．故选：C．【点评】本题考查了反比例函数系数k的几何意义，三角形相似的判定和性质，证得＝是解题的关键．11．（2019春•姑苏区期末）如图，四边形OABC和四边形BDEF都是正方形，反比例函数y＝在第一象限的图象经过点E，若两正方形的面积差为12，则k的值为（）A．12B．6C．﹣12D．8【分析】设正方形OABC、BDEF的边长分别为a和b，则可表示出D（a，a﹣b），F（a+b，a），根据反比例函数图象上点的坐标特征得到E（a+b，），由于点E与点D的纵坐标相同，所以＝a﹣b，则a2﹣b2＝k，然后利用正方形的面积公式易得k＝12．【解答】解：设正方形OABC、BDEF的边长分别为a和b，则D（a，a﹣b），F（a+b，a），所以E（a+b，），所以＝a﹣b，∴（a+b）（a﹣b）＝k，∴a2﹣b2＝k，∵两正方形的面积差为12，∴k＝12．故选：A．【点评】本题考查了反比例函数比例系数k的几何意义：在反比例函数y＝图象中任取一点，过这一个点向x轴和y轴分别作垂线，与坐标轴围成的矩形的面积是定值|k|．也考查了正方形的性质．七．反比例函数图象上点的坐标特征（共7小题）12．（2016春•常熟市期末）已知点P（a，b）是反比例函数图象上异于点（﹣2，﹣2）的一个动点，则的值为（）A．B．1C．D．4【分析】由点P是反比例函数图象上异于点（﹣2，﹣2）的一点即可得出ab＝4，且a ≠﹣2，b≠﹣2，将分式通分后代入ab的值即可得出结论．【解答】解：∵点P（a，b）是反比例函数图象上异于点（﹣2，﹣2）的一个动点，∴ab＝4，且a≠﹣2，b≠﹣2．∵＝＝＝＝．故选：A．【点评】本题考查了反比例函数图象上点的坐标特征，解题的关键是求出＝．本题属于基础题，难度不大，解决该题型题目时，根据点在反比例函数图象上，利用反比例函数图象上点的坐标特征找出该点横纵坐标之间的关系是关键．13．（2017•河南模拟）如图所示，在Rt△AOB中，∠AOB＝90°，2OB＝3OA，点A在反比例函数y＝的图象上，若点B在反比例函数y＝的图象上，则k的值为（）A．3B．﹣3C．﹣D．﹣【分析】过点A作AC⊥x轴于点C，过点B作BD⊥x轴于点D，由同角的余角相等可得出∠OBD＝∠AOC，结合∠BDO＝∠OCA可证出△OBD∽△AOC，根据相似三角形的性质可得出OD＝AC、BD＝OC，再根据反比例函数图象上点的坐标特征可得出OC•AC ＝2、OD•BD＝﹣k，代入OD＝AC、BD＝OC可求出k值．【解答】解：过点A作AC⊥x轴于点C，过点B作BD⊥x轴于点D，如图所示．∵∠BOD+∠OBD＝90°，∠BOD+∠AOC＝90°，∴∠OBD＝∠AOC．∵∠BDO＝∠OCA，∴△OBD∽△AOC，∴＝＝＝，∴OD＝AC，BD＝OC．∵点A在反比例函数y＝的图象上，点B在反比例函数y＝的图象上，∴OC•AC＝2，OD•BD＝﹣k，解得：k＝﹣．故选：D．【点评】本题考查了相似三角形的判定与性质以及反比例函数图象上点的坐标特征，根据相似三角形的性质找出OD＝AC、BD＝OC是解题的关键．14．（2017春•常熟市期末）如图，已知点A是反比例函数y＝在第一象限图象上的一个动点，连接OA，以OA为长，OA为宽作矩形AOCB，且点C在第四象限，随着点A 的运动，点C也随之运动，但点C始终在反比例函数y＝的图象上，则k的值为（）A．﹣3B．3C．﹣D．3【分析】设A（a，b），则ab＝，分别过A，C作AE⊥x轴于E，CF⊥x轴于F，根据相似三角形的判定证得△AOE∽△COF，由相似三角形的性质得到OF＝b，CF＝b，则k＝﹣OF•CF＝﹣3．【解答】解：设A（a，b），∴OE＝a，AE＝b，∵在反比例函数y＝图象上，∴ab＝，分别过A，C作AE⊥x轴于E，CF⊥x轴于F，∵矩形AOCB，∴∠AOE+∠COF＝90°，∴∠OAE＝∠COF＝90°﹣∠AOE，∴△AOE∽△COF，∵OC＝OA，∴＝＝＝，∴OF＝AE＝b，CF＝OE＝a，∵C在反比例函数y＝的图象上，且点C在第四象限，∴k＝﹣OF•CF＝﹣a•b＝﹣3ab＝﹣3，故选：A．【点评】本题主要考查了矩形的性质，相似三角形的判定和性质，反比例函数的几何意义和求法，正确作出辅助线证得△AOE∽△COF是解题的关键，同时注意k的符号．15．（2019秋•大余县期末）在函数（k为常数）的图象上有三个点（﹣2，y1），（﹣1，y2），（，y3），函数值y1，y2，y3的大小为（）A．y1＞y2＞y3B．y2＞y1＞y3C．y2＞y3＞y1D．y3＞y1＞y2【分析】先判断出﹣k2﹣2＜0的符号，再根据反比例函数的性质进行比较．【解答】解：∵﹣k2﹣2＜0，∴函数图象位于二、四象限，∵（﹣2，y1），（﹣1，y2）位于第二象限，﹣2＜﹣1，∴y2＞y1＞0；又∵（，y3）位于第四象限，∴y3＜0，∴y2＞y1＞y3．故选：B．【点评】本题考查了反比例函数图象上点的坐标特征，要明确，当k＜0在每个象限内，y随x的增大而增大．16．（2018春•常熟市期末）如图，点A在反比例函数y＝﹣的图象上，点B在反比例函数y＝的图象上，AB∥x轴，连接OB，过点A作AC⊥x轴于点C，交OB于点D，若AC＝3DC，则k的值为（）A．﹣4B．﹣6C．﹣8D．﹣9【分析】过点B作BE⊥x轴于E，延长线段BA，交y轴于F，得出四边形AFOC是矩形，四边形OEBF是矩形，得出S矩形AFOC＝2，S矩形OEBF＝k，根据平行线分线段成比例定理证得AB＝2OC，即OE＝3OC，即可求得矩形OEBF的面积，根据反比例函数系数k的几何意义即可求得k的值．【解答】解：如图，过点B作BE⊥x轴于E，延长线段BA，交y轴于F，∵AB∥x轴，∴AF⊥y轴，∴四边形AFOC是矩形，四边形OEBF是矩形，∴AF＝OC，BF＝OE，∴AB＝CE，∵点A在函数y＝﹣的图象上，∴S矩形AFOC＝2，同理可得S矩形OEBF＝k，∵AB∥OC，∴＝＝，∴AB＝2OC，∴CE＝2OC，∴S矩形OEBF＝3S矩形AFOC＝6，即k＝﹣6．故选：B．【点评】本题考查了反比例函数图象上点的坐标特征，矩形的判定和性质，平行线分线段成比例定理，作出辅助线构建矩形，运用反比例函数系数k的几何意义是解题的关键．17．（2018春•工业园区期末）如图，等边△ABC的顶点A，B分别在函数y＝﹣图象的两个分支上，且AB经过原点O．当点A在函数y＝﹣的图象上移动时，顶点C始终在函数y＝的图象上移动，则k的值为（）A．8B．6C．D．2【分析】根据反比例函数图象的对称性可得OA＝OB，设OA＝x，则AC＝2x，OC＝x，根据等边三角形三线合一可证明△AOE∽△OCF，根据相似三角形面积比等于相似比的平方可得结论．【解答】解：∵函数y＝﹣图象关于原点对称，∴OA＝OB，连接OC，过A作AE⊥x轴于E，过C作CF⊥x轴于F，∵△ABC是等边三角形，∴AO⊥OC，∴∠AOC＝90°，∠AOC＝30°，∴∠AOE+∠COF＝90°，设OA＝x，则AC＝2x，OC＝x，∵AE⊥x轴，CF⊥x轴，∴∠AEO＝∠OFC＝∠AOE+∠OAE＝90°，∴∠COF＝∠OAE，∴△AOE∽△OCF，∴＝＝＝，∵顶点A在函数y＝﹣图象的分支上，∴S△AOE＝1，∴S△OCF＝3，∵顶点C始终在函数y＝的图象上，∴k＝6，故选：B．【点评】本题考查了综合运用反比例函数图象上点的坐标特征，反比例函数图象关于原点对称，相似三角形的判定与性质及等边三角形等知识点，难度不大，属于中档题．18．（2019春•苏州期末）若点A（﹣2，y1）、B（﹣1，y2）、C（1，y3）都在反比例函数（k为常数）的图象上，则y1、y2、y3的大小关系为（）A．y1＜y2＜y3B．y1＜y3＜y2C．y2＜y1＜y3D．y3＜y2＜y1【分析】由k2+3＞0，可知反比函数在每个象限内，y随x的增大而减小，A（﹣2，y1）、B（﹣1，y2）在第三象限内，C（1，y3）在第一象限内，分别判断即可．【解答】解：∵k2+3＞0，∴反比函数在每个象限内，y随x的增大而减小，A（﹣2，y1）、B（﹣1，y2）在第三象限内，∵﹣1＞﹣2，∴y1＞y2，∴y3＞y1＞y2，故选：C．【点评】本题考查反比例函数的图象及性质；熟练掌握k对反比例函数图象的影响，特别注意要在每个象限内求解是解题的关键．八．反比例函数综合题（共1小题）19．（2019•临河区二模）在平面直角坐标系xOy中，将一块含有45°角的直角三角板如图放置，直角顶点C的坐标为（1，0），顶点A的坐标（0，2），顶点B恰好落在第一象限的双曲线上，现将直角三角板沿x轴正方向平移，当顶点A恰好落在该双曲线上时停止运动，则此时点C的对应点C′的坐标为（）A．（，0）B．（2，0）C．（，0）D．（3，0）【分析】过点B作BD⊥x轴于点D，易证△ACO≌△BCD（AAS），从而可求出B的坐标，进而可求出反比例函数的解析式，根据解析式与A的坐标即可得知平移的单位长度，从而求出C的对应点．【解答】解：过点B作BD⊥x轴于点D，∵∠ACO+∠BCD＝90°，∠OAC+∠ACO＝90°，∴∠OAC＝∠BCD，在△ACO与△BCD中，∴△ACO≌△BCD（AAS）∴OC＝BD，OA＝CD，∵A（0，2），C（1，0）∴OD＝3，BD＝1，∴B（3，1），∴设反比例函数的解析式为y＝，将B（3，1）代入y＝，∴k＝3，∴y＝，∴把y＝2代入，∴x＝，当顶点A恰好落在该双曲线上时，此时点A移动了个单位长度，∴C也移动了个单位长度，此时点C的对应点C′的坐标为（，0）故选：A．【点评】本题考查反比例函数的综合问题，涉及全等三角形的性质与判定，反比例函数的解析式，平移的性质等知识，综合程度较高，属于中等题型．九．三角形的重心（共1小题）20．（2018春•工业园区期末）如图，△ABC的中线BE，CD相交于点O，若△DOE的面积。

2019年八上各区压轴题

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2019八年级期末压轴题合集

八年级压轴题 期末复习试卷复习练习(Word版 含答案)

八年级数学压轴题 期末复习试卷复习练习(Word版 含答案)

八年级数学压轴题 期末复习试卷测试题(Word版 含解析)

最新2019-2020年人教版八年级数学下册期末压轴题练习卷(有答案)

(2019秋)北师大版八年级上册期末压轴题系列专题练习(有答案)-(数学)-精编.doc

北师大版八年级(上)期末数学压轴题系列专题练习(含答案)

2019-2020武汉市各区八年级上学期期末考试压轴题汇总

八年级数学压轴题 期末复习试卷测试卷附答案

2018~2019学年度第一学期期末考试武汉市部分区八年级数学压轴题

2016-2019年八年级期末考压轴题专练(解答题)

2019-2020学年度北京市八年级上数学期末考试压轴题汇总

2019-2020人教版数学八年级上册期末压轴题培优：全等三角形(含答案)

2019年上海市初二期末压轴题图文解析

湖北省武汉市各区2019—2020学年度年八年级上学期数学压轴题汇编(无答案)

八年级数学压轴题 期末复习试卷复习练习(Word版 含答案)

郑州市2019-2020学年八年级下期期末压轴题精讲精练

(八年级下册数学)(期末压轴题汇编)

2016-2019年八年级期末考压轴题专练(填空题)

2016-2019年八年级期末考压轴题专练(选择题)

2019年八上各区压轴题

八年级压轴题期末复习试卷复习练习(Word版含答案)

八年级数学压轴题期末复习试卷复习练习(Word版含答案)

八年级数学压轴题期末复习试卷测试题(Word版含解析)

八年级数学压轴题期末复习试卷测试卷附答案

八年级数学压轴题期末复习试卷复习练习(Word版含答案)