九年级数学找规律专题练习
初三找规律练习题

初三找规律练习题
在初三数学学习中,找规律是一个非常基础且重要的内容。
通过找规律,可以提高解题的速度和准确性,也有助于培养逻辑思维和问题解决能力。
本文将为大家提供一些初三找规律练习题,帮助同学们巩固和提高这方面的能力。
1. 数列规律题
(1) 2,4,8,16,32,... 下一个数是多少?
(2) 1,3,6,10,15,... 下一个数是多少?
(3) 1,4,9,16,25,... 下一个数是多少?
2. 图形规律题
(1) 下面的图形中,哪个是不同的?
□ □ □ □
□ □ □ ■
■ □ ■ □
□ □ □ □
(2) 下面的图形中,第几个是和其他不同的?
▲ ▲
▲▲ ▲▲
▲▲▲ ▲▲▲
▲▲▲▲ ▲▲▲▲
(3) 继续下面的图形,形成一个规律:
★
★★
★★★
★★★★
★★★★★
3. 数字逻辑题
(1) 请写出下面数字序列的规律: 2,4,8,16,32,64
(2) 请写出下面数字序列的规律: 1,4,9,16,25,36
(3) 请写出下面阴影图案的规律并填写问号处的数字:
■■■
■■■
■?■
■■■
以上是一些初三找规律练习题,同学们可以根据自己的理解和思考,分析规律,并给出答案。
通过反复练习,可以提高自己的观察力和发
现规律的能力。
希望同学们能够善于思考,积极解题,提高数学能力。
祝愿大家在数学学习中取得好成绩!。
(word完整版)初三数学找规律试题集锦

初三数学找规律试题集锦1.(2009年孝感)对于每个非零自然数n,抛物线2211 (1)(1) nn nn ny x x+++=-+与x轴交于A n、B n两点,以n nA B表示这两点间的距离,则112220092009A B A B A B+++L的值是A.20092008B.20082009C.20102009D.20092010【答案】D2.(2009仙桃)如图所示,直线y=x+1与y轴相交于点A1,以OA1为边作正方形OA1B1C1,记作第一个正方形;然后延长C1B1与直线y=x+1相交于点A2,再以C1A2为边作正方形C1A2B2C2,记作第二个正方形;同样延长C2B2与直线y=x+1相交于点A3,再以C2A3为边作正方形C2A3B3C3,记作第三个正方形;…依此类推,则第n个正方形的边长为________________.【答案】n3.(2009年泸州)如图1,已知Rt△ABC中,AC=3,BC= 4,过直角顶点C作CA1⊥A B,垂足为A1,再过A1作A1C1⊥BC,垂足为C1,过C1作C1A2⊥AB,垂足为A2,再过A2作A2C2⊥BC,垂足为C2,…,这样一直做下去,得到了一组线段CA1,A1C1,12C A,…,则CA1= ,=5554CAAC【答案】512,45.图14(2009年桂林市、百色市)如图,在△ABC 中,∠A =α.∠ABC 与∠ACD 的 平分线交于点A 1,得∠A 1;∠A 1BC 与∠A 1CD 的平分线相交于点A 2,得∠A 2; ……;∠A 2008BC 与∠A 2008CD 的平分线相交于点A 2009,得∠A 2009 .则∠A 2009= .【答案】20092α5 (2009年淄博市)如图,网格中的每个四边形都是菱形.如果格点三角形ABC 的面积为S ,按照如图所示方式得到的格点三角形A 1B 1C 1的面积是7S ,格点三角形A 2B 2C 2的面积是19S ,那么格点三角形A 3B 3C 3的面积为 .【答案】37S6.(2009年日照)正方形A 1B 1C 1O ,A 2B 2C 2C 1,A 3B 3C 3C 2,…按如图所示的方式放置.点A 1,A 2,A 3,…和点C 1,C 2,C 3,…分别在直线y kx b =+(k >0)和x 轴上,已知点B 1(1,1),B 2(3,2),则B n 的坐标是______________.B A CD 第18题图A 1A 2 A A 1 A 2 A 3B 3 B 2 B 1 BC 1 C 2 C 3 (第17题)C【答案】(12-n ,12-n ).7.(2009年湖州) 如图,已知Rt ABC △,1D 是斜边AB 的中点,过1D 作11D E AC ⊥于E 1,连结1BE 交1CD 于2D ;过2D 作22D E AC ⊥于2E ,连结2BE 交1CD 于3D ;过3D 作33D E AC ⊥于3E ,…,如此继续,可以依次得到点45D D ,,…,n D ,分别记112233BD E BD E BD E △,△,△,…,n n BD E △的面积为123S S S ,,,…n S .则n S =________ABC S △(用含n 的代数式表示).【答案】()211n +8.(2009 黑龙江大兴安岭)如图,边长为1的菱形ABCD 中,︒=∠60DAB .连结对角线AC ,以AC 为边作第二个菱形11D ACC ,使 ︒=∠601AC D ;连结1AC ,再以1AC 为边作第三个菱形221D C AC ,使 ︒=∠6012AC D ;……,按此规律所作的第n 个菱形的边长为 .【关键词】菱形的性质与判定 【答案】()13-nBC AE 1 E 2 E 3D 4D 1D 2 D 39.(2009年本溪)16.如图所示,已知:点(00)A ,,B ,(01)C ,在ABC △内依次作等边三角形,使一边在x 轴上,另一个顶点在BC 边上,作出的等边三角形分别是第1个11AA B △,第2个122B A B △,第3个233B A B △,…,则第n 个等边三角形的边长等于 .16题图D 1。
中考数学专题训练:规律探索——数式规律(附参考答案)

中考数学专题训练:规律探索——数式规律(附参考答案)1.按一定规律排列的单项式:a,√2a2,√3a3,√4a4,√5a5,…,第n个单项式是( ) A.√n B.√n−1a n-1C.√n a n D.√n a n-12.在如图所示的运算程序中,若开始输入x的值为48,我们发现第一次输出的结果为24,第二次输出的结果为12……则第2 023次输出的结果为( )A.6 B.3C.622 021D.322 0223.将从1开始的连续奇数按如图所示的规律排列,例如,位于第4行第3列的数为27,则位于第32行第13列的数是( )A.2 025 B.2 023C.2 021 D.2 0194.根据图中数字的规律,若第n个图中的q=143,则p的值为( )A.100 B.121C.144 D.1695.按一定规律排列的单项式:a2,4a3,9a4,16a5,25a6,…,第n个单项式是( ) A.n2a n+1B.n2a n-1C.n n a n+1D.(n+1)2a n6.根据图中数字的排列规律,在第⑦个图中,a-b-c的值是( )A.62 B.64C.-66 D.-1907.将从1开始的连续自然数按以下规律排列:若有序数对(n,m)表示第n行,从左到右第m个数,如(3,2)表示6,则表示99的有序数对是______________.8.根据图中数字的规律,则x+y的值是_______..例9.对于正整数a,我们规定:若a为奇数,则f(a)=3a+1;若a为偶数,则f(a)=a2=5.若a1=8,a2=f(a1),a3=f(a2),a4=f(a3),…,如f(15)=3×15+1=46,f(10)=102依此规律进行下去,得到一列数a1,a2,a3,a4,…,a n,…,(n为正整数),a1+a2+a3+…+a2 022=__________.参考答案1.C 2.A 3.B 4.B 5.A 6.A 7.(10,18) 8.593 9.4 725。
初中数学中考复习专题:找规律专项练习及答案解析(50道)

初中数学中考复习专题:找规律专项练习及答案解析(50道)以下是为大家整理的初中数学中考复习专题:找规律专项练习及答案解析(50道)的相关范文,本文关键词为初中,数学,中考,复习,专题,规律,专项,练习,答案,解析,,您可以从右上方搜索框检索更多相关文章,如果您觉得有用,请继续关注我们并推荐给您的好友,您可以在中考初中中查看更多范文。
初中数学中考复习专题:找规律专项练习及答案解析(50道)一、选择题1、连结多边形不相邻的两个顶点的线段,叫做多边形的对角线.观察上述图形并阅读相关文字,思考回答问题:显然四边形对角线有2条;五边形的对角线有5条;对于六边形的对角线条数,光靠“数”数,也能数出来,但已感到较麻烦!需寻找规律!从一个顶点A 出发,显然有3条,同理从b出发也3条,每个顶点出发都是3条,但从c顶点出发,就有重复线段!用此方法算出六边形的对角线条数为a;且能归纳出n边形的对角线条数的计算方法;若一个n边形有35条对角线,则a和n的值分别为()A.12,20b.12,15c.9,10D.9,122、寻找规律计算1-2+3-4+5-6+…+20XX-20XX等于()A.0b.-1c.-1008D.10083、观察下列各式并找规律,再猜想填空:,则______.4、观察一列数:是(),,,,,……根据规律,请你写出第10个数A.c.b.D.共20页,第1页二、填空题5、观察一下几组勾股数,并寻找规律:①3,4,5;②5,12,13;③7,24,25;④9,40,41;……请你写出有以上规律的第⑤组勾股数:6、找规律填空:……7、已知察上面的计算过程,寻找规律并计算:=.…,观8、观察分析下列数据,寻找规律:0,据应是_________.,,3,2,……那么第10个数9、找规律.一张长方形桌子可坐6人,按下图方式讲桌子拼在一起。
①2张桌子拼在一起可坐______人;(1分)3张桌子拼在一起可坐______人;(1分)n张桌子拼在一起可坐______人。
九年级数学找规律专题练习word精品
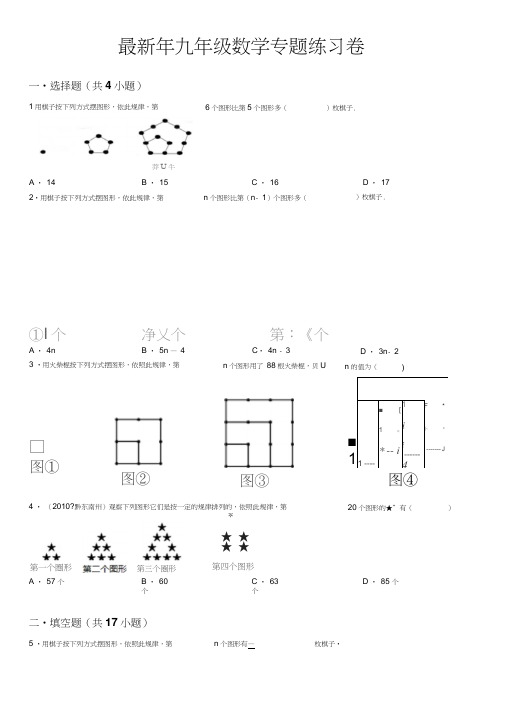
最新年九年级数学专题练习卷一•选择题(共4小题)1用棋子按下列方式摆图形,依此规律,第①I 个净乂个第:《个4 • (2010?黔东南州)观察下列图形它们是按一定的规律排列的,依照此规律,第二•填空题(共17小题)5 •用棋子按下列方式摆图形,依照此规律,第第一个圏形第三个圏形 *★ ★ ★ ★第四个图形A • 57 个B • 60个C • 63个D • 85 个6个图形比第5个图形多()枚棋子.A • 142•用棋子按下列方式摆图形,依此规律,第n 个图形比第(n - 1)个图形多(B • 15C • 16D • 17)枚棋子.A • 4nB • 5n — 43 •用火柴棍按下列方式摆图形,依照此规律,第□ 图①图②D • 3n - 2n 的值为()■1 1 ---- ■ [1耳* -- i 1if------4F *卜 *i ------- J图③图④20个图形的★”有()n 个图形有—枚棋子•莽U 牛C • 4n - 3n 个图形用了 88根火柴棍,贝U第1个 第2个 第3个6. (2010?徐州)用棋子按下列方式摆图形,依照此规律,第n 个图形比第(n - 1)个图形多 ______________________ 枚棋子.旃1个第1!个 第3个OOOOO O•o«o»oe上面是用棋子摆成的 上”字•依照此规律,第四个图形需要黑子 ______________________________ 个,白子 __________________ 个.9•用同样大小的黑色棋子按下图所示的方式摆图形,按照这样的规律摆下去,则第6个图形需棋子 _________________________ 枚.第一个團形第二个團形第三个團形第四个團形个.它们是按- 定规律排列的, 依照此规律, 第9个图形共有*12.观察下列图形:★ ★ ★★★★ ★★ ★ ★ * * * ★* ★★ ★ W ★★ ★ ★ ★* * * * *1 W 殆v J那$牛帯它们是按- 定规律排列的, 依照此规律, 第10个图形共有个^7•用棋子按下列方式摆图形,依此规律,第 6个图形比第5个图形多 ___________________ 枚棋子.O •OOOO ①ooooe②第1个團第2个團第3个團10.用同样大小的黑色棋子按如图所示的方式摆图形, 枚.按照这样的规律摆下去,则第2010个图形需棋子第1个图第2个图第3个图11 .观察下列图形:* * *it ♦★ ** 杳*★★★ >★★ 會****★ * ★★ * ★ * * *★ . - T 匸汁; 芻2个圍形 第3个图形 篦4个圏形14.观察下列图形:A A A A A A A A A A A AA A △ A A A A △ A A A △ 笫i 个图賂 蜡2个图昭 第3牛图形 n 个图形共有13.下列图形: 它们是按照一定规律排列的,依照此规律,第 5个图形中共有 它们是按一定规律排列的,依照此规律,第个. 2011个图形中共有 ________________ 个.* * ★ * * it★ ★ * * ** * ** * ★ + * * * * * * * ★* * **♦ ★ X l事4牛BB恵15 •观察下列图形:它们是按一定规律排列的,依照此规律,第 16.观察下列图形: © ◎©©lr-1• • • • •• • •• • • •• • • • • • • • •.* * • •■ • • • • • • • • • *… • • •• • •■ ■• « *18. (2012?青海)观察下列一组图形:* * *■ * 盘■# * *★ * ** * ** * •* * ★* * ***會*它们是按一 定规律排列的,依照此规律,第n 个图形中共有个^19.观察下列图形:OOOOOOOOOOOOO OOO OOOO …OOOOO OOOOOOOOO牛图形第3牛图形如rea 形它们是按一定规律排列的,依照此规律,第17•下列图形是用棋子摆成的图案,摆第 1 要37枚棋子,按照这样的方式摆下去,则摆第n 个图形共有 ___________________ 个笑脸.个图形需要7枚棋子,摆第2个图形需要19枚棋子,摆第3个图形需 5个图形需要____________________________ 枚棋子.它们是按一定规律排列的,依照此规律,第8个图形中共有O_ _ 个.20.观察下列图形它们是按一定规律构造的,依照此规律,第100个图形中共有__________________ 个三角形.21.观察下列图形:*★ ★*♦★♦* *★ * ** * ** * * ** *★ * ★* * *** ♦第1个图形第2个图形第3个'图形篤4个圏形它们是按一定规律排列的,依照此规律,第2010个图形中共有___________________ 个★.三.解答题(共9小题)222. (2012?山西)综合与实践:如图,在平面直角坐标系中,抛物线y - x +2x+3与x轴交于A、B两点,与y轴交于点C,点D是该抛物线的顶点.(1)求直线AC的解析式及B、D两点的坐标;(2)点P是x轴上一个动点,过P作直线I// AC交抛物线于点Q,试探究:随着P点的运动,在抛物线上是否存在点Q,使以点A、P、Q、C为顶点的四边形是平行四边形?若存在,请直接写出符合条件的点Q的坐标;若不存在,请说明理由.23. (2011?潼南县)如图,在平面直角坐标系中,△ ABC是直角三角形,/ ACB=90 , AC=BC , OA=1 , OC=4,抛2物线y=x +bx+c经过A, B两点,抛物线的顶点为D.(1)求b, c的值;)点E是直角三角形ABC斜边AB上一动点(点A、B除外),过点E作x轴的垂线交抛物线于点F,当线段EF的长度最大时,求点E的坐标;(3)在(2)的条件下:①求以点E、B、F、D为顶点的四边形的面积;M点的坐标.②在抛物线上是否存在一点卩,使厶EFP是以EF为直角边的直角三角形?若存在,求出所有点在,说明理由.24. (1)用棋子按下列方式摆图形,依照此规律,第n个图形有 __________________ 枚棋子. (2) 观察下列等式:第一行3=4 - 1第二行5=9 - 4第三行7=16 - 9第四行9=25 - 16按照上述规律,第n行的等式为______________________(3) 计算:(-J 2011舜012.4第1个第2个第3个25. 用棋子摆下面一组正方形图案:① ② ③图形序列①②③④⑤⑩每边棋子颗数23棋子总颗数48()照这样的规律摆下去,当每边有颗棋子时,这个图形所需要棋子总颗数是___________________________ ,第100个图形需要的棋子颗数是___________________ .26. 观察下列图形:★★★**★*★ *★ ★ ★ ★ * * * * * ** * * * * 金 *★*★*第】个图形第2个图形第3个图形第4个图形它们是按一定规律排列的,依照此规律,第16个图形共有个★27.探索规律:用棋子摆下面一组正方形图案P的坐标;若不存OOOO o O o O OOOO o OO o O o o O o O o O(3)如果某一图形共有 99枚棋子,你知道它是第几个图形吗?30.探索规律:用棋子按下面的方式摆出正方形(1)(2) (3)(1)按图示规律填写下表:图形编号(1)(2)(3)(4)(5)(6)棋子个数(2)按照这种方式摆下去,摆第 n 个正方形需要多少个棋子.OOOO o O o OOOOO图形序列(1) (2)(3)(4) (5)(12)每边棋子颗数23613 棋子总颗数 482048(2)照这样的规律摆下去,当每边有 60颗棋子时,这个图形所需要棋子总颗数是 __________________________ 颗,第(n )个图形需要的棋子总颗数是 _________________________ 颗.28 •用棋子摆出下列一组图形:B 田(1)C2) (3)图形编号1 2 3,456图形中的棋子② 照这样的方式摆下去,写出摆第n 个图形棋子的枚数;③ 如果某一图形共有 99枚棋子,你知道它是第几个图形吗?29 •用棋子摆出下列一组图形:S 田⑴ ⑵ ⑶L> *图形编号 1 2 3 4 5 6图形中的棋子)照这样的方式摆下去,写出摆第 n 个图形棋子的枚数;(用含n 的代数式表示)® ②(1)依照规律填写表中空格:①填写下表:最新九年级数学专题练习参考答案与试题解析一•选择题(共4小题)1用棋子按下列方式摆图形,依此规律,第6个图形比第5个图形多()枚棋子.A. 14B • 15C • 16|D • 17考点:规律型:图形的变化类•专题:规律型•分析:观察图形可以知道第二图比第一图多个多13,由此即可求解•4个,第三个比第二个多7个,第四个比第三个多10,第五个比第四解答:解::•第二图比第一图多4个,第三个比第二个多7个,第四个比第三个多10,第五个比第四个多13, •••第6个图形比第5个图形多16个.故选C.点评:此题主要考查了学生通过特例分析从而归纳总结出一般结论的能力•对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的•通过分析找到各部分的变化规律后直接利用规律求解.2•用棋子按下列方式摆图形,依此规律,第n个图形比第(n- 1)个图形多()枚棋子.B. 5n —4C. 4n —3D. 3n—2处L卩協占个訥%牛筆K个A . 4n考点:规律型:图形的变化类.分析:对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的. 解答:解:设第n 个图形的棋子数为 S n .第1个图形,S 1=1 ; 第2个图形,S 2=1+4 ; 第3个图形,S 3=1+4+7 ; ,第 n 个图形,S n =1+4+ --+3n - 2;第 n - 1 个图形,S n -1=1+4+ -+[3 (n - 1)- 2]; 则第n 个图形比第(n - 1)个图形多(3n -2)枚棋子; 故选D .点评:主要考查了图形的变化;解题的关键是让学生通过特例分析从而归纳总结出一般结论的能力.3•用火柴棍按下列方式摆图形,依照此规律,第 n 个图形用了 88根火柴棍,则n 的值为()考点:规律型:图形的变化类.分析:根据图形中火柴棒的个数得出变化规律得出第 n 个图形火柴棒为:n (n+3)根,进而求出n 的值即可. 解答:解:根据图形可得出:第一个图形火柴棒为:1 x( 1+3) =4根;第二个图形火柴棒为:2X (2+3) =10根; 第三个图形火柴棒为: 3X(3+3) =18根; 第四个图形火柴棒为: 4X(4+3) =28根;故第n 个图形火柴棒为:n (n+3)根,故88=n (n+3). 则n 的值为:8 . 故选:C .点评:此题主要考查了图形的变化类,根据已知图形表示出第n 个图形火柴棒个数是解题关键.考点:规律型:图形的变化类.分析:排列组成的图形都是三角形.第一个图形中有1X 3=3个^,第二个图形中有 2X 3=6个^, 第三个图形中有 3X 3=9个^, 第20个图形共有20X 3=60个★.解答:解:根据规律可知第n 个图形有3n 个^,所以第20个图形共有20X 3=60个★.另解:通过观察发现每行五星组成的三角形的边上分别有(n+1)个五星,共有3 (n - 1)个,但每个角上□ 團①图②图③ 图④C . 84. (2010?黔东南州)观察下列图形它们是按-定的规律排列的,依照此规律,第***★ ★★ ★ ★* ★★ ★★吝第一个圏形第一个图形 第二个图形第四个图形A . 57 个B . 60 个C . 63 个20个图形的★”有()D . 85 个的五星重复加了两次,故五星的个数为 3 (n - 1)- 3=3n个,故第20个图象共有60个★.故选B .本题考查了图形的变化类问题,解决此类探究性问题,关键在观察、分析已知数据,寻找它们之间的相互联系,探寻其规律.本题的关键规律为第n个图形有3n个★.•填空题(共17小题)却个第2个第3个考点:规律型:图形的变化类.专题:规律型.分析:对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的. 解答:解:设第n个图形的棋子数为Sn.第1个图形,S i=i ;第2个图形,S2=1+4 ;第3个图形,S3=1+4+7 ;第n 个图形,S n=1+4+7+ "+ (3n- 2)="(込).2点评:主要考查了图形的变化类问题,同时还考查了学生通过特例分析从而归纳总结出一般结论的能力.6. (2010?徐州)用棋子按下列方式摆图形,依照此规律,第n个图形比第(n- 1)个图形多3n- 2 枚棋子.汕个第2个湖个考点:规律型:图形的变化类.专题:规律型.分析:对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的. 解答:解:设第n个图形的棋子数为Sn.第1个图形,S1=1 ;第2个图形,S2=1+4 ;第3个图形,S3=1+4+7 ;则第n个图形比第(n- 1)个图形多(3n-2)枚棋子.点评:主要考查了学生通过特例分析从而归纳总结出一般结论的能力.7.用棋子按下列方式摆图形,依此规律,第6个图形比第5个图形多16枚棋子.5•用棋子按下列方式摆图形,依照此规律,第n个图形有二^枚棋子.第1个團 第2个團 第3个團考点:规律型:图形的变化类. 专题:规律型.分析:在4的基础上,依次多 3个,得到第n 个图中共有的棋子数.解答: 解:观察图形,发现:在 4的基础上,依次多 3个.即第n 个图中有4+3 (n - 1) =3n+1 .当n=6时,即原 式=19 .故第6个图形需棋子19枚.点评:此题能够观察图形找到规律.10•用同样大小的黑色棋子按如图所示的方式摆图形, 按照这样的规律摆下去, 则第2010个图形需棋子 6031枚.考点:规律型:图形的变化类. 专题:规律型.分析: 观察图形可以知道第二图比第一图多4个,第三个比第二个多 7个,第四个比第三个多 10,第五个比第四个多13,由此即发现第n 个图形比第(n - 1)个图形多3n -2棋子,代入n=6求解即可.解答:解:设第n 个图形的棋子数为 S n .第1个图形,S i =i ;第2个图形,S 2=1+4 ; 第3个图形,S 3=1+4+7 ;则第n 个图形比第(n - 1)个图形多3n - 2棋子. 当 n=6 时,3n - 2=3>6- 2=16. 故答案为:16.点评:此题主要考查了学生通过特例分析从而归纳总结出一般结论的能力•对于找规律的题目首先应找出哪些部 分发生了变化,是按照什么规律变化的•通过分析找到各部分的变化规律后直接利用规律求解.OOOO ®O OO O O O•o«o«②OOOO O O O•o«o»oe③上面是用棋子摆成的 上”字•依照此规律,第四个图形需要黑子5个,白子 14个.考点:规律型:图形的变化类. 专题:规律型.分析:根据已知得出黑棋子的变化规律为2, 3, 4…,白棋子为5, 8, 11-即可得出规律:摆成第 n 个上”字需要黑子n+1个,白子3n+2个,代入当n=4即可.解答:解:第一个字有 2个黑色棋子,5个白色棋子;第二个子有3个黑色棋子,8个白色棋子; 第三个字有4个黑色棋子,11个白色棋子,按照这样的规律摆下去,摆成第n 个 上”字需要黑子n+1个,白子3n+2个;当n=4时,黑色棋子有 n+1=4+1=5个,白色棋子有 3n+2=3 >4+2=14个, 故答案为:5, 14.点评:此题主要考查了图形与数字的变化类,根据已知图形得出数字变化规律是解题关键.9.用同样大小的黑色棋子按下图所示的方式摆图形,按照这样的规律摆下去,则第6个图形需棋子 19 枚.考点::规律型:图形的变化类.专题:: 规律型.分析:: 解决这类问题首先要从简单图形入手,抓住随着编号”或序号”增加时,后一个图形与前一个图形相比,在数量上增加(或倍数)情况的变化,找出数量上的变化规律,从而推出一般性的结论.解答::解:第一个图需棋子3+1-4 ; 第二个图需棋子3疋+1-7 ; 第三个图需棋子3X3+1-10;第n个图需棋子3n+1枚.将n-2010 时,3 >2010+仁6031 . 故答案为:6031 .点评:. 此题考查了规律型中的图形变化问题,主要培养学生的观察能力和空间想象能力.11 .观察下列图形:★* ★ * * * *★第一个图形第二个團形第三个團形第四个團形它们是按一定规律排列的,依照此规律,第9个图形共有金28个.考点:规律型:图形的变化类.专题:规律型.分析:观察图形可到这样一个规律,第二个图形比第一个图形多第一个图形是4个,则第二个是乙第三个是10,… 不难发现得到一个首项是4,公差是3的等差数列.3个,第三个图形比第二个图形多3个…解答:解:通过观察,第一个图形有4个第二个图形有7个第三个图形有10个依次是4, 7, 10…得到一个首项是4,公差是3的等差数列. 所以第九个图形有4+(9 - 1)>3-28 (个). 故答案为:28点评:此题主要考查了学生分析问题、观察总结规律的能力.关键是通过观察分析得出规律,此题是得到一个首项是4,公差是3的等差数列.12.观察下列图形:*★ ★ ★*★ ★ ■k *★* * ★ ★* ★★ *★ ★ ★ * * * *★ ★ ★ ★ ★* :牛常丽科J牛IBIV駢n啊8母它们是按一-定规律排列的,依照此规律,第10个图形共有30个^ 考点:规律型:图形的变化类.第1个图第2个图第3个图分析:本题是一道关于数字猜想的问题,关键是通过归纳与总结,得到其中的规律. 解答:解:•••第一个图形有1 >3=3个,第二个图形有2X3=6个,第三个图形有3X3=9个,第四个图形有4X3=12个,•••第10个图形共有:10X3=30.故答案为:30.点评:此题主要考查了图形的变化规律,解决问题的关键是通过归纳与总结,得到其中的规律.13.下列图形::它们是按一定规律排列的,依照此规律,第n个图形共有1+3n 个* W**★**★*★ *** * *W ★ ★★ * * * * * 竟 * * **★★*篤]个圍形第3个图形第4个圉形考点:规律型:图形的变化类.专题:规律型.「条线上后个图形比前一个图形多一个,分析:■把五角星分成两部分,顶点处的一个不变,其它的分三条线,每- 根据此规律找出第n个图形中五角星的个数的关系式即可;解答:解:观察发现,第1个图形五角星的个数是,1+3=4 , 第2个图形五角星的个数是,1+3 X2=7 ,第3个图形五角星的个数是,1+3 X3=10,第4个图形五角星的个数是,1+3用=13,依此类推,第n个图形五角星的个数是,1+3 Xi=1+3n ;故答案为:1+3n .并找出第n个图形五角星的个数的表达点评:本题考查了图形变化规律的问题,把五角星分成两部分进行考虑, 式是解题的关键.14.观察下列图形:A A AAA A A A AA A A血△屋A A AAA A A A A笫i牛图賂略2个圈昭第它们是按照定规律排列的,依照此规律,第5个图形中共有17个考点:: 规律型:图形的变化类.分析:' 仔细观察每一个图形得到图形中三角形的个数与图形的个数之间的关系即可得到结果.解答::解:第一个图形有2+3=个三角形;第二个图形有2+3+3个三角形;第三个图形有2+3+3+3个三角形;第n个图形有2+3+3+ --+3=3n+2个三角形,故当n=5时,有三角形3 X)+2=17个.故答案为17.点评:. 此题主要考查了学生分析问题、观察总结规律的能力.关键是通过观察分析得出规律.15•观察下列图形:它们是按一定规律排列的,依照此规律,第2011个图形中共有6034 个.* * ** *音* * * * ** * * * * * * * * ★★ ★ * * ★* * ** **X 1考点:规律型:图形的变化类. 专题: 规律型.分析:■把五角星分成两部分,顶点处的一个不变,其它的分三条线,每- 根据此规律找出第 n 个图形中五角星的个数的关系式,然后把「条线上后一个图形比前一个图形多一个, n=2011代入进行计算即可求解.解答:解:观察发现,第 1个图形五角星的个数是,1+3=4 , 第2个图形五角星的个数是,1+3 X 2=7 ,第3个图形五角星的个数是,1+3 X 3=10, 第4个图形五角星的个数是,1+3用=13,依此类推,第n 个图形五角星的个数是, 1+3 Xi=3n+1 ,•••当 n=2011 时,3 X 011 + 仁6034 . 故答案为:6034.点评:本题考查了图形变化规律的问题,把五角星分成两部分进行考虑, 式是解题的关键.并找出第n 个图形五角星的个数的表达16.观察下列图形:©©©©©n~3它们是按一定规律排列的,依照此规律,第n 个图形共有 3n — 1个笑脸.考点:规律型:图形的变化类. 专题:规律型.分析:观察图形可知前 4个图形中分别有:2, 5, 8,11个笑脸,所以可得规律为:第 n 个图形中共有3n - 1个笑 脸. 解答:解:由图形可知:n=1,笑脸=3XI -仁2, n=2,笑脸的个数=3 >2 - 1=5, n=3,笑脸的个数=3 X 3- 1=8, n=4,笑脸的个数=3X I -仁11,•••规律 3n - 1, 故答案为3n - 1.点评:本题主要考查了探究性问题,关键在观察、分析已知数据,寻找它们之间的相互联系,探寻其规律,难度 适中.17•下列图形是用棋子摆成的图案,摆第1个图形需要7枚棋子,摆第2个图形需要19枚棋子,摆第3个图形需要37枚棋子,按照这样的方式摆下去,则摆第5个图形需要91枚棋子.考点:规律型:图形的变化类.分析:; 根据相邻各图形之间棋子的个数得出变化规律,即可得出答案. 解答::解:•••第1个图形需要7=1+6 X1枚棋子,摆第2个图形需要19枚棋子,摆第3个图形需要37枚棋子, •••第2个比第1个多12个,即1+6 X (1+2)个,第3个比第2个多18个,即1+6 X( 1+2+3)个, 第4个比第三个多 24个,即1+6 X( 1+2+3+4)个. 则摆第5个图形需要:1+6 X( 1+2+3+4+5 ) =91 .故答案为:91.点评:. 此题主要考查了图形的变化,找出图形变化规律是解决问题的关键.18. (2012?青海)观察下列一组图形:考点:规律型:图形的变化类. 专题: 规律型.分析:■把五角星分成两部分,顶点处的一个不变,其它的分三条线,每- 根据此规律找出第 n 个图形中五角星的个数的关系式.•条线上后 个图形比前一个图形多一个,解答:解:观察发现,第 1个图形五角星的个数是:1+3=4 , 第2个图形五角星的个数是:1+3 X2=7 ,第3个图形五角星的个数是:1+3 X 3=10, 第4个图形五角星的个数是:1+3 X 4=13,依此类推,第n 个图形五角星的个数是:1+3 Xi=3n+1 . 故答案为:3n+1 .点评:本题考查了图形变化规律的问题,把五角星分成两部分进行考虑, 式是解题的关键. 并找出第n 个图形五角星的个数的表达19.观察下列图形:♦ * ★ * * * ★ * * ★ *■ * * * * * * ♦ * * ★ * * ★ ****它们是按一定规律排列的,依照此规律,第OOOOOOO OOOOOO OOO OOOOOO OOO OOOO ooooo弟1牛图个图晤第百卞00它们是按一定规律排列的,依照此规律,第考点:规律型:图形的变化类.分析:观察图形可看出:每幅图可看作一个由圆圈组成的正方形再加一个圆圈,因此,可利用正方形的面积公式n个图形中共有3n+1 个★.8个图形中共有O 65个.3是解决本题的关再加1计算出结果.解答:解:n=1时,圆的个数为1+1=2个;n=2时,圆的个数为 2疋+1=5个; n=3时,圆的个数为 3X 3+1=10个; n=8时,圆的个数应该是 8 >8+1=65个.故答案为:65.点评:解决这类问题首先要从简单图形入手,抓住随着 编号”或序号”增加时,后一个图形与前一个图形相比,在数量上增加(或倍数)情况的变化,找出数量上的变化规律,从而推出一般性的结论.20.观察下列图形它们是按一定规律构造的,依照此规律,第 100个图形中共有 399个三角形.第1个團形 第2个團冊 第3个图形考点: 规律型:图形的变化类.专题: 规律型.分析: 易得第1个图形中三角形的个数,进而得到其余图形中三角形的个数在第 上增加了几个4即可.1个图形中三角形的个数的基础解答:解:第1个图形中有3个三角形; 第2个图形中有3+4=7个三角形; 第3个图形中有3+2X 4=11个三角形;第 100 个图形中有 3+ (100 - 1) >4=399, 故答案为399.点评:考查图形的规律性问题;得到不变的量及变化的量与n 的关系是解决本题的关键.第1个图形 第2个图形 第3亍图形它们是按一定规律排列的,依照此规律,第2010个图形中共有 6031个★.考点:规律型:图形的变化类. 专题:规律型.分析: 找到每个图形中★的总数是在第一个图形中★的总数的基础上增加几个 解答:解:第1个图形中有4个^;第2个图形中有4+3个^; 第3个图形中有4+2X 3个^;第2010个图形中有 4+2009 X 3=6031个^; 故答案为6031 .点评:考查图形的变化规律;得到其余图形★的数目是在第一图形★的数目的基础上增加几个 键. 三.解答题(共9小题) 22. (2012?山西)综合与实践:如图,在平面直角坐标系中,抛物线 y= - x +2x+3与x 轴交于A 、B 两点,与y 轴 交于点C ,点D 是该抛物线的顶点.3即可.21.观察下列图形:2(1)求直线AC的解析式及B、D两点的坐标;(2)点P是x轴上一个动点,过P作直线I// AC交抛物线于点Q,试探究:随着P点的运动,在抛物线上是否存在点Q,使以点A、P、Q、C为顶点的四边形是平行四边形?若存在,请直接写出符合条件的点Q的坐标;若不存在,请说明理由.(3)请在直线AC上找一点皿,使厶BDM的周长最小,求出M点的坐标.考点:二次函数综合题.专题:综合题.分析:(1)根据抛物线的解析式可得出A、B、C、D的坐标,设AC解析式为y=k i x+b i ( k i书),利用待定系数法求解即可.(2)先根据题意结合图形,画出点P和点Q的位置,然后利用平行线的性质,及抛物线上点的坐标特点可求出三个Q的坐标.(3)因为BD的长固定,要使△ BDM的周长最小,只需满足BM+DM的值最小即可,作点B关于AC的对称点B',连接B'D,则与AC交点即是点M的位置,然后利用相似三角形的性质求出B'的坐标,得出B'D 的解析式,继而联立AC与B'D的解析式可得出点M的坐标.解答:解:(1 )当y=0 时,-x +2x+3=0,解得xx - 1, x2=3 . •••点A在点B的左侧,••• A、B 的坐标分别为(-1, 0), (3, 0).当x=0 时,y=3 .• C点的坐标为(0, 3)设直线AC的解析式为y=k 1x+b1 (k1旳),贝叫,| _ kj+bpOfki=3解得* ,卫i二3•直线AC的解析式为y=3x+3 .2 2••• y= - x +2x+3= -( x- 1) +4,•顶点D的坐标为(1 , 4).(2)抛物线上有三个这样的点Q,① 当点Q 在Q1位置时,Q1的纵坐标为3,代入抛物线可得点 Q1的坐标为(2, 3); _ ② 当点Q 在点Q2位置时,点Q2的纵坐标为-3,代入抛物线可得点 Q2坐标为(1+V7, - 3); ③ 当点Q 在Q3位置时,点Q3的纵坐标为-3,代入抛物线解析式可得,点Q3的坐标为(1 - _,- 3);综上可得满足题意的点 Q 有三个,分别为:Q i (2, 3), Q 2 (1+JV , - 3) , Q 3 (1 -V?,- 3).(3)过点B 作BB 丄AC 于点F ,使B F=BF ,贝U B 为点B 关于直线 AC 的对称点.连接 BD 交直线AC 于点M ,则点M 为所求, 过点B 作B E 丄x 轴于点E .•••/ 1和/ 2都是/ 3的余角, •••/ 1 = / 2.••• Rt △ AOC s Rt △ AFB ,CO CA由A(- 1 , 0), B (3, 0) , C (0, 3)得 OA=1 , OB=3 , OC=3, • AC=,AB=4 . • 一 二 • •Bf 4由/ 1 = / 2 可得 Rt △ AOC s Rt △ B ,EB ,AO CO CA••」一 | 即一:;:'vlo设直线B'D 的解析式为y=k 2x+b 2 (k 2老).k2+b 2=4OE=BE - OB==- 3=1911 9• B 点的坐标为(-…,一二).•BB2•••直线B'D 的解析式为:y=J^x+'13 139-------35■::,23. (2011?潼南县)如图,在平面直角坐标系中,2物线y=x +bx+c 经过A , (1) 求b , c 的值; (2) 点E 是直角三角形EF 的长度最大时,求点(3) 在(2)的条件下:① 求以点E 、B 、F 、D 为顶点的四边形的面积; ② 在抛物线上是否存在一点 卩,使厶EFP 是以EF 为直角边的直角三角形?若存在,求出所有点在,说明理由.考点:二次函数综合题.分析:(1)由/ ACB=90 ° AC=BC , OA=1 , OC=4,可得A (- 1, 0) B (4, 5),然后利用待定系数法即可求得b ,c 的值;(2)由直线AB 经过点A (- 1,0), B (4, 5),即可求得直线 AB 的解析式,又由二次函数 y=x - 2x - 3 , 设点E (t , t+1 ),则可得联立B'D 与AC的直线解析式可得:y=3x+3解得点评:此题考查了二次函数的综合应用,涉及了相似三角形的判定与性质、平行四边形的性质,解答本题需要我 们熟练各个知识点的内容,认真探究题目,谨慎作答.△ ABC 是直角三角形,/ ACB=90 , AC=BC , OA=1 , OC=4,抛B 两点,抛物线的顶点为 D . ABC 斜边AB 上一动点(点 A 、B 除外),过点E 作x 轴的垂线交抛物线于点 F ,当线段 E 的坐标;P 的坐标;若不存y=点F的坐标,则可求得EF的最大值,求得点E的坐标;2(3)①顺次连接点E、B、F、D得四边形EBFD,可求出点F的坐标(卫,-丄卧,点D的坐标为(1,2 4-4)由S四边形EBFD=S A BEF+S A DEF即可求得;②过点E作a丄EF交抛物线于点P,设点P ( m, m2- 2m- 3),可得m2- 2m- 3=5,即可求得点P的坐2 标,又由过点F作b丄EF交抛物线于P3,设P3 (n, n2-2n - 3),可得n2- 2n - 2=-丄求得点P的坐标,4 则可得使△ EFP是以EF为直角边的直角三角形的P的坐标.解答:解:(1)由已知得:A (- 1, 0), B (4, 5),2•••二次函数y=x +bx+c的图象经过点A (- 1, 0) , B (4 , 5),.- b+c 二0[16+4b+u二5解得:b= - 2 , c= - 3;(2)如图:•••直线AB 经过点A (- 1 , 0) , B (4 , 5),.直线AB的解析式为:y=x+1 , •••二次函数y=x2- 2x- 3 ,2.设点E (t , t+1 ),贝U F (t , t - 2t - 3),.EF= (t+1)-( t2- 2t- 3) = -( t - ;) 2+ ''2 4•••当t=时,EF的最大值为仝,2 4•••点E的坐标为(’J');2 2--),点D的坐标为(1, - 4)41 25 3 1 25 3 75S 四边形EBFD=S A BEF+S A DEF==x y x(4 -匚)+ /丁x(匚—1)= ;可求出点F的坐标(:②如图:。
初三专题---找规律
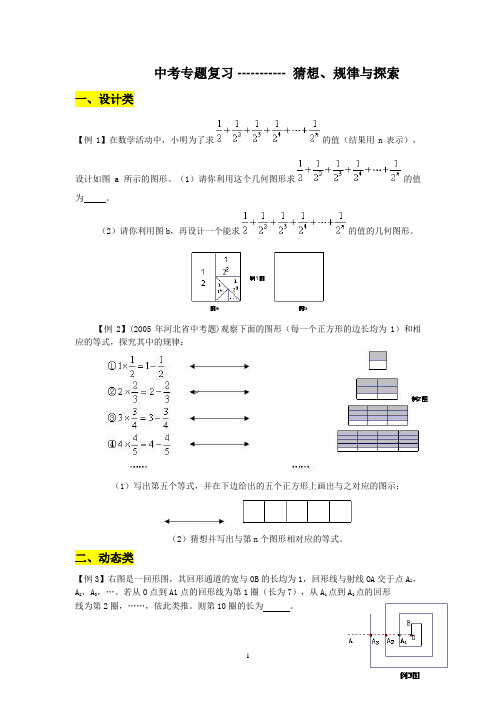
中考专题复习 ----------- 猜想、规律与探索一、设计类【例1】在数学活动中,小明为了求的值(结果用n表示),设计如图a所示的图形。
(1)请你利用这个几何图形求的值为。
(2)请你利用图b,再设计一个能求的值的几何图形。
【例2】(2005年河北省中考题)观察下面的图形(每一个正方形的边长均为1)和相应的等式,探究其中的规律:(1)写出第五个等式,并在下边给出的五个正方形上画出与之对应的图示;(2)猜想并写出与第n个图形相对应的等式。
二、动态类【例3】右图是一回形图,其回形通道的宽与OB的长均为1,回形线与射线OA交于点A1,A 2,A3,…。
若从O点到A1点的回形线为第1圈(长为7),从A1点到A2点的回形线为第2圈,……,依此类推。
则第10圈的长为。
【例4】)已知甲运动方式为:先竖直向上运动1个单位长度后,再水平向右运动2个单位长度;乙运动方式为:先竖直向下运动2个单位长度后,再水平向左运动3个单位长度。
在平面直角坐标系内,现有一动点P 第1次从原点O 出发按甲方式运动到点P 1,第2次从点P 1出发按乙方式运动到点P 2,第3次从点P 2出发再按甲方式运动到点P 3,第4次从点P 3出发再按乙方式运动到点P 4,……。
依此运动规律,则经过第11次运动后,动点P 所在位置P 11的坐标是 。
三、数字类【例5】瑞士中学教师巴尔末成功地从光谱数据,,,,……,中得到巴尔末公式,从而打开了光谱奥妙的大门。
请你按这种规律写出第七个数据是 。
【例6】观察下列算式:122=,224=,328=,4216=,….根据上述算式中的规【例7】按下列规律排列的一列数对(1,2)(4,5)(7,8),…,第5个数对是 。
【例8】一组按规律排列的数:,,,,,…请你推断第9个数是【例9】把数字按如图所示排列起来,从上开始,依次为第一行、第二行、第三行……,中间用虚线围的一列,从上至下依次为1、5、13、25、…,则第10个数为 。
初中数学找规律习题大全

1找规律专项训练一:数式问题1.(湛江)已知 22 222,3 3 323,4 4 424,⋯⋯,若 8a82a( a 、 b 为正整数)则 a b33 88 1515bb.2.(贵阳)有一列数 a 1, a 2, a 3,a 4, a 5,⋯, a n ,其中 a 1= 5× 2+ 1, a 2=5× 3+ 2,a 3= 5× 4+ 3, a 4= 5× 5+ 4, a 5= 5× 6+ 5,⋯,当 a n = 2009 时, n 的值等于()A . 2010B .2009C .401D . 3343.(沈阳)有一组单项式:a2,- a 3 , a 4 ,- a 5,⋯.观察它们构成规律,用你发现的规律写出第 10 个单2 34项式为.4.(牡丹江)有一列数1 2 3 47 个数是.2 ,,, ,⋯,那么第510 175.(南充)一组按规律排列的多项式:a b , a 2b 3 , a 3 b 5 , a 4b 7 ,⋯⋯,其中第 10 个式子是 ()A . a 10b 19B . a 10b 19C . a 10b 17D . a 10b 216.(安徽)观察下列等式:1 1 12 22 3 331, 23, 34,⋯⋯2234( 1)猜想并写出第 n 个等式;( 2)证明你写出的等式的正确性.7.(绵阳)将正整数依次按下表规律排成四列,则根据表中的排列规律,数 2009 应排的位置是第行第列.第 1 列第 2 列 第 3 列 第 4 列第 1 行 12 3第 2 行65 4第 3 行 7 8 9 第 4 行 121110⋯⋯8.(台州)将正整数 1,2,3,⋯从小到大按下面规律排列.若第 4 行第 2 列的数为 32,则① n▲ ;②第 i 行第 j 列的数为▲ (用 i , j 表示).第 1列第 2 列第 3 列⋯第 n 列1123⋯n第 行2第 2 行n 1n 2n 3⋯2n第 3 行2n 12n 22n 3⋯3n⋯⋯⋯⋯⋯⋯二:定义运算问题1.(定西)在实数范围内定义运算“”,其法则为: a b a2b2,求方程( 43)x24 的解.2.有一列数,,,,,从第二个数开始,每一个数都等于1与它前面那个数的倒数的差,若a12,a1 a2a3a n 则 a2007为()A. 2007B. 2C.1D. 1 2三:剪纸问题1.(2004年河南)如图( 9),把一个正方形三次对折后沿虚线剪下则得到的图形是()2.(2004年浙江湖州)小强拿了一张正方形的纸如图(10)①,沿虚线对折一次得图②,再对折一次得图③,然后用剪刀沿图③中的虚线(虚线与底边平行)剪去一个角,再打开后的形状应是()3.(2004年浙江衢州)如图(11),将一张正方形纸片剪成四个小正方形,然后将其中的一个正方形再剪成四个小正方形,再将其中的一个正方形剪成四个小正方形,如此继续下去,⋯⋯,根据以上操作方法,请你填写下表:3操作次数 N 1 2 3 4 5 ⋯N ⋯正方形的个数47 10⋯⋯3. (莆田) 如图, 在 x 轴的正半轴上依次截取 OA 1 A 1 A 2 A 2 A 3 A 3 A 4 A 4 A 5 ,过点 A 1、A 2、A 3、 A 4、A 5分别作 x 轴的垂线与反比例函数 y2 x 0 的图象相交于点P 1、 P 2、 P 3、 P 4、 P 5 ,得直角三角形xOP 1 A 1、 A 1P 2 A 2、 A 2 P 3 A 3、A 3P 4 A 4、 A 4 P 5 A 5,并设其面积分别为2yxS 、S 、S 、S 、S , .y12345则S 5的值为P 1P 2P 3P 4 P 5O12 A 345xA A A A (第 10 题图)4.(长春)用正三角形和正六边形按如图所示的规律拼图案,即从第二个图案开始,每个图案都比上一个 图案多一个正六边形和两个正三角形,则第 n 个图案中正三角形的个数为 (用含 n 的代数式表示) .(第 4题)5.(丹东)如图 6,用同样大小的黑色棋子按图所示的方式摆图案,按照这样的规律摆下去,第 1004个图案需棋子枚.⋯⋯图案 1图案 2图案 3图 6的三角形都是全等的),请写出第 n 个图中最小的三角形的个数有6.(抚顺)观察下列图形(每幅图中最小....个.第1个图第2个图第3个图第4个图(第 16 题图)7.(哈尔滨)观察下列图形:它们是按一定规律排列的,依照此规律,第16 个图形共有个★.五:对称问题1.(伊春)在平面直角坐标系中,已知 3 个点的坐标分别为 A1 (1,1) 、 A2 (0 ,2) 、 A3 ( 1 ,1). 一只电子蛙位于坐标原点处,第 1 次电子蛙由原点跳到以1A1为对称中心的对称点 P1,第 2 次电子蛙由 P 点跳到以 A2为对称中心的对称点P2,第 3 次电子蛙由 P2点跳到以 A3为对称中心的对称点 P3,⋯,按此规律,电子蛙分别以 A1、 A2、 A3为对称中心继续跳下去.问当电子蛙跳了 2009 次后,电子蛙落点的坐标是P2009( _______,_______ ) .2. ( 2004 年宁波)仔细观察下列图案,如图(12),并按规律在横线上画出合适的图形。
2024年中考数学复习重难点题型训练—规律探索题(含答案解析)

2024年中考数学复习重难点题型训练—规律探索题(含答案解析)类型一数式规律1.(2023·云南·统考中考真题)按一定规律排列的单项式:2345,a ,第n 个单项式是()AB1n -CnD1n -【答案】Ca ,指数为1开始的自然数,据此即可求解.【详解】解:按一定规律排列的单项式:2345,a ,第nn ,故选:C .【点睛】本题考查了单项式规律题,找到单项式的变化规律是解题的关键.2.(2023·山东·统考中考真题)已知一列均不为1的数123n a a a a ,,,,满足如下关系:1223121111a a a a a a ++==--,34131111n n na a a a a a +++==-- ,,,若12a =,则2023a 的值是()A .12-B .13C .3-D .2【答案】A【分析】根据题意可把12a =代入求解23a =-,则可得312a =-,413a =,52a =……;由此可得规律求解.【详解】解:∵12a =,∴212312a +==--,3131132a -==-+,411121312a -==+,51132113a +==-,…….;由此可得规律为按2、3-、12-、13四个数字一循环,∵20234505.....3÷=,∴2023312a a ==-;故选A .【点睛】本题主要考查数字规律,解题的关键是得到数字的一般规律.3.(2023·湖南常德·统考中考真题)观察下边的数表(横排为行,竖排为列),按数表中的规律,分数202023若排在第a 行b 列,则a b -的值为()11122113223114233241……A .2003B .2004C .2022D .2023【答案】C【分析】观察表中的规律发现,分数的分子是几,则必在第几列;只有第一列的分数,分母与其所在行数一致.【详解】观察表中的规律发现,分数的分子是几,则必在第几列;只有第一列的分数,分母与其所在行数一致,故202023在第20列,即20b =;向前递推到第1列时,分数为201912023192042-=+,故分数202023与分数12042在同一行.即在第2042行,则2042a =.∴2042202022.a b -=-=故选:C .【点睛】本题考查了数字类规律探索的知识点,解题的关键善于发现数字递变的周期性和趋向性.4.(2023·四川内江·统考中考真题)对于正数x ,规定2()1xf x x =+,例如:224(2)213f ⨯==+,1212212312f ⨯⎛⎫== ⎪⎝⎭+,233(3)312f ⨯==+,1211313213f ⨯⎛⎫== ⎪⎝⎭+,计算:11111(1)1011009932f f f f f f ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+++++++ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭(2)(3)(99)(100)(101)f f f f f +++++= ()A .199B .200C .201D .202【答案】C【分析】通过计算11(1)1,(2)2,(3)223f f f f f ⎛⎫⎛⎫=+=+= ⎪ ⎪⎝⎭⎝⎭,⋯可以推出11111(1)(2)(3)(99)(100)(101)1011009932f f f f f f f f f f f ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫++++++++++++ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭结果.【详解】解:2(1)1,11f ==+ 12441212(2),,(2)2,112323212f f f f ⨯⎛⎫⎛⎫====+= ⎪ ⎪+⎝⎭⎝⎭+122331113(3),,(3)2,113232313f f f f ⨯⨯⎛⎫⎛⎫====+= ⎪ ⎪+⎝⎭⎝⎭+…2100200(100)1100101f ⨯==+,1212100()11001011100f ⨯==+,1(100)(2100f f +=,11111(1)(2)(3)(99)(100)(101)1011009932f f f f f f f f f f f ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫++++++++++++ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭21001=⨯+201=故选:C .【点睛】此题考查了有理数的混合运算,熟练掌握运算法则,找到数字变化规律是解本题的关键.5.(2021·湖北鄂州市·中考真题)已知1a 为实数﹐规定运算:2111a a =-,3211a a =-,4311a a =-,5411a a =-,……,111n n a a -=-.按上述方法计算:当13a =时,2021a 的值等于()A.23-B.13C.12-D.23【答案】D 【分析】当13a =时,计算出23421,,3,32a a a ==-=⋅⋅⋅⋅⋅⋅,会发现呈周期性出现,即可得到2021a 的值.【详解】解:当13a =时,计算出23421,,3,32a a a ==-=⋅⋅⋅⋅⋅⋅,会发现是以:213,,32-,循环出现的规律,202136732=⨯+ ,2021223a a ∴==,故选:D .【点睛】本题考查了实数运算规律的问题,解题的关键是:通过条件,先计算出部分数的值,从中找到相应的规律,利用其规律来解答.6.(2021·湖北随州市·中考真题)根据图中数字的规律,若第n 个图中的143q =,则p的值为()A.100B.121C.144D.169【答案】B 【分析】分别分析n 的规律、p 的规律、q 的规律,再找n 、p 、q 之间的联系即可.【详解】解:根据图中数据可知:1,2,3,4n =,……22221,2,3,4,p =……222221,31,41,51,q =----……则2p n =,2(1)1q n =+-,∵第n 个图中的143q =,∴2(1)1=143q n =+-,解得:11n =或13n =-(不符合题意,舍去)∴2=121p n =,故选:B .【点睛】本题主要考查数字之间规律问题,将题中数据分组讨论是解决本题的关键.7.(2021·山东济宁市·中考真题)按规律排列的一组数据:12,35,□,717,926,1137,…,其中□内应填的数是()A.23B.511C.59D.12【答案】D 【分析】分子为连续奇数,分母为序号的平方1+,根据规律即可得到答案.【详解】观察这排数据发现,分子为连续奇数,分母为序号的平方1+,∴第n 个数据为:2211n n -+当3n =时W 的分子为5,分母为23110+=∴这个数为51102=故选:D .【点睛】本题考查了数字的探索规律,分子和分母分别寻找规律是解题关键.8.(2021·湖北十堰市·)将从1开始的连续奇数按如图所示的规律排列,例如,位于第4行第3列的数为27,则位于第32行第13列的数是()A.2025B.2023C.2021D.2019【答案】B 【分析】根据数字的变化关系发现规律第n 行,第n 列的数据为:2n(n-1)+1,即可得第32行,第32列的数据为:2×32×(32-1)+1=1985,再依次加2,到第32行,第13列的数据,即可.解:观察数字的变化,发现规律:第n行,第n列的数据为:2n(n-1)+1,∴第32行,第32列的数据为:2×32×(32-1)+1=1985,根据数据的排列规律,第偶数行从右往左的数据一次增加2,∴第32行,第13列的数据为:1985+2×(32-13)=2023,故选:B.【点睛】本题考查了数字的变化类,解决本题的关键是观察数字的变化寻找探究规律,利用规律解决问题.9.(2020•天水)观察等式:2+22=23﹣2;2+22+23=24﹣2;2+22+23+24=25﹣2;…已知按一定规律排列的一组数:2100,2101,2102,…,2199,2200,若2100=S,用含S的式子表示这组数据的和是()A.2S2﹣S B.2S2+S C.2S2﹣2S D.2S2﹣2S﹣2【分析】根据已知条件和2100=S,将按一定规律排列的一组数:2100,2101,2102,…,2199,2200,求和,即可用含S的式子表示这组数据的和.【解析】∵2100=S,∴2100+2101+2102+…+2199+2200=S+2S+22S+…+299S+2100S=S(1+2+22+…+299+2100)=S(1+2100﹣2+2100)=S(2S﹣1)=2S2﹣S.10.(2023·湖南岳阳·统考中考真题)观察下列式子:21110-=⨯;22221-=⨯;23332-=⨯;24443-=⨯;25554-=⨯;…依此规律,则第n (n 为正整数)个等式是.【答案】()21n n n n -=-【分析】根据等式的左边为正整数的平方减去这个数,等式的右边为这个数乘以这个数减1,即可求解.【详解】解:∵21110-=⨯;22221-=⨯;23332-=⨯;24443-=⨯;25554-=⨯;…∴第n (n 为正整数)个等式是()21n n n n -=-,故答案为:()21n n n n -=-.【点睛】本题考查了数字类规律,找到规律是解题的关键.11.(2023·山东临沂·统考中考真题)观察下列式子21312⨯+=;22413⨯+=;23514⨯+=;……按照上述规律,2n =.【答案】()()111n n -++【分析】根据已有的式子,抽象出相应的数字规律,进行作答即可.【详解】解:∵21312⨯+=;22413⨯+=;23514⨯+=;……∴()()2211n n n ++=+,∴()()2111n n n -++=.故答案为:()()111n n -++【点睛】本题考查数字类规律探究.解题的关键是从已有的式子中抽象出相应的数字规律.12.(2023·四川成都·统考中考真题)定义:如果一个正整数能表示为两个正整数m ,n 的平方差,且1m n ->,则称这个正整数为“智慧优数”.例如,221653=-,16就是一个智慧优数,可以利用22()()m n m n m n -=+-进行研究.若将智慧优数从小到大排列,则第3个智慧优数是;第23个智慧优数是.【答案】1545【分析】根据新定义,列举出前几个智慧优数,找到规律,进而即可求解.【详解】解:依题意,当3m =,1n =,则第1个一个智慧优数为22318-=当4m =,2n =,则第2个智慧优数为224214-=当4m =,1n =,则第3个智慧优数为224115-=,当5m =,3n =,则第5个智慧优数为225316-=当5m =,2n =,则第6个智慧优数为225221-=当5m =,1n =,则第7个智慧优数为225324-=……6m =时有4个智慧优数,同理7m =时有5个,8m =时有6个,12345621+++++=第22个智慧优数,当9m =时,7n =,第22个智慧优数为2297814932-=-=,第23个智慧优数为9,6m n ==时,2296813645-=-=,故答案为:15,45.【点睛】本题考查了新定义,平方差公式的应用,找到规律是解题的关键.13.(2023·山东聊城·统考中考真题)如图,图中数字是从1开始按箭头方向排列的有序数阵.从3开始,把位于同一列且在拐角处的两个数字提取出来组成有序数对:()3,5;()7,10;()13,17;()21,26;()31,37…如果单把每个数对中的第一个或第二个数字按顺序排列起来研究,就会发现其中的规律.请写出第n 个数对:.【答案】()221,22n n n n ++++【分析】根据题意单另把每个数对中的第一个或第二个数字按顺序排列起来研究,可发现第n 个数对的第一个数为:()11n n ++,第n 个数对的第二个位:()211n ++,即可求解.【详解】解:每个数对的第一个数分别为3,7,13,21,31,…即:121⨯+,231⨯+,341⨯+,451⨯+,561⨯+,…则第n 个数对的第一个数为:()2111n n n n ++=++,每个数对的第二个数分别为5,10,17,26,37,…即:221+;231+;241+;251+;261+…,则第n 个数对的第二个位:()221122n n n ++=++,∴第n 个数对为:()221,22n n n n ++++,故答案为:()221,22n n n n ++++.【点睛】此题考查数字的变化规律,找出数字之间的排列规律,利用拐弯出数字的差的规律解决问题.14.(2023·内蒙古通辽·统考中考真题)点Q 的横坐标为一元一次方程37322x x +=-的解,纵坐标为a b +的值,其中a ,b 满足二元一次方程组2428a b a b -=⎧⎨-+=-⎩,则点Q 关于y 轴对称点Q '的坐标为___________.【答案】()5,4--【分析】先分别解一元一次方程37322x x +=-和二元一次方程组2428a b a b -=⎧⎨-+=-⎩,求得点Q的坐标,再根据直角坐标系中点的坐标的规律即可求解.【详解】解:37322x x +=-,移项合并同类项得,525x =,系数化为1得,5x =,∴点Q 的横坐标为5,∵2428a b a b -=⎧⎨-+=-⎩①②,由2+⨯①②得,3=12b -,解得:4b =-,把4b =-代入①得,24=4a +,解得:0a =,∴=04=4a b +--,∴点Q 的纵坐标为4-,∴点Q 的坐标为()5,4-,又∴点Q 关于y 轴对称点Q '的坐标为()5,4--,故答案为:()5,4--.【点睛】本题考查解一元一次方程和解二元一次方程组、代数值求值、直角坐标系中点的坐标的规律,熟练掌握解一元一次方程和解二元一次方程组的方法求得点Q 的坐标是解题的关键.15.(2023·湖北恩施·统考中考真题)观察下列两行数,探究第②行数与第①行数的关系:2-,4,8-,16,32-,64,……①0,7,4-,21,26-,71,……②根据你的发现,完成填空:第①行数的第10个数为;取每行数的第2023个数,则这两个数的和为.【答案】1024202422024-+【分析】通过观察第一行数的规律为(2)n -,第二行数的规律为(2)1n n -++,代入数据即可.【详解】第一行数的规律为(2)n -,∴第①行数的第10个数为10(2)1024-=;第二行数的规律为(2)1n n -++,∴第①行数的第2023个数为2023(2)-,第②行数的第2023个数为2023(2)2024-+,∴202422024-+,故答案为:1024;202422024-+.【点睛】本题主要考查数字的变化,找其中的规律,是今年考试中常见的题型.16.(2021·湖南怀化市·中考真题)观察等式:232222+=-,23422222++=-,2345222222+++=-,……,已知按一定规律排列的一组数:1002,1012,1022,……,1992,若1002=m ,用含m 的代数式表示这组数的和是___________.【答案】100(21)m -【分析】根据规律将1002,1012,1022,……,1992用含m 的代数式表示,再计算0199222+++ 的和,即可计算1001011011992222++++ 的和.【详解】由题意规律可得:2399100222222++++=- .∵1002=m∴23991000222222=2m m +++++== ,∵22991001012222222+++++=- ,∴10123991002222222=++++++ 12=2m m m m =+=.102239910010122222222+=++++++ 224=2m m m m m =++=.1032399100101102222222222=++++++++ 3248=2m m m m m m =+++=.……∴1999922m =.故10010110110199992222222m m m ++++=+++ .令012992222S ++++= ①12310022222S ++++= ②②-①,得10021S-=∴10010110110199992222222m m m ++++=+++ =100(21)m -故答案为:100(21)m -.【点睛】本题考查规律问题,用含有字母的式子表示数、灵活计算数列的和是解题的关键.17.(2022·湖南怀化)正偶数2,4,6,8,10,……,按如下规律排列,2468101214161820……则第27行的第21个数是______.【答案】744【分析】由图可以看出,每行数字的个数与行数是一致的,即第一行有1个数,第二行有2个数,第三行有3个数••••••••第n行有n个数,则前n行共有(1)2n n+个数,再根据偶数的特征确定第几行第几个数是几.【详解】解:由图可知,第一行有1个数,第二行有2个数,第三行有3个数,•••••••第n行有n个数.∴前n行共有1+2+3+⋯+n=(1)2n n+个数.∴前26行共有351个数,∴第27行第21个数是所有数中的第372个数.∵这些数都是正偶数,∴第372个数为372×2=744.故答案为:744.【点睛】本题考查了数字类的规律问题,解决这类问题的关键是先根据题目的已知条件找出其中的规律,再结合其他已知条件求解.18.(2021·四川眉山市·中考真题)观察下列等式:1311 212x===+⨯;2711623x ===+⨯;313111234x ===+⨯;……根据以上规律,计算12320202021x x x x ++++-= ______.【答案】12016-【分析】根据题意,找到第n 个等式的左边为1与1n(n 1)+的和;利用这个结论得到原式=112+116+1112+…+1120202021⨯﹣2021,然后把12化为1﹣12,16化为12﹣13,120152016⨯化为12015﹣12016,再进行分数的加减运算即可.【详解】11(1)n n =++,20201120202021x =+⨯12320202021x x x x ++++- =112+116+1112+…+1120202021⨯﹣2021=2020+1﹣12+12﹣13+…+12015﹣12016﹣2021=2020+1﹣12016﹣2021=12016-.故答案为:12016-.【点睛】本题考查了二次根式的化简和找规律,解题关键是根据算式找的规律,根据数字的特征进行简便运算.19.(2022·安徽)观察以下等式:第1个等式:()()()22221122122⨯+=⨯+-⨯,第2个等式:()()()22222134134⨯+=⨯+-⨯,第3个等式:()()()22223146146⨯+=⨯+-⨯,第4个等式:()()()22224158158⨯+=⨯+-⨯,……按照以上规律.解决下列问题:(1)写出第5个等式:________;(2)写出你猜想的第n 个等式(用含n 的式子表示),并证明.【答案】(1)()()()2222516101610⨯+=⨯+-⨯(2)()[][]22221(1)21(1)2n n n n n +=+⋅+-+⋅,证明见解析【分析】(1)观察第1至第4个等式中相同位置的数的变化规律即可解答;(2)观察相同位置的数变化规律可以得出第n 个等式为()[][]22221(1)21(1)2n n n n n +=+⋅+-+⋅,利用完全平方公式和平方差公式对等式左右两边变形即可证明.(1)解:观察第1至第4个等式中相同位置数的变化规律,可知第5个等式为:()()()2222516101610⨯+=⨯+-⨯,故答案为:()()()2222516101610⨯+=⨯+-⨯;(2)解:第n 个等式为()[][]22221(1)21(1)2n n n n n +=+⋅+-+⋅,证明如下:等式左边:()2221441n n n +=++,等式右边:[][]22(1)21(1)2n n n n +⋅+-+⋅[][](1)21(1)2(1)21(1)2n n n n n n n n =+⋅+++⋅⋅+⋅+-+⋅[](1)411n n =+⋅+⨯2441n n =++,故等式()[][]22221(1)21(1)2n n n n n +=+⋅+-+⋅成立.【点睛】本题考查整式规律探索,发现所给数据的规律并熟练运用完全平方公式和平方差公式是解题的关键.20.(2021·贵州铜仁市·中考真题)观察下列各项:112,124,138,1416,…,则第n 项是______________.【答案】12nn +【分析】根据已知可得出规律:第一项:1111122=+,第二项:2112242=+,第三项:3113382=+…即可得出结果.【详解】解:根据题意可知:第一项:1111122=+,第二项:2112242=+,第三项:3113382=+,第四项:41144162=+,…则第n 项是12n n +;故答案为:12nn +.【点睛】此题属于数字类规律问题,根据已知各项的规律得出结论是解决此类题目的关键.0.618≈这个数叫做黄金比,著名数学家华罗庚优选法中的“0.618法”就应用了黄金比.设12a =,b =11111S a b =+++,2222211S a b =+++,…,10010010010010011S a b=+++,则12100S S S +++= _______.【答案】5050【分析】利用分式的加减法则分别可求S 1=1,S 2=2,S 100=100,•••,利用规律求解即可.【详解】解: 12a =,b =11122ab =⨯=∴,1112211112a ba ba b b ba bS a a ++++=+==+++++++ ,222222222222222222221112a b a b S a b a b a b a b ++++=+=⨯=⨯=+++++++,…,10101001001001010101010010011100100111a b S a b a b a b +++=+=⨯=+++++∴12100S S S +++= 121005050++⋯⋯+=故答案为:5050【点睛】本题考查了分式的加减法,二次根式的混合运算,求得1ab =,找出的规律是本题的关键.22.(2021·江西中考真题)下表在我国宋朝数学家杨辉1261年的著作《详解九章算法》中提到过,因而人们把这个表叫做杨辉三角,请你根据杨辉三角的规律补全下表第四行空缺的数字是______.【答案】3【分析】通过观察每一个数字等于它上方相邻两数之和.【详解】解:通过观察杨辉三角发现每一个数字等于它上方相邻两数之和的规律,例如:第3行中的2,等于它上方两个相邻的数1,1相加,即:211=+;第4行中的3,等于它上方两个相邻的数2,1相加,即:321=+;⋅⋅⋅⋅⋅⋅由此规律:故空缺数等于它上方两个相邻的数1,2相加,即空缺数为:3,故答案是:3.【点睛】本题考查了杨辉三角数的规律,解题的关键是:通过观察找到数与数之间的关系,从来解决问题.23.(2022·山东泰安)将从1开始的连续自然数按以下规律排列:若有序数对(),n m 表示第n 行,从左到右第m 个数,如()3,2表示6,则表示99的有序数对是_______.【答案】()10,18【分析】分析每一行的第一个数字的规律,得出第n 行的第一个数字为211n +-(),从而求得最终的答案.【详解】第1行的第一个数字:()2111=+-1第2行的第一个数字:()22121=+-第3行的第一个数字:()25131=+-第4行的第一个数字:()210141=+-第5行的第一个数字:()217151=+-…..,设第n 行的第一个数字为x ,得()211x n =+-设第1n +行的第一个数字为z ,得21z n =+设第n 行,从左到右第m 个数为y 当99y =时221(1)991n n +-≤<+∴22(1)98n n -≤<∵n 为整数∴10n =∴21182x n =+-=()∴9982118m =-+=故答案为:()10,18.【点睛】本题考查数字规律的性质,解题的关键是熟练掌握数字规律的相关性质.24.(2022·浙江舟山)观察下面的等式:111236=+,1113412=+,1114520=+,……(1)按上面的规律归纳出一个一般的结论(用含n 的等式表示,n 为正整数)(2)请运用分式的有关知识,推理说明这个结论是正确的.【答案】(1)1111(1)n n n n =+++(2)见解析【分析】(1)根据所给式子发现规律,第一个式子的左边分母为2,第二个式子的左边分母为3,第三个式子的左边分母为4,…;右边第一个分数的分母为3,4,5,…,另一个分数的分母为前面两个分母的乘积;所有的分子均为1;所以第(n+1)个式子为1111(1)n n n n =+++.(2)由(1)的规律发现第(n+1)个式子为1111(1)n n n n =+++,用分式的加法计算式子右边即可证明.(1)解:∵第一个式子()1111123621221=+=+++,第二个式子()11111341231331=+=+++,第三个式子()11111452041441=+=+++,……∴第(n+1)个式子1111(1)n n n n =+++;(2)解:∵右边=111111(1)(1)(1)(1)n n n n n n n n n n n n ++=+==+++++=左边,∴1111(1)n n n n =+++.【点睛】此题考查数字的变化规律,分式加法运算,解题关键是通过观察,分析、归纳发现其中各分母的变化规律.类型二图形规律25.(2023·重庆·统考中考真题)用长度相同的木棍按如图所示的规律拼图案,其中第①个图案用了9根木棍,第②个图案用了14根木棍,第③个图案用了19根木棍,第④个图案用了24根木棍,……,按此规律排列下去,则第⑧个图案用的木棍根数是()A .39B .44C .49D .54【答案】B 【分析】根据各图形中木棍的根数发现计算的规律,由此即可得到答案.【详解】解:第①个图案用了459+=根木棍,第②个图案用了45214+⨯=根木棍,第③个图案用了45319+⨯=根木棍,第④个图案用了45424+⨯=根木棍,……,+⨯=根,第⑧个图案用的木棍根数是45844故选:B.【点睛】此题考查了图形类规律的探究,正确理解图形中木棍根数的变化规律由此得到计算的规律是解题的关键.25.(2023·重庆·统考中考真题)用圆圈按如图所示的规律拼图案,其中第①个图案中有2个圆圈,第②个图案中有5个圆圈,第③个图案中有8个圆圈,第④个图案中有11个圆圈,…,按此规律排列下去,则第⑦个图案中圆圈的个数为()A.14B.20C.23D.26【答案】B【分析】根据前四个图案圆圈的个数找到规律,即可求解.=⨯-;【详解】解:因为第①个图案中有2个圆圈,2311=⨯-;第②个图案中有5个圆圈,5321=⨯-;第③个图案中有8个圆圈,8331=⨯-;第④个图案中有11个圆圈,11341…,⨯-=;所以第⑦个图案中圆圈的个数为37120故选:B.【点睛】本题考查了图形类规律探究,根据前四个图案圆圈的个数找到第n个图案的规律为31n -是解题的关键.27.(2023·山东日照·统考中考真题)数学家高斯推动了数学科学的发展,被数学界誉为“数学王子”,据传,他在计算1234100+++++ 时,用到了一种方法,将首尾两个数相加,进而得到100(1100)12341002⨯++++++= .人们借助于这样的方法,得到(1)12342n n n ++++++= (n 是正整数).有下列问题,如图,在平面直角坐标系中的一系列格点(),i i i A x y ,其中1,2,3,,,i n = ,且,i i x y 是整数.记n n n a x y =+,如1(0,0)A ,即120,(1,0)a A =,即231,(1,1)a A =-,即30,a = ,以此类推.则下列结论正确的是()A .202340a =B .202443a =C .2(21)26n a n -=-D .2(21)24n a n -=-【答案】B 【分析】利用图形寻找规律()211,1n A n n ---,再利用规律解题即可.【详解】解:第1圈有1个点,即1(0,0)A ,这时10a =;第2圈有8个点,即2A 到()91,1A ;第3圈有16个点,即10A 到()252,2A ,;依次类推,第n 圈,()211,1n A n n ---;由规律可知:2023A 是在第23圈上,且()202522,22A ,则()202320,22A 即2023202242a =+=,故A 选项不正确;2024A 是在第23圈上,且()202421,22A ,即2024212243a =+=,故B 选项正确;第n 圈,()211,1n A n n ---,所以2122n a n -=-,故C 、D 选项不正确;故选B .【点睛】本题考查图形与规律,利用所给的图形找到规律是解题的关键.28.(2022·江西)将字母“C”,“H”按照如图所示的规律摆放,依次下去,则第4个图形中字母“H”的个数是()A.9B.10C.11D.12【答案】B 【分析】列举每个图形中H 的个数,找到规律即可得出答案.【详解】解:第1个图中H 的个数为4,第2个图中H 的个数为4+2,第3个图中H 的个数为4+2×2,第4个图中H 的个数为4+2×3=10,故选:B.【点睛】本题考查了规律型:图形的变化类,通过列举每个图形中H 的个数,找到规律:每个图形比上一个图形多2个H 是解题的关键.29.(2022·重庆)用正方形按如图所示的规律拼图案,其中第①个图案中有5个正方形,第②个图案中有9个正方形,第③个图案中有13个正方形,第④个图案中有17个正方形,此规律排列下去,则第⑨个图案中正方形的个数为()A.32B.34C.37D.41【答案】C 【分析】第1个图中有5个正方形,第2个图中有9个正方形,第3个图中有13个正方形,……,由此可得:每增加1个图形,就会增加4个正方形,由此找到规律,列出第n 个图形的算式,然后再解答即可.【详解】解:第1个图中有5个正方形;第2个图中有9个正方形,可以写成:5+4=5+4×1;第3个图中有13个正方形,可以写成:5+4+4=5+4×2;第4个图中有17个正方形,可以写成:5+4+4+4=5+4×3;...第n 个图中有正方形,可以写成:5+4(n-1)=4n+1;当n=9时,代入4n+1得:4×9+1=37.故选:C.【点睛】本题主要考查了图形的变化规律以及数字规律,通过归纳与总结结合图形得出数字之间的规律是解决问题的关键.30.(2021·广西玉林市·中考真题)观察下列树枝分杈的规律图,若第n 个图树枝数用n Y 表示,则94Y Y -=()A.4152⨯B.4312⨯C.4332⨯D.4632⨯【答案】B【分析】根据题目中的图形,可以写出前几幅图中树枝分杈的数量,从而可以发现树枝分杈的变化规律,进而得到规律21nn Y =-,代入规律求解即可.【详解】解:由图可得到:11223344211213217211521n n Y Y Y Y Y =-==-==-==-==-则:9921Y =-,∴944942121312Y Y -=--+=⨯,故答案选:B.【点睛】本题考查图形规律,解答本题的关键是明确题意,利用数形结合的思想解答31.(2021·黑龙江大庆市·中考真题)如图,3条直线两两相交最多有3个交点,4条直线两两相交最多有6个交点,按照这样的规律,则20条直线两两相交最多有______个交点【答案】190【分析】根据题目中的交点个数,找出n 条直线相交最多有的交点个数公式:1(1)2n n -.【详解】解:2条直线相交有1个交点;3条直线相交最多有1123322+==⨯⨯个交点;4条直线相交最多有11236432++==⨯⨯个交点;5条直线相交最多有1123410542+++==⨯⨯个交点;⋯20条直线相交最多有120191902⨯⨯=.故答案为:190.【点睛】本题考查的是多条直线相交的交点问题,解答此题的关键是找出规律,即n 条直线相交最多有1(1)2n n -.32.(2023·四川遂宁·统考中考真题)烷烃是一类由碳、氢元素组成的有机化合物,在生产生活中可作为燃料、润滑剂等原料,也可用于动、植物的养护.通常用碳原子的个数命名为甲烷、乙烷、丙烷、……、癸烷(当碳原子数目超过10个时即用汉文数字表示,如十一烷、十二烷……)等,甲烷的化学式为4CH ,乙烷的化学式为26C H ,丙烷的化学式为38C H ……,其分子结构模型如图所示,按照此规律,十二烷的化学式为.【答案】1226C H 【分析】根据碳原子的个数,氢原子的个数,找到规律,即可求解.【详解】解:甲烷的化学式为4CH ,乙烷的化学式为26C H ,丙烷的化学式为38C H ……,碳原子的个数为序数,氢原子的个数为碳原子个数的2倍多2个,十二烷的化学式为1226C H ,故答案为:1226C H .【点睛】本题考查了规律题,找到规律是解题的关键.33.(2023·山西·统考中考真题)如图是一组有规律的图案,它由若干个大小相同的圆片组成.第1个图案中有4个白色圆片,第2个图案中有6个白色圆片,第3个图案中有8个白色圆片,第4个图案中有10个白色圆片,…依此规律,第n 个图案中有个白色圆片(用含n 的代数式表示)【答案】()22n +【分析】由于第1个图案中有4个白色圆片4221=+⨯,第2个图案中有6个白色圆片6222=+⨯,第3个图案中有8个白色圆片8223=+⨯,第4个图案中有10个白色圆片10224=+⨯,⋯,可得第(1)n n >个图案中有白色圆片的总数为22n +.【详解】解:第1个图案中有4个白色圆片4221=+⨯,第2个图案中有6个白色圆片6222=+⨯,第3个图案中有8个白色圆片8223=+⨯,第4个图案中有10个白色圆片10224=+⨯,⋯,∴第(1)n n >个图案中有()22n +个白色圆片.故答案为:()22n +.【点睛】此题考查图形的变化规律,通过从一些特殊的数字变化中发现不变的因素或按规律变化的因素,然后推广到一般情况.解题关键是总结归纳出图形的变化规律.34.(2023·黑龙江绥化·统考中考真题)在求123100++++ 的值时,发现:1100101+=,299101+= ,从而得到123100++++= 101505050⨯=.按此方法可解决下面问题.图(1)有1个三角形,记作11a =;分别连接这个三角形三边中点得到图(2),有5个三角形,记作25a =;再分别连接图(2)中间的小三角形三边中点得到图(3),有9个三角形,记作39a =;按此方法继续下去,则123n a a a a ++++= .(结果用含n 的代数式表示)【答案】22n n -/22n n -+【分析】根据题意得出()14143n a n n =+-=-,进而即可求解.【详解】解:依题意,()1231,5,9,14143n a a a a n n ===⋅⋅⋅=+-=-,,∴123n a a a a ++++= ()21432122n n n n n n +-==-=-,故答案为:22n n -.【点睛】本题考查了图形类规律,找到规律是解题的关键.35.(2022·山东泰安)观察下列图形规律,当图形中的“○”的个数和“.”个数差为2022时,n 的值为____________.【答案】不存在【分析】首先根据n=1、2、3、4时,“•”的个数分别是3、6、9、12,判断出第n 个图形中“•”的个数是3n;然后根据n=1、2、3、4,“○”的个数分别是1、3、6、10,判断出第n 个“○”的个数是()12n n +;最后根据图形中的“○”的个数和“.”个数差为2022,列出方程,解方程即可求出n 的值是多少即可.【详解】解:∵n=1时,“•”的个数是3=3×1;n=2时,“•”的个数是6=3×2;n=3时,“•”的个数是9=3×3;n=4时,“•”的个数是12=3×4;……∴第n 个图形中“•”的个数是3n;又∵n=1时,“○”的个数是1=1(11)2⨯+;n=2时,“○”的个数是2(21)32⨯+=,n=3时,“○”的个数是3(31)62⨯+=,n=4时,“○”的个数是4(41)102⨯+=,……∴第n 个“○”的个数是()12n n +,由图形中的“○”的个数和“.”个数差为2022()1320222n n n +∴-=①,()1320222n n n +-=②解①得:无解解②得:12n n ==故答案为:不存在【点睛】本题考查了图形类规律,解一元二次方程,找到规律是解题的关键.36.(2022·四川遂宁)“勾股树”是以正方形一边为斜边向外作直角三角形,再以该直角三角形的两直角边分别向外作正方形,重复这一过程所画出来的图形,因为重复数次后的形状好似一棵树而得名.假设如图分别是第一代勾股树、第二代勾股树、第三代勾股树,按照勾股树的作图原理作图,则第六代勾股树中正方形的个数为______.【答案】127【分析】由已知图形观察规律,即可得到第六代勾股树中正方形的个数.【详解】解:∵第一代勾股树中正方形有1+2=3(个),第二代勾股树中正方形有1+2+22=7(个),第三代勾股树中正方形有1+2+22+23=15(个),......∴第六代勾股树中正方形有1+2+22+23+24+25+26=127(个),故答案为:127.【点睛】本题考查图形中的规律问题,解题的关键是仔细观察图形,得到图形变化的规律.37.(2021·湖南常德市·中考真题)如图中的三个图形都是边长为1的小正方形组成的网格,其中第一个图形有11⨯个正方形,所有线段的和为4,第二个图形有22⨯个小正方形,所有线段的和为12,第三个图形有33⨯个小正方形,所有线段的和为24,按此规律,则第n 个网格所有线段的和为____________.(用含n 的代数式表示)【答案】2n 2+2n【分析】本题要通过第1、2、3和4个图案找出普遍规律,进而得出第n 个图案的规律为S n =4n+2n ×(n-1),得出结论即可.【详解】解:观察图形可知:第1个图案由1个小正方形组成,共用的木条根数141221,S =⨯=⨯⨯第2个图案由4个小正方形组成,共用的木条根数262232,S =⨯=⨯⨯第3个图案由9个小正方形组成,共用的木条根数383243,S =⨯=⨯⨯第4个图案由16个小正方形组成,共用的木条根数4104254,S =⨯=⨯⨯…由此发现规律是:第n 个图案由n 2个小正方形组成,共用的木条根数()22122,n S n n n n =+=+ 故答案为:2n 2+2n.【点睛】本题考查了规律型-图形的变化类,熟练找出前四个图形的规律是解题的关键.38.(2021·黑龙江绥化市·中考真题)下面各图形是由大小相同的三角形摆放而成的,图①中有1个三角形,图②中有5个三角形,图③中有11个三角形,图④中有19个三角形…,依此规律,则第n 个图形中三角形个数是_______.【答案】21n n +-【分析】此题只需分成上下两部分即可找到其中规律,上方的规律为(n-1),下方规律为n 2,结合两部分即可得出答案.【详解】解:将题意中图形分为上下两部分,则上半部规律为:0、1、2、3、4……n-1,下半部规律为:12、22、32、42……n 2,∴上下两部分统一规律为:21n n +-.故答案为:21n n +-.【点睛】本题主要考查的图形的变化规律,解题的关键是将图形分为上下两部分分别研究.类型三与函数有关规律39.(2023·山东烟台·统考中考真题)如图,在直角坐标系中,每个网格小正方形的边长均为1个单位长度,以点P 为位似中心作正方形123PA A A ,正方形456,PA A A ⋯,按此规律作下去,所作正方形的顶点均在格点上,其中正方形123PA A A 的顶点坐标分别为()()()123,0,2,1,1,0P A A ---,()32,1A --,则顶点100A 的坐标为()。
