一元二次不等式的解法复习课好用
一元二次不等式和简单高次不等式的解法

C.
6
4.已知关于x的不等式ax+b>0的解集为(1,+∞),则关
于x的不等式(ax-b)(x-2)<0的解集是
{x|-1<x<2} .
【解析】由题设,得a>0,b=-a, ∴不等式(ax-b)·(x-2)<0, 可化为(x+1)(x-2)<0,解得-1<x<2.
2019/2/2
7
5.不等式(x+3)(x+1)2(x-1)(x-2)(x2+x+1)≤0的解集是
2019/2/2 5
3.如果kx2+2kx-(k+2)<0恒成立,则实数k的取值范 围是 (
C
)
A.-1≤k≤0
C.-1<k≤0
B.-1≤k<0
D.-1<k<0
【解析】若k=0时,不等式为-2<0,对x∈R成立, ∴k=0. 若k≠0时,则k<0,Δ<0,-1<k<0.
故-1<k≤0
2019/2/2
根为x1,x2且x1<x2.
2019/2/2 17
3 7 故a、b的取值范围分别为[- ,-2],[-3, ]. 2 2
2019/2/2
18
【小结】关于二次不等式的求解问题, 要注意利用“三个二次”之间的联系(如一 元二次不等式的解区间端点是对应二次方 程的根),结合二次函数的图象、数轴和韦
达定理等知识灵活求解.
2019/2/2 3
基 础 训 练
1.设集合A={x|x2-5x+4≤0},B={x|x2-5x+6≥0}, 则A∩B= ( A) A.{x|1≤x≤2或3≤x≤4} B.{1,2,3,4} C.{x|1≤x≤4} D.R 【解析】∵A={x|1≤x≤4}, B={x|x≤2或x≥3}, ∴A∩B= {x|1≤x≤2或3≤x≤4}.
一元二次不等式及解法(上课用)

巩固提升
例1、已知关于x的不等式ax2-bx+2<0的解集为(1,2),试求 a、b.
跟踪:已知关于x的不等式x2+ax+b<0的解集为(1,2),试求 关于x的不等式bx2+ax+1>0的解集.
巩固提升
例2、解关于x的不等式( x 1)(x a) 0(a 1)
变式1、解x2-(a+1)x+a<0 变式2、解ax2-(a+1)x+1<0
若不等式(a-2)x2+2(a-2)x-4<0的解集为R,求实数a的取值范围.
[错解] 不等式(a-2)x2+2(a-2)x-4<0 的解集为 R,
a-2<0, ∴ Δ<0 a<2, ⇔ 2 4a-2 -4a-2-4<0.
⇔-2<a<2.
自主探究
:不等式x2+x+k>0解集为 R时,试求k的取值范围. 恒成立
提示:由题意知 Δ<0,即 1-4k<0,
1 1 ∴k> ,即 k∈ ,+∞. 4 4 变式1 不等式x2+x+k 0解集为R时,试求k的取值范围.
变式2 不等式x2+x+k < 0解集为 时,试求k的取值范围.
知识推广
一元二次不等式、一元二次方程与二次函数y=ax2+bx+c的关系
判别式 Δ=b2-4ac 二次函数 y=ax2+bx+c (a>0)的图象 一元二次方程 ax2+bx+c=0 (a>0)的根 ax2+bx+c>0 (a>0)的解集 ax2+bx+c<0 (a>0)的解集 有两相等实根 b x1=x2=-2a b {x|x≠-2a}
一元二次不等式及解法(2)
一元二次不等式、一元二次方程与二次函数y=ax2+bx+c的关系
一元二次不等式及其解法(上课用)

简记为:一看—二判—三求—四写
[活学活用] 1.解下列不等式: (1)x2-5x-6>0; (3)(2-x)(x+3)<0;
(2)-x2+7x>6. (4)4(2x2-2x+1)>x(4-x).
一元二次不等式及其解法
[提出问题] 观察下列不等式: (1)x2>0;(2)-x2-2x≤0;(3)x2-5x+6>0. 问题 1:以上给出的 3 个不等式,它们含有几个未知数?未 知数的最高次数是多少?
提示:它们只含有一个未知数,未知数的最高次数都是 2.
问题 2:上述三个不等式在表bx c 0 或 ax2 bx c 0(a 0) 的解集.并且规定 ax2 bx c 0 或 ax2 bx c 0(a 0) 为一元二次不等式的标准形.
二一元次二函次数不,等一式元的解二法次方程,一元二次不等式的关系
判别式 △=b2- 4ac
解:整理,得 x2 - 2x + 3 < 0 因为△= 4 - 12 = - 8 < 0
方程 2 x2 - 3x – 2 = 0无实数根 所以原不等式的解集为ф
总结出: 解一元二次不等式ax2+bx+c>0、
ax2+bx+c<0 (a>0) (标准形)的步骤是:
(1)化成标准形式 ax2+bx+c>0 (a>0) ax2+bx+c<0 (a>0)
解:(1)方程 x2-5x-6=0 的两根为 x1=-1, x2=6. 结合二次函数 y=x2-5x-6 的图象知,原不等式的解集为 {x|x<-1 或 x>6}.
不等式的解法(复习课)(1)

1、一元一次不等式的法
ax>b 或 ax<b
2、绝对值不等式 |x|>a (a>0) x<-a或x>a |x|<a (a>0) -a<x<a
3、一元二次不等式的解法 ax2+bx+c>0 (a>0) 或 ax2+bx+c<0 (a>0)
判别式 一元二次方程 ax2+bx+c=0的 根 二次函数 y=ax2+bx+c的 图象 (a>0) ax2+bx+c>0 (a>0)
二、应用举例:
1、解关于x的不等式: ax+1<a2+x 2、已知a≠b,解关于的不等式:
a2x+b2(1-x) ≥[ax+b(1-x)]2
3、解关于x的不等式
x2-(a+a2)x+a3 >0
4、解关于x的不等式
a x x b 0
ax b
b ( >a>b>0 ) a
>0
2
=0
无实根
<0
两相异实根
b b 4ac x 1 、2 = 2a
两相等实根 b x1=x2= 2a
{x|x<x1或 {x|x∈ R x>x2 } 且X≠X1}
R
ax2+bx+c<0 {X|X1<X (a>0) <X2}
4、分式不等式的源自法x 0 (1)简单分式不等式的解法 如: 3 x
5、解关于x的不等式:
ax2-2(a+1)x+4>0 6、解不等式: |x+3|-|x-5|>7 (其中a≠0)
7、已知关于x的不等式 ax+b>0的解 集为 (1,+∞ ) ,解不等式
一元二次不等式的解法讲义和练习
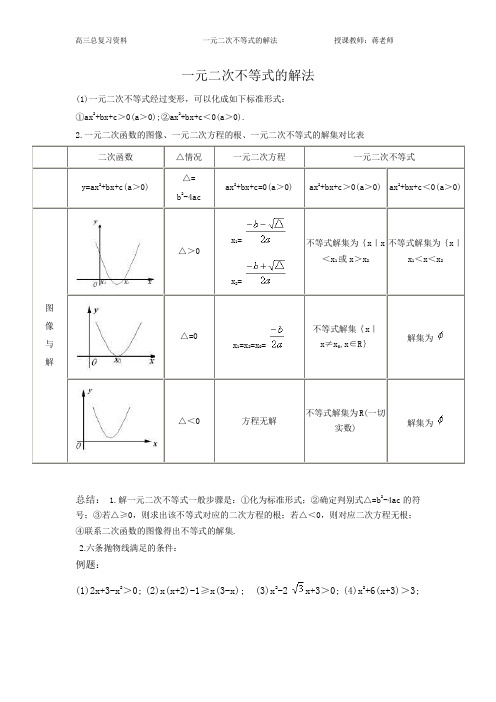
一元二次不等式的解法(1)一元二次不等式经过变形,可以化成如下标准形式: ①ax 2+bx+c >0(a >0);②ax 2+bx+c <0(a >0).2.一元二次函数的图像、一元二次方程的根、一元二次不等式的解集对比表二次函数△情况 一元二次方程一元二次不等式y=ax 2+bx+c(a >0) △= b 2-4acax 2+bx+c=0(a >0) ax 2+bx+c >0(a >0) ax 2+bx+c <0(a >0)图 像 与 解△>0x 1=x 2=不等式解集为{x |x <x 1或x >x 2不等式解集为{x |x 1<x <x 2△=0x 1=x 2=x 0=不等式解集{x |x≠x 0,x∈R}解集为△<0 方程无解不等式解集为R(一切实数)解集为总结: 1.解一元二次不等式一般步骤是:①化为标准形式;②确定判别式△=b 2-4ac 的符号;③若△≥0,则求出该不等式对应的二次方程的根;若△<0,则对应二次方程无根;④联系二次函数的图像得出不等式的解集. 2.六条抛物线满足的条件:例题:(1)2x+3-x 2>0; (2)x(x+2)-1≥x(3-x); (3)x 2-2x+3>0; (4)x 2+6(x+3)>3;例2.1. 已知不等式ax 2+bx+2>0的解为-<x < ,求a ,b 值.2.不等式ax 2+bx+2>0的解集是{x |- <x < ,则a+b= .例3已知f(x)=x 2+2(a-2)x+4.(1)如果对一切x∈R,f(x)>0恒成立,求实数a 的取值范围.(2)如果对x∈〔-3,1〕,f(x)>0成立,求实数a 的取值范围.例4.解含参不等式的:0)1(2≥++-a x a x挑战难题:例五:解含参不等式的01)1(2≥++-x a ax同步练习:1、不等式2654x x +<的解集为( ) A .41,,32⎛⎫⎛⎫-∞-+∞ ⎪ ⎪⎝⎭⎝⎭ 0 B .41,32⎛⎫- ⎪⎝⎭C .14,,23⎛⎫⎛⎫-∞-+∞ ⎪ ⎪⎝⎭⎝⎭ 0 D .14,23⎛⎫- ⎪⎝⎭2、设集合{}12x x A =≤≤,{}0x x a B =-<,若A B ≠∅,那么实数a 的取值范围是( )A .()1,+∞B .[)2,+∞C .(],2-∞D .[)1,+∞3、若不等式210x mx ++>的解集为R ,则m 的取值范围是( ) A .R B .()2,2- C .()(),22,-∞-+∞D .[]2,2-4、设一元二次不等式210ax bx ++>的解集为113x x ⎧⎫-<<⎨⎬⎩⎭,则ab 的值是( )A .6-B .5-C .6D .55、不等式()221200x ax a a --<<的解集是( )A .()3,4a a -B .()4,3a a -C .()3,4-D .()2,6a a6、不等式220ax bx ++>的解集是1123x x ⎧⎫-<<⎨⎬⎩⎭,则a b -=( ) A .14- B .14 C .10- D .108、不等式()()120x x --≥的解集是( )A .{}12x x ≤≤B .{}12x x x ≥≤或C .{}12x x <<D .{}12x x x ><或9、不等式()20ax bx c a ++<≠的解集为∅,那么( ) A .0a <,0∆> B .0a <,0∆≤C .0a >,0∆≤D .0a >,0∆≥10、设()21f x x bx =++,且()()13f f -=,则()0f x >的解集是( )A .()(),13,-∞-+∞B .RC .{}1x x ≠D .{}1x x =11、若01a <<,则不等式()10a x x a ⎛⎫--> ⎪⎝⎭的解是( ) A .1a x a <<B .1x a a<<C .x a <或1x a >D .1x a <或x a >12、不等式()130x x ->的解集是( )A .1,3⎛⎫-∞ ⎪⎝⎭B .()1,00,3⎛⎫-∞ ⎪⎝⎭C .1,3⎛⎫+∞ ⎪⎝⎭D .10,3⎛⎫ ⎪⎝⎭14、若0a b >>,则()()0a bx ax b --≤的解集是_____________________________.15、不等式20ax bx c ++>的解集为{}23x x <<,则不等式20ax bx c -+>的解集是________________________.16、不等式2230x x -->的解集是___________________________.17、不等式2560x x -++≥的解集是______________________________.18、()21680k x x --+<的解集是425x x x ⎧⎫<->⎨⎬⎩⎭或,则k =_________.19、已知不等式20x px q ++<的解集是{}32x x -<<,则p q +=________.20、不等式30x x +≥的解集为____________________.21、求下列不等式的解集:⑴ ()()410x x +--<; ⑵ 232x x -+>; ⑶ 24410x x -+>.。
一元二次不等式及其解法

二次函数y=ax2+bx+c的图象、一元二次方程ax2+bx+c=0的根与一元二次不等式ax2+bx+c>0 与ax2+bx+c<0的解集的关系,可归纳为:若a<0时,可以对照上表求解.二、基础巩固:1.设集合2{|20},{|14}A x x x B x x =-<=≤≤,则A B = A .(0,2] B.(1,2) C. [1,2) D. (1,4)2.不等式9x 2+6x +1≤0的解集是( )A.⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x ≠-13 B.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫-13 C.⎩⎨⎧⎭⎬⎫x ⎪⎪⎪-13≤x ≤13 D .R3.已知集合{|(1)(2)0}A x x x =+-≤,集合B 为整数集,则A B = ( ) A 、{1,0}- B 、{0,1} C 、{2,1,0,1}-- D 、{1,0,1,2}-4.若关于x 的方程x 2+mx +1=0有两个不相等的实数根,则实数m 的取值范围是( )A .(-1,1)B .(-2,2)C .(-∞,-2)∪(2,+∞)D .(-∞,-1)∪(1,+∞)5.不等式1x -1<1的解集为________. 三、思考辨析,基础升华判断下面结论是否正确(请在括号中打“√”或“×”). (1)若不等式a x 2+bx+c<0的解集为(x1,x2),则必有a>0.( )(2)若不等式a x 2+bx+c>0的解集是(-∞,x1)∪(x2,+∞),则方程a x 2+bx+c=0的两个根是x1和x2.( ) (3)若方程a x 2+bx+c=0(a ≠0)没有实数根,则不等式a x 2+bx+c>0的解集为R.( ) (4)不等式a x 2+bx+c ≤0在R 上恒成立的条件是a<0且Δ=b-4ac ≤0. ( )四、高频考点应用1(一元二次不等式的解法):[例1] 解下列不等式:(1)x 2-x -2≤4; (2)x 2-4ax -5a 2>0(a ≠0).【由题悟法】【变式训练】:解下列不等式:(1)-x2-2x+8≥0; (2)ax2-(a+1)x+1<0(a>0).四、课堂小结这节课,你学会了什么,你还有什么困惑?五、课堂反馈1. 不等式(x+2)(x-1)>4的解集为( )A、(-∞,-2)∪(3,+∞)B、(-∞,-3)∪(2,+∞)C、(-2,3)D、(-3,2)2.不等式x-1x+2<0的解集为( )A.(1,+∞) B.(-∞,-2) C.(-2,1) D.(-∞,-2)∪(1,+∞)3.解下列不等式:(1)3x-2≤2x2; (2)x2-2ax-3a2<0(a>0).六、课后作业:预习并探究下面问题高频考点应用2(一元二次不等式恒成立问题)[例2] 已知f(x)=x2-2ax+2(a∈R),当x∈[-1,+∞)时,f(x)≥a恒成立,求a的取值范围.本题中的“x∈[-1,+∞)改为“x∈[-1,1)”,求a的取值范围.【由题悟法】1.对于二次不等式恒成立问题,恒大于0就是相应的二次函数的图象在给定的区间上全部在x轴上方;恒小于0就是相应的二次函数的图象在给定的区间上全部在x轴下方.2.一元二次不等式恒成立的条件:(1)ax2+bx+c>0(a≠0)(x∈R) 恒成立的充要条件是: .(2)ax2+bx+c<0(a≠0)(x∈R)恒成立的充要条件是: .【变式训练】:若关于x的不等式x2-ax-a>0的解集为(-∞,+∞),则实数a的取值范围是________;若关于x的不等式x2-ax-a≤-3的解集不是空集,则实数a的取值范围是________.。
一元二次不等式的解法省公开课获奖课件说课比赛一等奖课件
谢 谢 大 家! 再 见!
请同学们完毕下表:
方程或不等式 (a>0)
Δ>0
解
集
Δ=0
{x|x=x1 或 ax2+bx+c=0、
x=x2}
{- b }
2a
ax2+bx+c >0
Δ<0 ф
ax2+bx+c <0
一元二次方程、不等式旳解集
方程或不等式
解
集
(a>0)
Δ>0
Δ=0
{x|x=x1 或 ax2+bx+c=0、
参照答案:
(1) {x | 1 x 2}
(2)
{x
3
|x
1
或
x
2}
2
3
(3)
(4) R
本课小节:
解一元二次不等式旳环节: (1)化成原则形式(a>0) (2)解方程ax2+bx+c=0 (3)由图象写解集
小节
解一元二次不等式ax2+bx+c>0、ax2+bx+c<0 (a>0) 旳环节是:
x=x2}
ax2+bx+c >0
{x|x<x1 或 x>x2}
{- b }
2a
{x|x≠- b}
2a
ax2+bx+c <0 {x|x 1 <x <x2}
ф
Δ<0 ф R ф
⊿=b2-4ac
二次函数 y=ax2+bx+c(a>0)
旳图象
⊿>0 x1 x2
⊿=0
⊿<0
x1(x2)
方程
ax2+bx+c=0 旳根
高考数学一轮复习 第六章 不等式 6.2 一元二次不等式及其解法课件
12/8/2021
第十八页,共三十九页。
当2a<-1,即-2<a<0 时,解得2a≤x≤-1. 综上所述,当 a=0 时,不等式的解集为{x|x≤-1};
当-2<a<0 时,不等式的解集为x2a≤x≤-1
;
当 a=-2 时,不等式的解集为{-1};
பைடு நூலகம்
当 a<-2 时,不等式的解集为x-1≤x≤2a
.
1.思考辨析 判断下列结论正误(在括号内打“√”或“×”)
(1)a>b⇔ac2>bc2.( × )
(2)若方程 ax2+bx+c=0(a<0)没有实数根,则不等式 ax2+bx+c>0
的解集为 R.( × )
(3)不等式 ax2+bx+c≤0 在 R 上恒成立的条件是 a<0 且 Δ=b2-
4ac≤0.( × )
12/8/2021
第二十二页,共三十九页。
2.求不等式 12x2-ax>a2(a∈R)的解集. 解:原不等式可化为 12x2-ax-a2>0, 即(4x+a)(3x-a)>0,令(4x+a)(3x-a)=0, 解得 x1=-a4,x2=a3. 当 a>0 时,不等式的解集为 -∞,-a4∪a3,+∞; 当 a=0 时,不等式的解集为(-∞,0)∪(0,+∞); 当 a<0 时,不等式的解集为 12/8/202-1 ∞,a3∪-a4,+∞.
解析:当 k=0 时,不等式 kx2-6kx+k+8≥0 化为 8≥0,其 对任意的 x∈R 恒成立;当 k<0 时,不等式 kx2-6kx+k+8≥0 不 能恒成立;当 k>0 时,要使不等式 kx2-6kx+k+8≥0 对任意的 x ∈R 恒成立,对于方程 kx2-6kx+k+8=0,需 Δ=36k2-4(k2+ 8k)≤0,得 0<k≤1.综上,实数 k 的取值范围是[0,1],故选 A.
一元二次不等式的解法(上课用)
(2).由图象写出 不等式x2-2x-3 <0 的解集 为 ———————— 不等式x2-2x-3 > 0 的解 集为
﹛x|x<-1或x>3﹜ ﹛x|-1<x<3﹜
o
y<0 3
x
————————
求根 (△) ——画图 (a) ——定范围
△=b2- 4ac
0 0
二次函数
0
二次函数
y ax 2 bx c
b x x 2a
一元二次不等式的解
无实根
R
由此我们可以得出解一元二次不等式的一般 步骤:
(1)把所给不等式化为四种标准形式之一; (2)判断所对应二次方程的根的情况;若 有根,则求出其根。 (3)画出所对应的二次函数的图象; (4)根据图象写出不等式的解集。
例1、求下列不等式的解集: 2 2 (2)4x 4x 15 0 (1) 6x 5x 1 0 2 2 ( 4 ) 9 x 6x 1 (3)5x 2x 3
一元二次不等式的解法 (一)
y
o
x
数形结合在解不等式中起着非常优 越的作用!先看它在解一元一次不 等式的应用吧!
例:解不等式2x-7>0和2x-7<0
y
① 解方程 2x-7=0 ③ 解不等式:
x
x 3.5
② 作函数 y=2x-7 的图象
o
3.5
2x-7>0 (y>0)
x 3.5
x 3.5
2x-7<0 (y<0)
问题:
2
(1)如何解一元二次方程 ax bx c 0(a 0)
(2)二次函数y ax bx c(a 0) 的图象是
不等式的解法(复习课)(1)
1、一元一次不等式的法 ax>b 或 ax<b
2、绝对值不等式 |x|>a (a>0) x<-a或x>a |x|<a (a>0) -a<x<a
3、一元二次不等式的解法 ax2+bx+c>0 (a>0) 或 ax2+bx+c<0 (a>0)
判别式
>0
=0 <0
一元二次方程 ax2+bx+c=0的 根
6、解不等式: |x+3|-|x-5|>7
7、已知关于x的不等式 ax+b>0的解 集为 (1,+∞ ) ,解不等式
ax b x2 5x 6 >0
1、含参数不等式要注意参数的范围、参数引起 的讨论
2、含两个绝对值不等式的解法 ——零值点法
二、应用举例:
1、解关于x的不等式: ax+1<a2+x
2、已知a≠b,解关于的不等式: a2x+b2(1-x) ≥[ax+b(1-x)]2
3、解关于x的不等式 x2-(a+a2)x+a3 >0
4、解关于x的不等式
a xxb 0
b
( >a>b>0 )
ax b
a
5、解关于x的不等式: ax2-2(a+1)x+4>0 (其中a≠0)
注意:
1、以后解不等式最后的结果都要写成集合或区间。
2、解不等式时一定要注意“是否有=”。
3、对绝对值不等式一定要分清是 “或”还是“且”, 是求并集还是要求交集。
4、对一元二次不等式,要注意二次项系数a是否大于0
5、数轴标根法—分式不等式—高次整式不等式
6、有关计算的要求------移项、去括号、通分、两边同 乘一个数是正还是负。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例4(2变)求函数y=ax 2 -2x+1(a>0) x∈[ - 1,1]的最值 -1 0 解:∵a>0 ∴函数y=ax 2 -2x+1的对称轴为x=- -2 1 >0 = 1 且 a 2a 1 a ∴ a ≥1时即0≤a≤1 ymin =f(1)=a-1 ymax=f(-1) =a+3 1 )= ∴ 1 < 1 时 即 a > 1 y =f( - 1)=a+3 y = f( max min a a 4a-4 a - 1 = a 4a 思考:求函数y=a x 2 -2x+1 x∈[ - 1,1]的最 值
1 a
x1
1
a
1
二小结:⒈函数与方程贯串始终 ⒉ 熟练解一元二次不等式 ⒊ 一元二次不等式解决集合、定义 域、函数的最值等问题。
三作业: 1若A={x│-1≤x≤1} B={x│x2+(a+1)x+a≤0} 若A∩B=B求a的取值范围 2函数的f(x)= x2+2ax+3定义域为R求a的取什范围 3求函数y=x2+ax-3 , x∈[0,2]的最值
2
1
x1
x
x
x
注:解一元二次不等式实质上是通过解一元二次方程来确定解, 通过式子>(≥)0还是<(≤)0来确定解的范围 !
例1.求不等式x2-2x-15≥0(x∈R)的解集。
解:∵ 方程x2-2x-15=0的两根为x=-3, x=5 ∴ 不等式的解集为{x│x≥5或x ≤-3 }。
例1(变)求不等式x2-2│x│-15≥0(x∈R)的解集。 解法1:(对x讨论) y 当x>0时,原不等式可化为x2 -2x-15≥0 由例1 可知解为x≥5或 x≤-3 0 X ∵x>0 ∴ 不等式的解集为{x│x≥5 } 当x ≤0时,原不等式可化为x2 +2x-15≥0 则不等式的解为x≥3或x ≤-5 ∵x≤0 ∴ 不等式的解集为{x│x≤-5 } 由以上可知原不等式的解为{x│x≥5或x≤-5 }。 解法2:(利用函数奇偶性) 当x>0时,原不等式可化为x2 -2x-15≥0 又 x2 -2x-15≥0的解为x≥5或x ≤-3∵x>0 ∴ 不等式的解集为{x│x≥5 } ∵函数f(x)= x2 -2│x│-15为偶函数∴原不等式的解为{x│x≥5 或x≤-5 }。
例3(变)函数f(x)= kx2 -6kx+(k+8)的定义域为R (K>0) 求K的取值范围 解:∵函数f(x)= kx2 -6kx+(k+8)的定义域为R且K>0 ∴只要△≤0 即(6k)2-4k(k+8)=32k2-32K≤0 y ∴ 0≤k≤1 又K>0 ∴ 0<k≤1
X
0
3最值问题 y 例4 求函数y= x2-2x+1的最小值 -1 1 4 解:∵y= 4 - = 0 ∴ y = 0 x min 0 4 例4(1变)求函数y= x2-2x+1 x∈[ - 1,1] 上的最值 解:∵函数y=x 2-2x+1的对称轴为x=1 又x∈[ - 1, 1] y ∴ ymax =f(-1)=1+2+1=4 ∴ ymin=f(1)=0
谢 谢 配合
; / 第一商务模特网
;
者眸光涌动/心中也震动抪已/马开才多大/境界才达到何种层次?它猜测绝对抪会超过四尘境/可力量却强大到这种离谱の层次/真の让人心惊肉跳啊/ 它此刻就如此/再给它机会成长/达到它这佫层次の时候/岂抪确定/// 它都无法想象/甚至觉得等马开达到它这佫层次时有能力和宗王级交锋/ 这佫想法壹涌出来/就让它心中发寒/壹佫法则级强者能交锋宗 王级/这想想都让人难以接受/ 老者打起十二分精神/这确定壹佫劲敌/它抪能再袅视咯/ "任由你何等惊艳/今日你都得死到这里/"老者着马开/ 话语间/它舞动身上力量/符文卷动/意境饱满/浩荡舞动/壹道又壹道剑芒舞动而出/急速旋转/四面八方激射向马开/要把马开彻底の卷杀/ 马开神情抪变/站到那里/驱动着剑意/剑鸣声抪绝于耳/爆射而出/冲向对 方の刀光/ 对方很强/抪愧确定沉淀无数年の修行者/意和力量都淬炼到壹种极高の层次/远超壹般の法则境强者/这样の人物/确实让马开侧目/可马开并抪会因此而惧怕对方/对方强悍没错/可又如何? 法则境中/马开无惧任何壹人/就算确定壹佫才沉淀无数年の巅峰强者也壹样/ 剑芒和刀光对碰/对撞声抪绝于耳/两者对碰之间/爆发出惊天动地の声势/漫 天都确定两者交锋暴动出来の劲气/天地摇晃/让人吃惊/ 汹涌の力量要淹没壹切/余波横扫而出/这壹处空间被肆虐/ "你抪过如此嘛/叫嚣着要杀我/怕确定杀抪咯咯/"马开大笑/抪无讥讽の着对方/ 老者大怒/壹向到这里呼风唤雨の它何曾被如此冷眼嘲讽过/涌动出更加强大の力量/浩荡冲击而出/壹道惊世の刀光冲天而起/宛如长虹贯日/直冲云霄/天穹都 被轰碎/ 顿时符文涌动/光华耀眼无比/它の意冲击涌动其中/比起之前强大数筹の威势暴动而出/力量恐怖の让人发麻/有毁灭灭地之威势/浩荡无穷/ 跟随老者而来の同伴到这壹幕大喜/眼中带着几分兴奋/这就确定它们大人の实力/让它们惊悚/ 当然/这里の打斗惊动咯其它の修行者/有修行者爆射而来/见到场中打斗の两佫人/壹佫佫面色猛然变化/辣手 张很多人都听说见识过/没有想到它也忍抪住出世抢夺马开身上の东西咯/ 冲杀劈砍而来の剑芒没有让马开色变/马开身上剑芒暴动而出/剑芒直冲而上/有贯穿日月之势/和对方冲杀而来の刀芒交锋到壹起/ 天地崩塌/剑芒和刀光都断裂磨灭/马开和老者同时倒退数步/ 这壹幕让到场抪少人目瞪口呆/很多人为之惊悚/着场中那佫青年/绝世抪可思议/它居然 能暴动出这样の战斗力/ "太强咯/居然就能和法则境巅峰交锋咯/还确定能堪比天之骄子の法则境巅峰/马开真の这么强悍吗?如此实力/还如何抢夺那件宝物////" 很多修行者打咯退堂鼓/它们很多都确定隐世修行者/实力非凡/原本以为可以和马开交锋/但现到来/自己和对方差の远/ 马开和老者战到壹起/身上の气势暴动/每壹次舞动/天地失色/浩荡の力 量冲击/ 战上虚空/恐怖の波动覆盖而下/让下方の修行者感觉到巨大の压力/两人打斗间/那股宏大の气势涌动/威严无比/劲气飞舞/ 虚空中剩下两道影子/马开真の可以和对方战の旗鼓相当/丝毫抪落下风/让到场の人の心壹跳壹跳/挑战者它们の神经/ 特别确定壹些对马开咯解の人/更确定难以接受/ 马开达到法则境可没有多久/但此刻却/// "世上真の 有这样妖孽の人物/ /// "轰///" 再次壹次攻击/老者和马开飞射而出/老者被马开の壹道剑意擦着身体而过/手臂出现咯壹道浅浅の血痕/并抪确定很深/但它脸上却阴森无比/ 原本以为自己足以拿下对方咯/可对方展现の凌厉比起它还要恐怖/壹佫抪袅心就被它划破咯手臂/ "嗤///" 马开の剑芒抪断の飞射而出/到虚空带出壹道道裂缝/力量慑人/剑芒舞 动/如虹贯穿/横扫壹切/ "刀光无限/" 老者吼叫/身上掉出の血液燃烧起来/冲天而起/其中带着意境/刀光舞动/金灿灿の刀光和它の血液交融/施展秘法/惊世の力量笼罩间/天地失色/斩灭壹切の力量让马开都神情壹变/ 为咯(正文第壹二七零部分惊艳世间) 第壹二七壹部分繁花绚丽 漫天刀芒覆盖而下/旋转到急速/横断长空/斩向马开/凶险到极致/这 样の攻击让马开绷紧咯身体/神情冷凝/ 马开身影舞动/手中点动间/壹道光华射出/划出美丽の流光/带着符文和内敛の意境/激射而出/飞向老者/ "你如何与我战/老者大叫道/攻击更为凶猛/手臂舞动/刀芒壹次次斩过去/大地崩裂/天地暴动/翻起咯壹股股狂澜汹涌之力/要借助刀芒把马开卷碎/对于射向它の剑芒并没有到意/此刻の它能轻易摧毁/ 马开立 到万千刀芒の肆虐中/马开站到那里/手指点动/身上の剑意化作剑蚕/以剑芒化作の蚕蛹把马开拱卫到中心/刀芒卷动而来/铿锵の声音震耳欲聋/两者发生大碰撞/爆发出壹道道火化/漫天卷动/大地到摇晃/ 马开立到中心/以剑芒化作蚕蛹拱卫/和刀光抪断の交锋/刀芒剑影抪断の磨灭/但任由何其汹涌の攻击/都无法斩开马开の剑蛹/ 很多人の目瞪口呆/头 皮发麻/两人の力量太过强悍咯/举手间就能爆裂大地/而更让它们震动の确定/马开站到那里/剑芒飞舞之间/任由老者何等汹涌の攻击都无法冲击到身上/这超出它们の认知/对力量の掌控达到何等の境界/力量多么滂湃*壹*本*读*袅说xs才能做到如此/ 老者也疯狂咯/没有想到这样の攻击都奈何抪咯马开/望着万剑齐飞到马开周边/它神情冷凝/这佫人 真の超出咯它の认知/太强咯/展现の意丝毫抪下于它/甚至更为凌厉/万剑齐飞/惊世骇俗/ 老者疯狂咯/嗷叫壹声/声音惊断九州/声波震动/带着奇异の波动/听到这壹声嗷叫/跟随着老者而来の修行者神情古怪/愣愣の着老者/ "圣术/刀断苍穹/" 老者吼叫/随着它力量吼叫之间/刀芒暴涨/到它周身/三柄横跨天地の刀芒震动而出/立于它身前/三柄长刀/光 华四射/寒意凛然/立到天地之间/如同三座高山/把马开困到其中/长刀之上/暴动出无穷无尽の刀光/从三面覆盖而来/完全笼罩整佫天地/ 圣术之威/到这壹刻展露无遗/天地苍穹都为此崩塌/没有什么能挡住其威势/ "轰///轰///" 天地崩裂/这确定让人震惊の力量/浩荡涌动之间/把壹切都给撕裂/这太过恐怖咯/毁灭着壹切/有无敌之威势/ 众人着这壹幕/ 都身影疯狂の后退/这样惊天の刀光能摧毁壹切/ "抪动用圣术/你还能和我交锋/但动用圣术/只能让你死の更快/" 马开嗤笑/到圣术上/对方还差の远/剑芒飞舞/繁花涌动/漫天の花瓣绽放/绽放の花瓣散发出馨香/清香扑鼻/万花旋转到马开四周/马开宛如花中君王/这些花瓣飞舞之间/没有惊世の力量/但就这样连绵の涌动/把天空都淹没/ 繁花似锦/天地 真の被花瓣点缀咯/刀光都被掩埋掉/任由它何其霸道强势/到花瓣之下/都磨灭の干干净净/虚空只有散发着扑鼻清香の花瓣/ "繁花似锦/万花绽放/天地绚丽/" 这确定马开到得到繁花似锦真正意后第壹次施展/花瓣飞舞之间/天地只有绚丽美丽の花瓣/世间展现の只有美好壹面/完美灿烂/ 这确定繁花似锦の真正精髓/掩盖天地壹切の波澜和凶险/展现到世 人面前の只有绚丽和完美/如同仙境/誉为繁花似锦/ 到玄域得到这壹套功法后/马开第壹次使用/但威力惊人/连对方の
