第7章-图
第七章_图论

非连通图的边连通度为 0
工
平凡图G, (G)=0
程
学
院
第七章 图论
与称为G的相对于完全图的补图,简称为G的补图,记作
工G` 若图G≌G,则称G为
程 自补图
学
院
第七章 图论
信 定义7-1.5
息
简单图G=<V,E>中,若每个结点均与其余结点相连,则称G为完全图。
有n个结点的完全图称为n阶完全图,记作Kn(n≥1) 。
科
学
。
如:
与
。。
。
。
工
。
。
程
。。
学
K3 考虑: Kn的边数为???
信 7-2 路与回路
息 定义7-2.1 设图G=<V,E>,G中结点与边的交替序列
科
=vi0ej1vi1ej2 … ejkvik
学 称点v,i0r为=0v,i1k ,到…的路,.k其中. :vviri-01,,vviikr分为别ej是r的的端始点和
与 终点. 中边的条数称为它的长度。
工 若vi0=vik ,则称该路为回路。 程 若中所有边各异,则称 为迹。
K6
院
定理7-1.4 Kn的边数为Cn2=n(n-1)/2。
第七章 图论
信 定义7-1.7
息 设G=<V,E>, G`=<V`,E`>为两个图(同时为无向图或有向图),若V` V且 E` E,则称G`为G的子图, G为G`的母图,记作G`G。
科 若V` V或E` E,则称G`为G的真子图。
d
d
d
息
e1
科 a e6
e4
c
e4
ca
7电磁场与电磁波-第七章(上)图片

第二节 平均坡印廷矢量
同样可导出:
则得坡印廷矢量的平均值:
第三节 理想介质中的均匀平面波
平面波:波阵面为平面的电磁波(等相位面为平 面)。 均匀平面波:等相位面为平面,且在等相位面上,电、 磁场场量的振幅、方向、相位处处相等的电磁波。 在实际应用中,纯粹的均匀平面波并不存在。但某 些实际存在的波型,在远离波源的一小部分波阵面,仍 可近似看作均匀平面波。 一、亥姆霍兹方程的平面波解 在正弦稳态下,在均匀、各向同性理想媒质的无源区 域中,电场场量满足亥姆霍兹方程,即:
量:
Ey
y
ZExz源自若Ex和Ey的相位相同或 相差180°,则合成波为直 线极化波。
沿z轴传播的电波 Ex和Ey的合成图 直线极化波示意图
x
特性:合成波电场大小随时间变化,但矢端
轨迹与x轴夹角不变。
常将垂直于大地的直线极化波称为垂直极化波, 而将与大地平行的直线极化波称为水平极化波。
圆极化
若Ex和Ey的振幅相同,相位差90°,合成波为圆 极化波。
设入射波电场为: 则入射波磁场为
则反射波电场为: 则反射波磁场为
由理想导体边界条件可知:
理想媒质中的合成场为:
合成波场量的实数表达式为:
讨论:1、合成波的性质:
Ex 合成波的性质: 合成波为纯驻 3 波 2 振幅随距离变化 电场和磁场最大值和最小 值位置错开λ/4 z
2
第一节 亥姆霍兹方程
时谐场所满足的波动方程即为亥姆霍兹方程。
一、时谐场场量的复数表示 对于时谐场,其场量E和H都是以一定的角频率 w随时间t按正弦规律变化。 在直角坐标系下,电场可表示为:
式中: 由复变函数,知:
为电场在各方向分量的幅度 为电场各分量的初始相位
建筑工程制图与识图第7章--建筑施工图的表达方法

图7.19 断面图按顺序排列
38页 退出
②杆件的断面图也可绘制在杆件的中断处,此种断面图无须 标注。如图7.20所示为钢筋混凝土梁的断面图画法。
23页 退出
图7.8 用一个剖切面剖切 采用两个或两个以上平行剖切画剖面图应注意以下两点: ①画剖面图时,应把几个平行的剖切平面视为一个剖切平面。 在剖面图中,不可画出两平行的剖切面所剖到的两断面在转折处 的分界线。同时,剖切平面转折处不应与图形轮廓线重合。 ②在剖切平面起、迄、转折处都应画上剖切位置线,投射方向 线与图形外的起、迄剖切位置线垂直,每个符号处应注上同样的编
2页 退出
7.1.1 多面正投影视图
由于房屋建筑形体一般都比较复杂,采用三面投影图难以表 达清楚,故需要多个视图才能表达清楚。
房屋建筑的视图应按正投影法并用第一角画法绘制。如图7. 1所示,在3个基本投影图的基础上,再增加3个投影图,从而得到 六面投影图。
图7.1 多面正投影视图的基本概念
3页 退出
包括各种软、硬塑料及有机玻璃等
19页 退出
26
防水材料
27
粉刷
构造层次多或比例大时,采用上图例 本图例采用较稀的点
20页 退出
(1)一般规定 ①建筑材料的图例画法,对其尺度比例不作具体规定。使用
时,应根据图样大小而定,如图7.6(c)所示。 ②建筑图例的图线应间隔均匀,疏密适度,做到图例正确,表
a.一张图纸内的图样只用一种图例时。 b.图形较小无法画出建筑材料图例时。
21页 退出
⑦需画出的建筑材料图例面积过大时,可在断面轮廓线内沿 轮廓线作局部表示,如图7.7(c)所示。
图7.7 建筑图例一般规定 ⑧当选用《房屋建筑制图统一标准》(GB/T50001-2010)标准 中未包括的建筑材料时,可自编图例。但不得与标准所列的图例 重复。绘制时,应在适当位置画出该材料图例,并加以说明。 (2)常用建筑材料图例 常用建筑材料应按表7.1所示图例画法绘制。
数据结构 第7章习题答案

第7章 《图》习题参考答案一、单选题(每题1分,共16分)( C )1. 在一个图中,所有顶点的度数之和等于图的边数的 倍。
A .1/2 B. 1 C. 2 D. 4 (B )2. 在一个有向图中,所有顶点的入度之和等于所有顶点的出度之和的 倍。
A .1/2 B. 1 C. 2 D. 4 ( B )3. 有8个结点的无向图最多有 条边。
A .14 B. 28 C. 56 D. 112 ( C )4. 有8个结点的无向连通图最少有 条边。
A .5 B. 6 C. 7 D. 8 ( C )5. 有8个结点的有向完全图有 条边。
A .14 B. 28 C. 56 D. 112 (B )6. 用邻接表表示图进行广度优先遍历时,通常是采用 来实现算法的。
A .栈 B. 队列 C. 树 D. 图 ( A )7. 用邻接表表示图进行深度优先遍历时,通常是采用 来实现算法的。
A .栈 B. 队列 C. 树 D. 图 ()8. 已知图的邻接矩阵,根据算法思想,则从顶点0出发按深度优先遍历的结点序列是( D )9. 已知图的邻接矩阵同上题8,根据算法,则从顶点0出发,按深度优先遍历的结点序列是A . 0 2 4 3 1 5 6 B. 0 1 3 5 6 4 2C. 0 4 2 3 1 6 5D. 0 1 2 34 6 5 ( D )10. 已知图的邻接表如下所示,根据算法,则从顶点0出发按深度优先遍历的结点序列是( A )11. 已知图的邻接表如下所示,根据算法,则从顶点0出发按广度优先遍历的结点序列是A .0 2 4 3 1 5 6B. 0 1 3 6 5 4 2C. 0 1 3 4 2 5 6D. 0 3 6 1 5 4 2⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡0100011101100001011010110011001000110010011011110A .0 1 3 2 B. 0 2 3 1 C. 0 3 2 1 D. 0 1 2 3(A)12. 深度优先遍历类似于二叉树的A.先序遍历 B. 中序遍历 C. 后序遍历 D. 层次遍历(D)13. 广度优先遍历类似于二叉树的A.先序遍历 B. 中序遍历 C. 后序遍历 D. 层次遍历(A)14. 任何一个无向连通图的最小生成树A.只有一棵 B. 一棵或多棵 C. 一定有多棵 D. 可能不存在(注,生成树不唯一,但最小生成树唯一,即边权之和或树权最小的情况唯一)二、填空题(每空1分,共20分)1. 图有邻接矩阵、邻接表等存储结构,遍历图有深度优先遍历、广度优先遍历等方法。
第7章状态机图

7 第章状态图
7.6 并发状态
7.6.1 并发状态的含义 7.6.2 同步状态
7.6.1 并发状态的含义
并发状态:在一个状态机或一个复合状态中,如果同时存 在相互可以独立的几组状态,则称这几组状态是并发状态 (concurrent state)。
例如:
7.6.2 同步状态
同步状态:指多个并发区间中的状态在转换过程彼此存在 同步关系,一个区间中的一个转换需要等到另一个区间中的 某个转换发生后才能进行。 例如:
• 初始状态表示一个状态机从此结点开始,但事物不会此状态 停留,会立即转换到初始状态所连接的第下一个状态。
• 初始状态只有输出,没有输入。
7.7.2 分叉与汇合
• 分叉 (fork) :指将一个转换分成两个或多个转换,用来描述 需要并发的状态。
• 汇合 (join) :指将从并发状态来的转换合并形成一个转换, 用来描述多个并发状态的控制同步。
7.8.5 状态机与其他的图比较
1)状态机图用于事物状态及其变换的建模;活动图用于过 程流程建模 。 2)状态结点表示事物一个状态,活动结点表示一个过程中 的一个动作。 3)交互图用于多个对象为完成一个任务的交互关系,状态 机图表示一个事物所处的状态,及其变换。 4)可以用状态机描述一个交互过程中所处的状态及其转换, 用活动图描述一个交互执行的流程。
3 交互状态建模:一个交互描述为完成某项功能,系统中 若干个对象相互交互消息的过程。一个交互过程也会存在 多种状态,及其状态的转换,可以用状态机图来描述交互 状态的转换。
订货交互的状态机:
7.8.2 状态机的用途
4 构件状态建模:构件封装了多个类,构件在其生命周期 中也会存在不同状态,可以用状态机对构件的状态及其转 换进行建模。
数据结构课后习题答案第七章
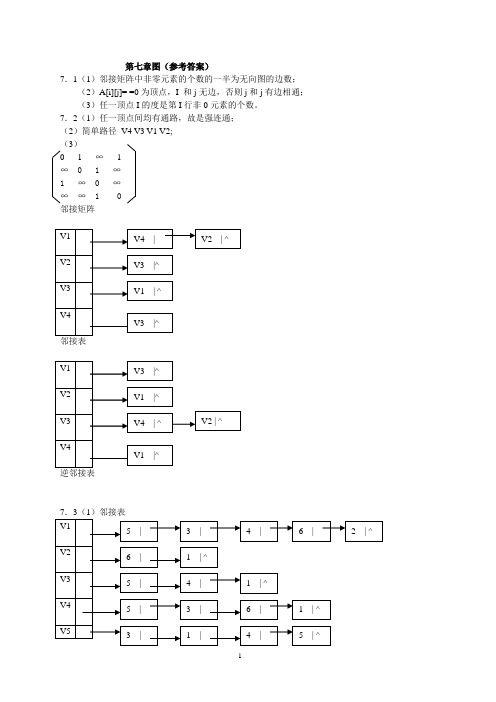
第七章图(参考答案)7.1(1)邻接矩阵中非零元素的个数的一半为无向图的边数;(2)A[i][j]= =0为顶点,I 和j无边,否则j和j有边相通;(3)任一顶点I的度是第I行非0元素的个数。
7.2(1)任一顶点间均有通路,故是强连通;(2)简单路径V4 V3 V1 V2;(3)0 1 ∞ 1∞ 0 1 ∞1 ∞ 0 ∞∞∞ 1 0邻接矩阵邻接表(2)从顶点4开始的DFS序列:V5,V3,V4,V6,V2,V1(3)从顶点4开始的BFS序列:V4,V5,V3,V6,V1,V27.4(1)①adjlisttp g; vtxptr i,j; //全程变量② void dfs(vtxptr x)//从顶点x开始深度优先遍历图g。
在遍历中若发现顶点j,则说明顶点i和j间有路径。
{ visited[x]=1; //置访问标记if (y= =j){ found=1;exit(0);}//有通路,退出else { p=g[x].firstarc;//找x的第一邻接点while (p!=null){ k=p->adjvex;if (!visited[k])dfs(k);p=p->nextarc;//下一邻接点}}③ void connect_DFS (adjlisttp g)//基于图的深度优先遍历策略,本算法判断一邻接表为存储结构的图g种,是否存在顶点i //到顶点j的路径。
设 1<=i ,j<=n,i<>j.{ visited[1..n]=0;found=0;scanf (&i,&j);dfs (i);if (found) printf (” 顶点”,i,”和顶点”,j,”有路径”);else printf (” 顶点”,i,”和顶点”,j,”无路径”);}// void connect_DFS(2)宽度优先遍历全程变量,调用函数与(1)相同,下面仅写宽度优先遍历部分。
第7章--双代号网络图
D
E
工程网络计划技术-18
工程项目管理—— 第7章 工程网络计划技术
A1 工作A、B分为三个施工 阶段,分段流水施工,A1 完成后进行A2、B1;A2完 成后进行A3、B2;A2、B1 完成后进行B2;A3、B2完 成后进行B3
第一种表示方法
厦门大学嘉庚学院土木工程系
A2 B1 B1 A2 B2 A3 B3 A3 B2 B3
节点的含义
工程网络计划技术-11
工程项目管理—— 第7章 工程网络计划技术
厦门大学嘉庚学院土木工程系
虚工作
箭线
工作表示 方法 代表工作 名称
3
1
节点
2
4
5
6
工作持续 时间
工程网络计划技术-12
工程项目管理—— 第7章 工程网络计划技术
厦门大学嘉庚学院土木工程系
(3)线路
1)线路含义及分类 线路—— 线路时间—— 关键工作—— 非关键工作—— 3)线路时差 ①→②→④→⑥(8天); A
10
A1
第二种表示方法
A1
A2
A3
11
A、B均完成后,C才能开 始;A、 B、C分三段作 业交叉进行;A、B分为 A1、A2、A3和B1、B2、B3 三个施工段,C分为C1、 C2、C3三个施工段
C1
C2
C3
B1
B2
B3 工程网络计划技术-19
工程项目管理—— 第7章 工程网络计划技术
厦门大学嘉庚学院土木工程系
垫层1
3
3
基础1
4
垫层2
断开不存在 的逻辑关系
基础1
没 有 逻 辑 关 系
4
基础2
5
6
第7章 图论 [离散数学离散数学(第四版)清华出版社]
![第7章 图论 [离散数学离散数学(第四版)清华出版社]](https://img.taocdn.com/s3/m/58b7923143323968011c9244.png)
6/27/2013 6:02 PM
第四部分:图论(授课教师:向胜军)
21
例:
a j i h c g d
1(a)
无 向 图
b
f
e
2(b)
7(j) 8(g) 9(d) 10(i)
6(e)
3(c) 4(h)
5(f)
6/27/2013 6:02 PM
第四部分:图论(授课教师:向胜军)
22
例:
1(b)
有向图
第四部分:图论(授课教师:向胜军)
6
[定义] 相邻和关联
在无向图G中,若e=(a, b)∈E,则称a与 b彼此相邻(adjacent),或边e关联 (incident) 或联结(connect) a, b。a, b称为边e的端点或 结束顶点(endpoint)。 在有向图D中,若e=<a, b>∈E,即箭头 由a到b,称a邻接到b,或a关联或联结b。a 称为e的始点(initial vertex),b称为e的终点 (terminal/end vertex)。
证明思路:将图中顶点的度分类,再利用定理1。
6/27/2013 6:02 PM 第四部分:图论(授课教师:向胜军) 9
[定理3] 设有向图D=<V, E>有n个顶点,m 条边,则G中所有顶点的入度之和等于所 有顶点的出度之和,也等于m。
即:
d ( v i ) d ( v i ) m.
i 1 i 1
n
n
证明思路:利用数学归纳法。
6/27/2013 6:02 PM
第四部分:图论(授课教师:向胜军)
10
一些特殊的简单图:
(1) 无向完全图Kn(Complete Graphs)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第7章-图-CAL-FENGHAI.-(YICAI)-Company One1第7章图实验图的基本操作及应用一、实验目的1、熟悉图的基本概念,理解图的各种类型2、掌握图的邻接矩阵、邻接表的表示方法3、掌握图的两种遍历方法4、加深理解图的最小生成树的基本思想。
5、掌握图的最小生成树的生成方法和实现算法6、加深对图的理解,熟悉图的实际应用二、实验内容(一)验证实验1、图的邻接矩阵表示(二)设计实验1、图的遍历问题案例描述:已知8个城市的交通路线图如下图1所示,从沈阳出发,要到其他7个城市推销产品。
给出到达每一个城市的一组城市顺序。
图1:8个城市的交通路线图设计方案:图的遍历有深度优先遍历和广度优先遍历两种算法。
在这里我们利用数据结构中图的邻接矩阵存储方式以及图的深度优先遍历的算法来解决该问题。
结构定义:typedef char vextype[LEN];typedef int edgetype;typedef struct{ vexntype vex[LEN];edgetype arc[VEXN][VEXN];int vexn,arcn;}Mgraph;2、某公司拟建一个局域网,需要连接6栋楼(0,1,2,3,4,5),其地理分布如下图2所示,各边上的权值代表楼宇间距离。
设计要求:根据下图中的楼宇分布,设计出布线造价最小的局域网络图,要求连接所有的顶点,并且总的布线费用最低。
实验提示:要想布线造价最小,可将图中各顶点间的距离看作其费用。
这样就可以用Prim算法构造一棵最小生成树来解决问题。
图2 图2的邻接矩阵运行时输入数据及运行结果显示如下:Input vexnum,arcnum:6,10V1,v2,w=0,1,6V1,v2,w=0,2,5V1,v2,w=0,5,1V1,v2,w=1,5,5V1,v2,w=1,3,3V1,v2,w=2,5,5V1,v2,w=2,4,2V1,v2,w=3,5,6V1,v2,w=3,4,6V1,v2,w=4,5,4输出最小生成树中的边及其权值如下:(0,5)1(5,4)4(4,2)2(5,1)5(1,3)3参考程序:(一)验证实验1、图的邻接矩阵表示实验程序:#include "Stdio.h"#include "Conio.h"#include"stdio.h"#define MaxNum 50 //图的最大顶点数设为50typedef char VexType[7]; //图的顶点类型设为字符数组,2个字符长度typedef int EdgeType; //弧(边)的权值设为整型typedef struct {VexType V[MaxNum]; //一维数组存储顶点信息EdgeType E[MaxNum][MaxNum]; //二维数组表示邻接矩阵,存储边的信息int n,e; //顶点数和边数}MGraph; //图类型定义int Locate(MGraph *G,char vex[]) //确定顶点在图G中的位置,即在G->V中的序{int i;for(i=0;i<G->n;i++)if(strcmp(G->V[i],vex)==0)return i;}void CreateGraph(MGraph *G){int i,j,k;char vex1[3],vex2[3];//保存输入的顶点printf("\n输入图的顶点数和边数(用逗号分隔):");scanf("%d,%d",&(G->n),&(G->e));//输入顶点数和边数printf("输入图的顶点信息(最长2个字符):");for (i=0;i<G->n;i++){/*G->V[i][0]=G->V[i][1]=0;*/scanf("\n%s",G->V[i]); //输入n个顶点的标识信息,建立顶点数组}for (i=0;i<G->n;i++)for (j=0;j<G->n;j++)G->E[i][j]=0; //对邻接矩阵元素进行初始化printf("\n输入图中每条边所依附的两个顶点的标识信息:");for (k=0;k<G->e;k++) //输入e条边{printf("\n输入第%d条边的第1个顶点:",k+1);scanf("%s",vex1);printf("输入第%d条边的第2个顶点:",k+1);scanf("%s",vex2);// scanf("%s\n%s",vex1,vex2);i=Locate(G,vex1);j=Locate(G,vex2);// scanf("\n%d,%d",&i,&j); //输入每条边所依附的顶点在二维数组中的下标,建立邻接矩阵G->E[i][j]=1; //如果同时输入G->E[j][i]=1;,则是建立无向图的邻接矩阵}}void PrintGraph(MGraph *G)//打印图的顶点和边的信息{int i,j;printf("\n图中顶点个数为:%d",G->n);printf("\n图中边数为:%d",G->e);printf("\n图中顶点为:");for (i=0;i<G->n;i++)printf("%c%c ",G->V[i][0],G->V[i][1]);printf("\n图中边为:");for(i=0;i<G->n;i++)for(j=0;j<G->n;j++)if(G->E[i][j])printf("[%c%c,%c%c] ",G->V[i][0], G->V[i][1], G->V[j][0], G->V[j][1]);}main(){MGraph mg;CreateGraph(&mg);PrintGraph(&mg);}(二)设计实验1、图的遍历问题案例描述:已知8个城市的交通路线图如下图1所示,从沈阳出发,要到其他7个城市推销产品。
给出到达每一个城市的一组城市顺序。
#define NULL 0#define VEXN 30 //顶点的最大个数#define LEN 10 //城市名称的最大长度#include <stdio.h>typedef char vexntype[LEN]; //顶点数据类型typedef int edgetype; //边数据类型typedef struct{vexntype vex[VEXN];edgetype arc[VEXN][VEXN];int vexn,arcn; //顶点个数和边数}Mgraph; //图的邻接矩阵表示结构int visit[VEXN]; //遍历标志数组Mgraph City_Graph(){int i,j,k;Mgraph G;printf("\n input vex number");scanf("%d",&G.vexn); //输入顶点数目printf("input edge numbef:");scanf("%d",&G.arcn); //输入总边数printf("input %d vex information such as Shenyang Beijing and soon:\n",G.vexn);for(i=0;i<G.vexn;i++)scanf("%s",&G.vex[i]);for(i=0;i<G.vexn;i++)for(j=0;j<G.vexn;j++)G.arc[i][j]=0;for(k=0;k<G.arcn;k++) //输入各顶点距离{printf("input edge %d such as i,j:",k+1);scanf("%d,%d",&i,&j);while(i<1||i>G.vexn||j<1||j>G.vexn) //输入各顶点距离{printf("Error vexn Number,input(i,j)again:");scanf("%d,%d",&i,&j);}G.arc[i-1][j-1]=1;G.arc[j-1][i-1]=1;}return G;}void DFS_G(Mgraph G,int i) //输出深度优先遍历序列{int j;printf("%s,",G.vex[i]);visit[i]=1;for(j=0;j<G.vexn;j++)if((G.arc[i][j]==1)&&(!visit[j]))DFS_G(G,j);}main(){Mgraph G;G=City_Graph(); //调用输入顶点和边的函数printf("\nDFS:\n"); //调用查询最短路径函数DFS_G(G,0);}运行测试:<输入>Input vex number:8Input edge number:9Input 8 vex information such as Shenyang Beijing and so on:沈阳北京天津大连营口鞍山抚顺丹东(输入:每一个顶点回车)Input edge1 such as i,j:1,2(在英文状态下输入)Input edge1 such as i,j:1,3Input edge1 such as i,j:2,3Input edge1 such as i,j:4,5Input edge1 such as i,j:5,6Input edge1 such as i,j:6,7Input edge1 such as i,j:7,8Input edge1 such as i,j:1,6Input edge1 such as i,j:1,7<输出>DFS:沈阳北京天津鞍山营口大连抚顺丹东2、某公司拟建一个局域网,需要连接6栋楼(0,1,2,3,4,5),其地理分布如下图2所示,各边上的权值代表楼宇间距离。
