2buck直流变换器的工作原理及动态建模
Buck-Boost变换器原理

浅谈Buck/Boost变换器Buck变换器原理Buck变换器又称降压变换器、是一种输出电压小于输入电压的单管不隔离直流变换器,串联开关稳压电源、三端开关型降压稳压器。
1.线路组成图1(a)所示为由单刀双掷开关S、电感元件L和电容C组成的Buck变换器电路图。
图1(b)所示为由以占空比D工作的晶体管T r、二极管D1、电感L、电容C组成的Buck变换器电路图。
电路完成把直流电压V s转换成直流电压V o的功能。
图1Buck变换器电路2.工作原理当开关S在位置a时,有图2 (a)所示的电流流过电感线圈L,电流线性增加,在负载R上流过电流I o,两端输出电压V o,极性上正下负。
当i s>I o时,电容在充电状态。
这时二极管D1承受反向电压;经时间D1T s后(,t on 为S在a位时间,T s是周期),当开关S在b位时,如图2(b)所示,由于线圈L中的磁场将改变线圈L两端的电压极性,以保持其电流i L不变。
负载R两端电压仍是上正下负。
在i L<I o时,电容处在放电状态,有利于维持I o、V o不变。
这时二极管D1,承受正向偏压为电流i L构成通路,故称D1为续流二极管。
由于变换器输出电压V o小于电源电压V s,故称它为降压变换器。
工作中输入电流is,在开关闭合时,i s>0,开关打开时,i s=0,故i s是脉动的,但输出电流I o,在L、D1、C作用下却是连续的,平稳的。
图2Buck变换器电路工作过程Boost变换器Boost变换器又称为升压变换器、是一种输出电压高于输入电压的单管不隔离直流变换器,并联开关电路、三端开关型升压稳压器。
1.线路组成线路由开关S、电感L、电容C组成,如图1所示,完成把电压V s升压到V o的功能。
图12.工作原理当开关S在位置a时,如图2(a)所示电流i L流过电感线圈L,电流线性增加,电能以磁能形式储在电感线圈L中。
此时,电容C放电,R上流过电流I o,R两端为输出电压V o,极性上正下负。
Buck变换器的结构及工作原理

Buck变换器的结构及工作原理高压水射流清洗技术是近年来在国际上兴起的一门高科技清洗技术,具有清洗速度快、效率高、成本低、清洁环保、不腐蚀损伤基体、适用范围广、易于实现自动化和智能化控制等优点,可清洗形状结构复杂的零部件[1]。
近年来,随着自动控制技术的不断发展,工业自动化水平日益提高。
为了提高高压水射流设备的清洗效率和清洗效果,有研究人员将自动控制技术运用到射流清洗过程中。
其清洗效果和清洗效率相对于传统的人工清洗有了很大的提升,但该过程对于控制系统的实时性、稳定性具有较高的要求。
因而作为控制系统的驱动部分,直流电源输出的快速性、稳定性也有较高的要求。
传统的驱动电源多以线性直流稳压电源为主,由于电压调整功能的器件始终工作于线性放大区,因而在应用过程中存在着功耗大、能量转换效率低、输出响应速度慢等问题。
这为线性直流电源的应用带来了很大的局限性。
近年来,随着电力电子功率器件的不断发展,开关电源得到了越来越广泛的应用,其相关的技术及发展现状如文献[2]所述。
开关电源具有较多的优点。
如内部功率损耗小、转换效率高。
随着超高频功率变换技术[3]的不断发展与应用,开关电源的转换效率可以大幅度提高,其转换效率可高达90%以上,即达到文献[4]所述合理使用能源、减少能量损耗的目的。
而且开关电源由于没有传统的工频变压器,散热器相对较小,因而具有体积小、重量轻的特点。
开关电源不仅具有以上所说的优点,与其相应的电路的控制方法也比较多,如循环控制方法[5]、滞环控制方法[6]、移相控制方法[7]等。
设计人员可以根据实际应用的要求和需要,灵活地选用各种类型的开关电源电路和控制方法。
本文针对传统线性直流稳压电源与开关直流电源的以上特点,结合射流清洗设备的触摸屏驱动电源输入输出响应要求。
设计了一种基于传统线性直流电源电路的开关电源电路结构,文中首先给出了相应的电路结构,并对相应的工作原理做了简要说明,其次给出了仿真结构图的搭建方法及结果分析,最后给出了所得结论。
直流直流降压变换器BUCK变换器PPT.

3、理想化处理:器件、电源和负载; •(1)课前,老师让同学们在出行中观察道路边的各种交通标志,能说说你们观察到了什么吗?
•后备箱
••2了.5解.8农要4药点、中毒在原因和D症C状,/D学习C一些变急救换的方器法。 中,降阶处理:假定电容上的端 •确认书压要简为明扼恒要,尽定快寄值到新,雇员手将中。二阶微分方程降为一阶微分方程
周期内电流连续且 无内阻 3.直流输出电压U0为恒 定 4.整个电路无功耗 5.电路已达稳态
8
3.2直流-直流降压变换器(BUCK变换器)(续4)
(一)、晶体管T导通工作模式
(0≤t≤t1=KT)
uL
ud
u0
L
diL dt
Ud
U0
L
I2 I1 t1
L
I t1
I (U d U0 )t1
L
I I2 I1
t2 t1
I (t2 t1)(U0 Ud ) L
由(一)、(二)可得:
I Udt1 (U0 Ud )(t2 t1)
L
L
将 t1 kT,t2 t1 (1 k)T 代入上式,则求得
U0
Ud 1 k
Ko 1 K
一、基本概念
3.1 概述
DC-DC变换器定义:只对直流参数进行变换的电路
1
3.1 概述(续1)
一般结构:
完成的功能:
• 直流电幅值变换
• 直流电极性变换
2
3.1 概述(续2)
二.理想直流变换器应具备的性能
1.输入/输出端的电压均为平滑直流,无交流谐波分量 2.输出阻抗为零
3
3.快速动态响应,抑制干扰的能力强 4.高效率/小型化
开关电源 之BUCK变换器工作原理及Multisim实例仿真
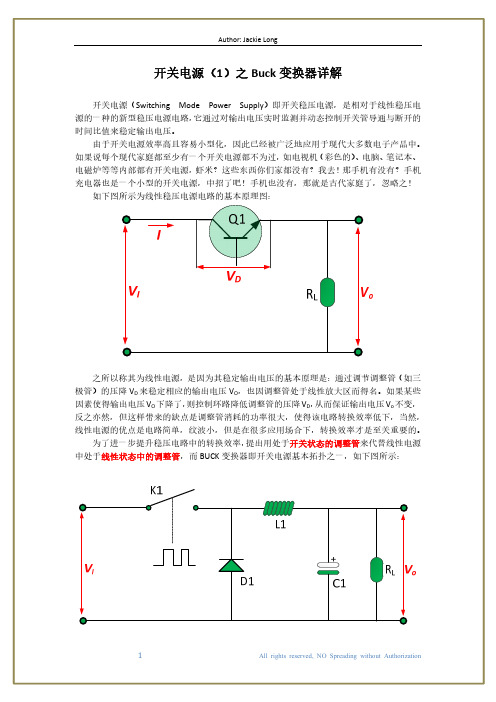
D1 1N5824
A PR1
PR3
V
3
V: 5.71 V V(p-p): 29.3 mV V(rms): 5.73 V V(dc): 5.70 V V(f req): 22.3 kHz
C1
R1
22பைடு நூலகம்µF
5Ω
根据上图仿真结果,则有:
1.14 5.7 0.58 12
93.36%
其中,开关 K1 代表三极管或 MOS 管之类的开关管(本文以 MOS 管为例),通过矩形波 控制开关 K1 只工作于截止状态(开关断开)或导通状态(开关闭合),理想情况下,这两种 状态下开关管都不会有功率损耗,因此,相对于线性电源的转换效率有很大的提升。
开关电源调压的基本原理即面积等效原理,亦即冲量相等而形状不同的脉冲加在具有惯 性环节上时其效果基本相同,如下图所示:
理想的 MOS 管在工作时(即导通或截止)的压降及流过其中的电流应如下图所示:
9
All rights reserved, NO Spreading without Authorization
DS
Author: Jackie Long
D
其中,VDS 表示 MOS 管两端的压降,而 ID 表示流经 MOS 管的电流,在任意时刻,VDS 与 ID 都会有一个参数为 0,因此消耗的功率 P=U×I 也应当是 0,但是实际 MOS 管的开关与 闭合都是需要过渡时间的,真实的开/关状态如下图所示:
同样是从输入电源 10V 中获取 5V 的输出电压,线性稳压电源的有效面积为 5×T,而对 应在开关稳压电源的单个有效周期内,其有效面积为 10×T×50%(占空比)=5×T,这样只要 在后面加一级滤波电路,两者的输出电压有效值(平均值)是相似的。
双向直流变换器建模ppt课件

① Buck 方向时, K2断开,电源V1提供负载R2能量:
VBuck V1 d
I Buck
V1 R2
d
② Boost 方向时,K1断开,电源V2提供负载R1能量:
VBoost V1 d
I Boost
V1 R1 D 2
d
③ 稳态时,电压之间的关系满足下式:V1 :V2 1: D
34
3 双向 Buck-Boost 变换器的小信号模型
1 iL
0
uc
27
2、 Boost 方向小信号模型的建立
(2)dTs ≤ t ≤ Ts(时间段记为dTs),状态空间 方程:
•
iL
0
• uc
1 C1
1 L
1 R1C1
iL uc
1 L 0
v2
v1
i2
0 1
1 iL
0
uc
28
2、 Boost 方向小信号模型的建立
L
iL
+
D1
+
V1
Q2
D2
V2
-
-
图1 双向Buck-Boost DC/DC变换器
3
1、 Buck 方向小信号模型的建立
1.1 列出状态方程
Buck 方向时电路结构如图2所示,忽略电感、
电容的寄生电路,开关管、二极管均假定为理想器
件。
i1
+
Q1
L
iL
+
V1
D2
C2 R2
V2
-
-
图2 Buck 方向在连续状态下的等效电路
基本建模法
建模方法
状态空间平均法 开关元件平均模型法 开关网络平均模型法
2buck直流变换器的工作原理及动态建模

DC/DC 变换器的概念7【】15【】19【】将一个固定的直流电压变换成可变的直流电压称之为DC/DC 变换,亦称为直流斩波。
用斩波器斩切直流的基本思想是:如果改变开关的动作频率,或者改变直流电流通和断的时间比例,就可以改变加到负载上的电压、电流的平均值。
Buck 变换器又称降压变换器、串连开关稳压电源、三端开关型降压稳压器。
基本的DC/DC 变换器按输入输出之间是否有电气隔离可分为两类:隔离型DC/DC 变换器和非隔离型DC/DC 变换器。
非隔离型DC/DC 变换器中存在四种基本的变换器拓扑,它们是降压式(Buck )型,升压式(Boost)型,升降压式(Buck-boost)型,Cuk 型,此外还有Sepic 型和Zeta 型变换器。
二电平Buck 直流变换器的工作原理及主电路图2【】13【】25【】26【】1 主电路拓扑Buck 变换器是一种输出电压等于或小于输入电压的单管非隔离直流变换器。
它的拓扑为电压源、串联开关和电流负载组合而成。
如图所示:图 Buck 电路主电路拓扑 为了分析稳态特性,简化推导公式的过程,特作如下假定。
(1) 开关晶体管、二极管均是理想元件。
也就是可以瞬间的导通和截至,而且导通时降压为零,截至时漏电流为零。
(2) 电感、电容是理想元件。
电感工作在线性区而未饱和,寄生电阻为零,电容的等效串联电阻为零。
(3) 输出电压中的纹波电压与输出电压的比值小到允许忽略。
Buck 变换器的工作原理:当开关管S 导通时,电容开始充电,i U 通过向负载传递能量,此时,L i 增加,电感内的电流逐渐增加,储存的磁场能量也逐渐增加,而续流二极管因反向偏置而截至;当S 关断时,由于电感电流L i 不能突变,故L i 通过二极管VD 续流,电感电流逐渐减小,由于二极管VD 的单向导电性,L i 不可能为负,即总有L 0i ,从而可在负载上获得单极性的输出电压。
根据晶体管的开关特性,在管子的基极加入开关信号,就能控制它的导通和截至,对于NPN 晶体管,当基极加入正向信号时,将产生积极电流b i ,基极正向电压电压升高,b i 也随之升高,b i 达到一定数值后,集电极电流c i 达到最大值,其后继续增加b i ,b i 基本上保持不变,这种现象称为饱和。
Buck变换器工作原理分析和总结
题目: Buck变换器工作原理分析与总结目录一、关于Buck变换器的简单介绍 (2)1、Buck变换器另外三种叫法 (2)2、Buck变换器工作原理结构图 (2)二、Buck变换器工作原理分析 (3)1、Buck变换器工作过程分析 (3)2、Buck变换器反馈环路分析 (4)3、Buck变换器的两种工作模式 (4)1)Buck变换器的CCM工作模式 (5)2)Buck变换器的DCM工作模式 (6)3)Buck变换器CCM模式和DCM模式的临界条件 (7)4)两种模式的特点 (8)4、Buck变换器电感的选择 (8)5、Buck变换器输出电容的选择和纹波电压 (9)三、Buck变换器工作原理总结 (10)Buck 变换器工作原理分析与总结一、关于Buck 变换器的简单介绍1、Buck 变换器另外三种叫法1. 降压变换器:输出电压小于输入电压。
2. 串联开关稳压电源:单刀双掷开关(晶体管)串联于输入与输出之间。
3. 三端开关型降压稳压电源:1) 输入与输出的一根线是公用的。
2) 输出电压小于输入电压。
2、Buck 变换器工作原理结构图GabcWMV Gd图1. Buck 变换器的基本原理图由上图可知,Buck 变换器主要包括:开关元件M1,二极管D1,电感L1,电容C1和反馈环路。
而一般的反馈环路由四部分组成:采样网络,误差放大器(Error Amplifier ,E/A ),脉宽调制器(Pulse Width Modulation ,PWM )和驱动电路。
二、Buck 变换器工作原理分析1、Buck 变换器工作过程分析图2. Buck 变换器的工作过程为了便于对Buck 变换器基本工作原理的分析,我们首先作以下几点合理的假设:1) 开关元件M1和二极管D1都是理想元件。
它们可以快速的导通和关断,且导通时压降为零,关断时漏电流为零;2) 电容和电感同样是理想元件。
电感工作在线性区而未饱和时,寄生电阻等于零。
Buck变换器的发展与工作原理
从一个电压(高)得到自己想要的电压值(低)的最简单的方法是通过电阻分压实现,如图1.1 所示。
图1.1 电阻分压电路这种方式最方便快捷,现在普通的电压采样基本采用这种方式,但是如果功率稍微大一点,由于R1 和R2 是串联的,所以在R1 上的损耗不可忽视,如果所要的电压值远低于输入电压,那末该电路的效率就会极其低下。
对该电路尝试进行变形,将R2 更换为三极管,也就是现在的LDO 模型,如图1.2 所示。
图1.2 LDO 模型通过变型,那末原来在电阻R2 上的损耗转移至分析三极管Q1 的损耗,由于Q1 承受输入和输出的压差,导致该电路的效率也比较低下。
为了提升效率,之前三极管是工作在线性状态,若将其更改为开关状态,使三极管惟独开关损耗和导通损耗,大大的降低其总损耗。
更改后的电路如图1.3 所示。
图1.3 开关电路图1.4 占空比和电压比的关系由图 1.4 可知,该电路工作周期时间为Ts,导通时间为Ton,占空比为D=Ton/Ts,输出电压与开关状态高度关联,S1 导通时有输出电压,S1 关断时没有输出电压。
可以看出输出负载总是需要连续的能量供给,开关S1 的导通与关断在图1.3 所示的电路中产生的断续能量波动对于输出端负载是不可接受的。
因此需要需要进行解耦,在变换器一定位置引入储能元器件电容,使输入端在S1 断开的情况下,输出端电容也可以进行持续的能量输出,保证输出电压的稳定。
图1.5 初步解耦电路由图1.5 所示的电路,根据电容两端的电压不能突变的原理,当S1 闭合的时候,路线中会产生一个非常大的冲击电流,它不仅导致噪声和EMI 问题,也可能会损坏S1 。
所以需要对其采取限流措施。
图1.6 电阻R2 限流的解耦电路如图1.6 所示,加入R2 限流电阻后,在S1 闭合瞬间就没有那末大的冲击电流了,但是由于R2 是串联在主功率回路中,电阻就会消耗功率,那末在开关上减小的功耗最终可能又消耗在所加的电阻上。
BUCK电路基本原理
1.BUCK电路基本拓扑
Buck变换器:也称降压式变换器,是一种输出电压小于输入电压的单管 不隔离直流变换器。
图中,Q为开关管,其驱动电压一般为PWM(Pulse width modulation脉宽调制)信号,信号周期为Ts,则信号频率为 f=1/Ts,导通时间为Ton,关断时间为Toff,则周期 Ts=Ton+Toff,占空比Dy= Ton/Ts。
4.闭环控制思想
1. 上图所示的电流电压双闭环的模式; 2.首先满足电压环的控制,使其输出快速达到给定 电压,而后通过调整负载满足电流环的控制; 3.当然在电路出现故障时,优先满足电流环,可能 会出现电压输出较低的情况。
5.PEU-BUCK电路
电感的电流总是由正方向流动 电流不会降到0
PWM控制,恒定开关频率工作 改变占空式调节输出
输出负载电流下降 从CCM-DCM
CCM CCM有最小输出负载电流要求
DCM
DCM不连续电流模式
在轻负载电流时
IAVE < ½ IRipple 电感的电流(能量)完全放电到0,
在电流降到0时刻,二极管自 然关断,阻挡电感电流的反向 流动,输出由电容提供,纹波 大. 开关频率及输出电压和负载电 流相关
2.基本工作原理
开关管导通,电感激磁,电流线性上升
L diL dt
Vin
Vo
I pk
(Vin
Vo )D Lf S
开关管关断,电感去磁, 电流线性
下降
L diL dt
Vo
Vo = D Vin
I pk
Vo (1 D) Lf S
伏秒值平衡: Vt =恒定 toff: 去磁
ton: 激磁 B
BUCK变换器 PPT
三、波形分析
❖ 按电感电流iL是否从零开始,有两种工作模式: ⑴、连续工作模式; ⑵、不连续工作模式。 各部分工作波形分别如图3(a)、(b)所示
图3 BUCK变换器两种工作模式波形图
连续工作模式
❖ 1、MOS导通D截止,电感电流增量: ❖ 2、MOS截止D导通,电感电流增量:
❖ 3、电路达到稳定状态下:
}
由上面公式可得:
Vo/Vs是电压增益,用M表示。 输出电压Vo随占空比D1变化,由于D1<1, 所以Vo<Vs。 由上式可得知:电压增益由开关接通的占空比 D1决定,说明变换器具有很好的控制性。 M与D1曲线图如下:
图4 电压增益M与开关占空比D1关系图
不连续工作模式
❖ 1、MOS管导通阶段:
和,寄生电阻零;电容等效串联电阻零。 ❖ 3、输出纹波电压与输出电压的比小到可以忽略。
2.2、工作过程
❖ 1、开关(晶体管)导通:
二极管D1截止;电感电流线性增加并储能;电容充电 储能;输出电压Vo。
❖ 2、开关(晶体管)关断:
二极管D1导通;电感释放能量;电容放电;输出Vo。
大家应该也有点累了,稍作休息
完全传递
(晶体管)串联于输入与输出之间。 ❖ 1.3、三端开关型降压稳压电源:
⑴、输入与输出的一根线是公用的。 ⑵、输出电压小于输入电压。
二、BUCK变换器的工作原理
图2 BUCK变换器电路工作过程
2.1、变换器工作于理想状态
❖ 在图2中作如下假设: ❖ 1、开关晶体管、二极管均为理想元件:快速导通
关断,且导通压降零,关断漏电流零。 ❖ 2、电感电容为理想元件:电感工作在线性区不饱
❖ 2、MOS管断开阶段:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
DC/DC 变换器的概念7【】15【】19【】将一个固定的直流电压变换成可变的直流电压称之为DC/DC 变换,亦称为直流斩波。
用斩波器斩切直流的基本思想是:如果改变开关的动作频率,或者改变直流电流通和断的时间比例,就可以改变加到负载上的电压、电流的平均值。
Buck 变换器又称降压变换器、串连开关稳压电源、三端开关型降压稳压器。
基本的DC/DC 变换器按输入输出之间是否有电气隔离可分为两类:隔离型DC/DC 变换器和非隔离型DC/DC 变换器。
非隔离型DC/DC 变换器中存在四种基本的变换器拓扑,它们是降压式(Buck )型,升压式(Boost)型,升降压式(Buck-boost)型,Cuk 型,此外还有Sepic 型和Zeta 型变换器。
二电平Buck 直流变换器的工作原理及主电路图2【】13【】25【】26【】1 主电路拓扑Buck 变换器是一种输出电压等于或小于输入电压的单管非隔离直流变换器。
它的拓扑为电压源、串联开关和电流负载组合而成。
如图所示:图 Buck 电路主电路拓扑 为了分析稳态特性,简化推导公式的过程,特作如下假定。
(1) 开关晶体管、二极管均是理想元件。
也就是可以瞬间的导通和截至,而且导通时降压为零,截至时漏电流为零。
(2) 电感、电容是理想元件。
电感工作在线性区而未饱和,寄生电阻为零,电容的等效串联电阻为零。
(3) 输出电压中的纹波电压与输出电压的比值小到允许忽略。
Buck 变换器的工作原理:当开关管S 导通时,电容开始充电,i U 通过向负载传递能量,此时,L i 增加,电感内的电流逐渐增加,储存的磁场能量也逐渐增加,而续流二极管因反向偏置而截至;当S 关断时,由于电感电流L i 不能突变,故L i 通过二极管VD 续流,电感电流逐渐减小,由于二极管VD 的单向导电性,L i 不可能为负,即总有L 0i ,从而可在负载上获得单极性的输出电压。
根据晶体管的开关特性,在管子的基极加入开关信号,就能控制它的导通和截至,对于NPN 晶体管,当基极加入正向信号时,将产生积极电流b i ,基极正向电压电压升高,b i 也随之升高,b i 达到一定数值后,集电极电流c i 达到最大值,其后继续增加b i ,b i 基本上保持不变,这种现象称为饱和。
在饱和状态下,晶体管的集射极电压很小,可以忽略不计。
因此晶体管的饱和状态相当于开关的接通状态。
当基极加入反向偏压时,晶体管截至,集电极电流c i 接近于零,而晶体管的集射极电压接近于电源电压。
晶体管的这种状态相当于开关的断开状态,通常称为截至状态,或称为关断状态。
Buck 变换器的工作模式5【】8【】27【】29【】由Buck 变换器的工作原理可以看出,电感可以工作在电流连续的方式下,也可能工作在电流不连续的工作状态。
以此为标准将Buck 变换器的工作模式分为两种:电感电流连续工作模式(continuous current mode, CCM)和电感电流断续模式(discontinuous current mode, DCM)。
电感电流连续是指输出滤波电感的电流总大于零,电感电流断续是指在快关管段期间有一段时间输出滤波的电流为零。
在这种工作方式之间有一个工作边界,称为电感电流临界连续状态,即在开关管关断末期,滤波电感的电流刚好降为零。
下面分别讨论电感电流处于不同模式时的变换器工作原理。
(1) 电感电流连续模式如图所示为电流连续导电模式下的相关波形:图 电流连续模式下电路波形在[]10t 区间,开关管S 处于导通状态,电源电压通过S 到二极管VD 两端,故二极管VD 截至。
电流流过电感,由于输出滤波电容保持不变,则电感两端呈现正电压L i 0U U U =-,由于i 0U U >所以,在该电压作用下输出滤波电感中电流L i 线性增长,知道1t 时刻,L i 达到最大值L1I 。
在S 导通期间,电感电流的增量及开关管的占空比D 分别为21000L()s 1s ()(1)t t U U U i dt T t D T L L L-∆=-=-=-⎰ 其中1s t D T =( 0D 1<<) (2-1)在[]1s t t 区间,S 关断,由于电感的储能作用,L i 经二极管VD 继续流通,此时加在输出滤波电感上的电压L 0U U =-,呈现负值,电感中电流L i 线性衰减,直到s T 时刻,L i 达到最小值L2I 。
在S 截至期间,电感电流的减小量为s 1000L()s 1s ()(1)T t U U U i dt T t D T L L L -∆=--=-=-⎰(2-2)由于稳态工作下的电感电流L i 波形必然周期性重复,因此S 导通期间L i 的增量必然等于S 截至期间的减小量,即L(+)L(-)i i ∆=∆,所以i 00s s (1)U U U DT D T L L-=-(2-3)整理得0iU D U =(2-4) 由式(2-4)可知,输出电压与开关管的占空比D 成正比,所以通过改变开关管的占空比可以控制输出平均电压的大小。
由于占空比总是小于1,所以输出电压总是小于输入电压,故常称为降压式变换器。
改变占空比就可以改变输出电压值。
(2)电感电流断续模式当电感较小,负载电阻较大或s T 较大时,将出现电感电流已下降到0,但新的周期却尚未开始的情况。
如图为电流断续模式下Buck 电路的相关波形图 电流断续模式下电路波形在[]10t 区间,开关管S 处于导通状态,与电感电流连续模式下的工作情况相同,此时()L L1i I +∆=。
在1T 时刻,S 关断,电感中电流L i 线性衰减,直到dis t 时刻下降到0,即(2-5) 式中,dis 1s(),(1)t t D D D T -∆=∆<-且。
由于L()L()=i i +-∆∆得 0(1)i U D D D U D D =∆<-+∆ ,其中(2-6)此时,变换器输出电流0I 任等于电感电流平均值,即2i 0L1dis i S S 011(1)22U D I I t U T Lf U =⨯=- (2-7) 上式表明。
电感电流断续时0i U U 不仅与占空比D 有关,而且与负载电流0I 有关。
若00I =,则D 多大,输出电压0U 必等于输入电压i U 。
(3)电感电流临界连续模式在有关电流断续工作模式的数学关系中,首先需要推导的是电感电流连续与断续的临界条件,其推导过程如下。
降压型电路电感电流处于连续与断续的临界状态时,在每个开关周期开始和结束的时刻,电感电流正好为零,如图2-4所示。
图 降压型电路电流临界连续工作时的波形稳态条件下,由于电容C 的开关周期平均电流为零,因此电感电流L i 在一个开关周期内的平均值等于负载电流为o o U I R =(2-8) 而电感电流L i 的开关周期平均值可以按下式计算:S L L 0()T I i t dt =⎰(2-9)0L I I ≥,即得到电感电流连续的临界条件。
这种计算方法需要导出()L I t 的表达式,还要计算定积分,比较繁琐。
我们采用一种简单的方法。
根据图2-4,电感电流在一个开关周期中的波形正好是一个三角形,它的高L I ∆,底边长为s T ,面积为I L S 12S I T =∆(2-10) 在几何意义上,电感电流的开关周期平均值等于和该三角形同底的矩形的高,因此电感电流开关周期平均值等于三角形面积除以s T ,即L L 12I I =∆(2-11) L I ∆的计算方法如下:电感电流在零时刻从零开始线性上升,在s DT 时刻达到L I ∆,上升的斜率为L i o di LU U dt =-(2-12) 有: i o L S U U I DT L-∆=(2-13)此时电感电流仍为连续,故有 o iU D U = 将其代入式(2-13),有L o S 1D I U T L -∆=(2-14)则可得电感电流开关平均值的表达式为 L o S 12D I U T L -=(2-15)电感电流连续的临界条件为 0L I I ≥将式(2-8)和式(2-9)带入上式有00s 12U D U T R L-≥ (2-16)整理得 S 12L D RT -≥(2-17)这就是用于判断降压型电路电感电流连续与否的临界条件。
随后需要推导的是电感电流断续条件下输出与出入电压的比例。
首先设开关S 关断后电感的续流时间为s aT ,如图3-7所示,其中()01a D ≤≤-。
图 电感电流断续工作时的波形 根据稳态条件下电感电压开关平均值为零的原理,有i o S o S ()U U DT U T α-= (2-18) 电感电流开关周期平均值为L L 1()2I I D α=∆+ (2-19) 而负载电流为 o o U I R=(2-20) 稳态条件下,电容C 的开关周期平均电流为零,故电感电流开关周期平均值等于 负载电流,即oL 1()2U I D Rα∆+= (2-21)从式(2-18)中,解出α的表达式,与式(2-15)一起代入式(2-21)中得i o o i S o ()12U U U U DT D L U R-= (2-22)整理得 2i i 2o o S 2()0U U L U U D T R --= (2-23) 令2S 2L K D T R=解方程,并略去负根,得o i 12U U K= (2-24) 值得注意的是,式(2-24)在电路工作在电感电流断续条件下成立,而电路工作在电感电流连续条件下不成立。
特别是,当电感电流处于临界连续状态时,S ()2L/RT =1-D /,代入式(2-17)得时0i U U D =。
从式(2-17)可以看出,电流断续时电压比与占空比D 和负载R 相关,也与电路参数L 和s T 有关。
主回路电感、电容参数整定3【】22【】33【】根据对二电平Buck 型直流变换器工作原理的分析以及电感电流连续和断续的临界条件的推导,可以计算出二电平Buck 型直流变换器滤波电感和滤波电容的参数。
稳态时,电感电流连续的临界条件为:o L I I ≥ (2-25)利用上节内容提到的三角形面积法我们得到电感电流的临界条件为:S 12L D RT -≥ 整理得s 12D L RT -≥(2-26) 在本次的设计中,给定工作电压i U 为40V ,输出电压0U 为20V ,负载电阻R 为50Ω,开关周期s f 为40kHz ,带入式2-26中得到电感电流临界值:s 3111500.00031H 244010D L RT -≥=⨯⨯=⨯(2-27) 即当主电路电感大于0.31mH 时, 电路工作在电感电流连续工作模式,当主电路电感小于0.31mH 时,则为电感电流断续工作模式。
