2018级数理统计考试题
2018级成考专本连读计算机科学与技术专业12月份考试资料概率论与数理统计复习资料

《概率论与数理统计》复习资料(一)一 填空题1在一次读书活动中,某同学从2本科技书和4本文艺书中任选2本,则选中的书都是文艺书的概率为______。
2设A ,B 是两事件,P (A )=1/4,P(B|A)=1/3,则P (AB )=________。
3概率很小的事件在一次试验中几乎是不可能发生的,这个原理称为 ________。
4 设随机变量~(0,1),X N 若(),P X a α>= 则()P X a <-= 。
5 设随机变量X 服从参数为1=10,=2n p 的二项分布,()E X = 。
二 选择题1 设随机变量2~(2,3),X N 1,,n X X 为简单随机样本,X -为样本均值,则下列统计量服从(0,1)N 的是( ) A 23X -- B 29X ----2 设12,A A 两个随机事件相互独立,当12,A A 同时发生时,必有A 发生,则( ) A 12()()P A A P A ≤ B 12()()P A A P A ≤C 12()=()P A A P AD 12()()()P A P A P A =3 设1,,n X X 为一组简单随机样本,则样本标准差为( ) A 211()n i i x x n -=-∑ B 211()-1n i i x x n -=-∑ C 11()-1n i i x x n -=-∑2 4 若A,B 为任意随机事件,则P(A ⋃ B)=( )A P(A)+P(B)B P(A)-P(AB)C P(A)-P(B)+P(AB)D P(A)+P(B)-P(AB)5 设,A B 为随机事件,A B ⊂,则AB 的逆事件为( )A AB -- B A -C B -D A6 设随机变量X 的方差()D X 存在,且()0,D X > 令2+3Y X =,则,X Y 的简单相关系数ρ= ( )A 0B 1C -1D 27设随机变量X 与Y 相互独立,且X ,Y 分别服从参数为1,4的泊松分布,则()D X Y -=( )A -3B-1 C 3D 5三 计算题设2~(5,3),X N 求以下概率(10),(210)P X P X ≤<<(用(0,1)N 的分布函数为()x Φ表示)。
概率论与数理统计(经管类)2018年10月真题及答案

概率论与数理统计(经管类)2018年10月真题及答案一、单选题(共10题,共40分)1.设随机事件A与B互不相容,且P(A)>0,P(B)>0,则()A.P(B|A)=0B.P(A|B)>0C..P(A|B)=P(A)D.P(AB)=P(A)P(B)2.设随机变量X~N(1,4),F(x)为X的分布函数,Φ(x)为标准正态分布函数,则F(3)=()A.Φ(0.5)B..Φ(0.75)C.Φ(1)D.Φ(3)3.设随机变量X的概率密度为f(x)=则P{0≤X≤}=()A.1/4B.1/3C.1/2D.3/44.设随机变量 X的概率密度为 f(x)=则常数c=()B.-1C.-1/2D.15.设下列函数的定义域均为(-∞,+∞),则其中可作为概率密度的是()A.B.C.D.6.设二维随机变量( X,Y)~ N(μ1, μ2,),则 Y ~()A.B.C.D.7.已知随机变量 X的概率密度为f(x)=则E(X)=()A.6B.3C.18.设随机变量X与Y相互独立,且X~B(16,0.5),Y服从参数为9的泊松分布,则D(X-2Y+3)=()A.-14B.-11C..40D..439.设随机变量Zn~B(n,p),n=1,2,其中0<p<1,=()A.B.C.D.10.设 x1,x2,x3,x4 为来自总体X的样本,=()A.B.C.D.二、填空题(共15题,共60分)11.设随机事件A与B相互独立,且P(A)=P(B)=1/3,则=_______.12.设袋内有5个红球、3个白球和2个黑球,从袋中任取3个球,则恰好取到1个红球、1个白球和1个黑球的概率为_________.13.设A为随机事件,P(A)=0.3,则_________.14.设X是连续型随机变量,则P{X=5}=_________.15.设随机变量 X的分布律为. 记 Y=X2,则 P{ Y=4} =_________.16.设随机变量X的分布函数为F(x),已知F(2)=0.5,F(-3)=0.1,则P{-3<X≤2} = _________.17.设随机变量 X的分布函数为 F(x)=则当 x>0 时,X的概率密度 f (x)=_________.18.若随机变量 X~B(4,1/3),则P{ X≥1} = _________.19.设二维随机变量(X,Y)的概率密度为 f (x,y)=则 P{ X +Y≤1} = _________.20.设随机变量X的分布律为21.设随机变量X~N(0,4),则E(X2)=_________.22.设随机变量X~N(0,1),Y~N(0,1),Cov(X,Y)=0.5,则D(X+Y)=_________.23.设X1,X2,,,Xn,,是独立同分布的随机变量序列,E(Xn)=μ,D(Xn)=σ2,n=1,2,,,则=_________.24.设 x1,x2,, , xn为来自总体X的样本,且 X~N( 0,1 ),则统计量_________.25.设 x1,x2,xn为样本观测值,经计算知nx 2 =64,1、正确答案: A2、正确答案: C3、正确答案: A4、正确答案: B5、正确答案: C6、正确答案: D7、正确答案: B8、正确答案: C9、正确答案: B10、正确答案: D11、正确答案:7/912、正确答案:1/413、正确答案:14、正确答案:015、正确答案:0.516、正确答案:0.417、正确答案:18、正确答案:65/8119、正确答案:1/420、正确答案:021、正确答案:422、正确答案:323、正确答案:0.524、正确答案:25、正确答案:36。
4月全国自考概率论与数理统计(二)试题及答案解析

1全国2018年4月高等教育自学考试概率论与数理统计(二)试题课程代码:02197一、单项选择题(本大题共10小题,每小题2分,共20分)在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1.设P (A )=21,P (B )=31,P (AB )=61,则事件A 与B ( )A .相互独立B .相等C .互不相容D .互为对立事件2.设随机变量X ~B (4,0.2),则P {X>3}=( ) A .0.0016 B .0.0272 C .0.4096D .0.81923.设随机变量X 的分布函数为F (x ),下列结论中不一定成立.....的是( ) A .F (+∞)=1 B .F (-∞)=0 C .0≤F (x )≤1D .F (x )为连续函数4.设随机变量X 的概率密度为f (x),且P {X ≥0}=1,则必有( ) A .f (x)在(0,+∞)内大于零 B .f (x)在(-∞,0)内小于零 C .⎰+∞=01f(x)dxD .f (x)在(0,+∞)上单调增加5.设随机变量X 的概率密度为f (x)=812221)x (e+-π,-∞<x<+∞,则X ~( )A .N (-1,2)B .N (-1,4)C .N (-1,8)D .N (-1,16)6.设(X ,Y )为二维连续随机向量,则X 与Y 不相关...的充分必要条件是( ) A .X 与Y 相互独立B .E (X +Y )=E (X )+E (Y )C .E (XY )=E (X )E (Y )D .(X ,Y )~N (μ1,μ2,21σ,22σ,0)27.设二维随机向量(X ,Y )~N (1,1,4,9,21),则Cov (X ,Y )=( ) A .21 B .3 C .18D .368.已知二维随机向量(X ,Y )的联合分布列为( )则E (X )= A .0.6 B .0.9 C .1 D .1.69.设随机变量X 1,X 2,…,X n ,…独立同分布,且i=1,2…,0<p<1.令∑===ni i n .n ,X Y 121Λ,,Φ(x )为标准正态分布函数,则=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧≤--∞→11lim n )p (np np Y P n ( ) A .0B .Φ(1)C .1-Φ(1)D .110.设总体X ~N (μ,σ2),其中μ,σ2已知,X 1,X 2,…,X n (n ≥3)为来自总体X 的样本,X 为样本均值,S 2为样本方差,则下列统计量中服从t 分布的是( ) A .221σS)n (X - B .221σμS)n (X --C .221σσμS)n (n/X -- D .22σσμSn/X -二、填空题(本大题共15小题,每小题2分,共30分)请在每小题的空格中填上正确答案。
2018年大学概率论与数理统计期末考试试卷及解析(7)

2018年大学概率论与数理统计期末考试试卷及解析(7)杭州电子科技大学学生考试(模拟)题解一、填空题(每空格2分)1.设事件B A ,相互独立,6.0)(,4.0)(==B P A P ,则概率)(B A P ?= 0.76 。
2.袋内装有6个白球,4个黑球。
从中任取三个,取出的三个球都是白球的概率= 1/6 。
3.设3.0}2010{),,10(~2=<<<="" 的值为="">4.设随机变量X 服从(0,2)上的均匀分布,则随机变量2X Y =在(0,4)上概率密度)(y f Y =y41。
5.设随机变量X 服从二项分布)3.0,10(b ,随机变量Y 服从正态分布)4,2(N ,且Y X ,相互独立,则)2(Y X E -= -1 ,)2(Y X D -= 18.1 。
二、试解下列各题 1.(求(1)X 的分布函数)(x F ;(2)概率}2{,}25.0{>≤X P X P ;(3))(,)(X D X E 。
解:≥<≤<≤--<=3,132,8.021,3.01,0)(x x x x x F 分分分1.........1.........1.........分分1...................2.0}3{}2{1.............3.0}1{}25.0{===>=-==≤X P X P X P X P3.12.035.023.0)(=?+?+-=X E 1分1.42.035.023.0)1()(2222=?+?+?-=X E 1分∴ 41.2)]([)()(22=-=X E X E X D 1分2、(16%)设二维随机变量),(Y X 的概率密度为<+=其它,01,1),(22y x y x f π试问:(1)Y X ,是否相互独立?(2)Y X ,是否相关?(3)求概率}{X Y P >。
临沂大学 2018-2019第二学期2018级《 概率论与数理统计》期末考试A附答案
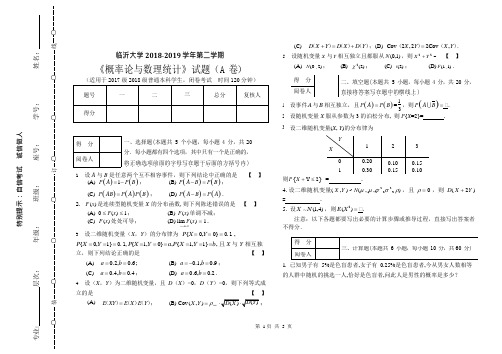
D (Y ) 31 2 1 2(C) D (X +Y )= D (X )+ D (Y );(D) Cov (2X , 2Y )= 2Cov (X ,Y ).临沂大学 2018-2019 学年第二学期5.设随机变量 X 与Y 相互独立且都服从 N (0,1) ,则 X 2 + Y 2 ~ 【 】《概率论与数理统计》试题(A 卷)(适用于 2017 级 2018 级普通本科学生,闭卷考试 时间 120 分钟)(A) N (0 , 2) ; (B) χ 2 (2) ;(C) t (2) ;(D) F (1 , 1) .得 分 一、选择题(本题共 5 个小题,每小题 4 分,共 20 分.每小题都有四个选项,其中只有一个是正确的, 将.正.确.选.项.前.面.的.字.母.写.在.题.干.后.面.的.方.括.号.内.)阅卷人1. 设 A 与 B 是任意两个互不相容事件,则下列结论中正确的是【 】(A) P ( A ) = 1- P (B ) ;(B) P ( A - B ) = P (B ) ;1. 设事件A 与B 相互独立,且 P ( A ) = P (B ) = 1,则 P (A B )= .2. 设随机变量 X 服从参数为 3 的泊松分布, 则 P {X =2}= .3. 设二维随机变量(X , Y )的分布律为YX123 00.20 0.10 0.15 10.30 0.150.10则 P {X + Y ≤ 2} = .(C) P ( A B ) = P ( A ) P (B ) ; (D) P ( A - B ) = P ( A ) . 2. F (x ) 是连续型随机变量 X 的分布函数,则下列陈述错误的是 【 】(A) 0 ≤ F (x ) ≤ 1 ;(B) F (x ) 单调不减; 4. 设二维随机变量( X ,Y ) ~ N (μ , μ ,σ 2,σ 2 , ρ) ,且 ρ = 0 ,则 D ( X + 2Y )=. 5. 设X N (1, 4) ,则E (X 2 ) = .(C) F (x ) 处处可导;(D) lim F (x ) = 1 .x →+∞注意:以下各题都要写出必要的计算步骤或推导过程,直接写出答案者 不得分.3. 设二维随机变量(X ,Y )的分布律为 P {X = 0,Y = 0} = 0.1 ,P {X = 0,Y =1} = 0.1,P {X =1,Y = 0} = a ,P {X =1,Y =1} =b , 且 X 与 Y 相互独立,则下列结论正确的是【 】(A) (C) a = 0.2,b = 0.6 ; (B) a = 0.4,b = 0.4 ;(D) a = -0.1,b = 0.9 ; a = 0.6,b = 0.2 .1. 已知男子有 5%是色盲患者,女子有 0.25%是色盲患者,今从男女人数相等的人群中随机的挑选一人,恰好是色盲者,问此人是男性的概率是多少?4.设(X ,Y )为二维随机变量,且 D (X )>0,D (Y )>0,则下列等式成 立的是【 】(A) E (XY )= E (X )·E (Y );(B) Cov ( X ,Y ) = ρXY ⋅ D ( X ) ⋅ ;特别提示:自信考试 诚信做人层次:年级:班级:座号:学号:姓名:装订线题号一二三总分复核人得分得 分 二、填空题(本题共 5 小题,每小题 4 分,共 20 分,直.接.将.答.案.写.在.题.中.的.横.线.上.)阅卷人得 分三、计算题(本题共 6 小题,每小题 10 分,共 60 分)阅卷人( ) ⎨⎧2x , 0 < x < 12.设连续型随机变量X 的概率密度为 f x = ⎨5.设随机变量 X 具有概率密度 f (x ) = ⎧x / 8, 0< x < 4试求随机变量⎩ 求(1)分布函数F (x ) (2)数学期望 E ( X ) .0, 其 他Y = 2X + 8 的概率密度.⎩ 0,其它.3. 设K 服从(0, 5)上的均匀分布,求方程4x 2 + 4xK + K + 2 = 0 有实根的概率6. 设总体X 的概率密度为⎪⎧ θ xθ -1, 0 < x < 1,f (x ;θ ) = ⎨⎪⎩ 0,其它.4. 设随机向量( X ,Y ) 的联合概率密度为:⎧ke -( x +2 y ) , f (x , y ) = ⎨x > 0, y > 0,其中θ > 0 为未知参数,X 1,X 2 , ,X n 是来自总体X 的一个样本,试求θ 的矩估计量.⎩ 0,其它 (1)试确定常数k ;(2)求Z = X +Y 的密度函数.特别提示:自信考试 诚信做人层次: 年级:班级:座号:学号:姓名:装订线D (Y ) B )= 7/9 1 2 1 2 1 2(A) E(XY )= E (X )·E (Y ); (B) Cov ( X ,Y ) = ρXY ⋅ D ( X ) ⋅ ;临沂大学 2018-2019 学年第二学期《概率论与数理统计》试题(A 卷)参考答案与平分标准(适用于 2017 级 2018 级普通本科学生,闭卷考试 时间 120 分钟) (C) D (X +Y )= D (X )+ D (Y );(D) Cov (2X , 2Y )= 2Cov (X ,Y ).5. 设随机变量 X 与Y 相互独立且都服从 N (0,1) ,则 X 2 + Y 2 ~【B 】(A) N (0 , 2) ;(B) χ 2 (2) ; (C) t (2) ; (D) F (1 , 1) .得 分 二、填空题(本题共 5 小题,每小题 4 分,共 20 分, 直.接.将.答.案.写.在.题.中.的.横.线.上.) 阅卷人11. 设事件A 与B 相互独立,且 P ( A ) = P (B ) = 3,则 P (A .2. 设随机变量 X 服从参数为 3 的泊松分布, 则 P {X =2}= 9e -3 .23. 设二维随机变量(X , Y )的分布律为1. 设 A 与 B 是任意两个互不相容事件,则下列结论中正确的是【D 】(A) P ( A ) = 1- P (B ) ;(B) P ( A - B ) = P (B ) ;(C) P ( A B ) = P ( A ) P (B ) ; (D) P ( A - B ) = P ( A ) .则 P {X + Y ≤ 2} = 0.6_.2. F (x ) 是连续型随机变量 X 的分布函数,则下列陈述错误的是【C 】4. 设二维随机变量( X ,Y ) ~ N (μ , μ ,σ 2,σ 2 , ρ) ,且 ρ = 0 ,则 D ( X + 2Y )(A) 0 ≤ F (x ) ≤ 1 ; (B) F (x ) 单调不减; =σ 2 + 4σ 2 .(C) F (x ) 处处可导;(D) lim F (x ) = 1 .x →+∞5. 设X N (1, 4) ,则E (X 2 ) = 5 .3.设二维随机变量(X ,Y )的分布律为 P {X = 0,Y = 0} = 0.1 ,注意:以下各题都要写出必要的计算步骤或推导过程,直接写出答案者 P {X = 0,Y =1} = 0.1,P {X =1,Y = 0} = a ,P {X =1,Y =1} =b , 且 X 与 Y 相互独立,则下列结论正确的是【C 】不得分.(A) (C) a = 0.2,b = 0.6 ; (B) a = 0.4,b = 0.4 ;(D) a = -0.1,b = 0.9 ; a = 0.6,b = 0.2 .1. 已知男子有 5%是色盲患者,女子有 0.25%是色盲患者,今从男女人数相等 4.设(X ,Y )为二维随机变量,且 D (X )>0,D (Y )>0,则下列等式成 立的是【B 】的人群中随机的挑选一人,恰好是色盲者,问此人是男性的概率是多少?特别提示:自信考试 诚信做人层次:年级:班级:座号:学号:姓名:装订线题号一二三总分复核人得分得 分一、选择题(本题共 5 个小题,每小题 4 分,共 20 分.每小题都有四个选项,其中只有一个是正确的, 将.正.确.选.项.前.面.的.字.母.写.在.题.干.后.面.的.方.括.号.内.)阅卷人Y X123 00.20 0.10 0.15 10.300.151.10得 分三、计算题(本题共 6 小题,每小题 10 分,共 60 分)阅卷人=xx x1⎩ 2+∞ ⎨x ⎩解 设A 1 = ”选到的人是男性”, A 2 = ”选到的人是女性”, B = ”选到的人 f (k ) =⎧1/ 5, 0 < k < 5,是色盲患者”, 则有⎨0,其它. P (A ) = 0.5,P (A ) = 0.5; P (B| A ) = 0.05,P (A ) = 0.025; .................. 5 分51 3于是,所求概率为P {k ≤ -1或K ≥ 2} =dk = . 1212则有贝叶斯公式得⎰2 5 54. 设随机向量( X ,Y ) 的联合概率密度为:P (A 1 | B ) = P (A 1 )P (B | A 1 )P (A )P (B | A ) + P (A )P (B | A )⎧ke -( x +2 y ) , f (x , y ) = ⎨ x > 0, y > 0 ,1 12 2⎩ 0,其它 =0.5⨯ 0.05 = 20 ................. 10 分 (1)试确定常数k ;(2)求Z = X +Y 的密度函数.0.5⨯ 0.05 + 0.5⨯ 0.0025 21 ⎧2x , 0 < x < 1解 (1) 根据概率密度函数的性质得+∞+∞ dx f (x , y )dy 1 , 2. 设连续型随机变量X 的概率密度为 f ( x ) = ⎨⎩ 0, 其 他⎰-∞ ⎰-∞ +∞ +∞ +∞ +∞ 另一方面, ⎰ dx ⎰ f (x , y )dy = k ⎰ e - x dx ⎰ e -2 ydy = 1 k ,求(1)分布函数F (x ) (2)数学期望 E ( X ) .-∞ -∞ -∞ -∞ 2于是k = 2. ............. 5 分解 (1) 首先F (x ) = ⎰-∞f (t )dt , 于是当x ≤ 0 时, F (x ) = 0 ,(2) 设 Z = X +Y 的概率密度函数为 f Z 机变量和的概率密度公式得 (z ) ,当0 < z < +∞ 时, 根据两个随 当0 < x < 1时, F (x ) = ⎰0 2t d t = x , f (z ) = f (x ,z - x )dx = z 2e -x -2(z -x )dx = z 2e x -2z d x = 2(e -z -e -2z).Z⎰-∞⎰⎰当x ≥ 1时, F (x ) = ⎰-∞ f (t )d t =⎰0 2t d t = 1.,对于其它情况,都有 f Z (z ) = 0 . 所以 ⎧⎪2(e -z -e -2z ),z > 0, ⎧ 0,x ≤ 0, f Z (z ) = ⎨ ………10 分于是F (x ) ⎪ 2, 0 < x < 1, ………5 分⎩⎪ 0, 其它. ⎪ 1, x ≥ 1. 5. 设随机变量 X 具有概率密度 f (x ) = ⎧x / 8, 0< x < 4试求随机变量(2) ⎩E ( X ) = ⎰+∞ xf (x )dx = ⎰1 2x 2dx =2 .............10 分 Y = 2X + 8 的概率密度.⎨0,其它. -∞ 0 3解 方法一 设Y 的概率密度函数为 f Y (y ) ,显然当x ≤ 0 时, y ≤ 8 ,当x ≥ 4 3. 设K 服从(0, 5)上的均匀分布,求方程4x 2 + 4xK + K + 2 = 0 有实根的概率解 方程4x 2+ 4xK + K + 2 = 0 有实根这一事件可表示为时, y ≥ 16 , 所以当y ≤ 8 或y ≥ 16 时,有 f Y (y ) = 0 .............. 4 分{16K 2-16(K + 2) ≥ 0} ,即{k ≤ -1或K ≥ 2}..而当0 < x < 4 时, y = 2x + 8 的取值范围是8 < y < 16 ,且y = 2x + 8 的反函数为 因为K 服从(0, 5)上的均匀分布,其概率密度函数为x = y - 8 , 且有dx = 1, 于是此时应有 f(y ) = f ⎛ y - 8 ⎫ ⋅ dx = y - 8............. 4 分2 dy 2Y 2⎪ dy 32 ⎝ ⎭特别提示:自信考试 诚信做人层次:年级:班级:座号:学号:姓名:装订线=θ ⎨ Y ⎬ ⎨ ⎬ ⎪ +∞ 1⎪⎧y - 8, 8 < y < 16,设样本X 1,X 2 , ,X n 的观察值为x 1,x 2 , ,x n ,样本均值的观察值为x于是 f Y (y ) = ⎪ 32 ⎪⎩ 0,其它. ………10 分 ⎛ x ⎫2方法二 设Y 的分布函数为F Y (y ) , 密度函数为 f Y (y ).显然当由分布函解方程x =得未知参数θ 的矩估计值为θ =⎪ ⎝ 1- x ⎭.………8 分 ⎛ X ⎫2数的定义可得当y ≤ 8 时,有相应的矩估计量为θ = ⎪ ⎝ 1- X ⎭.…………10 分F (y ) = P {Y ≤ y } = P {2X + 8 ≤ y } = P ⎧X ≤ y - 8⎫ = 0 , Y⎨ 2⎬ ⎩ ⎭当8 < y < 16 时,有F (y ) = P {Y ≤ y } = P {2X + 8 ≤ y } = P ⎧X ≤ y - 8⎫ = ⎰ y -8 x 2 dx = (y - 8)2当y ≥ 16 时,有⎩2 ⎭ 08 64 F (y ) = P {Y ≤ y } = P {2X + 8 ≤ y } = P ⎧X ≤ y - 8⎫ = ⎰4 x d x = 1⎧ 0,⎩ y ≤ 8, 2 ⎭ 0 8于是F ⎪(y - 8)2 (y ) = , 8 < y < 16, ………6 分 Y⎨ 64⎩⎪ 1, y ≥ 16. ⎧y - 8 , 8 < y < 16,所以 f (y ) = F ' (y ) = ⎪ 32 ………4 分Y Y⎨ ⎪⎩ 0,其它. 6. 设总体X 的概率密度为 ⎪⎧ θ x θ -1, 0 < x < 1,f (x ;θ ) = ⎨⎪⎩ 0,其它. 其中θ > 0 为未知参数,X 1,X 2 , ,X n 是来自总体X 的一个样本,试求θ 的矩估计量.解 总体的数学期望为E (X ) = ⎰ xf (x ;θ )dx = ⎰θx θ dx = θ4 分 -∞+1θ θ +1 特别提示:自信考试 诚信做人层次:年级: 班级:座号: 学号:姓名:装订线Y。
2018年数理统计大作业题目和答案--0348

2018年数理统计大作业题目和答案--03481、设总体X 服从正态分布),(2σμN ,其中μ已知,2σ未知,nX XX ,,,21Λ为其样本,2≥n ,则下列说法中正确的是( )。
(A )∑=-ni iXn 122)(μσ是统计量 (B )∑=ni iXn 122σ是统计量(C )∑=--ni iXn 122)(1μσ是统计量 (D )∑=ni iX n 12μ是统计量2、设两独立随机变量)1,0(~N X ,)9(~2χY ,则YX 3服从( )。
)(A )1,0(N)(B )3(t)(C )9(t)(D )9,1(F3、设两独立随机变量)1,0(~N X ,2~(16)Y χ,则Y服从( )。
)(A )1,0(N)(B (4)t)(C (16)t)(D (1,4)F4、设nX X,,1Λ是来自总体X 的样本,且μ=EX ,则下列是μ的无偏估计的是( ).)(A ∑-=-1111n i iX n )(B ∑=-ni i X n 111)(C ∑=ni iX n 21)(D ∑-=111n i iX n5、设4321,,,X X X X 是总体2(0,)N σ的样本,2σ未知,则下列随机变量是统计量的是( ).(A )3/Xσ; (B )414ii X=∑; (C )σ-1X;(D )4221/ii X σ=∑6、设总体),(~2σμN X ,1,,n X X L 为样本,S X ,分别为样本均值和标准差,则下列正确的是( ).2() ~(,)A X N μσ 2() ~(,)B nX N μσ22211()()~()nii C Xn μχσ=-∑ ()() ~()n X D t n Sμ-7、设总体X 服从两点分布B (1,p ),其中p 是未知参数,15,,X X ⋅⋅⋅是来自总体的简单随机样本,则下列随机变量不是统计量为( )( A ) . 12X X + ( B ) {}max ,15iX i ≤≤( C ) 52Xp+( D )()251X X -8、设1,,nX X ⋅⋅⋅为来自正态总体2(,)N μσ的一个样本,μ,2σ未知。
研究生一年级数理统计期末考试习题2-2018

研究生数理统计 习题二(2018版)1、设总体X 服从参数是(01)p p <<的几何分布,其分布律为()1(1)x P X x p p -==-,1,2,3,......x =,12(,,...,)n X X X 是来自总体X 的样本。
求(1)p 的矩估计;(2)p 的极大似然估计。
2、设总体X 的分布律为()22(1)(1),2,3,......x P X x x x θθ-==--=,其中01θ<<,θ是未知参数,12(,,...,)n X X X 是来自总体X 的样本。
求(1)θ的矩估计;(2)θ的极大似然估计。
3、设总体X服从对数正态分布,其密度函数为22(ln ),0()20,0x x f x x μσ⎧⎧⎫-->⎨⎬=⎩⎭≤⎩。
(1)验证21()exp 2E X μσ⎧⎫=+⎨⎬⎩⎭;(2)若12(,,...,)n X X X 是X 的样本,求()E X 的极大似然估计。
4、根据遗传学理论,基因总是成对出现并且具有两种型式A 及a 中的一种。
根据Hardy-Weinberg 定律,基因型AA ,Aa ,aa 在人群中的比分别为2(1),2(1)θθθ--和2θ。
为了考察某种基因在人群中的分布情况,求θ5、设总体X 的概率密度为()2e ,00,x x x f x λλ-⎧>=⎨⎩其他 ,其中参数()0λλ>未知,12,,,n X X X 是来自总体X 的简单随机样本。
(1)求参数λ的矩估计量;(2)求参数λ的最大似然估计量。
6、设总体X 的概率密度为23,0(;)0,x e x f x x θθθ-⎧>⎪=⎨⎪⎩其他,其中θ为未知参数且大于零,12,,...,n X X X 为来自总体X 的简单随机样本。
(1)求θ的矩估计量;(2)求θ的极大似然估计量。
7、设总体2~(,)X N μσ,其中μ已知,12(,,...,)n X X X 是来自总体X 的样本。
浙江7月高等教育自学考试概率论与数理统计(二)试题及答案解析

浙江省2018年7月高等教育自学考试概率论与数理统计(二)试题课程代码:02197一、填空题(每空2分,共32分)1.袋中装有3只白球、5只红球,在袋中取球两次,每次取1只,作不放回抽样,则取到2只红球的概率为________________2.设A 、B 是两个相互独立的事件,已知P(A)=0.3,P(B)=0.2,则P(A ∪B)=_______3.设正方形的边长在区间[0,2]服从均匀分布,则正方形面积A=X 2的期望为_________4.设X 的分布函数为F(x)=⎪⎩⎪⎨⎧>-其它,0100x ,x 1001, 其他则P{X>1500}=_________, P{2000<X ≤3000}=_________5.设D(X)=1,D(Y)=4,相关系数ρxy=12,则COV(X,Y)=_______6.设X 服从参数λ=3的泊松分布,则P{X<2}=_________7.设(X则Y 2+1的概率分布列为_______8.已知F 0.05(3,4)=6.59,则F 0.95(4,3)=________________;已知F ~F(5,9),则F1~_____ 布9.设(X ,Y)服从二维正态分布N(μ1,μ2,σ21,σ22,ρ),则X 的概率密度为____________,X ,Y 相互独立的充分且必要的条件是ρ=________________10.设X ~N(1,3),X 1、X 2,X 3,X 4是来自X 的样本,则31X -~________________分布,∑=-41i 2)31X (~________________分布,X 1+X 2~_________分布。
11.设x 21~x 2(2),x 22~x 2(3),且x 21、x 22相互独立,则x 21+x 22~_________分布。
二、计算题及应用题(共68分)1.一人携3发子弹去靶场打靶,命中一发或子弹打完他即离开靶场,他的射击命中率为p.设各次是否击中相互独立,求他离开靶场时己命中一发的概率(6分)2.设(X ,Y)的概率密度为f(x,y)=⎩⎨⎧≤≤≤≤+其它,01y 0,1x 0,Y X (1)求边缘概率密度f X (x),f Y (y)(4分)(2)问X 、Y 是否相互独立(需说明理由)(4分)(3)求E(X),D(X)(4分)(4)求概率P{Y ≤X/3}(4分)3.设随机变量X 的概率密度为(6分) f(x)=⎪⎩⎪⎨⎧<<-其它,01x 1,x 2320,其他求Y=3X+1的概率密度4.经验表明,有20%的顾客预订了餐厅的座位,但不来就餐,餐厅有30个座位,预订给了32位顾客(设各预订者是否来就餐相互独立),以X 表示预订了座位的顾客前来就餐的人数(1)写出X 的概率分布列(6分)(2)求前来就餐的顾客都有座位的概率(6分)5.0<θ<1,θ为未知参数,取到一个来自X 的样本X 1,X 2,…,X n(1)求θ的矩估计量(6分)(2)证明所得的矩估计量是无偏的(4分)6.设这两个总体依次服从正态分布N(μ1,σ2),N(μ2,σ2),μ1,μ2,σ2,均未知,试在水平 α=0.05下检验假设:H 0:μ1=μ2H 1: μ1≠μ2备用数据(x 2分布,t 分布的上侧α分位数):t 0.05(10)=1.8125 t 0.025(8)=2.3060 t 0.025(10)=2.22817.设随机变量X ~N(2,2),Y ~N(-1,4),且X ,Y 独立(1)求P{X<2,Y<4}(4分)(2)求E(XY)+D(X-Y)(4分)(3)求(X ,Y)的概率密度(4分)备用数据:Φ(0)=0.5Φ(1.25)=0.8944Φ(2.5)=0.9938Φ(x)为标准正态分布函数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018级数理统计考试题
1.设X ,Y 相互独立,其密度函数分别为21
()0X x x f x ≤≤⎧=⎨
⎩
0其它,
(5)
5
()0
5
y Y e y f y y --⎧>=⎨
≤⎩,求()E XY 2. 已知二维随机变量),(Y X
试验证X 与Y 不相关,但X 与Y
3. 为了防止意外,在矿内同时设有两报警系统A 与B ,每种系统单独使用时,其有效的概率系统A 为0.92,系统B 为0.93,在A 失灵的条件下,B 有效的概率为0.85,求:
(1)发生意外时,这两个报警系统至少一个有效的概率; (2)B 失灵的条件下,A 有效的概率。
4.设X 与Y 是独立同分布的随机变量,它们都服从均匀分布(0,1)U 。
试求 (1)Z X Y =+的分布函数与概率密度函数; (2)2U X Y =-的概率密度函数。
5. 设随机变量X 的分布密度为02()240ax
x f x bx c x <<⎧⎪
=+≤<⎨⎪⎩
其它,已知
3
()2,(13)4
E X P X =<<=,求:(1)常数A ,B ,C 的值; (2)方差()D X ;
(3)随机变量X Y e =的期望与方差。
