电网络分析理论线性时变因果无源总结和例题
国家电网考试之电网络分析理论：第二章补充内容
1 1 x1 0 求 H X 0， 1 1 x1 0
T
B １，１
2019/4/22
25
x1 x2
0 -1 -1 0 H 0 ， 1 1 X 0 X B 0 1 1 0
的
解：①求特征根：
1 5 I A 2 3
I A 4 3 10
2
2 3
2
2
I A 0
1 2 j3 , 2 1
2019/4/22
6
②求特征量 i I A 0 1 5 I A 2 3
A 2 1 2
I A1 0
I A2 1
2019/4/22
28
1 对2×2阵 x2 x1 取 1 1 成立！？ I A2 1 1 12 1
1 1 x1 1 1 1 x 1 2
P AP J
1
2 1 I A 1 4
1 A1 ,2 1 ,2 0
AP PJ
1 2 3
A1, A2 1,1 2
A1 1
·
的相图
轾 2 过 Z (0) = 犏 犏 2 臌
解：①求特征根
轾 l +1 - 2 [l I - A] = 犏 犏 l - 1 臌5 l I - A = l - 1 + 10 = l + 9 l I- A = 0 l 1 = j3 l 2 = l 1
电网络理论习题
电网络理论习题第一章1-1、图示电路中，N为电阻性定常而端口元件，其特性为u?Ri或i?Gu，其中R、G 为2×2矩阵，它们是已知的。
现在如图示接入方式接入电阻r1和r2。
求包括这两个电阻在内的二端口元件的特性。
（证明图示网络的线性、非时变性）r211`2r1N2`1-7、设电感器的电感矩阵L是：L??如果L12?L11?L21L12??L22??L21，试证明这个元件不是无源的。
进而证明元件是无源的充分必要条件是L对称正定。
1-8、图1-8的二端口由两个线性电阻器（无源元件）和一个理想流控电流源（有源元件）组成。
试证明在某些参数值下，它可以是无源二端口。
i1i2u1?i1r1r2u2图1-81-9、设互易n端口有混合参数矩阵H，求H应满足的条件。
1-10、设x是输入，y是输出，它们可以是n端口的电流或电压。
加法器、乘法器和延时元件的约束分别是：y?ax1?bx2，y?ax1x2，y(t)?ax(t??)式中，a、b、?都是正常数。
这些元件是不是线性的？是不是时变的？（题中输入x 可以是二维量，输出y是一维量，仍可以定义容许偶(x,y)。
）第二章2-5、建立图2-5所示网络的混合方程和改进节点方程。
aE3bG6ca3b6c?4V1V1C1G2dV20g7V2G5G8145782d0（a）图2-5（b）2-10、求图2-10所示双T型RC电路的转移函数V2(s)/V1(s)[提示：先求外节点方程]。
C314CR2CR2R2V1(s)V2(s)图2-102-14、N1（图2-14（a））与如下各网络N2按对应节点号相联的方式联结，试写出联结后所构成的新网络的节点方程。
（1）N2如图2-14（b）所示，其端口特性为：?U13?H11I1?H12U23??I2?H21I1?H22U23（2）N2为如图2-14（c）所示回转器，其特性为：?U1??rI2??U2?rI1I2N2I1rN14 2 （a）（b）（c）图2-1443210I12131U1I23U2补充：已知四端网络Na的不定导纳阵为Yia阵?(yij)4?4，求增加C,G后的不定导纳12CG3Na4第三章3-2、画出图3-2所示电路的信号流图。
电网络理论第六章 无源网络分析(
令K(1,n) =△，系数矩阵行列式，则输出端开路时
U0
1 I in Δ
Uin a1 Iin U2
Iin a2U2 I3
a1 Iin U2 Uin
-Iin + a2U2 I3
+
Iin
a1 a2
Io
a3 a4
a5 a6 a7
+
U2 a3 I3 U4 I3 a4U4 I5
（2） 输出端开路
C= A=
D=
Iin Uo Uin Uo
I in Io
Io 0
= K(1,n) C a1
C a1
= K(2,n) = Io 0
-1 a3
= K(1,n -1) = Uo 0
-1 a4 0
-1 an-1 0 -1
U B = in Io
C = K(2,n -1) = Uo 0 a1an
2
Z1 Z2
Zin1
(2)等效入端阻抗Zin2
Z 2 Z1 Zin2 Zin2 Z 2 + Z1 Zin2 Zin2 Zin2
Z in2 Z1 Z 1 Z1 Z 2 2 2
Uin = K(1,n) U o Io 0 I A C = in Io 0 = K(2,n) = Uo a1 A=
Io
a2 a3 a4 a5 a6 a7 a8
+
U in
-
Uo
-
Uin A = K(1,n -1) == I o Uo 0 an I in A D= = K(2,n -1) = I o Uo 0 a1an B=
（1） 输出端开路 1 输出端开路时 U 0 U in
【课件】国家电网考试之电网络分析理论：第一章网络理论基础小结
t 2
sin
t
2
0
任意
t [0的, 2 ]
其它
可得
i1
(
2
)
0,
i2
(
2
)
0
则
W ( 2
)
(M12
M 21)
2 0
sin
2
cos
2
2 sin
2
d
( M 12
M 21 )
2 0
2
图示电路含有非线性（非互易元件） 但仍为线性（互易）一端口网路。
设二极管D的模型为正向电阻 R 和
+i
反向电阻 R ，它们都是常数。
i1
i2
列出相应的KCL和KVL方程
u
R
R
i i1 i2
i1R i1R u
i2R i2R u
_
u i1 R R
i2
R
u R
i1i2 0
M12d
(i1i2
)
(M12
M 21)
t
i2
di1
d
d
1 2
L1i12
1 2
L2i22
M12i1i2
(M12
M 21)
t
i2
di1
d
d
（1）先说明M12 M 21 件是有源的。 电流是
假定
M
2
1s2inMt
21
取 i1
2 t
i2
10道例题！
例1 试说明受控源是有源元件 。
电网络分析简单题总结——仅供参考
电网络分析简单题总结——仅供参考1、电网络的基本变量有哪些,这些基本变量各有什么样的重要性质,基本变量是电流i、电压u、电荷q、磁通, ,重要性质有电流的连续性、在位场情况下电位的单值性、电荷的守恒性、磁通的连续性2、什么叫动态相关的网络变量偶,什么叫动态无关的网络变量偶,在电网络的变量偶中～哪些是动态相关的网络变量偶,哪些是动态无关的网络变量偶, 在任一端子上～基本网络变量之间存在着不依赖于元件性质的关系的一对变量称为动态相关网络变量偶。
例如和～因(u,,)(i，q)kkkk,()()dtdqtkku(),i(),tt为:、。
kkdtdt不存在不依赖于元件N的预先规定的关系的二基本变量被称为动态无关变量。
例如、、、。
(u,i)(u,q)(i,,)(q,,)kkkkkkkk3、电网络中有哪几类网络元件,这些网络元件是如何定义的,它们的特性方程分别是怎样的,电网络中有四类网络元件～分别是电阻类元件、电容类元件、电感类元件、忆组类元件。
如果一个n端口元件的端口电压向量u和端口电流向量i之间的f(u(t),i(t),t),0代数成分关系为～则称该元件为n端口电阻元件～其R f(u(t),i(t),t),0特性方程为。
R,如果一个n端口元件的端口电流向量i和端口磁链向量之间的f(i(t),,(t),t),0代数成分关系为～则称该元件为n端口电感元件～其L 特性方程为。
f(i(t),,(t),t),0L如果一个n端口元件的端口电压向量u和端口电荷向量q之间的代数成分关系为～则称该元件为n端口电容元件～其f(u(t),q(t),t),0C特性方程为。
f(u(t),q(t),t),0C如果一个n端口元件的端口电荷向量q和端口磁链向量之间的,代数成分关系为～则称该元件为n端口忆组元件～其f(q(t),,(t),t),0L特性方程为。
f(q(t),,(t),t),0L4、什么是端口型线性网络,端口型线性网络与传统的线性网络之间有什么样的关系,若一个n端口网络的输入/输出关系由积分算子微分算子D确定～当D既具有齐次性又具有可加性时～此网络称为端口型线性网络。
电力系统分析理论总结
15
SCU-SEEI-ltq
2019/9/28
四、频率调整和电压调整
电力系统的频率特性 电力系统的频率调整 电力系统有功功率的最优分配 无功平衡与电压水平的关系 电压调整的基本概念 电压调整的方法和手段
电压调整的基本概念
中枢点的三种调压方式
逆调压 顺调压 常调压
21
SCU-SEEI-ltq
2019/9/28
V i (V G k 1 V )/k2 (V G k 1PV N R Q)/X k2
22
SCU-SEEI-ltq
2019/9/28
调压措施
V b (V G k 1 V )/k2 (V G k 1PV N R Q)/X k2
40
SCU-SEEI-ltq
2019/9/28
PEQ
EQV X q
sin
EV
PE
sin
Xd
PVG
VGV XTL
sinTL
41
SCU-SEEI-ltq
2019/9/28
EQ0 V0Q0VX0q2P0VX0q2
Eq0EQ0X Xq d 1X Xq d V0co0s Eq 0EQ0X Xq d 1X Xq d V0co0s
(1)发电机调压,调节励磁VG
(2)变压器调压,选择变比 k1, k2
(3)无功补偿,改变无功分布Q (4)改变线路参数 X
23
SCU-SEEI-ltq
2019/9/28
电压调整的方法和手段
变压器分接头的选择 例 5-2 , 例 5-3
利用无功补偿调压(例 5-6)
电网络理论案例分析
解得： J1 5129 W / m ， J 2 2760 W / m
2
2
热圆盘的净辐射热量为： 1
Eb1 J 1 1072 W 1 1 1 A1 Eb2 J 2 148 W 1 2 2 A2
冷圆盘的净辐射热量为： 2
根据能量平衡，大房间壁所得到的净辐射热量为：
1 ——与电阻对应， 称为辐射换热的热阻。 由于这个热阻仅仅取决于空间参量， A1 X 1、 2
与表面的辐射特性无关，所以称为辐射空间热阻。 1.2 两灰体表面间的辐射换热 灰体表面单位面积的辐射换热量： ① 从表面 1 外部观察：能量收支差额为有效辐射 J 1 与投射辐射 G1 之差。 ② 从表面 1 内部观察：能量收支差额为本身辐射 1 Eb1 与吸收辐射 1G1 之差。 即：
3 (1 2 ) (1072 148) 1220 W
案例三
1、疏散模型研究现状
应急疏散电路模型
目前国内外对人员应急疏散规划的研究， 在理论上主要包括计算机仿真方法与数学分析 方法。 随着计算机技术的应用与发展， 一些基于计算机模拟的模型逐渐应用于疏散管理方面， 例如应用于建筑物的人员疏散模型有 EVACNET，BuildingEXODU，EGRESS，SIMULEX，SGEM， 主要对建筑物内人员的徒步疏散。机动车疏散模型有 MASSVAC，MEMBrain，REMS，CEMPS， DYNEV&I—DYNEV，SIM—Queue 等。这些模型都是从微观或宏观的层次对疏散过程中人员流 动或交通状况进行模拟，可用于预测出疏散时间，评估疏散方案。 数学分析的方法主要以网络流优化为基础， 无论是建筑物内疏散或大范围疏散都可以转 化为疏散网络的问题。疏散网络分为静态和动态两类。静态网络的结构与参数与时间无关， 其优化问题主要包括最短路径，最小费用流，最快流及最大流问题等。动态网络是传统静态 网络在时间维的扩展。
电网络理论试卷2精选全文
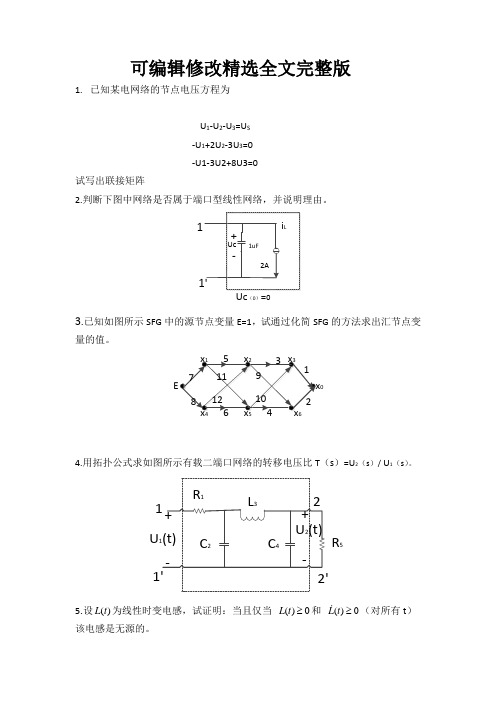
可编辑修改精选全文完整版1. 已知某电网络的节点电压方程为U 1-U 2-U 3=U S-U 1+2U 2-3U 3=0 -U1-3U2+8U3=0试写出联接矩阵2.判断下图中网络是否属于端口型线性网络，并说明理由。
1（0）03.已知如图所示SFG 中的源节点变量E=1，试通过化简SFG 的方法求出汇节点变量的值。
4.用拓扑公式求如图所示有载二端口网络的转移电压比T （s ）=U 2（s ）/ U 1（s ）。
R 1R 5C 2C 4L 3U 2(t)U 1(t)++--122'1'5.设()L t 为线性时变电感，试证明：当且仅当 ()0L t ≥和 ()0L t ≥（对所有t ）该电感是无源的。
6. 用Mason 公式求如图所示SFG 的图增益y T u。
d7.用灵敏度恒等式求下图所示网络的输入阻抗Zin 对各参数的灵敏度1inZ R S 。
答案： 1解：2解：1'12Ai L1uF（0）0U(t)i (t)+-Uc因为网路的端口型线性性质包括齐次性和可加性。
如图，()2dui t cdt=+ ，因为网路中含有独立的电流源，对输入输出有影响，所以端口网路不具备齐次性也不具备可加性，因此端口网路是端口型非线性网路。
3解：1.消去节点x1,x43131125x 0x 2x 3x 5x 61249102.消去节点x2,x53.消去节点x3,x6E4.解： 电路拓扑图为：根据拓扑电路图，找出全部2-树（1,1’），2-树（12,1’）, 2-树（12’,1’），列出树枝编号如下：2-树（1,1’） ：13 , 23,24,25,34,35 2-树（12,1’）:13 2-树（12’,1’）:无有载二端口网络的电压转移函数的拓扑公式为：2212,1'12',1'22'1212'21111,1'()()()()()T y T y U s U s T y ∑-∑-==∑ 得出结果：1322242413353531()11R SL T S C SC C S C C R SL L R L R SL =+++++5.解：220?0000:()1t ()()()[()]()()()21t ()()()2()(,)()()()()()ttt t t L t i t di W t u i d L i d L t i t d W t L t i t d t W t t u i d u t L t i t dtψττττττττψτττ-∞-∞===⋅=====+⎰⎰⎰0证明对于元件特性为()()()的线性时变电感，时刻电感元件的储能为：则时刻储能为：在[t ,t]时间区间，电源供给电感的能量为：其中02022200220000()()()()(),()(,)()()()()()111()()()()()()22211()(,)()()()()22()(,)0ttt t t t t t L t i t di t dL t i t L t dt dt W t t L i i d L i d L t i t L t i t L i d W t W t t L t i t L i d W t W t t τττττττττττττ===+=-++=++≥⎰⎰⎰⎰从而所以要该电感无源则成立即可故当且仅当00L t L t ≥≥（）和（）对所有的t 恒成立时，原命题成立得证6解：经分析可得图中回路有5个，不存在二阶回路，故1[d abc abe bcf ]1d abc bcf bdefbdef ∆=-----+=+++-前向路径有两条：11,1P abc =∆=22,1P d =∆=故11221P P y abc d T u d abc abe bcf bdef∆+∆+===∆+++++其回路如下:7. 解：由图可知：321321)(R R R R R R Z in +++=则321323211321323211)()(1)(32111321113211321132132111R R R R R R R R R S R R R R R S R R R R SSS S S S R R R R R R R R R R R R R R R R R R R R R R R R R Z R in+++=++-=++++++-+=-==++++++++。
电网络理论简答题总结
电网络理论考题总结（简答题）【1】N端口线性时变与非线性的电感元件、电容元件的定义，并举例。
线性时变电感：N端口元件满足关系，且为矩阵，与Ψ=L i(t)L(t)(N-1)×(N-1)磁链及电流无关。
线性时变电容：N端口元件满足关系，且为矩阵，与q=C v(t)C(t)(N-1)×(N-1)电荷及电压无关。
（电阻定义类似）☛☛☛一个不含时变元件的电路称为时不变电路，否则为时变电路。
若一个电容元件的库伏特性不是一条通过坐标原点的直线，该种电容就是非线性电容；电感的磁通链和电流间的函数关系为韦安特性，若电感元件的韦安特性不是一条过坐标原点的直线，则为非线性电感元件。
【2】N端口非线性电路的定义。
一是根据电路元件的特性来定义（含非线性元件即为非线性电路）；二是根据输入输出关系来定义（端口型定义，网络输入输出关系不同时存在可加性和齐次性时即为端口型非线性网络）。
【3】高阶有源滤波器的设计步骤。
（根据相应实例写步骤）一般：高阶：给出设计指标，根据设计指标选择逼近函数；确定阶数、找到对应的无源网络模型；选择实现方法（级联、多路反馈、无源模拟等）；参数退归一化；注意补偿、修正电路（直流通路）。
选取逼近函数类型；根据设计要求确定阶数；找到对应逼近函数的无源低通网络模型；选择实现方法（级联、多路反馈、无源模拟等）；根据要求的滤波器类型进行变换（如仿真电感、F D N R、L F等）；参数退归一化。
二阶：S a l l e n K e y---L P、H P、B P、高通、陷波或者双积分回路---K H NT T。
【4】高阶有源滤波器的分类。
按使用的器件：仿真电感、F D N R、C CⅡ、跨导电容、运放；按设计方法：级联法、多路反馈法、无源模拟法。
【5】高阶有源滤波器的设计方法，它们的共同点和特点。
❶级联法：级联滤波器易于调节和优化动态范围，但设计时各极、零点的搭配要慎重考虑，以实现较低灵敏度。
电网络理论考试习题
阅前提示：以后解答过程存在部分错误，请小心使用。
习题11. 一个非线性电阻元件的电压、电流分别为：u(t) = cos ωt ，i(t) = cos4ωt(u 、i 参考方向一致)。
求该电阻元件的构成关系。
i(t) = cos4ωt = 8cos 4ωt -8cos 2ωt+1 = 8u 4(t)-8u 2(t)+12．二端元件的电压、电流分别为u(t) = 2cost ，i(t) = 0.5-cost ，试确定元件类型(即属于电阻、电感、电容等中的哪一类)，并论证其无源性。
i(t) = 0.5-cost = 0.5-0.5u(t)0T d )cos 5.0(cos 2d )(i )(u )t ,t (W TT0<-=ττ-τ=τττ=⎰⎰电阻，有源。
3．有两个二端元件，其电压、电流关系方程分别为dt)t (di )t (2i u(t) (2) dt du(t)2u(t)i(t) )1(2== 试确定各元件类型，并论证各元件的无源性。
（1）因为dt du dt dq i 2==，所以q = u 2+A ，A 为常数，电容元件。
)t (u 32d d du u 2u d )(i )(u )t (W 3t t =ττ⨯=τττ=⎰⎰∞-∞-，当u<0时，W(t)<0，有源。
（2）因为dtdi 32dt d u 3=ψ=，所以ψ = 32i 3+A ，电感元件。
0)t (i 21id d di i 2d )(i )(u )t (W 4t 2t ≥=τ⨯τ=τττ=⎰⎰∞-∞-，无源。
4．如题图1所示二端口电路，其中非线性电阻r 的构成关系为u r = i r 3。
此二端口是有源的还是无源的。
p = u 1i 1+u 2i 2 = i = (i 1R 1+u R )i 1+(i 2R 2+u R )i 2 = i 12R 1+i 22R 2+i R 4≥00pd d )()()t (W tt=≥τ=τττ=⎰⎰∞-∞-i u ，无源。
国家电网考试之电网络分析理论：3、4章练习题.doc
1. （ 10%）已知题 2 图中四端网络N a的不定导纳阵为Y ia ( y ij ) 4 4，N b的 H 参数U 1 1 2 I 1，求 N a、 N b对应节点相联后的不定导纳矩阵。
为4 8 U 2I 21I1 I2 3 4 2+ Nb +U U2 11 Na2 - -42 题图2. （ 10 分）已知题 2 图中四端网络N a的不定导纳阵为Y ia ( y ij ) 4 4，N b的H参3 1数为I1 1 U 1 ，求 N a、 N b对应节点相联后的不定导纳矩阵。
U 222I 21I1 I2 3 4 2+ Nb +U U2 11 Na - -242 题图3 1 1 1 U n1I 11 22 1U n2 I 2 ，现二．（15 分）已知题图 2（a ）的全节点方程为Un3 I 3 1 1 1 11 02 1 U n4I 4把图（ a ）改造成图（ b ）， 求图（ b ）的节点电压方程 。
12I 1NI 2213N44题 2 图（ a ）题 2 图（ b ）3. 15%) 求题 1 图所示三端口网络的 Y 参数矩阵，并叙述判断多端口网络无源性的方法。
I 1αU-1I 3+ + 1Ω1Ω+ U 11 ΩU 3-1Ω-I 2β U 3+U 2-题 1 图4. （ 15%）已知四端口网络 Na 的不定导纳阵为 Y ia( y ij )4 4 ，求增加 C ， G后的不定导纳阵。
1 2CGN a34题 2 图5.（ 15%）图示两线性网络N1和N2，其节点方程（设均以大地为参考节点）分别为Y11 Y12Y13 u1 J1N1 :Y21 Y22Y23 u2 J2Y31 Y23Y33 u3 J3Y44 Y45Y46 u4 J4N2 :Y54 Y55Y56 u5 J5Y64 Y65Y66 u6 J6u1u4 N 1u2N2u5u3u6题2 图列出下列三种情况下的节点电压方程或改进节点电压方程（1）将节点对①－④，②－⑤用阻抗为零的导线联接；（7 分）（2）将节点对①－④，②－⑤用联线联接，设每根联接线的阻抗为Z l：（ 7 分）（3）将节点对①－④，②－⑤下图所示的互感元件联接。
电网络分析与综合学习报告 (1)
基本回路的方向规定为所含连支的方向。
2.2独立的基尔霍夫定律方程
割集：
割集：
割集：
注意：1、2、3为树枝
推广为一般情况：基本割集的基尔霍夫电流定律方程是一组独立方程，方程的数目等于树支数，基本割集是一组独立割集。
电网络理论读书报告
电网络理论主要包括：网络分析、网络综合、模拟电路故障诊断。其中网络分析主要是一致网络结构、网络参数和输入求输出，网络综合主要是已知网络输入和输出去确定网络的结构与参数，模拟电路故障分析是已知网络的输入和输出确定网络结构参数与故障分析。
第一章网络原件和网络的基本性质
1.1实际电路与电路模型
理想变压器：
阻抗匹配：
1.6网络的基本性质
线性和非线性
线性特性指均匀性，叠加性。
均匀性（齐次性）：
叠加性：
时变与时不变
一个网络在零初始条件下，其输出响应与输入信号施加于网络的时间起点无关，称为非时变网络，否则称为时变网络。
因果与非因果
因果网络当且仅当输入信号激励时，才会出现输出（响应）。也就是说，因果网络的（响应）不会出现在输入信号激励的以前时刻。也叫做非超前网络。
割集：是一组支路集合。并且满足：
(1)如果移去包含在此集合中的全部支路，则此图变成两个分离的部分；
(2)如果留下该集合中的任一支路,则剩下的图仍是连通的。
基本割集(fundamental cut-set)：由数的一条树支与相应的一组连支所构成的割集，称为基本割集。
基本割集的方向规定为所含树支的方向。
电网络理论是建立在电路模型基础上的一门科学，它所研究的直接对象不是实际电路，而是实际电路的模型。实际电路：为了某种目的，把电器件按照一定方式连接起来构成的整体。电路模型：实际电路的科学抽象，由理想化的网络原件连接而成的整体。器件：客观存在的物理实体，是实际电路的组成单元。元件：理想化的模型，其端子上的物理量服从一定的数学规律，是网络的基本构造单元。
【课件】国家电网考试之电网络分析理论：第一章网络理论基础(2)精简版
R0、L0、G0和C0 分别为传输线单位长度电阻、电感、电导 和电容。
非均匀多导体传输线方程
u x
R0
xi
L0
x
i t
i x
G0
xu
C0
x
u t
R0、L0、G0和C0 分别为传输线单位长度
的n阶电阻、电感、电导和电容矩阵。
传输线频非变频传变输传线输（线F（reFqrueeqnuceyn-Dcye-pInednedpaennt dTanrat nTsmrainsssmioinssLioinnesL）ines）
频变单导体传输线方程
U x
R0 I
j L0 I
dU (x) dx
R0 ( x) I
(x)
sL0(x)I (x)
I x
G0
U
jC0
U
dI ( x) dx
G0
(x)U
(x)
sC0
(x)U
(x)
频变多导体传输线方程
U x
跳过“传输线” 和“小信号模型”部 分！
传输线单多导导体体传传输输线线（（SMinugltlie－－CCoonndduuccttoorr
Transmission Lines） Transmission Lines）
单导体传输线方程
u x
R0i
L0
i t
i x
G0u
A(Q )
F x
Q
B(Q )
电网络分析理论线性时变因果无源总结和例题
则：dy3(t) 3 df3(t)
dt
dt
dy1(t) 3 df1(t) , dy2 (t) 3 df2 (t)
dt
dt dt
dt
d[ay1(t)] 3 d[af1(t)] , d[by2 (t)] 3 d[bf2 (t)]
dt
dt
dt
dt
二式相加得： d[ay1(t) by2 (t)] 3 d[af1(t) bf2 (t)]
设 f3(t) af1(t) bf2(t) y3(t) 则：y3(t) 8sin[ f3(t)] 8sin[af1(t) bf2(t)]
y3(t) 8sin[af1(t) bf2 (t)] a{8sin[ f1(t)]} b{8sin[ f2 (t)]} y3(t) 8sin[ f3(t)] ay1(t) by2(t)
6.连续时间系统与离散时间系统
如果系统的输入和输出都是时间的连续函数， 这个系统就称为连续时间系统；如果系统的 输入和输出都是时间离散函数，这个系统就 称为离散时间系统。
连续系统中传输和处理的是连续信号。
离散系统中传输和处理的是离散信号。 在实际工作中系统中长将两系统组合使用， 这种情况称为混合系统
满足（1）、（2）、（3）则系统为线性，
有一个不满足则系统为非线性。
2.时变系统与非时变系统
时不变特性是指系统的零输入状态输出波形 仅取决于输入波形与系统特性而与输入信号 接入系统的时间无关。设系统的输入 f (t) ，
输出为 y(t)
若 : f (t) y(t) f (t t0 ) y(t t0 ) t0为任意常数。
（2）可加性
若 : f1(t) y1(t) f2 (t) y2 (t) 则：f1(t) f2 (t) y1(t) y2 (t)
国家电网考试之电网络分析理论：3、4章练习题.doc
国家电网考试之电网络分析理论：3、4章练习题.doc1. （ 10%）已知题 2 图中四端网络N a的不定导纳阵为Y ia ( y ij ) 4 4，N b的 H 参数U 1 1 2 I 1，求 N a、 N b对应节点相联后的不定导纳矩阵。
为4 8 U 2I 21I1 I2 3 4 2+ Nb +U U2 11 Na2 - -42 题图2. （ 10 分）已知题 2 图中四端网络N a的不定导纳阵为Y ia ( y ij ) 4 4，N b的H参3 1数为I1 1 U 1 ，求 N a、 N b对应节点相联后的不定导纳矩阵。
U 222I 21I1 I2 3 4 2+ Nb +U U2 11 Na - -242 题图3 1 1 1 U n1I 11 22 1U n2 I 2 ，现二．（15 分）已知题图 2（a ）的全节点方程为Un3 I 3 1 1 1 11 02 1 U n4I 4把图（ a ）改造成图（ b ），求图（ b ）的节点电压方程。
12I 1NI 2213N44题 2 图（ a ）题 2 图（ b ）3. 15%) 求题 1 图所示三端口网络的 Y 参数矩阵，并叙述判断多端口网络无源性的方法。
I 1αU-1I 3+ + 1Ω1Ω+ U 11 ΩU 3-1Ω-I 2β U 3+U 2-题 1 图4. （ 15%）已知四端口网络 Na 的不定导纳阵为 Y ia( y ij )4 4 ，求增加 C ， G后的不定导纳阵。
1 2CGN a34题 2 图5.（ 15%）图示两线性网络N1和N2，其节点方程（设均以大地为参考节点）分别为Y11 Y12Y13 u1 J1N1 :Y21 Y22Y23 u2 J2Y31 Y23Y33 u3 J3Y44 Y45Y46 u4 J4N2 :Y54 Y55Y56 u5 J5Y64 Y6566 u6 J6u1u4 N 1u2N2u5u3u6题2 图列出下列三种情况下的节点电压方程或改进节点电压方程（1）将节点对①－④，②－⑤用阻抗为零的导线联接；（7 分）（2）将节点对①－④，②－⑤用联线联接，设每根联接线的阻抗为Z l：（7 分）（3）将节点对①－④，②－⑤下图所示的互感元件联接。
电网络分析简单题总结——仅供参考
电网络分析简单题总结——仅供参考1、电网络的基本变量有哪些,这些基本变量各有什么样的重要性质,基本变量是电流i、电压u、电荷q、磁通, ,重要性质有电流的连续性、在位场情况下电位的单值性、电荷的守恒性、磁通的连续性2、什么叫动态相关的网络变量偶,什么叫动态无关的网络变量偶,在电网络的变量偶中～哪些是动态相关的网络变量偶,哪些是动态无关的网络变量偶, 在任一端子上～基本网络变量之间存在着不依赖于元件性质的关系的一对变量称为动态相关网络变量偶。
例如和～因(u,,)(i，q)kkkk,()()dtdqtkku(),i(),tt为:、。
kkdtdt不存在不依赖于元件N的预先规定的关系的二基本变量被称为动态无关变量。
例如、、、。
(u,i)(u,q)(i,,)(q,,)kkkkkkkk3、电网络中有哪几类网络元件,这些网络元件是如何定义的,它们的特性方程分别是怎样的,电网络中有四类网络元件～分别是电阻类元件、电容类元件、电感类元件、忆组类元件。
如果一个n端口元件的端口电压向量u和端口电流向量i之间的f(u(t),i(t),t),0代数成分关系为～则称该元件为n端口电阻元件～其R f(u(t),i(t),t),0特性方程为。
R,如果一个n端口元件的端口电流向量i和端口磁链向量之间的f(i(t),,(t),t),0代数成分关系为～则称该元件为n端口电感元件～其L 特性方程为。
f(i(t),,(t),t),0L如果一个n端口元件的端口电压向量u和端口电荷向量q之间的代数成分关系为～则称该元件为n端口电容元件～其f(u(t),q(t),t),0C特性方程为。
f(u(t),q(t),t),0C如果一个n端口元件的端口电荷向量q和端口磁链向量之间的,代数成分关系为～则称该元件为n端口忆组元件～其f(q(t),,(t),t),0L特性方程为。
f(q(t),,(t),t),0L4、什么是端口型线性网络,端口型线性网络与传统的线性网络之间有什么样的关系,若一个n端口网络的输入/输出关系由积分算子微分算子D确定～当D既具有齐次性又具有可加性时～此网络称为端口型线性网络。
电网络理论习题
6.3 用梯形电路实现下列驱点函数(分别用 FosterⅠ、Ⅱ；CauerⅠ、Ⅱ这四种形式)：
(a)
Z ( s)
=
s4
s3 + 4s + 12s2 +
27
,
(b)
Z ( s)
=
(s2 + 1)(s2 + s(s2 + 2)
3)
.
6.4 试确定下列驱点函数能否用 RC 一端口来实现，能实现的实现之(FosterⅠⅡ、CauerⅠⅡ)。
1.5 一个二端电路元件的电压与电流的关系可写为 i = D d 2u dt 2
元件是有源的。
（D 为非零常数），证明该
1.6 图示二端口网络中，非线性电阻的特性为：
i1 1Ω
1Ω i2
+
+
+
(1) uR = iR2 ; (2) uR = iR3 . 试判断以上两种情况下此二端 口是无源的还是有源的？
3.7 用直接法列写题 3.2(b)电路的改进节点 方程。
4.1 求下列网络复杂性的阶数。
+
+
+
-
-
-
(a)
C4
+ r i1 -
i1 * L6
iS
+ u3-
R1
+
C3μ u3
L5 -
i5 *
M
R2 β i5
题图 3.6
+ -
+ (b)
++ u ku --
(c )
4.2 试写出图示电路的状态方程及输出方程。
式：
(a)
Zi d
=
【课件】国家电网考试之电网络分析理论：08电网络理论第六章参考
2020/1/29
14
极点位于虚轴上时
•若
Hi (s)
Ai s
，其原函数是阶跃函数,即
hi (t) Ai (t)
•若
Hi (s)
s
Ai
j
s
Ai
j
数为等幅振荡,即
，其对应的原函
hi (t) H sin(t )
::若极点是位于虚轴上的一阶以上极点时,则 当t ∞
时,hi(t) ∞。
得 c p(b11i b22i bnni ) D pN
::Δc中不含p的项之和就是Δ; 含p的c项 D之和pN即为D－ T1pNN。 0
如果取p＝1/T,得 例题
2020/1/29
12
四、网络函数的极零点图
• 把网络函数的极点和零点在s平面上的位置分 布图(零点用“O”表示,极点用“×”表示,r阶 极点用 表示),称为该网络函数的极零点图。
j sintd
h(t)
1
2
R() cost
X
( ) sin t d
2020/1/29
22
0
1
2
R(
)
c
ostX
(
)
sin
t
d
t 0
将上面两式相加或相减
h(t) 1
R() costd 1
X ()sintd,t 0
d
希尔伯特(Hilbert)变换。
2020/1/29
24
• 正弦稳态下 ，
H ( j ) e ( )
— (—) () j ()
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
（2）可加性
若 : f1(t) y1(t) f2 (t) y2 (t) 则：f1(t) f2 (t) y1(t) y2 (t)
统一处理方法
若 : f1(t) y1(t) f2 (t) y2 (t) 则：af1(t) bf2 (t) ay1(t) by2 (t) a,b为任意常数。
如果系统的输出不仅决定于该时刻的输入，而且 与它过去的状态（历史）有关，称这种性质为记 忆性。具有记忆性的系统称为记忆系统。
如果系统的输出仅决定于该时刻的输入，而且与系 统过去的状态（历史）无关，称这种系统为无记忆 性系统。
系统是有记忆的还是无记忆的，完全取决于组成 该系统的元件的性质。如果系统的组成含有记忆 元件（如：电容器、电感器、奇存器和存储器等， 就是记忆系统。
则 设
:dfyd3d1(ytd(t1t)t()t)atyft11y((1tt())t)bff12f((1tt())t,),dyddy2y3td(2(tt(t)t))ty则t2y(2：t()dt)yd3t(ft2f)(2t()tt)y3
(t
)
f3 (t )
d
[ay1 dt
(t
)]
t[ay1
(t
)]
af1
0
r1 0 ，r1r2 4 2r22 0 ，
2 r1 ，无源 ，
r2
2 r1 ，有源，可能为负 有源
r2
描述无记忆系统的方程为代数方程，描述有记忆 系统的方程为微分方程方程。
5.稳定系统与不稳定系统
对一个初始不储能的系统，如果输入有界
（有限值 f (t) ）输出也有界（有限 max
值 y(t) ）系统为稳定系统；反之，如 max
果输入有界（有限值 f (t) ），输出无 max
界（无限值），则该系统就是不稳定系统。
y1(t t0 ) 8sin[ f1(t t0 )] 8sin[ f2 (t)] y2 (t) f1(t t0 ) f2 (t) y2 (t) y1(t t0 )
∴ 该系统为时不变系统。
网络的有源性和无源性！
判断网络的有无源性
一端口，p（t） u（t）i（t）
n
n端口，p（t） u（T t）i（t） u（k t）i（k t） k 1 t
∴ 该系统为时变系统。
解：（2） 给 f1(t), f2 (t) 和任意常数 a,b
设 f1(t) y1(t), f2 (t) y2 (t)
则: dy1(t) 3 df1(t) , dy2 (t) 3 df2 (t)
dt
dt dt
dt
设 f3(t) af1(t) bf2 (t) y3(t)
例试判别下列零状态系统是否为线性系统是，是否为时不变系统。
(1) dy(t) ty(t) f (t) dt
(2) dy(t) 3 df (t)
dt
dt
(3) y(t) 8sin f (t)
解：（1） 给 f1(t), f2 (t) 和任意常数 a,b
设 f1(t) y1(t), f2 (t) y2 (t)
k 1
[i1，i2
]
r1
1 2
r2
1 2
r2
r2
i1
i2
0
注意：由Z阵可知该网络为非互易双口网络，在 判断网络的有源性时要重排二次型！
2
p（t） ukik u1i1 u2i2 i1r1i1 （i2 i1）r2i2 k 1
[i1，i2
]
r1
1 2
r2
1 2
r2
r2
i1
i2
dy1(t) 3 df1(t) dy1(t t0 ) 3 df1(t t0 ) dy2 (t)
dt
dt
dt
dt
dt
比较两式可知 f1(t) y1(t), f1(t t0 ) f2 (t) y2 (t) y1(t t0 )
∴ 该系统为时不变系统。
解：（3） 给 f1(t), f2 (t) 和任意常数 a,b 设f1(t) y1(t), f2 (t) y2 (t) 则: y1(t) 8sin[ f1(t)], y2 (t) 8sin[ f2 (t)]
设 f2 (t) f1(t
dy1(t) dt
ty1(t)
f1(t)
t0y)1d(ty)1,(ydt2则t(tt)：0,)d则yd1(：tt(t)dty0d2)tt(yyt11)((tt)tty02)f(1t()t
) f1
f (t
2 (t) t0
)
比较两式可知 f1(t) y1(t), f1(t t0 ) f2 (t) y2 (t) y1(t t0 )
6.连续时间系统与离散时间系统
如果系统的输入和输出都是时间的连续函数， 这个系统就称为连续时间系统；如果系统的 输入和输出都是时间离散函数，这个系统就 称为离散时间系统。
连续系统中传输和处理的是连续信号。
离散系统中传输和处理的是离散信号。 在实际工作中系统中长将两系统组合使用， 这种情况称为混合系统
则为时不变系统(亦称为非时变系统），否 则为时变系统
所谓时不变系统，就是当输入信号有一 个时移，在输出信号中将产生同样的时移， 而输出波形的形状没有变化。
实际上，系统内的参数如果不随时间变化， 其微分方程的系数全是常数，该系统就具 有时不变的性质，所以，恒定参数系统 （也称定常系统）是时不变系统；反之， 参数随时间变化的系统不具备时不变的性 质时就是时变系统。
（1）分解特性： y(t) yzi (t) yzs (t)
（2）零输入线性： 若 : f1(0) yzi1(t) f2 (0) yzi2 (t) 则：af1(0) bf2 (0) ayzi1(t) byzi2 (t) a,b为任意常数。
（3）零状态线性： 若 : f1(t) yzs1(t) f2 (t) yzs2 (t) 则：af1(t) bf2 (t) ayzs1(t) byzs2 (t) a,b为任意常数。
3.因果系统与非因果系统
系统的输出是由输入引起的，它的输出不能领先 于输入，这种性质称为因果性，这样的系统称为 因果系统。如果系统的输出出现在输入之前，则 为非因果系统。
因果系统的在任何时刻的输出仅取决于是现在与 过去的输入，而与将来的输入无关，因为系统的
输出无法预测将来的输入。
激励是产生响应的原因，响应是激励引起的结果。 所有实际物理系统在激励没有作用之前决不会有 输出响应，都属于因果系统。如果系统的响应出 现在输入之前，则为非因果系统。
(t
)
,
d[by2 dt
(t
)]
t[by2
(t
)]
bf
2
(t
)
二式相加得：
d[ay1
(t
) dt
by2
(t
)]
t[ay1
(t
)
by2
(t
)]
af1
(t
)
bf
2
(t
)
af1(t) bf2 (t) f3 (t) ay1(t) by2 (t) y3 (t)
∴ 该系统为线性系统。
解：（1） 设 f1(t)
满足（1）、（2）、（3）则系统为线性，
有一个不满足则系统为非线性。
2.时变系统与非时变系统
时不变特性是指系统的零输入状态输出波形 仅取决于输入波形与系统特性而与输入信号 接入系统的时间无关。设系统的输入 f (t) ，
输出为 y(t)
若 : f (t) y(t) f (t t0 ) y(t t0 ) t0为任意常数。
关于线性、时变、因果的说明
1. 线性系统与非线性系统
如果系统的输入与输出满足线性关系，则 称为线性系统，否则称为非线性系统。
线性也就是叠加性。它包括两方面的内容：
齐次性（比例性）和可加性。设系统的输入
为 f (t) 输出为 y(t ) 。
若 : f (t) y(t)
（1）奇次性 则：kf (t) ky(t) k为任意常数。
af1(t) bf2 (t) f3(t) y3(t) ay1(t) by2 (t)
∴ 该系统为非线性系统。
解：（3） 设 f2 (t) f1(t t0 ) y2 (t), 则：y2 (t) 8sin[ f2 (t)] y1(t) 8sin[ f1(t)] y1(t t0 ) 8sin[ f1(t t0 )]
把线性电路的初始状态看成等效激励， 则为因果系统。
设系统的输入（激励）为 f (t)（含等效
激励），输出（响应）为 y(t)
则因果和非因果系统可分别表示为：
f (t) tt0 y(t) tt0 0 (因果系统)
f (t) tt0 y(t) tt0 0 (非因果系统)
4. 记忆系统与非记忆系统
则为线性系统，否则为非线性系统
一般由线性元件组成的系统均为线性系统， 但并不是含有非线性元件的系统就一定是 非线性系统，有些含有非线性元件的系统 在一定的条件下也具有线性特征。判别的 标准是上述定义。奇次性和可加性有一个 不满足，系统就是非线性的。
当系统的初始状态不为零时，该系统的 线性条件具体反映在以下三方面
则：dy3(t) 3 df3(t)
dt
dt
dy1(t) 3 df1(t) , dy2 (t) 3 df2 (t)
dt
dt dt
dt
d[ay1(t)] 3 d[af1(t)] , d[by2 (t)] 3 d[bf2 (t)]
dt
dt
dt
dt
二式相加得： d[ay1(t) by2 (t)] 3 d[af1(t) bf2 (t)]
dt
dt
af1(t) bf2 (t) f3(t) ay1(t) by2 (t) y3(t)
∴ 该系统为线性系统。