半导体器件原理 第二章.2
半导体物理学第二章

电离能的大小:
• 硅中掺磷为0.044,掺硼为0.045(eV)。 • 锗中掺磷为0.0126,掺硼为0.01(eV)。 • 这种电离能很小,杂质可以在很低的温度下电离。故称之 为“浅能级杂质”,在室温几乎全部电离。 • 杂质能级用短线表示,因杂质浓度与硅相比很低,杂质原 子相互之间几乎无作用,杂质能级相同,量子的排斥原理 对低浓度的杂质掺杂不起作用。
•
h 0 0 . 53 氢原子玻尔轨道半径为 r0 Å, 2 q m0 * 根据杂质类氢模型将 r 0 代替 0 ,以 mn 代
2
替m0 ,可得杂质等效玻尔半径
,
h r 0 r 2 * q mn
2
0 r h m0 r 2 * r * r0 q mn mn
• 中性Au0为与周围四个Ge原子形成共价键,还可以依次由价带
再接受三个电子,分别形成EA1,EA2,EA3三个受主能级。价 带激发一个电子给Au0,使之成为单重电受主离化态Au-,电离 能为EA1-Ev ;从价带再激发一个电子给Au-使之成为二重电受 主离化态 Au= ,所需能量为EA2-Ev;从价带激发第三个电子给
杂质在GaAs中的位置
间隙式 替 族原子 替位式替V族原子
替代Ⅲ族时,周围是四个Ⅴ 族原子 替代Ⅴ族时,周围是四个Ⅲ 族原子
• IV族元素碳、硅、锗等掺入III-V族化合物中,若取代III族 元素起施主作用;若取代V族元素起受主作用。总效果是 施主还是受主与掺杂条件有关。
半导体的掺杂
受主:掺入在半导体中的杂质原子,能够向半导体中提供导电的空穴, 并成为带负电的离子。如Si中的B
EC
B
EA
EA EV
P型半导体
受主能级
第二章 半导体二极管及其应用

0
图2-12 双向限幅电路
开关作用 电子开关电路。在自动化控制电路和数字电路中有广泛地应 用。电子开关比机械开关的开关速度快得多,可达一秒钟上万 次,且无触点的颤动引起的火花,安全可靠。 图2-13所示的两个电路。
我们将在下一节详细讨论。
2. 检波 通常,无线电波中含有复杂的多种频率成分, 调幅收音机必须从中挑选出需要的音频信号, 为此要设置检波电路。半导体二极管检波电 路如图2-11所示。其中VD是检波二极管,C1 是高频滤波电容,R是检波电路负载电阻, C2是与下一级电路的耦合电容。
ui 调频 信号 VD C1
N型半导体和 P 型半导体
在本征半导体中掺入微量的杂质(某种元素), 形成杂质半导体。 在常温下即可 变为自由电子 掺入五价元素 掺杂后自由电子数目 Si Si 多 余 大量增加,自由电子导电 电 成为这种半导体的主要导 S p+ Si 子 电方式,称为电子半导体 i 动画 或N型半导体。 失去一个 电子变为 正离子 磷原子 在N 型半导体中自由电子 是多数载流子,空穴是少数 载流子。
二极管电路定性分析
导通 截止 若二极管是理想的,正向导通时正向管压降为零, 反向截止时二极管相当于断开。
定性分析:判断二极管的工作状态
否则,正向管压降
硅0.6~0.7V 锗0.2~0.3V
分析方法:将二极管断开,分析二极管两端电位 的高低或所加电压UD的正负。 若 V阳 >V阴或 UD为正( 正向偏置 ),二极管导通 若 V阳 <V阴或 UD为负( 反向偏置 ),二极管截止
N型半导体和 P 型半导体
第二章半导体材料的基本性质

第二章半导体材料的基本性质半导体材料是一类介于导体和绝缘体之间的材料,具有独特的电学性质和光学性质,广泛应用于电子器件和光电器件中。
本文将从电学性质和光学性质两个方面介绍半导体材料的基本性质。
一、电学性质1.带隙:半导体材料具有带隙,即价带和导带之间的能隙。
在绝缘体中,带隙较大,电子不易通过;在导体中,带隙为零,电子容易通过。
而在半导体中,带隙较小,介于绝缘体和导体之间,可以通过掺杂和加电场的方式改变其电导性能。
2.载流子:在半导体中,电子和空穴是载流子。
在纯净的半导体中,电子和空穴的数量相等,即n型和p型半导体中电子和空穴的浓度相等。
而在掺杂半导体中,通过掺杂可以使电子或空穴的浓度增加,从而改变其电导性质。
3.本征导电性:半导体材料在纯净状态下呈现本征导电性,即电导率较低。
本征导电性是由于半导体中的有限数量的载流子引起的。
n型半导体中主要是电子导电,p型半导体中主要是空穴导电。
本征导电性可以通过掺杂来改变。
4.外加电场下的导电性:在外加电场的作用下,半导体材料的导电性能发生变化。
当正电荷提供给半导体,将推动电子向正极移动,此时半导体变为n型半导体;当负电荷提供给半导体,将推动空穴向负极移动,此时半导体变为p型半导体。
这种现象被称为电场效应,也是半导体中众多器件如二极管和晶体管的基础。
二、光学性质1.吸收:半导体材料具有宽带隙能够吸收光的性质。
当光射入半导体中,部分光能会被电子吸收,使电子从价带跃迁到导带,此时光的能量将转化为电子的动能。
不同的半导体材料对不同波长的光吸收能力不同,这种特性使半导体材料成为光电器件的重要组成部分。
2.发光:除了吸收光能,有些半导体材料还可以发光。
当电子从导带跃迁到价带时,会释放出能量,部分能量以光的形式散发出来,形成发光现象。
不同的半导体材料对应不同的发光颜色,从红光到紫光等都可以通过不同材料的跃迁产生。
3.光电效应:半导体材料的光电效应是指当光照射到半导体表面时,会产生电流。
半导体器件原理和工艺2

半导体器件
晶体管的频率特性---小信号模型
▪ 小信号工作条件:
➢ 输入信号电压以及输出信号电压都远小于热电压 (kT/q)
vBE VBE vbe iC IC ic
半导体器件
小信号模型-1
i1
i2
v1
T
v2
短路输入导纳 短路反向跨导纳
短路正向跨导纳 短路输出导纳
半导体器件
h参数 短路输入阻抗
小信号模型-2
短路正向电流传输系 数、即电流增益
开路反向电压传输系 数,即电压反馈系致
半导体器件
开路输出导纳
小信号模型-3
共发射极h参数等效电路
b vbe
c vce e
半导体器件
小信号等效电路
▪ 混合模型
g
-g
gm
go
由E-M方程:
正向有源区
半导体器件
混合模型-1
▪ 跨导gm
1. gm正比于Ic,反比于T。 2. gm只决定于工作电流及工作温度,与器件所用材
半导体器件
Bardeen, Brattain, and Schockley 获1956年诺贝尔物理奖
晶体管的特性
半导体器件
半导体器件
理想NPN掺杂分布
▪ 集电结外延, 发射结离子 注入
eb
半导体器件
c
晶体管的静电特性
▪ 两个独立的PN结构成
N+
P
N
半导体器件
背靠背二极管
半导体器件
工作原理
半导体器件
特征频率和截止频率
▪ 特征频率fT和截止频率f 是根据hFE随频率的变化 关系定义的
半导体器件
特征频率和截止频率-1
第2章半导体器件习题答案
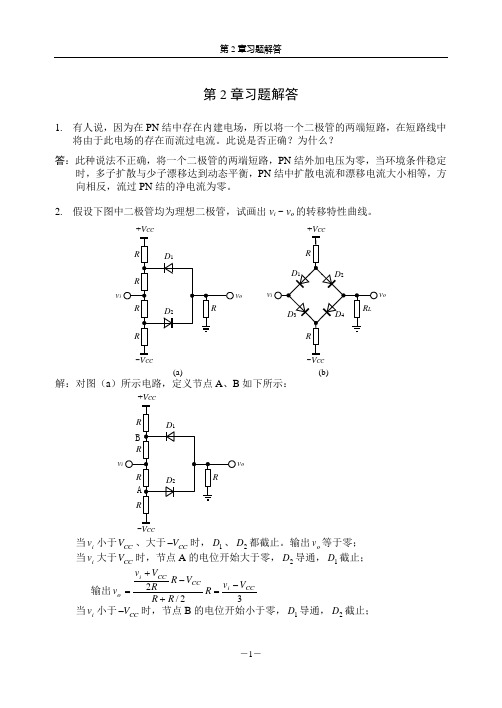
第2章习题解答1. 有人说,因为在PN 结中存在内建电场,所以将一个二极管的两端短路,在短路线中将由于此电场的存在而流过电流。
此说是否正确?为什么? 答:此种说法不正确,将一个二极管的两端短路,PN 结外加电压为零,当环境条件稳定时,多子扩散与少子漂移达到动态平衡,PN 结中扩散电流和漂移电流大小相等,方向相反,流过PN 结的净电流为零。
2. 假设下图中二极管均为理想二极管,试画出v i ~ v o 的转移特性曲线。
+V CC CCv iv oCC CCv v o(a) (b)解:对图(a )所示电路,定义节点A 、B 如下所示:+V CC CCv iv o当i v 小于CC V 、大于CC V -时,1D 、2D 都截止。
输出o v 等于零; 当i v 大于CC V 时,节点A 的电位开始大于零,2D 导通,1D 截止;输出32/2CC i CCCCi o V v R R R V R R V v v -=+-+=当i v 小于CC V -时,节点B 的电位开始小于零,1D 导通,2D 截止;输出32/2CC i iiCC o V v R R R v R R v V v +=++-=图(b )所示电路是一个双向限幅电路,输出正向限幅电压为:L LCCR R R V +,输出负向限幅电压为:L LCCR R R V +-当L L CC i R R R V v +≤时,输入与输出相同,当L L CC i R R R V v +>时,输出限幅在LLCC R R R V+-和L LCCR R R V + 两个电平上。
3. 下图是一种二极管整流电路,称为全波整流电路。
其中v 1 = v 2。
试分析它的工作原理,画出输出电压的波形并计算输出电压的平均值。
解:在输入信号的正半周,D 1导通、D 2截止,在输入信号的负半周, D 2导通、D 1截止,输入信号与输出的关系为:tωVVtω输出电压的平均值为:12sin()()om omV t d t Vπωωππ=⎰4.下图也是一种二极管整流电路,称为桥式整流电路。
半导体物理器件Chapter2-

势垒高度增加至 q(y0 VR) ,增高的势垒阻挡载流子通过PN结扩散,通
过PN结的电流非常小,结的阻抗很高。耗尽层宽度(突变结):
1
W
2k0
y0 VR
qNd
2
(2-23)
PN结
2.2加偏压的PN结
4)根据能带图和修正欧姆定律分析结的单向导电性
在电子扩散区和空穴扩散区,
区间电势差 y 0 。
未形成PN结之前的N区(P区)的电子(空穴)浓度为:
nN dnie(E F nE i)/K T
pNani(EiEFp)/KT
可以得到分别的费米能级为:
EFnEi
KTlnNd ni
EFp
Ei
KTln
Na ni
再由热电势
VT
KT q
,得: y01 q(EFnEFp)VTlnNn diN 2a
耗尽区
n 型电中性区
(c) 与(b)相对应的空间电荷分布
PN结
2.1热平衡PN结
3.几个概念
耗尽近似:在空间电荷区,与电离杂质浓度相比,自由
载流子浓度可以忽略,这种近似称为耗尽近似。因此空间电 荷区也称为耗尽区(又称为耗尽层)。在完全耗尽的区域, 自由载流子密度为零。
中性近似:假设耗尽区以外,在杂质饱和电离情况下,
单边突变结(一侧的杂质浓度远远大于另一侧的质浓度的突变结)
PN结
NaNd
引言
4.突变结与线性缓变结 2)线性缓变结: 两区之间杂质过渡是渐变的
adNDNA常数
dx
- ax
xj 0
x
ND NA
0
x
在线性区: N(x)a(xxj)
第二章半导体三极管与分立元件放大电路

IC IB
IE(1)IB
三、三极管的电流放大作用
(1)三极管的电流放大作用就是基极电流IB的微小变化控 制了集电极电流IC较大的变化。
(2)三极管放大电流时,被放大的IC是由电源VCC提供 的,并不是三极管自身生成的,放大的实质是小信号对大信 号的控制作用。
(3)三极管是一种电流控制器件。
UB
Rb 2V CC Rb1 Rb2
若电路满足I1≥(5~10)IB,UB≥(5~10)UBE由上式可知, UB由Rb1、Rb2分压而定,与温度变化基本无关。
如果温度升高使IC增大,则IE增大,发射极电位UE=IERe升 高,结果使UBE=UB-UE减小,IB相应减小,从而限制了IC的增 大,使IC基本保持不变。上述稳定工作点的过程可表示为
这个值时,放大性能下降或损坏管子。
(2)反向击穿电压(Reverse breakdown voltage) U(BR)CBO : 发射极开路时,集电极-基极之间允许施加的最高 反向电压,超过此值,集电结发生反向击穿。 U(BR)EBO : 集电极开路时,发射极-基极之间允许施加的最高反 向电压。 U(BR)CEO:基极开路时,集电极与发射极之间所能承受的最高反 向电压。为可靠工作,使用时VCC取U(BR)CEO的1/2或2/3。在输出特 性曲线中,iB=0的曲线开始急剧上翘所对应的电压即为U(BR)CEO , 其值比U(BR)CBO小。T↑,U(BR)↓。
图(b)的电路,由于C1的隔断直流作用,VCC不能通过Rb 使管子的发射结正偏即发射结零偏,因此三极管不工作在放大 区,无放大作用。
2.2.4 共射基本电路的静态工作点
一般,三极管的UBE可视为已知量,硅管│UBE│取0.7V, 锗管│UBE│取0.2V,VCC>>UBE。
功率半导体器件工作原理

邮编:412001TEL : ( 0733) 8498396 URL : 功率半导体器件工作原理1.基本开关过程:功率半导体器件除极少数特殊应用情况外,其余绝大多数都是应用在开关状态下。
应用在所有这些电力电子线路总的器件,它们的基本原理和工作方式都是相同的,我们所有对半导体器件和应用电力电子线路的研究,都是要使其尽可能的工作在低损耗状态。
也就是说应使器件工作在开关状态。
这是因为器件工作在开关状态时,其工作状态是最佳的,通态损耗是最小的。
大家知道,当一个器件在开关状态时,它具有这样的特性: ―导通状态:V =0,-∞<i <∞。
―关断状态: i =0,-∞<V <∞。
功率半导体器件虽然同是工作在开关状态,当其使用状态不同时,他们表现出不同的特性。
当晶闸管和电感一起组成一个回路时,开关可以主动地开通。
也就是说,它能够在任一时刻开通。
当开通时间趋进于零时,开关中不出现损耗,这主要是因为回路电感能够立即吸收所出现的电压差。
导通状态:v s =0;-∞<i s <∞; 关断状态:i s =0;-∞<v s <∞; 开关特性:当s v >0时,主动开通;当i s =0,被动关断2.功率半导体器件基本工作原理功率半导体器件它包括非常多的品种和类别,在这里我们主要介绍晶闸管的结构和工作原理。
晶闸管时具有PNPN 结构的半导体器件,见图1-1。
在阳极P 区和阴极N 区之间施加正向电压时,它具有阻断和导通两个稳定的工作状态。
由图1-2所示的电流-电压特性曲线可以看出,它有一个阻断区和一个导通区。
这一特性可以用于电流的接通和关断。
为了使晶闸管由阻断状态变为动态状态,必须使其电流增加到超过某个阈值。
要实现这个目标,通常我们有两种途径,其一,使用脉冲电流使其通过门极而加于两个中间区的一个来实现。
其二,不断的提高阳极电压,使其超过转折电压(UBO )。
邮编:412001TEL : ( 0733) 8498396 URL :图1-1(a )不加门极电流 (b )加门极电流I G >IGT 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
PN结在正向电压下电流很大,在反向电压下电流很小,这 说明PN结具有单向导电性,可作为二极管使用。
PN 结二极管的符号为:
本节主要讨论:
+
P区 N区
1、中性区与耗尽区边界处的少子的浓度与外加电压的关系。 这将被用做求解微分方程的边界条件。
2、PN 结耗尽区以外的两侧中性区内的少子浓度分布。
3、PN 结的正向电流。
1、正向电压下载流子的运动情况
外加正向电压V 后,PN结势垒高度由 qVbi 降为 qVbi V ,
xd 与 max 均减小,使扩散电流大于漂移电流,形成净的正向电
流。
外加电场
内建电场
P
N
平衡时
外加正向电压时
面积为Vbi 面积为Vbi -V
0
x
由于正向电流的来源是N 区电子和P 区空穴,他们都是 多子,所以正向电流很大。
正向电流密度由三部分组成:
1、空穴扩散电流密度:Jdp (推导在N 区中进行)。 2、电子扩散电流密度:Jdn (推导在P区中进行)。 3、势垒区复合电流密度:Jr (推导在势垒区中进行)。
P区
J
J dp N区
Jdp Jdn Jr
J dn
xp
Jr
0 xn
V
2、中性区与耗尽区边界的少子浓度与外加电压的关系 本小节所得的结果不仅可作为求解方程时所需的 边界条件,
4、势垒区复合电流
xn
J r
q
Rdx
xp
上式中净复合率 R 可近似表为:
R
np ni2
(n p 2ni )
已知在中性区里有:
n
R
n
p
p
(P区内) ( N区内)
在势垒区中,已知平衡时有:
no x po x ni2
当外加电压 V 时:
可见:
nx
px
ni2
exp qV kT Nhomakorabeapn ( x)
pno
exp
qV kT
1
exp
x
xn Lp
,
(x xn)
P区内的非平衡少子电子也有类似的分布:
np x
n po
exp
qV kT
1
exp
x
xp Ln
,
x xp
正向时PN结中的少子分布图:
np xp
n po
exp
qV kT
P区
pn xn
pno
exp
xn
J r
q
Rdx
xp
q R xd
qni xd
exp qV kT
1
2 exp qV 1
2kT
当 V = 0 时: J r 0
当V
>> kT / q 时: J r
qni xd
2
exp
qV 2kT
5、正向伏安特性与导通电压
为10μm 。 扩散方程的通解为:
pn
(x)
Aexp
x Lp
B
exp
x Lp
假设N区足够长 ( >> Lp ),则 pn ( x)的边界条件为:
pn ( xn )
pno
exp
qV kT
1,
pn x 0
利用此边界条件可解出系数 A、B ,于是可得N 区内的非 平衡少子空穴的分布为:
qV kT
1
总的PN 结扩散电流密度 Jd 为:
Jd
J dp
J dn
q
Dn Ln
n po
Dp Lp
pno
exp
qV kT
1
Jo
exp
qV kT
1
当 V 0 时, J d 0 ,
当
V kT q
( 室温时约为26 mV ) 时, J d
Jo
exp
qV kT
上式中:
Jo
q
Dp Lp
n po
exp
qV kT
,
pn x pno n p x n po
或对于非平衡少子,其边界条件为:
pn xn
pno
exp
qV kT
1,
np xp
n po
exp
qV kT
1,
pn x 0 np x 0
3、正向扩散电流
求扩散电流的步骤:以突变PN结的 Jdp 为例,先利用扩散
方程并结合边界条件求出N区内的非平衡少子分布 pn x ,再
qV kT
N区
n po
xp xn
pno x
假设中性区内无电场,故可略去空穴电流密度方程中的漂移
分量,将上面求得的 pn ( x) 代入后,得:
J dp
qD p
dpn dx
x xn
qDp pno Lp
exp
qV kT
1
同理可得P区内的电子扩散电流为:
J dn
qDnn po Ln
exp
当 V > 0 时,np > ni2 ,R > 0 , 发生净复合。 当 V < 0 时,np < ni2 ,R < 0 , 发生净产生。
为简化计算,可假设在势垒区中 n 与 p 相等,且不随 x
而变化。即:
n
p
ni
exp qV 2kT
R
ni
exp
qV kT
1
,
2
exp
qV 2kT
1
而且在其他章节也有很重要的用途。 已知在平衡PN结耗尽区两侧边界上的空穴浓度有如下关系:
pno
p po
exp
qVbi kT
当外加电压 V 后: Vbi Vbi V
pno pn pno pn
p po p p p po p p
从而得:
pn
pp
exp
q(Vbi kT
V
)
pp
exp
以上两式说明:当 PN 结有外加电压V 时,在小注入条件 下,中性区与耗尽区边界处的少子浓度等于平衡时的少子浓度 乘以 exp ( qV/kT ) 。上式对正、反向电压均适用。
假设中性区的长度远大于少子扩散长度,则可得 少子浓度 的边界条件:
pn xn
pno
exp qV kT
,
np xp
pno
Dn Ln
npo
qni2
Dp Lp N D
Dn Ln N A
对 Jo 的讨论: 与材料种类的关系: EG ↑,则 ni ↓,Jo ↓ 。 与掺杂浓度的关系: ND 、NA ↑,则 pno 、npo ↓,Jo ↓ (主要取决于低掺杂一侧的掺杂浓度)。 与温度的关系: T ↑,则 ni ↑,Jo ↑。
qVbi kT
exp
qV kT
在小注入条件下,p p p po , p p p po ,因而在N 型区与
耗尽区的边界处,即在 xn 处有:
pn
p po
exp
qVbi kT
exp qV kT
pno
exp
qV kT
同理,在 - xp 处有:
np
n po
exp qV kT
将其代入空穴电流密度方程中。
P 求 Jdn
N 求 Jdp
已知N区中的空穴扩散方程为:
pn t
Dp
2 pn x 2
R
将R 写作 R pn ; 直流情况下, pn 0 ;又因 2 pno 0 ,
故可得:
p
t
x 2
Dp
d 2pn dx 2
pn
p
0
d 2pn dx 2
pn L2p
上式中,Lp Dp p ,称为空穴的 扩散长度,其典型值
