第二章 PN结
第2章_PN结机理与特性

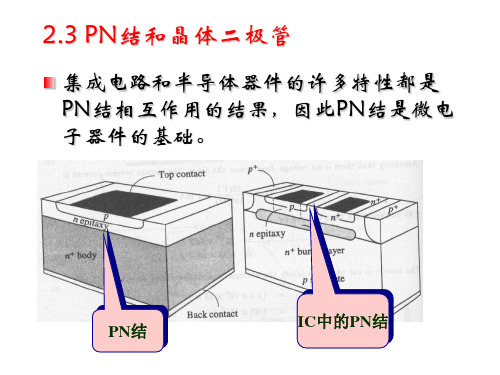
PN结隧道击穿示意图
雪崩击穿
雪崩击穿示意图
2.5.2 PN结雪崩击穿电压
雪崩击穿条件
∫
Xm
0
α eff dx = 1
单边突变结的雪崩击穿电压
1ε ε UB = S 0 2 q
3/4
8 Ci
−3/4 ND
线性缓变结的雪崩击穿电压
ε ε 2 6.29 −1/5 4 U B = S 0 qa j 3 Ci
第二章 PN结机理与特性
2.1 平衡PN结的机理与特性
2.1.1 PN结的制备与杂质分布
在N型(或P型)半导体单晶片衬底上,分别采用不同的 掺杂方法,使原来半导体的一部分变成P型,(或N 型),那么在P型半导体与N型半导体的交界面处就形 成了PN结,如图
合金法及其杂质分布 合金法制备PN结的基本过程如图所示
平衡PN结载流子浓度分布 a) U(x)分布 b)能带 c)载流子浓 度分布
2.2 正向PN结机理与特性
2.2.1 正向偏置与正向注入效应
正向偏置时PN结势垒变化及其能带图
2.2.2 正向PN结边界少子浓度和少子浓度 分布
1.边界少子浓度
正向PN结少子浓度分布示意图
边界少子浓度是指在空间电荷区靠N区边界XN处的空穴 浓度p(XN)和靠近P区边界XP处的电子浓度n(XP)。
平衡PN结费米能级时处处相等的(证明见教材)
2.1.3 平衡PN结的接触电势差
由于平衡PN结空间电荷区内存在自建电场, 使得N区和P区之间存在电势差,把这个电势 差称为PN结的接触电势差,用UD表示。
ND N A UD = ln q ni2
κT
2.1.4 平衡PN结的载流子浓度分布
第二章 p-n结

d 2ψ qN D =− 2 dx εs
0 < x ≤ xn
半导体的总电荷中性要求p侧每单位面积总负空间电荷必须 精确地和n侧每单位面积总正空间电荷相同:
N A x p = N D xn
总耗尽层宽度W即为
W = x p + xn
由
耗尽区 d ψ qN
2
dx
2
=
εs
A
− xp ≤ x < 0 和
d 2ψ qN =− D dx 2 εs
静 电 势 Ψ 电 子 势 能 Ei qψ p
qψ a qVbi EC EF Ei EV
(b) 在热平衡下突变结的能带图
Ei − E F p = ni exp( ) kT kT NA 1 ψ p ≡ − ( Ei − EF ) x≤− x p = − ln( ) 得到 q q ni
同理,可得n型中性区相对于费米能级的静电势为
热平衡状态下的p-n结
1 kT ND ψ n ≡ − ( Ei − EF ) x≥ xn = ln( ) q q ni
由上二式可计算出在不同掺杂浓度时,硅和砷化镓的 ψ p 和ψn 值的大小,如图所示.对于一给定掺杂的浓度,因为砷化镓有 较小的本征浓度,其静电势较高. 0.8
Ψ p 或Ψn / V
在热平衡时,p型和n型中性 区的总静电势差即为内建电 势Vbi
E ( x ) = − Em + qN D x
− xp ≤ x < 0
0 < x ≤ xn
εs
=
qN D
εs
( x − xn )
对耗尽区积分,可得到总电势变化,此即内建电势Vbi:
Vbi = −∫ E( x)dx = − ∫ E( x)dx
第2章 PN结

T 300K
对于锗PN结,通常可取VD=0.3—0.4V
对于硅PN结,通常可取 VD=0.6—0.7V
23
2.1.2 PN结的形成过程
扩散法制造PN结过程
N P
N-Si P-Si
杂 质 浓 度
ND -NA
PN结两边的杂质浓度是非均匀的 常按照一定的函数规律而变化。
xj
x
在一块N型硅片上用化学方法涂敷一层含有Al2O3的乙醇 溶液,在红外线灯下干燥后,置于1250℃的扩散炉中进行高 温处理若干小时,然后缓慢降温。 24
35
2.1.3平衡PN结的载流子浓度分布
平衡PN结势垒区两侧载流子浓度 Eip Ein qVD nn 0 exp P区电子浓度 n p 0 nn 0 exp kT kT
qVD N区空穴浓度 pn 0 p p 0 exp kT
空间电荷不能移动,也不能传导电流。
10
一、空间电荷区的形成
2.1.1 平衡PN结能带图
内建电场E内: 空间电荷所产生的电场, 此电场不是由外部因素引起的,而是由PN结内部 载流子运动形成的,由N区指向P区。
PN结的内建电势(接触电势)VD 由内建电场所导致的N区和P区的电位差。
11
平衡PN结能带图
ND N A
杂 质 浓 度
2.1.2 PN结的形成过程
杂 质 浓 度
ND -NA
xj
x
0
x
xj
dN ( x) a j dx
x x j
ND N A a j x x j
x
26
缓变结
A.线性缓变结近似
第2章_PN结
kT dn 由爱因斯坦关系 可得 Edx q n
kT 上式在整个势垒区积分 Edx xp q
xn
E
dV dx
n xn kT kT nn 0 V xn V x p ln ln q np0 n xp q
V xn V x p VD N D nn 0 N A p p0
第2章 PN 结
1
第2章 PN 结
PN 结是构成各种半导体器件的基本单元。 PN结中的载流子既有漂移运动,又有扩散运动; 既有产生,又有复合,这些性质集中反映在半导体 的导电特性中。
P区 NA
N区 ND
2
第2章 PN 结
1、PN 结的形成
在同一块N型(或P型)半导体单晶上,用特定 的工艺方法把P型(或N型)杂质掺入其中,使这块 单晶相连的二个不同区域分别具有N型区和P型区的 导电类型,在二者交界面以及交界面两侧的过渡区 即称为PN结。
40
(4)玻尔兹曼边界条件
即在势垒区两端,载流子分布满足玻尔兹曼分布。
(5)忽略半导体表面对电流的影响。
(6)只考虑一维情况。
41
理想PN结的伏安特性
正向偏压V>0时,P区边界-xp处的非平衡少子浓度
qV qVD qV n p x p n p 0 exp nn 0 exp kT kT P区边界 x x p 处的过剩载流子浓度
(1)小注入条件
满足下列条件的PN结)
即注入的非平衡少子浓度比平衡多子浓度小得多;
(2)耗尽层近似
即外加电压都降落在耗尽层(势垒区)上,耗尽层 以外的半导体是电中性的,因此注入的少子在 P区 和N区只作扩散运动;
最新第二章-PN结

漂移电流大于扩散电
-
内电场
外电场 U
+
流,可忽略扩散电流
UB+U 在一定的温度条件下,
由本征激发决定的少
E
R
子浓度是一定的
故少子形成 的漂移电流是恒定的,基本上与所加反向 电压的大小无关,这个电流也称为 反向饱和电流IS。
《半导体器件》中国计量学院光电学院
综上所述:PN结加正向电压时,呈现低 电阻,具有较大的正向扩散电流;PN结加反 向电压时,呈现高电阻,具有很小的反向漂 移电流。 即PN结具有单向导电特性。
第二章-PN结
一、PN结的形成 二、PN结的单向导电性 三、PN结的击穿特性 四、PN结的电容效应 五、 PN结的隧道效应
《半导体器件》中国计量学院光电学院
P型半导体和N型半导体相结合——PN结
PN结是构造半导体器件的基本单元。其 中,最简单的晶体二极管就是由PN结构 成的。
PN
异质结、同质结
《半导体器件》中国计量学院光电学院
发生击穿并不一定意味着PN结被损坏。 当PN结反向击穿时, 只要注意控制反向
电流的数值(一般通过串接电阻R实现),
不使其过大, 以免因过热而烧坏PN结, 当反向电压(绝对值)降低时, PN结的性 能就可以恢复正常。 稳压二极管正是利用了PN结的反向击 穿特性来实现稳压的, 当流过PN结的电 流变化时, 结电压基本保持不变。
关键在于耗尽层的存在
《半导体器件》中国计量学院光电学院
PN结的伏安特性
UD
I
伏安特性方程 ID IS(eUT 1)
ID
UBR U B
O
U
加正向电压时,UD只要大
于UT几倍以上,IDISeUD/UT
第2章_2_PN结
2.反向偏压作用 2.反向偏压作用
外加偏压几乎全落在空 间电荷区上. 间电荷区上.方向与空间 电荷区内建电场一致, 电荷区内建电场一致,使 空间电荷区变宽,相应 势垒高度也由qV 势垒高度也由qVD增至 q(VD+V)。 +V)。 由于电场增强,加强了 载流子的漂移运动,打 破了原先已达成的扩散 电流和漂移运动之间的 平衡。
2.3.4 pn结电容 pn结电容
PN结在交流条件下呈现出电容效应,限制了PN PN结在交流条件下呈现出电容效应,限制了PN 结的高频应用。
1. pn结势垒电容 pn结势垒电容
(1)pn结势垒电容定性分析 pn结势垒电容定性分析 随着外界电压的变化,出现了载流子电荷在势垒 区中的存入和取出,此现象相当于一个电容的充 放电。这种与势垒区相联系的电容称为势垒电容, 记为C 记为CT。势垒电容大小与结上所加直流偏压有关, 是一个可变电容。 dQ CT = dV
由于少子浓度很低,扩散长度为一定值, 所以当反偏时空间电荷区边界处少子梯度 较小,相应的反向电流也小。 当反向电压很大时,空间电荷区边界处少 子浓度趋于零后不再变化,该处少子浓度 梯度趋于常数,电流就基本保持不变。 所以PN结反偏时表现为电流较小,而且随 所以PN结反偏时表现为电流较小,而且随 外加电压的增加电流趋于饱和。
I = A(
qDnnp0 Ln
qDPP 0 kT n + )(e −1) = IS (ek pn结饱和电流 Np0和pn0分别为P区和N区平衡时的少子电子浓度和 分别为P区和N 少子空穴浓度。 Ln 和 Lp分别为电子和空穴的扩散长度。
Ln = Dnτ n
PN结在平衡状态下,在N型半导体中电子是多子, PN结在平衡状态下,在N 空穴是少子,在P 空穴是少子,在P型半导体中空穴是多子,电子 是少子 当形成PN结后,其交界面两侧的电子和空穴浓度 当形成PN结后,其交界面两侧的电子和空穴浓度 存在较大差异,这就导致P型区的空穴向N 存在较大差异,这就导致P型区的空穴向N型区扩 散,N型区的电子向P型区扩散。P 散,N型区的电子向P型区扩散。P区边界处因只 剩下失去了空穴的离化受主杂质而带负电,N 剩下失去了空穴的离化受主杂质而带负电,N区 边界处因只剩下失去了电子的离化施主杂质而带 正电,这些离化的杂质位于晶格之中不能运动, 它们就在P 它们就在P 结附近形成了一个带电区域,称为空 间电荷区。
第二章PN结资料

2.4 空间电荷区的复合电流和产生电流
• 低偏压:空间电荷区的复合电流占优势 • 偏压升高: 扩散电流占优势 • 更高偏压: 串联电阻的影响
I (A)
103
串联电阻
实验数据 104
105
106
107
斜率 q KT
108
109
斜率 q
2 KT
1 0 10 0.1 0.2 0.3 0.4 0.5 0.6 0.7
• 由于这个原因,也把空间电 荷区称为势垒区。
3.耗尽层 -突变结
• 突变结势垒中的电场、电势分布 • 耗尽层近似:在空间电荷区中,与电离杂质浓度相比,自由载流子浓度
可以忽略,这称为耗尽近似。 • 杂质完全电离:
• 在N侧和P侧泊松方程可以分别简化为:
d dx22 qN D0xxn d dx22 qN A0xxn
0
•
边界条件: pnxpn0 pn0expV V T1
xW n xxn
pnxpn0AexpL xpBexpL xp
A pn0 exp k q 0 V T 1 exp L xn p pn0 exp V V T 1 exp L xn p B0
p n x p n 0 p n 0 e x p V V T 1 e x p x n L p x x x n
I0expV V T1
Shockley方程
•
正向偏压:
I
I0
exp
V VT
• 反向偏压: I I 0 • I0称为饱和电流
• 正向偏压情况下的PN结
载流子浓度
P型
np pn0
N型 pn pn0
空间电荷层
xp 0 xn
x
(a)少数载流子分布
半导体第2章PN结总结

1. PN 结:由P 型半导体和N 型半导体实现冶金学接触(原子级接触)所形成的结构。
任何两种物质(绝缘体除外)的冶金学接触都称为结(junction ),W 时也叫做接触(contact )«2・PN 结是几乎所有半导体器件的基本单元。
除金属一半导体接触器件外,所有结型器件都 由PN 结构成匚3. 按照杂质浓度分布,PN 结分为突变结和线性缓变结.内建电场PFN%空间电荷区4. 空间电荷区:PN 结中,电子由N 区转移至P 区,空穴由P 区转移至N 区。
电子和空穴 的转移分别在N 区和P 区留下了未被补偿的施主藹子和受主离子。
它们是荷电的、固沱不 动的,称为空间电荷。
空间电荷存在的区域称为空间电荷区。
线性缓变结杂质分布XP 区留下N 区留下N ;,形成空间电荷区。
空间电荷 区产生的电场称为内建电场,方向为由N 区指向P 区。
电场的 存在会引起漂移电流,方向为由N 区指向P 区。
扩散电流,P 区—N 区 漂移电流:P 区—N 区达到平衡时,净电流=0。
于是就形成一个稳定的有一定 宽度的空间电荷区。
5. 内建电场:P 区和N 区的空间电荷之间建立了一个电场——空间电荷区电场,也叫内建 电场。
PN 结自建电场:在空间电荷区产生缓变基区自建电场:基区掺杂是不均匀的,产生出一个加速少数载流子运动的电场,电场沿 杂质浓度增加的方向,有助于电子在大部分基区范用内输运。
大注入内建电场:在空穴扩散区(这有利于提髙BJT 的电流增益和频率.速度性能)。
6. 内建电势差:由于内建电场,空间电荷区两侧存在电势差,这个电势差叫做内建电势差7. 费米能级:平衡PN结有统一的费米能级。
空穴扩散:P 区 一 N 区 电子扩散:P 区—N 区扩散电流方向为:P 区一N 区■% 0 ------ 1 ----------•—Z 一 W — ++ ++++ +++$空间电蓟区 中性区!1 1' ;'内雄电场\ ・ 空穴扩飆 甌『扩R 漁II空穴漂移流 电子漂核ft“(gpa)g 自建电场方向i 结空司电荷区处別空穴扩融区內大主入自注电场的形呢(用1%表示九逮掺杂p 型轻掺杂p 裂 本征准费米能级:当pn 结加上外加电压V后,在扩散区和势垒区范I 羽内,电子和空穴没有统 一的费米能级,分别用准费米能级.8. PN 结能带图 热平衡能带图平衡能带图非平衡能带图正偏压:P 正N 负 反偏压:P 负N 正J -P~L轻掺杂N 型重摻杂N 型P n(a)在接触前分开的P 型和N 型硅的能带图耗尽层(E)正偏反偏9.空间电荷区、耗尽区.势垒区・中性区势垒区:N区电子进入P区需要克服势垒g% ,P区空穴进入N区也需要克服势垒g必。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
半导体特征长度,德拜长度
LD =
(19)
ε s kT
q NB
2
=
qN B β
εs
能有效屏蔽外场的电 荷分布范围宽度
(20)
Si的德拜长度与掺杂浓度的关系
Si单边突变结耗尽层宽度和单位面积耗尽层电容 与掺杂浓度的关系。
W =
2ε s (Vbi ± V ) qN B
(21)
6) 耗尽层电容: 单位面积的耗尽层电容定义为: 单边突变结,单位面积电容:
5) 能带,载流子浓度: 内建势与载流子浓度间的关系:
qVbi = E g − (qVn + qV p )
NC NV N C NV ) − [kT ln( ) + kT ln( )] = kT ln( 2 nn 0 Pp 0 ni nn0 p p0 N AND = kT ln( ) ≈ kT ln( ) 2 2 ni ni
x V ( x) = Em ( x − ) 2W
2
0 ≤ x ≤ xn
内建势
V bi = V ( x n ) − V ( − x p )
电场对应的面积 (1)
1 1 Vbi = E mW ≡ E m ( x n + x p ) 2 2
| E m |=
(16)
qN D x n
εs
=
qN A x p
εs
C ≡ dQ / dV
εs d (qN BW ) = C ≡ dQ / dV = 2 d [(qN B / 2ε s )W ] W
= qε s N B (Vbi ± V − 2kT / q ) −1 / 2 2
1/C2~V 直线, 斜率:衬底杂质浓度, 1/C2=0时截距:内建势。
=
εs
2 LD
1/ C =
(3)
主要内容
pn结 异质结 金属-半导体接触 MIS 结构 (第四章)
(4)
2.1 p - n 结二级管
主要内容
耗尽区和耗尽电容 I-V特性 结的击穿 瞬变特性
(6)
1。耗尽区和耗尽电容
杂质分布描述
突变结—合金结、浅扩散结和离子注入结
突变结近似的杂质分布。
(7)
线性缓变结—深扩散结
线性缓变结近似的杂质分布。
kT ∂n ∂E F J n = qμ n ( nE + ) = μnn =0 q ∂x ∂x
∂EF =0 ∂x
同理
1 ∂E i E = q ∂x E F − E i = kT ln( n / ni )
净电子和空穴电流为零,要求费 米能级在整个样品中为常数。
∂EF J p = 0 = μp p ∂x
∂ 2V ∂E − q − 2 = ≈ NA εs ∂x ∂x
对以上方程一次积分,考虑边界条件(热平衡时,中性区的电场 为0), 得到电场分布
(13)
E( x) = −
qN A ( x + x p )
εs
− xp ≤ x < 0
= − Em −
qN A x
εs
E( x) =
qN D ( x − x n )
目标:给出PN结在加偏压后的电流-电压关系
Ln
XP W Xn
Lp
P I
N+
N区(远离扩散区): 多子(电子)的漂移电流 N区扩散区: 少子(空穴)电流与多子(电子)电流互相转换 结区:电流连续 P区扩散区:少子(电子)电流与多子(空穴)电流互相转换 P区(远离扩散区):多子(空穴)漂移电流
电子电流和空穴电流在不同区内各不相同,但二者之和保持不变。 只要求出通过pn结任何一个截面的总电流都可以。 (26)
PN结边界处的非平衡少数载流子浓度:
Δn p = n p − n p 0
⎛ qV = n po [ exp⎜ ⎝ kT
⎞ ⎟ − 1] ⎠
⎛ qV ⎞ Δp n = pn -pno = pno [ exp⎜ ⎟ − 1] ⎝ kT ⎠
(33)
正向偏压时, 边界的少数载 流子浓度比平 衡时要大,反 向偏压时要小.
总的电流密度
结两侧的 电势差
(28)
(1)准费米能级电势和结两侧的电势差 先考虑 半导体 热平衡时,波耳兹曼关系: 费米能级 本征能级
⎛ EF − Ei ⎞ ⎡ q(ψ - φ ) ⎤ n = n i exp⎜ ⎟ = n i exp⎢ kT ⎠ kT ⎥ ⎣ ⎦ ⎝ ⎛ Ei − EF ⎞ ⎡ q(φ -ψ ) ⎤ P = n i exp⎜ ⎟ = n i exp⎢ kT ⎠ kT ⎥ ⎝ ⎣ ⎦
第二章 半导体接触的物理机制
半导体器件的四种基础结构 – 平衡时的能带图 金属-半导体界面,
Ef
在金属和半导体之间形成的一种紧密 接触。是第一个被研究的半导体器件。 EC Ef 可作为整流接触-肖特基势垒,或用作 欧姆接触。也可以得到其他许多器 EV 件,如MESFET。
p-n 结
EC
EV
(2)
在p型和n型半导体之间形成的“结”, 具有整流特性,广泛用于电子电路的 Ef 整流、开关及其他工作中。若再加一 层p型半导体,两个p-n结构成p-n-p双 极晶体管。
Ge, Si, GaAs单边突变结的内建势
(18)
耗尽层的宽度 双边突变结
W =
单边突变结 2ε s N A + N D W = ( )Vbi q N AN D 轻掺杂一侧
2ε sVbi qN B
考虑到多数载流子分布尾,经过修正的单边突变结的W: β = q / kT
2ε s (Vbi − 2kT / q ) = LD 2( β Vbi − 2) W= qN B
(34)
正向和反向偏置下的能带图和载流子浓度分布
(3)耗尽区边界处少数载流子浓度的分布 根据连续性方程,稳态时, 对N区: 电子 净复 合率 空穴
∂n n ∂E ∂ nn + μn n n + Dn =0 - U + μn E 2 ∂x ∂x ∂x
2
乘以 μppn
∂ pn ∂p n ∂E - U − μp E − μp pn + Dp =0 2 ∂x ∂x ∂x
2
2 LD
2
( β Vbi ± β V − 2)
−1 / 2
εs
2
( β Vbi ± β V − 2)
2
F/cm2
反向和正向 偏置
(22)
2 d (1 / C 2 ) 2 LD β = = 2 dV qε s N B εs
(23)
Si单边突变结耗尽层宽度和单位面积耗尽层电 容与掺杂浓度的关系。
2-1 电流-电压特性--理想情况的肖克莱方程
电势分布,Vbi 为内建势
qN A 2 E m V1 = E m x + x + xp 2ε s 2 qN D 2 E m V2 = E m x − x + xp 2ε s 2
(15)
− xp ≤ x ≤0 0 ≤ x ≤ xn
如果pn结的两侧的掺杂浓度相差悬殊就形成了单边突变结。 若考虑单边突变结 ( Xp~0)得到电势分布: 总的耗尽层宽 度,此时~xn
(8)
通过绝缘层上的窗口向半导体本底扩散形成p-n结时,杂质要向 下扩散,也要向侧向扩散:柱形边缘分布和球形角分布
在扩散掩膜边缘附近形成结弯曲的平面 扩散工艺。
(9)
通过矩形掩膜扩散形成近似的柱面和球面区。
突变结
当半导体的杂质浓度从受主杂质NA突变为施主杂质ND时,得到突 变结. p n
(ND-NA)
2
+
乘以 μnnn 有偏压的非平衡条件下, 利用电中性条件: 非平衡的少子=非平衡多子(nn-nn0) ~(pn-pn0), 结合爱因斯坦关系 D=kTμ/q:
= −qμ n n∇φn
同理:
J p = −qμ p p∇φ p
电子和空穴的电流密度正比 于各自的准费米能级梯度
比较: 热平衡状态
φn = φ p = φ = 常数
Jn = J p = 0
(3)
正向和反向偏置下的能带图、电势分布。
(2)耗尽区边界的少数载流子浓度(边界条件) : 根据前面的图象:
异质结界面
Δ EC EC EF ΔEV EV
即在两种不同的半导体之间形成的 界面,可构成双异质结激光器等。
金属-绝缘体-半导体结构 如果绝缘体用氧化物,即MOS结构, 可 视为一个金属-氧化物界面和一个氧化 物-半导体界面的结合,ULSL中最重要 的MOSFET器件的基本结构。
Ef
EC Ef EV
ψ ≡ -E i /q φ ≡ -E F /q
热平衡时
(29)
本征能级电势 费米能级电势
np = n i
2
只有一个EF , 对应一个φ
外加电压, 结两侧的少数载流子密度变化, 非平衡:
np ≠ n i
2
电子和空穴不再有统一的费米能级,准平衡下,用各自的准费 米能级可以有与平衡时类似的表达式:
⎡ q(ψ - φn ) ⎤ n ≡ n i exp⎢ kT ⎥ ⎣ ⎦
平衡时,
能带图
nn0 pn0 = n p0 p p0 = ni
2
p p0 nn0 kT kT Vbi = ln( )= ln( ) q p n0 q n p0
结两侧空穴密度之间和电子密度之间的关系:
pn 0
(17)
qVbi (2) qV bi = p p 0 exp( − ) n p 0 = nn 0 exp(− ) kT kT
Ln
XP W Xn
Lp
P I
N+
Xn处(或Xp处)电子和空穴电流的和,即总电流。 I = Xn处的电子漂移电流 + Xn处的空穴扩散电流 = Xp处的电子(少子)扩散电流 + Xn处的空穴(少子)扩散电流 归纳为求少子扩散电流
