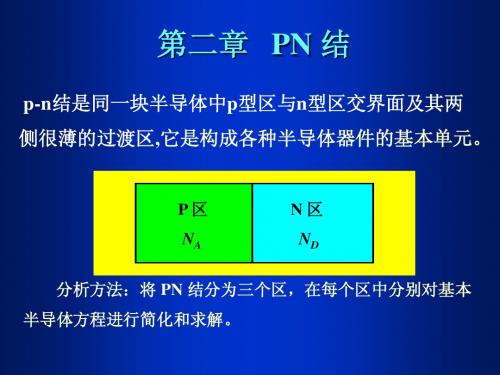
第二章 PN结 (2)
合集下载
第二章pn结.

则
xnEm(2 q (s2qsN D N(N N AN AA N A N DN DD V)D V )12D)1 2
xp(2q sNA(N N AD ND)VD)1 2
W xnxp(2qs(N N AD N N A D )V D )1 2
xn
Na Na Nd
W
xp
Nd Na Nd
W
➢ 缓变pn结的电场、电位分布
)
nn0
ni
exp(
EF kT
Ei
)
pn0
ni2 nn0
x xn x xn
电中性条件
qAxpNA qAxnND xpNA xnND
平衡态PN结空间电荷区内:
n(x)p(x)ni2
3.非平衡态pn结能,称非平 衡态pn结。
空间电荷区外侧的载流子浓度分布(假设pn结杂质分布均
匀、稳态直流条件下):
n区外侧非平衡空穴浓度分布:
p n (x ) p n (x ) p n 0 p n 0 [ e x p (q k V T ) 1 ]e x p (x n L p x ) ( x xn )
若以 x n 为坐标原点,则非平衡空穴浓度分布:
Ei
kT
ln
nn0 ni
nn0
n
i
e
x
p
(
E
F kT
E
i
)
VD
1 q {(Ei
EF )p区
(EF
Ei )n区 }
kT q
ln
pp0nn0
n
2 i
kT q
ln
NAND
n
2 i
2.平衡pn结的载流子浓度分布
本征费米能级是位置x的函数,即 E i ( x ) ,对非简并半导体而 言,pn结空间电荷区内的电子、空穴浓度为:
PN结

硅平面工艺的主体
国家级精品课程——半导体器件物理与实验
第二章 PN结
引
4-1 氧化工艺:
言
1957年,人们发现硅表面的二氧化硅层具有阻止杂质向硅内 扩散的作用。这一发现直接导致了氧化工艺的出现。 二氧化硅薄膜的作用: (1)对杂质扩散的掩蔽作用; (2)作为MOS器件的绝缘栅材料; (3)器件表面钝化作用;
二、电场和电势分布:
1. 内建电势差(势垒):
EC
漂移
扩散
EFp
ห้องสมุดไป่ตู้
Ei
EV
扩散
q 0 E C
EV
q 0 k T ln
EFn Ei
Na Nd ni2
( 2 1 1) ( 2 1 2)
两种证明方法:
(1)费米能级法:
漂移
Na Nd 0 VT ln ni2
q 0 ( Ei E Fp ) ( E Fn Ei ) , ( 2 1 3) Ei E Fp k T ln E Fn Ei k T ln p0 N k T ln a , ( 2 1 4) ni ni n0 N k T ln d , ( 2 1 5) ni ni
国家级精品课程——半导体器件物理与实验
第二章 PN结
2.1 热平衡(无偏压) PN结
二、电场和电势分布:
1. 内建电势差(势垒):
(2)静电势法: 取费米势为电势能的零点。
P型电 中性区 -xp 边界区
qNd
-qNa
xn
N型电 中性区
x
p0 ni exp / VT (1 10 10 )
在《半导体器件指南》一书中,定义了67种主要的半导体器 件及其相关的110多个变种。然而,所有这些器件都只由以 下的少数几种器件单元组成。
第二章PN结资料

2.4 空间电荷区的复合电流和产生电流
• 低偏压:空间电荷区的复合电流占优势 • 偏压升高: 扩散电流占优势 • 更高偏压: 串联电阻的影响
I (A)
103
串联电阻
实验数据 104
105
106
107
斜率 q KT
108
109
斜率 q
2 KT
1 0 10 0.1 0.2 0.3 0.4 0.5 0.6 0.7
• 由于这个原因,也把空间电 荷区称为势垒区。
3.耗尽层 -突变结
• 突变结势垒中的电场、电势分布 • 耗尽层近似:在空间电荷区中,与电离杂质浓度相比,自由载流子浓度
可以忽略,这称为耗尽近似。 • 杂质完全电离:
• 在N侧和P侧泊松方程可以分别简化为:
d dx22 qN D0xxn d dx22 qN A0xxn
0
•
边界条件: pnxpn0 pn0expV V T1
xW n xxn
pnxpn0AexpL xpBexpL xp
A pn0 exp k q 0 V T 1 exp L xn p pn0 exp V V T 1 exp L xn p B0
p n x p n 0 p n 0 e x p V V T 1 e x p x n L p x x x n
I0expV V T1
Shockley方程
•
正向偏压:
I
I0
exp
V VT
• 反向偏压: I I 0 • I0称为饱和电流
• 正向偏压情况下的PN结
载流子浓度
P型
np pn0
N型 pn pn0
空间电荷层
xp 0 xn
x
(a)少数载流子分布
pn结(2)

E Fn E Fp V np n e
2 V / k BT i
半导体器件物理
N型一侧
• 空穴分布连续性方程
p 2 pn pn pn 0 Dp 2 t x p
• 边界条件
x= Wn, pn =pn0; x=xn,
pn pn 0 exp(qV / kBT )
• 空穴扩散长度 Lp • 解(Wn -xn>>Lp)
半导体器件物理
pn结二极管(二)
理想pn结电流特性 实际电流曲线相对理想的偏离 二级管的温度特性
半导体器件物理
pn结二极管电流特性曲线
半导体器件物理
理想pn结电流特性
• 基本假设
– – – – 外加偏置电压全部降落在耗尽区 均匀掺杂突变结,载流子非简并 小注入电流 不考虑耗尽区载流子产生-复合
半导体器件物理
半导体器件物理
半导体器件物理
半导体器件物理
定性分析结果
半导体器件物理
准费米能级
• 载流子分布偏离平衡,存在 过剩载流子
– 假定电子在导带内平衡,空 穴在价带内平衡 – 电子和空穴各自平衡的时间 远小于产生-复合时间
n ni e
EFn Ei / kBT
• 电子、空穴的分布仍然满足 费米分布
np np0 np0 e
J n qDn
qV / kBT
1 e
x x p / Lp
d (n p n p 0 ) dx
xp
qDn n p 0 e qV / kBT 1 Ln
半导体器件物理
总电流
• 理想二极管方程(Shockley方程)
J J n J p J s eqV / kBT 1 Js qDp Lp qDn pn 0 np0 Ln qD p ni2 qDn ni2 Lp N D Ln N A
PN结 2013-11-8

2.1.3平衡PN结的载流子浓度分布
2.1.0 PN结初识 本征半导体 晶体结构 载流子浓度
Si Si
n 0 =p0 =n i =C T e
1/2
3/2 Eg / T
n0 p0 n
2 i
Si
Si
跟费米能 级的关系 能带图
E E ( F i) n0 ni e T E F =E i Ei E F p n e( T ) 0 i
多子:电子 少子:空穴
P 型半导体
- - - - - - - - - - - -
- - - - - -
多子:空穴
- - - - - -
少子:电子
PN 结
离子束刻蚀和离子注入
N区
PN结二极管制造过程
PN结结构
P区
Si 衬底
PN结二极管制造过程
PN结结构
P型硅 (P掺杂)
N区 P区
采用离子注入的方法实现
p 2 p p E p p0 Dp 2 p E p p Gp t x x x p
2. 单边稳态注入: p x p 0 e
x Lp
L , p D p p
3. 平衡状态下载流子浓度和费米能级的关系
E Ei n0 ni exp( F ) k0T E EF p0 ni exp( i ) k0T np=n i2
2.1.1 平衡PN结能带图
◎ 空间电荷区的形成
N型区与P型区的能带如何变化 ? N型区与P型区交界面处载流子如何运动 ?
• 空间电荷
• 空间电荷区 • 内建电场
◎PN 结的形成—费米能级
P型 N型
2.1.1 平衡PN结能带图
2.1.0 PN结初识 本征半导体 晶体结构 载流子浓度
Si Si
n 0 =p0 =n i =C T e
1/2
3/2 Eg / T
n0 p0 n
2 i
Si
Si
跟费米能 级的关系 能带图
E E ( F i) n0 ni e T E F =E i Ei E F p n e( T ) 0 i
多子:电子 少子:空穴
P 型半导体
- - - - - - - - - - - -
- - - - - -
多子:空穴
- - - - - -
少子:电子
PN 结
离子束刻蚀和离子注入
N区
PN结二极管制造过程
PN结结构
P区
Si 衬底
PN结二极管制造过程
PN结结构
P型硅 (P掺杂)
N区 P区
采用离子注入的方法实现
p 2 p p E p p0 Dp 2 p E p p Gp t x x x p
2. 单边稳态注入: p x p 0 e
x Lp
L , p D p p
3. 平衡状态下载流子浓度和费米能级的关系
E Ei n0 ni exp( F ) k0T E EF p0 ni exp( i ) k0T np=n i2
2.1.1 平衡PN结能带图
◎ 空间电荷区的形成
N型区与P型区的能带如何变化 ? N型区与P型区交界面处载流子如何运动 ?
• 空间电荷
• 空间电荷区 • 内建电场
◎PN 结的形成—费米能级
P型 N型
2.1.1 平衡PN结能带图
第二章 PN结
p pokTຫໍສະໝຸດ p po Vbi ln q pno
由于 p po
ni2 ni2 N A ,pno ,故得: nno N D
kT N A N D Vbi ln q ni2
由上式可见,Vbi 与掺杂浓度、ni (或EG 及温度T )有关。 在常用的掺杂浓度范围和室温下,硅的 Vbi 约为 0.75V ,锗的 约为 0.35V 。最后可得: 1
xd
也
3. 平衡的p-n结能带与载流子分布
1)平衡PN结能带
自建场和自建势
P区 N区
NApp0
NA-
ND+
nn0
x
xn
xp
dx C
dp J p qD p q p p 0 dx
dE f dx 0
1)p区导带底比n区高qVbi, P区价带顶比N区高qVbi 2)禁带宽度Eg保持处处相等 3)势垒区内能带弯曲 4)有统一的费米能级
可见:
空穴扩散:P 区 电子扩散:P 区
p po ni pno nno ni n po
N区 N区
扩散电流方向为:P 区
N区
P区留下 N A ,N区留下 N D ,形成 空间电荷区。空间电 荷区产生的电场称为 内建电场,方向为由N 区指向P 区。电场 的存在会引起漂移电流,方向为由N 区指向P 区。 扩散电流: P 区 漂移电流: P 区 N区 N区
0 max
q
s
xn N D
q
s
s
xp NA
由上式可求出 N 区与P 区的耗尽区宽度:
xn
s
qN D
max ,
xp
qN A
由于 p po
ni2 ni2 N A ,pno ,故得: nno N D
kT N A N D Vbi ln q ni2
由上式可见,Vbi 与掺杂浓度、ni (或EG 及温度T )有关。 在常用的掺杂浓度范围和室温下,硅的 Vbi 约为 0.75V ,锗的 约为 0.35V 。最后可得: 1
xd
也
3. 平衡的p-n结能带与载流子分布
1)平衡PN结能带
自建场和自建势
P区 N区
NApp0
NA-
ND+
nn0
x
xn
xp
dx C
dp J p qD p q p p 0 dx
dE f dx 0
1)p区导带底比n区高qVbi, P区价带顶比N区高qVbi 2)禁带宽度Eg保持处处相等 3)势垒区内能带弯曲 4)有统一的费米能级
可见:
空穴扩散:P 区 电子扩散:P 区
p po ni pno nno ni n po
N区 N区
扩散电流方向为:P 区
N区
P区留下 N A ,N区留下 N D ,形成 空间电荷区。空间电 荷区产生的电场称为 内建电场,方向为由N 区指向P 区。电场 的存在会引起漂移电流,方向为由N 区指向P 区。 扩散电流: P 区 漂移电流: P 区 N区 N区
0 max
q
s
xn N D
q
s
s
xp NA
由上式可求出 N 区与P 区的耗尽区宽度:
xn
s
qN D
max ,
xp
qN A
半导体器件物理:第2章 PN结

1. 费米能级观点;
P型电
N型电
中性区
中性区
2. 载流子输运观点。
x
图2-3 PN结示意图
边界区 耗尽区 边界区 (c)对应的空间电荷分布
国家级精品课程——半导体器件物理与实验
第二章 PN结
2.1 热平衡(无偏压) PN结
二、电场和电势分布:
1. 内建电势差(势垒):
EC
EFEpi
EV
漂移 扩散
x
m
qNd xn
s
qNa xp
s
(2 1 16)
耗尽区
Nd xn Na xp (2 117)
➢ P区耗尽层中单位面积内的负电荷数= N 区耗尽层中单位面积内的正电荷数;
➢ P区耗尽层中的负电荷数= N区耗尽层中 正电荷数;
国家级精品课程——半导体器件物理与实验
第二章 PN结
引言
5. 采用硅平面工艺制备PN结的主要工艺过程
国家级精品课程——半导体器件物理与实验
第二章 PN结
引言
5. 采用硅平面工艺制备PN结的主要工艺过程
国家级精品课程——半导体器件物理与实验
第二章 PN结
6. 突变结:
合 金 结
引言
N(x) Na Nd Na,(x xj) N(x) Na Nd Nd ,(x xj)
-xp
xn
x
-qNa
耗尽区
(x)
电场强
q Nd
s
dx
q Nd
s
x C2
度连续性边界条件:
,
(
(2 x)
1
1 4) 0,
x xn
P型电 P区 N区 N型电
中性区耗尽区 耗尽区 中性区 x
第2章_PN结
22
2、耗尽区
空间电荷区
耗尽近似:假设空
P
xp
电位 电子的电势能
FP
N
内建电场
xn
间电荷区内的载流子完
空间电荷完全由电离杂 质提供。这时空间电荷
0
q 0
全扩散掉,即完全耗尽,
区又可称为“耗尽区”。 E
qVFN ED
EC Ei EF E EiV EV
EC
能带 能带
23
设P型和N型侧的耗尽层宽度分别为xp和xn, 整个空间电荷层宽度表示为W=x n +x p 耗尽层宽度与扩散电势差有关,具体的计 算分情况讨论(了解) 对于P+N突变结
27
正向偏压PN结中费密能级的变化 图中的电子准费米能级如何随位置变化的?
28
PN结的反向特性 反向PN结
P区接负,N区接正 外加电场与内建电场方向相同 空间电荷区中的电场增强 反向电压使: 势垒区宽度变宽 势垒高度变高 0 qV0D↑q(VD+VR)
破坏扩散漂移运动平衡 漂移运动 强于 扩散运动
W =xn
20 1/2 qN D
空间电荷区的自建电场强度是非均匀电场, 电场强度是x的函数
24
2.2 加偏压的PN结
2.2.1 PN结的单向导电性 2.2.2 少数载流子的注入与输运
25
2.2.1 PN结的单向导电性
非平衡PN结
处于一定偏置状态下的 PN结称为非平衡PN结
当PN结两端加正向偏 压VF,即P区接电源的 正极,N区接电源的负 极,称为正向PN结。 反之,当PN结两端加反 向偏压VR则称反向PN结。
p n x n p n x n p n 0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
P区 N区
(2)反向PN结中载流子的运动
jp
1、反向电流很小 2、在少子扩散长度内有扩散和 产生 3、反向电流趋于不变
jn
Ln
Lp
2.2.3 非平衡PN结的能带图
(1)正偏
(2)反偏
2.2.4、V-I 特性方程
1、理想PN结模型
(1)小注入。即注入的非平衡少数载流子浓度远 低于平衡多子浓度,即掺杂浓度。 (2)外加电压全部降落在势垒区,势垒区以外为 电中性区。 (3)忽略势垒区载流子的产生-复合作用。通过势 垒区的电流密度不变。 (4)忽略半导体表面对电流的影响。 (5)只考虑一维情况。
由杂质离子形成 空间电荷区
内建电场促使 少子漂移 内建电场阻止 多子扩散
多子的扩散和少子的漂移达到动态平衡。
2.1.2、空间电荷区
N
基本概念:
XN
XP
P
空间电荷区XM
空间电荷 空间电荷区
2.1.3、平衡PN结能带图 (没有外加偏压)
空间电荷区
P
xp
电势
内建电场
N
xn
形成PN结前
VD
电子势能 能带
J J D J RG qLn
np0
n
e
qVF kT
ni 2 kT qxm e 2
qV F
2.3.11
讨论: ①势垒区复合电流随外加电压的增加比较缓慢,例如外加电压 增加0.1V,正向注入电流可增加50倍,而势垒区复合电流只增 加7倍,因此只有在比较低的正向电压,或者说比较小的正向电 流时,空间电荷区复合电流才起重要作用; ②势垒区复合电流正比于ni ,而正向注入的扩散电流却正比于 ni2,所以ni 越大,复合电流的影响就越小。硅的本征载流子浓 度比锗小,在小电流范围内复合电流的影响就必须考虑,它是 使硅晶体管小电流下β下降的原因。
(2)空间电荷区边界的少数载流子 浓度
np0 qVD qVD nn 0 exp pn 0 p p 0 exp kT kT
2.2 PN结直流V-I特性(肖克莱方程)
非平衡PN结
处于一定偏置状态下的PN结称 为非平衡PN结。 当P区接电源的正极,N区接电 源的负极,称为正向PN结。反 之,则称反向PN结。 外加电压基本降落在势垒区
2.1.4、PN结内建电势差
-Xp 0
空间电荷区
Xn
求VD :
电势
电子势能 能带
P
内建电场
N
VD
qVD
qVD
EC EF Ei
EV
2.1.4、PN结内建电势差 (1)突变结:
kT N A N D 式中 NA:P区掺杂浓度; VD ln ND:N区掺杂浓度 2 q ni
kT 0.026 V q
(3)、实际PN结近似 缓变PN结附近杂质浓度 有两种近似处理方法 A。线性缓变结近似 B。突变结近似
杂 质 浓 度
N
P
ND -NA
xj
x
2.1.1、PN结的形成及类型
线性缓变结近似 适用于表面杂质浓度 较低、结深较深的缓 变结
杂 质 浓 度
ND -NA
xj
杂 质 浓 度
x
ND N A a j x x j
pP 0 nN 0 e pN 0 nP 0
qVD kT
2.1.5、平衡PN结载流子浓度分布
势垒区本征费米能级 随x的变化
Ei x Eip qV x
EF Ei x kT
(1)空间电荷区内的载流子浓度
nx ni e
px ni e
Ei x EF kT
2.3.1
式中,n和p分别为电子和空穴的浓度,n1和p1为费密能级EF与复 合中心能级Et重和时的导带电子浓度和价带空穴浓度
势垒区载流子浓度
nx ni e
EF n Ei x
kT
2.3.2
px ni e
Ei x EF p kT
2.3.3
qVD
qVD
EC EF Ei EV
基本概念:
内建电场 内建电势差VD
形成PN结后 平衡PN结有统一的费米能级
2.1.3、PN结能带图
空间电荷区
平衡PN结能带图
电势
P
xp VD
内建电场
N
xn
空间电荷区又称 势垒区 耗尽层
注意:由“多子”变成“少子”
电子势能 能带
qVD
qVD
EC EF Ei EV
I0 (e
qVA / kT
1) I0e
qVA / kT
(7)当T升高时,JF增大,JR增大。
2.3 实际PN结的特性
2.3.1 PN结空间电荷区中的复合电流
正偏时,通过PN结的总电流为:
J J n J p J RG
势垒区复合电流
电子和空穴在空电区中, np ni2 通过复合中心复合的净复 U p n n1 n p p1 合率U可以写为
1 np ni2 U n p 2ni
2.3.5
np ni2 U p n n1 n p p1
2.3.1
式中的分子在空间电荷区中是不随位置变化的, U的极大值就 发生在n + p为极小值的地方。利用(2.3.2)、(2.3.3)式对x求极 小值可以得到,n + p的极小值发生在
对于锗PN结,通常可取VD=0.3—0.4V
ni :本征载流子浓度
T 300K
对于硅PN结,通常可取 VD=0.6—0.7V
2.1.4、PN结内建电势差 (2)线性缓变结
aX m 2 KT VD ln( ) q 2ni
式中,α:杂质浓度梯度( X=Xj), Xm:PN结势垒宽度
(3)推论
2.2.4、V-I 特性方程
2.2.4、V-I 特性方程 肖克莱方程
I I0 e
qVA / kT
1
qDP Pn 0 qDn n p 0 I0 A Ln LP
反向电流:
2.2.4、V-I 特性方程
单边结近似
NA>>ND
2 P i
对于P+N结
对于N+P结
Ln
,
n p 0 qV kT e 1 J J n qLn n
2.3.10
物理含义是:注入到P区的电子电流密度Jn ,就是单位时间内 在扩散长度Ln内复合的电子电荷量。这个电流是由非平衡少子 在扩散区内复合形成的,故称其为扩散电流,记为JD。 流过 N+P结的正向电流应为( 2.3.10)式和( 2.3.9)式之和, (2.3.10)式中的正向电压V也用 VF 表示,可得
2.1 PN结的形成及空间电荷区 2.1.1、PN结的形成及类型 1、PN 结含义: 在一块N型(或P型)半导体单晶上,用特定的工 艺方法把P型(或N型)杂质掺入其中,使这块单晶 相连的二个不同区域分别具有N型和P型的导电类型, 在二者交界面的过渡区即称为PN结。
PN结
P
N
半导体二极管
半导体二极管按结构分为点接触型和面接触型 点接触型(a)适用于高频电路,面接触型(b)适用于整流
微电子器件与IC设计
第2章 PN 结
半导体器件物理
据统计:半导体器件主要有67种,另外还有110个 相关的变种 所有这些器件都由少数基本模块构成: • pn结 •金属-半导体接触 • MOS结构 • 异质结 • 超晶格
两种或两种以上不同的极薄(几埃到几百埃)半导体单晶薄膜交替地生长在一起 而形成的周期性结构材料。在原子尺度上人工设计和 改变材料的结构参数和组分, 改变材料的能带结构和物理性能。
2.2.1、正向PN结
(1)势垒的变化
正向电压使 势垒区宽度变窄、 势垒高度变低 外加电场与内建电场方向相反 空间电荷区中的电场减弱 破坏扩散与漂移运动间的 平衡 扩散运动强于漂移运动 注入少子 注入的少子边扩散边复合
N
扩散
P
P区
漂移
正向偏置时,扩散大于漂移
扩散
电子: N区
空穴: P区
空穴扩散
2.2.2、反向PN结
(1)反向PN结的少子抽取 反向电压使 势垒区宽度变宽 势垒高度变高
外加电场与内建电场方向相同 增强空间电荷区中的电场 破坏扩散漂移运动平衡 漂移运动强于扩散运动 抽取少子
Ln
Lp
N
漂移
P
P区
扩散
反向偏置时,漂移大于扩散
漂移
空穴: N区
电子: P区
N区
扩散
2.2.2、反向PN结
(c)是硅平面工艺型二极管的结构 图,是集成电路中常见的一种形式。
2.1.1、PN结的形成及类型 2、PN结的类型 (1)、突变结
P区
N区
单边突变结 P+N结 N+P结
杂 质 浓 度
NA ND xj x
2.1.1、PN结的形成及类型(2来自、缓变结杂 质 浓 度
N
P
ND -NA
xj
x
2.1.1、PN结的形成及类型
2.2.4、V-I 特性方程
2.坐标 以xn、xp为坐标原点 分别建立坐标系。 步骤: ① 求解“非少子”的扩 散方程 ② →求“非少子”浓度 的边界值 ③ →求“非少子”浓度 梯度 ④ →分别求电子、空穴 的扩散电流密度 ⑤ →求PN结电流
电子 空穴
dx d P n j p qD p dx
E F n E F p
np ni2 e
由图2.2.2
(2)反向PN结中载流子的运动
jp
1、反向电流很小 2、在少子扩散长度内有扩散和 产生 3、反向电流趋于不变
jn
Ln
Lp
2.2.3 非平衡PN结的能带图
(1)正偏
(2)反偏
2.2.4、V-I 特性方程
1、理想PN结模型
(1)小注入。即注入的非平衡少数载流子浓度远 低于平衡多子浓度,即掺杂浓度。 (2)外加电压全部降落在势垒区,势垒区以外为 电中性区。 (3)忽略势垒区载流子的产生-复合作用。通过势 垒区的电流密度不变。 (4)忽略半导体表面对电流的影响。 (5)只考虑一维情况。
由杂质离子形成 空间电荷区
内建电场促使 少子漂移 内建电场阻止 多子扩散
多子的扩散和少子的漂移达到动态平衡。
2.1.2、空间电荷区
N
基本概念:
XN
XP
P
空间电荷区XM
空间电荷 空间电荷区
2.1.3、平衡PN结能带图 (没有外加偏压)
空间电荷区
P
xp
电势
内建电场
N
xn
形成PN结前
VD
电子势能 能带
J J D J RG qLn
np0
n
e
qVF kT
ni 2 kT qxm e 2
qV F
2.3.11
讨论: ①势垒区复合电流随外加电压的增加比较缓慢,例如外加电压 增加0.1V,正向注入电流可增加50倍,而势垒区复合电流只增 加7倍,因此只有在比较低的正向电压,或者说比较小的正向电 流时,空间电荷区复合电流才起重要作用; ②势垒区复合电流正比于ni ,而正向注入的扩散电流却正比于 ni2,所以ni 越大,复合电流的影响就越小。硅的本征载流子浓 度比锗小,在小电流范围内复合电流的影响就必须考虑,它是 使硅晶体管小电流下β下降的原因。
(2)空间电荷区边界的少数载流子 浓度
np0 qVD qVD nn 0 exp pn 0 p p 0 exp kT kT
2.2 PN结直流V-I特性(肖克莱方程)
非平衡PN结
处于一定偏置状态下的PN结称 为非平衡PN结。 当P区接电源的正极,N区接电 源的负极,称为正向PN结。反 之,则称反向PN结。 外加电压基本降落在势垒区
2.1.4、PN结内建电势差
-Xp 0
空间电荷区
Xn
求VD :
电势
电子势能 能带
P
内建电场
N
VD
qVD
qVD
EC EF Ei
EV
2.1.4、PN结内建电势差 (1)突变结:
kT N A N D 式中 NA:P区掺杂浓度; VD ln ND:N区掺杂浓度 2 q ni
kT 0.026 V q
(3)、实际PN结近似 缓变PN结附近杂质浓度 有两种近似处理方法 A。线性缓变结近似 B。突变结近似
杂 质 浓 度
N
P
ND -NA
xj
x
2.1.1、PN结的形成及类型
线性缓变结近似 适用于表面杂质浓度 较低、结深较深的缓 变结
杂 质 浓 度
ND -NA
xj
杂 质 浓 度
x
ND N A a j x x j
pP 0 nN 0 e pN 0 nP 0
qVD kT
2.1.5、平衡PN结载流子浓度分布
势垒区本征费米能级 随x的变化
Ei x Eip qV x
EF Ei x kT
(1)空间电荷区内的载流子浓度
nx ni e
px ni e
Ei x EF kT
2.3.1
式中,n和p分别为电子和空穴的浓度,n1和p1为费密能级EF与复 合中心能级Et重和时的导带电子浓度和价带空穴浓度
势垒区载流子浓度
nx ni e
EF n Ei x
kT
2.3.2
px ni e
Ei x EF p kT
2.3.3
qVD
qVD
EC EF Ei EV
基本概念:
内建电场 内建电势差VD
形成PN结后 平衡PN结有统一的费米能级
2.1.3、PN结能带图
空间电荷区
平衡PN结能带图
电势
P
xp VD
内建电场
N
xn
空间电荷区又称 势垒区 耗尽层
注意:由“多子”变成“少子”
电子势能 能带
qVD
qVD
EC EF Ei EV
I0 (e
qVA / kT
1) I0e
qVA / kT
(7)当T升高时,JF增大,JR增大。
2.3 实际PN结的特性
2.3.1 PN结空间电荷区中的复合电流
正偏时,通过PN结的总电流为:
J J n J p J RG
势垒区复合电流
电子和空穴在空电区中, np ni2 通过复合中心复合的净复 U p n n1 n p p1 合率U可以写为
1 np ni2 U n p 2ni
2.3.5
np ni2 U p n n1 n p p1
2.3.1
式中的分子在空间电荷区中是不随位置变化的, U的极大值就 发生在n + p为极小值的地方。利用(2.3.2)、(2.3.3)式对x求极 小值可以得到,n + p的极小值发生在
对于锗PN结,通常可取VD=0.3—0.4V
ni :本征载流子浓度
T 300K
对于硅PN结,通常可取 VD=0.6—0.7V
2.1.4、PN结内建电势差 (2)线性缓变结
aX m 2 KT VD ln( ) q 2ni
式中,α:杂质浓度梯度( X=Xj), Xm:PN结势垒宽度
(3)推论
2.2.4、V-I 特性方程
2.2.4、V-I 特性方程 肖克莱方程
I I0 e
qVA / kT
1
qDP Pn 0 qDn n p 0 I0 A Ln LP
反向电流:
2.2.4、V-I 特性方程
单边结近似
NA>>ND
2 P i
对于P+N结
对于N+P结
Ln
,
n p 0 qV kT e 1 J J n qLn n
2.3.10
物理含义是:注入到P区的电子电流密度Jn ,就是单位时间内 在扩散长度Ln内复合的电子电荷量。这个电流是由非平衡少子 在扩散区内复合形成的,故称其为扩散电流,记为JD。 流过 N+P结的正向电流应为( 2.3.10)式和( 2.3.9)式之和, (2.3.10)式中的正向电压V也用 VF 表示,可得
2.1 PN结的形成及空间电荷区 2.1.1、PN结的形成及类型 1、PN 结含义: 在一块N型(或P型)半导体单晶上,用特定的工 艺方法把P型(或N型)杂质掺入其中,使这块单晶 相连的二个不同区域分别具有N型和P型的导电类型, 在二者交界面的过渡区即称为PN结。
PN结
P
N
半导体二极管
半导体二极管按结构分为点接触型和面接触型 点接触型(a)适用于高频电路,面接触型(b)适用于整流
微电子器件与IC设计
第2章 PN 结
半导体器件物理
据统计:半导体器件主要有67种,另外还有110个 相关的变种 所有这些器件都由少数基本模块构成: • pn结 •金属-半导体接触 • MOS结构 • 异质结 • 超晶格
两种或两种以上不同的极薄(几埃到几百埃)半导体单晶薄膜交替地生长在一起 而形成的周期性结构材料。在原子尺度上人工设计和 改变材料的结构参数和组分, 改变材料的能带结构和物理性能。
2.2.1、正向PN结
(1)势垒的变化
正向电压使 势垒区宽度变窄、 势垒高度变低 外加电场与内建电场方向相反 空间电荷区中的电场减弱 破坏扩散与漂移运动间的 平衡 扩散运动强于漂移运动 注入少子 注入的少子边扩散边复合
N
扩散
P
P区
漂移
正向偏置时,扩散大于漂移
扩散
电子: N区
空穴: P区
空穴扩散
2.2.2、反向PN结
(1)反向PN结的少子抽取 反向电压使 势垒区宽度变宽 势垒高度变高
外加电场与内建电场方向相同 增强空间电荷区中的电场 破坏扩散漂移运动平衡 漂移运动强于扩散运动 抽取少子
Ln
Lp
N
漂移
P
P区
扩散
反向偏置时,漂移大于扩散
漂移
空穴: N区
电子: P区
N区
扩散
2.2.2、反向PN结
(c)是硅平面工艺型二极管的结构 图,是集成电路中常见的一种形式。
2.1.1、PN结的形成及类型 2、PN结的类型 (1)、突变结
P区
N区
单边突变结 P+N结 N+P结
杂 质 浓 度
NA ND xj x
2.1.1、PN结的形成及类型(2来自、缓变结杂 质 浓 度
N
P
ND -NA
xj
x
2.1.1、PN结的形成及类型
2.2.4、V-I 特性方程
2.坐标 以xn、xp为坐标原点 分别建立坐标系。 步骤: ① 求解“非少子”的扩 散方程 ② →求“非少子”浓度 的边界值 ③ →求“非少子”浓度 梯度 ④ →分别求电子、空穴 的扩散电流密度 ⑤ →求PN结电流
电子 空穴
dx d P n j p qD p dx
E F n E F p
np ni2 e
由图2.2.2
