2021版八年级数学上册第一章因式分解1.3公式法第2课时导学案人教版五四制
新人教版八年级上册数学导学案:因式分解—公式法(第2课时)
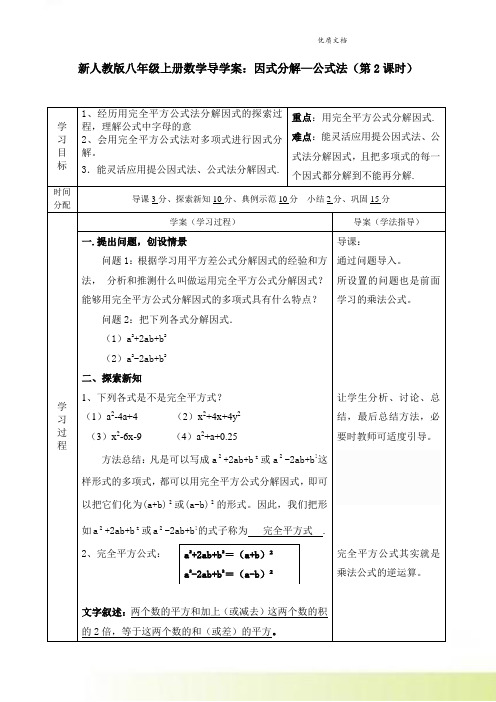
新人教版八年级上册数学导学案:因式分解—公式法(第2课时)学习目标1、经历用完全平方公式法分解因式的探索过程,理解公式中字母的意2、会用完全平方公式法对多项式进行因式分解。
3.能灵活应用提公因式法、公式法分解因式.重点:用完全平方公式分解因式.难点:能灵活应用提公因式法、公式法分解因式,且把多项式的每一个因式都分解到不能再分解.时间分配导课3分、探索新知10分、典例示范10分小结2分、巩固15分学习过程学案(学习过程)导案(学法指导)一.提出问题,创设情景问题1:根据学习用平方差公式分解因式的经验和方法,•分析和推测什么叫做运用完全平方公式分解因式?能够用完全平方公式分解因式的多项式具有什么特点?问题2:把下列各式分解因式.(1)a2+2ab+b2(2)a2-2ab+b2二、探索新知1、下列各式是不是完全平方式?(1)a2-4a+4 (2)x2+4x+4y2(3)x2-6x-9 (4)a2+a+0.25方法总结:凡是可以写成a2+2ab+b2或a2-2ab+b2这样形式的多项式,都可以用完全平方公式分解因式,即可以把它们化为(a+b)2或(a-b)2的形式。
因此,我们把形如a2+2ab+b2或a2-2ab+b2的式子称为完全平方式 .2、完全平方公式:文字叙述:两个数的平方和加上(或减去)这两个数的积的2倍,等于这两个数的和(或差)的平方。
a2+2ab+b2=(a+b)²a2-2ab+b2=(a-b)²导课:通过问题导入。
所设置的问题也是前面学习的乘法公式。
让学生分析、讨论、总结,最后总结方法,必要时教师可适度引导。
完全平方公式其实就是乘法公式的逆运算。
三、例题学习 例1 分解因式:(1)16x 2+24x+9 (2)-x 2+4xy-4y 2 例2 分解因式:(1)3ax 2+6axy+3ay 2 (2)(a+b )2-12(a+b )+36 四、课时小结1.如果多项式各项含有公因式,则第一步是提出这个公因式.2.如果多项式各项没有公因式,则第一步考虑用公式分解因式.3.公式法是用来把某些具有特殊形式的多项式分解因式,不是所有的多项式都可以用公式法。
1.3公式法第二课时教学设计2022-2023学年鲁教版(五四制)八年级数学上册

1.3 公式法第二课时教学设计 2022-2023 学年鲁教版(五四制)八年级数学上册一、教学目标•理解公式的概念和作用;•掌握列式中字母的含义和运算法则;•能够用公式解决实际问题。
二、教学重点•公式的使用及其作用;•列式中字母的含义和运算法则。
三、教学内容1. 公式的概念和作用•介绍公式的定义和作用,引导学生理解公式在数学中的重要性和应用场景。
2. 列式中字母的含义和运算法则•解释列式中字母的含义,引导学生理解字母在代数中的代表含义;•教授列式的运算法则,帮助学生掌握列式中字母的加减乘除运算规则。
3. 用公式解决实际问题•针对具体问题,引导学生分析问题,建立相应的列式;•培养学生应用公式解决实际问题的能力,提高他们的数学应用能力。
四、教学步骤第一步:导入与概念讲解(15分钟)1.教师与学生互动,引导学生回顾上节课学到的知识;2.讲解公式的概念和作用,并通过示例说明公式在数学中的应用。
第二步:字母的含义和运算法则(20分钟)1.让学生观察并分析列式中字母的含义,引导他们理解字母在代数中的代表含义;2.教授列式中字母的加减乘除运算法则,帮助学生掌握运算规则。
第三步:用公式解决实际问题(25分钟)1.选择一个具体的实际问题,与学生一起分析问题并建立列式;2.引导学生运用公式解决问题,并进行演示;3.让学生分组进行练习,互相讨论和解答问题。
第四步:作业布置及课堂小结(10分钟)1.布置课后作业,要求学生练习用公式解决实际问题;2.对本节课所学内容进行小结,提醒学生掌握重点和注意事项。
五、教学资源•教材《鲁教版八年级数学上册》•讲义和练习题六、教学评估•课堂讨论的质量和积极性•课后作业的完成情况和准确性•学生对公式的理解和应用情况七、教学反思本节课设计了导入、概念讲解、字母的含义和运算法则以及用公式解决实际问题等阶段,能够帮助学生全面掌握公式的概念、作用和应用。
同时,通过课堂小结和布置作业,能够及时发现学生的问题和困惑,并对下节课的教学做好准备。
八年级数学上册因式分解公式法时学案新人教

14.3.2 公式法(第二课时)学习目标:1、经历用完全平方公式法分解因式的探索过程,理解公式中字母的意2、会用完全平方公式法对多项式进行因式分解。
3、体会从正、逆两个方面认识和研究事物的方法。
学习重、难点: 学习重点:用完全平方公式分解因式;学习难点:正确运用平方差公式进行因式分解. 学习过程:一、创设情境、引入课题 前面我们在学习整式乘法时用到了完全平方公式,其公式内容为 。
像用平方差公式逆过来用可以分解因式一样,若把完全平方公式逆过来,就得到a 2+2ab+b 2=(a+b)2, a 2-2ab+b 2=(a-b)2。
这样,我们就可以利用它们对多项式进行因式分解了二、一起探究,尝试解决例3 把下列各式分解因式:⑴t 2+22t+121; ⑵m 2+41n 2-mn. 解:例4 把下列各式分解因式:⑴ax 2+2a 2x+a 3 ⑵(x+y)2-4(x+y)+4 ⑶(3m-1)2-4n 2我们看到,凡是可以写成a 2+2ab+b 2或a 2-2ab+b 2这样形式的多项式,都可以用完全平方公式分解因式,即可以把它们化为(a+b)2或(a-b)2的形式。
因此,我们把形如a 2+2ab+b 2或a 2-2ab+b 2的式子称为 。
三、随堂练习1.课后练习1,22. 1.23616x kx ++是一个完全平方式,则k 的值为( )A .48B .24C .-48D .±483.分解因式n n n +-2344= .4.一次课堂练习,小明同学做了如下四道因式分解题,你认为小明做的不够完整的一题是( ) A ,()123-=-x x x x B .()2222y x y xy x -=+- C .()y x xy xy y x -=-22 D .()()y x y x y x -+=-225.当a =3,a -b =1时,a 2-ab 的值是 .6.在多项式2a+1中添加一个单项式,使其成为一个完全平方式,则添加的单项式为 .7.分解因式:2mx 2+4mx+2m =四、拓展练习用简便方法计算:(1)20012-4002+1 (2) 9992 (3 ) 20022五布置作业 :课后习题1,2,3。
鲁教版 五四学制 八年级上册 数学导学案设计 第一章 因式分解 1.3公式法(2)(无答案)

第2课时自主预习: 1.完全平方公式的逆应用:a2+2ab+b2 .a2-2ab+b2= .2.形如的式子称为完全平方公式。
尝试练习:1.x2+()+24y=(x-2y)22.8x2+( )+8y2=8(x+y)23.对于多项式16x2+1,再加上一个单项式,可以变成一个完全平方式,则加上的单项式可以是。
(填一个即可)4.若m=2n+1,则m2-4mn+4n2的值是。
我的困惑。
课中导学典型例题:1、把下列各式因式分解:(1)16a2-16a2b+4ab2 (2)(a2+1)2-4a(a2+1)+4a2 (3)(x2+y2)2-4x2y2思路点拨(1)这个多项式有一个公因式4a,先提出4a,先提出4a,再用公式法因式分解;(2)这个多项式是一个完全平方式;(3)这个多项式时平方差的形式。
变式训练1.变式无论x,y为任何有理数,多项式(xy)2-x2(2y-1)的值总是()A.整数B.负数C.0D.非负数2.若x2+2xy+y2-a(x+y)+25是完全平方式,求a的值。
3.利用因式分解计算:2022+202×196+982课后巩固基础巩固1.下列因式分解正确的是()A.a4b-6a3b+9a2b=a2b(a2-6a+9)B.x2-x+ 14=(x-12)2C.x2-2x+4=(x-2)2D.4x2-y2=(4x+y)(4x-y)2.有下列式子:①-x2-xy-y2②12a2-ab+12b2③-4ab2-a2+4b2④4x2+9y2-12xy⑤3x2+6xy+3y2。
其中在实数范围内能用完全平方公式分解因式的有()个A.1B.2C.3D.43.分解因式:-x2+2x2-x= .4.若一个长方形的面积是x3+2x2+x(x>0),且一边长为x+1,则其邻边长为 .5.已知多项式4a2+b2-4ab+m有一个因式2a-b+1,则m的值为()A.1B.-1C.0D.4能力提升6.若|x2-4x+4|+|y2-6y+9|=0。
八年级数学上册第一章因式分解1.2提公因式法(第2课时)导学案(无答案)鲁教版五四制(2021年整

第二节山东省龙口市兰高镇八年级数学上册第一章因式分解1.2 提公因式法(第2课时)导学案(无答案)鲁教版五四制第三节第四节第五节编辑整理:第六节第七节第八节第九节第十节尊敬的读者朋友们:第十一节这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(山东省龙口市兰高镇八年级数学上册第一章因式分解1.2 提公因式法(第2课时)导学案(无答案)鲁教版五四制)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
第十二节本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为山东省龙口市兰高镇八年级数学上册第一章因式分解1.2 提公因式法(第2课时)导学案(无答案)鲁教版五四制的全部内容。
第十三节第十四节提公因式法(第二课时)学习目标:1。
继续学习用提公因式法分解因式(公因式是多项式)。
2. 在学习中体悟化归、整体的思想方法。
教学过程:一、根据问题,自主探究问题:1。
请在下列各式等号右边的括号前填入“+”或“—”,使等式成立。
1) 2 – a = ____( a – 2 ); 2) y – x = _____( x – y );3) b + a = ____( a+ b ); 4)(b – a)2 = ____(a – b)2 ;5) -m – n = ______( m + n); 6)-s2 + t2 = _____(s2– t2)。
2 仔细分析上面的等式,我们可以发现如下规律:括号前面添上正号,括到括号里面的__________________;括号前面添上负号,括到括号里面__________________。
3 a(2x - 3)与2b(2x—3),每项中都含有_______,因此可以把_______作为公因式。
多项式16(m – n )3 + 12(n - m)2可以变形为______________________或_________________________,因此可以把__________或_________作为公因式。
鲁教版(五四制)八年级上册数学1.1《因式分解》导学案设计(无答案)

1.1《因式分解》导学案因式分解(难点)1.因式分解的定义.把一个多项式化成几个整式的乘积的形式,这种变形叫做把这个多项式因式分解.(1)因式分解是恒等变形,因式分解的对象必须是多项式;(2)因式分解的结果要写成乘积的形式;(3)因式分解要彻底.例1.下面从左到右的变形属于因式分解的是()A.x+2y=(x+y)+y B.p(q+h)=pq+phC.4a2-4a+1=4a(a-1)+1 D.5x2y-10xy2=5xy(x-2y)答案:D.2.因式分解与整式的乘法互为逆运算.本节常考考点:一.因式分解的定义1.把一个多项式化为的形式,叫做把这个多项式分解因式.x+,把它分解因式后应当是()2. 已知31216x x-+有一个因式是4A.2+- B.2(4)(2)x x+++(4)(1)x x xC.2(4)(2)++ D.2x x+-+(4)(1)x x x3.下列各式从左到右的变形中,属于因式分解的是()A.x(2a+1)=2ax+x B.x2-2x+4=(x-2)2C.m2-n2=( m-n )( m+n) D.x2-36+9x=(x+6)(x-6)+9x4.一个多项式因式分解的结果为-m(m+3)(m-3),求这个多项式.二.简便运算与整除问题1.对于任意整数m,多项式(m+7)2﹣m2都能被()整除.A.2 B.7 C.m D.m+72.对于任意整数a,多项式(3a+5)2-4都能()A .被9整除B .被a 整除C .被a+1整除D .被a-1整除3.计算:20032﹣2002×2003= .4计算5.762﹣4.242= . 5. 证明:两个连续奇数的平方差是8的倍数。
三.含参问题1. 若x+5,x-3都是多项式x 2﹣kx ﹣15的因式,则k= . 2.3x 2+mxy-y ²=(3x+y )(x-y),则m= .3. 多项式可分解为()()5x x b --,则a ,b 的值分别为_________.4. 若(x+2)(x ﹣1)=x 2+mx+n ,则m+n=( )A .1B .﹣2C .﹣1D .25. 若)5)(3(+-x x 是q px x ++2的因式,则p 为( )A.-15B.-2C.8D.26.若将二次三项式ax ²+bx+c 因式分解后得到(x+8)(x-3),求a-b=c 的值.四.整体代入的思想1.若y2+4y﹣4=0,则3y2+12y﹣5的值为.2.写出一个二项式使它们都有公因式2a2b:_____.3. 若2330+-=__________.x x xx x266+-=,324.已知m+n=3,mn=-6,则m2n+mn2=_____________.5.若a+b=7,ab=10,则a2b+ab2的值应是()A.7B.10C.70D.176. 边长为a,b的长方形,它的周长为14,面积为10,则a2b+ab2-ab的值为()A.70 B.60 C.130 D.140五.数形结合的思想1. 将下列四个图形,拼成一个大长方形,再据此写出一个多项式的因式分解。
新人教版八年级上册数学14.3.2公式法(二)导学案

新人教版八年级上册数学14.3.2公式法(二)导学案学习目标:1.理解完全平方公式的特点.2.能较熟悉地运用完全平方公式分解因式.3.能灵活应用提公因式法、公式法分解因式.4.通过综合运用提公因式法,完全平方公式分解因式,进一步培养学生的观察和联想能力.通过知识结构图培养学生归纳总结的能力.学习重点:会用完全平方公式分解因式.学习难点:灵活应用公式分解因式学习活动:一、创设情境独立思考1、阅读课本P 117~118 页,思考下列问题:(1)怎样理解因式分解的完全平方公式?(2)课本P118页例5例6你能独立解答吗?二、师生合作解决问题【1】根据学习用平方差公式分解因式的经验和方法,•分析和推测什么叫做运用完全平方公式分解因式?能够用完全平方公式分解因式的多项式具有什么特点?【2】把下列各式分解因式.(1)a2+2ab+b2 (2)a2-2ab+b2两个数的平方和,加上(或减去)这两数的积的2倍,•等于这两个数的和(或差)的平方.完全平方公式的符号表示:a2+2ab+b2=(a+b)2,a2-2ab+b2=(a-b)2.下列各式是不是完全平方式?(1)a2-4a+4 (2)x2+4x+4y2 (3)4a2+2ab+14b2(4)a2-ab+b2 (5)x2-6x-9 (6)a2+a+0.25只有:(1)(3)(6)是完全平方式,你找对了吗?他们是这样分解的:(1)a2-4a+4=a2-2×2·a+22=(a-2)2(3)4a2+2ab+14b2=(2a)2+2×2a·12b+(12b)2=(2a+12b)2(6)a2+a+0.25=a2+2·a·0.5+0.52=(a+0.5)2三、归纳总结巩固新知(约15分钟)1、知识点的归纳总结:★两个数的平方和,加上(或减去)这两数的积的2倍,•等于这两个数的和(或差)的平方.★完全平方公式的符号表示.即:a2+2ab+b2=(a+b)2,a2-2ab+b2=(a-b)2.2、运用新知解决问题:(重点例习题的强化训练)[例5]分解因式:(1)16x2+24x+9 (2)-x2+4xy-4y2解:(1)16x2+24x+9=(4x)2+2·4x·3+32=(4x+3)2.(2):-x2+4xy-4y2=-(x2-4xy+4y2)=-[x2-2·x·2y+(2y)]2 =-(x-2y)2.[例6]分解因式:(1)3ax2+6axy+3ay2(2)(a+b)2-12(a+b)+36解:(1)3ax2+6axy+3ay2 =3a(x2+2xy+y2)=3a(x+y)2(2)(a+b)2-12(a+b)+36=[(a+b)+6]2=(a+b+6)2【练习1】课本P119页练习【练习2】课本P119页习题14.3第3题五、课堂小测(1)6a-a2-9;(2)-8ab-16a2-b2;(3)2a2-a3-a;(4)4x2+20(x-x2)+25(1-x)2。
新人教版八年级上册数学导学案:因式分解—公式法(第1课时)
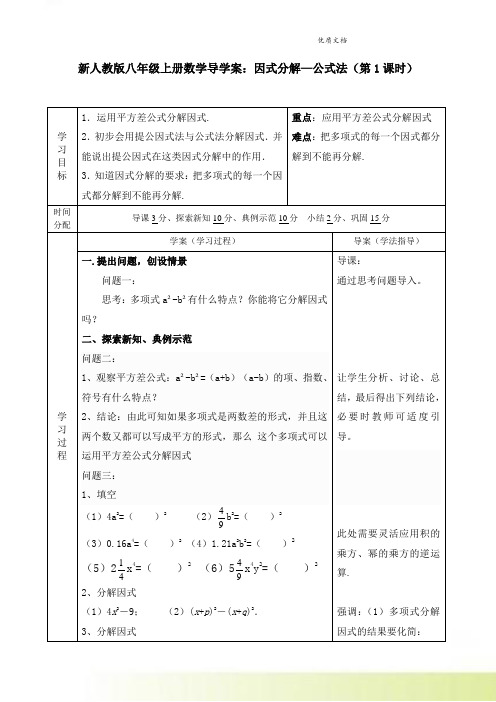
新人教版八年级上册数学导学案:因式分解—公式法(第1课时)学习目标1.运用平方差公式分解因式.2.初步会用提公因式法与公式法分解因式.并能说出提公因式在这类因式分解中的作用.3.知道因式分解的要求:把多项式的每一个因式都分解到不能再分解.重点:应用平方差公式分解因式难点:把多项式的每一个因式都分解到不能再分解.时间分配导课3分、探索新知10分、典例示范10分小结2分、巩固15分学习过程学案(学习过程)导案(学法指导)一.提出问题,创设情景问题一:思考:多项式a²-b²有什么特点?你能将它分解因式吗?二、探索新知、典例示范问题二:1、观察平方差公式:a²-b²=(a+b)(a-b)的项、指数、符号有什么特点?2、结论:由此可知如果多项式是两数差的形式,并且这两个数又都可以写成平方的形式,那么这个多项式可以运用平方差公式分解因式问题三:1、填空(1)4a2=()2(2)49b2=()2(3)0.16a4=()2 (4)1.21a2b2=()2(5)214x4=()2 (6)549x4y2=()22、分解因式(1)4x2-9;(2)(x+p)2-(x+q)2.3、分解因式导课:通过思考问题导入。
让学生分析、讨论、总结,最后得出下列结论,必要时教师可适度引导。
此处需要灵活应用积的乘方、幂的乘方的逆运算.强调:(1)多项式分解因式的结果要化简:(1)x 4-y 4 (2)a 3b-ab 三、课时小结1.如果多项式各项含有公因式,则第一步是提出这个公因式.2.如果多项式各项没有公因式,则第一步考虑用公式分解因式.3.第一步分解因式以后,所含的多项式还可以继续分解,•则需要进一步分解因式.直到每个多项式因式都不能分解为止 四、随堂练习1、 课本P 117练习1、2.2、 把下列各式分解因式(1)36(x+y )2 - 49(x-y )2 (2)(x-1)+b 2(1-x )(3)(x 2+x+1)2 - 1 (4)2()4x y --2()4x y +. (5) a 2(x -y)-4b 2(x -y)五、作业课本P 119习题14.3─第2题(2)在化简过程中要正确应用去括号法则,并注意合并同类项.小结先由学生总结,其他学生和老师补充。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
时导学案人教版五四制
学习目标:
1.学习用完全平方公式分解因式,并能灵活应用提公因式法、公式法分解因式.2.基本能做到:把多项式的每一个因式都分解到不能再分解.
教学过程:
一、根据问题,自主探究
1. 完成乘法公式:(a+b)2=_____________(a-b)2=______________
将完全平方公式反过来写:
___________________________;_______________________________
2. 形如a2+2ab+b2 或a2-2ab+b2的式子称为___________
把乘法公式反过来,就可以用来把某些多项式分解因式,这种分解因式的方法叫做运用_________
二、合作交流,成果展示
1 集体交流,并完成下面的问题
1)下列各式是不是完全平方式?
(1)a2-4a+4 (2)x2+4x+4y2 (3)4a2+2ab+1 4 b2
(4)a2-ab+b2 (5)x2-6x-9 (6)a2+a+0.25(2) 将下列各式分解因式:
(1)4x2+28x+49; (2)(m+n)2-(m +n)+1 4
.
(3)6ax2+12axy+6ay2(4)-x2+4xy-4y2
三、巩固拓展,升华认知
1.课本第12页随堂练习1、2题
2.把下列各式分解因式
(1)6a-a 2-9; (2)-8ab -16a 2-b 2; (3)2a 2-a 3-a ;
(4)4x 2+20(x-x 2)+25(1-x )2 (5)a a a 1812223-+-
(6) 2x 2y -8xy +8y (7)、1222-+-b ab a
四、小结反思,智慧生成
1. 通过本节的学习,你认为应当如何分解因式?
五、课堂检测,评价收获
1.若01222
=+-++b b a ,则22ab b a +的值为_______。
2.若22
++是一个完全平方式,那么m的值是__________
916
x mxy y
3. 若a2+2a+b2-6b+10=0,则a2-b2的值为______________.
4. 把下列各式分解因式.
(1)(m2+n2)2-4m2n2 (2)3(x-1)2-18(x-1)+27
(3)(a2-2ab+b2)+(- 4a+4b)+4 (4)-x2+(2x - 3)2
(5)(m-n)xx– 16(m-n)2003(6)(x2-2)2-4(x2-2)+4.
【感谢您的阅览,下载后可自由复制或修改编辑,敬请您的关注】。
