实验六:分段三次Hermit插值
分段三次埃尔米特插值

分段三次埃尔米特插值分段线性插值函数的导)(I x h 数是间断的,若在节点k x (k =0,1,…,n )上除已知函数值外还给k f 出导数值k k m f ='(k =0,1,…,n ),这样就可构造一个导数连续的分段插值函数)(I x h ,它满足条件:(1).[][]),(,)(I 11b a C b a C x h ∈代表区间一[]b a ,阶导数连续的函数集合. (2)k k h f x =)(I ,'')(I k k h f x -(k =0,1,…n ). (3))(I x h 在每个小区间上是三次[]1,+k k x x 多项式.由两点三次插值多项式可以知道在)(I x h 区间上表达[]1,+k k x x 式为'21111211211)()(21*)()21()()(I k k k k k k k k k k k k k k k k k k h f x x x x x x x x x x x x x x f x x x x x x x x x ---+--+--+--+--=++--++++)(+'1121)(+++---k k kk k f x x x x x x )(.分段三次埃尔米特插值比分段线性插值效果明显改善,但这种插值要求给出节点上的导数值,所要提供的信息太多,其光滑度也不高(只有一阶导数连续),改进这种以克服其缺点就导致三次样条插值的提出.三次样条插值上面讨论的分段插值函数都有一致收敛性,但光滑性比较差,对于像告诉飞机的机翼形线,船体放样等型值线往往要求有二阶光滑度,即有二阶连续导数.早起工程师制图是,把富有弹性的细长木条(所谓样条)用压铁固定在样点上,在其他地方让它自由的弯曲,然后画下长条的曲线,称为样条曲线.样条曲线实际上有分段三次曲线并接而成,在连接点即样点上要求二阶导数连续,从而数学上加以概括就得到数学样条这一概念.三次样条函数定义 若函数[]b a C x S ,)(2∈,并且在每个小区间上是[]1,+j j x x 三次多项式,其中是给定b x x x a n =<<<= 10节点,则称是节点)(x S 0x ,1x ,…,n x 上的三次样条函数.若在节点上j x 给定函数值)(j j x f y =(j =0,1,…,n ),并且成立j j y x S =)( (j =0,1,…,n ),(1.1) 则称为三次)(x S 样条插值函数.由定义知道要求出)(x S ,在每个小区间上要确定[]1,+j j x x 4个待定系数,一共有个小n 区间,所以应该确定4个参数n .根据在上二)(x S []b a ,阶导数的连续性,在节点j x (j =1,2,…,n -1)处应该满足连续性的条件)0()0(+=-j j x S x S ,)0()0(''+=-j j x S x S (1.2))0()0(''''+=-j j x S x S .一共有3n -3个条件,再加上要满)(x S 足插值条件(1.1),共有4n -2个条件,因此还需要2个条件才能确定)(x S .通常可以在区间[]b a ,端点0x a =,n x b =上各加上一个条件(称为边界条件),可根据实际问题要求给定.常见的有以下3种;(1)已知两端的一阶导数值,即'00')(f x S =,;')(n n f x S =. (1.3)(2)两端的二阶导数已知,即''00'')(f x S =,'''')(n n f x S =, (1.4)其特殊情况为0)()(''0''==n x S x S . (1.5)(3)当)(x f 是以n x -0x 为周期的周期函数时,则要求也是)(x S 周期函数.这时边界条件应满足)0()0(0-=+n x S x S ,)0()0('0'-=+n x S x S , )0()0(''0''-=+n x S x S . (1.6)而此时(1.1)中n y y =0.这样确定的样条函数称)(x S 为周期样条函数. 埃尔米特插值不少实际问题的插值问题不但要求在节点上函数值相等,而且还要求对应的导数值也相等,甚至要求高阶导数也相等,满足这种要求插值的多项式就是埃尔米特(Hermi t e )插值多项式.下面只讨论函数值与导数值个数一样的情况.设在节点上b x x x a n ≤<<<≤ 10,)(i i x f y =,)('j j x f m =(j =0,1,…,n ),要求插值多项式)(x H ,满足条件j j y x H =)(,j j m x H =)('(j =0,1,…,n ). (1.1)这里给出了2n +2个条件,可唯一确定一个次数不超过2n +1的多项式)()(12x H x H n =+,其形式为12121012)(++++++=n n n x a x a a x H .如果根据条件(1.1)来确定2n +2个系数0a ,1a ,…,12+n a ,显然非常复杂,因此,我们依旧采用拉格朗日插值多项式的基函数的方法.先求插值基函数)(x j α及)(x j β(j =0,1,…,n ),一共有2n +2个,每一个基函数都是2n +1次多项式,且满足条件⎪⎪⎭⎪⎪⎬⎫====⎩⎨⎧=≠==).,,1,0,()(,0)(;0)(,,1,,0)(''n k j x x x k j k j x jk k j k j k j jk k j δββαδα (1.2)于是满足条件(1.1)的插值多项式可以写成)()(12x H x H n +=用插值基函数表示的形式[]∑=-+=nj j j j j n x m x y x H 012)()()(βα. (1.3)由条件(1.2)可以知道,有k k n y x H =-)(12,kn m x H =+)('12,(k =0,1,…,n ).下面的问题就是求满足条件(1.2)的基函数以)(x j α及)(x j β.所以,我们可以利用拉格朗日插值基函数)(x l j .令)()()(2x l b ax x a j j +=,由条件(1.2)有1)()()(2=+=j j j j j x l b ax x α,[]0)()(2)()()(''=++=j j j j j j j j j x l b ax x al x l x α,整理得⎩⎨⎧=+=+0)(21'j j j x l a b ax . 解出)(2'j j x l a -=,)(21'j j j x l x b +=.由于)())(()()())(()()(110110n j j j j j j n j j j x x x x x x x x x x x x x x x x x l --------=+-+- ,利用两边取对数再求导数,有∑≠=-=njk k kj j jx x x l 0'1)(,所以有)()1)(21()(20x l x x x x x a j njk k kj j j ∑≠=---=. (1.4)同理,可以得到)()()(2x l x x x j j j -=β. (1.5)同时还证明满足条件(1.1)的插值多项式是唯一的.用反证法,假设及都满)(12x H n +)(12x H n +足条件(1.1),所以有)()()(1212x H x H x n n ++-=ϕ在每个节点上均有二重根,即)(x ϕ有2n +2重根.但是是不高)(x ϕ于2n +1次的多项式,所以0)(≡x ϕ.唯一性得到证明.。
分段线性插值和分段Hermit插值课程设计

一、前言本文建立在数值分析的理论基础上,能够在Matlab 环境中运行,给出了理论分析、具体实例、程序清单以及程序运行结果,对设计任务中的函数进行了分段线性插值和分段三次Hermit 插值,分别画出分段线性插值多项式和分段三次Hermit 插值多项式的图,最后对着两种不同类型的多项式进行比较和误差分析,找出这两种不同插值方法各自的优劣。
发现分段三次Hermit 插值比分段线性插值的效果要好,在步长越小时分段三次Hermit 插值与插值函数逼近效果更明显,相应的误差越小,而分段线性插值在步长越小时在个别点会出现较大的误差,但总体效果还是可以的,三次Hermit 插值总体上比分段线性插值更光滑,这也符合理论。
二、具体理论知识点(1)分段线性插值近似一条曲线的最简单的方法是过曲线上若干点作一条折线,这就是分段线性插值问题,它的确切提法是:设)(x f 在区间 ],[b a 上的差值数据为)(i i x f y = ,i i h x x n i -+=-≤≤1max 10,求一个函数)(x h φ满足:(1)[]b a C x h ,)(∈φ;(2)在每个子区间[]1,+i i x x )1,,1,0(-=n i 上1)(P x h ∈φ;(3) .,,1,0,)(n i y x i i h ==φ。
我们可以用Lagrange 插值的思想来构造分段线性插值函数)(x h φ,设满足上述条件(1)和(2)的所有函数构成的线性空间为h Φ。
先找线性空间 h Φ 的基函数)(,x l i n ),,1,0(n i =,使得:n j i x l ij j i n ,1,0,,)(,=∂=不难得出,)(,x l i n 的表达式为:[][]⎪⎩⎪⎨⎧∈∈--=,,,0,,,)(1101010,n n x x x x x x x x x x x l[][][]⎪⎪⎪⎩⎪⎪⎪⎨⎧∉∈--∈--=+-+++---,,,0,,,,,,)(11111111,i i i i i i i i i i i i i n x x x x x x x x x x x x x x x x x x l 1,2,1-=n i ,[][]⎪⎩⎪⎨⎧∈∈--=---,,,0,,,)(101101,n n n n n n x x x x x x x x x x x l所以有了基函数)(,x l i n ,满足条件(1)-(3)的分段线性插值函数)(x h φ就可写为:()∑=⋅=ni i n i h x l y x 0,)(φ(2)分段三次Hermit 插值分段三次Hermit 插值问题提法为:给定],[b a 上的1+n 个插值节点的插值数,仍记ii n i h x x -+-≤≤=110max ,并设被插值函数)(x f 在这些节点出的函数值()i i x f y = 和导数值()i i x f m '=都已知,要求)(x f 的一个插值函数)(x H h ,使之满足:(1)对n i ,,1,0 =,有i i h y x H =)(,i i h m x H =')(;(2)在每个子区间 []1,+i i x x 上,)(x H h 是不超过三次的多项式。
分段三次hermite函数

分段三次hermite函数
分段三次 Hermite 函数是一种用于插值数据、拟合数据以及数值微分的函数。
它的特点是可以通过选择足够的基函数来适应各种不同的非线性函数。
本文将深入探讨分段三次 Hermite 函数的定义、应用和优点。
一、定义
分段三次 Hermite 函数是一种三次多项式函数。
它由基函数和插值条件构成。
1. 基函数
1)常数项
2)线性项
3)二次项
这些基函数可以用于构建分段三次 Hermite 函数,使其适应不同的非线性函数。
2. 插值条件
1)值的匹配条件
二、应用
分段三次 Hermite 函数广泛应用于数值微分、插值和拟合。
下面将分别介绍这些应用。
分段三次 Hermite 函数可以用于插值数据。
通过确定插值条件,可以得到一个分段三次 Hermite 函数,使其在给定数据点处与目标函数匹配。
这种方法常常用于构建数值框架,如数值微分和数值积分。
3. 拟合
三、优点
1. 精确度高
2. 稳定性高
分段三次 Hermite 函数具有优良的稳定性。
它可以处理大量的数据,而不会出现精度问题或数值不稳定性。
3. 方便性高
4. 可扩展性高
分段三次 Hermite 函数具有非常强的可扩展性。
它可以扩展到高维空间,适应各种不同的数据类型,从而得到非常精确的结果。
数值分析实验六(分段三次Hermite插值)

数值分析实验六(分段三次Hermite插值)《数值分析》实验报告实验编号:实验六课题名称:分段三次Hermite插值一、算法介绍给定的函数为f(x)=1/(25*x*x+1),将给定区间分成10分,得到11个节点:x[0],x[1],...,x[10],构造插值函数的基函数。
当x在(x[0],x[1])区间上时,H[0] = (x-x[0])*[((x-x[1])/(x[0]-x[1]))^2]。
其余的区间为H[0]=0。
h[0]= [1+2*(x-x[0])/(x[1]-x[0])]*[((x-x[1])/(x[0]-x[1]))^2]。
当x在[x[i-1],x[i]] (i=1,2,3, (9)区间上时,H[i]=(x-x[i])*[((x-x[i-1])/(x[i]-x[i-1]))^2],h[i]=[1+2*(x-x[i])/(x[i-1]-x[i])]*[((x-x[i-1])/(x[i]-x[i-1]))^2)。
当x在(x[i],x[i+1]](i=1,2,3,…,10)区间上其余的区间为H[i]=(x-x[i])[((x-x[i+1])/(x[i]-x[i+1]))^2],h[i]=[1+2*(x-x[i])/(x[i+1]-x[i])]*[((x-x[i+1 ])/(x[i]-x[i+1]))^2]。
其余区间上均为H[i]=0,h[i]=0(i=1,2,…,10)。
当x在(x[9],x[10])区间上时,H[10] = (x-x[9])(((x-x[10])/(x[9]-x[10]))^2).其余的区间为H[10]=0.h[10]= (1+2*((x-x[9])/(x[10]-x[9])))(((x-x[10])/(x[9]-x[10]))^2).其余区间h[10]=0。
构造函数H(x) =∑(y[i]*h[i]+y'[i]*H[i],(i=0,1,…,10)。
二、程序代码// testV iew.cpp : implementation of the CT estV iew class//#include "stdafx.h"#include "test.h"#include "testDoc.h"#include "testView.h"#ifdef _DEBUG#define new DEBUG_NEW#undef THIS_FILEstatic char THIS_FILE[] = __FILE__;#endif/////////////////////////////////////////////////////////////////// //////////// CTestV iewIMPLEMENT_DYNCREA TE(CTestView, CView)BEGIN_MESSAGE_MAP(CTestView, CView)//{{AFX_MSG_MAP(CTestView)// NOTE - the ClassWizard will add and remove mapping macros here.// DO NOT EDIT what you see in these blocks of generated code!//}}AFX_MSG_MAP// Standard printing commandsON_COMMAND(ID_FILE_PRINT, CView::OnFilePrint)ON_COMMAND(ID_FILE_PRINT_DIRECT, CV iew::OnFilePrint) ON_COMMAND(ID_FILE_PRINT_PREVIEW,CView::OnFilePrintPreview)END_MESSAGE_MAP()/////////////////////////////////////////////////////////////////// //////////// CTestV iew construction/destructionCTestView::CTestV iew(){// TODO: add construction code here}CTestView::~CT estView(){}BOOL CTestView::PreCreateWindow(CREA TESTRUCT& cs){// TODO: Modify the Window class or styles here by modifying // the CREA TESTRUCT csreturn CV iew::PreCreateWindow(cs);}/////////////////////////////////////////////////////////////////// //////////// CTestV iew drawingvoid CTestView::OnDraw(CDC* pDC){CTestDoc* pDoc = GetDocument();ASSERT_V ALID(pDoc);// TODO: add draw code for native data hereint i,j,k;double x,y,p_x,p_y,l,xx[100],f[100],F[100],sum,p_sum;CPen MyPen,*OldPen;pDC->SetViewportOrg(400,400); //定义坐标原点for(i=-500;i<500;i++){pDC->SetPixel(0,i,RGB(0,0,0));pDC->SetPixel(i,0,RGB(0,0,0)); //画出坐标}pDC->TextOut(-210,5,"-1");pDC->TextOut(196,5,"1");//原函数MyPen.CreatePen(PS_SOLID,1,RGB(255,0,0));//定义画笔颜色OldPen=pDC->SelectObject(&MyPen);x=-1.0,y=1/(1+25*x*x);p_x=x*200;p_y=-y*200;pDC->MoveTo(p_x,p_y);for (x=-1.0;x<=1.0;x+=0.0001){y=1/(1+25*x*x);p_x=x*200;p_y=-y*200;pDC->LineT o(p_x,p_y);}pDC->SelectObject(OldPen);MyPen.DeleteObject();//分段三次Hermite插值MyPen.CreatePen(PS_SOLID,1,RGB(0,0,0)); OldPen=pDC->SelectObject(&MyPen); x=-1.0,y=1.0/(1+25*x*x);p_x=x*200;p_y=-y*200;pDC->MoveTo(p_x,p_y);x=-1.0;for(i=0;i<=10;i++){f[i]=1/(1+25*x*x);xx[i]=x;F[i]=-50*x/(1+25*x*x)/(1+25*x*x); //导数x+=0.2;}x=-1.0;for(j=0;j<=1000;j++){sum=0;for(i=0;i<=10;i++){if(x==xx[i]){sum=f[i];p_x=x*200,p_y=-sum*200;pDC->LineT o(p_x,p_y);break;}if(xxx[i]){y=(1+2*(x-xx[i])/(xx[i+1]-xx[i]))*(x-xx[i+1])*(x-xx[i+1])/(xx[i]-xx[i+1])/(xx[i]-xx[i+1]);sum+=f[i]*y;y=(1+2*(x-xx[i+1])/(xx[i]-xx[i+1]))*(x-xx[i])*(x-xx[i])/(xx[i+1]-xx[i])/(xx[i+1]-xx[i]);sum+=f[i+1]*y;y=(x-xx[i])*(x-xx[i+1])*(x-xx[i+1])/(xx[i]-xx[i+1])/(xx[i]-xx[i+1]);sum+=F[i]*y;y=(x-xx[i+1])*(x-xx[i])*(x-xx[i])/(xx[i+1]-xx[i])/(xx[i+1]-xx[i]);sum+=F[i+1]*y;p_x=x*200;p_y=-sum*200;pDC->LineT o(p_x,p_y);break;}}x+=0.002;}pDC->SelectObject(OldPen);MyPen.DeleteObject();/////////////////////////////////////////////////////////////////// //////////// CTestV iew printingBOOL CTestView::OnPreparePrinting(CPrintInfo* pInfo){// default preparationreturn DoPreparePrinting(pInfo);}void CTestView::OnBeginPrinting(CDC* /*pDC*/, CPrintInfo* /*pInfo*/){// TODO: add extra initialization before printing}void CTestView::OnEndPrinting(CDC* /*pDC*/, CPrintInfo* /*pInfo*/){// TODO: add cleanup after printing}/////////////////////////////////////////////////////////////////// //////////// CTestV iew diagnostics#ifdef _DEBUGvoid CTestView::AssertV alid() const{CView::AssertV alid();}void CTestView::Dump(CDumpContext& dc) const{CView::Dump(dc);CTestDoc* CT estV iew::GetDocument() // non-debug version is inline{ASSERT(m_pDocument->IsKindOf(RUNTIME_CLASS(CT estD oc)));return (CT estDoc*)m_pDocument;}#endif //_DEBUG/////////////////////////////////////////////////////////////////// //////////// CTestV iew message handlers三、运算结果截屏红色的曲线为原函数图像,黑色曲线为分段三次Hermite插值曲线四、算法分析上述图像中黑色的曲线为分段分段三次Hermite插值多项式所对应的图像,由图像可看出黑色的分段三次Hermited插值函数图像和拉格朗日、分段线性插值相比与红色被逼近函数的重合度最好,说明分段三次Hermite插值在函数的各节点两边插值函数的导数是相等的,保证了在各节点的平滑性,且不会出现Runge现象。
分段三次Hermite插值及其与三次样条的比较
分段三次Hermite插值及其与三次样条的⽐较分段三次 Hermite 插值多项式 (PCHIP)语法p = pchip(x,y,xq)pp = pchip(x,y)说明= pchip(,,)返回与xq中的查询点对应的插值p的向量。
p的值由x和y的保形分段三次插值确定。
= pchip(,)返回⼀个分段多项式结构体以⽤于ppval和样条实⽤⼯具unmkpp。
例1使⽤spline和pchip插⼊数据将spline和pchip为两个不同函数⽣成的插值结果进⾏⽐较。
创建由x值、点y处的函数值以及查询点xq组成的向量。
使⽤spline和pchip计算查询点处的插值。
绘制查询点处的插值函数值以进⾏⽐较。
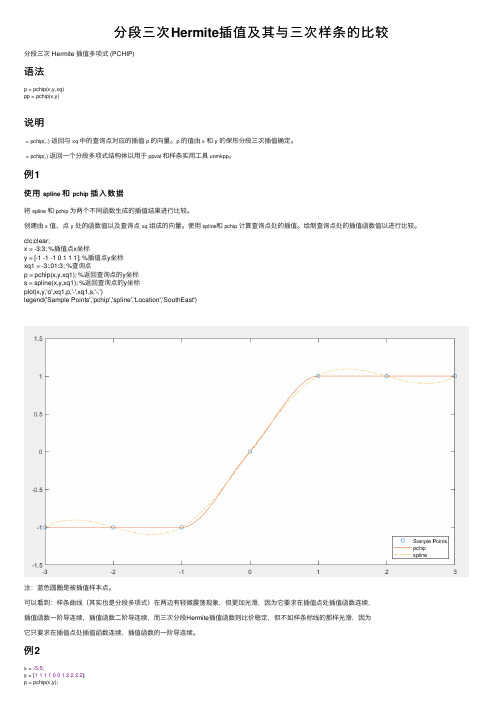
clc;clear;x = -3:3; %插值点x坐标y = [-1 -1 -1 0 1 1 1]; %插值点y坐标xq1 = -3:.01:3; %查询点p = pchip(x,y,xq1); %返回查询点的y坐标s = spline(x,y,xq1); %返回查询点的y坐标plot(x,y,'o',xq1,p,'-',xq1,s,'-.')legend('Sample Points','pchip','spline','Location','SouthEast')注:蓝⾊圆圈是被插值样本点。
可以看到:样条曲线(其实也是分段多项式)在两边有轻微震荡现象,但更加光滑,因为它要求在插值点处插值函数连续,插值函数⼀阶导连续,插值函数⼆阶导连续,⽽三次分段Hermite插值函数则⽐价稳定,但不如样条标线的那样光滑,因为它只要求在插值点处插值函数连续,插值函数的⼀阶导连续。
例2x = -5:5;y = [11110012222];p = pchip(x,y);xq = -5:0.2:5;pp = ppval(p,xq); %返回插值函数的查询点处的y坐标plot(x,y,'o',xq,pp,'-.')ylim([-0.22.2])例3x = -5:5;y = [11110012222];p = pchip(x,y);s = spline(x,y);xq = -5:0.1:5;pp = ppval(p,xq); %返回插值函数的查询点处的y坐标ss = ppval(s,xq); %返回插值函数的查询点处的y坐标figure(1);hold on;plot(x,y,'o',xq,pp,'-.',xq,ss,'b-')ylim([-0.22.2])figure(1);hold on ;legend('Sample Points','分段三次Hermite','分段三次样条','Location','SouthEast')PCHIP是分段三次hermit插值,但书中的该⽅法必须知道点的值和导数值,为什么PCHIP的变量只有函数值⽽没有导数值?在⽤pchip插值的过程中,matlab会基于所给的函数值来帮你估算各导数值。
三次Hermite插值

04 实例分析
CHAPTER
实例一:已知数据点的插值
总结词
利用已知数据点进行插值,可三次Hermite插值方法,利用已知的数据点来估计未知点的值。这 种方法能够更好地处理数据点的变化,并提高插值的精度。
CHAPTER
插值多项式的构造
定义
Hermite插值法是一种通过已知的离散数据点来构造一个多 项式,使其能够准确地经过这些数据点,并尽可能地平滑地 连接这些点的方法。
构造方法
Hermite插值多项式由两个部分组成,一个是线性函数,另 一个是二次函数。线性函数部分用于确保插值多项式能够准 确地经过数据点,而二次函数部分则用于保证插值多项式的 平滑性。
实例二:未知数据点的插值
总结词
在未知数据点的情况下,可以通过三次 Hermite插值方法,预测并估计未知点的值。
详细描述
在数据点未知的情况下,可以利用三次 Hermite插值方法,根据已知的数据点来预 测和估计未知点的值。这种方法能够为后续 的数据分析和处理提供重要的参考依据。
实例三:复杂函数的插值
三次Hermite插值能够提供高精度的插值结果,特别是在处理
复杂函数时。
稳定性好
02
该方法在处理大数据集时表现出良好的稳定性,不易受到噪声
和异常值的影响。
易于实现
03
三次Hermite插值的算法相对简单,易于在计算机上实现和优
化。
三次Hermite插值的局限性
对初始数据敏感
三次Hermite插值的结果对初始数据的选择 较为敏感,不同的初始数据可能导致不同的 插值结果。
实验六 分段三次Hermite插值画函数图像

实验六: 分段三次Hermite插值画函数图像学号: 姓名:指导老师:马季骕班级:计算机科学与技术(非师范)1、算法说明:分段三次Hermit插值的做法是在每一个小区间上作三次Hermit插值,因此在每一个插值节点上都需要构造两个插值基函数,然后再作它们的线性组合。
分段三次Hermit插值基函数如下:H(x)=Σ(yihi(x)+y’iHi(x))给定的函数为f(x)=1/(25*x*x+1),将给定区间分成10分,得到11个节点:x[0],x[1],...,x[10],构造插值函数的基函数。
当x在(x[0],x[1])区间上时,H[0] = (x-x[0])*[((x-x[1])/(x[0]-x[1]))^2]。
其余的区间为H[0]=0。
h[0]= [1+2*(x-x[0])/(x[1]-x[0])]*[((x-x[1])/(x[0]-x[1]))^2]。
当x在[x[i-1],x[i]] (i=1,2,3,...,9)区间上时,H[i]=(x-x[i])*[((x-x[i-1])/(x[i]-x[i-1]))^2],h[i]=[1+2*(x-x[i])/(x[i-1]-x[i])]*[((x-x[i-1])/(x[i]-x[i-1]))^2)。
当x在(x[i],x[i+1]](i=1,2,3, (10)区间上其余的区间为H[i]=(x-x[i])[((x-x[i+1])/(x[i]-x[i+1]))^2],h[i]=[1+2*(x-x[i])/(x[i+1]-x[i])]*[((x-x[i+1])/(x[i]-x[i+ 1]))^2]。
其余区间上均为H[i]=0,h[i]=0(i=1,2,…,10)。
当x在(x[9],x[10])区间上时,H[10] = (x-x[9])(((x-x[10])/(x[9]-x[10]))^2).其余的区间为H[10]=0.h[10]= (1+2*((x-x[9])/(x[10]-x[9])))(((x-x[10])/(x[9]-x[10]))^2).其余区间h[10]=0。
数值分析实验报告Hermite插值法、Runge现象,比较Language插值、分段线性插值、分段三次Hermie插值

山东师范大学数学科学学院实验报告x 0.1 0.5 1 1.5 2 2.5 3y 0.95 0.84 0.86 1.06 1.5 0.72 1.9y' 1 1.5 2 2.5 3 3.5 4求质点在时刻1.8时的速度,并画出插值多项式的图像。
1)运用Hermite插值法画出图像,如图4-1,并求质点在时刻1.8时的速度。
>>clear>>clc>>X=[0.1 0.5 1 1.5 2 2.5 3;0.95 0.84 0.86 1.06 1.5 0.72 1.9;1 1.5 2 2.5 3 3.5 4];>> x=0.1:0.01:3;>> H=Hermite1(X,x);>> plot(x,H)>> hold on>> plot(X(1,:),X(2,:),'r*')>> H1_8=Hermite(X,1.8);>> plot(1.8,H1_8,'go')>> legend('插值图像','原始点','目标点');图4-1二、验证高次插值的Runge现象问题分析和算法设计(一)Language插值代码function [Ln] =Lagrange(X,x)%请输入2*n+1矩阵X,X中第一行每个元素都是插值节点,X中第二行每个元素都是插值节点对应的函数值;%第二章P24例一拉格朗日插值n=size(X,2);d=0;for m=1:1:nif x==X(1,m);d=m;breakendend运行结果和总结 运行结果 例:给定函数55,11)(2≤≤-+=x xx f ; (1) 验证表2-10的误差结果(高次插值的Runge 现象);(2) 以0.1为步长分别进行Language 插值、分段线性插值、分段三次Hermite插值,画出三种插值函数以及f(x)的图像,比较三种插值结果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《数值分析》实验报告实验序号:实验六题目名称: 分段三次Hermit插值学号: 姓名: 、任课教师: 马季骕专业班级:计算机科学与技术(非师范)1、题目描述这是一种光滑的分段插值,给定[a,b]上的节点a=x0<x1<x2<…xn-1<xn=b和微商值f’(xi)=y’i(i=0,1,2…,n),作一个分段三次Hermit插值函数H(x),要求满足条件:(1)H(xi)=yi,H’(xi)=yi(i=0,1,2,…,n)。
(2)在每一个小区间[xi,xi+1]上是三次多项式。
根据前的结果做出个点的插值基函数2、算法分析●分段三次Hermit插值的算法思想:分段三次Hermit插值的做法是在每一个小区间上作三次Hermit插值,因此在每一个插值节点上都需要构造两个插值基函数,然后再作它们的线性组合。
分段三次Hermit插值基函数如下:H(x)=Σ(yihi(x)+y’iHi(x))●具体程序设计:for(i=0;i<=10;i++){ax[i]=-1+((2/10.0)*i); //选取节点ay[i]=1.0/(1+25*ax[i]*ax[i]); //函数值a[i]=(-50*ax[i])/((1+25*ax[i]*ax[i])*(1+25*ax[i]*ax[i]));//一阶导数值}x1=-1;y1=1/(1+25*x1*x1);while(x1<=1){m=0;x1=x1+0.00001;for(i=0;i<=10;i++){if(i==0&&x1>=ax[0]&&x1<=ax[1]){n=(1+2*((x1-ax[0])/(ax[1]-ax[0])))*((x1-ax[1])/(ax[0]-ax[ 1]))*((x1-ax[1])/(ax[0]-ax[1]));// 插值基函数h(x)tt=ay[0]*n; //插值基函数与其函数值线性组合h=(x1-ax[0])*((x1-ax[1])/(ax[0]-ax[1]))*((x1-ax[1])/(ax[0 ]-ax[1]));//插值基函数H(x)tt1=a[0]*h;//插值基函数与其一阶导数值线性组合m=tt+tt1+m;//把插值基函数做线性组合}else{if(x1>=ax[i-1]&&x1<=ax[i]){n=(1+2*((x1-ax[i])/(ax[i-1]-ax[i])))*((x1-ax[i-1])/(ax[i]-ax[i-1]))*((x1-ax[i-1])/(ax[i]-ax[i-1]));tt=ay[i]*n;h=(x1-ax[i])*((x1-ax[i-1])/(ax[i]-ax[i-1]))*((x1-ax[i -1])/(ax[i]-ax[i-1]));tt1=a[i]*h;m=tt+tt1+m;}else{if(x1>ax[i]&&x1<=ax[i+1]){n=(1+2*((x1-ax[i])/(ax[i+1]-ax[i])))*((x1-ax[i+ 1])/(ax[i]-ax[i+1]))*((x1-ax[i+1])/(ax[i]-ax[i+1]));tt=ay[i]*n;h=(x1-ax[i])*((x1-ax[i+1])/(ax[i]-ax[i+1]))*((x1 -ax[i+1])/(ax[i]-ax[i+1]));tt1=a[i]*h;m=tt+tt1+m;}else{if(i==9&&x1>ax[9]&&x1<=ax[10]){n=(1+2*((x1-ax[10])/(ax[9]-ax[10])))*((x1-ax [9])/(ax[10]-ax[9]))*((x1-ax[9])/(ax[10]-ax[9]));tt=ay[i]*n;h=(x1-ax[10])*((x1-ax[9])/(ax[10]-ax[9]))*(( x1-ax[9])/(ax[10]-ax[9]));tt1=a[i]*h;m=tt+tt1+m;}}}}}}3、运行结果截图:4、程序代码// SHIYAN456View.cpp : implementation of the CSHIYAN456View class//#include "stdafx.h"#include "SHIYAN456.h"#include "SHIYAN456Doc.h"#include "SHIYAN456View.h"#ifdef _DEBUG#define new DEBUG_NEW#undef THIS_FILEstatic char THIS_FILE[] = __FILE__;#endif///////////////////////////////////////////////////////////////// ////////////// CSHIYAN456ViewIMPLEMENT_DYNCREATE(CSHIYAN456View, CView)BEGIN_MESSAGE_MAP(CSHIYAN456View, CView)//{{AFX_MSG_MAP(CSHIYAN456View)ON_COMMAND(ID_FFunction, OnFFunction)ON_COMMAND(ID_Lagrange, OnLagrange)ON_COMMAND(ID_Subsection, OnSubsection)ON_COMMAND(ID_Hermite, OnHermite)//}}AFX_MSG_MAP// Standard printing commandsON_COMMAND(ID_FILE_PRINT, CView::OnFilePrint)ON_COMMAND(ID_FILE_PRINT_DIRECT, CView::OnFilePrint)ON_COMMAND(ID_FILE_PRINT_PREVIEW, CView::OnFilePrintPreview) END_MESSAGE_MAP()///////////////////////////////////////////////////////////////// ////////////// CSHIYAN456View construction/destructionCSHIYAN456View::CSHIYAN456View(){// TODO: add construction code here}CSHIYAN456View::~CSHIYAN456View(){}BOOL CSHIYAN456View::PreCreateWindow(CREATESTRUCT& cs){// TODO: Modify the Window class or styles here by modifying // the CREATESTRUCT csreturn CView::PreCreateWindow(cs);}///////////////////////////////////////////////////////////////// ////////////// CSHIYAN456View drawingvoid CSHIYAN456View::OnDraw(CDC* pDC){CSHIYAN456Doc* pDoc = GetDocument();ASSERT_VALID(pDoc);// TODO: add draw code for native data hereAfxGetMainWnd()->SetWindowText("实验四五六函数图像");for(int k=650;k<=690;k++){pDC->SetPixel(k,55,RGB(255,0,0));pDC->SetPixel(k,85,RGB(0,255,0));pDC->SetPixel(k,115,RGB(0,0,255));pDC->SetPixel(k,145,RGB(0,255,255));}pDC->TextOut(700,50,"原函数图像");pDC->TextOut(700,80,"Lagrange插值函数图像");pDC->TextOut(700,110,"分段线性插值函数图像");pDC->TextOut(700,140,"Hermite插值函数图像");for(int i=6;i<=600;i++)pDC->SetPixel(400,i,RGB(0,0,0));pDC->TextOut(395,4,"y");for(int j=100;j<=700;j++)pDC->SetPixel(j,500,RGB(0,0,0));pDC->TextOut(700,500,"x");//pDC->MoveTo(400,500);}///////////////////////////////////////////////////////////////// ////////////// CSHIYAN456View printingBOOL CSHIYAN456View::OnPreparePrinting(CPrintInfo* pInfo){// default preparationreturn DoPreparePrinting(pInfo);}void CSHIYAN456View::OnBeginPrinting(CDC* /*pDC*/, CPrintInfo* /*pInfo*/){// TODO: add extra initialization before printing}void CSHIYAN456View::OnEndPrinting(CDC* /*pDC*/, CPrintInfo*/*pInfo*/){// TODO: add cleanup after printing}///////////////////////////////////////////////////////////////// ////////////// CSHIYAN456View diagnostics#ifdef _DEBUGvoid CSHIYAN456View::AssertValid() const{CView::AssertValid();}void CSHIYAN456View::Dump(CDumpContext& dc) const{CView::Dump(dc);}CSHIYAN456Doc* CSHIYAN456View::GetDocument() // non-debug version is inline{ASSERT(m_pDocument->IsKindOf(RUNTIME_CLASS(CSHIYAN456Doc)));return (CSHIYAN456Doc*)m_pDocument;}#endif //_DEBUG///////////////////////////////////////////////////////////////// ////////////// CSHIYAN456View message handlersvoid CSHIYAN456View::OnFFunction(){// TODO: Add your command handler code hereCClientDC dr(this);COLORREF rgb=RGB(255,0,0);double x1,y1,x,y;x1=-1.0;y1=1/(1+25*x1*x1);x=x1*200+400;y=-y1*200+500;while(x1<=1){dr.MoveTo(int(x),int(y));x1=x1+0.00001;y1=1/(1+25*x1*x1);x=x1*200+400;y=-y1*200+500;dr.SetPixel(int(x),int(y),rgb);}}void CSHIYAN456View::OnLagrange(){// TODO: Add your command handler code hereCClientDC dr(this);COLORREF rgb=RGB(0,255,0);int i,j;double x1=0,y1=0,x=0,y=0,m=0,n=0,ax[100],ay[100]; for(i=0;i<=10;i++){ax[i]=-1+((2/10.0)*i);ay[i]=1.0/(1+25*ax[i]*ax[i]);}x1=-1;y1=1/(1+25*x1*x1);x=x1*200+400;y=-y1*200+500;dr.MoveTo(int(x),int(y));while(x1<=1){m=0;for(i=0;i<=10;i++){n=1;for(j=0;j<=10;j++){if(i!=j)n=((x1-ax[j])/(ax[i]-ax[j]))*n;}m=ay[i]*n+m;}x=x1*200+400;y=-m*200+500;dr.SetPixel(int(x),int(y),rgb);x1=x1+0.00001;}}void CSHIYAN456View::OnSubsection(){// TODO: Add your command handler code hereCClientDC dr(this);COLORREF rgb=RGB(0,0,255);int i;double x1=0,y1=0,x=0,y=0,m=0,n=0,ax[100],ay[100]; for(i=0;i<=20;i++){ax[i]=-1+((2/20.0)*i);ay[i]=1.0/(1+25*ax[i]*ax[i]);}x1=-1;y1=1/(1+25*x1*x1);x=x1*200+400;y=-y1*200+500;dr.MoveTo(int(x),int(y));while(x1<=1){m=0;x1=x1+0.00001;for(i=0;i<=20;i++){if(i==0&&x1>=-1&&x1<=-0.9){n=ay[0]*((x1-ax[1])/(ax[0]-ax[1]));m=n+m;}else{if(x1>=ax[i-1]&&x1<=ax[i]){n=ay[i]*((x1-ax[i-1])/(ax[i]-ax[i-1])); m=n+m;}else{if(x1>ax[i]&&x1<=ax[i+1]){n=ay[i]*((x1-ax[i+1])/(ax[i]-ax[i+1]));m=m+n;}else{if(i==19&&x1>ax[19]&&x1<=ax[20]){n=ay[20]*((x1-ax[19])-(ax[20]-ax[19]) );m=n+m;}}}}}x=x1*200+400;y=-m*200+500;dr.SetPixel(int(x),int(y),rgb);}}void CSHIYAN456View::OnHermite(){// TODO: Add your command handler code hereCClientDC dr(this);COLORREF rgb=RGB(0,255,255);int i;doublex1=0,y1=0,x=0,y=0,m=0,n=0,tt=0,tt1=0,h=0,ax[100],ay[100],a[100];for(i=0;i<=10;i++){ax[i]=-1+((2/10.0)*i);ay[i]=1.0/(1+25*ax[i]*ax[i]);a[i]=(-50*ax[i])/((1+25*ax[i]*ax[i])*(1+25*ax[i]*ax[i]));}x1=-1;y1=1/(1+25*x1*x1);x=x1*200+400;y=-y1*200+500;dr.MoveTo(int(x),int(y));while(x1<=1){m=0;x1=x1+0.00001;for(i=0;i<=10;i++){if(i==0&&x1>=ax[0]&&x1<=ax[1]){n=(1+2*((x1-ax[0])/(ax[1]-ax[0])))*((x1-ax[1])/( ax[0]-ax[1]))*((x1-ax[1])/(ax[0]-ax[1]));tt=ay[0]*n;h=(x1-ax[0])*((x1-ax[1])/(ax[0]-ax[1]))*((x1-ax[ 1])/(ax[0]-ax[1]));tt1=a[0]*h;m=tt+tt1+m;}else{if(x1>=ax[i-1]&&x1<=ax[i]){n=(1+2*((x1-ax[i])/(ax[i-1]-ax[i])))*((x1-ax [i-1])/(ax[i]-ax[i-1]))*((x1-ax[i-1])/(ax[i]-ax[i-1]));tt=ay[i]*n;h=(x1-ax[i])*((x1-ax[i-1])/(ax[i]-ax[i-1]))* ((x1-ax[i-1])/(ax[i]-ax[i-1]));tt1=a[i]*h;m=tt+tt1+m;}else{if(x1>ax[i]&&x1<=ax[i+1]){n=(1+2*((x1-ax[i])/(ax[i+1]-ax[i])))*(( x1-ax[i+1])/(ax[i]-ax[i+1]))*((x1-ax[i+1])/(ax[i] -ax[i+1]));tt=ay[i]*n;h=(x1-ax[i])*((x1-ax[i+1])/(ax[i]-ax[i+ 1]))*((x1-ax[i+1])/(ax[i]-ax[i+1]));tt1=a[i]*h;m=tt+tt1+m;}else{if(i==9&&x1>ax[9]&&x1<=ax[10]){n=(1+2*((x1-ax[10])/(ax[9]-ax[10])) )*((x1-ax[9])/(ax[10]-ax[9]))*((x1-ax[9])/(ax[10 ]-ax[9]));tt=ay[i]*n;h=(x1-ax[10])*((x1-ax[9])/(ax[10]-a x[9]))*((x1-ax[9])/(ax[10]-ax[9]));tt1=a[i]*h;m=tt+tt1+m;}}}}}x=x1*200+400;y=-m*200+500;dr.SetPixel(int(x),int(y),rgb);}}5、总结体会:通过本次实验我对分段三次Hermit插值有了更深刻更全面的掌握,它在给定了节点处的函数值和导数值以后,构造了一个整体上具有一阶连续微商的插值函数。
