2020~2021深圳市龙岗区第一学期九年级期末试卷
广东省深圳市2020-2021学年上学期九年级英语期末试卷分类汇编:信息匹配(部分答案)

广东省深圳市2020-2021学年上学期九年级英语期末试卷分类汇编信息匹配广东省深圳市光明区2020-2021 学年九年级上学期期末考试英语试题第三节信息匹配下面的材料A~F分别给出了六条建议。
请根据Noah、.Emelia 、Joshua、Reagan和Lily 五位同学的情况,帮助他们选择合适的建议,并在答题卡上将相应的字母编号涂黑。
(共5 小题,每小题1分)A. It can be sad when people don't believe what you say. You might think about why this has been happening. Be true to everyone. Over time, your honesty will speak for itself and people will know they can trust you.B. Tell your mom how you feel, Perhaps you both can find some time for just the two of you. Maybe each of your siblings wants the same. Be sure to share your mom—she loves every one of you!C. What exciting news for you and your sister! It shows your parents are confident with your musical talent. Talk to your parents and sister. Together, make a clear plan for the lessons. You'll do a good job.D. It's certainly possible for a person to be strong and gentle, often at the same time. If you practice kindness often, you may discover many chances to be strong and gentle at the same time,E. It's great that you want to say "thank you". Make a list of the people who do things for you. Another idea is to write thank-you notes, You may be surprised by how much a thank-you note can mean to someone!F. It's common for one to feel a little uncomfortable when he or she receives praise or attention. It shows people enjoy what you've done and they feel proud of you. You should feel proud of yourself, too\31. My parents are asking me to teach my sister piano. Any tips? ——Noah32.1 always feel strange when people clap for me. What should I do? ——Emelia33. People say I'm lying, even though Tm not. ——Joshua34.1 think I can be strong, but my friends think I'm gentle. ——Reagan35.1 have six siblings (兄弟姐妹),I want to spend time alone with my mom, but I can’t.——Lily 答案:31 — 35 CFADB广东省深圳市龙岗区2020-2021 学年九年级上学期期末考试英语试题第三节信息匹配下面的材料A-F分别介绍了六条网友回复信息, 请根据Tina, Mike,Betty, Toby和Nick的烦恼, 帮助他们选出最合适的回复, 并将其标号填入提前括号内。
广东省深圳市龙岗区2022年数学九年级第一学期期末检测试题含解析

2022-2023学年九上数学期末模拟试卷请考生注意:1.请用2B 铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。
写在试题卷、草稿纸上均无效。
2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。
一、选择题(每题4分,共48分)1.如图,CD 为O 的直径,弦AB CD ⊥于点E ,2DE =,8AB =,则O 的半径为( )A .5B .8C .3D .102.下列事件属于必然事件的是( )A .篮球队员在罚球线上投篮一次,未投中B .掷一次骰子,向上一面的点数是6C .任意画一个五边形,其内角和是540°D .经过有交通信号灯的路口,遇到红灯3.《孙子算经》中有一道题:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺,木长几何?”译文大致是:“用一根绳子去量一根木条,绳子剩余4.5尺;将绳子对折再量木条,木条剩余1尺,问木条长多少尺?”如果设木条长x 尺,绳子长y 尺,根据题意列方程组正确的是( )A . 4.5,12x y y x +=⎧⎪⎨+=⎪⎩B . 4.5,12x y y x =+⎧⎪⎨+=⎪⎩C . 4.5,12x y x y =+⎧⎪⎨=+⎪⎩D . 4.5,12x y y x +=⎧⎪⎨=-⎪⎩4.已知x 1=是一元二次方程2x mx 20+-=的一个解,则m 的值是( )A .1B .1-C .2D .2-5.一个正比例函数的图象过点(2,﹣3),它的表达式为( )A .32y x =-B .23y x =-C .32y x =D .23y x = 6.如图,在矩形ABCD 中,对角线AC 与BD 相交于点O ,AE BD ⊥,垂足为点E ,5AE =,且2EO BE =,则OA 的长为( )A.5B.25C.35D.1513 137.坡比常用来反映斜坡的倾斜程度.如图所示,斜坡AB坡比为().A.2:4 B.22:1 C.1:3 D.3:18.下列说法正确的个数是()①相等的弦所对的弧相等;②相等的弦所对的圆心角相等;③长度相等的弧是等弧;④相等的弦所对的圆周角相等;⑤圆周角越大所对的弧越长;⑥等弧所对的圆心角相等;A.1个B.2个C.3个D.4个9.如图,在△ABC中,中线AD、BE相交于点F,EG∥BC,交AD于点G,则AGAF的值是()A.23B.32C.34D.4310.若正六边形的半径长为4,则它的边长等于()A.4 B.2 C.3D.311.已知二次函数y=ax2+bx+c的y与x的部分对应值如下表:则下列判断中正确的是()x …﹣1 0 1 2 …y …﹣5 1 3 1 …A .抛物线开口向上B .抛物线与y 轴交于负半轴C .当x=3时,y <0D .方程ax 2+bx+c=0有两个相等实数根12.如图⊙O 的直径AB 垂直于弦CD ,垂足是E ,22.5A ∠=︒,4OC =,CD 的长为( )A .B .4C .D .8二、填空题(每题4分,共24分)13.若关于x 的方程kx 2+2x ﹣1=0有实数根,则k 的取值范围是_____.14.已知x-2y=3,试求9-4x+8y=_______15.如图,在△ABC 中,∠C=90°,AC=3,若cosA=35,则BC 的长为________.16.如图,一条公路的转弯处是一段圆弧AB ,点O 是这段弧所在圆的圆心,AB =40 m ,点C 是AB 的中点,且CD =10 m ,则这段弯路所在圆的半径为__________m .17.如图,在菱形ABCD 中,边长为10,60A ∠=︒.顺次连结菱形ABCD 各边中点,可得四边形1111D C B A ;顺次连结四边形1111D C B A 各边中点,可得四边形2222A B C D ;顺次连结四边形2222A B C D 各边中点,可得四边形3333A B C D ;按此规律继续下去….则四边形2019201920192019A B C D 的周长是_________.18.如图,AB 为⊙O 的直径,C 、D 为⊙O 上的点,弧AD=弧CD .若∠CAB =40°,则∠CAD =_____.三、解答题(共78分)19.(8分)如图所示,已知在平面直角坐标系xOy 中,抛物线22y ax ax c =++(其中a 、c 为常数,且0a <)与x 轴交于点A ,它的坐标是()3,0-,与y 轴交于点B ,此抛物线顶点C 到x 轴的距离为4.(1)求抛物线的表达式;(2)求CAB ∠的正切值;(3)如果点P 是抛物线上的一点,且ABP CAO ∠=∠,试直接写出点P 的坐标.20.(8分)在平面直角坐标系中,点O (0,0),点A (﹣3,0).已知抛物线y =﹣x 2+2mx+3(m 为常数),顶点为P . (1)当抛物线经过点A 时,顶点P 的坐标为 ;(2)在(1)的条件下,此抛物线与x 轴的另一个交点为点B ,与y 轴交于点C .点Q 为直线AC 上方抛物线上一动点.①如图1,连接QA 、QC ,求△QAC 的面积最大值;②如图2,若∠CBQ =45°,请求出此时点Q 坐标.21.(8分)已知:如图,AB 为⊙O 的直径,OD ∥AC .求证:点D 平分BC .22.(10分)如图,已知ABC ∆的三个顶点坐标为()2,3A -,()6,0B -,()1,0C -.(1)将ABC ∆绕坐标原点O 旋转180︒,画出旋转后的A B C '''∆,并写出点A 的对应点A '的坐标 ; (2)将ABC ∆绕坐标原点O 逆时针旋转90︒,直接写出点A 的对应点Q 的坐标 ;(3)请直接写出:以A 、B 、C 为顶点的平行四边形的第四个顶点D 的坐标 .23.(10分)如图,点D 在⊙O 的直径AB 的延长线上,CD 切⊙O 于点C ,AE ⊥CD 于点E(1)求证:AC 平分∠DAE ;(2)若AB =6,BD =2,求CE 的长.24.(10分)某商场为了方便消费者购物,准备将原来的阶梯式自动扶梯改造成斜坡式自动扶梯.如图所示,已知原阶梯式扶梯AB 长为10m ,坡角∠ABD =30°;改造后斜坡式自动扶梯的坡角∠ACB =9°,请计算改造后的斜坡AC 的长度,(结果精确到0.01(sin9°≈0.156,cos9°≈0.988,tan9°≈0.158)25.(12分)如图,抛物线y=ax2+bx+c经过△ABC的三个顶点,与y轴相交于(0,94),点A坐标为(-1,2),点B是点A关于y轴的对称点,点C在x轴的正半轴上.(1)求该抛物线的函数解析式;(2)点F为线段AC上一动点,过点F作FE⊥x轴,FG⊥y轴,垂足分别为点E,G,当四边形OEFG为正方形时,求出点F的坐标;(3)将(2)中的正方形OEFG沿OC向右平移,记平移中的正方形OEFG为正方形DEFG,当点E和点C重合时停止运动,设平移的距离为t,正方形的边EF与AC交于点M,DG所在的直线与AC交于点N,连接DM,是否存在这样的t,使△DMN是等腰三角形?若存在,求t的值;若不存在,请说明理由.26.如图,△ABC的三个顶点和点O都在正方形网格的格点上,每个小正方形的边长都为1.(1)将△ABC先向右平移4个单位,再向上平移2个单位得到△A1B1C1,请画出△A1B1C1;(2)请画出△A2B2C2,使△A2B2C2和△ABC关于点O成中心对称.参考答案一、选择题(每题4分,共48分)1、A【分析】作辅助线,连接OA ,根据垂径定理得出AE=BE=4,设圆的半径为r ,再利用勾股定理求解即可.【详解】解:如图,连接OA ,设圆的半径为r ,则OE=r-2,∵弦AB CD ⊥,∴AE=BE=4,由勾股定理得出:()22242r r =+-,解得:r=5,故答案为:A.【点睛】本题考查的知识点主要是垂径定理、勾股定理及其应用问题;解题的关键是作辅助线,灵活运用勾股定理等几何知识点来分析、判断或解答.2、C【分析】必然事件就是一定发生的事件,根据定义即可判断.【详解】解:A 、篮球队员在罚球线上投篮一次,未投中,是随机事件.B 、掷一次骰子,向上一面的点数是6,是随机事件.C 、任意画一个五边形,其内角和是540°,是必然事件.D 、经过有交通信号灯的路口,遇到红灯,是随机事件.故选:C .【点睛】本题考查了必然事件,解决本题需要正确理解必然事件、不可能事件、随机事件的概念.必然事件指在一定条件下一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件.不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.3、A【解析】本题的等量关系是:木长 4.5+=绳长,12⨯绳长1+=木长,据此可列方程组即可. 【详解】设木条长为x 尺,绳子长为y 尺,根据题意可得:4.5112x y y x +=⎧⎪⎨+=⎪⎩. 故选:A .【点睛】本题考查由实际问题抽象出二元一次方程组,解题的关键是明确题意,列出相应的二元一次方程组.4、A【解析】把x =1代入方程x 2+mx ﹣2=0得到关于m 的一元一次方程,解之即可.【详解】把x =1代入方程x 2+mx ﹣2=0得:1+m ﹣2=0,解得:m =1.故选A .【点睛】本题考查了一元二次方程的解,正确掌握一元二次方程的解的概念是解题的关键.5、A【分析】根据待定系数法求解即可.【详解】解:设函数的解析式是y =kx ,根据题意得:2k =﹣3,解得:k =﹣32. 故函数的解析式是:y =﹣32x . 故选:A .【点睛】本题考查了利用待定系数法求正比例函数的解析式,属于基础题型,熟练掌握待定系数法求解的方法是解题关键. 6、C【分析】由矩形的性质得到:,OA OB =设,BE x = 利用勾股定理建立方程求解x 即可得到答案. 【详解】解: 矩形ABCD , ,OA OB ∴=2,EO BE =设,BE x =则2,3,OE x OA OB x ===⊥,AE BD222∴=+(3)(2)5,x x2x∴=525,∴==x x∴=OA故选C.【点睛】本题考查的是矩形的性质,勾股定理,掌握以上知识点是解题的关键.7、A【分析】利用勾股定理可求出AC的长,根据坡比的定义即可得答案.【详解】∵AB=3,BC=1,∠ACB=90°,∴=∴斜坡AB坡比为BC:AC=1::4,故选:A.【点睛】本题考查坡比的定义,坡比是坡面的垂直高度与水平宽度的比;熟练掌握坡比的定义是解题关键.8、A【分析】根据圆的相关知识和性质对每个选项进行判断,即可得到答案.【详解】解:在同圆或等圆中,相等的弦所对的弧相等;故①错误;在同圆或等圆中,相等的弦所对的圆心角相等;故②错误;在同圆或等圆中,长度相等的弧是等弧;故③错误;在同圆或等圆中,相等的弦所对的圆周角相等;故④错误;在同圆或等圆中,圆周角越大所对的弧越长;故⑤错误;等弧所对的圆心角相等;故⑥正确;∴说法正确的有1个;故选:A.【点睛】本题考查了弧,弦,圆心角,圆周角定理,要求学生对基本的概念定理有透彻的理解,解题的关键是熟练掌握所学性质定理.9、C【分析】先证明AG =GD ,得到GE 为△ADC 的中位线,由三角形的中位线可得GE 12=DC 12=BD ;由EG ∥BC ,可证△GEF ∽△BDF ,由相似三角形的性质,可得12GF GE FD BD ==;设GF =x ,用含x 的式子分别表示出AG 和AF ,则可求得答案.【详解】∵E 为AC 中点,EG ∥BC ,∴AG =GD ,∴GE 为△ADC 的中位线,∴GE 12=DC 12=BD . ∵EG ∥BC ,∴△GEF ∽△BDF , ∴12GF GE FD BD ==, ∴FD =2GF .设GF =x ,则FD =2x ,AG =GD =GF +FD =x +2x =3x ,AF =AG +GF =3x +x =4x , ∴3344AG x AF x ==. 故选:C .【点睛】本题考查了三角形的中位线定理及相似三角形的判定与性质,熟练掌握相关定理及性质,是解答本题的关键. 10、A【解析】试题分析:正六边形的中心角为360°÷6=60°,那么外接圆的半径和正六边形的边长将组成一个等边三角形,故正六边形的半径等于1,则正六边形的边长是1.故选A .考点:正多边形和圆.11、C【解析】根据表格的数据,描点连线得,根据函数图像,得:抛物线开口向下;抛物线与y 轴交于正半轴;当x=3时,y <0 ;方程20ax bx c ++=有两个相等实数根.故选C.12、C【详解】∵直径AB 垂直于弦CD ,∴CE=DE=12CD , ∵∠A=22.5°,∴∠BOC=45°,∴OE=CE ,设OE=CE=x ,∵OC=4,∴x 2+x 2=16,解得:2,即:2∴2,故选C .二、填空题(每题4分,共24分)13、k≥-1【解析】首先讨论当0k =时,方程是一元一次方程,有实数根,当0k ≠时,利用根的判别式△=b 2-4ac=4+4k≥0,两者结合得出答案即可.【详解】当0k =时,方程是一元一次方程:210x -=,1,2x =方程有实数根; 当0k ≠时,方程是一元二次方程,24440b ac k =-=+≥,解得:1k ≥-且0k ≠.综上所述,关于x 的方程2210kx x +-=有实数根,则k 的取值范围是1k ≥-.故答案为 1.k ≥-【点睛】考查一元二次方程根的判别式,注意分类讨论思想在解题中的应用,不要忽略0k =这种情况.14、-3【分析】将代数式变形为9-4(x-2y ),再代入已知值可得.【详解】因为x-2y=3,所以9-4x+8y=9-4(x-2y )=9-4×3=-3 故答案为:-3【点睛】考核知识点:求整式的值.利用整体代入法是解题的关键.15、1【分析】由题意先根据∠C=90°,AC=3,cos ∠A=35,得到AB 的长,再根据勾股定理,即可得到BC 的长. 【详解】解:∵△ABC 中,∠C=90°,AC=3,cos ∠A=35, ∴335AB =, ∴AB=5,∴故此空填1.【点睛】本题考查的是锐角三角函数的定义,锐角A 的邻边b 与斜边c 的比叫做∠A 的余弦,记作cosA ,以此并结合勾股定理分析求解.16、25m【分析】根据垂径定理可得△BOD 为直角三角形,且BD=12AB ,之后利用勾股定理进一步求解即可. 【详解】∵点C 是AB 的中点,∴OC 平分AB ,∴∠BOD=90°,BD=12AB=20m , 设OB=x ,则:OD=(x-10)m ,∴()2221020x x =-+,解得:25x =,∴OB=25m ,故答案为:25m.【点睛】本题主要考查了垂径定理与勾股定理的综合运用,熟练掌握相关概念是解题关键.17、20185532+ 【分析】根据菱形的性质,三角形中位线的性质以及勾股定理求出四边形各边长,得出规律求出即可.【详解】∵菱形ABCD 中,边长为10,∠A=60°,设菱形对角线交于点O ,∴30DAO ∠=︒,∴152OD AD ==,353AO OD ==, ∴10BD =,103AC =,顺次连结菱形ABCD 各边中点,∴△AA 1D 1是等边三角形,四边形A 2B 2C 2D 2是菱形,∴A 1D 1=A A 1=12AB =5,C 1D 1 =123,A 2B 2=C 2D 2=C 2B 2=A 2D 2=12AB=5, ∴四边形A 2B 2C 2D 2的周长是:5×4=20, 同理可得出:A 3D 3=5×12,C 3D 3=12C 1D 1=12⨯3 A 5D 5=5212⎛⎫⨯ ⎪⎝⎭,C 5D 5=12C 3D 3=212⎛⎫⨯ ⎪⎝⎭3∴四边形A 2019B 2019C 2019D 2019553+故答案为:20185532+ 【点睛】 本题主要考查了菱形的性质以及矩形的性质和中点四边形的性质等知识,根据已知得出边长变化规律是解题关键.18、25°【分析】先求出∠ABC =50°,进而判断出∠ABD =∠CBD =25°,最后用同弧所对的圆周角相等即可得出结论.【详解】解:如图,连接BC ,BD ,∵AB 为⊙O 的直径,∴∠ACB =90°,∵∠CAB =40°,∴∠ABC =50°,∵弧AD=弧CD∴∠ABD =∠CBD =12∠ABC =25°, ∴∠CAD =∠CBD =25°.故答案为:25°.【点睛】本题考查的是圆周角定理,直径所对的圆周角是直角,直角三角形的性质,解本题的关键是作出辅助线.三、解答题(共78分)19、(1)223y x x =--+;(2)13;(2)点P 的坐标是()1,0或532,39⎛⎫- ⎪⎝⎭【分析】(1)先求得抛物线的对称轴方程,然后再求得点C 的坐标,设抛物线的解析式为y=a (x+1)2+4,将点(-2,0)代入求得a 的值即可;(2)先求得A 、B 、C 的坐标,然后依据两点间的距离公式可得到BC 、AB 、AC 的长,然后依据勾股定理的逆定理可证明∠ABC=90°,最后,依据锐角三角函数的定义求解即可;(2)记抛物线与x 轴的另一个交点为D .先求得D (1,0),然后再证明∠DBO=∠CAB ,从而可证明∠CAO=ABD ,故此当点P 与点D 重合时,∠ABP=∠CAO ;当点P 在AB 的上时.过点P 作PE ∥AO ,过点B 作BF ∥AO ,则PE ∥BF .先证明∠EPB=∠CAB ,则tan ∠EPB=13,设BE=t ,则PE=2t ,P (-2t ,2+t ),将P (-2t ,2+t )代入抛物线的解析式可求得t 的值,从而可得到点P 的坐标. 【详解】解:(1)抛物线的对称轴为x=-22a a =-1. ∵a <0,∴抛物线开口向下.又∵抛物线与x 轴有交点,∴C 在x 轴的上方,∴抛物线的顶点坐标为(-1,4).设抛物线的解析式为y=a (x+1)2+4,将点(-2,0)代入得:4a+4=0,解得:a=-1,∴抛物线的解析式为y=-x 2-2x+2.(2)将x=0代入抛物线的解析式得:y=2,∴B (0,2).∵C (-1,4)、B (0,2)、A (-2,0),∴BC=2,AB=22,AC=25,∴BC 2+AB 2=AC 2,∴∠ABC=90°.∴1tan 3BC CAB AB ∠==. 即CAB ∠的正切值等于13. (2)如图1所示:记抛物线与x 轴的另一个交点为D .∵点D 与点A 关于x=-1对称,∴D (1,0).∴tan ∠DBO=13. 又∵由(2)可知:tan ∠CAB=13.∴∠DBO=∠CAB.又∵OB=OA=2,∴∠BAO=∠ABO.∴∠CAO=∠ABD.∴当点P与点D重合时,∠ABP=∠CAO,∴P(1,0).如图2所示:当点P在AB的上时.过点P作PE∥AO,过点B作BF∥AO,则PE∥BF.∵BF∥AO,∴∠BAO=∠FBA.又∵∠CAO=∠ABP,∴∠PBF=∠CAB.又∵PE∥BF,∴∠EPB=∠PBF,∴∠EPB=∠CAB.∴tan∠EPB=1 3 .设BE=t,则PE=2t,P(-2t,2+t).将P(-2t,2+t)代入抛物线的解析式得:y=-x2-2x+2得:-9t2+6t+2=2+t,解得t=0(舍去)或t=59.∴P(-53,329).综上所述,点P的坐标为P(1,0)或P(-53,329).【点睛】本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求二次函数的解析式、勾股定理的逆定理、等腰直角三角形的性质、锐角三角函数的定义,用含t的式子表示点P的坐标是解题的关键.20、(1)(﹣1,4);(2)①278;②Q(﹣52,74).【分析】(1)将点A 坐标代入抛物线表达式并解得:m=-1,即可求解;(2)①过点Q 作y 轴的平行线交AC 于点N ,先求出直线AC 的解析式,点Q(x ,﹣x 2﹣2x+3),则点N(x ,x+3),则△QAC 的面积S=12×QN×OA=﹣32x 2﹣92x ,然后根据二次函数的性质即可求解; ②tan ∠OCB=OB CO =13,设HM=BM=x ,则CM=3x ,BC=BM+CM=4x=10,解得:x=104,CH=10x=52,则点H(0,12),同理可得:直线BH(Q)的表达式为:y=-12x+12,即可求解. 【详解】解:(1)将点A(﹣3,0)代入抛物线表达式并解得,0=﹣9-6m+3∴m =﹣1,故抛物线的表达式为:y =﹣x 2﹣2x+3=-(x+1)2+4…①,∴点P(﹣1,4),故答案为:(﹣1,4);(2)①过点Q 作y 轴的平行线交AC 于点N ,如图1,设直线AC 的解析式为y=kx+b ,将点A(﹣3,0)、C(0,3)的坐标代入一次函数表达式并解得,303k b b -+=⎧⎨=⎩, 解得13k b =⎧⎨=⎩, ∴直线AC 的表达式为:y =x+3,设点Q(x ,﹣x 2﹣2x+3),则点N (x ,x+3),△QAC 的面积S =12⨯QN×OA =12⨯(﹣x 2﹣2x+3﹣x ﹣3)×3=﹣32x 2﹣92x ,∵﹣32<0,故S有最大值为:278;②如图2,设直线BQ交y轴于点H,过点H作HM⊥BC于点M,tan∠OCB=OBCO=13,设HM=BM=x,则CM=3x,BC=BM+CM=4x10,解得:x10CH10=52,则点H(0,12),同直线AC的表达式的求法可得直线BH(Q)的表达式为:y=﹣12x+12…②,联立①②并解得:﹣x2﹣2x+3=﹣12x+12,解得x=1(舍去)或﹣52,故点Q(﹣52,74).【点睛】本题考查了待定系数法求二次函数和一次函数解析式,二次函数的图像与性质,锐角三角函数的定义,以及数形结合能力的培养.要会利用数形结合的思想把代数和几何图形结合起来,利用点的坐标的意义表示线段的长度,从而求出线段之间的关系.21、见解析.【分析】连接BC,根据圆周角定理求出∠ACB=90°,求出OD⊥BC,根据垂径定理求出即可.【详解】证明:连接CB,∵AB 为⊙O 的直径,∴∠ACB =90°,∵OD ∥AC ,∴∠OEB =∠ACB =90°,即OD ⊥BC ,∵OD 过O ,∴点D 平分BC .【点睛】本题考查了圆周角定理和垂径定理,能正确运用定理进行推理是解此题的关键.22、(1)()2,3-;(2)()3,2--;(3)()7,3-或()5,3--或()3,3.【解析】(1)根据题意作出图形,即可根据直角坐标系求出坐标;(2)根据题意作出图形,即可根据直角坐标系求出坐标;(3)根据平行四边形的性质作出图形即可写出.【详解】解:(1)旋转后的A B C '''∆图形如图所示,点A 的对应点Q 的坐标为:()2,3-;(2)如图点A 的对应点A ''的坐标()3,2--;(3)如图以A 、B 、C 为顶点的平行四边形的第四个顶点D 的坐标为:()7,3-或()5,3--或()3,3【点睛】此题主要考查坐标与图形,解题的关键是熟知图形的旋转作图及平行四边形的性质.23、(1)见解析;(2)【解析】(1)连接OC.只要证明AE∥OC即可解决问题;(2)根据角平分线的性质定理可知CE=CF,利用面积法求出CF即可;【详解】(1)证明:连接O C.∵CD是⊙O的切线,∴∠OCD=90°,∵∠AEC=90°,∴∠OCD=∠AEC,∴AE∥OC,∴∠EAC=∠ACO,∵OA=OC,∴∠OAC=∠OCA,∴∠EAC=∠OAC,∴AC平分∠DAE.(2)作CF⊥AB于F.在Rt△OCD中,∵OC=3,OD=5,∴CD=4,∵•OC•CD=•OD•CF,∴CF=,∵AC平分∠DAE,CE⊥AE,CF⊥AD,∴CE=CF=.【点睛】本题主要考查平行线的判定、角平分线的性质,熟练掌握这些知识点是解答的关键.24、32.05米【分析】先在Rt△ABD中,用三角函数求出AD,最后在Rt△ACD中用三角函数即可得出结论.【详解】解:在Rt△ABD中,∠ABD=30°,AB=10m,∴AD=ABsin∠ABD=10×sin30°=5(m),在Rt△ACD中,∠ACD=9°,sin9°=AD AC,∴AC=5sin9=50.156≈32.05(m),答:改造后的斜坡AC的长度为32.05米.【点睛】此题主要考查了解直角三角形的应用,熟练利用锐角三角函数关系得出是解题关键.25、(1)y=﹣x2+;(2)(1,1);(3)当△DMN是等腰三角形时,t的值为,3﹣或1.【解析】试题分析:(1)易得抛物线的顶点为(0,),然后只需运用待定系数法,就可求出抛物线的函数关系表达式;(2)①当点F在第一象限时,如图1,可求出点C的坐标,直线AC的解析式,设正方形OEFG的边长为p,则F (p,p),代入直线AC的解析式,就可求出点F的坐标;②当点F在第二象限时,同理可求出点F的坐标,此时点F不在线段AC上,故舍去;(3)过点M作MH⊥DN于H,如图2,由题可得0≤t≤2.然后只需用t的式子表示DN、DM2、MN2,分三种情况(①DN=DM,②ND=NM,③MN=MD)讨论就可解决问题.试题解析:(1)∵点B是点A关于y轴的对称点,∴抛物线的对称轴为y轴,∴抛物线的顶点为(0,),故抛物线的解析式可设为y=ax2+.∵A(﹣1,2)在抛物线y=ax2+上,∴a+=2,解得a=﹣,∴抛物线的函数关系表达式为y=﹣x2+;(2)①当点F在第一象限时,如图1,令y=0得,﹣x2+=0,解得:x1=3,x2=﹣3,∴点C的坐标为(3,0).设直线AC的解析式为y=mx+n,则有,解得,∴直线AC的解析式为y=﹣x+.设正方形OEFG的边长为p,则F(p,p).∵点F(p,p)在直线y=﹣x+上,∴﹣p+=p,解得p=1,∴点F的坐标为(1,1).②当点F在第二象限时,同理可得:点F的坐标为(﹣3,3),此时点F不在线段AC上,故舍去.综上所述:点F的坐标为(1,1);(3)过点M作MH⊥DN于H,如图2,则OD=t,OE=t+1.∵点E和点C重合时停止运动,∴0≤t≤2.当x=t时,y=﹣t+,则N(t,﹣t+),DN=﹣t+.当x=t+1时,y=﹣(t+1)+=﹣t+1,则M(t+1,﹣t+1),ME=﹣t+1.在Rt△DEM中,DM2=12+(﹣t+1)2=t2﹣t+2.在Rt△NHM中,MH=1,NH=(﹣t+)﹣(﹣t+1)=,∴MN2=12+()2=.①当DN=DM时,(﹣t+)2=t2﹣t+2,解得t=;②当ND=NM时,﹣t+=,解得t=3﹣;③当MN=MD时,=t2﹣t+2,解得t1=1,t2=3.∵0≤t≤2,∴t=1.综上所述:当△DMN是等腰三角形时,t的值为,3﹣或1.考点:二次函数综合题.26、解:(1)所画△A1B1C1如图所示.(2)所画△A2B2C2如图所示.【分析】(1)图形的整体平移就是点的平移,找到图形中几个关键的点,也就是A,B,C点,依次的依照题目的要求平移得到对应的点,然后连接得到的点从而得到对应的图形;(2)在已知对称中心的前提下找到对应的对称图形,关键还是找点的对称点,找法是连接点与对称中心O点并延长相等的距离即为对称点的位置,最后将对称点依次连接得到关于O点成中心对称的图形。
广东省深圳市2020-2021学年上学期九年级英语期末试卷分类汇编:完形填空(部分答案)

广东省深圳市2020-2021学年上学期九年级英语期末试卷分类汇编完形填空广东省深圳市光明区2020-2021 学年九年级上学期期末考试英语试题I .完形填空(10分)阅读下面短文,从短文后所给的A、B、C、D四个选项中选出能填入相应空白处的最佳选项,并在答题卡上将相应的字母编号涂黑。
(共10小题,每小题1分)I have lived beside the Loch Ness (尼斯湖)for many years. My house has a good, clear 1_ of the lake. In fact, it's only about a hundred meters from the lake. I've never been 2 the Loch Ness- monster. Until last Tuesday, I thought it was just a good story to attract tourists. But I've had to change my 3 after last Tuesday's experience.I got up as usual at about 7 and went into my garden. Something attracted my attention to the loch. There was almost no mist (薄雾)that morning, and I could see there was something 4_ quite fast, going north, in the middle of the loch. It 5 like a giant snake, with its head and part of its body above water. It was about thirty meters long. I rushed into the house to get my camera, _6 when I was back, it had gone.I waited and it 7 again, this time nearer the road and my house. I could see it very well. I managed to take several photographs of it. Most o£ the photos haven't come out, unluckily. But one or two of them show the creature quite 8 . At one point it swam straight towards me. It was a _9 that a truck passed at that moment. It perhaps heard the noise of the engine because it _10_ again. The whole incident (事件)lasted for about fifteen minutes, because I looked at my watch the last time, and it said a quarter past seven. I've never seen anything so strange in my life.1. A. message B. prize C. memory D. view2. A. interested in B. proud of C. bored with D. tired of3. A. life B. interest C. mind D. place4. A. moving B. writing C. reading D. drawing5. A. felt B. tasted C. seemed D. sounded6. A. so B. but C. if D. or7. A. ran away B. joined in C. passed out D. came along8. A. clearly B. easily C. quickly D. slowly9. A. honour B. chance C. shake D. pity10. A. failed B. sang C. disappeared D. came答案:1—5 DACAC 6 — 10 BDADC广东省深圳市龙岗区2020-2021 学年九年级上学期期末考试英语试题I. 完形填空(10分)阅读下面短文, 从短文后所给的A、B、C、D四个选项中选出能填入相应空白处的最佳选项, 并在答题卡上将相应的字母编号涂黑。
广东省深圳市龙岗区2020—2021学年九年级上学-期期末学业质量监测语文试题
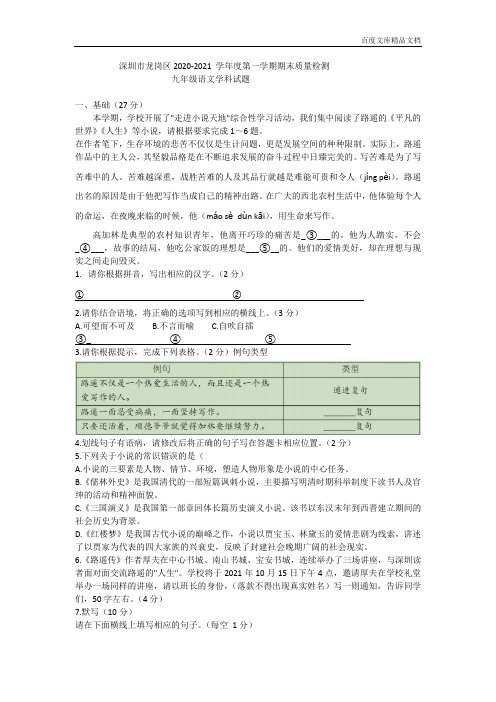
深圳市龙岗区2020-2021 学年度第一学期期末质量检测九年级语文学科试题一、基础(27分)本学期,学校开展了"走进小说天地"综合性学习活动,我们集中阅读了路遥的《平凡的世界》《人生》等小说,请根据要求完成1~6题。
在作者笔下,生存环境的悲苦不仅仅是生计问题,更是发展空间的种种限制。
实际上,路遥作品中的主人公,其坚毅品格是在不断追求发展的奋斗过程中日臻完美的。
写苦难是为了写苦难中的人。
苦难越深重,战胜苦难的人及其品行就越是难能可贵和令人(jìng pèi)。
路遥出名的原因是由于他把写作当成自己的精神出路。
在广大的西北农村生活中,他体验每个人的命运,在夜晚来临的时候,他(máo sèdùn kāi),用生命来写作。
高加林是典型的农村知识青年,他离开巧珍的痛苦是_③___的。
他为人踏实,不会_④___,故事的结局,他吃公家饭的理想是___⑤__的。
他们的爱情美好,却在理想与现实之间走向毁灭。
1.请你根据拼音,写出相应的汉字。
(2分)①②2.请你结合语境,将正确的选项写到相应的横线上。
(3分)A.可望而不可及B.不言而喻C.自吹自擂③_④⑤3.请你根据提示,完成下列表格。
(2分)例句类型4.划线句子有语病,请修改后将正确的句子写在答题卡相应位置。
(2分)5.下列关于小说的常识错误的是(A.小说的三要素是人物、情节、环境,塑造人物形象是小说的中心任务。
B.《儒林外史》是我国清代的一部短篇讽刺小说,主要描写明清时期科举制度下读书人及官绅的活动和精神面貌。
C.《三国演义》是我国第一部章回体长篇历史演义小说。
该书以东汉末年到西晋建立期间的社会历史为背景。
D.《红楼梦》是我国古代小说的巅峰之作,小说以贾宝玉、林黛玉的爱情悲剧为线索,讲述了以贾家为代表的四大家族的兴衰史,反映了封建社会晚期广阔的社会现实。
6.《路遥传》作者厚夫在中心书城、南山书城、宝安书城,连续举办了三场讲座,与深圳读者面对面交流路遥的"人生"。
广东省深圳市龙岗区东升学校2022-2023学年九年级上学期期末考试数学试卷(解析版)

2022-2023学年第一学期期末质量监测试题九年级数学(时间:90分钟 满分:100分 制卷人:八年级数学组)一.选择题:(共10小题,每小题3分,计30分)1. 如图所示的几何体的主视图是( )A.B. C. D.【答案】B【解析】【分析】找到从正面看所得到的图形即可,注意所有的看到的棱都应表现在主视图中.【详解】从几何体的正面看可得图形:.故选B .【点睛】本题考查三视图的知识,解决此类图的关键是由三视图得到相应的立体图形.从正面看到的图是正视图,从上面看到的图形是俯视图,从左面看到的图形是左视图,能看到的线画实线,被遮挡的线画虚线. 2. 下列命题中,是真命题的是( )A. 两条对角线互相平分的四边形是平行四边形B. 两条对角线相等的四边形是矩形C. 两条对角线互相垂直的四边形是菱形D. 两条对角线互相垂直且相等四边形是正方形【答案】A【解析】【分析】根据特殊四边形的判定方法进行判断.【详解】解:对角线互相平分的四边形是平行四边形,故选项A 符合题意;对角线相等的平行四边形是矩形,故选项B 不符合题意;对角线互相垂直的平行四边形是菱形,故选项C 不符合题意;的对角线互相垂直且相等的平行四边形是正方形,故选项D 不符合题意.故选:A .3. 在平面直角坐标系中,将抛物线y =x 2向上平移2个单位长度,再向右平移1个单位长度,得到的抛物线的解析式是( )A. y =(x ﹣1)2+2B. y =(x ﹣1)2﹣2C. y =(x +1)2﹣2D. y =(x +1)2+2【答案】A【解析】【分析】根据图象的平移规律,可得答案.【详解】解:将抛物线2y x =向上平移2个单位长度,再向右平移1个单位长度,得到的抛物线的解析式是()212y x =−+.故选:A .【点睛】本题主要考查了函数图象的平移,要求熟练掌握平移的规律:左加右减,上加下减.并用规律求函数解析式是解题的关键.4. 如图,ABC 和111A B C △是以点O 为位似中心的位似三角形,若1C 为OC 的中点,1113A B C S =△,则ABC 的面积为( )A. 15B. 12C. 9D. 6【答案】B【解析】 【分析】根据1C 为OC 的中点,则位似比为112OC OC =,再根据相似比等于位似比,面积比等于相似比的平方便可求解. 【详解】∵ABC 和111A B C △是以点O 为位似中心的位似三角形,1C 为OC 的中点,111A B C △面积是3, ∴112OC OC =, ∴11114A B C ABC S S =△△,∴314ABC S = , 解得:12ABC S =△.故选B .【点睛】本题考查位似比等于相似比,同时面积比是相似比的平方,掌握知识点是关键.5. 已知2x =3y ,那么下列结论中不正确的是( )A 32x y = B. 12x y y −= C. 1413x y +=+ D. 52x y y += 【答案】C【解析】【分析】根据内项之积等于外项之积对A 进行判断;根据分比性质对B 进行判断;根据合分比性质对C 进行判断;根据合比性质对D 进行判断.【详解】解:A .因为2x =3y ,所以32x y =,所以A 选项不符合题意; B .因为2x =3y ,则32x y =,所以32122x y y−−==,所以B 选项不符合题意; C .因为2x =3y ,则32x y =,所以1413x y +≠+,所以B 选项符合题意; D .因为2x =3y ,所以32x y =,则32522x y y ++==,所以D 选项不符合题意; 故选:C .【点睛】本题考查了比例的性质,掌握比例性质是解题的关键.6. 若反比例函数y =2k x −的图象分布在第二、四象限,则k 的取值范围是( ) A. k <﹣2B. k <2C. k >﹣2D. k >2 【答案】D【解析】【分析】根据反比例函数的图象和性质,由2﹣k <0即可解得答案.【详解】解:∵反比例函数y =2k x−的图象分布在第二、四象限, .∴2﹣k <0,解得k >2,故选择:D .【点睛】本题考查反比例函数的性质.掌握“反比例函数k y x=,当0k >时,图象经过第一、三象限;当0k <时,图象经过第二、四象限” .7. 如图,丁轩同学在晚上由路灯AC 走向路灯BD ,当他走到点P 时,发现身后他影子的顶部刚好接触到路灯AC 的底部,当他向前再步行20 m 到达Q 点时,发现身前他影子的顶部刚好接触到路灯BD 的底部,已知丁轩同学的身高是1.5 m ,两个路灯的高度都是9 m ,则两路灯之间的距离是( )A. 24 mB. 25 mC. 28 mD. 30 m【答案】D【解析】 详解】由题意可得:EP ∥BD ,所以△AEP ∽△ADB , 所以AP EP AP PQ BQ BD=++, 因为EP =1.5,BD =9, 所以1.59220AP AP =+, 解得:AP =5,因为AP=BQ ,PQ =20,所以AB=AP+BQ+PQ =5+5+20=30,故选:D .点睛:本题主要考查相似三角形的对应边成比例在解决实际问题中的应用,应用相似三角形可以间接地计算一些不易直接测量的物体的高度和宽度,解题时关键是找出相似三角形,然后根据对应边成比例列出方程,建立适当的数学模型来解决问题.8. 某农产品市场经销一种销售成本为每千克40元的水产品,据市场分析,若按每千克50元销售,一个月【能售出500千克,销售单价每涨1元,月销售量就减少10千克,设销售单价为每千克x元,月销售利润可以表示为()A. (x﹣40)[500﹣10(50﹣x)]元B. (x﹣40)(10x﹣500)元C. (x﹣40)(500﹣10x)元D. (x﹣40)[500﹣10(x﹣50)]元【答案】D【解析】【分析】由题意直接利用每千克利润×销量=总利润,进而即可得出代数式.【详解】解:设销售单价为每千克x元,则月销售利润=(x-40)[500-10(x-50)].故选:D.【点睛】本题主要考查根据实际问题抽象出二次函数,理解题意并正确表示出销量是解题的关键.9. 已知菱形OABC在平面直角坐标系的位置如图所示,顶点A(5,0),OBP是对角线OB上的一个动点,D(0,1),当CP+DP最短时,点P的坐标为()A. (0,0)B. (1,12) C. (65,35) D. (107,57)【答案】D【解析】【详解】解:如图连接AC,AD,分别交OB于G、P,作BK⊥OA于K.∵四边形OABC是菱形,∴AC⊥OB,GC=AG,OG=BG=A、C关于直线OB对称,∴PC+PD=P A+PD=DA,∴此时PC+PD最短.在RT △AOG 中,AG∴AC =∵OA •BK =12•AC •OB , ∴BK =4,AK =3, ∴点B 坐标(8,4),∴直线OB 解析式为12y x =,直线AD 解析式为115y x =−+, 由12115y x y x = =−+ ,解得:10757x y = =, ∴点P 坐标(107,57). 故选D .10. 如图,在正方形ABCD 中,BPC △是等边三角形,、BP CP 的延长线分别交AD 于点E F 、,连结,BD DP BD 、与CF 相交于点H .给出下列结论,①△ABE ≌△DCF;②△DPH 是等腰三角形;③PF AB =;④ABCDPBD S S ∆=四边形, 其中正确结论的个数是( )A. 4B. 3C. 2D. 1【答案】A【解析】 【分析】①利用等边三角形的性质以及正方形的性质得出∠ABE=∠DCF=30°,再直接利用全等三角形的判定方法得出答案;②利用等边三角形的性质结合正方形的性质得出∠DHP=∠BHC=75°,进而得出答案;③利用相似三角形的判定与性质结合锐角三角函数关系得出答案;④根据三角形面积计算公式,结合图形得到△BPD 的面积=△BCP 的面积+△CDP 面积-△BCD 的面积,得出答案.【详解】∵△BPC 是等边三角形,∴BP=PC=BC ,∠PBC=∠PCB=∠BPC=60°,在正方形ABCD 中,∵AB=BC=CD ,∠A=∠ADC=∠BCD=90°∴∠ABE=∠DCF=30°,在△ABE 与△CDF 中,A ADC ABE DC AB CD ∠=∠ ∠=∠ =, ∴△ABE ≌△DCF ,故①正确;∵PC=BC=DC ,∠PCD=30°,∴∠CPD=75°,∵∠DBC=45°,∠BCF=60°,∴∠DHP=∠BHC=1804560°−°−°=75°,∴PD=DH ,∴△DPH 是等腰三角形,故②正确;设PF=x ,PC=y ,则DC=AB=PC=y ,∵∠FCD=30°, ∴cos30CD y CF x y °==+,即)y x y +,整理得:1y x −解得:x y =,则PF AB =,故③正确; 如图,过P 作PM ⊥CD ,PN ⊥BC ,设正方形ABCD 的边长是4,∵△BPC 为正三角形,∴∠PBC=∠PCB=60°,PB=PC=BC=CD=4,∴∠PCD=30°,∴604PN PB sin =⋅°== 130422PM PC sin =⋅°=×=, S △BPD =S 四边形PBCD -S △BCD =S △PBC +S △PDC -S △BCD111222BC PN CD PM BC CD =⋅+⋅−⋅11144244222=××+××−××48=+−4,∴ABCD PBD S S ∆=四边形,故④正确; 故正确的有4个,故选:A .【点睛】本题考查了正方形的性质以及全等三角形的判定等知识,解答此题的关键是作出辅助线,利用锐角三角函数的定义表示出出FE 及PC 的长是解题关键.二.填空题:(共5小题,每小题3分,计15分)11. 若关于x 的一元二次方程260x mx −−=的一个根是3x =,则m 的值为______【答案】1【解析】【分析】根据一元二次方程的解的定义:使等式成立的x 的值,是方程的解,将3x =代入方程进行计算即可.【详解】解:把3x =代入260x mx −−=可得9360m −−=, 解得1m =,故答案为:1.【点睛】本题考查根据一元二次方程的根求参数的问题.熟练掌握一元二次方程的解的定义,是解题的关键.12. 如图,在ABC 中,36ABC S =△,点D 在.BC 上,6,9AC BD ==,且2AC BC CD =⋅,点E 为BD的中点,则AED S 的值为_____.【答案】272【解析】 【分析】利用2AC BC CD =⋅可求出3CD =,再计算出92DE =,然后根据三角形面积公式得到::AED ABC S S DE BC = ,从而可求出AED S .【详解】解:∵2,6,9AC BC CD AC BD =⋅==∴26(9)CD CD =+×,整理得29360CD CD +−=,解得12CD =−(舍去)或3CD =,∴3912BC CD BD =+=+=,∵点E 为BD 的中点, ∴1922DE BD ==, ∴::AED ABC S S DE BC = , 即9:36:122AED S ∆=, ∴272AED S ∆=. 故答案为:AED S .【点睛】本题考查了一元二次方程解法,等高三角形面积的比等于底边的比等知识,灵活运用线段之间的关系是解决问题的关键.13. 如图,坡面CD的坡比为1:,坡顶的平地BC 上有一棵小树AB ,当太阳光线与水平线夹角成60°时,测得小树的在坡顶平地上的树影BC =3米,斜坡上的树影CDAB 的高是_____________.【答案】【解析】【分析】此题是把实际问题转化为解直角三角形问题,首先根据题意作图(如图),得Rt △AFD ,Rt △CED ,然后由Rt △CED ,和坡面CD的坡比为1:,求出CE 和ED ,再由Rt △AFD 和三角函数求出AF .进而求出AB .【详解】解:由已知得Rt △AFD ,Rt △CED ,如图,且得:∠ADF =60°,FE =BC ,BF =CE ,在Rt △CED 中,设CE =x ,由坡面CD的坡比为,得:DE,则根据勾股定理得:x 2+2)=2,得x不合题意舍去, 所以,CEED =32米, 那么,FD =FE +ED =BC +ED =3+32=92米, 在Rt △AFD 中,由三角函数得:AF FD =tan ∠ADF ,的∴AF =FD •tan60°=92∴AB =AF ﹣BF =AF ﹣CE故答案为【点睛】本题考查解直角三角形的应用-坡度坡角问题,正确添加辅助线是解题关键.14. 如图,在正方形方格纸中,每个小正方形的边长都相等,A 、B 、C 、D 都在格点处,AB 与CD 相交于点P ,则cos APC ∠的值为_____.【解析】【分析】连接DE ,根据题意可得:AB DE ∥,从而利用平行线性质可得APC EDC ∠=∠,然后利用勾股定理的逆定理证明DCE △是直角三角形,从而可得90DCE ∠=°,再利用锐角三角函数的定义进行计算可得cos CDE ∠的值,即可解答.【详解】解:如图:连接DE ,的由题意得:AB DE ∥,∴APC EDC ∠=∠,在DCE △中,2222420CD =+=,222125CE =+=,2223425DE =+=,∴222CD CE DE +=,∴DCE △是直角三角形,∴90DCE ∠=°,∴cos CD CDE DE ∠=,∴cos cos APC CDE ∠=∠,. 【点睛】本题考查网格中的锐角三角函数,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.15. 如图,已知直线l :4y x =−+分别与x 轴、y 轴交于点A ,B ,双曲线()0,0k y k x x=>>与直线l 不相交,E 为双曲线上一动点,过点E 作EG x ⊥轴于点G ,EF y ⊥轴于点F ,分别与直线l 交于点C ,D ,且45COD ∠=°,则k =_____【答案】8【解析】【分析】求出点A 、B 的坐标分别为()40,、()04,,可得45OAB COD ∠=°=∠,证明ODA CDO ∽,根据相似三角形的性质可得2OD CD AD =⋅,然后设点(),E m n ,表示出点(),4C m m −和点()4,D n n −,再分别求出2OD 、CD 和AD ,代入2OD CD AD =⋅求出mn 即可.【详解】解:在一次函数4y x =−+中,当0x =时,4y =;当0y =时,4x =, ∴点A 、B 的坐标分别为()40,、()04,, ∴OA OB =,∴45OAB COD ∠=°=∠,∵ODA CDO ∠=∠,∴ODA CDO ∽, ∴OD AD CD OD=, ∴2OD CD AD =⋅,设点(),E m n ,则OG m =,EG n =,∴4AG m =−,∵45OAB ∠=°,90CGA ∠=°, ∴ACG 是等腰直角三角形,∴4CG AG m ==−,45ACG ∠=°,∴点(),4C m m −,()44CE n m m n =−−=+−,∵90EFO FOG OGE ∠=∠=∠=°,∴四边形OGEF 是矩形,∴90FEG ∠−°,FE OG m ==,∵45DCE ACG ∠=∠=°,∴DEC 是等腰直角三角形,∴4DE CE m n ==+−,∴44DF DE FE m n m n =−=+−−=−,∴点()4,D n n −,∴()22222241682816OD n n n n n n n =−+=+−+=−+,)4CD m n =+−,AD =,∴)228164n n m n −+=+−,∴8mn =,∴8k mn ==,故答案为:8. 【点睛】本题考查的是反比例函数与一次函数的交点问题,相似三角形的判定和性质,矩形的判定和性质,坐标与图形性质,勾股定理的应用等知识点,关键是通过设定点E 的坐标,确定相关线段的长度,进而求解.三.解答题(共7小题,计55分)16. 计算或解下列方程:(1)25410x x −−=(2)()2439x x x −=−(3)计算:112tan 454sin 602− −°+°−. 【答案】(1)11x =,215x =−(2)13x =,21x =(3)−【解析】【分析】(1)用公式法求解即可;(2)移项后用因式分解法求解即可;(3)代入特殊角三角函数值,根据负整数指数幂和二次根式的性质计算即可.【小问1详解】解:∵5a =,4b =−,1c =−,∴()()2244451360b ac ∆=−=−−××−=>,∴4610x ±, ∴146110x +==,2461105x −==−; 【小问2详解】解:()()24390x x x −−−=, ()()()43330x x x x −−+−=,()()3430x x x −−−=,即()()3330x x −−=, ∴30x −=或330x −=, ∴13x =,21x =.【小问3详解】解:原式2214=−×+ 22=−+=−【点睛】本题考查了解一元二次方程,实数的混合运算,特殊角三角函数值的运算,熟练掌握解一元二次方程的方法,牢记特殊角三角函数值是解题的关键.17. 为了解学生一周劳动情况,我市某校随机调查了部分学生的一周累计劳动时间,将他们一周累计劳动时间t (单位:时)划分为A :2t <,B :23t ≤<,C :34t ≤<,D :4t ≥四个组,并将调查结果绘制成如图所示的两幅不完整的统计图,根据图中所给信息解答下列问题:(1)这次抽样调查共抽取_____________人,条形统计图中的m=_____________;(2)在扇形统计图中,求B组所在扇形圆心角的度数,并将条形统计图补充完整;(3)已知该校有1300名学生,根据调查结果,请你估计该校一周累计劳动时间达到3小时及3小时以上的学生共有多少人?(4)学校准备从一周累计劳动时间较长的两男两女四名学生中,随机抽取两名学生为全校学生介绍劳动体会,请用列表法或画树状图法求恰好抽取到一名男生和一名女生的概率.【答案】(1)100;42(2)72°;条形统计图见解析(3)910;(4)2 3【解析】【分析】(1)用D组的人数除以它所占的百分比得到调查的总人数,然后用调查的总人数乘以C组人数所占的百分比得到m的值;(2)用360°乘以B组人数所占的百分比得到B组所在扇形圆心角的度数,再计算出B组人数,然后补全条形统计图;(3)用1300乘以样本中C组和D组的人数所占百分比的和即可;(4)画树状图展示所有12种等可能的结果,再找出一名男生和一名女生的结果数,然后根据概率公式计算.【小问1详解】解:这次抽样调查的总人数为2828%100÷=(人),所以10042%42m=×=;故答案为:100;42;【小问2详解】解:B组所在扇形圆心角的度数为36020%72°×=°;B组人数为10020%20×=(人),条形统计图补充完整为:【小问3详解】解:1300(28%42%)910×+=(人),所以估计该校一周累计劳动时间达到3小时及3小时以上的学生共有910人;【小问4详解】解:画树状图为:共有12种等可能的结果,其中一名男生和一名女生的结果数为8,所以恰好抽取到一名男生和一名女生的概率82 123==.【点睛】本题考查了列表法与树状图法:利用列表法或树状图法展示所有可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式计算事件A或事件B的概率.也考查了统计图.18. 深圳市某学校数学探究小组利用无人机在操场上开展测量教学楼高度的活动,如图,此时无人机在离地面30米的点D处,操控者站在点A处,无人机测得点A的俯角为30°,测得教学楼楼顶点C处的俯角为45°,又经过人工测量得到操控者和教学楼BC的距离为57米,求教学楼BC的高度.)【答案】24米【解析】【分析】过点D作DE⊥AB于E,过点C作CF⊥DE于F,根据正切的定义求出AE,根据题意求出BE,根据等腰直角三角形的性质求出DF,结合图形计算,得到答案.【详解】解:过点D 作DE ⊥AB 于E ,过点C 作CF ⊥DE 于F ,由题意得AB=57米,DE=30米,∠DAB=30°,∠DCF=45°,在Rt △ADE 中,tan ∠DAE=DE AE, ∴AE=tan DE DAE =∠≈51(米), ∵AB=57米,∴BE=AB-AE=6(米),∵CB ⊥BE ,FE ⊥BE ,CF ⊥EF ,∴四边形BCFE 为矩形,∴CF=BE=6(米),在Rt △DFC 中,∠CDF=45°,∴DF=CF=6(米),∴BC=EF=DE-DF=30-6=24(米).答:教学楼BC 的高度约为24米.【点睛】本题考查了解直角三角形的应用-仰角俯角问题,掌握仰角俯角的概念、熟记锐角三角函数的定义是解题的关键.19. 如图,矩形ABCD 中,点E 在边CD 上,将BCE 沿BE 折叠,点C 落在AD 边上的点F 处,过点F 作FG CD 交BE 于点G ,连接CG .(1)求证:四边形CEFG 是菱形;(2)若6,10AB AD ==,求四边形CEFG 的面积.【答案】(1)详见解析;(2)203【解析】【分析】(1)根据题意可得BCE BFE ≌,因此可得FG EC =,又FG CE ,则可得四边形CEFG 是平行四边形,再根据,CE FE =可得四边形CEFG 是菱形.(2)设EF x =,则,6CE x DE x ==−,再根据勾股定理可得x 的值,进而计算出四边形CEFG 的面积.【详解】(1)证明:由题意可得,BCE BFE ∴ ≌,∴,BEC BEF FE CE ∠=∠=, ∵FG CE ,∴FGE CEB ∠=∠,∴FGE FEG ∠=∠,∴FG FE =,∴FG EC =,∴四边形CEFG 是平行四边形,又∵,CE FE =∴四边形CEFG 是菱形;(2)∵矩形ABCD 中,6,10,AB AD BC BF === , ∴90,10BAF AD BC BF ∠=°===, ∴8AF =,∴2DF =,设EF x =,则,6CE x DE x ==−,∵90FDE ∠=°,∴()22226x x +−=, 解得,103x = , ∴103CE =, ∴四边形CEFG 的面积是:1020233CE DF ⋅×.【点睛】本题主要考查菱形的判定,关键在于首先证明其是平行四边形,再证明两条临边相等即可. 20. 如图,用长为22米的篱笆,一面利用墙(墙的最大可用长度为14米),围成中间隔有一道篱笆的长方形花圃,为了方便出入,在建造篱笆花圃时,在BC 上用其他材料做了宽为1米的两扇小门.(1)设花圃的宽AB 长为x 米,请你用含x 的代数式表示BC 的长为___米;(2)若此时花圃的面积刚好为452m ,求此时AB 的长度.【答案】(1)24-3x ;(2)AB=5m【解析】【分析】(1)用绳子的总长减去三个AB 的长,然后加上两个门的长即可表示出BC ;(2)由(1)得花圃长BC=(24-3x ),宽为x ,然后再根据面积为45,列一元二次方程方程解答即可.【详解】解:设花圃的宽AB 长为x 米,则长BC=22-3x+2=(24-3x )米故答案为24-3x ;(2)由题意可得:(24-3x )x=45,解得:x 1=3、x 2=5;∵当AB=3时,BC=24-3×3=15> 14,不符合题意,故舍去;当AB=5时,BC=9符合题意∴AB=5m .【点睛】本题主要考查一元二次方程的应用,弄清题意、用x 表示出BC 是解答本题的关键. 21. 定义:有一组邻边相等的凸四边形叫做“等邻边四边形”,回答下列问题.(1)如图1,四边形ABCD 中,∠A =90°,AB =1,CD ,∠BCD =∠DBC ,判断四边形ABCD 是不是“等邻边四边形”,并说明理由;(2)如图2,Rt ABC 中,∠ABC =90°,AB =2,BC =1,现将Rt △ABC 沿∠ABC 的平分线BB ′方向平移得到A B C ′′′ ,连结AA ′,BC ′,若平移后的四边形ABC A ′′是“等邻边四边形”,求'BB 的长.【答案】(1)是“等邻边四边形”,理由见详解;(2 或2 . 【解析】【分析】(1)根据∠BCD =∠DBC ,可得CD =BD ,由勾股定理可得AD =1,即可求证;(2)延长C B ′′ 交AB 于点D ,根据平移的性质和BB ′平分∠ABC ,,可得B D BD ′= ,从而BB ′=,然后分四种情况进行讨论——若2BC AB ′== 时;若2AA AB ′== 时;若AA A C ′′′=时;若BC A C ′′′== 时,即可求解.【详解】解:(1)是“等邻边四边形”,理由如下:∵∠BCD =∠DBC ,CD ,∴CD =BD ,∵∠A =90°,AB =1,在Rt ABD 中,由勾股定理得:1AD = ,∴AD =AB ,∴四边形ABCD 是 “等邻边四边形”;(2)如图2,延长C B ′′ 交AB 于点D ,∵将Rt △ABC 沿∠ABC 的平分线BB ′方向平移得到A B C ′′′ ,BC =1,∠ABC =90°,∴//A B AB ′′ ,90A B C ABC ′′′∠=∠=° ,1C B BC ′′== ,AA BB ′′= ,A C AC ′′= , ∴B D AB ′⊥ ,∵BB ′平分∠ABC ,∴45B BD ′∠=° ,∴904545BB D ′∠=°−°=° ,∴BB D B BD ′′∠=∠ , ∴B D BD ′= ,∴BB ′== ,设B D BD x ′==,∴1C D x ′=+ ,若2BC AB ′== 时,在Rt BDC ′ 中,由勾股定理得:()22212x x ++= ,解得:1x = ,2x =,∴BD =∴BB ′= ; 若2AA AB ′== 时,2BB AA ′′==; 若AA A C ′′′=时,在Rt ABC 中,由勾股定理得:AC =;∴AA A C AC ′′′===∴BB ′=;若BC A C ′′′== 时,在Rt BDC ′ 中,由勾股定理得:222BD C D BC ′′+= ,即()2221x x ++, 解得:11x = 或22x =− (舍去),∴BB ′= ;综上所述,若平移后的四边形ABC A ′′是“等邻边四边形”, 'BB 或2 或 .【点睛】本题主要考查了平移的性质,等腰三角形的判定和性质,勾股定理,理解“等邻边四边形”的定义是解题的关键.22. 在平面直角坐标系xOy 中,已知反比例函数1(0)k y k x=>的图像与正比例函数2(0)y mx m =>的图像交于点A 、点C ,与正比例函数3(0)y nx n =>的图像交于点B 、点D ,设点A 、D 的横坐标分别为s ,t (0s t <<).(1)如图1,若点A 坐标为(2,4).①求m ,k 的值;②若点D 的横坐标为4,连接AD ,求△AOD 的面积.(2)如图2,依次连接AB ,BC ,CD ,DA ,若四边形ABCD 为矩形,求mn 的值.(3)如图3,过点A 作AE x ⊥轴交CD 于点E ,以AE 为一边向右侧作矩形AEFG ,若点D 在边GF 上,试判断点D 是否为线段GF 的中点?并说明理由.【答案】(1)①2m =,8k =;②6(2)1 (3)D 为线段GF 的中点,理由见解析【解析】【分析】(1)①把A (2,4)分别代入入y 1=k x(k >0)和y 2=mx ,即可求得答案; ②如图1,延长DA 交y 轴于点K ,利用待定系数法求得直线AD 的解析式为y =-x +6,得出K (0,6),再由S △AOD =S △DOK -S △AOK ,即可求得答案; (2)由题意得:A (s ,ms ),D (t ,nt ),k =ms 2=nt 2①,再根据矩形性质可得OA =OD ,即s 2+m 2s 2=t 2+n 2t 2②,①②联立即可求得答案;(3)由题意得:A (s ,k s ),D (t ,k t ),C (-s ,-k s ),运用待定系数法可得直线CD 的解析式为y =k st x +k t -k s ,得出E (s ,2k t -k s ),再由矩形性质可得:FG ∥AE ∥y 轴,EF ∥AG ∥x 轴,进而得出F (t ,2k t -k s ),G (t ,k s ),即可得出结论.【小问1详解】解:①∵点A (2,4)在1k y x=上, ∴42k =,8k =; ∵点A (2,4)在2y mx =上,∴42m =,2m =②∵点D 的横坐标为4,∴当4x =时,824y==, ∴D (4,2) 分别过点A 、D 作x 轴的垂线交x 轴于点H 、K ,∵OHA OADK AHKD S S S ∆=+四边形梯形,ODA ODK OADKS S S ∆∆∆=+四边形,OHA ODK S S ∆∆= ∴()()()()112442622ODA AHKD S S DK AH OK OH ∆==+−=+−=梯形; 【小问2详解】解:∵直线AC ,BD 经过原点且与反比例函数1k y x =分别交于点A ,C ,B ,D ,反比例函数1k y x=的图像关于原点中心对称, ∴点A ,C 关于原点对称,点B 、D 关于原点对称,∴OA OC =,OB OD =,∴四边形ABCD 为平行四边形.当OA OD =时,四边形ABCD 是矩形.∵点A ,D 的横坐标分别为s ,t (0s t <<),∴点A 的坐标为(s ,k s ),点D 的坐标为(t ,k t), ∴22OA OD =, ∴222222k k s t s t +=+, ∴2222220k k s t s t +−−=, ∴2222220k k s t s t −+−= ∴()22222220k s t s t s t −−−=,∴()2222222k s t s t s t −−= ∴222s t k =又∵A (s ,k s)在2y mx =上, ∴k ms s =, ∴2k m s = D (t ,k t 在3y nx =上, ∴k nt t =,2k n t = ∴222221k k k mn s t s t=⋅==. 【小问3详解】解:由(2)知,,k A s s,,k D t t,则,k C s s −− 设CD 的表达式为y ax b =+ k at b t k as b s =+ −=−+ ,解得()k a ts k s t b ts = − =,∴CD的表达式为()k s tkxyts ts−=+,∵AE x⊥轴交CD于点E,∴当x s=时,()()2k s t k s t ksyts ts ts−−=+=∴E(s,() 2k s tst−),∵四边形AEFG是矩形∴(2),,,k k s t G t F ts st−∴()k t sk kGDs t ts−=−=,()()()22k s t k s t k t sk ksDFt ts ts ts ts−−−=−=−=∴GD DF=∴D为线段GF的中点.【点睛】本题是反比例函数综合题,考查了反比例函数的图像和性质,待定系数法,三角形面积,矩形的判定和性质,线段的中点坐标,反比例函数与正比例函数图像交点问题等,掌握反比例函数的图像及其性质是解题的关键.。
2020-2021学年度第一学期期末考试九年级语文试卷(附答案与解析)

2020-2021学年度第一学期期末考试语文试卷(附答案与解析)九年级(考试时间:120分钟 满分: 120分 请将答案写在答题卡上)一、基础知识与运用(15分)1.书法之美,美在其形,美在其意。
请你赏读下面两幅书法作品,按要求完成题目。
(3分)(1)新春佳节将至,人们少不了贴对联或相互祝福,请你从下列两幅对联横批或祝福语作品中任选一幅,用简化楷体将其工整、规范地写在米字格内。
(2分)⑵四位同学对以上两幅书法作品的理解正确的一项是( )(1分)A.甲同学:这是两幅草书作品,笔画连绵省简,龙飞凤舞。
B.乙同学:左幅为楷书作品,形体方正,笔画平直;右幅为隶书作品,横长竖短,呈宽扁状。
C.丙同学:左幅为楷书作品,形体方正,笔画平直;右幅为行书作品,笔画相互牵连,舒展、流畅。
D.丁同学:这是两幅篆书作品,笔画瘦长圆滑,有古代象形字的特点。
2.阅读下面的文段,按要求答题。
(6分) 在万宁蓝得醉人的海面上,岛屿.① (A. 星罗棋布 B, 鳞次栉比), 岛湖交相hu ī( ) 映。
东线高速兴隆出口处的石梅湾,由两个形如新月的海湾组成,长达六公里的碧海银滩,为植被茂密的低缓山坡所环抱,被世界旅游组织专家赞誉为中国最漂亮的海湾,以“东方夏威夷”的美称 ② (A. 骇人听闻 B 、闻名遐迩), 海天一色的景观醉美游人:大海真蓝啊,像一块晶莹剔透的宝石;大海真奇呀,像一块孕育丰富宝藏的圣地: , 。
(1) 给语段中加点的字注音,或根据拼音写汉字。
(2分)①交相hu ī 映( ) ②岛屿.( ) (2) 结合语境选择合适的成语,将字母序号填写在横线上。
(2分) , 。
(3) 仿照画线句,再补写一个句子,使之与前两句构成一组排比句。
(2分)3.央视热播的《中国诗词大会》在全国范围内引起了巨大反响,一时间,全国兴起了诗词学习热。
南海中学将于3月份举行“中国诗词大会”活动,下面是活动中的三项内容,请按要求完成。
(6分)(1)请你替学校拟写一则该活动的主题语。
广东省2020-2021学年上学期九年级英语期末试卷分类汇编:书面表达(部分答案)
广东省深圳市2020-2021学年上学期九年级英语期末试卷分类汇编书面表达广东省深圳市光明区2020-2021 学年九年级上学期期末考试英语试题IV. 书面表达(15分)2020年深圳公园文化节(Park Culture Season of Shenzhen)期间深圳市各大公园举办了各种文化活动。
你参加了哪项活动?请你根据以下提示,写一则活动评论。
(参考词汇:荧光夜跑shining run;沙滩音乐节beach music festival;网球公开赛open tennis tournament;欢乐剧场happy theater)要点:1. 你参加了哪项(些)活动?2. 活动的内容。
3. 谈谈你的感受和想法。
注意:1.80词左右,开头已给出,不计入总词数内;2.文中不得出现真实姓名和校名;3.可适当増加细节,以使条理清楚、行文连贯;4.标点正确,书面整洁。
Park Culture Season of Shenzhen is a yearly event. _________________________________ _______________________________________________________________________________ _______________________________________________________________________________ _______________________________________________________________________________ _______________________________________________________________________________ _______________________________________________________________________________ 答案:One possible version:Park Culture Season of Shenzhen is a yearly event. During the season, different kinds of events were held in the parks around the city. This year, I went to quite a few events, such as the music festival at the beach and the happy theater. At the music festival, I enjoyed many pieces of pop music and traditional music. At the happy theater, there were many plays for children. I had agood time there. Thanks to all people's hard work, Shenzhen has developed very fast in recent years. I feel proud of my city. I will work hard and try to play a role in building a better city in the future.1. 评分原则:A. 采用整体印象评分法。
深圳市2020—2021学年第一学期教学质量检测九年级语文试题
深圳市2020-2021学年第一学期教学质量检测九年级语文试卷说明:本试卷考试时长120分钟,满分120分.必须在答题卷上作答,在试题卷上作答无效.• • •一、基础(26分)班级组织了“小说天地”综合性学习活动,请根据要求完成1〜5题。
【活动一,小说开讲】听完一场小说讲座后,小福同学做了如下笔记,请根据笔记内容回答1〜3题。
笔记一:中国传统小说从说唱文学演变而来,小说是“小道”的观念①,古人曾将小说视为茶余饭后的谈资.后来小说逐渐形成以讲故事为主、设悬念吸引读者的特点.而中国现代以来的新小说受西方小说的影响,在叙事上向内转,出现淡化故事情节,加强心理描写的倾向.笔记二:中国传统的说书人遵循以小说“劝人向善”的准则,小说中蕴含了读者所认可的文化价值观,包括除暴安良、善恶有报以及仁义礼智信等.现代新小说继承了传统小说中的文化价值观,也吸收现代思想,例如平等、博爱、人对理想②zi zi的j而n的追求等.其内容与我国的社会主义核心价值观相通,在帮助读者树立正确价值观方面有着不可③轻觑的作用.青少年读者对小说的精神塑造是寓教于乐、涧物无声的.• •1 .字音字形考查。
(2分,每空1分)(1)根据拼音写词语:②zi zi bu judn ()(2)给加点词语注音:③轻觑()2 ,请从下列词语中选择最恰当的一项填入①处。
(2分)A,与日俱增 B.根深蒂固 C.不足为据 D.断章取义3 .文段画线句有语病,请写出修改后的正确表述。
(2分)【活动二,小说荐读】小福同学在班级小说荐读活动中列出了以下书单,请你根据书单内容回答4〜5题。
____ _____________4,这份书单中“现代小说”部分出现常识性错误,请你纠正,并用复句表述。
(2分)5 .书单推荐“网络小说”引发班级同学热烈讨论,有同学表示自己只读网络流行小说,不读经典名著。
请你就“网络流行小说阅读能否取代经典阅读”发表看法,要求观点明确,有说服力,’60字左右・(4分)6 .默写。
2020-2021九年级第一学期期末化学试卷
2020~2021 学年第一学期九年级期末考试化学试卷可能用到的相对原子质量:H-1 C-12 N-14 O-16 Na-23 Cl-35.5 K-39 Mn-55一、选择题(本大题共20 小题,每小题2 分,共40 分。
每小题只有一个选项符合题意,请将正确选项的序号填入下表相应的空格内。
)题号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 答案1.科学防疫,化学助力。
下列防疫工作中不属于化学研究范畴的是()A.制备消毒水B.配制生理盐水C.生产防护服D.测定病毒序列2.汽车加油站内不需要张贴的图标是()3.“低碳”生活开启现代生活新方式,“低碳”中的“碳”是指()A.碳元素B.碳单质C.二氧化碳D.含碳物质4.用洗洁精去除餐具上的油污,其原理属于()A.溶解B.乳化C.反应D.吸附5.生活中的下列物质中,不属于溶液的是()A.冰水B.汽水C.眼药水D.自来水6.某同学做氧化铜与稀硫酸反应的实验,操作示意图如下,其中操作有错误的是()A.加入氧化铜B.倾倒稀硫酸C.加热反应物D.洗涤试管7.2020 年12 月12 日,郑太高铁正式开通,高性能复合石墨滑板保证了高铁取电的安全稳定,该滑板没有用到的石墨性质是()A.润滑性B.还原性C.耐高温D.导电性8.下列试剂瓶标签上的化学式书写错误的是()9.下列物质中不能作制冷剂的是()A.液氮B.干冰C.硝酸铵D.生石灰10.化学反应前后有可能发生变化的是()A.分子数目B.物质种类C.原子数目D.元素质量11.中国天眼FAST 是目前世界唯一的天眼,它用到的高性能碳化硅是一种新型材料。
右图是硅的粒子结构示意图,下列说法正确的是()A.该粒子属于阳离子B.该粒子的中子数是14C.该粒子达到了相对稳定结构D.在化学反应中该粒子不容易得失电子12.自然界中的下列过程与二氧化碳的循环无关的是()A.酸雨的形成B.化石燃料的燃烧C.人和动植物的呼吸D.绿色植物的光合作用点燃13.黑火药是中国古代四大发明之一,其燃烧时发生的反应是S+2KNO+3C K2S+3X ↑ +N2 ↑,其中X3的化学式是()A.O2B.COC.CO2D.K2CO314.酸奶中的乳酸(化学式C3H6O3)对人体有保健作用下列关于乳酸的说法正确的是()A.乳酸中含有水B.乳酸中氧元素的质量分数最大C.乳酸中碳,氢,氧元素的质量比为1:2:1D.乳酸由3 个碳原子、6 个氢原子和3 个氧原子构成15.右图所示是某碳单质的结构,下列有关该碳单质的说法,正确的是()A.该碳单质是C60B.研磨后可以做装饰品C.它是世界上最硬的物质D.它与石墨的区别是分子构成不同16.我国南海有丰富的可燃冰资源,可燃冰主要含有甲烷水合物,下列有关说法正确的是()A.甲烷的化学式是C2H4B.甲烷燃烧产生黄色火焰C.甲烷不会造成温室效应D.可燃冰的能量高、热值大17.甲醇(CH3OH)制氢具有工艺简单、节能环保等优点,该反应的微观示意图如下,下列有关说法错误的是()A.该反应属于分解反应B.反应中有一种单质C.反应的生成物均可燃D.反应中各物质的质量比为8:1:918.下列实验不能达到相应目的的是()A.验证二氧化碳与水反应B.自制简易灭火器C.探究燃烧条件D.验满氧气19.2020 年11 月6 日,长征六号运载火箭在太原卫星发射中心成功发射,将13 颗卫星送入预定轨道,其采用的航空煤油来自煤,而普通航空煤油来自石油。
深圳市龙岗区2024届物理九年级第一学期期末检测试题含解析
深圳市龙岗区2024届物理九年级第一学期期末检测试题考生请注意:1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。
2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。
3.考生必须保证答题卡的整洁。
考试结束后,请将本试卷和答题卡一并交回。
一、单选题1.有一种电动玩具鱼(如图所示)内部电路主要有电源、小型电动机和小灯泡构成。
白天开关S1闭合,S2断开时,只有电动机工作,玩具鱼将会游动;晚上开关S1和S2都闭合时,电动机和灯泡都工作,玩具鱼既游动又发光;不玩时,只需将S1断开。
下列电路设计符合这种要求的是A.B.C.D.2.给手机电池充电,在充电过程中,该手机电池相当于电路中的()A.电源B.开关C.导线D.用电器3.“全国中小学安全教育平台”中强调了安全用电,下列做法正确的是()A.选用插座时,所有家用电器都使用两孔插座B.家用电器检修时,不用断开电源开关C.有人触电时,不能直接徒手去救,应先切断电源D.用验电笔验电时,手指不接触笔尾金属体4.细心的小明在阅读教材P53的J0407型直流电流表说明书的时候,发现在“规格”一栏中出现了“表头灵敏度为75mA”字样,通过关于表头灵敏度知识的学习,小明知道:表头的灵敏度是指表头指针满刻度偏转时流过表头的直流电流值。
因此,结合电路知识,在采用该电流表时,推测正确的是A.该电流表的量程为0~75mAB.该电流表可以直接接在电源两极之间C.该电流表可以测量大小为0.2A的电流D.该电流表的电流应该从“-”接线柱流入5..经常下厨的小关发现,同时用相同的煤和燃气灶加热质量相等、初温相同的水和食用油,油的温度总是升高得快些.这是因为A.水的比热容小,吸热后温度升高得慢B.油的比热容小,吸热后温度升高得快C.在相同的时间内,水吸收的热量较多D.在相同的时间内,油吸收的热量较多6.关于内能、温度和热量,下列说法正确的是A.物体的内能跟物体的运动速度、物体的温度和物质状态都有关系B.不同燃料燃烧时,放出热量越多的热值越大C.质量和初温相同的水和煤油,放出相同热量时煤油温度降低的多D.内能总是从内能多的物体向内能少的物体转移7.如图是某同学家中的部分电路,开始时各部分工作正常,将电饭煲的插头插入电源的三孔插座后,正在烧水的电热壶突然不能工作,但电灯仍正常发光拔出电饭煲的插头,电热壶仍不能工作,把测电笔分别插入插座的左、右孔,氖管均能发光.则可以判断出电路的故障是()A.电热壶所在电路的B、D两点间断路B.插座的接地线断路C.电路的C、D两点间导线断路D.电路的A、B两点间导线断路8.甲、乙两同学在平直的路面上同向行进,他们运动的s-t图像如图所示,由此可判断()A.图中的a点表示甲乙此时速度相间B.两同学都在做加速运动C.前5s甲、乙两同学通过的路程相等D.前5s乙同学运动较慢二、多选题9.如图所示,电源电压保持不变,R2=50Ω,闭合S1,断开S2,R1的电功率P1=0.1W,电压表示数为U1.开关都闭合时,电压表示数为6U1.用电阻R3替换R1、R2中的某一个,闭合开关S1,断开S2,电压表示数为U2,电路的总功率为P2,U2与U1相比,变化了0.5V.则下列结论正确的是()A.R3可能是110ΩB.R3可能是5ΩC.P2可能是0.54W D.P2可能是0.65W10.如图所示,电工师傅用检验灯泡L0(灯泡)取代保险丝来检查新安装的照明电路中每个支路的情况。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(
) <0,1<x2<2,则下列结论中正确的是(
)
A. a −1
B. b 2
C. 2a + b 0
抛物线 A
D. k 为任意实数,关于 x 的方程 ax2 + bx + c + k 2 = 0 没有实数根
A
F
D
y
3
2
(1,2)
GE
1
B
C
–1 O
1 2x
A.
B.
C.
D.
6.在一个不透明的袋子里装有红球、黄球共 20 个,这些球除颜色外都相同.小明通过多次实验发现,摸出红球的
16.计算: (−1)2021 +
12
cos
30
−
1 2
−1
.
17.在一个不透明的袋子中,放有四张质地完全相同的卡片,分别标有数字“-3,-2,1,6”. (1)随机抽出一张卡片是负数的概率是____________; (2)第一次从袋中随机地抽出一张卡片,把所抽到的数字记为横坐标 m,不放回袋中,再随机地从中抽出一
对应的函数表达式是( )
C
A. y = 2(x + 3)2 + 2
B. y = 2(x − 3)2 + 2
第 3 题图
C. y = 2(x+3)2 − 2
D. y = 2(x − 3)2 − 2
5. 函数 y = k 和 y = kx + 2(k 0) 在同一平面直角坐标系中的大致图象可能是(
)
x
龙岗区 2020-2021 学年第一学期期末质量监测试题
九年级数学
一、选择题(本部分共 10 小题,每小题 3 分,共 30 分)
1.方程 x2 = 2x 的解是(
)
A. x = 2
B. x1 = 0
ቤተ መጻሕፍቲ ባይዱ
C. x1 = 0, x2 = −2
D. x1 = 0, x2 = 2
2.下面四个几何体中,主视图为三角形的是( )
A.
B.
C.
D.
3. 如图,已知 Rt△ABC,∠C=90°,AB=5,BC=3,则下列结论正确的是 B
A. sin A = 3 4
B. cos B = 4 5
C. tan A = 3 5
D. sin B = 4 5
4. 将抛物线 y = 2x2 先向左平移 3 个单位,再向上平移 2 个单位,得到的新
20.在新冠肺炎抗疫期间,某药店决定销售一批口罩,经市场调研:某类型口罩进价每包为 20 元,当售价为每包 24 元时,周销售量为 160 包,若售价每提高 1 元,周销售量就会减少 10 包.设该类型售价为 x 元(不低于进价), 周利润为 y 元.请解答以下问题: (1)求 y 与 x 的函数关系式?(要求关系式化为一般式) (2)该药店为了获得周利润 750 元,且让利给顾客,售价应为多少元? (3)物价局要求利润不得高于 45%,当售价定为多少时,该药店获得利润最大,最大利润是多少元? 21.如图 1,□ABCD 的对角线 AC 平分∠BAD,AB=6.点 E 从 A 点出发沿 AB 方向以 1 个单位/秒的速度运动,点
频率稳定在 0.3 左右,则袋子中红球的个数最有可能是( )
A. 14
B. 12
C. 6
D. 4
7.疫情促进了快递行业高速发展,某家快递公司 2020 年 5 月份与 7 月份完成投递的快递总件数分别为 100 万件
和 144 万件,设该快递公司 5 月到 7 月投递总件数的月平均增长率为 x,则下列方程正确的是( )
A. 顺次连接矩形四边的中点所得到的四边形是菱形 B. 反比例函数的图象是轴对称图形 C.线段 AB 的长度是 2,点 C 是线段 AB 的黄金分割点且 AC<BC,则 AC= 5 −1
D.对于任意的实数 b ,方程 x2 − bx − 3 = 0 有两个不相等的实数根
9.如图,在正方形 ABCD 中,E、F 分别在 CD、AD 边上,且 CE=DF,连接 BE、CF 相交于 G 点. 则下列结论:
b3
b
12. 如图,四边形 ABCD 与四边形 EFGH 位似,其位似中心为点 O,且 OE=EA,则 GH =_________. CD
13.对于实数 a、b,定义新运算“ ”: a b = a2 − ab ,如 4 2 = 42 − 4 2 = 8 .若 x 4 = −4 ,则实数 x 的值
①BE=CF;② SBCG = S四边形DFGE ;③ CG2 = BG GE ;④当 E 为 CD 中点时,连接 DG,则∠FGD=45°. 正确结
论的个数是( )
A. 1
B. 2
C. 3
D. 4
10.如图,抛物线 y = ax2 + bx + c(a 0) 的图象经过点(1,2),与 x 轴交点的横坐标分别为 x1,x2,其中-1<x1
是__________.
14.如图,直角坐标系原点 O 为 Rt△ABC 斜边 AB 的中点,∠ACB=90°,A(-5,0),且 tan A = 1 ,反比例函数 2
y = k (k 0) 经过点 C,则 k 的值是______________. x
15.已知矩形 ABCD,AB=8,AD=6,E 是 BC 边上一点且 CE=2BE,F 是 CD 边的中点,连接 AF、BF、DE 相交于
M、N 两点,则△FMN 的面积是____________. y
D
F
C
C
M
N E
A
O
B
x
第 14 题图
A
B
第 15 题图
三、解答题(本大题共 7 题。其中 16 题 5 分,17 题 6 分,18 题 6 分,19 题 9 分,20 题 9 分,21 题 10 分,22 题 10 分,共 55 分)
(参考数据: sin 53 4,cos 53 3,tan 53 4 .)
5
5
3
A 45°
53°
B
C
于 G 点.过点 C 的反比例函数 y = k (k 0) 与直线 AD 交于 E、F 两点. x
(1)求证:△AOD≌△DGC; (2)求 E、F 两点坐标;
(3)填空:不等式 3x + 3 k 的取值范围是_____________. x
A. 100(1+ 2x) = 144 B. 100(1+ x)2 = 144 C. 100(1− 2x) = 144 D. 100(1− x)2 = 144
8.下列命题中,错误的是( )
第 9 题图
第 10 题图
二、填空题(本部分共 5 小题,每小题 3 分,共 15 分)
第 12 题图
11. 已知 a = 2 ,则 a + b =_________.
张,把所抽到的数字记为纵坐标 n.请用数状图或列表法求所得的点(m,n)在反比例函数 y = 6 上的概率. x
18.如图,从楼层底部 B 处测得旗杆 CD 的顶端 D 处的仰角是 53°,从楼层顶部 A 处测得旗杆 CD 的顶端 D 处的
仰角是 45°,已知楼层 AB 的楼高为 3 米. 求旗杆 CD 的高度约为多少米? D
