离散信号与系统的Z域分析
合集下载
第七章离散时间信号与系统的Z域分析总结
当 z > a 时，这是无穷递缩等比级数。
1 z X ( z) = 此时， = 1 − az −1 z − a
z > a 收敛域：
0
j Im[ z ]
a
*收敛域一定在模最大的极点 所在的圆外。
Re[ z ]
信号与系统
第7章 离散时间信号与系统的z域分析
13 /82
3.左边指数序列 x(n) = −b nu (−n − 1)
的形式 ，其中x2+Ax+B是实数范围内的不可约 多项式，而且k是正整数。这时称各分式为原 分式的“部分分式”。
信号与系统
第7章 离散时间信号与系统的z域分析
19 /82
M X ( z ) 通常， 可表成有理分式形式： b z −i ∑ i B( z ) = i =0N X ( z) = A( z ) 1 + ∑ ai z −i
z −n < ∞
n1 ≤ n ≤ n2 ;
信号与系统
第7章 离散时间信号与系统的z域分析
7 /82
因此，当时，只要，则 n= z − n 1/ z n , ≥0 同样，当时，只要，则 n <= 0 z z ,
n −n
z≠0 z≠∞ z
z −n < ∞
−n
<∞
所以收敛域至少包含，也就是除 0< z <∞ “有限平面” z= (0, ∞) z 。 ∞外的开域，即所谓
9 /82
(3)左边序列
x(n), n ≤ n2 x ( n) = n > n2 0,
X ( z)
n = −∞
= x ( n) z ∑ ∑ x ( n) z
−n n = −∞
n2
1 z X ( z) = 此时， = 1 − az −1 z − a
z > a 收敛域：
0
j Im[ z ]
a
*收敛域一定在模最大的极点 所在的圆外。
Re[ z ]
信号与系统
第7章 离散时间信号与系统的z域分析
13 /82
3.左边指数序列 x(n) = −b nu (−n − 1)
的形式 ，其中x2+Ax+B是实数范围内的不可约 多项式，而且k是正整数。这时称各分式为原 分式的“部分分式”。
信号与系统
第7章 离散时间信号与系统的z域分析
19 /82
M X ( z ) 通常， 可表成有理分式形式： b z −i ∑ i B( z ) = i =0N X ( z) = A( z ) 1 + ∑ ai z −i
z −n < ∞
n1 ≤ n ≤ n2 ;
信号与系统
第7章 离散时间信号与系统的z域分析
7 /82
因此，当时，只要，则 n= z − n 1/ z n , ≥0 同样，当时，只要，则 n <= 0 z z ,
n −n
z≠0 z≠∞ z
z −n < ∞
−n
<∞
所以收敛域至少包含，也就是除 0< z <∞ “有限平面” z= (0, ∞) z 。 ∞外的开域，即所谓
9 /82
(3)左边序列
x(n), n ≤ n2 x ( n) = n > n2 0,
X ( z)
n = −∞
= x ( n) z ∑ ∑ x ( n) z
−n n = −∞
n2
信号与系统第8章 离散时间系统的z域分析
零状态响应为
Yf
(z)
(1 z 1 z 2 ) 2 3z 1 z 2
1 1 z 1
1/ 6 0.5 5 / 6 1 z1 1 z1 1 0.5z1
yf [k] Z 1{Yf (z)}{1/ 6 0.5(1)k (5/ 6)(0.5)k}u[k]
y[k] yx[k] yf [k] {1/ 6 3.5(1)k (4 / 3)(0.5)k}u[k]
离散时间信号与系统的Z域分析
• 离散时间信号的Z域分析 • 离散时间系统的Z域分析 • 离散时间系统函数与系统特
性
离散时间信号的Z域分析
• 理想取样信号的拉普拉斯变换 • 单边Z变换定义 • 单边Z变换的收敛域 • 常用序列的Z变换 • 单边Z变换的性质 • Z反变换
理想取样信号的拉普拉斯变换
fs (t) f (t) (t kT) f (kT) (t kT)
Re(z)
三、常用序列的Z变换
1) Z{ (k)} 1, z 0
2) 3)
Z{u(k)} 1 1 z
Z{aku(k)}
1 , 1
1 a
z
z
1
1 z
a
4)
Z{e
j0k
u(k
)}
1
e
1
j0
z
1
z z e j0
5)
Z{e-
j0k u (k
)}
1
1 e- j0
z
1
z z e- j0
z e j0 z e j0
解代数方程
二阶系统响应的z域求解
y[k] a1 y[k 1] a2 y[k 2] b0 f [k] b1 f [k 1] k 0
初始状态为y[1], y[2] 对差分方程两边做Z变换，利用
中北大学精品课程-7_离散时间信号与系统的z域分析
7 离散时间信号与系统的Z域分析
例 利用部分分式法，求 1 X ( z) , z 2 的z反变换。 1 1 (1 2 z )(1 0.5z )
1 z2 X ( z) 1 1 (1 2 z )(1 0.5 z ) ( z 2)( z 0.5) X ( z) z A1 A2 z ( z 2)( z 0.5) z 2 z 0.5
7 离散时间信号与系统的Z域分析
§ 7.2 Z反变换
7 离散时间信号与系统的Z域分析
7.2.1部分分式展开法 1．z变换式的一般形式
bi z i 1 ai z i
i 1 i 0 N M
B( z ) X ( z) A( z )
7 离散时间信号与系统的Z域分析
因此，X(z)可以展成以下部分分式形式
7 离散时间信号与系统的Z域分析
第7章 离散时间信号与系统的Z域分析
7.1 离散信号的Z变换 7.2 Z反变换 7.3 Z变换的基本性质和定理 7.4 Z变换与拉普拉斯变换傅里叶变换的关系 7.5 序列的傅里叶变换的定义和性质 7.6 利用Z变换求解差分方程 7.7 离散系统的系统函数和频率响应
7.8 离散系统的信号的流图
双边序列指n为任意值时,x(n)皆有值的序列，即左边序列 和右边序列之和。
X ( z)
n
x ( n) z x ( n) z
n n 0
n
n
x ( n) z
1
第一项为右边序列(因果)其收敛域为： z 第二项为左边序列，其收敛域为： 当Rx-<Rx+时，其收敛域为
*第一项为有限长序列，第二项为z的负幂级数,
7 离散时间信号与系统的Z域分析
7.离散时间信号与系统的z域分析
第七章离散时间系统的Z域分析7.1 学习要求1.熟练掌握信号的Z域分析方法：Z变换的定义、收敛区及基本性质，能够应用长除法和部分分式分解法求Z反变换。
2.掌握序列的傅里叶变换的定义和基本性质，并了解Z变换与拉普拉斯变换、傅里叶变换的关系。
3.掌握离散系统响应的Z变换分析方法：深刻理解离散系统的系统函数的概念，掌握离散时间系统的时域和Z域框图与流图描述形式。
7.2 学习重点1.z变换,z反变换定义、基本性质、计算方法。
2.离散时间系统的z域分析。
3.离散时间系统的频率响应特性。
7.3知识结构7.4内容摘要7.4.1 Z变换1.定义∑∞-∞=-=n nz n x z X )()( 表示为：)()]([z X n x Z =。
2. 收敛域 (1) 有限长序列12(),()0,x n n n n x n n ≤≤⎧=⎨⎩其他当0,021>>n n 时，收敛条件为0>z ；当0,021<<n n 时，收敛条件为∞<z ；当0,021><n n 时，收敛条件为∞<<z 0。
(2) 右边序列11(),()0,x n n n x n n n ≥⎧=⎨<⎩当01>n 时，收敛域为1x R z >，1x R 为最小收敛半径；当01<n 时，收敛域为∞<<z R x 1。
(3) 左边序列2(),()0,x n n n x n n ≤⎧=⎨⎩其他 当02<n ，收敛域为2x R z <，2x R 为最大收敛半径； 当02>n ，收敛域为20x R z <<。
(4) 双边序列双边序列指n 为任意值时,)(n x 皆有值的序列，即左边序列和右边序列之和。
其z 变换：∑∑∑∞=--∞=--∞-∞=-+==1)()()()(n n nnn nzn x zn x zn x z X双边序列的收敛域为一环形区域21x x R z R <<。
离散时间信号与系统的Z域分析
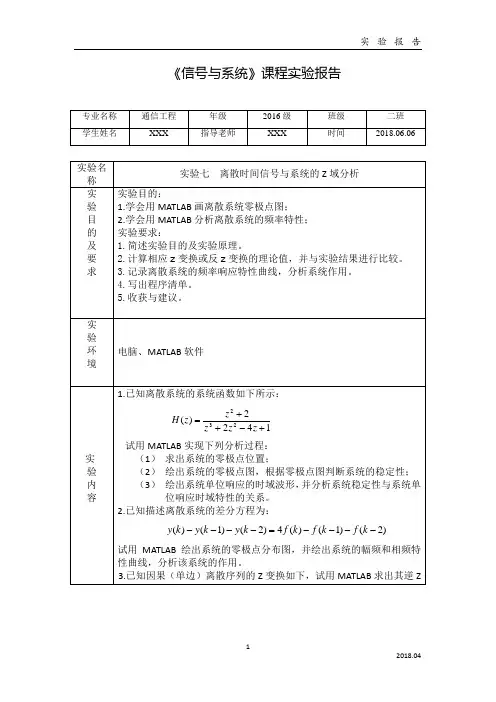
《信号与系统》课程实验报告变换。
zz z z z z F 2112)(232+++-=一、实验原理的验证 1、离散系统零极点图实验原理如下：离散系统可以用差分方程描述：∑∑==-=-Mm m Ni i m k f b i k y a 0)()(Z 变换后可得系统函数：NN MM z a z a a z b z b b z F z Y z H ----++++++==......)()()(110110 可以用root 函数可分别求零点和极点。
例7-4 求系统函数零极点图131)(45+-+=z z z z H实验结果如下：2、离散系统的频率特性实验原理如下：离散系统的频率特性可由系统函数求出，既令ωj e z =,函数freqz 可计算频率特性，调用格式是：[H ，W]=freqz(b,a,n)，b 和a 是系统函数分子分母系数，n 是π-0范围内n 个等份点，默认值为512，H 是频率响应函数值，W 是相应频率点； 例7-5 系统函数z z z H 5.0)(-=10个频率点的计算结果为幅频特性曲线相频特性曲线freqz语句直接画图例7-7已知系统函数114/11)1(4/5)(----=z z z H ，画频率响应和零极点图。
零极点图幅频特性曲线相频特性曲线二、已知离散系统的系统函数如下所示：1422)(232+-++=z z z z z H试用MATLAB 实现下列分析过程： （1）求出系统的零极点位置；（2）绘出系统的零极点图，根据零极点图判断系统的稳定性； （3）绘出系统单位响应的时域波形，并分析系统稳定性与系统单位响应时域特性的关系。
（1）由计算结果可知：系统的极点为p0=-3.3028、p1=1、p2=0.3028。
由计算结果可知：系统的零点为z0=1.4142i 、z1=-1.4142i 。
（2）系统的零极点图如下：程序清单如下： a=[1 2 -4 1]; b=[1 0 2]; ljdt(a,b)p=roots(a)q=roots(b)pa=abs(p)由图可知：第一个极点（p0）在单位圆外部，第二个极点（p1）在单位圆上，第三个极点（p2）在单位圆内部，因为有一个极点在单位圆外部，故该系统是不稳定的系统（稳定系统要求极点全部在单位圆内）。
《信号与系统》第六章 离散系统z域分析
(z
z2 1)(z
2)
z2
z2 z
2
其收敛域如下，分别求其相对应的原序列f(k)。 （1） |z| > 2 (2) |z|< 1 (3) 1< |z| < 2
解（1） 由于F(z)的收敛域在半径为2的圆外，故f(k) 为因果序列。用长除法将F(z)展开为z-1的幂级数：
z2/(z2-z-2)=1+ z-1 + 3z-2 + 5z-3 + …
例：f1(k)=2k(k)←→F1(z)=
z z2
, z>2
f2(k)=
–2k(–
k
–1)←→F2(z)=
z
z
2
, z<2
对单边z变换，其收敛域比较简单，一定
是某个圆以外的区域。可以省略。
常用序列的z变换： (k) ←→ 1 ，z>0
(k)
z ，z>1
–(– k –1)
z 1 ，z<1
书p276
若 f(k) ←→ F(z) , <z< ， 且有常数a0
则 akf(k) ←→ F(z/a) , a<z<a
证明：
Z[akf(k)]=
ak f (k)z k
f (k)
z k
F( z )
k
k
a
a
例1：akε(k) ←→ z
za
例2：cos(k)ε(k) ←→? cos(k)ε(k)=0.5(ejk+ e-jk)ε(k) ←→
方程取单边z变换yzz1yzy12z2yzy2y1z1fz2z2fz12224212121221212222212211??????????????????????????zzzzzzzzzzfzzzzzyyzzy1221221242kkyzzzzzzzzzykkzizi??????????????231212123121221kkyzzzzzzzykkzszs?????????????二系统函数zazbzfzyzhzs??2与时域的关系
第六章 离散系统的z域分析
3z 例： 2δ(k)+ 3ε(k) ←→ 2 + δ ε z −1
第1-12页 12页
z > 1
青岛科技大学信息科学技术学院
信号与系统 电子教案
6.2
z变换的性质 z变换的性质
二、移位特性
双边z 双边z变换
若： f (k) ←→F (z) ， α<z<β，且有整数 β 且有整数m>0， ， 则： f(k±m) ←→ z±mF(z)， α<z<β ± ， β
2 2
z > a
青岛科技大学信息科学技术学院
信号与系统 电子教案
6.2
z变换的性质 z变换的性质
四、卷积定理
若： f1 (k) ←→F1(z) ， α1<z<β1 β f2 (k) ←→F2(z) ， α2<z<β2 β 则： f1(k) * f2(k) ←→ F1(z)F2(z)， ， 例 收敛域至少为 相交部分 求单边序列 (k+1)akε(k)的z变换，(0<a<1)。 的 变换， 。 变换
三、z域尺度变换(序列乘ak) 域尺度变换(序列乘a
若： f (k) ←→F (z) ， α<z<β，且对整数m>0， β 且对整数 ， 则： ak f(k) ←→ F(z/a)， αa<z<βa ， β 变换。 例：求指数衰减正弦序列 aksin(βk)ε(k) 的z变换。 β 解:
6.1 z 变 换
b k , k < 0 f 2 (k ) = b k ε (−k − 1) = 0, k ≥ 0
解: 反因果序列的 变换为： 反因果序列的z变换为 变换为：
第1-12页 12页
z > 1
青岛科技大学信息科学技术学院
信号与系统 电子教案
6.2
z变换的性质 z变换的性质
二、移位特性
双边z 双边z变换
若： f (k) ←→F (z) ， α<z<β，且有整数 β 且有整数m>0， ， 则： f(k±m) ←→ z±mF(z)， α<z<β ± ， β
2 2
z > a
青岛科技大学信息科学技术学院
信号与系统 电子教案
6.2
z变换的性质 z变换的性质
四、卷积定理
若： f1 (k) ←→F1(z) ， α1<z<β1 β f2 (k) ←→F2(z) ， α2<z<β2 β 则： f1(k) * f2(k) ←→ F1(z)F2(z)， ， 例 收敛域至少为 相交部分 求单边序列 (k+1)akε(k)的z变换，(0<a<1)。 的 变换， 。 变换
三、z域尺度变换(序列乘ak) 域尺度变换(序列乘a
若： f (k) ←→F (z) ， α<z<β，且对整数m>0， β 且对整数 ， 则： ak f(k) ←→ F(z/a)， αa<z<βa ， β 变换。 例：求指数衰减正弦序列 aksin(βk)ε(k) 的z变换。 β 解:
6.1 z 变 换
b k , k < 0 f 2 (k ) = b k ε (−k − 1) = 0, k ≥ 0
解: 反因果序列的 变换为： 反因果序列的z变换为 变换为：
离散信号与系统的Z域分析
序列相加减（线性加权）后，所得序列z变换的ROC，有 可能比原序列z变换的ROC大。位移特性常用来分析单边 周期信号，单边周期信号总具有相似的形式。
8 离散信号与系统的 Z 域分析 p 16
例： F(z) = 1/(za) |z| a 求f [k]。 解：
1 F ( z) z 1 1 az
z 例： (3) u[k ] , z 3 z 3
k
类似于傅氏、拉氏变换的尺度变换特性。
1 1 s L f (at ) F ( j ) f (at ) F ( ), a a a a
F
8 离散信号与系统的 Z 域分析 p 18
a 0, a 0
例*：求aksin(0k) u[k] 的z变换及收敛域
1 cos 0 z 1 1 2 z 1 cos 0 z 2 sin 0 z 1 1 2 z 1 cos 0 z 2
五、单边z变换的主要性质
f [k ] F ( z), z R f
f1[k ] F1 ( z), z R f 1
1 2
sin 0 z 1 za 2 2 z 1 cos 0 z 2
8 离散信号与系统的 Z 域分析 p 19
五、单边z变换的主要性质
4. z域微分特性（时域线性加权）
dF ( z ) kf [k ] z dz
Z
Z Rf
m d m d F ( z) Z m m 或写成 : ( z ) F ( z ) k f [k ] ( z ) m dz dz
2 2
8 离散信号与系统的 Z 域分析 p 13
五、单边z变换的主要性质
2. 位移特性(记忆)
因果序列的位移
8 离散信号与系统的 Z 域分析 p 16
例： F(z) = 1/(za) |z| a 求f [k]。 解：
1 F ( z) z 1 1 az
z 例： (3) u[k ] , z 3 z 3
k
类似于傅氏、拉氏变换的尺度变换特性。
1 1 s L f (at ) F ( j ) f (at ) F ( ), a a a a
F
8 离散信号与系统的 Z 域分析 p 18
a 0, a 0
例*：求aksin(0k) u[k] 的z变换及收敛域
1 cos 0 z 1 1 2 z 1 cos 0 z 2 sin 0 z 1 1 2 z 1 cos 0 z 2
五、单边z变换的主要性质
f [k ] F ( z), z R f
f1[k ] F1 ( z), z R f 1
1 2
sin 0 z 1 za 2 2 z 1 cos 0 z 2
8 离散信号与系统的 Z 域分析 p 19
五、单边z变换的主要性质
4. z域微分特性（时域线性加权）
dF ( z ) kf [k ] z dz
Z
Z Rf
m d m d F ( z) Z m m 或写成 : ( z ) F ( z ) k f [k ] ( z ) m dz dz
2 2
8 离散信号与系统的 Z 域分析 p 13
五、单边z变换的主要性质
2. 位移特性(记忆)
因果序列的位移
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
N
|a|
Re z
ROC : z a
(2)
F ( z) z
k 0
N 1
k
1 z 1 z 1
ROC: z 0
按理说，有限长序列z变换的收敛域应为整个z平面，但 因为z≠0，需去除该点，所以 | z | > 0
8 离散信号与系统的 Z 域分析 p 7
四、常用因果序列的z变换
8 离散信号与系统的 Z 域分析 p 11
理解：
f [k ] {1, 2, 3, 4, 5, 6} f [k 2] {0, 0, 1, 2, 3, 4, 5, 6}
由左边移到 右边的部分
f [k 2]u[k ] {0, 0, 0, 2, 3, 4, 5, 6} f [k 2]u[k 2] {0, 0, 0, ( z)} a u[k 1]
1
k 1
8 离散信号与系统的 Z 域分析 p 17
五、单边z变换的主要性质
3. 指数加权特性
z a f [k ] F ( ) a
k Z
k
z a Rf
1 1 , z 1 a u[k ] , z a u[k ] 1 1 1 a z 1 z
双边z变换*
8 离散信号与系统的 Z 域分析 p 2
一、Z变换的定义
课本是从离散时间傅氏变换（DTFT）引出 z 变换的， 其思想：对于一些不存在傅氏变换的离散序列，可以乘上 一个衰减序列 r－k，使之衰减，于是有：
FT[ f [k ] r k ]
k
k jk f [ k ] r e j k f [ k ]( r e )
一、Z变换的定义
从拉普拉斯变换也可以引出 z 变换。对理想抽样信 号，求其拉氏变换，即得：
f s (t ) f (t ) (t kT ) f (kT ) (t kT )
k k
两边做拉氏变换
Fs (s) L[ f s (t )]
令e sT z, 为了方便，f [KT] 仍用 f [K]表示
解：
sin( 0 k )u[k ]
z
sin 0 z
1
1 2
1 2 z cos 0 z
z 1
利用z变换的指数加权特性，可得
k sin( 0 k )u[k ]
sin 0 ( z / ) 1 1 2( z / ) cos 0 ( z / )
1 1 a u[k ] , 1 z 1 1 az 1 ( ) a
k Z
z a
利用z域微分特性，可得
1 d 1 az 1 k 1 az Z{ka u[k ]} z ,z a 1 2 dz (1 az )
0
k
0
k
0
k
Z{ f [k 1]u[k ]} z 1F ( z) f [1] Z{ f [k 2]u[k ]} z 1Z{ f [k 1]u[k ]} f [2] z F ( z) z f [1] f [2]
8 离散信号与系统的 Z 域分析 p 15
2
z
1 cos 0 z 1 j sin 0 z 1 1 2 z 1 cos 0 z 2
cos( 0 k )u[k ] sin( 0 k )u[k ]
8 离散信号与系统的 Z 域分析 p 9
1 cos 0 z 1 1 2 z 1 cos 0 z 2 sin 0 z 1 1 2 z 1 cos 0 z 2
1 2
sin 0 z 1 za 2 2 z 1 cos 0 z 2
8 离散信号与系统的 Z 域分析 p 19
五、单边z变换的主要性质
4. z域微分特性（时域线性加权）
dF ( z ) kf [k ] z dz
Z
Z Rf
m d m d F ( z) Z m m 或写成 : ( z ) F ( z ) k f [k ] ( z ) m dz dz
即f [k 2]u[k ] f [k 2]u[k 2]
k 2 z f [k n]u[k ] F ( z ) z n z n
f [k ]
k n
1
1
f [k ] z k
由左边移到右 边部分的z变换
原来序列的z变换
8 离散信号与系统的 Z 域分析 p 12
n k Z f [k n]u[k ] z [ F ( z ) f [k ]z ] k n k 0 1
|z|> Rf |z|> Rf
8 离散信号与系统的 Z 域分析 p 14
五、单边Z变换的主要性质
非因果序列的位移
f [k ]
f [k 1]
f [k 2]
五、单边z变换的主要性质
f [k ] F ( z), z R f
f1[k ] F1 ( z), z R f 1
z
z
f 2 [k ] F2 ( z), z R f 2
z
1.线性特性
af1[k ] bf2 [k ] aF 1 ( z) bF 2 ( z)
课本中只讨论因果序列信号（右边序列信号的特例）， 对因果信号而言，若存在z变换，则其双边z变换与单边z 变换是相同的，收敛域也相同。 此处根据定义求z变换
(1) f [k ] [k ]
F ( z)
k k [ k ] z 1, z 0, 即全z平面
f [k ] [k m], m为正整数 .
F1 ( z )
k k m [ k m ] z z
z 0
8 离散信号与系统的 Z 域分析 p 8
四、常用因果序列的Z变换
1) Z{ [k ]} 1,
k
z0
2) Z{ u[k ]}
1 1 z
1 1 e
j 0
1
za
1
3) Z{e j0k u[k ]}
如果原序列是非因果序列（求单边变换时乘u[k]）：
Z f [k n]u[k ] z n [ F ( z ) k n n 1 k f [ k ] z ], z R f 1
Z f [k n]u[k ] z n [ F ( z ) f [k ]z k ], z R f k 0
z f [k ] F ( z)
三、单边z变换及其收敛域
单边z 变换 收敛域(ROC)：
使上式级数收敛的所有z的范围称为F(z)的收敛域 收敛域为z平面中某个圆 的外部区域。可仿照极点 法求其半径。
Im z
ROC Re z
F ( z ) f [k ]z k
k 0
z Rf
L{ f s (t )} f [k ]z k F ( z )
k
k
f (kT )e
ksT
z域到频域、s域的映射关系： z
8 离散信号与系统的 Z 域分析 p 4
re , z e
j
sT
二、z变换定义及符号表示
双边z变换 z反变换
F ( z ) f [k ]z k
z 例： (3) u[k ] , z 3 z 3
k
类似于傅氏、拉氏变换的尺度变换特性。
1 1 s L f (at ) F ( j ) f (at ) F ( ), a a a a
F
8 离散信号与系统的 Z 域分析 p 18
a 0, a 0
例*：求aksin(0k) u[k] 的z变换及收敛域
2 2
8 离散信号与系统的 Z 域分析 p 13
五、单边z变换的主要性质
2. 位移特性(记忆)
因果序列的位移
f [k n] u[k n] z nF(z) 非因果序列的位移
n 1
|z|> Rf
Z f [k n]u[k ] z n [ F ( z ) f [k ]z k ]
序列相加减（线性加权）后，所得序列z变换的ROC，有 可能比原序列z变换的ROC大。位移特性常用来分析单边 周期信号，单边周期信号总具有相似的形式。
8 离散信号与系统的 Z 域分析 p 16
例： F(z) = 1/(za) |z| a 求f [k]。 解：
1 F ( z) z 1 1 az
8 离散信号与系统的 Z 域分析 p 6
例：求以下序列的Z变换及收敛域。
(1) f [k ] a u[k ]
k
(2)
1 0 k N 1, N为有限值 f [k ] 0 其它
Im z
解：根据定义式：
(1)
F ( z) a z
k k 0
k
1 1 1 az
位移特性（常见二阶形式，常用于求解差分方程）
f [k n]u[k n] z F ( z), z R f
Z
Z f [k n]u[k ] z n [ F ( z ) k n
n
1
f [k ]z k ], z R f
Z{ f [k 1]} z F ( z ) f [1] Z{ f [k 2]} z F ( z ) z f [1] f [2]
k
1 k 1 f [k ] F ( z ) z dz c 2 πj
物理意义： 将离散信号分解为不同频率复指数esTk的线性组合 符号表示 正变换：F(z) = Z{f [k]} 或
8 离散信号与系统的 Z 域分析 p 5
|a|
Re z
ROC : z a
(2)
F ( z) z
k 0
N 1
k
1 z 1 z 1
ROC: z 0
按理说，有限长序列z变换的收敛域应为整个z平面，但 因为z≠0，需去除该点，所以 | z | > 0
8 离散信号与系统的 Z 域分析 p 7
四、常用因果序列的z变换
8 离散信号与系统的 Z 域分析 p 11
理解：
f [k ] {1, 2, 3, 4, 5, 6} f [k 2] {0, 0, 1, 2, 3, 4, 5, 6}
由左边移到 右边的部分
f [k 2]u[k ] {0, 0, 0, 2, 3, 4, 5, 6} f [k 2]u[k 2] {0, 0, 0, ( z)} a u[k 1]
1
k 1
8 离散信号与系统的 Z 域分析 p 17
五、单边z变换的主要性质
3. 指数加权特性
z a f [k ] F ( ) a
k Z
k
z a Rf
1 1 , z 1 a u[k ] , z a u[k ] 1 1 1 a z 1 z
双边z变换*
8 离散信号与系统的 Z 域分析 p 2
一、Z变换的定义
课本是从离散时间傅氏变换（DTFT）引出 z 变换的， 其思想：对于一些不存在傅氏变换的离散序列，可以乘上 一个衰减序列 r－k，使之衰减，于是有：
FT[ f [k ] r k ]
k
k jk f [ k ] r e j k f [ k ]( r e )
一、Z变换的定义
从拉普拉斯变换也可以引出 z 变换。对理想抽样信 号，求其拉氏变换，即得：
f s (t ) f (t ) (t kT ) f (kT ) (t kT )
k k
两边做拉氏变换
Fs (s) L[ f s (t )]
令e sT z, 为了方便，f [KT] 仍用 f [K]表示
解：
sin( 0 k )u[k ]
z
sin 0 z
1
1 2
1 2 z cos 0 z
z 1
利用z变换的指数加权特性，可得
k sin( 0 k )u[k ]
sin 0 ( z / ) 1 1 2( z / ) cos 0 ( z / )
1 1 a u[k ] , 1 z 1 1 az 1 ( ) a
k Z
z a
利用z域微分特性，可得
1 d 1 az 1 k 1 az Z{ka u[k ]} z ,z a 1 2 dz (1 az )
0
k
0
k
0
k
Z{ f [k 1]u[k ]} z 1F ( z) f [1] Z{ f [k 2]u[k ]} z 1Z{ f [k 1]u[k ]} f [2] z F ( z) z f [1] f [2]
8 离散信号与系统的 Z 域分析 p 15
2
z
1 cos 0 z 1 j sin 0 z 1 1 2 z 1 cos 0 z 2
cos( 0 k )u[k ] sin( 0 k )u[k ]
8 离散信号与系统的 Z 域分析 p 9
1 cos 0 z 1 1 2 z 1 cos 0 z 2 sin 0 z 1 1 2 z 1 cos 0 z 2
1 2
sin 0 z 1 za 2 2 z 1 cos 0 z 2
8 离散信号与系统的 Z 域分析 p 19
五、单边z变换的主要性质
4. z域微分特性（时域线性加权）
dF ( z ) kf [k ] z dz
Z
Z Rf
m d m d F ( z) Z m m 或写成 : ( z ) F ( z ) k f [k ] ( z ) m dz dz
即f [k 2]u[k ] f [k 2]u[k 2]
k 2 z f [k n]u[k ] F ( z ) z n z n
f [k ]
k n
1
1
f [k ] z k
由左边移到右 边部分的z变换
原来序列的z变换
8 离散信号与系统的 Z 域分析 p 12
n k Z f [k n]u[k ] z [ F ( z ) f [k ]z ] k n k 0 1
|z|> Rf |z|> Rf
8 离散信号与系统的 Z 域分析 p 14
五、单边Z变换的主要性质
非因果序列的位移
f [k ]
f [k 1]
f [k 2]
五、单边z变换的主要性质
f [k ] F ( z), z R f
f1[k ] F1 ( z), z R f 1
z
z
f 2 [k ] F2 ( z), z R f 2
z
1.线性特性
af1[k ] bf2 [k ] aF 1 ( z) bF 2 ( z)
课本中只讨论因果序列信号（右边序列信号的特例）， 对因果信号而言，若存在z变换，则其双边z变换与单边z 变换是相同的，收敛域也相同。 此处根据定义求z变换
(1) f [k ] [k ]
F ( z)
k k [ k ] z 1, z 0, 即全z平面
f [k ] [k m], m为正整数 .
F1 ( z )
k k m [ k m ] z z
z 0
8 离散信号与系统的 Z 域分析 p 8
四、常用因果序列的Z变换
1) Z{ [k ]} 1,
k
z0
2) Z{ u[k ]}
1 1 z
1 1 e
j 0
1
za
1
3) Z{e j0k u[k ]}
如果原序列是非因果序列（求单边变换时乘u[k]）：
Z f [k n]u[k ] z n [ F ( z ) k n n 1 k f [ k ] z ], z R f 1
Z f [k n]u[k ] z n [ F ( z ) f [k ]z k ], z R f k 0
z f [k ] F ( z)
三、单边z变换及其收敛域
单边z 变换 收敛域(ROC)：
使上式级数收敛的所有z的范围称为F(z)的收敛域 收敛域为z平面中某个圆 的外部区域。可仿照极点 法求其半径。
Im z
ROC Re z
F ( z ) f [k ]z k
k 0
z Rf
L{ f s (t )} f [k ]z k F ( z )
k
k
f (kT )e
ksT
z域到频域、s域的映射关系： z
8 离散信号与系统的 Z 域分析 p 4
re , z e
j
sT
二、z变换定义及符号表示
双边z变换 z反变换
F ( z ) f [k ]z k
z 例： (3) u[k ] , z 3 z 3
k
类似于傅氏、拉氏变换的尺度变换特性。
1 1 s L f (at ) F ( j ) f (at ) F ( ), a a a a
F
8 离散信号与系统的 Z 域分析 p 18
a 0, a 0
例*：求aksin(0k) u[k] 的z变换及收敛域
2 2
8 离散信号与系统的 Z 域分析 p 13
五、单边z变换的主要性质
2. 位移特性(记忆)
因果序列的位移
f [k n] u[k n] z nF(z) 非因果序列的位移
n 1
|z|> Rf
Z f [k n]u[k ] z n [ F ( z ) f [k ]z k ]
序列相加减（线性加权）后，所得序列z变换的ROC，有 可能比原序列z变换的ROC大。位移特性常用来分析单边 周期信号，单边周期信号总具有相似的形式。
8 离散信号与系统的 Z 域分析 p 16
例： F(z) = 1/(za) |z| a 求f [k]。 解：
1 F ( z) z 1 1 az
8 离散信号与系统的 Z 域分析 p 6
例：求以下序列的Z变换及收敛域。
(1) f [k ] a u[k ]
k
(2)
1 0 k N 1, N为有限值 f [k ] 0 其它
Im z
解：根据定义式：
(1)
F ( z) a z
k k 0
k
1 1 1 az
位移特性（常见二阶形式，常用于求解差分方程）
f [k n]u[k n] z F ( z), z R f
Z
Z f [k n]u[k ] z n [ F ( z ) k n
n
1
f [k ]z k ], z R f
Z{ f [k 1]} z F ( z ) f [1] Z{ f [k 2]} z F ( z ) z f [1] f [2]
k
1 k 1 f [k ] F ( z ) z dz c 2 πj
物理意义： 将离散信号分解为不同频率复指数esTk的线性组合 符号表示 正变换：F(z) = Z{f [k]} 或
8 离散信号与系统的 Z 域分析 p 5