沾益五中2014—2015学年度上学期八年级第二次月考数学试题
2014-2015学年度第二学期期中测试八年级数学试题附答案
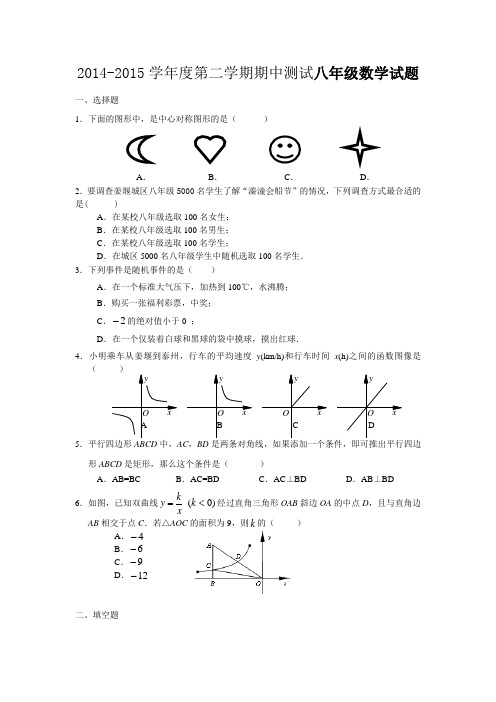
2014-2015学年度第二学期期中测试八年级数学试题一、选择题1.下面的图形中,是中心对称图形的是( )A. B . C .D .2.要调查姜堰城区八年级5000名学生了解“溱潼会船节”的情况,下列调查方式最合适的是( )A .在某校八年级选取100名女生;B .在某校八年级选取100名男生;C .在某校八年级选取100名学生;D .在城区5000名八年级学生中随机选取100名学生. 3.下列事件是随机事件的是( )A .在一个标准大气压下,加热到100℃,水沸腾;B .购买一张福利彩票,中奖;C .2-的绝对值小于0 ;D .在一个仅装着白球和黑球的袋中摸球,摸出红球.4.小明乘车从姜堰到泰州,行车的平均速度y (km/h)和行车时间x (h)之间的函数图像是(5.平行四边形ABCD 中,AC ,BD 是两条对角线,如果添加一个条件,即可推出平行四边形ABCD 是矩形,那么这个条件是( )A .AB=BCB .AC=BDC .AC ⊥BD D .AB ⊥BD 6.如图,已知双曲线 xky =)0(<k 经过直角三角形OAB 斜边OA 的中点D ,且与直角边AB 相交于点C .若△AOC 的面积为9,则k 的( )A .4-B .6-C .9-D .12-二、填空题7.当=x ________时,分式13-+x x 没有意义. 8.从1-,0,π,3四个数中随机任取一数,取到无理数的概率是 . 9.反比例函数xk y 1+=的图象在每一象限内y 随x 的增大而增大,则k 的取值范围是 . 10.若关于x 的分式方程233x m x x -=--有增根,则m = . 11.货车行驶25千米与小车行驶35千米所用时间相同,已知小车每小时比货车多行驶20千米,若设货车的速度为x 千米每小时,依题意可列的方程是 . 12.如图,在菱形ABCD 中,AC 、BD 相交于点O ,E 为AB 的中点,若OE =3,则菱形ABCD 的周长是_____________.13.某校根据去年初三学生参加中考的数学成绩的等级,绘制成如图的扇形统计图,则图中表示A 等级的扇形的圆心角的大小为_____________.14.如图,四边形ABCD 中,E ,F ,G ,H 分别是边AB ,BC ,CD ,DA 的中点.请你添加一个条件,使四边形EFGH 为矩形,应添加的条件是 . 15.如图,矩形ABCD 中,E 为BC 中点,AEC ∠的角平分线交AD 于F 点。
2014~2015学年8上数学第二次阶段考试卷及答案
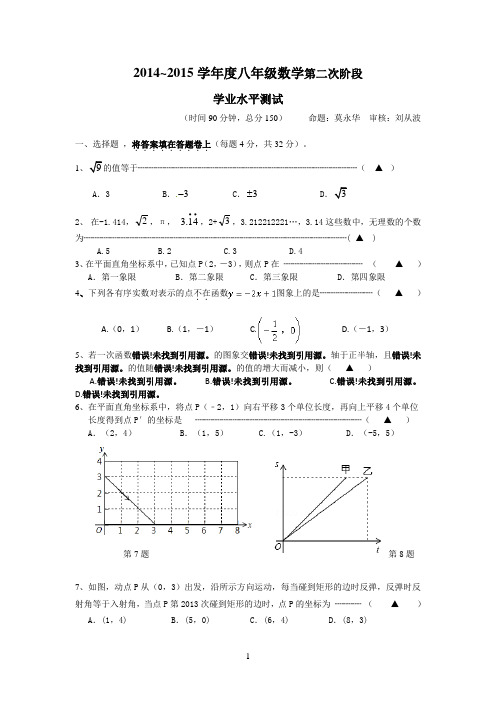
2014~2015学年度八年级数学第二次阶段学业水平测试(时间90分钟,总分150) 命题:莫永华 审核:刘从波一、选择题 ,将答案填在答题卷上.........(每题4分,共32分)。
1、9的值等于┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈( ▲ )A .3B .3-C .3±D .32、 在-1.414,2,π, ∙∙41.3,2+3,3.212212221…,3.14这些数中,无理数的个数为┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈( ▲ ) A.5 B.2 C.3 D.4 3、在平面直角坐标系中,已知点P (2,-3),则点P 在 ┈┈┈┈┈┈┈┈┈ ( ▲ ) A .第一象限 B .第二象限 C .第三象限 D .第四象限 4、下列各有序实数对表示的点不在..函数图象上的是┈┈┈┈┈┈( ▲ )A.(0,1)B.(1,-1)C.D.(-1,3)5、若一次函数错误!未找到引用源。
的图象交错误!未找到引用源。
轴于正半轴,且错误!未找到引用源。
的值随错误!未找到引用源。
的值的增大而减小,则( ▲ )A.错误!未找到引用源。
B.错误!未找到引用源。
C.错误!未找到引用源。
D.错误!未找到引用源。
6、在平面直角坐标系中,将点P (﹣2,1)向右平移3个单位长度,再向上平移4个单位长度得到点P′的坐标是 ┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈( ▲ ) A .(2,4) B .(1,5) C.(1,-3) D .(-5,5)第7题 第8题7、如图,动点P 从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当点P 第2013次碰到矩形的边时,点P 的坐标为 ┈┈┈ ( ▲ ) A .(1,4) B .(5,0) C .(6,4) D .(8,3)8、甲、乙两人在一次百米赛跑中,路程s (米)与赛跑时间t (秒)的关系如图所示,则下列说法正确的是( ▲ )A . 甲、乙两人的速度相同B . 甲先到达终点C . 乙用的时间短D . 乙比甲跑的路程多二、填空题,将答案填在答题卷上.........(每题4分,共40分)。
2013-2014年八年级数学12月月考试题(有答案)

( 2) a2 16( a b)2 .
解:( 1)原式= ( x y)( x y 2)
( 2)原式= (5a 4b)(4b 3a)
18. 先化简,再求值:( 7 分)
y( x y) ( x y) ( x y) 2 ,x其中 x = - 2,y = 1 . 2
解:原式= xy,当 x = - 2, y = 1 时,原式=- 1 2
22. 解下列方程与不等式( (1)3x(7-x)=18-x(3x-15) ; 解:( 1) x= 3 ( 2) x<- 1
8 分) ( 2) (x+3)(x-7)+8
> (x+5)(x-1).
23. ( 7 分)如图, OC是∠ AOB的角平分线, P 是 OC上
一点. PD⊥ OA交 OA于 D, PE⊥ OB交 OB于 E, F 是
24. ( 8 分) D 是 AB 上一点, DF 交 AC 于点 E, DE=EF ,AE=CE ,求证: A B∥CF。
证明:
A
∵∠ AED 与∠ CEF 是对顶角, ∴∠ AED= ∠ CEF, 在△ ABC 和△ CFE 中, ∵DE=FE ,∠ AED= ∠CEF, AE=CE ,
E
F
D
B 第 24 题 C
答案: D 2. 23 表示(★★★★★) .
A. 2 ×2× 2
B. 2 × 3
C. 3× 3 答案: A
D. 2+2+2
3. 在平面直角坐标系中。点 P( - 2, 3)关于 x 轴的对称点在(★★★★★) .
A. 第一象限 C. 第三象限 答案: C
B. 第二象限 D. 第四象限
4. 等腰但不等边的三角形的角平分线、高线、中线的总条数是(★★★★★)
2014-2015学年度第二学期八年级数学期中考试卷附答案

2014-2015学年度第二学期八年级数学期中考试卷(考试时间:100分钟 满分:120分)一、选择题:(每小题3分,共42分)下列各题都有A 、B 、C 、D 四个答案供选择,其中只有一个答案是正确的,请把认为正确的答案前面的字母编号写在相应的题号下。
1.下列式子是分式的是( )A.2x B.11+x C.y x +2 D.πxy2 2. 使分式2-x x有意义的x 的取值范围是( )A. 2x =B.2x ≠C.2x =-D.2x ≠-3. 某种感冒病毒的直径是0.00000012米,用科学记数法表示为( )米.A .71.210-⨯ B .71012.0-⨯ C .6102.1-⨯ D .61012.0-⨯ 4.点)0,2(在( )A.x 轴上B.y 轴上C.第一象限D.第四象限 5.点P (5,4-)关于x 轴对称点是( )A .(5,4) B.(5,4-) C.(4,5-) D.(5-,4-) 6.若点P(3,-1m )在第二象限,则m 的取值范围是( )A. m <1B. m <0C. m >0D. m >1 7.函数23-=x y 的图象不经过( )A.第一象限B.第二象限C.第三象限D.第四象限8.在同一坐标系中,函数x ky =和3+=kx y )0(≠k 的图像大致是( )9. 在平行四边形ABCD 中,A B C D ∠∠∠∠∶∶∶的值可以是( ) A.1234∶∶∶ B.1221∶∶∶ C.2211∶∶∶ D.2121∶∶∶ 10.下列说法错误的是( )学校: 班别: 姓名: 座号:………………………………………………………………装………………订………………线………………………………………………得分E A .平行四边形的对角相等 B.平行四边形的对角互补 C .平行四边形的对边相等 D.平行四边形的内角和是360°11.如图1,在平行四边形ABCD 中,CA ⊥AB ,若AB=3,BC=5,则平行四边形的面积等于( )A .6 B. 10 C. 12 D. 1512. 如图2,a b ∥,下列线段中是a b ,之间的距离的是( )A.AB B.AE C.EF D.BC图2 13.已知2111=-b a ,则b a ab -的值是( ) A .21 B.21- C.2 D.2-14.当一次函数32-=x y 的图像在第四象限时,自变量x 的取值范围是( ) A.0<x <23 B.x >0 C.x <23D.无法确定二、填空题:(每小题4分,共16分)15. 若分式方程212-=--x x m x 有增根,则这个增根是=x 16.若反比例函数xky = 的图象经过点(1,-2),则此函数的解析式为 。
【解析版】2014-2015年攀枝花五中八年级上月考数学试卷(10月)

③﹣ 27 的立方根是﹣ 3,故说法错误; ④互为相反数的两数的立方根互为相反数,故说法正确, 故选 C.
第 5 页(共 12 页)
8.能与数轴上的点一一对应的是( )
A. 整数
B. 有理数
9.下列各计算中,正确的是( )
A. b5•b5=2b5
B. x5+x5=x10
C. 无理数 C. m2•m3=m5
10.计算:(﹣ )1999•(﹣ 3)2000=( )
第 1 页(共 12 页)
D. 实数 D. a•b2=a2b2
2014-2015 学年四川省攀枝花五中八年级(上)月考数学试卷(10 月 份)
第 4 页(共 12 页)
点评:此题考查了立方根,熟练掌握立方根的定义是解本题的关键.
4.一个数的算术平方根与这个数的立方根的和为 0,则这个数是(
A. ﹣ 1
B. ±1
C. 0
) D. 不存在
考点:立方根;算术平方根. 专题:常规题型. 分析:根据算术平方根是非负数,一个数的立方根与它本身符号相同,而它们的和等于 0,可知这 个数是 0. 解答: 解:根据算术平方根非负数, 立方根不改变这个数的正负性, 相加等于 0,则这个数是 0. 故选 C. 点评:本题考查了立方根,与算术平方根非负数的性质,不是很难.
5.下列说法正确的是( ) A. 2 的平方根是 C. ﹣ 是 2 的平方根
B. 5 的算术平方根是± D. ± 是 5 的算术平方根
考点:平方根;算术平方根. 分析:根据平方根和算术平方根的定义判断即可. 解答: 解:A、2 的平方根是± ,错误;
B、5 的算术平方根是 ,错误; C、﹣ 是 2 的平方根,正确; D、 是 5 的算术平方根,错误; 故选 C. 点评:此题考查平方根问题,关键是根据平方根和算术平方根的定义分析.
2014-2015学年八年级(上)月考数学试卷(12月份)

2014-2015学年八年级(上)月考数学试卷(12月份)一、选择题(共10小题,每小题3分,计30分.每小题只有一个选项是符合题意的)1.下列运算正确的是( ) A. a3•a2=a6 B. y3÷y=y3 C.(m2n)3=m6n3 D.(x2)3=x5 2.剪纸是中华传统文化中的一块瑰宝,下列剪纸图案中不是轴对称图形的是( ) A.B.C.D.3.下列式子的变形,不是因式分解的有( )①(x+1)(x﹣2)=x2﹣x﹣2;②x2﹣2x+1=x(x﹣2)+1;③x2﹣9y2=(x+3y)(x﹣3y);④x2y﹣2xy+y=(x2﹣2x+1)y. A. 1个 B. 2个 C. 3个 D. 4个4.光年是一种长度单位,它表示光在一年中所通过的距离,已知光每秒的速度为3×105千米,一年以3×107秒计算,一光年约为( ) A. 3×1012千米 B. 9×1015千米 C. 9×1035千米 D. 9×1012千米 5.如图,在△ABC中,∠A=50°,∠ABC=70°,BD平分∠ABC,则∠BDC的度数是( ) A. 85° B. 80° C. 75° D. 70°6.如果单项式﹣x2a﹣3y2与x3y a+2b﹣7的和仍为单项式,那么它们的乘积为( ) A.﹣x6y4 B.﹣x3y2 C.﹣x6y4 D.x6y47.若A=10a2+3b2﹣5a+5,B=a2+3b2﹣8a+5,则A﹣B的值与﹣9a3b2的公因式为( ) A. a B.﹣3 C. 9a3b2 D. 3a8.对于任意整数n,多项式(n+7)2﹣(n﹣3)2的值都能( ) A.被20整除 B.被7整除 C.被21整除 D.被n+4整除9.如图,要设计一幅长为3xcm,宽为2ycm的长方形图案,其中有两横两竖的彩条,横彩条的宽度均为acm,竖彩条的宽度均为bcm,则空白区域的面积是( ) A.(6xy﹣6xa﹣4by+4ab)cm2 B.(6xy+6xa+4by﹣4ab)cm2 C.(6xy﹣6xb﹣4ay+4ab)cm2 D.(6xy+6xb+4ay﹣4ab10.计算(2+1)(22+1)(24+1)…(232+1)的结果为( ) A. 235+2 B. 264+1 C. 264﹣1 D. 232﹣1二、填空题(共8小题,每小题3分,计24分)11.若□×6xy=3x3y2,则□内应填的单项式是 .12.计算(15y3﹣9y2﹣3y)÷(﹣3y)= .13.已知2a+3b+4=0,则﹣4a﹣6b的值为 .14.若4x2+mx+9是一个完全平方式,则实数m的值是 . 15.如果(x2﹣mx+3)(3x﹣2)的展开式中不含x2项,则m的值是 .16.一个等腰三角形的周长为16,一边长是6,则它的腰长为 .17.若3x=m,9y=n,x,y为正整数,则32x+6y等于 . 18.在日常生活中如取款、上网等都需要密码.有一种用“因式分解”法产生的密码,方便记忆.原理是:如对于多项式x4﹣y4,因式分解的结果是(x﹣y)(x+y)(x2+y2),若取x=9,y=9时,则各个因式的值是:(x﹣y)=0,(x+y)=18,(x2+y2)=162,于是就可以把“018162”作为一个六位数的密码.对于多项式4x3﹣xy2,取x=10,y=10时,用上述方法产生的密码是: (写出一个即可). 三、解答题(共5小题,计46分.解答应写出过程)19.把下列各式分解因式:(1)x2﹣(y+2)2;(2)﹣20x3y+x4+100x2y2.20.如图,在Rt△ABC中,∠ABC=90°,在边AB上取一点D,使得DB=BC,过点D作EF⊥AC,分别交AC于点E,交CB的延长线于点F,求证:FC=AB+DB.21.先化简,再求值:(1)b(a+b)+(a+2b)(2a﹣b)﹣4ab,其中a=﹣3,b=4;(2)[(x+3y)(x﹣3y)+(x+3y)2]÷(﹣4x),其中x=1,y=.22.已知“两点之间,线段最短”,我们经常利用它来解决两线段和的最小值问题.(1)实践运用唐朝诗人李欣的诗《古从军行》开头两句说:“白日登山望烽火,黄昏饮马傍交河.”诗中隐含着一个有趣的数学问题﹣﹣将军饮马问题:如图1所示,诗中将军在观望烽火之后从山脚下的A点出发,走到河边饮马后,再到B点宿营,请问怎样走才能使总的路程最短?画出最短路径并说明理由.(2)拓展延伸如图2,点P,Q是△ABC的边AB、AC上的两个定点,请同学们在BC上找一点R,使得△PQR的周长最短(要求:尺规作图,不写作图过程保留作图痕迹).23.我们知道对于一个图形,通过不同的方法计算图形的面积时,可以得到一个数学等式,例如由图1可以得到(a+b)2=a2+2ab+b2.请解答下列问题:(1)直接写出图2中所表示的数学等式 ;(2)写出图3中所表示的数学等式,并利用所得到的结论,解决下面的问题:已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值;(3)图4中给出了若干个边长为a和边长为b的小正方形纸片,若干个长为a、宽为b的长方形纸片,请先写出数学等式:(2a+b)(a+2b)= ,再利用所给的纸片拼出一个几何图形,验证该公式.2014-2015学年陕西省安康市旬阳县桐木中学八年级(上)月考数学试卷(12月份)参考答案与试题解析一、选择题(共10小题,每小题3分,计30分.每小题只有一个选项是符合题意的)1.下列运算正确的是( ) A. a3•a2=a6 B. y3÷y=y3 C.(m2n)3=m6n3 D.(x2)3=x5考点:同底数幂的除法;同底数幂的乘法;幂的乘方与积的乘方.分析:根据同底数幂的乘法,可判断A,根据同底数幂的除法,可判断B,根据积的乘方,可判断C,根据幂的乘方,可判断D.解答:解:A、同底数幂的乘法底数不变指数相加,故A错误;B、底数不变指数相减,故B错误;C、积的乘方等每个因式分别乘方,再把所得的幂相乘,故C正确;D、幂的乘方底数不变指数相乘,故D错误;故选:C.点评:本题考查了同底数幂的除法,利用法则计算是解题关键.2.剪纸是中华传统文化中的一块瑰宝,下列剪纸图案中不是轴对称图形的是( ) A.B.C.D.考点:轴对称图形.分析:根据轴对称图形的定义直接判断得出即可.解答:解:A、是轴对称图形,故此选项错误;B、是轴对称图形,故此选项错误;C、是轴对称图形,故此选项错误;D、不是轴对称图形,故此选项正确.故选:D.点评:此题主要考查了轴对称图形的性质,如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴,这时,我们也可以说这个图形关于这条直线(成轴)对称.3.下列式子的变形,不是因式分解的有( )①(x+1)(x﹣2)=x2﹣x﹣2;②x2﹣2x+1=x(x﹣2)+1;③x2﹣9y2=(x+3y)(x﹣3y);④x2y﹣2xy+y=(x2﹣2x+1)y. A. 1个 B. 2个 C. 3个 D. 4个考点:因式分解的意义.分析:把一个多项式化为几个整式的积的形式,这种变形叫做把这个多项式因式分解.解答:解:①右边不是整式积的形式,不是因式分解;②右边不是整式积的形式,不是因式分解;③是因式分解;④右边的式子还有可以分解的多项式,不是因式分解;综上可得不是因式分解的是:①②④,共3个.故选C.点评:本题考查了因式分解的知识,解答本题的关键是掌握因式分解的定义.4.光年是一种长度单位,它表示光在一年中所通过的距离,已知光每秒的速度为3×105千米,一年以3×107秒计算,一光年约为( ) A. 3×1012千米 B. 9×1015千米 C. 9×1035千米 D. 9×1012千米考点:科学记数法—表示较大的数.分析:科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.解答:解:将3×105×3×107用科学记数法表示为:9×1012.故选:D.点评:此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.5.如图,在△ABC中,∠A=50°,∠ABC=70°,BD平分∠ABC,则∠BDC的度数是( ) A. 85° B. 80° C. 75° D. 70°考点:三角形内角和定理.分析:先根据∠A=50°,∠ABC=70°得出∠C的度数,再由BD平分∠ABC求出∠ABD的度数,再根据三角形的外角等于和它不相邻的内角的和解答.解答:解:∵∠ABC=70°,BD平分∠ABC,∴∠ABD=70°×=35°,∴∠BDC=50°+35°=85°,故选:A.点评:本题考查的是三角形的外角和内角的关系,熟知三角形的外角等于和它不相邻的内角的和是解题的关键.6.如果单项式﹣x2a﹣3y2与x3y a+2b﹣7的和仍为单项式,那么它们的乘积为( ) A.﹣x6y4 B.﹣x3y2 C.﹣x6y4 D.x6y4考点:单项式乘单项式;合并同类项.分析:根据合并同类项法则得出a,b的值,进而利用单项式乘以单项式运算法则求出即可.解答:解:∵单项式﹣x2a﹣3y2与x3y a+2b﹣7的和仍为单项式,∴,解得:,故单项式﹣x3y2与x3y2的乘积为:﹣x6y4.故选:C.点评:此题主要考查了单项式乘以单项式以及合并同类项法则,得出a,b的值是解题关键.7.若A=10a2+3b2﹣5a+5,B=a2+3b2﹣8a+5,则A﹣B的值与﹣9a3b2的公因式为( ) A. a B.﹣3 C. 9a3b2 D. 3a考点:公因式;整式的加减.分析:根据合并同类项,可化简整式,根据公因式是每項都含有的因式,可得答案.解答:解:A﹣B=9a2+3a,A﹣B的值与﹣9a3b2的公因式为3a,故选:D.点评:本题考查了公因式,先合并同类项,再判断公因式.8.对于任意整数n,多项式(n+7)2﹣(n﹣3)2的值都能( ) A.被20整除 B.被7整除 C.被21整除 D.被n+4整除考点:因式分解-运用公式法.分析:直接利用平方差公式分解因式得出即可.解答:解:(n+7)2﹣(n﹣3)2=[(n+7)﹣(n﹣3)][(n+7)+(n﹣3)]=10(2n+4)=20(n+2),故多项式(n+7)2﹣(n﹣3)2的值都能被20整除.故选:A.点评:此题主要考查了公式法分解因式,熟练应用平方差公式是解题关键.9.如图,要设计一幅长为3xcm,宽为2ycm的长方形图案,其中有两横两竖的彩条,横彩条的宽度均为acm,竖彩条的宽度均为bcm,则空白区域的面积是( ) A.(6xy﹣6xa﹣4by+4ab)cm2 B.(6xy+6xa+4by﹣4ab)cm2 C.(6xy﹣6xb﹣4ay+4ab)cm2 D.(6xy+6xb+4ay﹣4ab考点:整式的混合运算.专题:应用题.分析::由长方形面积减去阴影部分面积求出空白区域面积即可.解答:解:根据题意得:3x•2y﹣(3x﹣2a)(2y﹣2a)=(6xy﹣6xa﹣4by+4ab)cm2.故选A点评:此题考查了整式的混合运算,熟练掌握运算法则是解本题的关键.10.计算(2+1)(22+1)(24+1)…(232+1)的结果为( ) A. 235+2 B. 264+1 C. 264﹣1 D. 232﹣1考点:平方差公式.分析:把前面的1变为(2﹣1),再依次运用平方差公式进行计算即可.解答:解:原式=(2﹣1)(2+1)(22+1)(24+1)(28+1)(216+1)(232+1),=(22﹣1)(22+1)(24+1)(28+1)(216+1)(232+1),=(24﹣1)(24+1)(28+1)(216+1)(232+1),=(28﹣1)(28+1)(216+1)(232+1),=(216﹣1)(216+1)(232+1),=(232﹣1)(232+1),=264﹣1故选:C.点评:本题考查了平方差公式的应用,注意:(a+b)(a﹣b)=a2﹣b2.二、填空题(共8小题,每小题3分,计24分)11.若□×6xy=3x3y2,则□内应填的单项式是 x2y .考点:单项式乘单项式.分析:利用单项式的乘除运算法则,进而求出即可.解答:解:∵□×6xy=3x3y2,∴□=3x3y2÷6xy=x2y.故答案为:x2y.点评:此题主要考查了单项式的乘除运算,正确掌握运算法则是解题关键.12.计算(15y3﹣9y2﹣3y)÷(﹣3y)= ﹣5y2+3y+1 .考点:整式的除法.专题:计算题.分析:原式利用多项式除以单项式法则计算即可得到结果.解答:解:(15y3﹣9y2﹣3y)÷(﹣3y)=﹣5y2+3y+1,故答案为:﹣5y2+3y+1点评:此题考查了整式的除法,熟练掌握运算法则是解本题的关键. 13.已知2a+3b+4=0,则﹣4a﹣6b的值为 8 .考点:代数式求值.专题:计算题.分析:由已知等式变形求出2a+3b的值,原式变形后代入计算即可求出值.解答:解:由题意得:2a+3b=﹣4,则原式=﹣2(2a+3b)=8,故答案为:8点评:此题考查了代数式求值,熟练掌握运算法则是解本题的关键. 14.若4x2+mx+9是一个完全平方式,则实数m的值是 ±12 .考点:完全平方式.专题:常规题型.分析:先根据两平方项确定出这两个数,再根据完全平方公式的乘积二倍项即可确定k的值.解答:解:∵4x2+mx+9=(2x)2+mx+32,∴mx=±2×2x×3,解得m=±12.故答案为:±12.点评:本题主要考查了完全平方式,根据平方项确定出这两个数是解题的关键,也是难点,熟记完全平方公式对解题非常重要.15.如果(x2﹣mx+3)(3x﹣2)的展开式中不含x2项,则m的值是 .考点:多项式乘多项式.分析:根据多项式乘以多项式的法则,可表示为(x2﹣mx+3)(3x﹣2)=3x3﹣(3m+2)x2+(2m+9)x﹣6,再令 x2项系数为0,计算即可.解答:解:(x2﹣mx+3)(3x﹣2)=3x3﹣(3m+2)x2+(2m+9)x﹣6,如果(x2﹣mx+3)(3x﹣2)的展开式中不含x2项,则有,3m+2=0解得,m=﹣.故答案为:﹣.点评:本题主要考查多项式乘以多项式的法则.注意不要漏项,漏字母,有同类项的合并同类项.16.一个等腰三角形的周长为16,一边长是6,则它的腰长为 6或5 .考点:等腰三角形的性质;三角形三边关系.分析:题目给出等腰三角形有一边长为6,而没有明确腰、底分别是多少,所以要进行讨论,还要应用三角形的三边关系验证能否组成三角形.解答:解:∵等腰三角形的周长为16,∴当6为腰时,它的底长=16﹣6﹣6=3,3+6>6能构成等腰三角形,即它的腰长为6;当6为底时,它的腰长=(16﹣6)÷2=5,5+5>6能构成等腰三角形,即它的腰长也可以为5.故它的腰长为6或5.故填6或5.点评:本题考查了等腰三角形的性质和三角形的三边关系;本题从边的方面考查三角形,涉及分类讨论的思想方法.注意养成检验三边长能否组成三角形的好习惯,把不符合题意的舍去.17.若3x=m,9y=n,x,y为正整数,则32x+6y等于 m2n3 .考点:幂的乘方与积的乘方;同底数幂的乘法.分析:先求出32y=n,先根据同底数幂的乘法进行计算,再根据幂的乘方变形,最后整体代入求出即可.解答:解:∵3x=m,9y=n,∴32y=n,∴32x+6y=32x•36y=(3x)2•(32y)3=m2n3,故答案为:m2n3.点评:本题考查了同底数幂的乘法,幂的乘方的应用,能灵活运用法则进行变形是解此题的关键,用了整体代入思想.18.在日常生活中如取款、上网等都需要密码.有一种用“因式分解”法产生的密码,方便记忆.原理是:如对于多项式x4﹣y4,因式分解的结果是(x﹣y)(x+y)(x2+y2),若取x=9,y=9时,则各个因式的值是:(x﹣y)=0,(x+y)=18,(x2+y2)=162,于是就可以把“018162”作为一个六位数的密码.对于多项式4x3﹣xy2,取x=10,y=10时,用上述方法产生的密码是: 101030或103010或301010 (写出一个即可).考点:因式分解的应用.专题:开放型.分析:把所求的代数式分解因式后整理成条件中所给出的代数式的形式,然后整体代入即可.解答:解:4x3﹣xy2=x(4x2﹣y2)=x(2x+y)(2x﹣y),当x=10,y=10时,x=10;2x+y=30;2x﹣y=10,用上述方法产生的密码是:101030或103010或301010.故答案为:101030或103010或301010.点评:本题考查了提公因式法,公式法分解因式,读懂题目信息,正确进行因式分解是解题的关键,还考查了代数式求值的方法,同时还隐含了整体的数学思想和正确运算的能力.三、解答题(共5小题,计46分.解答应写出过程)19.把下列各式分解因式:(1)x2﹣(y+2)2;(2)﹣20x3y+x4+100x2y2.考点:提公因式法与公式法的综合运用.专题:计算题.分析:(1)原式利用平方差公式分解即可;(2)原式提取公因式,再利用完全平方公式分解即可.解答:解:(1)原式=(x+y+2)(x﹣y﹣2);(2)原式=x2(﹣20xy+x2+100y2)=x2(x﹣10y)2.点评:此题考查了提公因式法与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.20.如图,在Rt△ABC中,∠ABC=90°,在边AB上取一点D,使得DB=BC,过点D作EF⊥AC,分别交AC于点E,交CB的延长线于点F,求证:FC=AB+DB.考点:全等三角形的判定与性质.专题:证明题.分析:先根据角的互余关系求出∠A=∠F,再根据AAS证明△ABC≌△FBD,得出对应边相等,即可得出结论.解答:解:∵∠ABC=90°,EF⊥AC,∴∠A=∠C=90°,∠F+∠C=90°,∴∠A=∠F,在△ABC和△FBD中,,∴△ABC≌△FBD(AAS),∴BF=AB,∴FC=BF+BC=AB+BD.点评:本题考查了全等三角形的判定与性质;熟练掌握全等三角形的判定方法证明三角形全等是解决问题的关键.21.先化简,再求值:(1)b(a+b)+(a+2b)(2a﹣b)﹣4ab,其中a=﹣3,b=4;(2)[(x+3y)(x﹣3y)+(x+3y)2]÷(﹣4x),其中x=1,y=.考点:整式的混合运算—化简求值.专题:计算题.分析:(1)原式利用单项式乘以多项式,平方差公式计算,合并得到最简结果,把a与b的值代入计算即可求出值;(2)原式利用平方差公式及完全平方公式化简,再利用多项式除以单项式法则计算得到最简结果,把x与y的值代入计算即可求出值解答:解:(1)原式=ab+b2+2a2﹣ab+4ab﹣2b2﹣4ab=2a2﹣b2,当a=﹣3,b=4时,原式=18﹣16=2;(2)原式=(x2﹣9y2+x2+6xy+9y2)÷(﹣4x)=(2x2+6xy)÷(﹣4x)=﹣,当x=1,y=时,原式=﹣.点评:此题考查了整式的混合运算﹣化简求值,熟练掌握运算法则是解本题的关键.22.已知“两点之间,线段最短”,我们经常利用它来解决两线段和的最小值问题.(1)实践运用唐朝诗人李欣的诗《古从军行》开头两句说:“白日登山望烽火,黄昏饮马傍交河.”诗中隐含着一个有趣的数学问题﹣﹣将军饮马问题:如图1所示,诗中将军在观望烽火之后从山脚下的A点出发,走到河边饮马后,再到B点宿营,请问怎样走才能使总的路程最短?画出最短路径并说明理由.(2)拓展延伸如图2,点P,Q是△ABC的边AB、AC上的两个定点,请同学们在BC上找一点R,使得△PQR的周长最短(要求:尺规作图,不写作图过程保留作图痕迹).考点:轴对称-最短路线问题;作图—应用与设计作图.分析:(1)从点A出发向河岸引垂线,垂足为D,在AD的延长线上,取A′使得A′D=AD,连接A′B,与河岸相交y于C,则C点就是饮马的地方,此时AC+BC的值最小.(2)作P点关于BC的对称点P′,连接P′Q,交BC于R,此时△PQR的周长最短.解答:解:(1)如图1,从点A出发向河岸引垂线,垂足为D,在AD的延长线上,取A′使得A′D=AD,连接A′B,与河岸相交y于C,则C点就是饮马的地方;证明:如图1,如果将军在河边的另外任意点C′饮马,所走的路程就是AC′+C′B,因为AC′+C′B>A′B=AC+BC,所以在C点外任意一点饮马,所走的路程都要远些;(2)尺规作图,如图2:点评:此题主要考查了作图﹣应用与设计作图,关键是掌握在直线L上的同侧有两个点A、B,在直线L上有到A、B的距离之和最短的点存在,可以通过轴对称来确定,即作出其中一点关于直线L的对称点,对称点与另一点的连线与直线L的交点就是所要找的点.23.我们知道对于一个图形,通过不同的方法计算图形的面积时,可以得到一个数学等式,例如由图1可以得到(a+b)2=a2+2ab+b2.请解答下列问题:(1)直接写出图2中所表示的数学等式 (a+2b)(a+b)=a2+3ab+2b2 ;(2)写出图3中所表示的数学等式,并利用所得到的结论,解决下面的问题:已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值;(3)图4中给出了若干个边长为a和边长为b的小正方形纸片,若干个长为a、宽为b的长方形纸片,请先写出数学等式:(2a+b)(a+2b)= 2a2+5ab+2b2 ,再利用所给的纸片拼出一个几何图形,验证该公式.考点:多项式乘多项式.分析:(1)根据数据表示出矩形的长与宽,再根据矩形的面积公式写出等式的左边,再表示出每一小部分的矩形的面积,然后根据面积相等即可写出等式.(2)根据利用(1)中所得到的结论,将a+b+c=11,ab+bc+ac=38作为整式代入即可求出.(3)找规律,根据公式画出图形,拼成一个长方形,使它满足所给的条件解答:解:(1)根据题意,大矩形的面积为:(a+2b)(a+b)=a2+3ab+2b2,故答案为:(a+2b)(a+b)=a2+3ab+2b2.(2)根据题意,大矩形的面积为:(a+b+c)(a+b+c)=(a+b+c)2,各小矩形部分的面积之和=a2+2ab+b2+2bc+2ac+c2,∴等式为(a+b+c)2=a2+b2+c2+2ab+2ac+2bc.故a2+b2+c2 =(a+b+c)2﹣2ab﹣2ac﹣2bc=112﹣2×38=45;(3)(2a+b)(a+2b)=2a2+5ab+2b2;如图所示:(答案不唯一).点评:本题考查了完全平方公式的几何背景,根据矩形的面积公式分整体与部分两种思路表示出面积,然后再根据同一个图形的面积相等即可解答.。
【解析版】2014-2015年攀枝花五中八年级上月考数学试卷10月

2014-2015学年四川省攀枝花五中八年级(上)月考数学试卷(10月份)一、选择题.共30分1.16的平方根与﹣8的立方根之和是()A.﹣6 B.2 C.2或﹣6 D.02.下列说法正确的是()A.0和1的平方根等于本身B.0和1的算术平方根等于本身C.立方根等于本身的数是0 D.以上说法都不正确3.8的立方根是()A.﹣2 B.2 C.2或﹣6 D.04.一个数的算术平方根与这个数的立方根的和为0,则这个数是()A.﹣1 B.±1 C.0 D.不存在5.下列说法正确的是()A.2的平方根是B.5的算术平方根是±C.﹣是2的平方根D.±是5的算术平方根6.有下列四个说法:①1的算术平方根是1,②的立方根是±,③﹣27没有立方根,④互为相反数的两数的立方根互为相反数,其中正确的是()A.①②B.①③C.①④D.②④7.下列说法正确的是()A.无限不循环小数是无理数B.带根号的数都是无理数C.无限小数都是无理数D.π是无理数,但是分数,也就是有理数8.能与数轴上的点一一对应的是()A.整数B.有理数C.无理数D.实数9.下列各计算中,正确的是()A.b5•b5=2b5B.x5+x5=x10C.m2•m3=m5D.a•b2=a2b210.计算:(﹣)1999•(﹣3)2000=()A.B.3 C.﹣D.﹣3二.填空题.每道2分,共20分11.25的平方根是,的算术平方根是.12.125的立方根是,的立方根是.13.3是数a的一个平方根,2是数b的一个立方根,则a+b=,2a+b﹣1的平方根是.14.在实数0.3,﹣,﹣,,,0,0.2020020002…,﹣0.,﹣中,有理数有;无理数有.15.﹣=,±=.16.+=;|2﹣|+|3﹣|=.17.(﹣a5)•(﹣a2)2=,(﹣2x)3÷4x=.18.若x2=(﹣7)2,则x=;若=3,则x=.19.若+(y﹣3)2=0,则x+y=,x y﹣xy=.20.请你观察、思考下列计算过程:因为112=121,所以=11,同样,因为1112=12321,所以=111,则=,由此猜想=.三、解答题(共1小题,满分24分)21.计算题:①2a8•(3ab)3②42x2•x3÷7x4③(8a3b﹣5a2b2)÷4ab;④xy•(﹣x3y4+x2y6)⑤(a+3b)(a﹣3b);⑥(2x+y)2﹣(2x+3y)(2x﹣3y)四.解答题,共26分22.卫星绕地球表面做圆周运动的速度约为8×103米/秒,则卫星运行8×103秒所走的路程约是多少?23.先化简,再求值:2(x+1)(x﹣1)﹣x(2x﹣1),其中x=﹣2.24.已知与互为相反数,求(x﹣y)的值.25.已知(x﹣y)2=4,(x+y)2=64;求下列代数式的值:(1)x2+y2;(2)xy.26.问题:你能比较两个数20062007和20072006的大小吗?为了解决这个问题,我们先把它抽象成数学问题,写出它的一般形式,比较n n+1与(n+1)n的大小(n为正整数),从分析n=1,n=2,n=3,…的情形入手,通过归纳,发现规律,猜想出结论.(1)比较各组数的大小①1221;②2332;③3443;④4554(2)由(1)猜想出n n+1与(n+1)n的大小关系是;(3)由(2)可知:2006200720072006.五.附加题27.请认真分析下面一组等式的特征:1×3=22﹣1;3×5=42﹣1;5×7=62﹣1;7×9=82﹣1;…这一组等式有什么规律?将你猜想到的规律用一个只含字母n的式子表示出来?.2014-2015学年四川省攀枝花五中八年级(上)月考数学试卷(10月份)参考答案与试题解析一、选择题.共30分1.16的平方根与﹣8的立方根之和是()A.﹣6 B.2 C.2或﹣6 D.0考点:实数的运算.专题:计算题.分析:利用平方根及立方根定义计算即可得到结果.解答:解:根据题意得:16的平方根为±4,﹣8的立方根为﹣2,∴﹣4﹣2=﹣6;4﹣2=2,则16的平方根与﹣8的立方根之和是2或﹣6.故选C点评:此题考查了实数的运算,熟练掌握运算法则是解本题的关键.2.下列说法正确的是()A.0和1的平方根等于本身B.0和1的算术平方根等于本身C.立方根等于本身的数是0 D.以上说法都不正确考点:立方根;平方根;算术平方根.分析:根据1的平方根为±1对A进行判断;根据0的算术平方根为0,1的算术平方根为1对B、D 进行判断;根据0、±1的立方根等于它本身对C进行判断.解答:解:A、1的平方根为±1,所以A选项错误;B、0和1的算术平方根等于本身,所以B选项正确;C、立方根等于本身的数是0、±1,所以C选项错误;D、由于B选项正确,所以D选项错误.故选B.点评:本题考查了立方根:若一个数的立方等于a,那么这个数叫a的立方根,记作.也考查了平方根与算术平方根.3.8的立方根是()A.﹣2 B.2 C.2或﹣6 D.0考点:立方根.专题:计算题.分析:利用立方根定义计算即可得到结果.解答:解:8的立方根是2,故选B.点评:此题考查了立方根,熟练掌握立方根的定义是解本题的关键.4.一个数的算术平方根与这个数的立方根的和为0,则这个数是()A.﹣1 B.±1 C.0 D.不存在考点:立方根;算术平方根.专题:常规题型.分析:根据算术平方根是非负数,一个数的立方根与它本身符号相同,而它们的和等于0,可知这个数是0.解答:解:根据算术平方根非负数,立方根不改变这个数的正负性,相加等于0,则这个数是0.故选C.点评:本题考查了立方根,与算术平方根非负数的性质,不是很难.5.下列说法正确的是()A.2的平方根是B.5的算术平方根是±C.﹣是2的平方根D.±是5的算术平方根考点:平方根;算术平方根.分析:根据平方根和算术平方根的定义判断即可.解答:解:A、2的平方根是±,错误;B、5的算术平方根是,错误;C、﹣是2的平方根,正确;D、是5的算术平方根,错误;故选C.点评:此题考查平方根问题,关键是根据平方根和算术平方根的定义分析.6.有下列四个说法:①1的算术平方根是1,②的立方根是±,③﹣27没有立方根,④互为相反数的两数的立方根互为相反数,其中正确的是()A.①②B.①③C.①④D.②④考点:立方根;平方根;算术平方根.分析:①根据算术平方根的定义即可判定;②根据立方根的定义即可判定;③根据立方根的定义即可判定;④根据立方根、相反数的定义即可判定.解答:解:①1的算术平方根是1,故说法正确;②的立方根是,故说法错误;③﹣27的立方根是﹣3,故说法错误;④互为相反数的两数的立方根互为相反数,故说法正确,故选C.点评:此题考查了相反数,立方根和算术平方根的性质,要掌握一些特殊数字的特殊性质,如1,﹣1和0.相反数的定义:只有符号相反的两个数叫互为相反数;立方根的性质:一个正数的立方根是正数,一个负数的立方根是负数,0的立方根是0.算术平方根是非负数.7.下列说法正确的是()A.无限不循环小数是无理数B.带根号的数都是无理数C.无限小数都是无理数D.π是无理数,但是分数,也就是有理数考点:无理数.分析:根据无理数的概念,结合选项求解.解答:解:A、无限不循环小数是无理数,故本选项正确;B、开方开不尽的数为无理数,故本选项错误;C、无限不循环小数是无理数,故本选项错误;D、π是无理数,也是无理数,故本选项错误.故选A.点评:本题考查了无理数的知识,解答本题的关键是掌握无理数的三种形式:①开方开不尽的数,②无限不循环小数,③含有π的数.8.能与数轴上的点一一对应的是()A.整数B.有理数C.无理数D.实数考点:实数与数轴.分析:根据实数与数轴上的点是一一对应关系,即可得出.解答:解:根据实数与数轴上的点是一一对应关系.故选:D.点评:本题考查了实数与数轴的对应关系,任意一个实数都可以用数轴上的点表示;反之,数轴上的任意一个点都表示一个实数.数轴上的任一点表示的数,不是有理数,就是无理数.9.下列各计算中,正确的是()A.b5•b5=2b5B.x5+x5=x10C.m2•m3=m5D.a•b2=a2b2考点:同底数幂的乘法;合并同类项.分析:根据同底数幂的乘法性质,合并同类项的法则,对各选项分析判断后利用排除法求解.解答:解:A、b5•b5=b10,故此选项错误;B、应为x5+x5=2x5,故此选项错误;C、根据同底数的幂相乘,底数不变,指数相加,正确;D、应为a•b2=ab2,故此选项错误.故选C.点评:本题考查了合并同类项,同底数幂的乘法,理清指数的变化是解题的关键.10.计算:(﹣)1999•(﹣3)2000=()A.B.3 C.﹣D.﹣3考点:幂的乘方与积的乘方.分析:根据积的乘方计算即可.解答:解:(﹣)1999•(﹣3)2000=﹣3,故选D点评:此题考查积的乘方问题,关键是根据积的乘方的逆运算计算.二.填空题.每道2分,共20分11.25的平方根是±5,的算术平方根是3.考点:算术平方根;平方根.分析:根据平方根和算术平方根的定义解答即可.解答:解:25的平方根是±5,的算术平方根是3,故答案为:±5;3.点评:此题考查平方根和算术平方根的问题,关键是根据平方根和算术平方根的定义解答.12.125的立方根是5,的立方根是2.考点:立方根.分析:根据立方根的定义解答即可.解答:解:125的立方根是5,的立方根是2,故答案为:5;2点评:本题考查的是立方根的定义,根据立方根的定义解答此题的关键.13.3是数a的一个平方根,2是数b的一个立方根,则a+b=17,2a+b﹣1的平方根是±5.考点:立方根;平方根.分析:分别根据3是a的一个平方根,2是数b的一个立方根求出a、b的值,再求出a+b和2a+b﹣1的值,求出其平方根即可.解答:解:因为3是数a的一个平方根,2是数b的一个立方根,可得:a=9,b=8,把a=9,b=8代入a+b=17,2a+b﹣1=25,其平方根为±5.故答案为:17;±5.点评:本题考查的是立方根、平方根的定义,根据题意列出关于a、b的方程,求出a、b的值是解答此题的关键.14.在实数0.3,﹣,﹣,,,0,0.2020020002…,﹣0.,﹣中,有理数有0.3,﹣,,0,﹣0.;无理数有﹣,,0.2020020002…,﹣.考点:实数.分析:分别根据实数的分类及有理数、无理数的概念进行解答.解答:解:在实数0.3,﹣,﹣,,,0,0.2020020002…,﹣0.,﹣中,有理数有0.3,﹣,,0,﹣0.;无理数有﹣,,0.2020020002…,﹣,故答案为:0.3,﹣,,0,﹣0.;﹣,,0.2020020002…,﹣.点评:本题考查的是实数的分类,关键是根据实数的分类及无理数、有理数的定义解答.15.﹣=﹣4,±=±13.考点:算术平方根;平方根.分析:根据算术平方根和平方根的定义解答即可.解答:解:﹣=﹣4,±=±13,故答案为:﹣4;±13点评:此题考查算术平方根和平方根的问题,关键是根据算术平方根和平方根的定义解答.16.+=5;|2﹣|+|3﹣|=1.考点:实数的运算.分析:根据平方根、立方根、绝对值的性质解答.解答:解:=7﹣2=5;|2﹣|+|3﹣|=﹣2+3﹣=1.故答案为5,﹣1.点评:本题考查了实数的运算,熟悉平方根、立方根及绝对值的性质即可解答.17.(﹣a5)•(﹣a2)2=﹣a9,(﹣2x)3÷4x=﹣2x2.考点:整式的除法;同底数幂的乘法;幂的乘方与积的乘方.分析:根据整式的除法计算即可.解答:解:(﹣a5)•(﹣a2)2=﹣a9,(﹣2x)3÷4x=﹣2x2,故答案为:﹣a9;﹣2x2点评:此题考查整式的除法,关键是根据法则进行计算.18.若x2=(﹣7)2,则x=±7;若=3,则x=9.考点:算术平方根;平方根.分析:先算出(﹣7)2=49,再求平方根,根据算术平方根的定义求解即可.解答:解:∵x2=(﹣7)2,即x2=49,∴x=±7,∵=3,∴x=9.故答案为:±7,9.点评:本题主要考查了算术平方根与平方根,解题的关键是熟记算术平方根与平方根的定义.19.若+(y﹣3)2=0,则x+y=1,x y﹣xy=﹣2.考点:算术平方根;非负数的性质:偶次方.分析:根据非负数的性质列出方程求出x、y的值,代入所求代数式计算即可.解答:解:∵+(y﹣3)2=0,∴x+2=0,y﹣3=0,∴x=﹣2,y=3,将x=﹣2,y=3代入得:x+y=﹣2+3=1,x y﹣xy=(﹣2)3﹣(﹣2)×3=﹣2,故答案为:1,﹣2.点评:本题主要考查了非负数的性质,利用非负数的性质得出x,y是解答此题的关键.20.请你观察、思考下列计算过程:因为112=121,所以=11,同样,因为1112=12321,所以=111,则=1111,由此猜想=111111111.考点:算术平方根.专题:规律型.分析:首先观察已知等式,发现规律结果中,1的个数与其中间的数字相同,由此即可写出最后结果.解答:解:∵112=121,∴=11,∵1112=12321,∴=111,∴=1111,由此猜想=111111111.故答案为:1111,111111111.点评:此题主要考查了算术平方根的应用,此题注意要善于观察已有式子得出规律,从而写出最后结果.三、解答题(共1小题,满分24分)21.计算题:①2a8•(3ab)3②42x2•x3÷7x4③(8a3b﹣5a2b2)÷4ab;④xy•(﹣x3y4+x2y6)⑤(a+3b)(a﹣3b);⑥(2x+y)2﹣(2x+3y)(2x﹣3y)考点:整式的混合运算.分析:①根据积的乘方,单项式的乘法进行计算即可;②根据单项式的乘除法进行计算即可;③根据多项式除以单项式的法则,进行计算即可;④根据单项式乘多项式的法则进行计算即可;⑤根据平方差公式进行计算即可;⑥根据完全平方公式和平方差公式进行计算即可.解答:解:①原式=2a8•27a3b3=54a11b3;②原式=42x5÷7x4=6x;③原式=2a2b﹣ab;④xy•(﹣x3y4+x2y6)=﹣x4y5;⑤(a+3b)(a﹣3b)=a2﹣9b2;⑥(2x+y)2﹣(2x+3y)(2x﹣3y)=4x2+4xy+y2﹣4x2+9y2=4xy+10y2.点评:本题考查了整式的混合运算,涉及到的知识点有:平方差公式和完全平方公式,幂的乘方,积的乘方,单项式的乘法,多项式除以单项式,是基础知识要熟练掌握.四.解答题,共26分22.卫星绕地球表面做圆周运动的速度约为8×103米/秒,则卫星运行8×103秒所走的路程约是多少?考点:单项式乘单项式.分析:直接利用单项式乘以单项式运算法则求出即可.解答:解:由题意可得:8×103×8×103=6.4×107(m),答:卫星所走的路程约是6.4×107m.点评:此题主要考查了单项式乘以单项式,正确掌握运算法则是解题关键.23.先化简,再求值:2(x+1)(x﹣1)﹣x(2x﹣1),其中x=﹣2.考点:整式的混合运算—化简求值.专题:计算题.分析:根据平方差公式,单项式乘多项式的运算法则化简,然后把给定的值代入求值.解答:解:2(x+1)(x﹣1)﹣x(2x﹣1),=2(x2﹣1)﹣2x2+x,=2x2﹣2﹣2x2+x,=x﹣2,当x=﹣2时,原式=﹣2﹣2=﹣4.点评:这题考查了整式的混合运算,主要考查了整式的乘法以及合并同类项.注意运算顺序以及符号的处理.24.已知与互为相反数,求(x﹣y)的值.考点:非负数的性质:算术平方根;解二元一次方程组.分析:根据互为相反数的两个数的和等于0列出方程,再根据非负数的性质解答.解答:解:∵与互为相反数,∴+=0,∴,∴x﹣y=﹣3.点评:本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.25.已知(x﹣y)2=4,(x+y)2=64;求下列代数式的值:(1)x2+y2;(2)xy.考点:完全平方公式.专题:计算题.分析:(1)已知等式利用完全平方公式化简后,相加即可求出所求式子的值;(2)已知等式利用完全平方公式化简后,相减即可求出所求式子的值解答:解:(x﹣y)2=x2﹣2xy+y2=4①,(x+y)2=x2+2xy+y2=64②,(1)①+②得:x2+y2=34;(2)②﹣①得:4xy=60,即xy=15.点评:此题考查了完全平方公式,熟练掌握完全平方公式是解本题的关键.26.问题:你能比较两个数20062007和20072006的大小吗?为了解决这个问题,我们先把它抽象成数学问题,写出它的一般形式,比较n n+1与(n+1)n的大小(n为正整数),从分析n=1,n=2,n=3,…的情形入手,通过归纳,发现规律,猜想出结论.(1)比较各组数的大小①12<21;②23<32;③34>43;④45>54(2)由(1)猜想出n n+1与(n+1)n的大小关系是当n=1或2时,n n+1<(n+1)n;当n>2的整数时,n n+1>(n+1)n;(3)由(2)可知:20062007>20072006.考点:规律型:数字的变化类.分析:(1)根据乘方的意义分别计算后进行判断大小;(2)(3)根据(1)中的计算结果可归纳出当n=1或2时,n n+1<(n+1)n;当n>2的整数时,n n+1>(n+1)n.解答:解:(1)12<21;②23<32;③34>43;④45>54…(2)当n=1或2时,n n+1<(n+1)n;当n>2的整数时,n n+1>(n+1)n.(3)20062007>20072006.故答案为<,<,>,>,>;当n=1或2时,n n+1<(n+1)n;当n>2的整数时,n n+1>(n+1)n;>.点评:本题考查了有理数大小比较:正数大于0,负数小于0;负数的绝对值越大,这个数越小.五.附加题27.请认真分析下面一组等式的特征:1×3=22﹣1;3×5=42﹣1;5×7=62﹣1;7×9=82﹣1;…这一组等式有什么规律?将你猜想到的规律用一个只含字母n的式子表示出来?n(n+2)=(n+1)2﹣1.考点:规律型:数字的变化类.分析:等式的左边是相差为2的两个数相乘,右边是两个数的平均数的平方减去1.根据这一规律用字母表示即可.解答:解:∵1×3=22﹣1;3×5=42﹣1;5×7=62﹣1;7×9=82﹣1;…∴n(n+2)=(n+1)2﹣1.故答案为:n(n+2)=(n+1)2﹣1.点评:此题主要考查了数字的变化规律,等式的规律时,既要分别看左右两边的规律,还要注意看左右两边之间的联系.。
2015-2016年云南省曲靖市沾益县白水一中八年级(下)第二次月考数学试卷(解析版)

2015-2016学年云南省曲靖市沾益县白水一中八年级(下)第二次月考数学试卷一、选择题(每小题3分,共24分)1.(3分)下列计算正确的是()A.2a+3b=5ab B.(x+2)2=x2+4C.(ab3)2=ab6D.(﹣1)0=12.(3分)下列图形中有稳定性的是()A.正方形B.长方形C.直角三角形D.平行四边形3.(3分)以下列各组线段为边,能组成三角形的是()A.2cm,3cm,5cm B.3cm,3cm,6cmC.5cm,8cm,2cm D.4cm,5cm,6cm4.(3分)已知等腰三角形的两边长分别为3和6,则它的周长等于()A.12B.12或15C.15D.15或185.(3分)如图,已知△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2=()A.90°B.135°C.270°D.315°6.(3分)已知等腰三角形一腰上的高线与另一腰的夹角为50°,那么这个等腰三角形的顶角等于()A.15°或75°B.140°C.40°D.140°或40°7.(3分)点P(﹣1,2)关于y轴对称点的坐标是()A.(1,2)B.(﹣1,﹣2)C.(1,﹣2)D.(2,﹣1)8.(3分)化简a4•a2+(a3)2的结果是()A.a8+a6B.a6+a9C.2a6D.a12二、填空题(每题3分,共24分)9.(3分)计算(﹣a3)4•(﹣a)3的结果是.10.(3分)如图,AB、CD相交于点O,AD=CB,请你补充一个条件,使得△AOD≌△COB,你补充的条件是.11.(3分)已知M(a,3)和N(4,b)关于x轴对称,则(a+b)2012的值为.12.(3分)一个多边形的内角和是外角和的2倍,则这个多边形的边数为.13.(3分)若a m=2,a n=5,则a m+n等于.14.(3分)如图,在△ABC中,AB=5cm,AC=3cm,BC的垂直平分线分别交AB、BC于D、E,则△ACD的周长为cm.15.(3分)点(2,5)关于直线x=1的对称点的坐标为.16.(3分)若a﹣b=1,ab=﹣2,则(a+1)(b﹣1)=.三.解答题(72分)17.(8分)已知:如图△ABC中,AB=AC,∠C=30°,AB⊥AD,AD=4cm.求BC的长.18.(8分)如图,A、B是两个蓄水池,都在河流a的同侧,为了方便灌溉作物,要在河边建一个抽水站,将河水送到A、B两地,问该站建在河边什么地方,可使所修的渠道最短,试在图中确定该点.(保留作图痕迹)19.如图:某地有两所大学M、N和两条相交叉的公路a、b,现计划修建一座物资仓库,希望仓库到两所大学的距离相等,到两条公路的距离也相等.你能确定仓库应该建在什么位置吗?在所给的图形中画出你的设计方案.20.(8分)(1)计算:[x(x2y2﹣xy)﹣y(x2﹣x3y)]÷3x2y(2)化简求值:(a+b)(a﹣b)+(a+b)2,其中a=3,b=﹣.21.(8分)如图,在△ABC中,AB=AC,∠BAC=100°,MP、NO分别垂直平分AB、AC,求∠1,∠2的度数.22.(10分)如图,给出五个等量关系:①AD=BC②AC=BD③CE=DE④∠D=∠C⑤∠DAB=∠CBA.请你以其中两个为条件,另三个中的一个为结论,推出一个正确的结论(只需写出一种情况),并加以证明.23.(8分)已知:如图,CE⊥AB,BF⊥AC,CE与BF相交于D,且BD=CD.求证:∠BAD=∠CAD.24.(10分)如图,AD为△ABC的中线,BE为△ABD的中线.(1)∠ABE=15°,∠BAD=40°,求∠BED的度数;(2)在△BED中作BD边上的高;(3)若△ABC的面积为40,BD=5,则△BDE中BD边上的高为多少?25.(12分)两个大小不同的等腰直角三角形三角板如图①所示放置,图②是由它抽象出的几何图形,B,C,E在同一条直线上,联结DC,(1)请找出图②中的全等三角形,并给予说明(说明:结论中不得含有未标识的字母);(2)试说明:DC⊥BE.2015-2016学年云南省曲靖市沾益县白水一中八年级(下)第二次月考数学试卷参考答案与试题解析一、选择题(每小题3分,共24分)1.(3分)下列计算正确的是()A.2a+3b=5ab B.(x+2)2=x2+4C.(ab3)2=ab6D.(﹣1)0=1【解答】解:A、不是同类项,不能合并.故错误;B、(x+2)2=x2+4x+4.故错误;C、(ab3)2=a2b6.故错误;D、(﹣1)0=1.故正确.故选:D.2.(3分)下列图形中有稳定性的是()A.正方形B.长方形C.直角三角形D.平行四边形【解答】解:根据三角形具有稳定性,可得四个选项中只有直角三角形具有稳定性.故选:C.3.(3分)以下列各组线段为边,能组成三角形的是()A.2cm,3cm,5cm B.3cm,3cm,6cmC.5cm,8cm,2cm D.4cm,5cm,6cm【解答】解:根据三角形的三边关系,知A、2+3=5,不能组成三角形;B、3+3=6,不能够组成三角形;C、2+5=7<8,不能组成三角形;D、4+5>6,能组成三角形.故选:D.4.(3分)已知等腰三角形的两边长分别为3和6,则它的周长等于()A.12B.12或15C.15D.15或18【解答】解:∵等腰三角形的两边长分别是3和6,∴①当腰为6时,三角形的周长为:6+6+3=15;②当腰为3时,3+3=6,三角形不成立;∴此等腰三角形的周长是15.故选:C.5.(3分)如图,已知△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2=()A.90°B.135°C.270°D.315°【解答】解:∵∠C=90°,∴∠A+∠B=90°.∵∠A+∠B+∠1+∠2=360°,∴∠1+∠2=360°﹣90°=270°.故选:C.6.(3分)已知等腰三角形一腰上的高线与另一腰的夹角为50°,那么这个等腰三角形的顶角等于()A.15°或75°B.140°C.40°D.140°或40°【解答】解:当为锐角三角形时可以画图,高与右边腰成50°夹角,由三角形内角和为180°可得,顶角为40°;当为钝角三角形时可画图,此时垂足落到三角形外面,因为三角形内角和为180°,由图可以看出等腰三角形的顶角的补角为40°,三角形的顶角为140°.故选:D.7.(3分)点P(﹣1,2)关于y轴对称点的坐标是()A.(1,2)B.(﹣1,﹣2)C.(1,﹣2)D.(2,﹣1)【解答】解:点P(﹣1,2)关于y轴对称点的坐标为(1,2).故选:A.8.(3分)化简a4•a2+(a3)2的结果是()A.a8+a6B.a6+a9C.2a6D.a12【解答】解:原式=a6+a6=2a6.故选:C.二、填空题(每题3分,共24分)9.(3分)计算(﹣a3)4•(﹣a)3的结果是﹣a15.【解答】解:原式=﹣a12•a3,=﹣a15.故答案为:﹣a15.10.(3分)如图,AB、CD相交于点O,AD=CB,请你补充一个条件,使得△AOD≌△COB,你补充的条件是∠A=∠C或∠ADO=∠CBO.【解答】解:添加条件可以是:∠A=∠C或∠ADC=∠ABC.∵添加∠A=∠C根据AAS判定△AOD≌△COB,添加∠ADC=∠ABC根据ASA判定△AOD≌△COB,故填空答案:∠A=∠C或∠ADC=∠ABC.11.(3分)已知M(a,3)和N(4,b)关于x轴对称,则(a+b)2012的值为1.【解答】解:∵M(a,3)和N(4,b)关于x轴对称,∴a=4,b=﹣3,∴(a+b)2012=(4﹣3)2012=1.故答案为:1.12.(3分)一个多边形的内角和是外角和的2倍,则这个多边形的边数为6.【解答】解:∵多边形的外角和是360度,多边形的内角和是外角和的2倍,则内角和是720度,720÷180+2=6,∴这个多边形是六边形.故答案为:6.13.(3分)若a m=2,a n=5,则a m+n等于10.【解答】解:∵a m=2,a n=5,∴a m+n=a m a n=2×5=10.故答案为:1014.(3分)如图,在△ABC中,AB=5cm,AC=3cm,BC的垂直平分线分别交AB、BC于D、E,则△ACD的周长为8cm.【解答】解:∵DE为BC的垂直平分线,∴CD=BD,∴△ACD的周长=AC+CD+AD=AC+AD+BD=AC+AB,而AC=3cm,AB=5cm,∴△ACD的周长为3+5=8cm.故答案为:8.15.(3分)点(2,5)关于直线x=1的对称点的坐标为(0,5).【解答】解:所求点的纵坐标为5,横坐标为1﹣(2﹣1)=0,∴点(2,5)关于直线x=1的对称点的坐标为(0,5).16.(3分)若a﹣b=1,ab=﹣2,则(a+1)(b﹣1)=﹣4.【解答】解:∵(a+1)(b﹣1),=ab﹣a+b﹣1,=ab﹣(a﹣b)﹣1,当a﹣b=1,ab=﹣2,原式=﹣2﹣1﹣1=﹣4.三.解答题(72分)17.(8分)已知:如图△ABC中,AB=AC,∠C=30°,AB⊥AD,AD=4cm.求BC的长.【解答】解:∵AB=AC∴∠B=∠C=30°∵AB⊥AD∴BD=2AD=2×4=8(cm)∠B+∠ADB=90°,∴∠ADB=60°∵∠ADB=∠DAC+∠C=60°∴∠DAC=30°∴∠DAC=∠C∴DC=AD=4cm∴BC=BD+DC=8+4=12(cm).18.(8分)如图,A、B是两个蓄水池,都在河流a的同侧,为了方便灌溉作物,要在河边建一个抽水站,将河水送到A、B两地,问该站建在河边什么地方,可使所修的渠道最短,试在图中确定该点.(保留作图痕迹)【解答】解:作点A关于直线a对称的点C,连接BC交a于点P,则点P就是抽水站的位置.19.如图:某地有两所大学M、N和两条相交叉的公路a、b,现计划修建一座物资仓库,希望仓库到两所大学的距离相等,到两条公路的距离也相等.你能确定仓库应该建在什么位置吗?在所给的图形中画出你的设计方案.【解答】解:如图所示:点P、P′即为所求.20.(8分)(1)计算:[x(x2y2﹣xy)﹣y(x2﹣x3y)]÷3x2y(2)化简求值:(a+b)(a﹣b)+(a+b)2,其中a=3,b=﹣.【解答】解:(1)[x(x2y2﹣xy)﹣y(x2﹣x3y)]÷3x2y=(x3y2﹣x2y﹣x2y+x3y2)÷3x2y=(2x3y2﹣2x2y)÷3x2y=xy﹣;(2)(a+b)(a﹣b)+(a+b)2,=a2﹣b2+a2+2ab+b2=2a2+2ab把a=3,b=﹣代入上式可得:原式=2×32+2×3×(﹣)=16.21.(8分)如图,在△ABC中,AB=AC,∠BAC=100°,MP、NO分别垂直平分AB、AC,求∠1,∠2的度数.【解答】解:∵△ABC中,AB=AC,∠BAC=100°,∴∠B=∠C===40°,∵MP、NQ分别垂直平分AB、AC,∴∠1=∠B=40°,∠C=∠CAO=40°,∴∠2=∠BAC﹣∠1﹣∠CAO=100°﹣40°﹣40°=20°,∴∠1=40°,∠2=20°.22.(10分)如图,给出五个等量关系:①AD=BC②AC=BD③CE=DE④∠D=∠C⑤∠DAB=∠CBA.请你以其中两个为条件,另三个中的一个为结论,推出一个正确的结论(只需写出一种情况),并加以证明.【解答】解:已知:AD=BC,AC=BD,求证:∠DAB=∠CBA.证明:∵AD=BC,AC=BD,AB=AB,∴△ADB≌△BCA.∴∠DAB=∠CBA.23.(8分)已知:如图,CE⊥AB,BF⊥AC,CE与BF相交于D,且BD=CD.求证:∠BAD=∠CAD.【解答】证明:∵CE⊥AB,BF⊥AC,∴∠BED=∠CFD=90°,在△BED和△CFD中,,∴△BED≌△CFD(AAS),∴DE=DF,∵CE⊥AB,BF⊥AC,∴∠BAD=∠CAD.24.(10分)如图,AD为△ABC的中线,BE为△ABD的中线.(1)∠ABE=15°,∠BAD=40°,求∠BED的度数;(2)在△BED中作BD边上的高;(3)若△ABC的面积为40,BD=5,则△BDE中BD边上的高为多少?【解答】解:(1)∵∠BED是△ABE的外角,∴∠BED=∠ABE+∠BAD=15°+40°=55°;(2)过E作BC边的垂线,F为垂足,则EF为所求;(3)过A作BC边的垂线AG,∴AD为△ABC的中线,BD=5,∴BC=2BD=2×5=10,∵△ABC的面积为40,∴BC•AG=40,即×10•AG=40,解得AG=8,∵EF⊥BC于F,∴EF∥AG,∵E为AD的中点,∴EF是△AGD的中位线,∴EF=AG=×8=4.25.(12分)两个大小不同的等腰直角三角形三角板如图①所示放置,图②是由它抽象出的几何图形,B,C,E在同一条直线上,联结DC,(1)请找出图②中的全等三角形,并给予说明(说明:结论中不得含有未标识的字母);(2)试说明:DC⊥BE.【解答】解:(1)∵△ABC,△DAE是等腰直角三角形,∴AB=AC,AD=AE,∠BAC=∠DAE=90°.∠BAE=∠DAC=90°+∠CAE,在△BAE和△DAC中,∴△BAE≌△CAD(SAS).(2)由(1)得△BAE≌△CAD.∴∠DCA=∠B=45°.∵∠BCA=45°,∴∠BCD=∠BCA+∠DCA=90°,∴DC⊥BE.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
沾益县第五中学2014—2015学年度上学期八年级第二次月考
数学试卷(满分:120分;考试时间:120分钟)
班级:姓名:成绩: .
一、选择题(每小题3分,共24分)
1.下列交通标志中,是轴对称图形的是()
2.在△ABC中,若∠B=∠C=2∠A,则∠A的度数为()
A.72°
B.45°
C.36°
D.30°
3.如图,AB与CD相交于点E, AD=CB,若使△AED≌△CEB,则应补充的条件是()
A.∠A=∠C B.AE=CE C.DE=BE D.不用补充条件
4.已知△ABC 在直角坐标系中的位置如图所示,如果△A'B'C' 与△ABC 关于y轴对称,
那么点A的对应点A'的坐标为()
A.(-4,2) B.(-4,-2) C.(4,-2) D.(4,2)
5.已知等腰三角形其中一个内角为70°,那么这个等腰三角形的顶角度数为()
A、70°
B、70°或55°
C、40°或55°
D、70°或40°
6.将一副三角板按图中方式叠放,则∠M的度数为()
A.300
B. 750 C 600 D 450
(a-1,4)和P2(2,b-1)关于x轴对称,
7.在直角坐标系中,已知点P
1
则(a+b)的值是()
A.0 B.-1 C.1 D.不存在
8.如图,把长方形纸片ABCD 纸沿对角线折叠,设重叠部分为△EBD ,那么下列说法不正确的是( )
A.△EBD 是等腰三角形,EB=ED
B.折叠后∠ABE 和∠CBD 一定相等
C.折叠后得到的图形是轴对称图形
D.△EBA 和△EDC 一定是全等 二、填空题(每小题3分,共24分)
9.一个多边形的每一个外角都等于36°,则该多边形的内角和等于 。
10.如图,PM ⊥OA ,PN ⊥OB ,垂足分别为M 、N.PM =PN ,若∠BOC =30°,则∠AOB = 。
11.如图,在△ABC 和△FED 中,AD =FC ,AB =FE ,当添加条件 时,就可得到 △ABC ≌△FED 。
(只需填写一个你认为正确的条件)
12.从长为3cm 、5cm 、7cm 、10cm 的四根木条中选出三根组成三角形,共有 种选法。
13.若等腰三角形一腰上的高与另一腰的夹角为40°,则它的底角为 。
14.如图,△ABC 为等边三角形,AD 为BC 边上的高,E 为AC 边上的一点,且AE=AD ,则 ∠EDC = .
15.如图,在等边△ABC 中,点D 、E 分别在边AB 、BC 上.把△BDE 沿直线DE 翻折,使点 B 落在点B ′处,DB ′、EB ′分别与AC 交于点F 、G.若∠ADF =80°,则∠EGC = 。
16.若m 、n 为实数,且|21|m n +-,则2012(+)m n 的值为 。
三、解答题(72分)
17.解方程组 (5分)31328x y x y +=-⎧⎨-=⎩ ①, ②.
第10题
第11题
第15题
第14题
A B
D
18.解不等式组,并把解集在数轴上表示出来(6分)
()1133
8312
x x x x -+⎧+⎪
⎨⎪--<-⎩
≥①② 19.(7分)如图,两个四边形关于直线 对称,∠C =90°,试写出a ,b 的长度,并求出∠G 的度数。
20. (8分)如图,已知AD 、BC 相交于点O ,AB =CD ,AD =CB.求证:∠A =∠C
21. (8分)如图,16个相同的小正方形拼成一个正方形网格,现将其中的两个小方格涂黑。
请你用两种不同的方法分别在图中再涂黑两个小方格,使它们成为轴对称图形。
22. (9分)如图,在平面直角坐标系中,A(1,2),B(3,1),C(-2,-1)。
(1)在图中作出△ABC 关于y 轴对称的△A 1B 1C 1。
(2)写出点A 1,B 1,C 1的坐标(直接写出答案)。
A 1 B 1 C 1 (3)△A 1B 1C 1的面积为 。
23. (8分)在△ABC 中,∠BAC =50°,∠B=45°,AD 是△ABC 的一条角平分线,
求∠ADC 的度数.
第20题
第21题
第19题
第22题
24. (10分)已知:△ABC 中,∠B 、∠C 的角平分线相交于点D ,过D 作EF ∥BC 交AB 于点E ,交AC 于点F 。
求证:BE+CF =EF
25. (11分)两个等腰直角三角形的三角板如图①所示放置,图②是由它抽象出的几何图形,点B 、C 、E 在同一条直线上,连接DC 、EC 。
(1)请找出图②中的全等三角形,并给予证明(说明:结论中不得含有未标识的字母);
(2)求证:DC ⊥BE
第24题
第25题。
