初二数学-八年级数学-全等三角形的思维导图知识点结构总结
初中数学《全等三角形》单元教学设计以及思维导图

过程与方法:①在图形变换以及实际操作的过程中发展学生的空间观念,培养学生的几何直觉。
②使学生经历探索三角形全等的过程,体验用操作,归纳得出数学结论的过程。
③能够利用角平分线的性质和判定进行推理计算,并能在生活、生产中应用。
情感态度与价值观:①让学生观察、发现生活中的全等三角形并在实际操作中获得全等三角形的体验。
2、让学生观察图形、动手操作、分组讨论得出结论
活动三:探求全等三角形对应元素的找法
【活动步骤】
1、几何画板演示、提出问题:各对三角形是全等三角形,怎样改变其中一个三角形的位置,使它与另一个三角形完全重合?
2、学生动手操作摆放学具、分组讨论,得出结论:两个全等的三角形经过平移、翻折、旋转可以重合。
3、分组讨论找全等三角形对应元素的方法,班上交流,教师明确:
3、角平分线的性质和判定方法
主题单元问题设计
1、什么样的三角形叫全等三角形?
2、什么叫对应顶点、对应边、对应角?如何辨认全等三角形中的对应元素
3、全等三角形有哪些性质?
4、判定三角形全等有几种方法?
5、角平分线有什么性质?角的平分线的判定方法是什么?
专题划分
专题一:全等三角形(1课时)
专题二:三角形全等的判定(5课时)
(2)经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程。
4、关注他们的学习过程和在数学活动中表现出来的态度是否积极
专题二
三角形全等的判定
所需课时
5课时
专题学习目标
知识与技能:(1)探索三角形全等的五种判定方法,能利用三角形全等进行证明,掌握综合法证明的格式。
(2)理解并掌握五种判定三角形全等的方法,能灵活选用适当方法证明三角形全等问题
八年级数学思维导图
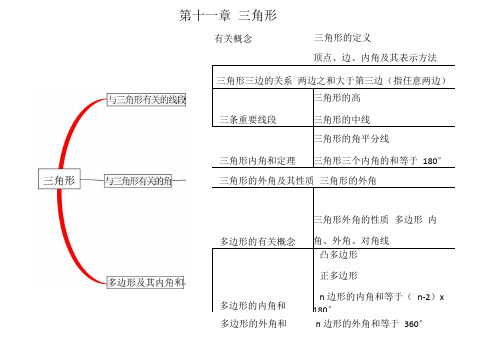
第十一章三角形
有关概念三角形的定义
三角形三边的关系两边之和大于第三边(指任意两边)
三条重要线段三角形的高三角形的中线
三角形内角和定理三角形的角平分线
三角形三个内角的和等于180°
三角形的外角及其性质三角形的外角
多边形的有关概念三角形外角的性质多边形内角、外角、对角线
多边形的内角和
凸多边形
正多边形
n 边形的内角和等于(n-2)x 180°
顶点、边、内角及其表示方法
多边形的外角和n 边形的外角和等于360°
第十二章全等三角形
全等三角形的对应边相等
第十三章轴对称
第十四章整式的乘法与因式分解
第十五章分式
第十六章二次根式
满足下列两个特点的二次根式,叫最简二次
根式.
1)被开方数不含分母,分母中不含二次
根式;
2)被开方数中不含开得尽方的因数或因
式. 定义:式子(a≥0)叫做二次根式
(a≥0)是一个非负数
最简二次根式(a≥0)
二次根式
二次根式性质
a≥0,b>0)
二次根式的
除法
(a≥0,b≥0)
二次根式
的混合运算运算
(a≥0,b>0)
二次根式的
加减
二次根式加减是,可以先将二次根式化成
最简二次根式,再合并同类二次根式
第十七章勾股定理
第十八章平行四边形
第十九章一次函数
第二十章数据的分析。
人教版 八年级上册数学 章节思维导图集 图片版
你现在的努力要对得起别人对你的好!
Math 实验室-1-人教版八年级数学上册章节思维导图
共5章
人教版八年级数学上册教材目录
第11章三角形的思维导图
11.1与三角形有关的线段
11.2与三角形有关的角
11.3多边形及其内角和
第12章全等三角形的思维导图
12.1全等三角形
12.2三角形全等的判定
12.3角的平分线的性质
第13章轴对称的思维导图
13.1轴对称
13.2画轴对称图形
13.3等腰三角形
13.4课题学习最短路径问题
第14章整式的乘法与因式分解的思维导图
14.1整式的乘法
14.2乘法公式
14.3因式分解
第15章分式的思维导图
15.1分式
15.2分式的运算
15.3
分式方程。
初中数学《全等三角形》单元教学设计以及思维导图

(4)提出问题:两个全等的三角形,任意摆放能重合吗怎样放置它们才能重合呢
(5)学生通过自己摆放图形,思考、分组讨论得出对应顶点、对应角、对应边的相关概念。
活动二:探究全等三角形的性质
】
【活动步骤】
1、提出问题:观察、思考图中两个三角形的对应边有什么关系对应角呢
①学生分组合作动手操作
②以小组为单位,把剪下的三角形重叠在一起,发现了什么
③思考:任意画一个三角形ABC,同样作出一个三角形A′B′C′,使AB=A′B′、AC=A′C′、BC=B′C′.那么这两个全等吗这反映了一个什么规律
④学生讨论交流,归纳结论,教师明确
三边对应相等的两个三角形全等,简写为“边边边”或“SSS”.
专题三:角平分线的性质 ( 2课时)
其中,专题 2 (或专题 中的活动 作为研究性学习)
专题一
全等三角形
所需课时
\
课内1课时,课外1课时
专题学习目标
1、知识与技能目标
(1)知道全等三角形的有关概念,掌握寻找全等三角形中的对应元素的基本方法。掌握全等三角形的性质。
(2)初步会用全等三角形的性质进行一些简单的计算。
(3)在探索角的平分线的性质中培养几何直觉
3、情感、态度与价值观:
在探讨作角的平分线的方法及角的平分线的性质的过程中,培养学生探究问题的兴趣,增强解决问题的信心,获得解决问题的成功体验,逐步培养学生的理性精神。
专题问题设计
1、如何画已知角的平分线
2、角平分线有什么性质
3、具有什么样特点的点在一个角的平分线上
3、角平分线的性质和判定方法
主题单元问题设计
八年级数学思维导图52711
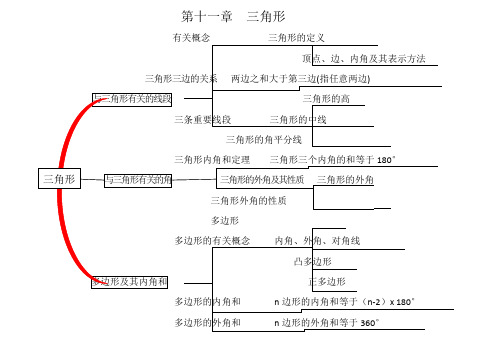
第十一章三角形
第十二章全等三角形
全等三角形的对应边相等
第十三章轴对称
第十四章整式的乘法与因式分解
第十五章分式
第十六章 二次根式
二次根式
定义:式子(a ≥0)叫做二次根式
(a ≥0)是一个非负数
(a ≥0)
运算二次根式的乘法二次根式的除法
二次根式的混合运算二次根式的加减
二次根式加减是,可以先将二次根式化成最简二次根式,再合并同类二次根式
满足下列两个特点的二次根式,叫最简二次根式.
(1)被开方数不含分母,分母
中不含二次根式;
(2)被开方数中不含开得尽方
的因数或因式.
最简二次根式
性质
(a ≥0,b ≥0)(a ≥0,b >0)
(a ≥0,b >0)
第十七章勾股定理
第十八章平行四边形。
初二数学知识点:全等三角形

初二数学知识点:全等三角形
初二数学知识点:全等三角形
大家都知道,能够完全重合的两个三角形叫做全等三角形(congruent triangles)。
那么接下来的全等三角形知识请同学认真记忆了。
一、知识框架:
二、知识概念:
1.基本定义:
⑴全等形:能够完全重合的两个图形叫做全等形.
⑵全等三角形:能够完全重合的两个三角形叫做全等三角形.
⑶对应顶点:全等三角形中互相重合的顶点叫做对应顶点.
⑷对应边:全等三角形中互相重合的边叫做对应边.
⑸对应角:全等三角形中互相重合的角叫做对应角.
2.基本性质:
⑴三角形的稳定性:三角形三边的长度确定了,这个三角形的形状、大小就全确定,这个性质叫做三角形的稳定性.
⑵全等三角形的性质:全等三角形的对应边相等,对应角相等.
3.全等三角形的判定定理:
⑴边边边():三边对应相等的两个三角形全等.
⑵边角边():两边和它们的夹角对应相等的两个三角形全等.
⑶角边角():两角和它们的夹边对应相等的两个三角形全等.
⑷角角边():两角和其中一个角的对边对应相等的两个三角形
全等.
⑸斜边、直角边():斜边和一条直角边对应相等的两个直角三角形全等.
4.角平分线:
⑴画法:
⑵性质定理:角平分线上的点到角的两边的距离相等.
⑶性质定理的逆定理:角的'内部到角的两边距离相等的点在角的平分线上.
5.证明的基本方法:
⑴明确命题中的已知和求证.(包括隐含条件,如公共边、公共角、对顶
角、角平分线、中线、高、等腰三角形等所隐含的边角关系)
⑵根据题意,画出图形,并用数字符号表示已知和求证.
⑶经过分析,找出由已知推出求证的途径,写出证明过程.。
初二数学八上第十二章全等三角形知识点总结复习和常考题型练习

第十二章全等三角形一、知识框架:二、知识概念:1。
基本定义:⑴全等形:能够完全重合的两个图形叫做全等形.⑵全等三角形:能够完全重合的两个三角形叫做全等三角形。
理解:①全等三角形形状与大小完全相等,与位置无关;②一个三角形经过平移、翻折、旋转可以得到它的全等形;③三角形全等不因位置发生变化而改变.⑶对应顶点:全等三角形中互相重合的顶点叫做对应顶点.⑷对应边:全等三角形中互相重合的边叫做对应边。
⑸对应角:全等三角形中互相重合的角叫做对应角.2.基本性质:⑴三角形的稳定性:三角形三边的长度确定了,这个三角形的形状、大小就全确定,这个性质叫做三角形的稳定性。
⑵全等三角形的性质:全等三角形的对应边相等,对应角相等。
理解:①长边对长边,短边对短边;最大角对最大角,最小角对最小角;②对应角的对边为对应边,对应边对的角为对应角。
(3)全等三角形的周长相等、面积相等。
(4)全等三角形的对应边上的对应中线、角平分线、高线分别相等。
3。
全等三角形的判定定理:⑴边边边(SSS):三边对应相等的两个三角形全等。
⑵边角边(SAS):两边和它们的夹角对应相等的两个三角形全等。
⑶角边角(ASA):两角和它们的夹边对应相等的两个三角形全等.⑷角角边(AAS):两角和其中一个角的对边对应相等的两个三角形全等。
⑸斜边、直角边(HL):斜边和一条直角边对应相等的两个直角三角形全等.4.证明两个三角形全等的基本思路:5.角平分线:⑴画法:⑵性质定理:角平分线上的点到角的两边的距离相等。
⑶性质定理的逆定理:角的内部到角的两边距离相等的点在角的平分线上. (4)三角形的三条角平分线交于三角形内部一点,并且这点到三边的距离相等6。
证明的基本方法:⑴明确命题中的已知和求证.(包括隐含条件,如公共边、公共角、对顶角、角平分线、中线、高、等腰三角形等所隐含的边角关系)⑵根据题意,画出图形,并用数字符号表示已知和求证。
⑶经过分析,找出由已知推出求证的途径,写出证明过程。
初中数学《全等三角形》单元教学设计以及思维导图

初中数学《全等三角形》单元教学设计以及思维导图全等三角形”是八年级数学教材第十一章的重要内容。
学生需要理解全等三角形的概念和性质,掌握五种判定全等的方法,并能熟练应用这些方法解决实际问题。
此外,学生还需要结合角的平分线的性质综合运用这些知识,为后续研究打下基础。
本主题单元共分为三个专题:全等三角形、三角形全等的判定、全等三角形的应用。
教学方式主要是通过小组讨论和交流,引导学生自主探究和归纳得出全等三角形的性质和判定定理,并能熟练应用。
研究重点是全等三角形的性质和判定的综合运用,难点是让学生理解证明的基本过程和运用综合法证明的格式。
研究目标包括知识与技能、过程与方法、情感态度与价值观三个方面。
学生需要了解全等三角形的概念和性质,掌握五种判定全等的方法,并能初步应用这些方法判定三角形全等。
同时,学生还需要在图形变换和实际操作中发展空间观念和几何直觉,体验用操作归纳得出数学结论的过程,并能在生活、生产中应用角平分线的性质和判定进行推理计算。
通过本单元研究,学生可以观察、发现生活中的全等三角形,并在实际操作中获得全等三角形的体验。
同时,通过探究判定三角形全等方法的活动,培养学生合作交流的意识和大胆猜想、乐于探索的品质及发现问题、解决问题的能力。
通过折纸、画图、文字与符号的互译活动,培养学生的联想、探索、概括归纳的能力,激发学生研究数学的兴趣。
对应课标要求学生理解全等三角形的概念和性质,掌握全等三角形的判定方法,并能运用综合法进行证明。
同时,学生还需要掌握角平分线的性质和判定方法。
1、教师用课件展示全等三角形的性质,引导学生观察、分析、总结。
2、学生自主探究、验证全等三角形的性质。
1)学生在纸板上画出两个全等三角形,并标出对应元素。
2)学生通过测量、计算、推理等方法验证全等三角形的性质,如对应角相等、对应边相等、对应顶点连线相等等。
3)学生归纳总结全等三角形的性质。
活动三:应用全等三角形的性质活动步骤】1、教师用课件展示一些实际问题,引导学生运用全等三角形的性质解决问题。
