第五章--传热过程基础
《食品工程原理》第五章 传热
传热
Heat Transfer
第一节 传热概述 第二节 热传导 第三节 对流传热 第四节 热交换 第五节 辐射传热
.
第一节 传热概述
5-1 传热的基本概念
1.传热基本方式
（1）热传导（conduction）
当物体内部或两直接接触的物体间有温度差时， 温度较高处的分子与相邻分子碰撞，并将能量的 一部分传给后者。
G P r 6 r .1 2 6 0 0 6 .4 7 .0 1 4 60 3
查表5-3 a = 0.53, m = 1/4
Nu=a(Pr·Gr)m
N u aL 0. 5(3 4 .1 460 )3 1/ 424.3 λ
αN λ u 24 0.3 .0 7 3.04 W 512/K (m ) L 0.1
δ1
δ2
.
本次习题
p.195
2. 5.
.
5-4 通过圆筒壁的稳态导热
5.4A 通过单层圆筒壁的稳态导热
Φλ2πrLdT
dr
Φ 2π
r2
Lr1
drλT2
r
T1
dT
Φ
2πLλ
lnr2 (T1
T2
)
r1
令
rmΦ rl2n2δ π rr12r1 m/rLλ T1T δln2rr12r2rδrm1
令 Am 2π rm L
.
M 3 Θ 1 L 1 a L T b M T 1 T 1 c M 3 Θ L 1 d M 3 L e L 2 T 2 Θ 1 f L L T 2 g
按因次一致性原则
对质量M 1 = c + d + e 对长度L 0 = a + b – c + d – 3e + 2f + g
循环流化床锅炉原理-第五章-传热
Deg
Tc1 =1+F L
L和Deg为稀相区的高度和截面直径
c=1.1 ，F=1.4，L/Deg>50时c1 =1
3.辐射换热系数计算公式
1 h rad＝ －1 (Ta－Tb ) eb ＋ew－1－ 1
第一节 密相区传热
循环流化床下部密相区与受热面间的传热机理 影响传热的各种因素
循环流化床下部 密相区与受热面 间的传热机理
(一)三个控制传热过程的因素
h=hgc +hpc +hrad
1．气体对流传热系数 2．辐射传热系数
hgc
hrad
3
. 颗粒对流传热系数 hpc
循环流化床下部 密相区与受热面 间的传热机理
循环流化床锅炉-传热
传热系统
密相区传热
稀相区传热 传热机理模型 传质
传热系数的准确性，对于循环流化床锅炉的设计、制造和运 行可靠性、安全性均起着举足轻重的作用。在锅炉设计中， 传热系数决定着受热面的布置、数量及结构，如果传热系数 选取不当，就难以达到稳定燃烧和最佳经济效益，甚至出现 受热面损坏的现象。与传统流化床一样，在循环流化床中存 在各种不同的传热过程： 1)颗粒与气流之间的传热(床内颗粒与床内气流)； 2)颗粒与颗粒之间的传热； 3)整个气固多相流与受热表面(包括壁面与悬吊在床内的 表面)之间的传热， 4)气固多相流与入床气流之间的传热。
s 为颗粒的导热率；dp为颗粒平均直 区颗粒密度； p和 g 径；cp和cg分别为颗粒和气体的定压比热容； 分别为颗粒和气体的密度；ut为截面平均流化速度； g0 为稀相区和密相区交界处的气体换热公式。
第五章 传热
液体被加热时，(/w)0.14=1.05，液体被冷却时，(/w)0.14=0.95
16
2. 圆直管强制滞流
Nu=1.86(RePrdi/l)1/3(/w)0.14 定性温度、定性尺寸和 (/w)0.14的处理同上 3. 圆直管过渡流
先按湍流计算，然后乘以校正因数
j=1-6×105/Re1.8<1
流体垂直流过单管时表面传热系数的变化
19
Nu=CRenPr0.4
Re 50~80 80~5000 ≥5000 C 0.93 0.715 0.226 n 0.4 0.46 0.6
2. 流体垂直流过管束 Nu=CeRenPr0.4 C、e、n的值由下表确定：
20
列序 1 2 3 4
直列 n 0.6 0.65 0.65 0.65
2
Pr
c p l
三、流体无相变对流表面传热系数的关联式
（一）流体在管内强制对流时的对流传热系数 1．流体在圆形直管内强制湍流时的对流传热系数 Nu=0.023Re0.8Prn 定性温度：流体进出口温度的算术平均值 定性尺寸：管内径 流体被加热时，n=0.4 流体被冷却时，n=0.3 对高粘度流体（粘度大于水粘度的2倍），用： Nu=0.027Re0.8Pr1/3(/w)0.14 定性温度：流体进出口温度的算术平均值 定性尺寸：管内径
E Et
Et：透过的能量
E：被反射的能量
33
由能量衡算：
Ea E Et E
Ea E
E E
Et E
1
a t 1
几种物体的定义：
黑体
镜体
a=1 =0 t=0 →例:黑煤a=0.97
a=0 =1 t=0 →例:磨光的铜镜面=0.97 t=0 a+=1
《传热学》资料第五章传热过程与传热器
《传热学》资料第五章传热过程与传热器一、名词解释1．传热过程:热量从高温流体通过壁面传向低温流体的总过程.2．复合传热:对流传热与辐射传热同时存在的传热过程.3．污垢系数:单位面积的污垢热阻.4．肋化系数: 肋侧表面面积与光壁侧表面积之比.5．顺流:两种流体平行流动且方向相同6．逆流: 两种流体平行流动且方向相反7．效能:换热器实际传热的热流量与最大可能传热的热流量之比.8．传热单元数:传热温差为1K时的热流量与热容量小的流体温度变化1K所吸收或放出的热流量之比.它反映了换热器的初投资和运行费用,是一个换热器的综合经济技术指标.9．临界热绝缘直径:对应于最小总热阻(或最大传热量)的保温层外径.二、填空题1．与的综合过程称为复合传热。
(对流传热，辐射传热)2．某燃煤电站过热器中，烟气向管壁传热的辐射传热系数为20 W／(m2．K)，对流传热系数为40 W／(m2．K)，其复合传热系数为。
(60W／(m2．K))3．肋化系数是指与之比。
(加肋后的总换热面积,未加肋时的换热面积)4．一传热过程的热流密度q＝1．8kW／m2，冷、热流体间的温差为30℃，则传热系数为，单位面积的总传热热阻为。
(60W／(m2．K)，0．017(m2.K)／W)5．一传热过程的温压为20℃，热流量为lkW，则其热阻为。
(0．02K／W)6．已知一厚为30mm的平壁，热流体侧的传热系数为100 W／(m2．K)，冷流体侧的传热系数为250W／(m2．K)，平壁材料的导热系数为0．2W／(m·K)，则该平壁传热过程的传热系数为。
(6．1W／(m2．K))7．在一维稳态传热过程中，每个传热环节的热阻分别是0．01K／W、0．35K／W和0．009lK ／W，在热阻为的传热环节上采取强化传热措施效果最好。
(0．35K／W)8．某一厚20mm的平壁传热过程的传热系数为45W／(m2．K)，热流体侧的传热系数为70W／(m2K)，冷流体侧的传热系数为200W／(m2．K)，则该平壁的导热系数为。
第五章-传热学
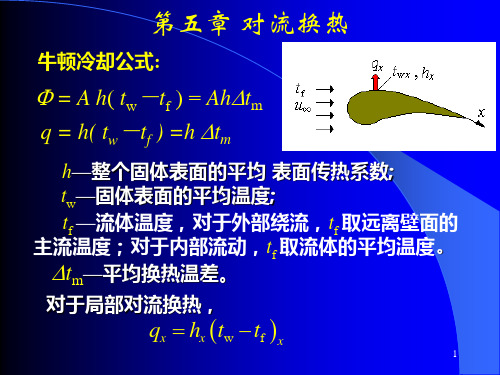
t w = f ( x, y , z , τ )
如果t 常数，则称为等壁温边界条件 如果 w=常数，则称为等壁温边界条件。 等壁温边界条件。
12
第二类边界条件给出边界上的热流密度分布规律 第二类边界条件给出边界上的热流密度分布规律： 给出边界上的热流密度分布规律：
qw = f ( x, y , z , τ )
8
单位时间内微元体热力学能的增加为 单位时间内微元体热力学能的增加为
dU Φλ + Φh = 于是根据微元体的能量守恒 dτ ( ut ) ( vt ) 2t 2t 可得 λ 2 + 2 dxdy ρ c p x + y dxdy x y t = ρcp dxdy τ t t t u v 2t 2t +v +t + ρcp + u = λ 2 + 2 x y x y x y τ
4
按照牛顿冷却公式
t q x = hx ( tw tf ) x= λ y w,x
hx =
qx
( tw tf ) x
λ
t y w, x
如果热流密度、 表面传热系数、 如果热流密度 、 表面传热系数 、 温度梯度及温差 都取整个壁面的平均值， 都取整个壁面的平均值，则有 λ t h= tw tf y w 上面两式建立了对流换热表面传热系数与温度场 之间的关系。 而流体的温度场又和速度场密切相关， 之间的关系 。 而流体的温度场又和速度场密切相关 ， 所以对流换热的数学模型应该包括描写速度场和温度 场的微分方程。 场的微分方程。 5
dU t = ρcp dxdy τ dτ
t t t 2t 2t ρcp + u +v = λ x 2 + y 2 x y τ
第五章传热ppt课件
1
第一节 概述
一、传热在食品工程中的应用
（１）食品生产中一般必要的加热、冷却过程； （２）为延长食品贮藏时间而进行的杀菌或冷藏； （３）以除去食品中水分为目的的蒸发或结晶过程的加热或冷 却； （４）为食品完成一定生物化学变化而进行的蒸煮、焙烤等。
2
第一节 概述
二、传热的基本方式
热的传递是由于系统内或物体内温度不同而引起的，根据 传热机理不同，传热的基本方式有三种：
7
一维温度场：若温度场中温度只沿着一个坐标方向变化。
一维温度场的温度分布表达式为：
t = f (x,τ)
(4-1a)
➢不稳定温度场：温度场内如果各点温度随时间而改变。
➢稳定温度场：若温度不随时间而改变。
➢等温面：温度场中同一时刻相同温度各点组成的面。
等温面的特点： （1）等温面不能相交； （2）沿等温面无热量传递。
24
2 多层圆筒壁的稳定热传导
对稳定导热过程，单位时间内由多层壁所传导的 热量，亦即经过各单层壁所传导的热量。
如图所示：以三层圆筒壁为例。
➢假定各层壁厚分别为b1= r2-
r1，b2=r3- r2，b3=r4- r3；
➢各 层 材 料 的 导 热 系 数 λ1，
λ2，λ3皆视为常数；
➢层与层之间接触良好，相互
3、热辐射
因热的原因而产生的电磁波在空间的传递，称为热辐射。
➢所有物体都能将热以电磁波的形式发射出去，而不需要任何
介质。
➢任何物体只要在绝对零度以上都能发射辐射能，但是只有在
物体温度较高的时候，热辐射才能成为主要的传热形式。
实际上，上述三种传热方式很少单独出现，而往往是相互
伴随着出现的。
化工原理第五章传热过程计算与换热器
5.4 传热效率和传热单元数
• 当传热系数K和比热cpc为常数时，积分上式可得
• 式中NTUc（Number of Transfer Unit）称为对冷流体而言的传热单 元数，Dtm为换热器的对数平均温差。
• 同理，以热流体为基准的传热单元数可表 示
• 在换热器中，传热单元数定义 为
5.4 传热效率和传热单元数
• 2．由选定的换热器型式计算传热系数K；
• 3．由规定的冷、热流体进出口温度计算参数e、CR； • 4．由计算的e、CR值确定NTU。由选定的流动排布型
式查取e—NTU算图。可能需由e—NTU关系反复计算 NTU；
• 5．计算所需的传热面积
。
5.5 换热器计算的设计型和操作型问题
• 例5-2 一列管式换热器中，苯在换热器的管内 流动，流量为1.25 kg/s，由80℃冷却至30℃； 冷却水在管间与苯呈逆流流动，冷却水进口温 度为20℃，出口温度不超过50℃。若已知换热 器的传热系数为470 W/（m2·℃），苯的平均 比热为1900 J/（kg·℃）。若忽略换热器的散 热损失，试分别采用对数平均温差法和传热效 率—传热单元数法计算所需要的传热面积。
• 如图5-4所示，按照冷、热流 体之间的相对流动方向，流体之 间作垂直交叉的流动，称为错流 ；如一流体只沿一个方向流动， 而另一流体反复地折流，使两侧 流体间并流和逆流交替出现，这
种情况称为简单折流。
•图 P2
•55
5.3 传热过程的平均温差计算
•通常采用图算法，分三步： •① 先按逆流计算对数平均温差Dtm逆； •② 求出平均温差校正系数φ；
•查图 φ
•③ 计算平均传热温差： • 平均温差校正系数 φ <1，这是由于在列管式换热器内增设了
传热学(第四版)第五章：对流传热的理论基础
温度边界层和速度边界层数值举例
空气，来流速度0.5 m/s 水，来流速度0.5 m/s
§5-2 对流传热与相似原理
1 问题的提出
能够得到理论解的对流传热问题非常少。试验是不可或缺 的手段，然而，经常遇到如下两个问题: h f (v, , c p , , , l ) (1) 变量太多 A 实验中应测哪些量（是否所有的物理量都测） B 实验数据如何整理（整理成什么样函数关系） (2) 实物试验很困难或太昂贵的情况，如何进行试验？
u
x
v
y
D D x x y y
（5）运动流体的能量守恒方程中引入了流场变量
第五章 对流换热
u和v 。
6
Navier-Stokes方程（1820年~1850年）
无因次化处理
预期解的形式
3 指导实验 • • 同名的已定特征数相等 单值性条件相似：初始条件、边界条件、几何条件、物理条件 实验中只需测量各特征数所包含的物理量,避免了测量的盲 目性——解决了实验中测量哪些物理量的问题 按特征数之间的函数关系整理实验数据，得到实用关联式 ——解决了实验中实验数据如何整理的问题 可以在相似原理的指导下采用模化试验 —— 解决了实物 试验很困难或太昂贵的情况下，如何进行试验的问题
厚度t 范围 — 热边界层 或温度边界层
t — 热边界层厚度
与t 不一定相等
第五章 对流换热 19
根据边界层理论，u v,
u v 0 x y u u u x v x v v u y v y
y x 简化对流传热问题如下：
Nusselt 1910年发表”管内换热理论解” Fourier 1822年发表“热的解析理论”
传热学2Chap5
(eKm A A
1)
tm
t t ln t
t
5.2 换热器中的传热过程
➢逆流
tm
t t ln t
t
t t1 t2 t t1 t2
统一表达形式
tm
tmax tmin ln tmax
tmin
tmax max t, t tmin min t, t
5.2 换热器中的传热过程
几点说明
算术平均温差
tm n i1
Φi / tmi
i 1
➢ 其他流型 温差修正系数 tm tm,逆
f P, R
P t2 t2 t1 t2
R t1 t1 t2 t2
反映了复杂流型的传热性能接近逆流的程度， <1
5.2 换热器中的传热过程
温差修正系数线算图
5.2 换热器中的传热过程
温差修正系数线算图
5.2 换热器中的传热过程
（2）平均传热温差tm计算 ➢顺流
基本假定： ① 换热器无散热损失，只有冷、热流体通过固体壁 面的传热 ② 流体流量及比热容都为常量 ③ 沿换热面传热系数不变 ④ 换热面沿流动方向导热不计 ⑤ 在换热器中，任一种流体都不能既有相变又有单 相介质换热
5.2 换热器中的传热过程
平均传热温差tm定义
A
A
第五章 传热过程及换热器
主要内容
传热过程及其控制 通过管壁（圆筒壁）的传热过程 通过肋壁的传热 传热过程的控制
换热器中的传热过程 换热器的分类 换热器的热计算
5.1 传热过程及其控制
传热过程
定义：高温流体通过固体壁把热量传给低温流体的过 程称为传热过程
传热方程 ？？
KA(t f 1 t f 2 ) KAtm
第五章传热
第五章传热主要内容：热量传递基础；传热过程的计算；传热设备。
重点内容：傅里叶传导定律；牛顿冷却对流传热定律；传热过程基本方程；换热器的计算；管壳式换热器的设计和选用。
难点内容：传热过程基本方程。
课时安排：20第一节概述一、传热过程由热力学第二定律可知，凡有温度差存在的地方，就必然有热量的传递。
化学工业与传热密切相关，化工生产过程中许多单元操作都需要加热和冷却。
化工生产中进行传热操作的目的——1．料液的加热和冷却，为达到反应所需的温度；2．为维持反应温度，需不断输入或输出热量；3．许多单元操作需输入或输出热量；4．化工设备的保温；5．生产过程中热能的综合利用及废热的回收。
化工生产对传热过程的要求：1．强化传热——要求传热速率高，降低设备成本；2．削弱传热——可减少热损失。
二、传热的基本方式（传热机理）传热原因——传热推动力（温度差）传热方向——在无外功输入时，由热力学第二定律，热流方向由高温处向低温处流动。
传热的三种基本方式：1．热传导——物体内部或两个直接接触物体之间的传热方式。
金属导体—自由电子运动不良导体，大部分液体—温度高的分子振动，与相邻分子碰撞，造成的动量传递。
气体—分子无规则运动热传导是静止物体内的一种传递方式，没有物质的宏观位移。
2．对流传热——是指流体由质点发生相对位移而引起的热交换。
对流传热仅发生在流体中，所以与流体的流动方式密切相关。
自然对流——质点位移是由于流体内部密度差引起的，使轻者浮，重者沉；强制对流——质点运动是由外力作用所致。
对流传热同时伴有热传导，事实上无法将其分开——又称给热。
化工中所讨论的给热，都是指流体与固体壁面之间的传热过程——间壁式换热3．热辐射——是一种通过电磁波传递能量的过程任何物体，只要在0K 以上都能发射电磁波，而不依靠任何介质，当被另一物体接收后，又重新变为热能。
热辐射不仅是能量转移，也伴随着能量形式的转移。
三、间壁式换热1． 间壁式换热过程—由对流、导热、对流三过程串联而成（1）热流体以对流方式将热量传递到间壁一侧； （2）热量以导热方式通过间壁； （3）热量以对流方式传至冷流体。
第五章-传热学
h
' h,x
' h,y
cpuxtvytdxdy
8
单位时间内微元体热力学能的增加为
dU
d
cp
t
dxdy
于是根据微元体的能量守恒
h
dU
d
可得
2t x2
2t y2
dxdy
cpuxtvytdxdy
cp
t
dxdy
cptux tvy ttu xv y
2t x2
2t y2
2
20
cp
uxt
v t y
＝
2t x2
2t y2
1
11 1
1
2
1 1
1
2
对流换热微分方程组简化为
h t tw tf y w
u v 0 x y
简化方程组只有4个方
程，但仍含有h、u、v、 p、t 等5个未知量，方
程组不封闭。如何求解？
uuxvuy1ddpxy2u2
u t x
v t y
26
第六节 相似理论基础
相似原理指导下的实验研究仍然是解决复杂对流换 热问题的可靠方法。
相似原理回答三个问题： （1）如何安排实验？ （2）如何整理实验数据？ （3）如何推广应用实验研究结果？
一、 相似原理的主要内容
1.物理现象相似的定义 2.物理现象相似的性质 3.相似特征数之间的关系 4.物理现象相似的条件
三、解的函数形式——特征数关联式
特征数是由一些物理量组成的无量纲数，例如毕 渥数Bi和付里叶数Fo。对流换热的解也可以表示成 特征数函数的形式，称为特征数关联式。
通过对流换热微分方程的无量纲化可以导出与对 流换热有关的特征数。
传热学第五章
h Atw t
以后除非特殊声明外,我们所说的对流换热系数皆指平均对流换
热系数,以 h 表示.
h(x)规律说明
Laminar region
x (x) h (x) 导热
Transition region
扰动
h(x)
Turbulent region
湍流部分的热阻很小,热阻主要集中在
粘性底层中.
2.按有无相变分
单相介质传热:对流换热时只有一种流体.
相变换热:传热过程中有相变发生.
物质有三态,固态,液态,气态或称三相.
相变换热有分为:
沸腾换热:(boiling heat transfer)物质由液态变为气态时发生 的换热.
凝结换热:(condensation heat transfer)物质由气态变为 液态时发生的换热. 熔化换热(melting heat transfer) 凝固换热(solidification heat transfer) 升华换热(sublimation heat transfer) 凝华换热（sublimation heat transfer ）
由上述分析可见,边界层控制着传热过程,故一些研究人员试图通过
破坏粘性底层来达到强化传热的目的,并取得了一些成果.
二、边界层微分方程组.
牛顿流体(Newtonian fluid),常物性,无内热源,耗散不计,稳态,
二维,略去重力.
完性分析已知：u，t，l 的量级为0(1) ， t 的量级为0(）
以此五个量为分析基础。
2.动量方程(momentum equation)
u v 0 x y
u
u
u x
v
u y
Fx
p x
化工原理(第五章传热第五节)
吉 首 大 学
流体在管束外横掠流动
化 工 原 理 由于各排的给热系数不同，则整个管束的平均给热系数应按 下式求出： a1A1+ a2A2 + a3A3 + … am = A1+A2 + A3 + … 式中：A1、A2、A3……分别为第一排，第二排，第三排…… 的传热面积； a1 、 a2 、 a3……分别为第一排，第二排，第三排…… 的传热系数。
d A2 π d 2dl d 2 = = d Am π d mdl d m
吉 首 大 学
1 = d2 ＋ b d2 ＋ 1 a2 a1 d1 λ dm K2
当间壁为平壁，或管壁很薄或管径较大时，dA1 、dA2 、dAm 和 dA 相等或近似相等，则： 1 = 1 ＋ b ＋ 1 a2 a1 λ K2
Q QR
Q A + QR + QD = Q Q A QR QD + + =1 Q Q Q
QA
吉 首 大 学
QD
A+ R + D =1
A、R 和 D 分别为物体吸收率、反射率和透过率。 单色吸收率、反射率和透过率
a(λ , T ) + r (λ , T ) + d (λ , T ) = 1
基本概念
化 工 原 理 黑体(绝对黑体)：能将辐射能全部吸收的物体，即 A=1, R=D=0。自然界中并不存在绝对黑体，例如没有光泽的黑墨 表面，其吸收率 A=0.96~0.98，定义黑体的目的是为了在计 算中确定一个比较的标准。 镜体(绝对白体)：能将辐射能全部反射的物体，即 R=1, A=D=0。自然界中也不存在绝对镜体，例如表面抛光的铜， 其反射率 R=0.97。 0.97 透热体：辐射能全部透过的物体，即D=1, A=R=0。例如对 称双原子气体 O2、N2、H2 等都是透热体。 灰体：能够以相等的吸收率吸收所有波长辐射能的物体。灰 体也是理想物体，其特点为：吸收率 A 与波长无关；为不透 热体 (A+R=1)。工业上常见的固体材料均可视为灰体。
第五章 传热
23
3．固体的导热系数
• 导热性能与导电性能密切相关，一般而言，良好 的导电体必然是良好的导热体，反之亦然。在所 有固体中，金属的导热性能最好。大多数金属的 导热系数随着温度的升高而降低，随着纯度的增 加而增大，也即合金比纯金属的导热系数要低。 • 非金属固体的导热系数与其组成、结构的紧密程 度及温度有关。大多数非金属固体的导热系数随 密度增加而增大；在密度一定的前提下，其导热 系数与温度呈线性关系，随温度升高而增大。 • 应予指出，在导热过程中导热体内的温度沿传热 方向发生变化，其导热系数也在变化，但在工程 计算中，为简便起见通常使用平均导热系数。
传热过程可依靠其中的一种或几种方式同时进行。 （一）热传导 热传导又称导热，是借助物质的分子或原子振动以及自由电子的热 运动来传递热量的过程。当物质内部在传热方向上无质点宏观迁移 的前提下，只要存在温度差，就必然发生热传导。可见热传导不仅 发生在固体中，同时也是流体内的一种传热方式。
在静止流体内部以及在作层流运动的流体层中垂直于流动方向上的 传热，是凭借流体分子的振动碰撞来实现的，换言之，这两类传热 过程也应属于导热的范畴。 很显然，导热过程的特点是：在传热过程中传热方向上无质点块的 宏观迁移。
△tm---推动力，冷热流体的平均温差。
应用：设计计算与校核计算；强化传热的途径
15
第二节 热传导
一、傅立叶定律
（一）导热的分类
由热传导引起的传热速率称为导热速率，其与导热体 内部的温度分布情况有关。导热体内部在空间和时间 上的温度分布称为温度场。 若温度场内各点的温度随时间变化，则称为不稳定温 度场。可用数学表达式表示为： t = f (x, y, z, θ)
22
2．液体的导热系数
• 液体可分为金属液体（液态金属）和非金属液体。 液态金属的导热系数比一般液体的高，其中熔融 的纯纳具有较高的导热系数，大多数金属液体的 导热系数随温度的升高而降低。在非金属液体中， 水的导热系数最大。除水和甘油外，大多数非金 属液体的导热系数亦随温度的升高而降低。通常 纯液体的导热系数较其溶液的要大。液体的导热 系数基本上与压强无关。
化工原理课件第五章 传热
温度场的通式
温度场的通式：
t f x, y, z,
式中： t —— 某点的温度，k；
X，y，z —— 这点的空间坐标；
θ —— 时间，s。
若在稳定温度场中， 表示式为：
t f x, y, z
稳定温度场和不稳定温度场
（1）不稳定温度场 —— 温度随时间而改变 的温度场，称为：不稳定温度场 。
称为：传热速率，用Q表示，单位：J/s， 即w（瓦）。
（三）辐射
1、辐射——是一种以电磁波传递能量的现象。 物体可以由不同原因发出辐射能。
2、热辐射——物体因热而发出辐射能的过程， 称为：热辐射radiation。
3、 只要物体的绝对温度大于 0K，便会不停地 将热量以电磁波的形式传递出去，同时也不断 地将其他物体辐射来的能量转为热量。辐射与 吸收能 量的差额转变为低温物体的热量。但 是，只有物体具有较高温度时， 辐射才为主 要形式。
传热面上不同局部面积的热通量可以不同。
3、热流量Q与热通量q的关系
式中：
q dQ dA
Q——热流量，单位为：J/s，即w（瓦） 。
q——热通量（热流密度），单位为：J/(m2·s)，即 w/m2。
A——传热面积， m2 。
热流量Q与热通量q的关系
（1）热通量q基于微元面dA，热通量q可以 用于局部地区。
1、热源——电热、饱和水蒸汽、烟道气、高 温载体等。
2、冷源——冷却水、空气、冷却盐水等。 冷却水——河水、海水、井水等。
二、传热的三种基本方式
• 1、热传导（导热） • 2、对流 • 3、辐射
（一）热传导（简称：导热）
1、热传导——热量从物体内部温度较高
的部分传递到温度较低的部分或者传递到与 之接触的另一物体的过程，称为：热传导， 简称：导热conduction。
河海大学传热学--第五章对流传热的理论基础PPT课件
34 18.07.2020 4:47 杨祥花
• 例1
河海大学常州校区热能与动力工程系—传热学
35 18.07.2020 4:47 杨祥花
§5-3 边界层型对流传热问题的数学描写
边界层概念：当粘性流体流过物体表面时，会形成速度梯
度很大的流动边界层；当壁面与流体间有温差时，也会产
生温度梯度很大的温度边界层（或称热边界层）
综合：对流换热微分方程组
u v 0 x y
( u u u x v u y) F x p x( x 2 u 2 y 2 u 2)
v v v
p 2 v 2 v
( u x v y) F y y( x2 y2)
tu x tv y tcp( x2t2 y2t2)
hx
第五章 对流传热 的理论基础
河海大学常州校区热能与动力工程系—传热学
1 18.07.2020 4:47 杨祥花
标题添加
点击此处输入相 关文本内容
前言
点击此处输入 相关文本内容
标题添加
点击此处输入相 关文本内容
河海大学常州校区热能与动力工程系—传热学
点击此处输入 相关文本内容
2 18.07.2020 4:47 杨祥花
???xtdyx???ytdxy1单位时间以导热的方式进入流体微元的单位时间以导热的方式进入流体微元的净热流量导热为河海大学常州校区热能与动力工程系传热学2018年1月3日5时2分杨祥花???????xdxxxtdxdydxxxx???????ydyyytdydxdyyyy22???xxdxtdxdyx22???yydytdxdyy2222导热????ttdxdyxy河海大学常州校区热能与动力工程系传热学2018年1月3日5时2分杨祥花2单位时间以对流方式进入元体的净热流对流为xpctudyypctvdx?xxdx???xxdxx???pcutdydxx?yydy???yydyy???pcvtdxdyy对流??????ppcutdycvtdxdxdyxy??????pputvtcdxdycdxdyxy???????????????pttuvcuvttdxdyxyxy
柴诚敬化工原理课后答案(05)第五章 传热过程基础
第五章 传热过程基础1．用平板法测定固体的导热系数，在平板一侧用电热器加热，另一侧用冷却器冷却，同时在板两侧用热电偶测量其表面温度，若所测固体的表面积为0.02 m 2，厚度为0.02 m ，实验测得电流表读数为0.5 A ，伏特表读数为100 V ，两侧表面温度分别为200 ℃和50 ℃，试求该材料的导热系数。
解：传热达稳态后电热器的加热速率应与固体的散热（导热）速率相等，即 Lt t SQ 21-=λ 式中 W 50W 1005.0=⨯==IV Qm 02.0C 50C 200m 02.0212=︒=︒==L t t S ，，， 将上述数据代入，可得()()()()C m W 333.0C m W 5020002.002.05021︒⋅=︒⋅-⨯⨯=-=t t S QL λ2．某平壁燃烧炉由一层400 mm 厚的耐火砖和一层200 mm 厚的绝缘砖砌成，操作稳定后，测得炉的内表面温度为1500 ℃，外表面温度为100 ℃，试求导热的热通量及两砖间的界面温度。
设两砖接触良好，已知耐火砖的导热系数为10.80.0006t λ=+，绝缘砖的导热系数为20.30.0003t λ=+，W /(m C)⋅︒。
两式中的t 可分别取为各层材料的平均温度。
解：此为两层平壁的热传导问题，稳态导热时，通过各层平壁截面的传热速率相等，即 Q Q Q ==21 （5-32） 或 23221211b t t S b t t SQ -=-=λλ （5-32a ） 式中 115000.80.00060.80.0006 1.250.00032t t t λ+=+=+⨯=+21000.30.00030.30.00030.3150.000152t t t λ+=+=+⨯=+代入λ1、λ2得2.0100)00015.0315.0(4.01500)0003.025.1(-+=-+t t t t解之得C 9772︒==t t())()C m W 543.1C m W 9770003.025.10003.025.11︒⋅=︒⋅⨯+=+=t λ则 ()22111m W 2017m W 4.09771500543.1=-⨯=-=b t t S Q λ3．外径为159 mm 的钢管，其外依次包扎A 、B 两层保温材料，A 层保温材料的厚度为50 mm ，导热系数为0.1 W /(m·℃)，B 层保温材料的厚度为100 mm ，导热系数为1.0 W /(m·℃)，设A 的内层温度和B 的外层温度分别为170 ℃和40 ℃，试求每米管长的热损失；若将两层材料互换并假设温度不变，每米管长的热损失又为多少？解：()()mW 150m W 100159100502159ln 0.11159502159ln 1.014017014.32ln 21ln 2123212121=++⨯++⨯+-⨯⨯=+-=r r r r t t L Q πλπλA 、B 两层互换位置后，热损失为()()mW 5.131m W 100159100502159ln 1.01159502159ln 0.114017014.32ln 21ln 2123212121=++⨯++⨯+-⨯⨯=+-=r r r r t t L Q πλπλ4．直径为57mm 3.5φ⨯mm 的钢管用40 mm 厚的软木包扎，其外又包扎100 mm 厚的保温灰作为绝热层。
传热过程基础知识
2020/10/29
6
5在空间的传递。
自然界中一切物体都在不停地发射辐射能，同时又不断地 吸收来自其它物体的辐射能，并将其转化为热能。物体之 间相互辐射和吸收能量的总结果，称为辐射传热。由于高 温物体发射的能量比吸收的多，而低温物体则相反，从而 使净热量从高温物体传递向低温物体。
导电固体：有许多的自由分子在晶格之间运动，正如这些 自由电子能传导电能一样，它们也能将热量从高温处传递 到低温区。
非导电固体：导热是通过晶格结构的振动(即原子、分子 在其平衡位置附近的振动)来实现的。物体中温度较高部分 的分子，因振动而与相邻的分子相碰撞，并将热能的一部 分传递给后者。
一般，通过晶格振动传递的热量比依靠自由电子迁移传递 的热量少，这就是良好的导电体也是良好导热体的原因。
❖纯金属：t↑，k↓ ❖金属： 纯度↑，k↑ 非金属：ρ，t ↑，k↑
〖说明〗
对大多数固体， k值与温度大致成线性关系：
k k0(1 t)
式中： k－固体在温度为 t℃时的导热系数，W/(m·℃) k0－固体在温度为 0℃时的导热系数，W/(m·℃) β－温度系数。 ❖ 大多数金属：β<0 ❖大多数非金属：β>0
因此，导热系数表征物体导热能力的大小，是物质的物性常
数之一。其大小取决于物质的组成结构、状态、温度和压强
等。
导热系数大小由实验测定，其数值随状态变化很大。
大 金属非金属固体液体气体 小
2020/10/29
17
5.3.3.1 固体的导热系数
金属：35～420W/(m·℃)，非金属：0.2～3.0W/ (m·℃) 固体中，金属是最好的导热体。
第五章对流传热理论基础
简化
流动
普朗特 速度边界层
类比
对流换热
波尔豪森 热边界层
38
传热学
一、流动边界层
1、流动边界层及其厚度 定义：当流体流过固体壁面时,由于流 体粘性的作用,使得在固体壁面附近存 在速度发生剧烈变化的薄层称为流动 边界层或速度边界层。
实际流动 ≈ 边界层区粘性流动+主流区无粘性理想流动
大空间自然对流 有限空间自然对流
沸腾换热 有相变
凝结换热
大容器沸腾 管内沸腾
管外凝结 管内凝结
14
传热学
六、研究对流传热的方法（确定h的方法）
四种：1）分析法；2）实验法；3）比拟法；4）数值法
适当介绍
重点介绍 一定介绍
不作介绍
1）分析法
解析：二维、楔形流、平板 边界层积分方程（近似解析）
2）实验法
u∞
y δ
0x xc
粘性底层
掠过平板时边界层的形成与发展
湍流核心 缓冲层
41
传热学
层流： 流体做有秩序的分层流动，各层互不干扰，只有分子扩散，
无大微团掺混
湍流： 流体微团掺混，紊乱的不规则脉动
粘性底层 :速度梯度较大、分子扩散—导热
湍流边界层
缓冲层 :导热+对流 湍流核心 :质点脉动强化动量传递，速度变化
换热表面的形状、大小、换热表面与流体运动方向的 相对位置及换热表面的状态（光滑或粗糙）
内部流动对流传热：管内或槽内 外部流动对流传热：外掠平板、圆管、管束
10
传热学
11
传热学
(5) 流体的热物理性质：
热导率 [W (m C)] 比热容 c [J (kg C)]
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第五章 传热过程基础1．用平板法测定固体的导热系数，在平板一侧用电热器加热，另一侧用冷却器冷却，同时在板两侧用热电偶测量其表面温度，若所测固体的表面积为0.02 m 2，厚度为0.02 m ，实验测得电流表读数为0.5 A ，伏特表读数为100 V ，两侧表面温度分别为200 ℃和50 ℃，试求该材料的导热系数。
解：传热达稳态后电热器的加热速率应与固体的散热（导热）速率相等，即 Lt t S Q 21-=λ 式中 W 50W 1005.0=⨯==IV Qm 02.0C 50C 200m 02.0212=︒=︒==L t t S ，，，将上述数据代入，可得()()()()C m W 333.0C m W 5020002.002.05021︒⋅=︒⋅-⨯⨯=-=t t S QL λ 2．某平壁燃烧炉由一层400 mm 厚的耐火砖和一层200 mm 厚的绝缘砖砌成，操作稳定后，测得炉的内表面温度为1500 ℃，外表面温度为100 ℃，试求导热的热通量及两砖间的界面温度。
设两砖接触良好，已知耐火砖的导热系数为10.80.0006t λ=+，绝缘砖的导热系数为20.30.0003t λ=+，W /(m C)⋅︒。
两式中的t 可分别取为各层材料的平均温度。
解：此为两层平壁的热传导问题，稳态导热时，通过各层平壁截面的传热速率相等，即 Q Q Q ==21 （5-32）或 23221211b t t S b t t SQ -=-=λλ （5-32a ）式中 115000.80.00060.80.0006 1.250.00032t t t λ+=+=+⨯=+ 21000.30.00030.30.00030.3150.000152t t t λ+=+=+⨯=+ 代入λ1、λ2得2.0100)00015.0315.0(4.01500)0003.025.1(-+=-+t t t t 解之得C 9772︒==t t()()()C m W 543.1C m W 9770003.025.10003.025.11︒⋅=︒⋅⨯+=+=t λ则 ()22111m W 2017m W 4.0977*******.1=-⨯=-=b t t S Q λ 3．外径为159 mm 的钢管，其外依次包扎A 、B 两层保温材料，A 层保温材料的厚度为50 mm ，导热系数为0.1 W /(m·℃)，B 层保温材料的厚度为100 mm ，导热系数为1.0 W /(m·℃)，设A 的内层温度和B 的外层温度分别为170 ℃和40 ℃，试求每米管长的热损失；若将两层材料互换并假设温度不变，每米管长的热损失又为多少？解： ()()m W 150m W 100159100502159ln 0.11159502159ln 1.014017014.32ln 21ln 2123212121=++⨯++⨯+-⨯⨯=+-=r r r r t t L Q πλπλA 、B 两层互换位置后，热损失为 ()()m W 5.131m W 100159100502159ln 1.01159502159ln 0.114017014.32ln 21ln 2123212121=++⨯++⨯+-⨯⨯=+-=r r r r t t L Q πλπλ4．直径为57mm 3.5φ⨯mm 的钢管用40 mm 厚的软木包扎，其外又包扎100 mm 厚的保温灰作为绝热层。
现测得钢管外壁面温度为120-℃，绝热层外表面温度为10 ℃。
软木和保温灰的导热系数分别为0.043⋅W/(m ℃)和0.07⋅W/(m ℃)，试求每米管长的冷损失量。
解：此为两层圆筒壁的热传导问题，则()()mW 53.24m W 04.00285.01.004.00285.0ln 07.010285.004.00285.0ln 043.011012014.32ln 1ln 1π223212121-=+++++--⨯⨯=+-=r r r r t t L Q λλ 5．在某管壳式换热器中用冷水冷却热空气。
换热管为Φ25 mm×2.5 mm的钢管，其导热系数为45 W/(m·℃)。
冷却水在管程流动，其对流传热系数为2 600 W/(m 2·℃)，热空气在壳程流动，其对流传热系数为52 W/(m 2·℃)。
试求基于管外表面积的总传热系数K ，以及各分热阻占总热阻的百分数。
设污垢热阻可忽略。
解：由o o o o m i i11K d d b d d αλα=++ 查得钢的导热系数 ()C m W 452︒⋅=λ2.5b =mm o 25d =mm ()mm 20mm 5.2225i =⨯-=dmm 5.22mm 22025m =+=d ()()C m W 6.50C m W 02.02600025.00225.045025.00025.0521122o ︒⋅=︒⋅⨯+⨯⨯+=K 壳程对流传热热阻占总热阻的百分数为oo o o 150.6100%100%100%97.3%152K K αα⨯=⨯=⨯= 管程对流传热热阻占总热阻的百分数为o o o i ii i o 50.60.025100%100%100% 2.4%126000.02d K d d d K αα⨯⨯=⨯=⨯=⨯ 管壁热阻占总热阻的百分数为oo o mm o 0.00250.02550.6100%100%100%0.3%1450.0225bd bd K d d K λλ⨯⨯⨯=⨯=⨯=⨯ 6．在一传热面积为40 m 2的平板式换热器中，用水冷却某种溶液，两流体呈逆流流动。
冷却水的流量为30 000kg/h ，其温度由22 ℃升高到36 ℃。
溶液温度由115 ℃降至55 ℃。
若换热器清洗后，在冷、热流体流量和进口温度不变的情况下，冷却水的出口温度升至40 ℃，试估算换热器在清洗前壁面两侧的总污垢热阻。
假设：（1）两种情况下，冷、热流体的物性可视为不变，水的平均比热容为4.174 kJ/(kg·℃)；（2）两种情况下，i o αα、分别相同；（3）忽略壁面热阻和热损失。
解：求清洗前总传热系数K()()C 7.52C 225536115ln 225536115m ︒=︒-----=∆t ()())C m W 231C m W 7.52403600223610174.430000223m ︒⋅=︒⋅⨯⨯-⨯⨯⨯=∆=t S Q K 求清洗后传热系数K '由热量衡算h p,h 12c p,c 21()()W C T T W C t t -=-h p,h 12c p,c 21()()W C T T W C t t ''-=- c p,c 2121h p,h ()W C T T t t W C ''=-- ()()C 9.37C 22402236551151151212211︒=︒⎥⎦⎤⎢⎣⎡----=-'---=t t t t T T T ()()C 1.38C 229.3740115ln 229.3740115m ︒=︒-----='∆t ()()()C m W 8.410C m W 1.38403600224010174.430000223︒⋅=︒⋅⨯⨯-⨯⨯⨯=K 清洗前两侧的总传热热阻C m 109.1W C m 8.4101231111232S ︒⋅⨯=︒⋅⎪⎭⎫ ⎝⎛-='-=-∑K K R 7．在一传热面积为25 m 2的单程管壳式换热器中，用水冷却某种有机溶液。
冷却水的流量为28 000kg/h ，其温度由25 ℃升至38 ℃，平均比热容为4.17 kJ/(kg·℃)。
有机溶液的温度由110 ℃降至65 ℃，平均比热容为1.72 kJ/(kg·℃)。
两流体在换热器中呈逆流流动。
设换热器的热损失可忽略，试核算该换热器的总传热系数并计算该有机溶液的处理量。
解：p,c 4.17C = kJ/(kg·℃)c p,c 21()Q W C t t =-()W 1022.4W 25381017.436002800053⨯=-⨯⨯⨯= 求m t ∆有机物 110 → 65水 38 ← 25————————————————t ∆ 72 40C 4.54C 4072ln 4072m ︒=︒-=∆t )()C m W 3.310C m W 4.54251022.4225︒⋅=︒⋅⨯⨯=K ()()h kg 10963.1s kg 452.5kg 651101072.11022.443521h h ⨯==-⨯⨯⨯=-=K T T c Q W p8．在一单程管壳式换热器中，用水冷却某种有机溶剂。
冷却水的流量为10 000 kg/h ，其初始温度为30 ℃，平均比热容为4.174 kJ/（kg·℃）。
有机溶剂的流量为14 000 kg/h ，温度由180 ℃降至120 ℃，平均比热容为1.72 kJ/（kg·℃）。
设换热器的总传热系数为500 W/(m 2·℃)，试分别计算逆流和并流时换热器所需的传热面积，设换热器的热损失和污垢热阻可以忽略。
解： ()()kW 3.401h kJ 104448.1h kJ 12018072.114000621h =⨯=-⨯⨯=-=T T Wc Q p 冷却水的出口温度为C 61.64C 30174.410000104448.161c c 2︒=︒⎪⎪⎭⎫ ⎝⎛+⨯⨯=+=t c W Q t p 逆流时()()C 102.2C 9039.115ln 39.25C 3012061.64180ln 3012061.64180m ︒=︒=︒-----=∆t 223m m 854.7m 2.102500103.401=⨯⨯=∆=t K Q S 逆并流时 ()()C 97.94C 15039.55ln 61.94C 3018061.64120ln 3018061.64120m ︒=︒=︒-----=∆t 223m m 452.8m 97.94500103.401=⨯⨯=∆=t K Q S 逆 9．在一单程管壳式换热器中，用冷水将常压下的纯苯蒸汽冷凝成饱和液体。
已知苯蒸汽的体积流量为1 600 m 3/h ，常压下苯的沸点为80.1 ℃，气化热为394 kJ/kg 。
冷却水的入口温度为20 ℃，流量为35 000 kg/h ，水的平均比热容为4.17 kJ/(kg·℃)。
总传热系数为450 W/(m 2·℃)。
设换热器的热损失可忽略，试计算所需的传热面积。
解：苯蒸气的密度为()33m kg 692.2m kg 1.8027308206.0781=+⨯⨯==RT PM ρh kg 2.4307h kg 692.21600h =⨯=WW 1071.4h kJ 10697.1h kJ 3942.430756h ⨯=⨯=⨯==γW Qc p,c 21()Q W C t t =-23535000 4.1710(20) 4.71103600t =⨯⨯-=⨯ 解出 231.6t =℃求m t ∆苯 80.1 → 80.1水 31.6 20————————————————t ∆ 48.5 60.1C 1.54C 5.481.60ln 5.481.60m ︒=︒-=∆t 225m m 3.19m 1.544501071.4=⨯⨯=∆=t K Q S10．在一单壳程、双管程的管壳式换热器中，水在壳程内流动，进口温度为30 ℃，出口温度为65 ℃。