2020厦门一中入学数学适应性测试(答案)
福建省厦门第一中学2024届高三适应性练习卷数学试题

福建省厦门第一中学2024届高三适应性练习卷数学试题一、单选题1.已知集合{}1,1,2,4A =-,{}11B x x =-≥,则R A B =I ð( ) A .{1} B .{1,2}-C .{1,2}D .{1,2,4}-2.“π2α>”是“πsin 12αα->-”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件3.已知函数()f x 的定义域为[)1,+∞,数列{}n a 满足()n a f n =,则“数列{}n a 为递增数列”是“函数()f x 为增函数”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件D .既不充分也不必要条件4.如图所示,九连环是中国传统民间智力玩具,以金属丝制成9个圆环,解开九连环共需要256步,解下或套上一个环算一步,且九连环的解下和套上是一对逆过程.九连环把玩时按照一定得程序反复操作,可以将九个环全部从框架上解下或者全部套上.将第n 个圆环解下最少需要移动的次数记为()*9,N n a n n ≤∈,已知121,1a a ==,按规则有()*12213,N n n n a a a n n --=++≥∈,则解下第5个圆环最少需要移动的次数为( )A .4B .7C .16D .315.古希腊数学家阿波罗尼奥斯所著的八册《圆锥曲线论(Conics )》中,首次提出了圆锥曲线的光学性质,其中之一的内容为:“若点P 为椭圆上的一点,1F 、2F 为椭圆的两个焦点,则点P 处的切线平分12F PF ∠外角”.根据此信息回答下列问题:已知椭圆22:184x y C +=,O 为坐标原点,l 是点(P 处的切线,过左焦点1F 作l 的垂线,垂足为M ,则OM 为( )A .B .2C .3D .6.数列{}n a 中,1log (2)(N )n n a n n *+=+∈,定义:使12k a a a ⋅⋅⋅L 为整数的数k (N )k *∈叫做期盼数,则区间[1,2023]内的所有期盼数的和等于( ) A .2023B .2024C .2025D .20267.在一次数学模考中,从甲、乙两个班各自抽出10个人的成绩,甲班的十个人成绩分别为1210x x x L 、、、,乙班的十个人成绩分别为1210,,,y y y L .假设这两组数据中位数相同、方差也相同,则把这20个数据合并后( ) A .中位数一定不变,方差可能变大 B .中位数可能改变,方差可能变大 C .中位数一定不变,方差可能变小 D .中位数可能改变,方差可能变小 8.若曲线 1e xax y +=有且仅有一条过坐标原点的切线,则正数a 的值为( )A .14B C .13D二、多选题9.若1b c >>,01a <<,则下列结论正确的是( ) A .a a b c < B .log log b c a a > C .a a cb bc <D .log log c b b a c a >10.若函数()3e xf x x =,则( )A .()f x 是奇函数B .()f x 有且仅有2个极值点C .()f x 有且仅有1个零点D .()f x 的一条切线方程为4e e y x =+11.已知()123123,,x x x x x x <<是函数()()()()1e e e e x xf x x m =-++-(m ∈R 且0m ≠)的三个零点,则1123e 21x x x --++的可能取值有( )A .0B .1C .2D .3三、填空题12.已知,αβ为锐角,tan 2,cos αβ=,则()tan 2αβ-=. 13.设函数2()f x x ax b =++,对于任意的实数a ,b ,总存在0[0,4]x ∈,使得()f x t ≥成立,则实数t 的取值范围是.14.已知函数()2e ln ln 2xf x a x a =-+,对任意的正实数x 都有()0f x ≥恒成立,则a 的取值范围是.四、解答题15.已知正项等比数列{}n a 满足34a =,1517a a +=,公比1q >. (1)求数列{}n a 的通项公式;(2)若213n n nn a c +⋅=,试判断:数列{}n c 有没有最大项?若有,求出第几项为最大项;若没有,请说明理由.16.ABC V 的内角,,A B C 的对边分别为,,a b c ,已知c ,且ABC V 的面积2224b c a S +-=. (1)求C ;(2)若ABC V 内一点P 满足AP AC =,BP CP =,求PAC ∠.17.如图,在四棱锥P ABCD -中,AB AD ⊥,CD AD ⊥,PA ⊥平面ABCD ,22PA AD CD AB ====,M 为PC 的中点.(1)求证://BM 平面P AD ;(2)设点N 在平面P AD 内,且MN ⊥平面PBD ,求直线BN 与平面ABCD 所成角的正弦值.18.已知双曲线22221x y a b-=(0a b >>)左、右焦点为12,F F ,其中焦距为()4,3D .(1)求双曲线的方程;(2)过右焦点2F 作直线交双曲线于M ,N 两点(M ,N 均在双曲线的右支上),过原点O 作射线OP ,其中OP MN ⊥,垂足为,E P 为射线OP 与双曲线右支的交点,求24MN OP -的最大值.19.对于数列{}n a ,数列{}1n n a a +-称为数列{}n a 的差数列或一阶差数列.{}n a 差数列的差数列,称为{}n a 的二阶差数列.一般地,{}n a 的k 阶差数列的差数列,称为{}n a 的1k +阶差数列.如果{}n a 的k 阶差数列为常数列,而1k -阶差数列不是常数列,那么{}n a 就称为k 阶等差数列. (1)已知20,24,26,25,20是一个k 阶等差数列{}n a 的前5项.求k 的值及6a ; (2)证明:二阶等差数列{}n b 的通项公式为()()()()()121321111222n b b n b b n n b b b =+--+---+; (3)证明:若数列{}n c 是k 阶等差数列,则{}n c 的通项公式是n 的k 次多项式,即0k in i i c n λ==∑(其中i λ(01i k =L ,,,)为常实数)。
厦门第一中学2023-2024学年高一下学期第一次适应性训练(月考)数学试题

厦门第一中学2023-2024学年高一下学期第一次适应性训练(月考)数学试题一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.若,,则等于()A. B.C. D.2.中,“”是“”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件3.在中,若,则的最大角与最小角之和是()A. B. C. D.4.在平行四边形中,,,设,,则()A. B.C. D.5.某学生为了测量学校旗杆的高度,在水平地面上一点处的测得仰角为,沿旗杆底部与处的直线向旗杆方向前进米的处测得的仰角为,那么旗杆高为()A. B. C. D.6.已知,,是平面直角坐标系内的三点,若,,则的面积为()A.15B.12C.D.67.在中,,,,则下列各式一定成立的是()A. B.C. D.8.在中,,,,是垂心,若,其中,,则动点的轨迹所覆盖图形的面积为()A.21B.14C.D.7二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,有选错的得0分,部分选对的得部分.9.某人向正东方向走了后向右转了,然后沿新方向走了,结果离出发点恰好,那么x的值是()A. B. C.3 D.610.在平面直角坐标系中,向量,如图所示,则()A.B.C.在方向上的投影向量的模为1D.存在实数,使得与共线11.在中,D,E分别是BC,AC的中点,且,则()A.面积最大值是6B.周长可能是14C.不可能是5D.二、填空题:本题共3小题,每小题5分,共15分.12.已知,,,则向量与的夹角为______.13.已知的内角、、的对边分别为、、,若的面积为,,则该三角形的外接圆直径________.14.已知非零平面向量,,满足:,的夹角为,与的夹角为,,,则的取值范围是______.三、解答题:解答应写出文字说明、证明过程或演算步骤.15.已知,,,,且.(1)求的值;(2)求向量与向量夹角的余弦.16.在中,角A、B、C对边分别为a、b、c,已知.(1)求的值;(2)求b的值.17.如图,A、B是海面上位于东西方向相距海里的两个观测点,现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距海里的C点的救援船立即前往营救,其航行速度为30海里/小时,试求:(1)轮船D与观测点B距离;(2)救援船到达D点所需要的时间.18.在中,角,,的对边分别为,,,若.(1)求角;(2)若,点满足,①求证::②求的最大值.19.在中,角,,的对边分别为,,,点,,分别位于,,所在直线上,满足,,(,,).(1)如图1,若三角形是边长为3的正三角形,且,求;(2)如图2,若,,交于一点,①求证:②若,,,,求.。
福建省厦门一中2020年中考数学模拟试卷(5月份)(含答案解析)
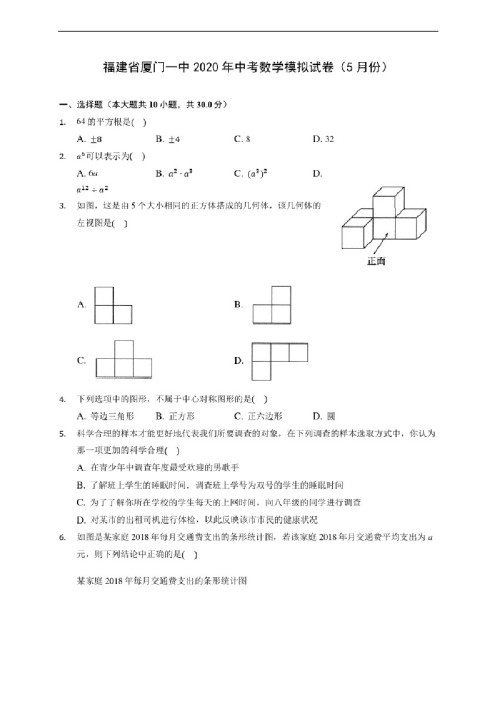
福建省厦门一中2020年中考数学模拟试卷(5月份)一、选择题(本大题共10小题,共30.0分)1.64的平方根是()A.±8B.±4C.8D.322./可以表示为(:1A.6uB. a2-a3C. (a3)2D.小2*23.如图,这是由5个大小相同的正方体搭成的几何体,该几何体的左视图是()正面B L0D•开4.下列选项中的图形,不属于中心对称图形的是()A.等边三角形B,正方形 C.正六边形D,圆5.科学合理的样本才能更好地代表我们所要调查的对象,在下列调查的样本选取方式中,你认为那一项更加的科学合理()A. 在青少年中调查年度最受欢迎的男歌手B. 了解班上学生的睡眠时间.调查班上学号为双号的学生的睡眠时间C.为了了解你所在学校的学生每天的上网时间,向八年级的同学进行调查D. 对某市•的出租司机进行体检,以此反映该市市民的健康状况6.如图是某家庭2018年每月交通费支出的条形统计图,若该家庭2018年月交通费平均支出为u元,则下列结论中正确的是()某家庭2018年每月交通费支出的条形统计图A. 200 < a< 220B. 220 < a < 240C. 240 < a < 260D. 260 < a < 2807. 如图allb.则直线i 到直线力的距离是()A. 13B. 14C. 17D. 258. 方程2x 2-5x-3 = 0根的情况是()A.方程有两个不相等的实根B.方程有两个相等的实根C.方程没有实根D.无法判断9. 如图.在下列四个选项中,能判定四边形ABCD 是平行四边形的是()A. AB = CD. AD//BCC. AB//DC. AD = BCD. AB//DC. AB = DC10.若一元二次方程ax 2 +bx + c = Q 的两根为勺=一3,x 2 =则二次函= ax 图象的对称轴是()A.直线% = -2 B.直线x = 2C.),轴D.不能确定+ * + c 的二、填空题(本大题共6小题,共18.0分)11. 不等式2x-8>。
2020-2021厦门市一中小学数学小升初第一次模拟试卷带答案
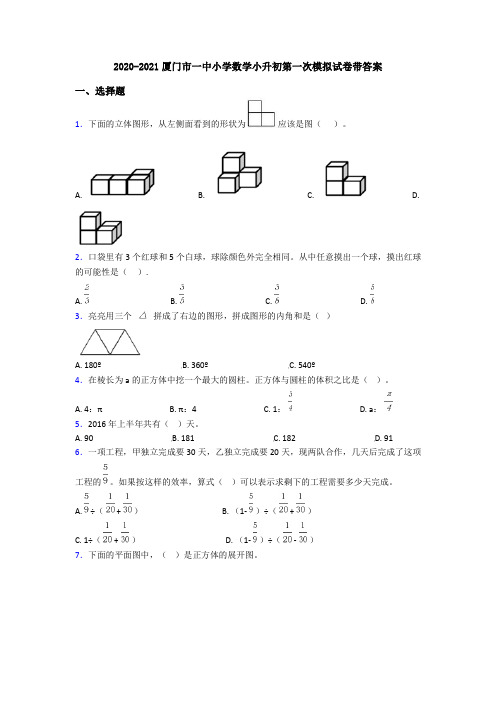
2020-2021厦门市一中小学数学小升初第一次模拟试卷带答案一、选择题1.下面的立体图形,从左侧面看到的形状为应该是图()。
A. B. C. D.2.口袋里有3个红球和5个白球,球除颜色外完全相同。
从中任意摸出一个球,摸出红球的可能性是().A. B. C. D.3.亮亮用三个拼成了右边的图形,拼成图形的内角和是()A. 180ºB. 360ºC. 540º4.在棱长为a的正方体中挖一个最大的圆柱。
正方体与圆柱的体积之比是()。
A. 4:πB. π:4C. 1:D. a:5.2016年上半年共有()天。
A. 90B. 181C. 182D. 916.一项工程,甲独立完成要30天,乙独立完成要20天,现两队合作,几天后完成了这项工程的。
如果按这样的效率,算式()可以表示求剩下的工程需要多少天完成。
A. ÷( + )B. (1- )÷( + )C. 1÷( + )D. (1- )÷( - )7.下面的平面图中,()是正方体的展开图。
A. B. C.D.8.用42cm长的铁丝围一个长方形,长和宽的比是2:1,这个长方形的长是()A. 14cmB. 7cmC. 28cmD. 21cm9.一个两位数,十位上的数字是a,个位上的数字是8,这个两位数表示()A. a+8B. 10a+8C. 8a10.下面三幅图中,图()表示6× 的意思。
A.B.C.11.学校有一块正方形草坪,正好能容纳100个小朋友做广播操。
这块草坪的面积大约是()。
A. 150平方米B. 1500平方分米C. 1500平方米12.一件商品原价100元,涨价10%后,再降价10%,现价()原价。
A. 高于B. 低于C. 等于D. 无法比较二、填空题13.一个圆柱的底面直径是2cm,高是3cm,它的侧面积是________m²。
14.一个直角三角形两个锐角度数的比是1:4,则这两个锐角分别是________度和________度。
【2020-2021自招】福建省厦门第一中学初升高自主招生数学模拟试卷【4套】【含解析】

第一套:满分150分2020-2021年福建省厦门第一中学初升高自主招生数学模拟卷一.选择题(共8小题,满分48分)1.(6分)如图,△ABC中,D、E是BC边上的点,BD:DE:EC=3:2:1,M在AC边上,CM:MA=1:2,BM交AD,AE于H,G,则BH:HG:GM=()A.3:2:1 B.5:3:1C.25:12:5 D.51:24:102.(6分)若关于x的一元二次方程(x-2)(x-3)=m有实数根x1,x2,且x1≠x2,有下列结论:①x1=2,x2=3;②1> ;m4③二次函数y=(x-x1)(x-x2)+m的图象与x轴交点的坐标为(2,0)和(3,0).其中,正确结论的个数是【】A.0B.1C.2D.33.(6分)已知长方形的面积为20cm2,设该长方形一边长为ycm,另一边的长为xcm,则y与x之间的函数图象大致是()A. B. C. D.4.(6分)如图,在平面直角坐标系中,⊙O 的半径为1,则直线y x 2=-与⊙O 的位置关系是( )A .相离B .相切C .相交D .以上三种情况都有可能 5.(6分)若一直角三角形的斜边长为c ,内切圆半径是r ,则内切圆的面积与三角形面积之比是( )A .B .C .D .6.(6分)如图,Rt △ABC 中,BC=,∠ACB=90°,∠A=30°,D 1是斜边AB 的中点,过D 1作D 1E 1⊥AC 于E 1,连结BE 1交CD 1于D 2;过D 2作D 2E 2⊥AC 于E 2,连结BE 2交CD 1于D 3;过D 3作D 3E 3⊥AC 于E 3,…,如此继续,可以依次得到点E 4、E 5、…、E 2013,分别记△BCE 1、△BCE 2、△BCE 3、…、△BCE 2013的面积为S 1、S 2、S 3、…、S 2013.则S 2013的大小为( ) A.31003 B.320136 C.310073 D.67147.(6分)抛物线y=ax 2与直线x=1,x=2,y=1,y=2围成的正方形有公共点,则实数a 的取值范围是( )A .≤a ≤1B .≤a ≤2C .≤a ≤1D .≤a ≤28.(6分)如图,矩形ABCD 的面积为5,它的两条对角线交于点O 1,以AB ,AO 1为两邻边作平行四边形ABC 1O 1,平行四边形ABC 1O 1的对角线交BD 于点02,同样以AB ,AO 2为两邻边作平行四边形ABC 2O 2.…,依此类推,则平行四边形ABC 2009O 2009的面积为( )A.n 25 B.n 22 C.n 31 D.n 23二.填空题:(每题7分,满分42分)9.(7分)方程组的解是 .10.(7分)若对任意实数x 不等式ax >b 都成立,那么a ,b 的取值范围为 .11.(7分)如图,圆锥的母线长是3,底面半径是1,A 是底面圆周上一点,从A 点出发绕侧面一周,再回到A 点的最短的路线长是 .12.(7分)有一张矩形纸片ABCD ,AD=9,AB=12,将纸片折叠使A 、C 两点重合,那么折痕长是 .13.(7分)设﹣1≤x ≤2,则|x ﹣2|﹣|x|+|x+2|的最大值与最小值之差为 .14.(7分)两个反比例函数y=,y=在第一象限内的图象如图所示.点P 1,P 2,P 3、…、P 2007在反比例函数y=上,它们的横坐标分别为x 1、x 2、x 3、…、x 2007,纵坐标分别是1,3,5…共2007个连续奇数,过P 1,P 2,P 3、…、P 2007分别作y 轴的平行线,与y=的图象交点依次为Q 1(x 1′,y 1′)、Q 1(x 2′,y 2′)、…、Q 2(x 2007′,y 2007′),则|P 2007Q 2007|= .三.解答题:(每天12分,满分60分)15.(12分).已知正实数,,x y z 满足:1xy yz zx ++≠ ,且222222(1)(1)(1)(1)(1)(1)4x y y z z x xy yz zx------++= .(1) 求111xy yz zx++的值. (2) 证明:9()()()8()x y y z z x xyz xy yz zx +++≥++.16.(12分)如图,ABC △是等腰直角三角形,CA CB =,点N 在线段AB 上(与A 、B 不重合),点M 在射线BA 上,且45NCM ∠=︒。
新课标2020届高中招生适应性考试(含答案) 数学测试卷.docx

新课标2020届高中招生适应性考试(含答案)数学测试卷注意事项:1.本试卷满分120分,考试时间120分钟.2.答题前,务必将自己的姓名、准考证号填写在答题卡规定的位置上.3.答选择题时,必须使用2B铅笔将答题卡上对应的答案标号涂黑,如需改动,用橡皮擦擦干净,再选涂其它答案标号;答非选择题时,必须使用0.5毫米黑色签字笔,将答案书写在答题卡规定的位置上;所有题目必须在答题卡上作答,在试卷上答题无效.4.不允许使用计算器进行运算,凡无精确度要求的题目,结果均保留准确值.5.凡作图题或辅助线均用签字笔画图.第Ⅰ卷(选择题共36分)一、选择题:本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是正确的,请将正确选项的字母填涂在答题卡上相应的位置.1.﹣3的相反数是A.3 B.﹣3 C.D.﹣2.下列计算正确的是A.a3+a3=2a3B.a3•a2=a6C.a6÷a2=a3D.(a3)2=a53.根据市统计局发布的统计数据显示,2018年全市生产总值为138000000000元,按可比价格计算,比上年增长7.3%,数据138000000000元用科学记数法表示为A.1.38×1010元B.1.38×1011元C.1.38×1012元D.0.138×1012元4.如图,AB∥CD,点E在线段BC上,CD=CE.若∠ABC=30°,则∠D为A.85°B.75°C.60°D.30°5.由五个大小相同的正方体组成的几何体如图所示,那么它的主视图是A.B.C. D.6.如图,点A,B,C在⊙O上,∠ACB=35°,则∠AOB的度数是A.75°B.70°C.65°D.35°7.甲、乙两班举行电脑汉字输入比赛,参赛学生每分钟输入汉字个数的统计结果如下表:某同学分析上表后得出如下结论:(1)甲、乙两班学生的成绩平均成绩相同;(2)乙班优秀的人数多于甲班优秀的人数(每分钟输入汉字≥150个为优秀);(3)甲班成绩的波动比乙班大.上述结论中,正确的是A.①②B.②③C.①③D.①②③8.某文具店一本练习本和一支水笔的单价合计为3元,小妮在该店买了20本练习本和10支水笔,共花了36元.如果设练习本每本为x元,水笔每支为y元,那么根据题意,下列方程组中,正确的是A.B.C.D.9.若正多边形的一个外角是60︒,则该正多边形的内角和为A.360︒B.540︒C.720︒D.900︒10.如图,将矩形ABCD沿GH折叠,点C落在点Q处,点D落在AB边上的点E处,若∠AEG=58°,则∠GHC等于A.112°B.110°C.108°D.106°11.如图,AB是圆锥的母线,BC为底面半径,已知BC=6cm,圆锥的侧面积为15πcm2,则sin∠ABC的值为A.B.C .D .12.如图,△ABC 是等边三角形,△ABD 是等腰直角三角形,∠BAD =90°,AE ⊥BD 于点E ,连CD 分别交AE ,AB 于点F ,G ,过点A 作AH ⊥CD 交BD 于点H .则下列结论:①∠ADC =15°;②AF =AG ;③AH =DF ;④△AFG ∽△CBG ;⑤AF =(﹣1)EF .其中正确结论的个数为 A .5 B .4C .3D .2第Ⅱ卷(非选择题 共84分)二、填空题(本大题共6小题,每小题3分,共18分.请将正确答案直接填在答题卡上相应的位置上).13.分解因式:3x 2﹣27= .14.数据5,5,4,2,3,7,6的中位数是 . 15.如图,在△ABC 和△DEF 中,点B ,F ,C ,E 在同一直线上,BF=CE ,AB ∥DE ,请添加一个条件,使△ABC ≌△DEF ,这个添加的条件可以是 (只需写一个,不添加辅助线).16.星期天,小明上午8:00从家里出发,骑车到图书馆去借书,再骑车回到家.他离家的距离y (千米)与时间t (分钟)的关系如图所示,则上午8:45小明离家的距离是 千米.17.如图,在△ABC 中,AC=BC=2,AB=1,将它沿AB 翻折 得到△ABD ,点P 、E 、F 分别为线段AB 、AD 、DB 的任意点, 则PE +PF 的最小值是 .18. 如图,过原点的直线交双曲线xy 33于A 、B 以AB 为边的等边三角形ABC 交x 轴于D ,D 是AC 中点, 19. 则C 点坐标为 .三、解答题:本大题共8小题,共66分.请把解答过程写在答题卡上相应的位置上.19.(6分)计算:|﹣2|﹣+23﹣(1﹣π)0.20.(6)解不等式组:,并在数轴上表示其解集.21.(8分)设x1,x2是关于x的方程x2-4x+k+1=0的两个实数根,是否存在实数k,使得x1x2>x1+x2成立?请说明理由.22.(8分)如图,在数学活动课上,小丽为了测量校园内旗杆AB的高度,站在教学楼的C处测得旗杆底端B的俯角为45°,测得旗杆顶端A的仰角为30°.已知旗杆与教学楼的距离BD=9m,请你帮她求出旗杆的高度(结果保留根号).23.(9分)杨老师为了了解所教班级学生课后复习的具体情况,对本班部分学生进行了一个月的跟踪调查,然后将调查结果分成四类:A:优秀;B:良好;C:一般;D:较差.并将调查结果绘制成以下两幅不完整的统计图.请根据统计图解答下列问题:(1)本次调查中,杨老师一共调查了名学生,其中C类女生有名,D类男生有名;(2)补全上面的条形统计图和扇形统计图;(3)在此次调查中,小平属于D类.为了进步,她请杨老师从被调查的A类学生中随机选取一位同学,和她进行“一帮一”的课后互助学习.请求出所选的同学恰好是一位女同学的概率.24.(9分)某商场购进甲、乙两种商品,甲种商品共用了2000元,乙种商品共用了2400元.已知乙种商品每件进价比甲种商品每件进价多8元,且购进的甲、乙两种商品件数相同.(1)求甲、乙两种商品的每件进价;(2)该商场将购进的甲、乙两种商品进行销售,甲种商品的销售单价为60元,乙种商品的销售单价为88元,销售过程中发现甲种商品销量不好,商场决定:甲种商品销售一定数量后,将剩余的甲种商品按原销售单价的七折销售;乙种商品销售单价保持不变.要使两种商品全部售完后共获利不少于2460元,问甲种商品按原销售单价至少销售多少件? 25.(9分)如图,在△ABC 中,∠ACB=90°,AC=BC ,D 是AB 边上一点(点D 与A ,B 不重合),连结CD ,将线段CD 绕点C 按逆时针方向旋转90°得到线段CE ,连结DE 交BC 于点F ,连接BE .(1)求证:△ACD ≌△BCE ;(2)当AD=1,DB=3时,求CF 的长.26.(11分)如图,在平面直角坐标系中,直线y =x +2与x 轴交于点A ,与y 轴交于点C ,抛物线y =x 2+bx +c 经过A 、C 两点,与x 轴的另一交点为点B .(1)求抛物线的函数表达式;(2)点D 为直线AC 上方抛物线上一动点;①连接BC 、CD ,设直线BD 交线段AC 于点E ,△CDE 的面积为S 1,△BCE 的面积为S 2,求的最大值;②过点D 作DF ⊥AC ,垂足为点F ,连接CD ,是否存在点D ,使得△CDF 与△ABC 相似,若存在,直接写出点D 的横坐标;若不存在,请说明理由.121212S S九年级数学试题答案及评分意见一、选择题 AABB CBDB CDBB 二、填空题13.3(x +3)(x ﹣3);14.5;15.AB=ED ;16.1.5;17.415;18.)3,33( . 三、19.(6分)计算:|﹣2|﹣+23﹣(1﹣π)0.解:原式=2﹣3+8﹣1…………………………………4分=6.…………………………………6分20.(6)解不等式组:,并在数轴上表示其解集.解:解不等式①,得:x ≤2;…………………………………1分 解不等式②,得:x >1,…………………………………2分 ∴不等式组的解集为:1<x ≤2.…………………………………4分 将其表示在数轴上,如图所示.…………………………………6分21.解:不存在.………………………………………………………………1分理由:由题意得Δ=16-4(k +1)≥0,解得k ≤3. ………………………………4分 ∵x 1,x 2是一元二次方程的两个实数根,∴x 1+x 2=4,x 1x 2=k +1,……………5分 由x 1x 2>x 1+x 2得k +1>4,∴k >3,………………………………7分 ∴不存在实数k 使得x 1x 2>x 1+x 2成立………………………………8分 22.解:在Rt △ACF 中, ∵tan ∠ACF=,∴tan30°=,∴=,∴AF=3m ,…………………………………3分在Rt △BCD 中,∵∠BCD=45°,∴BD=CD=9m ,……………………6分 ∴AB=AD +BD=3+9(m ).…………………………………8分23.解:(1)20、2、1;…………………………………3分(2)补全图形如下:……………………………………………………………………5分(3)因为A类的3人中,女生有2人,所以所选的同学恰好是一位女同学的概率为.…………………………………9分24.解:(1)设甲种商品的每件进价为x元,则乙种商品的每件进价为(x+8)元.………1分根据题意,得,=,…………………………………2分解得x=40.经检验,x=40是原方程的解.…………………………………3分答:甲种商品的每件进价为40元,乙种商品的每件进价为48元;…………………4分(2)甲乙两种商品的销售量为=50.…………………………………5分设甲种商品按原销售单价销售a件,则(60﹣40)a+(60×0.7﹣40)(50﹣a)+(88﹣48)×50≥2460,……………………7分解得a≥20.…………………………………8分答:甲种商品按原销售单价至少销售20件.…………………………………9分25.(9分)如图,在△ABC中,∠ACB=90°,AC=BC,D是AB边上一点(点D与A,B不重合),连结CD,将线段CD绕点C按逆时针方向旋转90°得到线段CE,连结DE交BC于点F,连接BE.(1)求证:△ACD≌△BCE;(2)当AD=1,DB=3时,求CF的长.解:(1)由题意可知:CD=CE ,∠DCE=90°,…………………………………2分 ∵∠ACB=90°,∴∠ACD=∠ACB ﹣∠DCB , ∠BCE=∠DCE ﹣∠DCB ,∴∠ACD=∠BCE ,…………………………………4分 在△ACD 与△BCE 中,∴△ACD ≌△BCE (SAS )…………………………………5分 (2)过C 作CG ꓕAB 于G ,…………………………………6分 ∵在△ABC 中,∠ACB=90°,AC=BC ,AD=1,DB=3, ∴CG=2,DG=1∴CD=CE=5,BC=22,…………………………………7分 易证△ECF 相似于△BCE , 可得ECCFBC EC =, 可得425=CF …………………………………9分 26.…………………………………3分G(2)①如图,令y =0, ∴-12x 2-32x +2=0, ∴x 1=-4,x 2=1, ∴B (1,0),过D 作DM ⊥x 轴交AC 于M ,过B 作BN ⊥x 轴交于AC 于N , ∴DM ∥BN , ∴△DME ∽△BNE , ∴12S DE DMS BE BN==, 设D (a ,-12a 2-32a +2), ∴M (a ,12a +2), ∵B (1.0), ∴N (1,52), ∴22121214225552a a S DM =(a )S BN--==-++; ∴当a =2时,12S S 的最大值是45;…………………………………7分(3))825,23();2,3(21--D D …………………………………11分11数学试卷第页,共5页。
【初升高】福建省厦门第一中学2020中考提前自主招生数学模拟试卷(9套)附解析

重点高中提前招生模拟考试数学试卷学校:___________姓名:___________班级:___________考号:___________注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上一、选择题1.不等式的解集是()A.﹣<x≤2 B.﹣3<x≤2 C.x≥2 D.x<﹣32.一个质地均匀的正方体骰子的六个面上分别刻有1到6的点数,将骰子抛掷两次,掷第一次,将朝上一面的点数记为x,掷第二次,将朝上一面的点数记为y,则点(x,y)落在直线y=﹣x+5上的概率为()A.B.C.D.3.如图所示,在正方形铁皮中,剪下一个圆和一个扇形,使余料尽量少.用圆做圆锥的底面,用扇形做圆锥的侧面,正好围成一个圆锥,若圆的半径为r,扇形的半径为R,那么()A.R=2r B.R=r C.R=3r D.R=4r4.如图所示,在边长为a的正方形中,剪去一个边长为b的小正方形(a>b),将余下部分拼成一个梯形,根据两个图形阴影部分面积的关系,可以得到一个关于a、b的恒等式为()A.(a﹣b)2=a2﹣2ab+b2B.(a+b)2=a2+2ab+b2C.a2﹣b2=(a+b)(a﹣b)D.a2+ab=a(a+b)5.若直线x+2y=2m与直线2x+y=2m+3(m为常数)的交点在第四象限,则整数m的值为()A.﹣3,﹣2,﹣1,0 B.﹣2,﹣1,0,1 C.﹣1,0,1,2 D.0,1,2,3 二、填空题(每小题4分,共24分)6.定义新运算:a⊕b=,则函数y=3⊕x的图象大致是.7.|π﹣3.14|+sin30°+3.14﹣8=.8.函数y=的自变量x的取值范围是.9.将边长为a的正三角形各边三等分,以这六个分点为顶点构成一个正六边形,则这个正六边形的面积为.10.如图,AB是⊙O的直径,C,D为⊙0上的两点,若∠CDB=30°,则∠ABC的度数为,cos∠ABC=.11.已知实数x,y满足x2+3x+y﹣3=0,则x+y的最大值为.12.古希腊数学家把数1,3,6,10,15,21,…叫做三角形数,它有一定的规律.若把第一个数记为a1,第二数记为a2,…,第n个数记为a n.计算a2﹣a1,a3﹣a2,a4﹣a3,…,由此推算a10﹣a9=,a2012=.三.解答题:(共52分)13.先化简:÷﹣,然后在0,1,2,3中选一个你认为合格的a值,代入求值.1012•桃源县校级自主招生)关于x的一元二次议程x2﹣x+p+1=0有两个实数根x1,x2.(1)求p的取值范围.(2)[1+x1(1﹣x2)][1+x2(1﹣x1)]=9,求p的值.15.某服装厂批发应夏季T恤衫,其单价y(元)与批发数量x(件)(x为正整数)之间的函数关系如图所示,(1)直接写出y与x的函数关系式;(2)一个批发商一次购进250件T恤衫,所花的钱数是多少元?(其他费用不计);(3)若每件T恤衫的成本价是20元,当100<x≤400件,(x为正整数)时,求服装厂所获利润w (元)与x(件)之间的函数关系式,并求一次批发多少件时所获利润最大,最大利润是多少?16.如图,抛物线y=ax2+c(a>0)经过梯形ABCD的四个顶点,梯形的底AD在x轴上,A点到原点的距离为2,梯形的高为3,C点到y轴的距离为1,(1)求抛物线的解析式;(2)点M为y轴上的任意一点,求点M到A,B两点的距离之和的最小值及此时点M的坐标;(3)在第(2)的结论下,抛物线上的P的使S△PAD=S△ABM成立,求点P的坐标.1012•桃源县校级自主招生)如图所示,四边形OABC是矩形,点A、C的坐标分别为(3,0),(0,1),点D是线段BC上的动点(与端点B、C不重合),过点D作直线y=﹣+b交折线OAB于点E.记△ODE的面积为S.(1)当点E在线段OA上时,求S与b的函数关系式;并求出b的范围;(2)当点E在线段AB上时,求S与b的函数关系式;并求出b的范围;(3)当点E在线段OA上时,若矩形OABC关于直线DE的对称图形为四边形OA1B1C1,试探究OA1B1C1与矩形OABC的重叠部分的面积是否发生变化?若不变,求出该重叠部分的面积;若改变,请说明理由.参考答案与试题解析一、选择题1.不等式的解集是()A.﹣<x≤2 B.﹣3<x≤2 C.x≥2 D.x<﹣3考点:解一元一次不等式组.分析:先解不等式组中的每一个不等式的解集,再利用求不等式组解集的口诀“大小小大中间找”来求不等式组的解集.解答:解:由①得:x>﹣3,由②得:x≤2,所以不等式组的解集为﹣3<x≤2.故选B.点评:解不等式组是考查学生的基本计算能力,求不等式组解集的时候,可先分别求出组成不等式组的各个不等式的解集,然后借助数轴或口诀求出所有解集的公共部分.2.一个质地均匀的正方体骰子的六个面上分别刻有1到6的点数,将骰子抛掷两次,掷第一次,将朝上一面的点数记为x,掷第二次,将朝上一面的点数记为y,则点(x,y)落在直线y=﹣x+5上的概率为()A.B.C.D.考点:列表法与树状图法;一次函数图象上点的坐标特征.分析:列举出所有情况,看落在直线y=﹣x+5上的情况占总情况的多少即可.解答:解:共有36种情况,落在直线y=﹣x+5上的情况有(1,4)(2,3)(3,2)(4,1)4种情况,概率是,故选C.1 2 3 4 5 61 (1,1)(1,2)(1,3)(1,4)(1,5)(1,6)2 (2,1)(2,2)(2,3)(2,4)(2,5)(2,6)3 (3,1)(3,2)(3,3)(3,4)(3,5)(3,6)4 (4,1)(4,2)(4,3)(4,4)(4,5)(4,6)5 (5,1)(5,2)(5,3)(5,4)(5,5)(5,6)6 (6,1)(6,2)(6,3)(6,4)(6,5)(6,6)点评:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=,注意本题是放回实验.3.如图所示,在正方形铁皮中,剪下一个圆和一个扇形,使余料尽量少.用圆做圆锥的底面,用扇形做圆锥的侧面,正好围成一个圆锥,若圆的半径为r,扇形的半径为R,那么()A.R=2r B.R=r C.R=3r D.R=4r考点:圆锥的计算;弧长的计算.专题:压轴题.分析:让扇形的弧长等于圆的周长即可.解答:解:根据扇形的弧长等于圆的周长,∴扇形弧长等于小圆的周长,即:=2πr,解得R=4r,故选D.点评:考查了扇形的弧长公式;圆的周长公式;用到的知识点为:圆锥的弧长等于底面周长.4.如图所示,在边长为a的正方形中,剪去一个边长为b的小正方形(a>b),将余下部分拼成一个梯形,根据两个图形阴影部分面积的关系,可以得到一个关于a、b的恒等式为()A.(a﹣b)2=a2﹣2ab+b2B.(a+b)2=a2+2ab+b2C.a2﹣b2=(a+b)(a﹣b)D.a2+ab=a(a+b)考点:平方差公式的几何背景.专题:计算题.分析:可分别在正方形和梯形中表示出阴影部分的面积,两式联立即可得到关于a、b的恒等式.解答:解:正方形中,S阴影=a2﹣b2;梯形中,S阴影=(2a+2b)(a﹣b)=(a+b)(a﹣b);故所得恒等式为:a2﹣b2=(a+b)(a﹣b).故选:C.点评:此题主要考查的是平方差公式的几何表示,运用不同方法表示阴影部分面积是解题的关键.5.若直线x+2y=2m与直线2x+y=2m+3(m为常数)的交点在第四象限,则整数m的值为()A.﹣3,﹣2,﹣1,0 B.﹣2,﹣1,0,1 C.﹣1,0,1,2 D.0,1,2,3考点:两条直线相交或平行问题.专题:计算题;压轴题.分析:由直线x+2y=2m与直线2x+y=2m+3(m为常数)的交点在第四象限,则交点坐标的符号为(+,﹣),解关于x、y的方程组,使x>0,y<0,即可求得m的值.解答:解:由题意得,解得,∵直线x+2y=2m与直线2x+y=2m+3(m为常数)的交点在第四象限,∴,解得:﹣3,又∵m的值为整数,∴m=﹣2,﹣1,0,1,故选B.点评:考查了平面直角坐标系中点的符号,是一道一次函数综合性的题目,是中档题.二、填空题(每小题4分,共24分)6.定义新运算:a⊕b=,则函数y=3⊕x的图象大致是.考点:一次函数的图象;反比例函数的图象.专题:新定义.分析:根据题意可得y=3⊕x=,再根据反比例函数的性质可得函数图象所在象限和形状,进而得到答案.解答:解:由题意得y=3⊕x=,当x≥3时,y=2;当x<3且x≠0时,y=﹣,图象如图:,故答案为:点评:此题主要考查了反比例函数的图象性质和一次函数的图象性质,要掌握它们的性质才能灵活解题.7.|π﹣3.14|+sin30°+3.14﹣8=π.考点:实数的运算;特殊角的三角函数值.专题:计算题.分析:原式第一项利用绝对值的代数意义化简,第二项利用特殊角的三角函数值计算,最后一项利用负整数指数幂法则计算即可得到结果.解答:解:原式=π﹣3.14++3.14﹣=π,故答案为:π点评:此题考查了实数的运算,熟练掌握运算法则是解本题的关键.8.函数y=的自变量x的取值范围是x<﹣1或x≥4.考点:函数自变量的取值范围.分析:根据被开方数为非负数和分母不能为0计算即可.解答:解:由题意得,x2﹣3x﹣4≥0,x+1≠0,解得,x<﹣1或x≥4,故答案为:x<﹣1或x≥4.点评:本题考查的是函数自变量的范围,一般从三个方面考虑:(1)当函数表达式是整式时,自变量可取全体实数;(2)当函数表达式是分式时,考虑分式的分母不能为0;(3)当函数表达式是二次根式时,被开方数为非负数.9.将边长为a的正三角形各边三等分,以这六个分点为顶点构成一个正六边形,则这个正六边形的面积为a2.考点:正多边形和圆.分析:由于正三角形各边三等分,就把整个三角形平均分成9个小正三角形,以这六个分点为顶点构成一个正六边形正好相当于6个小正三角形的面积.解答:解:如图所示:∵新的正六边形有三个顶点在正三角形的三边上,且是三边的等分点,∴连接正三角形的顶点与它对边的中点,可以看出新的正六边形的面积是六个小正三角形的面积之和,∵边长为a的正三角形各边三等分,∴小正三角形的边长为a,∴每个小正三角形的面积是×a×=a×a=a2,∴新的正六边形的面积=a2×6=a2;故答案为:a2.点评:此题考查了正三角形的性质、正三角形面积的计算方法;熟练掌握正三角形的性质,并能进行推理计算是解决问题的关键.10.如图,AB是⊙O的直径,C,D为⊙0上的两点,若∠CDB=30°,则∠ABC的度数为60°,cos∠ABC=.考点:圆周角定理;特殊角的三角函数值.分析:由于AB是⊙O的直径,由圆周角定理可知∠ACB=90°,则∠A和∠ABC互余,欲求∠ABC需先求出∠A的度数,已知了同弧所对的圆周角∠CDB的度数,则∠A=∠CDB,由此得解.解答:解:连接AC,∵AB是⊙O的直径,∴∠ACB=90°,即∠A+∠ABC=90°;又∵∠A=∠CDB=30°,∴∠ABC=90°﹣∠A=60°,∴cos∠ABC=.故答案为:60°.点评:此题主要考查了圆周角定理及其推论,半圆(弧)和直径所对的圆周角是直角,同弧所对的圆周角相等,还考查了三角函数,掌握圆周角定理是解题的关键.11.已知实数x,y满足x2+3x+y﹣3=0,则x+y的最大值为4.考点:二次函数的应用.专题:压轴题.分析:将函数方程x2+3x+y﹣3=0代入x+y,把x+y表示成关于x的函数,根据二次函数的性质求得最大值.解答:解:由x2+3x+y﹣3=0得y=﹣x2﹣3x+3,把y代入x+y得:x+y=x﹣x2﹣3x+3=﹣x2﹣2x+3=﹣(x+1)2+4≤4,∴x+y的最大值为4.故答案为:4.点评:本题考查了二次函数的性质及求最大值的方法,即完全平方式法.12.古希腊数学家把数1,3,6,10,15,21,…叫做三角形数,它有一定的规律.若把第一个数记为a1,第二数记为a2,…,第n个数记为a n.计算a2﹣a1,a3﹣a2,a4﹣a3,…,由此推算a10﹣a9=10,a2012=2025078.考点:规律型:数字的变化类.分析:先计算a2﹣a1=3﹣1=2;a3﹣a2=6﹣3=3;a4﹣a3=10﹣6=4,则a10﹣a9=10,a2=1+2,a3=1+2+3,a4=1+3+4,即第n个三角形数等于1到n的所有整数的和,然后计算n=2012的a的值.解答:解:∵a2﹣a1=3﹣1=2;a3﹣a2=6﹣3=3;a4﹣a3=10﹣6=4,∴a10﹣a9=10∵a2=1+2,a3=1+2+3,a4=1+2+3+4,…∴a2012=1+2+3+4+…+2012==2025078.故答案为:10,2025078.点评:本题考查了规律型:数字的变化类,通过从一些特殊的数字变化中发现不变的因素或按规律变化的因素,然后推广到一般情况是解答此题的关键.三.解答题:(共52分)13.先化简:÷﹣,然后在0,1,2,3中选一个你认为合格的a值,代入求值.考点:分式的化简求值.分析:先根据分式混合运算的法则把原式进行化简,再选出合适的x的值代入进行计算即可.解答:解:原式=•+a=a+a=2a.当a=2时,原式=4a.点评:本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.1012•桃源县校级自主招生)关于x的一元二次议程x2﹣x+p+1=0有两个实数根x1,x2.(1)求p的取值范围.(2)[1+x1(1﹣x2)][1+x2(1﹣x1)]=9,求p的值.考点:根的判别式;根与系数的关系.分析:(1)根据题意得出△≥0,求出即可;(2)根据根与系数的关系得出x1+x2=1,x1•x2=p+1,整理后得出(1﹣x1•x2)2+(x1+x2)(1﹣x1•x2)+x1•x2=9,代入求出即可.解答:解:(1)△=(﹣1)2﹣4(p+1)=﹣3﹣4p,当﹣3﹣4p≥0,即p≤﹣时,方程有两个实数根,即p的取值范围是p≤﹣;(2)根据根与系数的关系得:x1+x2=1,x1•x2=p+1,∵[1+x1(1﹣x2)][1+x2(1﹣x1)]=9,∴(1﹣x1•x2)2+(x1+x2)(1﹣x1•x2)+x1•x2=9,∴[1﹣(p+1)]2+1×[1﹣(p+1)]+(p+1)=9,解得:p±2,∵p≤﹣,∴p=﹣2.点评:本题考查了根与系数的关系,根的判别式的应用,能正确利用知识点进行计算是解此题的关键,题目比较典型.15.某服装厂批发应夏季T恤衫,其单价y(元)与批发数量x(件)(x为正整数)之间的函数关系如图所示,(1)直接写出y与x的函数关系式;(2)一个批发商一次购进250件T恤衫,所花的钱数是多少元?(其他费用不计);(3)若每件T恤衫的成本价是20元,当100<x≤400件,(x为正整数)时,求服装厂所获利润w (元)与x(件)之间的函数关系式,并求一次批发多少件时所获利润最大,最大利润是多少?考点:二次函数的应用.分析:(1)由题意设出一次函数的解析式,再根据点在直线上待定系数法求出函数解析式;(2)列出总利润的函数表达式,转化为求函数最值问题,最后求出最大利润;(3)根据利润=单件利润×批发数量,列出二次函数表达式,再运用二次函数性质解决最值问题.解答:解:(1)当0≤x<100时,y=60;当x≥100时,设y=kx+b,由图象可以看出过(100,60),(400,40),则,,∴y=;(2)∵250>100,∴当x=250件时,y=﹣×250+=50元,∴批发商一次购进250件T恤衫,所花的钱数是:50×250=12500元;(3)W=(﹣x+﹣20)×x=﹣x2+x=﹣(x﹣350)2+,∴当一次性批发350件时,所获利润最大,最大利润是元.点评:本题考查了待定系数法求函数关系式以及运用函数的性质解决问题,根据题意列出函数表达式是解决问题的关键.16.如图,抛物线y=ax2+c(a>0)经过梯形ABCD的四个顶点,梯形的底AD在x轴上,A点到原点的距离为2,梯形的高为3,C点到y轴的距离为1,(1)求抛物线的解析式;(2)点M为y轴上的任意一点,求点M到A,B两点的距离之和的最小值及此时点M的坐标;(3)在第(2)的结论下,抛物线上的P的使S△PAD=S△ABM成立,求点P的坐标.考点:二次函数综合题.分析:(1)易知A(﹣2,0),C(1,﹣3),将A、C两点的坐标代入y=ax2+c,利用待定系数法即可求出抛物线的解析式;(2)由于A、D关于抛物线对称轴即y轴对称,那么连接BD,BD与y轴的交点即为所求的M点,可先求出直线BD的解析式,即可得到M点的坐标;(3)设直线BC与y轴的交点为N,那么S△ABM=S梯形AONB﹣S△BMN﹣S△AOM,由此可求出△ABM和△PAD的面积;在△PAD中,AD的长为定值,可根据其面积求出P点纵坐标的绝对值,然后代入抛物线的解析式中即可求出P点的坐标.解答:解:(1)由题意可得:A(﹣2,0),C(1,﹣3),∵抛物线y=ax2+c(a>0)经过A、C两点,∴,解得,∴抛物线的解析式为:y=x2﹣4;(2)由于A、D关于抛物线的对称轴(即y轴)对称,连接BD,则BD与y轴的交点即为M点;设直线BD的解析式为:y=kx+b(k≠0),∵B(﹣1,﹣3),D(2,0),∴,解得,∴直线BD的解析式为y=x﹣2,当x=0时,y=﹣2,∴点M的坐标是(0,﹣2);(3)设BC与y轴的交点为N,则有N(0,﹣3),∵M(0,﹣2),B(﹣1,﹣3),∴MN=1,BN=1,ON=3,∴S△ABM=S梯形AONB﹣S△BMN﹣S△AOM=(1+2)×3﹣×1×1﹣×2×2=2,∴S△PAD=S△ABM=2.∵S△PAD=AD•|y P|=2,AD=4,∴|y P|=1.当P点纵坐标为1时,x2﹣4=1,解得x=±,∴P1(,1),P2(﹣,1);当P点纵坐标为﹣1时,x2﹣4=﹣1,解得x=±,∴P3(,﹣1),P4(﹣,﹣1);故存在符合条件的P点,且P点坐标为:P1(,1),P2(﹣,1),P3(,﹣1),P4(﹣,﹣1).点评:此题是二次函数的综合题型,其中涉及到二次函数解析式的确定、函数图象交点及图形面积的求法,轴对称的性质等.当所求图形不规则时,一般要将不规则图形转换为几个规则图形面积的和差来求.1012•桃源县校级自主招生)如图所示,四边形OABC是矩形,点A、C的坐标分别为(3,0),(0,1),点D是线段BC上的动点(与端点B、C不重合),过点D作直线y=﹣+b 交折线OAB于点E.记△ODE的面积为S.(1)当点E在线段OA上时,求S与b的函数关系式;并求出b的范围;(2)当点E在线段AB上时,求S与b的函数关系式;并求出b的范围;(3)当点E在线段OA上时,若矩形OABC关于直线DE的对称图形为四边形OA1B1C1,试探究OA1B1C1与矩形OABC的重叠部分的面积是否发生变化?若不变,求出该重叠部分的面积;若改变,请说明理由.考点:一次函数综合题.专题:压轴题.分析:(1)要表示出△ODE的面积,要分两种情况讨论,①如果点E在OA边上,只需求出这个三角形的底边OE长(E点横坐标)和高(D点纵坐标),代入三角形面积公式即可;(2)如果点E在AB边上,这时△ODE的面积可用长方形OABC的面积减去△OCD、△OAE、△BDE的面积;(3)重叠部分是一个平行四边形,由于这个平行四边形上下边上的高不变,因此决定重叠部分面积是否变化的因素就是看这个平行四边形落在OA边上的线段长度是否变化.解答:解:(1)∵四边形OABC是矩形,点A、C的坐标分别为(3,0),(0,1),∴B(3,1),若直线经过点A(3,0)时,则b=若直线经过点B(3,1)时,则b=若直线经过点C(0,1)时,则b=1①若直线与折线OAB的交点在OA上时,即1<b≤,如图1,此时E(2b,0)∴S=OE•CO=×2b×1=b;(2)若直线与折线OAB的交点在BA上时,即<b<,如图2此时E(3,),D(2b﹣2,1),∴S=S矩﹣(S△OCD+S△OAE+S△DBE)=3﹣[(2b﹣2)×1+×(5﹣2b)•(﹣b)+×3(b﹣)]=b﹣b2,∴S=;(3)如图3,设O1A1与CB相交于点M,OA与C1B1相交于点N,则矩形O1A1B1C1与矩形OABC的重叠部分的面积即为四边形DNEM的面积.由题意知,DM∥NE,DN∥ME,∴四边形DNEM为平行四边形根据轴对称知,∠MED=∠NED,又∠MDE=∠NED,∴∠MED=∠MDE,∴MD=ME,∴平行四边形DNEM为菱形.过点D作DH⊥OA,垂足为H,由题易知,D(2b﹣2,1),对于y=﹣+b,令y=0,得x=2b,则E(2b,0),∴DH=1,HE=2b﹣(2b﹣2)=2,设菱形DNEM的边长为a,则在Rt△DHN中,由勾股定理知:a2=(2﹣a)2+12,∴a=,∴S四边形DNEM=NE•DH=.∴矩形OA1B1C1与矩形OABC的重叠部分的面积不发生变化,面积始终为.点评:本题是一个动态图形中的面积是否变化的问题,看一个图形的面积是否变化,关键是看决定这个面积的几个量是否变化,本题题型新颖,是个不可多得的好题,有利于培养学生的思维能力,但难度较大,具有明显的区分度.重点高中提前招生模拟考试数学试卷学校:___________姓名:___________班级:___________考号:___________注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上一、选择题1.不等式的解集是()A.﹣<x≤2 B.﹣3<x≤2 C.x≥2 D.x<﹣32.一个质地均匀的正方体骰子的六个面上分别刻有1到6的点数,将骰子抛掷两次,掷第一次,将朝上一面的点数记为x,掷第二次,将朝上一面的点数记为y,则点(x,y)落在直线y=﹣x+5上的概率为()A.B.C.D.3.如图所示,在正方形铁皮中,剪下一个圆和一个扇形,使余料尽量少.用圆做圆锥的底面,用扇形做圆锥的侧面,正好围成一个圆锥,若圆的半径为r,扇形的半径为R,那么()A.R=2r B.R=r C.R=3r D.R=4r4.如图所示,在边长为a的正方形中,剪去一个边长为b的小正方形(a>b),将余下部分拼成一个梯形,根据两个图形阴影部分面积的关系,可以得到一个关于a、b的恒等式为()A.(a﹣b)2=a2﹣2ab+b2B.(a+b)2=a2+2ab+b2C.a2﹣b2=(a+b)(a﹣b)D.a2+ab=a(a+b)5.若直线x+2y=2m与直线2x+y=2m+3(m为常数)的交点在第四象限,则整数m的值为()A.﹣3,﹣2,﹣1,0 B.﹣2,﹣1,0,1 C.﹣1,0,1,2 D.0,1,2,3 二、填空题(每小题4分,共24分)6.定义新运算:a⊕b=,则函数y=3⊕x的图象大致是.7.|π﹣3.14|+sin30°+3.14﹣8=.8.函数y=的自变量x的取值范围是.9.将边长为a的正三角形各边三等分,以这六个分点为顶点构成一个正六边形,则这个正六边形的面积为.10.如图,AB是⊙O的直径,C,D为⊙0上的两点,若∠CDB=30°,则∠ABC的度数为,cos∠ABC=.11.已知实数x,y满足x2+3x+y﹣3=0,则x+y的最大值为.12.古希腊数学家把数1,3,6,10,15,21,…叫做三角形数,它有一定的规律.若把第一个数记为a1,第二数记为a2,…,第n个数记为a n.计算a2﹣a1,a3﹣a2,a4﹣a3,…,由此推算a10﹣a9=,a2012=.三.解答题:(共52分)13.先化简:÷﹣,然后在0,1,2,3中选一个你认为合格的a值,代入求值.1012•桃源县校级自主招生)关于x的一元二次议程x2﹣x+p+1=0有两个实数根x1,x2.(1)求p的取值范围.(2)[1+x1(1﹣x2)][1+x2(1﹣x1)]=9,求p的值.15.某服装厂批发应夏季T恤衫,其单价y(元)与批发数量x(件)(x为正整数)之间的函数关系如图所示,(1)直接写出y与x的函数关系式;(2)一个批发商一次购进250件T恤衫,所花的钱数是多少元?(其他费用不计);(3)若每件T恤衫的成本价是20元,当100<x≤400件,(x为正整数)时,求服装厂所获利润w (元)与x(件)之间的函数关系式,并求一次批发多少件时所获利润最大,最大利润是多少?16.如图,抛物线y=ax2+c(a>0)经过梯形ABCD的四个顶点,梯形的底AD在x轴上,A点到原点的距离为2,梯形的高为3,C点到y轴的距离为1,(1)求抛物线的解析式;(2)点M为y轴上的任意一点,求点M到A,B两点的距离之和的最小值及此时点M的坐标;(3)在第(2)的结论下,抛物线上的P的使S△PAD=S△ABM成立,求点P的坐标.1012•桃源县校级自主招生)如图所示,四边形OABC是矩形,点A、C的坐标分别为(3,0),(0,1),点D是线段BC上的动点(与端点B、C不重合),过点D作直线y=﹣+b交折线OAB于点E.记△ODE的面积为S.(1)当点E在线段OA上时,求S与b的函数关系式;并求出b的范围;(2)当点E在线段AB上时,求S与b的函数关系式;并求出b的范围;(3)当点E在线段OA上时,若矩形OABC关于直线DE的对称图形为四边形OA1B1C1,试探究OA1B1C1与矩形OABC的重叠部分的面积是否发生变化?若不变,求出该重叠部分的面积;若改变,请说明理由.参考答案与试题解析一、选择题1.不等式的解集是()A.﹣<x≤2 B.﹣3<x≤2 C.x≥2 D.x<﹣3考点:解一元一次不等式组.分析:先解不等式组中的每一个不等式的解集,再利用求不等式组解集的口诀“大小小大中间找”来求不等式组的解集.解答:解:由①得:x>﹣3,由②得:x≤2,所以不等式组的解集为﹣3<x≤2.故选B.点评:解不等式组是考查学生的基本计算能力,求不等式组解集的时候,可先分别求出组成不等式组的各个不等式的解集,然后借助数轴或口诀求出所有解集的公共部分.2.一个质地均匀的正方体骰子的六个面上分别刻有1到6的点数,将骰子抛掷两次,掷第一次,将朝上一面的点数记为x,掷第二次,将朝上一面的点数记为y,则点(x,y)落在直线y=﹣x+5上的概率为()A.B.C.D.考点:列表法与树状图法;一次函数图象上点的坐标特征.分析:列举出所有情况,看落在直线y=﹣x+5上的情况占总情况的多少即可.解答:解:共有36种情况,落在直线y=﹣x+5上的情况有(1,4)(2,3)(3,2)(4,1)4种情况,概率是,故选C.1 2 3 4 5 61 (1,1)(1,2)(1,3)(1,4)(1,5)(1,6)2 (2,1)(2,2)(2,3)(2,4)(2,5)(2,6)3 (3,1)(3,2)(3,3)(3,4)(3,5)(3,6)4 (4,1)(4,2)(4,3)(4,4)(4,5)(4,6)5 (5,1)(5,2)(5,3)(5,4)(5,5)(5,6)6 (6,1)(6,2)(6,3)(6,4)(6,5)(6,6)点评:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=,注意本题是放回实验.3.如图所示,在正方形铁皮中,剪下一个圆和一个扇形,使余料尽量少.用圆做圆锥的底面,用扇形做圆锥的侧面,正好围成一个圆锥,若圆的半径为r,扇形的半径为R,那么()A.R=2r B.R=r C.R=3r D.R=4r考点:圆锥的计算;弧长的计算.专题:压轴题.分析:让扇形的弧长等于圆的周长即可.解答:解:根据扇形的弧长等于圆的周长,∴扇形弧长等于小圆的周长,即:=2πr,解得R=4r,故选D.点评:考查了扇形的弧长公式;圆的周长公式;用到的知识点为:圆锥的弧长等于底面周长.4.如图所示,在边长为a的正方形中,剪去一个边长为b的小正方形(a>b),将余下部分拼成一个梯形,根据两个图形阴影部分面积的关系,可以得到一个关于a、b的恒等式为()A.(a﹣b)2=a2﹣2ab+b2B.(a+b)2=a2+2ab+b2C.a2﹣b2=(a+b)(a﹣b)D.a2+ab=a(a+b)考点:平方差公式的几何背景.专题:计算题.分析:可分别在正方形和梯形中表示出阴影部分的面积,两式联立即可得到关于a、b的恒等式.解答:解:正方形中,S阴影=a2﹣b2;梯形中,S阴影=(2a+2b)(a﹣b)=(a+b)(a﹣b);故所得恒等式为:a2﹣b2=(a+b)(a﹣b).故选:C.点评:此题主要考查的是平方差公式的几何表示,运用不同方法表示阴影部分面积是解题的关键.5.若直线x+2y=2m与直线2x+y=2m+3(m为常数)的交点在第四象限,则整数m的值为()A.﹣3,﹣2,﹣1,0 B.﹣2,﹣1,0,1 C.﹣1,0,1,2 D.0,1,2,3考点:两条直线相交或平行问题.专题:计算题;压轴题.分析:由直线x+2y=2m与直线2x+y=2m+3(m为常数)的交点在第四象限,则交点坐标的符号为(+,﹣),解关于x、y的方程组,使x>0,y<0,即可求得m的值.解答:解:由题意得,解得,∵直线x+2y=2m与直线2x+y=2m+3(m为常数)的交点在第四象限,∴,解得:﹣3,又∵m的值为整数,∴m=﹣2,﹣1,0,1,故选B.点评:考查了平面直角坐标系中点的符号,是一道一次函数综合性的题目,是中档题.二、填空题(每小题4分,共24分)6.定义新运算:a⊕b=,则函数y=3⊕x的图象大致是.考点:一次函数的图象;反比例函数的图象.专题:新定义.分析:根据题意可得y=3⊕x=,再根据反比例函数的性质可得函数图象所在象限和形状,进而得到答案.解答:解:由题意得y=3⊕x=,当x≥3时,y=2;当x<3且x≠0时,y=﹣,图象如图:,故答案为:点评:此题主要考查了反比例函数的图象性质和一次函数的图象性质,要掌握它们的性质才能灵活解题.7.|π﹣3.14|+sin30°+3.14﹣8=π.考点:实数的运算;特殊角的三角函数值.专题:计算题.分析:原式第一项利用绝对值的代数意义化简,第二项利用特殊角的三角函数值计算,最后一项利用负整数指数幂法则计算即可得到结果.解答:解:原式=π﹣3.14++3.14﹣=π,故答案为:π点评:此题考查了实数的运算,熟练掌握运算法则是解本题的关键.8.函数y=的自变量x的取值范围是x<﹣1或x≥4.考点:函数自变量的取值范围.分析:根据被开方数为非负数和分母不能为0计算即可.解答:解:由题意得,x2﹣3x﹣4≥0,x+1≠0,解得,x<﹣1或x≥4,故答案为:x<﹣1或x≥4.点评:本题考查的是函数自变量的范围,一般从三个方面考虑:(1)当函数表达式是整式时,自变量可取全体实数;(2)当函数表达式是分式时,考虑分式的分母不能为0;(3)当函数表达式是二次根式时,被开方数为非负数.9.将边长为a的正三角形各边三等分,以这六个分点为顶点构成一个正六边形,则这个正六边形的面积为a2.考点:正多边形和圆.分析:由于正三角形各边三等分,就把整个三角形平均分成9个小正三角形,以这六个分点为顶点构成一个正六边形正好相当于6个小正三角形的面积.解答:解:如图所示:∵新的正六边形有三个顶点在正三角形的三边上,且是三边的等分点,∴连接正三角形的顶点与它对边的中点,可以看出新的正六边形的面积是六个小正三角形的面积之和,∵边长为a的正三角形各边三等分,∴小正三角形的边长为a,∴每个小正三角形的面积是×a×=a×a=a2,∴新的正六边形的面积=a2×6=a2;故答案为:a2.点评:此题考查了正三角形的性质、正三角形面积的计算方法;熟练掌握正三角形的性质,并能进行推理计算是解决问题的关键.10.如图,AB是⊙O的直径,C,D为⊙0上的两点,若∠CDB=30°,则∠ABC的度数为60°,cos∠ABC=.考点:圆周角定理;特殊角的三角函数值.分析:由于AB是⊙O的直径,由圆周角定理可知∠ACB=90°,则∠A和∠ABC互余,欲求∠ABC需先求出∠A的度数,已知了同弧所对的圆周角∠CDB的度数,则∠A=∠CDB,由此得解.解答:解:连接AC,∵AB是⊙O的直径,∴∠ACB=90°,即∠A+∠ABC=90°;又∵∠A=∠CDB=30°,。
厦门第一中学2020-2021学年高一上学期入学测试数学试题(含答案和解析)

厦门_中2020级高一入学数学适应性练习C ⅛试时同为刃分钟.本卷満分】00分〉r 堆择莎G ¢10小題,毎JB 4分,卄40分〉 1. ^y-^y 分解因式时,应提取的公因式是()a×a i ÷ffl 2Γ -IaC. (α-l)2=α2-l有两个事件,事件总 拋掷一枚均匀的骰子,朝上的面点数为偶数'事件D 367人中至少有2人生日 相同.下列说法正确的是()4. 如图,AABC 的三个顶点在正方形网格的格点上,则(an 厶1的值是()5. 在某次演讲比赛中.五位评委给选手切同打分,得到互不相等的五个分数.若去掉一个最窈分,平均分 为*去掉一个最低分,平均分为屮 同时去掉一个最高分和一个最低分,平均分为二,则( )A. y> z>xB. x>z>yC. y>x> Z D ・ z> y>x6. 屈C 的周长 HQB 的中点.MC = A^ = 5,则^ABC 的面积是(>A. 24B. 20C. 15 D ・不确定7 •如图,"EC 中.厶lCff = 90o,Z4 = 30°,∕g=16,点P 是斜边ARh 任怠一点■过点P 作理丄力/垂足为A 交边ZC (或边仞》于点0设AP = x. ^APQ 的而积为”则y 与蛊之间的函数图象大致 A.C. 3X L y 3D. 3x 1y λ 2. 下列计算正确的是( A. (α 塔F= a 7b i B. -2⅛(4α-l) = -8σ⅛-2⅛ A. 事件儿〃都是随机事件 B. 事件/、E 都是必然爭件 C. 事件/是随机事件,事件〃是必然事件 D. 事件Zl 是必然事件,事件〃是随机事件2√10 亍3√O208.如图,已知册是半呵00的直径,/是EE 廷长线上一点・/C 切半圆OO 于点D,月C 丄力C 于点 G DFlEB 于总F,若Be = 2DF = 6∙则OO 的半径为( )9.如图,正三角形ABC 的边长为4,过点〃的直线/丄屈,且“ABC 与⑷C 关于直线Z 对称.D 为线段Bek 一动点,则4DYD 的最小值是( )A. 4馆 B ・6√2 C ・8 D ・4+ 2若10.二次函数y=α√ + ⅛Λ+c 的图象如图所示,对称轴是直线x = l.下列结论=① a be < 0: (2)3a÷c>0; (3)(Λ + C )2 -⅛2<0 ; ®a + b<m(am^b)(川为实数)・其中结CA ∙ 1个 B. 2个 C. 3个 D. 4个 二琪空莎(共4小题.毎题4分,计16分)12.如图,在A ABC 中,Z√ =40o , ZB = ZC, BP=CE, BD = CP,则SEE= ________________________13.如图,在平面直角坐标系中,蓋形屈CD 的顶点力、左往反比例函数^=-(⅛>0,Λ>0)的图象上, 己知久B 的横坐标分别为I 、4,且对角线X 轴,若菱形ABCD 的面积为30.则A 的值为 __________________________ .11・己知 3H 4 (Jr-I)(X-2)A R TrTT 则实数八一-论正确的个数为( )14.平面直克坐标系HOy中,已知点@0)在直线j=2rjr÷c2+2(c>0)上.且满足,十⅛2-2(l÷25c)+4c2+A=0,则C= ____________ •三.(共5小題,计44分〉15.(木题8分)为了解某县建档立卡贫困户对准扶贫政策落实的满意度,现从全县建档立卡贫困户中随机 捕取了部分贫国户进行了调査(把调查结果分为四个等级,A 级:非常满意:B 级三满意:C 级;基本满意: D 级;不满盘人并将调査结果绘制成如下两幅不完整的统计图.请根据统计图中的怕息解决下列问题;(1>本次抽样调查测试的建档立卡贫困户户数是 _______________〈2》图1中,Na 的度数是 ______________,并把图2条形图补充完整;〔3>某县建档立卡贫困户有IOOOO 户.如果全部参加这次满意度调查,请你估计满意(B 级)人数约为多 少户?U )调查人员想从5户建档立卡贫困户(分别记为G b 9 G M, W )中随机选取两户,调査它们对扶贫政 策的满意度,谙用列表或树状图的方法求出选中贫困户e 的概率・3乂 — y = 2a —516∙ “杪分〉己2 y 的方程组{“Ii+3的解都为正数・(1>当α=2时,解此方程组:(2>求α的取值范圉:(3>己知α+方一4,且6>0, Z= Ia -36 P 茨二的取值范围.17.(本題P 分)已知& F 分别在正方形ABCD 的边CD ∙ AD±f CD=4CE. ZEFB = ZFBC 9求1& (木題8分)如图1, 4B 是O O 的直径・£是朋延长线上一点,EC 切OO 于点G OP 丄Ao 交AC 于点P 交EC 的延长线于点D・猜准扶甘謂翳D D(1)求证;δPCD是等腰三角形;(2)CG丄力B于"点,交OO于G点,过D点作BF〃EC,交G)O于点F,交CG于0点,连接AF,3如国2.若SitlE=工,CQ = S9求力F值•519.(本題12分)己知二次函数y = χ2÷⅛r-c的图彖经过两点F(l,α), Q(2,10α).(1)如果弘b,疋都是整数,AC <b<Ka , Λ,b,€■的值,(2)设二次函数y = x2^bx-c的觀象与天轴的交点为A、B.与y轴的交点为C9如果关于X的方程√÷M-^=0的两个根都是整数,求厶ABC的面枳•厦门一中2020级离一入学数学适应性竦习鑫考答案一・选择禺(共M 小品每题4分,计恥分)1. B2. C3. C4. A5. A6. A7. D8. D9. C IO- C二、 壇空圈供4小圈毎题4分,计16分〉11. 1 2 12. 70° 13. y 14.三、 解答窗〈共5小圈 计g 分〉(须写出详»1的枠g ⅛t 程) 15.(本題8分)(1) 60(2) 54"(3) 3500 λ(4)所有可能出现的结果共有10种.选中e 的结果有4种4 2:■P (选中小=—=-10 516・(木題8分)①次2 +②得7工二7,即Jf=I,把兀=1代入①得.3-> = -l,即y = 4,ZJ-I>0 α+2> 0则原不等式组的解集为α>l:(3) Vd7 + 5 = 4, ⅛>0Λ ⅛ = 4 — α > O pV α>LΛ 1 <Λ <4, ∖t 2α — 3⅛ = 2a — 3(4—α) = 5α— I2,z= 2a —3b 、 解;<1)当a =2时.方程组为彳 3jc-y = -lx^2y = 9此方程的解为 x=l丁 = 4(2)解这个方程组的解为三 x = a-∖y = a +2tt-7<z<8・8 分17.(本題g 分) 如图,延长EF 交BC 的延长线于八设恥的中点为6连2,则OT 丄BFI 四边形ABCD 是正方形,不妨设其边长为4・・.ADHBC 上 A = ZBOT = 90°.'.AAFB = ΛOBT—BAFs^JOB2・•・ BF I = 2AF ・ BT设 Cr=k易证 REFSbCET :∙ DF=U ∙ AF=4-3k, BT = 4#Λ42÷(4+ 3^)2 = 2 X(4 —弘)(4 + k)15A 2-8⅛=O QΛJt = 或0 (舍去)Λtan∠ABF = ^=2AB 4 518.〈本题8分〉^OB = -BF OS BT解:(1)连接OC,≡11V EC切09于点C,:,OC丄DE∙,・•・ Zl-t-Z3 = 90°,又* OP丄O/,ΛZ2 + Z4=90o,-OA = OC,Λ Z1 = Z2,・•• Z3=Z4,又V∠4 = ∠5,,ΛZ3=Z5,ΛDP= DC,即为等腰三角形.(2)如图2,连接OC、BC,Λ DE与OO相切于点E,Λ ZOCS+ Z5CE= 90°,・•・ OC=OB,Λ ZOCB = ZOBC,Λ ZOBC^ ZBCE = 90°, 又VCG 丄√fg,ΛZOSC÷Z5CG = 90°lΛ ZBCE = ZBCG ,V BFHDE,Λ ZBCE = ZQBC,Λ ABCG= ZQEC.:∙ QC = QB = 5,V BF 〃DE,Λ ZABF= ZE,3V SinE = —,5Λ Sin ZABF = |,XOH=3、M=4,设QO的半径为r,:・在bOCH 中,^=81 + (r-4)2,解得:r = 10f3又VZ4∕B = 900, Sin ZABF = |,AJF= 12. 8 分19.(本题12分)解二点P(I卫)、ρ(2JOa)在二次函^y = X I^bX^^的图象上, 故l+bγ=α, 4A-2b-c=10« ,解得b = %-3, e=‰-2≡8n — 2 < 9,J—3(1)由CVbV&7知"9α — 3 < 8α解得1 vα∙<3,又“为整数.所以α = 2上=9α-3 = 15f c=8α-2 = 14;(2)设m ”是方程的两个整数根,且nι≤n.由根与系数的关系可得f ni = -b=3-9a∙ mn = -c = 2~^f消去血得9∕nπ-8(wz÷π) = -6,两边同时乘以9,得8b_720+龙)=_54,分解因式,得帥_8)(%_8) = 10・又g 〃是整数.所以后而三组解舍去, 故ZM = 1, ZT= 2. 因此 P b = -{m + Λ) = —= —mn = —2 , 二次函数的解析式为卩=,一3工+2・易求得点/、〃的坐标为(1,0)和(2,0),的坐标为(0,2). 所以^ABC 的面枳为∣×(2-1)×2=1. 12分 解得 9血一8 =1 /M = I/1 = 2 或“ :9加一8 = 一10,9Π-8=-1 Tl =— 9 1 JTl = - 32 Λ =—3 或“ 9m —8 = —510m =— 9 13 n =— 或电 9加一8 = 2。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
15.(本题 8 分)
(1)60……………………2 分
(2)54°……………………4 分
(3)3500 人……………………6 分
(4)所有可能出现的结果共有 10 种,选中 e 的结果有 4 种
4
∴P(选中 e)= = .……………………8 分
10
16.(本题 8 分)
解:(1)当 a=2 时,方程组为
17.(本题 8 分) 如图,延长 EF 交 BC 的延长线于 T,设 FB 的中点为 O,连 TO,则 OT⊥BF ∵四边形 ABCD 是正方形,不妨设其边长为 4 ∴AD∥BC,∠A=∠BOT=90° ∴∠AFB=∠OBT ∴△BAF∽△TOB
∴ AF BF ……………………2 分 OB BT
∵DE 与⊙O 相切于点 E, ∴∠OCB+∠BCE=90°, ∵OC=OB, ∴∠OCB=∠OBC, ∴∠OBC+∠BCE=90°, 又∵CG⊥AB, ∴∠OBC+∠BCG=90°, ∴∠BCE=∠BCG, ∵BF∥DE, ∴∠BCE=∠QBC, ∴∠BCG=∠QBC, ∴QC=QB=5, ∵BF∥DE, ∴∠ABF=∠E, ∵sinE= , ∴sin∠ABF= , ∴QH=3、BH=4, 设⊙O 的半径为 r, ∴在△OCH 中,r2=82+(r﹣4)2, 解得:r=10,
,
①×2+②得 7x=7,即 x=1, 把 x=1 代入①得,3﹣y=﹣1,即 y=4,
此方程的解为
;……………………2 分
(2)解这个方程组的解为:
,
由题意,得
,
则原不等式组的解集为 a>1;……………………5 分 (3)∵a+b=4,b>0, ∴b=4﹣a>0, ∵a>1, ∴1<a<4, ∵2a﹣3b=2a﹣3(4﹣a)=5a﹣12,z=2a﹣3b, 故﹣7<z<8.……………………8 分
又∵∠AFB=90°,sin∠ABF= ,
∴AF=12.……………………8 分 19.(本题 12 分)
解:点 P(1,a)、Q(2,10a)在二次函数 y=x2+bx﹣c 的图象上, 故 1+b﹣c=a,4+2b﹣c=10a, 解得 b=9a﹣3,c=8a﹣2;
(1<3, 又 a 为整数,所以 a=2,b=9a﹣3=15,c=8a﹣2=14;……………………5 分 (2)设 m,n 是方程的两个整数根,且 m≤n. 由根与系数的关系可得 m+n=﹣b=3﹣9a,mn=﹣c=2﹣8a, 消去 a,得 9mn﹣8(m+n)=﹣6,……………………7 分 两边同时乘以 9,得 81mn﹣72(m+n)=﹣54,分解因式,得(9m﹣8)(9n﹣8)=10.
∵OB= 1 BF 2
∴ BF 2 2 AF BT
设 CT=k 易证△DEF∽△CET ∴DF=3k,AF=4-3k,BT=4+k……………………4 分
∴ 42 4 3k 2 2 4 3k 4 k ……………………6 分
15k 2 8k 0 ∴ k 8 或0 (舍去)
15 ∴tan∠ABF= AF = 4 3k = 3 ……………………8 分
所以
或
或
或
,
解得 或
或
或
;
又∵m,n 是整数,所以后面三组解舍去, 故 m=1,n=2. 因此,b=﹣(m+n)=﹣3,c=﹣mn=﹣2, 二次函数的解析式为 y=x2﹣3x+2. 易求得点 A、B 的坐标为(1,0)和(2,0),点 C 的坐标为(0,2),
所以△ABC 的面积为
.……………………12 分
AB 4 5
18.(本题 8 分) 解:(1)连接 OC,
∵EC 切⊙O 于点 C, ∴OC⊥DE, ∴∠1+∠3=90°, 又∵OP⊥OA, ∴∠2+∠4=90°, ∵OA=OC, ∴∠1=∠2, ∴∠3=∠4,
又∵∠4=∠5, ∴∠3=∠5, ∴DP=DC,即△PCD 为等腰三角形.……………………4 分 (2)如图 2,连接 OC、BC,
厦门一中 2020 级高一入学数学适应性练习参考答案
一、选择题:(共 10 小题,每题 4 分,计 40 分)
1. B
2. C
3. C
4.A
5.A
6.A
7.D
8.D
9.C
10.C
二、填空题:(共 4 小题,每题 4 分,计 16 分)
11. 1 2
12.70°
13. 20 3
14. 3 1
三、解答题:(共 5 小题,计 44 分)(须写出详细的解答过程)
