平面几何习题大全
五年级下册数学《平面几何》练习题大全

五年级下册数学《平面几何》练习题大全
一、选择题
1. 以下哪个选项是平行四边形的一个性质?
A. 两组对边分别相等
B. 四条边都相等
C. 对角线互相平分
D. 有一个角是直角
2. 如果一个四边形的对边平行且相等,那么它一定是?
A. 矩形
B. 菱形
C. 平行四边形
D. 梯形
3. 在三角形中,若一个角的度数是90度,那么这个三角形是?
A. 锐角三角形
B. 直角三角形
C. 钝角三角形
D. 等边三角形
二、填空题
1. 矩形是一种特殊的平行四边形,它的特点是_____。
2. 在三角形中,如果一个角的度数大于90度,那么这个角被
称为_____角。
3. 若一个四边形的对边相等且平行,则这个四边形是_____。
三、解答题
1. 画出一个任意三角形,并标出它的三个内角。
2. 已知一个平行四边形的对边相等,证明它是矩形。
3. 若已知三角形ABC中,AB=AC,求证∠BAC=60度。
四、应用题
1. 小明的书桌是一个矩形,已知矩形的长是80cm,宽是40cm,求书桌的面积。
2. 小红有一个平行四边形的框架,已知对边相等,其中一个角是直角,求这个平行四边形的面积。
3. 如图,三角形ABC中,AB=AC,D是BC的中点,求证AD是∠BAC的角平分线。
请注意,以上题目只是示例,并不是完整的练习题大全。
您可以根据需要继续添加或修改题目。
平面几何练习题――点共圆

平面几何练习题 ――点共圆
1. 在直角ABC ∆的两条直角边AC 、BC 上各取一点D 和E ,由顶点C 分别向直线DE 、EA 、AB 、
BD 引垂线,求证,所得的4个垂足共圆;(1989年前苏联教委推荐题)
)
291988(.2候选题届年第共圆;
、、、、、、、、的中点,求证:、、为、、为垂心,为三条高的垂足,、、为三边的中点,、、中,在IMO R Q P Z Y X F E D HC HB HA R Q P H Z Y X F E D ABC ∆
)
191990(.3AMO Q P N M Q P AC AC N M CC AB AB ABC 届年第共圆;
、、、,求证:、于边的高线及其延长线交为直径的圆与以,
、及其延长线交于边的高线为直径的圆与,以给出平面上一个锐角‘
4.凸四边形ABCD 中,两对角线AC 和BD 互相垂直,两对边AB 与CD 不平行,且AB 与CD 的垂直平分线交于四边形内一点P ,证明:ABCD 为圆内接四边形的充要条件是ABP ∆的面积等于CDP ∆的面积。
(1998年第39届IMO )
)
361995(6,,,,,)()()(.5222111122112211221122112211221候选题届年第个顶点共圆。
求证:这两个三角形的也可构成一个三角形,线可构成一个三角形,直,直线,使得之间与位于、上取两点,在边之间与于位、上取两点,在边之间与位于,,上取两点的边在锐角IMO CC BB AA CC BB AA C CC C CC B BB B BB A AA A AA B C C C C AB A B B B B CA C A A A A BC ABC ∠=∠=∠=∠=∠=∠∆。
高三数学平面几何练习题及答案

高三数学平面几何练习题及答案一、选择题1. 已知直线l与x轴的交点为A(2, 0),与y轴的交点为B(0, -3)。
则直线l的斜率是:A. 3B. -3C. 1/3D. -1/3答案: B. -32. 已知平面上两点P(2, 4)、Q(5, 7),则向量PQ的坐标表示为:A. (3, 3)B. (2, 3)C. (5, 7)D. (7, 11)答案: A. (3, 3)3. 已知点A(-3, 4)、B(1, -2),则直线AB的斜率为:A. 2B. -2C. 3/2D. -3/2答案: D. -3/24. 在直角坐标系中,点P(3, 4)关于y轴的对称点为:A. (3, -4)B. (-3, 4)C. (4, 3)D. (-4, 3)答案: B. (-3, 4)5. 直线y = 2x + 3与直线y = -x + 1的交点坐标为:A. (1, 2)B. (2, 1)C. (-1, 2)D. (2, -1)答案: C. (-1, 2)二、填空题1. 已知向量AB = (-3, 2),向量BC = (-1, 4),则向量AC = ______。
答案: (-4, 6)2. 已知点A(2, 3)、B(5, 7),则直线AB的斜率为______。
答案: 4/33. 已知线段的中点坐标为M(3, -2),其中一端点为N(5, 1),则另一端点坐标为______。
答案: (1, -5)4. 平面上一点P(x, y),与坐标轴的距离之和为7,且x > 0,y > 0。
则点P可能的坐标是______。
答案: (4, 3)5. 直线y = 3x + 2与y轴交点的坐标为(0, b),则b = ______。
答案: 2三、解答题1. 已知四边形ABCD,其中AB为水平线段,CD为垂直线段。
已知AB的中点坐标为M(2, 3),CD的中点坐标为N(5, 4)。
求四边形ABCD的中心点坐标。
解答:四边形的中心点坐标为两个中点的坐标的平均值。
平面几何100题及答案(前80题)
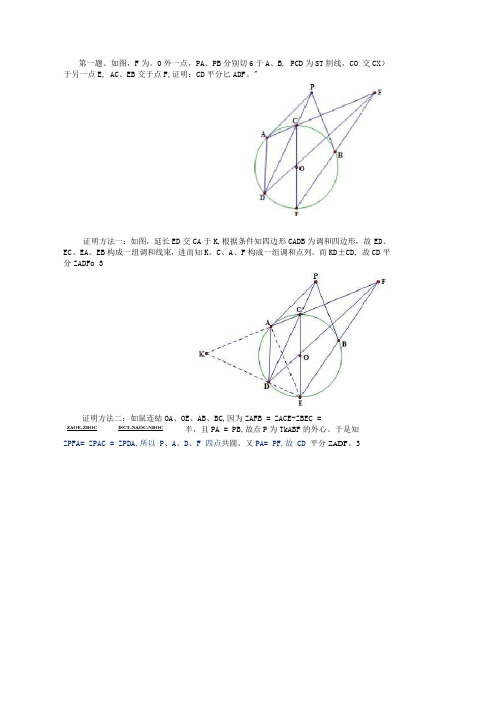
第一题、如图,F为。
0外一点,PA、PB分别切6于A、B, PCD为ST割线,CO 交CX)于另一点E, AC、EB交于点F,证明:CD平分匕ADF。
"证明方法一:如图,延长ED交CA于K,根据条件知四边形CADB为调和四边形,故ED、EC、EA、EB构成一组调和线束,进而知K、C、A、F构成一组调和点列。
而KD±CD, 故CD平分ZADFo 3证明方法二:如鼠连結OA、OE、AB、BC,因为ZAFB = ZACE-ZBEC =ZAOE-ZBOC ISCT-NAOC-NBOC 半,且PA = PB,故点P为TkABF的外心。
于是知ZPFA= ZPAC = ZPDA,所以P、A、D、F 四点共圆。
又PA= PF,故CD 平分Z A DF。
3第二题、如图,AB为©0直径,C、D为O。
上两点,且在AB同侧,。
在C、D两处的切城交于点E, BC、AD交于点F, EF交AB于证明:E、C、页、D四点共圆。
“证明:如图,延长白C、BD交于点K,则BC1AK, AD丄BK,从而知F^)AKAB的垂心。
又在圆内接六边形CCADDB中使用帕斯卡定理,知K、E、F三点共线,从而KM丄卽于価。
于是知匕CMF = ZCAF= ZCDE,所以E、C、页、D四点共圆。
K第三题、如图,AB为。
直径,C、D为伽上两点'且在AB同侧,O0在C. D两处的切线交于点E, BC、AD交于点F, EB交0。
于点G,证明;ZCEF = 2/AGF。
“证明:如图,根据条件知匕CF D =典牌=(脸-®;(i对-命)=Z CAB + / DBA = ZECF + ZEDF;且EC = ED;故点E 为△CED 外心。
于是知/EFC = ZECF = ZCAB = ZCGE,敌E、C、F、G四点共圆。
所以“ZCGF = ZCEF = 2(90° - ZECF)= 2(90° - ZCAB)= 2ZABC 二2ZAGC " 0lWZAGF = —=—,即得ZCEF = 2ZAGFo,2 2第四題、如图,AB为直径,P为AB延长线上一点,PC切于C,点C关于朋的对称点为点D, CE1AD于E, F为CE中点,AF交于K,求证:AP为ZXPCK外扬圆的切线。
平面几何练习题

平面几何练习题题一:求三角形边长和周长已知一个三角形的两边长分别为a和b,夹角为C°,求第三边c的长度和三角形的周长P。
解:根据余弦定理可知,余弦公式为:c² = a² + b² - 2ab·cos(C)。
根据上述公式,可以计算得到c的长度。
根据三角形的定义可知,三角形的周长P等于三边之和,即P = a + b + c。
题二:求三角形的面积已知一个三角形的底边长为b,高为h,求三角形的面积S。
解:根据三角形的面积公式可知,S = 0.5 * b * h。
题三:判断点是否在三角形内部已知一个三角形的三个顶点坐标分别为A(x₁,y₁),B(x₂,y₂),C(x₃,y₃),以及一个待判断的点D(x,y),判断点D是否在三角形ABC的内部。
解:利用行列式的性质可以判断点D是否在三角形ABC内部。
设点D的坐标为(x,y),则点D在三角形ABC内部的条件为:|(x₁ - x) (y₁ - y) 1||(x₂ - x) (y₂ - y) 1| > 0|(x₃ - x) (y₃ - y) 1|如果等式左侧的行列式结果大于0,则点D在三角形ABC内部;如果等式左侧的行列式结果小于0,则点D在三角形ABC的外部;如果等式左侧的行列式结果等于0,则点D在三角形ABC所在的边界上。
题四:求矩形的面积和周长已知一个矩形的长为L,宽为W,求矩形的面积S和周长P。
解:矩形的面积公式为S = L * W,周长公式为P = 2 * (L + W)。
题五:求圆的面积和周长已知一个圆的半径为r,求圆的面积S和周长C(circumference)。
解:圆的面积公式为S = π * r²,其中π取近似值3.14159;圆的周长公式为C = 2 * π * r。
题六:判断点是否在圆内部已知一个圆的圆心坐标为O(x₀,y₀),半径为r,以及一个待判断的点P(x,y),判断点P是否在圆O内部或者在圆的边界上。
2024年数学九年级上册平面几何基础练习题(含答案)

2024年数学九年级上册平面几何基础练习题(含答案)试题部分一、选择题:1. 在平面几何中,下列哪个图形既是轴对称图形又是中心对称图形?()A. 矩形B. 等腰三角形C. 梯形D. 正五边形2. 下列各角中,哪个角是补角?()A. 30°B. 45°C. 60°D. 120°3. 在直角坐标系中,点A(2, 3)关于原点对称的点是()A. (2, 3)B. (2, 3)C. (2, 3)D. (2, 3)4. 下列哪个条件能判定两个三角形全等?()A. 两边和其中一边的对角相等B. 两角和其中一边相等C. 两边和它们的夹角相等D. 两边和其中一边的对角相等5. 若平行线l1和l2之间的距离为5cm,直线l3与l1、l2均相交,且l3与l1、l2的夹角均为45°,则l3与l1、l2之间的距离为()A. 5cmB. 5√2 cmC. 2.5cmD. 2.5√2 cm6. 下列哪个图形是正多边形?()A. 边长为1,内角为108°的多边形B. 边长为1,内角为120°的多边形C. 边长为1,内角为135°的多边形D. 边长为1,内角为140°的多边形7. 在直角三角形中,若一个锐角的度数为30°,则另一个锐角的度数为()A. 30°B. 45°C. 60°D. 90°8. 下列哪个比例式成立?()A. a² : b² = (a+b)² : (ab)²B. a² : b² = (a+b) : (ab)C. a : b = (a+b)² : (ab)²D. a : b = (a+b) : (ab)9. 若等腰三角形的底边长为8cm,腰长为5cm,则该三角形的面积为()A. 20cm²B. 40cm²C. 30cm²D. 24cm²10. 在平面几何中,下列哪个说法是正确的?()A. 对角线互相垂直的四边形一定是矩形B. 对角线互相平分的四边形一定是平行四边形C. 对角线相等的四边形一定是矩形D. 对角线互相垂直平分的四边形一定是菱形二、判断题:1. 平行线的性质是:同位角相等,内错角相等,同旁内角互补。
平面几何习题
1、三角形ABC中,AD为中线,P为AD上任意一点,过p的直线交AB于M.交ac 于N,若AN=AM,求证PM/PN=AC/AB2、在三角形BCD中,BC=BD,延长BC至A,延长BD至E,使AC=BE,连接AD,AE,AD=AE,求BCD为等边3、三角形ABC中若圆O在变化过程中都落在三角形ABC内(含相切), A为60度,AC为8,AB为10,X为未知数,是AE的长.圆O与AB,AC相切,圆O与AB的切点为E, X的范围是?4、已知三角形ABE中C 、D分别为AB、BE上的点,且AD=AE,三角形BCD 为等边三角形,求证BC+DE=AC5、已知在三角形ABC中,AD是BC边上的中线,E是AD上的一点,且BE=AC,延长BE交AC与F,求证AF=EF6、在△ABC中,D是BC边中点,O是AD上一点,BO,CO的延长线分别交AC,AB 于E,F求证:EF平行BC。
7、已知:在△ABC和△A'B'C'中,AB=A'B', AC=A'C'.AD,A'D'分别是△ABC和△A'B'C'的中线,且AD=A'D'.求证:△ABC≌△A'B'C'8、四边形ABCD为菱形,E,F为AB,BC的中点,EP⊥CD,∠BAD=110º,求∠FPC的度数9、已知:E是正方形ABCD内的一点,且∠DAE=∠ADE=15°,求证:△EBC是等边三角形10、在三角形ABC中,经过BC的中点M,有垂直相交于M的两条直线,它们与AB,AC分别交于D、E,求证,BD+CE>DE11、AB是等腰直角三角形ABC的斜边,若点M在边AC上,点N在边BC上,沿直线MN把△MCN翻折,使点C落在AB上设其落点(1).如图一,当是AB的中点时,求证:PA/PB=CM/CN(2).如图二当P不是AB中点时,结论PA/PB=CM/CN是否成立?若成立,请给出证明12、三角形ABC中,BC=5,M和I分别是三角形ABC的重心和内心,若MI 平行于BC,则AB+AC的值是多少?13、已知圆O是三角形ABC的外接圆CD是AB边上的高,AE是圆O的直径。
平面几何练习题(1)(原创)(免财富)
平面几何练习题(1)一.如图,△ABC中,∠ABC=90°,∠ACB=α,△CDH中,∠CDH=90°,∠HCD=α,连接AH,取AH的中点M,连接MB、MD(1)求证:MB=MD(2)求∠BMD(用α表示)MH DCBA二.如图,△ABC中,∠ABC=90°,∠ACB=α,△CDH中,∠CDH=90°,∠HCD=α,连接AH,取AH的中点M,连接MB、MD(1)求证:MB=MD(2)求∠BMD(用α表示)MH DCB A三. 如图,△ABC 中,∠ABC=90°,∠ACB=α,△CDH 中,∠CDH=90°,∠HCD=α,连接AH ,取AH 的中点M ,连接MB 、MD (1)求证:MB=MD(2)求∠BMD (用α表示)ABCDHM四. 如图,△ABC 中,∠ABC=90°,∠ACB=α,△CDH 中,∠CDH=90°,∠HCD=α,连接AH ,取AH 的中点M ,连接MB 、MD (1)求证:MB=MD(2)求∠BMD (用α表示)MHDCBA中点M ,连接MB 、MD (1)求证:MB=MD(2)求∠BMD (用α表示)ABCDHM六. 如图,△ABC 中,∠ABC=90°,∠ACB=α,△CDH 中,∠CDH=90°,∠HCD=α,连接AH ,取AH 的中点M ,连接MB 、MD (1)求证:MB=MD(2)求∠BMD (用α表示)MHDCBAAB CDHM中点M ,连接MB 、MD (1)求证:MB=MD(2)求∠BMD (用α表示)八. 如图,△ABC 中,∠ABC=90°,∠ACB=α,△CDH 中,∠CDH=90°,∠HCD=α,连接AH ,取AH 的中点M ,连接MB 、MD (1)求证:MB=MD(2)求∠BMD (用α表示) MHDCBA。
中职教育数学《平面解析几何-复习课》练习题
第八章 平面解析几何(知识点)1. 直线:(1) 倾斜角α:一条直线l 向上的方向与x 轴的正方向所成的最小正角叫这条直线的倾斜角。
其范围是),0[π(2) 斜率:①倾斜角为090的直线没有斜率;②αtan =k(倾斜角的正切)③经过两点),(),,(222111y x P y x P 的直线的斜率1212x x y y K --= )(21x x ≠(3) 直线的方程①两点式:121121x x x x y y y y --=-- ② 截距式 1=+b y a x③ 斜截式:b kx y += ④点斜式:)(00x x k y y -=- ⑤一般式:0=++C By Ax注:1.若直线l 方程为3x+4y+5=0,则与l 平行的直线可设为3x+4y+C=0;与l 垂直的直线可设为4X-3Y+C=0 2.求直线的方程最后要化成一般式。
(4) 两条直线的位置关系①点),(00y x P 到直线0=++C By Ax 的距离:2200||B A C By Ax d +++=②0:1=++C By Ax l 与0:2=++C By Ax l 平行2221||BA C C d ++=2. 圆的方程(1) 标准方程:222)()(r b y a x =-+-(0>r)其中圆心),(b a ,半径r 。
(2) 一般方程:022=++++F Ey Dx y x (0422>-+F E D )圆心(2,2E D --) 半径:2422F EDr -+=(4)直线和圆的位置关系:主要用几何法,利用圆心到直线的距离d 和半径r 比较。
相交⇔<r d ; 相切⇔=r d ; 相离⇔>r d3. 二次曲线:定义一:平面内到一个定点和一条定直线的距离的比等于定长e 的点的集合,①当0<e<1时,是椭圆.②当e>1时,是双曲线.③当e=1时,是抛物线. 4. 椭圆注:等轴双曲线:(1)b a =(2)离心率2=e (3)渐近线x y ±=6. 抛物线(如右图示) 注:(1)p 的几何意义表示焦点到准线的距离。
高中数学练习题:平面几何
高中数学练习题:平面几何引子在高中数学中,平面几何是一个重要的知识点,也是学生们经常接触和练习的内容之一。
平面几何涉及到平面上的点、线、面等概念,通过运用几何定律和性质,解决与平面相关的问题。
掌握平面几何的基本概念与方法不仅有助于学生提高逻辑思维和推理能力,还能够拓宽学生的数学视野,使他们能够更好地应用数学知识解决实际问题。
本文将提供一系列高中平面几何的练习题,并逐一解析,帮助读者更好地理解和掌握平面几何的知识。
1. 点、线、面的基本概念H2:点的基本概念练习题 1:在平面上,画出以下图形:•两个不在同一直线上的点•三个共线的点•四个不在同一直线上的点H3:线的基本概念练习题 2:根据以下描述,判断相应的线段关系:•两个线段长度相等的关系是什么?•两个线段互相垂直的关系是什么?•如果一个线段是另一个线段的一半,它们之间的关系是什么?H3:面的基本概念练习题 3:根据以下描述,判断相应的平面关系:•两个平面都垂直于同一条直线的关系是什么?•如果两个平面相交,它们的交线是什么?•两个平行平面之间的夹角是多少?2. 直线与角的性质H2:平行线与相交线练习题 4:判断以下直线关系:•如果两条直线垂直相交,它们之间的夹角是多少?•如果一条直线与另一条直线平行,它们之间的夹角是多少?•如果两条直线相交,它们之间的夹角是多少?H2:三角形与四边形练习题 5:根据以下描述,判断相应的三角形和四边形特征:•如果一个四边形的对角线相等,它是什么形状的四边形?•如果一个三角形的三边相等,它是什么类型的三角形?•一个三角形的两个角相等,它是什么类型的三角形?H3:角的性质练习题 6:根据以下描述,判断相应角的性质:•如果一个角是直角,它的度数是多少?•如果一个角是锐角,它的度数是多少?•如果一个角是钝角,它的度数是多少?H3:三角形的性质练习题 7:根据以下描述,判断相应三角形的性质:•如果一个三角形的三个角都是锐角,它是什么类型的三角形?•如果一个三角形有一个角是钝角,它是什么类型的三角形?•如果一个三角形有一个角是直角,它是什么类型的三角形?3. 圆与圆的性质H2:圆的基本概念练习题 8:根据以下描述,判断相应的圆的性质:•什么是圆心?•什么是半径?•什么是直径?H2:角与圆的性质练习题 9:根据以下描述,判断相应角和圆的性质:•一个角的两条边与圆的切点相接,这个角叫什么?•如果一条边是直径,这个角叫什么?•如果一条边与圆的切点相接,而另一条边不过圆心,这个角叫什么?H3:切线与切点练习题 10:根据以下描述,判断相应的切线和切点的性质:•如果一条直线与圆的切点相接,这条直线叫什么?•如果一条直线与圆的切点相接,并且垂直于半径,这条直线叫什么?•如果一条直线与圆的切点相接,并且平行于半径,这条直线叫什么?4. 平面几何题目解析H2:练习题 11将一张纸对折两次得到四个重叠的小正方形,再按其中一条对角线剪开,得到两个相等的小三角形,请问这两个小三角形相似吗?解析首先,我们知道正方形的对角线可以将正方形分成两个相等的直角三角形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
命题在圆内接四边形ABCD中,O为圆心,己知∠AOB+∠COD=180.求证:由O向四边形ABCD所作的垂线段之和等于四边形ABCD的周长的一半。ﻫ证明(一)连OA,OB,OC,OD,过圆心O点分别作AB,BC,CD,DA的垂线,垂足依次为P,Q,R,S。
易证ΔAPO≌ΔORD,所以DR=OP,AP=OR,
故OP+OR=DR+AP=(CD+AB)/2。
同理可得:OQ+OS=(DA+BC)/2。
因此有OP+OQ+OR+OS=(AB+BC+CD+DA)/2。
证明(二)连OA,OB,OC,OD,因为∠AOB+∠COD=180°,OA=OD,所以易证
RtΔAPO≌RtΔORD,故得DR=OP,AP=OR,
即OP+OR=DR+AP=(CD+AB)/2。
平面几何习题大全
———————————————————————————————— 作者:
———————————————————————————————— 日期:
平面几何习题大全
下面的平面几何习题均是我两年来收集的,属竞赛范围。共分为五种类型,1,几何计算;2,几何证明;3,共点线与共线点;4,几何不等式;5,经典几何。
Sb=(BD*BF*sinB)/2=x*(1-z)*S,
Sc=(CD*CE*sinC)/2=y*(1-x)*S。
所以有
S1=S-Sa-Sb-Sc=S*[1-z*(1-y)-x*(1-z)-y*(1-x)]
=S*[1-(x+y+z)+yz+zx+xy],
据此命题[S≥4S1]转化为证明
4*[1-(x+y+z)+yz+zx+xy]≤1
F=[r2*r3*sinA+r3*r1*sinB+r1*r2*sinC]/2
=[a*r2*r3+b*r3*r1+c*r1*r2]/(4R)。
故命题转化为求证
a*r2*r3+b*r3*r1+c*r1*r2≤RΔ(1)
据恒等式:abc=4RΔ,则上式为
根据塞瓦定理得:
xyz=(1-x)*(1-y)*(1-z)
上述恒等式展开等价于
1+yz+zx+xy=2xyz+x+y+z
将其代入得:8xyz≤1.
由算术--几何平均不等式得:
2√[x(1-x)]≤1z)]≤1,
上述三式相乘得:
8√[xyz(1-x)*(1-y)*(1-z)]≤1,<==>8xyz≤1 .
证明设P点关于正△ABC的重心坐标为P(x,y,z),a为正△ABC的边长,则正△ABC的面积为S=(a^2√3)/4。ﻫ由三角形重心坐标定义易求得: ﻫAD=za/(y+z),CD=ya/(y+z),CE=xa/(z+x),AE=za/(z+x),AF=ya/(x+y),BF=xa/(x+y).ﻫ故得:
PK=(xa√3)/[2(x+y+z)], ﻫPN=(ya√3)/[2(x+y+z)],ﻫPM=(za√3)/[2(x+y+z)]. ﻫ故得:
S2=(PN*PM+PM*PK+PK*PN)*sin120/2=3S(yz+zx+xy)/[4(x+y+z)^2]。ﻫ所以待证不等式S2≥S1等价于: ﻫ(3/4)*(yz+zx+xy)/(x+y+z)^2≥2xyz/(y+z)(z+x)(x+y); ﻫ<====>3(y+z)(z+x)(x+y)(yz+zx+xy)≥8xyz(x+y+z)^2;ﻫ上式展开等价于ﻫ3x^3(y^2+z^2)+3y^3(z^2+x^2)+3z^3(x^2+y^2)-2xyz(x^2+y^2+z^2)-4xyz(yz+zx+xy)≥0;
几何不等式-3
命题设P是三角形ABC内一点,点P在三边BC,CA,AB上的射影分别为D,E,F。则三角形DEF叫做点P的垂足三角形。试证点P的垂足三角形DEF的面积不超过三角形ABC面积的四分之一。
证明 设P点垂足ΔDEF面积为F,ΔABC面积为Δ,
令PD=r1,PE=r2,PC=r3,BC=a,CA=b,AB=c,R表示三角形ABC的外接圆半径。则有
上式化简等价于ﻫx^2(x+2y+2z)(y-z)^2+y^2(y+2z+2x)(z-x)^2+z^2(z+2x+2y)(x-y)^2≥0.
因为P点在正△ABC内,故x>0,y>0,z>0,所以上式显然成立。命题得证。
几何不等式-2
命题设P是三角形ABC内一点,直线AP,BP,CP与三边的交点分别为D,E,F。则三角形DEF叫做点P的塞瓦三角形。试证点P的塞瓦三角形DEF的面积不超过三角形ABC面积的四分之一。
证明设三角形ABC的面积为S,塞瓦三角形DEF的面积为S1,三角形AEF的面积为Sa,三角形BFD的面积为Sb,三角形CDE的面积为Sc。令BD=xBC,CE=yCA,AF=zAB,则CD=(1-x)BC,AE=(1-y)CA,BF=(1-z)AB。那么
Sa=(AE*AF*sinA)/2=z*(1-y)*S,
几何计算-1
命题设点D是Rt△ABC斜边AB上的一点,DE⊥BC于点E,DF⊥AC于点F。若AF=15,BE=10,则四边形DECF的面积是多少?
解:设DF=CE=x,DE=CF=y.∵Rt△BED∽Rt△DFA,∴BE/DE=DF/AF
<==>10/y=x/15<==> xy=150.ﻩ
所以,矩形DECF的面积150.
同理可得:OQ+OS=(DA+BC)/2。
因此有OP+OQ+OR+OS=(AB+BC+CD+DA)/2。
几何不等式-1
命题设P是正△ABC内任意一点,△DEF是P点关于正△ABC的内接三角形[AP,BP,CP延长分别交BC,CA,AB于D,E,F],记面积为S1;△KNM是P点关于正△ABC的垂足三角形[过P点分别作BC,CA,AB垂线交于K,N,M],记面积为S2。求证:S2≥S1。
△AEF的面积X=AE*AF*sin60°/2=Syz/(z+x)(x+y);
△BFD的面积Y=BF*BD*sin60°/2=Szx/(x+y)(y+z);
△CDE的面积Z=CD*CE*sin60°/2=Sxy/(y+z)(z+x).
从而有S1=S-X-Y-Z=2xyzS/(y+z)(z+x)(x+y)。ﻫ因为P点是△KNM的费马点,从而易求得:
