初中-数学-北师大版-3 相似多边形同步练习(一)
北师大版九年级数学上册第四章4.3相似多边形 同步测试(含答案)

北师大版九年级数学上册第四章4.3相似多边形 同步测试一、选择题1.下列说法正确的是( )A. 矩形都是相似图形B. 各角对应相等的两个五边形相似C. 等边三角形都是相似三角形D. 各边对应成比例的两个六边形相似2.用一个2倍放大镜照一个△ABC ,下面说法中错误的是( )A .△ABC 放大后,是原来的2倍B .△ABC 放大后,各边长是原来的2倍C .△ABC 放大后,周长是原来的2倍D .△ABC 放大后,面积是原来的4倍3.在矩形ABCD 中,E ,F 分别为AB ,CD 的中点,如果矩形ABCD ∽矩形EFCB ,那么它们的相似比为( )A .2B .22C .2D .21 4.如果六边形ABCDEF ∽六边形A′B′C′D′E′F′,∠B=62°,那么∠B ′等于( )A. 28°B. 118°C. 62°D. 54°5.两个相似多边形的一组对分别是3cm 和4.5cm ,如果它们的面积之和是278cm ,那么较大的多边形的面积是( )A .44.8B .42C .52D .546.小张用手机拍摄得到(1),经放大后得到图(2),图(1)中的线段AB 在图(2)中的对应线段是( )A .FGB .FHC .EHD .EF7.在下面的图形中,相似的一组是( )A. B. C. D.4000m的多边形草坪,在嘉兴市政建设规划设计图纸上的面积为8.某块面积为22250cm,这块草坪某条边的长度是40m,则它在设计图纸上的长度是()A.4cm B.5cm C.10cm D.40cm9. 在下列命题中,正确的是()A. 邻边之比相等的两个平行四边形一定相似B. 有一个角是70∘两个等腰三角形一定相似C. 两个直角三角形一定相似D. 有一个角是60∘的两个菱形一定相似10.如果两个相似多边形面积的比为1:5,则它们的相似比为()A.1:25 B.1:5 C.1:2.5 D.1二、填空题11.相似多边形对应边之比叫做______.12.如果图形甲与图形乙相似,图形乙与图形丙相似,那么图形甲与图形丙=______,a=______.13.图中的两个四边形相似,则x y14.等边三角形ABC和三角形A′B′C′相似,相似比为5:2,若AB=10,B′C′等于15. 给出下列几何图形:①两个圆;②两个正方形;③两个矩形;④两个正六边形;⑤两个等边三角形;⑥两个直角三角形;⑦两个菱形.其中,一定相似的有(填序号).16.如图,E、F分别是平行四边形ABCD的边AD、BC的中点,若四边形AEFB与四边形ABCD相似,AB=4,则AD的长度为______.三、解答题17.在实际生活中,我们常常看到许多相似的图形,请找出图中所有的相似图形.18.把一个长方形(如图)划分成两个全等的长方形.若要使每一个小长方形与原长方形相似,问原长方形应满足什么条件?19.梯形ABCD 中,AD ∥BC ,E ,F 分别为AB ,CD 上一点,且梯形AEFD ∽梯形EBCF ,若AD =4,BC =9。
2022-2023学年北师大版九年级上册数学3 相似多边形同步练习

2022-2023学年北师大版九年级上册数学3 相似多边形同步练习一、单选题(共15题,共计45分)1、下列四组图形中,不是相似图形的是()A. B. C. D.2、下列各组图形中,一定相似的是()A.两个矩形B.两个菱形C.两个正方形D.两个等腰三角形3、如图,将矩形ABCD密铺在长为4cm.宽为2cm的矩形纸片右侧,若组成的新矩形与原矩形(图中阴影部分)相似,则AB=()cm.A.3B.6C.8D. ﹣14、下列生活现象中,属于相似变换的是()A.抽屉的拉开B.汽车刮雨器的运动C.荡秋千D.投影片的文字经投影变换到屏幕5、两个相似五边形,一组对应边的长分别为3cm和4.5cm,如果它们的面积之和是78cm2,则较大的五边形面积是()cm2。
A.44.8B.52C.54D.426、如图,这是圆桌正上方的灯泡(看作一个点)发出的光线照射到桌面后在地面上形成(圆形)的示意图. 已知桌面直径为1.2米,桌面离地面1米. 若灯泡离地面3米,则地面上阴影部分的面积()A.0.36π米2B.0.81π米2C.2π米2D.3.24π米27、下列说法中,错误的是( )A.正六边形都相似B.等腰直角三角形都相似C.矩形都相似D.正方形都相似8、若一个图形的面积为2,那么将它与成中心对称的图形放大为原来的两倍后的图形面积为()A.8B.6C.4D.29、两个多边形相似的条件是()A.对应角相等B.对应边相等C.对应角相等,对应边相等D.对应角相等,对应边成比例10、将矩形ABCD按如图方式铺在长为4cm.宽为2cm的矩形纸片(图中阴影部分)右侧,若组成的新矩形与原矩形(图中阴影部分)相似,则AB=()cm.A.3B.6C.8D. ﹣111、下列说法不正确的是()A.在平移变换中,图形中的每一个点都沿同一方向移动了相同的距离B.在旋转变换中,图形中的每一点都绕旋转中心旋转了相同的角度C.在相似变换中,图形中的每一个角都扩大(或缩小)相同的倍数D.在相似变换中,图形中的每一条线段都扩大(或缩小)相同的倍数12、如果两个相似多边形的面积之比为1:4,那么它们的周长之比是( )A.1:2B.1:4C.1:8D.1:1613、在研究相似问题时,甲、乙同学的观点如下:甲:将边长为3、4、5的三角形按图1的方式向外扩张,得到新三角形,它们的对应边间距为1,则新三角形与原三角形相似.乙:将邻边为3和5的矩形按图2的方式向外扩张,得到新的矩形,它们的对应边间距均为1,则新矩形与原矩形不相似.对于两人的观点,下列说法正确的是()A.两人都对B.两人都不对C.甲对,乙不对D.甲不对,乙对14、下列生活中的现象,属于相似变换的是()A.抽屉的拉开B.汽车刮雨器的运动C.坐在秋千上人的运动D.投影片的文字经投影变换到屏幕15、将一个菱形放在2倍的放大镜下,则下列说法中不正确的是()A.菱形的边长扩大到原来的2倍B.菱形的角的度数不变C.菱形的面积扩大到原来的2倍D.菱形的面积扩大到原来的4倍二、填空题(共10题,共计30分)16、已知正方形ABCD的面积为9cm2,正方形EFGH的面积为16cm2,则两个正方形边长的相似比为________.17、两个相似三角形________ 的比值叫做相似比.18、有一张矩形风景画,长为90cm,宽为60cm,现对该风景画进行装裱,得到一个新的矩形,要求其长、宽之比与原风景画的长、宽之比相同,且面积比原风景画的面积大44%.若装裱后的矩形的上、下边衬的宽都为acm,左、右边衬的宽都为bcm,那么ab=________ cm219、现有大小相同的正方形纸片若干张,小明想用其中的3张拼成一个如图所示的长方形,小芳也想拼一个与它形状相同但比它大的长方形,则她最少要用________ 张正方形纸片(每个正方形纸片不得剪开).20、图中的两个四边形相似,则=________°,a=________°.21、两个形状相同的图形,________ 不一定相等.22、把一个长方形按如图方式划分成三个全等的小长方形,每一个小长方形与原长方形相似,若小长方形的宽为2,则原长方形的宽x为________。
4.3相似多边形 同步练习 2021--2022学年北师大版九年级数学上册

4.3相似多边形同步练习一、选择题1.下列结论中正确的是()A.有两条边长是3和4的两个直角三角形相似B.一个角对应相等的两个等腰三角形相似C.两边对应成比例且一个角对应相等的两个三角形相似D.有一个角为60°的两个等腰三角形相似2.两个相似五边形的相似比为2:3,则它们的面积比为()A.2:3 B.3:2 C.4:9 D.9:43.下列各组图形一定相似的是()A.两个矩形B.两个等边三角形C.各有一角是80°的两个等腰三角形D.任意两个菱形4.下列各组图形相似的是()A.B.C.D.5.已知两个相似多边形的面积比是9:16,其中较小多边形的周长为36cm,则较大多边形的周长为()A.48 cm B.54 cm C.56 cm D.64 cm6.如果两个相似多边形的周长比为1:5,则它们的面积比为()A.1:2.5 B.1:5 C.1:25 D.1:7.如图所示的三个矩形中,是相似的是()A.甲与乙B.乙与丙C.甲与丙D.甲乙丙都相似8.如图,取一张长为a,宽为b的长方形纸片,将它对折两次后得到一张小长方形纸片,若要使小长方形与原长方形相似,则原长方形纸片的边a、b应满足的条件是()A.a=b B.a=2b C.a=2b D.a=4b9.已知A4纸的宽度为21cm,如图对折后所得的两个矩形都和原来的矩形相似,则A4纸的高度约为()A.24.8cm B.26.7cm C.29.7cm D.无法确定10.若四边形ABCD与四边形A′B′C′D′相似,AB与A′B′,AD与A′D′分别是对应边,AB =8cm,A′B′=6cm,AD=5cm,则A′D′等于()A.cm B.cm C.cm D.cm二、填空题11.两个相似多边形面积比是9:25,其中较小多边形的周长为36cm,则另一个多边形的周长是.12.有一张矩形风景画,长为90cm,宽为60cm,现对该风景画进行装裱,得到一个新的矩形,要求其长、宽之比与原风景画的长、宽之比相同,且面积比原风景画的面积大44%.若装裱后的矩形的上、下边衬的宽都为acm,左、右边衬的宽都为bcm,那么ab=.13.把一个正多边形放大到原来的2.5倍,则原图与新图的相似比为.14.在一张由复印机通过放大复印出来的纸上,一个面积为2cm2图案的一条边由原来的1cm变成3cm,则这次复印出来的图案的面积是cm2.三、解答题15.如图所示,四边形ABCD∽四边形A′B′C′D′,求未知边x的长度和α的大小.16.如图,现有一个边长是1的正方形ABCD,在它的左侧补一个矩形ABEF,使所得矩形CEFD∽矩形ABEF,求BE的长.17.我们通常用到的一种复印纸,整张称为A1纸,对折一分为二裁开成为A2纸,再一分为二成为A3纸,…,它们都是相似的矩形.求这种纸的长与宽的比值(精确到千分位).18.如图,如图用一根铁丝分成两段可以分别围成两个相似的五边形,已知它们的面积比是1:4,其中小五边形的边长为(x2﹣4)cm,大五边形的边长为(x2+2x)cm(其中x>0).求这这根铁丝的总长.19.试判断如图所示的两个矩形是否相似.20.两个相似五边形,一组对应边的长分别为3cm和4.5cm,如果它们的面积之和是78cm2,则这两个五边形面积各是多少cm2?21.把一个长方形(如图)划分成两个全等的长方形.若要使每一个小长方形与原长方形相似,问原长方形应满足什么条件?。
北师大版九年级数学《相似多边形》典型例题(含答案)
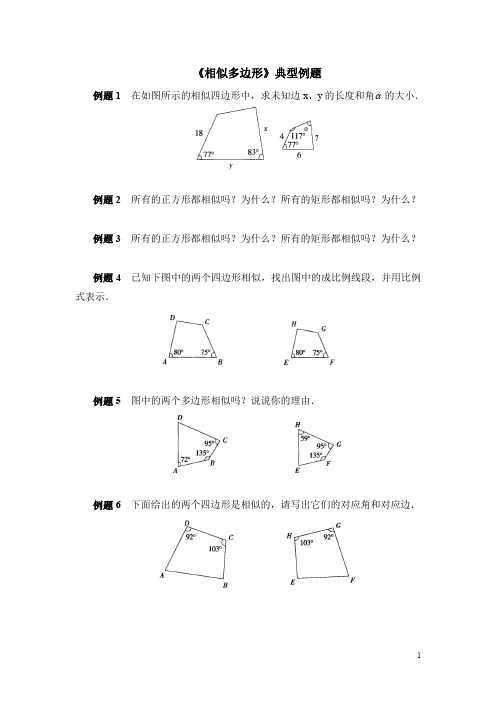
《相似多边形》典型例题例题1在如图所示的相似四边形中,求未知边x、y的长度和角 的大小.例题2所有的正方形都相似吗?为什么?所有的矩形都相似吗?为什么?例题3 所有的正方形都相似吗?为什么?所有的矩形都相似吗?为什么?例题4 已知下图中的两个四边形相似,找出图中的成比例线段,并用比例式表示.例题5图中的两个多边形相似吗?说说你的理由.例题6下面给出的两个四边形是相似的,请写出它们的对应角和对应边.例题7 已知图中的两个梯形相似,求出未知边x 、y 、z 的长度和βα∠∠、的度数.例题8 在如图所示的相似四边形中,求未知边x 、y 的长度和角α的大小.参考答案例题1 解答 ∵两个四边形相似,它们的对应边成比例,对应角相等. ∴67418y x ==, ∴27,5.31==y x .︒=︒+︒+︒-︒=83)1178377(360α.例题2 解答:所有的正方形都相似,因为正方形的每个角都是90°,因此对应角都相等,而每一个正方形的边长都相等,因此对应边成比例.所有的矩形不一定相似,虽然所有的矩形的角都相等,但对应的边不一定成比例,因此,矩形不一定相似.例题3 解答:所有的正方形都相似,因为正方形的每个角都是90°,因此对应角都相等,而每一个正方形的边长都相等,因此对应边成比例.所有的矩形不一定相似,虽然所有的矩形的角都相等,但对应的边不一定成比例,因此,矩形不一定相似.例题4 解答 HEDA GH CD FG BC EF AB === 例题5 解答 不相似.︒=︒-︒-︒-︒=∠587295135360D ,而︒=︒-︒-︒-︒=∠715995135360E ,不可能有“对应角相等”.例题6 解答 F A ∠→∠ E B ∠→∠ H C ∠→∠ G D ∠→∠FE AB → EH BC → HG CD → GF DA →例题7 分析 解题中要充分利用相似多边形的特征和梯形的性质. 解答 由于对应边成比例,所以232.38.45.442====z y x . 所以3,6,3===z y x .由于对应角相等,所以 ︒=∠-︒=∠=∠118180A D α,︒='∠-︒='∠=∠70180C B β.例题8 解答 ∵两个四边形相似,它们的对应边成比例,对应角相等. ∴67418y x ==,∴27,5.31==y x .︒=︒+︒+︒-︒=83)1178377(360α.。
八年级数学下册 《相似多边形》同步练习1 北师大版

4.4 相似多边形同步练习本课导学点击要点________相等、________成比例的两个多边形叫做相似多边形.学习策略解答本节习题应把握以下几方面:(1)了解相似多边形的含义;(2)进一步发展归纳、类比、反思、交流等方面的能力;(3)解题过程中注意对应关系.中考展望本节知识在中考中主要考查相似多边形的含义,多为选择题、填空题.随堂测评基础巩固一、训练平台(第1~5小题各6分,第6小题10分,共40分)1.两个多边形相似的条件是()A.对应角相等 B.对应边相等C.对应角相等,对应边相等 D.对应角相等,对应边成比例2.下列图形是相似多边形的是()A.所有的平行四边形; B.所有的矩形 C.所有的菱形; D.所有的正方形3.找出两类永远相似的图形_________、_________.4.在四边形ABCD与四边形A′B′C′D′中,∠A=∠A′,∠B=∠B′,∠C=∠C′,•∠D=∠D′,且,则四边形________∽四边形________,且它们的相似比是________.5.有一个角为120°的菱形与有一个角为________的菱形相似.6.把一个矩形剪去一个正方形,若剩余的矩形和原矩形相似,求原矩形的长与宽的比.能力升级二、提高训练(第1~3小题各6分,第4小题10分,共28分)1.下列命题正确的是()A.有一个角对应相等的平行四边形相似 B.对应边成比例的两个平行四边形相似 C.有一个角对应相等的两个等腰梯形相似;D.有一个角对应相等的两个菱形相似2.下列说法中正确的是()A.相似形一定是全等形 B.不全等的图形不是相似形C.全等形一定是相似形 D.不相似的图形可能是全等形3.如图所示,有三个矩形,其中是相似形的是()A.甲和乙 B.甲和丙 C.乙和丙 D.甲、乙和丙4.已知如图所示的两个梯形相似,求出未知的x,y,z的长和∠α,∠β的度数.三、探索发现(每小题12分,共24分)1.相片框(如图所示)中,内外两个矩形是否相似?2.暑假时,康子帮母亲到鱼店去买鱼,鱼店里有一种“竹笑鱼”,个个都长得非常相似,现在根据大小有两种不同的价格,如图所示,鱼长10cm的每条100日元,鱼长18cm的每条150日元,康子不知道买哪条更好些,你看怎么办?四、拓展创新(共8分)如图所示,甲、乙是两个不同的正方体,正方体都是相似体,•它们的一切对应线段之比都等于相似比(a:b),设S甲,S乙分别表示两个正方体的表面积,则,又设V甲,V乙分别表示这两个正方体的体积,则,下列几何体中,一定属于相似体的是()A.两个球体 B.两个圆柱体 C.两个圆锥体 D.两个长方体中考演练(中考预测题)把矩形对折后,和原来的矩形相似,那么这个矩形的长、宽之比为()A.2:1 B.4:1 C.:1 D.:1答案:本课导学各角对应各边对应随堂测评一、1.D 2.D 3.正方形等边三角形4.ABCD A′B′C′D′ 2:35.•60°或120° 6.(-1):2二、1.D 2.C 3.B4.x=3,y=3,z=6,∠α=70°,∠β=120°.三、1.不相似. 2.买18cm长的鱼更合算.四、A※C。
北师大版九年级数学4.3相似多边形1(含答案)
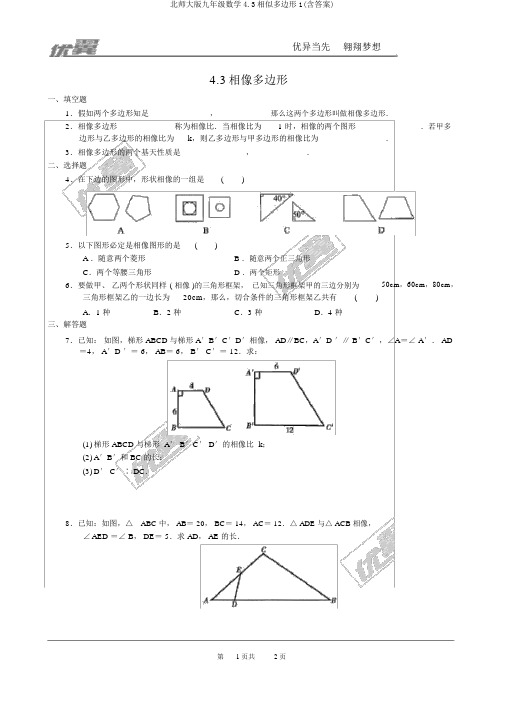
优异当先翱翔梦想4.3相像多边形一、填空题1.假如两个多边形知足____________, ____________那么这两个多边形叫做相像多边形.2.相像多边形 ____________称为相像比.当相像比为 1 时,相像的两个图形____________ .若甲多边形与乙多边形的相像比为k,则乙多边形与甲多边形的相像比为____________.3.相像多边形的两个基天性质是____________, ____________.二、选择题4.在下边的图形中,形状相像的一组是()5.以下图形必定是相像图形的是()A .随意两个菱形B .随意两个正三角形C.两个等腰三角形 D .两个矩形6.要做甲、乙两个形状同样( 相像 )的三角形框架,已知三角形框架甲的三边分别为三角形框架乙的一边长为20cm,那么,切合条件的三角形框架乙共有( A.1 种B.2 种C.3 种D.4 种)50cm,60cm,80cm,三、解答题7.已知:如图,梯形 ABCD 与梯形 A′B′C′D′相像, AD∥BC,A′D ′∥ B′C′,∠A=∠ A′. AD =4, A′D ′= 6, AB= 6, B′ C′= 12.求:(1)梯形 ABCD 与梯形 A′ B′C′ D′的相像比 k;(2)A′B′和 BC 的长;(3)D′ C′∶ DC.8.已知:如图,△ABC 中, AB= 20, BC= 14, AC= 12.△ ADE 与△ ACB 相像,∠AED =∠ B, DE= 5.求 AD, AE 的长.优异当先 翱翔梦想9.已知:如图,四边形 ABCD 的对角线订交于点 O , A ′, B ′, C ′, D ′分别是 OA , OB , OC ,OD 的中点,试判断四边形 ABCD 与四边形 A ′ B ′ C'D ′能否相像,并说明原因.10.以以下图甲所示,在矩形 ABCD 中, AB = 2AD .如图乙所示,线段EF = 10,在 EF 上取一点 M ,分别以 EM , MF 为一边作矩形EMNH 、矩形 MFGN ,使矩形 MFGN ∽矩形 ABCD ,设 MN = x ,当 x 为什么值时,矩形 EMNH 的面积 S 有最大值 ?最大值是多少 ?答案 :1.对应角相等,对应边的比相等.1 2.对应边的比,全等,k3.对应角相等,对应边的比相等. 4.C5. B6.C7. (1) k =2∶ 3; (2)A 'B '= 9, BC = 8; (3)3∶ 2. 8. AD30,AE50779.相像.10. x5时, S 的最大值为 2522。
北师大版数学九年级上册第四章第三节4.3 相似多边形 同步练习(包含答案)

第四章图形的相似第三节同步练习一、选择题1. 下图中,各组图形相似的是()A. ①③B. ③④C. ①②D. ①④2. 把一个图形按一定比例放大或缩小时,下列说法中正确的是()A. 图形中线段的长度与角的大小都保持不变B. 图形中线段的长度和角的大小都会改变C. 图形中线段的长度保持不变,角的大小可以改变D. 图形中线段的长度可以改变,角的大小保持不变3. 关于相似多边形的叙述不正确的是()A. 相似多边形对应边的比叫做相似比B. 边数不相同的多边形肯定不相似C. 相似多边形的对应角肯定相等D. 两个多边形不相似,它们肯定没有相等的角4. 一个多边形的边长分别为2,3,4,5,6,另一个和它相似的多边形的最长边为24,则这个多边形的最短边长为()A. 6B. 8C. 9D. 105. 若五边形ABCDE与五边形A1B1C1D1E1相似,且相似比为k1=5,则五边形A1B1C1D1E1与五边形ABCDE的相似比k2为()A. 2B. 15 C. 1.2 D. 16. 将一张矩形纸片ABCD沿AD和BC的中点连线EF对折,要使矩形AEFB与原矩形相似,则原矩形的长与宽的比是()A. 2∶1B. 2∶1C. 3∶1D. 2∶27. 已知五边形ABCDE∽五边形A1B1C1D1E1,且AB=2,BC=3,A1B1=4,则B1C1等于()A. 6B. 15C. 5D. 8 38. 在研究相似问题时,甲、乙同学的观点如下:甲:将边长为3,4,5的三角形按图1的方式向外扩张,得到新三角形,它们的对应边间距均为1,则新三角形与原三角形相似.乙:将邻边为3和5的矩形按图2的方式向外扩张,得到新矩形,它们的对应边间距均为1,则新矩形与原矩形不相似.对于两人的观点,下列说法正确的是()A. 两人都对B. 两人都不对C. 甲对,乙不对D. 甲不对,乙对9. 以下五个命题:①所有的正方形都相似;②所有的矩形都相似;③所有的三角形都相似;④所有的等腰直角三角形都相似;⑤所有的正五边形都相似.其中正确的有.(填序号)10. 如图,四边形ABCD与四边形A′B′C′D′相似,则∠α=,∠β=,AD=.11. 两个正方形的相似比为4∶1,其中较大的正方形的边长为12,则较小正方形的周长为多少?12. 甲同学手中有四根木棒,长度分别为18cm,21cm,12cm,9cm,乙同学手中有四根木棒,长度分别为6cm,7cm,4cm,3cm,甲同学说:以我手中的四根木棒组成的四边形一定与你手中四根棒组成的四边形相似,因为它们的对应边的比是3∶1.乙同学不同意他的看法,为什么?13. 如图,四边形ABCD与四边形EFGH相似吗?请说明理由.14. 如图所示,一个矩形长为a,宽为b(a≠b),若在矩形外侧增加宽度为c的边框,那么所得的矩形和原来的矩形相似吗?为什么?15. 两个正六边形,小正六边形的边长为3cm,大正六边形的周长为24cm.(1)这两个正六边形是否相似?为什么?(2)这两个正六边形中最长对角线的比是多少?16. 如图,已知梯形ABCD,AD∥BC,若EF∥BC,且所分成的梯形AEFD相似于梯形EBCF,AD=12,BC=18,求EF的长.17. 如图,将一张长、宽之比为2的矩形纸ABCD循环多次对折,可以得到矩形纸BCFE,AEML,GMFH,LGPN.(1)矩形ABCD,BCFE,AEML,GMFH,LGPN的长与宽的比改变了吗?(2)在这些矩形中,有成比例的线段吗?(3)你认为这些大小不同的矩形相似吗?1. C2. D3. D4. B5. B6. A7. A8. A9. ①④⑤10. 70° 120° 2811. 解:12 12. 解:因为两个四边形相似除了对应边成比例外,还要求对应角相等,所以虽然它们的对应边之比为3∶1,也不能保证它们相似.13. 解:不一定相似.理由:在四边形ABCD 中,由∠A =80°,∠B =90°,∠C =120°,得∠D =70°.在四边形EFGH 中,由∠F =90°,∠G =120°,∠H =70°,得∠E =80°,∴∠A =∠E ,∠B =∠F ,∠C =∠G ,∠D =∠H .∵根据已知条件无法判定对应边是否对应成比例.∴四边形ABCD 与四边形EFGH 不一定相似.14. 解:不相似.根据题意,外面矩形的长为a +2c ,宽为b +2c ,∵两个矩形的宽之比为b b +2c =1+b 2c ,长之比为a a +2c =1+a 2c ,又∵a ≠b ,∴a 2c ≠b 2c ,1+a 2c ≠1+b 2c ,即a a +2c ≠b b +2c ,∴两个矩形不相似.15. 解:(1)相似,对应角相等,对应边成比例.(2)大正六边形的边长是24÷6=4(cm).因两个正六边形相似,故两个正六边形最长对角线之比为3∶4.16. 解:∵梯形AEFD ∽梯形EBCF .∴EF AD =BC EF ,即EF 2=AD ·BC =12×18=216,∴EF =6(EF =-6不符题意,舍去).17. 解:(1)矩形ABCD ,BCFE ,AEML ,GMFH ,LGPN 的长与宽的比不改变.设纸的宽为a ,长为a ,则BC =a ,BE =22a ;AE =22a ,ME =2a ,MF =2a ,HF =42a ;LG =42a ,LN =4a ;∴BE BC =a ∶22a =;ME AE =22a ∶2a =;HF MF =2a ∶42a =;LN LG =42a ∶4a =;所以这五个矩形的长与宽的比不改变.(2)这些矩形中有成比例的线段.(3)这些大小不同的矩形都相似.。
最新2019-2020年度北师大版九年级数学上册《相似多边形》同步练习及答案解析-精品试题

北师大版九年级数学上册3.3相似多边形同步练习一、选择题1.用一个2倍放大镜照一个△ABC,下面说法中错误的是()A.△ABC放大后,是原来的2倍B.△ABC放大后,各边长是原来的2倍C.△ABC放大后,周长是原来的2倍D.△ABC放大后,面积是原来的4倍答案:A解析:解答:∵放大前后的三角形相似,∴放大后三角形的内角度数不变,面积为原来的4倍,周长和边长均为原来的2倍.故本题选A.分析:用2倍的放大镜放大一个△ABC,得到一个与原三角形相似的三角形;根据相似三角形的性质:相似三角形的面积比等于相似比的平方,周长比等于相似比.可知:放大后三角形的面积是原来的4倍,边长和周长是原来的2倍,而内角的度数不会改变.2.我国国土面积约为960万平方千米,画在比例尺为1:1000万的地图上的面积约是()A.960平方千米B.960平方米C.960平方分米D.960平方厘米答案:D解析:解答:16万平方千米平方厘米,=⨯9609.610设画在地图上的面积约为x平方厘米,则162x⨯=:(:万),9.61011000解得x=960.则画在地图上的面积约为960平方厘米.故选D.分析:相似多边形的面积比等于相似比的平方,据此求解,注意统一单位.3.如图,一张矩形纸片ABCD 的长AB=a ,宽BC=b .将纸片对折,折痕为EF ,所得矩形AFED 与矩形ABCD 相似,则a :b=( )A .2:1B .2:1C .3:3D .3:2答案:B解析:解答:∵矩形纸片对折,折痕为EF , ∴1122AF AB a ==, ∵矩形AFED 与矩形ABCD 相似, ∴AB AD AD AF =,即12a b b a =, ∴22a b=(), ∴2a b=. 故选B . 分析:根据折叠性质得到1122AF AB a ==,再根据相似多边形的性质得到AB AD AD AF =,即12a b b a =,然后利用比例的性质计算即可. 4.两个相似多边形的一组对分别是3cm 和4.5cm ,如果它们的面积之和是278cm ,那么较大的多边形的面积是( )A .44.8B .42C .52D .54答案:D解析:解答:设较大多边形与较小多边形的面积分别是m ,n .则2344.59n m ==(). 因而49n m =. 根据面积之和是78cm2.得到4789m m +=. 解得:254m cm =.故选D .分析:根据相似多边形相似比即对应边的比,面积的比等于相似比的平方,即可解决.5.两个相似多边形的面积之比为1:9,则它们的周长之比为( )A .1:3B .1:9C .1:3D .2:3答案:A解析:解答:∵两个相似多边形的面积之比为1:9,∴两个相似多边形的边长之比是1:3,∴它们的周长之比为1:3.故选A .分析:根据相似多边形的面积之比等于相似比的平方和相似多边形的周长之比等于相似比得出即可.6.如图所示,两个等边三角形,两个矩形,两个正方形,两个菱形各成一组,每组中的一个图形在另一个图形的内部,对应边平行,且对应边之间的距离都相等,那么两个图形不相似的一组是( )A .B .C .D .解析:解答:由题意得,A 中三角形对应角相等,对应边成比例,两三角形相似;C ,D 中正方形,菱形四条边均相等,所以对应边成比例,又角也相等,所以正方形,菱形相似;而B 中矩形四个角相等,但对应边不一定成比例,所以B 中矩形不是相似多边形 故选B .分析:此题考查相似多边形的判定问题,其对应角相等,对应边成比例.7.某块面积为24000m 的多边形草坪,在嘉兴市政建设规划设计图纸上的面积为2250cm ,这块草坪某条边的长度是40m ,则它在设计图纸上的长度是( )A .4cmB .5cmC .10cmD .40cm答案:C解析:解答:设这块草坪在设计图纸上的长度是xcm ,224000m 40000000m =,40m=4000cm , 根据题意得:2400000004000250x=(), 解得:x=10,即这块草坪在设计图纸上的长度是10cm .故选C .分析:首先设这块草坪在设计图纸上的长度是xcm ,根据题意可得这两个图形相似,根据相似图形的面积比等于相似比的平方,可列方程2400000004000250x=(),解此方程即可求得答案,注意统一单位.8.一个多边形的边长分别为2,3,4,5,6,另一个多边形和这个多边形相似,且最短边长为6,则最长边长为( )A .18B .12C .24答案:A解析:解答:设这个多边形的最长边是x,则26=,6x解得x=18.故选A.分析:根据题意找出最短边与最长边,然后根据相似多边形对应边成比例列式计算即可.9.若两个相似多边形的面积之比为1:4,则它们的周长之比为()A.1:4B.1:2C.2:1D.4:1答案:B解析:解答:∵两个相似多边形面积比为1:4,∴周长之比为112=:.4故选:B.分析:根据相似多边形的面积之比等于相似比的平方,周长之比等于相似比,就可求解.10.如果两个相似多边形面积的比为1:5,则它们的相似比为()A.1:25B.1:5C.1:2.5D.15:答案:D解析:解答:∵两个相似多边形面积的比为1:5,:.∴它们的相似比为15故选:D.分析:根据相似多边形的面积的比等于相似比的平方解答.11.对一个图形进行放缩时,下列说法中正确的是()A.图形中线段的长度与角的大小都保持不变B.图形中线段的长度与角的大小都会改变C.图形中线段的长度保持不变、角的大小可以改变D.图形中线段的长度可以改变、角的大小保持不变答案:D解析:解答:根据相似多边形的性质:相似多边形的对应边成比例,对应角相等,∴对一个图形进行收缩时,图形中线段的长度改变,角的大小不变,故选D.分析:根据相似图形的性质得出相似图形的对应边成比例,对应角相等,即可得出答案.12.下面给出了一些关于相似的命题,其中真命题有()(1)菱形都相似;(2)等腰直角三角形都相似;(3)正方形都相似;(4)矩形都相似;(5)正六边形都相似.A.1个B.2个C.3个D.4个答案:C解析:解答:(1)所有菱形的对应角不一定相等,故菱形不一定都相似;(2)等腰直角三角形都相似,正确;(3)正方形都相似,正确;(4)矩形对应边比值不一定相等,不矩形不一定都相似;(5)正六边形都相似,正确,故符合题意的有3个.故选:C.分析:利用相似图形的性质分别判断得出即可.13.如果两个相似多边形的面积比为16:9,那么这两个相似多边形的相似比为()A.16:9B.4:3C.2:3D.256:81解析:解答:根据题意得:164.93故选:B.分析:根据两个相似多边形的面积比为16:9,面积之比等于相似比的平方.14.下列判断正确的是()A.所有的直角三角形都相似B.所有的等腰直角三角形都相似C.所有的菱形都相似D.所有的矩形都相似答案:B解析:解答:A、所有的直角三角形只有直角相等,所以不一定都相似,故本选项错误;B、所有的等腰直角三角形都相似正确,故本选项正确;C、所有的菱形只有对应边成比例,对应角不一定相等,所以,不一定相似,故本选项错误;D、所有的矩形对应角相等,对应边不一定成比例,所以不一定相似,故本选项错误.故选B.分析:根据对应边成比例,对应角相等的图形叫做相似图形对各选项分析判断后利用排除法求解.15.如图,用放大镜将图形放大,这种图形的改变是()A.相似B.平移C.轴对称D.旋转答案:A解析:解答:根据相似图形的定义知,用放大镜将图形放大,属于图形的形状相同,大小不相同,所以属于相似变换.分析:根据轴对称变换、平移变换、旋转变换、相似变换的特点,结合图形即可得出答案.二、填空题16.若两个相似多边形的对应边之比为5:2,则它们的周长比是_____.答案:5:2解析:解答:∵两个相似多边形的对应边的比是5:2,∴这两个多边形的周长比是5:2.故答案为:5:2.分析:根据相似多边形的周长的比等于相似比解答即可.17.图中的两个四边形相似,则x y +=______,a=______.答案:63|85°解析:解答:由于两个四边形相似,它们的对应边成比例,对应角相等,所以18486x y ==:::,解得x=36,y=27,则362763x y +=+=. 360778311585a =︒-︒+︒+︒=︒().故答案为63;85°.分析:根据相似多边形的性质:对应角相等,对应边成比例即可求解.18.若两个相似多边形的面积比是16:25,则它们的周长比等于______.答案:4:5解析:解答:∵两个相似多边形面积的比为16:25,∴两个相似多边形周长的比等于4:5,∴这两个相似多边形周长的比是4:5.故答案为:4:5.分析:直接根据相似多边形周长的比等于相似比,面积的比等于相似比的平方进行解答即可.19.如图,在长8cm ,宽4cm 的矩形中截去一个矩形(阴影部分)使留下的矩形与原矩形相似,那么留下的矩形的面积为______2cm .答案:8解析:解答:设留下的矩形的宽为x ,∵留下的矩形与原矩形相似, ∴ 4 48x =, x=2,∴留下的矩形的面积为:2248cm ⨯=()故答案为:8.分析:本题需先设留下的矩形的宽为x ,再根据留下的矩形与矩形相似,列出方程即可求出留下的矩形的面积.20.如图,E 、F 分别是平行四边形ABCD 的边AD 、BC 的中点,若四边形AEFB 与四边形ABCD 相似,AB=4,则AD 的长度为______.答案:42解析:解答:设AE=x ,则AD=2x ,∵四边形ABCD 与矩四边形ABFE 是相似的, ∴AE AB AB AD=, ∴222AB x =, ∴24AB x ==, ∴22x =, ∴42AD =, 故答案为:42.分析:首先设AE=x ,则AD=2x ,进而利用四边形ABCD 与四边形ABFE 是相似的,则AE AB AB AD=,进而求出即可三、解答题21.如图,四边形ABCD 和四边形EFGH 相似,求∠α、∠β的大小和EH 的长度.答案:解答:∵四边形ABCD 和四边形EFGH 相似,∴∠α=∠B=83°,∠D=∠H=118°,360837811881β∠=︒-︒+︒+︒=︒(),EH AD HG DC =::, ∴242118EH =, ∴EH=28(cm ).答:∠α=83°,∠β=81°,EH=28cm .解析:分析:观察图形,根据相似多边形的对应角相等可得出∠α=∠B=83°,∠D=∠H=118°,再根据四边形的内角和等于360°可计算求出β的大小,然后根据相似多边形的对应边成比例即可求出EH 的长度.22.两个相似五边形,一组对应边的长分别为3cm 和4.5cm ,如果它们的面积之和是278cm ,则这两个五边形面积各是多少2cm ?答案:解答:设较小五边形与较大五边形的面积分别是2cm x ,2cm y . 则2344.59x y ==(),因而49x y =. 根据面积之和是278cm ,得到4789y y +=, 解得:54y =, 则454249x =⨯=.即较小五边形与较大五边形的面积分别是224cm ,254cm .解析:分析:根据相似多边形相似比即对应边的比,面积的比等于相似比的平方,即可解决.23.把一个长方形(如图)划分成两个全等的长方形.若要使每一个小长方形与原长方形相似,问原长方形应满足什么条件?答案:解答:设AE=ED=a ,AB=b ,∵每一个小长方形与原长方形相似, ∴2a b b a=, ∴222b a =,∵a,b 均为正数,∴2b a =, ∴2222AD a a AB b a===, ∴原长方形的长与宽之比为21:.解析:分析:设AE=ED=a ,AB=b ,根据每一个小长方形与原长方形相似,可知2a b b a =,再由a ,b 均为正数可知2b a =,故2222AD a a AB b a===,由此即可得出结论. 24.如图,把矩形ABCD 对折,折痕为MN ,矩形DMNC 与矩形ABCD 相似,已知2AD = ,求AB 的长.答案:解答:∵2AD =, ∴22MD NC ==,∵矩形DMNC 与矩形ABCD 相似, ∴NC MN AB AD =,即222AB AB =, ∴AB=1. 解析:分析:先根据2AD =求出MD 的长,再根据矩形DMNC 与矩形ABCD 相似得出矩形对应边的比例式,求出AB 的长即可.25.我们通常用到的一种复印纸,整张称为1A 纸,对折一分为二裁开成为2A 纸,再一分为二成为3A 纸,…,它们都是相似的矩形.求这种纸的长与宽的比值(精确到千分位). 答案:1.414解析:解答:设1A 纸的长为a ,宽为b ,2A 纸的长为b ,宽为2a , 由1A 、2A 纸的长与宽对应比成比例,得 12a b b a =, 故2 1.4141a b =≈. 故答案为:1.414.分析:分别设1A 纸的长为a ,宽为b ,2A 纸的长为b ,宽为2a ,再由相似多边形的对应边成比例列出比例式,求出a b 的值即可.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3 相似多边形同步练习(一)
一、选择题
1、下列说法中错误的是()
A. 相似多边形的对应边成比例
B. 相似多边形的对应角相等
C. 相似多边形的边数相同
D. 对应边成比例的两个多边形是相似多边形
2、两个相似五边形,一组对应边的长分别为3cm和4.5cm,则这两个多边形的相似比可能是()
A. 3
4
B.
5
6
C.
1
2
D.
2
3
3、如图所示的两个四边形相似,则∠α的度数是()
A. 60°
B. 75°
C. 87°
D. 120°
4、如图,四边形ABCD∠四边形A1B1C1D1,AB=12,CD=15,A1B1=9,则边C1D1的长是()
A. 10
B. 12
C. 45
4
D.
36
5
5、如图所示,正五边形FGHMN∠正五边形ABCDE,若AB∠FG=2∠3,则下列结论正确的是()
A. 2DE=3MN
B. 3DE=2MN
C. 3∠A=2∠F
D. 2∠A=3∠F
6、下列判断正确的是()
A. 两个对应角相等的多边形相似
B. 两个对应边成比例的多边形相似
C. 边数相同的正多边形都相似
D. 有一组角对应相等的两个平行四边形相似
7、如图,有三个矩形,其中相似的是()
A. 甲和乙
B. 甲和丙
C. 乙和丙
D. 没有相似的矩形
8、如图,两个菱形、两个等边三角形、两个矩形、两个正方形,各成一组,每组中的一个图形在另一个图形的内部,对应边平行,且对应边之间的距离都相等,那么两个图形不相似的一组是()
A. B. C. D.
9、下列说法中正确的是()
A. 两个直角三角形一定相似
B. 两个等腰三角形一定相似
C. 两个等腰直角三角形一定相似
D. 两个矩形一定相似
10、一个多边形的边长分别为2,3,4,5,6,另一个和它相似的多边形的最长边长为24,则这个多边形的最短边长为()
A. 6
B. 8
C. 12
D. 10
11、如图所示,一般书本的纸张是原纸张多次对开得到的,矩形ABCD沿EF对开后,再把矩形EFCD
沿MN对开,…,依此类推,若各种开本的矩形都相似,则AB
AD
等于()
A. 0.618
B.
C.
D. 2
二、填空题
12、如图,在四边形ABCD中,EF∠AB∠DC,AB=9,DC=4,若用EF把原四边形分成两个相似的小四边形,EF的长为______.
三、解答题
13、如图,在平面直角坐标系中,矩形OABC顶点的坐标分别为O(0,0),A(-2,0),B(-2,1),C(0,1),现把各点的坐标乘2,得到矩形ODEF,
(1)试证明:矩形OABC∠矩形ODEF;
(2)求矩形OABC与矩形ODEF的相似比.
答案第1页,共2页
参考答案
1、【答案】D
【分析】本题考查了相似多边形的性质。
【解答】D 错误,对应边成比例,对应角相等的两个多边形相似.
2、【答案】D
【分析】本题考查了相似多边形的性质。
【解答】两个多边形的相似比是
324.53=或者4.5332=,则相似比是23或32.故选D.
3、【答案】C
【分析】本题考查了相似多边形的性质。
【解答】根据相似多边形的特点可知对应角相等,所以∠α=360°-60°-138°-75°=87°.故选C. 4、【答案】C
【分析】本题考查了相似多边形的性质。
【解答】∠四边形ABCD∠四边形A 1B 1C 1D 1, ∴11AB CD A B C D =11
. ∠AB =12,CD =15,A 1B 1=9,
∠C 1D 1=91545124
⨯=.故选C. 5、【答案】B
【分析】本题考查了相似多边形的性质。
【解答】∠正五边形FGHMN∠正五边形ABCDE ,∠对应边成比例,对应角相等,∠DE∠MN =AB∠FG =2∠3,∠A =∠F ,∠3DE =2MN.故选B.
6、【答案】C
【分析】本题考查了相似多边形的判定。
【解答】C 正确,边数相同的正多边形都相似。
7、【答案】B
【分析】本题考查了相似多边形的判定。
【解答】三个矩形的角都是直角,甲、乙、丙短边与长边的比分别为2∠3,1.5∠2.5=3∠5,1∠1.5=2∠3,∠甲和丙相似.故选B.
8、【答案】C
【分析】本题考查了相似多边形的判定。
【解答】由题意得,B 中两个三角形对应角相等,对应边成比例,两个三角形相似;A ,D 中菱形、
正方形四条边均相等,所以对应边成比例,而角也相等,所以正方形、菱形都相似;而C中矩形的四个角相等,但对应边不成比例,所以C中的两个矩形不相似.
9、【答案】C
【分析】本题考查了相似多边形的判定。
【解答】C正确,两个等腰直角三角形一定相似。
10、【答案】B
【分析】本题考查了相似多边形的性质。
【解答】设这个多边形的最短边长为x.∠两个多边形相似,∠24∠6=x∠2,解得x=8.故选B.
11、【答案】B
【分析】根据相似多边形的对应边成比例求解.
【解答】设AB=x,AD=1,则AE=1
2
.根据题意,得矩形ABCD与矩形AEFB相似,所以
1
2
1
x
x
=,
解得x
=
2,故
AB
AD
=
2
.
12、【答案】6
【分析】根据相似多边形对应边成比例列式计算即可得解.【解答】解:由题意,得四边形DEFC∠四边形EABF,
则DC EF EF AB
=,
即EF2=DC·AB=4×9=36,
∠EF=6.
13、【答案】见解答。
【分析】本题考查了相似多边形的判定和性质。
【解答】解:(1)证明:由题意得D(-4,0),E(-4,2),F(0,2),∠OA=2,AB=1,BC=2,OC=1,OD=4,DE=2,EF=4,OF=2,∠OA∠OD=AB∠DE=BC∠EF=OC∠OF=1∠2.
又∠矩形OABC与矩形ODEF的角都是直角,∠矩形OABC∠矩形ODEF.
(2)∠OA∠OD=1∠2,∠矩形OABC与矩形ODEF的相似比为1∠2.。
