人教版九年级数学下册 26.1反比例函数培优训练(含答案)
初三数学反比例函数的专项培优练习题(含答案)含答案
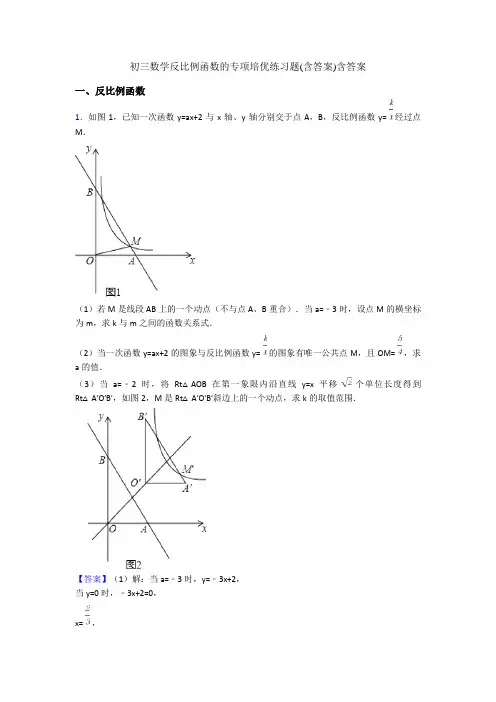
初三数学反比例函数的专项培优练习题(含答案)含答案一、反比例函数1．如图1，已知一次函数y=ax+2与x轴、y轴分别交于点A，B，反比例函数y= 经过点M．（1）若M是线段AB上的一个动点（不与点A、B重合）．当a=﹣3时，设点M的横坐标为m，求k与m之间的函数关系式．（2）当一次函数y=ax+2的图象与反比例函数y= 的图象有唯一公共点M，且OM= ，求a的值．（3）当a=﹣2时，将Rt△AOB在第一象限内沿直线y=x平移个单位长度得到Rt△A′O′B′，如图2，M是Rt△A′O′B′斜边上的一个动点，求k的取值范围．【答案】（1）解：当a=﹣3时，y=﹣3x+2，当y=0时，﹣3x+2=0，x= ，∵点M的横坐标为m，且M是线段AB上的一个动点（不与点A、B重合），∴0＜m＜，，DANG则，﹣3x+2= ，当x=m时，﹣3m+2= ，∴k=﹣3m2+2m（0＜m＜）（2）解：由题意得：，ax+2= ，ax2+2x﹣k=0，∵直线y=ax+2（a≠0）与双曲线y= 有唯一公共点M时，∴△=4+4ak=0，ak=﹣1，∴k=﹣，则，解得：，∵OM= ，∴12+（﹣）2=（）2，a=±（3）解：当a=﹣2时，y=﹣2x+2，∴点A的坐标为（1，0），点B的坐标为（0，2），∵将Rt△AOB在第一象限内沿直线y=x平移个单位得到Rt△A′O′B′，∴A′（2，1），B′（1，3），点M是Rt△A′O′B′斜边上一动点，当点M′与A′重合时，k=2，当点M′与B′重合时，k=3，∴k的取值范围是2≤k≤3【解析】【分析】（1）当a=﹣3时，直线解析式为y=﹣3x+2，求出A点的横坐标，由于点M的横坐标为m，且M是线段AB上的一个动点（不与点A、B重合）从而得到m的取值范围，由﹣3x+2= ,由X=m得k=﹣3m2+2m（0＜m＜）；（2）由ax+2= 得ax2+2x﹣k=0，直线y=ax+2（a≠0）与双曲线y= 有唯一公共点M时，△=4+4ak=0，ak=﹣1，由勾股定理即可；（3）当a=﹣2时，y=﹣2x+2，从而求出A、B两点的坐标，由平移的知识知A′，B′点的坐标，从而得到k的取值范围。
人教版九年级下册数学 26.1 反比例函数 课时训练(含答案)
人教版 九年级数学 26.1 反比例函数 课时训练一、选择题1. （2019·上海）下列函数中，函数值y 随自变量x 的值增大而增大的是( )A ．y ＝3xB ．y ＝－3x C ．y ＝3xD ．y ＝－3x2. 在函数y ＝x ＋4x 中，自变量x 的取值范围是( ) A. x ＞0 B. x ≥－4C. x ≥－4且x ≠0D. x ＞0且x ≠－43. 若一次函数y ＝mx ＋6的图象与反比例函数y ＝nx 在第一象限的图象有公共点，则有( )A. mn ≥－9B. －9≤mn ＜0C. mn ≥－4D. －4≤mn ≤04. （2020·内江）如图，点A 是反比例函数ky x=图象上的一点，过点A 作AC x ⊥轴，垂足为点C ，D 为AC 的中点，若AOD ∆的面积为1，则k 的值为（ ）A.43B.83C. 3D. 45. 如图，O 为坐标原点，四边形OACB 是菱形，OB 在x 轴的正半轴上，sin ∠AOB＝45，反比例函数y ＝48x 在第一象限内的图象经过点A ，与BC 交于点F ，则△AOF 的面积等于( )A. 60B. 80C. 30D. 406. （2020·常州）如图，点D 是OABC 内一点，CD 与x 轴平行，BD 与y 轴平行，BD ＝2，∠ADB ＝135°，S △ABD ＝2．若反比例函数y ＝kx (x ＞0)的图像经过A 、D 两点，则k 的值是( ) A ．2 2B ．4C ．3 2D ．67. 反比例函数y ＝1－6tx 的图象与直线y ＝－x ＋2有两个交点，且两交点横坐标的积为负数，则t 的取值范围是( ) A. t ＜16 B. t ＞16 C. t ≤16 D. t ≥168. (2019·江苏宿迁)如图，在平面直角坐标系xOy 中，菱形ABCD 的顶点A 与原点O 重合，顶点B 落在x 轴的正半轴上，对角线AC 、BD 交于点M ，点D 、M恰好都在反比例函数y =k x (x >0)的图象上，则ACBD的值为A ．2B ．3C ．2D ．5二、填空题9. 我们把直角坐标系中横坐标与纵坐标都是整数的点称为整点．反比例函数y ＝－3x 的图象上有一些整点，请写出其中一个整点的坐标________．10. （2020·安顺）如图，点A 是反比例函数3y x图象上任意一点，过点A 分别作x 轴，y 轴的垂线，垂足为B ，C ，则四边形OBAC 的面积为 .11. 如图，在平面直角坐标系中，菱形OABC 的面积为12，点B 在y 轴上，点C在反比例函数y ＝kx 的图象上，则k 的值为________．12. (2019·贵州安顺)如图，直线l ⊥x 轴于点P ，且与反比例函数y 1=1k x(x >0)及y 2=2k x(x >0)的图象分别交于A 、B 两点，连接OA 、OB ，已知△OAB 的面积为4，则k 1﹣k 2=__________．13. 如图，点A ，B 是双曲线y ＝6x 上的点，分别过点A ，B 作x 轴和y 轴的垂线段，若图中阴影部分的面积为2，则两个空白矩形面积的和．为________．14. 如图，直线y ＝－2x ＋4与双曲线y ＝kx 交于A 、B 两点，与x 轴交于点C ，若AB ＝2BC ，则k ＝________．15. (2019·浙江绍兴)如图，矩形ABCD 的顶点A ，C 都在曲线y kx(常数k >0，x >0)上，若顶点D 的坐标为(5，3)，则直线BD 的函数表达式是__________．16. （2019•北京）在平面直角坐标系xOy 中，点A （a ，b ）（a ＞0，b ＞0）在双曲线y =1k x 上，点A 关于x 轴的对称点B 在双曲线y =2k x，则k 1+k 2的值为__________．三、解答题17. （2019•吉林）已知y 是x 的反比例函数，并且当x =2时，y =6．（1）求y 关于x 的函数解析式； （2）当x =4时，求y 的值．18. 如图，直线y＝2x与反比例函数y＝kx(k≠0，x＞0)的图象交于点A(m，8)，AB⊥x 轴，垂足为B.(1)求k的值；(2)点C在AB上，若OC＝AC，求AC的长；(3)点D为x轴正半轴上一点，在(2)的条件下，若S△OCD＝S△ACD，求点D的坐标．19. 如图，在平面直角坐标系中，点O为坐标原点，菱形OABC的顶点A在x轴的正半轴上，顶点C的坐标为(1，3)．(1)求图象过点B的反比例函数的解析式；(2)求图象过点A、B的一次函数的解析式；(3)在第一象限内，当以上所求一次函数的图象在所求反比例函数的图象下方时，请直接写出自变量x的取值范围．20. （2019•甘肃）如图，一次函数y=kx+b的图象与反比例函数y=mx的图象相交于A（–1，n）、B（2，–1）两点，与y轴相交于点C．（1）求一次函数与反比例函数的解析式；（2）若点D与点C关于x轴对称，求△ABD的面积；（3）若M（x1，y1）、N（x2，y2）是反比例函数y=mx上的两点，当x1<x2<0时，比较y2与y1的大小关系．21. 如图，直线y＝2x＋6与反比例函数y＝kx(k＞0)的图象交于点A(m，8)，与x轴交于点B，平行于x轴的直线y＝n(0＜n＜6)交反比例函数的图象于点M，交AB于点N，连接BM.(1)求m的值和反比例函数的解析式；(2)观察图象，直接写出当x＞0时不等式2x＋6－kx＞0的解集；(3)直线y＝n沿y轴方向平移，当n为何值时，△BMN的面积最大？最大值是多少？人教版九年级数学26.1 反比例函数课时训练-答案一、选择题1. 【答案】A【解析】A、该函数图象是直线，位于第一、三象限，y随x的增大而增大，故本选项正确．B、该函数图象是直线，位于第二、四象限，y随x的增大而减小，故本选项错误．C、该函数图象是双曲线，位于第一、三象限，在每一象限内，y随x的增大而减小，故本选项错误．D、该函数图象是双曲线，位于第二、四象限，在每一象限内，y随x的增大而增大，故本选项错误．2. 【答案】C【解析】综合开平方时被开方数为非负数和分母不为0可得x取值范围，则x＋4≥0且x≠0，故x≥－4且x≠0.3. 【答案】A【解析】如解图，根据题意，两个函数的图象在第一象限有公共点，则关于x的方程nx＝mx＋6有实数根，方程化简为：mx2＋6x－n＝0，显然m≠0，Δ＝36＋4mn ≥0，所以mn ≥－9，由于一次函数与反比例函数y ＝nx 在第一象限的图象有公共点，所以n ＞0，显然当一次函数y 随x 的增大而增大时，两个函数图象在第一象限有交点，即mn ≥－9符合题意．4. 【答案】D【解析】本题考查了反比例函数系数k 的几何意义、反比例函数图象上点的坐标特征，解答本题的关键是明确题意，找出所求问题需要的条件，利用反比例函数的性质解答．先设出点A 的坐标，进而表示出点D 的坐标，利用△ADO 的面积建立方程求出2mn =，即可得出结论．∵点A 的坐标为（m ，2n ），∴2mn k =，∵D 为AC 的中点，∴D （m ，n ），∵AC ⊥x 轴，△ADO 的面积为1，∴()ADO 11121222S AD OC n n m mn =⋅=-⋅==，∴2mn =，∴24k mn ==，因此本题选D ．5. 【答案】D【解析】如解图所示，过点A 作AG ⊥OB ，垂足为G ，设A 点纵坐标为4m ，∵sin ∠AOB ＝45，∴OA ＝5m ，根据勾股定理可得OG ＝3m ，又∵点A 在反比例函数y ＝48x 上，∴3m ×4m ＝48，∴m 1＝2，m 2＝－2(不合题意，舍去)，∴AG ＝8，OG ＝6，OA ＝OB ＝10，∵四边形OBCA 是菱形，∴BC ∥OA ，∴S △AOF ＝12S 菱形OBCA ＝12×AG×OB ＝12×8×10＝40.故选D .6. 【答案】D【解析】【解析】过点D 、点A 分别作x 轴、y 轴的垂线，两条垂线相交于点E ，过点A 作AF ⊥x 轴于点F ，由∠BDF ＝135°，可证△DEA 为等腰直角三角形，因为S △ABD ＝12BD ·AE ，2＝12×2·AE ，所以AE ＝22，所以DE ＝AE ＝22，又由于BC 与OA 平行且相等，可证△CDB ≌△OAF ，所以AF ＝2，设A (2，2)，所以D (2－22，32)，所以(2－22)×32＝k ，解得k ＝6．7. 【答案】B【解析】将y ＝－x ＋2代入到反比例函数y ＝1－6tx 中，得：－x ＋2＝1－6t x ，整理，得：x 2－2x ＋1－6t ＝0，∵反比例函数y ＝1－6tx 的图象与直线y ＝－x ＋2有两个交点，且两交点横坐标的积为负数，∴⎩⎨⎧（－2）2－4（1－6t ）＞01－6t ＜0，解得t ＞16.8. 【答案】A【解析】设D (m ，km)，B (t ，0)， ∵M 点为菱形对角线的交点，∴BD ⊥AC ，AM =CM ，BM =DM ，∴M (2m t +，2km)，把M (2m t +，2k m )代入y =k x 得2m t +•2km=k ，∴t =3m ， ∵四边形ABCD 为菱形，∴OD =AB =t ，∴m2+(km)2=(3m)2，解得k=22m2，∴M(2m，2m)，在Rt△ABM中，tan∠MAB=2122BM mAM m==，∴2ACBD=．故选A．二、填空题9. 【答案】(1，－3)(答案不唯一，合理即可) 【解析】对于y＝－3x，依题意，说明只要x是3的约数即可，如(1，－3)，(－1，3)．10. 【答案】3【解析】在反比例函数3yx=中，3k=.由k的几何意义，可得四边形OBAC的面积为3.11. 【答案】－6【解析】如解图，连接AC交y轴于点D，因为四边形ABCO 是菱形，且面积为12，则△OCD的面积为3，利用反比例函数k的几何意义可得k＝－6.12. 【答案】8【解析】根据反比例函数k 的几何意义可知：△AOP 的面积为12k 1，△BOP 的面积为12k 2，∴△AOB 的面积为12k 1﹣12k 2，∴12k 1﹣12k 2=4，∴k 1﹣k 2=8，故答案为8．13. 【答案】8【解析】设两个空白矩形面积为S 1、S 2，则根据反比例函数的几何意义得：S 1＋2＝S 2＋2＝6，∴S 1＝S 2＝4，∴两个空白矩形的面积和为：S 1＋S 2＝8.14. 【答案】32 【解析】设A(x 1，k x 1)，B(x 2，k x 2)，∵直线y ＝－2x ＋4与y ＝k x交于A ，B 两点，∴－2x ＋4＝k x ，即－2x 2＋4x －k ＝0，∴x 1＋ x 2＝2，x 1x 2＝k2，如解图，过点A 作AQ ⊥x 轴于点Q ，BP ⊥AQ 于点P ，则PB ∥QC ，∴AP PQ ＝ABBC ＝2，即k x 1－k x 2k x 2＝2，∴x 2＝3x 1，∴x 1＝ 12，x 2 ＝ 32，∴k ＝ 2x 1x 2＝32.15. 【答案】y 35x 【解析】∵D (5，3)，∴A (3k ，3)，C (5，5k )，∴B (3k ，5k )，设直线BD 的解析式为y =mx +n ， 把D (5，3)，B (3k ，5k)代入， 得5335m n k k m n +=⎧⎪⎨+=⎪⎩，解得350m n ⎧=⎪⎨⎪=⎩， ∴直线BD 的解析式为y 35=x ． 故答案为y 35=x ．16. 【答案】0【解析】∵点A （a ，b ）（a ＞0，b ＞0）在双曲线y =1k x上，∴k 1=ab ； 又∵点A 与点B 关于x 轴对称，∴B （a ，–b ）， ∵点B 在双曲线y =2k x上，∴k 2=–ab ；∴k 1+k 2=ab +（–ab ）=0； 故答案为：0．三、解答题17. 【答案】（1）y =12x．（2）y =3． 【解析】（1）因为y 是x 的反例函数，所以设y =kx(k ≠0)， 当x =2时，y =6． 所以k =xy =12， 所以y =12x． （2）当x =4时，y =3．18. 【答案】(1)∵直线y ＝2x 与反比例函数y ＝kx (k ≠0，x ＞0)的图象交于点A (m ，8)，则2m ＝8， 解得m ＝4， ∴A (4，8)， ∴k ＝4×8＝32；(2)设AC ＝x ，则OC ＝x ，BC ＝8－x ，在Rt △OBC 中，由勾股定理得：OC 2＝OB 2＋BC 2， 即x 2＝42＋(8－x )2，解得x ＝5，∴AC ＝5； (3)设点D 的坐标为(x ，0)．分两种情况： ①当x ＞4时，如解图①，∵S △OCD ＝S △ACD ， ∴12OD ·BC ＝12AC ·BD ， ∴3x ＝5(x －4)，解得x ＝10；②当0＜x ＜4时，如解图②，同理得：3x ＝5(4－x )，解得x ＝52. ∴点D 的坐标为(10，0)或(52，0)．19. 【答案】(1)如解图，过点C作CD⊥OA于点D，则OD＝1，CD＝3，在Rt△OCD中，由勾股定理得OC＝OD2＋CD2＝2，∵四边形OABC为菱形，∴BC＝AB＝OA＝OC＝2，则点B的坐标为(3，3)，设反比例函数的解析式为y＝kx(k≠0)，∵其图象经过点B，∴将B(3，3)代入，得3＝k3，解得k＝33，∴该反比例函数的解析式为y＝33 x；(2)∵OA＝2，∴点A的坐标为(2，0)，由(1)得B (3，3)，设图象经过点A 、B 的一次函数的解析式为y ＝k ′x ＋b (k ′≠0)， 将A (2，0)，B (3，3)分别代入， 得⎩⎨⎧2k ′＋b ＝03k ′＋b ＝3，解得⎩⎨⎧k ′＝3b ＝－23，∴该一次函数的解析式为y ＝3x －23；(3)由图象可得，满足条件的自变量x 的取值范围是2＜x ＜3.20. 【答案】（1）一次函数的解析式为y =–x +1，反比例函数的解析式为y =–2x． （2）S △ABD =3．（3）y 1<y 2． 【解析】（1）∵反比例函数y =mx经过点B （2，–1），∴m =–2， ∵点A （–1，n ）在y =2x-上，∴n =2，∴A （–1，2）， 把A ，B 坐标代入y =kx +b ，则有221k b k b -+=+=-⎧⎨⎩，解得11k b =-=⎧⎨⎩，∴一次函数的解析式为y =–x +1，反比例函数的解析式为y =–2x． （2）∵直线y =–x +1交y 轴于C ，∴C （0，1）， ∵D ，C 关于x 轴对称，∴D （0，–1）， ∵B （2，–1），∴BD ∥x 轴，∴S △ABD =12×2×3=3．（3）∵M （x 1，y 1）、N （x 2，y 2）是反比例函数y =–2x上的两点，且x 1<x 2<0，s ∴y 1<y 2．21. 【答案】(1)∵直线y ＝2x ＋6经过点A (m ，8)， ∴2×m ＋6＝8，解得m ＝1， ∴A (1，8)，∵反比例函数经过点A (1，8)，∴k ＝8， ∴反比例函数的解析式为y ＝8x ； (2)不等式2x ＋6－kx ＞0的解集为x ＞1；(3)由题意，点M ，N 的坐标为M (8n ，n )，N (n －62，n )， ∵0＜n ＜6，∴n －62＜0，∴8n －n －62＞0，∴S △BMN ＝12|MN |×|y M |＝12×(8n －n －62)×n ＝－14(n －3)2＋254， ∴n ＝3时，△BMN 的面积最大，最大值为254.。
人教版九年级下册数学第二十六章 反比例函数含答案(满分必刷)
人教版九年级下册数学第二十六章反比例函数含答案一、单选题(共15题，共计45分)1、在平面直角坐标系中，反比例函数的图象在其所在的每个象限内y随x的增大而减小，则k的取值范围是A. B. C. D.2、如图，在直角坐标系中，正方形OABC的顶点O与原点重合，顶点A，C分别在x轴、y轴上，反比例函数y= (k≠0，x>0)的图象与正方形的两边AB、BC分别交于点E、F，FD⊥x轴，垂足为D，连接OE，OF，EF，FD与OE相交于点G.下列结论：①OF=OE；②∠EOF=60°；③四边形AEGD与△FOG面积相等；④EF=CF+AE；⑤若∠EOF=45°， EF=4，则直线FE的函数解析式为.其中正确结论的个数是（）A.2B.3C.4D.53、一台印刷机每年可印刷的书本数量y(万册)与它的使用时间x(年)成反比例关系，当x＝2时，y＝20，则y与x的函数图象大致是( )A. B. C. D.4、如图，在Rt△OAB中，∠OBA＝90°，OA在x轴上，AC平分∠OAB，OD平分∠AOB，AC与OD相交于点E，且OC＝，CE＝，反比例函数的图象经过点E，则k的值为（）A. B. C. D.5、如图，平行四边形AOBC中，对角线交于点E，双曲线y= （k＞0）经过A、E两点，若平行四边形AOBC的面积为24，则k的值是（）A.8B.7.5C.6D.96、在同平面直角坐标系中，函数y＝x﹣1与函数y＝的图象大致是（）A. B. C. D.7、已知点M(-2，4)在双曲线y= 上，则下列各点一定在该双曲线上的是（）A.(-2，-4)B.(4，-2)C.(2，4)D.(4，2)8、已知广州市的土地总面积约为7434 km2，人均占有的土地面积S（单位：km2/人）随全市人口n（单位：人）的变化而变化，则S与n的函数关系式为（）A.S=7434nB.S=C.n=7434SD.S=9、如图，以平行四边形ABCO的顶点O为原点，边OC所在直线为x轴，建立平面直角坐标系，顶点A、C的坐标分别是（2，4）、（3，0），过点A的反比例函数y= 的图象交BC于D，连接AD，则四边形AOCD的面积是（）A.6B.7C.9D.1010、二次函数y=ax2+bx+c（a≠0）的图象如图，则反比例函数与一次函数y=bx﹣c在同一坐标系内的图象大致是（）A. B. C.D.11、如图，在平面直角坐标系中，双曲线y＝，y＝﹣与⊙O相交，以交点为顶点的八边形ABCDEFGH是正八边形，则此正八边形的面积为（）A.32B.64C.16D.16+1612、若反比例函数y=的图象位于第二、四象限，则k的取值可以是( )A.0B.1C.2D.以上都不是13、已知常数k＜0，b＞0，则函数y=kx+b，的图象大致是下图中的（）A. B. C. D.14、如图，在平面直角坐标系中，等腰直角三角形ABC的顶点A、B分别在x 轴、y轴的正半轴上，∠ABC=90°，CA⊥x轴，点C在函数y= （x＞0）的图象上，若AB=2，则k的值为（）A.4B.2C.2D.15、下列各式不能确定为反比例函数关系的是（）A. B. C. D.二、填空题(共10题，共计30分)16、给出以下命题：①平分弦的直径垂直于这条弦；②已知点、、均在反比例函数的图象上，则；③若关于x的不等式组无解，则；④将点向左平移3个单位到点，再将绕原点逆时针旋转90°到点，则的坐标为．其中所有真命题的序号是________．17、若反比例函数的图象经过点，则m=________．18、点（2，5）在反比例函数的图象上，那么k＝________．19、双曲线y1， y2在第一象限的图象如图，已知y1＝，过y1上的任意一点A作x轴的平行线交y2于点B，交y轴于点C，若S△AOB＝，则y2的表达式是________.20、已知点（，），（，），（，）均在反比例函数的图象上，则，，的大小关系是________．（用“＜”连接）21、若反比例函数y=的图象经过第一、三象限，则 k的取值范围是________ ．22、已知反比例函数的图象具有下列特征：在所在的象限内，y随x 的增大而增大，那么m的取值范围是________.23、如图在平面直角坐标系中，周长为12的正六边形ABCDEF的对称中心与原点O重合，点A在x轴上．点B，在反比例函数y＝位于第一象限的图象上．则k的值为________．24、如图，矩形的面积为，它的对角线与双曲线相交于点，且，则________．25、如图，已知第一象限内的点A在反比例函数y= 上，第二象限的点B在反比例函数y= 上，且OA⊥OB，tanA= ，则k的值为________．三、解答题(共5题，共计25分)26、函数y=（m﹣2）x 是反比例函数，则m的值是多少？27、如图,一次函数的图象与反比例函数（x>0）的图象交于点P,PA⊥x轴于点A,PB⊥y轴于点B,一次函数的图象分别交x轴、y轴于点C、点=27,．D,且S△DBP（1）求点D的坐标;（2）求一次函数与反比例函数的表达式;（3）根据图象写出当x取何值时,一次函数的值小于反比例函数的值?28、已知函数y=（m﹣1）x|m|﹣2是反比例函数．（1）求m的值；（2）求当x=3时，y的值．29、如图，等边三角形ABC放置在平面直角坐标系中，已知A（0，0），B （4，0），反比例函数的图象经过点C.求点C的坐标及反比例函数的解析式.30、在平面直角坐标系中，反比例函数y= （k≠0）图象与一次函数y=x+2图象的一个交点为P，且点P的横坐标为1，求该反比例函数的解析式．参考答案一、单选题(共15题，共计45分)1、B2、B3、C4、D5、A6、C7、B8、B9、C10、A11、A12、A13、D14、A15、D二、填空题(共10题，共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题，共计25分)26、28、30、。
人教版 九年级下数学 第26章 反比例函数 培优训练(含答案)
人教版 九年级数学 第26章 反比例函数培优训练一、选择题（本大题共10道小题）1. 一司机驾驶汽车从甲地去乙地，他以80千米/小时的平均速度用了4小时到达乙地，当他按原路匀速返回时，汽车的速度v 千米/小时与时间t 小时的函数关系是( )A. v ＝320tB. v ＝320tC. v ＝20tD. v ＝20t2. 反比例函数y ＝－1x的图象上有两点P 1(x 1，y 1)，P 2(x 2，y 2)，若x 1<0<x 2，则下列结论正确的是( )A. y 1<y 2<0B. y 1<0<y 2C. y 1>y 2>0D. y 1>0>y 23. （2020·黑龙江龙东）如图，正方形ABCD 的两个顶点B ，D 在反比例函数y的图象上，对角线AC ，BD 的交点恰好是坐标原点O ，已知B（﹣1，1），则k 的值是（ ）A ．﹣5B ．﹣4C ．﹣3D ．﹣14. （2020·苏州）如图，平行四边形OABC 的顶点A 在x 轴的正半轴上，点()3,2D 在对角线OB 上，反比例函数()0,0ky k x x=>>的图像经过C 、D 两点.已知平行四边形OABC 的面积是152，则点B 的坐标为（ ）A.84,3⎛⎫ ⎪⎝⎭B.9,32⎛⎫ ⎪⎝⎭C.105,3⎛⎫ ⎪⎝⎭D.2416,55⎛⎫ ⎪⎝⎭5. (2019·海南)如果反比例函数y =2a x-(a 是常数)的图象在第一、三象限，那么a 的取值范围是 A ．a <0 B ．a >0C ．a <2D ．a >26. （2019•广西）若点（1，y 1），（2，y 2），（3，y 3）在反比例函数y =kx（k <0）的图象上，则y 1，y 2，y 3的大小关系是 A ．y 1＞y 2＞y 3 B ．y 3＞y 2＞y 1C ．y 1＞y 3＞y 2D ．y 2＞y 3＞y 17. （2020·长沙）2019年10月，《长沙晚报》对外发布长沙高铁两站设计方案，该方案以三湘四水，杜鹃花开 ，塑造出杜鹃花开的美丽姿态，该高铁站建设初期需要运送大量的土石方，某运输公司承担了运送总量为106 m 3土石方的任务，该运输公司平均运送土石方的速度v （单位：m 3/天）与完成运送任务所需的时间t （单位：天）之间的函数关系式是 · （ ）A ．tv 610＝B ．t 106＝vC ．26101t v ＝D ．26t 10＝v8. （2020·宜昌）已知电压U 、电流I 、电阻R 三者之间的关系式为：U =IR (或者RUI),实际生活中，由于给定已知量不同，因此会有不同的可能图象，图象不可能是（ ）.A ．B ．C ．D ．9. （2020·衡阳）反比例函数y =kx 经过点(2，1) ，则下列说法错误．．的是 （ ） A. k =2 B.函数图象分布在第一、三象限C.当x >0时，随x 的增大而增大D.当x >0时，y 随x 的增大而减小10. (2019·湖北咸宁)在平面直角坐标系中，将一块直角三角板如图放置，直角顶点与原点O 重合，顶点A ，B 恰好分别落在函数y =﹣1x (x <0)，y =4x(x >0)的图象上，则sin ∠ABO 的值为A ．13B ．33C ．54D ．55二、填空题（本大题共6道小题）11. 已知反比例函数y ＝kx(k ≠0)的图象如图所示，则k 的值可能是________(写一个即可)．12. 如图，过原点O 的直线与反比例函数y 1、y 2的图象在第一象限内分别交于点A 、B ，且A 为OB 的中点．若函数y 1＝1x，则y 2与x 的函数表达式是________．13. (2019·黑龙江齐齐哈尔)如图，矩形ABOC 的顶点B 、C 分别在x轴，y 轴上，顶点A 在第二象限，点B 的坐标为(﹣2，0)．将线段OC 绕点O 逆时针旋转60°至线段OD ，若反比例函数y =kx(k ≠0)的图象经过A 、D 两点，则k 值为__________．。
人教版九年级数学下《第26章反比例函数》专项训练含答案
第26章 反比例函数 专项训练 专训1 反比例函数与几何的综合应用名师点金：解反比例函数与几何图形的综合题，一般先设出几何图形中的未知数，然后结合函数的图象用含未知数的式子表示出几何图形与图象的交点坐标，再由函数解析式及几何图形的性质写出含未知数及待求字母系数的方程(组)，解方程(组)即可得所求几何图形中的未知量或函数解析式中待定字母的值．反比例函数与三角形的综合1．如图，一次函数y ＝kx ＋b 与反比例函数y ＝6x (x>0)的图象交于A(m ，6)，B(3，n)两点．(1)求一次函数的解析式；(2)根据图象直接写出使kx ＋b<6x 成立的x 的取值范围；(3)求△AOB 的面积．(第1题)2．如图，点A ，B 分别在x 轴、y 轴上，点D 在第一象限内，DC ⊥x 轴于点C ，AO ＝CD ＝2，AB ＝DA ＝5，反比例函数y ＝kx (k ＞0)的图象过CD 的中点E.(1)求证：△AOB ≌△DCA ； (2)求k 的值；(3)△BFG 和△DCA 关于某点成中心对称，其中点F 在y 轴上，试判断点G 是否在反比例函数的图象上，并说明理由．(第2题)反比例函数与四边形的综合类型1：反比例函数与平行四边形的综合3．如图，过反比例函数y ＝6x (x ＞0)的图象上一点A 作x 轴的平行线，交双曲线y ＝－3x (x ＜0)于点B ，过B 作BC ∥OA 交双曲线y ＝－3x (x ＜0)于点D ，交x轴于点C ，连接AD 交y 轴于点E ，若OC ＝3，求OE 的长．(第3题)类型2：反比例函数与矩形的综合4．如图，矩形OABC 的顶点A ，C 的坐标分别是(4，0)和(0，2)，反比例函数y ＝kx(x>0)的图象过对角线的交点P 并且与AB ，(第4题)BC 分别交于D ，E 两点，连接OD ，OE ，DE ，则△ODE 的面积为________． 5．如图，在平面直角坐标系中，矩形OABC 的对角线OB ，AC 相交于点D ，且BE ∥AC ，AE ∥OB.(1)求证：四边形AEBD 是菱形；(2)如果OA ＝3，OC ＝2，求出经过点E 的双曲线对应的函数解析式．(第5题)类型3：反比例函数与菱形的综合6．如图，在平面直角坐标系中，菱形ABCD 在第一象限内，边BC 与x 轴平行，A ，B 两点的纵坐标分别为3，1，反比例函数y ＝3x的图象(第6题)经过A ，B 两点，则菱形ABCD 的面积为( ) A ．2 B ．4C ．2 2D ．4 27．如图，在平面直角坐标系中，菱形ABCD 的顶点C 与原点O 重合，点B 在y 轴的正半轴上，点A 在反比例函数y ＝kx (k>0，x>0)的图象上，点D 的坐标为(4，3)．(1)求k 的值；(2)若将菱形ABCD 沿x 轴正方向平移，当菱形的顶点D 落在反比例函数y ＝kx(k>0，x>0)的图象上时，求菱形ABCD 沿x 轴正方向平移的距离．(第7题)类型4：反比例函数与正方形的综合8．如图，在平面直角坐标系中，点O 为坐标原点，正方形OABC 的边OA ，OC 分别在x 轴，y 轴上，点B 的坐标为(2，2)，反比例函数y ＝kx (x ＞0，k ≠0)的图象经过线段BC 的中点D(1)求k 的值；(2)若点P(x ，y)在该反比例函数的图象上运动(不与点D 重合)，过点P 作PR ⊥y 轴于点R ，作PQ ⊥BC 所在直线于点Q ，记四边形CQPR 的面积为S ，求S 关于x 的函数解析式并写出x 的取值范围．(第8题)反比例函数与圆的综合(第9题)9．如图，双曲线y ＝kx (k>0)与⊙O 在第一象限内交于P ，Q 两点，分别过P ，Q 两点向x 轴和y 轴作垂线，已知点P 的坐标为(1，3)，则图中阴影部分的面积为________．10．如图，反比例函数y ＝kx (k ＜0)的图象与⊙O 相交．某同学在⊙O 内做随机扎针试验，求针头落在阴影区域内的概率．(第10题)专训2 全章热门考点整合应用名师点金：反比例函数及其图象、性质是历年来中考的热点，既有与本学科知识的综合，也有与其他学科知识的综合，题型既有选择、填空，也有解答类型．其热门考点可概括为：1个概念，2个方法，2个应用及1个技巧．1个概念：反比例函数的概念1．若y ＝(m －1)x |m|－2是反比例函数，则m 的取值为( )A ．1B ．－1C ．±1D ．任意实数2．某学校到县城的路程为 5 km ，一同学骑车从学校到县城的平均速度v(km /h )与所用时间t(h )之间的函数解析式是( )A ．v ＝5tB ．v ＝t ＋5C ．v ＝5tD ．v ＝t53．判断下面哪些式子表示y 是x 的反比例函数：①xy ＝－13；②y ＝5－x ；③y ＝－25x ；④y ＝2ax (a 为常数且a ≠0)．其中________是反比例函数．(填序号)2个方法：方法1：画反比例函数图象的方法 4．已知y 与x 的部分取值如下表：解析式；(2)画出这个函数的图象．方法2：求反比例函数解析式的方法5．已知反比例函数y ＝kx 的图象与一次函数y ＝x ＋b 的图象在第一象限内相交于点A(1，－k ＋4)．试确定这两个函数的解析式．6．如图，已知A(－4，n)，B(2，－4)是一次函数y ＝kx ＋b 的图象和反比例函数y ＝mx的图象的两个交点．求：(1)反比例函数和一次函数的解析式；(2)直线AB 与x 轴的交点C 的坐标及△AOB 的面积； (3)方程kx ＋b －mx ＝0的解(请直接写出答案)；(4)不等式kx ＋b －mx<0的解集(请直接写出答案)．(第6题)2个应用应用1：反比例函数图象和性质的应用7．画出反比例函数y ＝6x 的图象，并根据图象回答问题：(1)根据图象指出当y ＝－2时x 的值；(2)根据图象指出当－2<x<1且x ≠0时y 的取值范围； (3)根据图象指出当－3<y<2且y ≠0时x 的取值范围．应用2：反比例函数的实际应用8．某厂仓库储存了部分原料，按原计划每小时消耗2吨，可用60小时．由于技术革新，实际生产能力有所提高，即每小时消耗的原料量大于计划消耗的原料量．设现在每小时消耗原料x(单位：吨)，库存的原料可使用的时间为y(单位：小时)．(1)写出y 关于x 的函数解析式，并求出自变量的取值范围．(2)若恰好经过24小时才有新的原料进厂，为了使机器不停止运转，则x应控制在什么范围内？1个技巧：用k 的几何性质巧求图形的面积9．如图，A ，B 是双曲线y ＝kx (k ≠0)上的两点，过A 点作AC ⊥x 轴，交OB于D 点，垂足为C.若△ADO 的面积为1，D 为OB 的中点，则k 的值为( )A .43B .83C ．3D ．4(第9题)(第10题)10．如图，过x 轴正半轴上的任意一点P 作y 轴的平行线交反比例函数y ＝2x 和y ＝－4x 的图象于A ，B 两点，C 是y 轴上任意一点，则△ABC 的面积为________．11．如图是函数y ＝3x 与函数y ＝6x 在第一象限内的图象，点P 是y ＝6x 的图象上一动点，PA ⊥x 轴于点A ，交y ＝3x 的图象于点C ，PB ⊥y 轴于点B ，交y ＝3x 的图象于点D.(1)求证：D 是BP 的中点；(2)求四边形ODPC 的面积．(第11题)答案专训11．解：(1)∵A(m ，6)，B(3，n)两点在反比例函数y ＝6x (x>0)的图象上，∴m ＝1，n ＝2，即 A(1，6)，B(3，2)．又∵A(1，6)，B(3，2)在一次函数y ＝kx ＋b 的图象上， ∴⎩⎨⎧6＝k ＋b ，2＝3k ＋b ，解得⎩⎨⎧k ＝－2，b ＝8， 即一次函数解析式为y ＝－2x ＋8.(第1题)(2)根据图象可知使kx ＋b<6x 成立的x 的取值范围是0<x<1或x>3.(3)如图，分别过点A ，B 作AE ⊥x 轴，BC ⊥x 轴，垂足分别为E ，C ，设直线AB 交x 轴于D 点．令－2x ＋8＝0，得x ＝4，即D(4，0)． ∵A(1，6)，B(3，2)，∴AE ＝6，BC ＝2.∴S △AOB ＝S △AOD －S △ODB ＝12×4×6－12×4×2＝8.2．(1)证明：∵点A ，B 分别在x 轴，y 轴上，点D 在第一象限内，DC ⊥x轴于点C ，∴∠AOB ＝∠DCA ＝90°.在Rt △AOB 和Rt △DCA 中，∵⎩⎨⎧AO ＝DC ，AB ＝DA ，∴Rt △AOB ≌Rt △DCA.(2)解：在Rt △ACD 中，∵CD ＝2，DA ＝5， ∴AC ＝DA 2－CD 2＝1.∴OC ＝OA ＋AC ＝2＋1＝3.∴D 点坐标为(3，2)．∵点E 为CD 的中点，∴点E 的坐标为(3，1)．∴k ＝3×1＝3. (3)解：点G 在反比例函数的图象上．理由如下：∵△BFG 和△DCA 关于某点成中心对称， ∴△BFG ≌△DCA.∴FG ＝CA ＝1，BF ＝DC ＝2，∠BFG ＝∠DCA ＝90°.∵OB ＝AC ＝1，∴OF ＝OB ＋BF ＝1＋2＝3.∴G 点坐标为(1，3)． ∵1×3＝3，∴点G(1，3)在反比例函数的图象上．3．解：∵BC ∥OA ，AB ∥x 轴，∴四边形ABCO 为平行四边形． ∴AB ＝OC ＝3.设A ⎝⎛⎭⎪⎫a ，6a ，则B ⎝ ⎛⎭⎪⎫a －3，6a ， ∴(a －3)·6a＝－3.∴a ＝2.∴A(2，3)，B(－1，3)．∵OC ＝3，C 在x 轴负半轴上，∴C(－3，0)， 设直线BC 对应的函数解析式为y ＝kx ＋b ， 则⎩⎨⎧－3k ＋b ＝0，－k ＋b ＝3，解得⎩⎪⎨⎪⎧k ＝32，b ＝92.∴直线BC 对应的函数解析式为y ＝32x ＋92.解方程组⎩⎪⎨⎪⎧y ＝32x ＋92，y ＝－3x ，得⎩⎨⎧x 1＝－1，y 1＝3，⎩⎨⎧x 2＝－2，y 2＝32. ∴D ⎝⎛⎭⎪⎫－2，32.设直线AD 对应的函数解析式为y ＝mx ＋n ，则⎩⎨⎧2m ＋n ＝3，－2m ＋n ＝32，解得⎩⎪⎨⎪⎧m ＝38，n ＝94.∴直线AD 对应的函数解析式为y ＝38x ＋94.∴E ⎝⎛⎭⎪⎫0，94.∴OE ＝94.4.154 点拨：因为C(0，2)，A(4，0)，由矩形的性质可得P(2，1)，把P 点坐标代入反比例函数解析式可得k ＝2，所以反比例函数解析式为y ＝2x .因为D点的横坐标为4，所以AD ＝24＝12.因为点E 的纵坐标为2，所以2＝2CE ，所以CE＝1，则BE ＝3.所以S △ODE ＝S 矩形OABC －S △OCE －S △BED －S △OAD ＝8－1－94－1＝154.5．(1)证明：∵BE ∥AC ，AE ∥OB ，∴四边形AEBD 是平行四边形．∵四边形OABC 是矩形，∴DA ＝12AC ，DB ＝12OB ，AC ＝OB.∴DA ＝DB.∴四边形AEBD 是菱形．(2)解：如图，连接DE ，交AB 于F ， ∵四边形AEBD 是菱形，∴DF ＝EF ＝12OA ＝32，AF ＝12AB ＝1.∴E ⎝ ⎛⎭⎪⎫92，1.设所求反比例函数解析式为y ＝kx，把点E ⎝ ⎛⎭⎪⎫92，1的坐标代入得1＝k 92，解得k ＝92.∴所求反比例函数解析式为y ＝92x.(第5题)(第7题) 6．D7．解：(1)如图，过点D作x轴的垂线，垂足为F.∵点D的坐标为(4，3)，∴OF＝4，DF＝3.∴OD＝5.∴AD＝5.∴点A的坐标为(4，8)．∴k＝xy＝4×8＝32. (2)将菱形ABCD沿x轴正方向平移，使得点D落在函数y＝32x(x>0)的图象上点D′处，过点D′作x轴的垂线，垂足为F′.∵DF＝3，∴D′F′＝3.∴点D′的纵坐标为3.∵点D′在y＝32x的图象上，∴3＝32x，解得x＝323，即OF′＝323.∴FF′＝323－4＝203.∴菱形ABCD沿x轴正方向平移的距离为20 3.8．解：(1)∵正方形OABC的边OA，OC分别在x轴，y轴上，点B的坐标为(2，2)，∴C(0，2)．∵D是BC的中点，∴D(1，2)．∵反比例函数y＝kx(x＞0，k≠0)的图象经过点D，∴k＝2.(2)当P在直线BC的上方，即0＜x＜1时，∵点P(x，y)在该反比例函数的图象上运动，∴y＝2 x .∴S四边形CQPR ＝CQ·PQ＝x·⎝⎛⎭⎪⎫2x－2＝2－2x；当P在直线BC的下方，即x＞1时，同理求出S四边形CQPR＝CQ·P Q ＝x·⎝⎛⎭⎪⎫2－2x ＝2x －2，综上，S ＝⎩⎨⎧2x －2（x ＞1），2－2x （0＜x ＜1）.9．410．解：∵反比例函数的图象关于原点对称，圆也关于原点对称，故阴影部分的面积占⊙O 面积的14，则针头落在阴影区域内的概率为14.专训2 1．B 2.C 3．①③④4．解：(1)反比例函数：y ＝－6x.(2)如图所示．(第4题)5．解：∵反比例函数y ＝kx 的图象经过点A(1，－k ＋4)，∴－k ＋4＝k1，即－k ＋4＝k ，∴k ＝2，∴A(1，2)．∵一次函数y ＝x ＋b 的图象经过点A(1，2)， ∴2＝1＋b ，∴b ＝1.∴反比例函数的解析式为y ＝2x ，一次函数的解析式为y ＝x ＋1.6．解：(1)将B(2，－4)的坐标代入y ＝m x ，得－4＝m2，解得m ＝－8.∴反比例函数的解析式为y ＝－8x. ∵点A(－4，n)在双曲线y ＝－8x上，∴n ＝2. ∴A(－4，2)．把A(－4，2)，B(2，－4)的坐标分别代入y ＝kx ＋b ，得 ⎩⎨⎧－4k ＋b ＝2，2k ＋b ＝－4，解得⎩⎨⎧k ＝－1，b ＝－2. ∴一次函数的解析式为y ＝－x －2. (2)令y ＝0，则－x －2＝0，x ＝－2. ∴C(－2，0)．∴OC ＝2.∴S △AOB ＝S △AOC ＋S △BOC ＝12×2×2＋12×2×4＝6.(3)x 1＝－4，x 2＝2.(4)－4<x<0或x>2.7．解：如图，由观察可知： (1)当y ＝－2时，x ＝－3；(2)当－2<x<1且x ≠0时，y<－3或y>6； (3)当－3<y<2且y ≠0时，x<－2或x>3.(第7题)点拨：解决问题时，画出函数图象．由图象观察得知结果．由图象解决相关问题，一定要注意数形结合，学会看图．8．解：(1)库存原料为2×60＝120(吨)，根据题意可知y 关于x 的函数解析式为y ＝120x.由于生产能力提高，每小时消耗的原料量大于计划消耗的原料量，所以自变量的取值范围是x>2.(2)根据题意，得y ≥24，所以120x≥24. 解不等式，得x ≤5，即每小时消耗的原料量应控制在大于2吨且不大于5吨的范围内．点拨：(1)由“每小时消耗的原料量×可使用的时间＝原料总量”可得y 关于x 的函数解析式．(2)要使机器不停止运转，需y ≥24，解不等式即可．(第9题)9．B 点拨：如图，过点B 作BE ⊥x 轴于点E ，∵D 为OB 的中点，∴CD 是△OBE 的中位线，则CD ＝12BE.设A ⎝ ⎛⎭⎪⎫x ，k x ，则B ⎝ ⎛⎭⎪⎫2x ，k 2x ，CD ＝k 4x ，AD ＝k x －k 4x .∵△ADO 的面积为1，∴12AD·OC＝1，即12⎝⎛⎭⎪⎫k x －k 4x ·x＝1.解得k ＝83. 10．311．(1)证明：∵点P 在双曲线y ＝6x 上，∴设P 点坐标为⎝ ⎛⎭⎪⎫6m ，m .∵点D 在双曲线y ＝3x 上，BP ∥x 轴，D 在BP 上，∴D 点坐标为⎝⎛⎭⎪⎫3m ，m .∴BD ＝3m ，BP ＝6m ， 故D 是BP 的中点．(2)解：由题意可知S △BOD ＝32，S △AOC ＝32，S 四边形OBPA ＝6.四边形ODPC ＝S四边形OBPA－S△BOD－S△AOC＝6－32－32＝3.∴S。
人教版九年级数学下《第26章反比例函数》专项训练含答案
第26章反比例函数专项训练专训1反比例函数与几何的综合应用名师点金：解反比例函数与几何图形的综合题，一般先设出几何图形中的未知数，然后结合函数的图象用含未知数的式子表示出几何图形与图象的交点坐标，再由函数解析式及几何图形的性质写出含未知数及待求字母系数的方程(组)，解方程(组)即可得所求几何图形中的未知量或函数解析式中待定字母的值．反比例函数与三角形的综合1．如图，一次函数y＝kx＋b与反比例函数y＝6x(x>0)的图象交于A(m，6)，B(3，n)两点．(1)求一次函数的解析式；(2)根据图象直接写出使kx＋b<6x成立的x的取值范围；(3)求△AOB的面积．(第1题)2．如图，点A，B分别在x轴、y轴上，点D在第一象限内，DC⊥x轴于点C，AO＝CD＝2，AB＝DA＝5，反比例函数y＝kx(k＞0)的图象过CD的中点E.(1)求证：△AOB≌△DCA；(2)求k的值；(3)△BFG和△DCA关于某点成中心对称，其中点F在y轴上，试判断点G 是否在反比例函数的图象上，并说明理由．(第2题)反比例函数与四边形的综合类型1：反比例函数与平行四边形的综合3．如图，过反比例函数y ＝6x (x ＞0)的图象上一点A 作x 轴的平行线，交双曲线y ＝－3x (x ＜0)于点B ，过B 作BC ∥OA 交双曲线y ＝－3x (x ＜0)于点D ，交x轴于点C ，连接AD 交y 轴于点E ，若OC ＝3，求OE 的长．(第3题)类型2：反比例函数与矩形的综合4．如图，矩形OABC 的顶点A ，C 的坐标分别是(4，0)和(0，2)，反比例函数y ＝kx(x>0)的图象过对角线的交点P 并且与AB ，(第4题)BC 分别交于D ，E 两点，连接OD ，OE ，DE ，则△ODE 的面积为________． 5．如图，在平面直角坐标系中，矩形OABC 的对角线OB ，AC 相交于点D ，且BE ∥AC ，AE ∥OB.(1)求证：四边形AEBD 是菱形；(2)如果OA ＝3，OC ＝2，求出经过点E 的双曲线对应的函数解析式．(第5题)类型3：反比例函数与菱形的综合6．如图，在平面直角坐标系中，菱形ABCD在第一象限内，边BC与x轴平行，A，B两点的纵坐标分别为3，1，反比例函数y＝3x的图象(第6题)经过A，B两点，则菱形ABCD的面积为( )A．2 B．4C．2 2 D．4 27．如图，在平面直角坐标系中，菱形ABCD的顶点C与原点O重合，点B在y轴的正半轴上，点A在反比例函数y＝kx(k>0，x>0)的图象上，点D的坐标为(4，3)．(1)求k的值；(2)若将菱形ABCD沿x轴正方向平移，当菱形的顶点D落在反比例函数y＝kx(k>0，x>0)的图象上时，求菱形ABCD沿x轴正方向平移的距离．(第7题)类型4：反比例函数与正方形的综合8．如图，在平面直角坐标系中，点O为坐标原点，正方形OABC的边OA，OC分别在x轴，y轴上，点B的坐标为(2，2)，反比例函数y＝kx(x＞0，k≠0)的图象经过线段BC的中点D(1)求k的值；(2)若点P(x，y)在该反比例函数的图象上运动(不与点D重合)，过点P作PR⊥y轴于点R，作PQ⊥BC所在直线于点Q，记四边形CQPR的面积为S，求S 关于x的函数解析式并写出x的取值范围．(第8题)反比例函数与圆的综合(第9题)9．如图，双曲线y＝kx(k>0)与⊙O在第一象限内交于P，Q两点，分别过P，Q两点向x轴和y轴作垂线，已知点P的坐标为(1，3)，则图中阴影部分的面积为________．10．如图，反比例函数y＝kx(k＜0)的图象与⊙O相交．某同学在⊙O内做随机扎针试验，求针头落在阴影区域内的概率．(第10题)专训2全章热门考点整合应用名师点金：反比例函数及其图象、性质是历年来中考的热点，既有与本学科知识的综合，也有与其他学科知识的综合，题型既有选择、填空，也有解答类型．其热门考点可概括为：1个概念，2个方法，2个应用及1个技巧．1个概念：反比例函数的概念1．若y＝(m－1)x|m|－2是反比例函数，则m的取值为( )A．1 B．－1C．±1 D．任意实数2．某学校到县城的路程为5 km，一同学骑车从学校到县城的平均速度v(km/h)与所用时间t(h)之间的函数解析式是( )A．v＝5t B．v＝t＋5C．v＝5tD．v＝t53．判断下面哪些式子表示y是x的反比例函数：①xy＝－13；②y＝5－x；③y＝－25x；④y＝2ax(a为常数且a≠0)．其中________是反比例函数．(填序号)2个方法：方法1：画反比例函数图象的方法4．已知y与x的部分取值如下表：解析式；(2)画出这个函数的图象．方法2：求反比例函数解析式的方法5．已知反比例函数y＝kx的图象与一次函数y＝x＋b的图象在第一象限内相交于点A(1，－k＋4)．试确定这两个函数的解析式．6．如图，已知A(－4，n)，B(2，－4)是一次函数y＝kx＋b的图象和反比例函数y＝mx的图象的两个交点．求：(1)反比例函数和一次函数的解析式；(2)直线AB与x轴的交点C的坐标及△AOB的面积；(3)方程kx＋b－mx＝0的解(请直接写出答案)；(4)不等式kx＋b－mx<0的解集(请直接写出答案)．(第6题)2个应用应用1：反比例函数图象和性质的应用7．画出反比例函数y＝6x的图象，并根据图象回答问题：(1)根据图象指出当y＝－2时x的值；(2)根据图象指出当－2<x<1且x≠0时y的取值范围；(3)根据图象指出当－3<y<2且y≠0时x的取值范围．应用2：反比例函数的实际应用8．某厂仓库储存了部分原料，按原计划每小时消耗2吨，可用60小时．由于技术革新，实际生产能力有所提高，即每小时消耗的原料量大于计划消耗的原料量．设现在每小时消耗原料x(单位：吨)，库存的原料可使用的时间为y(单位：小时)．(1)写出y关于x的函数解析式，并求出自变量的取值范围．(2)若恰好经过24小时才有新的原料进厂，为了使机器不停止运转，则x应控制在什么范围内？1个技巧：用k的几何性质巧求图形的面积9．如图，A，B是双曲线y＝kx(k≠0)上的两点，过A点作AC⊥x轴，交OB于D点，垂足为C.若△ADO的面积为1，D为OB的中点，则k的值为( )A.43B.83C．3 D．4(第9题)(第10题)10．如图，过x轴正半轴上的任意一点P作y轴的平行线交反比例函数y＝2 x 和y＝－4x的图象于A，B两点，C是y轴上任意一点，则△ABC的面积为________．11．如图是函数y＝3x与函数y＝6x在第一象限内的图象，点P是y＝6x的图象上一动点，PA⊥x轴于点A，交y＝3x的图象于点C，PB⊥y轴于点B，交y＝3x的图象于点D.(1)求证：D是BP的中点；(2)求四边形ODPC的面积．(第11题)答案专训11．解：(1)∵A(m ，6)，B(3，n)两点在反比例函数y ＝6x (x>0)的图象上，∴m ＝1，n ＝2，即 A(1，6)，B(3，2)．又∵A(1，6)，B(3，2)在一次函数y ＝kx ＋b 的图象上， ∴⎩⎨⎧6＝k ＋b ，2＝3k ＋b ，解得⎩⎨⎧k ＝－2，b ＝8， 即一次函数解析式为y ＝－2x ＋8.(第1题)(2)根据图象可知使kx ＋b<6x 成立的x 的取值范围是0<x<1或x>3.(3)如图，分别过点A ，B 作AE ⊥x 轴，BC ⊥x 轴，垂足分别为E ，C ，设直线AB 交x 轴于D 点．令－2x ＋8＝0，得x ＝4，即D(4，0)． ∵A(1，6)，B(3，2)，∴AE ＝6，BC ＝2.∴S △AOB ＝S △AOD －S △ODB ＝12×4×6－12×4×2＝8.2．(1)证明：∵点A ，B 分别在x 轴，y 轴上，点D 在第一象限内，DC ⊥x轴于点C ，∴∠AOB ＝∠DCA ＝90°.在Rt △AOB 和Rt △DCA 中，∵⎩⎨⎧AO ＝DC ，AB ＝DA ，∴Rt △AOB ≌Rt △DCA.(2)解：在Rt △ACD 中，∵CD ＝2，DA ＝5， ∴AC ＝DA 2－CD 2＝1.∴OC ＝OA ＋AC ＝2＋1＝3.∴D 点坐标为(3，2)．∵点E 为CD 的中点，∴点E 的坐标为(3，1)．∴k ＝3×1＝3. (3)解：点G 在反比例函数的图象上．理由如下：∵△BFG 和△DCA 关于某点成中心对称， ∴△BFG ≌△DCA.∴FG ＝CA ＝1，BF ＝DC ＝2，∠BFG ＝∠DCA ＝90°.∵OB ＝AC ＝1，∴OF ＝OB ＋BF ＝1＋2＝3.∴G 点坐标为(1，3)． ∵1×3＝3，∴点G(1，3)在反比例函数的图象上．3．解：∵BC ∥OA ，AB ∥x 轴，∴四边形ABCO 为平行四边形． ∴AB ＝OC ＝3.设A ⎝⎛⎭⎪⎫a ，6a ，则B ⎝ ⎛⎭⎪⎫a －3，6a ， ∴(a －3)·6a＝－3.∴a ＝2.∴A(2，3)，B(－1，3)．∵OC ＝3，C 在x 轴负半轴上，∴C(－3，0)， 设直线BC 对应的函数解析式为y ＝kx ＋b ， 则⎩⎨⎧－3k ＋b ＝0，－k ＋b ＝3，解得⎩⎪⎨⎪⎧k ＝32，b ＝92.∴直线BC 对应的函数解析式为y ＝32x ＋92.解方程组⎩⎪⎨⎪⎧y ＝32x ＋92，y ＝－3x ，得⎩⎨⎧x 1＝－1，y 1＝3，⎩⎨⎧x 2＝－2，y 2＝32. ∴D ⎝⎛⎭⎪⎫－2，32.设直线AD 对应的函数解析式为y ＝mx ＋n ，则⎩⎨⎧2m ＋n ＝3，－2m ＋n ＝32，解得⎩⎪⎨⎪⎧m ＝38，n ＝94.∴直线AD 对应的函数解析式为y ＝38x ＋94.∴E ⎝⎛⎭⎪⎫0，94.∴OE ＝94.4.154 点拨：因为C(0，2)，A(4，0)，由矩形的性质可得P(2，1)，把P 点坐标代入反比例函数解析式可得k ＝2，所以反比例函数解析式为y ＝2x .因为D点的横坐标为4，所以AD ＝24＝12.因为点E 的纵坐标为2，所以2＝2CE ，所以CE＝1，则BE ＝3.所以S △ODE ＝S 矩形OABC －S △OCE －S △BED －S △OAD ＝8－1－94－1＝154.5．(1)证明：∵BE ∥AC ，AE ∥OB ，∴四边形AEBD 是平行四边形．∵四边形OABC 是矩形，∴DA ＝12AC ，DB ＝12OB ，AC ＝OB.∴DA ＝DB.∴四边形AEBD 是菱形．(2)解：如图，连接DE ，交AB 于F ， ∵四边形AEBD 是菱形，∴DF ＝EF ＝12OA ＝32，AF ＝12AB ＝1.∴E ⎝ ⎛⎭⎪⎫92，1.设所求反比例函数解析式为y ＝kx，把点E ⎝ ⎛⎭⎪⎫92，1的坐标代入得1＝k 92，解得k ＝92.∴所求反比例函数解析式为y ＝92x.(第5题)(第7题) 6．D7．解：(1)如图，过点D作x轴的垂线，垂足为F.∵点D的坐标为(4，3)，∴OF＝4，DF＝3.∴OD＝5.∴AD＝5.∴点A的坐标为(4，8)．∴k＝xy＝4×8＝32.(2)将菱形ABCD沿x轴正方向平移，使得点D落在函数y＝32x(x>0)的图象上点D′处，过点D′作x轴的垂线，垂足为F′.∵DF＝3，∴D′F′＝3.∴点D′的纵坐标为3.∵点D′在y＝32x的图象上，∴3＝32x，解得x＝323，即OF′＝323.∴FF′＝323－4＝203.∴菱形ABCD沿x轴正方向平移的距离为20 3.8．解：(1)∵正方形OABC的边OA，OC分别在x轴，y轴上，点B的坐标为(2，2)，∴C(0，2)．∵D是BC的中点，∴D(1，2)．∵反比例函数y＝kx(x＞0，k≠0)的图象经过点D，∴k＝2.(2)当P在直线BC的上方，即0＜x＜1时，∵点P(x，y)在该反比例函数的图象上运动，∴y＝2 x .∴S四边形CQPR ＝CQ·PQ＝x·⎝⎛⎭⎪⎫2x－2＝2－2x；当P在直线BC的下方，即x＞1时，同理求出S四边形CQPR＝CQ·P Q ＝x·⎝⎛⎭⎪⎫2－2x ＝2x －2，综上，S ＝⎩⎨⎧2x －2（x ＞1），2－2x （0＜x ＜1）.9．410．解：∵反比例函数的图象关于原点对称，圆也关于原点对称，故阴影部分的面积占⊙O 面积的14，则针头落在阴影区域内的概率为14.专训2 1．B 2.C 3．①③④4．解：(1)反比例函数：y ＝－6x.(2)如图所示．(第4题)5．解：∵反比例函数y ＝kx 的图象经过点A(1，－k ＋4)，∴－k ＋4＝k1，即－k ＋4＝k ，∴k ＝2，∴A(1，2)．∵一次函数y ＝x ＋b 的图象经过点A(1，2)， ∴2＝1＋b ，∴b ＝1.∴反比例函数的解析式为y ＝2x ，一次函数的解析式为y ＝x ＋1.6．解：(1)将B(2，－4)的坐标代入y ＝m x ，得－4＝m2，解得m ＝－8.∴反比例函数的解析式为y ＝－8x. ∵点A(－4，n)在双曲线y ＝－8x上，∴n ＝2. ∴A(－4，2)．把A(－4，2)，B(2，－4)的坐标分别代入y ＝kx ＋b ，得 ⎩⎨⎧－4k ＋b ＝2，2k ＋b ＝－4，解得⎩⎨⎧k ＝－1，b ＝－2. ∴一次函数的解析式为y ＝－x －2. (2)令y ＝0，则－x －2＝0，x ＝－2. ∴C(－2，0)．∴OC ＝2.∴S △AOB ＝S △AOC ＋S △BOC ＝12×2×2＋12×2×4＝6.(3)x 1＝－4，x 2＝2.(4)－4<x<0或x>2.7．解：如图，由观察可知： (1)当y ＝－2时，x ＝－3；(2)当－2<x<1且x ≠0时，y<－3或y>6； (3)当－3<y<2且y ≠0时，x<－2或x>3.(第7题)点拨：解决问题时，画出函数图象．由图象观察得知结果．由图象解决相关问题，一定要注意数形结合，学会看图．8．解：(1)库存原料为2×60＝120(吨)，根据题意可知y 关于x 的函数解析式为y ＝120x.由于生产能力提高，每小时消耗的原料量大于计划消耗的原料量，所以自变量的取值范围是x>2.(2)根据题意，得y ≥24，所以120x≥24. 解不等式，得x ≤5，即每小时消耗的原料量应控制在大于2吨且不大于5吨的范围内．点拨：(1)由“每小时消耗的原料量×可使用的时间＝原料总量”可得y 关于x 的函数解析式．(2)要使机器不停止运转，需y ≥24，解不等式即可．(第9题)9．B 点拨：如图，过点B 作BE ⊥x 轴于点E ，∵D 为OB 的中点，∴CD 是△OBE 的中位线，则CD ＝12BE.设A ⎝ ⎛⎭⎪⎫x ，k x ，则B ⎝ ⎛⎭⎪⎫2x ，k 2x ，CD ＝k 4x ，AD ＝k x －k 4x .∵△ADO 的面积为1，∴12AD·OC＝1，即12⎝⎛⎭⎪⎫k x －k 4x ·x＝1.解得k ＝83. 10．311．(1)证明：∵点P 在双曲线y ＝6x 上，∴设P 点坐标为⎝ ⎛⎭⎪⎫6m ，m .∵点D 在双曲线y ＝3x 上，BP ∥x 轴，D 在BP 上，∴D 点坐标为⎝⎛⎭⎪⎫3m ，m .∴BD ＝3m ，BP ＝6m ， 故D 是BP 的中点．(2)解：由题意可知S △BOD ＝32，S △AOC ＝32，S 四边形OBPA ＝6.四边形ODPC ＝S四边形OBPA－S△BOD－S△AOC＝6－32－32＝3.∴S。
人教版数学九年级下册第二十六章《反比例函数》测试卷(含答案)
人教版数学九年级下册第二十六章《反比例函数》测试卷[时间：100分钟满分：120分]一、选择题(每小题3分，共30分)1. 下列函数中，y是x的反比例函数的是()A. y=－12xB. y=－29xC. y=86xD. y=1－6x2．反比例函数y＝5nx的图象经过点(2，3)，则n的值是()A. －2B. －1C. 0D. 13. 反比例函数y＝kx的图象经过点P(－1，2)，则这个函数的图象位于()A. 第二、三象限B. 第一、三象限C. 第三、四象限D. 第二、四象限4．已知反比例函数y＝3x，下列结论中不正确的是()A. 图象经过点(－1，－3)B. 图象在第一、三象限C. 当x＞1时，0＜y＜3D. 当x＜0时，y随着x的增大而增大5. 已知反比例函数y=－10x的图象上有两点P1(x1，y1)，P2(x2，y2)，若x1<0<x2，则下列结论正确的是()A. y1<y2<0B. y1<0<y2C. y1>y2>0D. y1>0>y26．如图所示，直线y＝x＋2与双曲线y＝kx相交于点A，点A的纵坐标为3，则k的值为()A. 1B. 2C. 3D. 4第6题第7题7．已知二次函数y＝－(x－a)2－b的图象如图所示，则反比例函数y＝abx与一次函数y＝ax＋b的图象可能是()A B C D8. 在一个可以改变体积的密闭容器内装有一定质量的二氧化碳，当改变容器的体积时，气体的密度也会随之改变，密度ρ(单位：kg/m 3)是体积V (单位：m 3)的反比例函数，它的图象如图所示，当V =10 m 3时，气体的密度是( )A. 1 kg/m 3B. 2 kg/m 3C. 100 kg/m 3D. 5 kg/m 3第8题 第9题9．如图，A ，B 两点在反比例函数y ＝1k x 的图象上，C ，D 两点在反比例函数y ＝2kx的图象上，AC ⊥x 轴于点E ，BD ⊥x 轴于点F ，AC ＝2，BD ＝3，EF ＝103，则k 2－k 1的值为( )A. 4B.143 C. 163D. 6 10. 某医药研究所开发一种新药，成年人按规定的剂量限用，服药后每毫升血液中的含药量y (毫克)与时间t (小时)之间的函数关系近似满足如图所示曲线，当每毫升血液中的含药量不少于0.25毫克时治疗有效，则服药一次治疗疾病有效的时间为( )A. 16小时B. 1578小时C. 151516小时 D. 17小时二、填空题(每小题3分，共24分)11．请写出一个图象在第二、四象限的反比例函数的解析式：．12. 若反比例函数y=(m－1)x|m|－2，则m的值是.13．若函数y＝2mx的图象在每个象限内y的值随x值的增大而增大，则m的取值范围为．14. 如图，Rt△ABC的两个锐角顶点A，B在函数y=kx(x>0)的图象上，AC∥x轴，AC=2.若点A的坐标为(2，2)，则点B的坐标为.15．已知反比例函数y＝4x，当函数值y≥－2时，自变量x的取值范围是________．16．若变量y与x成反比例，且当x＝3时，y＝－3，则y与x之间的函数关系式是________，在每个象限内函数值y随x的增大而________．17．某闭合电路，电源的电压为定值，电流I(A)与电阻R(Ω)成反比例．如图表示的是该电路中电流I与电阻R之间的函数关系的图象，当电阻R为6 Ω时，电流I为________A.第17题第18题18. 如图，四边形OABC是矩形，ADEF是正方形，点A，D在x轴的正半轴上，点C在y轴的正半轴上，点F在AB上，点B，E在反比例函数y＝kx的图象上，OA＝1，OC＝6，则正方形ADEF的边长为________．三、解答题(共66分)19. (8分)已知y与x－1成反比例，且当x＝－5时，y＝2.(1)求y与x的函数关系式；(2)当x＝5时，求y的值．20. (8分)你吃过拉面吗?实际上在做拉面的过程中就渗透着数学知识：一定体积的面团做成拉面，面条的总长度y(m)是面条的粗细(横截面积)S(mm2)的反比例函数，其图象如图所示.(1)写出y与S的函数关系式；(2)当面条粗为1.6 mm2时，求面条总长度.21. (12分)已知反比例函数y＝4 x .(1)若该反比例函数的图象与直线y＝kx＋4(k≠0)只有一个公共点，求k的值；(2)如图，反比例函数y＝4x(1≤x≤4)的图象记为曲线C1，将C1向左平移2个单位长度，得曲线C2，请在图中画出C2，并直接写出C1平移到C2处所扫过的面积．22. (12分)如图，一次函数y=kx＋b的图象分别与反比例函数y=ax的图象在第一象限交于点A(4，3)，与y轴的负半轴交于点B，且OA=OB.(1)求函数y=kx＋b和y=ax的表达式；(2)已知点C(0，5)，试在该一次函数图象上确定一点M，使得MB=MC，求此时点M的坐标.23. (12分)如图，在平面直角坐标系xOy中，直线y＝x－2与y轴相交于点A，与反比例函数y＝kx在第一象限内的图象相交于点B(m，2)．(1)求该反比例函数的关系式；(2)若直线y＝x－2向上平移后与反比例函数y＝kx在第一象限内的图象相交于点C，且△ABC的面积为18，求平移后的直线对应的函数关系式．24. (14分)为了预防流行性感冒，某学校对教室采用药熏消毒法进行消毒.已知药物燃烧时室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例；药物燃烧后，y与x成反比例(如图所示).请根据图中提供的信息，解答下列问题：(1)药物燃烧后y与x的函数关系式为；(2)当空气中每立方米的含药量低于1.6毫克时学生方可进教室，那么从消毒开始，至少需要经过几分钟后，学生才能回到教室；(3)当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时，才能有效杀灭空气中的病菌，那么此次消毒是否有效?为什么?。
人教版初三数学9年级下册 第26章 26.1.2反比例函数的图像与性质 课时训练(含答案)
26.1.2反比例函数的图像与性质一、选择题1. 若点(3,6)在反比例函数y=kx(k≠0)的图象上，那么下列各点在此图象上的是( ) A．(−3,6)B．(2,9)C．(2,−9)D．(3,−6)2. 在反比例函数y=k−1x的图象的每一条曲线上，y都随x的增大而减小，则k的取值范围是( )A．k>1B．k>0C．k≥1D．k<13. 下列反比例函数的图象一定在第一，三象限的是( )A．y=mx B．y=m+1xC．y=m2+1xD．y=−mx4. 已知函数y=kx的图象经过点(2,3)，下列说法正确的是( )A．y随x的增大而增大B．函数的图象只在第一象限C．当x<0时，必有y<0D．点(−2,−3)不在此函数图象上5. 已知A(x1,y1)，B(x2,y2)是反比例函数y=kx(k≠0)图象上的两点，当x1<x2<0时，y1> y2，那么一次函数y=kx−k的图象不经过( )A．第一象限B．第二象限C．第三象限D．第四象限6. 一次函数y=kx+b(k≠0)与反比例函数y=kx(k≠0)的图象在同一直角坐标系中的大致图象如图所示，则k，b的取值范围是( )A．k>0，b>0B．k<0，b>0C．k<0，b<0D．k>0，b<07. 如图，菱形OABC的顶点C的坐标为(3,4)．顶点A在x轴的正半轴上，反比例函数y=kx (x>0)的图象经过顶点B，则k的值为( )A．12B．20C．24D．328. 在反比例函数y=k(k<0)的图象上有两点A(x1,y1)，B(x2,y2)，且x1>x2>0，则y1−y2的x值为( )A．正数B．负数C．非正数D．非负数9. 已知抛物线y=x2−2x+m+1与x轴有两个不同的交点，则函数y=m的大致图象为x( )A．B．C．D．二、填空题10. 点(1,3)在反比例函数y=k的图象上，则k=，在图象的每一支上，y随x的增大x而．11. 如图所示，某反比例函数的图象经过点(−2,1)，则此反比例函数表达式为．12. 反比例函数y=2a−1的图象有一支位于第一象限，则常数a的取值范围是．x13. 已知点A(2,y1)，B(4,y2)都在反比例函数y=k(k<0)的图象上，则y1y2（填“>”“<”x或“=”）．14. 已知函数y=(m+1)x m2−5是反比例函数，且图象在第一、三象限内，则m=．15. 如图，在平面直角坐标系中，点P是反比例函数y=k(x>0)图象上的一点，分别过点P作xPA⊥x轴于点A，PB⊥y轴于点B，若四边形OAPB的面积为3，则k的值为．16. 反比例函数y=k+1，点(x1,y1)，(x2,y2)在其图象上，当x1<0<x2时，有y1>y2，则k x的取值范围是．图象上的概率17. 从2，3，4，5中任意选两个数，记作a和b，那么点(a,b)在函数y=12x是．18. 如图，已知点A(1,2)是反比例函数y=k图象上的一点，连接AO并延长交双曲线的另一分支x于点B，点P是x轴上一动点．若△PAB是等腰三角形，则点P的坐标是．19. 如图，已知直线y=k1x+b与x轴，y轴相交于P，Q两点，与y=k2的图象相交于Axn=0；③S△AOP= (−2,m)，B(1,n)两点，连接OA，OB给出下列结论：①k1k2<0；②m+12的解集是x<−2或0<x<1．其中正确结论的序号是．S△BOQ；④不等式k1x+b>k2x三、解答题20. 作出反比例函数y=−4的图象，并结合图象回答：x(1) 当x=2时，y的值；(2) 当1<x≤4时，y的取值范围；(3) 当1≤y<4时，x的取值范围．21. 已知反比例函数y=m−7的图象的一支位于第一象限．x(1) 判断该函数图象的另一支所在的象限，并求m的取值范围；(2) 如图，O为坐标原点，点A在该反比例函数位于第一象限的图象上，点B与点A关于x轴对称，若△OAB的面积为6，求m的值．22. 如图，在平面直角坐标系中，菱形ABCD的顶点C与原点O重合，点B在y轴的正半轴上，点A在函数y=k(k>0,x>0)的图象上，点D的坐标为(4,3)．x(1) 求k的值；(2) 若将菱形ABCD沿x轴正方向平移，当菱形的顶点D落在函数y=k(k>0,x>0)的图象x上时，求菱形ABCD沿x轴正方向平移的距离．23. 如图，P1，P2是反比例函数y=k(k>0)在第一象限图象上的两点，点A1的坐标为x(4,0)．若△P1OA1与△P2A1A2均为等腰直角三角形，其中点P1，P2为直角顶点．(1) 求反比例函数的解析式；(2) ①求P2的坐标；②根据图象直接写出在第一象限内当x满足什么条件时，经过点P1，P2的一次函数的函的函数值．数值大于反比例函数y=kx24. 如图，在平面直角坐标系中，点O为坐标原点，正方形OABC的边OA，OC分别在x轴、y轴上，点B的坐标为(2,2)，反比例函数y=k（x>0，k≠0）的图象经过线段BC的中点xD．(1) 求k的值(2) 若点P(x,y)在该反比例函数的图象上运动（不与点D重合），过点P作PR⊥y轴于点R，作PQ⊥BC所在直线于点Q，记四边形CQPR的面积为S，求S关于x的解析式，并写出x的取值范围．25. 已知反比例函数的图象过点(1,−2)．(1) 求这个函数的解析式，并画出图象．(2) 若点A(−5,m)在该图象上，则点A关于两坐标轴和原点的对称点是否也在图象上？26. 如图，一次函数y=kx+b的图象l分别与x轴，y轴交于点E，F，与双曲线y=−4x (x<0)交于点P(−1,n)，F是PE的中点．(1) 求直线l的解析式；(2) 若直线x=a与l交于点A，与双曲线交于点B（不同于A），问a为何值时，PA=PB？27. 如图1，已知正比例函数和反比例函数图象都经过点M(−2,−1)，P(−1,−2)为双曲线上的一点，Q为坐标平面上一动点．(1) 写出正比例函数和反比例函数的关系式．(2) 如图2，当点Q在第一象限中的双曲线上运动时，作以OP，OQ为邻边的平行四边形OPCQ，求平行四边形OPCQ周长的最小值．答案一、选择题1. 【答案】B2. 【答案】A3. 【答案】C4. 【答案】C5. 【答案】B6. 【答案】D7. 【答案】D8. 【答案】A9. 【答案】B二、填空题10. 【答案】3；减小11. 【答案】y=−2x12. 【答案】a>12的图象有一支位于第一象限，【解析】∵反比例函数y=2a−1x∴2a−1>0，解得a>1．213. 【答案】<14. 【答案】215. 【答案】316. 【答案】k<−117. 【答案】1618. 【答案】(−3,0)或(5,0)或(3,0)或(−5,0)19. 【答案】②③④三、解答题20. 【答案】(1) y=−2．(2) −4<y≤−1．(3) −4≤x<−1．21. 【答案】(1) 根据反比例函数的图象关于原点对称知，该函数图象的另一支在第三象限，且m−7>0，则m>7．(2) ∵点B与点A关于x轴对称，若△OAB的面积为6，∴△OAC 的面积为 3．设 A 12x ⋅m−7x=3，解得 m =13．22. 【答案】(1) 如图，过点 D 作 x 轴的垂线，垂足为 F ．因为点 D 的坐标为 (4,3)，所以 OF =4，DF =3．所以 OD =5．所以 AD =5．所以点 A 的坐标为 (4,8)．所以 k =4×8=32．(2) 如图，将菱形 ABCD 沿 x 轴正方向平移，使得点 D 落在函数 y =32x(x >0) 的图象上的Dʹ 处，过点 Dʹ 作 x 轴的垂线，垂足为 Fʹ．因为 DF =3，所以 DʹFʹ=3．所以点 Dʹ 的纵坐标为 3．因为点 Dʹ 在 y =32x的图象上，所以 3=32x ，解得 x =323，即 OFʹ=323．所以 FFʹ=323−4=203．所以菱形 ABCD 沿 x 轴正方向平移的距离为 203．23. 【答案】(1) y =4x ．(2) ① P 2 的坐标为 (2+22,22−2)；② 2<x <2+22．24. 【答案】(1) k =2．(2) S =2x−2,x >12−2x,0<x <1．25. 【答案】(1) y =−2x ，图略．(2) m =25，点 A −5,关于两坐标轴对称的点均不在函数图象上，关于原点对称的点在函数图象上．26. 【答案】(1) y =−2x +2．(2) 当 a =−2 时，PA =PB （提示：过点 P 作 PD ⊥AB ）．27. 【答案】(1) 正比例函数解析式为 y =12x ，反比例函数解析式为 y =2x ．(2) 平行四边形 OPCQ 周长的最小值是 2(OP +OQ )=2(5+2)=25+4．。
初三数学反比例函数的专项培优练习题(含答案)含答案解析
初三数学反比例函数的专项培优练习题(含答案)含答案解析一、反比例函数1．如图，在平面直角坐标系中，一次函数y1=ax+b（a≠0）的图象与y轴相交于点A，与反比例函数y2= （c≠0）的图象相交于点B（3，2）、C（﹣1，n）．（1）求一次函数和反比例函数的解析式；（2）根据图象，直接写出y1＞y2时x的取值范围；（3）在y轴上是否存在点P，使△PAB为直角三角形？如果存在，请求点P的坐标；若不存在，请说明理由．【答案】（1）解：把B（3，2）代入得：k=6∴反比例函数解析式为：把C（﹣1，n）代入，得：n=﹣6∴C（﹣1，﹣6）把B（3，2）、C（﹣1，﹣6）分别代入y1=ax+b，得：，解得：所以一次函数解析式为y1=2x﹣4（2）解：由图可知，当写出y1＞y2时x的取值范围是﹣1＜x＜0或者x＞3．（3）解：y轴上存在点P，使△PAB为直角三角形如图，过B作BP1⊥y轴于P1，∠B P1 A=0，△P1AB为直角三角形此时，P1（0，2）过B作BP2⊥AB交y轴于P2∠P2BA=90，△P2AB为直角三角形在Rt△P1AB中，在Rt△P1 AB和Rt△P2 AB∴∴P2（0，）综上所述，P1（0，2）、P2（0，）．【解析】【分析】（1）利用待定系数法求出反比例函数解析式，进而求出点C坐标，最后用再用待定系数法求出一次函数解析式；（2）利用图象直接得出结论；（3）分三种情况，利用勾股定理或锐角三角函数的定义建立方程求解即可得出结论．2．如图，在平面直角坐标系xOy中，一次函数y=kx+b（k≠0）的图象与反比例函数的图象交于二四象限内的A、B 两点，与x轴交于C点，点B的坐标为（6，n），线段OA=5，E为x轴负半轴上一点，且sin∠AOE=．（1）求该反比例函数和一次函数的解析式；（2）求△AOC的面积；（3）直接写出一次函数值大于反比例函数值时自变量x的取值范围．【答案】（1）解：作AD⊥x轴于D，如图，在Rt△OAD中，∵sin∠AOD= = ，∴AD= OA=4，∴OD= =3，∴A（﹣3，4），把A（﹣3，4）代入y= 得m=﹣4×3=﹣12，所以反比例函数解析式为y=﹣；把B（6，n）代入y=﹣得6n=﹣12，解得n=﹣2，把A（﹣3，4）、B（6，﹣2）分别代入y=kx+b得，解得，所以一次函数解析式为y=﹣x+2（2）解：当y=0时，﹣x+2=0，解得x=3，则C（3，0），所以S△AOC= ×4×3=6（3）解：当x＜﹣3或0＜x＜6时，一次函数的值大于反比例函数的值【解析】【分析】（1）作AD⊥x轴于D，如图，先利用解直角三角形确定A（﹣3，4），再把A点坐标代入y= 可求得m=﹣12，则可得到反比例函数解析式；接着把B（6，n）代入反比例函数解析式求出n，然后把A和B点坐标分别代入y=kx+b得到关于a、b的方程组，再解方程组求出a和b的值，从而可确定一次函数解析式；（2）先确定C点坐标，然后根据三角形面积公式求解；（3）观察函数图象，找出一次函数图象在反比例函数图象上方所对应的自变量的范围即可．3．如图，已知正比例函数y=2x和反比例函数的图象交于点A（m，﹣2）.（1）求反比例函数的解析式；（2）观察图象，直接写出正比例函数值大于反比例函数值时自变量x的取值范围；（3）若双曲线上点C（2，n）沿OA方向平移个单位长度得到点B，判断四边形OABC 的形状并证明你的结论.【答案】（1）解：设反比例函数的解析式为（k＞0）∵A（m，﹣2）在y=2x上，∴﹣2=2m，∴解得m=﹣1。
人教版九年级下数学《第26章反比例函数》单元培优检测题含答案
《反比例函数》单元培优检测题一．选择题1．已知点A（3，y1），B（﹣2，y2），C（1，y3）都在反比例函数y＝的图象上，那么（）A．y2＜y1＜y3B．y3＜y1＜y2C．y1＜y3＜y2D．y2＜y3＜y12．若反比例函数y＝（k≠0）的图象经过点P（2，﹣3），则该函数的图象不经过的点是（）A．（3，﹣2）B．（1，﹣6）C．（﹣1，6）D．（﹣1，﹣6）3．如图，在平面直角坐标系xOy中，反比例函数y＝的图象经过点T．下列各点P（4，6），Q（3，﹣8），M（2，﹣12），N（，48）中，在该函数图象上的点有（）A．4个B．3个C．2个D．1个4．如图，点M、N都在反比例函数的图象上，则△OMN的面积为（）A．1 B．C．2 D．35．在温度不变的条件下，通过一次又一次地对汽缸顶部的活塞加压，测出每一次加压后缸内气体的体积和气体对汽缸壁所产生的压强，如下表：则可以反映y与x之间的关系的式子是（）体积x（mL）100 80 60 40 20压强y（kPa）60 75 100 150 300A．y＝3 000x B．y＝6 000x C．y＝D．y＝6．反比例函数y＝和y＝在第一象限内的图象如图所示，点P在y＝的图象上，PC⊥x 轴，交y＝的图象于点A，PD⊥y轴，交y＝的图象于点B．当点P在y＝的图象上运动时，以下结论：①△ODB与△OCA的面积相等；②PA与PB始终相等；③四边形PAOB的面积不会发生变化；④当点A是PC的中点时，点B一定是PD的中点．其中一定正确的是（）A．①②③④B．①②③C．②③④D．①③④7．反比例函数y＝（a＞0，a为常数）和y＝在第一象限内的图象如图所示，点M在y ＝的图象上，MC⊥x轴于点C，交y＝的图象于点A；MD⊥y轴于点D，交y＝的图象于点B，当点M在y＝的图象上运动时，以下结论：①S△ODB ＝S△OCA；②四边形OAMB的面积不变；③当点A是MC的中点时，则点B是MD的中点．其中正确结论是（）A．①②B．①③C．②③D．①②③8．如图，△ABC的顶点A在反比例函数y＝（x＞0）的图象上，顶点C在x轴上，AB∥x轴，若点B的坐标为（1，3），S＝2，则k的值为（）△ABCA．4 B．﹣4 C．7 D．﹣79．函数y＝ax2﹣a与y＝﹣（a≠0）在同一直坐标系中的图象可能是（）A．B．C．D．10．如图所示双曲线y＝与y＝﹣分别位于第三象限和第二象限，A是y轴上任意一点，B是y＝﹣上的点，C是y＝上的点，线段BC⊥x轴于D，且4BD＝3CD，则下列说法：①双曲线y＝在每个象限内，y随x的增大而减小；②若点B的横坐标为﹣3，则C点的坐标为（﹣3，）；③k＝4；④△ABC的面积为定值7，正确的有（）A．1个B．2个C．3个D．4个二．填空题11．如图，在△AOB中，∠AOB＝90°，点A的坐标为（4，2），BO＝4，反比例函数y＝的图象经过点B，则k的值为．12．如图，在平面直角坐标系xOy中，函数y＝（x＞0）的图象经过Rt△OAB的斜边OA 的中点D，交AB于点C．若点B在x轴上，点A的坐标为（6，4），则△BOC的面积为．13．请写出一个图象与直线y＝x无交点的反比例函数的表达式：．14．已知A（m，3）、B（﹣2，n）在同一个反比例函数图象上，则＝．15．在反比例函数y＝（x＜0）中，函数值y随着x的增大而减小，则m的取值范围是．16．如图，点P在反比例函数y＝的图象上．若矩形PMON的面积为4，则k＝．三．解答题17．如图，已知一次函数y1＝k1x+b（k1≠0）与反比例函数y2＝（k2≠0）的图象交于A（4，1），B（n，﹣2）两点．（1）求一次函数与反比例函数的解析式；（2）请根据图象直接写出y1＜y2时x的取值范围．18．如图，在平面直角坐标系中，点A（2，4）在反比例函数y＝的图象上，点C的坐标是（3，0），连接OA，过C作OA的平行线，过A作x轴的平行线，交于点B，BC与双曲线y＝的图象交于D，连接AD．（1）求D点的坐标；（2）四边形AOCD的面积．19．如图，一次函数y＝kx+b与反比例函数y＝的图象交于A（1，4），B（4，n）两点．（1）求反比例函数和一次函数的解析式；（2）直接写出当x＞0时，kx+b＜的解集．（3）点P是x轴上的一动点，试确定点P并求出它的坐标，使PA+PB最小．20．如图，点A在反比例函数的图象在第二象限内的分支上，AB⊥x轴于点B，O是原点，且△AOB的面积为1．试解答下列问题：（1）比例系数k＝；（2）在给定直角坐标系中，画出这个函数图象的另一个分支；（3）当x＞1时，写出y的取值范围．21．如图，一次函数y＝kx+b的图象与反比例函数y＝的图象交于A（﹣2，1），B（1，n）两点．（1）求m，n的值；（2）当一次函数的值大于反比例函数的值时，请写出自变量x的取值范围．22．如图，四边形ABCD放在在平面直角坐标系中，已知AB∥CD，AD＝BC，A（﹣2，0）、B （6，0）、D（0，3），反比例函数的图象经过点C．（1）求点C的坐标和反比例函数的解析式；（2）将四边形ABCD向上平移2个单位后，问点B是否落在该反比例函数的图象上？23．如图，反比例函数的图象在第一象限内经过点A，过点A分别向x轴、y轴作垂线，垂足分别P、Q，若AP＝3，AQ＝1，求这个反比例函数的解析式．24．如图，在平面直角坐标系xOy中，直线y＝x+b与双曲线y＝相交于A，B两点，已知A（2，5）．求：（1）b和k的值；（2）△OAB的面积．参考答案一．选择题1．解：∵点A（3，y1），B（﹣2，y2），C（1，y3）都在反比例函数y＝的图象上，∴y1＝2，y2＝﹣3，y3＝6，∴y2＜y1＜y3，故选：A．2．【解答】解：∵反比例函数y＝（k≠0）的图象经过点P（2，﹣3），∴k＝2×（﹣3）＝﹣6∴解析式y＝当x＝3时，y＝﹣2当x＝1时，y＝﹣6当x＝﹣1时，y＝6∴图象不经过点（﹣1，﹣6）故选：D．3．解：∵反比例函数y＝的图象经过点T（3，8），∴k＝3×8＝24，将P（4，6），Q（3，﹣8），M（2，﹣12），N（，48）分别代入反比例函数y＝，可得Q（3，﹣8），M（2，﹣12）不满足反比例函数y＝，∴在该函数图象上的点有2个，故选：C．4．解：过M、N分别作MA⊥x轴，NB⊥x轴，S四边形OMNB ＝S△OMA+S四边形MABN＝S△OMN+S△ONB，∵M（1，2），N（2，1），∴MA＝OB＝2，OA＝NB＝1，则S△OMN＝×1×2+×（1+2）×（2﹣1）﹣×2×1＝，故选：B．5．解：由表格数据可得：此函数是反比例函数，设解析式为：y ＝， 则xy ＝k ＝6000，故y 与x 之间的关系的式子是y ＝，故选：D ．6．解：①∵点A 、B 均在反比例函数y ＝的图象上，且BD ⊥y 轴，AC ⊥x 轴， ∴S △ODB ＝，S △OCA ＝，∴S △ODB ＝S △OCA ，结论①正确；②设点P 的坐标为（m ，），则点B 的坐标（，），点A （m ，）， ∴PA ＝﹣＝，PB ＝m ﹣＝， ∴PA 与PB 的关系无法确定，结论②错误；③∵点P 在反比例函数y ＝的图象上，且PC ⊥x 轴，PD ⊥y 轴，∴S 矩形OCPD ＝k ，∴S 四边形PAOB ＝S 矩形OCPD ﹣S △ODB ﹣S △OCA ＝k ﹣1，结论③正确；④设点P 的坐标为（m ，），则点B 的坐标（，），点A （m ，）， ∵点A 是PC 的中点，∴k ＝2，∴P （m ，），B （，），∴点B 是PD 的中点，结论④正确．故选：D ．7．解：①由于A、B在同一反比例函数y＝图象上，则△ODB与△OCA的面积相等，都为×2＝1，正确；②由于矩形OCMD、三角形ODB、三角形OCA为定值，则四边形MAOB的面积不会发生变化，正确；③连接OM，点A是MC的中点，则△OAM和△OAC的面积相等，∵△ODM的面积＝△OCM的面积＝，△ODB与△OCA的面积相等，∴△OBM与△OAM的面积相等，∴△OBD和△OBM面积相等，∴点B一定是MD的中点．正确；故选：D．8．解：∵AB∥x轴，若点B的坐标为（1，3），∴设点A（a，3）＝（a﹣1）×3＝2∵S△ABC∴a＝∴点A（，3）∵点A在反比例函数y＝（x＞0）的图象上，∴k＝7故选：C．9．解：A、二次y＝ax2﹣a的图象开口方向向上，与y轴交于负半轴，则a＞0，则反比例函数y＝﹣的图象应该经过第二、四象限，故本选项正确．B、二次y＝ax2﹣a的图象开口方向向上，与y轴交于负半轴，则a＞0，则反比例函数y＝﹣的图象应该经过第二、四象限，故本选项错误．C、二次y＝ax2﹣a的图象开口方向向下，则a＜0．与y轴交于负半轴，则﹣a＜0，即a＞0，相矛盾，故本选项错误．D、二次y＝ax2﹣a的图象开口方向向下，与y轴交于正半轴，则a＜0，则反比例函数y＝﹣的图象应该经过第一、三象限，故本选项错误．故选：A．10．解：①y＝的图象在一、三象限，故在每个象限内，y随x的增大而减小，故①正确；②点B的横坐标为﹣3，则B（﹣3，1），由4BD＝3CD，可得CD＝，故C（﹣3，﹣），故②错误；③设点B的横坐标为a，则B（a，﹣），由4BD＝3CD，可得CD＝﹣，故C（a，），由C（a，）可得：k＝a×＝4，故③正确；＝＝﹣×（﹣a）×＝，故④错误；④BC＝﹣﹣＝﹣，S△ABC所以本题正确的有两个：①③；故选：B．二．填空题（共6小题）11．解：过点A作AC⊥x轴，过点B作BD⊥x轴，垂足分别为C、D，则∠OCA＝∠BDO＝90°，∴∠DBO+∠BOD＝90°，∵∠AOB＝90°，∴∠AOC+∠BOD＝90°，∴∠DBO＝∠AOC，∴△DBO∽△COA，∴＝＝，∵点A的坐标为（4，2），∴AC＝2，OC＝4，∴AO＝＝2，∴＝＝即BD＝8，DO＝4，∴B（﹣4，8），∵反比例函数y＝的图象经过点B，∴k的值为﹣4×8＝﹣32．故答案为﹣3212．解：∵点A的坐标为（6，4），而点D为OA的中点，∴D点坐标为（3，2），把D（3，2）代入y＝得k＝3×2＝6，∴反比例函数的解析式为y＝，∴△BOC的面积＝|k|＝×|6|＝3．故答案为：3；13．解：∵直线y＝x经过第一、三象限，∴与直线y＝x无交点的反比例函数的图象在第二、四象限，∴与直线y＝x无交点的反比例函数表达式为：y＝﹣故答案为：y＝﹣（答案不唯一）．14．解：设反比例函数解析式为y＝，根据题意得：k＝3m＝﹣2n∴＝﹣故答案为：﹣．15．解：∵反比例函数y ＝（x ＜0）中，函数值y 随着x 的增大而减小，∴m ﹣1＞0，∴m ＞1，故答案为m ＞1．16．解：设PN ＝a ，PM ＝b ，则ab ＝6，∵P 点在第二象限，∴P （﹣a ，b ），代入y ＝中，得 k ＝﹣ab ＝﹣4，故答案为：﹣4．三．解答题（共8小题）17．解：（1）∵反比例函数y 2＝（k 2≠0）的图象过点A （4，1），∴k 2＝4×1＝4，∴反比例函数的解析式为y 2＝．∵点B （n ，﹣2）在反比例函数y 2＝的图象上，∴n ＝4÷（﹣2）＝﹣2，∴点B 的坐标为（﹣2，﹣2）．将A （4，1）、B （﹣2，﹣2）代入y 1＝k 1x +b ， ，解得：， ∴一次函数的解析式为y ＝x ﹣1．（2）观察函数图象，可知：当x ＜﹣2和0＜x ＜4时，一次函数图象在反比例函数图象下方， ∴y 1＜y 2时x 的取值范围为x ＜﹣2或0＜x ＜4．18．解：（1）∵点A （2，4）在反比例函数y ＝的图象上，∴k ＝2×4＝8，∴反比例函数解析式为y ＝；设OA 解析式为y ＝k 'x ，则4＝k '×2，∴k '＝2，∵BC ∥AO ，∴可设BC 的解析式为y ＝2x +b ，把（3，0）代入，可得0＝2×3+b ，解得b ＝﹣6，∴BC 的解析式为y ＝2x ﹣6，令2x ﹣6＝，可得x ＝4或﹣1，∵点D 在第一象限，∴D （4，2）；（2）∵AB ∥OC ，AO ∥BC ，∴四边形ABCO 是平行四边形，∴AB ＝OC ＝3，∴S 四边形AOCD ＝S 四边形ABCO ﹣S △ABD＝3×4﹣×3×（4﹣2）＝12﹣3＝9．19．解：（1）把A （1，4）代入y ＝，得：m ＝4，∴反比例函数的解析式为y ＝；把B （4，n ）代入y ＝，得：n ＝1，∴B （4，1），把A（1，4）、（4，1）代入y＝kx+b，得：，解得：，∴一次函数的解析式为y＝﹣x+5；（2）根据图象得当0＜x＜1或x＞4，一次函数y＝﹣x+5的图象在反比例函数y＝的下方；∴当x＞0时，kx+b＜的解集为0＜x＜1或x＞4；（3）如图，作B关于x轴的对称点B′，连接AB′，交x轴于P，此时PA+PB＝AB′最小，∵B（4，1），∴B′（4，﹣1），设直线AB′的解析式为y＝px+q，∴，解得，∴直线AB′的解析式为y＝﹣x+，令y＝0，得﹣x+＝0，解得x＝，∴点P的坐标为（，0）．20．（1）解：由于△AOB的面积为1，则|k|＝2，又函数图象位于第一象限，k＞0，则k＝2，反比例函数关系式为y＝﹣．故答案为：﹣2；（2）如图所示：；（3）利用图象可得出：当x＞1时：﹣2＜y＜0．21．解：（1）把A（﹣2，1）代入反比例函数y＝得，m＝﹣2×1＝﹣2，∴反比例函数解析式为y＝﹣；把B（1，n）代入得，1×n＝﹣2，解得n＝﹣2；（2）由图象可知：x＜﹣2或0＜x＜1．22．解：（1）过C作CE⊥AB，∵DC∥AB，AD＝BC，∴四边形ABCD为等腰梯形，∴∠A＝∠B，DO＝CE＝3，CD＝OE，∴△ADO≌△BCE，∴BE＝OA＝2，∵AB＝8，∴OE＝AB﹣OA﹣BE＝8﹣4＝4，∴C（4，3），把C（4，3）代入反比例解析式得：k＝12，则反比例解析式为y＝；（2）由平移得：平移后B的坐标为（6，2），把x＝6代入反比例得：y＝2，则平移后点B落在该反比例函数的图象上．23．解：由题意得：S＝|k|＝3×1＝3；四边形APOQ又由于函数图象位于第一象限，k＞0，则k＝3．所以这个反比例函数的解析式为y＝．24．解：（1）∵直线y＝x+b与双曲线y＝相交于A，B两点，已知A（2，5），∴5＝2+b，5＝．解得：b＝3，k＝10．（2）如图，过A作AD⊥y轴于D，过B作BE⊥y轴于E，∴AD＝2．∵b＝3，k＝10，∴y＝x+3，y＝．由得：或，∴B点坐标为（﹣5，﹣2）．∴BE＝5．设直线y＝x+3与y轴交于点C．∴C点坐标为（0，3）．∴OC＝3．∴S△AOC＝OC•AD＝×3×2＝3，S△BOC＝OC•BE＝×3×5＝．∴S△AOB ＝S△AOC+S△BOC＝．。
人教版九年级数学下《第26章反比例函数》专项训练含答案
人教版九年级数学下《第26章反比例函数》专项训练含答案26章 反比例函数 专项训练专训1 反比例函数与几何的综合应用 名师点金：解反比例函数与几何图形的综合题，一般先设出几何图形中的未知数，然后结合函数的图象用含未知数的式子表示出几何图形与图象的交点坐标，再由函数解析式及几何图形的性质写出含未知数及待求字母系数的方程(组)，解方程(组)即可得所求几何图形中的未知量或函数解析式中待定字母的值．反比例函数与三角形的综合1．如图，一次函数y ＝kx ＋b 与反比例函数y ＝6x(x>0)的图象交于A(m ，6)，B(3，n)两点．(1)求一次函数的解析式；(2)根据图象直接写出使kx ＋b<6x成立的x 的取值范围；(3)求△AOB 的面积．(第1题)2．如图，点A ，B 分别在x 轴、y 轴上，点D 在第一象限内，DC ⊥x 轴于点C ，AO ＝CD ＝2，AB ＝DA ＝5，反比例函数y ＝kx(k ＞0)的图象过CD 的中点E.(1)求证：△AOB ≌△DCA ； (2)求k 的值；(3)△BFG 和△DCA 关于某点成中心对称，其中点F 在y 轴上，试判断点G 是否在反比例函数的图象上，并说明理由．(第2题)反比例函数与四边形的综合类型1：反比例函数与平行四边形的综合3．如图，过反比例函数y ＝6x(x ＞0)的图象上一点A 作x 轴的平行线，交双曲线y ＝－3x (x ＜0)于点B ，过B 作BC ∥OA 交双曲线y ＝－3x(x ＜0)于点D ，交x 轴于点C ，连接AD 交y 轴于点E ，若OC ＝3，求OE 的长．(第3题)类型2：反比例函数与矩形的综合4．如图，矩形OABC 的顶点A ，C 的坐标分别是(4，0)和(0，2)，反比例函数y ＝kx(x>0)的图象过对角线的交点P 并且与AB ，(第4题)BC 分别交于D ，E 两点，连接OD ，OE ，DE ，则△ODE 的面积为________． 5．如图，在平面直角坐标系中，矩形OABC 的对角线OB ，AC 相交于点D ，且BE ∥AC ，AE ∥OB.(1)求证：四边形AEBD 是菱形；(2)如果OA ＝3，OC ＝2，求出经过点E 的双曲线对应的函数解析式．(第5题)类型3：反比例函数与菱形的综合6．如图，在平面直角坐标系中，菱形ABCD 在第一象限内，边BC 与x 轴平行，A ，B 两点的纵坐标分别为3，1，反比例函数y ＝3x的图象(第6题)经过A ，B 两点，则菱形ABCD 的面积为( ) A ．2 B ．4C ．2 2D ．4 27．如图，在平面直角坐标系中，菱形ABCD 的顶点C 与原点O 重合，点B在y 轴的正半轴上，点A 在反比例函数y ＝kx(k>0，x>0)的图象上，点D 的坐标为(4，3)．(1)求k 的值；(2)若将菱形ABCD 沿x 轴正方向平移，当菱形的顶点D 落在反比例函数y ＝kx(k>0，x>0)的图象上时，求菱形ABCD 沿x 轴正方向平移的距离．(第7题)类型4：反比例函数与正方形的综合8．如图，在平面直角坐标系中，点O 为坐标原点，正方形OABC 的边OA ，OC 分别在x 轴，y 轴上，点B 的坐标为(2，2)，反比例函数y ＝kx(x ＞0，k ≠0)的图象经过线段BC 的中点D(1)求k 的值；(2)若点P(x ，y)在该反比例函数的图象上运动(不与点D 重合)，过点P 作PR ⊥y 轴于点R ，作PQ ⊥BC 所在直线于点Q ，记四边形CQPR 的面积为S ，求S 关于x 的函数解析式并写出x 的取值范围．(第8题)反比例函数与圆的综合(第9题)9．如图，双曲线y ＝kx(k>0)与⊙O 在第一象限内交于P ，Q 两点，分别过P ，Q 两点向x 轴和y 轴作垂线，已知点P 的坐标为(1，3)，则图中阴影部分的面积为________．10．如图，反比例函数y ＝kx(k ＜0)的图象与⊙O 相交．某同学在⊙O 内做随机扎针试验，求针头落在阴影区域内的概率．(第10题)专训2 全章热门考点整合应用名师点金：反比例函数及其图象、性质是历年来中考的热点，既有与本学科知识的综合，也有与其他学科知识的综合，题型既有选择、填空，也有解答类型．其热门考点可概括为：1个概念，2个方法，2个应用及1个技巧．1个概念：反比例函数的概念1．若y ＝(m －1)x |m|－2是反比例函数，则m 的取值为( )A ．1B ．－1C ．±1D ．任意实数2．某学校到城的路程为5 km ，一同学骑车从学校到城的平均速度v(km /h )与所用时间t(h )之间的函数解析式是( )A ．v ＝5tB ．v ＝t ＋5C．v＝5tD．v＝t53．判断下面哪些式子表示y是x的反比例函数：①xy＝－13；②y＝5－x；③y＝－25x；④y＝2ax(a为常数且a≠0)．其中________是反比例函数．(填序号)2个方法：方法1：画反比例函数图象的方法4．已知y与x的部分取值如下表：解析式；(2)画出这个函数的图象．方法2：求反比例函数解析式的方法5．已知反比例函数y＝kx的图象与一次函数y＝x＋b的图象在第一象限内相交于点A(1，－k＋4)．试确定这两个函数的解析式．6．如图，已知A(－4，n)，B(2，－4)是一次函数y＝kx＋b的图象和反比例函数y＝mx的图象的两个交点．求：(1)反比例函数和一次函数的解析式；(2)直线AB与x轴的交点C的坐标及△AOB的面积；(3)方程kx＋b－mx＝0的解(请直接写出答案)；(4)不等式kx＋b－mx<0的解集(请直接写出答案)．(第6题)2个应用应用1：反比例函数图象和性质的应用7．画出反比例函数y ＝6x的图象，并根据图象回答问题：(1)根据图象指出当y ＝－2时x 的值；(2)根据图象指出当－2<x<1且x ≠0时y 的取值范围； (3)根据图象指出当－3<y<2且y ≠0时x 的取值范围．应用2：反比例函数的实际应用8．某厂仓库储存了部分原料，按原计划每小时消耗2吨，可用60小时．由于技术革新，实际生产能力有所提高，即每小时消耗的原料量大于计划消耗的原料量．设现在每小时消耗原料x(单位：吨)，库存的原料可使用的时间为y(单位：小时)．(1)写出y 关于x 的函数解析式，并求出自变量的取值范围．(2)若恰好经过24小时才有新的原料进厂，为了使机器不停止运转，则x 应控制在什么范围内？1个技巧：用k 的几何性质巧求图形的面积9．如图，A ，B 是双曲线y ＝kx(k ≠0)上的两点，过A 点作AC ⊥x 轴，交OB于D 点，垂足为C.若△ADO 的面积为1，D 为OB 的中点，则k 的值为( )A .43B .83C ．3D ．4(第9题)(第10题)10．如图，过x 轴正半轴上的任意一点P 作y 轴的平行线交反比例函数y ＝2x 和y ＝－4x 的图象于A ，B 两点，C 是y 轴上任意一点，则△ABC 的面积为________．11．如图是函数y ＝3x 与函数y ＝6x 在第一象限内的图象，点P 是y ＝6x的图象上一动点，PA ⊥x 轴于点A ，交y ＝3x 的图象于点C ，PB ⊥y 轴于点B ，交y ＝3x的图象于点D.(1)求证：D 是BP 的中点； (2)求四边形ODPC 的面积．(第11题)答案专训11．解：(1)∵A(m ，6)，B(3，n)两点在反比例函数y ＝6x(x>0)的图象上，∴m ＝1，n ＝2，即 A(1，6)，B(3，2)．又∵A(1，6)，B(3，2)在一次函数y ＝kx ＋b 的图象上， ∴⎩⎨⎧6＝k ＋b ，2＝3k ＋b ，解得⎩⎨⎧k ＝－2，b ＝8，即一次函数解析式为y ＝－2x ＋8.(第1题)(2)根据图象可知使kx ＋b<6x成立的x 的取值范围是0<x<1或x>3.(3)如图，分别过点A ，B 作AE ⊥x 轴，BC ⊥x 轴，垂足分别为E ，C ，设直线AB 交x 轴于D 点．令－2x ＋8＝0，得x ＝4，即D(4，0)． ∵A(1，6)，B(3，2)，∴AE ＝6，BC ＝2.∴S △AOB ＝S △AOD －S △ODB ＝12×4×6－12×4×2＝8.2．(1)证明：∵点A ，B 分别在x 轴，y 轴上，点D 在第一象限内，DC ⊥x 轴于点C ，∴∠AOB ＝∠DCA ＝90°.在Rt △AOB 和Rt △DCA 中，∵⎩⎨⎧AO ＝DC ，AB ＝DA ，∴Rt △AOB ≌Rt △DCA.(2)解：在Rt △ACD 中，∵CD ＝2，DA ＝5， ∴AC ＝DA 2－CD 2＝1.∴OC ＝OA ＋AC ＝2＋1＝3. ∴D 点坐标为(3，2)．∵点E 为CD 的中点，∴点E 的坐标为(3，1)．∴k ＝3×1＝3. (3)解：点G 在反比例函数的图象上．理由如下：∵△BFG 和△DCA 关于某点成中心对称， ∴△BFG ≌△DCA.∴FG ＝CA ＝1，BF ＝DC ＝2，∠BFG ＝∠DCA ＝90°.∵OB ＝AC ＝1，∴OF ＝OB ＋BF ＝1＋2＝3.∴G 点坐标为(1，3)． ∵1×3＝3，∴点G(1，3)在反比例函数的图象上．3．解：∵BC ∥OA ，AB ∥x 轴，∴四边形ABCO 为平行四边形． ∴AB ＝OC ＝3.设A ⎝ ⎛⎭⎪⎫a ，6a ，则B ⎝ ⎛⎭⎪⎫a －3，6a ，∴(a －3)·6a＝－3.∴a ＝2.∴A(2，3)，B(－1，3)．∵OC ＝3，C 在x 轴负半轴上，∴C(－3，0)， 设直线BC 对应的函数解析式为y ＝kx ＋b ，则⎩⎨⎧－3k ＋b ＝0，－k ＋b ＝3，解得⎩⎪⎨⎪⎧k ＝32，b ＝92.∴直线BC 对应的函数解析式为y ＝32x ＋92.解方程组⎩⎪⎨⎪⎧y ＝32x ＋92，y ＝－3x ，得⎩⎨⎧x 1＝－1，y 1＝3，⎩⎨⎧x 2＝－2，y 2＝32.∴D ⎝⎛⎭⎪⎫－2，32.设直线AD 对应的函数解析式为y ＝mx ＋n ，则⎩⎨⎧2m ＋n ＝3，－2m ＋n ＝32，解得⎩⎪⎨⎪⎧m ＝38，n ＝94.∴直线AD 对应的函数解析式为y ＝38x ＋94.∴E ⎝ ⎛⎭⎪⎫0，94.∴OE ＝94.4.154点拨：因为C(0，2)，A(4，0)，由矩形的性质可得P(2，1)，把P 点坐标代入反比例函数解析式可得k ＝2，所以反比例函数解析式为y ＝2x.因为D 点的横坐标为4，所以AD ＝24＝12.因为点E 的纵坐标为2，所以2＝2CE，所以CE ＝1，则BE ＝3.所以S △ODE ＝S 矩形OABC －S △OCE －S △BED －S △OAD ＝8－1－94－1＝154.5．(1)证明：∵BE ∥AC ，AE ∥OB ， ∴四边形AEBD 是平行四边形．∵四边形OABC 是矩形，∴DA ＝12AC ，DB ＝12OB ，AC ＝OB.∴DA ＝DB.∴四边形AEBD 是菱形． (2)解：如图，连接DE ，交AB 于F ， ∵四边形AEBD 是菱形，∴DF ＝EF ＝12OA ＝32，AF ＝12AB ＝1.∴E ⎝ ⎛⎭⎪⎫92，1.设所求反比例函数解析式为y ＝kx ，把点E ⎝ ⎛⎭⎪⎫92，1的坐标代入得1＝k 92，解得k ＝92.∴所求反比例函数解析式为y ＝92x.(第5题)(第7题)6．D7．解：(1)如图，过点D 作x 轴的垂线，垂足为F. ∵点D 的坐标为(4，3)，∴OF ＝4，DF ＝3.∴OD ＝5. ∴AD ＝5.∴点A 的坐标为(4，8)．∴k ＝xy ＝4×8＝32.(2)将菱形ABCD 沿x 轴正方向平移，使得点D 落在函数y ＝32x(x>0)的图象上点D′处，过点D′作x 轴的垂线，垂足为F′.∵DF ＝3，∴D′F′＝3.∴点D′的纵坐标为3.∵点D′在y ＝32x 的图象上，∴3＝32x ，解得x ＝323，即OF′＝323.∴FF′＝323－4＝203.∴菱形ABCD 沿x 轴正方向平移的距离为203.8．解：(1)∵正方形OABC 的边OA ，OC 分别在x 轴，y 轴上，点B 的坐标为(2，2)，∴C(0，2)．∵D 是BC 的中点，∴D(1，2)．∵反比例函数y ＝k x(x ＞0，k ≠0)的图象经过点D ，∴k ＝2.(2)当P 在直线BC 的上方，即0＜x ＜1时，∵点P(x ，y)在该反比例函数的图象上运动，∴y ＝2x. ∴S 四边形CQPR ＝CQ ·PQ＝x·⎝ ⎛⎭⎪⎫2x －2＝2－2x ；当P 在直线BC 的下方，即x ＞1时，同理求出S 四边形CQPR ＝CQ·PQ ＝x·⎝⎛⎭⎪⎫2－2x ＝2x －2，综上，S ＝⎩⎨⎧2x －2（x ＞1），2－2x （0＜x ＜1）.9．410．解：∵反比例函数的图象关于原点对称，圆也关于原点对称，故阴影部分的面积占⊙O 面积的14，则针头落在阴影区域内的概率为14.专训21．B 2.C3．①③④4．解：(1)反比例函数：y ＝－6x.(2)如图所示．(第4题)5．解：∵反比例函数y ＝k x的图象经过点A(1，－k ＋4)， ∴－k ＋4＝k 1，即－k ＋4＝k ，∴k ＝2，∴A(1，2)． ∵一次函数y ＝x ＋b 的图象经过点A(1，2)，∴2＝1＋b ，∴b ＝1.∴反比例函数的解析式为y ＝2x， 一次函数的解析式为y ＝x ＋1.6．解：(1)将B(2，－4)的坐标代入y ＝m x ，得－4＝m 2， 解得m ＝－8.∴反比例函数的解析式为y ＝－8x. ∵点A(－4，n)在双曲线y ＝－8x上，∴n ＝2. ∴A(－4，2)．把A(－4，2)，B(2，－4)的坐标分别代入y ＝kx ＋b ，得⎩⎨⎧－4k ＋b ＝2，2k ＋b ＝－4，解得⎩⎨⎧k ＝－1，b ＝－2.∴一次函数的解析式为y ＝－x －2.(2)令y ＝0，则－x －2＝0，x ＝－2.∴C(－2，0)．∴OC ＝2.∴S △AOB ＝S △AOC ＋S △BOC ＝12×2×2＋12×2×4＝6. (3)x 1＝－4，x 2＝2.(4)－4<x<0或x>2.7．解：如图，由观察可知：(1)当y ＝－2时，x ＝－3；(2)当－2<x<1且x ≠0时，y<－3或y>6；(3)当－3<y<2且y ≠0时，x<－2或x>3.(第7题)点拨：解决问题时，画出函数图象．由图象观察得知结果．由图象解决相关问题，一定要注意数形结合，学会看图．8．解：(1)库存原料为2×60＝120(吨)，根据题意可知y 关于x 的函数解析式为y ＝120x. 由于生产能力提高，每小时消耗的原料量大于计划消耗的原料量，所以自变量的取值范围是x>2.(2)根据题意，得y ≥24，所以120x≥24. 解不等式，得x ≤5，即每小时消耗的原料量应控制在大于2吨且不大于5吨的范围内．点拨：(1)由“每小时消耗的原料量×可使用的时间＝原料总量”可得y 关于x 的函数解析式．(2)要使机器不停止运转，需y ≥24，解不等式即可．(第9题)9．B 点拨：如图，过点B 作BE ⊥x 轴于点E ，∵D 为OB 的中点，∴CD 是△OBE 的中位线，则CD ＝12BE.设A ⎝ ⎛⎭⎪⎫x ，k x ，则B ⎝⎛⎭⎪⎫2x ，k 2x ，CD ＝k 4x ，AD ＝k x －k 4x .∵△ADO 的面积为1，∴12AD·OC＝1，即12⎝ ⎛⎭⎪⎫k x －k 4x ·x＝1.解得k ＝83. 10．311．(1)证明：∵点P 在双曲线y ＝6x上， ∴设P 点坐标为⎝ ⎛⎭⎪⎫6m ，m . ∵点D 在双曲线y ＝3x上，BP ∥x 轴，D 在BP 上， ∴D 点坐标为⎝ ⎛⎭⎪⎫3m ，m .∴BD ＝3m ，BP ＝6m ， 故D 是BP 的中点．(2)解：由题意可知S △BOD ＝32，S △AOC ＝32，S 四边形OBPA ＝6. ∴S 四边形ODPC ＝S 四边形OBPA －S △BOD －S △AOC ＝6－32－32＝3.。
人教版数学九年级下册第26章测试题含答案
人教版数学九年级下册第26章测试题含答案26.1角反比例函数一、单选题1.函数 y =m x 与y=-mx 2+m (m≠0)在同一直角坐标系中的大致图像可能是（ ） A. B. C.D.2.若反比例函数 y =1−k x 的图像分布在第二、四象限，则k 的取值范围是（ ） A. k ＜ 12 B. k ＞ 12 C. k ＞1 D. k ＜1 3.已知反比例函数 y =−6x ，下列说法中正确的是（ ）A. 该函数的图像分布在第一、三象限B. 点（-4，-3）在函数图像上C. y 随x 的增大而增大D. 若点（-2，y 1）和（-1，y 2）在该函数图像上，则y 1＜y 24.关于反比例函数y ＝﹣ 12x ，下列说法不正确的是（ ）A. 函数图象分别位于第二、四象限B. 函数图象关于原点成中心对称C. 函数图象经过点（﹣6，﹣2）D. 当x ＜0时，y 随x 的增大而增大 5.函数y ＝kx ﹣3与y ＝ （k≠0）在同一坐标系内的图象可能是（ ）A. B. C. D.6.已知反比例函数的图象经过点（1，3），则这个反比例函数的表达式为（ ）A. y= -3xB. y= 3xC. y= 13xD. y=- 13x7.若点 A(−3,y 1) ， B(−2,y 2) ， C(3,y 3) 在反比例函数 y =−1x 的图象上，则 y 1,y 2,y 3 大小关系是（ ）A. y 1<y 2<y 3B. y 1<y 3<y 2C. y 2<y 1<y 3D. y 3<y 1<y 28.下列关系式中，表示y 是x 的反比例函数的是（ ）A. y =3x 2B. y =x 2C. y =1x +2D. y =1x 9.若反比例函数y=2m−1x 的图象在第二，四象限，则m 的值是( ) A. m> 12 B. m< 12 C. m>2 D. m<210.下列关系式中，y 是x 的反比例函数的是( )A. y=5xB. y x =3C. y= −1x D. y=x 2-3 11.当压力F(N)一定时，物体所受的压强P(Pa)与受力面积S(m 2)的函数关系式为P= F S (S≠0)，这个反比例函数的图象大致是( ) A. B. C.D.二、填空题12.若点 A(−2,4) 在反比例函数 y =k x 的图象上，则 k 的值为________. 13.如果反比例函数 y =2−k x （ k 为常数）的图象在二、四象限，那么 k 的取值范围是________14.已知反比例函数 的图象在第二、四象限内，那么k 的取值范围是________.15.如图，经过原点的直线与反比例函数y= k x (k>0)相交于A ，B 两点，BC ⊥x 轴。
人教版数学九年级下26.1《反比例函数》基础测试题(含答案及解析)
人教版数学九年级下26.1《反比例函数》基础测试题（含答案及解析）反比例函数基础测试题时间：60分钟总分：100题号一二三总分得分一、选择题（本大题共10小题，共30.0分）1.下列函数中，是反比例函数的是()A. y=kxB. 3x+2y=0C. xy−√2=0 D. y=2x+12.下列式子中，y是x的反比例函数的是()A. y=1x2B. y=x2 C.y=xx+1 D.xy=13.反比例函数y=−32x中常数k为()A. −3B. 2C. −12D. −324.下列函数关系式中属于反比例函数的是()A. y=3xB. y=−2xC. y=x2+3D. x+y=55.下列关系式中：①y=2x；②yx=5；③y=−7x ；④y=5x+1；⑤y=x2−1；⑥y=1x2；⑦xy=11，y是x的反比例函数的共有()A. 4个B. 3个C. 2个D. 1个C. 矩形的长为a，宽为20，其面积S与a的关系D. 矩形的面积为40，长a与宽b之间的关系6.下列四个关系式中，y是x的反比例函数的是()A. y=4xB. y=13xC. y=1x2D. y=1x+1二、填空题（本大题共10小题，共30.0分）7.若y=(m−3)x m2−2m−4是反比例函数，则m=______ ．8.反比例函数y=(2m−1)x m2−2，在每个象限内，y随x的增大而增大，则m的值是______ ．9.函数y=(m+1)x m2−2m−4是y关于x的反比例函数，则m=______．10.若反比例函数y=(2k−1)x3k2−2k−1经过第一、三象限，则k=______11.已知函数y=(k−3)x 8−k2为反比例函数，则k=______ ．12.如果函数y=kx2k2+k−2是反比例函数，那么k=______ ．13.反比例函数y=(m+2)x m2−10的图象分布在第二、四象限内，则m的值为______ ．14.若函数y=(m−1)x m2−2是反比例函数，则m的值等于______ ．15.若函数y=(3+m)x8−m2是反比例函数，则m=______ ．16.若函数y=(m+1)x m2+3m+1是y关于x的反比例函数，则m的值为______ ．三、解答题（本大题共5小题，共40.0分）17.函数y=(m−1)x m2−m−1是反比例函数．(1)求m的值；(2)指出该函数图象所在的象限，在每个象限内，y随x的增大如何变化？,2)是否在这个函数的图象上．(3)判断点(1218.已知y是x的反比例函数，且当x=2时，y=−3，请你确定该反比例函数的解析式，并求当y=6时，自变量x的值．19.若函数y=(m+1)x m2+3m+1是反比例函数，求m的值．20.已知函数y=(m2+2m−3)x|m|−2．(1)若它是正比例函数，则m=______ ；(2)若它是反比例函数，则m=______ ．21.当k为何值时，y=(k−1)x k2−2是反比例函数？答案和解析【答案】1. C2. D3. D4. B5. C6. D7. C8. A9. D10. B11. −112. −113. 314. 2 315. −316. −1或1 217. −318. −119. 320. −221. 解：(1)由题意：{m2−m−1=−1m−1≠0，解得m=0．(2)∵反比例函数的解析式为y=−1x，∴函数图象在二四象限，在每个象限内，y随x 的增大而增大．(3)当x=12时，y=−2≠2，∴点(12,2)不在这个函数的图象上．22. 解：设反比例函数y=kx(k≠0)，∵当x=2时，y=−3，∴k=xy=2×(−3)=−6，∴y与x之间的函数关系式y=−6x．把y=6代入y=−6x，则x=−1．23. 解：由函数y=(m+3)x m2+3m+1为反比例函数可知m2+3m+1=−1，且m+1≠0解得m=−1(舍去)，m=−2，m的值是−2．24. 3；−125. 解：y=(k−1)x k2−2是反比例函数，得{k2−2=−1k−1≠0，解得k=−1，当k=−1时，y=(k−1)x k2−2是反比例函数．【解析】1. 解：A、不是反比例函数，故此选项错误；B、不是反比例函数，故此选项错误；C、是反比例函数，故此选项正确；D、不是反比例函数，故此选项错误；故选：C．根据反比例函数的概念形如y=kx(k为常数，k≠0)的函数称为反比例函数进行分析即可．此题主要考查了反比例函数的概念，判断一个函数是否是反比例函数，首先看看两个变量是否具有反比例关系，然后根据反比例函数的意义去判断，其形式为y=kx(k为常数，k≠0)或y=kx−1(k为常数，k≠0)．2. 【分析】本题考查了反比例函数，利用反比例函数的定义是解题关键.根据反比例函数的意义，可得答案．【解答】解：y=1x，y=x−1，yx=1是反比例函数．故选D．3. 解：反比例函数y=−32x中常数k为−32，故选D．找出反比例函数解析式中k的值即可．此题考查了反比例函数的定义，熟练掌握反比例函数解析式的一般形式是解本题的关键．4. 解：A、该函数是正比例函数，故本选项错误；B、该函数符合反比例函数的定义，故本选项正确；C、该函数是二次函数，故本选项错误；D、该函数是一次函数，故本选项错误；故选：B．根据反比例函数的定义进行判断．本题考查了反比例函数的定义，反比例函数的(k≠0)．一般形式是y=kx5. 解：①y=2x是正比例函数；=5可化为y=5x，不是反比例函数；②yx③y=−7符合反比例函数的定义，是反比例x函数；④y=5x+1是一次函数；⑤y=x2−1是二次函数；⑥y=1不是反比例函数；x2⑦xy=11可化为y=11，符合反比例函数的x定义，是反比例函数．故选C．分别根据反比例函数、二次函数及一次函数的定义对各小题进行逐一分析即可．本题考查的是反比例函数的定义，熟知形如y=kx(k为常数，k≠0)的函数称为反比例函数是解答此题的关键．6. 解：根据题意得2m+1=−1，解得m=−1．故选D．根据反比例函数的定义.即y=kx(k≠0)，只需令2m+1=−1即可．本题考查了反比例函数的定义，重点是将一般式y=kx(k≠0)转化为y=kx−1(k≠0)的形式．7. 解：(1)由题意可得：m=346.2n，是反比例函数关系；(2)由题意可得：I=UR，是反比例函数关系；(3)设腰长为x，底边长为y，由题意可得：x= C−y2，不是反比例函数关系；(4)设底边长为x，底边上的高为h，根据题意可得：x=5h，是反比例函数关系．故选：C．根据题意分别得出两变量的关系式，进而利用反比例函数的定义得出答案．此题主要考查了反比例函数的定义，正确得出各函数关系是解题关键．8. 解：根据题意，得2πrL=4，则L=42πr =2πr．所以这个圆柱的母线长L和底面半径r之间的函数关系是反比例函数．故选A．根据题意，由等量关系“矩形的面积=底面周长×母线长”列出函数表达式再判断它们的关系则可．本题考查了反比例函数的定义和圆柱侧面积的求法，涉及的知识面比较广．9. 解：A、根据题意，得S=a2，所以正方形的面积S与边长a的关系是二次函数关系；故本选项错误；B、根据题意，得l=4a，所以正方形的周长l与边长a的关系是正比例函数关系；故本选项错误；C、根据题意，得S=20a，所以正方形的面积S与边长a的关系是正比例函数关系；故本选项错误；D、根据题意，得b=40a，所以正方形的面积S与边长a的关系是反比例函数关系；故本选项正确．故选D．根据每一个选项的题意，列出方程，然后由反比例函数的定义进行一一验证即可．本题考查了反比例函数的定义.反比例函数的一般形式是y=kx(k≠0)．10. 解：y=13x=13x是反比例函数，故选：B．根据反比例函数的定义，可得答案．本题考查了反比例函数的定义，利用反比例函数的定义是解题关键．11. 解：由函数y=(m−3)x m2−2m−4是反比例函数，可知m2−2m−4=−1，m−3≠0，解得：m=−1．故答案为：−1．根据反比例函数的定义可知m2−2m−4=−1，m−3≠0，继而求出m的值．本题考查了反比例函数的定义，属于基础题，(k≠0)转化为y=重点是将一般式y=kxkx−1(k≠0)的形式．m2−2=−1，12. 解：根据题意得：{2m−1<0解得：m=−1．故答案为−1．根据反比例函数的定义列出方程求解，再根据它的性质决定解的取舍．本题考查了反比例函数的性质.对于反比例函，当k>0时，在每一个象限内，函数数y=kx值y随自变量x的增大而减小；当k<0时，在每一个象限内，函数值y随自变量x的增大而增大．13. 解：∵函数y=(m+1)x m2−2m−4是y关于x的反比例函数，∴m2−2m−4=−1且m+1≠0，解得m=3．故答案是：3．根据反比例函数的一般形式得到m2−2m−4=−1且m+1≠0，由此来求m的值即可．本题考查了反比例函数的定义，反比例函数的(k≠0)．一般形式是y=kx14. 解：∵是反比例函数，∴3k2−2k−1=−1，，解得k=0，或k=23∵反比例函数y=(2k−1)x3k2−2k−1经过第一、三象限，∴2k−1>0，解答k>0.5，∴k=2．3．故答案为：23让反比例函数中x的指数为−1，系数大于0列式求值即可．考查反比例函数的定义及反比例函数图象的性质；用到的知识点为：反比例函数的一般形式为y=kx−1(k≠0)；反比例函数中的比例系数大于0，图象的两个分支在一、三象限．15. 解：∵函数y=(k−3)x 8−k2为反比例函数，∴8−k2=−1且k−3≠0．解得k=−3．故答案是：−3．根据反比例函数的定义得到8−k2=−1且k−3≠0．本题考查了反比例函数的定义，反比例函数的一般形式是y =k x (k ≠0)．16. 解：根据题意得{2k 2+k −2=−1k ≠0， 解得k =−1或12．一般地，如果两个变量x 、y 之间的关系可以表示成y =k x 或写成y =kx −1(k 为常数，k ≠0)的形式，那么称y 是x 的反比例函数． (1)将反比例函数解析式的一般式y =k x (k ≠0)，转化为y =kx −1(k ≠0)的形式，根据反比例函数的定义条件可以求出k 的值； (2)特别注意不要忽略k ≠0这个条件． 17. 解：根据题意得，m 2−10=−1且m +2<0，解得m 1=3，m 2=−3且m <−2， 所以m =−3．故答案为：−3．根据反比例函数的定义可得m 2−10=−1，根据函数图象分布在第二、四象限内，可得m +2<0，然后求解即可．本题考查了反比例函数的定义，反比例函数的性质，对于反比例函数y =k x (k ≠0)，(1)k >0，反比例函数图象在一、三象限；(2)k<0，反比例函数图象在第二、四象限内．18. 解：∵y=(m−1)x m2−2是反比例函数，∴m2−2=−1，m−1≠0，∴m=−1．故答案为−1．根据反比例函数的定义先求出m的值，再根据系数不为0进行取舍．本题考查了反比例函数的定义，重点是将一般式y=kx(k≠0)转化为y=kx−1(k≠0)的形式．19. 解：根据题意得：{8−m2=−1 3+m≠0，解得：m=3．故答案是：3．根据反比例函数的一般形式：x的次数是−1，且系数不等于0，即可求解．本题考查了反比例函数的定义，重点是将一般式y=kx(k≠0)转化为y=kx−1(k≠0)的形式．20. 解：∵函数y=(m+1)x m2+3m+1是y关于x 的反比例函数，∴{m+1≠0m2+3m+1=−1，解得m=−2．故答案为：−2．根据反比例函数的定义列出关于m的不等式组，求出m的值即可．本题考查的是反比例函数的定义，熟知形如y=kx(k为常数，k≠0)的函数称为反比例函数是解答此题的关键．21. (1)根据反比例函数的定义可得{m2−m−1=−1m−1≠0，解得m=0．(2)利用反比例函数的性质即可解决问题；(3)利用待定系数法即可解决问题；本题考查反比例函数图象上的点的特征，反比例函数的性质等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．22. 由题意y是x的反比例函数，可设y=kx(k≠0)，然后利用待定系数法进行求解；把y=6代入函数解析式求得相应的x的值即可．此题主要考查利用待定系数法求函数的解析式，是一道基础题，比较简单．23. 根据反比例函数的定义先求出m的值．本题考查了反比例函数的定义，重点是将一般式y=kx(k≠0)转化为y=kx−1(k≠0)的形式．24. 解：(1)y=(m2+2m−3)x|m|−2是正比例函数，m2+2m−3≠0，|m|−2=1m=3，(2)y=(m2+2m−3)x|m|−2是反比例函数，m2+2m−3≠0，|m|−2=−1，m=−1，故答案为：3，−1．(1)根据y=kx(k是常数，k≠0)是正比例函数，可得m的值；(2)根据y=k(k是常数，k≠0)是反比例函x数，可得m的值．本题考查了反比例函数，注意k不能为0．25. 根据反比例函数的定义，可得答案．本题考查了反比例函数的定义，重点是将一般(k≠0)转化为y=kx−1(k≠0)的形式y=kx式．。
人教版九年级数学下册26.1--26.2基础过关测试题含答案
人教版九年级数学下册26.1--26.2基础过关测试题含答案26.1.1反比例函数一、选择题1.已知y 与x 成反比例，当x = 3时，y = 4，那么当y = 3时，x 的值为（ ）；A. 4B. -4C. 3D. -32.若n x m y ++=2)5(是反比例函数，则m 、n 的取值是 （ ）A.3,5-=-=n mB.3,5-=-≠n mC. 3,5=-≠n mD.4,5-=-≠n m 3.下列函数，①y ＝2x ，②y ＝x ，③y ＝x －1，④y ＝11x +是反比例函数的个数有( )A ．0个B ．1个C ．2个D ．3个 4.在圆的面积公式S=πr 2中，是常量的是（ ）A ．SB ．πC ．RD ．S 和r 5.下列各问题中的两个变量成反比例的是（ ）；A.某人的体重与年龄B.时间不变时，工作量与工作效率C.矩形的长一定时，它的周长与宽D.被除数不变时，除数与商6.已知A （2-，a ）在满足函数xy 2=，则___=a （ ）A. 1-B. 1C. 2-D. 27.已知点(3，1)是双曲线y ＝k x(k ≠0)上一点，则下列各点中在该图象上的点是( )A ．(13，－9) B ．(3，1) C ．(－1，3) D ．(6，－12)下列表述：①若信件质量为27克，则邮资为2.40元；②若邮资为2.40元，则信件质量为35克；③p 是q 的函数；④q 是p 的函数，其中正确的是（ ）A ．①④B ．①③C ．③④D ．①②③④ 9.下列关系式中，哪个等式表示y 是x 的反比例函数 （ ）A. xk y = B. 2xB y =C.121+=x yD.12=-xy 10.附城二中到联安镇为5公里，某同学骑车到达，那么时间t 与速度（平均速度）v 之间的函数关系式是 （ ）A.st v =B. s t v +=C. ts v = D.st v = 二、填空题11.有一面积为60的梯形，其上底长是下底长的 13，设下底长为x ，高为y ，则y 与x 的函数关系式是 ； 12.如果函数y =222-+k kkx 是反比例函数，那么k =________，此函数的解析式是 ； 13.反比例函数y ＝21039n n x--的图象每一象限内，y 随x 的增大而增大，则n＝_______．14．已知一次函数y ＝3x +m 与反比例函数y ＝3m x-的图象有两个交点，当m ＝_____时，有一个交点的纵坐标为6．15.正比例函数y ＝x 与反比例函数y ＝1x的图象相交于A 、C 两点，AB ⊥x 轴于B ，CD •⊥x 轴于D ，如图所示，则四边形ABCD 的为_______．三、综合题16.一水池内有污水60m 3，设放净全池污水所需的时间为t (小时），每小时的放水量为w m 3，（1）试写出t 与w 之间的函数关系式，t 是w 反比例函数吗？ （2）求当w = 15时，t 的值.17.如图，已知一次函数y＝kx+b(k≠0)的图象与x轴、y轴分别交于A、B•两点，且与反比例函数y＝m(m≠0)的图象在第一象限交于C点，CDx垂直于x轴，垂足为D，•若OA＝OB＝OD＝1．(1)求点A、B、D的坐标；(2)求一次函数和反比例函数的解析式．18.已知某易拉罐厂设计一种易拉罐，在设计过程中发现符合要求的（1）上表反映了哪两个变量之间的关系？哪个是自变量？哪个是因变量？（2）当易拉罐底面半径为2.4cm 时，易拉罐需要的用铝量是多少？ （3）根据表格中的数据，你认为易拉罐的底面半径为多少时比较适宜？说说你的理由．（4）粗略说一说易拉罐底面半径对所需铝质量的影响．19.已知y ＝y 1－y 2，y 1成正比例，y 与x 成反比例，且当x ＝1时，y ＝－14，x ＝4时，y ＝3．求(1)y 与x 之间的函数关系式． (2)自变量x 的取值范围． (3)当x ＝14时，y 的值．26.1.1反比例函数 同步测试答案一、选择题1.A2.A3.B4.B5.D6.A7.B8.A9.A 10.C 二、填空题11.y = 90x12.-1或21 xy x y 211=-=或13.n ＝－3； 14．m ＝5； 15.2 三、综合题16. （1）t = 60w，（2）t = 4.17.解：(1)∵OA ＝OB ＝OD ＝1，∴点A 、B 、D 的坐标分别为A (－1，0)，B (0，1)，D (1，0)． (2)∵点AB 在一次函数y ＝kx +b (k ≠0)的图象上，∴解得∴一次函数的解析式为y＝x+1，∵点C在一次函数y＝x+1的图象上，•且CD⊥x轴，∴C点的坐标为(1，2)，(m≠0)的图象上，又∵点C在反比例函数y＝mx∴m＝2，•∴反比例函数的解析式为y＝．；18.解：（1）易拉罐底面半径和用铝量的关系，易拉罐底面半径为自变量，用铝量为因变量；（2）当底面半径为2.4cm时，易拉罐的用铝量为5.6cm²；（3）易拉罐底面半径为2.8cm时比较合适，因为此时用铝量较少，成本低；（4）当易拉罐底面半径在1.6~2.8cm变化时，用铝量随半径的增大而减小，当易拉罐半径在2.8~4.0cm之间变化时，用铝量随半径的增大而增大.19.(1)y＝2x－提示：设y＝k1x－，再代入求k1，k2的值．(2)自变量x取值范围是x＞0．(3)当x＝1时，y＝24－162＝255．；26.2 实际问题与反比例函数同步测试班级：姓名：1.在一个可以改变体积的密闭容器内装有一定质量的某种气体，当改变容器的体积时，气体的密度也会随之改变，密度ρ(单位：kg/m3)与体积V(单位：m3)满足函数解析式ρ＝mV(m为常数，m≠0)，其图象如图所示，则m的值为（）A.9B.－9C.4D.－42.某学校要种植一块面积为100 m2的长方形草坪，要求相邻两边长均不小于5 m，则草坪的一边长y(单位：m)随与其相邻的一边长x(单位：m)的变化而变化的图象可能是（）3.已知，，是反比例函数上的三点，若，，则下列关系式不正确的是（）A.B.C.D.4.某气球内充满了一定质量的气体，当温度不变时，气球内气体的气压是气体体积的反比例函数，其图象如图所示．当气球内的气压大于时，气球将爆炸．为了安全起见，气球的体积应（）A. 大于B. 小于C. 大于D. 小于5.如图，的边，边上的高，的面积为，则与的函数图象大致是（）A. B. C. D.6.如图，正比例函数与反比例函数的图象交于，两点，轴于点，连接，则的面积为（）A. B. C. D.7.如图，若正方形的顶点和正方形的顶点都在函数的图象上，则点的坐标是______．8. 某医药研究所开发一种新药，成年人按规定的剂量限用，服药后每毫升血液中的含药量y（毫克）与时间t（小时）之间的函数关系近似满足如图所示曲线，当每毫升血液中的含药量不少于0.25毫克时治疗有效，则服药一次治疗疾病有效的时间为（）9.在反比例函数的图像所在的每个象限中，如果函数值随自变量的值增大而增大，那么常数的取值范围是_______.10.如图，直线与双曲线交于点，则_______．（若结果为分数，写成a/b形式，如：1/2）11.将油箱注满k 升油后，轿车可行驶的总路程s(单位：千米)与平均耗油量a(单位：升/千米)之间是反比例函数关系s ＝k a (k 是常数，k ≠0)．已知某轿车油箱注满油后，以平均耗油量为每千米耗油0.1升的速度行驶，可行驶700千米．(1)求该轿车可行驶的总路程s 与平均耗油量a 之间的函数解析式(关系式)；(2)当平均耗油量为0.08升/千米时，该轿车可以行驶多少千米？12.工匠制作某种金属工具要进行材料煅烧和锻造两个工序,即需要将材料煅烧到800 ℃,然后停止煅烧进行锻造操作.经过8 min 时,材料温度降为600 ℃.煅烧时,温度y( ℃)与时间x(min)成一次函数关系;锻造时,温度y(℃)与时间x(min)成反比例函数关系(如图),已知该材料初始温度是32 ℃.(1)分别求出材料煅烧和锻造时y 与x 的函数关系式,并且写出自变量x 的取值范围;(2)根据工艺要求,当材料温度低于480 ℃时,须停止操作,那么锻造的操作时间有多长?参考答案1-6.ACAAAD7.8.161515 9.10.211.(1)由题意得：a ＝0.1时，s ＝700，代入反比例函数关系s ＝k a 中，解得k ＝sa ＝70，∴函数关系式为s ＝70a（2）当a ＝0.08时，s ＝700.08＝875.答：该轿车可以行驶875千米．12.解:(1)设锻造时y 与x 的函数关系式为y=(k ≠0), 则600=,∴k=4 800,∴锻造时y 与x 的函数关系式为y=. 当y=800时,800=,解得x=6, ∴点B 的坐标为(6,800),自变量的取值范围是x>6.设煅烧时y与x的函数关系式为y=ax+b(a≠0),则解得∴煅烧时y与x的函数关系式为y=128x+32(0≤x≤6).(2)当y=480时,x==10,10-6=4(min),∴锻造的操作时间有4 min.。
26.1 反比例函数、定义图象与性质(知识解读+达标检测)(教师版)25学年九年级数学下册(人教版)
26.1 反比例函数、定义图象与性质【考点1 反比例函数的定义】【考点2 反比例函数系数K 的几何意义】【考点3 反比例函数的图象】【考点4 反比例函数图象的对称性】【考点5 反比例函数的性质】【考点6 反比例函数图象点坐标特征】【考点7 待定系数法求反比例函数解析式】【考点8 反比例函数与一次函数的交点问题】知识1 反比例函数的定义如果两个变量的每一组对应值的乘积是一个不等于零的常数，那么就说这两个变量成反比例.即xy k =，或表示为ky x=，其中k 是不等于零的常数.一般地，形如ky x=(k 为常数，0k ¹)的函数称为反比例函数，其中x 是自变量，y 是函数，自变量x 的取值范围是不等于0的一切实数.注意：（1）在k y x =中，自变量x 是分式k x 的分母，当0x =时，分式kx无意义，所以自变量x的取值范围是，函数y 的取值范围是0y ¹.故函数图象与x 轴、y 轴无交点. （2）k yx=()可以写成()的形式，自变量x 的指数是－1，在解决有关自变量指数问题时应特别注意系数这一条件.（3）k y x=()也可以写成的形式，用它可以迅速地求出反比例函数的比例系数k ，从而得到反比例函数的解析式.【考点1 反比例函数的定义】【典例1】（2023春•东台市期中）下列函数中，是反比例函数的为（ ）A．y＝2x+1B．y＝C．y＝D．2y＝x【答案】C【解答】解：A、该函数属于一次函数，故本选项错误；B、该函数是y与x2成反比例关系，故本选项错误；C、该函数符合反比例函数的定义，故本选项正确；D、由已知函数得到y＝x，属于正比例函数，故本选项错误；故选：C．【变式1-1】（2023春•邗江区期末）下列式子中，表示y是x的反比例函数的是（ ）A．xy＝1B．y＝C．y＝D．y＝【答案】A【解答】解：A、由原式得到y＝，符合反比例函数的定义．故本选项正确；B、该函数式表示y与x2成反比例关系，故本选项错误；C、该函数式表示y与x成正比例关系，故本选项错误；D、该函数不属于反比例函数，故本选项错误；故选：A．【变式1-2】（2023秋•怀化期末）下列函数不是反比例函数的是（ ）A．y＝3x﹣1B．y＝﹣C．xy＝5D．y＝【答案】B【解答】解：A、y＝3x﹣1＝是反比例函数，故本选项错误；B、y＝﹣是正比例函数，故本选项正确；C、xy＝5是反比例函数，故本选项错误；D、y＝是反比例函数，故本选项错误．故选：B．【典例2】（2023秋•岳阳县期末）若函数y＝（m+4）x|m|﹣5是反比例函数，则m的值为（ ）A．4B．﹣4C．4或﹣4D．0【答案】A【解答】解：由题意得，|m|﹣5＝﹣1，且m+4≠0，解得：m＝4．故选：A．【变式2-1】】（2023秋•惠来县期末）函数y＝x k﹣1是反比例函数，则k＝（ ）A．3B．2C．1D．0【答案】D【解答】解：由题意得：k﹣1＝﹣1，解得：k＝0，故选：D．【变式2-2】（2023秋•邯山区校级期末）若y＝x2m+1为关于x的反比例函数，则m的值是（ ）A．0B．﹣1C．0.5D．1【答案】B【解答】解：∵y＝x2m+1为关于x的反比例函数，∴2m+1＝﹣1，解得m＝﹣1，故选：B．【变式2-3】（2023•雁峰区校级一模）若函数y＝（n﹣2）是反比例函数，则n为（ ）A．±2B．2C．﹣2D．以上都不对【答案】C【解答】解：由题意得：n2﹣5＝﹣1，且n﹣2≠0，解得：n＝﹣2．故选：C知识点2 反比例的图象和性质1、 反比例函数的图象特征：反比例函数的图象是双曲线，它有两个分支，这两个分支分别位于第一、三象限或第二、四象限；反比例函数的图象关于原点对称，永远不会与x 轴、y 轴相交，只是无限靠近两坐标轴.注意：（1）若点(a b ，)在反比例函数ky x=的图象上，则点(a b --，)也在此图象上，所以反比例函数的图象关于原点对称；（2）在反比例函数(k 为常数，0k ¹) 中，由于，所以两个分支都无限接近但永远不能达到x 轴和y 轴．2、画反比例函数的图象的基本步骤：（1）列表：自变量的取值应以0为中心，在0的两侧取三对（或三对以上）互为相反数的值，填写y 值时，只需计算右侧的函数值，相应左侧的函数值是与之对应的相反数；（2）描点：描出一侧的点后，另一侧可根据中心对称去描点；（3）连线：按照从左到右的顺序连接各点并延伸，连线时要用平滑的曲线按照自变量从小到大的顺序连接，切忌画成折线.注意双曲线的两个分支是断开的，延伸部分有逐渐靠近坐标轴的趋势，但永远不与坐标轴相交；（4）反比例函数图象的分布是由k 的符号决定的：当0k >时，两支曲线分别位于第一、三象限内，当0k <时，两支曲线分别位于第二、四象限内． 3、反比例函数的性质（1）如图1，当0k >时，双曲线的两个分支分别位于第一、三象限，在每个象限内，y 值随x 值的增大而减小；（2）如图2，当0k <时，双曲线的两个分支分别位于第二、四象限，在每个象限内，y 值随x 值的增大而增大； 注意：（1）反比例函数的增减性不是连续的，它的增减性都是在各自的象限内的增减情况，反比例函数的增减性都是由反比例系数k 的符号决定的；反过来，由双曲线所在的位置和函数的增减性，也可以推断出k 的符号.（2）反比例的图象关于原点的对称【考点2 反比例函数系数K的几何意义】【典例3】（2023•和平区校级三模）如图，点A在双曲线上，AB⊥x轴于B，且△AOB的面积S＝2，则k的值为（ ）△AOBA．2B．4C．﹣2D．﹣4【答案】D＝2，【解答】解：∴S△AOB∴|k|＝4，∵函数在二、四象限，∴k＝﹣4．故选：D．【变式3-1】（2023秋•怀化期末）如图，点A在双曲线y＝上，AB⊥y轴于B，S＝3，△AOB 则k＝（ ）A．3B．6C．18D．不能确定【答案】B【解答】解：设A的坐标是（m，n），则mn＝k．AB＝m，OB＝n．＝AB•OB＝mn＝3∵S△AOB∴k＝mn＝6．故选：B【变式3-2】（2023•海州区校级二模）若图中反比例函数的表达式均为，则阴影面积为2的是（ ）A．B．C．D．【答案】B【解答】解：选项A中，阴影面积＝xy＝4≠2，故选项A不符合题意；选项B中，阴影面积为，故选项B符合题意；选项C中，阴影面积为2×，故选项C不符合题意；选项D中，阴影面积为4×，故选项D不符合题意；故选：B．【变式3-3】（2023春•高新区期末）如图，两个反比例函数和在第一象限内的图象分别是C1和C2，设点P在C1上，PA⊥x轴于点A，交C2于点B，已知△POB的面积为4，则k的值为（ ）A ．16B ．14C ．12D ．10【答案】A【解答】解：∵PA ⊥x 轴于点A ，交C 2于点B ，∴S △POA ＝，S △BOA ＝＝4，∵POB 的面积为4，∴S △POB ＝|k |﹣4＝4，∵k ＞0，∴k ＝16．故选：A ．【考点3 反比例函数的图象】【典例4】（2023秋•南华县期末）反比例函数与一次函数y ＝kx +1在同一坐标系的图象可能是（ ）A ．B ．C ．D ．【答案】B【解答】解：A、由反比例函数的图象可知，k＞0，由一次函数的图象可知k＜0，两结论矛盾，故本选项错误；B、由反比例函数的图象可知，k＜0，由一次函数的图象可知k＞0，故本选项正确，符合题意；C、由反比例函数的图象可知，k＜0，由一次函数的图象可知k＞0，故本选项错误，不符合题意；D、由反比例函数的图象可知，k＞0，由一次函数的图象可知k＜0，由一次函数在y轴上的截距可知k＝﹣1，故本选项错误．故选：B．【变式4-1】（2023秋•大渡口区校级期末）在同一坐标系中，函数和y＝kx﹣2的图象大致是（ ）A．B．C．D．【答案】B【解答】解：k＞0时，一次函数y＝kx﹣2的图象经过第一、三、四象限，反比例函数的两个分支分别位于第一、三象限，选项A、C不符合题意，选项B符合题意；k＜0时，一次函数y＝kx﹣2的图象经过第二、三、四象限，反比例函数的两个分支分别位于第二、四象限，选项D不符合题意．故选：B．【变式4-2】（2023•庐阳区校级三模）反比例函数y＝﹣与一次函数y＝kx﹣3在同一坐标系中的大致图象可能是（ ）A．B．C．D．【答案】C【解答】解：当k＞0时，一次函数y＝kx﹣3的图象经过第一、三、四象限，反比例函数y＝﹣图象在第二、四象限，当k＜0时，一次函数y＝kx﹣3的图象经过第二、三、四象限，反比例函数y＝﹣图象在第一、三象限，四个选项中只有C符合，故选：C．【变式4-3】（2023•济南模拟）函数y＝﹣kx+k与函数y＝（k≠0）在同一直角坐标系中的大致图象可能是（ ）A．B．C．D．【答案】B【解答】解：当k＞0时，反比例函数的图象位于第一、三象限，一次函数的图象交y轴于正半轴，y随着x的增大而减小，B选项符合，A、C选项错误；当k＜0时，反比例函数的图象位于第二、四象限，一次函数的图象交y轴于负半轴，y 随着x的增大而增大，D错误；故选：B【考点4 反比例函数图象的对称性】【典例5】（2023秋•细河区期末）如图，双曲线y＝与直线y＝mx相交于A、B两点，B点坐标为（﹣2，﹣3），则A点坐标为（ ）A．（﹣2，﹣3）B．（2，3）C．（﹣2，3）D．（2，﹣3）【答案】B【解答】解：∵点A与B关于原点对称，∴A点的坐标为（2，3）．故选：B．【变式5-1】（2023•海口二模）如图，直线与双曲线相交于A（﹣2，1）、B 两点，则点B坐标为（ ）A．（2，﹣1）B．（1，﹣2）C．（1，）D．（，﹣1）【答案】A【解答】解：∵点A与B关于原点对称，∴B点的坐标为（2，﹣1）．故选：A．【变式5-2】（2023秋•新城区期末）若正比例函数y＝﹣2x与反比例函数y＝的图象交于（1，﹣2），则另一个交点坐标为（ ）A．（2，1）B．（﹣1，2）C．（﹣2，﹣1）D．（﹣2，1）【答案】B【解答】解：∵正比例函数与反比例函数的图象均关于原点对称，∴两函数的交点关于原点对称，∵一个交点的坐标是（1，﹣2），∴另一个交点的坐标是（﹣1，2）．故选：B．【考点5 反比例函数的性质】【典例6】（2023•章贡区校级模拟）对于反比例函数y＝，下列结论错误的是（ ）A．函数图象分布在第一、三象限B．函数图象经过点（﹣3，﹣2）C．函数图象在每一象限内，y的值随x值的增大而减小D．若点A（x1，y1），B（x2，y2）都在函数图象上，且x1＜x2，则y1＞y2【答案】D【解答】解：A、k＝6＞0，图象分布在第一，三象限，此选项不符合题意；B、∵（﹣3）×（﹣2）＝6，∴函数图象经过点（﹣3，﹣2），此选项不符合题意；C、∵k＝6＞0，∴函数图象在每一象限内，y的值随x值的增大而减小，此选项不符合题意；D、虽然点A（x1，y1），B（x2，y2）都在函数图象上，且x1＜x2，但不知道A，B所在的象限，故y1，y2不能判断大小，此选项符合题意；故选：D．【变式6-1】（2023春•淮安区校级期末）反比例函数的图象分布在第二、四象限，则a的取值范围是（ ）A．a＜1B．a＞1C．a≤1D．a≥1【答案】A【解答】解：∵反比例函数的图象分布在第二、四象限，∴a﹣1＜0，解得：a＜1．故选：A．【变式6-2】（2022秋•兴县期末）对于反比例函数y＝﹣，下列描述不正确的是（ ）A．图象位于二、四象限B．当x＞0时，y随x的增大而增大C．图象必经过（﹣2，）D．当x＞﹣1时，y＞3【答案】D【解答】解：∵k＝﹣3＜0，图象分布在第二、四象限，A选项不符合题意；当x＞0时，y随x的增大而增大，B选项不符合题意；当x＝﹣2时，，故图象经过点（﹣2，），C选项不符合题意；若x＞﹣1，则y＞3或y＜0，故D选项符合题意；故选：D．【变式6-3】（2023•瑞安市开学）对于反比例函数，当﹣1＜y≤2，且y≠0时，自变量x的取值范围是（ ）A．x≥1或x＜﹣2B．x≥1或x≤﹣2C．0＜x≤1或x＜﹣2D．﹣2＜x＜0或x≥1【答案】A【解答】解：由题知，因为反比例函数表达为，所以其函数图象位于第一、三象限，且在每个象限内y随x的增大而减小．则当﹣1＜y＜0时，对应的图象在第三象限，且x的取值范围是x＜﹣2．当0＜y≤2时，对应的图象在第一象限，其x的取值范围是x≥1．所以x的取值范围是：x≥1或x＜﹣2．故选：A．【考点6 反比例函数图象点坐标特征】【典例7】（2023•西湖区校级开学）若点A（x1，y1），B（x2，y2），C（x3，y3），都在反比例函数（k为常数，k＞0）的图象上，其中y2＜0＜y1＜y3，则x1，x2，x3的大小关系是（ ）A．x1＜x2＜x3B．x2＜x3＜x1C．x1＜x3＜x2D．x2＜x1＜x3【答案】B【解答】解：∵k＝8＞0，y2＜0＜y1＜y3，∴点B在第二象限，点A、C在第一象限，且在每一个象限内，y随x的增大而减小，∴x2＜0，x3＞x1＞0，∴x2＜x3＜x1．故选：B．（2023•义乌市校级开学）以下四个点中，不在反比例函数y＝图象上的是（ ）【变式7-1】A．（2，2）B．（﹣2，﹣2）C．（3，）D．（﹣4，）【答案】D【解答】解：因为反比例函数的表达式是y＝，所以横纵坐标的积等于4的点，在这个反比例函数的图象上．又2×2＝4，﹣2×（﹣2）＝4，，．所以D选项中的点的坐标不在反比例函数的图象上．故选：D．【变式7-2】（2023春•沐川县期末）若点A（﹣1，y1），B（2，y2），C（3，y3）在反比例函数y＝﹣的图象上，则y1，y2，y3的大小关系是（ ）A．y1＞y2＞y3B．y1＞y3＞y2C．y2＞y3＞y1D．y3＞y2＞y1【答案】B【解答】解：∵点A（﹣1，y1），B（2，y2），C（3，y3）在反比例函数y＝﹣的图象上，∴y1＝4，y2＝﹣2，y3＝﹣，∴y2＜y3＜y1．故选：B．【变式7-3】（2023秋•平度市期末）已知函数，当﹣2＜x＜﹣1时，y的取值范围是（ ）A．1＜y＜2B．C．﹣2＜y＜﹣1D．【答案】A【解答】解：∵在y＝﹣中，﹣2＜0，∴第二象限内，y随x的增大而减小，∴当x＝﹣1时，y有最大值2，当x＝﹣2时，y有最小值1，∴当﹣2＜x＜﹣1时，1＜y＜2，故选：A．【考点7 待定系数法求反比例函数解析式】【典例8】（2023秋•道县期末）已知反比例函数y＝（k≠0）的图象经过点A（﹣2，6）．（1）求这个反比例函数的表达式；（2）若（1，y1），（3，y2）是这个反比例函数图象上的两个点，请比较y1，y2的大小．【答案】（1）；（2）y1＜y2．【解答】解：（1）把A（﹣2，6）代入，得，解得：k＝﹣12．∴这个反比例函数的解析式为；（2）y1＜y2．理由如下：∵k＝﹣12＜0，∴在每一个象限内，函数值y随x的增大而增大．∵点（1，y1），（3，y2）都在第四象限，且1＜3，∴y1＜y2．【变式8-1】（2023•高阳县校级模拟）y与x成反比例，当x＝2时y＝1，则y与x的函数关系式为（ ）A．y＝2x B．y＝2﹣x C．D．【答案】D【解答】解：设（k≠0）．根据题意得：，解得：k＝2，即函数解析式是．故选：D．【变式8-2】（2023春•灌云县期末）已知y与x+2成反比例函数关系，且当x＝﹣1时，y＝3．（1）求y与x之间的函数表达式；（2）当x＝0时，求y的值．【答案】（1）y＝；（2）y＝．【解答】解：（1）∵y与x+2成反比例函数关系，∴设该函数的解析式为y＝，∵x＝﹣1时，y＝3，∴k＝3，∴y与x之间的函数表达式为：y＝；（2）当x＝0时，y＝．【变式8-3】（2023春•东阳市期末）已知反比例函数的图象的一支如图所示，它经过点（3，﹣2）．（1）求此反比例函数的表达式，并补画该函数图象的另一支．（2）求当y≤4，且y≠0时自变量x的取值范围．【答案】（1）反比例函数的表达式为y＝﹣，图象见详解；（2）x≤﹣或x＞0．【解答】解：（1）把点（3，﹣2）代入y＝（k≠0），﹣2＝，解得：k＝﹣6，∴反比例函数的表达式为y＝﹣，补充其函数图象如下：（2）当y＝4时，﹣＝4，解得：x＝﹣，∴当y≤4，且y≠0时，x≤﹣或x＞0．【考点8 反比例函数与一次函数的交点问题】【典例9】（2023•西山区二模）如图，在同一平面直角坐标系中，直线y1＝x+1与双曲线y2＝相交于点A（1，2）和点B（﹣2，﹣1），则当y1＞y2时，x的取值范围是（ ）A．x＜﹣2或x＞1B．﹣2＜x＜1C．﹣2＜x＜0或x＞1D．x＜﹣2或0＜x＜1【答案】C【解答】解：直线y1＝x+1与双曲线y2＝相交于点A（1，2）和点B（﹣2，﹣1），由图象可知，当y1＞y2时，﹣2＜x＜0或x＞1；故选：C．【变式9-1】（2023秋•乐亭县期末）一次函数y1＝k1x+b和反比例函数y2＝（k1•k2≠0）的图象如图所示，若y1＞y2，则x的取值范围是（ ）A．x＜﹣2或x＞1B．x＜﹣2或0＜x＜1C．﹣2＜x＜0或0＜x＜﹣2D．﹣2＜x＜0或x＞2【答案】B【解答】解：由图象可知，当y1＞y2，x的取值范围为x＜﹣2或0＜x＜1．故选：B．【变式9-2】（2023春•高新区期末）反比例函数y＝与正比例函数y＝2x一个交点为（1，2），则另一个交点是（ ）A．（﹣1，﹣2）B．（﹣2，﹣1）C．（1，2）D．（2，1）【答案】A【解答】解：∵反比例函数y＝与正比例函数y＝2x一个交点为（1，2），∴另一个交点与点（1，2）关于原点对称，∴另一个交点是（﹣1，﹣2）．故选：A．【变式9-3】（2023秋•辽阳期末）如图，正比例函数y＝k1x（k1为常数，且k1≠0）和反比例函数（k2为常数，且k2≠0）的图象相交于A（2，m）和B两点，则不等式的解集为（ ）A．x＜﹣2或x＞2B．﹣2＜x＜2C．﹣2＜x＜0或x＞2D．x＜﹣2或0＜x＜﹣2【答案】C【解答】解：根据反比例函数关于原点的对称性，可知B（﹣2，﹣m），∴的解集为﹣2＜x＜0或x＞2，故选：C．1．如图，反比例函数y=k的图象经过A(―1,―2)，则以下说法错误的是（）xA．k=2B．图象也经过点B(2,1)C．若x<―1时，则y<―2D．x>0，y随x的增大而减小2．若反比例函数y=2m―1x的图象经过第二、四象限，则m的取值范围是（ ）A．m≤12B．m≥12C．m<12D．m>123．若反比例函数y=k(k≠0)的图象经过点(―2,3)，则图象必经过另一点（ ）xA．(2,3)B．(2,―3)C．(3,2)D．(―2,―3)4．如图，过反比例函数y=k(x<0)图象上的一点A作AB⊥x轴于点B，连接AO，若xSΔAOB=4，则k的值是（ ）A．4B．―4C．8D．―8【答案】D【分析】本题考查了反比例函数值k的几何意义，熟练掌握反比例函数图象上点的坐标特征是解答本题的关键．根据反比例函数k 值的几何意义可知2S△AOB=8=|k||，再根据图象所在象限确定k 的符号即可．【详解】解：∵|k|=2S△AOB=2×4=8，∴k=±8，∵函数图象在第二象限，∴k=―8．故选：D．5．如图，一次函数y1=kx+b与反比例函数y2=c的图象交于A，B两点，则不等式kx+bx>c的解集是（ ）xA．―3<x<2B．x<―3或x>2C．―3<x<0或x>2D．0<x<26．已知点A(x1,y1)，B(x2,y2)，C(x3,y3)在反比例函数y=―4的图象上．其中x1<x2<0<xx3．下列结论正确的是（）A．y3<y1<y2B．y1<y2<y3C．y3<y2<y1D．y2<y1<y3又∵x 1<x 2<0<x 3，∴y 1>0，y 2>0，y 3<0，y 1<y 2，∴y 3<y 1<y 2，故选：A ．7．如图，反比例函数y =kx (k ≠0)的图象的一个分支上有一点A ，AB 平行于x 轴，交y 轴于点B ，△ABO 的面积是1，则反比例函数的表达式是（ ）A ．y =12x B ．y =2xC ．y =2x 或y =―2xD ．y =14x8．下列函数中，当x>0时，y随x的增大而减小的是（）A．y=x B．y=x+1C．y=x2D．y=1x9．对于反比例函数y=3，下列说法中错误的是（）xA．y随x的增大而减小B．图象位于一、三象限C．图象与坐标轴无交点D．图象关于原点对称10．在同一直角坐标系中，函数y=kx+1与y=k(k≠0)的图象可能是（ ）xA．B．C．D．二、填空题11．已知y是x的反比例函数，并且当x=2时，y=6，求当x=4时，y=．12．已知点(x1,y1)，(x2,y2)都在反比例函数y=2的图象上，当x1<0<x2，则y1xy2．（填“>”，“<”或“=”）【答案】<【分析】本题主要考查了比较反比例函数值的大小，根据解析式可知反比例函数图象经过第一、三象限，据此可得答案．13．如图，点A 在双曲线y =1x 上，点B 在双曲线y =3x 上，且AB ∥ x 轴，过点A 、B 分别向x 轴作垂线，垂足分别为点D 、C ，那么四边形ABCD 的面积是．则点E 、A 、B 在同一直线上，∵点A 在双曲线y =1x 上，点∴矩形EODA 的面积为1，矩形∴矩形ABCD 的面积为3―1=14．如图，已知直线y =―4x 与双曲线y =kx 交于A ，B 两点，若点A 的纵坐标为4，则点B 的坐标为．15．对于函数y =8x ，当―2≤y ≤―1时，x 的取值范围是 ．16．如图，一次函数y1=―x+2的图象与反比例函数y2=k(k≠0)的图象交于点A(―1,m)和x点B(n,―1)．(1)求反比例函数的解析式；(2)当y1>y2时，直接写出x的取值范围．17．如图，反比例函数y1=k与一次函数y2=―x+b的图象交于两点A(1,3)、B(3,1)．x(1)反比例函数和一次函数的解析式；(2)观察图象，请直接写出满足y1≤y2的取值范围；(3)若x轴上的存在一点Q，使△QAB的周长最小，请直接写出点Q的坐标．∵∴B关于x轴的对称点B′的坐标为设直线AB′的解析式为y=∴m+n=33m+n=―1，解得∴直线AB′的解析式为y=令y=0，则x=52，。
九年级数学反比例函数的专项培优练习题(含答案)含详细答案
九年级数学反比例函数的专项培优练习题(含答案)含详细答案一、反比例函数1．平行四边形ABCD的两个顶点A、C在反比例函数y= （k≠0）图象上，点B、D在x轴上，且B、D两点关于原点对称，AD交y轴于P点（1）已知点A的坐标是（2，3），求k的值及C点的坐标；（2）在（1）的条件下，若△APO的面积为2，求点D到直线AC的距离．【答案】（1）解：∵点A的坐标是（2，3），平行四边形ABCD的两个顶点A、C在反比例函数y= （k≠0）图象上，点B、D在x轴上，且B、D两点关于原点对称，∴3= ，点C与点A关于原点O对称，∴k=6，C（﹣2，﹣3），即k的值是6，C点的坐标是（﹣2，﹣3）；（2）解：过点A作AN⊥y轴于点N，过点D作DM⊥AC，如图，∵点A（2，3），k=6，∴AN=2，∵△APO的面积为2，∴，即，得OP=2，∴点P（0，2），设过点A（2，3），P（0，2）的直线解析式为y=kx+b，，得，∴过点A（2，3），P（0，2）的直线解析式为y=0.5x+2，当y=0时，0=0.5x+2，得x=﹣4，∴点D的坐标为（﹣4，0），设过点A（2，3），B（﹣2，﹣3）的直线解析式为y=mx+b，则，得，∴过点A（2，3），C（﹣2，﹣3）的直线解析式为y=1.5x，∴点D到直线AC的直线得距离为：= ．【解析】【分析】（1）根据点A的坐标是（2，3），平行四边形ABCD的两个顶点A、C在反比例函数y= （k≠0）图象上，点B、D在x轴上，且B、D两点关于原点对称，可以求得k的值和点C的坐标；（2）根据△APO的面积为2，可以求得OP的长，从而可以求得点P的坐标，进而可以求得直线AP的解析式，从而可以求得点D的坐标，再根据点到直线的距离公式可以求得点D到直线AC的距离．2．已知点A，B分别是x轴、y轴上的动点，点C，D是某个函数图象上的点，当四边形ABCD（A，B，C，D各点依次排列）为正方形时，称这个正方形为此函数图象的伴侣正方形．例如：如图，正方形ABCD是一次函数y=x+1图象的其中一个伴侣正方形．（1）若某函数是一次函数y=x+1，求它的图象的所有伴侣正方形的边长；（2）若某函数是反比例函数y= （k＞0），他的图象的伴侣正方形为ABCD，点D（2，m）（m＜2）在反比例函数图象上，求m的值及反比例函数解析式；（3）若某函数是二次函数y=ax2+c（a≠0），它的图象的伴侣正方形为ABCD，C、D中的一个点坐标为（3，4）．写出伴侣正方形在抛物线上的另一个顶点坐标________，写出符合题意的其中一条抛物线解析式________，并判断你写出的抛物线的伴侣正方形的个数是奇数还是偶数________．【答案】（1）解：如图1，当点A在x轴正半轴，点B在y轴负半轴上时，∵OC=0D=1，∴正方形ABCD的边长CD= ；∠OCD=∠ODC=45°，当点A在x轴负半轴、点B在y轴正半轴上时，设小正方形的边长为a，易得CL=小正方形的边长=DK=LK，故3a=CD= ．解得a= ，所以小正方形边长为，∴一次函数y=x+1图象的伴侣正方形的边长为或（2）解：如图2，作DE，CF分别垂直于x、y轴，易知△ADE≌△BAO≌△CBF此时，m＜2，DE=OA=BF=m，OB=CF=AE=2﹣m，∴OF=BF+OB=2，∴C点坐标为（2﹣m，2），∴2m=2（2﹣m），解得m=1．反比例函数的解析式为y= ．（3）（3，4）；y=﹣ x2+ ；偶数【解析】【解答】解：（3）实际情况是抛物线开口向上的两种情况中，另一个点都在（3，4）的左侧，而开口向下时，另一点都在（3，4）的右侧，与上述解析明显不符合①当点A在x轴正半轴上，点B在y轴正半轴上，点C坐标为（3，4）时：另外一个顶点为（4，1），对应的函数解析式是y=﹣ x2+ ；②当点A在x 轴正半轴上，点 B在 y轴正半轴上，点D 坐标为（3，4）时：不存在，③当点A 在 x 轴正半轴上，点 B在 y轴负半轴上，点C 坐标为（3，4）时：不存在④当点A在x 轴正半轴上，点B在y轴负半轴上，点D坐标为（3，4）时：另外一个顶点C为（﹣1，3），对应的函数的解析式是y= x2+ ；⑤当点A在x轴负半轴上，点B在y轴负半轴上，点D坐标为（3，4）时，另一个顶点C的坐标是（7，﹣3）时，对应的函数解析式是y=﹣；⑥当点A在x轴负半轴上，点B在y轴负半轴上，点C坐标为（3，4）时，另一个顶点D的坐标是（﹣4，7）时，对应的抛物线为y= x2+ ；∵由抛物线的伴侣正方形的定义知，一条抛物线有两个伴侣正方形，是成对出现的，∴所求出的任何抛物线的伴侣正方形个数为偶数．【分析】解答此题时，要特别注意认真读题，分析题意，注意已知条件点A，B分别是x 轴、y轴上的动点，点C，D是某个函数图象上的点。
26.1.1 反比例函数培优练习 - 2023—2024学年人教版数学九年级下册(含答案)
1
2
4
y
4
2如图，平行四边形 的顶点 在函数 的图像上，边 与 轴交于点 ， 轴于点 ．若 的面积为8，则 的值为（）
A．2B． C． D．4
6.对于反比例函数 ，下列说法错误的是（）
A．它的图像在第一、三象限
B．它的函数值 随 的增大而减小
C．点 为图像上的任意一点，过点 作 轴于点 ． 的面积是 ．
26.1.1 反比例函数 培优练习
一、选择题
1.下列关系式中， 是x的反比例函数的是（）
A． B． C． D．
2．下列四个点，在反比例函数 的图象上的是（）
A． B． C． D．
3.若点 A(1,3)是反比例函数 图象上的一点，则常数k的值为 ( )
A.3
4.函数y与自变量x的部分对应值如表所示，则下列函数表达式中，符合表中对应关系的可能是（）
①y＝ ；②y＝ ；③xy＝2；④y＝7x－1；⑤y＝ .
2.已知某盐厂晒出了3000吨盐，厂方决定把盐全部运走.
(1)写出运走盐所需的时间t（天）与运走速度v(吨/天）之间的函数关系式；
(2)该盐厂有工人80名，每天最多可运走500吨盐，则预计盐最快可在几天内运完？
(3)若该盐厂的工人工作了3天后，天气预报预测在未来的几天内可能有暴雨，于是盐厂决定在2天内把剩下的盐全部运走，则需要从其他盐厂调来多少人？
B．经过点 且平行于 轴的直线
C．经过点 且平行于 轴的直线
D．经过点 且平行于 轴的直线
二、填空题
1.函数（k是常数， ）叫做反比例函数，k叫做．
2.在函数 中，自变量 的取值范围是．
3.已知A，B两点分别在反比例函数 和 的图象上，若点A与点B关于x轴对称，则m的值是______．
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1 / 9
人教版九年级数学第二学期26.1反比例函数培优训练
一、单选题
1．若点(1,2)-在反比例函数(0)k y k x =
≠的图象上，那么下列各点在此图象上的是( ) A ．(1,2)-- B ．(1,2) C ．(1,2)- D ．(4,1)-
2．已知反比例函数2y x =-
，下列结论不正确的是 A ．图象必经过点(-1,2) B ．y 随x 的增大而增大
C ．图象在第二、四象限内
D ．若x ＞1，则y ＞-2 3．在函数()0k y k x
=<的图象上有()11,A y ，()21,B y -，()32,B y -三个点，则下列各式中正确的是（ ） A ．123y y y <<
B ．132y y y <<
C ．321y y y <<
D ．231y y y << 4．当0x <时，反比例函数2y x
=-的图象（ ） A ．在第一象限，y 随x 的增大而减小 B ．在第二象限，y 随x 的增大而增大
C ．在第三象限，y 随x 的增大而减小
D ．在第四象限，y 随x 的增大而减小 5．已知反比例函数y =，当1＜x ＜3时，y 的最小整数值是（ ）
A ．3
B ．4
C ．5
D ．6
6．如图，已知点P 在反比例函数k y x
=
上，PA x ⊥轴，垂足为点A ，且AOP ∆的面积为4，则k 的值为（ ）
A ．8
B ．4
C ．8-
D ．4-
7．若正比例函数y=﹣2x 与反比例函数y=
k x 图象的一个交点坐标为（﹣1，2），则另一个交点的坐标为（ ） A ．（2，﹣1） B ．（1，﹣2） C ．（﹣2，﹣1） D ．（﹣2，1）
8．已知反比例函数k y x
=的图象分别位于第二、第四象限，()11,A x y 、()22,B x y 两点在该图象上，下列命题：①过点A 作AC x ⊥轴，C 为垂足，连接OA .若ACO ∆的面积为3，则6k
=-；②若120x x <<，
则12y y >；③若120x x +=，则120y y +=其中真命题个数是（ ）
A ．0
B ．1
C ．2
D ．3
二、填空题 9．在反比例函数1k y x
-=
的图象的每一支上，y 都随x 的增大而减少，则k 的取值范围是______. 10．如图，在平面直角坐标系中，点A ，B 在反比例函数()0k y k x =≠的图象上运动，且始终保持线段
AB =M 为线段AB 的中点，连接OM ．则线段OM 长度的最小值是_____(用含k 的代数式表示)．
11．如图，点A 在函数y ＝
4x
（x>0）的图象上，且OA ＝4，过点A 作AB ⊥x 轴于点B ，则△ABO 的周长为______．
12．如图，一次函数2y x =+与反比例函数k y x
=
的图像在第一象限交于点M ，若OM =，则k 的值是_______.
3 / 9
13．已知，点P （a ，b ）为直线3y x =-与双曲线2y x =-的交点，则11b a
-的值等于__． 14．如图，⊙A 和⊙B 都与x 轴和y 轴相切，圆心A 和圆心B 都在反比例函数
1
y x =
的图象上，则图中阴影部分的面积等于_________（结果保留π）．
15．直线y ＝kx(k ＞0)与双曲线y ＝
6x
交于A(x 1，y 1)和B(x 2，y 2)两点，则3x 1y 2－9x 2y 1的值为________． 16．如图，正方形的顶点A ，C 分别在y 轴和x 轴上，边BC 的中点F 在y 轴上，若反比例函数y ＝6x 的图象恰好经过CD 的中点E ，则OA 的长为______．
三、解答题
17．如图，一次函数y 1＝kx +b （k ≠0）和反比例函数y 2=
m x (m ≠0)的图象相交于点A （﹣4，2），B （n ，﹣
4）
（1）求一次函数和反比例函数的表达式；
（2）观察图象，直接写出不等式y 1＜y 2的解集．
18．在平面直角坐标系xOy 中，直线l ：y ＝kx +b （k ≠0）与反比例函数y 4x
=
的图象的一个交点为M （1，m ）． （1）求m 的值； （2）直线l 与x 轴交于点A ，与y 轴交于点B ，连接OM ，设△AOB 的面积为S 1，△MOB 的面积为S 2，若S 1≥3S 2，求k 的取值范围．
19．如图，点A 是直线2y x =与反比例函数1m y x
-=
（m 为常数）的图象的交点．过点A 作x 轴的垂线，垂足为B ，且2OB =．
（1）求点A 的坐标及m 的值；
（2）已知点(0,)(08)P n n <≤，过点P 作平行于x 轴的直线，交直线2y x =于点()11,C x y ，交反比例函数1m y x
-=（m 为常数）的图象于点()22,D x y ，交垂线AB 于点()33,E x y ．若231x x x <<，结合函数的图象，直接写出123x x x ++的取值范围．
5 / 9
20．如图，直线y=mx+n 与双曲线y=k x
相交于A （﹣1，2）、B （2，b ）两点，与y 轴相交于点C ．
（1）求m ，n 的值；
（2）若点D 与点C 关于x 轴对称，求△ABD 的面积；
（3）在坐标轴上是否存在异于D 点的点P ，使得S △PAB =S △DAB ？若存在，直接写出P 点坐标；若不存在，说明理由。
21．如图，已知将反比例函数14y x =-
（x ＜0），沿y 轴翻折得到反比例函数2k y x =（x ＞0），一次函数y ＝ax+b 与2k y x
=交于A （1，m ），B （4，n ）两点；
（1）求反比例函数y 2和一次函数y ＝ax+b 的解析式；
（2）连接OA ，过B 作BC ⊥x 轴，垂足为C ，点P 是线段AB 上一点，若直线OP 将四边形OABC 的面积分成1：2两部分，求点P 的坐标．
22．如图，已知直线y ＝x ﹣3与双曲线y ＝
k x
（k ＞0）交于A 、B 两点，点A 的纵坐标为1． （1）求点B 的坐标； （2）直接写出当x 在什么范围内时，代数式x 2﹣3x 的值小于k 的值；
（3）点C （2，m ）是直线AB 上一点，点D （n ，4）是双曲线y ＝
k x 上一点，将△OCD 沿射线BA 方向平移，得到△O ′C ′D ′．若点O 的对应点O ′落在双曲线y ＝k x
上，求点D 的对应点D ′的坐标．
23．如图，双曲线y 1＝1k x 与直线y 2＝2
x k 的图象交于A 、B 两点．已知点A 的坐标为（4，1），点P （a ，b ）是双曲线y 1＝1k x
上的任意一点，且0＜a ＜4． （1）分别求出y 1、y 2的函数表达式；
（2）连接PA 、PB ，得到△PAB ，若4a ＝b ，求三角形ABP 的面积；
（3）当点P 在双曲线y 1＝
1k x
上运动时，设PB 交x 轴于点E ，延长PA 交x 轴于点F ，判断PE 与PF 的大小关系，并说明理由．
7 / 9
1 / 9 参考答案
1．C2．B3．B4．B5．A6．C7．B8．D
9．1k >
10
11
．．
12．3
13．-32
14．π
15．36
16．6
17．(1) y ＝﹣x ﹣2，;(2) x ＞2或﹣4＜x ＜0
18．（1）m =4；（2）﹣2≤k ＜0或0＜k ≤1．
19．（1）A （2，4）；m=9；（2）6＜x 1+x 2+x 3≤7
20．（1）m =﹣1，n =1；（2）3；（3）存在，P 点坐标为（﹣1，0）或（3，0）或（0，3） 21．（1）24y x =，y ＝﹣x+5；（2）P 的坐标是P 3441,1515⎛⎫ ⎪⎝⎭或P 5322,1515⎛⎫ ⎪⎝⎭
. 22．（1）B (﹣1，﹣4)；（2）0＜x ＜4或﹣1＜x ＜0；（3）D ′(3，6)
23．（1）双曲线y 1＝4x
；直线为y 2＝14x ；（2）15；（3）PE ＝PF ，理由略．。