绪论 画法几何及阴影透视课件
合集下载
第一节 阴影的基本知识 画法几何及阴影透视课件

光线 阳面 阴线 阴面
影(或称落影)
影线
承影面
3
二、正投影图中加绘阴影的作用
(a) 未画阴影的正投影图
(b) 画出了阴影的正投影图
4
5
三、阴影在建筑表现图中的效果
(a) 未画阴影、图面单调呆板
(b) 加绘阴影、图面生动美观
6
四、常用光线
1
L l′ l" l' l"
45°
2 1
45°
1
45° 45°
57
1. 平行于投影面的多边形在该投影面上的落影
a' e'
b'
c' Bv
Av
d'
Ev
Dv
X
Cv
O
ab
c
de
58
59
2. 平面多边形在其平行平面上的落影
a' a'p e' e'p d'
b' b'p
c'
d'p
c'p
ab c PH ed
60
3. 平行于光线的平面图形的落影
a'
e' e'p
b'
c'
d'
第1节 阴影的基本知识和 点、直线、平面的阴影
§9-1 阴影的基本知识 §9-2 点的落影 §9-3 直线的落影 §9-4 平面的阴影
1
§9-1
阴影的基本知识
一、 阴和影的形成 二、正投影图中加绘阴影的作用 三、阴影在建筑表现图中的效果 四、光线和常用光线 五、求常用光线的真实倾角
2
一、阴和影的形成
影(或称落影)
影线
承影面
3
二、正投影图中加绘阴影的作用
(a) 未画阴影的正投影图
(b) 画出了阴影的正投影图
4
5
三、阴影在建筑表现图中的效果
(a) 未画阴影、图面单调呆板
(b) 加绘阴影、图面生动美观
6
四、常用光线
1
L l′ l" l' l"
45°
2 1
45°
1
45° 45°
57
1. 平行于投影面的多边形在该投影面上的落影
a' e'
b'
c' Bv
Av
d'
Ev
Dv
X
Cv
O
ab
c
de
58
59
2. 平面多边形在其平行平面上的落影
a' a'p e' e'p d'
b' b'p
c'
d'p
c'p
ab c PH ed
60
3. 平行于光线的平面图形的落影
a'
e' e'p
b'
c'
d'
第1节 阴影的基本知识和 点、直线、平面的阴影
§9-1 阴影的基本知识 §9-2 点的落影 §9-3 直线的落影 §9-4 平面的阴影
1
§9-1
阴影的基本知识
一、 阴和影的形成 二、正投影图中加绘阴影的作用 三、阴影在建筑表现图中的效果 四、光线和常用光线 五、求常用光线的真实倾角
2
一、阴和影的形成
《画法几何与阴影透视》教学课件—03直线与平面、平面与平面的相对位置

画法几何与阴影透视
3 第 章直线与平面、平面与平面的相对位置
3.1 直线与平面、平面与平面平行及其应用举例
3.1.1 直线和平面平行 几何条件:若平面外的一条直线与平面内的一条 直线平行,则该直线与该平面平行。这是解决直线与 平面平行作图问题的依据。 有关线、面平行的作图问题有:判别已知线面是 否平行;作直线与已知平面平行;作平面与已知直线 平行。
画法几何与阴影透视
V
判断直线的可见性
b
n
N
B
a
k
P
m
K
A
c
PH a
bk
C
n a
kb
M
c H
m
交点只有一个,其他投影重叠处都是重影。可见性判别的基本方法依然是交叉二直线c
重影点的可见性判别。对于特殊情况可以直接判断。如右图判别V投影的可见性,在H投
影图中去比较交点K左侧直线和平面的前后,直线在平面之前,故V投影图中m′k′段可
画法几何与阴影透视
3.2.3 一般位置直线与一般位置平面相交
一般位置线面相交由于直线和平面的投影都没有积聚性 ,求交点时无积聚性投影可以利用,因此通常要采用辅助 平面法求一般位置线面的交点。一般位置线、面相交求交 点的步骤: (l)含已知直线作特殊位置的辅助平面; (2)求辅助平面与已知平面的交线; (3)求交线与已知直线的交点,交点即为所求。 (4)判别可见性。
11
画法几何与阴影透视 B
平面与平面相交
M
K A
L
F
N
C
两平面的交线是一条直线,这条直线为两平面所共有。 交线的特性:交线总是可见的,是可见与不可见的分界线。
画法几何与阴影透视
3.2.1直线与平面相交的特殊情况
3 第 章直线与平面、平面与平面的相对位置
3.1 直线与平面、平面与平面平行及其应用举例
3.1.1 直线和平面平行 几何条件:若平面外的一条直线与平面内的一条 直线平行,则该直线与该平面平行。这是解决直线与 平面平行作图问题的依据。 有关线、面平行的作图问题有:判别已知线面是 否平行;作直线与已知平面平行;作平面与已知直线 平行。
画法几何与阴影透视
V
判断直线的可见性
b
n
N
B
a
k
P
m
K
A
c
PH a
bk
C
n a
kb
M
c H
m
交点只有一个,其他投影重叠处都是重影。可见性判别的基本方法依然是交叉二直线c
重影点的可见性判别。对于特殊情况可以直接判断。如右图判别V投影的可见性,在H投
影图中去比较交点K左侧直线和平面的前后,直线在平面之前,故V投影图中m′k′段可
画法几何与阴影透视
3.2.3 一般位置直线与一般位置平面相交
一般位置线面相交由于直线和平面的投影都没有积聚性 ,求交点时无积聚性投影可以利用,因此通常要采用辅助 平面法求一般位置线面的交点。一般位置线、面相交求交 点的步骤: (l)含已知直线作特殊位置的辅助平面; (2)求辅助平面与已知平面的交线; (3)求交线与已知直线的交点,交点即为所求。 (4)判别可见性。
11
画法几何与阴影透视 B
平面与平面相交
M
K A
L
F
N
C
两平面的交线是一条直线,这条直线为两平面所共有。 交线的特性:交线总是可见的,是可见与不可见的分界线。
画法几何与阴影透视
3.2.1直线与平面相交的特殊情况
(精选)画法几何与阴影透视

• 如果直线段的影落在相交的两承影面上,则直线段的影为 一折线,除了要求出直线两端点的影,还要求出折影点的 影。
9
平面的影子
10
1.4 平面 一、平面图形的阴影
• 平面图形阴影的形成——平面图形的影子的影线,是平面图形边线的
影子。
L
平面是不透明的,在光线的照射下,平面多边形迎光的一面为阳面,
背光的一面为阴面,故多边形各边均为阴线;求平面多边形的落影也就是
c0 a0
作图步骤:
一. 求A、B、C三点的落影 三点均落在H面上
二.连接各点的落影,则三 角形a0b0c0即为所求
三.H面投影各顶点的顺序与
b0
落影的顺序不同,平面的H 面投影为阴面投影
而平面的V面投影为阳面
投影
19
[例]已知四边形例A7B求C四D的边投形影的,阴求影它的阴影
作图步骤:
一. 求A、B两点的落影
d’ b’c’
落在所垂直的H面上为45°方向,落 在所平行的V面上为铅垂方向(A点 影和其自身重合)
二.作正垂线BC的落影
全部落在所垂直的V面上,为45°方 向
三.作侧垂线CD的落影
全部落在所平行的V面上为侧垂方向
四.作铅垂线DE的落影
与AB线作图相同
五.在影线的可见范围内涂色
45
根据特殊位置平面有积聚性的投影直接判别
16
• (3)判别一般位置平面的阴阳面 • 根据两个投影及平面影子顶点的旋转顺序来进行判别。 • 初步判别:平面的两个投影各顶点旋转顺序一致,则同是
阴面或同是阳面;反之,则一阴一阳。 • 进一步判别:平面影子的顶点与平面投影的顶点旋转顺序
一致的为阳面,不一致的为阴面。
求多边形各边的落影。
9
平面的影子
10
1.4 平面 一、平面图形的阴影
• 平面图形阴影的形成——平面图形的影子的影线,是平面图形边线的
影子。
L
平面是不透明的,在光线的照射下,平面多边形迎光的一面为阳面,
背光的一面为阴面,故多边形各边均为阴线;求平面多边形的落影也就是
c0 a0
作图步骤:
一. 求A、B、C三点的落影 三点均落在H面上
二.连接各点的落影,则三 角形a0b0c0即为所求
三.H面投影各顶点的顺序与
b0
落影的顺序不同,平面的H 面投影为阴面投影
而平面的V面投影为阳面
投影
19
[例]已知四边形例A7B求C四D的边投形影的,阴求影它的阴影
作图步骤:
一. 求A、B两点的落影
d’ b’c’
落在所垂直的H面上为45°方向,落 在所平行的V面上为铅垂方向(A点 影和其自身重合)
二.作正垂线BC的落影
全部落在所垂直的V面上,为45°方 向
三.作侧垂线CD的落影
全部落在所平行的V面上为侧垂方向
四.作铅垂线DE的落影
与AB线作图相同
五.在影线的可见范围内涂色
45
根据特殊位置平面有积聚性的投影直接判别
16
• (3)判别一般位置平面的阴阳面 • 根据两个投影及平面影子顶点的旋转顺序来进行判别。 • 初步判别:平面的两个投影各顶点旋转顺序一致,则同是
阴面或同是阳面;反之,则一阴一阳。 • 进一步判别:平面影子的顶点与平面投影的顶点旋转顺序
一致的为阳面,不一致的为阴面。
求多边形各边的落影。
(精选)画法几何与阴影透视

c0 a0
作图步骤:
一. 求A、B、C三点的落影 三点均落在H面上
二.连接各点的落影,则三 角形a0b0c0即为所求
三.H面投影各顶点的顺序与
b0
落影的顺序不同,平面的H 面投影为阴面投影
而平面的V面投影为阳面
投影
19
[例]已知四边形例A7B求C四D的边投形影的,阴求影它的阴影
作图步骤:
一. 求A、B两点的落影
17
(3)当平面是一般位置面时,若平面图形在某一投影面上 投影的各顶点旋转顺序与该平面落影的各顶点旋转顺序相同,则 平面在该投影面上的投影为阳面投影,反之则为阴面投影
阴面的投影 顺 序 不
阳面的投影
顺 序
相
同
同 均为顺阳序面相
的
同
阳面的投影
阳面的投影
投 影
根据各顶点旋转顺序判断
18
[例]已知三角形ABC的例投6影,求它的阴影
《建筑阴影和透视》
第一章 阴影和几何元素的阴影(3)
1
线的影子
2
五、一条直线在两个平面上的影子特性 (1) 直线在两个平行平面上的落影
c'
b'q
d'q
c'q
b'q
a'p
ap
bp
cq
bq
c
一条直线在两 个平行平面上 两段影子互相 平行。
3
(2)直线落在两相交承影面上 落影为两段相交的折线
K A0
• W与面光上线的W影面子投投影影l’a’o’’ 方向一致。
• V面(第三投影面)投 影 (第a’二0与投承影影面面)的积H聚面投 影呈对称形状。
7
某投影面垂直线落于任何物体表面上的影,在另外两个 投影面上的投影,总是成对称形状。
画法几何与阴影透视(课件七)
如前所述,当建筑物位于物空间时, 其透视始终是缩小的图像,而当建筑 物位于中空间时,其透视为放大的图 像。现在如右下图所示,当建筑物和 视点的相对位置关系不变,而将画面 在物空间和中空间两空间中进行移动, 这样我们将在画面上得到一系列大小 不同的相似透视图像,
画法几何与阴影透视
天津大学
(下册) 许松照 编著
画法几何与阴影透视
天津大学
(下册) 许松照 编著
第二章 透视的分类和视点的选定
本章需要掌握的基本知识:
一、透视分类的依据
二、视觉范围与视点选定
本章的具体内容:
一、透视分类的依据
建筑物都有长、宽、高,我们把建 筑物的长、宽、高三组主要方向的轮 廓线定义为主要向线。
主要向线与画面如果不平行,则存 在灭点(该灭点称之为主向灭点); 主向线与画面如果平行,则不存在灭 点。
b、过转角a和c向pp作垂线,得透 视图的近似宽度B;
c、在近似宽度内,选定心点的投 影Sg,由Sg作PP的垂线SSg,即中心 线的投影。使SSg的长度约等于近似画 面宽度的1.5~2.0倍。
注意:该方法步骤的第一步中角度 需要反复试验,而没有某一定数。
画法几何与阴影透视
天津大学
(下册) 许松照 编著
视平线提高,则视觉范围增加(如右 图所示),有时为了表现某一区域的 整体效果,则故意将视点定在高空, 这样视高就会很大,这样所绘制出的 透视称为鸟瞰图。
3、画面与建筑物的相对位置关系
1)、画面与建筑物立面的偏角大小 对透视形象的影响(如下图所示)
画法几何与阴影透视
4、在平面图中确定视点、画面的步骤 方法一: 先确定视点,然后确定画
面(如右上图所示)
a、先确定站点s,使由站点s向建筑 平面图所作两边缘视线sa和sc间的夹 角约为30度~40度;
画法几何与阴影透视
天津大学
(下册) 许松照 编著
画法几何与阴影透视
天津大学
(下册) 许松照 编著
第二章 透视的分类和视点的选定
本章需要掌握的基本知识:
一、透视分类的依据
二、视觉范围与视点选定
本章的具体内容:
一、透视分类的依据
建筑物都有长、宽、高,我们把建 筑物的长、宽、高三组主要方向的轮 廓线定义为主要向线。
主要向线与画面如果不平行,则存 在灭点(该灭点称之为主向灭点); 主向线与画面如果平行,则不存在灭 点。
b、过转角a和c向pp作垂线,得透 视图的近似宽度B;
c、在近似宽度内,选定心点的投 影Sg,由Sg作PP的垂线SSg,即中心 线的投影。使SSg的长度约等于近似画 面宽度的1.5~2.0倍。
注意:该方法步骤的第一步中角度 需要反复试验,而没有某一定数。
画法几何与阴影透视
天津大学
(下册) 许松照 编著
视平线提高,则视觉范围增加(如右 图所示),有时为了表现某一区域的 整体效果,则故意将视点定在高空, 这样视高就会很大,这样所绘制出的 透视称为鸟瞰图。
3、画面与建筑物的相对位置关系
1)、画面与建筑物立面的偏角大小 对透视形象的影响(如下图所示)
画法几何与阴影透视
4、在平面图中确定视点、画面的步骤 方法一: 先确定视点,然后确定画
面(如右上图所示)
a、先确定站点s,使由站点s向建筑 平面图所作两边缘视线sa和sc间的夹 角约为30度~40度;
《画法几何与阴影透视》教学课件—09形体的阴与影
5)、着色(受光区应着 亮色)。
W
V
c〞
C
s〞
Cw
c
KH
AH
A
S B ﹙b﹚a
s
BH
H
画法几何与阴影透视
(4)雨蓬与隔板的阴影
作影思路:
1)、根据A点的落影Aw,
D
定出空间光线S及其投
C
影s、s′、s〞;
2)、由光线的方向定出 雨蓬及隔板的阴线;
3)、依次作出上述阴 线的影线;
5)、着色。
Dv
Cv
P
ap′
ap
PH
a
画法几何与阴影透视
点在一般位置平面上的落影
a′
s′
2′
P′
ap′
1′
2
sap
FH P
1
a
画法几何与阴影透视 a′
(3)当承影面为 立体表面时,点的落 影为含该点的光线与 立体的交点。
t
C
D
a
画法几何与阴影透视
(3)圆柱的阴影
作阴影步骤:
1)、根据光线方向确定阴、 阳面,从而定出阴线;
S
Ⅳ Ⅲ
Ⅴ
s
2)、逐段求出各段阴线的
落影;(即为圆柱落影的
Ⅱ
轮廓线)
3)、着色。
Ⅳo
Ⅴo
Ⅲo
Ⅰ
4
Ⅱo
3
5
Ⅰo
2
s
1
画法几何与阴影透视 (4)圆筒内壁的阴影
S s
31
21 Ⅰ
41
51 Ⅵ
Ⅴ
Ⅴ0
Ⅳ
Ⅱ
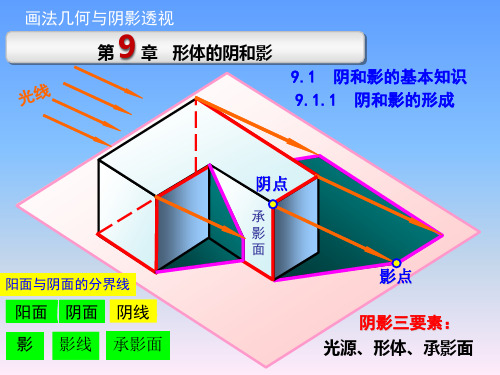
【例9.2】 已知直线Aa为铅垂线;平面P为倾斜面,平面P在水平面上的投影为四 边形DefG;光线方向为S,S在水平面上的投影为s,求直线Aa的落影。
W
V
c〞
C
s〞
Cw
c
KH
AH
A
S B ﹙b﹚a
s
BH
H
画法几何与阴影透视
(4)雨蓬与隔板的阴影
作影思路:
1)、根据A点的落影Aw,
D
定出空间光线S及其投
C
影s、s′、s〞;
2)、由光线的方向定出 雨蓬及隔板的阴线;
3)、依次作出上述阴 线的影线;
5)、着色。
Dv
Cv
P
ap′
ap
PH
a
画法几何与阴影透视
点在一般位置平面上的落影
a′
s′
2′
P′
ap′
1′
2
sap
FH P
1
a
画法几何与阴影透视 a′
(3)当承影面为 立体表面时,点的落 影为含该点的光线与 立体的交点。
t
C
D
a
画法几何与阴影透视
(3)圆柱的阴影
作阴影步骤:
1)、根据光线方向确定阴、 阳面,从而定出阴线;
S
Ⅳ Ⅲ
Ⅴ
s
2)、逐段求出各段阴线的
落影;(即为圆柱落影的
Ⅱ
轮廓线)
3)、着色。
Ⅳo
Ⅴo
Ⅲo
Ⅰ
4
Ⅱo
3
5
Ⅰo
2
s
1
画法几何与阴影透视 (4)圆筒内壁的阴影
S s
31
21 Ⅰ
41
51 Ⅵ
Ⅴ
Ⅴ0
Ⅳ
Ⅱ
【例9.2】 已知直线Aa为铅垂线;平面P为倾斜面,平面P在水平面上的投影为四 边形DefG;光线方向为S,S在水平面上的投影为s,求直线Aa的落影。
画法几何与阴影透视ppt课件
9
画法几何与阴影透视
(下册)
思考:求画面迹点有什么作用? (5)、直线上离画面无限远的点,其 透视称为直线的灭点。 思考:灭点该如何求解? 2、直线与画面的相对位置关系: (1)、直线在画面上
如果直线在画面上,则其透视及基 透视有什么特征? (2)、直线与画面平行
如果直线与画面平行,则其透视特 性有:
11
画法几何与阴影透视
(下册)
b、点在画面相交线上所分线段的长 度之比,在透视上不能保持原长度比 例; c、一组平行直线有一个共同的灭点, 其基透视也有一个共同的基灭点; (一组平行直线其透视和基透视分别 相交于其灭点和基灭点) d、画面相交线的三种典型形式:
a)、垂直于画面的直线,其透视和 基透视的公共点为什么?其透视有什 么特征?
13
画法几何与阴影透视
(下册)
三、平面形的透视、平面的迹线与灭线 1、平面形的透视 平面形的透视,其实质就是构成 平面形周边的各轮廓线的透视。 平面形的透视的基本属性: 1)、如果平面形是直线多边形, 那么其透视一般仍为直线多边形; 2)、如果平面形所在的平面通过 视点,其透视则为一条直线,而基透 视仍为多边形。(如右图所示) 2、平面的迹线与灭线 如果空间直线面与画面相交,则 称其交线为画面的画面迹线; 如果空间直线面与基面相交,则 称其交线为基面的基面迹线。 注意:如果空间直线面既与画面相 交,又与基面相交,则两条迹线必与 基线交于一点。
5、直线、平面间各种几何关系的 透视表现
a、直线如位于平面上,或平行 于平面,则直线的灭点在该平面的灭 线上;
b、如果平面上的直线或平行于 平面的直线,又同时平行于画面,那 么这种直线的灭点就是平面灭线上的 无限远点,从而直线的透视成为该平 面灭线的平行线;
画法几何与阴影透视
(下册)
思考:求画面迹点有什么作用? (5)、直线上离画面无限远的点,其 透视称为直线的灭点。 思考:灭点该如何求解? 2、直线与画面的相对位置关系: (1)、直线在画面上
如果直线在画面上,则其透视及基 透视有什么特征? (2)、直线与画面平行
如果直线与画面平行,则其透视特 性有:
11
画法几何与阴影透视
(下册)
b、点在画面相交线上所分线段的长 度之比,在透视上不能保持原长度比 例; c、一组平行直线有一个共同的灭点, 其基透视也有一个共同的基灭点; (一组平行直线其透视和基透视分别 相交于其灭点和基灭点) d、画面相交线的三种典型形式:
a)、垂直于画面的直线,其透视和 基透视的公共点为什么?其透视有什 么特征?
13
画法几何与阴影透视
(下册)
三、平面形的透视、平面的迹线与灭线 1、平面形的透视 平面形的透视,其实质就是构成 平面形周边的各轮廓线的透视。 平面形的透视的基本属性: 1)、如果平面形是直线多边形, 那么其透视一般仍为直线多边形; 2)、如果平面形所在的平面通过 视点,其透视则为一条直线,而基透 视仍为多边形。(如右图所示) 2、平面的迹线与灭线 如果空间直线面与画面相交,则 称其交线为画面的画面迹线; 如果空间直线面与基面相交,则 称其交线为基面的基面迹线。 注意:如果空间直线面既与画面相 交,又与基面相交,则两条迹线必与 基线交于一点。
5、直线、平面间各种几何关系的 透视表现
a、直线如位于平面上,或平行 于平面,则直线的灭点在该平面的灭 线上;
b、如果平面上的直线或平行于 平面的直线,又同时平行于画面,那 么这种直线的灭点就是平面灭线上的 无限远点,从而直线的透视成为该平 面灭线的平行线;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章 绪论
§1-1 本课程的研究对象和目的 §1-2 投影的方法
§1-1 本课程的研究对象、任务、学习方法
一、本课程的研究对象 1.画法几何 2.建筑透视阴影 二、本课程的任务 1.培养空间想象能力和空间分析能力。 2.研究解决空间几何问题的图解法。 3 .培养绘制建筑物透视阴影的能力。 4.培养踏实、细致、耐心的工程技术人员素质。 三、学习方法 1.循序渐进,多做练习,准确绘图。 2.养成正确使用绘图工具和绘图仪器的习惯。 3.养成认真细致的学习态度和工作作风。
90°
a
b
c
三、工程上常用用的几种投影图 1. 多面正投影图
(2)多面正投影图
2.轴测图
S Z
O X
Y
3. 标高图
25
20
15
25
20 15
25 20 15
4.透视图
本章结束
建筑透视阴影
V1
F1 V2
BC
D
G
Fx
Dº Cº
Fy
V3
Fl
V4
Bº
J
Байду номын сангаас
2
E
A1
Jº G E
F2
FL
一、投影的方法
投射线
b a 投影
一、投影的分类 1.中心投影法
S 投射中心 投射线
形体
a b
物体的中 心投影
c
2.平行投影法 (1)斜投影法
投 射 线 方 向
a b
c
90°
(2)正投影法 投 射 线 方 向
§1-1 本课程的研究对象和目的 §1-2 投影的方法
§1-1 本课程的研究对象、任务、学习方法
一、本课程的研究对象 1.画法几何 2.建筑透视阴影 二、本课程的任务 1.培养空间想象能力和空间分析能力。 2.研究解决空间几何问题的图解法。 3 .培养绘制建筑物透视阴影的能力。 4.培养踏实、细致、耐心的工程技术人员素质。 三、学习方法 1.循序渐进,多做练习,准确绘图。 2.养成正确使用绘图工具和绘图仪器的习惯。 3.养成认真细致的学习态度和工作作风。
90°
a
b
c
三、工程上常用用的几种投影图 1. 多面正投影图
(2)多面正投影图
2.轴测图
S Z
O X
Y
3. 标高图
25
20
15
25
20 15
25 20 15
4.透视图
本章结束
建筑透视阴影
V1
F1 V2
BC
D
G
Fx
Dº Cº
Fy
V3
Fl
V4
Bº
J
Байду номын сангаас
2
E
A1
Jº G E
F2
FL
一、投影的方法
投射线
b a 投影
一、投影的分类 1.中心投影法
S 投射中心 投射线
形体
a b
物体的中 心投影
c
2.平行投影法 (1)斜投影法
投 射 线 方 向
a b
c
90°
(2)正投影法 投 射 线 方 向
