初二数学截长补短法精题绝练(超实用版)
初二数学截长补短法精题绝练(超实用版)

因式分解易错点新解在分解因式时,应注意观察题目本身的特点,灵活选择恰当的方法,正确熟练地进行因式分解,采用“一提二套三查”法,即:首先看它是否有公因式,有公因式的要先提取公因式,再看这个多项式是几项式,若是二项式,就考虑能否运用平方差公式分解因式;若是三项式,就考虑能否运用完全平方公式分解因式,同时,在分解因式时,一定要分解到每一个因式都不能再分解为止。
然而同学们在实际运用中总是存在一定的错误,为了更好的帮助同学们理解因式分解,我将从几个易错点入手带领大家走出误区。
易错点一:用提公因式法分解因式时易漏项易错点导析:运用提公因式法分解因式,当多项式的某一项和公因式相同时,提取公因式后剩余的项为1,而部分初学者却让1“不翼而飞”了。
例如:28422(42)a b ab a a ab b -+=-,原多项式中有三项,但提取公因式后另一个因式仅有两项了,这是错误的,正确的是:28422(421)a b ab a a ab b -+=-+,为避免这种错误,可以用整式的乘法进行检验。
【例】分解因式:2212246a b ab ab -+错解:22122466(24)12(2)a b ab ab ab a b ab a b -+=-=-错解分析:此题中的公因式为6ab ,提公因式后,漏掉了为1的项,注意用整式的乘法进行检验,就可避免此类错误。
正解:22122466(241)a b ab ab ab a b -+=-+易错点2:运用完全平方公式时漏解出错易错点导析:我们知道,完全平方公式有两个,两数和的完全平方和两数差的完全平方,二者不能互相代替,有的同学对完全平方公式的特点把握不准,因而在解答相关题目时出现漏解错误,只有正确理解完全平方公式,熟记完全平方公式的结构特点,才能有效避免这类错误。
【例】若21364y ay ++是完全平方公式,求a 的值。
错解:2221136()642y ay y ay ++=++,所以1262ay y =⨯⨯,即12662a =⨯⨯= 错误分析:本题的错误之处是漏掉了a 为负数的情况。
初二数学 全全等三角形截长补短测试附解析

初二数学 全全等三角形截长补短测试附解析一、全等三角形截长补短1.已知:在ABC 中,90BAC ︒∠=,AB AC =.将ABC 按如图所示的位置放置在平面直角坐标系中,使得点(0,)A m 落在y 轴的负半轴上,使得点(,0)B n 落在x 轴的正半轴上,点C 在第二象限,并且,m n 满足2268250m n m n ++-+=.(1)由题意可知OA =_____,OB =_____(直接写答案);(2)求点C 的坐标;(3)ABC 的斜边BC 交y 轴于D ,直角边AC 交x 轴于E .在AC 上截取AF CE =,连接DF .探究线段DF AD BE 、、的数量关系并证明你的结论.2.已知,90POQ ∠=,分别在边OP ,OQ 上取点A ,B ,使OA OB =,过点A 平行于OQ 的直线与过点B 平行于OP 的直线相交于点C .点E ,F 分别是射线OP ,OQ 上动点,连接CE ,CF ,EF .(1)求证:OA OB AC BC ===;(2)如图1,当点E ,F 分别在线段AO ,BO 上,且45ECF ∠=时,请求出线段EF ,AE ,BF 之间的等量关系式;(3)如图2,当点E ,F 分别在AO ,BO 的延长线上,且135ECF ∠=时,延长AC 交EF 于点M ,延长BC 交EF 于点N .请猜想线段EN ,NM ,FM 之间的等量关系,并证明你的结论.3.在四边形ABDE 中,C 是BD 边的中点.(1)如图(1),若AC 平分BAE ∠,90ACE ∠=︒,则线段AE 、AB 、DE 的长度满足的数量关系为______;(直接写出答案)(2)如图(2),AC 平分BAE ∠,EC 平分AED ∠,若120ACE ∠=︒,则线段AB 、BD 、DE 、AE 的长度满足怎样的数量关系?写出结论并证明.4.如图所示,//AB DC AB AD BE ⊥,,平分ABC CE ∠,平分BCD ∠;(1)求AB CD 、与BC 的数里关系,并说明你的理由.(2)若把AB AD ⊥条件去掉,则(1)中AB CD 、与BC 的数里关系还成立吗?并说明你的理由.5.如图所示,已知AC 平分∠BAD ,180B D ∠+∠=︒,CE AB ⊥于点E ,判断AB 、AD 与BE 之间有怎样的等量关系,并证明.6.如图,在菱形ABCD 中,∠A =60°,E 为菱形ABCD 内对角线BD 左侧一点,连接BE 、CE 、DE .(1)若AB =6,求菱形ABCD 的面积;(2)若∠BED =2∠A ,求证:CE =BE+DE .7.已知等腰△ABC 中,AB=AC ,点D 在直线AB 上, DE ∥BC ,交直线AC 与点E ,且BD=BC ,CH ⊥AB ,垂足为H .(1)当点D 在线段AB 上时,如图1,求证DH=BH+DE ;(2)当点D 在线段BA 延长线上时,如图2,当点D 在线段AB 延长线上时,如图3,直接写出DH ,BH ,DE 之间的数量关系,不需要证明.8.如图,正方形ABCD 的对角线相交于点O .点E 是线段DO 上一点,连接CE .点F 是∠OCE 的平分线上一点,且BF ⊥CF 与CO 相交于点M ,点G 是线段CE 上一点,且CO=CG .(1)若OF=4,求FG 的长;(2)求证:BF=OG+CF .9.如图,在梯形ABCD 中,AD ∥BC ,AE 平分∠BAD ,BE 平分∠ABC ,且AE 、BE 交CD 于点E .试说明AD =AB ﹣BC 的理由.10.在平行四边形ABCD 中,DE 平分ADC ∠交BC 于点E ,连接AE .点O 是DE 的中点,连接CO 并延长交AD 于点F ,在CF 上取点G ,连接AG .(1)若4tan 3B =,5AB =,6BC =,求ABE △的周长. (2)若60B EAG ∠=∠=︒,求证:AF CG =.【参考答案】***试卷处理标记,请不要删除一、全等三角形截长补短1.(1)3,4;(2)(3,1)C -;(3)BE=DF+AD ,理由见解析【分析】(1)由非负数的性质求出m ,n 即可;(2)如图,作CH ⊥y 轴于点H ,只要证明△ACH ≌△BAO 即可解决问题;(3)在OB 上取一点K ,使得OK=DH ,则△CHD ≌△AOK ,再证明DF=EK ,AD=BK 即可解决问题.【详解】解:(1)∵2268250m n m n ++-+=∴22(3)(4)0m n ++-=,∵2(3)0+≥m ,2(4)0n -≥,∴3,4m n =-=,∴(0,3)A -,(4,0)B∴OA=3,OB=4,故答案为:3,4(2)如图,作CH ⊥y 轴于点H ,∵∠CHA=∠AOB=∠CAB=90°,∴∠CAH+∠ACH=90°,∠CAH+∠BAO=90°,∴∠ACH=∠BAO ,∵AC=BC ,∴△ACH ≌△BAO ,∴AH=OB=4,CH=OA=3,∴OH=1,∴(3,1)C -(3)结论为:BE=DF+AD理由:如图,在OB 上取一点K ,使得OK=DH ,∵CH=OA ,∠CHD=∠AOK=90°,DH=OK ,∴△CHD ≌△AOK (SAS ),∴CD=AK ,∵AD=BK ,AB=AC ,∴△AKB ≌△CDA (SSS ),∴∠KAB=∠ACD=45°,∴∠EAK=45°=∠FCD ,∵CE=AF ,∴CF=AE ,∵CD=AK ,∴△CDF ≌△AKE (SAS )∴DF=KE ,∵BE=EK+BK ,∴BE=DF+AD【点睛】本题考查三角形综合题、等腰直角三角形的性质、全等三角形的判定和性质、非负数的性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.2.(1)见解析;(2)EFAE BF =+;(3)222MN EN FM =+,见解析 【分析】(1)连接AB ,通过90POQ ∠=,OA OB =得到AOB 为等腰直角三角形,进而得到45OAB OBA ∠=∠=,根据过点A 平行于OQ 的直线与过点B 平行于OP 的直线相交于点C ,可推出45CBA ∠=,45BAC ∠=,最后通过证明AOB ≌ACB △,可以得出结论;(2)在射线AP 上取点D ,使AD BF =,连接CD ,通过证明CAD ≌CBF ,得到CD CF =,ACD BCF ∠=∠,再结合45ECF ∠=,90ACB ∠=推导证明ECD ≌ECF △,得到ED EF =,最后等量代换线段即可求解;(3)延长AO 到点D ,使得AD BF =,连接CD ,通过证明CAD ≌CBF ,得到CD CF =,ACD BCF ∠=∠,再结合135ECF ∠=,推导证明ECD ≌ECF △,得到D CFM ∠=∠,根据D CFB ∠=∠,等量代换可知CFM CFB ∠=∠,又因为//AC OQ ,推出MCF CFB ∠=∠,进而得到MC MF =,同理可证CN EN =,最后根据勾股定理即可求解.【详解】解:(1)证明:连接AB.90POQ∠=,OA OB=,∴AOB为等腰直角三角形,∴45OAB OBA∠=∠=,又//BC OP,且90POQ∠=,∴BC OQ⊥,∴90CBF∠=,∴45CBA∠=,同理,45BAC∠=,在AOB与ACB△中OAB CABAB ABOBA CBF∠=∠⎧⎪=⎨⎪∠=∠⎩,∴AOB≌ACB△()ASA,∴90AOB ACB∠=∠=,OA OB AC BC===;(2)如图1,在射线AP上取点D,使AD BF=,连接CD.在CAD与CBF中CA CBCAD CBFAD BF=⎧⎪∠=∠⎨⎪=⎩,∴CAD≌CBF()SAS,∴CD CF=,ACD BCF∠=∠,45ECF∠=,90ACB∠=,∴45ACE BCF∠+∠=,∴45ACE ACD ECD∠+∠=∠=,∴ECD ECF∠=∠,在ECD与ECF△中CD CF ECD ECF CE CE =⎧⎪∠=∠⎨⎪=⎩∴ECD ≌ECF △()SAS ,∴ED EF =,又ED AD AE BF AE =+=+,∴EF AE BF =+. (3)222MN EN FM =+.证明如下:如图2,延长AO 到点D ,使得AD BF =,连接CD .∴90CAD CBF ∠=∠=,在CAD 与CBF 中CA CB CAD CBF AD BF =⎧⎪∠=∠⎨⎪=⎩,∴CAD ≌CBF ()SAS ,∴CD CF =,ACD BCF ∠=∠,90ACD DCB ∠+∠=,∴90BCF DCB DCF ∠+∠==∠,∴90FCD BCA ∠=∠=,135ECF ∠=,∴36090135135ECD ∠=--=,∴ECF ECD ∠=∠,在ECD 与ECF △中EC EC ECD ECF CD CF =⎧⎪∠=∠⎨⎪=⎩,∴ECD ≌ECF △()SAS ,∴D CFM ∠=∠,CAD≌CBF,∴D CFB∠=∠,∴CFM CFB ∠=∠,//AC OQ,∴MCF CFB∠=∠,∴CFM MCF∠=∠,∴MC MF=,同理可证:CN EN=,∴在Rt MCN△中,由勾股定理得:22222MN CN CM EN FM=+=+.【点睛】本题综合考查了全等三角形的性质和判定,勾股定理以及正方形的有关知识,通过添加辅助线构造全等三角形,通过证明全等三角形得到线段之间的关系是解题的关键.3.(1)AE=AB+DE;(2)AE=AB+DE+12BD,证明见解析.【分析】(1)在AE上取一点F,使AF=AB,由三角形全等的判定可证得△ACB≌△ACF,根据全等三角形的性质可得BC=FC,∠ACB=∠ACF,根据三角形全等的判定证得△CEF≌△CED,得到EF=ED,再由线段的和差可以得出结论;(2)在AE上取点F,使AF=AB,连结CF,在AE上取点G,使EG=ED,连结CG,根据全等三角形的判定证得△ACB≌△ACF和△ECD≌△ECG,由全等三角形的性质证得CF=CG,进而证得△CFG是等边三角形,就有FG=CG=12BD,从而可证得结论.【详解】解:(1)如图(1),在AE上取一点F,使AF=AB.∵AC平分∠BAE,∴∠BAC=∠FAC.在△ACB和△ACF中,AB AFBAC FACAC AC⎧⎪∠∠⎨⎪⎩===∴△ACB≌△ACF(SAS).∵C 是BD 边的中点,∴BC =CD .∴CF =CD .∵∠ACE =90°,∴∠ACB +∠DCE =90°,∠ACF +∠ECF =90°.∴∠ECF =∠ECD .在△CEF 和△CED 中,CF CD ECF ECD CE CE ⎧⎪∠∠⎨⎪⎩=== ∴△CEF ≌△CED (SAS ).∴EF =ED .∵AE =AF +EF ,∴AE =AB +DE .故答案为:AE =AB +DE ;(2)AE =AB +DE +12BD . 证明:如图(2),在AE 上取点F ,使AF =AB ,连结CF ,在AE 上取点G ,使EG =ED ,连结CG .∵C 是BD 边的中点,∴CB =CD =12BD . ∵AC 平分∠BAE ,∴∠BAC =∠FAC .在△ACB 和△ACF 中,AB AF BAC FAC AC AC ⎧⎪∠∠⎨⎪⎩=== ∴△ACB ≌△ACF (SAS ).∴CF =CB ,∠BCA =∠FCA .同理可证:△ECD ≌△ECG∵CB =CD ,∴CG =CF .∵∠ACE =120°,∴∠BCA +∠DCE =180°−120°=60°.∴∠FCA +∠GCE =60°.∴∠FCG =60°.∴△FGC 是等边三角形.∴FG =FC =12BD . ∵AE =AF +EG +FG , ∴AE =AB +DE +12BD . 【点睛】本题主要考查了全等三角形的判定与性质的运用,能熟练应用三角形全等的判定和性质是解决问题的关键.4.(1)AB CD BC +=,见解析;(2)成立,见解析【分析】(1)先写出数量关系,过E 作EF BC ⊥于F ,然后证明CDE CFE ∆≅∆和ABE FBE ≅∆∆,便可得结论了.(2)成立, 在BC 上截取CF CD =证明CDE CFE ∆≅∆和ABE FBE ≅∆∆,便可得到结论.【详解】()1AB CD BC +=理由是:过E 作EF BC ⊥于FCE 为角平分线DCE FCE ∴∠=∠//AB DC AB AD ⊥,90D ∴∠=EF BC ⊥D CFE ∴∠=∠CE CE =()CDE CFE AAS ∆≅∆CD CF ∴=同理可证()ABE FBE AAS ∆≅∆AB BF ∴=CF BF AB +=AB CD BC ∴+=()2成立理由:在BC 上截取CF CD =CE 为角平分线DCE FCE ∴∠=∠CE CE =()CDE CFE SAS ∆≅∆CD CF ∴= D CFE ∠=∠//AB DC180D A ∴∠+∠=又180CFE EFB ∠+=A EFB ∴∠=∠ 又BE 是角平分线 ABE FBE ∴∠=∠BE BE =()BAE BFE AAS ∆≅∆AB FB ∴=∴ CF BF AB +=AB CD BC ∴+=5.2AB AD BE =+,证明见解析【分析】在AB 上截取EF ,使EF=BE ,联结CF .证明()BCE ECF SAS ≌,得到 B BFC ∠=∠,又证明 AFC ADC ≌,得到 AF AD =,最后结论可证了.【详解】证明:在AB 上截取EF ,使EF=BE ,联结CF .CE AB ⊥90BEC FEC ∴∠=∠=︒在BCE 和ECF △ BE EF BEC FEC CE CE =⎧⎪∠=∠⎨⎪=⎩()BCE ECF SAS ∴≌ B BFC ∴∠=∠180B D ∠+∠=︒180BFC AFC ∠+∠=︒又D AFC ∴∠=∠AC 平分∠BADFAC DAC ∴∠=∠在AFC △ 和ADC 中AFC D FAC DAC AC AC ∠=∠⎧⎪∠=∠⎨⎪=⎩() AFC ADC AAS ∴≌AF AD ∴=AB AF BE EF =++2AB AD BE ∴=+【点睛】本题考查三角形全等知识的综合应用,关键在于寻找全等的条件,作适当的辅助线加以证明.6.(1)3;(2)见解析【分析】(1)过点B 作BH ⊥AD 于H ,由直角三角形的性质可求BH 的长,由菱形的面积公式可求解;(2)延长DE 至M ,使ME =BE ,连接MB ,由题意可证△ABD 是等边三角形,△BCD 是等边三角形,△BEM 是等边三角形,可得∠CBD =∠ABD =60°=∠MBE ,AB =BD =BC ,BM =BE ,由“SAS”可证∴△MBD ≌△EBC ,可得MD =EC ,即可得结论.【详解】解:(1)如图,过点B 作BH ⊥AD 于H ,∵四边形ABCD 是菱形,∴AB =AD =6,∵∠A =60°,BH ⊥AD ,∴∠ABH =30°,∴AH =12AB =3,BH =3AH =33, ∴菱形ABCD 的面积=AD×BH =6×33=183;(2)如图,延长DE 至M ,ME =BE ,连接MB ,∵四边形ABCD 是菱形,∴AB =AD =CD =BC ,∠A =60°=∠BCD ,∴△ABD 是等边三角形,△BCD 是等边三角形,∴∠CBD =∠ABD =60°,AB =BD =BC ,∵∠BED =2∠A =120°,∴∠BEM =60°,又∵BE =ME ,∴△BEM 是等边三角形,∴BM =BE ,∠MBE =∠DBC =60°,∴∠MBD =∠EBC ,∴△MBD ≌△EBC (SAS ),∴MD =EC ,∴CE =BE+DE .【点睛】本题主要考查了菱形的性质应用,结合等边三角形的性质是解题的关键.7.(1)见详解;(2)图2:=DH BH DE -,图3:+DE DH BH =【分析】(1)在线段AH 上截取HM BH =,连接CM ,CD ,证明DMC DEC △≌△,可得到DE DM =,即可求解.(2)当点D 在线段BA 延长线上时,在BA 的延长线上截取MH BH =,连接CM ,DC ,由题意可证BHC CHM △≌△,可得B CMB ∠=∠,由题意可得=B AED ∠∠,即可证DMC DEC △≌△,可得DE DM =,则可得DH BH DE =-;当点D 在线段AB 延长线上时,在线段AB 上截取BH HM =,连接CM ,CD ,由题意可证BHC CHM △≌△,可得B CMB ∠=∠,由题意可得B AED ∠=∠,即可证DMC DEC △≌△,可得DE DM =,则可得DE DH BH =+.【详解】解:(1)证明:在线段AH 上截取HM BH =,连接CM ,CD∵CH AB ⊥,HM BH =∴CM BC =∴B CMB ∠=∠∵AB AC =∴B ACB ∠=∠∵//DE BC∴ADE B AED ACB ∠=∠=∠=∠,CDE BCD ∠=∠∴AED BMC ∠=∠∴DEC DMC ∠=∠∵BD BC =∴BDC BCD EDC ∠=∠=∠∵CD CD =∴CDM CDE △≌△∴=DM DE∴+BH DE DM HM DH =+=(2)当点D 在线段BA 延长线上时,DH BH DE =-如图2:在BA 的延长线上截取MH BH =,连接CM ,DC∵AB AC =∴A ABC CB =∠∠∵BD BC =∴BDC DCB =∠∠∵//DE BC∴E ACB B EDB ===∠∠∠∠∵=CH CH ,BH MH =,BHC CHM =∠∠∴BHC CHM △≌△∴=B M ∠∠∴E M =∠∠∵+MDC B DCB =∠∠∠,EDC BDC EDB =+∠∠∠∴MDC EDC =∠∠又∵E M =∠∠,DC CD =∴DEC DMC △≌△∴DE DM =∵=DH MH DM -∴DH BH DE =-当点D 在线段AB 延长线上时,DE DH BH =+如图3:当点D 在线段AB 延长线上时,在线段AB 上截取BH HM =,连接CM ,CD∵BH HM =,CH CH =,90CHB MHC ==︒∠∠∴MHC BHC △≌△∴ABC BMC =∠∠∵AB AC =∴A ABC CB =∠∠∵BD BC =∴BDC BCD ∠=∠∵//BC DE∴BCD CDE ∠=∠,ACB AED ∠=∠∴BDC CDE ∠=∠,BMC AED =∠∠,且CD CD =∴CDM CDE △≌△∴DE DM =∵DM DH HM =+∴DE DH BH =+【点睛】本题主要考查了三角形综合题,等腰三角形的性质,全等三角形的性质和判定,合理添加辅助线证全等是解题的关键.8.(1)4;(2)见解析【分析】(1)根据条件证明△OCF ≌△GCF ,由全等的性质就可以得出OF=GF 而得出结论; (2)在BF 上截取BH=CF ,连接OH ,通过条件可以得出△OBH ≌△OCF ,可以得出OH=OF ,从而得出OG ∥FH ,OH ∥FG ,进而可以得出四边形OHFG 是平行四边形,就可以得出结论.【详解】解:(1)∵CF 平分∠OCE ,∴∠OCF=∠ECF .∵OC=CG ,CF=CF ,∵在△OCF 和△GCF 中,OC GC OCF ECF CF CF ⎧⎪∠∠⎨⎪⎩=== ∴△OCF ≌△GCF (SAS ),∴FG=OF=4即FG 的长为4.(2)证明:在BF 上截取BH=CF ,连接OH .∵四边形ABCD 为正方形,∴AC ⊥BD ,∠DBC=45°,∴∠BOC=90°,∴∠OCB=180°-∠BOC-∠DBC=45°.∴∠OCB=∠DBC .∴OB=OC .∵BF ⊥CF ,∴∠BFC=90°.∵∠OBH=180°-∠BOC-∠OMB=90°-∠OMB ,∠OCF=180°-∠BFC-∠FMC=90°-∠FMC ,且∠OMB=∠FMC ,∴∠OBH=∠OCF .∵在△OBH 和△OCF 中OB OC OBH OCF BH CF ⎧⎪∠∠⎨⎪⎩=== ∴△OBH ≌△OCF (SAS ).∴OH=OF ,∠BOH=∠COF .∵∠BOH+∠HOM=∠BOC=90°,∴∠COF+∠HOM=90°,即∠HOF=90°. ∴1180452OHF OFH HOF ∠=∠=︒-∠=︒() ∴∠OFC=∠OFH+∠BFC=135°.∵△OCF ≌△GCF ,∴∠GFC=∠OFC=135°,∴∠OFG=360°-∠GFC-∠OFC=90°. ∴1180452FGO FOG OFG ∠=∠=︒-∠=︒() , ∴∠GOF=∠OFH ,∠HOF=∠OFG .∴OG ∥FH ,OH ∥FG ,∴四边形OHFG 是平行四边形(两组对边分别平行的四边形是平行四边形).∴OG=FH .∵BF=FH+BH ,∴BF=OG+CF【点睛】本题考查了正方形的性质的运用,全等三角形的判定及性质的运用,平行四边形的判定及性质的运用,解答时采用截取法作辅助线是关键.9.见解析【分析】在AB 上找到F 使得AF =AD ,易证△AEF ≌△AED ,可得AF =AD ,∠AFE =∠D ,根据平行线性质可证∠C =∠BFE ,即可证明△BEC ≌△BEF ,可得BF =BC ,即可解题.【详解】证明:在AB 上找到F 使得AF =AD ,∵AE 平分∠BAD ,∴∠EAD =∠EAF ,∵在△AEF 和△AED 中,AD AF EAD EAF AE AE =⎧⎪∠=∠⎨⎪=⎩,∴△AEF ≌△AED ,(SAS )∴AF =AD ,∠AFE =∠D ,∵AD ∥BC ,∴∠D +∠C =180°,∵∠AFE +∠BFE =180°∴∠C =∠BFE ,∵BE 平分∠BAD ,∴∠FBE =∠C ,∵在△BEC 和△BEF 中,BFE C FBE CBE BE BE ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△BEC ≌△BEF ,(AAS )∴BF =BC ,∵AB =AF +BF ,∴AB =AD +BC ,即AD =AB ﹣BC .【点睛】本题考查了全等三角形的判定,考查了全等三角形对应边、对应角相等的性质,本题中求证△AEF ≌△AED 和△BEC ≌△BEF 是解题的关键.10.(1)256;(2)见解析【分析】(1)构建直角三角形,得出AH 、BH ,然后利用角平分线的性质以及平行四边形的性质,进行等量互换,即可得解;(2)首先在AB 上截取BQ BE =,然后判定DOF EOC ≌△△和AEQ GAF ≌△△,进行等量转换,即可得证.【详解】(1)过点A 作AH BC ⊥于点H ,如图所示: 4tan 3B ∠=,5AB =, 4AH ∴=,3BH =DE 平分ADC ∠,12∠∠∴=,AD BC ∵∥,13∠∠∴=23∴∠=∠,5DC EC ∴==,1BE ∴=,2EH ∴=,25AE ∴=256ABE C ∴=+△;(2)在AB 上截取BQ BE =,连接EQ ,如图所示:CD CE =,CO DE ⊥,OD DE ∴=①AD BC ∵∥,DFO ECO ∴∠=∠,ADE CED ∠=∠②③由①②③得:DOF EOC ≌△△,DF CE ∴=,又AD BC =,AD DF BC CE ∴-=-,即AF BE =60EAG ∠=︒,60BAE FAG ∴∠+∠=︒,60DFC ∠=︒,60FGA FAG ∴∠+∠=︒,CD=CFBAE FGA ∴∠=∠④又120FAG AQE ∠=∠=︒,EQ AF =⑤⑥由④⑤⑥得:AEQ GAF ≌△△,AQ FG ∴=,又AB CF =,AB AQ CF FG ∴-=-,即BQ CG =,AF CG ∴=.【点睛】此题主要考查利用三角函数值构建直角三角形以及全等三角形的判定与性质,熟练掌握,即可解题.。
全等三角形截长补短法的经典例题

全等三角形截长补短法的经典例题初中最容易拉开分数差距的就是数学考试,而初二数学难点就差在几何上了。
初中数学哪些题最容易拉开差距?毫无疑问——几何辅助线!几何辅助线答题成为孩子们成绩的分水岭!很多资深数学老师经常挂在嘴边一句话,得几何者得数学。
为了学好几何,孩子们就必须要在头脑中建立几何辅助线模型,学会做辅助线,构造模型。
说来说去其实也就那几个模型,学会了按照模型设计辅助线,初中数学考试答题迎刃而解。
截长补短法,是初中数学几何题中一种辅助线的添加方法。
截长:即在一条较长的线段上截取一段较短的线段在线段AB上截取AD=AC补短:在较短的线段上补一段线段使其和较长的线段相等延长AC,使得AD=AB例1.如图①,已知在△ABC中,∠C=2∠B,AD平分∠BAC交BC于点D。
求证:AB=AC+CD方法1(截长法)证明:如图②,在AB上取AE=AC,连接DE∵AD平分∠BAC∴∠1=∠2∴在△ADE和△ADC中AE= AC∠1=∠2AD=AD∴△ADE≌△ADC(SAS)ED=CD,∠AED=∠C=2∠B又∵∠AED=∠BH∠BDE∴∠B=∠BDE,∴EB=ED∴EB=CD∴AB=AE+EB∴AB=AC+CD方法2补短法:证明如图③,延长AC到E,使CE=CD,连接DE.则∠CDE=∠E ∠ACB=∠CDE+∠E=2∠E又∵∠ACB=2∠B∴∠B=∠E∴在△ABD和AED中∠B=∠E∠1=∠2AD= AD∴△ABD≌AED(AS)∴AB=AE又∵AE=AC+CE,CE=CD∴AB=AC+CD例题1,三角形中,出现角平分线,然后证明AB=AC+CD例2.如图①,在△ABC中,∠BAC=60°,AD是∠BAC的平分线,且AC =AB+BD.求∠ABC的度数例题2,三角形中,出现了角平分线,已知线段的等量关系AC=AB+BD,再求角度的经典例题,同样可以截长补短来解决。
例3.如图,∠ABC+∠BCD=180°,E为AD上的一点,BE、CE分别平分∠ABC、∠BCD。
初二数学全全等三角形截长补短提优专项训练
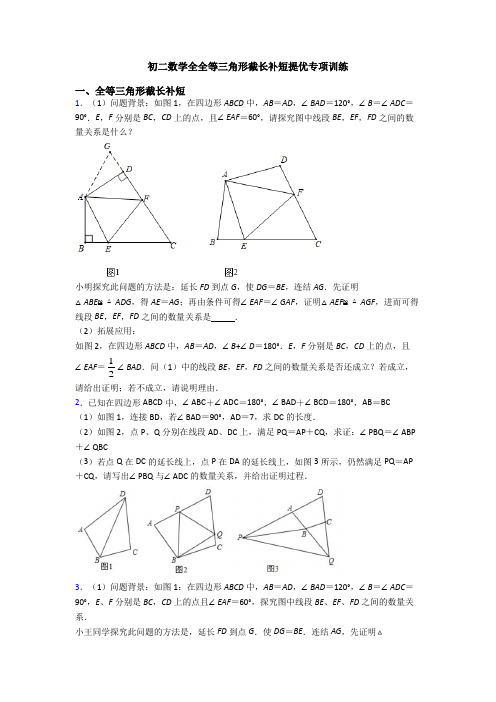
初二数学全全等三角形截长补短提优专项训练一、全等三角形截长补短1.(1)问题背景:如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°.E,F分别是BC,CD上的点,且∠EAF=60°,请探究图中线段BE,EF,FD之间的数量关系是什么?小明探究此问题的方法是:延长FD到点G,使DG=BE,连结AG.先证明△ABE≌△ADG,得AE=AG;再由条件可得∠EAF=∠GAF,证明△AEF≌△AGF,进而可得线段BE,EF,FD之间的数量关系是.(2)拓展应用:如图2,在四边形ABCD中,AB=AD,∠B+∠D=180°.E,F分别是BC,CD上的点,且∠BAD.问(1)中的线段BE,EF,FD之间的数量关系是否还成立?若成立,∠EAF=12请给出证明;若不成立,请说明理由.2.已知在四边形ABCD中,∠ABC+∠ADC=180°,∠BAD+∠BCD=180°,AB=BC(1)如图1,连接BD,若∠BAD=90°,AD=7,求DC的长度.(2)如图2,点P、Q分别在线段AD、DC上,满足PQ=AP+CQ,求证:∠PBQ=∠ABP +∠QBC(3)若点Q在DC的延长线上,点P在DA的延长线上,如图3所示,仍然满足PQ=AP +CQ,请写出∠PBQ与∠ADC的数量关系,并给出证明过程.3.(1)问题背景:如图1:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E、F分别是BC,CD上的点且∠EAF=60°,探究图中线段BE、EF、FD之间的数量关系.小王同学探究此问题的方法是,延长FD到点G.使DG=BE.连结AG,先证明ABE ≌ADG ,再证明AEF ≌AGF ,可得出结论,他的结论应是______________;(2)探索延伸:如图2,若在四边形ABCD 中,AB =AD ,∠B +∠D =180°.E ,F 分别是BC ,CD 上的点,且∠EAF 12=∠BAD ,上述结论是否仍然成立,并说明理由; (3)实际应用:如图3,在某次军事演习中,舰艇甲在指挥中心(O 处)北偏西30°的A 处,舰艇乙在指挥中心南偏东70°的B 处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以45海里/小时的速度前进,同时舰艇乙沿北偏东50°的方向以60海里/小时的速度前进,2小时后,指挥中心观测到甲、乙两地分别到达E 、F 处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离.4.如图所示,已知AC 平分∠BAD ,180B D ∠+∠=︒,CE AB ⊥于点E ,判断AB 、AD 与BE 之间有怎样的等量关系,并证明.5.如图,在正方形ABCD 中,点E 、F 均为中点,连接AF 、DE 交于点P ,连接PC ,证明:2PE PF PC +=.6.如图,//AD BC ,点E 在线段AB 上,DE 、CE 分别是ADC ∠、BCD ∠的角平分线,若3AD =,2BC =,求CD 的长.7.已知等腰ABC ∆中,AB AC =,点D 在直线AB 上,//DE BC ,交直线AC 于点E ,且BD BC =,CH AB ⊥,垂足为H .(1)当点D 在线段AB 上时,如图1,求证BH DE DH +=;(2)当点D 在线段BA 的延长线上时,如图2;当点D 在线段AB 延长线时,如图3,线段BH ,DE ,DH 又有怎样的数量关系?请直接写出你的猜想,不需要证明. 8.已知△ABC 中,AB =AC ,∠A =108°,BD 平分∠ABC ,求证:BC =AC +CD .9.在平行四边形ABCD 中,DE 平分ADC ∠交BC 于点E ,连接AE .点O 是DE 的中点,连接CO 并延长交AD 于点F ,在CF 上取点G ,连接AG .(1)若4tan 3B =,5AB =,6BC =,求ABE △的周长. (2)若60B EAG ∠=∠=︒,求证:AF CG =.10.阅读下面材料,完成(1)﹣(3)题数学课上,老师出示了这样一道题:如图,四边形ABCD ,AD ∥BC ,AB =AD ,E 为对角线AC 上一点,∠BEC =∠BAD =2∠DEC ,探究AB 与BC 的数量关系.某学习小组的同学经过思考,交流了自己的想法:小柏:“通过观察和度量,发现∠ACB =∠ABE ”;小源:“通过观察和度量,AE 和BE 存在一定的数量关系”;小亮:“通过构造三角形全等,再经过进一步推理,就可以得到线段AB 与BC 的数量关系”.……老师:“保留原题条件,如图2, AC 上存在点F ,使DF =CF =k AE ,连接DF 并延长交BC 于点G ,求AB FG的值”. (1)求证:∠ACB =∠ABE ;(2)探究线段AB 与BC 的数量关系,并证明;(3)若DF =CF =k AE ,求AB FG的值(用含k 的代数式表示).【参考答案】***试卷处理标记,请不要删除一、全等三角形截长补短1.(1)EF =BE +DF ;(2)结论EF =BE +DF 仍然成立;证明见解析.【分析】(1)延长FD 到点G .使DG=BE .连结AG ,即可证明△ABE ≌△ADG ,可得AE=AG ,再证明△AEF ≌△AGF ,可得EF=FG ,即可解题;(2)延长FD 到点G .使DG=BE .连结AG ,即可证明△ABE ≌△ADG ,可得AE=AG ,再证明△AEF ≌△AGF ,可得EF=FG ,即可解题.【详解】(1)EF =BE +DF ,理由如下:在△ABE 和△ADG 中,90DG BE B ADG AB AD ︒=⎧⎪∠=∠=⎨⎪=⎩,∴△ABE ≌△ADG (SAS ),∴AE =AG ,∠BAE =∠DAG ,∵∠EAF =12∠BAD , ∴∠GAF =∠DAG +∠DAF =∠BAE +∠DAF =∠BAD ﹣∠EAF =∠EAF ,∴∠EAF =∠GAF ,在△AEF 和△GAF 中,AE AG EAF GAF AF AF =⎧⎪∠=∠⎨⎪=⎩,∴△AEF ≌△AGF (SAS ),∴EF =FG ,∵FG =DG +DF =BE +DF ,∴EF =BE +DF ;故答案为:EF =BE +DF .(2)结论EF =BE +DF 仍然成立;理由:延长FD 到点G .使DG =BE .连结AG ,如图2,∵∠B +∠ADC =180°,∠ADC +∠ADG =180°,∴∠B =∠ADG ,在△ABE 和△ADG 中,DG BE B ADG AB AD =⎧⎪∠=∠⎨⎪=⎩,∴△ABE ≌△ADG (SAS ),∴AE =AG ,∠BAE =∠DAG ,∵∠EAF =12∠BAD , ∴∠GAF =∠DAG +∠DAF =∠BAE +∠DAF =∠BAD ﹣∠EAF =∠EAF ,∴∠EAF =∠GAF ,在△AEF 和△GAF 中,AE AG EAF GAF AF AF =⎧⎪∠=∠⎨⎪=⎩,∴△AEF ≌△AGF (SAS ),∴EF =FG ,∵FG =DG +DF =BE +DF ,∴EF =BE +DF .【点睛】本题是四边形综合题,考查了全等三角形的判定和性质,直角三角形的性质,添加恰当辅助线构造全等三角形是解题的关键.2.(1)7DC =;(2)见解析;(3)1902PBQ ADC ∠=︒+∠,证明见解析 【分析】(1)根据已知条件得出BDC 为直角三角形,再根据HL 证出△≌△Rt BAD Rt BCD ,从而证出AD CD =即可得出结论;(2)如图2,延长DC 到 K ,使得CK=AP ,连接BK ,通过证△BPA ≌△BCK (SAS )得到:∠1=∠2,BP=BK .然后根据SSS 证明得≌PBQ BKQ ,从而得出21PBQ CBQ CBQ ∠=∠+∠=∠+∠,然后得出结论;(3)如图3,在CD 延长线上找一点K ,使得KC=AP ,连接BK ,构建全等三角形:△BPA ≌△BCK (SAS ),由该全等三角形的性质和全等三角形的判定定理SSS 证得:△PBQ ≌△BKQ ,则其对应角相等:∠PBQ=∠KBQ ,结合四边形的内角和是360°可以推得:∠PBQ=90°+12∠ADC . 【详解】(1)证明:如图1,∵180ABC ADC ∠+∠=︒,90BAD ∠=︒,∴90BCD BAD ∠=∠=︒,在Rt BAD 和Rt BCD 中,BD BD AB BC =⎧⎨=⎩∴()△≌△Rt BAD Rt BCD HL ,∴AD DC =,∴7DC =;(2)如图2,延长DC 至点K ,使得CK AP =,连接BK∵180ABC ADC ∠+∠=︒,∴180BAD BCD ∠+∠=︒,∵180BCD BCK ∠+∠=︒,∴BAD BCK ∠=∠,∵AP CK =,AB BC =,∴()△≌△BPA BCK SAS , ∴12∠=∠,BP BK =,∵PQ AP CQ =+,QK CK CQ =+,∴PQ QK =,∵BP BK =,BQ BQ =,∴()≌PBQ BKQ SSS ,∴21PBQ CBQ CBQ ∠=∠+∠=∠+∠,∴PBQ ABP QBC ∠=∠+∠;(3)1902PBQ ADC ∠=︒+∠; 如图3,在CD 延长线上找一点K ,使得KC AP =,连接BK ,∵180ABC ADC ∠+∠=︒,∴180BAD BCD ∠+∠=︒,∵180BAD PAB ∠+∠=︒,∴PAB BCK ∠=∠,在BPA △和BCK 中,AP CK BAP BCK AB BC =⎧⎪∠=∠⎨⎪=⎩∴()△≌△BPA BCK SAS , ∴ABP CBK ∠=∠,BP BK =,∴PBK ABC ∠=∠,∵PQ AP CQ =+,∴PQ QK =,在PBQ △和BKQ 中,BP BK BQ BQ PQ KQ =⎧⎪=⎨⎪=⎩∴()≌PBQ BKQ SSS ,∴PBQ KBQ ∠=∠,∴22360PBQ PBK PBQ ABC ∠+∠=∠+∠=︒,∴()2180360PBQ ADC ∠+︒-∠=︒, ∴1902PBQ ADC ∠=︒+∠. .【点睛】本题考查了全等三角形的判定与性质.在应用全等三角形的判定时,要注意三角形间的公共边和公共角,必要时添加适当辅助线构造三角形.3.(1)EF =BE +DF ;(2)结论EF =BE +DF 仍然成立;(3)此时两舰艇之间的距离是210海里【分析】(1)延长FD 到点G ,使DG=BE .连结AG ,即可证明ABE ≌ADG ,可得AE=AG ,再证明AEF ≌AGF ,可得EF=FG ,即可解题; (2)延长FD 到点G ,使DG=BE .连结AG ,即可证明ABE ≌ADG ,可得AE=AG ,再证明AEF ≌AGF ,可得EF=FG ,即可解题; (3)连接EF ,延长AE 、BF 相交于点C ,然后与(2)同理可证.【详解】解:(1)EF =BE +DF ,证明如下:在ABE 和ADG 中,B ADG AB AD ⎪∠=∠⎨⎪=⎩, ∴ABE ≌ADG (SAS ),∴AE =AG ,∠BAE =∠DAG ,∵∠EAF 12=∠BAD , ∴∠GAF =∠DAG +∠DAF =∠BAE +∠DAF =∠BAD ﹣∠EAF =∠EAF , ∴∠EAF =∠GAF ,在AEF 和GAF 中,AE AG EAF GAF AF AF =⎧⎪∠=∠⎨⎪=⎩,∴AEF ≌AGF (SAS ),∴EF =FG ,∵FG =DG +DF =BE +DF ,∴EF =BE +DF ;故答案为 EF =BE +DF .(2)结论EF =BE +DF 仍然成立;理由:延长FD 到点G .使DG =BE .连结AG ,如图2,在ABE 和ADG 中,DG BE B ADG AB AD =⎧⎪∠=∠⎨⎪=⎩,∴ABE ≌ADG (SAS ),∴AE =AG ,∠BAE =∠DAG ,∵∠EAF 12=∠BAD , ∴∠GAF =∠DAG +∠DAF =∠BAE +∠DAF =∠BAD ﹣∠EAF =∠EAF ,∴∠EAF =∠GAF ,在AEF 和GAF 中,EAF GAF AF AF ⎪∠=∠⎨⎪=⎩, ∴AEF ≌AGF (SAS ),∴EF =FG ,∵FG =DG +DF =BE +DF ,∴EF =BE +DF ;(3)如图3,连接EF ,延长AE 、BF 相交于点C ,∵∠AOB =30°+90°+(90°﹣70°)=140°,∠EOF =70°,∴∠EOF 12=∠AOB , 又∵OA =OB ,∠OAC +∠OBC =(90°﹣30°)+(70°+50°)=180°,∴符合探索延伸中的条件,∴结论EF =AE +BF 成立,即EF =2×(45+60)=210(海里).答:此时两舰艇之间的距离是210海里.【点睛】本题考查了全等三角形的判定以及全等三角形对应边相等的性质,本题中求证△AEF ≌△AGF 是解题的关键.4.2AB AD BE =+,证明见解析【分析】在AB 上截取EF ,使EF=BE ,联结CF .证明()BCE ECF SAS ≌,得到 B BFC ∠=∠,又证明 AFC ADC ≌,得到 AF AD =,最后结论可证了.【详解】证明:在AB 上截取EF ,使EF=BE ,联结CF .CE AB ⊥90BEC FEC ∴∠=∠=︒在BCE 和ECF △BE EF BEC FEC CE CE =⎧⎪∠=∠⎨⎪=⎩()BCE ECF SAS ∴≌ B BFC ∴∠=∠180B D ∠+∠=︒180BFC AFC ∠+∠=︒又D AFC ∴∠=∠AC 平分∠BADFAC DAC ∴∠=∠在AFC △ 和ADC 中AFC D FAC DAC AC AC ∠=∠⎧⎪∠=∠⎨⎪=⎩() AFC ADC AAS ∴≌AF AD ∴=AB AF BE EF =++2AB AD BE ∴=+【点睛】本题考查三角形全等知识的综合应用,关键在于寻找全等的条件,作适当的辅助线加以证明.5.见解析【分析】延长DE 至N ,使得EN PF =,连接CN ,先证明()ADF DCE SAS △≌△,可得AFD DEC ∠=∠,即CFP CEN ∠=∠,再通过证明()CEN CFP SAS △≌△,可得CN CP =,ECN PCF ∠=∠,即可证明NCP是等腰直角三角形,即PN PE NE =+=,从而得证PE PF +=.【详解】证明:如图,延长DE 至N ,使得EN PF =,连接CN ,在正方形ABCD 中, E 、F 分别是BC 、CD 的中点,CE DF ∴=,在ADF 和DCE 中,,90,,AD CD ADF DCE DF CE =⎧⎪∠=∠=︒⎨⎪=⎩()ADF DCE SAS ∴△≌△,AFD DEC ∴∠=∠,CFP CEN ∴∠=∠,在CEN 和CFP 中,,,,CE CF CEN CFP EN PF =⎧⎪∠=∠⎨⎪=⎩()CEN CFP SAS ∴△≌△,CN CP ∴=,ECN PCF ∠=∠,90PCF BCP ∠+∠=︒,90ECN BCP NCP ∴∠+∠=∠=︒,NCP ∴△是等腰直角三角形, 2PN PE NE PC ∴=+=.即2PE PF PC +=.【点睛】本题考查了正方形的性质和全等三角形的综合问题,掌握全等三角形的性质以及判定定理是解题的关键.6.5【分析】如图,在DC 上截取DF DA =,连接EF ,先证明ADE FDE △≌△,得到AE EF =,5A ∠=∠,然后证明CEF CEB △≌△,得到CF BC =,即可求出答案.【详解】解:如图,在DC 上截取DF DA =,连接EF ,DE 是ADC ∠的角平分线,12∠∠∴=,在△ADE 和△FDE 中,,12,,AD DF DE DE =⎧⎪∠=∠⎨⎪=⎩()ADE FDE SAS ∴△≌△,AE EF ∴=,5A ∠=∠,//AD BC ,180A B ∴∠+∠=︒,56180∠+∠=︒,6B ∴∠=∠, CE 是BCD ∠的角平分线,34∴∠=∠,在CEF △和CEB △中,6,34,,B CE CE ∠=∠⎧⎪∠=∠⎨⎪=⎩()CEF CEB AAS ∴△≌△,CF BC ∴=,325CD DF CF AD BC ∴=+=+=+=.【点睛】本题考查了角平分线的性质,平行线的性质,全等三角形的判定和性质,证明ADE FDE △≌△是解题关键.7.(1)见解析;(2)图2:BH DE DH -=;图3:DE BH DH -=【分析】(1)在线段AH 上截取HM=BH ,连接CM ,CD ,证明△DMC ≌△DEC ,即可可得DE=DM 则结论可得;(2)当点D 在线段BA 延长线上时,在BA 的延长线上截取MH=BH ,连接CM ,DC ,由题意可证△BHC ≌△CHM ,可得∠B=∠CMB ,由题意可得∠B=∠AED ,即可证△DMC ≌△DEC ,可得DE=DM ,则可得DH=BH-DE ;当点D 在线段AB 延长线上时,在线段AB 上截取BH=HM ,连接CM ,CD ,由题意可证△BHC ≌△CHM ,可得∠B=∠CMB ,由题意可得∠B=∠AED ,即可证△DMC ≌△DEC ,可得DE=DM ,则可得DE=DH+BH ..【详解】解:(1)证明:在AH 上截取HM BH =,连接CM ,CD .∵CH AB ⊥,HM BH =∴CM BC =.∴B CMB ∠=∠.∵AB AC =∴B ACB ∠=∠.∵//DE BC ,∴ADE B AED ACB ∠=∠=∠=∠,CDE BCD ∠=∠.∴AED BMC ∠=∠.∴DEC DMC ∠=∠.∵BD BC =,∴BDC BCD EDC ∠=∠=∠.∵CD CD =,∴ΔΔCDM CDE ≅.∴DM DE =.∴DE BH DM HM DH +=+=.(2)当点D 在线段BA 延长线上时,DH=BH-DE如图:在BA 的延长线上截取MH=BH ,连接CM ,DC∵AB=AC∠ABC=∠ACB,∵BD=BC,∴∠BDC=∠DCB∵DE∥BC∠E=∠ACB=∠B=∠EDB∵CH=CH,BH=MH,∠BHC=∠CHM∴△BHC≌△CHM∴∠B=∠M∴∠E=∠M∵∠MDC=∠B+∠DCB,∠EDC=∠BDC+∠EDB ∴∠MDC=∠EDC又∵∠E=∠M,DC=CD∴△DEC≌△DMC∴DE=DM∵DH=MH-DM∴DH=BH-DE当点D在线段AB延长线上时,DE=BH+DH如图在线段AB上截取BH=HM,连接CM,CDBH=HM,CH=CH,∠CHB=∠MHC=90°∴△MHC≌△BHC∴∠ABC=∠BMC∵AB=AC∴∠ABC=∠ACB ,∵BD=BC∴∠BDC=∠BCD∵BC ∥DE∴∠BCD=∠CDE ,∠ACB=∠AED∴∠BDC=∠CDE ,∠BMC=∠AED ,且CD=CD∴△CDM ≌△CDE∴DE=DM∵DM=DH+HM∴DE=DH+BH .【点睛】本题考查了三角形综合题,等腰三角形的性质,全等三角形的性质和判定.添加恰当的辅助线证全等是本题的关键.8.见解析【分析】在线段BC 上截取BE =BA ,连接DE .则只需证明CD =CE 即可.结合角度证明∠CDE =∠CED .【详解】证明:在线段BC 上截取BE =BA ,连接DE .∵BD 平分∠ABC ,∴∠ABD =∠EBD 12=∠ABC . 在△ABD 和△EBD 中,BE BA ABD EBD BD BD =⎧⎪∠=∠⎨⎪=⎩,∴△ABD ≌△EBD .(SAS )∴∠BED =∠A =108°,∠ADB =∠EDB .又∵AB =AC ,∠A =108°,∠ACB =∠ABC 12=⨯(180°﹣108°)=36°, ∴∠ABD =∠EBD =18°.∴∠ADB =∠EDB =180°﹣18°﹣108°=54°.∴∠CDE =180°﹣∠ADB ﹣∠EDB=180°﹣54°﹣54°=72°.∴∠DEC =180°﹣∠DEB=180°﹣108°=72°.∴∠CDE =∠DEC .∴CD =CE .∴BC =BE +EC =AB +CD .【点睛】本题考查全等三角形的判定和性质,等腰三角形的判定,添加恰当辅助线是本题的关键. 9.(1)256+;(2)见解析【分析】 (1)构建直角三角形,得出AH 、BH ,然后利用角平分线的性质以及平行四边形的性质,进行等量互换,即可得解;(2)首先在AB 上截取BQ BE =,然后判定DOF EOC ≌△△和AEQ GAF ≌△△,进行等量转换,即可得证.【详解】(1)过点A 作AH BC ⊥于点H ,如图所示:4tan 3B ∠=,5AB =, 4AH ∴=,3BH =DE 平分ADC ∠,12∠∠∴=,AD BC ∵∥,13∠∠∴=23∴∠=∠,5DC EC ∴==,1BE ∴=,2EH ∴=,25AE ∴=256ABE C ∴=△;(2)在AB 上截取BQ BE =,连接EQ ,如图所示:CD CE =,CO DE ⊥,OD DE ∴=①AD BC ∵∥,DFO ECO ∴∠=∠,ADE CED ∠=∠②③由①②③得:DOF EOC ≌△△,DF CE ∴=,又AD BC =,AD DF BC CE ∴-=-,即AF BE =60EAG ∠=︒,60BAE FAG ∴∠+∠=︒,60DFC ∠=︒,60FGA FAG ∴∠+∠=︒,CD=CFBAE FGA ∴∠=∠④又120FAG AQE ∠=∠=︒,EQ AF =⑤⑥由④⑤⑥得:AEQ GAF ≌△△,AQ FG ∴=,又AB CF =,AB AQ CF FG ∴-=-,即BQ CG =,AF CG ∴=.【点睛】此题主要考查利用三角函数值构建直角三角形以及全等三角形的判定与性质,熟练掌握,即可解题.10.(1)见解析;(2)CB=2AB ;(3)23AB k FG = 【分析】(1)利用平行线的性质以及角的等量代换求证即可;(2)在BE 边上取点H ,使BH=AE ,可证明△ABH ≌△DAE ,△ABE ∽△ACB ,利用相似三角形的性质从而得出结论;(3)连接BD 交AC 于点Q ,过点A 作AK ⊥BD 于点K ,得出12AD DK CB DB ==,通过证明△ADK ∽△DBC 得出∠BDC=∠AKD=90°,再证DF=FQ ,设AD=a ,因此有DF=FC=QF=ka ,再利用相似三角形的性质得出AC=3ka ,3AB ka =,1122FG DF ka ==,从而得出答案.【详解】解:(1)∵∠BAD=∠BEC∠BAD=∠BAE+∠EAD∠BEC=∠ABE+BAE∴∠EAD=∠ABE∵AD ∥BC∴∠EAD=∠ACB∴∠ACB=∠ABE(2)在BE 边上取点H ,使BH=AE∵AB=AD∴△ABH ≌△DAE∴∠AHB=∠AED∵∠AHB+∠AHE=180°∠AED+∠DEC=180°∴∠AHE=∠DEC∵∠BEC=2∠DEC∠BEC=∠HAE+∠AHE∴∠AHE=∠HAE∴AE=EH∴BE=2AE∵∠ABE=∠ACB∠BAE=∠CAB∴△ABE ∽△ACB∴EB AE CB AB= ∴CB=2AB ; (3)连接BD 交AC 于点Q ,过点A 作AK ⊥BD 于点K∵AD=AB ∴12DK BD = ∠AKD=90° ∵12AB AD BC == ∴12AD DK CB DB == ∵AD ∥BC∴∠ADK=∠DBC ∴△ADK ∽△DBC ∴∠BDC=∠AKD=90° ∵DF=FC∴∠FDC=∠DFC ∵∠BDC=90°∴∠FDC+∠QDF=90° ∠DQF+∠DCF=90° ∴DF=FQ 设AD=a∴DF=FC=QF=ka ∵AD ∥BC∴∠DAQ=∠QCB ∠ADQ=∠QBC ∴△AQD ∽△CQB ∴12AD QA BC CQ == ∴AQ=ka=QF=CF ∴AC=3ka∵△ABE ∽△ACB ∴AE AB AB AC = ∴3AB ka = 同理△AFD ∽△CFG12DF AF FG FC == ∴1122FG DF ka ==AB FG k=. 【点睛】本题是一道关于相似的综合题目,难度较大,根据题目作出合适的辅助线是解此题的关键,解决此题还需要较强的数形结合的能力以及较强的计算能力.。
八年级数学——截长补短练习题

截长补短一.解答题(共13小题)1.(2016秋•丰宁县期中)如图,在△ABC中,∠A=100°,∠ABC=40°,BD是∠ABC的平分线,延长BD至E,使DE=AD.求证:BC=AB+CE.2.(2016秋•和平区期中)如图,AC平分∠BAD,CE⊥AB于点E,∠B+∠D=180°.求证:AE=AD+BE.∠∠∠∠.3.(2012•海曙区校级模拟)已知梯形ABCD中,AD∥BC,AB=BC=DC,点E、F分别在AD、AB上,且∠∠∠∠=12(1)求证:BF=EF﹣ED;(2)连接AC,若∠B=80°,∠DEC=70°,求∠ACF的度数.4.(2013•重庆模拟)如图,梯形ABCD中,AD∥BC,点E在BC上,AE=BE,且AF⊥AB,连接EF.(1)若EF⊥AF,AF=4,AB=6,求AE的长.(2)若点F是CD的中点,求证:CE=BE﹣AD.5.如图,四边形ABCD中,∠ABC=90°,点E是AB上的点,∠ECD=45°,连接ED,过D作DF⊥BC于F,DF=BC.求证:ED﹣FC=BE.6.如图,在四边形ABCD中,AD∥BC,AB=DC,∠ABC=∠BCD,E为AD中点,连接BE,CE(1)求证:BE=CE;(2)若∠BEC=90°,过点B作BF⊥CD,垂足为点F,交CE于点G,连接DG,求证:BG=DG+CD.7.(2017秋•卢氏县校级月考)如图,在△ABC中,∠B=2∠C,AD是△ABC的角平分线,∠1=∠C,求证:AC=AB+CE.8.如图,四边形ABCD中,∠A=∠B=90°,E是AB的中点,DE平分∠ADC.(1)求证:CE平分∠BCD;(2)求证:AD+BC=CD;(3)若AB=12,CD=13,求S△CDE.9.已知:如图,在正方形ABCD中,AD=AB,∠D=∠ABC=∠BAD=90°,E,F分别为DC,BC边上的点,且∠EAF=45°,连接EF,求证:EF=BF+DE.10.已知如图,在△ABC中,∠B=60°,AD、CE是△ABC的角平分线,并且它们交于点O,(1)求:∠AOC的度数;(2)求证:AC=AE+CD.11.如图,已知AB=AC,∠BAC=60°,∠BDC=120°,求证:AD=BD+CD.12.如图,AD∥BC,EA,EB分别平分∠DAB,∠CBA,CD过点E,求证:AB=AD+BC.∠BDC.求证:AC=BD+CD.13.(2014秋•株洲县期末)如图,已知△ABC中,AB=AC,D是△ABC外一点且∠ABD=60°,∠ADB=90°﹣12截长补短参考答案与试题解析一.解答题(共13小题)1.(2016秋•丰宁县期中)如图,在△ABC中,∠A=100°,∠ABC=40°,BD是∠ABC的平分线,延长BD至E,使DE=AD.求证:BC=AB+CE.【解答】解:在BC上截取BF=AB,连DF,∵BD是∠ABC的平分线,∴∠1=∠2.则在△ABD与△FBD中,{∠∠=∠∠∠1=∠2∠∠=∠∠,∴△ABD≌△FBD(SAS),∴DF=DA=DE,又∵∠A=100°,∠ABC=40°,∴∠ACB=∠ABC=40°,∠DFC=180°﹣∠A=80°,∴∠FDC=60°,∵∠EDC=∠ADB=180°﹣∠ABD﹣∠A=180°﹣20°﹣100°=60°,∴∠FDC=∠EDC,∴△DCE≌△DCF(SAS),∴CE=CF,∴BC=BF+CF=AB+CE,即BC=AB+CE.2.(2016秋•和平区期中)如图,AC平分∠BAD,CE⊥AB于点E,∠B+∠D=180°.求证:AE=AD+BE.【解答】证明:如图,过点C作CF⊥AD交AD的延长线于F,∵AC平分∠BAD,CE⊥AB,∴CE=CF,∵∠B+∠ADC=180°.∠ADC+∠CDF=180°(平角定义),∴∠CDF=∠B,在△CDF和△CBE中,{∠∠∠∠=∠∠∠∠=∠∠∠∠=90°∠∠=∠∠,∴△CDF≌△CBE(AAS),∴DF=BE,在Rt△ACF和Rt△ACE中,{∠∠=∠∠∠∠=∠∠,∴Rt△ACF≌Rt△ACE(HL),∴AE=AF,∵AF=AD+DF,∴AE=AD+BE.3.(2012•海曙区校级模拟)已知梯形ABCD中,AD∥BC,AB=BC=DC,点E、F分别在AD、AB上,且∠∠∠∠=12∠∠∠∠.(1)求证:BF=EF﹣ED;(2)连接AC,若∠B=80°,∠DEC=70°,求∠ACF的度数.【解答】(1)证明:旋转△BCF使BC与CD重合,∵AD∥BC,AB=DC,即梯形ABCD为等腰梯形,∴∠A=∠ADC,∠A+∠ABC=180°,∴∠ADC+∠ABC=180°,由旋转可知:∠ABC=∠CDF′,∴∠ADC+∠CDF′=180°,即∠ADF′为平角,∴A,D,F′共线,∵FC=F′C,EC=EC,∠ECF'=∠BCF+∠DCE=∠ECF,∴△FCE≌△F′CE,∴EF′=EF=DF′+ED,∴BF=EF﹣ED;(2)解:∵AB=BC,∠B=80°,∴∠ACB=50°,由(1)得∠FEC=∠DEC=70°,∴∠ECB=70°,而∠B=∠BCD=80°,∴∠DCE=10°,∴∠BCF=30°,∴∠ACF=∠BCA﹣∠BCF=20°.4.(2013•重庆模拟)如图,梯形ABCD中,AD∥BC,点E在BC上,AE=BE,且AF⊥AB,连接EF.(1)若EF⊥AF,AF=4,AB=6,求AE的长.(2)若点F是CD的中点,求证:CE=BE﹣AD.【解答】解:(1)作EM⊥AB,交AB于点M.∵AE=BE,EM⊥AB,×6=3;∴AM=BM=12∵EF⊥AF,∴∠AME=∠MAF=∠AFE=90°,∴四边形AMEF是矩形,∴EF=AM=3;在Rt△AFE中,AE=√∠∠2+∠∠2=5;(2)延长AF、BC交于点N.∵AD∥EN,∴∠DAF=∠N;∵F是CD的中点,∴DF=FC,∵∠AFD=∠NFC,∴△ADF≌△NCF(AAS),∴AD=CN;∵∠B+∠N=90°,∠BAE+∠EAN=90°,又AE=BE,∠B=∠BAE,∴∠N=∠EAN,AE=EN,∴BE=EN=EC+CN=EC+AD,∴CE=BE﹣AD.5.如图,四边形ABCD 中,∠ABC =90°,点E 是AB 上的点,∠ECD =45°,连接ED ,过D 作DF ⊥BC 于F ,DF =BC .求证:ED ﹣FC =BE .【解答】证明:延长EB 至G ,使BG =CF ,连接CG ,∵DF ⊥BC ,∴∠CBG =∠DFC =90°,在△BCG 和△FDC 中{∠∠=∠∠∠∠∠∠=∠∠∠∠∠∠=∠∠∴△BCG ≌△FDC ,∴CD =CG ,∠1=∠2,∵∠1+∠DCF =90°,∴∠2+∠DCF =90°,∵∠DCE =45°,∴∠ECG =45°,∴∠DCE =∠ECG ,在△DEC 和△EGC 中,{∠∠=∠∠∠∠∠∠=∠∠∠∠∠∠=∠∠∴△DEC ≌△EGC (SAS ),∴ED =EG ,∴ED ﹣FC =BE .6.如图,在四边形ABCD 中,AD ∥BC ,AB =DC ,∠ABC =∠BCD ,E 为AD 中点,连接BE ,CE(1)求证:BE=CE;(2)若∠BEC=90°,过点B作BF⊥CD,垂足为点F,交CE于点G,连接DG,求证:BG=DG+CD.【解答】解:∵等腰梯形ABCD中,AD∥BC,AB=DC,E为AD中点,∴∠BAE=∠CDE,AE=DE,在△BAE与△CDE中,{∠∠=∠∠∠∠∠∠=∠∠∠∠∠∠=∠∠,∴△BAE≌△CDE(SAS),∴BE=CE;(2)延长CD和BE的延长线交于H,∵BF⊥CD,∠BEC=90°,∴∠HEC=90°,∴∠EBF+∠H=∠ECH+∠H=90°,∴∠EBF=∠ECH,在△BEG和△CEH中,{∠∠∠∠=∠∠∠∠∠∠=∠∠∠∠∠∠=∠∠∠∠=90°,∴△BEG≌△CEH(ASA),∴EG=EH,BG=CH=DH+CD,∵△BAE≌△CDE,∴∠AEB=∠GED,∠HED=∠AEB,∴∠GED=∠HED,在△GED和△HED中,{∠∠=∠∠∠∠∠∠=∠∠∠∠∠∠=∠∠,∴△GED≌△HED(SAS),∴DG=DH,∴BG=DG+CD7.(2017秋•卢氏县校级月考)如图,在△ABC中,∠B=2∠C,AD是△ABC的角平分线,∠1=∠C,求证:AC=AB+CE.【解答】证明:∵∠AED=∠1+∠C,∠1=∠C,∴∠AED=2∠C,ED=EC,AC∵∠B=2∠C,∴∠AED=∠B,∵AD是△ABC的角平分线,∴∠DAB=∠DAC,在△DAB和△DAE中,{∠∠=∠∠∠∠∠∠∠∠=∠∠∠∠∠∠=∠∠,∴△DAB≌△DAE,∴AB=AE,BD=DE=EC∴AC=AE+EC=AB+CE.8.如图,四边形ABCD中,∠A=∠B=90°,E是AB的中点,DE平分∠ADC.(1)求证:CE平分∠BCD;(2)求证:AD+BC=CD;(3)若AB=12,CD=13,求S△CDE.【解答】(1)证明:作EM⊥CD垂足为M,∵ED平分∠ADM,EA⊥AD,EM⊥CD,∴AE=EM,∵AE=EB,∴EM=EB,∵EB⊥BC,EM⊥CD,∴EC平分∠BCD.(2)证明:由(1)可知:AE=EM=EB,在RT△DEA和RT△DEM中,{∠∠=∠∠∠∠=∠∠,∴△DEA≌△DEM,∴DA=DM,同理可证:CB=CM∴CD=DM+MC=AD+BC.(3)解:由(1)可知:EM=AE=EB=12AB=6,∵EM⊥CD,CD=13,∴S△EDC=12•DC•EM=12×13×6=39.9.已知:如图,在正方形ABCD中,AD=AB,∠D=∠ABC=∠BAD=90°,E,F分别为DC,BC边上的点,且∠EAF=45°,连接EF,求证:EF=BF+DE.【解答】证明:∵四边形ABCD为正方形,∴AB=AD,∠BAC=∠D=∠ABC=90°,∴把△AED绕点A顺时针旋转90°得到△ABG,如图,∴AG=AE,BG=DE,∠EAG=90°,∠ABG=∠D=90°,∴点G在CB的延长线上,∴BF+BG=GF,∵∠EAF=45°,∴∠GAF=45°,在△AEF和△AGF中,{∠∠=∠∠∠∠∠∠=∠∠∠∠∠∠=∠∠,∴△AEF≌△AGF,∴EF=FG,∴EF=BF+BG=BF+DE.10.已知如图,在△ABC中,∠B=60°,AD、CE是△ABC的角平分线,并且它们交于点O,(1)求:∠AOC的度数;(2)求证:AC=AE+CD.【解答】(1)解:∵∠B =60°,∴∠BAC +∠ACB =180°﹣60°=120°,∵AD 、CE 是△ABC 的角平分线,∴∠OAC +∠OCA =12(∠BAC +∠ACB )=12×120°=60°, 在△AOC 中,∠AOC =180°﹣(∠OAC +∠OCA )=180°﹣60°=120°;(2)证明:如图,在AC 上截取AF =AE ,∵AD 是△ABC 的角平分线,∴∠OAE =∠OAF ,在△AOE 和△AOF 中,{∠∠=∠∠∠∠∠∠=∠∠∠∠∠∠=∠∠,∴△AOE ≌△AOF (SAS ),∴∠AOF =∠AOE ,∵∠AOE =180°﹣∠AOC =180°﹣120°=60°,∴∠AOF =60°,∵∠COF =∠AOC ﹣∠AOF =120°﹣60°=60°,∠COD =∠AOE =60°,∴∠COD =∠COF ,∵CE 是△ABC 的平分线,∴∠OCD =∠OCF ,在△COD 和△COF 中,{∠∠∠∠=∠∠∠∠∠∠=∠∠∠∠∠∠=∠∠∠∠,∴△COD ≌△COF (ASA ),∴CF =CD ,∵AC =AF +CF ,∴AC =AE +CD .11.如图,已知AB =AC ,∠BAC =60°,∠BDC =120°,求证:AD =BD +CD .【解答】解:延长DB ,使BE =CD ,连接AE ,BC ,∵∠BAC +∠ACD +∠BDC +∠ABD =360°,∠BAC =60°,∠BDC =120°,∴∠ABD +∠ACD =180°,∴A ,B ,D ,C 四点共圆,∴∠ACB =∠ADE ,∵∠ABD +∠ABE =180°,∴∠ABE =∠ACD ,∵AB =AC ,∴△ABC 是等边三角形,∴∠ACB =60°,∴∠ADE =60°,在△ABE 和△ACD 中,{∠∠=∠∠∠∠∠∠=∠∠∠∠∠∠=∠∠, ∴△ABE ≌△ACD (SAS ),∴AE =AD ,∴△ADE 是等边三角形,∴AD =DE ,∵DE =BD +BE ,∴AD =BD +CD .12.如图,AD ∥BC ,EA ,EB 分别平分∠DAB ,∠CBA ,CD 过点E ,求证:AB =AD +BC .【解答】解:过E 作EF ∥AD ,交AB 于F ,则∠DAE=∠AEF,∠EBC=∠BEF,∵EA、EB分别平分∠DAB和∠CBA,∴∠EAF=∠AEF,∠EBF=∠BEF,∴AF=EF=FB,又∵EF∥AD∥BC,∴EF是梯形ABCD的中位线,,∴EF=∠∠+∠∠2∴AF+FB=2EF,∴AB=AD+BC.∠BDC.求证:AC=BD+CD.13.(2014秋•株洲县期末)如图,已知△ABC中,AB=AC,D是△ABC外一点且∠ABD=60°,∠ADB=90°﹣12【解答】证明:以AD为轴作△ABD的对称△AB′D(如图),则有B′D=BD,AB′=AB=AC,∠BDC,∠B′=∠ABD=60°,∠ADB′=∠ADB=90°﹣12所以∠ADB′+∠ADB+∠BDC=180°﹣∠BDC+∠BDC=180°,所以C、D、B′在一条直线上,所以△ACB′是等边三角形,所以CA=CB′=CD+DB′=CD+BD.。
截长补短法例题完整

截长补短法例题(可以直接使用,可编辑优秀版资料,欢迎下载)截长补短法例1. 已知,如图1-1,在四边形ABCD 中,BC >AB ,AD =DC ,BD 平分∠ABC .求证:∠BAD +∠BCD =180°.分析:因为平角等于180°,因而应考虑把两个不在一起的通过全等转化成为平角,图中缺少全等的三角形,因而解题的关键在于构造直角三角形,可通过“截长补短法”来实现.证明:过点D 作DE 垂直BA 的延长线于点E ,作DF ⊥BC 于点F ,如图1-2∵BD 平分∠ABC ,∴DE =DF ,在Rt △ADE 与Rt △CDF 中,⎩⎨⎧==CD AD DF DE ∴Rt △ADE ≌Rt △CDF (HL ),∴∠DAE =∠DCF .又∠BAD +∠DAE =180°,∴∠BAD +∠DCF =180°,即∠BAD +∠BCD =180°F E D C B A 图1-2 A B C D图1-1例2. 已知,如图3-1,∠1=∠2,P 为BN 上一点,且PD ⊥BC 于点D ,AB +BC =2BD .求证:∠BAP +∠BCP =180°.分析:与例1相类似,证两个角的和是180°,可把它们移到一起,让它们是邻补角,即证明∠BCP =∠EAP ,因而此题适用“补短”进行全等三角形的构造.证明:过点P 作PE 垂直BA 的延长线于点E ,如图3-2∵∠1=∠2,且PD ⊥BC ,∴PE =PD ,在Rt △BPE 与Rt △BPD 中,⎩⎨⎧==BP BP PD PE ∴Rt △BPE ≌Rt △BPD (HL ),∴BE =BD .∵AB +BC =2BD ,∴AB +BD +DC =BD +BE ,∴AB +DC =BE即DC =BE -AB =AE .在Rt △APE 与Rt △CPD 中,⎪⎩⎪⎨⎧=∠=∠=DC AE PDC PEA PD PEA B C D P 12N图3-1P 12NA B C D E 图3-2AD B CE 图2-1 ∴Rt △APE ≌Rt △CPD (SAS),∴∠PAE =∠PCD又∵∠BAP +∠PAE =180°,∴∠BAP +∠BCP =180°例3. 如图2-1,AD ∥BC ,点E 在线段AB 上,∠ADE =∠CDE ,∠DCE =∠ECB .求证:CD =AD +BC .分析:结论是CD =AD +BC ,可考虑用“截长补短法”中的“截长”,即在CD 上截取CF =CB ,只要再证DF =DA 即可,这就转化为证明两线段相等的问题,从而达到简化问题的目的.证明:在CD 上截取CF =BC ,如图2-2在△FCE 与△BCE 中,⎪⎩⎪⎨⎧=∠=∠=CE CE BCE FCE CB CF∴△FCE ≌△BCE (SAS ),∴∠2=∠1.又∵AD ∥BC ,∴∠ADC +∠BCD =180°,∴∠DCE +∠CDE =90°,∴∠2+∠3=90°,∠1+∠4=90°,∴∠3=∠4. 在△FDE 与△ADE 中,⎪⎩⎪⎨⎧∠=∠=∠=∠43DEDE ADE FDE ∴△FDE ≌△ADE (ASA ),∴DF =DA ,∵CD =DF +CF ,∴CD =AD +BC .例4. 已知:如图4-1,在△ABC 中,∠C =2∠B ,∠1=∠2. 求证:AB =AC +CD .分析:从结论分析,“截长”或“补短”都可实现问题的转化,即延长AC 至E 使CE =CD ,或在AB 上截取AF =AC .证明:方法一(补短法)延长AC 到E ,使DC =CE ,则∠CDE =∠CED ,如图4-2 AD B CEF 1234图2-2D C B A 12图4-1 ED CB A 12图4-2∴∠ACB =2∠E ,∵∠ACB =2∠B ,∴∠B =∠E ,在△ABD 与△AED 中,⎪⎩⎪⎨⎧=∠=∠∠=∠AD AD E B 21∴△ABD ≌△AED (AAS ),∴AB =AE .又AE =AC+CE =AC +DC ,∴AB =AC +DC .方法二(截长法)在AB 上截取AF =AC ,如图4-3在△AFD 与△ACD 中,⎪⎩⎪⎨⎧=∠=∠=AD AD AC AF 21∴△AFD ≌△ACD (SAS ),∴DF =DC ,∠AFD =∠ACD . 又∵∠ACB =2∠B ,∴∠FDB =∠B ,∴FD =FB .∵AB =AF +FB =AC +FD ,∴AB =AC +CD .F D C B A 12图4-3超重和失重 问题超重和失重是两个很重要的物理现象。
初二数学 全全等三角形截长补短练习题及答案

初二数学 全全等三角形截长补短练习题及答案一、全等三角形截长补短1.如图,在ABC 中,AC BC =,AD 平分CAB ∠.(1)如图1,若90ACB =︒,求证:AB AC CD =+;(2)如图2,若AB AC BD =+,求ACB ∠的度数;(3)如图3,若100ACB ∠=︒,求证:AB AD CD =+.2.已知:线段AB 及过点A 的直线l ,如果线段AC 与线段AB 关于直线l 对称,连接BC 交直线l 于点D ,以AC 为边作等边△ACE ,使得点E 在AC 的下方,作射线BE 交直线l 于点F ,连接CF .(1)根据题意将图1补全;(2)如图1,如果∠BAD =α(30°<α<60°).①∠BAE=_______,∠ABE=_______(用含有α代数式表示);②用等式表示线段FA ,FE 与FC 的数量关系,并证明.(3)如图2,如果60°<α<90°,直接写出线段FA ,FE 与FC 的数量关系,不证明.3.如图,在ABC 中,AB AC =,30ABC ∠<︒,D 是边BC 的中点,以AC 为边作等边三角形ACE ,且ACE △与ABC 在直线AC 的异侧,连接BE 交DA 的延长线于点F ,连接FC 交AE 于点M .(1)求证:FB FC =;(2)求证:FEA FCA ∠=∠;(3)若8FE =,2AD =,求AF 的长.4.如图,ABC 中,点D 在AC 边上,且1902BDC ABD ∠=+∠.(1)求证:DB AB =;(2)点E 在BC 边上,连接AE 交BD 于点F ,且AFD ABC ∠=∠,BE CD =,求ACB ∠的度数.(3)在(2)的条件下,若16BC =,ABF 的周长等于30,求AF 的长.5.已知等边三角形ABC ,D 为△ABC 外一点,BDC 120∠=︒,BD=DC ,MDN 60∠=︒,射线DM 与直线AB 相交于点M ,射线DN 与直线AC 相交于点N . (1)当点M 、N 在边AB 、AC 上,且DM=DN 时,直接写出BM 、NC 、MN 之间的数量关系;(2)当点M 、N 在边AB 、AC 上,且DM ≠DN 时,猜想①中的结论还成立吗?若成立,请证明;(3)当点M 、N 在边AB 、CA 的延长线上时,请画出图形,并求出BM 、NC 、MN 之间的数量关系.6.如图,四边形ABCD 为矩形,F 为对角线BD 上一点,过点F 作FE BD ⊥交AD 于点H ,交BA 的延长线于点E ,连接AF ,当FD FE =时,求证:2AH AB AF +=.7.如图,在正方形ABCD 中,点E 、F 均为中点,连接AF 、DE 交于点P ,连接PC ,证明:2PE PF PC +=.8.如图所示,平行四边形ABCD和平行四边形CDEF有公共边CD,边AB和EF在同一条直线上,AC⊥CD且AC=AF,过点A作AH⊥BC交CF于点G,交BC于点H,连接EG.(1)若AE=2,CD=5,则△BCF的面积为;△BCF的周长为;(2)求证:BC=AG+EG.9.如图1,在正方形ABCD中,点P为AD延长线上一点,连接AC、CP,过点C作CF⊥CP 交于C,交AB于点F,过点B作BM⊥CF于点N,交AC于点M.(1)若AP=78AC,BC=4,求S△ACP;(2)若CP﹣BM=2FN,求证:BC=MC;(3)如图2,在其他条件不变的情况下,将“正方形ABCD”改为“矩形ABCD”,且AB≠BC,AC=AP,取CP中点E,连接EB,交AC于点O,猜想:∠AOB与∠ABM之间有何数量关系?请说明理由.10.已知△ABC中,AB=AC,∠A=108°,BD平分∠ABC,求证:BC=AC+CD.【参考答案】***试卷处理标记,请不要删除一、全等三角形截长补短1.(1)见详解;(2)108°;(3)见详解【分析】(1)如图1,过D 作DM ⊥AB 于M ,由 CA =CB ,90ACB =︒,得ABC 是等腰直角三角形,根据角平分线的性质得到CD =MD ,∠ABC =45°,根据全等三角形的性质得到AC =AM ,于是得到结论;(2)如图2,设∠ACB =α,则∠CAB =∠CBA =90°−12α,在AB 上截取AK =AC ,连结DK ,根据角平分线的定义得到∠CAD =∠KAD ,根据全等三角形的性质得到∠ACD =∠AKD =α,根据三角形的内角和即可得到结论;(3)如图3,在AB 上截取AH =AD ,连接DH ,根据等腰三角形的性质得到∠CAB =∠CBA =40°,根据角平分线的定义得到∠HAD =∠CAD =20°,求得∠ADH =∠AHD =80°,在AB 上截取AK =AC ,连接DK ,根据全等三角形的性质得到∠ACB =∠AKD =100°,CD =DK ,根据等腰三角形的性质得到DH =BH ,于是得到结论.【详解】(1)如图1,过D 作DM ⊥AB 于M ,∴在ABC 中,AC BC =,∴∠ABC =45°,∵∠ACB =90°,AD 是角平分线,∴CD =MD ,∴∠BDM =∠ABC =45°,∴BM =DM ,∴BM =CD ,在RT △ADC 和RT △ADM 中,CD MD AD AD ⎧⎨⎩==, ∴RT △ADC ≌RT △ADM (HL ),∴AC =AM ,∴AB =AM +BM =AC +CD ,即AB =AC +CD ;(2)设∠ACB =α,则∠CAB =∠CBA =90°−12α,在AB 上截取AK =AC ,连结DK ,如图2,∵AB =AC +BD ,AB=AK+BK∴BK =BD ,∵AD 是角平分线,∴∠CAD =∠KAD ,在△CAD 和△KAD 中,AC AK CAD KAD AD AD ⎧⎪∠∠⎨⎪⎩=== ∴△CAD ≌△KAD (SAS ),∴∠ACD =∠AKD =α,∴∠BKD =180°−α,∵BK =BD ,∴∠BDK =180°−α,∴在△BDK 中,180°−α+180°−α+90°−12α=180°, ∴α=108°,∴∠ACB =108°;(3)如图3,在AB 上截取AH =AD ,连接DH ,∵∠ACB =100°,AC =BC ,∴∠CAB =∠CBA =40°,∵AD 是角平分线,∴∠HAD =∠CAD =20°,∴∠ADH =∠AHD =80°,在AB 上截取AK =AC ,连接DK ,由(1)得,△CAD ≌△KAD ,∴∠ACB =∠AKD =100°,CD =DK ,∴∠DKH =80°=∠DHK ,∴DK =DH =CD ,∵∠CBA =40°,∴∠BDH =∠DHK -∠CBA =40°,∴DH =BH ,∴BH =CD ,∵AB =AH +BH ,∴AB =AD +CD .【点睛】本题考查了全等三角形的判定和性质,等腰三角形的性质,角平分线的定义,三角形的内角和,正确的作出辅助线是解题的关键.2.(1)作图见解析;(2)①260α-︒,120α︒-;②FA=FC +FE ,证明见解析;(3)AF=FC-EF .【分析】(1)先根据轴对称的性质作出线段AC ,再分别以A 、C 为圆心,AC 长为半径画弧,两弧交于点E ,可得等边△ACE ,最后根据题意画出图形即可;(2)①根据轴对称的性质可得∠BAC=2∠BAD=2α,根据等边三角形的性质可知∠EAC=60°,根据角的和差关系即可表示出∠BAE ;根据轴对称的性质和等边三角形的性质可得AB=AE ,根据等腰三角形的性质及三角形内角和定理即可表示出∠ABE ;②在FA 上截取FG=EF ,连接EG ,利用三角形内角和定理可得∠AFB=60°,即可证明△EFG 是等边三角形,根据角的和差故选可得∠AEG=∠CEF ,利用SAS 可证明△AEG ≌△CEF ,即可得出AG=CF ,根据线段的和差关系即可得结论;(3)由60°<α<90°可知点E 在直线l 右侧,根据题意画出图形,在FA 上截取FG=EF ,根据轴对称的性质可得AF ⊥BC ,BF=CF ,根据(2)中结论可得∠FBC=∠FCB=30°,利用三角形外角性质可得∠GFE=60°,可证明三角形EFG 是等边三角形,利用SAS 可证明△AEF ≌△CEG ,可得FA=CG ,根据线段的和差关系即可得答案.【详解】(1)补全图形如下:(2)①260α-︒,120.α︒-①∵AB 、AC 关于直线l 对称,∴∠BAD=∠CAD ,AB=AC ,∵△ACE 是等边三角形,∴∠EAC=60°,AE=AC=EC ,∵∠BAD=α,∴∠BAC=BAD+∠CAD=2∠BAD=2α,∴∠BAE=∠BAC-∠EAC=2α-60°.∵AB=AC ,AC=AE ,∴AB=AE ,∴∠ABE=12(180°-∠BAE )=120°-α. 故答案为:2α-60°,120°-α②数量关系是FA =FC +FE ,证明如下:在FA 上截取FG=EF ,连接EG ,由①得,∠ABE=120°-α,∠BAD=α,∴∠AFB=180°-∠ABE-∠BAD=60°,∴△EFG 为等边三角形,∴EG=FE=FG ,∠GEF=60°,∵△AEC 是等边三角形,∴∠AEC=60°,AE=CE ,∴∠AEC=∠GEF=60°,∴∠AEC-∠GEC=∠GEF-∠GEC ,即∠AEG=∠CEF ,在△AEG 和△CEF 中,EG EF AEG CEF AE CE =⎧⎪∠=∠⎨⎪=⎩,∴△AEG ≌△CEF ,∴AG=FC∴FA=AG+FG=FC+FE ,(3)AF=FC-EF .∵60°<α<90°,∴如图所示,点E 在直线l 右侧,在FA 上截取FG=EF ,连接EG ,∵AB 、AC 关于直线l 对称,点F 在直线l 上,∴AF ⊥BC ,BF=CF ,∴∠ABC=∠ACB=90°-α,由(2)可知∠ABE=120°-α,∴∠FBC=∠FCB=120°-α-(90°-α)=30°,∴∠EFG=∠FBC+∠FCB=60°,∴△EFG 是等边三角形,∴∠FEG=60°,∵∠AEC=60°,∴∠AEF+∠AEG=∠CEG+∠AEG=60°,∴∠AEF=∠CEG ,在△AEF 和△CEG 中,EF EG AEF CEG AE CE =⎧⎪∠=∠⎨⎪=⎩,∴△AEF ≌△CEG ,∴AF=CG ,∴AF=FC-EF .【点睛】本题考查轴对称的性质、等边三角形的判定与性质及全等三角形的判定与性质,根据轴对称的性质正确得出对应边并熟练掌握相关性质及判定定理是解题关键.3.(1)见解析;(2)见解析;(3)4【分析】(1)利用AD 所在直线是BC 的垂直平分线,点F 在直线AD 上即可得出结论. (2)由ACE △是等边三角形,得AC=AE=AB 推得ABF FEA ∠=∠.易证ABF ≌ACF (SSS ),ABF FCA FEA ∠=∠=∠即可,(3)延长AD 至点P 处,使DP AD ,连接CP .先证直角三角形ADC ≌PDC△(SAS ),推出AC CP CE ==,ACD PCD ∠=∠.再证60EFC EAC ∠=∠=︒.求出,FBD 30FCD ∠=∠=︒.用ACD ∠表示30ECF ACD ∠=︒+∠.而30FCP ACD ∠=︒+∠,得ECF FCP ∠=∠.可证ECF △≌PCF (SAS ),可推得AF EF AP =-即可.【详解】(1)证明:∵AB AC =,D 是边BC 的中点,∴AD 所在直线是BC 的垂直平分线,又∵点F 在直线AD 上∴FB FC =.(2)证明:∵ACE △是等边三角形,∴60EAC ACE ∠=∠=︒,AC AE =.∵AB AC =,∴AB AE =,∴ABF FEA ∠=∠.由(1)可知,FB FC =,又∵AF AF =,AB AC =,∴ABF ≌ACF (SSS ),∴ABF FCA ∠=∠,∴FEA FCA ∠=∠.(3)解:如图,延长AD 至点P 处,使DP AD ,连接CP .∵AB AC =,D 是边BC 的中点,∴90ADC PDC ∠=∠=︒.∵ACE △是等边三角形,∴AC CE =,60EAC ∠=︒.∵AD DP =,ADC PDC ∠=∠,CD CD =,∴ADC ≌PDC △(SAS ),∴AC CP CE ==,ACD PCD ∠=∠.由(2)可知,FEA FCA ∠=∠,∵AMC FME ∠=∠,∴60EFC EAC ∠=∠=︒.由(1)可知,BF CF =,∴()18060260BFD CFD ∠=∠=︒-︒÷=︒,∴906030FCD ∠=︒-︒=︒.∵FCA FCD ACD ∠=∠-∠,∴30FCA ACD ∠=︒-∠.∵ECF ECA FCA ∠=∠-∠,∴()303030ECF ECA ACD ECA ACD ACD ∠=∠-︒-∠=∠-︒+∠=︒+∠. ∵FCP FCD PCD ∠=∠+∠,∴30FCP ACD ∠=︒+∠,∴ECF FCP ∠=∠.∵FC FC =,CE CP =,∴ECF △≌PCF (SAS ),∴FE FP =,∴2FE FA AP AF AD =+=+,∴2822=4AF EF AD =-=-⨯.【点睛】本题考查线段垂直平分线性质,等边三角形性质,三角形全等判定与性质,掌握线段垂直平分线性质,等边三角形性质,三角形全等判定与性质,会利用引辅助线构造三角形全等转化线与线关系,角与角关系来解决问题.4.(1)见解析;(2)ACB ∠=60°;(3)AF =11【分析】(1)根据三角形内角与外角之间的关系建立等式,运用等量代换得出A BDA ∠=∠,证得DB AB =;(2)作CH =BE ,连接DH ,根据角的数量关系证得EAC C ∠=∠,再由三角形全等判定得△BDH ≌△ABE ,最后推出△DCH 为等边三角形,即可得出ACB ∠=60°;(3)借助辅助线AO ⊥CE ,构造直角三角形,并结合平行线构造△BFE ∽△BDH ,建立相应的等量关系式,完成等式变形和求值,即可得出AF 的值.【详解】(1)证明:∵∠BDC =90°+12∠ABD ,∠BDC=∠ABD+∠A , ∴ ∠A =90°-12∠ABD . ∵∠BDC +∠BDA =180°,∴∠BDA =180°-∠BDC =90°-12∠ABD . ∴ ∠A =∠BDA =90°-12∠ABD . ∴DB =AB .解:(2)如图1,作CH =BE ,连接DH ,∵∠AFD=∠ABC,∠AFD=∠ABD+∠BAE,∠ABC=∠ABD+∠DBC,∴∠BAE=∠DBC.∵由(1)知,∠BAD=∠BDA,又∵∠EAC=∠BAD-∠BAE,∠C=∠ADB-∠DBC,∴∠CAE=∠C.∴AE=CE.∵BE=CH,∴BE+EH=CH+EH.即BH=CE=AE.∵AB=BD,∴△BDH≌△ABE.∴BE=DH.∵BE=CD,∴CH=DH=CD.∴△DCH为等边三角形.∴∠ACB =60°.(3)如图2,过点A作AO⊥CE,垂足为O.∵DH∥AE,∴∠CAE=∠CDH=60°,∠AEC=∠DHC=60°.∴△ACE是等边三角形.设AC=CE=AE=x,则BE=16-x,∵DH∥AE,∴△BFE∽△BDH.∴16BF BE EF x BD BH DH x-===. ∴1616x x BF BD AB x x--==, ()21616x x EF DH x x--==. ∵△ABF 的周长等于30,即AB +BF +AF =AB +16x AB x -+x -()216x x-=30, 解得AB =16-8x .在Rt △ACO 中,AC =2x ,AO , ∴BO =16-2x . 在Rt △ABO 中,AO 2+BO 2=AB 2, 即2221616428x x x x ⎛⎫⎛⎫+-=- ⎪ ⎪⎝⎭⎝⎭. 解得10x =(舍去)225621x =. ∴AC =25621. ∴AF =11.【点睛】 本题考查了三角形角的性质、等边三角形的性质与判定以及全等三角形的判定与性质的综合应用,解题的关键是能熟练掌握三角形的性质与全等判定并借助辅助线构造特殊三角形的能力,.5.(1)BM+NC=MN ,证明见解析;(2)成立,证明见解析;(3)NC-BM=MN ,证明见解析.【分析】(1)由DM=DN ,∠MDN=60°,可证得△MDN 是等边三角形,又由△ABC 是等边三角形,CD=BD ,易证得Rt △BDM ≌Rt △CDN ,然后由直角三角形的性质,即可求得BM 、NC 、MN 之间的数量关系 BM+NC=MN ;(2)在CN 的延长线上截取CM 1=BM ,连接DM 1.可证△DBM ≌△DCM 1,即可得DM=DM 1,易证得∠CDN=∠MDN=60°,则可证得△MDN ≌△M 1DN ,然后由全等三角形的性质,即可得结论仍然成立;(3)首先在CN 上截取CM 1=BM ,连接DM 1,可证△DBM ≌△DCM 1,即可得DM=DM 1,然后证得∠CDN=∠MDN=60°,易证得△MDN ≌△M 1DN ,则可得NC-BM=MN .【详解】解(1)BM 、NC 、MN 之间的数量关系:BM+NC=MN .证明如下:∵BD=DC ,DM=DN ,MDN 60∠=︒∴∠BDC=∠DCB=180302BDC ,△MDN 为等边三角形, ∴MN=MD=DN ,∵△ABC 是等边三角形,∴∠ABC=∠ACB=60°,∴∠ABD=∠ACD=90°,∴Rt △BDM ≌Rt △CDN (HL ),∴∠BDM =∠CDN=302BDC MDN , ∴11,22BM DM NC DN , ∴BM+NC=MN . (2)猜想:结论仍然成立.证明:在CN 的反向延长线上截取CM 1=BM ,连接DM 1.∵∠MBD=∠M 1CD=90°,BD=CD ,∴△DBM ≌△DCM 1,∴DM=DM 1,∠MBD=∠M 1CD ,∵∠MDN=60°,∠BDC=120°,∴∠M 1DN=∠MDN=60°,∴△MDN ≌△M 1DN ,∴MN=M1N=M 1C+NC=BM+NC ,(3)证明:在CN 上截取CM 1=BM ,连接DM 1.与(2)同理可证△DBM ≌△DCM 1,∴DM=DM 1,与(2)同理可证∠CDN=∠MDN=60°,∴△MDN ≌△M 1DN ,∴MN=M 1N ,∴NC-BM=MN .【点睛】本题考查了等边三角形,直角三角形,等腰三角形的性质以及全等三角形的判定与性质等知识.此题综合性很强,难度较大,解题的关键是注意数形结合思想的应用与辅助线的作法.6.见解析【分析】过点F 作FN AF ⊥交AB 的延长线于点N ,先证明()EFN DFA ASA △≌△,可得N DAF ∠=∠,FN AF =,从而可以证明()AHF NBF ASA △≌△,可证得AH BN =,即可得证2AH AB +=.【详解】证明:如图,过点F 作FN AF ⊥交AB 的延长线于点N ,EF DF ⊥,EA AD ⊥,90E ABD ∴∠+∠=︒,90ADF ABD ∠+∠=︒,E ADF ∴∠=∠,90AFN EFD ∠=∠=︒,AFD EFN ∴∠=∠,在EFN 和DFA 中,,,,EFN DFA EF DF E ADF ∠=∠⎧⎪=⎨⎪∠=∠⎩()EFN DFA ASA ∴△≌△,N DAF ∴∠=∠,FN AF =,又90AFN ∠=︒, 2AN AF ∴=,90AFN EFB ∠=∠=︒,AFH BFN ∴∠=∠,在AHF △和NBF 中,,,,AFH NFB AF NF HAF N ∠=∠⎧⎪=⎨⎪∠=∠⎩()AHF NBF ASA ∴△≌△,AH BN ∴=,2AH AB BN AB AN AF ∴+=+==.【点睛】本题考查了全等三角形的综合问题,掌握全等三角形的性质以及判定定理是解题的关键. 7.见解析【分析】延长DE 至N ,使得EN PF =,连接CN ,先证明()ADF DCE SAS △≌△,可得AFD DEC ∠=∠,即CFP CEN ∠=∠,再通过证明()CEN CFP SAS △≌△,可得CN CP =,ECN PCF ∠=∠,即可证明NCP 是等腰直角三角形,即2PN PE NE PC =+=,从而得证2PE PF PC +=.【详解】证明:如图,延长DE 至N ,使得EN PF =,连接CN ,在正方形ABCD 中,E 、F 分别是BC 、CD 的中点,CE DF ∴=,在ADF 和DCE 中,,90,,AD CD ADF DCE DF CE =⎧⎪∠=∠=︒⎨⎪=⎩()ADF DCE SAS ∴△≌△,AFD DEC ∴∠=∠,CFP CEN ∴∠=∠,在CEN 和CFP 中,,,,CE CF CEN CFP EN PF =⎧⎪∠=∠⎨⎪=⎩()CEN CFP SAS ∴△≌△,CN CP ∴=,ECN PCF ∠=∠,90PCF BCP ∠+∠=︒,90ECN BCP NCP ∴∠+∠=∠=︒,NCP ∴△是等腰直角三角形, 2PN PE NE PC ∴=+=.即2PE PF PC +=.【点睛】本题考查了正方形的性质和全等三角形的综合问题,掌握全等三角形的性质以及判定定理是解题的关键.8.(1)3,23234+2)见解析【分析】(1)根据平行和垂直的特点求出BF ,AF ,再根据勾股定理求出CD ,根据FP 与BA 的比值求出面积,再根据勾股定理求CF ,BC 即可得到周长.(2)在AD 上截取AM=AG ,连接CM ,证△FAG ≌△CAM ;证△EFG ≌△DCM .【详解】解:(1)面积为3;周长为23234+∵四边形ABCD 和四边形CDEF 都是平行四边形,∴EF=CD ,AB=CD ,AB ∥CD∴EF=AB=CD=5∴AE=EF-AE=5-2=3∴BF=5-3=2过F 作FP ⊥BC则FP :AH=BF :AB=2:5,∴::2:5BCF BCA S S FP AH == ,∵AC ⊥CD ,AB ∥CD,∴AB ⊥AC ,即∠BAC=90°,∵AC=AF=3,∴CF=223332+= ,BC=223534+= ,∴2213552BCF BCA S S CD AC ==⨯⨯= ∴△BCF 的面积为3,△BCF 周长为23234++(2)在AD 上截取AM=AG ,连接CM ,∵四边形ABCD 是平行四边形,∴AD ∥BC ,AD=BC∵AH ⊥BC∴AD ⊥AH∴∠DAH=90°∵∠BAC=90°∴∠DAH=∠BAC∴∠DAH-∠CAH =∠BAC-∠CAH∴∠BAH=∠CAD∵AF=AC∴△FAG ≌△CAM∴FG=CM ,∠ACM=∠AFG∵四边形CDEF 是平行四边形,∴EF ∥CD ,EF=CD ,∴∠DCF+∠AFC=180°,∵AF=AC , ∠BAC=90°,∴∠AFC=∠ACF=45°,∴∠DCF=180°-∠AFC=135°,∴∠ACM=∠AFG=45°,∴∠DCM=∠FCD-∠ACF-∠ACM=45°,∴∠AFG=∠DCM ,∴△EFG ≌△DCM ,∴EG=DM ,∵AD=AM+DM ,∴AD=AG+EG ,∵AD=BC ,∴BC=AG+EG .【点睛】此题考查平行四边形的性质,平行线分线段成比例和勾股定理的应用.9.(1);(2)证明见解析;(3)∠AOB=3∠ABM ,理由见解析.【分析】(1)由正方形的性质得出AB=BC=CD=4,∠ADC=∠CDP=∠ABC=∠BCD=90°,由勾股定理求出AC ,得出AP ,即可求出S △ACP ;(2)在CF 上截取NG=FN ,连接BG ,则CF ﹣CG=2FN ,证出∠BCF=∠DCP ,由ASA 证明△BCF ≌△DCP ,得出CF=CP ,证出CG=BM ,由SAS 证明△ABM ≌△BCG ,得出∠AMB=∠BGC ,因此∠BMC=∠BGF ,由线段垂直平分线的性质得出BF=BG ,得出∠BFG=∠BGF ,因此∠BMC=∠CBM ,即可得出结论;(3)连接AE ,先证出∠BCA=2∠PAE ,再证明A 、D 、E 、C 四点共圆,由圆周角定理得出∠DCP=∠PAE ,得出∠BCF=∠PAE ,证出∠BCA=2∠ABM ,然后由三角形的外角性质即可得出结论.【详解】解:(1)∵四边形ABC 是正方形,∴AD ∥BC ,AB=BC=CD=4,∠ADC=∠CDP=∠ABC=∠BCD=90°,∴,∴AP=78AC=78,∴S△ACP =12AP×CD=12×2; (2)在CF 上截取NG=FN ,连接BG ,如图1所示:则CF ﹣CG=2FN ,∵CF ⊥CP ,∴∠PCF=90°,∴∠BCF=∠DCP ,在△BCF和△DCP中,ABC CDP BC DCBCF DCP∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△BCF≌△DCP(ASA),∴CF=CP,∵CP﹣BM=2FN,∴CG=BM,∵∠ABC=90°,BM⊥CF,∴∠ABM=∠BCG,∠BFG=∠CBM,在△ABM和△BCG中,AB BCABI CBG BM CG=⎧⎪∠=∠⎨⎪=⎩,∴△ABM≌△BCG(SAS),∴∠AMB=∠BGC,∴∠BMC=∠BGF,∵GN=FN,BM⊥CF,∴BF=BG,∴∠BFG=∠BGF,∴∠BMC=∠CBM,∴BC=MC;(3)∠AOB=3∠ABM;理由如下:连接AE,如图2所示:∵AC=AP,E是CP的中点,∴AE⊥CP,∠PAE=∠CAE,∵AD∥BC,∴∠BCA=∠PAC=2∠PAE,∵CF⊥CP,∴∠PCF=90°,∴∠BCF=∠DCP,∵∠ADC=∠AEC=90°,∴A、D、E、C四点共圆,∴∠DCP=∠PAE,∴∠BCF=∠PAE,又∵∠ABM=∠BCF,∴∠ABM=∠BCF=∠PAE,∴∠BCA=2∠ABM,∵∠AOB=∠BCF+∠BCA,∴∠AOB=3∠ABM.【点睛】本题是四边形综合题目,考查了正方形的性质、勾股定理、全等三角形的判定与性质、线段垂直平分线的性质、等腰三角形的判定与性质、四点共圆、圆周角定理等知识;本题综合性强,有一定难度,特别是(2)中,需要通过作辅助线两次证明三角形全等才能得出结论.10.见解析【分析】在线段BC 上截取BE =BA ,连接DE .则只需证明CD =CE 即可.结合角度证明∠CDE =∠CED .【详解】证明:在线段BC 上截取BE =BA ,连接DE .∵BD 平分∠ABC ,∴∠ABD =∠EBD 12=∠ABC . 在△ABD 和△EBD 中,BE BA ABD EBD BD BD =⎧⎪∠=∠⎨⎪=⎩,∴△ABD ≌△EBD .(SAS )∴∠BED =∠A =108°,∠ADB =∠EDB .又∵AB =AC ,∠A =108°,∠ACB =∠ABC 12=⨯(180°﹣108°)=36°, ∴∠ABD =∠EBD =18°.∴∠ADB =∠EDB =180°﹣18°﹣108°=54°.∴∠CDE =180°﹣∠ADB ﹣∠EDB=180°﹣54°﹣54°=72°.∴∠DEC=180°﹣∠DEB=180°﹣108°=72°.∴∠CDE=∠DEC.∴CD=CE.∴BC=BE+EC=AB+CD.【点睛】本题考查全等三角形的判定和性质,等腰三角形的判定,添加恰当辅助线是本题的关键.。
初二数学 全全等三角形截长补短练习题及解析

初二数学 全全等三角形截长补短练习题及解析一、全等三角形截长补短1.阅读与理解:折纸,常常能为证明一个命题提供思路和方法.例如,在ABC 中,AB AC >(如图),怎样证明C B ∠>∠呢?分析:把AC 沿A ∠的角平分线AD 翻折,因为AB AC >,所以,点C 落在AB 上的点C '处,即AC AC '=,据以上操作,易证明ACD AC D '△△≌,所以AC D C '∠=∠,又因为AC D B '∠>∠,所以C B ∠>∠.感悟与应用:(1)如图(a ),在ABC 中,90ACB ∠=︒,30B ∠=︒,CD 平分ACB ∠,试判断AC 和AD 、BC 之间的数量关系,并说明理由;(2)如图(b ),在四边形ABCD 中,AC 平分BAD ∠,16AC =,8AD =,12DC BC ==,①求证:180B D ∠+∠=︒;②求AB 的长.2.如图,已知 B (-1, 0) , C (1, 0) , A 为 y 轴正半轴上一点, AB = AC ,点 D 为第二象限一动点,E 在 BD 的延长线上, CD 交 AB 于 F ,且∠BDC = ∠BAC .(1)求证: ∠ABD = ∠ACD ;(2)求证: AD 平分∠CDE ;(3)若在 D 点运动的过程中,始终有 DC = DA + DB ,在此过程中,∠BAC 的度数是否变化?如果变化,请说明理由;如果不变,请求出∠BAC 的度数?3.阅读材料并完成习题:在数学中,我们会用“截长补短”的方法来构造全等三角形解决问题.请看这个例题:如图1,在四边形ABCD 中,∠BAD=∠BCD=90°,AB=AD ,若AC=2cm ,求四边形ABCD 的面积. 解:延长线段CB 到E ,使得BE=CD ,连接AE ,我们可以证明△BAE ≌△DAC ,根据全等三角形的性质得AE=AC=2, ∠EAB=∠CAD ,则∠EAC=∠EAB+∠BAC=∠DAC+∠BAC=∠BAD=90°,得S 四边形ABCD =S △ABC +S △ADC =S △ABC +S △ABE =S △AEC ,这样,四边形ABCD 的面积就转化为等腰直角三角形EAC 面积.(1)根据上面的思路,我们可以求得四边形ABCD 的面积为 cm 2.(2)请你用上面学到的方法完成下面的习题.如图2,已知FG=FN=HM=GH+MN=2cm ,∠G=∠N=90°,求五边形FGHMN 的面积. 4.(1)方法选择如图①,四边形ABCD 是⊙O 的内接四边形,连接AC ,BD ,AB BC AC ==,求证:BD AD CD =+.小颖认为可用截长法证明:在DB 上截取DM AD =,连接AM ……小军认为可用补短法证明:延长CD 至点N ,使得DN AD =……请你选择一种方法证明.(2)类比探究探究1如图②,四边形ABCD 是⊙O 的内接四边形,连接AC ,BD ,若BC 是⊙O 的直径,AB AC =,试用等式表示线段AD ,BD ,CD 之间的数量关系,并证明你的结论. 探究2如图③,四边形ABCD 是⊙O 的内接四边形,连接AC ,BD .若BC 是⊙O 的直径,::::BC AC AB a b c =,则线段AD ,BD ,CD 之间的等量关系式是______.5.如图,ABC 是边长为2的等边三角形,BDC 是顶角为120°的等腰三角形,以点D 为顶点作60MDN ∠=︒,点M 、N 分别在AB 、AC 上.(1)如图①,当//MN BC 时,则AMN 的周长为______;(2)如图②,求证:BM NC MN +=.6.数学课上,张老师出示了问题:如图1,四边形ABCD 是正方形,点E 是边BC 的中点.∠AEF=90°,且EF 交正方形外角∠DCG 的角平分线CF 于点F ,求证:AE=EF .经过思考,小明展示了一种正确的解题思路:取AB 的中点M ,连接ME ,则AM=EC ,易证△AME ≌△ECF ,所以AE=EF .在此基础上,同学们作了进一步的研究:(1)小颖提出:如图2,如果把“点E 是边BC 的中点”改为“点E 是边BC 上(除B ,C 外)的任意一点”,其它条件不变,那么结论“AE=EF”仍然成立,你认为小颖的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;(2)小华提出:如图3,点E 是BC 的延长线上(除C 点外)的任意一点,其他条件不变,结论“AE=EF”仍然成立.你认为小华的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由.7.如图,在四边形ABCD 中,AB =AD ,∠B =∠D =90°,E 、F 分别是边BC 、CD 上的点,且∠EAF =12∠BAD .求证:EF =BE +FD .8.如图所示,平行四边形ABCD 和平行四边形CDEF 有公共边CD ,边AB 和EF 在同一条直线上,AC ⊥CD 且AC=AF ,过点A 作AH ⊥BC 交CF 于点G ,交BC 于点H ,连接EG .(1)若AE=2,CD=5,则△BCF 的面积为 ;△BCF 的周长为 ;(2)求证:BC=AG+EG .9.已知△ABC 中,AB =AC ,∠A =108°,BD 平分∠ABC ,求证:BC =AC +CD .10.如图1,在ABC ∆中,ACB ∠是直角,60B ∠=︒,AD 、CE 分别是BAC ∠、BCA ∠的平分线,AD 、CE 相交于点F .(1)求出AFC ∠的度数;(2)判断FE 与FD 之间的数量关系并说明理由.(提示:在AC 上截取CG CD =,连接FG .)(3)如图2,在△ABC ∆中,如果ACB ∠不是直角,而(1)中的其它条件不变,试判断线段AE 、CD 与AC 之间的数量关系并说明理由.【参考答案】***试卷处理标记,请不要删除一、全等三角形截长补短1.(1)BC−AC=AD;理由详见解析;(2)①详见解析;②AB=14【分析】(1)在CB上截取CE=CA,连接DE,证△ACD≌△ECD得DE=DA,∠A=∠CED=60°,据此∠CED=2∠CBA,结合∠CED=∠CBA+∠BDE得出∠CBA=∠BDE,即可得DE=BE,进而得出答案;(2)①在AB上截取AM=AD,连接CM,先证△ADC≌△AMC,得到∠D=∠AMC,CD=CM,结合CD=BC知CM=CB,据此得∠B=∠CMB,根据∠CMB+∠CMA=180°可得;②设BN=a,过点C作CN⊥AB于点N,由CB=CM知BN=MN=a,CN2=BC2−BN2=AC2−AN2,可得关于a的方程,解之可得答案.【详解】解:(1)BC−AC=AD.理由如下:如图(a),在CB上截取CE=CA,连接DE,∵CD平分∠ACB,∴∠ACD=∠ECD,又CD=CD,∴△ACD≌△ECD(SAS),∴DE=DA,∠A=∠CED=60°,∴∠CED=2∠CBA,∵∠CED=∠CBA+∠BDE,∴∠CBA=∠BDE,∴DE=BE,∴AD=BE,∵BE=BC−CE=BC−AC,∴BC−AC=AD.(2)①如图(b),在AB上截取AM=AD,连接CM,∵AC平分∠DAB,∴∠DAC=∠MAC,∵AC=AC,∴△ADC≌△AMC(SAS),∴∠D=∠AMC,CD=CM=12,∵CD=BC=12,∴CM=CB,∴∠B=∠CMB,∵∠CMB +∠CMA =180°,∴∠B +∠D =180°;②设BN =a ,过点C 作CN ⊥AB 于点N ,∵CB =CM =12,∴BN =MN =a ,在Rt △BCN 中,2222212CN BC BN a --==,在Rt △ACN 中,2222216(8)CN AC AN a --+==, 则22221216(8)a a --+=,解得:a =3,即BN =MN =3,则AB =8+3+3=14,∴AB=14.【点睛】本题考查了四边形的综合题,以及全等三角形的判定与性质、勾股定理、等腰三角形的判定与性质;本题有一定难度,需要通过作辅助线证明三角形全等才能得出结果. 2.(1)见解析;(2)见解析;(3)∠BAC 的度数不变化.∠BAC=60°.【解析】【分析】(1)根据三角形内角和定理等量代换可得结论;(2)作AM ⊥CD 于点M ,作AN ⊥BE 于点N ,证明△ACM ≌△ABN 即可;(3)用截长补短法在CD 上截取CP=BD ,连接AP ,证明△ABD ≌△ACP ,由全等性质可知△ADP 是等边三角形,易知∠BAC 的度数.【详解】(1)∵∠BDC=∠BAC ,∠DFB=∠AFC ,又∵∠ABD+∠BDC+∠DFB=∠BAC+∠ACD+∠AFC=180°,∴∠ABD=∠ACD ;(2)过点A 作AM ⊥CD 于点M ,作AN ⊥BE 于点N .则∠AMC=∠ANB=90°.∵OB=OC,OA⊥BC,∴AB=AC,∵∠ABD=∠ACD,∴△ACM≌△ABN (AAS)∴AM=AN.∴AD平分∠CDE.(到角的两边距离相等的点在角的平分线上);(3)∠BAC的度数不变化.在CD上截取CP=BD,连接AP.∵CD=AD+BD,AD=PD.∵AB=AC,∠ABD=∠ACD,BD=CP,∴△ABD≌△ACP.∴AD=AP;∠BAD=∠CAP.∴AD=AP=PD,即△ADP是等边三角形,∴∠DAP=60°.∴∠BAC=∠BAP+∠CAP=∠BAP+∠BAD=60°.【点睛】本题考查了三角形的综合,主要考查了三角形内角和定理、全等三角形的证明和性质,等腰等边三角形的性质和判定,采用合适的方法添加辅助线构造全等三角形是解题的关键. 3.(1)2;(2)4【分析】(1)根据题意可直接求等腰直角三角形EAC的面积即可;≌,则有(2)延长MN到K,使NK=GH,连接FK、FH、FM,由(1)易证FGH FNKFK=FH ,因为HM=GH+MN 易证FMK FMH ≌,故可求解. 【详解】(1)由题意知21=22ABC ADC ABC ABE AEC ABCD AC S SS S S S =+=+==四边形, 故答案为2; (2)延长MN 到K ,使NK=GH ,连接FK 、FH 、FM ,如图所示:FG=FN=HM=GH+MN=2cm ,∠G=∠N=90°,∴∠FNK=∠FGH=90°,∴FGH FNK ≌, ∴FH=FK ,又FM=FM ,HM=KM=MN+GH=MN+NK ,∴FMK FMH ≌,∴MK=FN=2cm ,∴12=242FGH HFM MFN FMK FGHMN S SS S S MK FN =++=⨯⋅=五边形. 【点睛】 本题主要考查全等三角形的性质与判定,关键是根据截长补短法及割补法求面积的运用. 4.(1)见解析;(2)①2BD CD =+,见解析,②c a BD CD AD b b=+ 【分析】(1)根据题中所给的截长法或补短法思路解题,利用全等三角形的性质解题即可.(2)探究1 要求AD 、BD 、CD 之间的数量关系,结合(1)中所给方法,在BD 上截取BM CD =,再利用全等三角形及等腰直角三角形的性质进行求解.探究2 要求AD 、BD 、CD 之间的数量关系,以AD 为边构造直角三角形,再利用相似的性质求解. 【详解】(1)截长法 证明:如图①-1,在DB 上截取DM AD =,连接AM , AB BC AC ==,ABC ∴是等边三角形,60ABC ACB BAC ∴∠=∠=∠=︒.60ADB ACB ∴∠=∠=︒,DM AD =,AMD ∴△是等边三角形,60MAD ∴∠=︒,AM AD =.BAM CAD ∴∠=∠,()BAM CAD SAS ∴△≌△,BM CD ∴=,BD DM BM AD CD ∴=+=+;补短法 证明:如图①-2,延长CD 至点N ,使得DN AD =, DAN DNA ∴∠=∠.AB AC BC ==,ABC ∴为等边三角形,60ABC ACB BAC ∠=∠=∠=︒. 60ADB ACB ∴∠=∠=︒,60BDC BAC ∠=∠=︒, 18060ADN BDC ADB ∴∠=︒-∠-∠=︒,ADN ∴为等边三角形,AD AN =,60DAN ∠=︒. BAD CAN ∴∠=∠.在BAD 和CAN △中,AB AC BAD CAN AD AN =⎧⎪∠=∠⎨⎪=⎩,()BAD CAN SAS ∴△≌△,BD CN ∴=,又CN CD DN CD AD =+=+,BD CD AD ∴=+.(2)探究1 解:2BD AD CD =+;证明:如图②,在BD 上截取BM CD =,连接AM , BC 是O 的直径,AB AC =,90BAC ∴∠=︒,45ABC ACB ∠=∠=︒.45ADM ACB ∴∠=∠=︒,在BAM 和CAD 中,,AB AC ABM ACD BM CD =⎧⎪∠=∠⎨⎪=⎩()BAM CAD SAS ∴△≌△,AM AD ∴=,BAM CAD ∠=∠.45AMD ADM ∴∠=∠=︒,90MAD ∠=︒. AMD ∴△是等腰直角三角形,2MD AD ∴=. BD MD BM =+,2BD AD CD ∴=+;探究2 解:c a BD CD AD b b=+. 如图③,过点A 作AM AD ⊥交BD 于点M , BC 是O 的直径,90BAC ∴∠=︒,BAC MAD ∴∠=∠, BAM CAD ∴∠=∠,ABM DCA ∠=∠,BAM CAD ∴△∽△,BM AB c CD AC b ∴==,c BM CD b ∴=, 又ADM ACB ∠=∠,MAD BAC ∠=∠,ADM ACB ∴△∽△,DM BC a AD AC b ∴==,a DM AD b∴=, BD BM MD =+,c a BD CD AD b b∴=+.【点睛】本题是圆的综合题,考查了圆周角定理,全等三角形的判定和性质,相似三角形的判定与性质,等边三角形的判定与性质,等腰直角三角形的判定与性质,正确作出辅助线,熟练运用图形的性质是解题的关键.5.(1)4;(2)见解析【分析】(1)首先证明△BDM ≌△CDN ,进而得出△DMN 是等边三角形,∠BDM=∠CDN=30°,NC=BM=12DM=12MN ,即可解决问题; (2)延长AC 至点E ,使得CE BM =,连接DE ,首先证明BDM CDE △≌△,再证明MDN EDN △≌△,得出MN NE =,进而得出结果即可.【详解】解:(1)∵ABC 是等边三角形,//MN BC ,60AMN ABC ∴∠=∠=︒,60ANM ACB ∠=∠=︒∴AMN 是等边三角形,AM AN ∴=,则BM NC =,∵BDC 是顶角120BDC ∠=︒的等腰三角形,30DBC DCB ∴∠=∠=︒,90DBM DCN ∴∠=∠=︒,在BDM 和CDN △中, ,,,BM CN MBD DCN BD CD =⎧⎪∠=∠⎨⎪=⎩()BDM CDN SAS ∴△≌△,DM DN ∴=,BDM CDN ∠=∠,∵60MDN ∠=︒,∴DMN 是等边三角形,30BDM CDN ∠=∠=︒,1122NC BM DM MN ∴===,MN MB NC ∴=+, ∴AMN 的周长4AB AC =+=.(2)如图,延长AC 至点E ,使得CE BM =,连接DE ,∵ABC 是等边三角形,BDC 是顶角120BDC ∠=︒的等腰三角形,60ABC ACB ∴∠=∠=︒,30DBC DCB ∠=∠=︒,90ABD ACD ∠∴∠==︒,90DCE ∴∠=︒,在BDM 和CDE △中,,,,BD CD MBD ECD BM CE =⎧⎪∠=∠⎨⎪=⎩()BDM CDE SAS ∴△≌△,MD ED ∴=,MDB EDC ∠=∠,120120MDE MDB EDC ∴∠=︒-∠+∠=︒,∵60MDN ∠=︒,60NDE ∴∠=︒,在MDN △和EDN △中,,60,,MD ED MDN NDE DN DN =⎧⎪∠=∠=︒⎨⎪=⎩()MDN EDN SAS ∴△≌△.MN NE ∴=,又∵NE NC CE NC BM =+=+,BM NC MN ∴+=.【点睛】本题考查了全等三角形的判定与性质及等边三角形的性质及等腰三角形的性质,掌握全等三角形的性质与判定,等边三角形及等腰三角形的性质是解题的关键.6.(1)正确.证明见解析;(2)正确.证明见解析.【分析】(1)在AB 上取一点M ,使AM EC =,连接ME ,根据已知条件利用ASA 判定AME ECF ,因为全等三角形的对应边相等,所以AE EF =. (2)在BA 的延长线上取一点N ,使AN CE =,连接NE ,根据已知利用ASA 判定ANE ECF ,因为全等三角形的对应边相等,所以AE EF =. 【详解】 解:(1)正确.证明:在AB 上取一点M ,使AM EC =,连接ME .BM BE ∴=,45BME ∴∠=°,135AME , CF 是外角平分线,45DCF ∴∠=︒,135ECF ∴∠=°,AME ECF ,90AEB BAE ,90AEB CEF ∠+∠=︒, BAE CEF ∴∠=∠, ()AME ECF ASA ,AE EF ∴=.(2)正确.证明:如图示,在BA 的延长线上取一点N ,使AN CE =,连接NE .BN BE ∴=,45N NEC , CF 平分DCG ∠,45FCE ,N ECF ,四边形ABCD 是正方形,//AD BE ∴,DAE BEA ,DAE BEA,即9090NAE CEF,ANE ECF ASA,()∴=.AE EF【点睛】此题主要考查了正方形的性质,角平分线的性质及全等三角形的判定方法,熟悉相关性质是解题的关键.7.证明见解析.【分析】延长EB到G,使BG=DF,连接AG.先说明△ABG≌△ADF,然后利用全等三角形的性质和已知条件证得△AEG≌△AEF,最后再运用全等三角形的性质和线段的和差即可解答.【详解】延长EB到G,使BG=DF,连接AG.∵∠ABG=∠ABC=∠D=90°,AB=AD,∴△ABG≌△ADF.∴AG=AF,∠1=∠2.∠BAD.∴∠1+∠3=∠2+∠3=∠EAF=12∴∠GAE=∠EAF.又∵AE=AE,∴△AEG≌△AEF.∴EG=EF.∵EG=BE+BG.∴EF=BE+FD【点睛】本题考查了全等三角形的判定与性质,做出辅助线构造全等三角形是解答本题的关键.8.(1)3,23234+2)见解析【分析】(1)根据平行和垂直的特点求出BF,AF,再根据勾股定理求出CD,根据FP与BA的比值求出面积,再根据勾股定理求CF,BC即可得到周长.(2)在AD上截取AM=AG,连接CM,证△FAG≌△CAM;证△EFG≌△DCM.【详解】+解:(1)面积为3;周长为23234∵四边形ABCD 和四边形CDEF 都是平行四边形,∴EF=CD ,AB=CD ,AB ∥CD∴EF=AB=CD=5∴AE=EF-AE=5-2=3∴BF=5-3=2过F 作FP ⊥BC则FP :AH=BF :AB=2:5,∴::2:5BCF BCA S S FP AH == ,∵AC ⊥CD ,AB ∥CD,∴AB ⊥AC ,即∠BAC=90°,∵AC=AF=3,∴CF=223332+= ,BC=223534+= ,∴2213552BCF BCA S S CD AC ==⨯⨯= ∴△BCF 的面积为3,△BCF 周长为23234++(2)在AD 上截取AM=AG ,连接CM ,∵四边形ABCD 是平行四边形,∴AD ∥BC ,AD=BC∵AH ⊥BC∴AD ⊥AH∴∠DAH=90°∵∠BAC=90°∴∠DAH=∠BAC∴∠DAH-∠CAH =∠BAC-∠CAH∴∠BAH=∠CAD∵AF=AC∴△FAG ≌△CAM∴FG=CM ,∠ACM=∠AFG∵四边形CDEF 是平行四边形,∴EF ∥CD ,EF=CD ,∴∠DCF+∠AFC=180°,∵AF=AC , ∠BAC=90°,∴∠AFC=∠ACF=45°,∴∠DCF=180°-∠AFC=135°,∴∠ACM=∠AFG=45°,∴∠DCM=∠FCD-∠ACF-∠ACM=45°,∴∠AFG=∠DCM ,∴△EFG ≌△DCM ,∴EG=DM ,∵AD=AM+DM ,∴AD=AG+EG ,∵AD=BC ,∴BC=AG+EG .【点睛】此题考查平行四边形的性质,平行线分线段成比例和勾股定理的应用.9.见解析【分析】在线段BC 上截取BE =BA ,连接DE .则只需证明CD =CE 即可.结合角度证明∠CDE =∠CED .【详解】证明:在线段BC 上截取BE =BA ,连接DE .∵BD 平分∠ABC ,∴∠ABD =∠EBD 12=∠ABC . 在△ABD 和△EBD 中,BE BA ABD EBD BD BD =⎧⎪∠=∠⎨⎪=⎩,∴△ABD ≌△EBD .(SAS )∴∠BED =∠A =108°,∠ADB =∠EDB .又∵AB=AC,∠A=108°,∠ACB=∠ABC12=⨯(180°﹣108°)=36°,∴∠ABD=∠EBD=18°.∴∠ADB=∠EDB=180°﹣18°﹣108°=54°.∴∠CDE=180°﹣∠ADB﹣∠EDB=180°﹣54°﹣54°=72°.∴∠DEC=180°﹣∠DEB=180°﹣108°=72°.∴∠CDE=∠DEC.∴CD=CE.∴BC=BE+EC=AB+CD.【点睛】本题考查全等三角形的判定和性质,等腰三角形的判定,添加恰当辅助线是本题的关键.10.(1)∠AFC=120°;(2)FE与FD之间的数量关系为:DF=EF.理由见解析;(3)AC=AE+CD.理由见解析.【分析】(1)根据三角形的内角和性质只要求出∠FAC,∠ACF即可解决问题;(2)根据在图2的 AC上截取CG=CD,证得△CFG≌△CFD (SAS),得出DF= GF;再根据ASA 证明△AFG≌△AFE,得EF=FG,故得出EF=FD;(3)根据(2) 的证明方法,在图3的AC上截取AG=AE,证得△EAF≌△GAF (SAS)得出∠EFA=∠GFA;再根据ASA证明△FDC≌△FGC,得CD=CG即可解决问题.【详解】(1)解:∵∠ACB=90°,∠B=60°,∴∠BAC=90°﹣60°=30°,∵AD、CE分别是∠BAC、∠BCA的平分线,∴∠FAC=15°,∠FCA=45°,∴∠AFC=180°﹣(∠FAC+∠ACF)=120°(2)解:FE与FD之间的数量关系为:DF=EF.理由:如图2,在AC上截取CG=CD,∵CE是∠BCA的平分线,∴∠DCF=∠GCF,在△CFG 和△CFD 中,CG CD DCF GCF CF CF =⎧⎪∠=∠⎨⎪=⎩,∴△CFG ≌△CFD (SAS ),∴DF =GF .∠CFD =∠CFG由(1)∠AFC =120°得,∴∠CFD =∠CFG =∠AFE =60°,∴∠AFG =60°,又∵∠AFE =∠CFD =60°,∴∠AFE =∠AFG ,在△AFG 和△AFE 中,AFE AFG AF AFEAF GAF ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴△AFG ≌△AFE (ASA ),∴EF =GF ,∴DF =EF ;(3)结论:AC =AE+CD .理由:如图3,在AC 上截取AG =AE ,同(2)可得,△EAF ≌△GAF (SAS ),∴∠EFA =∠GFA ,AG =AE∵∠BAC+∠BCA=180°-∠B=180°-60°=120°∴∠AFC =180°﹣(∠FAC+∠FCA)=180°-12(∠BAC+∠BCA)=180°-12×120°=120°, ∴∠EFA =∠GFA =180°﹣120°=60°=∠DFC ,∴∠CFG =∠CFD =60°,同(2)可得,△FDC ≌△FGC (ASA ),∴CD =CG ,∴AC =AG+CG =AE+CD .【点睛】本题考查了全等三角形的判定和性质的运用,全等三角形的判定和性质是证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件,要注意三角形间的公共边和公共角,必要时添加适当辅助线构造全等三角形.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
因式分解易错点新解
在分解因式时,应注意观察题目本身的特点,灵活选择恰当的方法,正确熟练地进行因式分解,采用“一提二套三查”法,即:首先看它是否有公因式,有公因式的要先提取公因式,再看这个多项式是几项式,若是二项式,就考虑能否运用平方差公式分解因式;若是三项式,就考虑能否运用完全平方公式分解因式,同时,在分解因式时,一定要分解到每一个因式都不能再分解为止。
然而同学们在实际运用中总是存在一定的错误,为了更好的帮助同学们理解因式分解,我将从几个易错点入手带领大家走出误区。
易错点一:用提公因式法分解因式时易漏项
易错点导析:运用提公因式法分解因式,当多项式的某一项和公因式相同时,提取公因式后剩余的项为1,而部分初学者却让1“不翼而飞”了。
例如:28422(42)a b ab a a ab b -+=-,原多项式中有三项,但提取公因式后另一个因式仅有两项了,这是错误的,正确的是:28422(421)a b ab a a ab b -+=-+,为避免这种错误,可以用整式的乘法进行检验。
【例】分解因式:2212246a b ab ab -+
错解:22122466(24)12(2)a b ab ab ab a b ab a b -+=-=-
错解分析:此题中的公因式为6ab ,提公因式后,漏掉了为1的项,注意用整式的乘法进行检验,就可避免此类错误。
正解:22122466(241)a b ab ab ab a b -+=-+
易错点2:运用完全平方公式时漏解出错
易错点导析:我们知道,完全平方公式有两个,两数和的完全平方和两数差的完全平方,二者不能互相代替,有的同学对完全平方公式的特点把握不准,因而在解答相关题目时出现漏解错误,只有正确理解完全平方公式,熟记完全平方公式的结构特点,才能有效避免这类错误。
【例】若
21364y ay ++是完全平方公式,求a 的值。
错解:2221136()642y ay y ay ++=++,所以1262ay y =⨯⨯,即12662a =⨯⨯=
错误分析:本题的错误之处是漏掉了a 为负数的情况。
正解:因为
2221136()642y ay y ay ++=++,所以1262ay y =±⨯⨯,即12662a =±⨯⨯=±
易错点3:提公因式时易出现符号错误
易错点导析:当多项式第一项的系数是负数时,通常先提取“-”号,使括号内第一项的系数变为正数,同时多项式的各项都要变号,再将多项式提公因式进行分解因式,按上述两个步骤进行,一般不会出错,但当同学们对分解因式较熟练之后会直接取负公因式,这样虽然可以使运算量减少,一步就可以达到分解因式的目的,但由于既需要考虑符号的变化,又需要考虑公因式的确定,因此很多同学往往只注重了公因式的确定而忽略了符号的变化出现错误,避免错误的方法是先提取“-”号,再确定括号内多项式的公因式。
【例】分解因式:3251015a a a -+-
错解:322510155(23)a a a a a a -+-=-+-
易错分析:本题的错误之处是提取负公因式手,括号内的多项式只有第一项变号,而其余两项没有变号,由于公因式含有“-”号,故多项式中的每一项都应改变符号。
正解:322510155(23)a a a a a a -+-=--+
易错点4:分解因式不彻底,半途而废
易错点导析:分解因式时必须进行到每一个因式都不能再分解为止,否则会“半途而废”。
例如:442222()()x y x y x y -=+-,其中因式22x y -还可以继续分解,正确的应是44222222()()()()()x y x y x y x y x y x y -=+-=++-。
在进行因式分解时,能分解的因式而没有进行因式分解是初学者易犯的通病,应当注意,结果要彻底是指:(1)其中一个因式能继续分解因式的,必须继续分解;(2)因式中带有中括号,必须去掉中括号,有同类项的要合并同类项,把每一个因式化为最简因式,使结果只含有小括号。
【例】分解因式:2232()2()()n m n m m n m n +++++
错解: []22322()2()()()22()n m n m m n m n m n n m m n +++++=++++
22
()(22)()(33)m n n m m n m n m n =++++=++错解分析:本题的错误之处是分解不彻底,其中因式33m n +还可以再分解为3()m n +
正解:[]22322()2()()()22()n m n m m n m n m n n m m n +++++=++++ 22()(22)3()()m n n m m n m n m n =++++=++
总之,因式分解的错误原因很多,要认真审题,牢记分解方法,并能灵活运用,以下口诀同学们在分解过程中不妨试一试,方能避免错误:
因式分解并不难,分解方法要记全;各项若有公因式,首先提取莫迟缓; 各项若无公因式,乘法公式看一看; 以上方法若不行,分组分解做试验; 因式分解若不完,继续分解到完全。
