河北省邢台市第一中学高一直升班上学期期末数学试题(解析版)
河北省邢台市第一中学2019_2020学年高一数学上学期第一次月考试题(直升班,含解析)

河北省邢台市第一中学2019-2020学年高一数学上学期第一次月考试题(直升班,含解析)一、选择题;(每小题5分,共60分) 1.不等式021x x ≤-+的解集是 ( ) A. (1)(12]-∞--U ,, B. [12]-, C. (1)[2)-∞-+∞U ,, D. (12]-, 【答案】D 【解析】 【分析】将“不等式21x x -+≤0”转化为“不等式组()()12010x x x ⎧+-≤⎨+≠⎩”,由一元二次不等式的解法求解.【详解】依题意,不等式化为()()12010x x x ⎧+-≤⎨+≠⎩,解得﹣1<x≤2, 故选D .【点睛】本题主要考查不等式的解法,关键是将分式不等式转化为二次不等式来求解 2. 在实数范围内,下列命题正确的是( ) A. 若,a b >则1ba< B. 若,a b c d ><,则a c b d +>+ C. 若a b >,则lg()0a b -> D. 若0,ab a b >>,则11a b< 【答案】D 【解析】解:A 选项中,不符合不等式的性质,因此错误.当a<0不成立. B 选项中,只有同向不等式可以相加,因此结果为a d b c +>+,因此错误 选项C 中,当a-b>1时,对数值大于零,因此错误.只有D 成立. 3.若,则1x+1y 的最小值为( ).A.120 B.15C.12D. 2【解析】 试题分析:,,,(当且仅当).考点:对数的运算、基本不等式. 4.下列结论正确的是( ) A. 当0x >且1x ≠时,1lg 2lg x x+≥ B. 当0x >时2x x≥ C. 当2x ≥时,1x x+的最小值是2 D. 当02x <≤时,1x x-无最大值 【答案】B 【解析】 【分析】利用基本不等式的性质、函数的单调性即可得出. 【详解】解:A .当1>x >0时,lgx <0,lgx 1lgx+≥2不成立; B .当0x >时2x x≥,正确; C .当x ≥2时,x 1x+>2,不成立; D .当0<x ≤2时,函数y =x 1x -单调递增,当x =2时,有最大值21322-=,不正确. 故选B .考点:基本不等式.5.已知正项数列{a n }满足a 1=2,a 2=1,且11n n n n a aa a +-+=2,则a 12的值为( ) A.16B. 6C.13D. 3【答案】A 【解析】首项将112n n n n a a a a +-+=变形为11112n n n a a a +-+=,通过等差中项的性质即可判定1{}na 是以首项12,公差12的等差数列.再利用等差数列的通项公式即可得出12a 的值. 【详解】因为112n n n n a a a a +-+=,所以11112n n na a a +-+=. 所以1{}n a 是以首项1112=a ,公差211112a a -=的等差数列. 所以11(1)2221n n n a =+-=. 即2n a n =,1216a =. 故选:A【点睛】本题主要考查等差数列的性质,通过等差中项判定数列为等差数列是解题的关键,属于中档题.6.已知等差数列{}n a 的公差0d <,若462824,10a a a a =+=,则该数列的前n 项和n S 的最大值为( ) A. 50 B. 45C. 40D. 35【答案】B 【解析】试题分析:284610a a a a +=+=,又4624a a =,0d <,所以466,4a a ==,所以19,1a d ==-,所以100,10n a n n =-+≥≤,故前9或10项的和最大,91989452S a d ⨯=+=. 考点:等差数列.7.在等差数列{a n }中,若a 1+a 4+a 7=39,a 2+a 5+a 8=33,则a 3+a 6+a 9的值为( ) A. 30 B. 27C. 24D. 21【答案】B 【解析】 【分析】首先由等差中项的性质知:413a =,511a =,因为54d a a =-,36963a a a a ++=,再计算6a 带入即可.【详解】因为1474339a a a a ++==,所以413a =. 因为2585333a a a a ++==,所以511a =. 所以542d a a =-=-.659a d a =+=3696327a a a a ++==.故选:B【点睛】本题主要考查等差数列的性质,数列掌握等差中项的性质为解题的关键,属于简单题.8.在ABC ∆中,a x =2b =,45B ∠=o .若该三角形有两个解,则x 的取值范围是A. 2x >B. 02x <<C. 2x <<D.2x <<【答案】C 【解析】试题分析:由AC=b=2,要使三角形有两解,就是要使以C 为圆心,半径为2的圆与BA 有两个交点,当A=90°时,圆与AB 相切;当A=45°时交于B 点,也就是只有一解,∴45°<A <90°,sin 1A <<,由正弦定理以及asinB=bsinA .可得:a=x=,∵(A ∈.∴x 的取值范围是2x <<考点:正弦定理解三角形9.设函数())f n n =,()ln(g n n =,则()f n 与()g n 的大小关系是( ) A. ()()f n g n >B. ()()f n g n <C. ()()f n g n ≥D.()()f n g n ≤【答案】B 【解析】 【分析】n 和n 不相等,所以()()f n g n ≠,再将1n =带入()f n 和()g n 即可比较大小.n 和n ()()f n g n ≠.令1n =,())1)ln10f n n ==<=,()ln(ln10g n n ===.所以()()f n g n <. 故选:B【点睛】本题主要考查对数函数的性质和应用,利用特值法为解题的关键,属于中档题. 10. 如果把直角三角形的三边都增加同样的长度,则这个新的三角形的形状为 ( ) A. 锐角三角形 B. 直角三角形C. 钝角三角形D. 由增加的长度决定 【答案】A 【解析】试题分析:不妨设ABC ∆为直角三角形,90C =o ,则222+=a b c ,设三边增加的长度为()0m m >,则新三角形A B C '''∆的三边长度分别为,,a m b m c m +++,则()()()()()222cos 2a m b m c m C a m b m '+++-+=++,而()()()()222220a m b m c m a b c m m +++-+=+-+>,所以cos 0C '>,因此新三角形为锐角三角形. 考点:余弦定理.【此处有视频,请去附件查看】11.已知函数()()633,7;,7x a x x f x a x -⎧--≤=⎨⎩>,数列{}n a 满足()()n a f n n N +=∈,且{}n a 是递增数列.则实数a 的取值范围是( ). A. 9,34⎛⎫ ⎪⎝⎭B. 9,34⎡⎤⎢⎥⎣⎦C. ()1,3D. ()2,3【答案】D 【解析】【详解】由{}n a 是递增数列得30,1 3.1a a a ><<>-⎧⇒⎨⎩又由()()78f f <,得()2733.a a --<解得9 2.a a -<或>故实数a 的取值范围是()2,3.12.设数列{a n }满足a 1=0且111n n a a +-=--,bn ={b n }的前n 项和为T n ,则T 2019的值是( )A. 1C. 1D.12【答案】C 【解析】 【分析】首先根据111n na a +-=--得到数列1{}1n a -是以首项为1,公差为1的等差数列,就可以求出1n n a n-=,再把1n a +带入n b 求出通项公式,最后利用裂项法即可求出2019T .【详解】因为111n na a +-=--,所以111111n n a a +-=-- 所以数列1{}1na -是以首项为1,公差为1的等差数列.所以11(1)1nn n a =+-=-. 所以1n n a n-=. n b ===,2019(1T =++……1+=-故选:C【点睛】本题主要考查了等差数列的证明,同时考查了裂项法求和,属于中档题. 二、填空题:(每小题5分,共20分)13.已知ABC ∆的一个内角为120o ,并且三边长构成公差为4的等差数列,则ABC ∆的面积为_______________.【答案】【解析】【详解】试题分析:设三角形的三边长为a-4,b=a,c=a+4,(a<b<c),根据题意可知三边长构成公差为4的等差数列,可知a+c=2b ,C=1200,,则由余弦定理,c 2= a 2+ b 2-2abcosC ,10a ∴=,∴ 三边长为6,10,14,,b 2= a 2+ c 2-2accosB,即14(a+c )2=a 2+c 2-2accosB, cosB=1114,可知S=11sin 61422ac B =⨯⨯==考点:本试题主要考查了等差数列与解三角形的面积的求解的综合运用.点评:解决该试题的关键是利用余弦定理来求解,以及边角关系的运用,正弦面积公式来求解.巧设变量a-4,a,a+4会简化运算. 14.已知等差数列{a n }的前n 项和为S n ,且4813S S =,那么816S S =_____. 【答案】310【解析】【分析】 首先根据4813S S =,设4S k =,8=3S k ,再根据等差数列的性质得到4S ,84S S -,128S S -,1612S S -构成等差数列,计算出16S 即可求出答案.【详解】设4S k =,8=3S k ,由等差数列的性质得:4S ,84S S -,128S S -,1612S S -构成等差数列.所以842S S k -=,1283S S k -=,16124S S k -=. 所以126S k =,1610S k =.816310S S =. 故答案为:310【点睛】本题主要考查等差数列的性质,熟练掌握n S ,2n n S S -,32n n S S -,……,构成等差数列为解题的关键,属于中档题.15.在锐角△ABC 中,角A 、B 、C 所对的边分别为a 、b 、c ,且a2+b 2=1,c =1,a ﹣b 的取值范围为_____.【答案】1( 【解析】 【分析】根据221a b +=,1c =,由余弦定理知6C π=,再根据正弦定理得到2sin a A =,2sin b B =,2sin()6b A π+=-,最后利用三角函数的性质就可求出相应的范围.【详解】因为221a b +=,1c =,所以222a b c +-=.222cos 222a b c C ab ab +-===. 因为02C <<π,所以6C π=.又因为12sin sin sin 6a b A B π===, 所以2sin a A =,2sin b B =,56B A π=-.2sin b A B -=-52sin()6A A π=--552(sin cos cos sin )66A A A ππ=--cos 2sin()6A A A π=-=-.因为025062A A πππ⎧<<⎪⎪⎨⎪<-<⎪⎩,所以32A ππ<<.663A πππ<-<,1sin()262A π<-<b -∈. 故答案:【点睛】本题主要考查正弦定理和余弦定义的应用,同时考查了三角函数的值域问题,属于中档题.16.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,且满足4bsinA =,若a ,b ,c成等差数列,且公差大于0,则cosA ﹣cosC 的值为_____.【解析】 【分析】首先4sin b A =,通过正弦定理可求出sin B 的值,又根据a ,b ,c 成等差数列,且公差大于0,得到3cos 4B =和sin sin 2A C +=.设cos cos A C m -=,平方相交化简即可求出答案.【详解】因为4sin b A =,由正弦定理得:4sin sin B A A =.因为sin 0A ≠,所以sin B =. 又因为a ,b ,c 成等差数列,且公差大于0, 所以2b a c =+,A B C <<. 所以B 是锐角,.sin sin 2sin A C B +==. 设cos cos 0A C m -=>.2222(cos cos )cos cos 2cos cos A C A C A C m -=+-=①,2227(sin sin )sin sin 2sin sin 4A C A C A C +=++=②, ①+②得:2722cos cos 2sin sin 4A C A C m -+=+2722cos()4A C m -+=+,2722cos 4B m +=+因为3cos 4B =,所以274m =,m =.【点睛】本题主要考查了正弦定理,同时考查了三角函数的两角和差公式和同角的三角函数关系,属于中档题.三、解答题:(本大题共6小题,共70分)17.设锐角ABC ∆的内角,,A B C 的对边分别为,,a b c 2sin b A =. (Ⅰ)求B 的大小;(Ⅱ)若ABC ∆2c =,求a 和b 的值. 【答案】(1)3π;(2)2,2. 【解析】本试题主要是考查了解三角形的运用.解:(Ⅰ)解:2sin 2sin sin sin 2(0,)23b A A B A B B B ππ==∴=∈∴=Q ........ 4分(Ⅱ)2221sin 222cos 42S ac B a b a c ac B b =====∴=+-=∴= ................................................ 10分 18.已知不等式ax 2﹣3x +2>0的解集为{x |x <1或x >b } (1)求a 、b ;(2)解关于x 的不等式ax 2+(ac +b )x +bc <0. 【答案】(1)2,(2)见解析 【解析】 【分析】(1)由题知1,b 是方程2320ax x -+=的根,利用根系关系即可求出a ,b 的值. (2)由(1)知不等式为2(2)20x c x c +++>,讨论c -和2-的大小,写出对应的解集即可.【详解】(1)由题意知0a >且1,b 是方程2320ax x -+=的根,所以312b a b a ⎧+=⎪⎪⎨⎪=⎪⎩,解得1a =,2b =.(2)不等式可化为2(2)20x c x c +++>,即()(2)0x c x ++>. 当2c -<-,即2>c 时,不等式的解集为{|2}x c x -<<-, 当2c -=-,即2c =时,不等式的解集为{|2}x x ≠-, 当2c ->-,即2c <时,不等式的解集为{|2}x x c -<<-.【点睛】本题第一问考查不等式的解法,第二问考查含参不等式的解法,分类讨论为解题的关键,属于中档题.19.已知正项等差数列{a n }的前n 项和为S n ,且满足a 1+a 513=a 32,S 7=56.(1)求数列{a n }的通项公式a n ;(2)若数列{b n }满足b 1=a 1且b n +1﹣b n =a n +1,求数列{b n }的通项公式. 【答案】(1)a n =2n ,n ∈N *.(2)b n =n 2+n ,n ∈N *. 【解析】 【分析】(1)根据已知215313a a a +=,756S =可求出36a =和48a =,再求出公差,即可求出通项公式.【详解】(1)由题意,数列{}n a 是等差数列且215313a a a +=, 即233123a a =, 因为0n a >, 所以36a =. 又因为1747477275622a a a S a +⋅====(), 所以48a =,公差432d a a =-=.所以数列{}n a 的通项公式3(3)62(3)2n a a n d n n =+-=+-=,*n N ∈. (2)根据(1),有112b a ==,112(1)n n n b b a n ++-==+. 所以2122b b -=⨯,3223b b -=⨯,……12n n b b n --=各式左右分别相加,可得:12223n b b -=⨯+⨯+……2n +⨯.所以22223n b =+⨯+⨯+…2n +⨯2(123=+++……2(1))22n n n n n ++==+. 数列{}n b 的通项公式为2n b n n =+,*n N ∈.【点睛】本题第一问考查等差数列的性质和求和公式,第二问考查了叠加法求数列通项公式,属于中档题.20.某投资商到邢台市高开区投资72万元建起一座汽车零件加工厂,第一年各种经费12万元,以后每年增加4万元,每年的产品销售收入50万元.(Ⅰ)若扣除投资及各种费用,则该投资商从第几年起开始获取纯利润?(Ⅱ)若干年后,该投资商为投资新项目,需处理该工厂,现有以下两种处理方案:① 年平均利润最大时,以48万元出售该厂; ② 纯利润总和最大时,以16万元出售该厂. 你认为以上哪种方案最合算?并说明理由.【答案】(1)从第3年起;(2)两种方案获利都是144万元,但方案①只需要6年,而方案②需要10年,所以选择方案①最合算. 【解析】本试题主要考查了函数在实际生活中的运用.解:由题意知,每年的经费是以12为首项、4为公差的等差数列,设纯利润与年数的关系为()f n ,则()()215012472240722n n f n n n n n ⎡⎤-=-+⨯-=-+-⎢⎥⎣⎦. ………………3分(Ⅰ)令()0f n >,即2240720n n -+->,解得218n <<.由*n N ∈可知,该工厂从第3年起开始获得纯利润; …………………………5分(Ⅱ)按方案①:年平均利润为()3636402()402216f n n n nn n=-+≤-⨯⨯=,当且仅当36n n=,即6n =时取等号,故按方案①共获利61648144⨯+=万元,此时6n =; ………………………………8分按方案②:()()2224072210128f n n n n =-+-=--+,当10n =时,,故按方案②共获利万元,此时10n =.比较以上两种方案,两种方案获利都144万元,但方案①只需要6年,而方案②需要10年,所以选择方案①最合算. ………………………………12分21.在锐角△ABC 中,222b a c cos A C ac sinAcosA--+=(). (1)求角A ;(2)若a =sinB +cos (712π-C )取得最大值时,求B 和b . 【答案】(1)4π(2)B 3π=,b =【解析】 【分析】(1)利用余弦定理化简222cos sin cos b a c A C ac A A--+=()即可求出sin 21A =,再根据三角函数的性质即可求出角A . (2)首先将7sin cos()12B C π+-)6B π+,再根据角B的范围即可求出最大值和角B ,最后利用正弦定理即可求出b 的值.【详解】(1)因为222cos sin cos b a c A C ac A A --+=(), 所以2222cos 2si c )n os a c b A C ac A A-++=-((). 由余弦定理可得cos 2cos sin cos BB A A--=,因为ABC V 是锐角三角形,所以cos 0B >. 所以2sin cos 1A A =,sin 21A =. 所以22A π=,4A π=.(2)由(1)知34B C π+=,34B C π=-. 所以7sin cos()sin cos()126B C B B ππ+-=+- sin cos cos sin sin66B B B ππ=++3sin )26B B B π=+=+. 因为3042B ππ<-<,02B π<<, 所以42B ππ<<,521263B πππ<+<.所以当62B ππ+=,即3B π=)6B π+即3B π=时,7sin cos()12B C π+-由正弦定理可得sin sin b aB A=,sin sin a B b A ===【点睛】本题主要考查正弦定理和余弦定理的应用,同时考查了三角函数的化简和三角函数的最值问题,属于中档题.22.设正数列{}n a 的前{}n a 项和为n,且1n a =+. (1)求数列{}n a 的通项公式.(2)若数列32n n a b +=,设n T 为数列11n n b b +⎧⎫⎨⎬⎩⎭的前n 项的和,求n T .(3)若1n n T b λ+≤对一切*N n ∈恒成立,求实数λ的最小值. 【答案】(1)21n a n =-(2)24nn +(3)116【解析】分析:(1)利用,n n S a 的关系,求解n a (2)裂项相消求解n T(3)分离变量转化为求1nn T b +的最值.详解::(1)∵正数列{}n a 的前n 项和为n S,且1n a =+,∴111n n n n S S a S --=+=+,∴)211n S -=,1=,∵11a =,解得11a =,11n n =+-=,∴2n S n =,∴()221121n n n a S S n n n -=-=--=-,当1n =时,1211n a -==,∴21n a n =-. (2)3213122n n a n b n +-+===+, ∴()()111111212n n b b n n n n +==-++++, ∴1111123341n T n =-+-++-+L 11122224n n n n =-=+++ (3)1n n T b λ+≤对一切*N n ∈恒成立, ∴()224nn n λ≤++,∴()211422444n n n n n λ≥=++++116≥= 当且仅当2n =时取等号,故实数λ的最小值为116点睛:11n 1n 2n nn S a S S -=⎧=⎨-≥⎩,,,一定要注意,当n 1=时要验证是否满足数列.求分式结构11n n b b +,数列n b 为等差数列的前n 项和,用裂项相消.。
2022-2023学年河北省邢台市高一上册期末数学模拟试题(含解析)

当
log2
x 1
2得
x
5或
5 4
,则 2
x4
5,
由题知, log2 x3 1 log2 x4 1 0 ,故 x3 1 x4 1 1 ,
所以
x3
1 x4 1
1
,
故
x1
x2
x3
x4
2
1 1 x4 1
x4
1 x4 1
x4
1
,
因为1 x4 1 4 ,
设 t x4 1,则由对勾函数的性质可知,
x,
∴ y g 9 x2 log1 9 x2 ,
2
由 9 x2 0 ,解得 3 x 3 ,
所以 y g 9 x2 log1 9 x2 的定义域为 3,3 ,
2
令 u 9 x2 , 3 x 3 ,
u 9 x2 在 3, 0 上单调递增,在 0, 3 上单调递减, 又 y log1 u 在 0, 上单调递减,
1 y
的最小值为
4,由于不等式的恒成立关系可得
m2
3m
4
,解一元二
次不等式即可.
【详解】因为
1 x
1 y
1 x
1 y
x
y
2
y x
x y
2
2
y x 4, xy
当且仅当 y x ,即 x y 1 时取得等号,
xy
2
因为
1 x
1 y
m2
3m
恒成立,所以
m2
3m
4,
解得 1 m 4 ,
故选:BCD.
x1 x2 x3 x4 ,则 x1 x2 x3 x4 的取值范围是( )
A.
河北邢台一中2022年高一上数学期末经典模拟试题含解析

(2)函数 ,因为 ,则函数 在区间 递减,在区间 递增 ,函数 在区间 递增.∴综上可知,函数 的增区间为 , ,减区间为 .
(3)由 得 .又函数 在 递增,在 递减, 且 , .
若 ,即 时, ;
若 ,即 时, .
∴综上,当 时, ;当 时, .
故选:A
2、C
【解析】由对数函数的性质及分式的性质解不等式即可得解.
【详解】由题意得 ,解得 ,
所以 的定义域为 .
故选:C.
【点睛】本题考查了具体函数定义域的求解,属于基础题.
3、B
【解析】根据正弦、余弦、正切函数的周期性和单调性逐一判断即可得出答案.
【详解】解:对于A,函数 的最小正周期为 ,不符合题意;
一、选择题(本大题共10小题;在每小题给出的四个选项中,只有一个选项符合题意,请将正确选项填涂在答题卡上.)
1.已知扇形 的圆心角为 ,面积为8,则该扇形的周长为()
A.12B.10
C. D.
2. 的定义域为()
A. B.
C. D.
3.下列函数中,以 为最小正周期且在区间 上单调递减的是()
A. B.
∴ = ,即22k2+15k+2=0,解得k=- 或k=-
所以,满足题意的直线l方程为y=- +2或y=- x+2
(Ⅱ)将直线l的方程y= x+2代入圆方程得x2+(kx+2)2-12x+32=0
整理得(1+k2)x2+4(k-3)x+36=0. ①
直线与圆交于两个不同的点A,B等价于
△=[4(k-3)2]-4×36(1+k2)=42(-8k2-6k)>0,
2020-2021学年邢台市高一上学期期末数学试卷(附答案解析)

2020-2021学年邢台市高一上学期期末数学试卷一、单选题(本大题共12小题,共60.0分) 1.已知集合A ={y ︱y =3},B ={x ︱x 2>1},,则A ∩C R B = ( )A. [−1,1]B. (0,1)C. [0,1]D.2.关于x 的不等式x 2+2ax +4≥0对一切x ∈R 恒成立,且函数f(x)=log a (x −a +2)在区间(1,+∞)上恒为正值,则a 的取值范围是( )A. [1,2]B. [−2,1]C. (1,2]D. (1,2)3.如图E 、F 是正方形ABCD 两边的三等分点,向正方形ABCD 内任投一点M ,记点M 落在阴影区域的概率为p ,则a =p 是函数y =ax 2+2x +1有两个零点的( )A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 非充分非必要条件4.已知函数f(x)=x 2−3x +c ,(x ∈[1,3]的值域为( )A. [f(1),f(3)]B. [f(1),f(32)]C. [c −94,f(3)]D. [f(32),f(3)]5.定义2×2矩阵[a 1a 2a3a 4]=a 1a 4−a 2a 3,若f(x)=[cos 2x −sin 2x√3cos(π2+2x)1],则f(x)的图象向右平移π3个单位得到函数g(x),则函数g(x)解析式为( )A. g(x)=−2cos2xB. g(x)=−2sin2xC. g(x)=2sin(2x −π6)D. g(x)=−2cos(2x −π6)6.已知下列四个关系:①a >b ⇔ac 2>bc 2; ②a >b ⇒1a <1b ;③a >b >0,c >d ⇒ad >bc ; ④a >b >0⇒a c <b c . 其中正确的有( )A. 1个B. 2个C. 3个D. 4个7.已知定义在R 上的函数f(x)满足f(x +1)=−f(x),且x ∈(−1,1]时f(x)={1,(−1<x ≤0)−1,(0<x ≤1),则f(3)=( )A. −1B. 0C. 1D. 1或08.已知函数f(x)=3x2−ax+1在区间[12,1]上为减函数,则a 的取值范围为( )A. [2,+∞)B. (−∞,1]C. (−∞,2]D. [1,+∞)9.下列函数中,既是偶函数,又是(0,+∞)上的增函数是( )A. y =x 12B. y =log 12|x| C. y =2x +2−xD. y =2x −2−x10. 将函数f(x)=2sin(2x −π3)的图象向左平移π6个单位得到函数g(x),则下列结论正确的是( )A. 函数g(x)的最小正周期为2πB. 函数g(x)的图象关于原点对称C. 函数g(x)在区间[−π6,π3]上单调递增D. 函数f(x)在[−π6,π3]上的最小值为−√3211. 定义:M l 表示函数y =f(x)在I 上的最大值,已知奇函数f(x)满足f(x +4)=f(4−x),且当x ∈(0,4]时,f(x)=x ,正数a 满足M [0,a]≥2M [a,2a],则( )A. M [0,a]=2B. M [0,a]=9C. a 的取值范围为[4,9]D. a 的取值范围为[6,9]12. 已知函数f(x)={1,x 为有理数0,x 为无理数,给出下列三个命题:①函数f(x)为偶函数; ②函数f(x)是周期函数;③存在x i (i =1,2,3),使得(x i ,f(x i ))为顶点的三角形是等边三角形. 其中正确命题的个数是( )A. 0B. 1C. 2D. 3二、单空题(本大题共4小题,共20.0分)13. 函数f(x)=6x 3+9x +1满足f(a)+f(a −1)>2,则实数的取值范围是__________ 14. 已知全集U 为一切实数,若集合,集合B ={y|y =(12)x ,x ≥−2} ,则((∁U A)∩B =_________.15. 已知一扇形的圆心角为60°,半径为2cm ,则扇形的面积是______ cm 2. 16. 《周脾算经》中给出了弦图,所谓弦图是由四个全等的直角三角形和中间一个正方形拼成一个大的正方形.若图中直角三角形的两个锐角分别为α,β,且小正方形与大正方形的面积之比为9:16,则cos(α−β)= ______ . 三、解答题(本大题共6小题,共70.0分) 17. 化简:sin(2π−α)cos(3π+α)cos(32π+α)sin(−π+α)sin(3π−α)cos(−π−α).18. 计算(1)(23)0+2−2×(214)− 12−(0.01)0.5(2)log 25625+lg 1100+lne .19. 已知函数().(1)若的定义域和值域均是,求实数的值; (2)若对任意的,,总有,求实数的取值范围.20. 已知函数f(x)=sin(x +π6). (1)若f(α−π6)=35,α∈(π2,π),求f(α);(2)把f(x)的图象向左平移π6个单位长度,然后把图象上各点的横坐标变为原来的12(纵坐标不变),得到函数y =g(x)的图象,求函数g(x)的单调增区间.21. 设函数f(x)=acos2x +(a −1)(cosx +1)其中a >0,记f(x)||的最大值为A . (Ⅰ)当0<a <15时,讨论f(x)的单调性; (Ⅱ)求A .22.某景区为提高经济效益,现对某一景点进行改造升级,从而扩大内需,提高旅游增加值,经过x−blnx+市场调查,旅游增加值y万元与投入x(x≥10)万元之间满足:y=f(x)=ax2+10150 bln10,a,b为常数.当x=10万元时,y=19.2万元;当x=30万元时,y=50.5万元.(1)求f(x)的解析式;(2)求该景点改造升级后旅游利润T(x)=f(x)−x的最大值.(参考数据:ln2=0.7,ln3=1.1,ln5=1.6)参考答案及解析1.答案:D解析:试题分析:根据题意,由于集合A ={y ︱y =3}={y|y >0},B ={x ︱x 2>1}={x|x >1,或x <−1},故可知C R B ={x|1≥x ≥−1},那么可知A ∩C R B =,选D考点:集合的补集点评:本题考查集合的表示方法、集合的补集,两个集合的交集的定义和求法,求出C R B ={x|1≥x ≥−1},是解题的关键.2.答案:C解析:解:①若关于x 的不等式x 2+2ax +4≥0对一切x ∈R 恒成立,则判别式△≤0, 即4a 2−4×4≤0,所以a 2−4≤0,解得−2≤a ≤2.即甲:−2≤a ≤2. ②函数f(x)=log a (x −a +2)在区间(1,+∞)上恒为正值, 即{a >11−a +2≥1,解得:1<a ≤2, 由①②得:1<a ≤2, 故选:C .先求出关于x 的不等式x 2+2ax +4≥0对一切x ∈R 恒成立解得a 的范围,函数f(x)=log a (x −a +2)在区间(1,+∞)上恒为正值,进一步进行判断即可.本题主要考查利用二次函数和对数函数的性质是解决本题的关键.3.答案:A解析:解:∵E 、F 是正方形ABCD 两边的三等分点,∴向正方形ABCD 内任投一点M ,记点M 落在阴影区域的概率为p =13, 若函数y =ax 2+2x +1有两个零点, 则判别式△=4−4a ≥0,即a ≤1,则a =p 是函数y =ax 2+2x +1有两个零点的充分不必要条件, 故选:A求出概率p ,结合函数零点的关系以及成充分条件和必要条件的定义进行判断即可.本题主要考查充分条件和必要条件的判断,根据概率的计算以及函数零点的关系是解决本题的关键.4.答案:C解析:解:函数f(x)=x 2−3x +c =(x −32)2−94+c对称轴x =32,开口向上, ∵x ∈[1,3],∴当x =32时,f(x)取得最小值为c −94. 当x =3时,f(x)取得最大值为f(3). 故得f(x)值域为[c −94,f(3)]. 故选C根据二次函数的单调性求解即可.本题考查了二次函数的单调性的运用求值域的问题.属于基础题.5.答案:A解析:解:由题意可得f(x)=[cos 2x −sin 2x√3cos(π2+2x)1]=cos 2x −sin 2x −√3cos(π2+2x) =cos2x +√3sin2x =2cos(2x −π3),则f(x)的图象向右平移π3个单位得到函数g(x)=2cos[2(x −π3)−π3]=2 cos(2x −π)=−2cos2x , 故选:A .利用三角恒等变换化简函数f(x)的解析式,再利用函数y =Asin(ωx +φ)的图象变换规律,求得函数g(x)解析式.本题主要考查三角恒等变换,函数y =Asin(ωx +φ)的图象变换规律,属于中档题.6.答案:A解析:本题考查了不等式的性质,考查特殊值法的应用,是一道基础题. 取特殊值判断①②③,根据指数函数的性质判断④. 解:对于①c =0时,不成立,故①错误; 对于②令a =1,b =−1,不成立,故②错误; 对于③令a =1,b =−1,不成立,故③错误; 对于④,由于a >b >1,当x <0时,a x <b x , 故a c <b c 正确, 故选A .7.答案:A解析:解:∵f(x +1)=−f(x),∴f(x +2)=f(x),即函数的周期是2,又x ∈(−1,1]时f(x)={1,(−1<x ≤0)−1,(0<x ≤1),∴f(3)=f(1)=−1, 故选A .本题是一个根据函数性质求函数值的题,由题设条件f(x)满足f(x +1)=−f(x),知自变量相差1函数值互为相反数,可由此推出函数的周期是2,再由x ∈(−1,1]时f(x)={1,(−1<x ≤0)−1,(0<x ≤1),求f(3)的值.本题考查求利用函数的周期性求函数的值,解题的关键是寻求出函数的周期,利用函数的周期将要求函数值用已知解析式的区间上的函数值表示出来,从而求函数值.考查了转化化归的思想与计算能力.8.答案:A解析:本题考查复合函数单调性的判定和性质,涉及二次函数、指数函数的性质,属于一般题.设t =x 2−ax +1,由复合函数的单调性可得t =x 2−ax +1在[12,1]上内单调递减,结合二次函数的性质可得结论. 解:设t =x 2−ax +1, 因为函数y =3t 在R 为增函数,若函数f (x )=3x2−ax+1在区间[12,1]上内单调递减,则t =x 2−ax +1在区间[12,1]上内单调递减, 则a2≥1,a ≥2. 故选A .9.答案:C解析:解:y =x 12为非奇非偶函数,不符合题意;y=log12|x|在(0,+∞)上是减函数,不符合题意;y=2x+2−x为偶函数,且x>0时,t=2x>1,根据复合函数及对勾函数单调性可知y=t+1t(t> 1)单调递增,符合题意;y=2x−2−x为奇函数,不符合题意.故选:C.结合奇偶性的定义及单调性的定义分别检验各选项即可判断.本题主要考查了函数单调性及奇偶性的判断,属于基础试题.10.答案:B解析:解:函数f(x)=2sin(2x−π3)的图象向左平移π6个单位得到:函数g(x)=2sin(2x+π3−π3)=2sin2x,所以:①函数的最小正周期为T=2π2=π,故选项A错误.②函数的图象关于原点对称.③令:−π2+2kπ≤2x≤2kπ+π2(k∈Z),整理得:−π4+kπ≤x≤kπ+π4(k∈Z),当k=0时,函数的单调递增区间为:[−π4,π4 ],故选项C错误.④当−π6≤x≤π3,所以:−π3≤2x≤2π3,所以函数的最小值:即当2x=−π3时,函数的最小值为−√3.选项D错误.故选:B.首先通过三角函数关系式的平移变换,把函数的关系式,变形成正弦型函数,进一步利用正弦型函数的性质的应用求出结果.本题考查的知识要点:三角函数关系式的变换,正弦型函数的性质的应用,主要考察学生的运算能力和转换能力,属于基础题型.11.答案:D解析:解:由题意,f(−x)=−f(x),且f(0)=0.∵f(x+4)=f(4−x),∴f(x+16)=f(x),可得f(x)是周期函数T=16.当x∈(0,4]时,f(x)=x,作出图象,根据M I表示函数y=f(x)在I上的最大值,对于A,B选项:根据图象可知M[0,a]=4,∴A,B错误;对于C:D选项:要满足M[0,a]≥2M[a,2a]成立,即2≥M[a,2a],由图象可得,a≥6且2a≤18,∴a的取值范围为[6,9],故选:D.根据奇函数f(x)满足f(x+4)=f(4−x),可得周期T=16,当x∈(0,4]时,f(x)=x,作出图象,结合图象,逐项判断各选项即可.本题考查函数的周期性的运用,考查函数的图象和性质,运用数形结合的思想方法是解题的关键.12.答案:D解析:解:函数f(x)={1,x为有理数0,x为无理数,对于①,定义域为R,x为有理数,−x为有理数,f(−x)=1=f(x);x为无理数,−x为无理数,f(−x)=0=f(x),则f(−x)=f(x),x ∈R , 则f(x)为偶函数;对于②,存在非零有理数T , 当x 为有理数时,x +T 为有理数, f(x +T)=1=f(x);当x 为无理数时,x +T 为无理数, f(x +T)=0=f(x); 则f(x)为周期函数;对于③,设三个点(x 1,0)(x 2,1)(x 3,0),且x 1+x 3=2x 2,x 3−x 2=√33,比如x 1=1−√33,x 2=1,x 3=1+√33.易满足三点构成三角形是等边三角形,故③正确. 故正确的个数为3. 故选:D .①由偶函数的定义进行判断. ②由周期函数的定义证明③由解析式做出大致图象:根据图象进行判断即可.本题主要考查了特殊函数的性质的理解和运用,考查函数的奇偶性和周期性,属于中档题.13.答案:解析:因为是奇函数,所以f(x)+f(−x)=2,即有f(−x)=2−f(x),f(a)+f(a −1)>2 <=>f(a)>2−f(a −1)=f(1−a),易知f(x)在R 上单调增加,a >1−a 解得:。
2022-2023学年河北省邢台市第一中学高一上学期期末考试数学试题(解析版)

2022-2023学年河北省邢台市第一中学高一上学期期末考试数学试题一、单选题1.()sin 1320︒-=( )A .12B .12-C D .【答案】C【分析】利用诱导公式进行化简求值.【详解】()()480480sin120sin 1320sin 1800sin ︒︒︒︒︒+-=-==故选:C.2.已知集合212112x x A x +-⎧⎫⎪⎪⎛⎫=≥⎨⎬ ⎪⎝⎭⎪⎪⎩⎭,304x B x x ⎧⎫+=≥⎨⎬-⎩⎭,则()RA B =( )A .{}34x x -<<B .{}33x x -<<C .{}34x x -<≤D .{}33x x -<≤【答案】D【分析】分别解不等式求出集合A 和集合B ,然后再求()RAB 即可.【详解】不等式212112x x +-⎛⎫≥ ⎪⎝⎭等价于2121122x x +-⎛⎫⎛⎫≥ ⎪⎪⎝⎭⎝⎭, ∵12xy ⎛⎫= ⎪⎝⎭在R 上单调递减,∴2120x x +-≤,解得43x -≤≤,∴{}21211432x x A x x x +-⎧⎫⎪⎪⎛⎫=≥=-≤≤⎨⎬ ⎪⎝⎭⎪⎪⎩⎭, 不等式304x x +≥-等价于()()34040x x x ⎧+-≥⎨-≠⎩,解得3x ≤-或>4x , ∴{3034x B xx x x ⎧⎫+=≥=≤-⎨⎬-⎩⎭或}4x >, ∴{}34B x x =-<≤R , ∴(){}33A B x x ⋂=-<≤R . 故选:D.3.下列函数中,既是奇函数又在定义域上是减函数的是( ) A .ln y x =- B .()tan y x =- C .3y x =- D .1y x=【答案】C【分析】根据奇函数和减函数的特征,结合选项进行判定. 【详解】对于选项A ,ln y x =-不是奇函数,排除A ;对于选项B ,()tan y x =-是奇函数,但是在其定义域上不是减函数,排除B ; 对于选项C ,3y x =-是奇函数,在其定义域上也是减函数,符合题意; 对于选项D ,1y x=是奇函数,但是在其定义域上不是减函数,排除D. 故选:C.4.函数()()1ln 23f x x x =---的零点所在区间为( )A .()4,3--B .()3,e --C .()e,2--D .()2,1--【答案】B【分析】根据公共定义域内判断函数的单调性及复合函数的单调性, 得出函数()f x 的单调性,再利用函数零点的存在性定理即可求解. 【详解】由题意可知,()f x 的定义域为(),0-∞, 令u x =-,则ln y u =,由u x =-在(),0-∞上单调递减, ln y u =在定义域内单调递增,所以()ln y x =-在(),0-∞单调递减.所以函数()()1ln 23f x x x =---在(),0-∞上单调递减.所以()()()12214ln 442ln 4ln e 03333f -=---⨯--=->-=>⎡⎤⎣⎦ ()()()13ln 332ln 31ln e 103f -=---⨯--=->-=⎡⎤⎣⎦()()()1e e ln e e 21033f -=---⨯--=-<⎡⎤⎣⎦ ()()()1442ln 222ln 2ln e 0333f -=---⨯--=-<-<⎡⎤⎣⎦ ()()()151ln 112033f -=---⨯--=-<⎡⎤⎣⎦故()3(e)0f f -⋅-<,根据零点的存在性定理,可得 函数()()1ln 23f x x x =---的零点所在区间为()3,e --.故选:B.5.命题0:p x ∃∈R ,使得200680kx kx k -++<成立.若p 是假命题,则实数k 的取值范围是( ) A .[]0,1B .(]0,1C .()(),01,-∞⋃+∞D .][(),01,∞∞-⋃+【答案】A【分析】根据p 是假命题,得出p ⌝为真命题,利用恒成立知识求解.【详解】因为p 是假命题,所以p ⌝为真命题,即x ∀∈R ,使得2680kx kx k -++≥成立. 当0k =时,显然符合题意;当0k ≠时,则有0k >,且()236480k k k -+≤,解得01k <≤.故选:A.6.已知幂函数()y f x =的图象过()4,2A 、()cos1,B m 、()sin1,C n 三点,则m 与n 的大小关系为( ) A .m n > B .m n < C .m n = D .不能确定【答案】B【分析】设()af x x =,根据点A 在函数()f x 的图象上可求得a 的值,可得出()f x 的解析式,分析函数()f x 的定义域与单调性,比较cos1与sin1,利用函数()f x 的单调性可得出m 、n 的大小关系.【详解】设()af x x =,则()442a f ==,可得12a =,()12f x x ∴= 所以,函数()f x 是定义在[)0,∞+上的增函数, 因为ππ0cos1cos sin sin144<<=<,所以,()()cos1sin1f f <,即m n <. 故选:B.7.已知tan π22α⎛⎫-=- ⎪⎝⎭,则π3π1cos sin 22π14ααα⎛⎫⎛⎫+--+ ⎪ ⎪⎝⎭⎝⎭=⎛⎫+ ⎪⎝⎭( )A.2B.C .12D .1【答案】C【分析】利用诱导公式可求得tan2α,利用三角恒等变换化简所求代数式,可求得结果.【详解】因为tan πtan 222αα⎛⎫-=-=- ⎪⎝⎭,则tan 22α=,若cossin022αα+=,则tan12α=-,矛盾,故cossin022αα+≠.因此,()π3π1cos sin 1sin cos 1cos sin 22π1cos sin 1cos sin 14ααααααααααα⎛⎫⎛⎫+--+ ⎪ ⎪++++⎝⎭⎝⎭==---+⎛⎫+ ⎪⎝⎭ 222coscos sin 12cos 12sincos112222222tan112sin 2sin cos 2sin cos sin 2222222ααααααααααααα⎛⎫++-+ ⎪⎝⎭====⎛⎫⎛⎫--++ ⎪ ⎪⎝⎭⎝⎭.故选:C.8.“一骑红尘妃子笑,无人知是荔枝来”描述了封建统治者的骄奢生活,同时也讲述了古代资源流通的不便利.如今我国物流行业蓬勃发展,极大地促进了社会经济发展和资源整合.已知某类果蔬的保鲜时间y (单位:小时)与储藏温度x (单位:C )满足函数关系e ax b y +=(,a b 为常数),若该果蔬在5C 的保鲜时间为216小时,在20C 的保鲜时间为8小时,那么在10C 时,该果蔬的保鲜时间为( )小时. A .72 B .36C .24D .16【答案】A【分析】根据题意列出5,20x x ==时,a b 所满足等式,利用指数幂的运算分别可求解出5e ,e a b 的值,然后即可计算出10x =时y 的值,则对应保鲜时间可求. 【详解】当5x =时,5e 216a b +=;当20x时,20e 8a b +=,则520e 21627e 8a b a b ++==,整理可得51e 3a=,于是e 2163648b =⨯=, 当10x =时,10521e(e )e 648729a ba b y +==⋅=⨯=. 故选:A二、多选题9.下到说法错误的是( )A .若α终边上一点的坐标为()()3,40k k k ≠,则3cos 5α= B .α为第二或第三象限角的充要条件是sin tan 0αα<C .将函数()πcos 23f x x ⎛⎫=- ⎪⎝⎭的图象向左平移π3个单位长度,得到函数()cos2g x x =的图象D .若1sin cos 5αα+=,且0απ<<,则4tan 3α=-【答案】AC【分析】结合选项逐个判定,利用定义可知A 错误,结合象限符号可得B 正确,根据平移规则可得C 错误,利用平方关系和商关系可得D 正确. 【详解】对于A ,3355cos k k α===±,故不正确; 对于B ,α为第二象限时,sin 0,tan 0αα><,所以sin tan 0αα<;α为第三象限角时,sin 0,tan 0αα<>,所以sin tan 0αα<;反之,sin tan 0αα<,则sin ,tan αα异号,所以α为第二或第三象限角,故正确;对于C ,将函数()πcos 23f x x ⎛⎫=- ⎪⎝⎭的图象向左平移π3个单位长度,得到的函数解析式为()πcos 23g x x ⎛⎫=+ ⎪⎝⎭,故不正确;对于D ,因为1sin cos 5αα+=,所以12sin cos 25αα=-,所以222sin cos tan 12sin cos tan 125αααααα==-++,解得3tan 4α=-或4tan 3α=-. 因为1sin cos 05αα+=>,12sin cos 025αα=-<,且0πα<<,所以sin >cos αα, 所以4tan 3α=-,故D 正确.故选:AC.10.已知a ,b 为正数,41a b +=,则下列说法正确的是( ) A .114a b+的最小值为4 B .11a b+的最小值为9 C .()()411a b ++的最大值为94D .()()11a b ++的最大值为94【答案】ABC【分析】选项A 和选项B 使用基本不等式“1”的妙用求解,选项C 和选项D 构造“和为定值”对“积的最大值”进行求解. 【详解】对于A ,()1111442444a b a b a b a b b a ⎛⎫+=++=++ ⎪⎝⎭,∵0a >,0b >,∴40a b >,04b a >,∴由基本不等式424a b b a +≥=, 当且仅当44a b b a =,即18a =,12b =时,等号成立, ∴114222444a b a b b a+=++≥+=,114a b +的最小值为4,故选项A 正确;对于B ,()1111445a b a b a b a b b a ⎛⎫+=++=++ ⎪⎝⎭, ∵0a >,0b >,∴40a b >,0b a >,∴由基本不等式44a b b a +≥, 当且仅当4a bb a =,即16a =,13b =时,等号成立, ∴1145549a ba b b a +=++≥+=,11a b+的最小值为9,故选项B 正确; 对于C ,∵0a >,0b >,∴410a +>,10+>b ,∴由基本不等式()()()()222411421294112224a b a b a b +++⎡⎤+++⎛⎫⎛⎫++≤===⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎣⎦, 当且仅当411a b +=+,即18a =,12b =时,等号成立,∴()()411a b ++的最大值为94,故选项C 正确;对于D ,∵0a >,0b >,∴440a +>,10+>b ,∴由基本不等式()()()()()()2244111145911441442424a b a b a b a b +++⎡⎤++⎛⎫++=++≤⋅=⋅=⎢⎥ ⎪⎝⎭⎣⎦,当且仅当441a b +=+,即14a =-,2b =时,等号成立,这与0a >矛盾,上式无法取等号,故选项D 错误. 故选:ABC.11.已知函数()()4log 1,11,14x x x f x x ⎧->⎪=⎨⎛⎫≤⎪ ⎪⎝⎭⎩,则下列结论正确的是( )A .若()1f a =,则5a =B .202320222022f f ⎛⎫⎛⎫= ⎪⎪⎝⎭⎝⎭C .若()2f a ≥,则12a ≤-或17a ≥D .若方程()f x k =有两个不同的实数根,则14k ≥ 【答案】BCD【分析】解方程可()1f a =判断A 选项;求出20232022f f ⎛⎫⎛⎫ ⎪⎪⎝⎭⎝⎭的值,可判断B 选项;解不等式()2f a ≥可判断C 选项;数形结合可判断D 选项.【详解】对于A 选项,当1a ≤时,由()114af a ⎛⎫== ⎪⎝⎭,可得0a =,当1a >时,由()()4log 11f a a =-=,可得5a =. 综上所述,若()1f a =,则5a =或0,A 错; 对于B 选项,41420231log log 2022020222022f ⎛⎫==< ⎪⎝⎭, 所以,14log 20221420231log 2022202220224f f f ⎛⎫⎛⎫⎛⎫⎛⎫=== ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭,B 对;对于C 选项,当1a ≤时,由()21224aa f a -⎛⎫==≥ ⎪⎝⎭,可得21a -≥,解得12a ≤-,此时12a ≤-,当1a >时,由()()4log 12f a a =-≥,可得116a -≥,解得17a ≥,此时17a ≥, 综上所述,若()2f a ≥,则12a ≤-或17a ≥,C 对;对于D 选项,作出函数y k =与函数()f x 的图象如下图所示:由图可知,当14k ≥时,直线y k =与函数()f x 的图象有两个交点, 此时方程()f x k =有两个不等的实根,D 对. 故选:BCD.12.设函数()f x 的定义域为D ,如果对任意的1x D ∈,存在2x D ∈,使得12()()2f x f x c +=(c 为常数),则称函数()y f x =在D 上的均值为c ,下列函数中在其定义域上的均值为1的有( ) A .3y x = B .tan y x =C .2sin y x =D .24y x -【答案】ABD【分析】根据题意将问题转化为关于2x 的方程是否存在有解问题,然后逐个分析判断即可 【详解】由题意可得1c =,则12()()12f x f x +=,即12()()2f x f x +=,将问题转化为关于2x 的方程是否存在有解问题,对于A ,3y x =的定义域为R ,则对于任意1R x ∈,关于2x 的方程为33122x x +=,则33212x x =-,2x ,方程一定有解,所以A 正确,对于B ,tan y x =的定义域为,2D x x k k Z ππ⎧⎫=≠+∈⎨⎬⎩⎭,值域为R ,则对于任意1x D ∈,总存在2x D ∈,使得12tan tan 2x x +=,所以B 正确,对于C ,2sin y x =的定义域为R ,值域为[2,2]-,当12x π=-时,1()2f x =-,此时不存在2x R ∈,使12()()2f x f x +=,所以C 错误,对于D ,y {}22D x x =-≤≤,值域为[0,2],则对于任意1x D ∈,关于2x 的方2,整理得(22242x =-,则总存在2x D ∈满足上式,所以D 正确,故选:ABD三、填空题13.已知集合(){}222810A x ax a x =+-+=有且仅有两个子集,则a 的取值集合为___________.【答案】{}0,2,8【分析】根据题意集合A 有一个元素,考虑0a =和0a ≠两种情况,计算得到答案即可.【详解】由题意,集合(){}222810A x ax a x =+-+=有且仅有两个子集,则集合A 只有一个元素,当0a =时,810x -+=,解得18x,符合题意; 当0a ≠时,()2284210a a ∆=--⨯⨯=,解得2a =或8a =, 当2a =时,{}2144102A x x x ⎧⎫=-+==⎨⎬⎩⎭,符合题意,当8a =时,{}21168104A x x x ⎧⎫=++==-⎨⎬⎩⎭,符合题意.综上所述,a 的取值集合为{}0,2,8. 故答案为:{}0,2,8.14.已知函数()()212log 2f x x x t =-++的定义域是(),6m m +,则函数()f x 的单调增区间为__________. 【答案】()1,4【分析】先根据定义域求出,m t 的值,再结合复合函数求出单调区间.【详解】因为函数()()212log 2f x x x t =-++的定义域是(),6m m +,所以,6m m +是方程220x x t -++=的两个根,所以()()22206260m m t m m t ⎧-++=⎪⎨-++++=⎪⎩,解得28m t =-⎧⎨=⎩,即()()212log 28f x x x =-++. 令()222819n x x x =-++=--+,0n >,则12log y n=为减函数,函数()219n x =--+是开口向下,对称轴为1x =的二次函数,且()1,4x ∈时,为减函数;所以函数()f x 的单调增区间为()1,4. 故答案为:()1,4.15.如图,在Rt PBO 中,90PBO ∠= ,以O 为圆心、OB 为半径作圆弧交OP 于A 点.若圆弧AB 等分POB 的面积,且AOB α∠=弧度,则tan αα=________.【答案】12【详解】设扇形的半径为r ,则扇形的面积为212r α,直角三角形POB 中, tan PB r α=, POB ,面积为1tan 2r r α⨯,由题意得211222r rtan r αα⨯=⨯,∴tan 2αα=,∴1tan 2αα=,故答案为12. 点睛:本题考查扇形的面积公式及三角形的面积公式的应用,考查学生的计算能力,属于基础题;设出扇形的半径,求出扇形的面积,再在直角三角形中求出高PB ,计算直角三角形的面积,由条件建立等式,解此等式求出tan α与α的关系,即可得出结论. 16.函数()f x 为定义在()(),00,∞-+∞上的奇函数,且()31f =,对于任意()1212,0,,x x x x ∈+∞≠,都有()()1122120x f x x f x x x ->-成立,则()3f x x≤的解集为__________. 【答案】(](]30,3-∞-⋃,【分析】构造函数,利用函数的单调性和奇偶性进行求解.【详解】设函数()()g x xf x =,因为()f x 为奇函数,所以()g x 为偶函数; 因为()()1122120x f x x f x x x ->-,所以()()12120g x g x x x ->-,即()g x 在()0,∞+为增函数;因为(3)3(3)3g f ==,()g x 为偶函数,所以(3)3g -=,且()g x 在(),0∞-为减函数;当0x >时,()3f x x ≤等价于()3(3)g x g ≤=,所以03x <≤; 当0x <时,()3f x x ≤等价于()3(3)g x g ≥=-,所以3x ≤-;即()3f x x≤的解集为(](]30,3-∞-⋃,. 故答案为:(](]30,3-∞-⋃,.四、解答题17.设a ∈R ,集合(){}(){}22log 2,30A x x a B x x a x =+<=-+<,(1)若2a =,求A B ⋃(2)若()3A B ∈⋂R ,求a 的取值范围. 【答案】(1){}|25A B x x ⋃=-<< (2)30a -<≤【分析】(1)先根据2a =,化简两个集合,再求两个集合的并集; (2)由3在集合A 中,不在集合B 中,可求取值范围.【详解】(1)当2a =时,(){}{}{}{}22|log 22|22|50|05A x x x x B x x x x x =+<=-<<=-<=<<,,所以{}{}{}|22|05|25A B x x x x x x ⋃=-<<⋃<<=-<<.(2)集合(){}2|30B x x a x =-+<,所以(){}2|30.B x x a x =-+≥R因为()3A B ∈⋂R ,所以3A ∈且3B ∈R.则()()22log 323330a a ⎧+<⎪⎨-+≥⎪⎩,即03430a a <+<⎧⎨-≥⎩,解得30a -<≤.18.函数()()sin 0,0,02f x A x A πωϕωϕ⎛⎫=+>><< ⎪⎝⎭部分图象如图所示,已知41x x π-=.再从条件①112x π=、条件②26x π=、条件③32x π=这三个条件中选择两个作为已知.(1)求函数()f x 的解析式; (2)求6f x π⎛⎫-⎪⎝⎭的单调增区间. 【答案】(1)()2sin 26f x x π⎛⎫=- ⎪⎝⎭(2)5,36k k ππππ⎡⎤++⎢⎥⎣⎦,k ∈Z【分析】(1)先由41x x π-=求出ω,分三种情况讨论求解,代入点的坐标求出,A ϕ,从而得到解析式; (2)先求6f x π⎛⎫-⎪⎝⎭的解析式,整体代换可求6f x π⎛⎫- ⎪⎝⎭的单调增区间. 【详解】(1)因为41x x π-=,由图可知T π=,所以22Tπω==.所以()()sin 2f x A x ϕ=+. 若选择条件①②,即112x π=,26x π=.因为()1sin 0126f x f A ππϕ⎛⎫⎛⎫==+= ⎪ ⎪⎝⎭⎝⎭.由图可知26k πϕπ+=,k ∈Z ,即26k πϕπ=-+.因为02πϕ<<,所以6πϕ=-,所以()sin 26f x A x π⎛⎫=- ⎪⎝⎭.又因为()2sin 166f x f A ππ⎛⎫=== ⎪⎝⎭,所以2A =,所以()2sin 26f x x π⎛⎫=- ⎪⎝⎭.若选择条件①③,即112x π=,32x π=. 因为()1sin 0126f x f A ππϕ⎛⎫⎛⎫==+= ⎪ ⎪⎝⎭⎝⎭.由图可知26k πϕπ+=,k ∈Z ,即26k πϕπ=-+.因为02πϕ<<,所以6πϕ=-,所以()sin 26f x A x π⎛⎫=- ⎪⎝⎭.又因为()3sin 126f x f A ππ⎛⎫=== ⎪⎝⎭,所以2A =,所以()2sin 26f x x π⎛⎫=- ⎪⎝⎭.若选择条件②③,即26x π=,32x π=. 因为()()23f x f x =,由图可知,当2323x x x +π==时,()f x 取得最大值, 即3f A π⎛⎫= ⎪⎝⎭,sin 23A A πϕ⎛⎫⨯+= ⎪⎝⎭,由2sin 13πϕ⎛⎫+=⎪⎝⎭,得2232k ϕππ+=+π,k ∈Z , 因为02πϕ<<,所以6πϕ=-. 又()216f x f π⎛⎫== ⎪⎝⎭,所以2A =,所以()2sin 26f x x π⎛⎫=- ⎪⎝⎭.(2)()2sin[2()]2sin(2)2sin(2)66666f x x x x πππππ-=--=-=--,故()6f x π-的单调增区间即为2sin(2)6x π-的单调递减区间.由3222262k x k πππππ+≤-≤+,k ∈Z ,得536k x k ππππ+≤≤+,k ∈Z .所以()6f x π-的单调递增区间为5,36k k ππππ⎡⎤++⎢⎥⎣⎦,k ∈Z . 19.已知函数()5ππ3πsin 22sin cos 644f x x x x ⎛⎫⎛⎫⎛⎫=---+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.(1)求()f x 的最小正周期及对称轴方程;(2)ππ,46x ⎡⎤∈-⎢⎥⎣⎦时,()()g x af x b =+的最大值为7,最小值为1,求a ,b 的值.【答案】(1)最小正周期为πT =,对称轴方程为ππ23k x =+,k ∈Z (2)4a =,5b =或4a =-,3b =【分析】(1)使用两角和差的正余弦公式、二倍角公式、辅助角公式进行化简后,即可求得最小正周期和对称轴方程;(2)结合正弦函数的图象和性质,分别对0a >和a<0两种情况进行讨论即可. 【详解】(1)()5ππ3πsin 22sin cos 644f x x x x ⎛⎫⎛⎫⎛⎫=---+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭1cos 2sin 222x x x x x x ⎛⎫⎛⎫=-- ⎪⎪ ⎪⎪⎝⎭⎝⎭⎝⎭()()1cos 22sin cos cos sin 2x x x x x x =----()221cos22cos sin 22x x x x =+--1cos 22cos 22x x x =-12cos 22x x =- πsin 26x ⎛⎫=- ⎪⎝⎭∴()πsin 26f x x ⎛⎫=- ⎪⎝⎭,则()f x 的最小正周期为2ππ2T ==,∵sin y x =的对称轴为直线ππ+2=x k ,k ∈Z , ∴由ππ2π62x k -=+,k ∈Z ,解得ππ23k x =+,k ∈Z , ∴()f x 的对称轴方程为ππ23k x =+,k ∈Z . (2)πsi 2()(n 6)x b g x af x b a =+=⎛⎫-+ ⎪⎝⎭,∵ππ,46x ⎡⎤∈-⎢⎥⎣⎦,∴ππ2[,]23x ∈-,∴π2ππ2[,]636x -∈-,∴π1sin(2)[1,]62x -∈-,当0a >时,()()g x af x b =+的最大值为12a b +,最小值为a b -+,∴由1721a b a b ⎧+=⎪⎨⎪-+=⎩,解得45a b =⎧⎨=⎩,当a<0时,()()g x af x b =+的最大值为a b -+,最小值为12a b +,∴由7112a b a b -+=⎧⎪⎨+=⎪⎩,解得43a b =-⎧⎨=⎩,综上所述,4a =,5b =或4a =-,3b =.20.比亚迪是我国乃至全世界新能源电动车的排头兵,新能源电动车汽车主要采用电能作为动力来源,目前比较常见的主要有两种:混合动力汽车、纯电动汽车.有关部门在国道上对比亚迪某型号纯电动汽车进行测试,国道限速60km/h .经数次测试,得到该纯电动汽车每小时耗电量Q (单位:wh )与速度x (单位:km/h )的数据如下表所示:为了描述该纯电动汽车国道上行驶时每小时耗电量Q 与速度x 的关系,现有以下三种函数模型供选择:①3211()250Q x x x cx =-+;②22()13xQ x ⎛⎫=- ⎪⎝⎭;3()300log a Q x x b =+.(1)当060x ≤≤时,请选出你认为最符合表格中所列数据的函数模型(需说明理由),并求出相应的函数表达式;(2)现有一辆同型号纯电动汽车从重庆育才中学行驶到成都七中,其中,国道上行驶50km ,高速上行驶300km .假设该电动汽车在国道和高速上均做匀速运动,国道上每小时的耗电量Q 与速度x 的关系满足(1)中的函数表达式;高速路上车速x (单位:km/h )满足[80,120]x ∈,且每小时耗电量N (单位:wh )与速度x (单位:km/h )的关系满足2()210200(80120)N x x x x =-+≤≤).则当国道和高速上的车速分别为多少时,该车辆的总耗电量最少,最少总耗电量为多少? 【答案】(1)选①3211()250Q x x x cx =-+,321()216050Q x x x x =-+ (2)当这辆车在高速上的行驶速度为80km/h ,在国道上的行驶速度为50km/h 最少,最少为51250wh .【分析】(1)利用表格中数据进行排除即可得解;(2)在分段函数中分别利用均值不等式和二次函数求出最值即可得解.【详解】(1)解:对于③3()300log a Q x x b =+,当0x =时,它无意义,故不符合题意,对于②22()13xQ x ⎛⎫=- ⎪⎝⎭,当10x =时,1022(10)13Q ⎛⎫=- ⎪⎝⎭,又100122033<⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝=⎭,所以1022(10)113Q ⎛⎫=-< ⎪⎝⎭,故不符合题意,故选①3211()250Q x x x cx =-+, 由表中的数据可得,3211021010142050c ⨯-⨯+⨯=,解得160c = ∴321()216050Q x x x x =-+. (2)解:高速上行驶300km ,所用时间为300h x, 则所耗电量为()2300300100()()2102006003000f x N x x x x x x x ⎛⎫=⋅=⋅-+=+- ⎪⎝⎭, 由对勾函数的性质可知,()f x 在[80,120]上单调递增,∴min 100()(80)60080300045750wh 80f x f ⎛⎫==⨯+-= ⎪⎝⎭,国道上行驶50km ,所用时间为50h x,则所耗电量为32250501()()2160100800050g x Q x x x x x x x x ⎛⎫=⋅=⋅-+=-+ ⎪⎝⎭, ∵060x ≤≤,∴当50x =时,min ()(50)5500wh g x g ==,∴当这辆车在高速上的行驶速度为80km/h ,在国道上的行驶速度为50km/h 时,该车从重庆育才中学行驶到成都七中的总耗电量最少,最少为45750550051250wh +=. 21.已知函数()log (0a f x x a =>,且1)a ≠.(1)若函数()f x 的图象与函数()h x 的图象关于直线y x =对称,且点()4,256P 在函数()h x 的图象上,求实数a 的值; (2)已知函数()1,,162322x x g x f f x ⎛⎫⎛⎫⎡⎤=∈ ⎪⎪⎢⎥⎝⎭⎝⎭⎣⎦.若()g x 的最大值为12,求实数a 的值. 【答案】(1)4a = (2)12或2【分析】(1)根据两个函数图象对称的特征求出()xh x a =,代入点的坐标可得实数a 的值;(2)先化简()g x ,利用换元法和二次函数知识,结合最大值求出实数a 的值.【详解】(1)因为函数()log (0=>a f x x a ,且1a ≠)的图象与函数()h x 的图象关于直线y x =对称, 所以()xh x a =(0a >,且1a ≠),因为点(4,256)P 在函数()h x 的图象上,所以4256a =,解得4a =,或4a =-(舍去). (2)()()()log log log log log 5log 22232aa a a a a x xg x x x =⋅=--()()()2222log 6log log 5log 2log 3log 4log 2(2)2a a a a a a a x x x =-⋅+-=-.令log a t x =. ①当01a <<时,由1162x ≤≤,有4log 2log log 2a a a x ≤≤-, 二次函数()()226log 25log 2a a t t t ϕ=-+的对称轴为3log 2a t =,最大值为()()()()()2222log 2log 26log 25log 212log 212a a a a a ϕ-=++==,解得12a =或2a =(舍去);②当1a >时,由1162x ≤≤,有log 2log 4log 2a a a x -≤≤, 二次函数()22()6log 25log 2a a t t t ϕ=-+的对称轴为3log 2a t =,可得最大值为()()()()()2222log 2log 26log 25log 212log 212a a a a a ϕ-=++==,解得2a =或12a =(舍去),综上,实数a 的值为12或2. 22.已知函数()14x b f x a =++的定义域为R ,其图像关于点11,22⎛⎫⎪⎝⎭对称.(1)求实数a ,b 的值; (2)求122022202320232023f f f ⎛⎫⎛⎫⎛⎫+++⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭的值;(3)若函数()412log 22x g x f x x +⎛⎫=++ ⎪-⎝⎭,判断函数()g x 的单调性(不必写出证明过程),并解关于t的不等式()()2121g t g t -++>. 【答案】(1)2,2a b ==- (2)1011(3)103t -<<【分析】(1)根据对称性列方程解出a 和b ; (2)根据对称性分组计算;(3)构造函数,根据函数的单调性和奇偶性求解不等式.【详解】(1)有条件可知函数()f x 经过点11,22⎛⎫ ⎪⎝⎭ ,()()112210122f f f ⎧⎛⎫= ⎪⎪⎪⎝⎭∴⎨⎪+=⨯⎪⎩,即12112411114b a b b aa ⎧+=⎪⎪+⎨⎪+++=⎪++⎩ , 解得:2,2a b ==- ,()2414242xx xf x -=+=++ ; (2)由于120222************1,1,,1202320232023202320232023+=+=+= , 1202222021101110121,1,,1202320232023202320232023f f f f f f ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫∴+=+=+= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭, 1220221011202320232023f f f ⎛⎫⎛⎫⎛⎫+++= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭; (3)由于42log 2x y x +=- 是奇函数,根据函数平移规则,()()12h x g x =- 也是奇函数, 并且由于()f x 是增函数,42log 2xy x+=- 也是增函数,()h x ∴ 也是增函数,定义域为()2,2- 不等式()()2121g t g t -++> 等价于()()11212022g t g t --++-> ,即()()2120h t h t -++> ,()()()2122h t h t h t ->-+=-- ,由于()h x 是增函数,2122212222t t t t ->--⎧⎪∴-<-<⎨⎪-<+<⎩,解得103t -<< ;综上,(1)2,2a b ==-;(2)1220221011202320232023f f f ⎛⎫⎛⎫⎛⎫+++= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭;(3)103t -<<.。
学河北省邢台市高一(上)期末数学试卷(解析版)
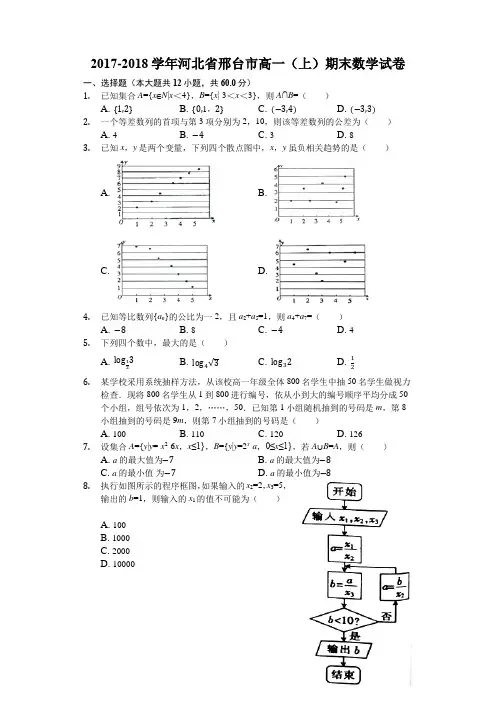
2017-2018学年河北省邢台市高一(上)期末数学试卷一、选择题(本大题共12小题,共60.0分)1.已知集合A={x∈N|x<4},B={x|-3<x<3},则A∩B=()A. {1,2}B. {0,1,2}C. (−3,4)D. (−3,3)2.一个等差数列的首项与第3项分别为2,10,则该等差数列的公差为()A. 4B. −4C. 3D. 83.已知x,y是两个变量,下列四个散点图中,x,y虽负相关趋势的是()A. B.C. D.4.已知等比数列{a n}的公比为一2,且a2+a5=1,则a4+a7=()A. −8B. 8C. −4D. 45.下列四个数中,最大的是()A. log123 B. log4√3 C. log32 D. 126.某学校采用系统抽样方法,从该校高一年级全体800名学生中抽50名学生做视力检查.现将800名学生从1到800进行编号,依从小到大的编号顺序平均分成50个小组,组号依次为1,2,……,50.已知第1小组随机抽到的号码是m,第8小组抽到的号码是9m,则第7小组抽到的号码是()A. 100B. 110C. 120D. 1267.设集合A={y|y=-x2-6x,x≤1},B={y|y=2x-a,0≤x≤1},若A∪B=A,则()A. a的最大值为−7B. a的最大值为−8C. a的最小值为−7D. a的最小值为−88.执行如图所示的程序框图,如果输入的x2=2,x3=5,输出的b=1,则输入的x1的值不可能为()A. 100B. 1000C. 2000D. 100009. 函数f(x)=x 44x −4−x 的大致图象为( ) A. B.C. D.10. 某商场在周末推出购物满100元赠送一次抽奖机会的活动,抽奖是这样进行的:一盒子内放有大小完全相同编号为2,4,5,6,8,9的6个小球,每次从中随机摸出3个小球.若这3个小球的编号可以构成等比数列,则获得一等奖:若这3个小球的编号可以构成等差数列,则获得二等奖.在此次抽奖活动中,获得一等奖与二等奖的概率分别为( )A. 120,14B. 120,15C. 110,14D. 110,15 11. 设S n ,T n 分别为数列{a n },{b n }的前n 项和S n =2a n -1,且49a n −b n =n ⋅2n ,则当T n 取得最大值时,n =( )A. 23B. 24C. 25D. 26 12. 若函数f(x)={(a −1)x −88,x ≤a 1+1gx,x>a ,在R 上是单调函数,则a 的取值范围为( )A. (1,10]B. (1,+∞)C. (0,10]D. [10,+∞)二、填空题(本大题共4小题,共20.0分)13. 若从区间[-4,7]上任意选取一个实数x ,则log 5x <1的概率为______.14. 已知函数f(x)=√4−x +√4x −1,则f (-x )的定义域为______.15. 冬泳能增强人体对冷刺激的适应能力,能提高自身的免疫力,也能增强消化系统功能.为了解某社区参加冬泳参与者的年龄分布情况,某调查小组随机统计了100个该社区冬泳参与者的年龄(他们的年龄都在区间[10,60]内),并绘制出了如图所示的频率分布直方图,则由图可知,这100人年龄在区间[30,50)内的人数为______.16. 在数列{a n }中,a 1=12,且a n+13n+4=3a n 3n+1.记S n =∑ai 3i+1n i=1,T n =∑ai 3i n i=1,则下列判断正确的是______.(填写所有正确结论的编号)①数列{an 3n+1}为等比例数列;②存在正整数n ,使得a n 能被11整除; ③S 10>T 243;④T 21能被51整除.三、解答题(本大题共6小题,共70.0分)17. 将甲、乙两名篮球运动员在五场比赛中所得的分数的数据绘制成茎叶图,如图所示,分别计算在这五场比赛中甲、乙得分的平均数与方差,并据此判断谁的平均水平更好,谁的稳定性更好?18. 已知函数f (x )=log 3x ,g (x )=9x .(1)若f [g (a )]=g [f (a )],求g (1a )的值;(2)若f (x )+g (x )>m 对x ∈(1,2)恒成立,求m 的取值范围.19. 设S n 为等差数列{a n }的前n 项和,a 6=11,公差d <3且a 3+a 7=a 4a 5-45.(1)求S n ;(2)求数列{n S n (a n +3)}的前50项和T 50.20. 某餐馆将推出一种新品特色菜,为更精准确定最终售价,这种菜按以下单价各试吃单价x (元) 1819 20 21 22 销量y (份) 61 56 50 48 45 (2)预计今后的销售中,销量与单价服从(1)中的线性回归方程,已知每份特色菜的成本是15元,为了获得最大利润,该特色菜的单价应定为多少元?(附:,)21.设数列{a n},{b n}满足b n=2n,a1b1+a2b2+⋯+a n b n=n2b n.(1)求数列{a n}的通项公式;(2)求数列{a n+1−a nb n }的前n项和Sn.22.已知函数f(x)=2x-3,g(x)=ax2-2x(a∈R,且a≥0).(1)当a>2时,证明:函数f(x)的零点与函数g(x)的零点之和小于3;(2)若对任意x1,x2∈[1,2],f(x1)≠g(x2),求a的取值范围.答案和解析1.【答案】B【解析】解:集合A={x∈N|x<4}={0,1,2,3},B={x|-3<x<3},则A∩B={0,1,2}.故选:B.用列举法写出集合A,再根据交集的定义写出A∩B.本题考查了交集的运算问题,是基础题.2.【答案】A【解析】解:在等差数列{a n}中,由已知得a1=2,a3=10,∴d=.故选:A.由已知结合等差数列的通项公式求解.本题考查等差数列的通项公式,是基础的计算题.3.【答案】C【解析】解:对于A,散点图中的点从左向右是上升的,且在一条直线附近,是正相关关系;对于B,散点图中的点不成带状分布,没有明显的相关关系;对于C,散点图中的点从左向右是下降的,且在一条直线附近,是负相关关系;对于D,散点图中的点不成带状分布,没有明显的相关关系.故选:C.根据散点图中各点的分布情况,判断是否具有相关性和正负相关关系.本题考查了利用散点图判断相关性问题,是基础题.4.【答案】D【解析】解:∵等比数列{a n}的公比为-2,a2+a5=1,∴a4+a7=a2q2+a5q2=q2(a2+a5)=4,故选:D.由题意可得a4+a7=q2(a2+a5)=4,问题得以解决.本题考查了等比数列的通项公式,考查了运算能力,属于基础题.5.【答案】C【解析】解:<log1=0,log4=log163<log164=,log32>=.∴四个数中最大的是log32.故选:C.利用对数函数、指数函数的单调性直接求解.本题考查四个数的大小的判断,考查对数函数、指数函数的单调性等基础知识,考查运算求解能力,考查函数与方程思想,是基础题.6.【答案】B【解析】解:样本间隔为800÷50=16,∵第1小组随机抽到的号码是m,第8小组抽到的号码是9m,∴9m=m+16(8-1),解得m=14,则第7小组抽到的号码是16×(7-1)+14=110故选:B.求出样本间隔,利用系统抽样的定义进行求解即可.本题主要考查系统抽样的应用,根据条件求出样本间隔是解决本题的关键.7.【答案】B【解析】解:y=-(x+3)2+9,且x≤1;∴y≥9;∴A={y|y≥9};∵0≤x≤1;∴1≤2x≤2;∴1-a≤2x-a≤2-a;∴B={y|1-a≤y≤2-a};∵A∪B=A;∴B⊆A;∴1-a≥9;∴a≤-8;∴a的最大值为-8.故选:B.可解出A={y|y≥9},B={y|1-a≤y≤2-a},而根据A∪B=A即可得出A⊆B,从而得出1-a≥9,得出a≤-8,从而得出a的最大值为-8.考查描述法的定义,二次函数的图象,指数函数的单调性,以及并集、子集的定义.8.【答案】C【解析】解:模拟程序的运行可知该程序的功能是利用循环结构计算并输出变量b的值;且x2=2,x3=5,a=,b=,∴b=,∴x1是x2•x3的倍数;由程序运行结果为输出b=1,∴输入的x1的值不可能为2000.故选:C.由已知中的程序语句,模拟程序的运行过程,分析循环中各变量值的变化情况,即可得出答案.本题考查了程序框图的应用问题,解题时应模拟程序框图的运行过程,以便得出正确的结论.9.【答案】A【解析】解:函数是奇函数,排除选项BD,当x=2时,f(2)=,对应点在y=1的上方,排除C.故选:A.判断函数的奇偶性排除选项,特殊值对于点的位置排除选项即可.本题考查函数与方程的应用,函数的图象的判断,是基本知识的考查.10.【答案】D【解析】解:一盒子内放有大小完全相同编号为2,4,5,6,8,9的6个小球,每次从中随机摸出3个小球.基本事件总数n==20,这3个小球的编号可以构成等比数列,包含的基本事件(a,b,c)有(2,4,8),(4,6,9),共有两个,若这3个小球的编号可以构成等比数列,则获得一等奖,∴在此次抽奖活动中,获得一等奖的概率p1==,这3个小球的编号可以构成等差数列,包含的基本事件(a,b,c)有:(2,4,6),(2,5,8),(4,5,6),(4,6,8),共有4个,若这3个小球的编号可以构成等差数列,则获得二等奖.∴在此次抽奖活动中,获得二等奖的概率为p2=.故选:D.基本事件总数n==20,这3个小球的编号可以构成等比数列,包含的基本事件(a,b,c)有(2,4,8),(4,6,9),共有两个,这3个小球的编号可以构成等差数列,包含的基本事件(a,b,c)有(2,4,6),(2,5,8),(4,5,6),(4,6,8),共有4个,由此能求出在此次抽奖活动中,获得一等奖与二等奖的概率.本题考查概率的求法,考查古典概型、列举法等基础知识,考查运算求解能力,考查函数与方程思想,是基础题.11.【答案】B【解析】解:∵S n=2a n-1,∴当n=1时,S1=a1=1,当n≥2时,S n=2(S n-S n-1)-1,即S n=2S n-1+1,即S n+1=2(S n-1+1),由S1+1=2得:{S n+1}是以2为首项,以2为公比的等比数列,故S n+1=2n即S n=2n-1,则a n=S n-S n-1=2n-1,又由得:故当n≤24时,b n>0,当n>24时,b n<0,故当T n取得最大值时,n=24故选:B.根据已知利用构造等比等比数列法,可得S n+1=2n,进而可得a n=2n-1,求出{b n}的通项公式后,分析数列值由正变负的临界点,可得答案.本题考查的知识点是数列的递推公式,求数列通项公式,难度中档.12.【答案】A【解析】解:若函数,在R上是单调函数,由y=lgx,x>a是增函数,所以,当a>1时,lga-a2+a+89>0,画出函数y=1+lga,以及y=a2-a-88的图象如图:可得,a∈(1,10].故选:A.判断函数的单调性,利用函数的单调性的性质,列出不等式,即得所求.本题主要求函数的单调性的性质,分段函数的应用,属于中档题.13.【答案】511【解析】解:由log5x<1解得0<x<1,在区间[-3,2]上随机选取一个实数x,对应事件的为区间长度为:7+4=11,而满足事件“0<x<1”发生的事件的长度为:1,由几何概型的公式得到所求概率为;故答案为:由题意,利用区间的长度比求概率即可.本题考查了几何概型的概率求法;明确事件的测度为区间的长度是关键.14.【答案】[-4,0]【解析】解:要使f(x)有意义,则;解得0≤x≤4;∴f(x)的定义域为[0,4];∴0≤-x≤4;∴-4≤x≤0;∴f(-x)的定义域为[-4,0].故答案为:[-4,0].可看出,要使f(x)有意义,则需满足,从而得出f(x)的定义域,进而得出f(-x)的定义域.考查函数定义域的概念及求法,指数函数的单调性.15.【答案】50【解析】解:由频率分布直方图得年龄在区间[30,50)内的频率为:(0.028+0.022)×10=0.5,∴这100人年龄在区间[30,50)内的人数为100×0.5=50.故答案为:50.由频率分布直方图得年龄在区间[30,50)内的频率为0.5,由此能求出这100人年龄在区间[30,50)内的人数.本题考查频数的求法,考查频率分布直方图等基础知识,考查运算求解能力,考查数形结合思想,是基础题.16.【答案】①②④【解析】解:=,可得=3•,可得数列{}为首项为3,公比为3的等比数列,故①正确;由=3n,即a n=(3n+1)•3n,可得n=7时,a7=22•37,能被11整除,故②正确;S n==3+9+…+3n==(3n-1),T n===4+7+…+(3n+1)=n(3n+5),由S10=(310-1)=88572,T243=×243×734=89181,S10<T243,故③错误;T21=×21×68=51×14能被51整除,故④正确.故答案为:①②④.由等比数列的定义可得数列{}为首项为3,公比为3的等比数列,可判由等比数列的通项公式计算可判断②;分别运用等差数列和等比数列的求和公式计算可判断③;由等差数列的求和公式计算可判断④.本题考查等比数列和等差数列的定义和通项公式、求和公式,考查化简变形能力和运算能力,推理能力,属于基础题.17.【答案】解:∵x =8+7+9+12+145=10, ∴S 甲2=42+32+12+22+425=6.8. ∵x 乙=8+9+10+14+195=12, ∴S 乙2=42+32+22+22+725=16.4. ∵x 乙>x 甲,S 甲2<S 乙2,∴乙的平均水平更好,甲的稳定性更好.【解析】分别求出甲、乙得分的平均数与方差,由此能判断谁的平均水平更好,谁的稳定性更好.本题考查判断谁的平均水平更好,谁的稳定性更好的判断,考查平均数、方差的性质等基础知识,考查运算求解能力,考查函数与方程思想,是基础题. 18.【答案】解:(1)由题意知a >0,若f [g (a )]=g [f (a )],则f (9a )=g (log 3a ),即log 39a =9log 3a ,即log 332a =(3log 3a )2,即2a =a 2,得a =2或a =0(舍).则g (1a )=g (12)=912=√9=3.(2)若f (x )+g (x )>m 对x ∈(1,2)恒成立,则log 3x +9x >m 对x ∈(1,2)恒成立,设h (x )=log 3x +9x ,则当x ∈(1,2)时,h (x )为增函数,∴h (1)<h (x )<h (2),即9<h (x )<log 32+92,则m ≤9.即实数m 的取值范围是(-∞,9].(1)根据对数和指数幂的运算法则进行化简求出a 的值,代入计算即可. (2)根据不等式恒成立,转化求求函数的最值,求出函数的值域即可.本题主要考查对数函数和指数函数的性质,以及不等式恒成立,构造函数,转化为求函数的值域是解决本题的关键.19.【答案】解:(1)∵a 3+a 7=2a 5=a 4a 5-45,又a 6=11,∴2(11-d )=(11-2d )(11-d )-45,解得d =2或d =272, ∵d <3,∴d =2, ∴a 1=11-2×5=1, ∴a 2=2n -1,S n =n(1+2n−1)2=n 2. (2)∵n S n (a n +3)=1n(2n+2)=12(1n −1n+1), ∴T 50=12(1−12+12−13+⋯+150−151)=12(1−151)=2551.【解析】(1)运用等差数列的通项公式,解方程可得公差和首项,即可得到所求通项公式;(2)运用等差数列的求和公式可得,运用数列的裂项相消求和,即可得到所求和.本题考查等差数列的通项公式和求和公式的运用,考查数列的裂项相消求和,考查化简运算能力,属于基础题.20.【答案】解;(1)∵x =15(18+19+20+21+22)=20,y =15(61+56+50+48+45)=52,∑(5i=1x i −x)(y i −y)=−40,∑(5i=1x i −x)2=10, ∴,,所以y 关于x 的线性回归方程为:.∴当x=1928=24时,z取最大值,∴单价应定为24元,可获得最大利润.【解析】(1)分别求出x,y的平均数,求出相关系数,求出回归方程即可;(2)求出利润z关于x的解析式,结合二次函数的性质求出对应x的值即可.本题考查了求回归方程问题,考查二次函数的性质,是一道中档题.21.【答案】解:(1)当n=1时,a1=1.当n≥2时,a1b1+a2b2+⋯+a n b n=n2b n①,a1b1+a2b2+⋯+a n−1b n−1=(n−1)2b n−1②,①-②得a n b n=n2b n−(n−1)2b n−1,∴a n=n2b n−(n−1)2b−1b n =n2−12(n−1)2=n2+2n+12.经验证a1=1符合上式,故a n=n2+2n−12.(2)a n+1−a n=12(2n+3),∴S n=12(52+722+⋯+2n+32n),1 2S n=12(522+733+⋯+2n+32n+1),∴1 2S n=12(52+222+223+⋯+22n−2n+32n+1),则S n=52+2×122−12n+11−12−2n+32n+1=52+2×122−12n+11−12−2n+32n+1=72−2n+72n+1.【解析】(1)直接利用递推关系式求出数列的通项公式.(2)利用乘公比错位相减法在数列求和中的应用.本题考查的知识要点:数列的通项公式的求法及应用,乘公比错位相减法在数列求和中的应用,主要考查学生的运算能力和转化能力,属于基础题型.22.【答案】(1)证明:f(x)的零点为log23,当a>2时,g(x)的零点为0,2a,∵log23<2,且当a>2时,0<2a<1,∴log23+2a<3,(2)解:由已知可得两个函数的值域交集为空,当x ∈[1,2]时,f (x )=2x -3∈[-1,1].若a =0,g (x )=-2x ∈[-4,-2],满足题意.若a >0,g(x)=a(x −1a )2−1a ,当1a ≤1即a ≥1时,g (x )在[1,2]上单调递增,∴g (x )∈[a -2,4a -4],∵a ≥1,∴4a -4≥0,∴a -2>1,即a >3.当1a ≥2即0<a ≤12时,g (x )在[1,2]上单调递减,∴g (x )∈[4a -4,a -2],∵a -2<0,∴a −2≤−32,∴0<a ≤12满足题意.当1<1a <2即12<a <1时,g(x)min =g(1a )=−1a ,且−1a ∈(−2,−1),则{g(2)<−1g(1)<−1,∴a <34,又12<a <1,∴12<a <34.综上,a 的取值范围为[0,34)∪(3,+∞).【解析】(1)分别求得f (x ),g (x )的零点,由对数的运算性质,即可得证;(2)由已知可得两个函数的值域交集为空,对a 进行分类讨论,可得结果. 本题考查函数的零点求法,考查不等式恒成立问题解法,注意运用分类讨论思想方法,以及函数的单调性,考查运算能力,属于中档题。
2019-2020学年河北省邢台市高一上学期期末数学试题(解析版)
2019-2020学年河北省邢台市高一上学期期末数学试题一、单选题1.已知集合{|22}A x x =-≤≤,{}2|log 2B x x =<,则()R A B =I ð( ) A .{|20}x x -≤≤B .{|20}x x -≤<C .{|24}x x 剟D .{|02}x x <„【答案】A【解析】解对数不等式求得集合B ,由此求得U B ð,进而求得()R A B I ð. 【详解】因为2log 2x <,所以22log log 4x <,所以{}|04B x x =<<,所以R {|0B x x =≤ð或4}x ≥,所以()R {|20}A B x x ⋂=-剟ð.故选:A 【点睛】本小题主要考查集合交集和补集的概念和运算,考查对数不等式的解法,属于基础题. 2.函数log (1)3a y x =++的图象恒过定点M ,则M 的坐标为( ) A .(-1,3) B .(0,3)C .(3,-1)D .(3,0)【答案】B【解析】根据对数型函数过定点,求得M 点的坐标. 【详解】令log (1)0a x +=,则0x =,故M 的坐标为(0,3). 故选:B 【点睛】本小题主要考查对数型函数过定点问题,属于基础题.3.若函数()27x f x x =+-的零点所在的区间为(,1)()k k k +∈Z ,则k =( ) A .3 B .4C .1D .2【答案】D【解析】结合零点存在性定理和函数()f x 的单调性,求得k 的值. 【详解】∵(2)4270,(3)8370,f f =+-<⎧⎨=+->⎩且()f x 单调递增,∴()f x 的零点所在的区间为(2,3),∴2k =. 故选:D 【点睛】本小题主要考查零点存在性定理的运用,考查函数的单调性,属于基础题. 4.若函数2(1)5f x x -=+,则(2)f -=( ) A .9 B .6 C .4 D .3【答案】B【解析】求得2-对应x 的值,由此求得函数值. 【详解】由12x -=-,解得1x =-,所以()()22156f -=-+=. 故选:B 【点睛】本小题主要考查函数值的求法,属于基础题. 5.下列函数中,既以π为周期,又在区间0,2π⎛⎫⎪⎝⎭上单调递减的函数是( ) A .cos2x y =- B .|sin |y x =C .tan 1e xy ⎛⎫= ⎪⎝⎭D .cos 24x y π⎛⎫=+⎪⎝⎭ 【答案】C【解析】逐一分析四个选项中函数的单调性和最小正周期,由此确定正确选项. 【详解】 A 中函数在0,2π⎛⎫⎪⎝⎭上单调递增,不合题意;B 中函数在区间0,2π⎛⎫⎪⎝⎭上单调递增,不合题意;C 中函数满足题意;D 中函数的最小正周期为4π,不合题意; 综上所述,选项C 满足题意. 故选:C 【点睛】本小题主要考查函数的周期性和单调性,属于基础题.6.已知()lg sin143a ︒=,22tan 371tan 37b ︒︒=-,22c -=,则( ) A .b c a >> B .a b c >>C .c a b >>D .b a c >>【答案】A【解析】利用“0,1分段法”,结合对数函数、三角恒等变换、指数函数的知识,比较出三者的大小关系. 【详解】因为()lg sin143lg10a ︒=<=,22tan 37tan 7411tan 37b ︒︒︒==>-,212(0,1)4c -==∈,所以b c a >>. 故选:A 【点睛】本小题主要考查利用对数函数、三角恒等变换、指数函数的知识比较大小,属于基础题. 7.函数()ln(sin cos )f x x x =-+( )A .,3ππ⎛⎤⎥⎝⎦ B .73,44ππ⎛⎫-- ⎪⎝⎭C .73,,444ππππ⎛⎫⎛⎤--⋃ ⎪ ⎥⎝⎭⎝⎦D .7,(0,]44πππ⎛⎫--⋃ ⎪⎝⎭ 【答案】C【解析】根据偶次方根的被开方数为非负数、对数真数大于零,结合三角不等式的解法,求得函数的定义域. 【详解】由sin cos 0,0,20,x x x x ππ->⎧⎪-⎨⎪+⎩……得522,,442,k x k k x ππππππ⎧+<<+∈⎪⎨⎪-⎩Z 剟故73,,444x ππππ⎛⎫⎛⎤∈--⋃ ⎪ ⎥⎝⎭⎝⎦. 故选:C 【点睛】本小题主要考查函数定义域的求法,属于基础题. 8.函数2212xx y --+=-的单调递增区间为( )A .(,1]-∞-B .[1,)-+∞C .(,1]-∞D .[1,)+∞【答案】B【解析】利用复合函数单调性同增异减,判断出函数的单调递增区间. 【详解】 因为函数221y xx =--+的单调递减区间为[1,)-+∞,所以原函数的单调递增区间为[1,)-+∞.故选:B 【点睛】本小题主要考查指数型复合函数单调性的求法,属于基础题.9.已知()f x 是定义在(26,)a a -上的奇函数,且()f x 在[0,)a 上单调递减,则不等式(31)(14)f x f x --…的解集为( )A .12,37⎛⎤- ⎥⎝⎦B .23,74⎡⎫⎪⎢⎣⎭ C .12,47⎡⎫-⎪⎢⎣⎭ D .12,47⎛⎤-⎥⎝⎦ 【答案】D【解析】根据奇函数的定义域的特点求得a ,根据奇函数的单调性以及函数的定义域化简所求不等式,由此求得不等式的解集. 【详解】因为()f x 是奇函数,所以260a a -+=,则2a =,所以()f x 的定义域为(2,2)-.又()f x 在[0,2)上单调递减,从而在(2,2)-上单调递减,所以由(31)(14)f x f x --…,可得231,3114,142,x x x x -<-⎧⎪--⎨⎪-<⎩„所以1247x -<„,即不等式(31)(14)f x f x --…的解集为12,47⎛⎤- ⎥⎝⎦.故选:D 【点睛】本小题主要考查根据函数的单调性、奇偶性解不等式,属于基础题.10.函数()sin()(0,0)f x x ωϕωϕπ=+><<的部分图象如图所示,BC ∥x 轴当70,12x π⎡⎤∈⎢⎥⎣⎦时,若不等式()sin 2f x m x -„恒成立,则m 的取值范围是( )A .32⎫+∞⎪⎢⎪⎣⎭B .1,2⎡⎫+∞⎪⎢⎣⎭C .3,)+∞D .[1,)+∞【答案】A【解析】根据,B C 两点的对称性求得()f x 的一条对称轴方程,由此结合()f x 的周期性求得ω的值,结合π,03⎛⎫⎪⎝⎭求得ϕ,进而求得()f x 的解析式,利用分离常数法化简()sin 2f x m x -„,结合三角函数值域的求法,求得m 的取值范围.【详解】因为//BC x ,所以()f x 的图像的一条对称轴方程为2723212x πππ+==,71212344ππππω-==⨯,所以2ω=.由于函数()f x 图像过π,03⎛⎫ ⎪⎝⎭,由23k πϕππ⨯+=+,k Z ∈,且0ϕπ<<,得3πϕ=,所以()sin 23f x x π⎛⎫=+ ⎪⎝⎭.()sin 2f x m x -„,等价于()sin 2f x x m -„,令()sin 2sin 23g x x x π⎛⎫=+- ⎪⎝⎭,70,12x π⎡⎤∈⎢⎥⎣⎦,()sin 2coscos 2sinsin 2cos 2336g x x x x x πππ⎛⎫=+-=+ ⎪⎝⎭. 由70,12x π⎡⎤∈⎢⎥⎣⎦,得42,663x πππ⎡⎤+∈⎢⎥⎣⎦,()g x 3,所以3m …故选:A【点睛】本小题主要考查根据三角函数的图像求三角函数的解析式,考查三角函数最值的求法,考查三角恒等变换,考查化归与转化的数学思想方法,属于中档题.11.已知锐角θ满足22tan tan 60θθ--=,224sin 3sin cos cos a θθθθ=--,则函数2sin ()=sin x af x x a+-( )A .没有最大值也没有最小值B .只有最大值,且最大值为114C .只有最小值,且最小值为194- D .最大值是114,最小值是194-【答案】D【解析】解一元二次方程求得tan θ,利用“1”的代换以及齐次方程的方法,求得a ,由此求得()f x 解析式,利用分离常数法以及换元法,结合函数的单调性,求得()f x 的最大值和最小值. 【详解】由22tan tan 60θθ--=,得tan 2θ=或3tan 2θ=-(舍), 则22224tan 3tan 194sin 3sin cos cos tan 15a θθθθθθθ--=--==+, 则9272sin 55()299sin sin 55x f x x x +==+--,令sin x t =,则[1,1]t ∈-,令275()295g t t =+-, 易知关于t 的函数275()295g t t =+-在区间[1,1]-上单调递减,所以()f x 的最大值是114,最小值是194-. 故选:D 【点睛】本小题主要考查同角三角函数的基本关系式和齐次方程,考查分式型函数最值的求法,属于中档题.12.设函数1e 1,0,()(1)(2),0,x x f x f x f x x +⎧-=⎨--->⎩…则(2020)f =( )A .eB .11e- C .1-e D .-e【答案】C【解析】首先根据分段函数解析式判断出当0x >时,()f x 是周期为6的周期函数,由此求得()2020f 的值. 【详解】当x >0时,由()(1)(2)f x f x f x =---,可得(1)()(1)f x f x f x +=--,两式相加得(1)(2)f x f x +=--,则当x >0时,(6)()f x f x +=,故(2020)(4)(1)(1)(0)1e f f f f f ==-=--=-.故选:C 【点睛】本小题主要考查分段函数求函数值,考查函数的周期性,属于基础题.二、填空题13.已知()f x 是R 上的奇函数,且当(1,0)x ∈-时,()4x f x =-,则45log 4f ⎛⎫= ⎪⎝⎭_________.【答案】45【解析】利用奇函数的性质以及题目所给(1,0)x ∈-时,()f x 的解析式,化简求得45log 4f ⎛⎫ ⎪⎝⎭的值.【详解】 因为4454log log 45f f ⎛⎫⎛⎫=- ⎪ ⎪⎝⎭⎝⎭,44log (1,0)5∈-, 所以544log 44544log log 4455f f⎛⎫⎛⎫=-== ⎪ ⎪⎝⎭⎝⎭. 故答案为:45【点睛】本小题主要考查函数的奇偶性,属于基础题.14.已知集合{}22,4,46A a a =-+,{2,}B a =,A B B =I ,则实数a 的取值的集合为_________. 【答案】{3,4}【解析】分成24,46a a a a ==-+两种情况,结合集合元素的互异性,求得a 的取值的集合. 【详解】当4a =时,2466a a -+=,符合;当246a a a -+=,解得2a =,3a =,由集合元素的互异性,2a =舍去.故4a =或3a =. 故答案为:{3,4} 【点睛】本小题主要考查根据交集的结果求参数,考查集合元素的互异性,属于基础题. 15.已知一扇形的半径为2,弧长为π,则该扇形的圆心角所对的弦长是_________.【答案】【解析】首先计算出圆心角,然后根据勾股定理求得圆心角所对的弦长. 【详解】设扇形的弧长为l ,圆心角为θ,由l r θ=,得2θπ=,即2πθ=,故所对的弦长是=.故答案为:【点睛】本小题主要考查扇形弧长、弦长有关计算,属于基础题.16.已知函数()sin f x a x x =+的图象关于直线76x π=对称,则函数7()()5g x f x =-在7,22ππ⎡⎤-⎢⎥⎣⎦上的所有零点之和为________.【答案】143π 【解析】首先根据()f x 关于直线76x π=对称求得a 的值,即求得()f x 解析式.由此画出()f x 与75y =的图象,结合三角函数图象的对称性,求得函数7()()5g x f x =-在7,22ππ⎡⎤-⎢⎥⎣⎦上的所有零点之和. 【详解】由题意,函数()sin )f x a x x x θ==+(θ为辅助角).由于()f x 图象的一条对称轴的方程为76x π=,得23322a a +=+,解得1a =,所以()2sin 3f x x π⎛⎫=+ ⎪⎝⎭,结合函数7()2sin(322f x x x πππ⎫⎛⎫=+-⎪⎪⎭⎝⎭剟与75y =的图象可知,方程()0g x =有4个根1x ,2x ,3x ,4x (1234x x x x <<<),且1x ,2x 关于6π对称,3x ,4x 关于136π对称,即12263x x ππ+=⨯=,341313263x x ππ+=⨯=,所以1234143x x x x π+++=.故答案为:143π 【点睛】本小题主要考查三角函数辅助角公式,三角函数图像与性质,考查函数零点问题的求解策略,考查数形结合的数学思想方法,属于中档题.三、解答题17.已知角θ的终边经过点(2,3)P -,求下列各式的值. (1)2sin 3cos sin θθθ-;(2)23cos 2cos cos(2)222πθπθθπ⎛⎫⎛⎫-+++-- ⎪ ⎪⎝⎭⎝⎭. 【答案】(1) 23-(2)0 【解析】(1)根据θ终边上一点的坐标,求得tan θ的值.将所求表达式化为只含tan θ的式子,由此求得所求表达式的值.(2)利用诱导公式、二倍角公式以及“1”的代换的方法,将所求表达式化为只含tan θ的式子,由此求得所求表达式的值. 【详解】(1)由角θ的终边经过点P (2,-3),可知3tan 2θ=- 则2sin 2tan 23cos sin 3tan 3θθθθθ==---.(2)23cos 2cos cos(2)222πθπθθπ⎛⎫⎛⎫-+++-- ⎪ ⎪⎝⎭⎝⎭ 22sin 2sin cos 222sin cos 3sin 3θθθθθθ=-+--=-+-222222sin cos 3sin 2tan 3tan 33sin cos tan 1θθθθθθθθ-+-+=-=-++ 393013=-=. 【点睛】本小题主要考查三角函数的定义,考查同角三角函数的基本关系式,考查化归与转化的数学思想方法,属于基础题. 18.计算或化简:(1)112320412730.1log 321664π-⎛⎫⎛⎫++-- ⎪ ⎪⎝⎭⎝⎭;(2)6log 3332log log 2log 36⋅--- 【答案】(1)99(2)-3【解析】(1)利用指数、对数运算,化简所求表达式. (2)利用指数、根式、对数运算,化简所求表达式. 【详解】(1)原式11233225249131log 216104-⎡⎤⎛⎫⎛⎫⎛⎫=++--⎢⎥ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦7351001442=++-- =99.(2)原式323log 313=---31422=-- =-3. 【点睛】本小题主要考查指数、根式和对数运算,属于基础题. 19.已知1()f x ax b x=++是定义在{|0}x x ∈≠R 上的奇函数,且(1)5f =. (1)求()f x 的解析式;(2)判断()f x 在1,2⎛⎫+∞ ⎪⎝⎭上的单调性,并用定义加以证明. 【答案】(1) 1()4(0)f x x x x =+≠ (2) ()f x 在1,2⎛⎫+∞ ⎪⎝⎭上单调递增.见解析 【解析】(1)利用奇函数的性质以及()15f =,列式求得,a b 的值,进而求得函数解析式.(2)利用单调性的定义,通过计算()()120f x f x -<,证得()f x 在1,2⎛⎫+∞⎪⎝⎭上递增. 【详解】(1)∵()f x 为奇函数,∴()()0f x f x -+=,∴0b =.由(1)5f =,得4a =, ∴1()4(0)f x x x x =+≠. (2)()f x 在1,2⎛⎫+∞⎪⎝⎭上单调递增. 证明如下: 设1212x x <<,则()()()121212114f x f x x x x x -=-+- ()12121241x x x x x x -=- ∵1212x x <<,∴120x x -<,12410x x ->,∴()121212410x x x x x x --<, ∴()()120f x f x -<,∴()f x 在1,2⎛⎫+∞⎪⎝⎭上单调递增. 【点睛】本小题主要考查根据函数的奇偶性求参数,考查利用函数单调性的定义证明函数的单调性,属于基础题.20.已知函数()sin cos 3f x x x a π⎛⎫=++ ⎪⎝⎭在区间0,2π⎡⎤⎢⎥⎣⎦上有且只有两个不同的零点1x 和2x ,记1202x x x +=,将()f x 的图象向右平移0x 个单位长度得到函数()g x 的图象. (1)求()g x 的解析式及a 的取值范围;(2)求()g x 在0,2π⎡⎤⎢⎥⎣⎦上的单调区间. 【答案】(1) 1()sin 226g x x a π⎛⎫=+ ⎪⎝⎭0a <„. (2) 单调递增区间为06,π⎡⎤⎢⎥⎣⎦,单调递减区间为,62ππ⎡⎤⎢⎥⎣⎦. 【解析】(1)利用两角和的余弦公式、辅助角公式化简()f x 解析式,根据()f x 在区间0,2π⎡⎤⎢⎥⎣⎦上有且只有两个不同的零点1x 和2x 列不等式组,解不等式组求得a 的取值范围.求得0x 的值,根据函数图像变换的知识求得()g x 的解析式.(2)利用三角函数单调性的求法,求得()g x 在0,2π⎡⎤⎢⎥⎣⎦上的单调区间. 【详解】(1)由题意,1()sin cos sin cos 322f x x x a x x x a π⎛⎫⎛⎫=++=-+ ⎪ ⎪ ⎪⎝⎭⎝⎭11sin 2(1cos 2)sin 244234x x a x a π⎛⎫=--+=+-+ ⎪⎝⎭ 当0,2x π⎡⎤∈⎢⎥⎣⎦时,42,333x πππ⎡⎤+∈⎢⎥⎣⎦, 若232x ππ+=,解得12x π=.因为()f x 在区间0,2π⎡⎤⎢⎥⎣⎦上有且只有两个不同的零点1x 和2x ,则(0)0,10,122f a f a π=⎧⎪⎨⎛⎫=> ⎪⎪⎝⎭⎩„0a <„. 又120212x x x π+==,则11()sin 2sin 2212326g x x a x a πππ⎡⎤⎛⎫⎛⎫=-+=+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦. (2)由(1)可知,1()sin 226g x x a π⎛⎫=++ ⎪⎝⎭,当0,2x π⎡⎤∈⎢⎥⎣⎦时,72666x πππ+剟,当262x ππ+=时,6x π=, 则由正弦函数的单调性可知, 当0,6x π⎡⎤∈⎢⎥⎣⎦时,函数()g x 单调递增;当,62x ππ⎡⎤∈⎢⎥⎣⎦时,函数()g x 单调递减. 即()g x 的单调递增区间为06,π⎡⎤⎢⎥⎣⎦,单调递减区间为,62ππ⎡⎤⎢⎥⎣⎦. 【点睛】本小题主要考查三角恒等变换,考查三角函数图像变换,考查三角函数单调区间的求法,属于中档题.21.已知二次函数()21f x ax x =++,且()()141f x f x x --=-. (1)求()f x 的解析式;(2)若()()g x f x mx =-在[]1,2上的最大值为-1,求m 的值以及()g x 的最小值.【答案】(1) 2()21f x x x =++ (2) 6m =,最小值为178-. 【解析】(1)利用()()141f x f x x --=-列方程,对比系数后求得a 的值.(2)由(1)求得()g x 表达式,根据二次函数的对称轴进行分类讨论,结合()g x 在区间[]1,2上的最大值列方程,由此求得m 的值以及()g x 的最小值.【详解】(1)由()(1)41f x f x x --=-,得221(1)(1)141ax x a x x x ++-----=-,所以2141ax a x -+=-,所以2a =,故2()21f x x x =++,(2)22()212(1)1g x x x mx x m x =++-=+-+. ①当1342m -≤,即7m …时,max ()(2)1121g x g m ==-=-,得6m =, 此时()g x 的图象的对称轴为1544m x -==,min 517()48g x g ⎛⎫==- ⎪⎝⎭. ②当1342m ->,即7m >时,max ()(1)41g x g m ==-=-,得5m =,无解. 综上所述,6m =,()g x 的最小值为178-. 【点睛】本小题主要考查函数解析式的求法,考查二次函数在闭区间上的最大值和最小值问题,考查分类讨论的数学思想方法,属于中档题.22.如图,某小区为美化环境,建设美丽家园,计划在一块半径为R (R 为常数)的扇形区域上,建个矩形的花坛CDEF 和一个三角形的水池FCG .其中GC GF =,O 为圆心,120AOB ∠=︒,C ,G ,F 在扇形圆弧上,D ,E 分别在半径OA ,OB 上,记OG 与CF ,DE 分别交于M ,N ,GOC θ∠=.(1)求△FCG 的面积S 关于θ的关系式,并写出定义域;(2)若R =10米,花坛每平方米的造价是300元,试问矩形花坛的最高造价是多少?(取3=1.732) 【答案】(1) 2sin (1cos )03S R πθθθ⎛⎫=-<< ⎪⎝⎭. (2)17320元 【解析】(1)利用圆的几何性质证得GM CF ⊥,利用θ表示出,FC GM ,由此求得三角形FCG 面积的表达式,并求得θ的取值范围.(2)求得MN ,由此求得矩形CDEF 面积的表达式,利用辅助角公式,结合三角函数求最值的方法,求得矩形CDEF 面积的最大值,从而求得最高造价.【详解】(1)连接OF ,因为GC GF =,所以GOF GOC ∠=∠,易得OOF GOC V V ≌,所以MGF MGC ∠=∠.因为GC GF =,所以GM CF ⊥,所以cos GM R OM R R θ=-=-,sin MC R θ=, 所以21sin (1cos )023S FC GM R πθθθ⎛⎫=⋅=-<< ⎪⎝⎭.(2)因为sin 333ON ND MC R θ===,所以cos sin MN OM ON R θθ=-=,所以222sin cos CDEF S FC MN R θθθ⎛⎫=⋅=- ⎪ ⎪⎝⎭矩形2112sin 2(1cos 2)232R θθ⎡⎤=-⨯-⎢⎥⎣⎦2sin 2363R πθ⎡⎛⎫=+-⎢ ⎪⎝⎭⎣⎦. 因为52,666πππθ⎛⎫+∈ ⎪⎝⎭,所以当6πθ=时,CDEF 矩形S 最大.故矩形花坛的最高造价是230017320R =元. 【点睛】本小题主要考查三角函数在实际生活中的应用,考查扇形中的三角形、矩形面积计算,考查三角函数辅助角公式以及三角函数最值的求法,属于中档题.。
河北省邢台市2022-2023学年高一上学期期末数学试题(含答案解析)
二、多选题 9.已知命题 p :“ x R, x 2 2x3 x 4 0 ”,则( )
A. p : x R, x2 2x3 x4 0
B. p : x R, x 2 2x 3 x 4 0
C. p 是假命题
D. p 是真命题
10.将
y
sin
x
π 6
的图象上的所有点的横坐标伸长到原来的
4.在定义域内存在 x1, x2 x1 x2 ,使得 f x1 f x2 成立的幂函数称为“亲幂函数”,
则下列函数是“亲幂函数”的是( )
A. f x x
B. f x 2x
C.
f
x
1
x3
D. f x x2
5.已知函数
f
x
Asin
x
A
0,
0,
π 2 的部分图象如图所示,则(
1
π
9 5
π, 2
当
x
0,
π 2
时, sin
x
0 ,则
f
x
2sinx
1 ,所以
f
x
在
0,
π 2
上单调递增,
所以 f log32 f
8 9
f
π
9 5
,则
f
π log32
f
8 9
f
5 3
2
,即
c<a<b
.
故选:D.
9.AD
答案第 3页,共 13页
【分析】根据含量词的命题的否定方法判断 AB,通过分解因式判断命题 p 的真假. 【详解】因为命题为:“ x R, x 2 2x3 x 4 0 ”,
定函数”.下列函数中,是区间 D 上的“稳定函数”的有( )
2017-2018学年河北省邢台市高一(上)期末数学试卷(解析版)
2017-2018学年河北省邢台市高一(上)期末数学试卷一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.(5分)已知集合A={x∈N|x<4},B={x|﹣3<x<3},则A∩B=()A.{1,2}B.{0,1,2}C.(﹣3,4)D.(﹣3,3)2.(5分)一个等差数列的首项与第3项分别为2,10,则该等差数列的公差为()A.4B.﹣4C.3D.83.(5分)已知x,y是两个变量,下列四个散点图中,x,y虽负相关趋势的是()A.B.C.D.4.(5分)已知等比数列{a n}的公比为一2,且a2+a5=1,则a4+a7=()A.﹣8B.8C.﹣4D.45.(5分)下列四个数中,最大的是()A.B.C.log 32D.6.(5分)某学校采用系统抽样方法,从该校高一年级全体800名学生中抽50名学生做视力检查.现将800名学生从1到800进行编号,依从小到大的编号顺序平均分成50个小组,组号依次为1,2,……,50.已知第1小组随机抽到的号码是m,第8小组抽到的号码是9m,则第7小组抽到的号码是()A.100B.110C.120D.1267.(5分)设集合A={y|y=﹣x2﹣6x,x≤1},B={y|y=2x﹣a,0≤x≤1},若A∪B=A,则()A.a的最大值为﹣7B.a的最大值为﹣8C.a的最小值为﹣7D.a的最小值为﹣88.(5分)执行如图所示的程序框图,如果输入的x2=2,x3=5,输出的b=1,则输入的x1的值不可能为()A.100B.1000C.2000D.100009.(5分)函数的大致图象为()A.B.C.D.10.(5分)某商场在周末推出购物满100元赠送一次抽奖机会的活动,抽奖是这样进行的:一盒子内放有大小完全相同编号为2,4,5,6,8,9的6个小球,每次从中随机摸出3个小球.若这3个小球的编号可以构成等比数列,则获得一等奖:若这3个小球的编号可以构成等差数列,则获得二等奖.在此次抽奖活动中,获得一等奖与二等奖的概率分别为()A.,B.,C.,D.,11.(5分)设S n,T n分别为数列{a n},{b n}的前n项和S n=2a n﹣1,且,则当T n取得最大值时,n=()A.23B.24C.25D.2612.(5分)若函数,在R上是单调函数,则a的取值范围为()A.(1,10]B.(1,+∞)C.(0,10]D.[10,+∞)二、填空题(本大题共4小题,每小题5分,共20分,把答案填在答题卡中的横线上)13.(5分)若从区间[﹣4,7]上任意选取一个实数x,则log5x<1的概率为.14.(5分)已知函数,则f(﹣x)的定义域为.15.(5分)冬泳能增强人体对冷刺激的适应能力,能提高自身的免疫力,也能增强消化系统功能.为了解某社区参加冬泳参与者的年龄分布情况,某调查小组随机统计了100个该社区冬泳参与者的年龄(他们的年龄都在区间[10,60]内),并绘制出了如图所示的频率分布直方图,则由图可知,这100人年龄在区间[30,50)内的人数为.16.(5分)在数列{a n}中,a1=12,且=.记S n=,T n=,则下列判断正确的是.(填写所有正确结论的编号)①数列{}为等比例数列;②存在正整数n,使得a n能被11整除;③S10>T243;④T21能被51整除.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)17.(10分)将甲、乙两名篮球运动员在五场比赛中所得的分数的数据绘制成茎叶图,如图所示,分别计算在这五场比赛中甲、乙得分的平均数与方差,并据此判断谁的平均水平更好,谁的稳定性更好?18.(12分)已知函数f(x)=log3x,g(x)=9x.(1)若f[g(a)]=g[f(a)],求g()的值;(2)若f(x)+g(x)>m对x∈(1,2)恒成立,求m的取值范围.19.(12分)设S n为等差数列{a n}的前n项和,a6=11,公差d<3且a3+a7=a4a5﹣45.(1)求S n;(2)求数列的前50项和T50.20.(12分)某餐馆将推出一种新品特色菜,为更精准确定最终售价,这种菜按以下单价各试吃1天,得(1)求销量y关于x的线性回归方程;(2)预计今后的销售中,销量与单价服从(1)中的线性回归方程,已知每份特色菜的成本是15元,为了获得最大利润,该特色菜的单价应定为多少元?(附:,)21.(12分)设数列{a n},{b n}满足,.(1)求数列{a n}的通项公式;(2)求数列的前n项和S n.22.(12分)已知函数f(x)=2x﹣3,g(x)=ax2﹣2x(a∈R,且a≥0).(1)当a>2时,证明:函数f(x)的零点与函数g(x)的零点之和小于3;(2)若对任意x1,x2∈[1,2],f(x1)≠g(x2),求a的取值范围.2017-2018学年河北省邢台市高一(上)期末数学试卷参考答案与试题解析一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.【解答】解:集合A={x∈N|x<4}={0,1,2,3},B={x|﹣3<x<3},则A∩B={0,1,2}.故选:B.2.【解答】解:在等差数列{a n}中,由已知得a1=2,a3=10,∴d=.故选:A.3.【解答】解:对于A,散点图中的点从左向右是上升的,且在一条直线附近,是正相关关系;对于B,散点图中的点不成带状分布,没有明显的相关关系;对于C,散点图中的点从左向右是下降的,且在一条直线附近,是负相关关系;对于D,散点图中的点不成带状分布,没有明显的相关关系.故选:C.4.【解答】解:∵等比数列{a n}的公比为﹣2,a2+a5=1,∴a4+a7=a2q2+a5q2=q2(a2+a5)=4,故选:D.5.【解答】解:<1=0,log4=log163<log164=,log 32>=.∴四个数中最大的是log32.故选:C.6.【解答】解:样本间隔为800÷50=16,∵第1小组随机抽到的号码是m,第8小组抽到的号码是9m,∴9m=m+16(8﹣1),解得m=14,则第7小组抽到的号码是16×(7﹣1)+14=110故选:B.7.【解答】解:y=﹣(x+3)2+9,且x≤1;∴y≤9;∴A={y|y≤9};∵0≤x≤1;∴1≤2x≤2;∴1﹣a≤2x﹣a≤2﹣a;∴B={y|1﹣a≤y≤2﹣a};∵A∪B=A;∴B⊆A;∴2﹣a≥9;∴a≤﹣7;∴a的最大值为﹣7.故选:A.8.【解答】解:模拟程序的运行可知该程序的功能是利用循环结构计算并输出变量b的值;且x2=2,x3=5,a=,b=,∴b=,∴x1是x2•x3的倍数;由程序运行结果为输出b=1,∴输入的x1的值不可能为2000.故选:C.9.【解答】解:函数是奇函数,排除选项BD,当x=2时,f(2)=,对应点在y=1的上方,排除C.故选:A.10.【解答】解:一盒子内放有大小完全相同编号为2,4,5,6,8,9的6个小球,每次从中随机摸出3个小球.基本事件总数n==20,这3个小球的编号可以构成等比数列,包含的基本事件(a,b,c)有(2,4,8),(4,6,9),共有两个,若这3个小球的编号可以构成等比数列,则获得一等奖,∴在此次抽奖活动中,获得一等奖的概率p1==,这3个小球的编号可以构成等差数列,包含的基本事件(a,b,c)有:(2,4,6),(2,5,8),(4,5,6),(4,6,8),共有4个,若这3个小球的编号可以构成等差数列,则获得二等奖.∴在此次抽奖活动中,获得二等奖的概率为p2=.故选:D.11.【解答】解:∵S n=2a n﹣1,∴当n=1时,S1=a1=1,当n≥2时,S n=2(S n﹣S n﹣1)﹣1,即S n=2S n﹣1+1,即S n+1=2(S n﹣1+1),由S1+1=2得:{S n+1}是以2为首项,以2为公比的等比数列,故S n+1=2n即S n=2n﹣1,则a n=S n﹣S n﹣1=2n﹣1,又由得:故当n≤24时,b n>0,当n>24时,b n<0,故当T n取得最大值时,n=24故选:B.12.【解答】解:若函数,在R上是单调函数,由y=lgx,x>a是增函数,所以,当a>1时,lga﹣a2+a+89>0,画出函数y=1+lga,以及y=a2﹣a﹣88的图象如图:可得,a∈(1,10].故选:A.二、填空题(本大题共4小题,每小题5分,共20分,把答案填在答题卡中的横线上)13.【解答】解:由log5x<1解得0<x<1,在区间[﹣3,2]上随机选取一个实数x,对应事件的为区间长度为:7+4=11,而满足事件“0<x<1”发生的事件的长度为:1,由几何概型的公式得到所求概率为;故答案为:14.【解答】解:要使f(x)有意义,则;解得0≤x≤4;∴f(x)的定义域为[0,4];∴0≤﹣x≤4;∴﹣4≤x≤0;∴f(﹣x)的定义域为[﹣4,0].故答案为:[﹣4,0].15.【解答】解:由频率分布直方图得年龄在区间[30,50)内的频率为:(0.028+0.022)×10=0.5,∴这100人年龄在区间[30,50)内的人数为100×0.5=50.故答案为:50.16.【解答】解:=,可得=3•,可得数列{}为首项为3,公比为3的等比数列,故①正确;由=3n,即a n=(3n+1)•3n,可得n=7时,a7=22•37,能被11整除,故②正确;S n==3+9+…+3n==(3n﹣1),T n===4+7+…+(3n+1)=n(3n+5),由S10=(310﹣1)=88572,T243=×243×734=89181,S10<T243,故③错误;T21=×21×68=51×14能被51整除,故④正确.故答案为:①②④.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)17.【解答】解:∵,∴.∵,∴.∵,,∴乙的平均水平更好,甲的稳定性更好.18.【解答】解:(1)由题意知a>0,若f[g(a)]=g[f(a)],则f(9a)=g(log3a),即log39a=,即log332a=()2,即2a=a2,得a=2或a=0(舍).则g()=g()===3.(2)若f(x)+g(x)>m对x∈(1,2)恒成立,则log3x+9x>m对x∈(1,2)恒成立,设h(x)=log3x+9x,则当x∈(1,2)时,h(x)为增函数,∴h(1)<h(x)<h(2),即9<h(x)<log32+92,则m≤9.即实数m的取值范围是(﹣∞,9].19.【解答】解:(1)∵a3+a7=2a5=a4a5﹣45,又a6=11,∴2(11﹣d)=(11﹣2d)(11﹣d)﹣45,解得d=2或d=,∵d<3,∴d=2,∴a1=11﹣2×5=1,∴a2=2n﹣1,.(2)∵,∴.20.【解答】解;(1)∵=(18+19+20+21+22)=20,=(61+56+50+48+45)=52,,,∴,,所以y关于x的线性回归方程为:.(2)获得的利润z=(x﹣15)y=﹣4x2+192x﹣1980,∴当时,z取最大值,∴单价应定为24元,可获得最大利润.21.【解答】解:(1)当n=1时,a1=1.当n≥2时,①,②,①﹣②得,∴.经验证a1=1符合上式,故.(2),∴,,∴,则.22.【解答】(1)证明:f(x)的零点为log23,当a>2时,g(x)的零点为0,,∵log23<2,且当a>2时,0<,∴,∴函数f(x)零点与函数g(x)的零点之和小于3.(2)解:由已知可得两个函数的值域交集为空,当x∈[1,2]时,f(x)=2x﹣3∈[﹣1,1].若a=0,g(x)=﹣2x∈[﹣4,﹣2],满足题意.若a>0,,当即a≥1时,g(x)在[1,2]上单调递增,∴g(x)∈[a﹣2,4a﹣4],∵a≥1,∴4a﹣4≥0,∴a﹣2>1,即a>3.当即时,g(x)在[1,2]上单调递减,∴g(x)∈[4a﹣4,a﹣2],∵a﹣2<0,∴,∴满足题意.当即时,,且,则,∴,又,∴.综上,a的取值范围为.。
河北省邢台市高一数学上学期期末试卷(含解析)-人教版高一全册数学试题
2015-2016学年某某省某某市高一(上)期末数学试卷一、选择题(共12小题,每小题5分,满分60分)1.设全集U={0,1,2,3,4},∁U A={1,2},B={1,3},则A∪B等于()A.{2} B.{1,2,3} C.{0,1,3,4} D.{0,1,2,3,4}2.某工厂的一个车间包装一种产品,在一定的时间内,从自动包装传送带上,每隔30min抽一包产品,称其重量是否合格,记录抽查产品的重量的茎叶图如图所示(以重量的个位数为叶),则抽查产品重量的中位数和众数分别为()A.96,98 B.96,99 C.98,98 D.98,993.若函数f(x)=ln(x),则f(e﹣2)等于()A.﹣1 B.﹣2 C.﹣e D.﹣2e4.对变量x,y有观测数据(x i,y i)(i=1,2,3,4,5),得表1;对变量u,v有观测数据(u i,v i)(i=1,2,3,4,5),得表2.由这两个表可以判断()表1:x 1 2 3 4 5y 2.9 3.3 3.6 4.4 5.1表2:u 1 2 3 4 5v 25 20 21 15 13A.变量x与y正相关,u与v正相关B.变量x与y负相关,u与v正相关C.变量x与y负相关,u与v负相关D.变量x与y正相关,u与v负相关5.从装有3个红球和2个黑球的口袋内任取2个球,那么对立的两个事件是()A.至少有1个黑球与都是红球B.至少有1个黑球与都是黑球C.至少有1个黑球与至少有1个红球D.恰有1个黑球与恰有2个黑球6.函数f(x)=2x﹣x2的零点所在的一个区间是()A.(﹣,0)B.(,)C.(,)D.(4,+∞)7.已知a=0.85.2,b=0.85.5,c=5.20.1,则这三个数的大小关系为()A.b<a<c B.a<b<c C.c<a<b D.c<b<a8.执行如图所示的程序框图,输出的结果是()A.lg97 B.lg98 C.lg99 D.29.某单位有840名职工,现采用系统抽样方法,抽取42人做问卷调查,将840人从1到840进行编号,求得间隔数k==20,即每20人抽取一个人,其中21号被抽到,则抽取的42人中,编号落入区间[421,720]的人数为()A.12 B.13 C.14 D.1510.假定某运动员每次投掷飞镖正中靶心的概率为0.4,现采用随机模拟的方法估计该运动员两次投掷飞镖两次都命中靶心的概率:先利用计算器产生0到9之间取整数值的随机数,指定2,3,5,7表示命中靶心,1,4,6,8,9,0表示未命中靶心,再以每两个随机数为一组,代表两次的结果,经随机模拟产生了20组随机数:93 28 12 45 85 69 68 34 31 2573 93 02 75 56 48 87 30 11 35据此估计,该运动员两次投掷飞镖都正中靶心的概率为()A.0.16 B.0.20 C.0.35 D.0.4011.已知映射f:M→N,其中集合M={(x,y)|xy=1,x>0},且在映射f的作用下,集合M 中的元素(x,y)都变换为(log2x,log2y),若集合N中的元素都是集合M中元素在映射f 下得到的,则集合N是()A.{(x,y)|x+y=0} B.{(x,y)|x+y=0,x>0} C.{(x,y)|x+y=1} D.{(x,y)|x+y=1,x>0}12.已知函数f(x)=,则满足f[f(a)]=3的实数a的个数为()A.4 B.8 C.12 D.16二、填空题(共4小题,每小题5分,满分20分)13.利用计算机产生0~1之间的均匀随机数x,则事件“3x﹣2≥0”发生的概率为.14.执行如图的程序,若输出的结果是2,则输入的x=.15.已知一个样本x,1,y,5的平均数为2,方差为5,则xy=.16.已知函数f(x)=ln(x+)+ax7+bx3﹣4,其中a,b为常数,若f(﹣3)=4,则f (3)=.三、解答题(共6小题,满分70分)17.已知一次函数y=f(x)满足f(x+1)=x+3a,且f(a)=3.(1)求函数f(x)的解析式;(2)若g(x)=x•f(x)+λf(x)+1在(0,2)上具有单调性,某某数λ的取值X围.18.某地有2000名学生参加数学学业水平考试,现将成绩(满分:100分)汇总,得到如图所示的频率分布表.(1)请完成题目中的频率分布表,并补全题目中的频率分布直方图;成绩分组频数频率[50,60] 100(60,70](70,80] 800(80,90](90,100] 200(2)将成绩按分层抽样的方法抽取150名同学进行问卷调查,甲同学在本次测试中数学成绩为95分,求他被抽中的概率.19.已知函数f(x)=b•a x(a>0且a≠1,b∈R)的图象经过点A(1,),B(3,2).(1)试确定f(x)的解析式;(2)记集合E={y|y=b x﹣()x+1,x∈[﹣3,2]},λ=()0+8+,判断λ与E关系.20.中华龙鸟是生存于距今约1.4亿年的早白垩世现已灭绝的动物,在一次考古活动中,考古学家发现了中华龙鸟的化石标本共5个,考古学家检查了这5个标本股骨和肱骨的长度,得到如下表的数据:股骨长度x/cm 38 56 59 64 73肱骨长度y/cm 41 63 70 72 84若由资料可知肱骨长度y与股骨长度x呈线性相关关系.(1)求y与x的线性回归方程y=x+(,精确到0.01);(2)若某个中华龙鸟的化石只保留有股骨,现测得其长度为37cm,根据(1)的结论推测该中华龙鸟的肱骨长度(精确到1cm).(参考公式和数据:b=,a=﹣, x i y i=19956, x=17486)21.在一个不透明的袋中有5个形状、大小、质地均相同的小球,小球的编号分别为1,2,3,4,5.(1)从袋中随机抽取两个小球;①用列举法写出全部基本事件;②求取出的两个小球编号之和不大于5的概率;(2)从袋中随机取一个小球记下它的编号m,再将小球放入袋中,然后再从袋中随机取一个小球,记下它的编号n,求函数f(x)=x2﹣2•x+m+1无零点的概率.22.已知函数f(x)=1+,g(x)=log2x.(1)设函数h(x)=g(x)﹣f(x),求函数h(x)在区间[2,4]上的值域;(2)定义min{p,q}表示p,q中较小者,设函数H(x)=min{f(x),g(x)}(x>0).①求函数H(x)的单调区间及最值;②若关于x的方程H(x)=k有两个不同的实根,某某数k的取值X围.2015-2016学年某某省某某市高一(上)期末数学试卷参考答案与试题解析一、选择题(共12小题,每小题5分,满分60分)1.设全集U={0,1,2,3,4},∁U A={1,2},B={1,3},则A∪B等于()A.{2} B.{1,2,3} C.{0,1,3,4} D.{0,1,2,3,4}【考点】并集及其运算.【专题】计算题;集合思想;定义法;集合.【分析】根据全集U及A的补集确定出A,求出A与B的并集即可.【解答】解:∵全集U={0,1,2,3,4},∁U A={1,2},B={1,3},∴A={0,3,4},A∪B={0,1,3,4},故选:C.【点评】此题考查了交、并、补集的混合运算,熟练掌握各自的定义是解本题的关键.2.某工厂的一个车间包装一种产品,在一定的时间内,从自动包装传送带上,每隔30min抽一包产品,称其重量是否合格,记录抽查产品的重量的茎叶图如图所示(以重量的个位数为叶),则抽查产品重量的中位数和众数分别为()A.96,98 B.96,99 C.98,98 D.98,99【考点】茎叶图.【专题】计算题;数形结合;综合法;概率与统计.【分析】抽查产品重量分别为89,96,97,98,98,99,103,即可求出抽查产品重量的中位数和众数.【解答】解:抽查产品重量分别为89,96,97,98,98,99,103,∴抽查产品重量的中位数和众数分别为98,98,故选:C.【点评】本题考查抽查产品重量的中位数和众数,考查学生的计算能力,属于中档题.3.若函数f(x)=ln(x),则f(e﹣2)等于()A.﹣1 B.﹣2 C.﹣e D.﹣2e【考点】对数的运算性质;函数的值.【专题】计算题;函数思想;综合法;函数的性质及应用.【分析】将x=e﹣2代入函数的表达式求出即可.【解答】解:∵函数f(x)=ln(x),∴f(e﹣2)=ln(e﹣2)=﹣2,故选:B.【点评】本题考察了求函数值问题,考察对数函数的性质,是一道基础题.4.对变量x,y有观测数据(x i,y i)(i=1,2,3,4,5),得表1;对变量u,v有观测数据(u i,v i)(i=1,2,3,4,5),得表2.由这两个表可以判断()表1:x 1 2 3 4 5y 2.9 3.3 3.6 4.4 5.1表2:u 1 2 3 4 5v 25 20 21 15 13A.变量x与y正相关,u与v正相关B.变量x与y负相关,u与v正相关C.变量x与y负相关,u与v负相关D.变量x与y正相关,u与v负相关【考点】相关系数.【专题】图表型;对应思想;数学模型法;概率与统计.【分析】由图标直接看出,随着x的增大,对应的y值增大,随着u的增大,v减小,由此可知两组变量的相关性.【解答】解:由图表可知,随着x的增大,对应的y值增大,其散点图呈上升趋势,故x与y 正相关;随着u的增大,v减小,其散点图呈下降趋势,故u与v负相关.故选:A.【点评】本题考查两个变量的相关性,考查读取图标的能力,是基础题.5.从装有3个红球和2个黑球的口袋内任取2个球,那么对立的两个事件是()A.至少有1个黑球与都是红球B.至少有1个黑球与都是黑球C.至少有1个黑球与至少有1个红球D.恰有1个黑球与恰有2个黑球【考点】互斥事件与对立事件.【专题】计算题;转化思想;综合法;概率与统计.【分析】A是对立事件;B和不是互斥事件;D是互斥但不对立事件.【解答】解:从装有3个红球和2个黑球的口袋内任取2个球,在A中:至少有1个黑球与都是红球,不能同时发生,也不能同时不发生,故A是对立事件;在B中,至少有1个黑球与都是黑球,能够同时发生,故B不是互斥事件,更不是对立事件;在C中,至少有1个黑球与至少有1个红球,能够同时发生,故C不是互斥事件,更不是对立事件;在D中,恰有1个黑球与恰有2个黑球,不能同时发生,但能同时不发生,故D是互斥但不对立事件.故选:A.【点评】本题考查互斥事件与对立事件的判断,是基础题,解题时要认真审题,注意对立事件的合理运用.6.函数f(x)=2x﹣x2的零点所在的一个区间是()A.(﹣,0)B.(,)C.(,)D.(4,+∞)【考点】函数零点的判定定理.【专题】计算题;转化思想;数形结合法;函数的性质及应用.【分析】将方程2x﹣x2=0的零点问题转化成函数y=x2与函数y=2x图象的交点问题,画出图象可得.【解答】解:∵f(x)=2x﹣x2,∴f(x)的零点问题转化为关于x的方程2x﹣x2=0,可化为2x=x2.分别画出函数y=x2和y=2x的图象,如图所示:由图可知,它们的交点情况是:恰有3个不同的交点.f(x)的最小零点在A点处,在区间(﹣1,﹣0.75)内,第二个零点是x=2,d在区间(,)内,第三个零点是x=4.故选:B.【点评】本题考查了根的存在性及根的个数判断,以及函数与方程的思想,解答关键是运用数形结合的思想,属于中档题.7.已知a=0.85.2,b=0.85.5,c=5.20.1,则这三个数的大小关系为()A.b<a<c B.a<b<c C.c<a<b D.c<b<a【考点】指数函数的图象与性质.【专题】函数思想;综合法;函数的性质及应用.【分析】分别考察指数函数y=0.8x以及y=5.2x,即可比较三个幂值的大小.【解答】解:∵指数函数y=0.8x在R上为单调减函数,∴0.85.5<0.85.2<1,∴b<a<1,∵c=5.20.1>5.20=1∴b<a<c,故选:A.【点评】题考查了指数函数的图象和性质,利用函数单调性比较大小,取中间量比较大小的技巧.8.执行如图所示的程序框图,输出的结果是()A.lg97 B.lg98 C.lg99 D.2【考点】程序框图.【专题】计算题;图表型;数学模型法;算法和程序框图.【分析】模拟执行程序框图,依次利用对数的运算性质计算每次循环得到的b的值,计算a 的值,当a=100时不满足条件a<100,退出循环,输出b的值为lg99.【解答】解:模拟执行程序框图,可得a=2,b=lg2,满足条件a<100,b=lg2+lg=lg3,a=3满足条件a<100,b=lg3+lg=lg4,a=4…满足条件a<100,b=lg98+lg=lg99,a=100不满足条件a<100,退出循环,输出b的值为lg99.故选:C.【点评】本题主要考查了循环结构的程序框图,利用对数的运算性质计算每次循环得到的b的值是解题的关键,属于基础题.9.某单位有840名职工,现采用系统抽样方法,抽取42人做问卷调查,将840人从1到840进行编号,求得间隔数k==20,即每20人抽取一个人,其中21号被抽到,则抽取的42人中,编号落入区间[421,720]的人数为()A.12 B.13 C.14 D.15【考点】系统抽样方法.【专题】计算题;方程思想;综合法;概率与统计.【分析】根据系统抽样方法,从840人中抽取42人,那么从20人抽取1人.从而得出从编号421~720共300人中抽取的人数即可.【解答】解:使用系统抽样方法,从840人中抽取42人,即从20人抽取1人.∴从编号421~720共300人中抽取=15人.故选:D.【点评】本题主要考查系统抽样的定义和方法,属于基础题.10.假定某运动员每次投掷飞镖正中靶心的概率为0.4,现采用随机模拟的方法估计该运动员两次投掷飞镖两次都命中靶心的概率:先利用计算器产生0到9之间取整数值的随机数,指定2,3,5,7表示命中靶心,1,4,6,8,9,0表示未命中靶心,再以每两个随机数为一组,代表两次的结果,经随机模拟产生了20组随机数:93 28 12 45 85 69 68 34 31 2573 93 02 75 56 48 87 30 11 35据此估计,该运动员两次投掷飞镖都正中靶心的概率为()A.0.16 B.0.20 C.0.35 D.0.40【考点】列举法计算基本事件数及事件发生的概率.【专题】计算题;转化思想;综合法;概率与统计.【分析】在20组随机数中,打出表示该运动员两次投掷飞镖都正中靶心的个数,据此估计,能求出该运动员两次投掷飞镖都正中靶心的概率.【解答】解:20组随机数中,表示该运动员两次投掷飞镖都正中靶心的有:25,73,75,35,共4个,∴据此估计,该运动员两次投掷飞镖都正中靶心的概率为:p==0.2.故选:B.【点评】本题考查概率的求法,则基础题,解题时要认真审题,注意列举法的合理运用.11.已知映射f:M→N,其中集合M={(x,y)|xy=1,x>0},且在映射f的作用下,集合M 中的元素(x,y)都变换为(log2x,log2y),若集合N中的元素都是集合M中元素在映射f 下得到的,则集合N是()A.{(x,y)|x+y=0} B.{(x,y)|x+y=0,x>0} C.{(x,y)|x+y=1} D.{(x,y)|x+y=1,x>0}【考点】映射.【专题】计算题;函数思想;分析法;函数的性质及应用.【分析】由题意可知N中元素的横纵坐标之和为0,以此确定N中元素的条件即可.【解答】解:∵xy=1,x>0,∴log2x+log2y=log2xy=log21=0,由此排除C,D,由题意可知,N中的元素横坐标是任意实数,故选:A.【点评】本题考查映射的概念,注意对题目隐含条件的挖掘是解题的关键,属中档题.12.已知函数f(x)=,则满足f[f(a)]=3的实数a的个数为()A.4 B.8 C.12 D.16【考点】分段函数的应用.【专题】计算题;转化思想;换元法;函数的性质及应用.【分析】令f(a)=t,现在来求满足f(t)=3的t,容易判断f(t)为偶函数,所以可先求t≥0时的t,解出为t=1,或3.根据偶函数的对称性知,t<0时,满足f(t)=3的解为﹣1,或﹣3,而接着就要判断以下几个方程:f(a)=1,f(a)=﹣1,f(a)=3,f(a)=﹣3解的个数,由于f(x)是偶函数,所以只需判断a≥0时以上几个方程解的个数即可,而a<0时方程解的个数和a≥0时解的个数相同,最后即可得出满足f[f(a)]=3的实数a的个数.【解答】解:易知f(x)=﹣x2+4|x|为偶函数,令f(a)=t,则f[f(a)]=3变形为f(t)=3,t≥0时,f(t)=﹣t2+4t=3,解得t=1,或3;∵f(t)是偶函数;∴t<0时,f(t)=3的解为,t=﹣1或﹣3;综上得,f(a)=±1,±3;当a≥0时,﹣a2+4a=1,方程有2解;﹣a2+4a=﹣1,方程有1解;﹣a2+4a=3,方程有2解;﹣a2+4a=﹣3,方程有1解.∴当a≥0时,方程f(a)=t有6解;∵f(x)是偶函数,∴a<0时,f(a)=t也有6解;综上所述,满足f[f(a)]=3的实数a的个数为12.故选C.【点评】本题考查偶函数的概念及偶函数图象的对称性,以及解偶函数方程和判断偶函数方程解的个数所用到的方法:只需求出x≥0时方程的解.二、填空题(共4小题,每小题5分,满分20分)13.利用计算机产生0~1之间的均匀随机数x,则事件“3x﹣2≥0”发生的概率为.【考点】几何概型.【专题】计算题;转化思想;定义法;概率与统计.【分析】由题意可得概率为线段长度之比,计算可得.【解答】解:由题意可得总的线段长度为1﹣0=1,在其中满足3x﹣2≥0即x≥的线段长度为1﹣=,∴所求概率P=,故答案为:.【点评】几何概型的概率估算公式中的“几何度量”,可以为线段长度、面积、体积等,而且这个“几何度量”只与“大小”有关,而与形状和位置无.14.执行如图的程序,若输出的结果是2,则输入的x= 0或2 .【考点】伪代码;选择结构.【专题】计算题;分类讨论;算法和程序框图.【分析】本题考查条件语句,先根据算法语句写出分段函数,然后讨论x的正负,根据函数值求出自变量即可.【解答】解:根据条件语句可知程序的功能是计算y=,当x<1时,2x+1=2,解得:x=0,当x≥1时,x2﹣x=2,解得:x=2或﹣1(舍去),故答案为:0或2.【点评】本题主要考查了分段函数,以及条件语句,算法语句是新课标新增的内容,在近两年的新课标地区高考都考查到了,这启示我们要给予高度重视,属于基础题.15.已知一个样本x,1,y,5的平均数为2,方差为5,则xy= ﹣4 .【考点】极差、方差与标准差;众数、中位数、平均数.【专题】计算题;转化思想;综合法;概率与统计.【分析】利用平均数和方差公式列出方程组,由此能求出xy的值.【解答】解:∵一个样本x,1,y,5的平均数为2,方差为5,∴,解得xy=﹣4.故答案为:﹣4.【点评】本题考查代数式求值,是基础题,解题时要认真审题,注意方差、平均数的性质的合理运用.16.已知函数f(x)=ln(x+)+ax7+bx3﹣4,其中a,b为常数,若f(﹣3)=4,则f (3)= ﹣12 .【考点】函数的值.【专题】计算题;函数思想;综合法;函数的性质及应用.【分析】由f(﹣3)=ln(﹣3+)﹣37a﹣33b﹣4=4,得到[ln(3+)+37a+33b=﹣8,从而求出f(3)的值即可.【解答】解:∵函数f(x)=ln(x+)+ax7+bx3﹣4,其中a,b为常数,由f(﹣3)=4,得:则f(﹣3)=ln(﹣3+)﹣37a﹣33b﹣4=4,∴[ln(3+)+37a+33b=﹣8,∴f(3)=ln(3+))+37a+33b﹣4=﹣8﹣4=﹣12,故答案为:﹣12.【点评】本题考察了求函数值问题,考察对数函数的性质,是一道基础题.三、解答题(共6小题,满分70分)17.已知一次函数y=f(x)满足f(x+1)=x+3a,且f(a)=3.(1)求函数f(x)的解析式;(2)若g(x)=x•f(x)+λf(x)+1在(0,2)上具有单调性,某某数λ的取值X围.【考点】函数单调性的性质;函数解析式的求解及常用方法;二次函数的性质.【专题】函数的性质及应用.【分析】(1)本题可以直接设一次函数的解析式,然后通过代入法,利用系数对应相等,建立方程组求解;(2)结合二次函数的图象和性质,构造不等式,解得实数λ的取值X围.【解答】解:(1)设f(x)=kx+b(k≠0),则f(x+1)=k(x+1)+b=kx+k+b=x+3a,故k=1,b=3a﹣1,又∵f(a)=3,即a+3a﹣1=3,解得:a=1,b=2,∴f(x)=x+2;(2)∵g(x)=x•(x+2)+λ(x+2)+1=x2+(λ+2)x+2λ+1的图象是开口朝上,且以直线x=为对称轴的抛物线,若g(x)在(0,2)上具有单调性,则≤0,或≥2,解得:λ≤﹣6,或λ≥﹣2.【点评】本题考查的知识点是二次函数的图象和性质,等于系数法求函数的解析式,难度中档.18.某地有2000名学生参加数学学业水平考试,现将成绩(满分:100分)汇总,得到如图所示的频率分布表.(1)请完成题目中的频率分布表,并补全题目中的频率分布直方图;成绩分组频数频率[50,60] 100(60,70](70,80] 800(80,90](90,100] 200(2)将成绩按分层抽样的方法抽取150名同学进行问卷调查,甲同学在本次测试中数学成绩为95分,求他被抽中的概率.【考点】频率分布直方图;列举法计算基本事件数及事件发生的概率.【专题】综合题;数形结合;数学模型法;概率与统计.【分析】(1)根据频率分布直方图,利用频率、频数与样本容量的关系,填写频率分布表,计算,补全频率分布直方图即可;(2)用分层抽样方法,该同学被抽中的概率是与每一个同学的几率相等,为.【解答】解:(1)完成题目中的频率分布表,如下;成绩分组频数频率[50,60] 100 0.05(60,70] 600 0.30(70,80] 800 0.40(80,90] 300 0.15(90,100] 200 0.10补全题目中的频率分布直方图,如下;(2)将成绩按分层抽样的方法抽取150名同学进行问卷调查,甲同学在本次测试中数学成绩为95分,他被抽中的概率为=0.075.【点评】本题考查了频率分布直方图的应用问题,也考查了古典概型的概率计算问题,是基础题目.19.已知函数f(x)=b•a x(a>0且a≠1,b∈R)的图象经过点A(1,),B(3,2).(1)试确定f(x)的解析式;(2)记集合E={y|y=b x﹣()x+1,x∈[﹣3,2]},λ=()0+8+,判断λ与E关系.【考点】函数解析式的求解及常用方法.【专题】函数思想;综合法;函数的性质及应用.【分析】(1)由图象经过点A(1,),B(3,2)可得ba=,ba3=2,联立解方程组可得;(2)令t=()x,二次函数区间的最值求y=t2﹣t+1,t∈[,8]值域可得E,再由指数的运算化简可得λ,可得答案.【解答】解:(1)∵函数f(x)=b•a x(a>0且a≠1,b∈R)的图象经过点A(1,),B (3,2),∴ba=,ba3=2,联立解得a=2,b=,故f(x)的解析式为f(x)=•2x=2x﹣2;(2)由(1)可得y=b x﹣()x+1=()x﹣()x+1=[()x]2﹣()x+1,令t=()x,由x∈[﹣3,2]可得t∈[,8],故y=t2﹣t+1,t∈[,8],由二次函数可知当t=时,y取最小值,当t=8时,y取最大值57,故E=[,57],化简可得λ=()0+8+=1+﹣=,故λ与E关系为λ∈E【点评】本题考查函数解析式求解方法,涉及换元法和二次函数区间的最值,属中档题.20.中华龙鸟是生存于距今约1.4亿年的早白垩世现已灭绝的动物,在一次考古活动中,考古学家发现了中华龙鸟的化石标本共5个,考古学家检查了这5个标本股骨和肱骨的长度,得到如下表的数据:股骨长度x/cm 38 56 59 64 73肱骨长度y/cm 41 63 70 72 84若由资料可知肱骨长度y与股骨长度x呈线性相关关系.(1)求y与x的线性回归方程y=x+(,精确到0.01);(2)若某个中华龙鸟的化石只保留有股骨,现测得其长度为37cm,根据(1)的结论推测该中华龙鸟的肱骨长度(精确到1cm).(参考公式和数据:b=,a=﹣, x i y i=19956, x=17486)【考点】线性回归方程.【专题】计算题;应用题;函数思想;综合法;概率与统计.【分析】(1)求出,代入回归系数公式解出,,得到回归方程;(2)把x=37代入回归方程求出y即为肱骨长度的估计值.【解答】解:(1)=(38+56+59+64+73)=58, =(41+63+70+72+84)=66,∴==1.23, =66﹣1.23×58=﹣5.34.∴y与x的线性回归方程是y=1.23x﹣5.34.(2)当x=37时,y=1.23×37﹣5.34≈40.∴此中华龙鸟的肱骨长度约为40cm.【点评】本题考查了线性回归方程的求法和数值估计,属于基础题.21.在一个不透明的袋中有5个形状、大小、质地均相同的小球,小球的编号分别为1,2,3,4,5.(1)从袋中随机抽取两个小球;①用列举法写出全部基本事件;②求取出的两个小球编号之和不大于5的概率;(2)从袋中随机取一个小球记下它的编号m,再将小球放入袋中,然后再从袋中随机取一个小球,记下它的编号n,求函数f(x)=x2﹣2•x+m+1无零点的概率.【考点】列举法计算基本事件数及事件发生的概率.【专题】计算题;转化思想;综合法;概率与统计.【分析】(1)①从袋中随机抽取两个小球,利用列举法能求出全部基本事件.②取出的两个小球编号之和不大于5,利用列举法求出包含的基本事件个数,由此能求出取出的两个小球编号之和不大于5的概率.(2)从袋中随机取一个小球记下它的编号m,再将小球放入袋中,然后再从袋中随机取一个小球,记下它的编号n,利用列举法能求出函数f(x)=x2﹣2•x+m+1无零点的概率.【解答】解:(1)①从袋中随机抽取两个小球,有以下10种取法:12,13,14,15,23,24,25,34,35,45.②取出的两个小球编号之和不大于5,包含的基本事件为:12,13,14,23,共4个,∴取出的两个小球编号之和不大于5的概率:p==.(2)从袋中随机取一个小球记下它的编号m,再将小球放入袋中,然后再从袋中随机取一个小球,记下它的编号n,基本事件总数为:5×5=25,∵函数f(x)=x2﹣2•x+m+1无零点,∴△=4n﹣1﹣4m﹣4=4(n﹣m)﹣5<0,即n﹣m<,∴条件的(m,n)有(1,1),(1,2),(1,3),(1,4),(1,5),(2,1),(2,2),(2,3),(2,4),(2,5),(3,2),(3,3),(3,4),(3,5),(4,3),(4,4),(4,5),(5,4),(5,5),∴函数f(x)=x2﹣2•x+m+1无零点的概率p=.【点评】本题考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.22.已知函数f(x)=1+,g(x)=log2x.(1)设函数h(x)=g(x)﹣f(x),求函数h(x)在区间[2,4]上的值域;(2)定义min{p,q}表示p,q中较小者,设函数H(x)=min{f(x),g(x)}(x>0).①求函数H(x)的单调区间及最值;②若关于x的方程H(x)=k有两个不同的实根,某某数k的取值X围.【考点】分段函数的应用;函数的最值及其几何意义.【专题】函数的性质及应用.【分析】(1)根据函数f(x)=1+在[2,4]上为减函数,g(x)=log2x在[2,4]上为增函数,可得函数h(x)的单调性,进而求出最值,可得函数的值域;(2)结合函数f(x)=1+在(0,+∞)上为减函数,g(x)=log2x在(0,+∞)上为增函数,且当x=4时,f(x)=g(x),可得函数H(x)的解析式,进而得到答案.【解答】解:(1)∵函数f(x)=1+在[2,4]上为减函数,g(x)=log2x在[2,4]上为增函数,∴函数h(x)=g(x)﹣f(x)=log2x﹣1﹣在[2,4]上为增函数,当x=2时,函数取最小值﹣2,当x=4时,函数取最大值0,故函数h(x)在区间[2,4]上的值域为[﹣2,0];word(2)当x=4时,f(x)=g(x),由函数f(x)=1+在(0,+∞)上为减函数,g(x)=log2x在(0,+∞)上为增函数,故当x∈(0,4)时,g(x)<f(x),当x∈(4,+∞)时,g(x)>f(x),故H(x)=min{f(x),g(x)}=.故①求函数H(x)的单调递增区间为(0,4],单调递减区间为[4,+∞),当x=4时,取最大值2,无最小值;②当x→+∞时,H(x)→1,故若关于x的方程H(x)=k有两个不同的实根,则k∈(1,2)【点评】本题考查的知识点是分段函数的应用,分段函数分段处理,是解答此类问题的关键.- 21 - / 21。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
河北省邢台市第一中学高一直升班上学期期末数学试题一、单选题1.已知集合2{|1}A x x ==,2{|2}B x x x ==,则A B =( )A .{1,0,1,2}-B .{0}C .{1,1,2}-D .{1,2}【答案】A【解析】解二次方程,化简集合A ,B ,进而求并集即可. 【详解】因为{}1,1A =-,{}0,2B =, 所以{}1,0,1,2A B ⋃=-. 故选A 【点睛】本题考查并集的概念及运算,考查一元二次方程的解法,属于基础题. 2.若45角的终边上有一点(4,1)a a -+,则a =( ) A .3 B .32-C .1D .32【答案】D【解析】利用三角函数定义可得a 的方程,解之即可. 【详解】 因为01tan4514a a +==-,所以32a =. 故选D 【点睛】本题考查任意角的三角函数的定义,属于基础题. 3.已知sin tan 0αα<,tan 0cos αα<,则角α的终边在( ) A .第一象限 B .第二象限C .第三象限D .第四象限【答案】C【解析】利用三角函数式的符号推断角α的终边所在象限. 【详解】因为sin tan 0αα<,所以角α在第二或第三象限,又tan 0cos αα<,所以角α在第三或第四象限, 故角α在第三象限.故选C 【点睛】本题主要考查三角函数在各个象限中的符号,属于基础题.4.已知幂函数()y f x =的图像经过点(2,2,则2(log f =( )A .BC .12D .1【答案】A【解析】设()af x x =,点⎛ ⎝⎭在图像上,解得a 值,进而得到结果. 【详解】设()af x x =,则1222a-==,故12a =-,112211222f -⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭故选A 【点睛】本题考查幂函数的表达式,考查计算能力,属于基础题.5.设向量12,e e 是平面内的一组基底,若向量123a e e =--与12b e e λ=-共线,则λ=( ) A .13B .13-C .3-D .3【答案】B【解析】由题得存在R μ∈,使得a b μ=,得到关于μ,λ的方程组,解之即得解. 【详解】因为a 与b 共线,所以存在R μ∈,使得a b μ=,即()12123e e e e μλ--=-,故3μ=-,1λμ-=-,解得13λ=-. 【点睛】本题主要考查向量共线的应用,意在考查学生对该知识的理解掌握水平和分析推理能力.6.小婷经营一花店,每天的房租、水电等固定成本为100元,每束花的进价为6元,若日均销售量Q (束)与销售单价x (元)的关系为1005Q x =-,则当该店每天获利最大时,每束花应定价为( ) A .15元 B .13元C .11元D .10元【答案】B【解析】设每天获利y 元,可得()()10056100020y x x x =---<≤(),结合二次函数的图像与性质求最值即可. 【详解】设每天获利y 元,则()()()210056100513145y x x x =---=--+ 由0x >,10050Q x =-≥,得020x <≤, 故当13x =时,每天获利最大. 故选B 【点睛】解决函数模型应用的解答题,还有以下几点容易造成失分:①读不懂实际背景,不能将实际问题转化为函数模型.②对涉及的相关公式,记忆错误.③在求解的过程中计算错误.另外需要熟练掌握求解方程、不等式、函数最值的方法,才能快速正确地求解.含有绝对值的问题突破口在于分段去绝对值,分段后在各段讨论最值的情况. 7.设函数1,{|21,}()1,{|2,}x x x k k Z g x x x x k k Z -∈=-∈⎧=⎨∈=∈⎩,则下列结论不正确的是( )A .()g x 的值域为{1,1}-B .()g x 不是单调函数C .()g x 是奇函数D .()g x 是周期函数 【答案】C【解析】利用分段函数的图像与性质逐一判断即可. 【详解】,A B 选项显然正确;因为x 与x -的奇偶性相同,所以()()g x g x -=,故()g x 是偶函数,C 选项不正确;()g x 是以2为周期的周期函数,D 选项正确.故选C 【点睛】本题考查分段函数的图像与性质,涉及到函数的值域,函数的单调性,奇偶性,周期性,考查逻辑推理能力与数形结合能力.8.已知1(0,5)P ,2(2,1)P -,3(1,4)P -,则向量12PP 在向量13PP 方向上的投影是( ) A .4 B .210C .22D.105【答案】C【解析】求出1213PP PP ,的坐标,利用12131213·cos PP PP PP PP θ=即可得到结果.【详解】因为()122,6PP =-,()131,1PP =--,1213·4PP PP =,132PP =,所以12131213·cos 222PP PP PP PP θ===. 故选C 【点睛】本题考查了平面向量投影的定义,解题时应根据定义代入计算即可,是基础题. 9.函数()sin()f x x ωφ=+(0,)2πωφ><的部分图像如图所示,以下说法:①()f x 的单调递减区间是[21,25]k k ++,k Z ∈; ②()f x 的最小正周期是4;③()f x 的图像关于直线3x =-对称; ④()f x 的图像可由函数sin 4y x π=的图像向左平移一个单位长度得到.正确的个数为( )A .1B .2C .3D .4【答案】B【解析】由图像可知()f x 的周期为8,可得ω,进而得到ϕ,结合正弦型函数的图像与性质逐一判断即可. 【详解】由图像可知()f x 的周期为8,故284ππω==,()sin 4f x x πϕ⎛⎫=+ ⎪⎝⎭, 将点()1,1代入解析式,得1sin 4πϕ⎛⎫=+⎪⎝⎭,故242k ππϕπ+=+,所以24k πϕπ=+,k Z ∈因为2πϕ<,所以4πϕ=,所以()sin 44f x x ππ⎛⎫=+⎪⎝⎭,故①②错,③④正确.故选B 【点睛】已知函数sin()(0,0)y A x B A ωϕω=++>>的图象求解析式(1)max min maxmin,22y y y y A B -+==. (2)由函数的周期T 求2,.T πωω= (3)利用“五点法”中相对应的特殊点求ϕ.10.设6log 3a =,lg5b =,14log 7c =,则,,a b c 的大小关系是( ) A .a b c << B .a b c >>C .b a c >>D .c a b >>【答案】A【解析】构造函数()log 2x xf x =,利用单调性比较大小即可. 【详解】构造函数()21log 1log 212log xx x f x x==-=-,则()f x 在()1,+∞上是增函数, 又()6a f =,()10b f =,()14c f =,故a b c <<. 故选A 【点睛】本题考查实数大小的比较,考查对数函数的单调性,考查构造函数法,属于中档题. 11.已知奇函数()y f x =的图像关于点(,0)2π对称,当[0,)2x π∈时,()1cos f x x =-,则当5(,3]2x ππ∈时,()f x 的解析式为( )A .()1sin f x x =--B .()1sin f x x =-C .()1cos f x x =--D .()1cos f x x =-【答案】C 【解析】当5,32x ππ⎛⎤∈ ⎥⎝⎦时,30,2x ππ⎡⎫-∈⎪⎢⎣⎭,结合奇偶性与对称性即可得到结果.【详解】因为奇函数()y f x =的图像关于点,02π⎛⎫⎪⎝⎭对称,所以()()0f x f x π++-=, 且()()f x f x -=-,所以()()f x f x π+=,故()f x 是以π为周期的函数.当5,32x ππ⎛⎤∈⎥⎝⎦时,30,2x ππ⎡⎫-∈⎪⎢⎣⎭,故()()31cos 31cos f x x x ππ-=--=+因为()f x 是周期为π的奇函数,所以()()()3f x f x f x π-=-=- 故()1cos f x x -=+,即()1cos f x x =--,5,32x ππ⎛⎤∈ ⎥⎝⎦故选C 【点睛】本题考查求函数的表达式,考查函数的图象与性质,涉及对称性与周期性,属于中档题. 12.在ABC ∆中,2AB =,3AC =,5cos 6A =,若O 为ABC ∆的外心(即三角形外接圆的圆心),且AO mAB nAC +=,则2n m -=( ) A .199B .4122-C .111-D .1711【答案】D【解析】设,D E 分别为,AB AC 的中点,连接,OD OE ,则OD AB ⊥,OE AC ⊥,从而得到·0?0OD AB OE AC ==,,坐标化构建m ,n 的方程组,解之即可. 【详解】设,D E 分别为,AB AC 的中点,连接,OD OE ,则OD AB ⊥,OE AC ⊥,又OD AD AO =-,即11222mOD AB mAB nAC AB nAC -=--=-,同理122nOE AE AO AC mAB -=-=-, 因为212·||?02mOD AB AB nAB AC -=-=, 所以124502m n -⨯-=,又212·||?02nOE AC AC mAB AC -=-=, 所以129502nm -⨯-=,联立方程组124502129502mn n m -⎧⨯-=⎪⎪⎨-⎪⨯-=⎪⎩, 解得922811m n ⎧=-⎪⎪⎨⎪=⎪⎩,所以17211n m -=. 故选D【点睛】本题考查了数量积运算性质、向量垂直与数量积的关系、三角形外心的性质、向量基本定理,考查了推理能力与计算能力,属于中档题.二、填空题13.已知半径为2的扇形OAB 的弦长AB =__________. 【答案】π【解析】利用勾股定理可知圆心角为直角,结合弧长公式得到结果. 【详解】在OAB ∆中,2228AB OA OB =+=, 故2AOB π∠=,故弧长22l ππ=⨯=故答案为π 【点睛】本题考查弧长公式,考查计算能力,属于基础题. 14.函数1()1x f x x +=-,[2,6]x ∈的最大值为__________. 【答案】3【解析】利用函数的单调性即可得到最大值. 【详解】因为()12111x f x x x +==+--在[]2,6上单调递减, 所以()()max 23f x f == 故答案为3 【点睛】本题考查一次分式函数的图像与性质,考查单调性的应用,考查常数分离法,属于基础题.15.已知()tan αβ1+=,()tan αβ7-=,则tan2β=______. 【答案】34-【解析】利用两角差正切公式即可得到结果. 【详解】()()()()()()tan tan 173tan2tan 1tan tan 1174αβαββαβαβαβαβ+---⎡⎤=+--===-⎣⎦++-+⨯,故答案为34- 【点睛】本题考查两角和与差的正切公式,考查计算能力,属于基础题.16.若函数222,1()43,1x a x f x x ax a x ⎧-<=⎨-+≥⎩恰有2个零点,则a 的取值范围是__________. 【答案】1{|12}3a a α≤<≥或或写成1[,1)[2,)3⋃+∞ 【解析】对a 分类讨论,结合指数函数与二次函数的图像与性质进行分析即可. 【详解】①当2a ≥时,因为当1x <时,22x <,故()2xf x a =-无零点,所以,当1x ≥时,()()()22433f x x ax a x a x a =-+=--有2个零点,1x a =,23x a =,故2a ≥;②当02a <<时,因为当1x <时,()2xf x a =-有1个零点2log x a =,所以当1x ≥时,()()()3f x x a x a =--只能有1个零点,3x a =,故131a a <⎧⎨≥⎩,解得113a ≤<;③当0a ≤时,()f x 无零点综上,实数a 的取值范围是1{|12}3a a a ≤<≥或. 故答案为1{|12}3a a α≤<≥或 【点睛】已知函数有零点求参数取值范围常用的方法和思路(1)直接法:直接根据题设条件构建关于参数的不等式,再通过解不等式确定参数范围; (2)分离参数法:先将参数分离,转化成求函数值域问题加以解决;(3)数形结合法:先对解析式变形,在同一平面直角坐标系中,画出函数的图象,然后数形结合求解.三、解答题17.已知集合A 是函数2log (62)y x =-的定义域,集合{|11}B x x a =-<-≤.(1)当1a =-时,求A B ;(2)当AB B =时,求实数a 的取值范围.【答案】(1){|23}AB x x =-<<(2){|12}a a ≤<【解析】(1) 当1a =-时,化简集合A 与B ,进而求并集即可; (2)由A B B ⋂=可知B A ⊆,转化为不等式组,即可得到结果. 【详解】 (1)依题意得:620210xx ->⎧⎨-≥⎩, 即0322x x <⎧⎨≥⎩,解得03x ≤<,即{|03}A x x =≤< 当1a =-时,{|111}{|20}B x x x x =-<+≤=-<≤ 所以{|23}A B x x ⋃=-<< (2)集合{|11}B x a x a =-<≤+ 由A B B ⋂=,得B A ⊆, 故1013a a -≥⎧⎨+<⎩,解得12a ≤<.故实数a 的取值范围为{|12}a a ≤<. 【点睛】本题考查了集合的包含关系,考查集合的运算以及不等式的解法,考查计算能力,是一道基础题.18.已知α为第二象限角,3sin()cos()tan()22()tan()sin()f ππαααπααπαπ-+-=----. (1)化简:()f α; (2)若3tan 4α=-,求()f α的值. 【答案】(1)()cos f αα=-(2)45【解析】(1)利用诱导公式化简即可得到结果; (2)利用同角关系即可得到()f α的值.【详解】(1)因为()()()()3sin cos tan 22tan sin f ππαααπααπαπ⎛⎫⎛⎫-+- ⎪ ⎪⎝⎭⎝⎭=---- 所以()()()cos sin tan tan sin f αααααπαπ=⎡⎤-+-+⎣⎦所以()cos sin tan cos tan sin f ααααααα==--(2)因为sin 3tan cos 4ααα==-, 所以3sin cos 4αα=-,代入得216cos 25α=,因为α为第二象限角,所以4cos 5α=-,故()4cos 5f αα=-=【点睛】本题考查三角函数的恒等变形,考查诱导公式与同角基本关系式,考查计算能力. 19.设单位向量1,e 2e 的夹角是3π,且()122,a e e =-+1245b e e =-. (1)求||a ; (2)求a 与b 的夹角.【答案】(1)7a =;(2)2π【解析】1)根据平面向量的数量积求a 的模长a ;(2)根据向量的数量积的运算律计算0a b =得出a b ⊥,即a 与b 的夹角为2π. 【详解】解:(1)单位向量1e ,2e 的夹角是3π, 则121e e ==,12111cos 32e e π=⨯⨯=; 又()122a e e =-+,所以2221122144414172a e e e e =++=⨯+⨯+=,所以7a =;(2)由1245b e e =-,则()()1212245a b e e e e =-+-221122865e e e e =-++1816512=-⨯+⨯+⨯0=,所以a b ⊥, 所以a 与b 的夹角为2π. 【点睛】本题考查了平面向量的数量积与模长和夹角的计算问题,属于基础题. 20.已知函数的图像经过点.(1)求的值以及的单调递减区间;(2)当时,求使成立的的取值集合.【答案】(1)a=1,的单调递减区间为;(2)【解析】(1)根据函数f (x )的图象过点求出a 的值,再化f (x )为正弦型函数,求出它的单调递减区间; (2) 由,得,结合正弦函数图像,解三角不等式即可.【详解】解:(1)因为函数的图像经过点,所以,解得又,由,得故的单调递减区间为(2)由,得 当时,故,解得: 故使成立的的取值集合为.【点睛】本题考查了三角函数的图象与性质的应用问题,也考查了三角恒等变换问题,是基础题. 21.设sin ,sin ,4a x x π⎛⎫⎛⎫=+⎪ ⎪⎝⎭⎝⎭cos ,sin ,4b x x π⎛⎫⎛⎫=- ⎪ ⎪⎝⎭⎝⎭()2f x a b =. (1)当,02x ⎡⎤∈-⎢⎥⎣⎦π时,求()f x 的最大值和最小值; (2)已知323f α⎛⎫-= ⎪⎝⎭,且当22παπ≤≤时,求()f α的值. 【答案】(1)min ()2f x =-max ()1f x =;(2)()25f α-=【解析】(1)利用平面向量数量积的运算,三角函数恒等变换的应用可得()224f x x π⎛⎫=+ ⎪⎝⎭,利用正弦函数的性质可求出函数在给定区间上的最值;(2)由已知可得3cos sin αα-=,从而得到22cos sin 03αα=>,再根据22παπ≤≤,即可得到sin 0α<,cos 0α<,从而求出5cos sin 3αα+=-,即可求出cos2α,再根据两角和的正弦公式计算可得; 【详解】解:(1)因为sin ,sin ,4a x x π⎛⎫⎛⎫=+⎪ ⎪⎝⎭⎝⎭cos ,sin ,4b x x π⎛⎫⎛⎫=- ⎪ ⎪⎝⎭⎝⎭()2f x a b =. 所以()22sin cos sin sin 44f x a b x x x x ππ⎡⎤⎛⎫⎛⎫==++- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦12sin 2sin sin 2424x x x πππ⎧⎫⎡⎤⎛⎫⎛⎫=++-+⎨⎬ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦⎩⎭sin 22sin cos 44x x x ππ⎛⎫⎛⎫=+++ ⎪ ⎪⎝⎭⎝⎭sin 2sin 24x x π⎛⎫=++ ⎪⎝⎭sin 2sin 22x x π⎛⎫=++ ⎪⎝⎭sin 2cos2x x =+24x π⎛⎫=+ ⎪⎝⎭()24f x x π⎛⎫∴=+ ⎪⎝⎭因为,02x ⎡⎤∈-⎢⎥⎣⎦π,所以432,44x πππ⎡⎤+∈-⎢⎥⎣⎦所以当38x π=-即242x ππ+=-时,()f x 取最小值,min ()f x = 当0x =即244x ππ+=时,()f x 取最大值,max ()1f x =;(2)因为2f α⎛⎫-= ⎪⎝⎭,243f απα⎛⎫⎛⎫∴-=-+=⎪ ⎪⎝⎭⎝⎭cos sin 3αα∴-=,两边平方得,112cos sin 3αα∴-=,22cos sin 3αα∴=,2sin 23α∴=又22παπ≤≤,cos 0α∴<,sin 0α<,()225cos sin 12cos sin 133αααα∴+=+=+=cos sin 3αα∴+=-()()cos 2cos sin cos sin ααααα⎛∴=+-== ⎝⎭()2sin 2cos cos 2sin sin 2cos 2444f πππαααααα⎛⎫⎫∴=+=+=+=⎪⎪⎝⎭⎭ 【点睛】本题主要考查了平面向量数量积的运算,三角函数恒等变换的应用以及正弦函数的图象和性质,考查了计算能力和转化思想,属于中档题. 22.已知函数()log )a f x x =(0a >且1a ≠). (1)判断函数()f x 的奇偶性;(2)判断函数()f x 在(0,+)∞上的单调性,并证明你的结论;(3)当1a >时,若不等式()0f f mx +-<对于(0,+)x ∈∞恒成立,求m 的最大值.【答案】(1)奇函数(2)详见解析(3)1 【解析】(1)利用奇偶性的定义判断即可; (2)利用单调性的定义判断即可;(3mx >对0x >恒成立,然后变量分离,转求最值即可. 【详解】(1)因为函数())log a f x x =的定义域为R ,所以()))()log log log aa af x x x f x ⎛⎫-===-=-所以函数()f x 为奇函数. (2)()))log log log aa af x x x ⎛⎫===-当1a >时,()f x 在()0,+∞上是减函数,当01a <<时,()f x 在()0,+∞上是增函数,证明如下:()))log log aaf x x x ==-任取120x x <<,则()()))1221log log aaf x f x x x -=-因为210x x >>,所以2221x x >>21x x >所以当1a >时,))21log log aax x >,()()120f x f x ->,所以()()12f x f x >,故函数()f x 在()0,+∞上是减函数.所以当01a <<时,))21log log aax x <,所以()()120f x f x -<,所以()()12f x f x <,故函数()f x 在()0,+∞上是增函数.(3)由(1)知,()f x 是奇函数,()0ff mx +-<,即()ff mx <.当1a >时,由(2)知,()f x 在()0,+∞上是减函数,从而在(),-∞+∞上是减函数,mx >对0x >恒成立,即m <0x >恒成立.因为y =()0,+∞上是减函数,所以y =()1,+∞. 所以1m ≤,故实数m 的最大值为1. 【点睛】本题主要考查了对数型函数的奇偶性和单调性的判断,要注意对底数的讨论,总体来说本题很基础、很典型,是不得不练的好题.。
