安徽省合肥一六八中学2020学年高二数学上学期期中试题 理(宏志班)
安徽省合肥市第一六八中学高二数学上学期期中试卷理(凌志班)

高二数学试题(凌志班)一、选择题(本大题共12 小题,每题 5 分,共 60 分)1.下边四个命题:①分别在两个平面内的两直线是异面直线;②若两个平面平行,则此中一个平面内的任何一条直线必平行于另一个平面;③假如一个平面内的两条直线平行于另一个平面,则这两个平面平行;④假如一个平面内的任何一条直线都平行于另一个平面,则这两个平面平行.此中正确的命题是()A.①②B.②④C.①③ D .②③2.过点P( 1,3)且垂直于直线x 2 y 3 0 的直线方程为()A.2x y 1 0B.2x y 50C .x2y 5 0D.x 2 y 703.如图,矩形O'A'B'C'是水平搁置的一个平面图形的直观图,此中O'A'=3cm , O'C'=1cm ,则原图形的面积是()A.B.C.2 D . 6cm4. 点( 4,﹣ 2)到直线的距离是()A. 1B.2C.D. 65.已知空间两条不一样的直线m,n 和两个不一样的平面,, 则以下命题中正确的选项是 ( )A .若m / / , n , 则m //n B.若m, m n, 则nC .若m / / , n / / ,则m / /nD .若m / /, m, I n, 则m / /n 6.直线 l 过点 P( 1,0),且与以 A( 2,1),为端点的线段总有公共点,则直线l 斜率的取值范围是()A.B.C.D.[1 , +∞)7.已知ab0, bc 0,则直线ax by c 经过()A .第一、二、三象限B.第一、二、四象限C .第一、三、四象限D.第二、三、四象限8.正方体 ABCD— A1 B1C1D1中, E、F 分别是 AA1与 CC1的中点,则直线ED与 D1F 所成角余弦值大小是()A .1B .1C.1D.3 53229. 在三棱柱ABC A1B1C1中,各棱长相等,侧掕垂直于底面,点 D 是侧面 BB1C1C 的中心,则 AD 与平面 BB1C1C 所成角的大小是( )A .30o B. 45o C. 60o D. 90o10.将正方形 ABCD沿对角线 BD折成直二面角A- BD- C,有以下四个结论:① AC⊥ BD;②△ ACD是等边三角形;③ AB与平面 BCD成 60°的角;④ AB 与 CD所成的角是 60°.此中正确结论的个数是()A. 1B.2C.3D.411.如图 : 直三棱柱ABC—A1B1C1的体积为 V,点 P、Q分别在侧棱AA1和CC 1上, AP=C1Q,则四棱锥 B—APQC的体积为()A.VB.VC.VD.V(11题)234512.如图,正方体ABCD—A1B1C1D1的棱长为1,线段 B1D1上有两个动点1E、F,且 EF=2,则以下结论错误的选项是()A. AC⊥ BEB.EF∥平面ABCD(12 题)C .三棱锥A—BEF的体积为定值D .△AEF的面积与△BEF的面积相等二、填空题(本大题共 4 小题,每题 5 分,共 20 分)13.一个几何体的三视图及其尺寸( 单位: cm)以下图,则该几何体的侧面积为 _ ______cm 214.已知直线l1 : ax 2 y 6 0 与l2: x a 1 y a210 平行,则实数a的取值是.15.若直线 l为: 3y=x+6,则直线 l 的倾斜角为.16. 球的半径为5cm,被两个互相平行的平面所截得圆的直径分别为6cm 和 8cm,则这两个平面之间的距离是cm.三、解答题17.(本小题10 分)如图,在三棱柱ABC-A1B1 C1中,△ ABC与△ A1B1C1都为正三角形且AA1⊥面ABC, F、 F1分别是 AC, A1C1的中点.求证: (1) 平面 AB1F1∥平面 C1BF;(2)平面 AB1F1⊥平面 ACC1A1.(17 题)18.(本小题 12 分)设直线l 的方程为( a+1) x+ y+2- a=0 ( a∈R).(1)若 l 在两坐标轴上截距相等,求直线l 的方程;(2)若 l 不经过第二象限,务实数 a 的取值范围.19. (本小题12 分)已知直线.( 1)若,务实数的值;( 2)当时,求直线与之间的距离.20.(本小题 12 分)如图,DC⊥平面ABC,EB∥DC,AC=BC=EB= 2DC= 2,∠ACB=120°,P, Q分别为 AE,AB的中点.(1)证明:PQ∥平面ACD;(2)求AD与平面ABE所成角的正弦值(19 题)21.(本小题12 分)以下图,边长为 2 的等边△ PCD所在的平面垂直于矩形ABCD所在的平面, BC= 2 2, M为 BC的中点.(1)证明: AM⊥ PM;(2)求二面角 P- AM- D的大小.(21题)222.如图,△ ABC中, AC= BC=AB,ABED是边长为 1 的正方形,平面ABED⊥底面ABC,2若 G, F 分别是 EC, BD的中点.(1)求证: GF∥底面 ABC;(2)求证:AC⊥平面 EBC;(22 题)( 3)求几何体ADEBC的体积 V.理科凌志班参照答案一、选择题: 1-5 BABBD 6-10 BCACC 11-12 BD二、填空题13 . 80 14.-1 15 .30°16.1或7三、解答题17 . 证明 :(1)在正三棱柱ABC- A1B1C1中,∵F、 F1分别是 AC、 A1C1的中点,∴B1F1∥ BF, AF1∥C1F.又∵ B1F1∩ AF1= F1, C1F∩ BF= F,∴平面 AB1F1∥平面 C1BF.(2) 在三棱柱ABC- A1B1C1中, AA1⊥平面 A1B1C1,∴ B1F1⊥ AA1.又 B1F1⊥ A1C1, A1C1∩ AA1=A1,∴B1F1⊥平面 ACC1A1,而 B1F1? 平面 AB1F1,∴平面 AB1F1⊥平面 ACC1A1.18. (1) 3x+y= 0 或x+y+ 2= 0;( 2)a≤- 1.19. ( 1)由知,解得;( 2)当时,有解得,或a=-1(舍去),即,距离为.20.( 1)证明:由于 P, Q分别为 AE, AB的中点,所以 PQ∥ EB.又 DC∥ EB,所以 PQ∥ DC,又 PQ?平面 ACD,进而 PQ∥平面 ACD.(2)如图,连结CQ,DP,由于 Q为 AB的中点,且AC= BC,所以 CQ⊥ AB.由于 DC⊥平面 ABC, EB∥ DC,所以 EB⊥平面 ABC,所以 CQ⊥EB.故 CQ⊥平面 ABE.1由(1) 有 PQ∥DC,又 PQ= EB =DC,所以四边形CQPD为平行四边形,故DP∥CQ,2所以 DP⊥平面 ABE,∠DAP为 AD和平面 ABE所成的角,在 Rt △ DPA 中, AD =5, DP =1,sin ∠ DAP =5,所以 AD 和平面 ABE 所成角的正弦值为55521.(1) 证明:以下图,取CD 的中点 E ,连结 PE , EM , EA ,∵△ PCD 为正三角形,∴PE ⊥ CD ,PE = PDsin ∠ PDE = 2sin60 °= 3.∵平面 PCD ⊥平面 ABCD ,∴PE ⊥平面 ABCD ,而 AM? 平面 ABCD ,∴ PE ⊥ AM.∵四边形 ABCD 是矩形,∴△ ADE ,△ ECM ,△ ABM 均为直角三角形,由勾股定理可求得 EM = 3,AM = 6 ,AE = 3,2 2 2∴EM + AM = AE . ∴ AM ⊥ EM.又 PE ∩ EM =E ,∴ AM ⊥平面 PEM ,∴ AM ⊥PM.(2) 解:由 (1) 可知 EM ⊥ AM , PM ⊥ AM ,∴∠ PME 是二面角 P -AM - D 的平面角.∴tan ∠ PME =PE3 == 1,∴∠ PME = 45° .EM3∴二面角 P -AM - D 的大小为 45° .22.(1) 证明:连结 AE ,以以下图所示.∵ADEB 为正方形,∴AE ∩ BD =F ,且 F 是 AE 的中点,又 G 是 EC 的中点,∴GF ∥ AC ,又 AC? 平面 ABC , GF?平面 ABC ,∴GF ∥平面 ABC.(2) 证明:∵ ADEB 为正方形,∴ EB ⊥ AB ,又∵平面 ABED ⊥平面 ABC ,平面 ABED ∩平面 ABC =AB , EB? 平面 ABED ,∴BE ⊥平面 ABC ,∴ BE ⊥ AC.2又∵ AC = BC = 2 AB ,222∴CA + CB = AB ,∴AC ⊥ BC.又∵ BC ∩ BE = B ,∴ AC ⊥平面 BCE.22 (3) 取 AB 的中点 H,连 GH,∵ BC= AC=2 AB=2,1∴CH⊥ AB,且 CH=2,又平面ABED⊥平面 ABC111.∴GH⊥平面 ABCD,∴ V=3× 1×2=6。
安徽省合肥市2023-2024学年高二上学期期中数学试题含解析

安徽省合肥2023-2024学年上学期高二年级数学期中考试(答案在最后)(考试总分:150分考试时长:120分钟)一、单选题(本题共计8小题,总分40分)1.经过((),3,0A B 两点的直线的倾斜角为()A.5π6 B.π6 C.2π3D.π3【答案】A 【解析】【分析】根据直线上任意两点可求出斜率,从而求出倾斜角.【详解】由题意得033303AB k -==--,所以直线的倾斜角为5π6;故选:A2.以点()1,2A -为圆心,且与直线0x y +=相切的圆的方程为()A.221(1)(2)2x y -++=B.229(1)(2)2x y -++=C.221(1)(2)2x y ++-=D.229(1)(2)2x y ++-=【答案】A 【解析】【分析】根据给定条件,利用点到直线的距离公式求出圆的半径即可得解.【详解】由直线0x y +=为圆的切线,得圆的半径r ==所以所求圆的方程为221(1)(2)2x y -++=.故选:A3.已知(2,1,3),(1,3,9)a x b == ,如果a 与b为共线向量,则x =()A.1B.12C.13 D.16【答案】D 【解析】【分析】由a 与b为共线向量则a b λ= 求解即可.【详解】因为a 与b 为共线向量,所以a b λ=,即21339x λλλ=⎧⎪=⎨⎪=⎩,解得1316x λ⎧=⎪⎪⎨⎪=⎪⎩,故选:D4.经过两条直线1:2l x y +=,2:21l x y -=的交点,且直线的一个方向向量()3,2v =-的直线方程为()A.2350x y +-=B.220x y ++=C.220x y +-=D.70x y --=【答案】A 【解析】【分析】联立方程组求得两直线的交点坐标为(1,1),再由题意,得到23k =-,结合直线的点斜式方程,即可求解.【详解】联立方程组221x y x y +=⎧⎨-=⎩,解得1,1x y ==,即两直线的交点坐标为(1,1),因为直线的一个方向向量(3,2)v =- ,可得所求直线的斜率为23k =-,所以所求直线方程为21(1)3y x -=--,即2350x y +-=.故选:A.5.如图,在正方体1111ABCD A B C D -中,M ,N 分别为AB ,B 1C 的中点,若AB =a ,则MN 的长为()A.32a B.33a C.55a D.155a 【答案】A 【解析】【分析】根据空间向量的基本定理,用AB ,AD ,1AA表示MN ,将线段长度问题转换为向量模长问题.【详解】设AB i = ,AD j = ,1AA k =,则{},,i j k 构成空间的一个正交基底.()1111122222MN MB BC CN i j j k i j k =++=++-+=++,故2222211134444MN a a a a =++= ,所以MN =32a .故选:A6.已知()22112225,24x y x y ++=+=,则()()221212x x y y -+-的最小值为()A.55B.15C.655D.365【答案】B 【解析】【分析】利用直线与圆的位置关系及两点距离公式计算即可.【详解】易知()()221212x x y y -+-为圆()2225x y ++=上一点()11,A x y 与直线24x y +=上一点()22,B x y 的距离的平方,易知圆心()2,0C -,半径5r =,点C 到直线24x y +=的距离222465512d --==+,则()22min15ABd r =-=.故选:B7.在我国古代的数学名著《九章算术》中,堑堵指底面为直角三角形,且侧棱垂直于底面的三棱柱,鳖臑指的是四个面均为直角三角形的三棱锥.如图,在堑堵111ABC A B C -中,190,2,4ACB AB AA ︒=∠==,当鳖臑1A ABC -的体积最大时,直线1B C 与平面11ABB A 所成角的正弦值为()A.346B.31010C.26D.1010【答案】C 【解析】【分析】先根据鳖臑1A ABC -体积最大求出AC 和BC 的值,建系求出各点坐标,利用向量即可求出直线1B C 与平面11ABB A 所成角的正弦值.【详解】在堑堵111ABC A B C -中,90ACB ∠=︒,2AB =,14AA =,1112||||||||||2313ABC A V AC BC AA AC BC -⋅⋅⋅⋅==⋅ ,222||||||||||()2||||2||4AC BC B C AC B B A C C C C A ++=+⋅⋅≤ ,22||4||BC AC += ,||||2AC BC ∴⋅≤,当且仅当||||2AC BC ==是等号成立,即当鳖臑1A ABC -的体积最大时,||||2AC BC ==,以C 为原点,CA 为x 轴,CB 为y 轴,1CC 为z轴,建立空间直角坐标系,14)B ,(0,0,0)C,A,B,1(0,4)B C =-,BA =,1(0,0,4)BB = ,设平面11ABB A 的法向量n(,,)x y z =,则1040n BA n BB z ⎧⋅=-=⎪⎨⋅==⎪⎩ ,取1x =,得(1,1,0)n = ,设直线1B C 与平面11ABB A 所成角为θ,则11||6|s |in ||C C B n B n θ⋅==⋅,∴直线1B C 与平面11ABB A 所成角的正弦值为26.故选:C .8.已知椭圆22196x y +=,12,F F 为两个焦点,O 为原点,P 为椭圆上一点,123cos 5F PF ∠=,则||PO =()A.25B.2C.35D.2【答案】B 【解析】【分析】根据椭圆的定义结合余弦定理求出221212,PF PF PF PF +的值,利用()1212PO PF PF =+,根据向量模的计算即可求得答案.【详解】由题意椭圆22196x y +=,12,F F 为两个焦点,可得3,a b c ===则1226PF PF a +==①,即221212236PF PF PF PF ++=,由余弦定理得2222121212122cos F F PF PF PF PF F PF =+-∠=,123cos 5F PF ∠=,故212123()2(1)125PF PF PF PF +-+=,②联立①②,解得:22121215,212PF PF PF PF =∴+=,而()1212PO PF PF =+ ,所以1212PO PO PF PF ==+,即12122PO PF PF =+===,故选:B【点睛】方法点睛:本题综合考查了椭圆和向量知识的结合,解答时要注意到O 为12F F 的中点,从而可以利用向量知识求解||PO .二、多选题(本题共计4小题,总分20分)9.已知平面α的一个法向量为()1,2,1n =-,以下四个命题正确的有()A.若直线l 的一个方向向量为()2,4,2u =--,则//l αB.若直线l 的一个方向向量为()2,4,2u =--,则l α⊥C.若平面β的一个法向量为()1,0,1m =,则//αβD.若平面β的一个法向量为()1,0,1m =,则αβ⊥【答案】BD 【解析】【分析】由0n u ⋅≠ ,2u n =- 可判断AB ;由0n m ⋅=可判断CD【详解】对于AB :平面α的一个法向量为()1,2,1n =-,直线l 的一个方向向量为()2,4,2u =--,所以282120n u ⋅=---=-≠,所以n 与u不垂直,又2u n =-,所以//u n,所以l α⊥,故A 错误,B 正确;对于CD :平面α的一个法向量为()1,2,1n =-,平面β的一个法向量为()1,0,1m =,,所以1010n m ⋅=+-=,所以n m ⊥ ,所以αβ⊥,故C 错误,D 正确;故选:BD10.已知方程224820x y x y a +-++=,则下列说法正确的是()A.当10a =时,表示圆心为(2,4)-的圆B.当10a <时,表示圆心为(2,4)-的圆C.当0a =时,表示的圆的半径为D.当8a =时,表示的圆与y 轴相切【答案】BCD 【解析】【分析】将圆的一般方程化为标准方程,结合选项,逐项判定,即可求解.【详解】由题意,方程224820x y x y a +-++=,可化为()()2224202x y a -++=-,可圆的圆心坐标为(2,4)-,A 中,当10a =时,此时半径为2020a -=,所以A 错误;B 中,当10a <时,此时半径大于2020a ->,表示圆心为(2,4)-的圆,所以B 正确;C 中,当0a =时,表示的圆的半径为r =,所以C 正确;D 中,当8a =时,可得2024a -=,方程表示的圆半径为2r =,又圆心坐标为()2,4-,所以圆心到y 轴的距离等于半径,所以圆与y 轴相切,所以D 正确.故选:BCD.11.已知()1,,m a b a b =+- (a ,b ∈R )是直线l 的方向向量,()1,2,3n =是平面α的法向量,则下列结论正确的是()A.若l α∥,则510a b -+=B.若l α∥,则10a b +-=C .若l α⊥,则20a b +-= D.若l α⊥,则30a b --=【答案】ACD 【解析】【分析】选项A 、B :根据0m n ⋅=求解;选项C 、D :根据m n ∥,向量的平行求解;【详解】对于A ,B ,若l α∥则m n ⊥ ,所以0m n ⋅=,即()()1230a b a b +++-=,即510a b -+=,A 正确,B 错误;对于C 、D ,若l α⊥,则m n∥,所以1123a b a b+-==,即20a b +-=且30a b --=,C 、D 正确.故选:ACD.12.的圆柱被与其底面所成的角为45θ=︒的平面所截,截面是一个椭圆,则()A.椭圆的长轴长为4B.椭圆的离心率为4C.椭圆的方程可以为22142x y +=D.椭圆上的点到焦点的距离的最小值为2-【答案】ACD 【解析】【分析】结合图象根据椭圆的长轴,短轴的几何意义求椭圆的a b ,,由此判断各选项.【详解】设椭圆的长半轴长为a ,椭圆的长半轴长为b ,半焦距为c ,由图象可得2cos 45a = ∴2a =,又b =,222c a b =-,∴c =∴椭圆的长轴长为4,A 对,椭圆的离心率为2,B 错,圆的方程可以为22142x y +=,C 对,椭圆上的点到焦点的距离的最小值为2D 对,故选:ACD .三、填空题(本题共计4小题,总分20分)13.两直线330x y +-=与640x my ++=平行,则它们之间的距离为__________.【答案】2【解析】【分析】根据给定条件,利用平行线间距离公式求解即得.【详解】两直线330x y +-=与640x my ++=平行,则36m =,即2m =,直线640x my ++=化为:320x y ++=2=.所以所求距离为102.故答案为:214.圆224x y +=与圆22260x y y ++-=的公共弦长为__________.【答案】【解析】【分析】将两圆方程作差可得出相交弦所在直线的方程,求出圆224x y +=的圆心到相交弦所在直线的距离,利用勾股定理可求得相交弦长.【详解】设圆221:4C x y +=与圆222:260C x y y ++-=相交于A ,B 两点,圆1C 的半径12r =,将两圆的方程相减可得1y =,即两圆的公共弦所在的直线方程为1y =,又圆心1C 到直线AB 的距离1d =,12r =,所以22212AB d r ⎛⎫+= ⎪⎝⎭,解得AB =故答案为:15.如图,平行六面体1111ABCD A B C D -的底面ABCD 是边长为1的正方形,且1160A AD A AB ∠=∠=o,12AA =,则线段1AC 的长为_____.【答案】【解析】【分析】以1,,AB AD AA 为基底表示出空间向量1AC uuu r ,利用向量数量积的定义和运算律求解得到21AC ,进而得到1AC 的长.【详解】()()222111AC AB BC CC AB AD AA =++=++ 222111222AB AD AA AB AD AB AA AD AA =+++⋅+⋅+⋅ 1140212cos 60212cos 6010=++++⨯⨯+⨯⨯=,1AC ∴=,即线段1AC..16.古希腊著名数学家阿波罗尼斯发现:平面内到两个定点距离之比为定值λ(0λ>且1λ≠)的点的轨迹是圆,此圆被称为“阿氏圆”.在平面直角坐标系xOy 中,点()0,3A ,满足2=MA MO 的动点M 的轨迹为C ,若在直线:30l ax y a -+=上存在点P ,在C 上存在两点A 、B ,使得PA PB ⊥,则实数a 的取值范围是______.【答案】[7,1]-【解析】【分析】根据求轨迹方程的步骤:1.设点的坐标;2.找等量关系列方程;3.化简.先求出动点M 的轨迹方程,然后根据题意要使在直线:30l ax y a -+=上存在点P ,在C 上存在两点A 、B ,使得PA PB ⊥成立,则点P到圆心的距离小于等于,利用点到直线的距离公式即可求解.【详解】设(,)M x y ,因为()0,3A ,()0,0C ,又因为2=MA MO ,所以2222(3)4()x y x y +-=+,化简整理可得:22(1)4x y ++=,动点M 的轨迹是以(0,1)C -为圆心,以2为半径的圆,因为直线:30l ax y a -+=过定点(3,0)-,若在直线:30l ax y a -+=上存在点P ,在C 上存在两点A 、B ,使得PA PB ⊥,由数形结合可知:当A 、B 为圆的切点时点P,所以点P,2≤,解之可得:71a -≤≤,所以实数a 的取值范围是[7,1]-,故答案为:[7,1]-.四、解答题(本题共计6小题,总分70分)17.在平行四边形ABCD 中,(1,2)A -,()1,3B ,(3,1)C -,点E 是线段BC 的中点.(1)求直线CD 的方程;(2)求过点A 且与直线DE 垂直的直线.【答案】(1)250x y --=;(2)350x y +-=.【解析】【分析】(1)根据给定条件,求出点D 的坐标,再求出直线CD 的方程作答.(2)求出点E 坐标及直线DE 的斜率,再利用垂直关系求出直线方程作答.【小问1详解】在平行四边形ABCD 中,(1,2)A -,()1,3B ,(3,1)C -,则(2,4)AD BC ==-,则点(1,2)D -,直线CD 的斜率2(1)1132CD k ---==-,则有1(1)(3)2y x --=-,即250x y --=,所以直线CD 的方程是250x y --=.【小问2详解】依题意,点(2,1)E ,则直线DE 的斜率21312DE k --==-,因此过点A 且与直线DE 垂直的直线斜率为113DE k -=-,方程为12(1)3y x -=-+,即350x y +-=,所以所求方程是350x y +-=.18.如图,在正方体1111ABCD A B C D -中,E 为1DD 的中点.(1)证明:直线1//BD 平面ACE ;(2)求异面直线1CD 与AE 所成角的余弦值.【答案】(1)证明见解析(2)1010【解析】【分析】(1)根据线线平行,结合线面平行的判定即可求证,(2)建立空间直角坐标系,利用向量的夹角即可求解线线角.【小问1详解】如图,连接BD 交AC 于点O ,连接EO ,由于E 为1DD 的中点,O 为AC 的中点,则//EO 1BD ,又因为EO ⊂平面1,ACE BD ⊄平面ACE ,所以1BD //平面ACE【小问2详解】以D 为原点,1,,DA DC DD 所在直线为x 轴、y 轴、z 轴,建立如图所示的空间直角坐标系.设正方体的棱长为2a ,则()0,2,0C a ()()()10,0,2,2,0,0,0,0,D a A a E a ,所以()10,2,2CD a a =- ,()2,0,AE a a =-,设1CD 与AE 所成角为θ,则111cos cos ,10CD AE CD AE CD AEθ⋅===所以1CD 与AE所成角的余弦值为10.19.已知圆C 的圆心坐标()1,1,直线:1l x y +=被圆C.(1)求圆C 的方程;(2)从圆C 外一点()2,3P 向圆引切线,求切线方程.【答案】(1)()()22111x y -+-=(2)2x =或3460x y -+=【解析】【分析】(1)计算出圆心C 到直线l 的距离,利用勾股定理求出圆C 的半径,由此可得出圆C 的方程;(2)对切线的斜率是否存在进行分类讨论,在第一种情况下,写出切线方程,直接验证即可;在第二种情况下,设出切线方程为()32y k x -=-,利用圆心到切线的距离等于圆的半径,由此可得出所求切线的方程.【小问1详解】解:圆心C 到直线l的距离为2d ==,所以,圆C的半径为1r ==,因此,圆C 的方程为()()22111x y -+-=.【小问2详解】解:当切线的斜率不存在时,则切线的方程为2x =,且直线2x =与圆C 相切,合乎题意;当切线的斜率存在时,设切线方程为()32y k x -=-,即320kx y k -+-=,1=,解得34k =,此时,切线的方程为3460x y -+=.综上所述,所求切线的方程为2x =或3460x y -+=.20.如图,在四棱台1111ABCD A B C D -中,底面为矩形,平面11AAD D ⊥平面11CC D D ,且1111122CC CD DD C D ====.(1)证明:AD ⊥平面11CC D D ;(2)若11π3A CD ∠=,求平面1A AC 与平面ABC 夹角的余弦值.【答案】(1)证明见解析(2)34【解析】【分析】(1)连结1DC ,进而利用勾股定理证明11DC DD ⊥,结合题中条件利用线面垂直的判断定理证明即可;(2)以1D 为坐标原点,建立空间直角坐标系,求出平面1A AC 与平面ABC 的法向量,计算即可.【小问1详解】如图,在梯形11CC D D 中,因为1111122CC CD DD C D ====,作11DH D C ⊥于H ,则11D H =,所以11cos 2DD H ∠=,所以11π3DD C ∠=,连结1DC ,由余弦定理可求得123DC =因为2221111DC DD D C +=,所以11DC DD ⊥,因为平面11AA D D ⊥平面11CC D D 且交于1DD ,1DC ⊂平面11CC D D ,所以1DC ⊥平面11AA D D因为AD ⊂平面11AA D D ,所以1AD DC ⊥,因为1,AD DC DC DC D ⊥⋂=,1DC DC ⊂,平面11CC D D ,所以AD ⊥平面11CC D D .【小问2详解】连结11A C ,由(1)可知,11A D ⊥平面11CC D D ,所以1AC 与平面11CC D D 所成的角为11A CD ∠,即11π3A CD ∠=,在11Rt ACD △中,因为123CD =,所以116A D =因为11//A C AC ,所以平面1A AC 与平面11A ACC 是同一个平面.以1D为坐标原点,建立空间直角坐标系如图所示,则,()(()116,0,0,3,0,4,0A C C 所以()(1116,4,0,3AC AC =-=-设平面1A AC 的法向量为(),,n a b c =,则有,1110n A C n A C ⎧⋅=⎪⎨⋅=⎪⎩ ,即3206330a b a b c -+=⎧⎪⎨-++=⎪⎩,令2a =,则3,3b c ==,故(3n =由题意可知()0,0,1m =是平面ABC 的一个法向量所以33cos ,144m n m n m n ⋅===⨯,故平面1A AC 与平面ABC 夹角的余弦夹角的值为4.21.如图,相距14km 的两个居民小区M 和N 位于河岸l (直线)的同侧,M 和N 距离河岸分别为10km 和8km .现要在河的小区一侧选一地点P ,在P 处建一个生活污水处理站,从P 排直线水管PM ,PN 分别到两个小区和垂直于河岸的水管PQ ,使小区污水经处理后排入河道.设PQ 段长为t km (0<t <8).(1)求污水处理站P 到两小区的水管的总长最小值(用t 表示);(2)请确定污水处理站P 的位置,使所排三段水管的总长最小,并求出此时污水处理站分别到两小区水管的长度.【答案】(1))08t <<(2)P 点距河岸5km ,距小区M 到河岸的垂线km ,此时污水处理站到小区M 和N 的水管长度分别为10km 和6km .【解析】【分析】(1)本题实质为在一直线上求一点到两定点距离之和最小,其求法为利用三角形两边之和大于第三边:先作N 关于直线的对称点1N ,再利用11PM PN PM PN MN +=+≥得最小值)08t <<(2)由(1)知三段水管的总长)108L PM PN PQ MN PQ t t =++≥+=+<<,因此总长最小就是求)08y t t =+<<最小值,这种函数最小值可利用判别式法求解,即从方程有解出发,利用判别式不小于零得解.【详解】(1)如图,以河岸l 所在直线为x 轴,以过M 垂直于l 的直线为y 轴建立直角坐标系,则可得点()()0,10,M N ,设点(,)P s t ,过P 作平行于x 轴的直线m ,作N 关于m 的对称点1N ,则()13,28N t -.所以2211(830)(12810)PM PN PM PN MN t +=+≥=-+--)21812908t t t =-+<<即为所求.(2)设三段水管总长为L ,则由(1)知)2121812908L PM PN PQ MN PQ t t t t =++≥+=+-+<<,所以22()4(18129)L t t t -=-+在()0,8t ∈上有解.即方程223(272)(516)0t L t L +-+-=在()0,8t ∈上有解.故22(272)12(516)0L L ∆=---≥,即218630L L --≥,解得21L ≥或3L ≤-,所以L 的最小值为21,此时对应的5(0,8)t =∈.故()13,2N ,1MN 方程为3103y x =-,令5y =得3x =,即()53,5P ,从而22(53)(510)10PM =+-=,22(5383)(58)6PN =-+-=.所以满足题意的P 点距河岸5km ,距小区M 到河岸的垂线53km ,此时污水处理站到小区M 和N 的水管长度分别为10km 和6km .22.已知椭圆2222:1(0)x y C a b a b+=>>的上顶点与左、右焦点连线的斜率之积为45-.(1)求椭圆C 的离心率;(2)已知椭圆C 的左、右顶点分别为,A B ,且6AB =,点M 是C 上任意一点(与,A B 不重合),直线,MA MB 分别与直线:5l x =交于点,,P Q O 为坐标原点,求OP OQ ⋅ .【答案】(1)3(2)1619【解析】【分析】(1)由椭圆标准方程可写出顶点以及焦点坐标,由斜率之积可得2245b c =,即可求出离心率;(2)设出点M 坐标,写出直线MA 和MB 的方程求出交点,P Q 坐标,利用223649x y -=化简OP OQ ⋅ 的表达式即可求得结果.【小问1详解】根据题意可得椭圆C 的上顶点的坐标为()0,b ,左、右焦点的坐标分别为()(),0,,0c c -,由题意可知45b b c c ⎛⎫⋅-=- ⎪⎝⎭,即2245b c =,又222a b c =+,所以2295a c =,即225,93c c a a ==,可得椭圆C 的离心率3e =.【小问2详解】由6AB =,得26a =,即3,2a c b ===,所以椭圆C 的方程为22194x y +=.如图所示:设()00,M x y ,则2200194x y +=,即22003649x y -=,又()(),3,03,0A B -,则直线MA 的方程为()0033y y x x =++,直线MB 的方程为()0033y y x x =--;因为直线,MA MB 分别与直线:5l x =交于点,P Q ,可得0000825,,5,33y y P Q x x ⎛⎫⎛⎫ ⎪ ⎪+-⎝⎭⎝⎭,所以()()220000220000163648216641615,5,2525253399999x y y y OP OQ x x x x -⎛⎫⎛⎫⋅=⋅=+=+=-= ⎪ ⎪+---⎝⎭⎝⎭.。
2020年安徽省合肥一中高二(上)期中数学试卷
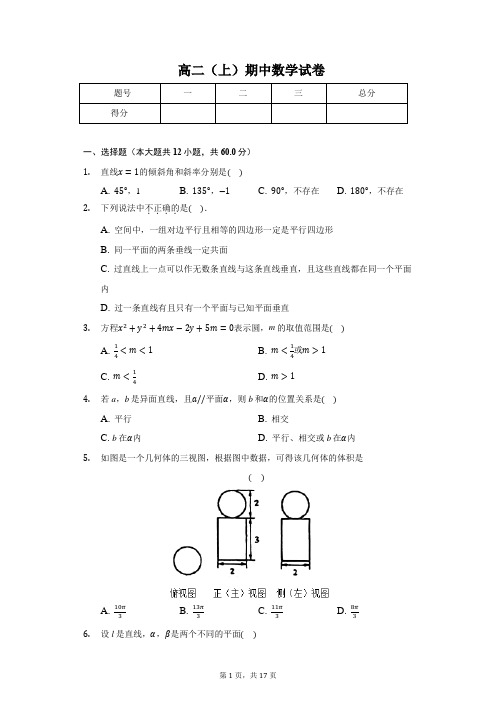
高二(上)期中数学试卷题号一二三总分得分一、选择题(本大题共12小题,共60.0分)1.直线x=1的倾斜角和斜率分别是()A. 45°,1B. 135°,−1C. 90°,不存在D. 180°,不存在2.下列说法中不正确的....是().A. 空间中,一组对边平行且相等的四边形一定是平行四边形B. 同一平面的两条垂线一定共面C. 过直线上一点可以作无数条直线与这条直线垂直,且这些直线都在同一个平面内D. 过一条直线有且只有一个平面与已知平面垂直3.方程x2+y2+4mx−2y+5m=0表示圆,m的取值范围是()A. 14<m<1 B. m<14或m>1C. m<14D. m>14.若a,b是异面直线,且a//平面α,则b和α的位置关系是()A. 平行B. 相交C. b在α内D. 平行、相交或b在α内5.如图是一个几何体的三视图,根据图中数据,可得该几何体的体积是()A. 10π3B. 13π3C. 11π3D. 8π36.设l是直线,α,β是两个不同的平面()A. 若l//α,l//β,则α//βB. 若l//α,l⊥β,则α⊥βC. 若α⊥β,l⊥α,则l⊥βD. 若α⊥β,l//α,则l⊥β7.若直线x−y+1=0与圆(x−a)2+y2=2有公共点,则实数a的取值范围是()A. [−3,−1]B. [−1,3]C. [−3,1]D. (−∞,−3]∪[1,+∞)8.圆x2+2x+y2+4y−3=0上到直线x+y+1=0的距离为√2的点共有()A. 1个B. 2个C. 3个D. 4个9.平面α截球O的球面所得圆的半径为1,球心O到平面α的距离为√2,则此球的体积为()A. √6πB. 4√3πC. 4√6πD. 6√3π10.直三棱柱ABC−A1B1C1中,∠BCA=90°,M,N分别是A1B1,A1C1的中点,BC=CA=CC1,则BM与AN所成角的余弦值为()A. 110B. 25C. √3010D. √2211.已知点A(2,−3),B(−3,−2),直线m过P(1,1),且与线段AB相交,求直线m的斜率k的取值范围为()A. k≥34或k≤−4 B. k≥34或k≤−14C. −4≤k≤34D. 34≤k≤412.如图,点P在正方体ABCD−A1B1C1D1的面对角线BC1上运动(P点异于B、C1点),则下列四个结论:①三棱锥A−D1PC的体积不变:②A1P//平面ACD1:③DP⊥BC1;④平面PDB1⊥平面ACD1.其中正确结论的个数是()A. 1个B. 2个C. 3个D. 4个二、填空题(本大题共4小题,共20.0分)13.如果直线ax+2y+2=0与直线3x−y−2=0平行,那么系数a的值为______.14.已知点B与点A(1,2,3)关于M(0,−1,2)对称,则点B的坐标是______.15.圆(x+2)2+y2=4与圆(x−2)2+(y−1)2=9的位置关系为______.16.已知⊙M:x2+(y−2)2=1,Q是x轴上的动点,QA,QB分别切⊙M于A,B两点,求动弦AB的中点P的轨迹方程为______.三、解答题(本大题共6小题,共72.0分)17.已知集合A={y|y=x2−32x+1,34≤x≤2},B={x|x+m2≥1},p:x∈A,q:x∈B,并且p是q的充分条件,求m的取值范围.18.已知直线l1,l2的方程分别为2x−y=0,x−2y+3=0,且l1,l2的交点为P.(1)求P点坐标;(2)若直线l过点P,且与x,y轴正半轴围成的三角形面积为92,求直线l的方程.19.圆C经过点A(2,−1),和直线x+y=1相切,且圆心在直线y=−2x上.(1)求圆C的方程;(2)圆内有一点B(2,−52),求以该点为中点的弦所在的直线的方程.20.如图,在底面是菱形的四棱锥P−ABCD中,∠ABC=60°,PA=AC=a,PB=PD=√2a,点E在PD上,且PE:ED=2:1.(1)求该四棱锥的体积;(2)若F为棱PC的中点,证明:BF//平面AEC.21.如图1,在Rt△ABC中,∠C=90°,D,E分别为AC,AB的中点,点F为线段CD上的一点,将△ADE沿DE折起到△A1DE的位置,使A1F⊥CD,如图2.(1)求证:DE//平面A1CB;(2)求证:A1F⊥BE;(3)线段A1B上是否存在点Q,使A1C⊥平面DEQ?说明理由.22. 已知过点A(−1,0)的动直线l 与圆C :x 2+(y −3)2=4相交于P ,Q 两点,M 是PQ 中点,l 与直线m :x +3y +6=0相交于N . (1)求证:当l 与m 垂直时,l 必过圆心C ; (2)当PQ =2√3时,求直线l 的方程;(3)探索AM ⃗⃗⃗⃗⃗⃗ ⋅AN ⃗⃗⃗⃗⃗⃗ 是否与直线l 的倾斜角有关?若无关,请求出其值;若有关,请说明理由.答案和解析1.【答案】C【解析】解:∵直线x=1垂直于x轴,倾斜角为90°,而斜率不存在,故选:C.利用直线x=1垂直于x轴,倾斜角为90°,选出答案.本题考查直线的倾斜角和斜率的关系,以及直线的图象特征与直线的倾斜角、斜率的关系.2.【答案】D【解析】【分析】根据证明平行四边形的条件判断A,由线面垂直的性质定理和定义判断B和C,利用实际例子判断D.本题考查了平面几何和立体几何中的定理和定义,只要抓住定理中的关键条件进行判断,可借助于符合条件的几何体进行说明,考查了空间想象能力和对定理的运用能力.【解答】解:A、一组对边平行且相等就决定了是平行四边形,故A不符合题意;B、由线面垂直的性质定理知,同一平面的两条垂线互相平行,因而共面,故B不符合题意;C、由线面垂直的定义知,这些直线都在同一个平面内即直线的垂面,故C不符合题意;D、由实际例子,如把书本打开,且把书脊垂直放在桌上,则由无数个平面满足题意,故D符合题意.故选:D.3.【答案】B【解析】【分析】根据二元二次方程表示圆的条件,可以求得若方程x2+y2+4mx−2y+5m=0表示圆,必有16m2+4−20m>0,即可求出m的取值范围.本题考查二元二次方程表示圆的条件,若方程x2+y2+Dx+Ey+F=0表示圆,则有D2+E2−4F>0.【解答】解:根据二元二次方程表示圆的条件,方程x2+y2+4mx−2y+5m=0表示圆,必有16m2+4−20m>0,解可得,m<14或m>1,故选:B.4.【答案】D【解析】解:如图,在正方体ABCD−A1B1C1D1中,BB1的中点为E,CC1的中点为F,设D1C1=a,平面ABCD为α,则a//α.观察图形,知:a与AD为异在直线,AD⊂α;a与AA1为异面直线,AA1与α相交;a与EF是异面直线,EF//α.∴若a,b是异面直线,且a//平面α,则b和α的位置关系是平行、相交或b在α内.故选:D.作出正方体,借助正方体能够比较容易地得到结果.本题考查直线与平面的位置关系的判断,解题时要认真审题,注意平面的公理及其推论的灵活运用.5.【答案】B【解析】解:由几何体的三视图得,几何体是低下是一个圆柱,底面半径为1,圆柱体的高为3,上面是半径为1的一个球∴该几何体的体积为π×3+43π=133π故选:B.先由三视图判断出几何体的直观图的形状为上面是球,下面是圆柱;然后利用圆柱、球的体积公式求出该几何体的体积.解决由三视图求几何体的表面积、体积问题,一般先将三视图转化为几何体的直观图,再利用面积、体积公式求.6.【答案】B【解析】解:若l//α,l//β,则α//β或α,β相交,故A不正确;根据线面平行的性质可得:若l//α,经过l的直线与α的交线为m,则l//m,∵l⊥β,∴m⊥β,根据平面与平面垂直的判定定理,可得α⊥β,故B正确;若l⊥α,α⊥β,则l⊂β或l//β,故C错误;作出正方体ABCD−A′B′C′D′,设平面ABCD为α,ADD′A′为β,则α⊥β,观察正方体,得到:B′C′//α,且B′C′//β;A′D′//α,且A′D′⊂β;A′B′//α,且A′B′与β相交.∴面α、β及直线l满足:α⊥β,l//α,则一定有l//β或l⊂β或l与β相交,故D不正确.故选:B.对4个选项分别进行判断,即可得出结论.“由已知想性质,由求证想判定”,也就是说,根据已知条件去思考有关的性质定理;根据要求证的结论去思考有关的判定定理,往往需要将分析与综合的思路结合起来.7.【答案】C【解析】【分析】根据直线x−y+1=0与圆(x−a)2+y2=2有公共点,可得圆心到直线x−y+1=0的距离不大于半径,从而可得不等式,即可求得实数a取值范围.本题考查直线与圆的位置关系,解题的关键是利用圆心到直线的距离不大于半径,建立不等式.【解答】解:∵直线x−y+1=0与圆(x−a)2+y2=2有公共点≤√2∴圆心到直线x−y+1=0的距离为|a+1|√2∴|a+1|≤2∴−3≤a≤1故选:C.8.【答案】C【解析】解:圆x2+2x+y2+4y−3=0的圆心(−1,−2),半径是2√2,圆心到直线x+=√2,y+1=0的距离是|−1−2+1|√2故圆上的点到直线x+y+1=0的距离为√2的共有3个.故选:C.先求圆心和半径,再看圆心到直线的距离,和√2比较,可得结果.本题考查直线和圆的位置关系,点到直线的距离公式,考查数形结合的思想,是中档题.9.【答案】B【解析】【分析】利用平面α截球O的球面所得圆的半径为1,球心O到平面α的距离为√2,求出球的半径,然后求解球的体积.本题考查球的体积的求法,考查空间想象能力、计算能力.【解答】解:因为平面α截球O的球面所得圆的半径为1,球心O到平面α的距离为√2,所以球的半径为:√(√2)2+1=√3.(√3)3=4√3π.所以球的体积为:4π3故选B.10.【答案】C【解析】【分析】本题考查异面直线对称角的求法,作出异面直线所成角的平面角是解题的关键,同时考查余弦定理的应用.画出图形,找出BM与AN所成角的平面角,利用解三角形求出BM与AN所成角的余弦值.【解答】解:直三棱柱ABC−A1B1C1中,∠BCA=90°,M,N分别是A1B1,A1C1的中点,如图:BC的中点为O,连结ON,B1C1=OB,则MNOB是平行四边形,BM与AN所成角等于∠ANO,MN=//12∵BC=CA=CC1,设BC=CA=CC1=2,∴CO=1,AO=√5,AN=√5,MB=√B1M2+BB12=√(√2)2+22=√6,在△ANO中,由余弦定理可得:cos∠ANO=AN 2+NO2−AO22AN⋅NO=62×√5×√6=√3010.故选:C.11.【答案】A【解析】【分析】本题考查一元二次不等式组表示平面区域的问题,注意直线m与线段AB相交,即A、B在直线的两侧或直线上.根据题意,设直线m的方程为y−1=k(x−1),分析可得若直线m与线段AB相交,即A、B在直线的两侧或直线上,则有[(−3)−2k+k−1][(−2)−(−3)k+k−1]≤0,解可得k的范围,即可得答案.【解答】解:根据题意,直线m过P(1,1),设直线m的方程为y−1=k(x−1),即y−kx+k−1=0,若直线m与线段AB相交,即A、B在直线的两侧或直线上,则有[(−3)−2k+k−1][(−2)−(−3)k+k−1]≤0,解可得:k≥34或k≤−4;故选A.12.【答案】C【解析】解:对于①,由题意知AD1//BC1,从而BC1//平面AD1C,故BC 1上任意一点到平面AD1C的距离均相等,所以以P为顶点,平面AD1C为底面,则三棱锥A−D1PC的体积不变,故①正确;对于②,连接A1B,A1C1,A1C1//AD1且相等,由于①知:AD1//BC1,所以面BA1C1//面ACD1,从而由线面平行的定义可得,故②正确;对于③,由于DC ⊥平面BCB 1C 1,所以DC ⊥BC 1, 若DP ⊥BC 1,则BC 1⊥平面DCP ,BC 1⊥PC ,则P 为中点,与P 为动点矛盾,故③错误; 对于④,连接DB 1,由DB 1⊥AC 且DB 1⊥AD 1,可得DB 1⊥面ACD 1,从而由面面垂直的判定知,故④正确. 故选:C .利用空间中线线、线面、面面间的位置关系,结合线线、线面、面面平行和垂直的判断与性质求解.本题考查命题真假的判断,解题时要注意三棱锥体积求法中的等积法、线面平行、线线垂直的判定,要注意转化的思想的使用,是中档题.13.【答案】−6【解析】解:∵直线ax +2y +2=0与直线3x −y −2=0平行, ∴它们的斜率相等,∴−a2=3 ∴a =−6故答案为:−6根据它们的斜率相等,可得−a2=3,解方程求a 的值. 本题考查两直线平行的性质,两直线平行,斜率相等.14.【答案】(−1,−4,1)【解析】解:设点B 的坐标为(x,y ,z),∵点B 与点A(1,2,3)关于M(0,−1,2)对称, ∴点M(0,−1,2)对为点A(1,2,3)和点B(x,y ,z)的中点, 由中点坐标公式可得,{ 0=x+12−1=y+222=z+32,解得{x =−1y =−4z =1,∴点B 的坐标是(−1,−4,1). 故答案为:(−1,−4,1).根据点的对称性,将问题转化为两点的中点坐标问题,利用中点坐标公式列出方程组,求解即可得到点B 的坐标公式.本题考查了空间中的点的坐标.中点考查了中点坐标公式,解空间坐标问题时,要注意类比平面坐标,对于一些运算公式和法则两者是通用的.属于基础题.15.【答案】相交【解析】解:圆C(x +2)2+y 2=4的圆心C(−2,0),半径r =2; 圆M(x −2)2+(y −1)2=9的圆心M(2,1),半径R =3.∴|CM|=√(−2−2)2+1=√17,R −r =3−2=1,R +r =3+2=5. ∴R −r <√17<R +r . ∴两圆相交. 故答案为:相交.由两圆的方程可得圆心坐标及其半径,判断圆心距与两圆的半径和差的关系即可得出. 本题考查了判断两圆的位置关系的方法,属于基础题.16.【答案】x 2+(y −74)2=116(32≤y <2)【解析】解:连接MB ,MQ ,设P(x,y),Q(|a|,0),点M 、P 、Q 在一条直线上, 得2−a =y−2x.①由射影定理,有|MB|2=|MP|⋅|MQ|, 即√x 2+(y −2)2⋅√a 2+4=1.②由①及②消去a ,可得x 2+(y −74)2=116和x 2+(y −94)2=116. 又由图形可知y <2, 因此x 2+(y −94)2=116舍去.因此所求的轨迹方程为x 2+(y −74)2=116(32≤y <2). 故答案为:x 2+(y −74)2=116(32≤y <2).连接MB ,MQ ,设P(x,y),Q(|a|,0),点M 、P 、Q 在一条直线上,利用斜率相等建立等式,进而利用射影定理|MB|2=|MP|⋅|MQ|,联立消去a ,求得x 和y 的关系式,根据图形可知y <2,进而可求得动弦AB 的中点P 的轨迹方程.本题主要考查了直线与圆的位置关系,求轨迹方程问题.解题过程中灵活利用了射影定理.17.【答案】解:化简集合A ={y|y =x 2−32x +1,34≤x ≤2},配方,得y =(x −34)2+716.因为x ∈[716,2],∴y min =716,y max =2∴y ∈[716,2]∴A ={y|716≤y ≤2}, 化简集合B ,由x +m 2≥1,得x ≥1−m 2,B ={x|x ≥1−m 2}, 因为命p 题是命题q 的充分条件, ∴A ⊆B ∴1−m 2≤716解得m ≥34或m ≤−34, 故实数的取值范围是(−∞,−34]∪[34.【解析】根据二次函数的性质求出A 的范围,化简集合B ,根据A ⊆B ,得到关于m 的不等式,解出即可.本题考查了二次函数的性质,考查集合的包含关系,是一道基础题.18.【答案】解:(1)由{2x −y =0x −2y +3=0得P(1,2).(2)①当过点P(1,2)的直线与坐标轴平行时,不合题意;②当过点P(1,2)的直线与坐标轴不平行时,可设所求直线方程为y −2=k(x −1), 当x =0时,y =2−k ;当y =0时,x =1−2k .故三角形的面积s △=12|(1−2k )(2−k)|=92,由2−k >0,1−2k >0, 解得k =−1或−4.故所求的直线方程为y −2=−1×(x −1)或y −2=−4×(x −1), 即x +y −3=0或4x +y −6=0;综上,所求直线方程为x +y −3=0或4x +y −6=0;【解析】(1)把2条直线的方程联立方程组,求出方程组的解,可得交点坐标. (2)用点斜式求直线的方程,并求出它在坐标轴上的截距,再根据直线与x ,y 轴正半轴围成的三角形面积为92,求出斜率的值,可得直线l 的方程.本题主要考查求直线的交点坐标,用点斜式求直线的方程,直线的截距,属于基础题.19.【答案】解:(1)设圆心(m,−2m),方程为:(x −m)2+(y +2m)2=r 2∵圆过A(2,−1),∴有(2−m)2+(−1+2m)2=r 2 又√2=r ,解得m =1,r =√2,∴圆的方程为(x −1)2+(y +2)2=2.(2)由题意,(x −1)2+(y +2)2=2的圆心坐标为C(1,−2),则k CB =−2+521−2=−12,∴以B(2,−52)为中点的弦所在的直线的斜率为2,∴所求直线方程为y+52=2(x−2),即4x−2y−13=0.【解析】(1)设出圆心坐标,利用圆C经过点A(2,−1),和直线x+y=1相切,建立方程组,可求圆C的方程;(2)求出以B(2,−52)为中点的弦所在的直线的斜率,利用点斜式可得方程.本题考查圆的方程,考查直线与圆的位置关系,考查学生的计算能力,属于中档题.20.【答案】(1)解:设AC∩BD=O,连接PO,则O既为AC的中点,也为BD的中点,∵∠ABC=60°,AC=a,∴BD=√3a,AO=12AC=12a,BO=12BD=√32a.∵PB=PD=√2a,∴PO⊥BD,PO2=PB2−BO2=54a2,∴PA2+AO2=PO2,即PA⊥AC.∵PO⊥BD,AC⊥BD,PO∩AC=O,PO、AC⊂平面PAC,∴BD⊥平面PAC,又BD⊂平面ABCD,∴平面ABCD⊥平面PAC.∵平面ABCD∩平面PAC=AC,PA⊂平面PAC,∴PA⊥平面ABCD.∴四棱锥的体积V=13PA⋅S菱形ABCD=13PA⋅12AC⋅BD=13×a×12×a×√3a=√36a3.(2)证明:取PE的中点M,连结FM、BM,则FM//CE.由PE:ED=2:1,知E是MD的中点,∵O为BD的中点,∴BM//OE.∵FM∩BM=M,CE∩OE=E,FM、BM⊂平面BFM,CE、OE⊂平面AEC,∴平面BFM//平面AEC.又BF⊂平面BFM,∴BF//平面AEC.【解析】(1)设AC∩BD=O,连接PO,在菱形ABCD中,易求得BD=√3a,AO=12a,BO=√32a,由勾股定理可证明PA⊥AC;由PO⊥BD,AC⊥BD,可推出BD⊥平面PAC,PA⋅结合面面垂直的判定定理与性质定理可得PA⊥平面ABCD,故四棱锥的体积V=13S.菱形ABCD(2)取PE的中点M,连结FM、BM,则FM//CE,BM//OE,从而推出平面BFM//平面AEC,再由面面平行的性质定理即可得证.本题考查空间中线与面的位置关系、棱锥体积的求法,熟练掌握空间中线面、面面平行或垂直的判定定理与性质定理是解题的关键,考查学生的空间立体感、逻辑推理能力和运算能力,属于中档题.21.【答案】解:(1)∵D,E分别为AC,AB的中点,∴DE//BC,又DE⊄平面A1CB,∴DE//平面A1CB.(2)由已知得AC⊥BC且DE//BC,∴DE⊥AC,∴DE⊥A1D,又DE⊥CD,∴DE⊥平面A1DC,而A1F⊂平面A1DC,∴DE⊥A1F,又A1F⊥CD,∴A1F⊥平面BCDE,∴A1F⊥BE.(3)线段A1B上存在点Q,使A1C⊥平面DEQ.理由如下:如图,分别取A1C,A1B的中点P,Q,则PQ//BC.∵DE//BC,∴DE//PQ.∴平面DEQ即为平面DEP.由(Ⅱ)知DE⊥平面A1DC,∴DE⊥A1C,又∵P是等腰三角形DA1C底边A1C的中点,∴A1C⊥DP,∴A1C⊥平面DEP,从而A1C⊥平面DEQ,故线段A1B上存在点Q,使A1C⊥平面DEQ.【解析】(1)D ,E 分别为AC ,AB 的中点,易证DE//平面A 1CB ;(2)由题意可证DE ⊥平面A 1DC ,从而有DE ⊥A 1F ,又A 1F ⊥CD ,可证A 1F ⊥平面BCDE ,问题解决;(3)取A 1C ,A 1B 的中点P ,Q ,则PQ//BC ,平面DEQ 即为平面DEP ,由DE ⊥平面,P 是等腰三角形DA 1C 底边A 1C 的中点,可证A 1C ⊥平面DEP ,从而A 1C ⊥平面DEQ . 本题考查直线与平面平行的判定,直线与平面垂直的判定与性质,考查学生的分析推理证明与逻辑思维能力,综合性强,属于难题.22.【答案】解:(1)∵l 与m 垂直,且k m =−13,∴k 1=3,故直线l 方程为y =3(x +1),即3x −y +3=0.∵圆心坐标(0,3)满足直线l 方程, ∴当l 与m 垂直时,l 必过圆心C .(2)①当直线l 与x 轴垂直时,易知x =−1符合题意.②当直线l 与x 轴不垂直时,设直线l 的方程为y =k(x +1),即kx −y +k =0, ∵PQ =2√3,∴CM =√4−3=1,则由CM =√k 2+1=1,得k =43,∴直线l :4x −3y +4=0.故直线l 的方程为x =−1或4x −3y +4=0.(3)∵CM ⊥MN ,∴AM ⃗⃗⃗⃗⃗⃗ ⋅AN ⃗⃗⃗⃗⃗⃗ =(AC ⃗⃗⃗⃗⃗ +CM ⃗⃗⃗⃗⃗⃗ )⋅AN ⃗⃗⃗⃗⃗⃗ =AC ⃗⃗⃗⃗⃗ ⋅AN ⃗⃗⃗⃗⃗⃗ +CM ⃗⃗⃗⃗⃗⃗ ⋅AN ⃗⃗⃗⃗⃗⃗ =AC ⃗⃗⃗⃗⃗ ⋅AN⃗⃗⃗⃗⃗⃗ . ①当l 与x 轴垂直时,易得N(−1,−53),则AN ⃗⃗⃗⃗⃗⃗ =(0,−53),又AC ⃗⃗⃗⃗⃗ =(1,3), ∴AM ⃗⃗⃗⃗⃗⃗ ⋅AN ⃗⃗⃗⃗⃗⃗ =AC ⃗⃗⃗⃗⃗ ⋅AN⃗⃗⃗⃗⃗⃗ =−5. ②当l 的斜率存在时,设直线l 的方程为y =k(x +1), 则由{y =k(x +1)x +3y +6=0得N(−3k−61+3k ,−5k1+3k ),则AN ⃗⃗⃗⃗⃗⃗ =(−51+3k ,−5k 1+3k ). ∴AM ⃗⃗⃗⃗⃗⃗ ⋅AN ⃗⃗⃗⃗⃗⃗ =AC ⃗⃗⃗⃗⃗ ⋅AN ⃗⃗⃗⃗⃗⃗ =−51+3k +−15k 1+3k=−5. 综上所述,AM ⃗⃗⃗⃗⃗⃗ ⋅AN⃗⃗⃗⃗⃗⃗ 的值与直线l 的斜率无关,且AM ⃗⃗⃗⃗⃗⃗ ⋅AN ⃗⃗⃗⃗⃗⃗ =−5.【解析】(1)根据l 与m 垂直,则两条直线的斜率之积为−1,进而根据直线过点A(−1,0),我们可求出直线的方程,将圆的圆心坐标代入直线方程验证后,即可得到结论; (2)根据半弦长、弦心距、圆半径构造直角三角形,满足勾股定理,结合PQ =2√3,易得到弦心距,进而根据点到直线的距离公式,构造关于k 的方程,解方程即可得到k 值,进而得到直线l 的方程;(3)根据已知条件,我们可以求出两条直线的交点N 的坐标(含参数k),然后根据向量数量积公式,即可求出AM ⃗⃗⃗⃗⃗⃗ ⋅AN⃗⃗⃗⃗⃗⃗ 的值,进而得到结论.本题考查的知识点是直线与圆相交的性质及向量在几何中的应用,其中在处理圆的弦长问题时,根据半弦长、弦心距、圆半径构造直角三角形,满足勾股定理,进行弦长、弦心距、圆半径的知二求一,是解答此类问题的关键.。
2019-2020学年安徽省合肥市一六八中学高二上学期期中数学(理)试题(解析版)

2019-2020学年安徽省合肥市一六八中学高二上学期期中数学(理)试题一、单选题1.经过圆上任意三个不同的点可以作出( )个平面. A .0个 B .1个C .2个D .1个或无数个【答案】B【解析】当空间的三个不同的点不共线时,过这三个点能确定1个平面,由此得解. 【详解】当空间的三个不同的点不共线时,过这三个点能确定1个平面. 所以经过圆上任意三个不同的点可以作出1个平面. 故选:B . 【点睛】本题考查平面的基本性质及其推论的应用,解题时要认真审题,仔细解答,注意全面考虑,不要遗漏.2.已知光线从点(3,4)A -射出,到x 轴上的点B 后,被x 轴反射,这时反射光线恰好过点(1,6)C ,则BC 所在直线的方程为( )A .5270x y -+=B .2570x y -+=C .5270x y +-=D .2570x y +-=【答案】A【解析】设(3,4)A -点关于x 轴的对称点为A ',根据反射定律,A '在直线BC 上,即可求出BC 所在的直线方程. 【详解】设(3,4)A -点关于x 轴的对称点为(3,4)A '--, 根据对称性,点A '在直线BC 上,(1,6)C , 所以BC 所在的直线方程为56(1)2y x -=-, 即5270x y -+=.故选:A. 【点睛】本题考查直线方程的求法,利用对称性是解题的关键,属于基础题.3.如图所示,在正方体1111ABCD A B C D 中,M ,N 分别是1BB ,BC 的中点,则图中阴影部分在平面11ADD A 上的正投影是( )A .B .C .D .【答案】A【解析】根据投影的定义,分别找出点,,D M N 在平面11ADD A 上的投影,即可求解,得到答案. 【详解】由题意,阴影部分为三角形DMN ,其中点D 在投影面上,它的投影是其本身, 点N 在平面11ADD A 上的投影是AD 的中点, 点M 在平面11ADD A 上的投影是1AA 的中点, 所以三角形DMN 的投影为选项A 符合题意. 故选:A . 【点睛】本题主要考查了平行投影及平行投影的作法,其中解答中熟记平行投影的定义,准确确定点在平面上的投影是解答的关键,着重考查了空间想象能力,属于基础题. 4.设长方体的三条棱长分别为a 、b 、c ,若长方体所有棱长度之和为24,一条对角线长度为5,体积为2,则111a b c ++等于( ). A .114B .411C .112D .211【答案】A【解析】解:设长方体的长、宽、高分别为a ,b ,c ,由题意可知, a+b+c=6…①, abc=2…②, a 2+b 2+c 2=25…③由①式平方-②可得ab+bc+ac=112…④, ④÷②得:111a b c ++=114故选A 5.设a 、b 是不同的两条直线,α、β是不同的两个平面,分析下列命题,其中正确的是( ).A .a α⊥,b β⊂,a b αβ⊥⇒⊥B .α∥β,a α⊥,b ∥βa b ⇒⊥C .αβ⊥,a α⊥,b ∥a b β⇒⊥D .αβ⊥,a αβ⋂=,a b b β⊥⇒⊥ 【答案】B【解析】解:因为利用空间中点线面的位置关系可知,选项A 中,不符合面面垂直的判定定理,错误选项C 中,可能a,b 相交成一般角,错误,选项D 中,可能线面相交不成直角,错误.选B6.连结Rt ABC V 的直角顶点C 与斜边AB 的两个三等分点,D E ,所得线段,CD CE 的长分别为sin α和cos 02παα⎛⎫<<⎪⎝⎭,则AB 长为( )A .43B C D 【答案】B【解析】设1,,3AC b BC a AD EB AB x =====,可得2229a b x +=,以及cos ,cos A B ,分别在,ACD BCE ∆∆中,由余弦定理求出22,CD CE ,利用221CD CE +=,即可求解.【详解】设1,,3AC b BC a AD EB AB x =====, 则2229,cos ,cos 33b a a b x A B x x+===, 在ACD ∆中,2222cos CD AC AD AC AD A =+-⋅22222sin 233b b b x b x x x α=+-⋅⋅=+,①同理在BCE ∆中,222cos 3a x α=+,②①+②得,22222111()25,35a b x x x =++=∴=, 35AB x ==. 故选:B.【点睛】本题考查余弦定理解三角形,利用直角三角形边角关系是解题的关键,属于中档题. 7.已知四棱锥底面四边形中顺次三个内角的大小之比为2:3:4,此棱锥的侧棱与底面所成的角相等,则底面四边形的最小角是( ).A .18011oB .60oC .18013oD .无法确定的【答案】B 【解析】【详解】解:因为棱锥的侧棱与底面所成的角相等,所以四棱锥底面四边形内接于一个圆,因为四棱锥底面四边形顺次三个内角的大小之比为2:3:4,设对应角为2,3,42423k k k k k k ππ∴+=∴=,因此此则底面四边形的最小角是60o ,选B8.《九章算术》是我国古代的数学专著,是“算经十书”(汉唐之间出现的十部古算书)中最重要的一种.在《九章算术》中,将底面是直角三角形的直三棱柱称为“堑堵”.已面积为3π,则这个三棱柱的体积是( ) A .16B .13C .12D .1【答案】C【解析】设11,BC B C 中点分别为1,M M ,取1MM 中点O ,则O 为111ABC A B C -的外接球的球心,由球O 表面积,得出球O 半径,求出1MM ,即可求解. 【详解】设11,BC B C 中点分别为1,M M ,取1MM 中点O ,Q 三棱柱111ABC A B C -底面是直角三角形,1AB AC ==,111111,,//AB AC A B AC MM AA ∴⊥⊥,1,M M 分别为111,Rt ABC Rt A B C ∆∆的外接圆圆心, 1AA ⊥Q 平面ABC , 1MM ∴⊥平面ABC ,O ∴为111ABC A B C -的外接球的球心, Q 球O 的表面积为3π,∴球O 的半径3OB =, 22122()12BC MM OM OB ∴==-=, 1112111122ABC A B C V -∴=⨯⨯=.故选:C.【点睛】本题以数学文化为背景,考查多面体与球“接”“切”问题,确定球心位置是解题的关键,9.球面上有三点,,A B C 组成这个球的一个截面的内接三角形的三个顶点,其中18AB =,24BC =,30AC =,球心到这个截面的距离为球半径的一半,则该球的表面积为( ) A .1200π B .1400πC .1600πD .1800π【答案】A【解析】设所求球的球心为O ,半径为R ,根据已知ABC ∆是以AC 为斜边的直角三角形,设AC 中点为1O ,则1O 是截面圆的圆心,从而有1OO ⊥平面ABC ,在1Rt OO A ∆中,建立R 的方程,求解即可. 【详解】设所求球的球心为O ,半径为,R AC 中点为1O , 连1,OO OA ,18AB =Q ,24BC =,30AC =,222,AB BC AC AB BC ∴+=∴⊥,1O ∴为过,,A B C 三点截面圆的圆心,1OO ∴⊥平面1,ABC OO AC ∴⊥,在1Rt OO A ∆中,22222211154R AO R OO AO ==+=+,解得2300R =,球O 的表面积为241200R ππ=. 故选:A.【点睛】本题考查球的表面积,利用球的性质是解题的关键,属于中档题. 10.两条异面直线,a b 所成的角3π,直线a c ⊥,则直线b 与c 所成的角的范围为( )A .,63ππ⎡⎤⎢⎥⎣⎦B .,32ππ⎡⎤⎢⎥⎣⎦ C .,62ππ⎡⎤⎢⎥⎣⎦D .2,63ππ⎡⎤⎢⎥⎣⎦【解析】将异面直线所成的角转化为平面角,然后由题意,找出与直线a 垂直的直线c ,判定与直线b 的夹角. 【详解】在直线a 上任取一点O ,过O 做//b b ',则,a b '确定一平面α,过O 点做直线c 的平行线c ',所有平行线c '在过O 与直线a 垂直的平面β内, 若存在平行线1c '不在β内,则1c '与c '相交又确定不同于β的平面, 这与过一点有且仅有一个平面与一条直线垂直矛盾,所以c '都在平面β内, 则,l αβαβ⊥=I ,在直线b '上任取不同于O 的一点P ,作PP l '⊥于P ',则PP β'⊥,POP '∠为是b '与β所成的角为30°, 若c l '⊥,则,c c b α'''⊥⊥,若c '不垂直l 且不与l 重合, 过P '作P A c ''⊥,垂足为A ,连PA ,,PP c P A PP P '''''⊥=Ic '∴⊥平面PP A ',c PA '⊥,即OA PA ⊥,3cos 2OA OP AOP OP OP '∠=<=,30AOP ∠>︒, 综上b '与c '所成角的范围为[30,90]︒︒,所以直线b 与c 所成角的范围为,62ππ⎡⎤⎢⎥⎣⎦.故选:C.【点睛】本题考查异面直线所成角,空间角转化为平面角是解题的关键,利用垂直关系比较角的大小,属于中档题.11.如图所示,三棱锥P ABC -的底面在平面α内,且AC PC ⊥,平面PAC ⊥平面PBC ,点P A B ,,是定点,则动点C 的轨迹是( )A .一条线段B .一条直线C .一个圆D .一个圆,但要去掉两个点 【答案】D【解析】因为平面PAC ⊥平面PBC ,AC ⊥PC ,平面PAC∩平面PBC=PC , AC ⊂平面PAC ,所以AC ⊥平面PBC.又因为BC ⊂平面PBC ,所以AC ⊥BC.所以∠ACB=90°. 所以动点C 的轨迹是以AB 为直径的圆,除去A 和B 两点. 选D.点睛:求轨迹实质是研究线面关系,本题根据面面垂直转化得到线线垂直,再根据圆的定义可得轨迹,注意轨迹纯粹性. 12.已知矩形,ABCD 1,2AB BC ==将ABD ∆沿矩形的对角线BD 所在的直线进行翻折,在翻折过程中( )A .存在某个位置,使得直线AC 与直线BD 垂直B .存在某个位置,使得直线AB 与直线CD 垂直C .存在某个位置,使得直线AD 与直线BC 垂直D .对任意位置,三对直线“AC 与BD ”,“AB 与CD ”,“AD 与BC ”均不垂直 【答案】B【解析】最简单的方法是取一长方形动手按照其要求进行翻着,观察在翻着过程,即可知选项B 是正确的二、填空题13.经过平面α外一点和平面α内一点与平面α垂直的平面有_____个. 【答案】1个或无数个论,即可求出结论. 【详解】设平面α外一点为A ,平面α内一点为O , 若OA α⊥,则过OA 任一平面都垂直α, 所以过OA 存在无数个平面与平面α垂直;若OA 不垂直α,过点A 作唯一的直线l 与平面α垂直,OA 与l 确定唯一的平面与α垂直,所以过OA 存在唯一的平面与平面α垂直. 故答案为:1个或无数个. 【点睛】本题考查直线与平面的位置关系,考查直线与平面垂直的性质、平面和平面垂直的判定,考查直观想象能力,属于中档题.14.若动点()11,A x y ,()22,B x y 分别在直线1:270+-=l x y 和2:250+-=l x y 上移动,则AB 的中点到原点的距离的最小值为__________.【解析】先设AB 的中点坐标为(),x y ,根据题意,得到AB 中点所在直线方程,由点到直线距离公式,即可得出结果. 【详解】设AB 的中点坐标为(),x y ,因为()11,A x y ,()22,B x y ,所以121222x x x y y y +⎧=⎪⎪⎨+⎪=⎪⎩,又()11,A x y ,()22,B x y 分别在直线1:270+-=l x y 和2:250+-=l x y 上移动,所以1122270250x y x y +-=⎧⎨+-=⎩,两式相加得()()12122120+++-=x x y y ,所以42120+-=x y ,即260x y +-=即为AB 中点所在直线方程,因此原点到直线260x y +-=的距离,即为AB 的中点到原点的距离的最小值;=故答案为:655【点睛】本题主要考查求直线上的点到原点距离的最值问题,熟记点到直线距离公式即可,属于常考题型.15.如图,正方体ABCDA B C D ''''有12条棱,选取其中6条棱,每条棱上取一点,使这6个点正好成为正八面体的6个顶点.(注:正八面体共有6个顶点.)比如就从点A 出发,来进行构建.在与点A 相邻的三条棱上分别取一点,使其到点A 的距离都为棱长的四分之三,得到3个点:E F G 、、.同理,对与点A 相对的点C '进行类似的操作,得到另外3个点:E F G '''、、.显然,位于正方体界面上的6条线段相等,即EF FG GE E F F G G E ''=====''''从正方体内部穿过的线段也有六条:EF '、EG '、FE '、FG '、GE '、GF '.这样一共得到12条线段,它们就是所要构建的正八面体的12条棱.通过计算它们的长度全都相等,即构建的是正八面体.在此正八面体中EF '与FG '所成角的余弦值是_________.【答案】12【解析】设正方体的边长为4,可证四边形FGF G ''为平行四边形,从而有//GF FG '',EF G '∠(或补角)为异面直线EF '与FG '所成的角,解EF G '∆即可.【详解】设正方体的边长为4,连,A D B C '',333,//,3244AF AG AA GF A D GF A D '''===∴==Q , 同理//,32G F B C G F '''''=在正方体ABCD A B C D ''''-中,//A D B C '',//,GF F G GF F G ''''∴=,四边形FGF G ''为平行四边形, //,GF FG EF G '''∴∠(或补角)为异面直线EF '与FG '所成的角,连2222,,17,32CE CG CE BE BC EF CE CF ''=+==+=同理32,232,GF GE AE EF G ''===∴∆为等边三角形,160,cos 2EF G EF G ''∴∠=︒∠=EF '∴与FG '所成角的余弦值是12.故答案为:12.【点睛】本题考查异面直线所成的角,空间角转化为平面角是解题的关键,考查直观想象能力,属于基础题.16.在三棱柱111ABCA B C 中,侧棱1AA ⊥平面11AB C ,11AA =,底面ABC V 是边长为4的正三角形,则此三棱柱的体积为__________.【答案】211【解析】由已知可得11AB AC =并求出其值,进而求出11AB C ∆的面积,利用1111113ABC A B C A A B C V V --=,结合已知求出111A AB C V -,即可得出结论.【详解】1AA ⊥Q 平面11AB C ,1111,AA AB AA AC ∴⊥⊥,11111111,4,15AA A B AC AB AC ===∴=Q , 取11B C 中点D ,连AD ,则11AD B C ⊥,1122111111()11,21122AB C B C AD AB S B C AD ∆∴=-==⨯⨯=, 11111111111133211ABC A B C A A B C A AB C AB C V V V AA S ---∆∴===⨯=.故答案为:211.【点睛】本题考查三棱柱的体积,注意柱体和椎体体积间的关系,以及等体积法的应用,属于中档题.三、解答题17.如图,在Rt AOB V 中,30OAB ∠=︒,斜边4AB =,Rt AOC V 可以通过Rt AOB V 以直线AO 为轴旋转得到,且平面AOB ⊥平面AOC .动点D 在斜边AB 上.(1)求证:平面COD ⊥平面AOB ;(2)当D 为AB 的中点时,求异面直线AO 与CD 所成角的正切值. 【答案】(1)证明见解析;(215【解析】(1)平面AOB ⊥平面AOC ,OC OA ⊥,可证OC ⊥平面AOB ,即可证明结论;(2)取OB 中点E ,连DE ,则//DE AO ,CDE ∠(或补角)为异面直线AO 与CD 所成的角,解Rt CDE ∆,即可求出结论. 【详解】(1)平面AOB ⊥平面AOC ,平面AOB I 平面AOC OA =,,OC OA OC ⊥⊂平面,AOC OC ∴⊥平面AOB ,OC ⊂Q 平面,COD ∴平面COD ⊥平面AOB ;(2)取OB 中点E ,连DE ,D 为AB 的中点,//DE AO ∴,CDE ∠(或补角)为异面直线AO 与CD 所成的角,,,,OA OB OA OC OB OC O OA ⊥⊥=∴⊥Q I 平面BOC ,DE ∴⊥平面BOC ,CE ⊂平面,BOC DE CE ∴⊥,在Rt AOB V 中,30OAB ∠=︒,斜边4AB =,2223,2,3,()52OB OA OB OC DE CE OC ∴===∴==+=, 15tan 3CE CDE DE ∴∠==, 所以异面直线AO 与CD 所成角的正切值为15.【点睛】本题考查空间线、面位置关系,证明直线与平面垂直,注意空间垂直间的相互转化,求异面直线所成的角,要掌握空间角的解题步骤,“做”“证”“算”缺一不可,考查直观想象能力,属于中档题.18.在直角坐标系中,射线OA: x -y=0(x≥0),OB: x+2y=0(x≥0),过点P(1,0)作直线分别交射线OA 、OB 于A 、B 两点. (1)当AB 中点为P 时,求直线AB 的方程; (2)当AB 中点在直线12y x =上时,求直线AB 的方程. 【答案】(1)220x y +-=;(2)5250x y --= 【解析】【详解】(1)因为,A B 分别为直线与射线:0(0)OA x y x -=≥及:20(0)OB x y x +=≥的交点, 所以可设(,),(2,)A a a B b b -,又点(1,0)P 是AB 的中点,所以有21,2{0.2a ba b-=+=即2,3{2.3ab==-∴A、B两点的坐标为2242(,),(,)3333A B-,∴223324233ABk--==--,所以直线AB的方程为02(1)y x-=--,即220x y+-=(2)①当直线AB的斜率不存在时,则AB的方程为1x=,易知,A B两点的坐标分别为1(1,1),(1,),2A B-所以AB的中点坐标为1(1,)4,显然不在直线12y x=上,即AB的斜率不存在时不满足条件.②当直线AB的斜率存在时,记为k,易知0k≠且1k≠,则直线AB的方程为(1).y k x=-分别联立(1),{y k xx y=--=及(1),{20.y k xx y=-+=可求得,A B两点的坐标分别为(,),11k kAk k--2(,)1212k kBk k-++所以AB的中点坐标为(,)22122224k k k kk k k k+--+-+又AB的中点在直线12y x=上,所以1()222422212k k k kk k k k-=+-+-+解得52k=所以直线AB的方程为5(1)2y x=-,即5250x y--=19.H城市要在某小区前一块广场ABCDE(如图)上规划出一块长方形地面(不改变方位),改善人们室外活动生活.问:如何设计才能使开发面积最大?并求出最大面积.(已知210BC m=,240CD m=,300DE m=,180EA m=)【答案】设计见解析,面积最大值为254150m.【解析】把问题转化为在线段AB上找一点P,过P点分别做,AE BC的平行线与,DE CD围成长方形面积最大的问题,建立坐标系,设点P坐标,将长方形的面积表达式求出,再求其最值即可.【详解】以BC 所在的直线为x 轴,AE 所在的直线为y 轴建立直角坐标系, 则(0,60),(90,0)A B ,AB 所在的直线方程为19060x y +=, 即2603y x =-,设2(,60),0903P x x x -≤≤, 过P 点分别做,AE BC 的平行线与,DE CD 交于,F Q , 开发的矩形PQDF 的面积为2(300)(240)(300)(180)3S x y x x =--=-+22222054000(15)5415033x x x =-++=--+∴当15,50x y ==时,S 取得最大值为254150m ,答:长方形顶点P 距AE 边15m ,距BC 边50m 时,面积最大为254150m .【点睛】本题考查函数应用问题,根据几何关系转化成代数关系是解题的关键,考查数学建模、数学抽象、数学计算能力,属于中档题.20.在边长为4cm 的正方形ABCD 中,E F 、分别为BC CD 、的中点,M N 、分别为AB CF 、的中点,现沿AE AF EF 、、折叠,使B C D 、、三点重合,重合后的点记为B ,构成一个三棱锥.(1)请判断MN 与平面AEF 的位置关系,并给出证明; (2)证明:AB ⊥平面BEF ; (3)求四棱锥E AFNM -的体积.【答案】(1)//MN 平面AEF .证明见解析;(2)证明见解析;(3)2. 【解析】(1)//MN 平面AEF .在三棱锥中可得//MN AF ,即可证明结论; (2)由翻折前,AB BE AD DF ⊥⊥,在三棱锥中,AB BE AB BF ⊥⊥,即可证明结论;(3)由34ABF MNAF S S ∆=梯形,可得3344E AFNM E ABF A BEF V V V ---==,即可求解. 【详解】(1)//MN 平面AEF .证明如下:,M N Q 分别为,AB BF 中点,//MN AF ∴,AF ⊂Q 平面AEF ,MN ⊄平面AEF ,//MN ∴平面AEF ;(2)在正方形ABCD 中,,AB BE AD DF ⊥⊥, 在三棱锥中,,AB BE AB BF BE BF B ⊥⊥=I ,,BE BF ⊂平面BEF ,AB ∴⊥平面BEF ;(3)13//,,24ABF MNAF MN AF MN AF S S ∆=∴=Q 梯形, 23331142244432E AFNM E ABFA BEF V V V ---∴===⨯⨯⨯⨯= ∴四棱锥E AFNM -的体积的体积为2.【点睛】本题考查空间线、面的位置关系,证明直线与平面平行、直线与平面垂直,注意翻折前后不变量的应用,以及利用等体积法求椎体的体积,考查逻辑推理、直观想象能力,属于基础题.21.如图,在直三棱柱111ABCA B C 中,AC BC ⊥,14CC =,M 是棱1CC 上的一点.(1)求证:BC AM ⊥;(2)若N 是AB 的中点,且//CN 平面1AB M ,求CM 的长. 【答案】(1)证明见解析;(2)2CM =.【解析】(1)由已知可得1CC BC ⊥,结合AC BC ⊥,可得BC ⊥平面11AAC C ,即可证明结论;(2)取1AB 中点D ,连,MD ND ,则//ND CM ,由//CN 平面1AB M ,可证//CN MD ,得到四边形CMDN 为平行四边形,即可求CM 的长.【详解】(1)在直三棱柱111ABCA B C 中,1CC ⊥平面ABC ,1CC BC ∴⊥,又11,,,AC BC AC CC C AC CC ⊥=⊂I 平面11AAC C ,BC ∴⊥平面11AAC C ,AM ⊂Q 平面11AAC C ,BC AM ⊥∴;(2)取1AB 中点D ,连,MD ND ,N 是AB 的中点,11111//,22DN BB DN BB CC ∴==,又11//,//BB CC DN CM ∴, ,DN CM ∴可确定平面,CMDN CN ∴⊂平面CMDN ,//CN Q 平面1AB M ,平面1AB M I 平面CMDN DM =,//,CN DM ∴∴四边形CMDN 为平行四边形,1122CM DN CC ∴===.【点睛】本题考查异面直线垂直的证明,注意空间垂直间的相互转化,以及直线与平面平行性质定理的应用,意在考查直观想象、逻辑分析能力,属于中档题.22.如图,正方形ABCD 所在平面与平面四边形ABEF 所在平面互相垂直,ABE ∆是等腰直角三角形,AB AE =,FA FE =,45AEF ∠=︒.(1)设线段CD AE 、的中点分别为P M 、,求证://PM 平面BCE ; (2)求二面角F BD A --所成角的正弦值.【答案】(1)证明见解析;(2)11. 【解析】(1)取BE 中点N ,连,MN CN ,得1//,2MN AB MN AB =,可证四边形CPMN 为平行四边形,进而有//MP CN ,即可证明结论;(2)设2AB AE ==,由已知可得AE ⊥平面ABCD ,过F 做//FQ AE ,交AB 于Q ,得FQ ⊥平面ABCD ,过Q 做QO BD ⊥垂足为O ,连FO ,可证BD ⊥平面FOQ ,得到FOQ ∠为二面角F BD A --的平面角,解Rt OFQ ∆即可. 【详解】(1)取BE 中点N ,连,MN CN ,又M 为AE 的中点,1//,2MN AB MN AB ∴=,在正方形ABCD 中,P 是CD 中点, //,CP MN CP MN ∴=,∴四边形CPMN 为平行四边形,//MP CN ∴,MP ⊄平面BCE ,CN ⊂平面BCE , //PM ∴平面BCE ;(2)设2AB AE ==,ABE ∆是等腰直角三角形,AB AE =,AE AB ∴⊥,平面ABCD ⊥平面ABEF ,平面ABCD I 平面ABEF AB =,AE ⊂平面ABEF ,AE ∴⊥平面ABCD ,过F 做//FQ AE ,交AB 于Q ,FQ ∴⊥平面ABCD , FA FE =Q ,45AEF ∠=︒,,45,45EF AF EAF AF FAQ ∴⊥∠=︒∴=∠=︒,在Rt AFQ ∆中,1,3FQ AQ BQ ===, 过Q 做QO BD ⊥垂足为O ,连FO ,FQ ⊥Q 平面,ABCD FQ BD ∴⊥,FQ OQ Q =I ,BD ∴⊥平面,FOQ BD OF ⊥,FOQ ∠为二面角F BD A --的平面角,在Rt BOQ ∆中,323,45,2BQ OBQ OQ =∠=︒∴=, 在Rt FOQ ∆中,22222OF FQ OQ =+=, 22sin FQ FOQ OF ∴∠==, ∴二面角F BD A --所成角的正弦值22.【点睛】本题考查空间线、面位置关系,证明直线与平面平行以及求二面角,利用垂直关系做出二面角的平面角是解题的难点,要注意空间垂直间的相互转化,属于中档题.。
2018-2019学年高二数学上学期期中试题理宏志班

合肥一六八中学2018—2019学年第一学期期中考试高二数学试题(宏志班)一、选择题(共60题,每题5分。
每题仅有一个正确选项。
)1.已知a、b是两条平行直线,且a∥平面β,则b与β的位置关系是()A.平行B.相交C.b在平面β内D.平行或b在平面β内2.在下列命题中,不是公理的是()A.平行于同一条直线的两条直线互相平行B.如果一条直线上的两点在一个平面内,那么这条直线在此平面内C.空间中,如果两个角的两边分别对应平行,那么这两角相等或互补D.如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线3.如果ac>0,bc>0,那么直线ax+by+c=0不通过()A.第一象限B.第二象限C.第三象限D.第四象限4.直线(a2+1)x﹣y+1=0(其中a∈R)的倾斜角的取值范围是()A.[0,]B.[,)C.(,]D.[,π)5.一个几何体的三视图如图所示,则该几何体的体积为()A.12πB.24πC.D.72π6.半径为5的球内有一个高为8的内接正四棱锥,则这个球与该内接正四棱锥的体积之比为()A.B.C.D.7.三棱柱ABC﹣A'B'C′的所有棱长都等于2,并且AA'⊥平面ABC,M是侧棱BB′的中点,则直线MC′与A′B所成的角的余弦值是()A.B.C.D.8.直线l过点P(1,0),且与以A(2,1),为端点的线段总有公共点,则直线l 斜率的取值范围是()A.B.C.D.[1,+∞)9.在正方体ABCD﹣A1B1C1D1中,E是棱CC1的中点,F是四边形BCC1B1内的动点,且A1F∥平面D1AE,下列说法正确的个数是()①点F的轨迹是一条线段②A1F与D1E不可能平行③A1F与BE是异面直线④当F与C1不重合时,平面A1FC1不可能与平面AED1平行A.1B.2C.3D.410.在平面直角坐标系中,记d为点P(cosθ,sinθ)到直线x﹣my﹣2=0的距离.当θ、m变化时,d的最大值为()A.1B.2C.3D.411.生于瑞士的数学巨星欧拉在1765年发表的《三角形的几何学》一书中有这样一个定理:“三角形的外心、垂心和重心都在同一直线上,而且外心和重心的距离是垂心和重心距离之半.”这就是著名的欧拉线定理.设△ABC中,设O、H、G分别是外心、垂心和重心,下列四个选项错误的是()A.HG=2OGB.++=C.设BC边中点为D,则有AH=3ODD.S△ABG=S△BCG=S△ACG12.如图1,直线EF将矩形纸ABCD分为两个直角梯形ABFE和CDEF,将梯形CDEF沿边EF翻折,如图2,在翻折的过程中(平面ABFE和平面CDEF不重合)下面说法正确的是()。
安徽省合肥市第一六八中学高二数学上学期期中试卷理(宏志班)

高二数学试题(宏志班)一、选择题(共60 题,每题 5 分。
每题仅有一个正确选项。
)1.已知 a、 b 是两条平行直线,且a∥平面β,则 b 与β的地点关系是()A.平行B.订交C. b 在平面β内D.平行或b在平面β 内2.在以下命题中,不是公义的是()A.平行于同一条直线的两条直线相互平行B.假如一条直线上的两点在一个平面内,那么这条直线在此平面内C.空间中,假如两个角的两边分别对应平行,那么这两角相等或互补D.假如两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线3.假如 ac> 0,bc> 0,那么直线ax+by+c=0 不经过()A.第一象限B.第二象限 C .第三象限D.第四象限4.直线( a2+1) x﹣y+1=0(此中 a∈R)的倾斜角的取值范围是()A. [0 ,]B.[,) C .(,] D .[,π)5.一个几何体的三视图如下图,则该几何体的体积为()A.12πB.24πC.D.72π6.半径为 5 的球内有一个高为8 的内接正四棱锥,则这个球与该内接正四棱锥的体积之比为()A.B.C.D.7.三棱柱ABC﹣A'B'C ′的全部棱长都等于2,并且AA' ⊥平面ABC, M是侧棱BB′的中点,则直线 MC′与 A′B所成的角的余弦值是()A.B.C.D.8.直线 l 过点 P( 1, 0),且与以 A( 2,1),为端点的线段总有公共点,则直线l斜率的取值范围是()A.B.C.D.[1,+∞)9.在正方体ABCD﹣ A1B1C1D1中, E 是棱 CC1的中点, F 是四边形BCC1B1内的动点,且A1F∥平面D1AE,以下说法正确的个数是()①点 F 的轨迹是一条线段②A1F 与 D1E 不行能平行③ A1F 与 BE是异面直线④当 F 与 C1不重合时,平面 A1FC1不行能与平面 AED1平行A. 1B.2C. 3D. 410.在平面直角坐标系中,记 d 为点 P(cosθ, sin θ)到直线x﹣ my﹣2=0 的距离.当θ、m变化时, d 的最大值为()A. 1B.2C. 3D. 411.生于瑞士的数学巨星欧拉在1765 年发布的《三角形的几何学》一书中有这样一个定理:“三角形的外心、垂心和重心都在同向来线上,并且外心和重心的距离是垂心和重心距离之半.”这就是有名的欧拉线定理.设△ABC中,设O、H、 G 分别是外心、垂心和重心,以下四个选项错误的选项是()A. HG=2OG B.+ + =C.设 BC边中点为D,则有 AH=3OD D. S△ABG=S△BCG=S△ACG12.如图 1,直线 EF 将矩形纸A BCD分为两个直角梯形ABFE和 CDEF,将梯形 CDEF沿边 EF翻折,如图 2,在翻折的过程中(平面ABFE和平面 CDEF不重合)下边说法正确的选项是()A.存在某一地点,使得CD∥平面 ABFEB.存在某一地点,使得DE⊥平面 ABFEC.在翻折的过程中,BF∥平面 ADE恒成立D.在翻折的过程中,BF⊥平面 CDEF恒成立二、填空题(共20 分,每题 5 分)13 、已知直线l1: ax 2 y 60 与l2: x a 1 y a210 平行,则实数 a 的取值是________14.球的半径为 5cm,被两个相互平行的平面所截得圆的直径分别为6cm和 8cm,则这两个平面之间的距离是cm.15.我国古代数学名著《数书九章》中有“天池盆测雨”题:在下雨时,用一个圆台形的天池盆接雨水.天池盆盆口直径为二尺八寸,盆底直径为一尺二寸,盆深一尺八寸.若盆中积水深九寸,则平川降雨量是________寸.( 注:① 平川降雨量等于盆中积水体积除以盆口面积;② 一尺等于十寸 )16.在正方体ABCD﹣ A1B1C1D1中, E 为棱 AB上一点,且AE=1, BE=3,以 E 为球心,线段EC的长为半径的球与棱A1D1, DD1分別交于F, G两点,则△ AFG的面积为 ________三、解答题(共70 分,每题必需要有必需的解答过程)17.( 10 分)设直线l的方程为 ( a+ 1) x+y+ 2-a= 0 ( a∈R).(1)若 l 在两坐标轴上截距相等,求直线l 的方程;(2)若 l 不经过第二象限,务实数 a 的取值范围.18. ( 12 分)在平面直角坐标系xOy中,OBC的边BC所在的直线方程是l : x y 3 0 ,( 1)假如一束光芒从原点O 射出,经直线 l 反射后,经过点(3, 3) ,求反射后光芒所在直线的方程;( 2)假如在OBC 中,BOC 为直角,求OBC 面积的最小值.19. ( 12 分)如图是一个以A1B1C1为底面的直三棱柱被一平面所截获得的几何体,截面为ABC,已知 A1B1=B1C1=2,∠ A1B1C1=90°, AA1=4, BB1= 3, CC1= 2,求:( Ⅰ ) 该几何体的体积;( Ⅱ ) 截面 ABC的面积.20( 12 分) . 如图,已知正三棱锥P﹣ABC的侧面是直角三角形,PA=6,极点 P 在平面 ABC内的正投影为点D,D 在平面 PAB内的正投影为点E,连结 PE并延伸交AB 于点 G.(Ⅰ)证明:G是 AB的中点;(Ⅱ)在图中作出点 E 在平面 PAC内的正投影F,并求四周体PDEF的体积.21.( 12 分)如图,四周体 ABCD中,△ ABC是正三角形,△ ACD是直角三角形,∠ ABD=∠ CBD,AB=BD.(1)证明:平面 ACD⊥平面 ABC;(2)过 AC的平面交 BD于点 E,若平面 AEC把四周体 ABCD分红体积相等的两部分,求二面角D﹣ AE﹣C 的余弦值.22. ( 12 分)如图,在三棱锥中,是正三角形,为此中心.面面,,,是的中点,.( 1)证明:面;( 2)求与面所成角的正弦值.合肥一六八中学2018— 2019 学年第一学期期中考试高二数学试题(宏志班)参照答案一.选择题题号123456789101112答案D C A B C B A B C C C C二、填空题13.- 114. 1 或 715. 316. 4三、解答题17. ( 1) 3x+y=0 或x+y+ 2= 0;(2)a≤- 1.y01x03 18( 1)设点O对于直线l的对称点为A(x0, y0),由题意应有x0,解得y0y0,x030322所以点 A(3,3) .由于反射后光芒经过点A(3,3)和点 (3, 3),所以反射后光芒所在直线的方程为 x 3.(2)设OD为OBC 的一条高,则3,设 BOD(0) ,可得|OD |22|BC ||BD|| DC | | OD | tan θ| OD |,所以OBC 的面积S1|BC||OD | tan θ21(| OD | tan θ| OD |) | OD |12| OD | tan θ| OD ||OD | |OD |29,当且仅2tan θ2tan θ2当时,等号成立.49 .所以,OBC 面积的最小值是219.(Ⅰ)过 C 作平行于 A1B1C1的截面 A2B2C,交 AA1, BB1分别于点 A2, B2.由直三棱柱性质及∠A1B1C1= 90°可知 B2C⊥平面 ABB2A2,则该几何体的体积V==× 2×2×2+× ×(1 + 2)×2× 2=6,(Ⅱ)在△ ABC中, AB==,BC==,AC== 2 .则 S△ABC=×2×=20.(Ⅰ)证明:∵ P﹣ ABC为正三棱锥,且 D为极点 P 在平面 ABC内的正投影,∴ PD⊥平面 ABC,则 PD⊥ AB,又 E 为 D 在平面 PAB内的正投影,∴ DE⊥面 PAB,则 DE⊥ AB,∵ PD∩DE=D,∴ AB⊥平面 PDE,连结 PE并延伸交 AB于点 G,则 AB⊥PG,又 PA=PB,∴ G是 AB 的中点;(Ⅱ)在平面 PAB内,过点 E 作 PB的平行线交 PA于点 F, F 即为 E 在平面 PAC内的正投影.∵正三棱锥 P﹣ ABC的侧面是直角三角形,∴ PB⊥PA, PB⊥PC,又 EF∥PB,所以 EF⊥ PA,EF⊥ PC,所以 EF⊥平面 PAC,即点 F 为 E 在平面 PAC内的正投影.连结 CG,由于 P 在平面 ABC内的正投影为 D,所以 D是正三角形 ABC的中心.由(Ⅰ)知, G是 AB的中点,所以 D在 CG上,故 CD= CG.由题设可得PC⊥平面 PAB, DE⊥平面 PAB,所以 DE∥ PC,所以 PE= PG,DE=PC.由已知,正三棱锥的侧面是直角三角形且PA=6,可得 DE=2, PG=3,PE=2.在等腰直角三角形EFP中,可得EF=PF=2.所以四周体PDEF的体积 V=× DE× S△PEF=× 2×× 2× 2=.21.( 1)证明:如下图,取 AC的中点 O,连结 BO,OD.∵△ ABC是等边三角形,∴ OB⊥ AC.△ ABD与△ CBD中, AB=BD=BC,∠ ABD=∠CBD,∴△ ABD≌△ CBD,∴ AD=CD.∵△ ACD是直角三角形,∴ AC是斜边,∴∠ ADC=90°.∴DO= AC.2222∴ DO+BO=AB=BD.∴∠ BOD=90°.∴ OB⊥OD.又 DO∩AC=O,∴ OB⊥平面ACD.又 OB? 平面 ABC,∴平面 ACD⊥平面 ABC.(2)解:设点 D, B 到平面 ACE的距离分别为 h D, h E.则= .∵平面 AEC把四周体 ABCD分红体积相等的两部分,∴===1.∴点 E 是 BD的中点.成立如下图的空间直角坐标系.不如取AB=2.则 O( 0,0,0),A( 1,0,0),C(﹣ 1,0,0),D( 0,0,1),B( 0,,0),E.=(﹣ 1, 0, 1),=,=(﹣ 2,0, 0).设平面 ADE的法向量为=( x,y,z),则,即,取=.同理可得:平面ACE的法向量为=( 0, 1,).∴ cos===﹣.∴二面角D﹣ AE﹣C 的余弦值为.22. ( 1)连结,由于是正三角形的中心,所以在上且,又,所以在中有,所以,又平面,平面,所以平面.( 2)解法一:作交的延伸线于,作交的延伸线于,由面面知面,所以,又,所以所以面,所以面面,作,则面连结,则为与面所成角,∴,即所求角的正弦值为.解法二:以中点为原点,成立如下图的空间直角坐标系.∵,∴,,,,∴,,,.设面的法向量为,则安徽省合肥市第一六八中学高二数学上学期期中试卷理(宏志班)取,∴,即所求角的正弦值为.-11-。
2019-2020学年安徽省合肥一六八中学高二上学期期末考试数学(理)试题(解析版)
2019-2020学年安徽省合肥一六八中学高二上学期期末考试数学(理)试题一、单选题1.设集合{1,2,3}M =,{}2|230N x Z x x =∈--<,则M N ⋃=( )A .{}1,2,3B .{}1,0,1,2,3-C .{}0,1,2,3D .{}1,2【答案】C【解析】解二次不等式求得集合N ,再求并集即可. 【详解】由2230x x --<解得()1,3x ∈-,又x ∈Z , 故{}0,1,2N =, 故{}0,1,2,3M N ⋃=. 故选:C . 【点睛】本题考查并集的求解,涉及一元二次不等式的求解. 2.抛物线22y x =的焦点坐标为( ) A .1,02⎛⎫ ⎪⎝⎭B .1,04⎛⎫⎪⎝⎭C .10,4⎛⎫ ⎪⎝⎭D .10,8⎛⎫ ⎪⎝⎭【答案】D【解析】将抛物线方程化为标准形式,得出p 的值,结合开口方向即可得焦点坐标. 【详解】由于抛物线的方程为22y x =,即212x y =, 可得抛物线开口向上,14p =, 可得抛物线22y x =的焦点坐标为10,8⎛⎫⎪⎝⎭,故选D. 【点睛】本题主要考查了求抛物线的焦点坐标,将抛物线方程化为标准形式是解题的关键,属于基础题.3.光线沿直线21y x =+射到直线y x =上, 被y x =反射后的光线所在的直线方程为 A .112y x =- B .1122y x =- C .1122y x =+ D .112y x =+ 【答案】B【解析】【考点】与直线关于点、直线对称的直线方程. 专题:计算题;综合题.分析:先求出y=2x+11与y=x 的交点(-1,-1),然后求出反射光线与X 轴的交点(1,0),然后两点确定直线.解答:解:直线y=2x+1与y=x 的交点为(-1,-1),又直线y=2x+1与y 轴的交点(0,1)被y=x 反射后,经过(1,0) 所以反射后的光线所在的直线方程为:---y 010=---x 111即 y=12x-12故选B .点评:本题考查与直线关于电、直线对称的直线方程,考查学生发现问题解决问题的能力,是基础题. 4.给出下列命题:①若两条直线和第三条直线所成的角相等,则这两条直线平行; ②若两条直线与第三条直线垂直,则这两条直线互相平行; ③若两条直线与第三条直线平行,这两条直线互相平行; ④若两条直线均与一个平面平行,则这两条直线互相平行. 其中正确的命题的个数是( ) A .1 B .2C .3D .4【答案】A【解析】由空间三条直线构成等腰三角形可判断①;由空间直线的位置关系可判断②;由线面平行的定义可判断③由线线平行的公理4可判断④. 【详解】在空间中,若两条直线和第三条直线所成的角相等,可能这三条直线构成等腰三角形, 可得这两条直线不一定互相平行,故①错;在空间中,若两条直线都与第三条直线垂直,则这两条直线互相平行或相交或异面,故②错;若两条直线都与同一个平面平行,则这两条直线互相平行或相交或异面,故③错; 在空间中,若两条直线都与第三条直线平行,由公理4可得这两条直线互相平行,故④对.故选:A 【点睛】本题考查了空间中直线的平行垂直关系,考查了学生逻辑推理,空间想象能力,属于基础题.5.已知直线0x y m -+=与圆O :221x y +=相交于A ,B 两点,若OAB ∆为正三角形,则实数m 的值为( )A .BC .2或 D .2【答案】D【解析】 由题意得,圆22:1O x y +=的圆心坐标为(0,0),半径1r =.因为OAB ∆为正三角形,则圆心O 到直线0x y m -+=的距离为22r =,即2d ==,解得2=m 或2m =-,故选D. 6.下列命题中正确命题的个数是( )①对于命题:p x R ∃∈,使得210x x ++<,则:p x R ⌝∃∈,均有210x x ++>; ②命题“已知x ,y R ∈,若3x y +≠,则2x ≠或1y ≠”是真命题;③设a r ,b r是非零向量,则“a b =r r ”是“a b a b +=-r r r r ”的必要不充分条件;④3m =是直线()320m x my ++-=与直线650mx y -+=互相垂直的充要条件. A .1 B .2C .3D .4【答案】A【解析】①根据特称命题的否定是全称命题,判断①错误;②原命题与它的逆否命题真假性相同,判断它的逆否命题的真假性即可; ③利用向量的平行四边形法则,转化为平行四边形的对角线的关系,判断即可; ④计算直线()320m x my ++-=与直线650mx y -+=互相垂直的等价条件为0,3m =,即可.【详解】对于命题:p x R ∃∈,使得210x x ++<,则:p x R ⌝∃∈,均有210x x ++≥,故①不正确;命题“已知x ,y R ∈,,若3x y +≠,则2x ≠或1y ≠”的逆否命题为:“已知x ,y R ∈,,若2x =且=1y ,则3x y +=”为真命题,故②正确;设a r ,b r是非零向量,则“a b =r r ”是“a b a b +=-r r r r ”的既不充分也不必要条件,故③不正确;直线()320m x my ++-=与直线650mx y -+=互相垂直,则0,3m =,故④不正确. 故选:A 【点睛】本题考查了命题的否定,逆否命题,充要条件等知识点,考查了学生逻辑推理,概念理解,数学运算的能力,属于基础题.7.《九章算术》将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.下图所示的阳马P ABCD -中,侧棱PD ⊥底面ABCD ,且PD CD BC ==,则当点E 在下列四个位置:PA 中点、PB 中点、PC 中点、PD 中点时分别形成的四面体E BCD -中,鳖臑有( )个.A .0B .1C .2D .3【答案】C【解析】根据题意,结合线面垂直的判定以及性质,对点所在的位置进行逐一分析即可. 【详解】 设2PD =①当点E 在P A 中点时:6,2BE EC BC ===,不满足勾股定理,即此时EBC ∆不为直角三角形,不满足题意;②当点E 在PB 中点时:3DE BE EC ===2,2BD DC BC ===,由勾股定理,此时,,DEB EBC DEC ∆∆∆均不是直角三角形,不满足题意;③当点E 在PC 中点时:因为,DE EC DE BC ⊥⊥,故DE ⊥面BEC ,则DE BE ⊥,故,DEC DEB ∆∆均为直角三角形,又,,BC CD BC PD ⊥⊥故BC ⊥面PDC ,则BC CE ⊥,故,BEC DCB ∆∆均为直角三角形, 满足题意;④当点E 在PD 中点时:因为PD ⊥面ABCD ,故,PD DB PD DC ⊥⊥,故,DEC DEB ∆∆均为直角三角形, 又BC ⊥DC ,BC ⊥DP ,故BC ⊥面PDC ,则BC CE ⊥,故,BEC DCB ∆∆均为直角三角形 满足题意.综上所述,当点E 在PC 中点或PD 中点时,满足题意. 故选:C . 【点睛】本题考查由线线垂直,线面垂直的判定和性质,属综合基础题. 8.方程(x+y-1)224x y +-=0所表示的曲线是 ( )A .B .C .D .【答案】D【解析】试题分析:由题意得方程()22140x y x y +-+-=,得10x y +-=或,且,所以方程(22140x y x y +-+-=所表示的曲线为选项D ,故选D .【考点】曲线与方程.9.已知P 是双曲线()222210,0x y a b a b-=>>上的点,1F 、2F 是其焦点,双曲线的离心率是54,且120PF PF ⋅=u u u r u u u u r ,若12PF F △的面积为9,则此双曲线的实轴长为( ) A .4B .6C .8D .10【答案】C【解析】由双曲线的离心率求得34b a =,再根据12PF F △的面积为9,得到128||||1P PF F =,在12PF F △中,由勾股定理和双曲线的定义知,b=3,即得解.【详解】双曲线的离心率是5344c b a a ==∴=又12120PF PF PF PF ⋅=∴⊥u u u r u u u u r u u u r u u u u r12PF F ∴△的面积12121||||9||||182S P P PF F PF F ==∴= 在12PF F △中,由勾股定理可得:222221212124||+||=(||+||)2||||436c PF PF PF PF PF PF a =-=-3,4b a ∴==故双曲线的实轴长为:8 故选:C 【点睛】本题考查了双曲线的性质综合,考查了学生综合分析,转化与划归,数学运算的能力,属于中档题.10.若抛物线22y px =的焦点为F ,点A 、B 在抛物线上,且23AFB π∠=,弦AB 的中点M 在准线l 上的射影为'M ,则'MM AB的最大值为( )A .3B .3C D【答案】C【解析】转化:11|'|(||||)(||||)22MM AG BH AF BF =+=+,利用余弦定理:||AB =,即得解. 【详解】如图所示,由题意得(1,0)F ,22111(||||)(||||)(||||)'222=||||2||||2||||cos3AG BH AF BF AF BF MM AB AB AB AF BF AF BF π+++==+-22211(||||)(||||)22||||||||(||||)||||AF BF AF BF AF BF AF BF AF BF AF BF ++==+++-221(||||)2(||||)(||||)4AF BF AF BF AF BF +≤++-1(||||)3233(||||)AF BF AF BF +==+当且仅当:||||AF BF =时,'MM AB有最大值33. 故选:C 【点睛】本题考查了抛物线的综合问题,考查了学生综合分析,转化化归,数学运算的能力,属于中档题.11.已知点P 是双曲线()222210,0y x a b a b-=>>下支上的一点,1F 、2F 分别是双曲线的上、下焦点,M 是12PF F △的内心,且121213MPF MPF MF F S S S =+V V V ,则双曲线的离心率为( ) A .2 B 3C .3D 21【答案】C【解析】设12PF F △的内切圆的半径为r ,121213MPF MPF MF F S S S =+V V V ,即12121111||||+||2232PF r PF r F F r ⨯=,故得解. 【详解】设22c a b =+,12PF F △的内切圆的半径为r ,则21212||||,||2c PF PF a F F -==12121212111||,||,||222F F MPF MPF M S PF r S PF r S F F r ===V V V 由于121213MPF MPF MF F S S S =+V V V 故12121111||||+||2232PF r PF r F F r ⨯= 因此:3ce a== 故选:C 【点睛】本题考查了双曲线的焦点三角形的综合问题,考查了学生综合分析,转化与划归,数学运算的能力,属于中档题.12.在Rt ABC V 中,已知D 是斜边AB 上任意一点(如图①),沿直线CD 将ABC V 折成直二面角B CD A --(如图②).若折叠后,A B 两点间的距离为d ,则下列说法正确的是( )A .当CD 为Rt ABC V 的中线时,d 取得最小值B .当CD 为Rt ABC V 的角平分线时,d 取得最小值 C .当CD 为Rt ABC V 的高线时,d 取得最小值 D .当D 在Rt ABC V 的斜边AB 上移动时,d 为定值 【答案】B【解析】试题分析:如图设,,BC a AC b ACD θ==∠=,则022BCD ππθθ⎛⎫∠=-<< ⎪⎝⎭, 过A 作CD 的垂线AG ,过B 作CD 的延长线的垂线BH , 所以AG sin b θ=,cos CG b θ=,BH cos a θ=,CH sin a θ=,sin cos HG CH CG a b θθ=-=-;直线AG BH 和是异面直线,所成的角为90︒;线段HG 是公垂线段, 所以222AB 2cos90d AG BH HG AG BH ==++-⋅︒()()()222sin cos sin cos b a a b θθθθ=++-22222222sin cos sin cos sin 2b a a b ab θθθθθ+++- 22sin 2a b ab θ+-当=4πθ时,即当CD 为Rt ABC V 的角平分线时,d 取得最小值.故选B.【考点】平面与平面之间的位置关系;两条异面直线上两点间的距离.二、填空题13.若三个点()2,1-,()2,3-,()2,1-中恰有两个点在双曲线C :()22210x y a a-=>上,则双曲线C 的离心率为______. 6【解析】由双曲线的图象关于原点对称,可知点()2,1-,()2,1-在双曲线上,将点的坐标代入双曲线方程可求得a ,进而可求出离心率. 【详解】三个点()2,1-,()2,3-,()2,1-中恰有两个点在双曲线C :()22210x y a a-=>上,又双曲线的图象关于原点对称,所以()2,3-不在双曲线上,点()2,1-,()2,1-在双曲线上,则()24110a a -=>,解得2a =,又1b =,所以离心率为216112b a ⎛⎫+=+= ⎪⎝⎭. 故答案为:6. 【点睛】本题考查双曲线的几何性质,考查离心率的求法,属于基础题.14.一个半径为1的小球在一个内壁棱长为46的正四面体封闭容器内可向各个方向自由运动,则该小球表面永远不可能接触到的容器内壁的面积是 . 【答案】723【解析】【详解】试题分析:如图甲,考虑小球挤在一个角时的情况,作平面111A B C //平面ABC ,与小球相切于点D ,则小球球心O 为正四面体111P A B C -的中心,111PO A B C 面⊥,垂足D 为111A B C 的中心.因11111113P A B C A B C V S PD -∆=⋅1114O A B C V -=⋅111143A B C S OD ∆=⋅⋅⋅, 故44PD OD ==,从而43PO PD OD =-=-=. 记此时小球与面PAB 的切点为1P ,连接1OP ,则2222113122PP PO OP =-=-= 考虑小球与正四面体的一个面(不妨取为PAB )相切时的情况,易知小球在面PAB 上最靠近边的切点的轨迹仍为正三角形,记为1P EF ,如图乙.记正四面体的棱长为a ,过1P 作1PM PA ⊥于M .因16MPP π∠=,有113cos 262PM PP MPP =⋅==1226PE PA PM a =-=-. 小球与面PAB 不能接触到的部分的面积为1PAB P EF S S ∆∆-223(6))a a =--3263a =- 又6a =124363183PAB PEF S S ∆∆-==. 由对称性,且正四面体共4个面,所以小球不能接触到的容器内壁的面积共为3 【考点】(1)三棱锥的体积公式;(2)分情况讨论及割补思想的应用.15.在圆2210210x y x y +--+=内,过点()2,1有n 条弦的长度成等差数列,最短弦长为数列的首项1a ,最长弦长为n a ,若公差5311,d ⎛⎫∈ ⎪⎝⎭,那么n 的取值集合为________. 【答案】{}8,9,10【解析】先由圆的几何性质,最短的弦为垂直于OA 的弦,最长弦为直径,得到1,n a a ,因此公差21d n =-,结合公差11,35d ⎛⎫∈ ⎪⎝⎭,即得解.【详解】设()2,1A ,圆心()5,1O ,半径为=5r ,最短的弦为垂直于OA 的弦,且||=3OA ∴18a =,最长弦为直径:10n a =, 公差:21217111513d n n n =∴<<∴<<-- 因此:n 的取值集合为{}8,9,10. 【点睛】本题考查了圆的性质和数列综合,考查了学生综合分析,转化于划归,数学运算的能力,属于中档题.16.存在实数φ,使得圆面225x y +≤恰好覆盖函数sin y x k πφ⎛⎫=+ ⎪⎝⎭图象的最高点或最低点共三个,则正数k 的取值范围是________. 【答案】(]1,2【解析】根据题意,可知函数sin y x k πφ⎛⎫=+⎪⎝⎭图象的最高点或最低点在1y =±上,结合圆面方程可以列出方程组,即得解. 【详解】根据题意,可知函数sin y x k πφ⎛⎫=+⎪⎝⎭图象的最高点或最低点在1y =±上,则: 221225y x x y =±⎧∴-≤≤⎨+≤⎩又由题意:22T kkππ==,因此4<2T T ≤,解得正数k 的取值范围是:(]1,2 故答案为:(]1,2 【点睛】本题考查的是三角函数的周期性的应用,解答本题的关键是熟练使用三角函数周期性的定义以及求法,考查了学生综合分析,转化和划归,数学运算的能力,属于中档题.三、解答题17.已知命题:p x R ∃∈,使240x x a -+<成立,命题:,21q x R x x a ∀∈-++≥恒成立.(1)若命题p ⌝为真,求实数a 的取值范围;(2)若p 或q 为真,p 且q 为假,求实数a 的取值范围. 【答案】(1)4a ≥;(2)34a <<【解析】(1)写出非P 命题,通过二次函数恒成立问题,求解参数的范围; (2)先求出每个命题真假分别对应的参数范围,再分类讨论,先交后并即可. 【详解】(1)p ⌝为真,即240x x a -+≥恒成立, 故0∆≤,即1640a -≤, 解得4a ≥,故a 的取值范围为:4a ≥(2)由(1)可知命题p 为假命题,则4a ≥ 故命题p 为真,则4a <,对命题q ,若其为真,则21x x a -++≥ 恒成立 则()()21213x x x x a -++≥--+=≥ 解得:3a ≤故命题q ,若其为假,则3a >; 又由p 或q 为真,p 且q 为假, 则p ,q 中一个为真,一个为假即43a a <⎧⎨>⎩或43a a ≥⎧⎨≤⎩解得()3,4a ∈故实数a 的取值范围为34a <<. 【点睛】本题考查由命题的真假,求参数的取值范围,涉及二次函数恒成立,绝对值不等式. 18.在ABC ∆中,BC 边上的高所在直线的方程为210x y -+=,A ∠的平分线所在直线方程为0y =,若点B 的坐标为(1,2). (1)求点A 和点C 的坐标;(2)求AC 边上的高所在的直线l 的方程.【答案】(1)(5,6)C -(2)10x y -+=【解析】试题分析:(1)联立直线210x y -+=和0y =,可求得A 点的坐标,利用点斜式可得直线BC 的方程,利用角平分线可得直线AC 的斜率,利用点斜式可写出直线AC 的方程,联立直线,BC AC 的方程可求得交点C 的坐标.(2)由直线AC 的斜率可得高的斜率,利用点斜式可求得高所在直线方程. 试题解析:(1)由已知点A 应在BC 边上的高所在直线与A ∠的角平分线所在直线的交点, 由210{x y y -+==得1{x y =-=,故()1,0A -.由1AC AB k k =-=-,所以AC 所在直线方程为()1y x =-+,BC 所在直线的方程为()221y x -=--,由()()1{221y x y x =-+-=--,得()5,6C -.(2)由(1)知,AC 所在直线方程10x y ++=,所以l 所在的直线方程为()()120x y ---=,即10x y -+=.19.如图,在多面体ABCDEF 中,底面ABCD 是边长为2的菱形,60BAD ∠=︒,四边形BDEF 是矩形,平面BDEF ⊥平面ABCD ,4BF =,H 是CF 的中点.(1)求证:AC ⊥平面BDEF ;(2)求直线DH 与平面CEF 所成角的正弦值; 【答案】(1)证明见解析(2)399133【解析】(1)由面面垂直的性质可证AC ⊥平面BDEF ;(2)以AC 、BD 的交点为坐标原点,DB 方向为x 轴,AC 方向为y 轴,建立空间直角坐标系,求出面CEF 的法向量,即可求直线DH 与平面CEF 所成角的正弦值. 【详解】(1)证明:Q 四边形ABCD 是菱形,AC BD ∴⊥.又Q 平面BDEF ⊥平面ABCD ,平面BDEF ⋂平面ABCD BD =, 且AC ⊂平面ABCD ,AC ∴⊥平面BDEF ;(2)以AC 、BD 的交点为坐标原点,DB 方向为x 轴,AC 方向为y 轴,建立空间直角坐标系,1333,0)(1,0,3)(1,0,3),(1,0,0)(,)222C E FD H --,,,,则()1,3,4CF =-u u u r ,()2,0,0EF =u u u r .设面CEF 的法向量为(),,n x y z =r则34020n CF x y z n EF x ⎧⋅=-+=⎪⎨⋅==⎪⎩u u u v v u u u v v ,不妨令1y =, 得到面CEF 的法向量为3n ⎛= ⎝⎭r ,3322DH ⎛⎫=⎪ ⎪⎝⎭u u u u r 因此:4399cos ,||||n DH n DH n DH ⋅==⋅r u u u u rr u u u u r ru u u u r 即DH u u u u r 与面CEF 4399【点睛】本题考查了面面垂直的判定以及线面角的求解,考查了学生逻辑推理,转化与化归,数学运算的能力,属于中档题.20.设抛物线()2:20C x py p =>的焦点为F ,准线为l ,A 为C 上一点,已知以F为圆心,FA 为半径的圆F 交l 于M.N 点.(1)若60MFN ∠=︒,AMN n 的面积为83,求抛物线方程;(2)若A .M.F 三点在同一直线m 上,直线n 与m 平行,且n 与C 只有一个公共点,求坐标原点到直线n 、m 距离的比值.【答案】(1)24x y =;(2)1:3【解析】(1)由抛物线的定义,以及圆的对称性可得FMN n 为等边三角形,可由其高线求得边长,进而表达出面积,列方程解得p 即可求得抛物线方程.(2)由A.M.F 三点共线,可得直线m 斜率,和直线m 方程;根据直线n 与C 只有一个公共点,设出直线n 方程,联立抛物线方程,0=n ,可求得n 方程;据此利用点到直线距离公式求得距离之比. 【详解】(1)由对称性以及60MFN ∠=︒可知MFN △是等边三角形.又F 点到MN 的距离为p,故||MN p =, 由抛物线定义知:点A 到准线l的距离||||3d FA MN p ===又AMN S n 818||2323MN d p =⇔⨯⨯=⇔=. 故抛物线方程为:24x y =.(2)由对称性设2000(,)(0)2x A x x p >,则(0,)2p F 点A ,M 关于点F 对称,得22220000(,)3222x x p M x p p x p p p --⇒-=-⇔=,得:3,)2pA ,直线m斜率3p p k -== 所以直线m方程为02x -+=. ∵//m n ,设直线n方程为:0x t -+=, 又因为直线n 与抛物线只有一个公共点,所以202x t x py⎧+=⎪⎨=⎪⎩,消去y得2033x px pt --=, 由0∆=,得t p =直线3:306n x y p --=, 坐标原点到n ,m 距离的比值为33:1:3p p =. 【点睛】本题考查抛物线,涉及抛物线的定义,直线与抛物线的位置关系,属抛物线中的基础题. 21.已知平面PAB ⊥平面ABC ,P 、P 在平面ABC 的同侧,二面角Q AC B --的平面角为钝角,Q 到平面ABC 的距离为6,PAB △是边长为2的正三角形,4BC =,23AQ CQ ==,30ACB ∠=︒.(1)求证:面PAC ⊥平面PAB ;(2)求二面角P AC Q --的平面角的余弦值.【答案】(1)证明见解析(2)3236【解析】(1)由正弦定理,可求得90BAC ∠=︒,即AC AB ⊥,再由平面PAB ⊥平面ABC ,可得AC ⊥平面P AB ,可证得面PAC ⊥平面P AB ;(2)以A 为坐标原点,AB u u u r,AC u u u r 方向为x 轴、y 轴的正方向,建立空间直角坐标系. 求出平面ACQ , 平面P AC 的法向量,即可求得二面角. 【详解】 (1)424sin sin 30BAC ==∠︒,所以sin 1BAC ∠=,90BAC ∠=︒AC AB ∴⊥,又Q 平面PAB ⊥平面ABC ,AB =平面PAB ABC I ,AC ⊂平面ABC ,AC ∴⊥平面P AB ,AC ⊂Q 面P AC ,∴面PAC ⊥面P AB(2)以A 为坐标原点,AB u u u r,AC u u u r 方向为x 轴、y 轴的正方向,建立空间直角坐标系.则()2,0,0B ,()0,23,0C ,()1,0,3P,()3,3,6Q -,设平面ACQ 的法向量为(),,m x y z =u r ,则2303360AC m y AQ m x y z ⎧⋅==⎪⎨⋅=-++=⎪⎩u u u v v u u u v v, 令1z =,()2,0,1m ∴=u r设平面P AC 的法向量为(),,n x y z =r ,则23030AC n y PA n x z ⎧⋅==⎪⎨⋅=+=⎪⎩u u u v v u u uv v , 令1z =:()3,0,1n ∴=-r,设二面角P AC Q --的平面角为θ,则323cos cos ,m n θ-==u r r . 而此二面角为锐角,故二面角P AC Q --的平面角的余弦值为3236-. 【点睛】本题考查了面面垂直的判定以及线面角的求解,考查了学生逻辑推理,转化与划归,数学运算的能力,属于中档题.22.设椭圆()2222:10x y C a b a b+=>>的长轴长42,离心率为e ,定义直线b y e =±为椭圆的类准线,若椭圆C 的类准线方程为26y =±,(1)求椭圆C 的方程;(2)如图,不垂直于x 轴的直线6:5l y kx =-与椭圆C 交于A 、B 两点,点()2,1P 在直线l 的左上方,且PA PB ⊥,直线PA 、PB 分别与y 轴交于点M 、N ,若线段MN 长度是4,求k .【答案】(1)22182x y +=(2)12【解析】(1)根据题设条件,列出a,b,c 的等量关系,联立即得解;(2)由4MN =,得到MNP △是等腰直角三角形,0MP NP k k ∴+=,联立65y kx =-与22480x y +-=,利用韦达定理即得解. 【详解】由题意知:2a c e a b a b e ⎧⎪=⎪⎪=∴==⎨⎪⎪=⎪⎩22182x y ∴+= (2)4MN =Q ,MNP ∴V 是等腰直角三角形0MP NP k k ∴+=设()11,A x y ,()22,B x y联立y kx m =+与22480x y +-=得:()222418480kx kmx m +++-=122841km x x k -∴+=+,21224841m x x k -=+ 212111022PB PA y y k k x x --+=+=--Q 代入,化简得:224140km k m k ++--=65m =-,12k ∴=或1110k =检验,当1110k =时,点P 在直线l 上,不合题意.12k ∴=. 【点睛】本题考查了直线和圆锥曲线综合,考查了学生综合分析,转化与化归,数学运算的能力,属于中档题.。
【20套试卷合集】合肥一六八中学2019-2020学年数学高二上期中模拟试卷含答案
2019-2020学年高二上数学期中模拟试卷含答案2.已知0tan cos <⋅θθ,那么角θ是( )A .第一或第二象限角B .第二或第三象限角C .第一或第四象限角D .第三或第四象限角 3.如果命题“)(q p 或⌝”为假命题,则( ) A .,p q 中至少有一个为真命题 B .,p q 均为假命题C .,p q 均为真命题D .,p q 中至多有一个为真命题4.下列命题中,真命题的是( )A .0,x R ∃∈使得00xe ≤ B . 命题2,2x x R x ∀∈> 的否定是真命题C .2{|10}{|40}(2,0)x x x x -<⋂->=-D . 1,1a b >>的充分不必要条件是1ab > 5.如图所示的程序框图,若输出的S 是30,则①可以为( )A .2n ≤B .3n ≤C .4n ≤D .5n ≤6.已知数据123 n x x x x ⋅⋅⋅,,,,是某市普通职工n (3 )n n N +≥∈,个人的年收入,设这n 个数据的中位数为x ,平均数为y ,方差为z ,如果再加上世界首富的年收入1n x +,则这1n +个数据中,下列说法正确的是( )A .年收入平均数可能不变,中位数可能不变,方差可能不变B .年收入平均数大大增大,中位数可能不变,方差变大C .年收入平均数大大增大,中位数可能不变,方差也不变D .年收入平均数大大增大,中位数一定变大,方差可能不变7.已知抛物线28y x =的焦点为F ,准线为l ,经过点F x 轴上方的部分相交于点A ,AK l ⊥,垂足为K ,则AKF △的面积是( )A .12B .C .16D .8.已知1F 、2F 为椭圆22221(0)x y a b a b +=>>的焦点,B 为椭圆短轴上的端点,若212121()2BF BF F F →→→⋅≥,则椭圆的离心率的取值范围是( )A .1(0,)2B .C .(0,2 D .1(0,]29.若[],1,1b c ∈-,则方程2220x bx c ++=有实数根的概率为( )A .12B .23 C .34 D .5610.已知条件:2p x y +≠-,条件:1q x ≠-或1y ≠-,则p 是q 的( )A .充要条件B .既不充分也不必要条件C .充分不必要条件D .必要不充分条件11.平面向量的集合A 到A 的映射f 由()2()f x x x a a →→→→→=-⋅确定,其中a →为常向量.若映射f 满足()()f x f y x y →→→→⋅=⋅对,x y A →→∈恒成立,则a →的坐标不可能...是( ) A .(0,0) B. C. D.1(2- 12.已知二元函数2cos (,)(,),sin 2x f x x R R x x θθθθ=∈∈++则(,)f x θ的最大值和最小值分别是( )B.C. -D.第Ⅱ卷 (非选择题共100分)二、填空题:本大题共4小题,每小题5分,共20分. 13.已知抛物线214y x =-,则它的焦点坐标为 . 14.根据某固定测速点测得的某时段内过往的200辆机动车的行驶速度(单位:/km h )绘制的频率分布直方图如右图所示.该路段限速标志牌提示机动车辆正常行驶速度为60/-120/km h km h ,则该时段内非正常行驶的机动车辆数为 .15.已知,,m n n m +成等差数列,,,mn n m 成等比数列,则椭圆221x y m n+=的离心率是 . 16.已知椭圆22221x y a b +=的两个焦点为12,F F ,点P 为椭圆上的点,则能使12F PF 2π∠=的点P 的个数可能有 个. (把所有的情况填全)三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤. 17.(本小题满分10分) 已知函数2()sin(2)2cos 6f x x x π=--.(1)求函数)(x f 的最小正周期;(2)当[,]63x ππ∈-时,求函数)(x f 的最值及相应的自变量x 的取值.18.(本小题满分10分)(1)根据茎叶图判断哪个班的平均身高较高; (2)计算甲班的样本方差;(3)现从乙班这10名同学中随机抽取两名身高不低于 173cm 的同学,求身高为176cm 的同学被抽中的概率.19. (本小题满分12分)已知命题:p 方程2260x x a a -+-=有一正根和一负根,命题:q 函数2(3)1y x a x =+-+的图像与x 轴有公共点,若命题“p q 或” 为真命题,而命题“p q 且”为假命题,求实数a 的取值范围.20.(本小题满分12分)如图,四边形PCBM 是直角梯形,90PCB ∠=︒,PM ∥BC ,1,2PM BC ==,又1AC =, 120,ACB AB PC ∠=︒⊥,直线AM 与直线PC 所成的角为60︒.(1)求证:PC AC ⊥;(2)求点B 到平面MAC 的距离.21.(本小题满分13分)已知数列}{n a 的前n 项和为n S ,且满足2()n n S a n n N +=-∈. (1)求数列}{n a 的通项公式;(2)若(21)(1)n n b n a =++,数列{}n b 的前n 项和为,n T 求满足不等式225621n T n -≥-的 最小n 值.22.(本小题满分13分)已知椭圆C 的方程为22221(0)x y a b a b+=>>,点A 在椭圆C 上,且其离心率e =.(1)求该椭圆的标准方程;(2)设动点()00,P x y 满足2OP OM ON →→→=+,其中,M N 是椭圆C 上的点,直线OM 与ON 的斜率之积为12-,求22002x y +的值; (3)在(2)的条件下,问:是否存在两个定点,A B ,使得PA PB +为定值?若存在,给出证明;若不存在,请说明理由.高二数学试卷答题卷(文科)选择题(本大题共12小题,每小题5分,共60分;在每小题给出的四个选项中,只有一项是符合目要求的.)二、填空题(本大题4小题,每小题5分,共20分;把正确答案填在横线上.)13._________________________;14._________________________;15._________________________;16._________________________;三、解答题(本大题共6小题,共70分;解答应写出文字说明、证明过程或演算步骤.)(2)由63x ππ-<<,得22333x πππ-≤-≤∴由图像知当233x ππ-=即3x π=时,有max 112y =-=;当232x ππ-=-即12x π=-时,有min (1)11y =--=. ……………… 10分18.解:(1)由茎叶图可知:甲班身高集中于160179-之间,而乙班身高集中于170180- 之间,因此乙班平均身高高于甲班. ………………2分(2) 15816216316816817017117917918217010x +++++++++==甲班的样本方差为()()()()222221[(158170)16217016317016817016817010-+-+-+-+-()()()()()22222170170171170179170179170182170]57.2+-+-+-+-+-=………………6分(3)设身高为176cm 的同学被抽中的事件为A ,从乙班10名同学中抽中两名身高不低于173cm 的同学有:(181,173),(181,176) (181,178),(181,179),(179,173),(179,176),(179,178),(178,173) (178, 176) ,(176,173)共10个基本事件,而事件A 含有4个基本事件;()42105P A ∴==.………………10分 19.解:∵命题:p 方程2260x x a a -+-=有一正根1x 和一负根2x∴22212(1)4(6)060a a x x a a ⎧∆=--->⎪⎨⋅=-<⎪⎩解得06a << ………………3分 ∵命题:q 函数2(3)1y x a x =+-+的图象与x 轴有公共点∴2(3)40a ∆=--≥∴1a ≤或5a ≥ ………………5分∵命题“p q 或”为真命题,而命题“p q 且”为假命题∴命题p q 和一真一假01当命题p 为真命题,命题q 为假命题时,则 0615a a <<⎧⎨<<⎩15a ∴<< ………………7分 02当命题p 为假命题,命题q 为真命题时,则 0615a a a a ≤≥⎧⎨≤≥⎩或或06a a ∴≤≥或 ………………10分由0102可知:实数a 的取值范围为0a ≤或15a <<或6a ≥.………………12分 20.解:(1)∵,PC BC PC AB ⊥⊥,∴PC ⊥平面ABC ,∴PC AC ⊥.………………4分 (2)取BC 的中点N ,连MN .∵PM //=CN ,∴MN //=PC ,∴MN ⊥平面ABC .作NH ⊥AC ,交AC 的延长线于H ,连结MH ∵直线AM 与直线PC 所成的角为60︒, ∴在Rt AMN ∆中,60AMN ∠=︒在Rt AMN ∆中,cot 601MN AN AMN =⋅∠=︒= 在Rt NCH ∆中,sin 1sin 60NH CN NCH =⋅∠=⨯︒= 在Rt M NH ∆中,∵MH =作NE MH ⊥于E .∵AC ⊥平面MNH ,∴AC NE ⊥,∴NE ⊥平面MAC ,∴点N 到 平面MAC的距离为MN NH NE MH ⋅==. ∵点N 是线段BC 的中点,∴点B 到平面MAC 的距离是点N 到平面 MAC.……………12分 (说明:等体积法解对同样给分)21.解:(1)因为2,1,n n S a n n =-=令解得11a =因为2,n n S a n =-所以112(1),(2,)n n S a n n n N --+=--≥∈ 两式相减得121+=-n n a a所以112(1),(2,)n n a a n n N -++=+≥∈又因为112a +=,所以{1}n a +是首项为2,公比为2的等比数列所以n n a 21=+,所以21nn a =-. ………………5分 (2)因为(21)21n n b n a n =+++,所以(21)2nn b n =+⋅所以231325272(21)2(21)2n nn T n n -=⨯+⨯+⨯+⋅⋅⋅+-⋅++⋅①23123252(21)2(21)2n n n T n n +=⨯+⨯+⋅⋅⋅+-⋅++⋅ ②①—②得:231322(222)(21)2n n n T n +-=⨯+++⋅⋅⋅+-+⋅2122262(21)212n n n +-⨯=+⨯-+⋅-11122(21)22(21)2n n n n n +++=-+-+⋅=---⋅所以12(21)2n n T n +=+-⋅若2256,21n T n -≥-则12(21)22256,21n n n ++-⋅-≥-[高&考%资(源#] 即1822,n +≥所以18n +≥,解得7n ≥,所以满足不等式2256,21n T n -≥-的最小n 值为7. ………………13分22.解:(1)由2c e a ==及222a b c =+得22222a b c ==又点2A 在椭圆C 上 223112a b ∴+= 解得224,2a b ==故椭圆的标准方程为22142x y +=. ………………4分 (2)设()()1122,,,M x y N x y ,则由2OP OM ON →→→=+,得()()()001122,,2,x y x y x y =+,2019-2020学年高二上数学期中模拟试卷含答案本试题分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,考试时间120分钟。
安徽省合肥一六八中学2018_2019学年高二数学上学期期中试题理宏志班201811230250
合肥一六八中学2018—2019学年第一学期期中考试高二数学试题(宏志班)一、选择题(共60题,每题5分。
每题仅有一个正确选项。
)1.已知a、b是两条平行直线,且a∥平面β,则b与β的位置关系是( )A.平行 B.相交C.b在平面β内 D.平行或b在平面β内2.在下列命题中,不是公理的是( )A.平行于同一条直线的两条直线互相平行B.如果一条直线上的两点在一个平面内,那么这条直线在此平面内C.空间中,如果两个角的两边分别对应平行,那么这两角相等或互补D.如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线3.如果ac>0,bc>0,那么直线ax+by+c=0不通过( )A.第一象限B.第二象限 C.第三象限 D.第四象限4.直线(a2+1)x﹣y+1=0(其中a∈R)的倾斜角的取值范围是( )A.[0,] B.[,) C.(,] D.[,π)5.一个几何体的三视图如图所示,则该几何体的体积为( )A.12π B.24π C. D.72π6.半径为5的球内有一个高为8的内接正四棱锥,则这个球与该内接正四棱锥的体积之比为( )A.B.C.D.7.三棱柱ABC﹣A'B'C′的所有棱长都等于2,并且AA'⊥平面ABC,M是侧棱BB′的中点,则直线MC′与A′B所成的角的余弦值是( )A.B.C.D.8.直线l过点P(1,0),且与以A(2,1),为端点的线段总有公共点,则直线l斜率的取值范围是( )A. B.C. D.[1,+∞)9.在正方体ABCD﹣A1B1C1D1中,E是棱CC1的中点,F是四边形BCC1B1内的动点,且A1F∥平面D1AE,下列说法正确的个数是( )①点F的轨迹是一条线段②A1F与D1E不可能平行③A1F与BE是异面直线④当F与C1不重合时,平面A1FC1不可能与平面AED1平行A.1 B.2 C.3 D.410.在平面直角坐标系中,记d为点P(cosθ,sinθ)到直线x﹣my﹣2=0的距离.当θ、m变化时,d的最大值为( )A.1 B.2 C.3 D.411.生于瑞士的数学巨星欧拉在1765年发表的《三角形的几何学》一书中有这样一个定理:“三角形的外心、垂心和重心都在同一直线上,而且外心和重心的距离是垂心和重心距离之半.”这就是著名的欧拉线定理.设△ABC中,设O、H、G分别是外心、垂心和重心,下列四个选项错误的是( )A.HG=2OG B.++=C.设BC边中点为D,则有AH=3OD D.S△ABG=S△BCG=S△ACG12.如图1,直线EF将矩形纸ABCD分为两个直角梯形ABFE和CDEF,将梯形CDEF沿边EF翻折,如图2,在翻折的过程中(平面ABFE和平面CDEF不重合)下面说法正确的是( )A .存在某一位置,使得CD ∥平面ABFEB .存在某一位置,使得DE ⊥平面ABFEC .在翻折的过程中,BF ∥平面ADE 恒成立D .在翻折的过程中,BF ⊥平面CDEF 恒成立二、填空题(共20分,每题5分)13、已知直线1:260l ax y ++=与()22:110l x a y a +-+-=平行,则实数a 的取值是________14.球的半径为5cm ,被两个相互平行的平面所截得圆的直径分别为6cm 和8cm ,则这两个平面之间的距离是 cm .15. 我国古代数学名著《数书九章》中有“天池盆测雨”题:在下雨时,用一个圆台形的天池盆接雨水.天池盆盆口直径为二尺八寸,盆底直径为一尺二寸,盆深一尺八寸.若盆中积水深九寸,则平地降雨量是________寸.(注:① 平地降雨量等于盆中积水体积除以盆口面积;② 一尺等于十寸)16.在正方体ABCD﹣A 1B 1C 1D 1中,E 为棱AB 上一点,且AE=1,BE=3,以E 为球心,线段EC 的长为半径的球与棱A 1D 1,DD 1分別交于F ,G 两点,则△AFG 的面积为________ 三、解答题(共70分,每题必需要有必要的解答过程)17.(10分) 设直线l 的方程为(+1)x +y +2-=0 (∈R). a a a (1)若l 在两坐标轴上截距相等,求直线l 的方程; (2)若l 不经过第二象限,求实数的取值范围. a18.(12分)在平面直角坐标系xOy 中,OBC ∆的边BC 所在的直线方程是03:=--y x l , (1)如果一束光线从原点O 射出,经直线l 反射后,经过点)3,3(,求反射后光线所在直线的方程;(2)如果在OBC ∆中,BOC ∠为直角,求OBC ∆面积的最小值.19.(12分)如图是一个以A1B1C1为底面的直三棱柱被一平面所截得到的几何体,截面为ABC,已知A1B1=B1C1=2,∠A1B1C1=90°,AA1=4,BB1=3,CC1=2,求:(Ⅰ)该几何体的体积;(Ⅱ)截面ABC的面积.20(12分).如图,已知正三棱锥P﹣ABC的侧面是直角三角形,PA=6,顶点P在平面ABC内的正投影为点D,D在平面PAB内的正投影为点E,连接PE并延长交AB于点G.(Ⅰ)证明:G是AB的中点;(Ⅱ)在图中作出点E在平面PAC内的正投影F,并求四面体PDEF的体积.21.(12分)如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.(1)证明:平面ACD⊥平面ABC;(2)过AC的平面交BD于点E,若平面AEC把四面体ABCD分成体积相等的两部分,求二面角D﹣AE﹣C的余弦值.22.(12分)如图,在三棱锥中,是正三角形,为其中心.面面,,,是的中点,.(1)证明:面;(2)求与面所成角的正弦值.合肥一六八中学2018—2019学年第一学期期中考试高二数学试题(宏志班)参考答案一.选择题 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案DCABCBABCCCC二、填空题 13. -114. 1或7 15. 3 16. 4三、解答题17.(1)3x +y =0或x +y +2=0;(2)a ≤-1.18(1)设点O 关于直线l 的对称点为),(00y x A ,解得⎩⎨⎧-==3300y x,所以点)3,3(-A .因为反射后光线经过点)3,3(-A 和点)3,3(,所以反射后光线所在直线的方程为3=x .(2)设OD 为OBC ∆的一条高,则当且仅所以,OBC ∆面积的最小值是19.(Ⅰ)过C 作平行于A 1B 1C 1的截面A 2B 2C ,交AA 1,BB 1分别于点A 2,B 2. 由直三棱柱性质及∠A 1B 1C 1=90°可知B 2C ⊥平面ABB 2A 2, 则该几何体的体积V ==×2×2×2+××(1+2)×2×2=6, (Ⅱ)在△ABC 中,AB ==,BC ==,AC==2.则S△ABC=×2×=20.(Ⅰ)证明:∵P﹣ABC为正三棱锥,且D为顶点P在平面ABC内的正投影,∴PD⊥平面ABC,则PD⊥AB,又E为D在平面PAB内的正投影,∴DE⊥面PAB,则DE⊥AB,∵PD∩DE=D,∴AB⊥平面PDE,连接PE并延长交AB于点G,则AB⊥PG,又PA=PB,∴G是AB的中点;(Ⅱ)在平面PAB内,过点E作PB的平行线交PA于点F,F即为E在平面PAC内的正投影.∵正三棱锥P﹣ABC的侧面是直角三角形,∴PB⊥PA,PB⊥PC,又EF∥PB,所以EF⊥PA,EF⊥PC,因此EF⊥平面PAC,即点F为E在平面PAC内的正投影.连结CG,因为P在平面ABC内的正投影为D,所以D是正三角形ABC的中心.由(Ⅰ)知,G是AB的中点,所以D在CG上,故CD=CG.由题设可得PC⊥平面PAB,DE⊥平面PAB,所以DE∥PC,因此PE=PG,DE=PC.由已知,正三棱锥的侧面是直角三角形且PA=6,可得DE=2,PG=3,PE=2.在等腰直角三角形EFP中,可得EF=PF=2.所以四面体PDEF的体积V=×DE×S△PEF=×2××2×2=.21.(1)证明:如图所示,取AC的中点O,连接BO,OD.∵△ABC是等边三角形,∴OB⊥AC.△ABD与△CBD中,AB=BD=BC,∠ABD=∠CBD,∴△ABD≌△CBD,∴AD=CD.∵△ACD是直角三角形,∴AC是斜边,∴∠ADC=90°.∴DO=AC.∴DO2+BO2=AB2=BD2.∴∠BOD=90°.∴OB⊥OD.又DO∩AC=O,∴OB⊥平面ACD.又OB⊂平面ABC,∴平面ACD⊥平面ABC.(2)解:设点D,B到平面ACE的距离分别为h D,h E.则=.∵平面AEC把四面体ABCD分成体积相等的两部分,∴===1.∴点E是BD的中点.建立如图所示的空间直角坐标系.不妨取AB=2.则O(0,0,0),A(1,0,0),C(﹣1,0,0),D(0,0,1),B(0,,0),E .=(﹣1,0,1),=,=(﹣2,0,0).设平面ADE的法向量为=(x,y,z),则,即,取=.同理可得:平面ACE的法向量为=(0,1,).∴cos===﹣.∴二面角D﹣AE﹣C的余弦值为.22.(1)连结,因为是正三角形的中心,所以在上且,又,所以在中有,所以,又平面,平面,所以平面.(2)解法一:作交的延长线于,作交的延长线于,由面面知面,所以,又,所以所以面,所以面面,作,则面连结,则为与面所成角,∴,即所求角的正弦值为.解法二:以中点为原点,建立如图所示的空间直角坐标系.∵,∴,,,,∴,,,.设面的法向量为,则取,∴,即所求角的正弦值为.- 11 -。
安徽省合肥市一六八中学2020年高二数学理上学期期末试卷含解析
安徽省合肥市一六八中学2020年高二数学理上学期期末试卷含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 某地政府召集5家企业的负责人开会,其中甲企业有2人到会,其余4家企业各有1人到会,会上有3人发言,则这3人来自3家不同企业的可能情况的种数为()A.14 B. 16 C.20 D. 48参考答案:B略2. 若直线()A. B.[-1,3]C.[-3,1] D.参考答案:C3. 圆的圆心坐标和半径分别为 ( )....参考答案:C略4. 已知函数在上是单调函数,则实数的取值范围是()A.B. C.D.参考答案:B 5. 设等比数列前项的积为,若是一个确定的常数,那么数列,,,中也是常数的项是A. B. C. D.参考答案:C6. 甲乙两人有三个不同的学习小组A,B,C可以参加,若每人必须参加并且仅能参加一个学习小组,则两人参加同一个小组的概率为()A. B. C. D.参考答案:A依题意,基本事件的总数有种,两个人参加同一个小组,方法数有种,故概率为. 7. 如图,正方体中,分别为BC, CC1中点,则异面直线与所成角的大小为参考答案:D8. 如图是一个组合体的三视图,根据图中数据,可得该几何体的表面积(接触面积忽略不计)是()A.32πB.36πC.40πD.48π参考答案:D【考点】棱柱、棱锥、棱台的体积;由三视图求面积、体积.【分析】由已知中的三视图可得该几何体是一个球与圆柱的组合体,分别计算其表面积,相加可得答案.【解答】解:由已知中的三视图可得该几何体是一个球与圆柱的组合体,球的半径为2,故表面积为:4?π?22=16π,圆柱的底面半径为2,高为6,故表面积为:2π?2?(2+6)=32π,故该几何体的表面积S=48π,故选:D【点评】本题考查的知识点是圆柱的体积和表面积,球的体积和表面积,简单几何体的三视图,难度中档.9. 如图,AB是⊙O的直径,PB,PE分别切⊙O于B,C.若∠ACE=40°,则∠P=( )A.60°B.70°C.80°D.90°参考答案:C10. 已知定义在R上的可导函数f(x)满足:f′(x)+f(x)<0,则与f(1)(e是自然对数的底数)的大小关系是()A.>f(1)B.<f(1)C.≥f(1)D.不确定参考答案:A【考点】63:导数的运算.【分析】构造函数g(x)=e x f(x),利用导数研究其单调性,注意到已知f′(x)+f(x)<0,可得g(x)为单调减函数,最后由,代入函数解析式即可得答案.【解答】解:设g(x)=e x f(x),∵f′(x)+f(x)<0,∴g′(x)=e x(f′(x)+f(x))<0∴函数g(x)为R上的减函数;∵,∴g(m﹣m2)>g(1)即,∴>f(1)故选:A.二、填空题:本大题共7小题,每小题4分,共28分11. 命题P:“内接于圆的四边形对角互补”,则P的否命题是,非P是。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
合肥一六八中学 2020 学年第一学期期中考试高二数学试题(宏志班)一、选择题(共 60 题,每题 5 分。
每题仅有一个正确选项。
) 1.已知 a、b 是两条平行直线,且 a∥平面 β,则 b 与 β 的位置关系是( )A.平行B.相交C.b 在平面 β 内D.平行或 b 在平面 β 内2.在下列命题中,不是公理的是( )A.平行于同一条直线的两条直线互相平行B.如果一条直线上的两点在一个平面内,那么这条直线在此平面内C.空间中,如果两个角的两边分别对应平行,那么这两角相等或互补D.如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线3.如果 ac>0,bc>0,那么直线 ax+by+c=0 不通过( )A.第一象限 B.第二象限 C.第三象限D.第四象限4.直线(a2+1)x﹣y+1=0(其中 a∈R)的倾斜角的取值范围是( )A.[0, ]B.[ , ) C.( , ] D.[ ,π)5.一个几何体的三视图如图所示,则该几何体的体积为( )A.12πB.24πC.D.72π6.半径为 5 的球内有一个高为 8 的内接正四棱锥,则这个球与该内接正四棱锥的体积之比为 ()A.B.C.D.7.三棱柱 ABC﹣A'B'C′的所有棱长都等于 2,并且 AA'⊥平面 ABC,M 是侧棱 BB′的中点, 则直线 MC′与 A′B 所成的角的余弦值是( )A.B.C.D.8.直线 l 过点 P(1,0),且与以 A(2,1), 斜率的取值范围是( )为端点的线段总有公共点,则直线 lA.B.C.D.[1,+∞)9.在正方体 ABCD﹣A1B1C1D1 中,E 是棱 CC1 的中点,F 是四边形 BCC1B1 内的动点,且 A1F∥平面 D1AE,下列说法正确的个数是( )①点 F 的轨迹是一条线段②A1F 与 D1E 不可能平行 ③A1F 与 BE 是异面直线 ④当 F 与 C1 不重合时,平面 A1FC1 不可能与平面 AED1 平行A.1B.2C.3D.410.在平面直角坐标系中,记 d 为点 P(cosθ,sinθ)到直线 x﹣my﹣2=0 的距离.当 θ、m 变化时,d 的最大值为( )A.1B.2C.3D.411.生于瑞士的数学巨星欧拉在 1765 年发表的《三角形的几何学》一书中有这样一个定理:“三角形的外心、垂心和重心都在同一直线上,而且外心和重心的距离是垂心和重心距离之半.”这就是著名的欧拉线定理.设△ABC 中,设 O、H、G 分别是外心、垂心和重心,下列四个选项错误的是( )A.HG=2OG C.设 BC 边中点为 D,则有 AH=3ODB. + + = D.S△ABG=S△BCG=S△ACG12.如图 1,直线 EF 将矩形纸 ABCD 分为两个直角梯形 ABFE 和 CDEF,将梯形 CDEF 沿边 EF 翻 折,如图 2,在翻折的过程中(平面 ABFE 和平面 CDEF 不重合)下面说法正确的是( )A.存在某一位置,使得 CD∥平面 ABFEB.存在某一位置,使得 DE⊥平面 ABFEC.在翻折的过程中,BF∥平面 ADE 恒成立D.在翻折的过程中,BF⊥平面 CDEF 恒成立 二、填空题(共 20 分,每题 5 分)13、已知直线 l1 : ax 2 y 6 0 与 l2 : x a 1 y a2 1 0 平行,则实数 a 的取值 是________ 14.球的半径为 5cm,被两个相互平行的平面所截得圆的直径分别为 6cm 和 8cm,则这两个平面之间的距离是cm.15. 我国古代数学名著《数书九章》中有“天池盆测雨”题:在下雨时,用一个圆台形的天 池盆接雨水.天池盆盆口直径为二尺八寸,盆底直径为一尺二寸,盆深一尺八寸.若盆中积 水深九寸,则平地降雨量是________寸.(注:① 平地降雨量等于盆中积水体积除以盆口面 积;② 一尺等于十寸)16.在正方体 ABCD﹣A1B1C1D1 中,E 为棱 AB 上一点,且 AE=1,BE=3,以 E 为球心,线段 EC 的长为半径的球与棱 A1D1,DD1 分別交于 F,G 两点,则△AFG 的面积为________三、解答题(共 70 分,每题必需要有必要的解答过程)17.(10 分) 设直线 l 的方程为( a +1)x+y+2- a =0 ( a ∈R). (1)若 l 在两坐标轴上截距相等,求直线 l 的方程; (2)若 l 不经过第二象限,求实数 a 的取值范围.18.(12 分)在平面直角坐标系 xOy 中,OBC 的边 BC 所在的直线方程是 l : x y 3 0 , (1)如果一束光线从原点 O 射出,经直线 l 反射后,经过点 (3, 3) ,求反射后光线所在直线的方程;(2)如果在 OBC 中, BOC 为直角,求 OBC 面积的最小值.19.(12 分)如图是一个以 A1B1C1 为底面的直三棱柱被一平面所截得到的几何体,截面为 ABC, 已知 A1B1=B1C1=2,∠A1B1C1=90°,AA1=4,BB1=3,CC1=2,求:(Ⅰ)该几何体的体积; (Ⅱ)截面 ABC 的面积. 20(12 分).如图,已知正三棱锥 P﹣ABC 的侧面是直角三角形,PA=6,顶点 P 在平面 ABC 内 的正投影为点 D,D 在平面 PAB 内的正投影为点 E,连接 PE 并延长交 AB 于点 G. (Ⅰ)证明:G 是 AB 的中点; (Ⅱ)在图中作出点 E 在平面 PAC 内的正投影 F,并求四面体 PDEF 的体积.21.(12 分)如图,四面体 ABCD 中,△ABC 是正三角形,△ACD 是直角三角形,∠ABD=∠CBD, AB=BD. (1)证明:平面 ACD⊥平面 ABC; (2)过 AC 的平面交 BD 于点 E,若平面 AEC 把四面体 ABCD 分成体积相等的两部分,求二面角 D﹣AE﹣C 的余弦值.22.(12 分)如图,在三棱锥中, 是正三角形, 为其中心.面,, 是 的中点,.面,(1)证明: 面 ; (2)求 与面 所成角的正弦值.一.选择题题号 12答案 DC合肥一六八中学 2020 学年第一学期期中考试 高二数学试题(宏志班)参考答案345678910 11 12ABCBABCCCC二、填空题 13. -1 14. 1 或 7 15. 3 16. 4 三、解答题 17.(1)3x+y=0 或 x+y+2=0;(2)a≤-1.18(1)设点 O关于直线 l的对称点为A(x0 ,y0 ),由题意应有 x0 2y0 1 x0 y0 3 20,解得 x0 y03 3,所以点 A(3, 3) .因为反射后光线经过点 A(3, 3) 和点 (3, 3) ,所以反射后光线所在直线的方程为 x 3.(2)设 OD 为 OBC 的一条高,则| OD | 3 ,设 BOD (0 ) ,可得22| BC || BD | | DC || OD | tan θ | OD | ,所以 OBC 的面积 S 1 | BC | | OD |tan θ2 1 (| OD | tan θ | OD |) | OD | 1 2 | OD | tan θ | OD | | OD || OD |2 9 , 当 且 仅2tan θ2tan θ2当 时,等号成立. 4所以, OBC 面积的最小值是 9 . 219.(Ⅰ)过 C 作平行于 A1B1C1 的截面 A2B2C,交 AA1,BB1 分别于点 A2,B2.由直三棱柱性质及∠A1B1C1=90°可知 B2C⊥平面 ABB2A2,则该几何体的体积 V== ×2×2×2+ × ×(1+2)×2×2=6,(Ⅱ)在△ABC 中,AB==,BC==,AC==2 .则 S△ABC= ×2 ×=20.(Ⅰ)证明:∵P﹣ABC 为正三棱锥,且 D 为顶点 P 在平面 ABC 内的正投影,∴PD⊥平面 ABC,则 PD⊥AB,又 E 为 D 在平面 PAB 内的正投影,∴DE⊥面 PAB,则 DE⊥AB,∵PD∩DE=D,∴AB⊥平面 PDE,连接 PE 并延长交 AB 于点 G,则 AB⊥PG,又 PA=PB,∴G 是 AB 的中点;(Ⅱ)在平面 PAB 内,过点 E 作 PB 的平行线交 PA 于点 F,F 即为 E 在平面 PAC 内的正投影.∵正三棱锥 P﹣ABC 的侧面是直角三角形,∴PB⊥PA,PB⊥PC,又 EF∥PB,所以 EF⊥PA,EF⊥PC,因此 EF⊥平面 PAC,即点 F 为 E 在平面 PAC 内的正投影.连结 CG,因为 P 在平面 ABC 内的正投影为 D,所以 D 是正三角形 ABC 的中心.由(Ⅰ)知,G 是 AB 的中点,所以 D 在 CG 上,故 CD= CG.由题设可得 PC⊥平面 PAB,DE⊥平面 PAB,所以 DE∥PC,因此 PE= PG,DE= PC.由已知,正三棱锥的侧面是直角三角形且 PA=6,可得 DE=2,PG=3 ,PE=2 . 在等腰直角三角形 EFP 中,可得 EF=PF=2. 所以四面体 PDEF 的体积 V= ×DE×S△PEF= ×2× ×2×2= .21.(1)证明:如图所示,取 AC 的中点 O,连接 BO,OD. ∵△ABC 是等边三角形,∴OB⊥AC. △ABD 与△CBD 中,AB=BD=BC,∠ABD=∠CBD, ∴△ABD≌△CBD,∴AD=CD. ∵△ACD 是直角三角形, ∴AC 是斜边,∴∠ADC=90°.∴DO= AC. ∴DO2+BO2=AB2=BD2. ∴∠BOD=90°. ∴OB⊥OD. 又 DO∩AC=O,∴OB⊥平面 ACD. 又 OB⊂ 平面 ABC, ∴平面 ACD⊥平面 ABC.(2)解:设点 D,B 到平面 ACE 的距离分别为 hD,hE.则 = .∵平面 AEC 把四面体 ABCD 分成体积相等的两部分,∴= = =1.∴点 E 是 BD 的中点. 建立如图所示的空间直角坐标系.不妨取 AB=2.则 O(0,0,0),A(1,0,0),C(﹣1,0,0),D(0,0,1),B(0, ,0),E.=(﹣1,0,1), =, =(﹣2,0,0).设平面 ADE 的法向量为 =(x,y,z),则,即,取 =.同理可得:平面 ACE 的法向量为 =(0,1, ).∴cos===﹣ .∴二面角 D﹣AE﹣C 的余弦值为 .22.(1)连结 ,因为 是正三角形 的中心,所以 在 上且,又,所以在 中有,所以,又 平面 , 平面 ,所以 平面 .(2)解法一:作交 的延长线于 ,作交 的延长线于 ,由面面 知 面 ,所以,又,所以所以 面 ,所以面面 ,作,则 面连结 ,则 为 与面 所成角,∴,即所求角的正弦值为 .解法二:以 中点为原点,建立如图所示的空间直角坐标系.∵,∴,,,,∴,,,.设面 的法向量为,则取,∴,即所求角的正弦值为.。
