柱面坐标变换
三重积分柱面坐标变换公式

三重积分柱面坐标变换公式在进行三重积分运算时,柱面坐标变换是一种常用的方法,可以简化积分的计算过程。
柱面坐标通常用于描述空间中的圆柱体或圆锥体问题,因此对于涉及到这些几何形状的三重积分问题,柱面坐标的应用是非常有用的。
柱面坐标的定义柱面坐标是一种三维坐标系,其中一个点的位置由径向距离、极角和高度三个参数决定。
在柱面坐标系中,通常用(ρ,φ,z)表示一个点的位置,其中ρ 表示点到 z 轴的距离,φ 表示点在 xy 平面上的极角,z 表示点在 z 轴上的高度。
三重积分的柱面坐标变换公式假设在三维空间中有一个函数f(ρ, φ, z),我们要计算其在柱面坐标系下的三重积分。
此时,需要进行坐标变换以便在柱面坐标系下进行积分计算。
三重积分的柱面坐标变换公式如下:$$ \\iiint f(ρ, φ, z) dV = \\iiint f(ρ, φ, z) ρ dz dρ dφ $$其中,dV 表示体积元素,ρ 从 0 到ρ,φ 从 0 到2π, z 的范围由具体问题决定。
柱面坐标变换公式的应用举例举一个简单的例子来说明柱面坐标变换的应用。
假设有一个函数f(ρ, φ, z) =ρ^2,我们要计算其在半径为 1,高度为 2 的圆柱体内的体积。
根据柱面坐标变换公式,可以得到:$$ \\iiint f(ρ, φ, z) dV = \\int_{0}^{2π} \\int_{0}^{1} \\int_{0}^{2} (ρ^2) ρ dz dρ dφ $$经过计算可得最终结果为8π/3。
结语柱面坐标变换公式在处理涉及柱面形状的三重积分问题时具有重要作用,能够简化积分计算过程,提高计算效率。
熟练掌握柱面坐标变换公式对于解决相关数学问题是非常有帮助的。
希望本文所介绍的柱面坐标变换公式能够对你的数学学习有所帮助。
柱坐标变换的雅可比行列式

柱坐标变换的雅可比行列式柱坐标系是三维坐标系的一种,它以极坐标系和笛卡尔坐标系为基础,其三个坐标分量分别表示点的径向距离、仰角和方位角。
在求解某些函数的梯度、散度和旋度等问题中,使用柱坐标系可以更加方便和简洁。
而柱坐标变换的雅可比行列式则是柱坐标系中坐标变换的重要工具和判别条件。
柱坐标变换的雅可比行列式可以用来描述从一个坐标系到另一个坐标系的变换对函数积分测量的影响。
在柱坐标系中,雅可比矩阵为三阶正交矩阵,而雅可比行列式则可以用来计算变换后体积元的缩放因子。
具体地,设在柱坐标系下函数 $f(\rho, \theta, z)$,可得坐标变换$$\begin{cases}x &= \rho \sin \theta \\y &= \rho \cos \theta \\z &= z\end{cases}$$则该坐标变换的雅可比行列式为$$J=\begin{vmatrix}\dfrac{\partial x}{\partial \rho} & \dfrac{\partial x}{\partial \theta} & \dfrac{\partial x}{\partial z} \\\dfrac{\partial y}{\partial \rho} & \dfrac{\partial y}{\partial \theta} & \dfrac{\partial y}{\partial z} \\\dfrac{\partial z}{\partial \rho} & \dfrac{\partial z}{\partial \theta} & \dfrac{\partial z}{\partial z}\end{vmatrix}=\begin{vmatrix}\sin \theta & \rho \cos \theta & 0 \\\cos \theta & -\rho \sin \theta & 0 \\0 & 0 & 1\end{vmatrix}=-\rho$$因此,在柱坐标系下,体积元的缩放因子为 $-\rho$。
柱面坐标变换和球面坐标变换

柱面坐标变换和球面坐标变换
在数学和物理学中,柱面坐标和球面坐标是描述空间中点位置的两种不同坐标系。
通过对这两种坐标系进行变换,可以在不同问题中更好地描述和分析相关的物理现象。
柱面坐标变换
柱面坐标通常用于描述平面内的点位置,其坐标形式为(r, θ, z),其中r是点到z轴的距离,θ是与x轴的夹角,z是点在z轴上的投影位置。
柱面坐标与直角坐标系之间的变换关系如下:
假设直角坐标系中的点为(x, y, z),柱面坐标系中的点为(r, θ, z),则有以下变换关系:
r = √(x^2 + y^2)
θ = arctan(y/x)
z = z
柱面坐标变换在解决某些旋转对称问题时非常有用,比如圆柱体或圆锥体的体积计算和空间内的电场分布等问题。
球面坐标变换
球面坐标通常用于描述空间中的点位置,其坐标形式为(r, θ, φ),其中r是点到原点的距离,θ是与x轴的夹角,φ是与z轴的夹角。
球面坐标与直角坐标系之间的变换关系如下:
假设直角坐标系中的点为(x, y, z),球面坐标系中的点为(r, θ, φ),则有以下变换关系:
r = √(x^2 + y^2 + z^2)
θ = arctan(y/x)
φ = arccos(z/r)
球面坐标变换在处理一些涉及球形对称性问题时非常有用,比如天文学中的行星运动和化学中的原子排列等问题。
综上所述,柱面坐标变换和球面坐标变换是描述空间中点位置的两种重要坐标系,它们在解决不同问题中起着关键作用。
通过深入理解两种坐标系之间的变换关系,我们可以更好地解释和分析物理现象,并在应用中更加灵活地使用不同的坐标系来描述问题。
柱面坐标变换和球面坐标变换一样吗

柱面坐标变换和球面坐标变换一样吗在数学和物理学领域,柱面坐标和球面坐标是常用的坐标系,它们在描述空间中的点和矢量时发挥着重要的作用。
虽然柱面坐标和球面坐标都是三维空间中的坐标系统,但它们之间存在一些显著的不同之处。
柱面坐标变换柱面坐标系是一个应用广泛的坐标系,其中一个点的位置由径向距离、极角和高度组成。
在柱面坐标系中,点的坐标表示为$(r, \\theta, z)$,其中r是点到z轴的距离,$\\theta$是与x轴的夹角,z是点到xy平面的距离。
柱面坐标系到直角坐标系的变换公式如下:$$ \\begin{aligned} x & = r \\cdot \\cos(\\theta) \\\\ y & = r \\cdot\\sin(\\theta) \\\\ z & = z \\end{aligned} $$球面坐标变换球面坐标系是另一种常用的坐标系,其中一个点的位置由半径、极角和方位角组成。
在球面坐标系中,点的坐标表示为$(\\rho, \\phi, \\theta)$,其中$\\rho$是点到原点的距离,$\\phi$是点到z轴的夹角,$\\theta$是与x轴的夹角。
球面坐标系到直角坐标系的变换公式如下:$$ \\begin{aligned} x & = \\rho \\cdot \\sin(\\phi) \\cdot \\cos(\\theta) \\\\ y & = \\rho \\cdot \\sin(\\phi) \\cdot \\sin(\\theta) \\\\ z & = \\rho \\cdot\\cos(\\phi) \\end{aligned} $$比较与总结尽管柱面坐标和球面坐标都用于描述三维空间中的点,但它们之间有一些显著的不同。
柱面坐标主要用于旋转对称的问题,球面坐标则适用于球对称的问题。
在坐标变换公式中,柱面坐标的r是一个平面距离,而球面坐标的$\\rho$是一个空间距离。
柱面坐标变换公式推导过程是什么

柱面坐标变换公式推导过程是什么在数学和物理学中,柱面坐标系是一种常用的坐标系,它是平面极坐标系的三维扩展。
在柱面坐标系中,我们用径向距离、方位角和高度来描述空间中的点。
坐标系介绍柱面坐标系中,一个点的位置由三个坐标确定: - r:点到z轴的直线距离(径向距离) - $\\phi$:点在x-y平面上的投影与x轴的夹角(方位角) - z:点在z轴上的高度这三个坐标$(r, \\phi, z)$描述了三维空间中的一个点的位置。
坐标变换公式推导过程从直角坐标系到柱面坐标系的变换令$x = r\\cos(\\phi)$, $y = r\\sin(\\phi)$,可得 - $r = \\sqrt{x^2 + y^2}$ - $\\phi = \\arctan\\left(\\frac{y}{x}\\right)$根据z轴高度不变,z=z,所以直角坐标系到柱面坐标系的变换可以表示为:$$ \\begin{cases} r = \\sqrt{x^2 + y^2} \\\\ \\phi =\\arctan\\left(\\frac{y}{x}\\right) \\\\ z = z \\end{cases} $$从柱面坐标系到直角坐标系的变换直角坐标系到柱面坐标系的变换是一个非线性变换,可以使用雅可比矩阵来表示。
考虑柱面坐标$(r, \\phi, z)$到直角坐标(x,y,z)的变换,我们有:$$ \\begin{bmatrix} x \\\\ y \\\\ z \\end{bmatrix} = \\begin{bmatrix}r\\cos(\\phi) \\\\ r\\sin(\\phi) \\\\ z \\end{bmatrix} $$其中,雅可比矩阵为:$$ J = \\begin{bmatrix} \\cos(\\phi) & -r\\sin(\\phi) & 0 \\\\ \\sin(\\phi) & r\\cos(\\phi) & 0 \\\\ 0 & 0 & 1 \\end{bmatrix} $$柱面坐标系下的梯度算子与拉普拉斯算子在柱面坐标系中,梯度算子和拉普拉斯算子的表达式为: - 梯度算子:$$ \ abla f = \\frac{\\partial f}{\\partial r}\\mathbf{e}_r +\\frac{1}{r}\\frac{\\partial f}{\\partial \\phi}\\mathbf{e}_\\phi + \\frac{\\partial f}{\\partial z}\\mathbf{e}_z $$- 拉普拉斯算子:$$ \\Delta f = \\frac{1}{r}\\frac{\\partial}{\\partial r}\\left(r\\frac{\\partial f}{\\partial r}\\right) + \\frac{1}{r^2}\\frac{\\partial^2 f}{\\partial \\phi^2} + \\frac{\\partial^2 f}{\\partial z^2} $$结论本文介绍了柱面坐标系的定义,并推导了从直角坐标系到柱面坐标系的变换公式,以及柱面坐标系下的梯度算子和拉普拉斯算子的表达式。
柱坐标、球坐标下的三重积分

解:由图知:直角系:
D
y
x
2
4 x2
6x2 y2
I dx
dy
f (x, y, z)dz
2
4x2
x2 y2
柱标系: I
2
d
2
rdr
6r 2
f (r cos , r sin , z)dz
0
0
r
杂例
在三种坐标系下化三重积分 f (x, y, z)dv为三次积分,
z
其中:z 6 x2 y2, z x2 y2 z 6 x2 y2 6
四、柱坐标、球坐标下的三重积分
1. 柱坐标:(θ,r,z)
zz
变换为:x r cos , y r sin , z z
即:(x, y, z) (r cos , r sin , z),其中:
0 r ,0 2 ,| J || (x, y, z) | r ( , r, z)
x
注:柱坐标— 极坐标平面竖起一根Z轴。x
上顶: z 1 x2 y2
下底: z = 0
z
Dxy: x 2 y 2 1
x y
I dxdy
zdz
Dxy
用哪种坐标? 柱面坐标 .
.
2π
1
1r 2
I = 0 dθ 0 rdr0 zdz
Dxy 0
1
4
x
z0
1y
注:用柱坐标求 fdv分成两个步骤:
第一步:先一后二,对z积分后将二重积分化为极坐 标下的二重积分;
元素区域由六个坐标面围成:
半平面及+d ;
半径为r及 r+dr的园柱面;
平面 z及 z+dz;
dz
柱面坐标变换

柱面坐标变换在数学和物理学中,柱面坐标系是一种常用的坐标系,通常用来描述圆柱体或圆锥体上的点。
柱面坐标系包括径向距离r、方位角$\\theta$和高度z三个坐标参数。
柱面坐标变换是从笛卡尔坐标系到柱面坐标系的转换过程,通过该变换可以描述更为复杂的空间几何关系。
坐标系介绍•径向距离r:表示点到z轴的投影长度,通常$r\\geq 0$。
•方位角 $\\theta$:表示点在x−y平面上的极角,通常$0\\leq \\theta < 2\\pi$。
•高度z:表示点在z轴上的坐标。
柱面坐标变换公式若一个点在柱面坐标系下的位置为$(r, \\theta, z)$,其对应的笛卡尔坐标为P(x,y,z),则柱面坐标系到笛卡尔坐标系的变换公式如下:$$ x = r\\cos(\\theta) $$$$ y = r\\sin(\\theta) $$z=z其中,x、y、z分别是点在笛卡尔坐标系下的坐标。
而逆变换(笛卡尔坐标系到柱面坐标系)的公式如下:$$ r = \\sqrt{x^2 + y^2} $$$$ \\theta = \\arctan\\left(\\frac{y}{x}\\right) $$示例考虑一个在柱面坐标系下的点$(4, \\frac{\\pi}{3}, 2)$,我们要将其转换到笛卡尔坐标系下。
根据上述变换公式,我们可以得到:$$ x = 4\\cos\\left(\\frac{\\pi}{3}\\right) = 2 $$$$ y = 4\\sin\\left(\\frac{\\pi}{3}\\right) = 2\\sqrt{3} $$z=2因此,该点在笛卡尔坐标系下的坐标为$(2, 2\\sqrt{3}, 2)$。
应用柱面坐标变换在数学和物理学的问题中具有重要的应用,特别是在三维空间中的曲线积分、曲面积分等计算中。
通过使用柱面坐标变换,可以简化许多复杂的计算过程,使得问题的求解更加直观和简便。
8.3.1 三重积分-直角坐标系切片法,柱面坐标系
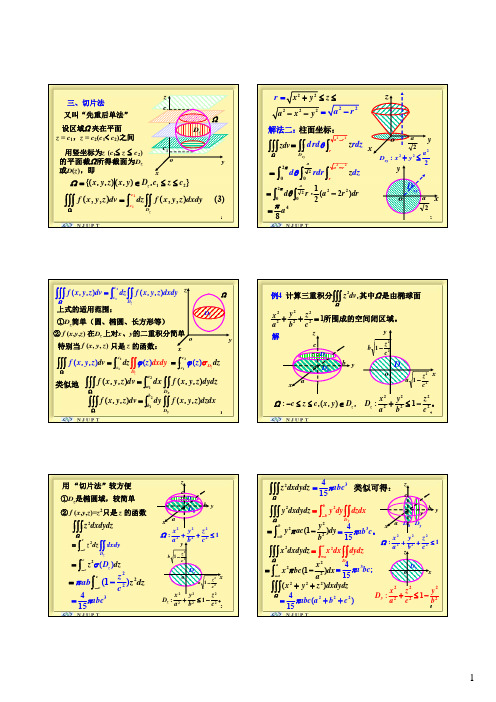
三、切片法又叫“先重后单法”设区域Ω夹在平面z =c 1,z =c 2(c 1<c 2)之间Ω1c 2c z用竖坐标为z c ≤z ≤c zD 1},),(),,{(21c z c D y x z y x z ≤≤∈=Ωyxo (12)的平面截Ω所得截面为D z 或D (z ),即21(,,)(,,) (3)zc c D f x y z dv dz f x y z dxdy Ω=⎰⎰⎰⎰⎰⎰柱解法二:面坐标:⎰⎰⎰zdv ∙yzxo2a 2a 22222x y z a x y +≤≤--22a r=-r =22r ra z d rd rdz θ-=⎰⎰⎰22a yxo⎰⎰-⋅=202220)2(21a dr r a r d πθΩ48a π=xyD 22:2xy D x y +≤xyD 22220a r ra z d rdr dzπθ-=⎰⎰⎰ΩzyozD ⎰⎰⎰⎰⎰⎰=zD c c dxdy z y x f dz dv z y x f ),,(),,(21Ω特别当f (x , y , z ) 只是z 的函数:②f (x ,y ,z ) 在D z 上对x 、y 的二重积分简单①D z 简单(圆、椭圆、长方形等)上式的适用范围:3x类似地⎰⎰⎰⎰⎰⎰=ΩxD a adydzz y x f dx dv z y x f ),,(),,(21⎰⎰⎰⎰⎰⎰=ΩyD b bdzdxz y x f dy dv z y x f ),,(),,(2121(,,)()zc c D dxd dv d f y z y x z z ϕΩ=⎰⎰⎰⎰⎰⎰21()z c c D z dzϕσ=⎰解2222222,14z dv y z x a b c ΩΩ++=⎰⎰⎰计算三重积分其中是由椭球面所围成的空间例闭区域。
zc y 21z b -4,),(,:z D y x c z c ∈≤≤-Ω。
2222221:c z b y a x D z -≤+D 0D z xyz ab o zD 221cz a -x o2c ⎰⎰⎰Ωdxdydzz 2D 0D z z x yz ab oc ①D z 是椭圆域,较简单②f (x ,y ,z )=z 2只是z 的函数用“切片法”较方便1:222222≤++cz b y a x Ω2cz 53154abcπ=zD 221c z a -yx o221c zb -。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
柱面坐标变换
一、概述
柱面坐标变换是一种将三维空间中的点从直角坐标系转换到柱面坐标系的方法。
在计算机图形学和计算机视觉等领域中,柱面坐标变换被广泛应用于图像处理、目标跟踪、物体识别等方面。
二、柱面坐标系
柱面坐标系是一种常见的三维坐标系,它由径向距离$r$、极角
$\theta$和高度$h$三个参数组成。
在柱面坐标系中,一个点$(x,y,z)$可以表示为$(r,\theta,h)$,其中$r=\sqrt{x^2+y^2}$,$\theta=\arctan(\frac{y}{x})$,$h=z$。
三、直角坐标系到柱面坐标系的转换
将直角坐标系中的点$(x,y,z)$转换到柱面坐标系中需要进行以下步骤:
1. 计算径向距离$r$
$$r=\sqrt{x^2+y^2}$$
2. 计算极角$\theta$
$$\theta=\arctan(\frac{y}{x})$$
需要注意的是,在计算$\theta$时需要考虑$x$和$y$的符号。
当$x>0,y>0$时,$\theta=\arctan(\frac{y}{x})$;当$x<0,y>0$时,$\theta=\pi+\arctan(\frac{y}{x})$;当$x<0,y<0$时,$\theta=-\pi+\arctan(\frac{y}{x})$;当$x>0,y<0$时,
$\theta=\arctan(\frac{y}{x})$。
3. 计算高度$h$
$$h=z$$
四、柱面坐标系到直角坐标系的转换
将柱面坐标系中的点$(r,\theta,h)$转换到直角坐标系中需要进行以下步骤:
1. 计算$x$和$y$
$$x=r\cos\theta$$
$$y=r\sin\theta$$
2. 计算$z$
$$z=h$$
五、应用举例
柱面坐标变换在计算机视觉和计算机图形学中有着广泛的应用。
以下是一些常见的应用举例:
1. 图像处理:在图像处理中,柱面坐标变换可以用于纠正鱼眼镜头等广角镜头畸变问题。
2. 目标跟踪:在目标跟踪中,柱面坐标变换可以将目标从直角坐标系转换到柱面坐标系,从而更好地描述目标的形状和运动轨迹。
3. 物体识别:在物体识别中,柱面坐标变换可以将物体从直角坐标系转换到柱面坐标系,从而更好地描述物体的形状和特征。
六、总结
柱面坐标变换是一种将三维空间中的点从直角坐标系转换到柱面坐标
系的方法。
它在计算机视觉和计算机图形学等领域中有着广泛的应用。
通过对柱面坐标系和直角坐标系之间的转换方法进行了解和掌握,可
以更好地应用柱面坐标变换解决实际问题。
