回溯法实验(n皇后问题)(迭代法)

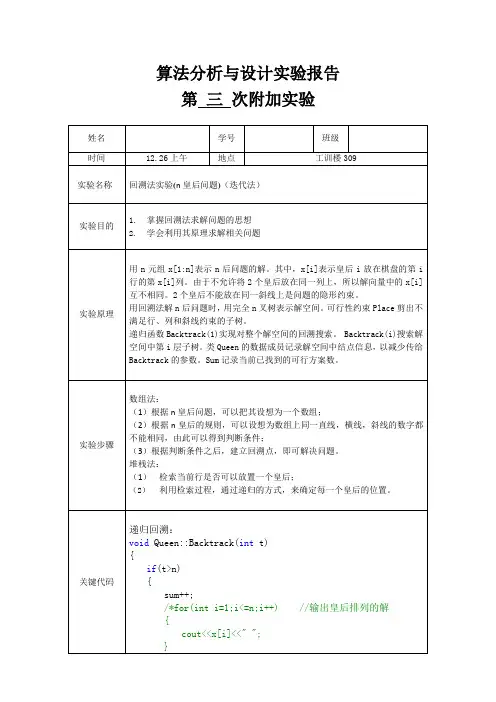
算法分析与设计实验报告第三次附加实验
附录：
完整代码（回溯法）
//回溯算法递归回溯n皇后问题#include<iostream>
#include<time.h>
#include<iomanip>
#include"math.h"
using namespace std;
class Queen
{
friend int nQueen(int); //定义友元函数，可以访问私有数据
private:
bool Place(int k); //判断该位置是否可用的函数
void Backtrack(int t); //定义回溯函数
int n; //皇后个数
int *x; //当前解
long sum; //当前已找到的可行方案数
};
int main()
{
int m,n;
for(int i=1;i<=1;i++)
{
cout<<"请输入皇后的个数："; //输入皇后个数
cin>>n;
cout<<"皇后问题的解为："<<endl;
clock_t start,end,over; //计算程序运行时间的算法
start=clock();
end=clock();
over=end-start;
start=clock();
m=nQueen(n); //调用求解的函数
cout<<n<<"皇后问题共有";
cout<<m<<"个不同的解！"<<endl; //输出结果
end=clock();
printf("The time is %6.3f",(double)(end-start-over)/CLK_TCK); //显示运行时间
cout<<endl;
}
system("pause");
return 0;
}
bool Queen::Place(int k)//传入行号
{
for(int j=1;j<k;j++)
{
if((abs(k-j)==abs(x[j]-x[k]))||(x[j]==x[k]))//如果两个在同一斜线或者在同一列上，说明冲突，该位置不可用
{
return false;
}
}
return true;
}
void Queen::Backtrack(int t)
{
if(t>n)
{
sum++;
/*for(int i=1;i<=n;i++) //输出皇后排列的解
{
cout<<x[i]<<" ";
}
cout<<endl;*/
}
else
{//回溯探索第i行的每一列是否有元素满足要求for(int i=1;i<=n;i++)
{
x[t]=i;
if(Place(t))
{
Backtrack(t+1);
}
}
}
}
int nQueen(int n)
{
Queen X; //定义Queen类的对象X
//初始化X
X.n=n;
X.sum=0;
int *p=new int[n+1]; //动态分配
for(int i=0;i<=n;i++) //初始化数组
{
p[i]=0;
}
X.x=p;
X.Backtrack(1);
delete[] p;
return X.sum;//输出解的个数
}
完整代码（回溯法）
//回溯算法迭代回溯n皇后问题
#include<iostream>
#include<time.h>
#include<iomanip>
#include"math.h"
using namespace std;
class Queen
{
friend int nQueen(int); //定义友元函数
private:
bool Place(int k); //定义位置是否可用的判断函数
void Backtrack(void); //定义回溯函数
int n; // 皇后个数
int *x; // 当前解
long sum; // 当前已找到的可行方案数
};
int main()
{
int n,m;
for(int i=1;i<=1;i++)
{
cout<<"请输入皇后的个数：";
cin>>n;
cout<<n<<"皇后问题的解为："<<endl;
clock_t start,end,over; //计算程序运行时间的算法
start=clock();
end=clock();
over=end-start;
start=clock();
m=nQueen(n); //调用求解皇后问题的函数
cout<<n<<"皇后问题共有";
cout<<m<<"个不同的解!"<<endl;
end=clock();
printf("The time is %6.3f",(double)(end-start-over)/CLK_TCK); //显示运
行时间
cout<<endl;
}
system("pause");
return 0;
}
bool Queen::Place(int k)
{
for (int j=1;j<k;j++)
{
if ((abs(k-j)==abs(x[j]-x[k]))||(x[j]==x[k])) //如果两个皇后在同一斜线或者在同一列上，说明冲突，该位置不可用
{
return false;
}
}
return true;
}
void Queen::Backtrack() //迭代法实现回溯函数
{
x[1] = 0;
int k = 1;
while(k>0)
{
x[k] += 1; //先将皇后放在第一列的位置上
while((x[k]<=n)&&!(Place(k))) //寻找能够放置皇后的位置
{
x[k] += 1;
}
if(x[k]<=n) //找到位置
{
if(k == n) //如果寻找结束输出结果
{
/*for (int i=1;i<=n;i++)
{
cout<<x[i]<<" ";
}
cout<<endl; */
sum++;
}
else//没有结束则找下一行
{
k++;
x[k]=0;
}
}
else//没有找到合适的位置则回溯
{ k--; }
}
}
int nQueen(int n)
{
Queen X; //定义Queen类的对象X
//初始化X
X.n=n;
X.sum=0;
int *p=new int[n+1];
for(int i=0;i<=n;i++)
{
p[i]=0;
}
X.x=p;
X.Backtrack();
delete []p;
return X.sum; //返回不同解的个数
}。