多元函数求导法则
§8.4 多元复合函数的求导法则与隐函数的求导公式
M
26
机动 目目录录 上上页页 下下页页 返返回回 结结束束
定理2 若函数 F (x, y, z) 满足:
① 在点
的某邻域内具有连续偏导数 ,
② F (x0 , y0, z0) 0 ③ Fz (x0 , y0, z0) 0
则方程
在点
某一邻域内可唯一确
定一个单值连续函数 z = f (x , y) , 满足
机动 目目录录 上上页页 下下页页 返返回回 结结束束
导数的另一求法 — 利用隐函数求导
sin y ex xy 1 0, y y(x) 两边对 x 求导
两边再对 x 求导
y x0
ex y cos y x (0,0)
sin y ( y)2 cos y y
令 x = 0 , 注意此时 y 0 , y 1
8
目录 上页 下页 返回 结束
例3 设 z uv sin t , u et , v cos t , 求全导数 dz .
dt
解 dz z du
z
dt u dt
t
z
vet
cos t
e t (cost sin t) cos t
uvt tt
注意：多元抽象复合函数求导在偏微分方程变形与 验证解的问题中经常遇到, 下列两个例题有助于掌握 这方面问题的求导技巧与常用导数符号.
x y
解 z
z v
x
v x
eu sin v eu cos v 1
z
z
z v
y
v y
eu sin v eu cos v 1
uv x yx y
7
目录 上页 下页 返回 结束
例2 u f (x, y, z) ex2 y2 z2 , z x2sin y, 求 u , u x y
多元函数的求导法则-精选
z z u z v y u y v y
x yx y
eusinvx eucovs1
e x y [x six n y ) (co x y s )( ]
山东农业大学
高等数学
主讲人： 苏本堂
例2. u f(x ,y ,z ) e x 2 y 2 z 2 ,z x 2 sy i,求nu , u x y
山东农业大学
高等数学
主讲人： 苏本堂
推广: 设下面所涉及的函数都可微 .
1) 中间变量多于两个的情形. 例如, zf(u,v,w ),
u ( t ) ,v ( t ) ,w ( t )
z
d z z du z dv z dw d t u d t v dt w dt
在点 t 可导, 且有链式法则 dzzduzdv dt u dt v dt
z
uv
证: 设 t 取增量△t , 则相应中间变量 t t
有增量△u ,△v ,
zzuzvo() (( u)2( v)2)
u vΒιβλιοθήκη 山东农业大学高等数学
主讲人： 苏本堂
zzuzv o ( ) (( u)2( v)2)
山东农业大学
高等数学
主讲人： 苏本堂
第四节多元复合函数的求导法则
一、多元复合函数求导的链式法则 二、多元复合函数的全微分
山东农业大学
高等数学
主讲人： 苏本堂
一、多元复合函数求导的链式法则
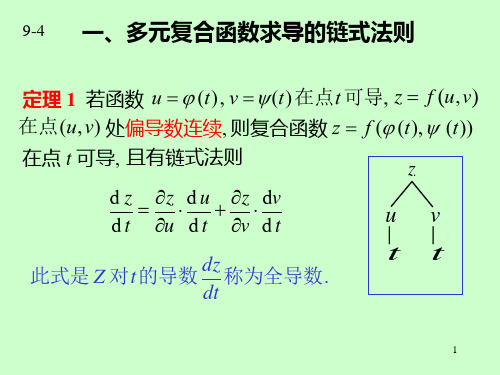
定理. 若函数 u (t),v (t)在 t可 点 ,z导 f(u,v) 在点 (u,v)处偏导连续, 则复合函数 zf((t) ,(t))
e xy[x six ny ) (co x y s )]d(y 所以 zexy[ysixn y()co x sy)(]
多元函数求导
z 求 y x
x 1 1 z 1 ′′ ′′ ′′ ′′ = f1′ + x[ y f11 + f12] 2 f2′ 2 [ yf 21 + f 22 ] y y y y yx 1 y 2 g′ 3 g′′ x x
2
1 y 1 x ′′ ′′ = f1′ + x y f11 2 f2′ 3 f22 2 g′ 3 g′′ x x y y
第三节 多元复合函数的求导法则
一元复合函数 y = f (u), u = (x) 求导法则 微分法则
d y d= f ′(u) du= f ′(u)′ (x) dx
推广
（1）多元复合函数求导的链式法则 ） （2）多元复合函数的全微分 ）
1
可导, 可导 且有链式法则 z = f (φ (t), ψ (t)) 在点 t d z z du z d v = + dt u dt v dt
x2 + y2 +z2
x y
+2ze
x2 + y2 +z2 x2 cos y x2 + y2 +x4 sin2 y
7
= 2 ( y + x sin y cos y ) e
例 3. 设 z = u v + sin t , u = e ,
t
dz 求全导数 . dt
解:
z
t t
d z z du z d v z = + + dt u dt v dt t
2
x y z x y z f 2′ f 2′ u f 2′ v ′′ ′′ = f 21 + xyf 22 ; + = u z v z z 2w ′′ ′′ ′′ ′′ = f11 + xyf12 + yf 2′+ yz( f 21 + xyf 22 ) 于是 xz
9.4 多元复合函数求导法则(新)
∂z 2 x = e cos y + ∂x x
∂z 1 x = −e sin y + ∂y y
18
z = f (u, v) =
u2v 2 2 , u +v ≠ 0 2 2 u +v
u =t , v =t
t 但，z = f (t, t ) = 2
dz 1 = dt 2
0,
u2 +v2 = 0
∂z du ∂z dv ≠ ∂u ⋅ dt + ∂v ⋅ dt = 0⋅1+ 0⋅1 = 0
2
常用导数符号
∂z = fv (u, v) = fv = f2′ ∂v ∂2 z ′′ = fvv (u, v) = fvv = f22 2 ∂v
称为混合偏导数
′′ ′′ ′′ ′′ 当 f12 和 f21 均连续时有 f12 = f21
3
推广: 推广 设下面所涉及的函数都可微 . 1、中间变量多于两个的情形 、中间变量多于两个的情形.
8
例 3.
u = f (x, y, z) = e
x2 + y2 +z2
, z = x sin y, 已知
2
∂u ∂u , . 可微，求 ∂x ∂ y
u
x y z
∂u ∂ f = 解: ∂x ∂x
x y
2 2 x2 + y2 +x4 sin 2 y
= 2 x (1+ 2 x sin y) e
∂u ∂ f ∂ f ∂z = + ⋅ ∂y ∂y ∂z ∂y
x
y x
y
5
z = eu sin v, u = xy , v = x + y , 求 例2. 设
多元复合函数的求导法则详解
多元复合函数的求导法则详解具体来说，有两种常见的多元复合函数情况，即链式法则和求导法则。
下面将结合具体例子详细解释这两种求导法则。
链式法则：链式法则适用于一个函数内部嵌套一个函数的情况。
我们用一个简单的例子来说明。
假设有一个函数f(x)=x²+1，另一个函数g(y)=y³。
现在我们要求复合函数h(x)=g(f(x))的导数。
首先，我们可以计算出 f(x) 的导数 df/dx = 2x。
然后我们计算g(y) 的导数dg/dy = 3y²。
接下来，我们利用链式法则来求解 h(x) 的导数。
根据链式法则，h(x) 的导数可以表示为 h'(x) = (dg/df) *(df/dx)。
在这个例子中，(dg/df) 表示 g'(f(x))。
我们可以通过将 f(x) 的结果代入到 g(y) 中来计算 (dg/df)。
即将 f(x) 的结果代入到 g(y)中得到h(x) = g(f(x)) = (f(x))³ = (x²+1)³。
然后我们计算 g'(f(x))，也就是求 g(f(x)) 的导数。
根据前面的计算， g(y) 的导数dg/dy = 3y²。
将 f(x) 的结果代入 dg/dy 中，即f(x) = x²+1，我们得到dg/df = 3(x²+1)²。
接下来，我们将 (dg/df) 和 df/dx 代入链式法则的公式中，即h'(x) = (dg/df) * (df/dx) = 3(x²+1)² * 2x = 6x(x²+1)²。
因此，我们得出 h(x) 的导数为h'(x) = 6x(x²+1)²。
这个例子说明了链式法则的使用方法，即先计算每个嵌套函数的导数，然后将这些导数代入到链式法则的公式中，得到最终的复合函数的导数。
94多元复合函数的求导法则
vet u sin t cost
et cost et sin t cost
et (cost sin t) cost.
【解Ⅱ】 将u,v函数表达式代入 z 后化为t 的一元函 数再对t 求导(略)
13/20
【例3】 设w f (x y z, xyz)， f 具有二阶
无论 z 是自变量 u、v 的函数或是中间变量 u、v
的函数，它的全微分形式是一样的. dz z du z dv
２.全微分形式不变性的简单应用
u v
(1)由全微分形式不变性，易得全微分四则运算公式，
d(u v) du dv,
d(u v) udv vdu,
d
z v
v x
dx
z u
u y
z v
v y
dy
uv x yx y
z u
u x
dx
y
dy
z v
v x
dx
v y
dy
z u
du
z v
dv.
17/20
１. 全微分形式不变性的实质
f11 y(x z) f12 xy2zf22 yf2.
【注意】 用观察法可一步写出一阶偏导数结果.
15/20
[课本例5略]
要求: 复合函数的一阶偏导数的求法及 练习题要会做.
[练习] 习题9-4 P82 1——10
[作业] 习题9-4 P82 2、4、6、9、10
v 用x，y的表达式代入，则得到
第四节 多元函数的求导法则
z u z v u v lim lim u 0 0 u x v x v 0 x u0 x v
z u z v . u x v x
同理可证
z z u z v . y u y v y
是x, y的复合函数 .
如何求复合函数 f [ ( x, y), ( x, y )] z 的导数？
定理 设 u ( x, y), v ( x, y) 在点 x, y)有偏导数 ( ,
而z f (u, v ) 在对应点 u, v ) 有连续偏导数，则复合 ( 函数
z f [ ( x, y ), ( x, y )] 在点( x, y) 有偏导数
du 函 数F，f，均 可 微 ， 求 . dx
四、小结
1、链式法则
2、全微分形式不变性
（理解其实质）
思考题
设 z f ( u, v , x ) ，而u ( x ) ，v ( x ) ，
dz f du f dv f ， 则 dx u dx v dx x dz f 试问 与 是否相同？为什么？ dx x
x 0 x 0
所以 z z u z v u v lim lim( ) x 0 x x 0 u x v x x x
z u z v u v lim lim lim lim lim lim u x 0 x v x 0 x x 0 x 0 x x 0 x 0 x
y
z f (sin x , e xy , ln x 2 y 2 )，f 具有连续偏 例3 设
z z 导数，求 和 . x y
多元复合函数的复合关系是多种多样的，我们不可 能把所有的公式都写出来，也没有必要，只要把握住 函数间的复合关系，及函数对某个自变量求偏导时，
4多元复合函数的求导法则
4多元复合函数的求导法则多元复合函数的求导法则可以通过链式法则来进行推导和应用。
链式法则是微积分中一种基本的求导法则，用于求解复合函数的导数。
在多元函数的情况下，链式法则也同样适用。
1.一元函数的链式法则首先回顾一下一元函数的链式法则。
对于一个一元函数f(g(x))，其中g(x)是x的函数，我们可以使用链式法则求导：(f(g(x)))'=f'(g(x))*g'(x)这个法则的核心思想在于，我们把函数f的导数与待求函数对x的导数相乘。
2.二元函数的链式法则推广到二元函数的情况，假设我们有一个二元函数z=f(x,y)，其中x 是自变量，y是中间变量。
我们可以通过链式法则来求导。
首先，我们考虑z关于x的偏导数，记作∂z/∂x。
由链式法则可得：∂z/∂x = (∂f/∂x)(dx/dx) + (∂f/∂y)(dy/dx)由于dx/dx=1，dy/dx是变量关于中间变量的导数，我们可以令∂z/∂x 简化为：∂z/∂x = (∂f/∂x) + (∂f/∂y)(dy/dx)同理，我们也可以求z关于y的偏导数∂z/∂y：∂z/∂y = (∂f/∂x)(dx/dy) + (∂f/∂y)(dy/dy)由于dy/dy=1，dx/dy是变量关于中间变量的导数，我们可以令∂z/∂y简化为：∂z/∂y = (∂f/∂x)(dx/dy) + (∂f/∂y)3.多元函数的链式法则如果函数z与多个自变量有关，即z=f(x1, x2, ..., xn)，我们可以使用类似的方式计算其偏导数。
对于z关于x1的偏导数∂z/∂x1，我们需要乘以x1关于中间变量的导数。
具体来说，我们可以写出：∂z/∂x1 = (∂f/∂x1)(dx1/dx1) + (∂f/∂x2)(dx2/dx1) + ... +(∂f/∂xn)(dxn/dx1)同理，我们也可以对z关于其他自变量求偏导数，得到类似的表达式。
4.链式法则的应用链式法则在实际问题中有广泛的应用，特别是在多元函数的求导计算中。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
多元函数求导法则
理论与实验课教案首页
第17 次课授课时间2016年12月23日第3～5节课教案完成时间2016年12月16日
课程名
称高等数学
教
员
职
称
副教
授
专业层
次药学四年制
本科
年
级
201
6
授课方
式
理
论
学
时
3
授课题目（章，节）
第七章多元函数及其微分法§3.全微分§4.多元复合函数与隐函数的偏导数
基本教材、主要参考书和相关网站基本教材：《高等数学》，顾作林主编，人民卫生出版社，2011年，第五版
主要参考书：《医科高等数学》，张选群主编，高教出版社，2009年，第二版
— 2 —
教学目标与要求：
了解：全微分存在的必要条件和充分条件；一阶全微分形式的不变性；全微分的概念掌握：全微分的求法；复合函数、隐函数的偏导数的求法
教学内容与时间分配：
复习5分钟全微分概念5分钟
可微与可导间的关系5分钟全微分的算法及应用25分钟
复合函数求导法则（推广及特例4种）40分钟
一阶全微分形式的不变性15分钟隐函数求导法20分钟
小结5分钟
— 3 —
教学重点与难点：
重点：全微分的概念；复合函数求导规则；隐函数求导法
难点：全微分的概念；全微分存在的充分条件；锁链法则的理解；函数结构图的分析
教学方法与手段：
教学方法：讲授式为主，启发式和讨论式相结合，借助示意图及实例分析，加深对抽象概念理解。
教学手段：传统教学手段（板书）与现代化教学手段（多媒体）相结合，既有演算推导过程，又提高单位时间授课信息量。
教学组长审阅意见：
签名：年月日教研室主任审阅意见：
签名：年月日
— 4 —
理论与实验课教案续页
基本内容教学方法手段和时间分配
— 5 —
理论与实验课教案续页
— 7 —
理论与实验课教案末页
小结1. 掌握全微分公式及应用；
2. 多元复合函数的求导法则；
3. 一阶全微分形式的不变性；
4. 隐函数求导法。
思
考题及作业题
作业：习题七15（1）；25(2,4)；26(1)；29(2)；32(2)；33（2）；34
预习：第七章第七节多元函数的极值
第八节经验公式与最小二乘法
— 8 —
实
施
情
况
及
效
果
分
析
教员签名：年
月日
— 9 —。