高考数学 6年高考母题精解精析 专题16 不等式选讲02 理
全国高考理科数学试题分类汇编16:不等式选讲 Word版含答案

2013年全国高考理科数学试题分类汇编16:不等式选讲一、填空题1 .(2013年普通高等学校招生统一考试重庆数学(理)试题(含答案))若关于实数x 的不等式53x x a -++<无解,则实数a 的取值范围是_________【答案】(],8-∞2 .(2013年高考陕西卷(理))(不等式选做题) 已知a , b , m , n 均为正数, 且a +b =1, mn =2,则(am +bn )(bm +an )的最小值为_______.【答案】23 .(2013年高考江西卷(理))(不等式选做题)在实数范围内,不等式211x --≤的解集为_________【答案】[]0,44 .(2013年高考湖北卷(理))设,,x y z R ∈,且满足:2221x y z ++=,23x y z ++=,则x y z ++=_______.二、解答题5 .(2013年普通高等学校招生统一考试新课标Ⅱ卷数学(理)(纯WORD 版含答案))选修4—5;不等式选讲设,,a b c 均为正数,且1a b c ++=,证明: (Ⅰ)13ab bc ca ++≤; (Ⅱ)2221a b c b c a++≥. 【答案】6 .(2013年普通高等学校招生统一考试辽宁数学(理)试题(WORD 版))选修4-5:不等式选讲已知函数()f x x a =-,其中1a >.(I)当=2a 时,求不等式()44f x x ≥=-的解集;(II)已知关于x 的不等式()(){}222f x a f x +-≤的解集为{}|12x x ≤≤,求a 的值.【答案】7 .(2013年普通高等学校招生统一考试福建数学(理)试题(纯WORD 版))不等式选讲:设不等式*2()x a a N -<∈的解集为A ,且32A ∈,12A ∉. (1)求a 的值; (2)求函数()2f x x a x =++-的最小值.【答案】解:(Ⅰ)因为32A ∈,且12A ∉,所以322a -<,且122a -≥ 解得1322a <≤,又因为*a N ∈,所以1a = (Ⅱ)因为|1||2||(1)(2)|3x x x x ++-≥+--=当且仅当(1)(2)0x x +-≤,即12x -≤≤时取得等号,所以()f x 的最小值为38 .(2013年普通高等学校招生全国统一招生考试江苏卷(数学)(已校对纯WORD 版含附加题))D.[选修4-5:不定式选讲]本小题满分10分.已知b a ≥>0,求证:b a ab b a 223322-≥-[必做题]第22、23题,每题10分,共20分.请在相应的答题区域内作答,若多做,解答时应写出文字说明、证明过程或演算步骤.【答案】D 证明:∵=---b a ab b a 223322()=---)(223223b b a ab a ())(22222b a b b a a ---())2)()(()2(22b a b a b a b a b a --+=--=又∵b a ≥>0,∴b a +>0,0≥-b a 02≥-b a ,∴0)2)()((≥--+b a b a b a∴0222233≥---b a ab b a∴b a ab b a 223322-≥-9 .(2013年高考新课标1(理))选修4—5:不等式选讲 已知函数()f x =|21||2|x x a -++,()g x =3x +.(Ⅰ)当a =2时,求不等式()f x <()g x 的解集;(Ⅱ)设a >-1,且当x ∈[2a -,12)时,()f x ≤()g x ,求a 的取值范围. 【答案】当a =-2时,不等式()f x <()g x 化为|21||22|30x x x -+---<,设函数y =|21||22|3x x x -+---,y =15, 212, 1236, 1x x x x x x ⎧-<⎪⎪⎪--≤≤⎨⎪->⎪⎪⎩, 其图像如图所示从图像可知,当且仅当(0,2)x ∈时,y <0,∴原不等式解集是{|02}x x <<. (Ⅱ)当x ∈[2a -,12)时,()f x =1a +,不等式()f x ≤()g x 化为13a x +≤+, ∴2x a ≥-对x ∈[2a -,12)都成立,故2a -≥2a -,即a ≤43, ∴a 的取值范围为(-1,43].10.(2013年高考湖南卷(理))在平面直角坐标系xOy 中,将从点M 出发沿纵、横方向到达点N 的任一路径成为M 到N 的一条“L 路径”.如图6所示的路径1231MM M M N MN N 与路径都是M 到N 的“L 路径”.某地有三个新建的居民区,分别位于平面xOy 内三点(3,20),(10,0),(14,0)A B C -处.现计划在x 轴上方区域(包含x 轴)内的某一点P 处修建一个文化中心.(I)写出点P 到居民区A 的“L 路径”长度最小值的表达式(不要求证明);(II)若以原点O 为圆心,半径为1的圆的内部是保护区,“L 路径”不能进入保护区,请确定点P 的位置,使其到三个居民区的“L 路径”长度值和最小.【答案】解: .0),,(≥y y x P 且设点(Ⅰ) d L A P 路径”的最短距离的“到点点)20,3(,|20 -y | + |3 -x |=+d 垂直距离,即等于水平距离,其中.,0R x y ∈≥(Ⅱ)本问考查分析解决应用问题的能力,以及绝对值的基本知识.点P 到A,B,C 三点的“L 路径”长度之和的最小值d = 水平距离之和的最小值h + 垂直距离之和的最小值v.且h 和v 互不影响.显然当y=1时,v = 20+1=21;时显然当]14,10[-∈x ,水平距离之和h=x – (-10) + 14 – x + |x-3| 24≥,且当x=3时, h=24.因此,当P(3,1)时,d=21+24=45.所以,当点P(x,y)满足P(3,1)时,点P 到A,B,C 三点的“L 路径”长度之和d 的最小值为45.。
新课标通用版高考数学总复习精品课件:第16章 不等式选讲(2课时)

考纲原文下载
命题规律分析
知识梳理整合
挖教材赢高考
高频考点透析
直通高考2020
第5页
经典品质/超越梦想
高考总复习/新课标版 数学·理
命题规律分析
考纲原文下载
命题规律分析
知识梳理整合
挖教材赢高考
高频考点透析
直通高考2020
第6页
经典品质/超越梦想
高频考点
高考试题 考查年份 试卷 题号 分值
高考总复习/新课标版 数学·理
第2页
经典品质/超越梦想
高考总复习/新课标版 数学·理
§16.1 绝对值不等式
考纲原文下载
命题规律分析
知识梳理整合
挖教材赢高考
高频考点透析
直通高考2020
第3页
经典品质/超越梦想
高考总复习/新课标版 数学·理 考 纲 原文下载
考纲原文下载
命题规律分析
知识梳理整合
挖教材赢高考
高频考点透析
直通高考2020
高频考点 1 绝对值不等式的解法 【例 1.1】 (1)(2018 年高考·课标全国卷Ⅲ) 设函数 f(x)=|2x+1|+|x-1|.
图1 ①画出 y=f(x)的图像; ②当 x∈[0,+∞)时,f(x)≤ax+b,求 a+b 的最小值.
考纲原文下载
命题规律分析
知识梳理整合
挖教材赢高考
高频考点透析
答案 1.(1)≥2ab a=b (2)≥ ab a=b
(3)算术 几何 (4)≥3 abc a=b=c (5)a1+a2+n …+an≥n a1a2…an 2.(1)ab≥0 (2)(a-b)(b-c)≥0
考纲原文下载 命题规律分析 知识梳理整合
高考数学一轮复习第十六章不等式选讲练习理
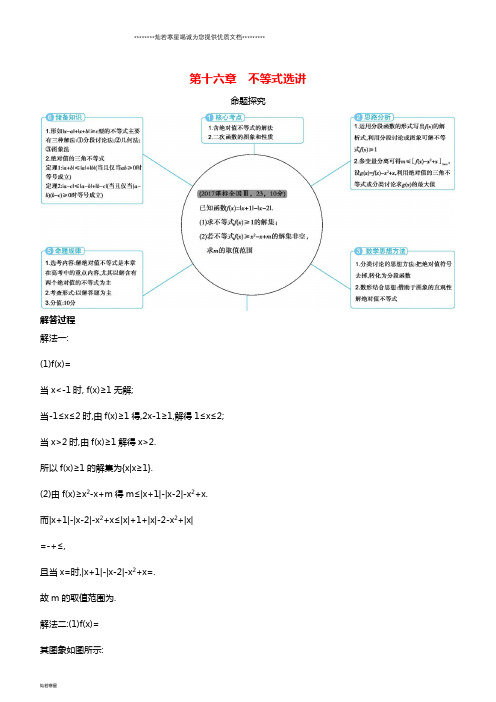
第十六章不等式选讲命题探究解答过程解法一:(1)f(x)=当x<-1时, f(x)≥1无解;当-1≤x≤2时,由f(x)≥1得,2x-1≥1,解得1≤x≤2;当x>2时,由f(x)≥1解得x>2.所以f(x)≥1的解集为{x|x≥1}.(2)由f(x)≥x2-x+m得m≤|x+1|-|x-2|-x2+x.而|x+1|-|x-2|-x2+x≤|x|+1+|x|-2-x2+|x|=-+≤,且当x=时,|x+1|-|x-2|-x2+x=.故m的取值范围为.解法二:(1)f(x)=其图象如图所示:由图可知f(x)≥1的解集为{x|x≥1}.(2)原式等价于存在x∈R使得f(x)-x2+x≥m成立, 即m≤[f(x)-x2+x]max,设g(x)=f(x)-x2+x,由(1)知g(x)=(i)当x≤-1时,g(x)=-x2+x-3,其图象开口向下,对称轴方程为x=>-1,∴g(x)≤g(-1)=-5;(ii)当-1<x<2时,g(x)=-x2+3x-1,其图象开口向下,对称轴方程为x=∈(-1,2),∴g(x)≤g=;(iii)当x≥2时,g(x)=-x2+x+3,其图象开口向下,对称轴方程为x=<2,∴g(x)≤g(2)=1.综上,g(x)max=,∴m的取值范围为考纲解读分析解读 1.本章主要考查绝对值的几何意义,绝对值不等式的解法及不等式证明的基本方法.2.绝对值不等式及不等式的证明均为高考的常考点.本章在高考中以解答题为主,往往涉及含有两个绝对值的问题,考查分类讨论、等价转化和数形结合等思想方法,分值约为10分,难度中等.五年高考考点一含绝对值不等式的解法1.(2017课标全国Ⅰ,23,10分)已知函数f(x)=-x2+ax+4,g(x)=|x+1|+|x-1|.(1)当a=1时,求不等式f(x)≥g(x)的解集;(2)若不等式f(x)≥g(x)的解集包含[-1,1],求a的取值范围.解析本题考查绝对值不等式的求解.(1)当a=1时,不等式f(x)≥g(x)等价于x2-x+|x+1|+|x-1|-4≤0.①当x<-1时,①式化为x2-3x-4≤0,无解;当-1≤x≤1时,①式化为x2-x-2≤0,从而-1≤x≤1;当x>1时,①式化为x2+x-4≤0,从而1<x≤.所以f(x)≥g(x)的解集为.(2)当x∈[-1,1]时,g(x)=2.所以f(x)≥g(x)的解集包含[-1,1]等价于当x∈[-1,1]时f(x)≥2.又f(x)在[-1,1]的最小值必为f(-1)与f(1)之一,所以f(-1)≥2且f(1)≥2,得-1≤a≤1.所以a的取值范围为[-1,1].2.(2016课标全国Ⅲ,24,10分)已知函数f(x)=|2x-a|+a.(1)当a=2时,求不等式f(x)≤6的解集;(2)设函数g(x)=|2x-1|.当x∈R时, f(x)+g(x)≥3,求a的取值范围.解析(1)当a=2时, f(x)=|2x-2|+2.解不等式|2x-2|+2≤6得-1≤x≤3.因此f(x)≤6的解集为{x|-1≤x≤3}.(5分)(2)当x∈R时,f(x)+g(x)=|2x-a|+a+|1-2x|≥|2x-a+1-2x|+a=|1-a|+a,当x=时等号成立,所以当x∈R时, f(x)+g(x)≥3等价于|1-a|+a≥3.①(7分) 当a≤1时,①等价于1-a+a≥3,无解.当a>1时,①等价于a-1+a≥3,解得a≥2.所以a的取值范围是[2,+∞).(10分)3.(2015课标Ⅰ,24,10分)选修4—5:不等式选讲已知函数f(x)=|x+1|-2|x-a|,a>0.(1)当a=1时,求不等式f(x)>1的解集;(2)若f(x)的图象与x轴围成的三角形面积大于6,求a的取值范围.解析(1)当a=1时,f(x)>1化为|x+1|-2|x-1|-1>0.当x≤-1时,不等式化为x-4>0,无解;当-1<x<1时,不等式化为3x-2>0,解得<x<1;当x≥1时,不等式化为-x+2>0,解得1≤x<2.所以f(x)>1的解集为.(5分)(2)由题设可得,f(x)=所以函数f(x)的图象与x轴围成的三角形的三个顶点分别为A,B(2a+1,0),C(a,a+1),△ABC的面积为(a+1)2. 由题设得(a+1)2>6,故a>2.所以a的取值范围为(2,+∞).(10分)教师用书专用(4—12)4.(2015山东,5,5分)不等式|x-1|-|x-5|<2的解集是( )A.(-∞,4)B.(-∞,1)C.(1,4)D.(1,5)答案 A5.(2014湖南,13,5分)若关于x的不等式|ax-2|<3的解集为x-<x<,则a= .答案-36.(2015重庆,16,5分)若函数f(x)=|x+1|+2|x-a|的最小值为5,则实数a= .答案-6或47.(2014广东,9,5分)不等式|x-1|+|x+2|≥5的解集为.答案{x|x≤-3或x≥2}8.(2013江西,15(2),5分)(不等式选做题)在实数范围内,不等式||x-2|-1|≤1的解集为.答案[0,4]9.(2013重庆,16,5分)若关于实数x的不等式|x-5|+|x+3|<a无解,则实数a的取值范围是.答案(-∞,8]10.(2015江苏,21D,10分)[选修4—5:不等式选讲]解不等式x+|2x+3|≥2.解析原不等式可化为或解得x≤-5或x≥-.综上,原不等式的解集是.11.(2014课标Ⅱ,24,10分)选修4—5:不等式选讲设函数f(x)=+|x-a|(a>0).(1)证明:f(x)≥2;(2)若f(3)<5,求a的取值范围.解析(1)证明:由a>0,得f(x)=+|x-a|≥=+a≥2.所以f(x)≥2.(2)f(3)=+|3-a|.当a>3时,f(3)=a+,由f(3)<5得3<a<.当0<a≤3时,f(3)=6-a+,由f(3)<5得<a≤3.综上,a的取值范围是.12.(2014辽宁,24,10分)选修4—5:不等式选讲设函数f(x)=2|x-1|+x-1,g(x)=16x2-8x+1,记f(x)≤1的解集为M,g(x)≤4的解集为N.(1)求M;(2)当x∈M∩N时,证明:x2f(x)+x[f(x)]2≤.解析(1)f(x)=当x≥1时,由f(x)=3x-3≤1得x≤,故1≤x≤;当x<1时,由f(x)=1-x≤1得x≥0,故0≤x<1.所以f(x)≤1的解集为M=.(2)证明:由g(x)=16x2-8x+1≤4得16≤4,解得-≤x≤.因此N=,故M∩N=.当x∈M∩N时, f(x)=1-x,于是x2f(x)+x·[f(x)]2=xf(x)[x+f(x)]=x·f(x)=x(1-x)=-≤.考点二不等式的证明1.(2017课标全国Ⅱ,23,10分)已知a>0,b>0,a3+b3=2.证明:(1)(a+b)(a5+b5)≥4;(2)a+b≤2.证明本题考查不等式的证明.(1)(a+b)(a5+b5)=a6+ab5+a5b+b6=(a3+b3)2-2a3b3+ab(a4+b4)=4+ab(a2-b2)2≥4.(2)因为(a+b)3=a3+3a2b+3ab2+b3=2+3ab(a+b)≤2+(a+b)=2+,所以(a+b)3≤8,因此a+b≤2.2.(2017江苏,21D,10分)已知a,b,c,d为实数,且a2+b2=4,c2+d2=16,证明:ac+bd≤8. 证明本小题主要考查不等式的证明,考查推理论证能力.由柯西不等式可得:(ac+bd)2≤(a2+b2)(c2+d2).因为a2+b2=4,c2+d2=16,所以(ac+bd)2≤64,因此ac+bd≤8.3.(2016课标全国Ⅱ,24,10分)已知函数f(x)=+,M为不等式f(x)<2的解集.(1)求M;(2)证明:当a,b∈M时,|a+b|<|1+ab|.解析(1)f(x)=(2分)当x≤-时,由f(x)<2得-2x<2,解得x>-1;(3分)当-<x<时, f(x)<2;(4分)当x≥时,由f(x)<2得2x<2,解得x<1.(5分)所以f(x)<2的解集M={x|-1<x<1}.(6分)(2)证明:由(1)知,当a,b∈M时,-1<a<1,-1<b<1,从而(a+b)2-(1+ab)2=a2+b2-a2b2-1=(a2-1)(1-b2)<0. 因此|a+b|<|1+ab|.(10分)4.(2015课标Ⅱ,24,10分)选修4—5:不等式选讲设a,b,c,d均为正数,且a+b=c+d,证明:(1)若ab>cd,则+>+;(2)+>+是|a-b|<|c-d|的充要条件.证明(1)因为(+)2=a+b+2,(+)2=c+d+2,由题设a+b=c+d,ab>cd得(+)2>(+)2.因此+>+.(2)(i)若|a-b|<|c-d|,则(a-b)2<(c-d)2,即(a+b)2-4ab<(c+d)2-4cd.因为a+b=c+d,所以ab>cd.由(1)得+>+.(ii)若+>+,则(+)2>(+)2,即a+b+2>c+d+2.因为a+b=c+d,所以ab>cd.于是(a-b)2=(a+b)2-4ab<(c+d)2-4cd=(c-d)2.因此|a-b|<|c-d|.综上,+>+是|a-b|<|c-d|的充要条件.教师用书专用(5—9)5.(2013陕西,15A,5分)(不等式选做题)已知a,b,m,n均为正数,且a+b=1,mn=2,则(am+bn)(bm+an)的最小值为.答案 26.(2015湖南,16(3),6分)选修4—5:不等式选讲设a>0,b>0,且a+b=+.证明:(1)a+b≥2;(2)a2+a<2与b2+b<2不可能同时成立.证明由a+b=+=,a>0,b>0,得ab=1.(1)由基本不等式及ab=1,有a+b≥2=2,即a+b≥2.(2)假设a2+a<2与b2+b<2同时成立,则由a2+a<2及a>0得0<a<1;同理,0<b<1,从而ab<1,这与ab=1矛盾.故a2+a<2与b2+b<2不可能同时成立.7.(2014课标Ⅰ,24,10分)选修4—5:不等式选讲若a>0,b>0,且+=.(1)求a3+b3的最小值;(2)是否存在a,b,使得2a+3b=6?并说明理由.解析(1)由=+≥,得ab≥2,且当a=b=时等号成立.故a3+b3≥2≥4,且当a=b=时等号成立.所以a3+b3的最小值为4.(2)由(1)知,2a+3b≥2≥4.由于4>6,从而不存在a,b,使得2a+3b=6.8.(2014福建,21(3),7分)选修4—5:不等式选讲已知定义在R上的函数f(x)=|x+1|+|x-2|的最小值为a.(1)求a的值;(2)若p,q,r是正实数,且满足p+q+r=a,求证:p2+q2+r2≥3.解析(1)因为|x+1|+|x-2|≥|(x+1)-(x-2)|=3,当且仅当-1≤x≤2时,等号成立,所以f(x)的最小值等于3,即a=3.(2)证明:由(1)知p+q+r=3,又因为p,q,r是正实数,所以(p2+q2+r2)(12+12+12)≥(p×1+q×1+r×1)2=(p+q+r)2=9,即p2+q2+r2≥3.9.(2013课标全国Ⅱ,24,10分)选修4—5:不等式选讲设a,b,c均为正数,且a+b+c=1,证明:(1)ab+bc+ca≤;(2)++≥1.证明(1)由a2+b2≥2ab,b2+c2≥2bc,c2+a2≥2ca得a2+b2+c2≥ab+bc+ca. 由题设得(a+b+c)2=1,即a2+b2+c2+2ab+2bc+2ca=1.所以3(ab+bc+ca)≤1,即ab+bc+ca≤.(2)易证+b≥2a,+c≥2b,+a≥2c,故+++(a+b+c)≥2(a+b+c),即++≥a+b+c.所以++≥1.三年模拟A组2016—2018年模拟·基础题组考点一含绝对值不等式的解法1.(2018湖南长沙第二次模拟,23)已知函数f(x)=|x+a2|+|x-a-1|.(1)证明:f(x)≥;(2)若f(4)<13,求a的取值范围.解析(1)证明:f(x)=|x+a2|+|x-a-1|≥|(x+a2)-(x-a-1)|=|a2+a+1|=+≥.(2)因为f(4)=|a2+4|+|a-3|=所以f(4)<13⇔或解得-2<a<3,即a的取值范围是(-2,3).2.(2017广东汕头潮阳黄图盛中学第三次质检,23)已知函数f(x)=|2x-a|+|2x+3|,g(x)=|x-1|+2.(1)解不等式|g(x)|<5;(2)若对任意x1∈R,都有x2∈R,使得f(x1)=g(x2)成立,求实数a的取值范围.解析(1)由||x-1|+2|<5,得-5<|x-1|+2<5,∴-7<|x-1|<3,∴不等式的解集为{x|-2<x<4}.(2)因为任意x1∈R,都有x2∈R,使得f(x1)=g(x2)成立,所以{y|y=f(x)}⊆{y|y=g(x)},又f(x)=|2x-a|+|2x+3|≥|(2x-a)-(2x+3)|=|a+3|,g(x)=|x-1|+2≥2,所以|a+3|≥2,解得a≥-1或a≤-5,所以实数a的取值范围为a≥-1或a≤-5.考点二不等式的证明3.(2017山西重点中学协作体期末,23)已知|x1-2|<1,|x2-2|<1.(1)求证:2<x1+x2<6,|x1-x2|<2;(2)若f(x)=x2-x+1,求证:|x1-x2|<| f(x1)-f(x2)|<5|x1-x2|.证明(1)∵|x1-2|<1,∴-1<x1-2<1,即1<x1<3,同理1<x2<3,∴2<x1+x2<6.∵|x1-x2|=|(x1-2)-(x2-2)|≤|x1-2|+|x2-2|.∴|x1-x2|<2.(2)|f(x1)-f(x2)|=|--x1+x2|=|x1-x2||x1+x2-1|,∵2<x1+x2<6,∴1<x1+x2-1<5,∴|x1-x2|<|f(x1)-f(x2)|<5|x1-x2|.4.(2017湖北八校联考,23)设函数f(x)=|x-a|,a∈R.(1)当a=2时,解不等式f(x)≥6-|2x-5|;(2)若关于x的不等式f(x)≤4的解集为[-1,7],且两正数s和t满足2s+t=a,求证:+≥6.解析(1)当a=2时,f(x)≥6-|2x-5|即为|x-2|+|2x-5|≥6,∴①或②或③由①得,x≥;②无解;由③得,x≤,所以,原不等式的解集为∪.(2)不等式f(x)≤4即为-4≤x-a≤4,∴a-4≤x≤a+4,∴a-4=-1且a+4=7,∴a=3,∴+=(2s+t)=≥=6当且仅当s=,t=2时,等号成立.B组2016—2018年模拟·提升题组(满分:40分时间:40分钟)解答题(共40分)1.(2018四川内江第一次模拟,23)已知函数f(x)=|3x-1|+|x-2|的最小值为m.(1)求m的值;(2)设实数a,b满足2a2+b2=m,证明:2a+b≤.解析(1)∵f(x)=∴f(x)在上单调递增,在上单调递减,∴f(x)的最小值为f=.∴m=.(2)由(1)知,2a2+b2=.∵2ab≤a2+b2,∴(2a+b)2=4a2+b2+4ab≤4a2+b2+2(a2+b2)=3(2a2+b2)=5,∴2a+b≤.2.(2018安徽淮南第二中学、宿城第一中学第四次考试,23)已知函数h(x)=-|x-3|.(1)若h(x)-|x-2|≤n对任意的x>0恒成立,求实数n的最小值;(2)若函数f(x)=求函数g(x)=f(x)+h(x)的值域.解析(1)h(x)-|x-2|≤n对任意的x>0恒成立,等价于-|x-3|-|x-2|≤n对任意的x>0恒成立,等价于-n≤(|x-2|+|x-3|)min.因为|x-2|+|x-3|≥|x-2-(x-3)|=1,当且仅当x∈[2,3]时取到等号,所以-n≤1,得n≥-1.所以实数n的最小值为-1.(2)因为f(x)=g(x)=f(x)+h(x),所以g(x)=f(x)-|x-3|=当0<x<3时,+x+2≥2+2=2+2,当x≥3时,x+3≥6.综上,g(x)≥2+2.所以函数g(x)=f(x)+h(x)的值域为[2+2,+∞).3.(2017福建六校联考)已知函数f(x)=|2x+1|+|2x-3|.(1)求不等式f(x)≤6的解集;(2)若关于x的不等式f(x)-log2(a2-3a)>2恒成立,求实数a的取值范围.解析(1)原不等式等价于或或解得<x≤2或-≤x≤或-1≤x<-,∴不等式f(x)≤6的解集为{x|-1≤x≤2}.(2)不等式f(x)-log2(a2-3a)>2恒成立⇔log2(a2-3a)+2<f(x)=|2x+1|+|2x-3|恒成立⇔log2(a2-3a)+2<f(x)min 恒成立,∵|2x+1|+|2x-3|≥|(2x+1)-(2x-3)|=4,∴f(x)的最小值为4,∴log2(a2-3a)+2<4,即解得-1<a<0或3<a<4.∴实数a的取值范围为(-1,0)∪(3,4).4.(2016河南八市重点高中联考,24)已知函数f(x)=|x+m|-|5-x|(m∈R).(1)当m=3时,求不等式f(x)>6的解集;(2)若不等式f(x)≤10对任意实数x恒成立,求m的取值范围.解析(1)当m=3时,f(x)>6,即|x+3|-|x-5|>6.∴或或解得x≥5或4<x<5.故不等式f(x)>6的解集为{x|x>4}.(2)f(x)=|x+m|-|5-x|≤|(x+m)+(5-x)|=|m+5|.由题意得|m+5|≤10,即-10≤m+5≤10,解得-15≤m≤5.故m的取值范围为[-15,5].C组2016—2018年模拟·方法题组方法1 含绝对值不等式的解法1.(2018四川成都第七中学一诊,23)已知函数f(x)=m-|x-1|-|x+1|.(1)当m=5时,求不等式f(x)>2的解集;(2)若函数y=x2+2x+3与y=f(x)的图象恒有公共点,求实数m的取值范围.解析(1)当m=5时, f(x)=所以不等式f(x)>2的解集为.(2)二次函数y=x2+2x+3=(x+1)2+2,该函数在x=-1时取到最小值2,因为f(x)=在x∈[-1,1]时取到最大值m-2,所以要使二次函数y=x2+2x+3与函数y=f(x)的图象恒有公共点,只需m-2≥2,即m≥4.所以实数m的取值范围是[4,+∞).2.(2017广东韶关1月调研,23)已知函数f(x)=|x+m|+|2x-1|(m∈R).(1)当m=-1时,求不等式f(x)≤2的解集;(2)设关于x的不等式f(x)≤|2x+1|的解集为A,且⊆A,求实数m的取值范围.解析(1)当m=-1时,f(x)=|x-1|+|2x-1|,则f(x)≤2⇒|x-1|+|2x-1|≤2,上述不等式可化为或或解得或或∴0≤x≤或<x<1或1≤x≤.∴原不等式的解集为.(2)∵f(x)≤|2x+1|的解集包含,∴当x∈时,不等式f(x)≤|2x+1|恒成立,即|x+m|+|2x-1|≤|2x+1|在上恒成立,∴|x+m|+2x-1≤2x+1在上恒成立,即|x+m|≤2在上恒成立,∴-2≤x+m≤2在上恒成立,∴-x-2≤m≤-x+2在上恒成立,∴(-x-2)max≤m≤(-x+2)min,∴-≤m≤0,∴实数m的取值范围是.方法2 与绝对值不等式相关的最值问题的求解策略3.(2017湖南三湘名校联盟三模,23)已知函数f(x)=|2x-a|-|x-1|.(1)当a=1时,求f(x)的最小值;(2)存在x∈[0,2]时,使得不等式f(x)≤0成立,求实数a的取值范围.解析(1)当a=1时,f(x)=|2x-1|-|x-1|=∴f(x)在上单调递减,在上单调递增,∴x=时, f(x)取到最小值-.(2)不等式f(x)≤0,即|2x-a|≤|x-1|,两边平方并化简得(3x-a-1)(x-a+1)≤0.a=2时,f(x)≤0即x=1∈[0,2],符合题意;a<2时,a-1<, f(x)≤0的解集为,∴∩[0,2]≠⌀,∴a-1≤2且≥0,∴-1≤a<2;a>2时,a-1>, f(x)≤0的解集为,∴∩[0,2]≠⌀,∴a-1≥0且≤2,∴2<a≤5.综上所述,a的取值范围是-1≤a≤5.方法3 不等式的证明4.(2017山西孝义九校质量监测,23)已知函数f(x)=|x+4|-|x-1|,若不等式f(x)>3的解集为P.(1)求P;(2)若a,b∈P,且a<b<1,证明:+≥9.解析(1)f(x)=则当x≤-4时,-5>3不成立;当-4<x<1时,2x+3>3,解得x>0,∴0<x<1;当x≥1时,5>3成立,故P={x|x>0}.(2)证明:∵a>0,b>a,∴a(b-a)≤=,当且仅当b=2a时取等号,又b<1,故+≥+=[b2+(1-b2)]·=5++≥9,当且仅当即a=,b=时取等号.。
高考数学考试大纲解读 专题16 不等式选讲 理

专题16 不等式选讲选考内容 (二)不等式选讲1.理解绝对值的几何意义,并能利用含绝对值不等式的几何意义证明以下不等式: (1)a b a b +≤+ . (2) a b a c c b -≤-+-.(3)会利用绝对值的几何意义求解以下类型的不等式:; ; ax b c ax b c x a x b c +≤+≥-+-≥.2.了解下列柯西不等式的几种不同形式,理解它们的几何意义,并会证明. (1)柯西不等式的向量形式:||||||.⋅≥⋅αβαβ (2)22222()(+)()a b c d ac bd +≥+.(3(此不等式通常称为平面三角不等式.) 3.会用参数配方法讨论柯西不等式的一般情形:4.会用向量递归方法讨论排序不等式.5.了解数学归纳法的原理及其使用范围,会用数学归纳法证明 一些简单问题. 6.会用数学归纳法证明伯努利不等式:了解当n 为大于1的实数时伯努利不等式也成立.7.会用上述不等式证明一些简单问题.能够利用平均值不等式、 柯西不等式求一些特定函数的极值.8.了解证明不等式的基本方法:比较法、综合法、分析法、反证法、放缩法.1.从考查题型来看,涉及本知识点的题目主要以选考的方式,在解答题中出现,考查解绝对值不等式、证明不等式等.2.从考查内容来看,主要考查绝对值不等式的解法、不等式的证明,求最值问题等.3.从考查热点来看,重点在于考查学生解不等式及利用不等式求解最值问题等,绝对值不等式与函数问题的综合是高考的趋势,值得关注.考向一 绝对值不等式的求解样题1 (2017新课标全国Ⅰ理科)已知函数2–4()x ax f x =++,11()x x g x =++-||||.(1)当a =1时,求不等式()()f x g x ≥的解集;(2)若不等式()()f x g x ≥的解集包含[–1,1],求a 的取值范围.所以a 的取值范围为[1,1]-.【名师点睛】零点分段法是解答绝对值不等式问题常用的方法,也可以将绝对值函数转化为分段函数,借助图象解题.考向二含绝对值不等式的恒成立问题样题2 已知函数.(1)当时,求的解集;(2)若不等式对任意实数恒成立,求的取值范围.样题3 已知函数.(1)若不等式的解集为,求实数的值;(2)若不等式对任意恒成立,求实数的取值范围.【解析】(1)由题意知,不等式的解集为,由得,∴,解得.(2)不等式等价于,因为不等式对任意恒成立,所以,因为,所以,解得或.考向三不等式的证明样题4 已知函数的单调递增区间为.(1)求不等式的解集;(2)设,证明:.。
专题十六 不等式选讲(讲解部分) 高考数学(课标版,理科)复习课件

考向突破 考向 不等式的证明
例 (2020届广西玉林第二次月考,23)已知正数a,b满足 1 + 1 =1.
a 4b
(1)证明: 25 ≤ab;
4(4a b)
(2)若存在实数x,使得|x+2|- x- 1 =a+b,求a,b.
4
解析
(1)证明:∵4a+b=(4a+b)
1 a
1 4b
=4+
a b
5 4
a
=
5 4
+a -
5 4
y
a时取?
”
,即g(y)的最小值为
5 4
+a,
当x∈(-∞,a]时,
f(x)=x(a-x)=-
x-
a 2
2
+
a2 4
,
∴x= a 时, f(x)取得最大值,为 a2 ,
2
4
故原问题转化为 a2 ≤ 5 +a⇒a2-4a-5≤0⇒-1≤a≤5,
44
又a>0,∴a∈(0,5].
例2 (2018湖北重点高中联考,23)已知函数f(x)=x|x-a|,a∈R. (1)若f(1)+f(-1)>1,求a的取值范围; (2)若a>0,∀x,y∈(-∞,a],都有不等式f(x)≤ y 5+|y-a|恒成立,求a的取值范
4
围.
解析 (1)f(1)+f(-1)>1⇒|1-a|-|1+a|>1
3.分析法 从要证的结论出发,逐步寻求使它成立的充分条件,直至所需条件为已知条 件或一个明显成立的事实(定义、公理或已证明的定理、性质等),从而得 出要证的命题成立. 4.反证法 先假设要证的命题不成立,以此为出发点,结合已知条件,应用公理、定 义、定理、性质等,进行正确的推理,得到和命题的条件(或已证明的定 理、性质、明显成立的事实等)矛盾的结论,以说明假设不正确,从而证明 原命题成立. 5.放缩法 证明不等式时,通过把不等式中的某些部分的值放大或缩小,简化不等式, 从而达到证明的目的.
第十六章 不等式选讲

x-
1 2
,A
为不等式
f( x)
<x+
1 2
的解集.
(1)求 A;
(2) 当 a∈A 时,试比较 | log2(1-a) | 与 | log2(1+a) | 的大小.
ìï ï
1 2
- 2x,x≤0,
1-2
解析
( 1) f(
x) =
ï í ï
1 2
,0<x<
1 2
,
当 x≤0 时,
îïï2x-
1 2
对应学生用书起始页码 P281
一、含绝对值不等式的解法
������������������������������������������������������������������������������������������������������������������������������������������������������������
基本不等式的推广
如果
a,b,c∈R+
,
那
么
a+b+c 3
≥
3
abc ,当且仅当
a=b=c
时等号成立.
对于 n 个正数 a1 ,a2 ,…,an ,它们的算术平均值不小于它
们的
几
何
平
均
值,
即
a1
+a
2
+…+a n
n
≥
n a1 ·a2 ·…·an ,当且
仅当 a1 = a2 = … = an 时等号成立.
| 2x-3 | + | 2x-1 | 的最小值为 M.
(1) 若 m,n∈[ -M,M] ,求证:2 | m+n | ≤ | 4+mn | ;
高考数学大讲义第十六章 不等式选讲 理

第十六章不等式选讲第一节绝对值不等式对应学生用书P1871.绝对值三角不等式(1)定理1:若是a,b是实数,那么|a+b|≤|a|+|b|,当且仅当ab≥0时,等号成立.(2)定理2:若是a,b,c是实数,那么|a-c|≤|a-b|+|b-c|,当且仅当(a-b)(b-c)≥0时,等号成立.2.绝对值不等式的解法(1)含绝对值的不等式|x|<a与|x|>a的解集(2)|ax+b|≤①|ax+b|≤c⇔-c≤ax+b≤c;②|ax+b|≥c⇔ax+b≥c或ax+b≤-c.(3)|x-a|+|x-b|≥c(c>0)和|x-a|+|x-b|≤c(c>0)型不等式的解法:①利用绝对值不等式的几何意义求解,表现了数形结合的思想;②利用“零点分段法”求解,表现了分类讨论的思想;③通过构造函数,利用函数的图像求解,表现了函数与方程的思想.1.关于绝对值三角不等式,易轻忽等号成立的条件.对|a+b|≥|a|-|b|,当且仅当a>-b>0时,等号成立,对|a|-|b|≤|a-b|≤|a|+|b|,若是a<-b<0当且仅当|a|≥|b|且ab≥0时左侧等号成立,当且仅当ab≤0时右边等号成立.2.形如|x-a|+|x-b|≥c(c>0)的不等式解法在讨论时应注意分类讨论点处的处置及c的符号判定,假设c<0那么不等式解集为R.[试一试]1.已知不等式|2x -t |+t -1<0的解集为(-12,12),那么t =________________. 解析:|2x -t |<1-t ,t -1<2x -t <1-t ,2t -1<2x <1,t -12<x <12,∴t =0. 答案:02.不等式|x +1|-|x -2|>k 的解集为R ,那么实数k 的取值范围为________.解析:法一:依照绝对值的几何意义,设数x ,-1,2在数轴上对应的点别离为P ,A ,B ,那么原不等式等价于|PA |-|PB |>k 恒成立.∵|AB |=3,即|x +1|-|x -2|≥-3.故当k <-3时,原不等式恒成立.法二:令y =|x +1|-|x -2|,则y =⎩⎪⎨⎪⎧ -3,x ≤-1,2x -1,-1<x <23,x ≥2,,要使|x +1|-|x -2|>k 恒成立,从图像中能够看出,只要k <-3即可.故k <-3知足题意.答案:(-∞,-3)含绝对值不等式的经常使用解法1.大体性质法:对a ∈R +,|x |<a ⇔-a <x <a ,|x |>a ⇔x <-a 或x >a .2.平方式:两边平方去掉绝对值符号.3.零点分区间法(或叫概念法):含有两个或两个以上绝对值符号的不等式,可用零点分区间法脱去绝对值符号,将其转化为与之等价的不含绝对值符号的不等式(组)求解.4.几何法:利用绝对值的几何意义,画出数轴,将绝对值转化为数轴上两点的距离求解.5.数形结合法:在直角坐标系中作出不等式两边所对应的两个函数的图像,利用函数图像求解.[练一练]1.在实数范围内,不等式|2x-1|+|2x+1|≤6的解集为____________.解析:法一:分类讨论去绝对值号解不等式.当x >12时,原不等式转化为4x ≤6⇒x ≤32;当-12≤x ≤12时,原不等式转化为2≤6,恒成立;当x <-12时,原不等式转化为-4x ≤6⇒x ≥-32.综上知,原不等式的解集为⎩⎨⎧⎭⎬⎫x |-32≤x ≤32. 法二:利用几何意义求解.原不等式可化为⎪⎪⎪⎪⎪⎪x -12+⎪⎪⎪⎪⎪⎪x +12≤3,其几何意义为数轴上到12,-12两点的距离之和不超过3的点的集合,数形结合知,当x =32或x =-32时,到12,-12两点的距离之和恰好为3,故当-32≤x ≤32时,知足题意,那么原不等式的解集为⎩⎨⎧⎭⎬⎫x |-32≤x ≤32. 答案:⎩⎨⎧x ⎪⎪⎪⎭⎬⎫-32≤x ≤32 2.假设存在实数x 使|x -a |+|x -1|≤3成立,那么实数a 的取值范围是________. 解析:利用绝对值不等式的性质求解.∵|x -a |+|x -1|≥|(x -a )-(x -1)|=|a -1|,要使|x -a |+|x -1|≤3有解,可使|a -1|≤3,∴-3≤a -1≤3,∴-2≤a ≤4.答案:[-2,4]对应学生用书P188考点一 绝对值不等式的解法 1.不等式|解析:原不等式等价于|x -2|>|x -1|,那么(x -2)2>(x -1)2,解得x <32. 答案:⎝ ⎛⎭⎪⎫-∞,322.(2021·西安质检)假设关于x的不等式|x-a|<1的解集为(1,3),那么实数a的值为________.解析:原不等式可化为a-1<x<a+1,又知其解集为(1,3),因此通过对照可得a=2.答案:23.若是关于x的不等式|x-3|-|x-4|<a的解集不是空集,那么实数a的取值范围是________.解析:注意到||x -3|-|x -4||≤|(x -3)-(x -4)|=1,-1≤|x -3|-|x -4|≤1.假设不等式|x -3|-|x -4|<a 的解集是空集,那么有|x -3|-|x -4|≥a 对任意的x ∈R 都成立,即有(|x -3|-|x -4|)min ≥a ,a ≤-1.因此,由不等式|x -3|-|x -4|<a 的解集不是空集可得,实数a 的取值范围是a >-1.答案:(-1,+∞)[备课札记][类题通法]利用零点分类讨论法解绝对值不等式时,注意分类讨论时要不重不漏.考点二 绝对值不等式的证明[典例] M .(1)求M ;(2)当a ,b ∈M 时,证明:2|a +b |<|4+ab |.解:(1)f (x )=|x +1|+|x -1|=⎩⎪⎨⎪⎧ -2x ,x <-1,2,-1≤x ≤1,2x ,x >1,当x <-1时,由-2x <4,得-2<x <-1;当-1≤x ≤1时,f (x )=2<4,∴-1≤x ≤1;当x >1时,由2x <4,得1<x <2,∴M =(-2,2).(2)证明:a ,b ∈M 即-2<a <2,-2<b <2.∵4(a +b )2-(4+ab )2=4(a 2+2ab +b 2)-(16+8ab +a 2b 2)=(a 2-4)·(4-b 2)<0,∴4(a +b )2<(4+ab )2,∴2|a +b |<|4+ab |.[备课札记]本例中f(x)若变为“f(x)=|x+1|+|x-1|-a”且f(x)≥0对x∈R恒成立,求a的取值范围.解:由f (x )≥0知a ≤|x +1|+|x -1|,又|x +1|+|x -1|≥|(x +1)-(x -1)|=2,∴a ≤2.故a 的取值范围为(2,+∞).[类题通法]证明绝对值不等式要紧有三种方式(1)利用绝对值的概念去掉绝对值符号,转化为一般不等式再证明;(2)利用三角不等式||a |-|b ||≤|a ±b |≤|a |+|b |进行证明;(3)转化为函数问题,数形结合进行证明.[针对训练]设函数f (x )=|x -1|+|x -2|.(1)求证:f (x )≥1;(2)假设f (x )=a 2+2a 2+1成立,求x 的取值范围.解:(1)证明:f (x )=|x -1|+|x -2|≥|(x -1)-(x -2)|=1.(2)∵a 2+2a 2+1=a 2+1+1a 2+1=a 2+1+1a 2+1≥2,∴要使f (x )=a 2+2a 2+1成立,需且只需|x -1|+|x -2|≥2,即⎩⎪⎨⎪⎧ x <1,1-x +2-x ≥2或⎩⎪⎨⎪⎧ 1≤x <2,x -1+2-x ≥2或⎩⎪⎨⎪⎧x ≥2,x -1+x -2≥2, 解得x ≤12或x ≥52, 故x 的取值范围是⎝ ⎛⎦⎥⎤-∞,12∪⎣⎢⎡⎭⎪⎫52,+∞. 考点三 绝对值不等式的综合应用[典例](1)当a =-2时,求不等式f (x )<g (x )的解集;(2)设a >-1,且当x ∈⎣⎢⎡⎭⎪⎫-a 2,12时,f (x )≤g (x ),求a 的取值范围. [解] (1)当a =-2时,不等式f (x )<g (x )化为|2x -1|+|2x -2|-x-3<0.设函数y =|2x -1|+|2x -2|-x -3,那么y =⎩⎪⎨⎪⎧ -5x ,x <12,-x -2,12≤x ≤1,3x -6,x >1.其图像如下图.从图像可知,当且仅当x ∈(0,2)时,y <0.因此原不等式的解集是{x |0<x <2}.(2)当x ∈⎣⎢⎡⎭⎪⎫-a 2,12时,f (x )=1+a . 不等式f (x )≤g (x )化为1+a ≤x +3.因此x ≥a -2对x ∈⎣⎢⎡⎭⎪⎫-a 2,12都成立. 故-a 2≥a -2,即a ≤43. 从而a 的取值范围是⎝⎛⎦⎥⎤-1,43. [备课札记][类题通法]1.研究含有绝对值的函数问题时,依照绝对值的概念,分类讨论去掉绝对值符号,转化为分段函数,然后数形结合解决是经常使用的思维方式.2.关于求y =|x -a |+|x -b |或y =|x +a |-|x -b |型的最值问题利用绝对值三角不等式更方便.形如y =|x -a |+|x -b |的函数只有最小值,形如y =|x -a |-|x -b |的函数既有最大值又有最小值.[针对训练](2021·镇江模拟)已知f (x )=|x +a |+|x -2|.(1)当a =-1时,解关于x 的不等式f (x )>5;(2)已知关于x 的不等式f (x )+a <2 014(a 是常数)的解集是非空集合,求实数a 的取值范围.解:(1)构造函数g (x )=|x -1|+|x -2|-5,则g (x )=⎩⎪⎨⎪⎧-2x -2x ≤1,-41<x <2,2x -8x ≥2.令g (x )>0,那么x <-1或x >4,∴原不等式的解集为(-∞,-1)∪(4,+∞).(2)∵f (x )+a =|x +a |+|x -2|+a ≥|a +2|+a ,又关于x 的不等式f (x )+a <2 014的解集是非空集合,∴|a +2|+a <2 014,解得a <1 006.对应学生用书P189[课堂练通考点]1.(2021·江西高考)在实数范围内,不等式||x -2|-1|≤1的解集为________. 解析:依题意得-1≤|x -2|-1≤1,即|x -2|≤2,解得0≤x ≤4.答案:[0,4]2.(2021·重庆高考)假设关于实数x 的不等式|x -5|+|x +3|<a 无解,那么实数a 的取值范围是________.解析:|x -5|+|x +3|≥|(x -5)-(x +3)|=8,故a ≤8.答案:(-∞,8]3.(2021·南昌模拟)假设对任意的a ∈R ,不等式|x |+|x -1|≥|1+a |-|1-a |恒成立,那么实数x 的取值范围是________.解析:由|1+a |-|1-a |≤2得|x |+|x -1|≥2,当x <0时,-x +1-x ≥2,x ≤-12;当0≤x ≤1时,x +1-x ≥2,无解;当x >1时,x +x -1≥2,x ≥32.综上,x ≤-12或x ≥32. 答案:(-∞,-12]∪[32,+∞) 4.(2021·西安检测)已知函数f (x )=|x -2|,g (x )=-|x +3|+m .假设函数f (x )的图像恒在函数g (x )图像的上方,那么m 的取值范围为________.解析:函数f (x )的图像恒在函数g (x )图像的上方,即为|x -2|>-|x +3|+m 对任意实数x 恒成立,即|x -2|+|x +3|>m 恒成立.因为对任意实数x 恒有|x -2|+|x +3|≥|(x -2)-(x+3)|=5,因此m<5,即m的取值范围是(-∞,5).答案:(-∞,5)5.(2021·长春模拟)已知实数t ,假设存在t ∈[12,3]使得不等式|t -1|-|2t -5|≥|x -1|+|x -2|成立,求实数x 的取值范围.解:∵t ∈[12,3],∴|t -1|-|2t -5|=⎩⎪⎨⎪⎧ -t +4,t ≥52,3t -6,1<t <52,t -4,t ≤1,可得其最大值为32. ∴只需解不等式|x -1|+|x -2|≤32即可,当x ≥2时,可解得2≤x ≤94,当1<x <2时不等式恒成立,当x ≤1时可解得34≤x ≤1,综上可得x 的取值范围为[34,94]. [课下提升考能]1.(2021·福建高考)设不等式|x -2|<a (a ∈N *)的解集为A ,且32∈A ,12∉A . (1)求a 的值;(2)求函数f (x )=|x +a |+|x -2|的最小值. 解:(1)因为32∈A ,且12∉A ,因此⎪⎪⎪⎪⎪⎪32-2<a , 且⎪⎪⎪⎪⎪⎪12-2≥a , 解得12<a ≤32.又因为a ∈N *,因此a =1. (2)因为|x +1|+|x -2|≥|(x +1)-(x -2)|=3,当且仅当(x +1)(x -2)≤0,即-1≤x ≤2时取到等号.因此f (x )的最小值为3.2.设函数f (x )=|x -a |+2x ,其中a >0.(1)当a =2时,求不等式f (x )≥2x +1的解集;(2)假设x ∈(-2,+∞)时,恒有f (x )>0,求a 的取值范围.解:(1)a =2时,|x -2|+2x ≥2x +1,∴|x -2|≥1,∴x ≥3或x ≤1.∴不等式的解集为(-∞,1]∪[3,+∞).(2)依题意,f (x )=⎩⎪⎨⎪⎧3x -a ,x ≥a ,x +a ,x <a ,∵a >0,∴当x >-2时,f (x )≥x +a >-2+a ,要使f (x )>0,只需-2+a ≥0即可,∴a ≥2.故a 的取值范围为[2,+∞).3.已知函数f (x )=|x -a |-2|x -1|(a ∈R ).(1)当a =3时,求函数f (x )的最大值;(2)解关于x 的不等式f (x )≥0.解:(1)当a =3时,f (x )=|x -3|-2|x -1|=⎩⎪⎨⎪⎧ -x -1,x ≥3,-3x +5,1<x <3,x +1,x ≤1.当x ≤1时,f (x )=x +1,因此f (x )在(-∞,1]上单调递增;当1<x <3时,f (x )=-3x +5,因此f (x )在(1,3)上单调递减;当x ≥3时,f (x )=-x -1,因此f (x )在[3,+∞)上单调递减.因此当x =1时,函数f (x )取得最大值2.(2)由f (x )≥0得|x -a |≥2|x -1|,两边平方得,(x -a )2≥4(x -1)2,即3x 2+2(a -4)x +4-a 2≤0,得[x -(2-a )][3x -(2+a )]≤0,故①当a >1时,不等式的解集为2-a ,2+a 3; ②当a =1时,不等式的解集为{x |x =1};③当a <1时,不等式的解集为[2+a 3,2-a ]. 4.已知函数f (x )=|x -1|.(1)解关于x 的不等式f (x )+x 2-1>0;(2)假设g (x )=-|x +3|+m ,f (x )<g (x )的解集非空,求实数m 的取值范围. 解:(1)由题意原不等式可化为:|x -1|>1-x 2,即x-1>1-x2或x-1<x2-1,由x-1>1-x2得x>1或x<-2;由x-1<x2-1得x>1或x<0.综上,原不等式的解为x>1或x<0.(2)原不等式等价于|x -1|+|x +3|<m 的解集非空.令h (x )=|x -1|+|x +3|,即h (x )min <m ,又|x -1|+|x +3|≥|x -1-x -3|=4,因此h (x )min =4,因此m >4.5.设函数f (x )=|x +1|+|x +2|-a .(1)当a =5时,求函数f (x )的概念域;(2)假设函数f (x )的概念域为R ,试求a 的取值范围.解:(1)当a =5时,f (x )=|x +1|+|x +2|-5,由|x +1|+|x +2|-5≥0 得⎩⎪⎨⎪⎧ x ≥-1,2x -2≥0,或⎩⎪⎨⎪⎧ -2≤x <-1,-4≥0,或⎩⎪⎨⎪⎧x <-2,-8-2x ≥0, 解得x ≥1或x ≤-4.即函数f (x )的概念域为{x |x ≥1或x ≤-4}.(2)由题可知|x +1|+|x +2|-a ≥0恒成立,即a ≤|x +1|+|x +2|恒成立,而|x +1|+|x +2|≥|(x +1)-(x +2)|=1,因此a ≤1,即a 的取值范围为(-∞,1].6.已知函数f (x )=|x -2|+2|x -a |(a ∈R ).(1)当a =1时,解不等式f (x )>3;(2)不等式f (x )≥1在区间(-∞,+∞)上恒成立,求实数a 的取值范围.解:(1)当a =1时,原不等式可化为 ①⎩⎪⎨⎪⎧x ≥2,x -2+2x -2>3,解得x >73;②⎩⎪⎨⎪⎧1<x <2,2-x +2x -2>3,现在无解; ③⎩⎪⎨⎪⎧ x ≤1,2-x +2-2x >3,解得x <13, ∴不等式的解集为(-∞,13)∪(73,+∞). (2)当a >2时,f (x )=⎩⎪⎨⎪⎧-3x +2+2a ,x ≤2,-x +2a -2,2<x <a ,3x -2-2a ,x ≥a ;当a =2时,f (x )=⎩⎪⎨⎪⎧-3x +6,x ≤2,3x -6,x >2; 当a <2时,f (x )=⎩⎪⎨⎪⎧ -3x +2+2a ,x ≤a ,x -2a +2,a <x <2,3x -2-2a ,x ≥2.∴f (x )的最小值为f (2)或f (a ), 则⎩⎪⎨⎪⎧ f a ≥1,f 2≥1,解得a ≤1或a ≥3. 故实数a 的取值范围为(-∞,1]∪[3,+∞).7.(2021·郑州模拟)已知函数f (x )=|x -a |.(1)假设不等式f (x )≤3的解集为{x |-1≤x ≤5},求实数a 的值;(2)在(1)的条件下,假设f (x )+f (x +5)≥m 对一切实数x 恒成立,求实数m 的取值范围. 解:(1)由f (x )≤3得,|x -a |≤3,解得a -3≤x ≤a +3.又已知不等式f (x )≤3的解集为{x |-1≤x ≤5}, 因此⎩⎪⎨⎪⎧a -3=-1,a +3=5,解得a =2. (2)当a =2时,f (x )=|x -2|,设g (x )=f (x )+f (x +5), 于是g (x )=|x -2|+|x +3|=⎩⎪⎨⎪⎧ -2x -1,x <-3,5,-3≤x ≤2,2x +1,x >2,因此当x <-3时,g (x )>5;当-3≤x ≤2时,g (x )=5;当x >2时,g (x )>5. 综上可得,g (x )的最小值为5.从而假设f(x)+f(x+5)≥m,即g(x)≥m对一切实数x恒成立,那么m的取值范围为(-∞,5].8.设二次函数f(x)=ax2+bx+c(a,b,c∈R)知足以下条件:①当x∈R时,f(x)的最小值为0,且f(x-1)=f(-x-1)恒成立;②当x∈(0,5)时,x≤f(x)≤2|x-1|+1恒成立.(1)求f(1)的值;(2)求f(x)的解析式;(3)求最大的实数m(m>1),使得存在实数t,当x∈[1,m]时,f(x+t)≤x恒成立.解:(1)在②中令x=1,有1≤f(x)≤1,故f(1)=1.(2)由①知二次函数的图像关于直线x=-1对称,且开口向上,故设此二次函数为f(x)=a(x+1)2(a>0).因为f (1)=1,因此a =14,因此f (x )=14(x +1)2. (3)f (x )=14(x +1)2的图像开口向上, 而y =f (x +t )的图像是由y =f (x )的图像向左或向右平移|t |个单位取得的,要在区间[1,m ]上使得y =f (x +t )的图像在y =x 的图像下方,且m 最大,那么1和m 应当是方程14(x +t +1)2=x 的两个根.令x =1代入方程,得t =0或-4.当t =0时,方程的解为x 1=x 2=1(这与m >1矛盾,舍去);当t =-4时,方程的解为x 1=1,x 2=9,因此m =9.又当t =-4时,对任意x ∈[1,9],y =f (x -4)-x =14(x -3)2-x =14(x 2-10x +9)=14(x -5)2-4≤0,即f (x -4)≤x 恒成立.因此最大的实数m 为9.第二节不等式的证明及柯西不等式对应学生用书P189 1.不等式证明的方式(1)比较法:①求差比较法:明白a >b ⇔a -b >0,a <b ⇔a -b <0,因此要证明a >b 只要证明a -b >0即可,这种方式称为求差比较法.②求商比较法:由a >b >0⇔a b >1且a >0,b >0,因此当a >0,b >0时,要证明a >b ,只要证明ab>1即可,这种方式称为求商比较法.(2)综合法:利用某些已经证明过的不等式和不等式的性质,推导出所要证明的不等式,这种方式叫综合法.即“由因导果”的方式. (3)分析法: 证明不等式时,有时能够从求证的不等式动身,分析使那个不等式成立的充分条件,把证明不等式转化为判定这些充分条件是不是具有的问题,若是能够确信这些充分条件都已经具有,那么就能够够判定原不等式成立,这种方式叫作分析法.即“执果索因”的方式.(4)反证法和放缩法:①先假设要证的命题不成立,以此为起点,结合已知条件,应用公理、概念、定理、性质等,进行正确的推理,取得和命题的条件(或已证明的定理、性质、明显成立的事实等)矛盾的结论,以说明假设不正确,从而证明原命题成立,这种方式叫作反证法. ②证明不等式时,通过把不等式中的某些部份的值放大或缩小,简化不等式,从而达到证明的目的,这种方式叫作放缩法.2.几个经常使用大体不等式(1)柯西不等式:①柯西不等式的代数形式:设a 1,a 2,b 1,b 2均为实数,那么(a 21+a 22)(b 21+b 22)≥(a 1b 1+a 2b 2)2(当且仅当a 1b 2=a 2b 1时,等号成立).②柯西不等式的向量形式:设α,β为平面上的两个向量,那么|α||β|≥|α·β|.③二维形式的三角不等式:设x 1,y 1,x 2,y 2∈R ,那么 x 21+y 21+x 22+y 22≥ x 1-x 22+y 1-y 22.④柯西不等式的一样形式:设a 1,a 2,…,a n ,b 1,b 2,…,b n 为实数,那么(a 21+a 22+…+a 2n )(b 21+b 22+…+b 2n )≥(a 1b 1+a 2b 2+…+a n b n )2,当且仅当b i =0或存在一个数k ,使a i =kb i (i =1,2,…,n )时,等号成立.(2)平均值不等式:①定理:若是a ,b ,c 为正数,那么a +b +c 3≥3abc ,当且仅当a =b =c 时,等号成立.②咱们称a +b +c 3为正数a ,b ,c 的算术平均值,3abc 为正数a ,b ,c 的几何平均值,定理中的不等式为三个正数的算术—几何平均值不等式,简称为平均值不等式.③一样形式的算术—几何平均值不等式:若是a 1,a 2,…,a n 为n 个正数,那么a 1+a 2+…+a n n ≥n a 1a 2…a n ,当且仅当a 1=a 2=…=a n 时,等号成立. 1.利用柯西不等式或平均值不等式时易轻忽等号成立的条件. 2.易混淆分析法与综合法,分析法是执果索因,综合法是由因导果.[试一试]1.已知x 2+y 2=10,那么3x +4y 的最大值为______.解析:∵(32+42)(x 2+y 2)≥(3x +4y )2,当且仅当3y =4x 时等号成立,∴25×10≥(3x +4y )2,∴(3x +4y )max =510.答案:510 2.已知a ,b ,c ∈R +,那么1a +1b +1c 与1ab +1bc +1ac的大小关系是________. 解析:21a +1b +1c =1a +1b +1b +1c +1c +1a ≥2ab +2bc +2ca. 因此1a +1b +1c ≥1ab +1bc +1ac. 答案:1a +1b +1c ≥1ab +1bc +1ac放缩法证明不等式的技术(1)放缩法原理简单,但放缩技术性强,而且应用普遍,经常使用的放缩法有增项、减项,利用分式的性质、函数的性质、不等式的性质等.其理论依据是不等式的传递性,利用此方式时要注意把握放大或缩小的度.(2)常见的放缩技术有:①1k k -1>1k 2>1k k +1(k ≥2,k ∈N *);②2k-1+k>22k>2k+k+1(k≥2,且k∈N*).[练一练]设M=1210+1210+1+1210+2+…+1211-1,那么M与1的大小关系是__________.解析:∵210+1>210,210+2>210,…,211-1>210,∴M=1210+1210+1+1210+2+…+1211-1<1210+1210+…+1210=1.210个答案:M<1对应学生用书P190考点一比较法证明不等式1.设t=a2解析:∵s-t=a+b2+1-a-2b=b2-2b+1=(b-1)2≥0,∴s≥t.答案:s≥t2.已知c>b>a,求证:a2b+b2c+c2a<ab2+bc2+ca2.证明:ab2+bc2+ca2-(a2b+b2c+c2a)=a(b2-c2)+b(c2-a2)+c(a2-b2)=a(b2-c2)+b(c2-b2+b2-a2)+c(a2-b2)=a(b2-c2)+b(c2-b2)+b(b2-a2)+c(a2-b2)=(c2-b2)(b-a)+(b2-a2)(b-c)=(b-a)·(c-b)[b+c-(b+a)]=(b-a)(c-b)(c-a).∵c>b>a,∴b-a>0,c-b>0,c-a>0.∴ab2+bc2+ca2>a2b+b2c+c2a.即a2b+b2c+c2a<ab2+bc2+ca2.3.求证:当a ,b ∈(0,+∞)时,a a b b ≥(ab )a +b 2.证明:a a b b ab a +b 2=a a -b 2b b -a 2=⎝ ⎛⎭⎪⎫a b a -b 2, 当a =b 时,⎝ ⎛⎭⎪⎫a b a -b 2=1. 当a >b >0时,a b >1,a -b2>0, 则⎝ ⎛⎭⎪⎫a b a -b 2>1. 当b >a >0时,0<a b <1,a -b2<0,则⎝ ⎛⎭⎪⎫a b a -b 2>1. 综上可知,当a ,b ∈(0,+∞)时,a a b b ≥(ab )a +b 2成立.[备课札记][类题通法]关于多项式的大小比较问题通常能够用比较法,而比较法中最经常使用的是作差法和作商法.作差法中作差后的关键是对差的符号进行判定,通常运用配方、因式分解等方式,作商法要注意两式的符号.考点二 综合法与分析法[典例] (1)已知a ,b ,c 均为正数,且a +b +c =1,求证:1a +1b +1c≥9. (2)已知a >b >c ,且a +b +c =0,求证:b 2-ac <3a .[证明]:(1)法一:1a +1b +1c =(a +b +c )1a +1b +1c ≥3·3abc ·3·31abc =9(当且仅当a =b=c =13时等号成立).法二:1a +1b +1c =a +b +c a +a +b +c b +a +b +c c =3+⎝ ⎛⎭⎪⎫b a +a b +⎝ ⎛⎭⎪⎫c a +a c +⎝ ⎛⎭⎪⎫c b +b c ≥3+2+2+2=9(当且仅当a =b =c =13时等号成立.) (2)要证b 2-ac <3a ,只需证b 2-ac <3a 2.∵a +b +c =0,只需证b 2+a (a +b )<3a 2,只需证2a 2-ab -b 2>0,只需证(a -b )(2a +b )>0,只需证(a -b )(a -c )>0.∵a >b >c ,∴a -b >0,a -c >0.∴(a -b )(a -c )>0显然成立,故原不等式成立. 在本例(1)的条件下 求证:(a +1a )2+(b +1b)2+(c +1c )2≥1003. 证明:⎝ ⎛⎭⎪⎫a +1a 2+⎝ ⎛⎭⎪⎫b +1b 2+⎝ ⎛⎭⎪⎫c +1c 2 =13(12+12+12)·⎝ ⎛⎭⎪⎫a +1a 2+⎝ ⎛⎭⎪⎫b +1b 2+⎝ ⎛⎭⎪⎫c +1c 2 ≥13⎣⎢⎡⎦⎥⎤1×⎝ ⎛⎭⎪⎫a +1a +1×⎝ ⎛⎭⎪⎫b +1b +1×⎝ ⎛⎭⎪⎫c +1c 2 =13⎣⎢⎡⎦⎥⎤1+a +b +c ⎝ ⎛⎭⎪⎫1a +1b +1c 2 =13⎣⎢⎡⎦⎥⎤1+⎝ ⎛⎭⎪⎫3+b a +a b +c b +b c +c a +a c 2 ≥13⎣⎢⎢⎡⎦⎥⎥⎤1+⎝ ⎛⎭⎪⎪⎫3+2 b a ·a b +2 c b ·bc +2 a c ·c a2 =13×(1+9)2=1003. 当且仅当a =b =c =13时,等号成立. [备课札记][类题通法]分析法与综合法常常结合利用,实际是以分析法为主,借助综合法,使证明的问题明朗化.[针对训练]已知a>0,b>0,2c>a+b,求证:c-c2-ab<a<c+c2-ab.证明:法一(分析法)要证c-c2-ab<a<c+c2-ab,即证-c2-ab<a-c<c2-ab,即证|a-c|<c2-ab,即证(a-c)2<c2-ab,即证a2-2ac<-ab.因为a>0,因此只要证a-2c<-b,即证a+b<2c.由已知条件知,上式显然成立,因此原不等式成立.法二(综合法)因为a+b<2c,因此a-2c<-b.又因为a>0,因此a2-2ac<-ab,因此(a-c)2<c2-ab,因此|a-c|<c2-ab,因此-c2-ab<a-c<c2-ab,因此c-c2-ab<a<c+c2-ab.考点三放缩法证明不等式[典例] 123n x1+x2+x3+…+x n=1.求证:1x1-x31+1x2-x32+1x3-x33+…+1x n-x3n>4.[证明] ∵0<x i<1,∴1x i-x3i>1x i,其中i=1,2,3,…,n,1x1-x31+1x2-x32+1x3-x33+…+1x n-x3n>1x1+1x2+1x3+…+1x n≥nn1x1x2x3…x n.∴∵ n x 1x 2x 3…x n ≤x 1+x 2+x 3+…+x n n =1n , ∴ n1x 1x 2x 3…x n ≥n , ∴1x 1-x 31+1x 2-x 32+1x 3-x 33+…+1x n -x 3n >n 2≥22=4, ∴1x 1-x 31+1x 2-x 32+1x 3-x 33+…+1x n -x 3n >4.[备课札记][类题通法]放缩法证明不等式时,常见的放缩依据和技术是不等式的传递性.缩小分母、扩大分子,分式值增大;缩小分子、扩大分母,分式值减小;每一次缩小其和变小,但需大于所求;每一次扩大其和变大,但需小于所求,即不能放缩不够或放缩过头.[针对训练]设n 是正整数,求证:12≤1n +1+1n +2+ (12)<1. 证明:由2n ≥n +k >n (k =1,2,…,n ),得12n ≤1n +k <1n. 当k =1时,12n ≤1n +1<1n; 当k =2时,12n ≤1n +2<1n; …当k =n 时,12n ≤1n +n <1n, ∴12=n 2n ≤1n +1+1n +2+…+12n <n n=1. 考点四 柯西不等式求最值[典例] (2021·南通模拟)假设正数a ,b ,c 知足a +b +c =1,那么13a +2+13b +2+13c +2的最小值为________.解析:由柯西不等式知:⎝ ⎛⎭⎪⎫13a +2+13b +2+13c +2[(3a +2)+(3b +2)+(3c +2)]≥⎝ ⎛⎭⎪⎪⎫13a +2×3a +2+13b +2×3b +2+13c +2×3c +22=32=9. ∴⎝ ⎛⎭⎪⎫13a +2+13b +2+13c +2[3(a +b +c )+6]≥9, 即⎝ ⎛⎭⎪⎫13a +2+13b +2+13c +2×9≥9. ∴13a +2+13b +2+13c +2≥1. 当且仅当3a +2=3b +2=3c +2,即a =b =c =13时,取到最小值1. 答案:1[备课札记][类题通法]利用柯西不等式求最值的一样结构为:(a 21+a 22+…+a 2n )⎝ ⎛⎭⎪⎫1a 21+1a 22+…+1a 2n ≥(1+1+…+1)2=n 2.在利用柯西不等式时,要注意右边为常数且应注意等号成立的条件.[针对训练]已知实数a ,b ,c ,d 知足a +b +c +d =3,a 2+2b 2+3c 2+6d 2=5,求证:1≤a ≤2. 证明:由柯西不等式得(2b 2+3c 2+6d 2)⎝ ⎛⎭⎪⎫12+13+16≥(b +c +d )2,即2b2+3c2+6d2≥(b+c+d)2,由已知可得2b2+3c2+6d2=5-a2,b+c+d=3-a,∴5-a2≥(3-a)2,即1≤a≤2.当且仅当2b12=3c13=6d16,即2b=3c=6d时等号成立.对应学生用书P192[课堂练通考点]1.(2021·陕西高考)已知a,b,m,n均为正数,且a+b=1,mn=2,那么(am+bn)(bm+an )的最小值为________.解析:(am +bn )(bm +an )=ab (m 2+n 2)+mn (a 2+b 2)≥2abmn +mn (a 2+b 2)=4ab +2(a 2+b 2)=2(2ab +a 2+b 2)=2(a +b )2=2(当且仅当m =n =2时取等号). 答案:2 2.已知x 2a 2+y 2b 2=1(a >b >0),那么利用柯西不等式判定a 2+b 2与(x +y )2的大小关系为________.解析:∵x 2a 2+y 2b 2=1,∴a 2+b 2=(a 2+b 2)⎝ ⎛⎭⎪⎫x 2a 2+y 2b 2≥⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫a ·x a +⎝ ⎛⎭⎪⎫b ·y b 2 =(x +y )2.答案:a 2+b 2≥(x +y )23.设x ,y ,z 均为实数,那么2x +y -z x 2+2y 2+z 2的最大值是________. 解析:由柯西不等式知(x 2+2y 2+z 2)[ 22+⎝ ⎛⎭⎪⎪⎫122+(-1)2 ]≥(2x +y -z )2⇒2x +y -z x 2+2y 2+z 2≤222. 当且仅当x2=2y =-z >0时等号成立. 答案:222 4.(2021·全国卷Ⅱ)设a ,b ,c 均为正数,且a +b +c =1,证明:(1)ab +bc +ac ≤13; (2)a 2b +b 2c +c 2a ≥1.证明:(1)由a2+b2≥2ab,b2+c2≥2bc,c2+a2≥2ca 得a2+b2+c2≥ab+bc+ca.由题设得(a+b+c)2=1,即a2+b2+c2+2ab+2bc+2ca=1,因此3(ab +bc +ca )≤1,即ab +bc +ca ≤13. (2)因为a 2b +b ≥2a ,b 2c +c ≥2b ,c 2a+a ≥2c , 故a 2b +b 2c +c 2a +(a +b +c )≥2(a +b +c ),即a 2b +b 2c +c 2a ≥a +b +c .因此a 2b +b 2c +c 2a ≥1.[课下提升考能]1.已知x ,y ,z ∈R ,假设x 4+y 4+z 4=1.求证:x 2+y 2+z 2≤ 3.证明:x ,y ,z ∈R ,且x 4+y 4+z 4=1为定值,利用柯西不等式取得 (x 2+y 2+z 2)2≤(12+12+12)[(x 2)2+(y 2)2+(z 2)2]. 从而(x 2+y 2+z 2)2≤3⇒x 2+y 2+z 2≤3. 当且仅当x 21=y 21=z 21时取“=”号, 又x 4+y 4+z 4=1,因此x 2=y 2=z 2=33时取“=”号. 2.(2021·大连模拟)已知a >0,b >0,c >0,a +b >c . 求证:a 1+a +b 1+b >c 1+c. 证明:∵a >0,b >0,∴a 1+a >a 1+a +b ,b 1+b >b 1+a +b. ∴a 1+a +b 1+b >a +b1+a +b .而函数f (x )=x 1+x =1-11+x在(0,+∞)上递增,且a +b >c ,∴f (a +b )>f (c ),则a +b 1+a +b >c1+c ,因此a 1+a +b 1+b >c 1+c, 故原不等式成立.3.已知a ≥b >0,求证:2a 3-b 3≥2ab 2-a 2b . 证明:2a 3-b 3-(2ab 2-a 2b )=2a (a 2-b 2)+b (a 2-b 2)=(a 2-b 2)(2a +b )=(a -b )(a +b )(2a +b ).因为a ≥b >0,因此a -b ≥0,a +b >0,2a +b >0, 从而(a -b )(a +b )(2a +b )≥0,即2a 3-b 3≥2ab 2-a 2b .4.已知a ,b ,c ∈R +.求证:b 2a +c 2b +a 2c ≥c ba +a cb +b ac .证明:∵a ,b ,c ∈R +,∴b 2a +c 2b ≥2 b 2a ·c 2b =2c ba , 同理,c 2b +a 2c ≥2a c b ,a 2c +b 2a ≥2b ac, 三式相加可得b 2a +c 2b +a 2c ≥c ba +a cb +b ac .5.已知f (x )=1+x 2,a ≠b ,求证|f (a )-f (b )|<|a -b |.证明:∵|f (a )-f (b )|=|1+a 2-1+b 2|= |a 2-b 2|1+a 2+1+b 2=|a -b ||a +b |1+a 2+1+b 2. 又|a +b |≤|a |+|b |=a 2+b 2<1+a 2+1+b 2. ∴|a +b |1+a 2+1+b 2<1.∵a ≠b ,∴|a -b |>0,∴|f (a )-f (b )|<|a -b |.6.(2021·金华模拟)已知x,y,z是正实数.求证:x2y+z+y2x+z+z2x+y≥x+y+z2.证明:∵x ,y ,z 是正实数,令a =⎝ ⎛⎭⎪⎪⎫x y +z ,y x +z ,z x +y , b =(y +z ,x +z ,x +y ),∵|a·b|2≤|a|2|b|2,∴⎝ ⎛⎭⎪⎪⎫x y +z ·y +z +y x +z ·x +z +z x +y ·x +y 2≤⎝ ⎛⎭⎪⎫x 2y +z +y 2x +z +z 2x +y [(y +z )+(x +z )+(x +y )],当且仅当x =y =z 时,等号成立.即(x +y +z )2≤2⎝ ⎛⎭⎪⎫x 2z +y +y 2x +z +z 2x +y ·(x +y +z ), ∴x 2y +z +y 2x +z +z 2x +y ≥x +y +z2. 7.设a ,b ,c 均为正实数.求证:12a +12b +12c ≥1b +c +1c +a +1a +b . 证明:∵a ,b ,c 均为正实数,∴12⎝ ⎛⎭⎪⎫12a +12b ≥12ab ≥1a +b,当且仅当a =b 时等号成立; 12⎝ ⎛⎭⎪⎫12b +12c ≥12bc ≥1b +c ,当且仅当b =c 时等号成立; 12⎝ ⎛⎭⎪⎫12c +12a ≥12ca ≥1c +a,当且仅当c =a 时等号成立; 三个不等式相加即得12a +12b +12c ≥1b +c +1c +a +1a +b , 当且仅当a =b =c 时等号成立.8.(1)设x 是正实数,求证:(x +1)(x 2+1)(x 3+1)≥8x 3;(2)假设x ∈R ,不等式(x +1)(x 2+1)(x 3+1)≥8x 3是不是仍然成立?若是成立,请给出证明,若是不成立,请举出一个使它不成立的x 值.解:(1)证明:x是正实数,由大体不等式知,x+1≥2x,1+x2≥2x,x3+1≥2x3,故(x+1)(x2+1)(x3+1)≥2x·2x·2x3=8x3(当且仅当x=1时等号成立).(2)假设x∈R,不等式(x+1)(x2+1)(x3+1)≥8x3仍然成立.由(1)知,当x >0时,不等式成立; 当x ≤0时,8x 3≤0.而(x +1)(x 2+1)(x 3+1)=(x +1)2(x 2+1)(x 2-x +1) =(x +1)2(x 2+1)⎝ ⎛⎭⎪⎫x -122+34≥0, 现在不等式仍然成立.。
高考数学命题热点名师解密专题:不等式选讲(理)

专题37 不等式选讲一.【学习目标】1.理解绝对值的几何意义,并能利用含绝对值不等式的几何意义证明以下不等式: ①|a +b |≤|a |+|b |; ②|a -b |≤|a -c |+|c -b |.2.会利用绝对值的几何意义求解以下类型的不等式: |ax +b |≤c ;|ax +b |≥c ;|x -a |+|x -b |≥c .3.会用绝对值不等式、基本不等式证明一些简单问题;能够利用基本不等式求一些特定函数的最(极)值. 4.了解证明不等式的基本方法:比较法、综合法、分析法、反证法、放缩法等. 二.【知识要点】1.绝对值的概念和几何意义代数:|a |=⎩⎪⎨⎪⎧a (a ≥0),-a (a <0).几何意义:|a |表示数轴上坐标为±a 的点A 到原点的距离.2.绝对值不等式性质 |a |-|b |≤|a ±b |≤|a |+|b |.(1)|a +b |≤|a |+|b |,当且仅当ab ≥0时取等号; (2)|a -b |≤|a |+|b |,当且仅当ab ≤0时取等号. 3.绝对值不等式的解法原则是转化为不含绝对值的不等式求解.基本型:a >0,|x |<a ⇔-a<x<a ;|x |>a ⇔x<-a 或x>a .(1)c >0,|ax +b |≤c ⇔,|ax +b |≥c ⇔.(2)c >0,|x -a |+|x -b |≥c ,|x -a |+|x -b |≤c .三种解法:图解法(数形结合)、零点分区法(定义)、绝对值的几何意义(数轴). 4.比较法证明不等式 (1)作差比较法:知道a >b ⇔a -b >0,a <b ⇔a -b <0,因此要证明a >b ,只要证明a-b>0即可,这种方法称为作差比较法. (2)作商比较法:由a >b >0⇔ab >1且a >0,b >0,因此当a >0,b >0时要证明a >b ,只要证明1a b即可,这种方法称为作商比较法.5.综合法证明不等式从已知条件出发,利用定义、公理、定理、性质等,经过一系列的推理、论证而得出命题成立,即“由因导果”的方法.这种证明不等式的方法称为综合法或顺推法.6.分析法证明不等式证明命题时,我们还常常从要证的结论出发,逐步寻求使它 成立的充分条件,直至所需条件为已知条件或一个明显成立的事实(定义、公理、性质、或已证明的定理 等),从而得出要证的命题成立,这种证明方法叫做分析法,这是一种执果索因的思考和证明方法.7.反证法证明不等式先假设要证的命题不成立,以此为出发点,结合已知条件,应用公理、定义、定理、性质等,进行正确的推理,得到和命题的条件(或已证明的定理、性质、明显成立的事实等) 矛盾的结论,以说明假设不正确,从而证明原命题成立,我们把它称为反证法. 8.放缩法证明不等式证明不等式时,通过把不等式中的某些部分的值放大或缩小,简化不等式,从而达到证明的目的,我们把这种方法称为放缩法. 三.方法总结1.含绝对值不等式的求解策略(1)解含有绝对值的不等式的指导思想是设法去掉绝对值符号.常用的方法是:①由定义分段讨论(简称零点分区间法);②利用绝对值不等式的性质(题型法);③平方法;④数形结合法等.(2)解含参数的不等式,如果转化不等式的形式或求不等式的解集时与参数的取值范围有关,就必须分类讨论.注意:①要考虑参数的总取值范围.②用同一标准对参数进行划分,做到不重不漏.(3)含绝对值不等式的证明,要善于应用分析转化法.(4)灵活运用绝对值不等式的两个重要性质定理|a|-|b|≤|a±b|≤|a|+|b|,特别注意等号成立的条件.2.作差比较法是证明不等式最基本、最重要的方法,其关键是变形,通常通过因式分解,利用各因式的符号进行判断,或进行配方,利用非负数的性质进行判断.3.综合法证明不等式时,主要利用基本不等式、函数的单调性以及不等式的性质,在严密的推理下推导出结论,综合法往往是分析法的逆过程,所以在实际证明时,用分析法分析,用综合法表述证明推理过程.4.某些不等式的条件与结论,或不等式的左右两边联系不明显,用作差法又难以对差进行变形,难以运用综合法直接证明,这时常用分析法,以便发现联系.分析的过程中,综合条件、定理等因素进行探索,把分析与综合结合起来,形成分析综合法.5.有些不等式,从正面证如果不易说清楚,可以考虑反证法,凡是含有“至少”“唯一”或者含有其他否定词的命题,适宜用反证法.6.放缩法是一种常用的证题技巧,放缩必须有目标,而目标可以从求证的结论中和中间结果中寻找.常用的放缩技巧有添舍放缩,拆项对比放缩,利用函数的单调性和重要不等式放缩等.四.典例分析(一)解绝对值不等式例1.设函数.(1)若,解不等式;(2)求证:.【答案】(1);(2)详见解析.【解析】(1)因为,所以,即或故不等式的解集为(2)由已知得:所以在上递减,在递增即所以练习1已知函数,.(Ⅰ)若恒成立,求的最小值;(Ⅱ)若,求不等式的解集.【答案】(1)2(2)练习2.已知函数.(I)当时,求不等式的解集;(II)求证:.【答案】(I);(II)详见解析.【解析】(Ⅰ)当时,,由,得解得的解集为;(Ⅱ),当且仅当时等号成立.练习3.已知,其中。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、填空题:
1.(2010年高考陕西卷理科15)(不等式选做题)不等式323≥--+x x 的解集为
____________.
【答案】{
}1≥x x
【解析】(方法一)当3-<x 时,∵原不等式即为()()35323≥-⇒≥-++-x x ,这显然不可能,∴3-<x 不适合.
当23≤≤-x 时,∵原不等式即为()()1323≥⇒≥-++x x x ,又23≤≤-x ,∴21≤≤x 适合.
当2>x 时,∵原不等式即为()()35323≥⇒≥--+x x ,这显然恒成立,∴2>x 适合. 故综上知,不等式的解集为{}221>≤≤x x x 或,即{}
1≥x x .
(方法二)设函数()23--+=x x x f ,则∵()⎪⎩
⎪
⎨⎧>≤≤-+-<-=,2,5,23,12,
3,5x x x x x f ∴作函数()x f
的图象,如图所示,并作直线3=y 与之交于点A . 又令312=+x ,则1=x ,即点A 的横坐标为1. 故结合图形知,不等式的解集为{}
1≥x x .
二、解答题:
1.(2010年高考福建卷理科21)(本小题满分7分)选修4-5:不等式选讲 已知函数()||f x x a =-。
(Ⅰ)若不等式()3f x ≤的解集为{}|15x x -≤≤,求实数a 的值;
(Ⅱ)在(Ⅰ)的条件下,若()(5)f x f x m ++≥对一切实数x 恒成立,求实数m 的取值范围。
(Ⅱ)当2a =时,()|2|f x x =-,设()=()(5)g x f x f x ++,于是
()=|x-2||3|g x x ++=21,<35,3221,>2x x x x x ---⎧⎪
-≤≤⎨⎪+⎩
,所以
当x<-3时,g(x)>5;当-3x 2≤≤时,g(x)>5;当x>2时,g(x)>5。
2.(2010年高考江苏卷试题21)选修4-5:不等式选讲 (本小题满分10分)
设a 、b 是非负实数,求证:33
22
()a b ab a b +≥
+。
3.
(2010年全国高考宁夏卷24)(本小题满分10分)选修4-5,不等式选讲 设函数()241f x x l =-+ (Ⅰ)画出函数()y f x =的图像
(Ⅱ)若不等式()f x ≤ax 的解集非空,求a 的取值范围。
(24) 解: (Ⅰ)由于
252()23x x f x x -+<⎧=⎨
-≥⎩,,x 2则函数
()y f x =的图像如图所示。
4.(2010年高考辽宁卷理科24)(本小题满分10分)选修4-5:不等式选讲 已知c b a ,,均为正数,证明:36)111(2
2
2
2
≥+++++c
b a
c b a ,并确定c b a ,,为何值时,等号成立。
【2009年高考试题】 7. (2009广东14)不等式
1|
2||
1|≥++x x 的实数解为 .
7.【答案】32
x -2x ≤-≠且 【解析】
112x x
+≥+23
02)2()1(0
22122-≤⇔⎩⎨⎧≠++≥+⇔⎩⎨
⎧≠++≥+⇔x x x x x x x 且2-≠x . 8.(2009福建选考21(
3))
解不等式∣2x-1∣<∣x ∣+1
9.(2009海南宁夏选作(24)) 如力,O 为数轴的原点,A ,B ,M 为数轴上三点,C 为线段OM 上的动点。
设x 表示C 与原点的距离, y 表示C
到A 距离的4倍与C 到B 距离的6倍的和。
(I )将y 表示为x 的函数;
(Ⅱ)要使y 的值不超过70,x 应该在什么范围内取值?
10.(2009辽宁选作24)
设函数.|||1|)(a x x x f -+-= (I )若3)(,1≥-=x f a 解不等式;
(II )如果a x f x 求,2)(,≥∈∀R 的取值范围。
(II )若|1|2)(,1-==x x f a ,不满足题设条件。
若21,,.1,()1,
1,()2(1),1,x a x a a f x a a x f x x a x -+-≤⎧⎪
<=-<<⎨⎪-+≥⎩的 1a -最小值;
若21,1,.1,()1,
1,()2(1),,x a x a f x a x a f x x a x a -+-≤⎧⎪
>=-<<⎨⎪-+≥⎩
的
:1a -最小值
所以)2(,≥∈∀x f x R 的充要条件是a a 从而,2|1|≥-的取值范围为)3()1,(∞+--∞ 。
【2008年高考试题】
1.(2008广东,14)(不等式选讲选做题)已知R ∈a ,若关于x 的方程0|||
4
1
|2
=+-++a a x x 有实根,则a 的取值范围是 。
3.(2008宁夏,24,10分)(选修4 – 5:不等式选讲)已知函数.|4||8|)(---=x x x f (1)在图中作出函数)(x f y =的图象; (2)解不等式.2|4||8|>---x x
3.【解析】(1)⎪⎩
⎪
⎨⎧>-≤<+-≤=.8,4
,84,122,4,
4)(x x x x x f
图象如下:
(2)不等式,2|4||8|>---x x 即,2)(>x f 由2122=+-x 得.5=x 由函数)(x f 图象可知,原不等式的解集为).5,(-∞
4.(2008江苏,21D ,10分)(选修4 – 5:不等式选讲)设c b a ,,为正实数,求证:
.321
11333≥+++abc c b a
6
.(2008·山东高考题)若不等式4|3|<-b x 的解集中的整数有且仅有1、2、3,则b 的取值范围为 。
11.(2008广东选作14)已知R a ∈,若关于x 的方程0|||4
1
|2
=+-++a a x x 有实根, 则a 的取值范围是 .
11.【答案】10,4⎡⎤
⎢⎥⎣⎦
【解析】:
111
14()0444
a a a a ∆=--+≥⇒-+≤,利用绝对值的几何意义,知104
a ≤≤。
【2007年高考试题】
2.(2007广东,14)(不等式选讲选做题)设函数)2(,3|12|)(-++-=f x x x f 则= ;若5)(≤x f ,则x 的取值范围是 。
5.(2007海南、宁夏,22C ,10分)(选修4 –5:不等式选讲)设函数.|4||12|)(--+=x x x f (1)解不等式2)(>x f ; (2)求函数)(x f y =的最小值。
- 11 -。
