C电子跃迁选择精讲
跃迁类型和选择定则
同样,氦的21S0到基态11S0也不能进行电和磁的单光子跃迁, 它们之间主要的是双光子跃迁过程。 在激光的强相干场中,双光子过程才变得重要。 现在经常利用功率较大的可调频率激光器来研究双光子和多 光子跃迁等极小概率过程。
2(1)
591.4
3888.6 7065.2 169082.185 169081.189 169081.111 10830
2(2,1,0)
2(1)
159850.318
1(0)
(cm–1)
图 2.1.1 HeI 的衰变图和能级图
磁偶极辐射和电四极辐射的选择定则
定则 1 2 3 4 电偶极跃迁E1
ΔJ = 0, ±1,
辐射跃迁矩阵元:
ˆ M ba = ψ b e−ik ⋅r ε ⋅∇ ψ a
kr的数量级为10-3,是一个小量。
e
− ik ⋅r
1 = 1 − (ik ⋅ r ) + (ik ⋅ r ) 2 − 2!
如果忽略一次以上项,即取 则有
E1 ba
e
− ik ⋅r
≈1
( Dba = −erba )
M
mωba ˆ = ε ⋅ Dba e
2
电偶极矩-er在空间反演下变号,宇称为奇,P = -1。由于 宇称守恒,初态和末态波函数的宇称必须改变。
e
− ik ⋅r
1 = 1 − (ik ⋅ r ) + (ik ⋅ r ) 2 − 2!
磁偶极和电四极辐射由展开式第二项贡献,要多乘一项 k·r。因而磁偶极和电四极辐射作用算符是偶宇称的,P = 1, 由于宇称守恒,初态和末态波函数的宇称应不变。 由此可以得到电多极辐射和磁多极辐射的宇称,以及原 子分子初态和末态宇称Pf和Pi与光子角动量有如下关系:
7跃迁和选择定则电偶极跃迁
F
=
−∇U
=
−
i
∂U ∂x
+
j ∂U ∂y
+ k ∂U ∂z
其直角坐标分量
Fx
= − ∂U ∂x
= µx ∂∂Bxx
+ µy
∂By ∂x
+ µz
∂Bz ∂x
Fy
= − ∂U ∂y
= µx ∂∂Byx
+ µy
∂By ∂y
+ µz
∂Bz ∂y
Fz
= − ∂U ∂z
= µx ∂∂Bzx
+ µy
f
= exp −
ω kBT
exp
−
ω kBT
= Bif I (ω) Afi + Bfi I (ω)
I (ω) = Afi
1
Bif
ω
exp
kBT
−
B fi Bif
§2.7 跃迁和选择定则—Einstein辐射唯象理论
Planck黑体辐射公式
I (ω)
=
ω3 π 2c3
exp
∂By ∂z
+ µz
∂Bz ∂z
如果磁场是均匀的,梯度为零,则磁矩所受力为零。
§3.1 轨道磁矩和Stern-Gerlach实验—磁矩与磁场相互作用
磁矩受到的力矩: τ= µ × B
B
力矩的作用将引起角动量的变化
τ= dL= µ × B
dt
在均匀磁场中磁矩虽然不受净平移力的作用,但仍要受 到一个力矩作用
原子分子的低激发态的能级寿命一般在10-8 ~ 10-9 s,相 应的能级宽度为Γ = 10-8 ~ 10-7 eV。
对于稳定的基态,τ=∞,相应的 Γ = 0。
7跃迁和选择定则—电偶极跃迁.pdf

/
Ef
原子分子的低激发态的能级寿命一般在10-8 ~ 10-9 s,相 应的能级宽度为Γ = 10-8 ~ 10-7 eV。
对于稳定的基态,τ=∞,相应的 Γ = 0。
§2.7 跃迁和选择定则—原子光谱
满足电偶极跃迁的选择定则
( ) 谱线位置 =ω Ei − Ef /
谱线强度 I ∝ Niλfi
I
0
谱线宽度:(1) 自然宽度;
(2) 多普勒展宽;
I0/2
(3) …..;
(4) 光谱仪的分辨本领。
0
Ei
( ) =ω Ei − Ef /
Ef
E
E1 E0 E2
多普勒展宽
第三章 电子自旋和原子能级的精细结构
角动量空间取向量子化
=L l(l +1) Lz = ml
对于给定量子数 l,
受激辐射系数 Bfi
自发辐射的跃迁概率 Afi
自发辐射系数 Afi
在温度 T下,达到平衡,设处于上能级状态的原子数 为 Ni ,处在下能级状态的原子数为 Nf
激发的原子数 ∝ Bif I (ω)N f
退激发的原子数 ∝ ( Afi + Bfi I (ω)) Ni
A. Einstein (1879-1955)
Ef
uf
自发辐射
dNi / Ni = − Afidt
= Ni (t) Ni0 exp(− Afit)
其中 Ni0 = Ni t=0
§2.7 跃迁和选择定则—能级的平均寿命
每个原子的退激发是独立进行的,激发态存在的时间的 长短是随机的。但退激发的速率是确定的,因而大量原子的 退激发服从统计规律。 我们可以计算激发态i的平均寿命。
跃迁类型和选择定则

. ..
5(1) 4(1) 3(1)
537.0 6675.2
. ..
5(2) 4(2) 3(2)
. ..
5(1) 4(1) 3(1)
. ..
5(2,1,0)
. ..
5(3,2,1) 4(3,2,1) 4(2,1,0) 3(3,2,1) 3(2,1,0)
5875.6
3(0)
538.9
2(0) 171129.148
这就是电偶极近似。与这一部分对应的跃迁称 为电偶极跃迁(用E1表示)。
e
− ik ⋅r
1 = 1 − (ik ⋅ r ) + (ik ⋅ r ) 2 − 2!
第二项包含两部分,分别含有来源于电荷运动的电流产生 的磁偶极矩和电荷分布产生的电四极矩,相应的辐射是磁偶极 辐射(M1)和电四极辐射(E2)。 第二项之后还有磁四极辐射(M2)和电八极辐射(E3) 等。 我们把除电偶极辐射之外的辐射称为禁戒辐射。 这里的禁戒指的是对电偶极辐射禁戒,它可以通过其它种 辐射跃迁,只是跃迁概率比电偶极辐射小很多。
2(1)
591.4
3888.6 7065.2 169082.185 169081.189 169081.111 10830
2(2,1,0)
2(1)
159850.318
1(0)
(cm–1)
图 2.1.1 HeI 的衰变图和能级图
磁偶极辐射和电四极辐射的选择定则
定则 1 2 3 4 电偶极跃迁E1
ΔJ = 0, ±1,
宇称: 在空间反演下,
r → −r
q q I n 'l ' m ';nlm = (−1)l +l '+1 I n 'l ' m ';nlm
跃迁类型和选择定则

将原子和电偶极辐射场作为一个整体系统处理,用k表示 辐射的波矢,ε表示偏振态,-er是电偶极矩。 如果系统处在有nk,ε个量子的初始态(用i标记)中,则单 位时间内系统跃迁到有nk,ε+1个量子的终态(用f标记)的跃迁 速率为
λif =
( Ei − E f
3πε 0 c
)
3
4 3
∫ψ
* f
(-er )ψ i dτ (nk,ε + 1)
M ˆ M ba1E2 = ψ b (ik ⋅ r )(ε ⋅∇) ψ a M E = M ba1 + M ba2
其中
M
M1 ba
=−
ωba
2 c
ψ b ly ψ a
E M ba2
2 imωba =− ψ b xi zi ψ a 2 c
原子序数为Z的类氢离子的磁偶极跃迁的跃迁速率与电 偶极跃迁速率之比为:
三、跃迁类型和选择定则
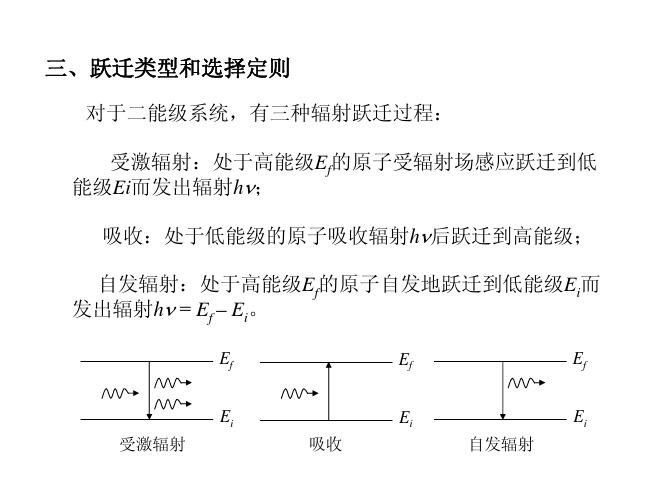
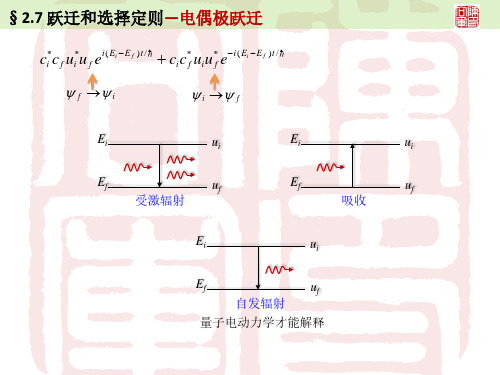
对于二能级系统,有三种辐射跃迁过程: 受激辐射:处于高能级Ef的原子受辐射场感应跃迁到低 能级Ei而发出辐射hν; 吸收:处于低能级的原子吸收辐射hν后跃迁到高能级; 自发辐射:处于高能级Ef的原子自发地跃迁到低能级Ei而 发出辐射hν = Ef – Ei。
Ef Ei 受激辐射 吸收 Ef Ei 自发辐射 Ef Ei
2
电偶极矩-er在空间反演下变号,宇称为奇,P = -1。由于 宇称守恒,初态和末态波函数的宇称必须改变。
e
− ik ⋅r
1 = 1 − (ik ⋅ r ) + (ik ⋅ r ) 2 − 2!
磁偶极和电四极辐射由展开式第二项贡献,要多乘一项 k·r。因而磁偶极和电四极辐射作用算符是偶宇称的,P = 1, 由于宇称守恒,初态和末态波函数的宇称应不变。 由此可以得到电多极辐射和磁多极辐射的宇称,以及原 子分子初态和末态宇称Pf和Pi与光子角动量有如下关系:
四、跃迁类型和选择定则

2
106
四、跃迁类型和选择定则 --电多极和磁多极
在原子分子物理涉及电磁相互作用的跃迁中,磁偶极和电 四极跃迁速率比电偶极跃迁速率小很多。
如果两个能级之间电偶极跃迁是允许的,则电偶极辐射是 主要的,磁偶极和电四极跃迁可以忽略不考虑,它们对能级寿 命、宽度影响很小。
只有当电偶极跃迁是禁戒的情况下,才要考虑磁偶极和 电四极跃迁,能级预计寿命在10-3秒量级或更长,因此称为亚 稳能级。
Ea
Ea
吸收
自发辐射
四、跃迁类型和选择定则
吸收和受激辐射可以用非相对论量子力学来处理,把它们 当作是在电磁辐射场作用下原子在不同能级之间跃迁。
但普通的量子力学无法解释自发辐射:当原子在初始时刻 处于某激发能级的定态上,如没有外界作用,原子的哈密顿 量是守恒的,原子应该保持在该定态,电子不会跃迁到较低 能级。
严格处理要用量子电动力学。
象对兰姆移位和电子反常磁矩的解释一样,与零点能相联 系的真空涨落电磁场造成了自发辐射。
四、跃迁类型和选择定则 --原子与辐射场相互作用
设辐射场是角频率为的平面单色波
A(,r,t) A0() exp i k r t . c.c
A0是描述辐射强度和极化的矢量,
A0 () A0 ()ˆ
2
Ze2
4 0 r
是无外场时类氢单电子原子的定态哈密顿量,
H (t) i e A m
为含时的微扰项。
四、跃迁类型和选择定则 --原子与辐射场相互作用
利用含时微扰论,可以得到吸收的跃迁速率:
Wba
4 2 e2
m2c
4
0
I (ba ) 2
ba
Mba (ba ) 2
和受激辐射的跃迁速率:
跃迁类型和选择定则
2 2 2
电四极跃迁的跃迁速率与电偶极跃迁速率之比为
λE2 3 ⎛ ω r ⎞ 3 ⎛ Zα ⎞ ≈ ⎜ = ⎜ ≈ 10−6 λE1 40 ⎝ c ⎟ 40 ⎝ 2 ⎟ ⎠ ⎠
λif =
( Ei − E f
3πε 0 c
)
3
4 3
∫ψ
* f
(-er )ψ i dτ (nk,ε + 1)
2
式中Ei – Ef = hν,上式已对k和ε的各个方向取了平均,相当 于原子与各向同性的非偏振辐射的相互作用。
跃迁速率包括两项: 第一项对应于受激辐射,在通常光源作用下可以忽略,只有 在较强光场中才明显出现。 第二项对应于自发辐射,即外界不存在辐射 (nk,ε= 0)时的辐 射速率。 如果存在简并态,自发辐射的速率变为
磁偶极跃迁M1
0→0
电四极跃迁E2
ΔJ = 0, ±1, ±2 0 → 0,1
1 2
0 → 0 ΔJ = 0, ±1,
→
1 2
ΔM=0,±1 宇称改变 有单电子跃迁 Δl = ±1 ΔS=0
ΔL = 0, ±1, 0→0
ΔM=0,±1 宇称不变 无单电子跃迁 Δl = 0, Δn = 0 ΔS=0 ΔL=0
j = 0 (无辐射) 的跃迁,称为单极跃迁,只能通过电子碰撞 或其他无辐射方式跃迁。
定则2同样来自角动量守恒以及原子波函数相对量子化 轴的角向对称性。 定则3来自宇称守恒。 电偶极辐射的宇称:
λif
( Ei − E f ) =
3πε 0 c
4 3
跃迁类型和选择定则
例如,氦原子的21S0和 23S1态,无法通过电偶极跃迁到基态11S0 (偶极禁戒),这两个状态为亚稳态。
ns1S
20×104
np1Po
nd1D
ns3S
np3Po
nd3D
. ..
5(0) 515.6 4(0)
5047.7 184859.06 18×104 7281.3 3964.7 520 166271.70 16×104 0 584.3
这就是电偶极近似。与这一部分对应的跃迁称 为电偶极跃迁(用E1表示)。
e
− ik ⋅r
1 = 1 − (ik ⋅ r ) + (ik ⋅ r ) 2 − 2!
第二项包含两部分,分别含有来源于电荷运动的电流产生 的磁偶极矩和电荷分布产生的电四极矩,相应的辐射是磁偶极 辐射(M1)和电四极辐射(E2)。 第二项之后还有磁四极辐射(M2)和电八极辐射(E3) 等。 我们把除电偶极辐射之外的辐射称为禁戒辐射。 这里的禁戒指的是对电偶极辐射禁戒,它可以通过其它种 辐射跃迁,只是跃迁概率比电偶极辐射小很多。
同样,氦的21S0到基态11S0也不能进行电和磁的单光子跃迁, 它们之间主要的是双光子跃迁过程。 在激光的强相干场中,双光子过程才变得重要。 现在经常利用功率较大的可调频率激光器来研究双光子和多 光子跃迁等极小概率过程。
P = Pf / Pi=(-1) j 对Ej =(-1) j+1 对Mj
后三个选择定则是近似成立的。定则4只对所涉及的每个 态都能用单一电子组态描述才成立,定则5和定则6适用于多 电子原子的LS耦合。 氢原子基态12S1/2的两条超精细劈裂能级之间的跃迁是磁 偶极辐射的一个例子,它们的所有量子数都满足磁偶极辐射 的选择定则,定则3和定则4使电偶极辐射禁戒。
光电效应电子的跃迁精品PPT课件
写在最后
经常不断地学习,你就什么都知道。你知道得越多,你就越有力量 Study Constantly, And You Will Know Everything. The More
You Know, The More Powerful You Will Be
Thank You
在别人的演说中思考,在自己的故事里成长
在复习本单元知识时要提醒学生注意宏观领域中的经验和规律在微观领域都遇到严重的障碍微观领域的研究方法应是从实验事实出发经过分析总结提出假设建立模型再经过实验的验证并发现新的问题从而对假设进行修正
第十五单元 原子物理
知识框架
考试说明
复习建议
1.本单元概念、公式多,在复习单元知识时应注意: (1)辨析概念:通过对比,使学生真正理解各物理量之间的区 别与联系. (2)总结方法:在复习本单元知识时要提醒学生注意,宏观领 域中的经验和规律在微观领域都遇到严重的障碍,微观领域的研 究方法应是从实验事实出发经过分析总结,提出假设,建立模 型,再经过实验的验证,并发现新的问题,从而对假设进行修 正.
2.光的波动性和粒子性与经典波和经典粒子的概念不同. (1)光波是概率波,在光的干涉现象中,明条纹是由于光子到达的 概率较大形成的,暗条纹是光子到达的概率较小形成的,这与经典波 的叠加原理不同; (2)光的粒子性是指光的能量不连续性,能量是一份一份的,没有 一定的形状
关于光的波粒二象性的理解正确的是( ) A.大量光子的效果往往表现出粒子性,个别光子的行 为往往表现出波动性 B.光在传播时是波,而与物质相互作用时就转变成粒 子 C.高频光是粒子,低频光是波 D.波粒二象性是光的根本属性,有时它的波动性显著, 有时它的粒子性显著
► 探究点三 能级的分析与计算
物理高考跃迁知识点
物理高考跃迁知识点在物理高考中,跃迁(Transition)是一个重要的知识点,涉及到原子、分子的能级变化以及辐射现象等内容。
本文将介绍物理高考中的跃迁知识点,包括跃迁的基本概念、能级理论、光谱与跃迁、以及应用等方面。
一、跃迁的基本概念跃迁是指原子、分子在能级间的转变过程。
在跃迁中,物体吸收或辐射能量,从一个能级转移到另一个能级。
根据能级间的差异,跃迁可分为电子能级跃迁和核能级跃迁两种形式。
1. 电子能级跃迁电子能级跃迁是指原子或分子中的电子从一个能级跃迁到另一个能级。
根据能级差异的大小,电子能级跃迁可以分为激发态和基态跃迁。
激发态跃迁是指电子从低能级跃迁到高能级,吸收能量;基态跃迁则是电子从高能级跃迁到低能级,释放能量。
2. 核能级跃迁核能级跃迁是指原子核中的质子、中子在能级间转变的过程。
核能级跃迁主要发生在放射性核素的衰变过程中,包括α衰变、β衰变和γ衰变等。
二、能级理论能级理论是解释跃迁现象的理论基础,主要包括玻尔原子模型和量子力学理论。
1. 玻尔原子模型玻尔原子模型是根据物理学家玻尔的理论提出的,它将原子看作是由电子围绕着核心旋转的结构。
根据玻尔原子模型,原子的电子能级是离散的,电子只能在特定的能级上运动,而不能处于能级之间的状态。
2. 量子力学理论量子力学理论是描述微观粒子行为的理论,它基于概率的观念,描述了电子在原子、分子中的运动状态。
根据量子力学理论,电子的能量是量子化的,也即电子只能占据离散的能级。
三、光谱与跃迁光谱与跃迁之间存在着紧密的关系。
原子、分子的跃迁过程会伴随特定波长的电磁辐射的发射或吸收,从而形成了不同类型的光谱。
1. 发射光谱当原子或分子从激发态跃迁回基态时,会发射对应能级差的能量,形成发射光谱。
发射光谱的特征波长与原子、分子的能级结构有关,通过对发射光谱的观测与分析,可以推断物质的组成以及它们的能级差。
2. 吸收光谱当原子或分子从基态吸收能量跃迁到激发态时,会吸收对应波长的电磁辐射,形成吸收光谱。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(s) (a) + (a) + (s) (s) (a) +
(a) (s) +
(s) +
(a) -
(a) (s) + (s) + (a) (a) (s) +
J’ 5
同核分子的电子态(包括带相同电荷的异核分子,奇偶性必须相反:
g↔u, g ←|→ g, u ←|→ u
第7页/共33页
(2)适用于耦合情况(a)和(b)的选择定则
量子数L是有意义的,其选择定则是:
DL= 0,±1
当上下两个态都是S态时,电子波函数有对称性限制:
S+↔S+, S- ↔S-, S+ ←|→S-
Hund情况(c)矢量图
第3页/共33页
(4)Hund 情况(d)
具有角动量L的电子轨道运动半径比 核间距大很多,核与内层电子看起来像一 个点电荷,故核间电场弱得以致L不与它耦 合,而与分子转动R矢量耦合成N, N再与 电子自旋S耦合成分子总角动量J。
N = R+L, R+L-1, …, |R-L|
总角动量J的选择定则:
DJ = 0,±1, 但J = 0←|→ J = 0
一级近似下,分子的总波函数的宇称与耦合情况无关。偶极矩对空间 反演是奇函数,所以上下两个态的波函数的宇称必须相反,即:
+↔-, + ←|→ +, - ←|→ -
同核分子的交换对称性:
s↔s, a ↔ a, s ←|→ a
但是,对于同一电子态中的振动跃迁, 因为同核双原子分子没有永久电偶极矩 而被禁阻;对于不同电子态间,因为电 核重新分布时有瞬间的电偶极矩产生, 伴随电子跃迁同时有振动跃迁发生。
Hund情况(b)矢量图
第2页/共33页
(3)Hund 情况(c) 核间电场不足以破坏原子中的L-S耦合,
两个原子的li和si各自先耦合成电子总角动量 Ji,然后它们在核间轴方向分量相加成W, 再与分子转动角动量R合成分子的总角动量J。
量子数L是没有意义的。
重原子分子组成的分子激发态中 会有这种耦合情况。
对于S = 0→S = 0 跃迁,D N = 0被禁阻。
2. 电子跃迁符号规定
(1)高态写在前面,低态写在后面; (2)若想标明吸收或发射,用箭头←或→表示; (3)与基态有相同多重性的谱项前用大写字母:A, B, C,…;
与基态自旋多重度不同的谱项用小写字母:a, b, c, … (4)对于电子跃迁中振动量子数变化,如:V’=2与V”=3振动态间的跃迁,
对于S = 0→S = 0 跃迁,D N = 0被禁阻。
R支从R(0)开始,随着J值的增大向 高波数(紫端)延伸;
R (2)
+
R (1)
P (3)
J”
4
P (2)
-
+
R (0) P (1)
3 2
-
1
+
0
P支从P(1)开始,随着J值的增大向 低波数(红端)延伸。
第10页/共33页
1P – 1S+跃迁
(1)Hund 情况(a) L≠0的电子态耦合。
L-S耦合比较强,电子运动和核运动耦合弱。 L和S在核间轴上的投影, L和S耦合成电子总角动量W; 核转动角动量R与W耦合成总角动量J。
J = W, W+1, W+2, …
S=整数或者半整数 S,W,J =整数或者半整数
Hund情况(a)矢量图.
第1页/共33页
记作2-3谱带或者(2,3)带,前面的数字表示高态量子数,后面的数 字表示低态量子数。
第9页/共33页
单重态-单重态跃迁 S=0, Hund case (a) 和(b)没有区别。
1S+ - 1S+跃迁
+
R (3)
+ +
考虑case (b):
J’ 4
3 2 1 0
P (4)
DJ = 0,±1, 但J = 0←|→ J = 0; +↔-, + ←|→ +, - ←|→ -; D N= 0,±1;
自旋作用很弱,由自旋引起的能级 分裂可以忽略。
H和He的某些激发态有这种耦合情况。
Hund情况(d)矢量图
第4页/共33页
(5)Hund 情况(e) L-S 耦合很强,耦合成 Ja. 但是,L-
S 在核间轴上的耦合很弱。Ja 和核转动 角动量R 耦合成总角动量J.
J = R + Ja, R + Ja − 1, R + Ja − 2, . . . , |R − Ja|.
Hund情况(e)矢量图
第5页/共33页
B)不耦合情况:L型双重分裂
洪特耦合是理想化极限状态。
L≠0的电子态在零级近似下是双重简并的,并且简并电子态的每个转动能级 在零级近似下也是双重简并的。当考虑电子运动与分子转动的相互作用时,简并 就消除了,每个转动能级将分裂为两个能量略有差别的子能级。
J= N
自旋量子数S的选择定则是:
DS=0 (3)只适用于耦合情况(a)的选择定则
自旋量子数S的轴向分量量子数S不变:
D S= 0
总电子角动量轴向分量量子数W也守恒,其选择定则为:
D W = 0,±1
对于W = 0→W = 0 跃迁,D J = 0被禁阻。
第8页/共33页
(4)只适用于耦合情况(b)的选择定则 总角动量量子数N: D N= 0,±1
-+
+ -
-+ + -+
+
-
+
-
+
R(4) R(3) R(2) R(1) R(0)
Q(1) Q(2) Q(3) Q(4)
P(2) P(3) P(4)
第11页/共33页
DJ =DN= 0,±1
J’ 5
考虑L分裂
+↔-, + ←|→ +, - ←|→ -;
4
1P
3
2
1
J” 4
3
(s) (a) +
+-
-+
5
+-
-+
4
+-
-+
3
+-
-+
2
+-
-+
1
(a)
(b)
1P 态的转动能级的L双重分裂
L双重分裂
转动能级的(+)(-)指的是分子总 波函数的宇称。 L双重分裂的大小与量子数J有关。
第6页/共33页
6.3 选择定则 跃迁的例子
1. 选择定则
el *el d 考虑不同的耦合情况。
(1)一般选择定则
(2)Hund 情况(b)
L=0或者电子的轨道运动在核间轴方向上的磁场比较弱。 电子轨道角动量L的轴间分量L与分子转动角动量R合成N, N与电子自旋S耦合成总角动量J。
几乎所有的S态都属于这种情况。
J= N+S, N+S-1,…,|N-S| N=L,L+1,L+2,…
对于每个给定得N值,将产生2S+1个J值。 即:在洪特情况(b)中,由于自旋通分子 转动的耦合使同一个N值得转动能级分裂 为不同J值得子能级,其数目等于多重度。
