第四章 原子的精细结构 21节 碱金属双线1
第四章碱金属原子

线
第
第
第
第
系
四
三
二
一
限
条
条
条
条
碱金属原子三个线系的精细结构示意图
31
复习:
•碱金属原子与氢原子价电子的运动 有何不同? •碱金属原子光谱项怎样表示?
32
二、定性解释
光谱线的任何分裂都是能级分裂的结果,那么
推论1;谱线的分裂意味着能级的分裂 推论2;s 能级是单层的,所有p,d,f 能
级都是双层的,并且当量子数n 增大时,双层能级间隔减小。
3、锂的四个线系
主
线
系:
~pn
R (2 s )2
R (n p )2
,n
=
2,
3,
4…
第二辅线系:
~ sn
R (2
)2
R (n
)2
,n =3,4,5…
p
s
第一辅线系:
~ dn
R (2
)2
(n
R
)2
,n
=3,4,5…
p
d
柏格曼系:
锂原子的价电子的轨道:n ≥ 2 钠原子的价电子的轨道:n ≥ 3 原子实的有效电荷数 :Z*=Z-(Z-1)=1
18
价电子远离原子实运动
相当于价电子在n 很大的轨道上运动, 价电子与原子实间的作用很弱,原子实电 荷对称分布,正负电荷中心重合在一起。 有效电荷为+e,价电子好象处在一个单位 正电荷的库仑场中运动,与氢原子模型完 全相似,所以光谱和能级与氢原子相同。
19
-e
价电子远离原子实
20
§21碱金属双线

式中 l r me
电子的轨道角动量 电子的静止能量
U 电子磁矩(内禀磁矩)s在磁场中的势能: s B
E0=mec2
1 s s( s 1), s ; s g s B s s s(s 1) gs B ; 2 1 Zg s B e s l 所以,在电子坐标系中 U 3 4 0 E0 r
钠的黄色D线
但要计算钠3P能级的分裂 却不很容易,(5)式不能直 接用.因为钠的原子核外 有10个电子屏蔽着,使最 后一个单电子感受到的Ze 并非核的电荷,而是有效 电荷z有效e。Z有效=3.5
需要指出,对原子的自旋角动量、轨道角动量和 总角动量有贡献的电子数目不止一个时,理论上 可以证明自旋轨道相互作用引起的附加能量U也 正比于 S L,但公式(5)有的可用,但(6)不能。
(4)
把式(4)和(3)代入式(2),得到自旋一轨道耦合 项: ( Z )4 E [ j ( j 1) s( s 1) l (l 1)] 0 U , l 0 (5) 3 1
4n
对于单电子:
l (l )(l 1) 2
( Z )4 E0 U 3 ; 2n (2l 1)(l 1) ( Z )4 E0 U 3 ; 2n l (2l 1)
假设是圆轨道;可证明,对任意形状的轨道都适用 电流i在中心处(电子所在位置)产生的磁场大小为: 1 2i 1 Ze B 2 4 0 c r 4 0 c 2 r 2
B Ze 1 Ze ( ) r l 2 3 3 4 0 c r 4 0 E0 r 1
1 当j l , l 0 2 1 当j l , l 0 2
双能级差值
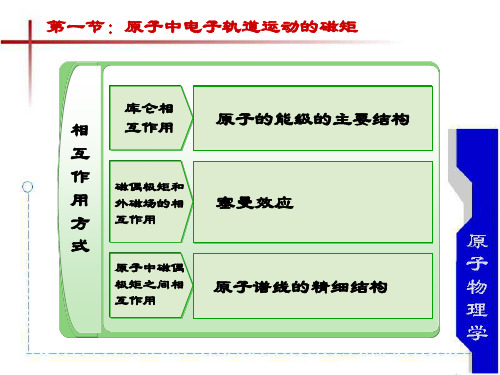
碱金属原子光谱的精细结构
l
分量,与j垂直的分量对外的平均效 果抵消了(由于绕j转动的缘故)。
j
对外起作用的是它沿j的延线的分量, j
这就是电子的总磁矩
单电子磁矩与角动量的关系
对图示进行分析,利用三角形的余弦定理
可求出 j
lˆ l(l 1)
l
sˆ s(s 1)
ˆj
j( j 1)
1、载流闭合回路的磁矩 μ (IS)n 对应力矩: τ μ B
经典物理:封闭矩形线圈
1、载流闭合回路的磁矩 (IS)n 力矩τ μ B
2、回转运动电子的角动量与磁矩 μ e L L
2m
1、载流闭合回路的磁矩 (IS)n 力矩τ μ B
观察到两个取向;
难道是轨道角动量矢量合成?
第四章:原子的精细结构:电子的自旋
第一节 原子中电子轨道运动磁矩 第二节 史特恩—盖拉赫实验 第三节 电子自旋的假设 第四节 碱金属双线 第五节 塞曼效应 第六节 氢原子能谱研究进展
埃伦费斯特和他的学生,1924年,莱顿. 左起: 第开, 古兹密特, 汀柏根, 埃 伦费斯特, 克罗尼格, 和费米。
原子处于基态。
沿着-x方向观察:
沿X水平方向运动的氢原子束,其速度:v
3kT m
为了使进入磁场的氢原子 束受到力的作用,这个磁 场必须是不均匀的磁场区 (0.1nm的线度范围内)。
N
S
磁场沿Z 方向是变化的,即
Bz 0, Bz Bz 0
z
x y
在磁场中,磁矩在磁场中的势能:
ˆj2 lˆ2 sˆ2
ˆj2 sˆ2 lˆ2
g j gl
21_碱金属原子光谱的精细结构.ppt

2
11 d V E p s 2 2 sp m c rd r
2
Ze 1 V r 40 r
2
1 d V 22 j j 1 1 s s 1 2 m c r d r
第二辅线系: ns 2p
伯格曼线系: nf 3d
Li 原子光谱的精细结构精细结构
间隔逐渐缩小
间隔不变
ns2p
因而设想 s: 单层 p: 双层
np2s 因而设想 s: 单层 p: 双层 且双层间隔随n 增加而减小
nd2p
因而设想 p、d、f: 皆为双层, 且 双层间隔随n 增加而减小
B ?
e
r
e
r
Ze
Ze
j Ze Ze
r 0 j B 3 4 r
r Ze r 0 j 0 B 3 3 4 r B 0 0 E 4 r 1 E Ze r j Ze E 2 c 4 0 r3 2 Ze 1 d V r e E F Vr 4 r d r r 0
1 2
Ze
p m s,z s
1 2
E s,zB
B
B
s,z
s,z
1 e E B s 2m
1e E B s 2m
2.2 自旋与轨道运动相互作用 能量的计算
E B s
e s ps m
2 2
给定n, l, s = ½,
可修改原子物理学——碱金属原子光谱的精细结构.doc
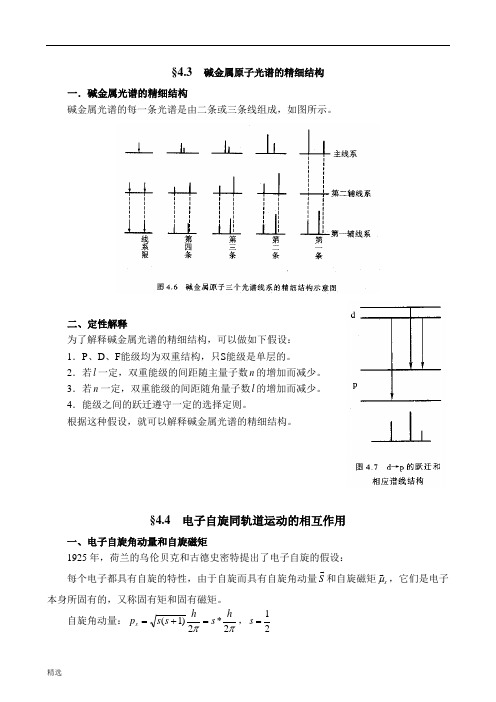
§4.3 碱金属原子光谱的精细结构一.碱金属光谱的精细结构碱金属光谱的每一条光谱是由二条或三条线组成,如图所示。
二、定性解释为了解释碱金属光谱的精细结构,可以做如下假设: 1.P 、D 、F 能级均为双重结构,只S 能级是单层的。
2.若l 一定,双重能级的间距随主量子数n 的增加而减少。
3.若n 一定,双重能级的间距随角量子数l 的增加而减少。
4.能级之间的跃迁遵守一定的选择定则。
根据这种假设,就可以解释碱金属光谱的精细结构。
§4.4 电子自旋同轨道运动的相互作用一、电子自旋角动量和自旋磁矩1925年,荷兰的乌伦贝克和古德史密特提出了电子自旋的假设:每个电子都具有自旋的特性,由于自旋而具有自旋角动量S 和自旋磁矩s μ,它们是电子本身所固有的,又称固有矩和固有磁矩。
自旋角动量:ππ2*2)1(h s h s s p s =+=,21=s外场方向投影:π2h m S sz =, 21±=s m 共2个, 自旋磁矩:s s p me-=μBs s hs s m e p me μπμ32)1(-=+-=-= 外场方向投影:B z z S meμμ±=-=共两个⇒偶数,与实验结果相符。
1928年,Dirac 从量子力学的基本方程出发,很自然地导出了电子自旋的性质,为这个假设提供了理论依据。
二、电子的总角动量电子的运动=轨道运动+自旋运动轨道角动量:ππ2*2)1(hl h l l p l =+= 12,1,0-=n l 自旋角动量:ππ2*2)1(hs h s s p s =+= 21=s 总角动量: s l j p p p += ππ2*2)1(hj h j j p j =+= s l j +=,1-+s l ,……s l -当s l >时,共12+s 个值当s l <时,共12+l 个值由于 21=s当0=l 时,21==s j ,一个值。
当 3,2,1=l 时,21±=l j ,两个值。
第4章 原子的精细结构(修改)

n*
m*
当 n 时,系限。
~ ~ Tm*
1.有效量子数
n* m*
H原子:主量子数n是整数
有效量子数。
碱金属原子:n*、m* 不是整数有效量子数
2.量子数亏损
n* 、m* 和整数之间有一个差值,用l 表示,
l n n* 量子数亏损
l
l
与 n 无关, 与 l
0、1、2、3……
有关,l
s, p,d, f
二、定性解释
为了解释碱金属光谱的精细结 构,可以做如下假设: 1.P、D、F能级均为双重结 构,只S能级是单层的。 2.若一定,双重能级的间距 随主量子数的增加而减少。 3.若一定,双重能级的间距 随角量子数的增加而减少。 4.能级之间的跃迁遵守一定 的选择定则。 根据这种假设,就可以解释碱 金属光谱的精细结构。
合力
Fz
q
dE dz
l cos
pz
dE dz
pz p cos : p 在外场方向的投影
2.磁矩
iA 方向与 i方向满足右手螺旋关系。
均匀磁场中: F 0 M B
非均匀磁场中:
磁场方向沿 z 轴,随z 的变化为dB
dz
合力
Fz
dB cos
dz
z
dB dz
z cos : 在外场方向的投影
§4.7 碱金属原子的精细结构
电子的运动=轨道运动+自旋运动
一、电子的总角动量
轨道角动量: L l(l 1) h 2
自旋角动量: S s(s 1) h
2
总角动量: J L S
l 0,1,2n 1
s1 2
J j( j 1) h
2
j l s,l s 1 ,…… l s
4[1].3 4.4 碱金属原子光谱的精细结构
![4[1].3 4.4 碱金属原子光谱的精细结构](https://img.taocdn.com/s3/m/85ff3522192e45361066f5dc.png)
p j = pl + ps或p j = pl + ps
h h +s 或pj = l 2π 2π h h = (l + s ) 或 (l s ) 2π 2π h = j , j = l + s或 l s 2π
j:电子的总角动量量子数
h pj = l 2π
h s 2π
由电磁学理论,考虑电子的自旋磁距后附加的能量为
1 3 1 1 如l = 1,j = 1 + = 或1 - = 2 2 2 2
h h pl = 2 = 1.41 2π 2π 1 3 h h ps = × = 0.87 2 2 2π 2π
3 5 h h pj = × = 1.94 2 2 2π 2π h 1 3 h 或= × = 0.87 2 2 2π 2π
附加光谱项和精细结构裂距
T
T
j =l +
1 2
l = a 2
l +1 =a 2
Tls上=-a l 2
j =l
1 2
T0
nl
Tls下=a
l +1 2
双层能级间隔用波数表示
1 Rα 2 z 4 ~ v = T1 T2 = a (l + ) = 3 米 1 2 n l (l + 1)
~ v 与n 3和l (l + 1)成反比,与z 4成正比
对电子: 可得:
0 z ev B= sin α 2 4π r
mrv sin α = pl
ze 1 1 B= 3 pl (ε 0 0 = 2 ) 2 4πε 0 mc r c 1
3, θ 的取值 cos
p j = pl + ps 2 pl ps cos θ
第四章原子的精细结构:电子的自旋

不加磁场
加磁场经典预言
加磁场实验结果
斯特恩-盖拉赫实验对氢原子的结果 斯特恩盖拉赫实验时空间量子化的最直接的证明,它是第 一次量度原子的基态性质的实验,又是这个实验,进一步开辟 了原子束及分子束实验的新领域。
三、实验问题
1、先看例子(Ag、Zn l 0 )在屏上能看到几束
理论上:( 2l 1 1 )只有一个值
x vt
1 Fz 2 zt t 2m
d O
P
S1 S2
S N
z1
z2
x
D
通真空泵
原子束在经过磁场区(长度D)到达出口处时,已偏离x轴z1 距离,那时与x轴的偏角为:
Fz t dz1 Fz d arctan arctan arctan 2 dx mv mv d
§18 原子中电子轨道运动的磁矩
一、经典表示式
1、磁矩 从经典电磁学知道,一载流线圈有一个磁矩μ ,它可以表示成:
ˆ IS iSen
i
-----电流大小
S
-----载流线圈所围面积
ˆ en -----垂直与该面积的单位矢量,即和导线线圈平面垂直
因 和 S
线圈平面。
子的1/1836,实际核磁子值
因为核磁矩比电子磁矩
小得多,所以原子磁矩主要由电子磁矩组成。玻尔磁子
也可作为原子磁矩的单位。
2、磁相互作用比电相互作用小
4 0 2 e 1 e 2 B ec 2 2me 2 4 0 c me e 1 1 ea1 c c ea1 2 2
它在z方向的分量只有两个:
1 sz 2
1 : 即:自旋量子数在z方向的分量只能取 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§21 碱金属双线
掌握碱金属双线产生的原因
掌握旋-轨相互作用导致的能级分裂的计算方法
① 自旋角动量与旋-轨相互作用;
② 碱金属双线中能量与光谱的计算。
理论讲授
2学时
第三章 原子的精细结构:电子的自旋
§21 碱金属双线
一、碱金属原子谱线的精细结构:定性考虑
Li 原子的光谱精细结构:在高分辨率光谱仪下为双线或三线结构。
其中,主线 系、二辅系为双线结构,一辅系、柏格曼系为三线结构。
主线系: S nP 2→ ,3,2=n 二辅系(锐线系)P nS 2→ ,4,3=n 一辅系(漫线系)P nD 2→ ,4,3=n 柏格曼系(基线系)D nF 3→ ,5,4=n
前项为动项,后项为固定项。
推想:①有主线、二辅系,S 能级为单层的,l 能级为双层的;
②随l 增加,能级分裂越来越小;
③遵从一定的选择定则。
