大学物理质点和质点系的动量定理
合集下载
04 3-1 质点和质点系的动量定理
t2
F1＋F2 dt (m1v1 m2v2 ) (m1v10 m2v20 )
t1
作用在两质点组成的系统的合外力的冲量等于系统内两质 点动量之和的增量，即系统动量的增量。
2、多个质点的情况
t2 t2 n n n Fi外 dt＋ Fi内 dt m i v i m i v i 0 i 1 i 1 t1 i 1 t1 i 1 n
3-4 动能定理
一、功与功率
1、功
•恒力的功 力对质点所作的功等于该力在位移 方向上的分量与位移大小的乘积
F m
F
S
m
说明 •功是标量，没有方向，只有大小，但有正负 p/2，功W为正值，力对物体作正功； p /2，功W=0， 力对物体不作功； p /2，功W为负值，力对物体作负功，或 物体克服该力作功。 •单位：焦耳(J) 1J=1N· m
i i i
ex ex 若质点系所受的合外力为零 F Fi 0
则系统的总动量守恒，即
讨论
ex dp ex i F , F 0, P C dt
p pi
保持不变 .
i
1）系统的动量守恒是指系统的总动量不变，系 统内任一物体的动量是可变的, 各物体的动量必相 对于同一惯性参考系 .
W＝F S dW＝F dS
•变力的功 分成许多微小的位移元，在每一个 位移元内，力所作的功为
Z
dr
b
F
dW F dr F cos dr
总功
a O
Y
W
•合力的功
B
A
B X F dr F cosdr
大学物理 动量 动量守恒定律汇总
Fdt (m dm)v (mv dm 0) vdm vkdt
F k v 200 4 8 10
2
N
12
3-9 一小船质量M=100kg，船头到船尾长度l=3.6m。现 有一质量m=50kg的人从船尾走到船头时，船头将移动多 少距离？假定水的阻力不计。
Fi外
Fij
j
i
内力-----是质点系内各质点间的作用力； 外力------是质点系外物体对质点系内质点的力。
由牛顿第三定律，内力必定是成对出现，且每对内力 都沿两质点连线的方向。
3
i质点合力
t2
t1
( Fi外 f ji )dt mi vi 2 mi vi1
j 1
n 1
F i外 f
9
n
例2.5 一弹性球，质量m＝0.20kg，速度 v＝5m/s， 与墙碰撞后弹回.设弹回时速度大小不变，碰撞前后的 运动方向和墙的法线所夹的角都是α，设球和墙碰撞 的时间Δt＝0.05s，α＝60°，求在碰撞时间内，球和 墙的平均相互作用力. 解：以球为研究对象.设墙对 球的平均作用力为 f ，球在 碰撞前后的速度为 v1和 v 2 ， 由动量定理可得
2
t1 t2
Fx dt mv2 x mv1x
Iy Iz
t1 t2
Fy dt mv2 y mv1 y Fz dt mv2 z mv1z
2
t1
3
二 质点系的动量定理
如果研究的对象为多个质 点，则称为质点系 对质点系，受力可分为 “内力”和“外力”。
质点系
Fj外
Fji
§2.2 动量 动量守恒定律
力对时间的累积效应
大学物理——第2章-质点和质点系动力学
2 2 2 α + a1 cos2 α
a1 = cot α 方 向: tanθ = ax g
由式④得:
ay
θ 为 a 与 x 正向夹角
FN = m(g + a1) cosα
10
例2-2 阿特伍德机 (1)如图所示滑轮和绳子的质量均不计,滑 轮与绳间的摩擦力以及滑轮与轴间的摩擦力 均不计.且 m > m2 . 求重物释放后,物体 1 的加速度和绳的张力. 解: 以地面为参考系 画受力图,选取坐标如图
ar
ar
m1 m2
a
m g FT = m a1 1 1 m2g + FT = m2a2
a1 = ar a
FT 0
a2 = ar + a
m1 m2 ar = m + m (g + a) 1 2 a1 FT = 2m1m2 (g + a) P 1 m1 + m2
a2
y FT
y
P0 2
12
8
桥梁是加速度 a
例2-1 升降机以加速度a1上升,其中光滑斜面上有一物体m沿 斜面下滑. 求:物体对地的加速度 a ? y 斜面所受正压力的大小? 解: 由于升降机对地有加速度,为一非惯性 系,故选地面为参考系,设坐标如图.
FN
a1
a2
a = a2 + a1
在 x , y 方向上有:
G
α
x
ax = a2 a1 sin α a = a cosα 1 y
m1 m2
FT 0
m g FT = m a 1 1 m2 g + FT = m2a
m1 m2 a= g m1 + m2
2m m2 1 FT = g m + m2 1
a1 = cot α 方 向: tanθ = ax g
由式④得:
ay
θ 为 a 与 x 正向夹角
FN = m(g + a1) cosα
10
例2-2 阿特伍德机 (1)如图所示滑轮和绳子的质量均不计,滑 轮与绳间的摩擦力以及滑轮与轴间的摩擦力 均不计.且 m > m2 . 求重物释放后,物体 1 的加速度和绳的张力. 解: 以地面为参考系 画受力图,选取坐标如图
ar
ar
m1 m2
a
m g FT = m a1 1 1 m2g + FT = m2a2
a1 = ar a
FT 0
a2 = ar + a
m1 m2 ar = m + m (g + a) 1 2 a1 FT = 2m1m2 (g + a) P 1 m1 + m2
a2
y FT
y
P0 2
12
8
桥梁是加速度 a
例2-1 升降机以加速度a1上升,其中光滑斜面上有一物体m沿 斜面下滑. 求:物体对地的加速度 a ? y 斜面所受正压力的大小? 解: 由于升降机对地有加速度,为一非惯性 系,故选地面为参考系,设坐标如图.
FN
a1
a2
a = a2 + a1
在 x , y 方向上有:
G
α
x
ax = a2 a1 sin α a = a cosα 1 y
m1 m2
FT 0
m g FT = m a 1 1 m2 g + FT = m2a
m1 m2 a= g m1 + m2
2m m2 1 FT = g m + m2 1
第四章 动量定理与动量守恒定律
v dpi v v (e) v (i) = Fi = Fi + Fi dt
m1
v ex Fi
v in m i m2 Fi
求和, 求和 有
合外力 合内力
v v (e) v (i) dpi d v ∑ dt = dt ∑ pi = ∑Fi + ∑Fi
因为内力成对出现, 上式可写为: 因为内力成对出现 上式可写为
I x = ∫ Fxdt = mvx mvx0
t0 t
t
I y = ∫ Fydt = mvy mvy0
t0 t
I z = ∫ Fzdt = mvz mvz0
t0
May 31, 2010 Page #
ANHUI UNIVERSITY
大学物理学
第四章 第四章动量定理与动量守恒定律
(3) 在碰撞或冲击问题中 牛顿定律无法直接应用 而动 在碰撞或冲击问题中, 牛顿定律无法直接应用, 量定理的优点在于避开了细节而只讨论过程的总体效果. 量定理的优点在于避开了细节而只讨论过程的总体效果 (4) 动量定理仅适用于惯性系 且与惯性系的选择无关 动量定理仅适用于惯性系, 且与惯性系的选择无关. 如图, 锤从高度为h 例 如图 一重锤从高度为 =1.5m的地方由 的地方由 静止下落, 静止下落,锤与被加工的工件的碰撞后的 末速度为零. 若打击时间分别为10 末速度为零 若打击时间分别为 -1s, 10-2s, 10-3s, 10-4s,试计算这几种情形下平均冲力 , 与重力的比值. 与重力的比值 如图坐标系, 设重锤质量为m 解: 取如图坐标系 设重锤质量为 . 重锤初速度
10-1s 6.5 10-2s 56
Page #
由此解得
计算结果如下
t
大学物理第二章动能定理
例题3. 如图，一轻绳跨过一定滑轮，两边分别拴有质量
为m及M的物体，M离地面的高度为h: (1)若滑轮质量及
摩擦力不计，m与桌面的摩擦也不计，开始时两物体均静
止，求M落到地面时的速度(m始终在桌面上); (2)若m与
桌面的静摩擦系数和滑动摩擦系数均为，结果又如何？
解：
m
(1)不计摩擦,系统(m,M,地球)机械能守恒:
v
m
0 M f c
f
s
s
Wf Wf 0
N
v c
N
WN WN 0
质点系动能定理：
质点系的动能的增量等于作用于质点系的一切外力与
内力做功之和.
W ex
W in
n i1
1 2
mi vi2
n i1
1 2
mi vi20
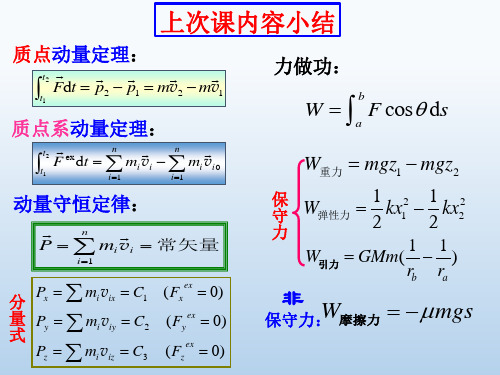
2.2.1 质点系动量定理
作用于质点系的合外力的冲量等于质点系动量的增量.
t2
系统内所有质点对同一参考点角动量的矢量和称为
质点系的角动量.
L Li ri pi ri mivi
i
i
i
dL dt
d dt
Li
i
Mi外
i
Mi内
i
0
M外
M 外
dL dt
积分得：
t2 t1
M外dt
L2
L1
注意：只有外力矩对质点系的角动量变化有贡献，
内力矩对质点系的角动量变化没有贡献.
W
F dr
l
F dr
acb
F dr
bda
0
a
c
F dr F dr F dr
acb
adb
bda
d
大学物理质点和质点系的动量定理
t1
I
O
F t2 t
O
I
t1 t2 t
t1
动量定理常应用于碰撞问题
F
t1 mv2 mv1 t2 t1 t2 t1
在△p一定时, △t 越小,则F越大
t2
Fdt
mv
mv1
F
mv2
注意
第三章 动量守恒和能量守恒
9/14
物理学
第五版
3-1 质点和质点系的动量定理 例 1 一质量为0.05kg、速率为10m/s的刚球,以与钢 板法线呈45º 角的方向撞击在钢板上,并以相同的速率和 角度弹回来.设碰撞时间为0.05s.求在此时间内钢板所受 到的平均冲力 F 解:由动量定理得 F t mv mv mv1 2 1 建立如图坐标系 x
t2
物体由于运动具有的机械效果 Objects with the mechanical effect because of moving 冲量(Impluse) (矢量Vector)
I
t1
Fdt
力对时间的累积效应
The time accumulation effects of forces
作用于质点系的合外力等于质点系动量随 时间的变化率. The combined external force acting on the mass point system is equal to the momentum variation rate of the mass point system with respect to time.
则
y
两边同乘以ydy， 则
2
y
1 3 1 d yv 2 y gdy ydy yv d yv gy yv 3 2 dt y yv 1 2 2 g y d y yv d yv v ( gy ) 2 0 0 3
I
O
F t2 t
O
I
t1 t2 t
t1
动量定理常应用于碰撞问题
F
t1 mv2 mv1 t2 t1 t2 t1
在△p一定时, △t 越小,则F越大
t2
Fdt
mv
mv1
F
mv2
注意
第三章 动量守恒和能量守恒
9/14
物理学
第五版
3-1 质点和质点系的动量定理 例 1 一质量为0.05kg、速率为10m/s的刚球,以与钢 板法线呈45º 角的方向撞击在钢板上,并以相同的速率和 角度弹回来.设碰撞时间为0.05s.求在此时间内钢板所受 到的平均冲力 F 解:由动量定理得 F t mv mv mv1 2 1 建立如图坐标系 x
t2
物体由于运动具有的机械效果 Objects with the mechanical effect because of moving 冲量(Impluse) (矢量Vector)
I
t1
Fdt
力对时间的累积效应
The time accumulation effects of forces
作用于质点系的合外力等于质点系动量随 时间的变化率. The combined external force acting on the mass point system is equal to the momentum variation rate of the mass point system with respect to time.
则
y
两边同乘以ydy， 则
2
y
1 3 1 d yv 2 y gdy ydy yv d yv gy yv 3 2 dt y yv 1 2 2 g y d y yv d yv v ( gy ) 2 0 0 3
3-1 质点和质点系的动量定理
在直角坐标系中， 在直角坐标系中，动量定理分量形式
v v v v I = Ixi + I y j + Izk
I x = ∫ Fx dt = mv x − mv0 x
t0 t t
I y = ∫ Fy dt = mv y − mv0 y
t0 t
I z = ∫ Fz dt = mvz − mv0 z
t0
t2
参考系
t2 时刻
动量定理
v v mv1 mv2 S系 系 v v v v S’系 m( v1 − u ) m( v2 − u ) 系
∫t
t2
1
v v v F (t )dt = mv 2 − mv1
动量定理常应用于碰撞问题
v v v ∫t1 mv2 − mv1 F= = t 2 − t1 t 2 − t1
例 1 一质量为 0.05kg、速率为 、速率为10m·s-1 的刚球 , 以 角的方向撞击在钢板上, 与钢板法线呈 45º 角的方向撞击在钢板上 并以相同的 速率和角度弹回来. 速率和角度弹回来 设碰撞时间为 0.05s . 求在此时间 内钢板所受到的平均冲力 F . 建立如图坐标系, 解 建立如图坐标系 由动量定理得
答：冲量的方向是动量增量的方向。 冲量的方向是动量增量的方向。
问题二：冲量大小或动量增量与哪两个因素有关？ 问题二：冲量大小或动量增量与哪两个因素有关？ 与哪两个因素有关
答：力与时间的增量；要产生同样的动量的增量， 力与时间的增量；要产生同样的动量的增量， 力大力小都可以：力大则时间短些； 力大力小都可以：力大则时间短些；力小则时间 长些。只要力的时间累积即冲量一样， 长些。只要力的时间累积即冲量一样，就产生同 样的动量增量。 样的动量增量。
2动量定理2
N = 3×10 ×(9.8 + 2×9.8×1.5 / 0.01)
3
顿 = 1.9×10 牛
6
解法二：考虑从锤自由下落到静止的整个过程， 解法二：考虑从锤自由下落到静止的整个过程， 动量变化为零。 动量变化为零。 重力作用时间为
动量定理
τ + 2h/ g
支持力的作用时间为τ 根据动量定理，整个过程合外力的冲量为零， 根据动量定理，整个过程合外力的冲量为零，即
动量定理
Ix = ∫t1 F dt = mv2x mv1x x
t2
I y = ∫t1 Fy dt = mv2 y mv y 1
t2
Iz = ∫t1 F dt = mv2z mv z z 1
t2
显然，动量定理在某一方向上也成立。 显然，动量定理在某一方向上也成立。
在一维情况下,力的整个作用 在一维情况下 力的整个作用 时间内， 时间内，平均力的冲量等于变 力的冲量
解： t时刻，链条下垂部分长度为 y 设
m2
λ
o
y
以链条为一系统有：
下垂部分所受重 力 P1 = m1 g ,
桌上部分所受重 力 P2 = m2 g , 桌上部分所受支持 力 FN = m2 g ,
m1
y
所以系统所受合外力为：F ex = m1 g , 其中 m1 = λ y
在dt间隔内，由动量定理可得： F ex dt = λ ygdt = dp
一.冲量 质点动量定理
重写牛顿第二定律的微分形式
Fdt = dp = d(mv)
考虑一过程， 考虑一过程，时间从t1-t2，两端积分
∫t F dt = ∫p d p = p2 p1 = mv2 mv1
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
mi vi
n i 1
(m1v10 mi vi0
m2 v 20
)
第三章 动量守恒和能量守恒
6/14
物理学
第五版
3-1 质点和质点系的动量定理
I p p t2 F exdt t1
n
mi vi
i 1
n
mi vi0
i 1
0
质点系动量定理:作用于系统的合外力的冲量等于
Newton’s Second law :When a mass point with momentum
p is under the effect of the combined external force F, the
time variation of the momentum is equal to the external
动量(Momentum)冲量 (Impulse) 动量定理
(Theorem of momentum)
动量守恒
(Momentum conservation)
动能(Kinetic energy) 功(Work) 动能定理
(Theorem of kinetic energy)
机械能守恒
(Mechanical energy conservation)
第三章 动量守恒和能量守恒
1/14
物理学
第五版
3-1 质点和质点系的动量定理
一 动量(Momentum)冲量(Impulse) 质点的动量定理(Theorem of momentum of amass point)
牛顿第二定律:动量为p的质点,在和外里F的作用下,其 动量随时间的变化率等于作用在质点上的合外力.
mvcos (mvcos) 2mvcos
m v2
Fyt mv2y mv1y mvsinα mvsin 0
y
F
Fx
2mv cos
t
14.1N
方向沿x轴反向
第三章 动量守恒和能量守恒
11/14
物理学
第五版
3-1 质点和质点系的动量定理
例 2 一柔软链条长为l,单位长度的质量为.链条放
物理学
第五版
3-1 质点和质点系的动量定理
例 1 一质量为0.05kg、速率为10m/s的刚球,以与钢
板法线呈45º角的方向撞击在钢板上,并以相同的速率和
角度弹回来.设碰撞时间为0.05s.求在此时间内钢板所受
到的平均冲力 F
解:由动量定理得 Ft
建立如图坐标系
mv2
mv1
x
mv1
Fxt mv2x mv1x
在桌上,桌上有一小孔,链条一端由小孔稍伸下,其余部分
堆在小孔周围.由于某种扰动,链条因自身重量开始落下.
求链条下落速度与落下距离之间的关系.设链与各处的
摩擦均略去不计,且认为链条软得可以自由伸开 .
解 以竖直悬挂的链条
和桌面上的链条为一系统,
m2
建立如图坐标
O
则 F ex m1g yg
m1
第三章 动量守恒和能量守恒
8/14
物理学
第五版
注意
3-1 质点和质点系的动量定理
区分外力和内力 内力仅能改变系统内某个物体的动量， 但不能改变系统的总动量.
第三章 动量守恒和能量守恒
9/14
物理学
第五版
3-1 质点和质点系的动量定理
讨论
F
1、F 为恒 力
F
I Ft
2、F 为变力
F
I
第三章 动量守恒和能量守恒
3/14
物理学
第五版
3-1 质点和质点系的动量定理
I
t2 t1
Fdt
mv2
mv1
质点的动量定理:在给定的时间间隔内,外力作
用在质点上的冲量,等于质点在此时间内动量 的增量.
Theorem of momentum of a mass point: In the given time interval, the impulse on a mass point by a external force is equal to the increment in the momentum of that mass point in the same time interval
第三章 动量守恒和能量守恒
4/14
物理学
第五版
3-1 质点和质点系的动量定理
在直角坐标系分量表示
In cartesian coordinate componet equations
I
x
t2 t1
Fxdt
mv2x
mv1x
I
y
t2 t1
Fydt
mv2 y
mv1y
dt
3
2
g y y2 d y yv yv d yv
0
0
v ( 2 gy)
1 2
3
第三章 动量守恒和能量守恒
13/14
物理学
第五版
选择进入下一节：
本章目录
3-0 教学基本要求
3-1 质点和质点系的动量定理 3-2 动量守恒定律 *3-3 系统内质量移动问题
3-4 动能定理
3-5 保守力与非保守力 势能
物理学
第五版
3-1 质点和质点系的动量定理
力的累积效应
The accumulative effects of forces
对时间积累
The time accumulative effects of forces
对空间积累
The space accumulative effects of forces
force on the same direction
第三章 动量守恒和能量守恒
5/14
物理学
第五版
3-1 质点和质点系的动量定理
二 质点系的动量定理
(Theorem of momentum of the mass point system)
对两质点分别应用质点动量定理
t2
t1
t2
t1
(F1
momentum of that system.
N
F ex Fi 11
I t2 F exdt t1
n
n
p0 mi vi0
p mivi
i 1
i 1
第三章 动量守恒和能量守恒
7/14
物理学
第五版
3-1 质点和质点系的动量定理
对于无限小的时间间隔内,质点系动量定理.
第三章 动量守恒和能量守恒
14/14
I
I
t2 t1
Fdt F
(t2
t1)
O t1
t2 t O t1
t2 t
动量定理常应用于碰撞问题
F
t2 t1
Fdt
mv2
mv1
t2 t1
t2 t1
mv1
mv mv 2
注意
在△p一定时, △t 越小,则F越大
F
第三章 动量守恒和能量守恒
10/14
y
由质点系动量定理得
F exdt dp
y
第三章 动量守恒和能量守恒
12/14
物理学
第五版
3-1 质点和质点系的动量定理
F ex yg F exdt dp
又 dp d(yv)
m2
O
ygdt d( yv)
则
yg dyv
dt
两边同乘以ydy， 则
m1
y
y
y2gdy ydy dyv yv dyv 1 gy3 1 yv2
I
z
t2 t1
Fzdt
mv2 z
mv1z
说明
质点在某方向上的动量增量,仅与质点
(Description) 在该方向上所受外力的冲量有关．
The momentum increment of the mass point on some
direction only depends on the impulse of the extermal
(F2
F12 )dt
F21)dt
m1v1
m2v2
m1v10
m2v20
质点系
F1
F12
m1
F2
F21
m2
因内力
t2
t1
(F1
F2F)1d2tF(2m11v10 m2v2 )
t2
F
exdt
t1
n i 1
物体由于运动具有的机械效果
Objects with the mechanical effect because of moving
冲量(Impluse) (矢量Vector)
I
t2
Fdt
t1
力对时间的累积效应
The time accumulation effects of forces
forcFeactindgponthde (pmarvtic)le.
Fdt
dp
d
(mv)Biblioteka dtdm 0 dt
t2