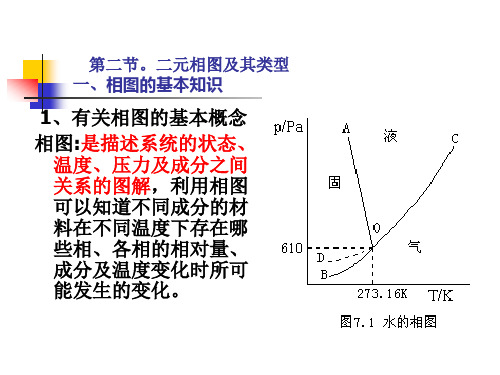
1 相图基本知识 一元相图
合集下载
一元相图
（二）同质多晶现象
同质多晶现象：同一化学成分，由于形成的条件不同，晶体结构上有很大差别，这种 现象叫同质多晶现象。 多晶转变：当温度和压力的条件产生变化时，同质多晶间会发生相互转变，这种现象 叫多晶转变。 如金刚石和石墨，α石英和β石英等。这些虽然都是在熔点之下产生的，但在相图中是 很明确地表示出来的。
P/kPaCFra bibliotek液A
固
101.325/kPa 0.610/kPa D B 273.16K 273.25K T/K K G O
汽
图1-2-1
（2）相图中各曲线的斜率及位置的规律 相会于三相点的各单变量平衡曲线的相互排列规律是：其中任一个单变量平衡曲线在三相点 外的延长部分必须在其它二曲线之间通过，或必须服从克—克方程。
101325
N’ D’ D
M
O
C
β-石英
N
（a)
时间
L
393 436 603 846 1143 1743 1873 1943 1986
T/K
T/K T/K 石英玻璃 1986
图1-2-6 SiO2系统相图
T/K 1986 α方石英
1743
ΔV=0.2% ΔV=2.8% 603 (b) 时间 (c) β-方石英 436 393 时间 (d) 时间 ΔV=0.2%
图1-2-1 这就证明了平衡曲线位置的排列顺序。
（3）亚稳区和亚稳相 过冷现象：如果实验时小心控制条件，可使水冷至 273.15K以下仍无冰出现，这种现象称为过冷现象。
亚稳区：这时图1-2-1中的AO线可延伸到D点。OD线
在OB线之上，这表示过冷水的蒸汽压要比同温度下的冰 的蒸汽压大。过冷水不如冰稳定，因此，在OD线上水和 蒸汽是处于亚稳的平衡状态。过冷水可作为亚稳相，同样
第五章1-相结构与一元相图2013春
1.气体所有气体均作为一相； 2.液体中纯粹液体和真溶液为一相，互不相 容的液体为二相； 3.固体中熔融的固相溶液为一相，固态时有 几种物质就为几相；
上海大学材料学院，施鹰
2
Aluminum-Copper Alloy
多晶Al2O3陶瓷
含 4 wt.% C 铸铁的显微结构
每个相可以是纯金属、固溶 体或化合物 材料的组织：对于构成材料 相的类型、形状、数量、大 小、分布等特征的描述。
上海大学材料学院，施鹰
9
5.3 吉布斯相律
1876年，J.W.Gibbs 用热力学作为工具，导 出了多相平衡系统的普遍规律 → 相率
关于相平衡系统的普遍规律。揭示了系统自由度数 f 与独立组分数 C 和相数 P 间的关系。
相律的表达式为
f=c–p+n
式中 f 为系统的自由度数；c 为独立组元数；p为平衡相数；n 为外界条件数(如温度、压力、电场、重力场等)。
Pure Water
20 40 60 80 100 Co =Composition (wt% sugar)
12
相图中的信息：Effect of T & Composition (Co)
• Changing T can change # of phases: path A to B. • Changing Co can change # of phases: path B to D. B (100°C,70) D (100°C,90) 100
20 40 60 70 80 100 C =Composition (wt% sugar) o 上海大学材料学院，施鹰
相图的发展
相图都是根据大量实验建立起来的。建立相图的关键是 要准确地测出各成分的相变临界点(临界温度)。 测临界点的方法通常有热分析法、金相分析、X射线结构 分析、磁性法、膨胀法、电阻法等。通常是几种方法配合使 用以保证测试的精度。 1900年，形成完善的Fe－C相图； 20世纪30－40年代，由于X射线衍射等一批现代分析手段 的出现和完善，相图的准确性和测定速度大幅度提高； 《二元合金相图》；《三元合金相图》；《陶瓷学家用相 图》 20世纪70年代后，电脑成功应用于计算和预测新材料体系 上海大学材料学院，施鹰 相图，指导新材料设计。
第五章 相图
第三节 二元共晶相图及合金凝固
（2）共晶合金（分析要点） ① 凝固过程（冷却曲线、相变、组织示意图）。 ② 共晶线上两相的相对量计算。 ③ 室温组织（α＋β）及其相对量计算。
2h
图4-28 Pb-Sn共晶合金平衡凝固过程示意图
1) 在液体中α 和β 同时具有析出条件，都可以析出。
2) 由于α 和β 析出过程在成分上可以互相补充和促进， 共同析出。
二元匀晶相图
一、匀晶相图及其分析 （1）匀晶转变：由液相直接结晶出单相固溶体的 转变。 （2）匀晶相图：具有匀晶转变特征的相图。 Cu-
Ni、 Cu-Au、 Au-Ag、Fe-Cr等
（3）相图分析（以Cu-Ni相图为例） 两点：纯组元的熔点； 两线：L, S相线； 三区：L, α, L+α。
固溶体合金的平衡结晶
金相法
膨胀法 电阻法
热分析法（以Cu-Ni系相图为例）：
配制一系列成分不同的Cu-Ni合金； 测定上述合金的冷却曲线 找出各合金的临界点 以温度为纵坐标、以成分为横坐标的图中，将各临 界点连接起来即得到Cu-Ni合金相图
二.相图的建立
名称 晶格类型 熔点 合金1 合金2 合金3 …….. 合金9 合金10 合金11 A金属 fcc 高 100% 90% 80% …….. 20% 10% 0% B金属 fcc 低 0% 10% 20% ……. 80% 90% 100%
二、包晶体转变
过程
成分为P点合金的凝固 β 相的形核在α 相晶体和液体 的边界处，由于β 相的成分介于 液体和α 相之间，所以它是靠消 耗部分已有的α 相和部分液体来 实现。 β 相的生长在液体和α 相的交 界面处最有利，沿边界同时消耗 液体和α 相来长大，形成的β 相 包围在α 相外围，将α 相与液体 分隔开，所以把这种转变称为包 晶转变。
材料科学基础_第5章_相 图
点在二元相图中对应一个点。 5. 连接各相同意义的临界点(开始点或终了点)，并做出相应
的曲线。 6.用相分析法测出向图中各相区所含的相，将他们的名称填
入相应的相区内，就得到了Cu—Ni合金的二元相图。
30
热分析法建立的Cu—Ni相图
31
5.1.4 相图热力学基础
➢ 相平衡的热力学条件 ➢ 相平衡：
1、热分析法 原理：根据系统在冷却过程中温度随时间的变化情况来
判断系统中是否发生了相变化。 做法： (1) 将样品加热成液态； (2) 令其缓慢而均匀地冷却，记录冷却过程中系统在不
同时刻的温度数据； (3) 以温度为纵坐标，时间为横坐标，绘制成温度－时
间曲线，即步冷曲线(冷却曲线)； (4) 由若干条组成不同的系统的冷却曲线就可以绘制出
90 80 70
60
B% 50 40
30 20
10
10 20 30 40 C% 50 60
70 80 90
A
C
90 80 70 60 50 40 30 20 10
← A% 25
(3) 等腰成分三角形 当三元系中某一组元含量较少，而另两组元含量较大
时，合金成分点将靠近等边成分三角形的某一边。为了使 该部分相图清晰的表示出来，常采用等腰三角形，即将两 腰的刻度放大,而底边的刻度不变。
相图。
29
5.1.3 相图的建立
➢ 下面以热分析法为例说明如何测绘Cu—Ni相图，其步骤如 下：
1. 按质量分数先配制一系列具有代表性成分不同的Cu—Ni 合金。
2. 测出上述所配合金及纯Cu、纯Ni的冷却曲线。 3. 求出各冷却曲线上的临界点。 （曲线的转折点） 4. 将各临界点投到对应的合金成分-温度坐标中，每个临界
的曲线。 6.用相分析法测出向图中各相区所含的相，将他们的名称填
入相应的相区内，就得到了Cu—Ni合金的二元相图。
30
热分析法建立的Cu—Ni相图
31
5.1.4 相图热力学基础
➢ 相平衡的热力学条件 ➢ 相平衡：
1、热分析法 原理：根据系统在冷却过程中温度随时间的变化情况来
判断系统中是否发生了相变化。 做法： (1) 将样品加热成液态； (2) 令其缓慢而均匀地冷却，记录冷却过程中系统在不
同时刻的温度数据； (3) 以温度为纵坐标，时间为横坐标，绘制成温度－时
间曲线，即步冷曲线(冷却曲线)； (4) 由若干条组成不同的系统的冷却曲线就可以绘制出
90 80 70
60
B% 50 40
30 20
10
10 20 30 40 C% 50 60
70 80 90
A
C
90 80 70 60 50 40 30 20 10
← A% 25
(3) 等腰成分三角形 当三元系中某一组元含量较少，而另两组元含量较大
时，合金成分点将靠近等边成分三角形的某一边。为了使 该部分相图清晰的表示出来，常采用等腰三角形，即将两 腰的刻度放大,而底边的刻度不变。
相图。
29
5.1.3 相图的建立
➢ 下面以热分析法为例说明如何测绘Cu—Ni相图，其步骤如 下：
1. 按质量分数先配制一系列具有代表性成分不同的Cu—Ni 合金。
2. 测出上述所配合金及纯Cu、纯Ni的冷却曲线。 3. 求出各冷却曲线上的临界点。 （曲线的转折点） 4. 将各临界点投到对应的合金成分-温度坐标中，每个临界
相图—基本定义：相,成份,平衡,一元相图
７．活化能
图８给出了两个不同温度下的分子（或原子）能量的基本分布。可以看出
是能量为Ea或者能量比Ea大的分子或原子的比例。阿累尼乌斯等式告 诉我们当且仅当相互反应的物质间至少存在临界能Ea。因为含有这种能量的或者
更大能量的粒子的比例是
，所以反应速率正比于该式。
当Ea值增加的时候，需要的能量也增加，并且分子要获得这种能量也变得更
（１）在反应结束时，化学上并不发生改变 （２）只能需要极少的量 （３）催化活性是常常正比于它的表面积 （４）催化剂是有选择性的：如果出现不同的反应，催化剂可以在不影响其
积分:
或者,
得: +常数
当t=0时,取c=co,我们有常数=ln co.并且:
或者:
也可以写作:
图3 反应率与浓度的关系
从上面我们可以看到在H2O2分解的反应中, (ln c)-t 的图像是一条直线(图3.)。 它是一级反应的特征-----浓度指数(n)是“1”。
4
一级反应: 放射性衰变 等式:
课件（八）
记住:在所有的动力学和热力学的计算中,必须使用“绝对温度尺度”开尔文 (K)表示,它与摄氏温度的关系为: K = oC + 273.16 因此, 0K = –273.16 oC,它与热力学绝对温度对应.logk VS 1/T的线性图揭示 出了以下关系:
在后面的推导重,这个经验关系可以方便地写成:
其中A是比例常数,有时被叫作反应常数；R是气体常数其值等于8.31 J/mole K； E是反应活化能,单位是J/mole K；而e是自然对数的底数。因为ln x = 2.3 log10x, 我们可以将上式重新写成:
6. 阿累尼乌斯理论
阿累尼乌斯提出的分子反应理论主要为定性的理论,这让我们得出了速率常 数的经验表达式。后来的理论(这在3.091课程范围之外) 阐述更详细并且使原来 的观点更加定量。
一元相图
1.Al2O3－SiO2系相图
Al2O3-SiO2系相图从1909年发表第一篇相图开始至今
已有十几篇，Al2O3-SiO2系在耐火材料中应用相当广
泛，从耐火砖划分可见，硅质、半硅质、粘土质、高 铝质。
(1) 对硅砖而言，从相图可见，液相线非常陡，说明 在硅砖中引入少量Al2O3会使SiO2熔点急剧降低，如按 重量百分比在硅砖中引入1%Al2O3则在1595℃产生 18.2%L相，因此对硅砖生产要严格控制Al2O3含量，防
§1-2 相图基本类型
一、一元相图
晶型Ⅰ 晶型Ⅱ 熔体
具有双向转变的单元相图
具有单向转变的单元相图
实际一元相图
经常接触的一元实际相图：SiO2、ZrO2、C2S、H2O、石墨等。
870 C 1470 C 1723 C 石英 鳞石英 - 方石英 熔体 573C 163 C 180 ~ 270C 急冷 石英 - 鳞石英 - 方石英 石英玻璃 117 C - 鳞石英
SiO2 多晶转变的体积变化
一级变体 间的转变 计算采取 的温度 /℃ 1000 1000 1000 1000 在该温度下 转变时体积 效应/% +16.0 +15.4 +15.5 -0.9 二级变体 间的转变 计算采取 的温度 /℃ 573 117 163 150 在该温度下转 变时体积效应 /% +0.82 +0.2 +0.2 +2.8
原料制造的硅质耐火制品。制品SiO2含量应在93~96 wt%。 应用：焦炉、热风炉和玻璃熔窑等。 工业制造要点：制造稳定致密的硅砖，希望制品中鳞石英 越多越好，这是硅砖烧成的核心问题，所以硅砖烧成
1、相图的基本知识及匀晶相图
1 K0 RX mCo / K0+GX T A mCo1 TA exp ÷ K D 0
G m Co 1 K R D K0
化简得：
(8)
② 影响成分过冷的因素 ·合金本身 m、Co越大，D越小，K0<1 时K0值越小，K0>1时K0值越大。成分 过冷倾向增大。 – ·外界条件 G越小(实际温度分布越平 缓）， 凝固速度R越大，成分过冷倾 向增大。临界过冷度G1，成分过冷消 失
2．液体中仅借扩散而混合的情况 • 当凝固速度很快，无搅拌时，固体中无扩散而液体中 仅靠扩散而混合。这种情况比较符合实际凝固情况
Ke=1
X C S C 0 1 L
11
C0
1 K0 RX C L C 0 1 exp K D 0
式中 R：凝固速度 δ：边界层厚度 D：扩散系数 • A 当凝固速度非常缓慢时， Rδ/D 0 ，Ke K0 即为液体中溶质完全混合的情况。 • B．当凝固速度非常大时，e - Rδ/D 0 ， Ke=1，为液 体中溶质仅有通过扩散而混合的情况。 • C．当凝固速度介于上面二者之间， K0＜Ke＜ 1， 液体中溶质部分混合的情况。 • Ke方程式图解
临界过冷度g1成分过冷消失六固溶体凝固时的生成形态当在液固界面前沿有较小的成分过冷区时平面生长生长就不稳定如液固界面有些偶然的突起的部分它们就伸入过冷区中其生长速度加快而进一步凸向液体使界面出现胞状组织如界面前沿的成分过冷区甚大凸出部分就能继续伸向过冷液相中生长同时在其侧面产生分枝形成树枝状组织
相图的基本知识
□ ○
正常凝固过程
在讨论金属合金的实际凝固问题时,一般不考虑固相内 部的原子扩散，而仅讨论液相中的溶质原子混合均匀程度问 题。以下讨论的均为正常凝固过程。
G m Co 1 K R D K0
化简得：
(8)
② 影响成分过冷的因素 ·合金本身 m、Co越大，D越小，K0<1 时K0值越小，K0>1时K0值越大。成分 过冷倾向增大。 – ·外界条件 G越小(实际温度分布越平 缓）， 凝固速度R越大，成分过冷倾 向增大。临界过冷度G1，成分过冷消 失
2．液体中仅借扩散而混合的情况 • 当凝固速度很快，无搅拌时，固体中无扩散而液体中 仅靠扩散而混合。这种情况比较符合实际凝固情况
Ke=1
X C S C 0 1 L
11
C0
1 K0 RX C L C 0 1 exp K D 0
式中 R：凝固速度 δ：边界层厚度 D：扩散系数 • A 当凝固速度非常缓慢时， Rδ/D 0 ，Ke K0 即为液体中溶质完全混合的情况。 • B．当凝固速度非常大时，e - Rδ/D 0 ， Ke=1，为液 体中溶质仅有通过扩散而混合的情况。 • C．当凝固速度介于上面二者之间， K0＜Ke＜ 1， 液体中溶质部分混合的情况。 • Ke方程式图解
临界过冷度g1成分过冷消失六固溶体凝固时的生成形态当在液固界面前沿有较小的成分过冷区时平面生长生长就不稳定如液固界面有些偶然的突起的部分它们就伸入过冷区中其生长速度加快而进一步凸向液体使界面出现胞状组织如界面前沿的成分过冷区甚大凸出部分就能继续伸向过冷液相中生长同时在其侧面产生分枝形成树枝状组织
相图的基本知识
□ ○
正常凝固过程
在讨论金属合金的实际凝固问题时,一般不考虑固相内 部的原子扩散，而仅讨论液相中的溶质原子混合均匀程度问 题。以下讨论的均为正常凝固过程。
相图
1 相图的基本知识
根据相图可确定不同 成分的材料在不同温度下 组成相的种类、各相的相 对量、成分及温度变化时 可能发生的变化。 仅在热力学平衡条件 下成立，不能确定结构、 分布状态和具体形貌。
§1 相 律
相律：研究相态变化的规律。 相数(P )，组元数(C )，自由度数（f ） 一、相与相数（P）
• ① ② ③
注意：在材料学中 各微区的成分不完全均匀，存在成分偏聚 同一相的不同晶粒也存在界面 材料中的相，均匀是指成分、结构、及性质要 么宏观上完全相同，要么呈现连续变化没有突 变现象。
基本概念
• 单组元晶体(纯晶体)：由一种化合物或金属组成的 晶体。该体系称为单元系 • 从一种相转变为另一种相的过程称为相变（phase transformation）。 若转变前后均为固相，则成为固 态相变（solid phase transformation ）。 • 从液相转变为固相的过程称为凝固(solidification)。 若凝固后的产物为晶体称为结晶(crystallization)。 • 相图(phase diagram)：表示合金系中合金的状态与 温度、成分之间的关系的图形，又称为平衡图或状 态图。 • 单组元相图(single phase diagram)是表示在热力学平 衡条件下所存在的相与温度，压力之间的对应关系 的图形。
• 整理上式： • 式中: Sm为1mol物质由相变为相的熵变;
•
Vm为1mol物质由相变为相的体积变化.
• 因为是平衡相变,有: • Sm=Lm/T • Lm: 物质的相变潜热; • T: 平衡相变的温度. • 代入(2)式: • dp/dT=Lm/TVm (3) • (3)式称为克拉贝龙方程. • 克拉贝龙方程适用于纯物质任何平衡相变过程,应用范围 很广.
相图的基本知识及单元系相图
5.1 相图的基本知识
相律的应用
① 利用相律可以判断在一定条件下系统最多可能平衡共存的相数 f＝C－P＋1 P＝C－f＋1
压力给定时，最多平衡相数比组元数多1 P＝C＋1 （压力给定时，最多平衡相数比组元数多1） 单元系，C=1 P=2 最多两相共存。 例：单元系，C=1，P=2 最多两相共存。
利用它可解释纯金属与二元合金结晶时的差别。 ② 利用它可解释纯金属与二元合金结晶时的差别。 纯金属结晶， 固共存， 说明结晶为恒温。 纯金属结晶，液－固共存，f=0，说明结晶为恒温。 二元系金属结晶两相平衡， 二元系金属结晶两相平衡，f= 2－2＋1=1，说明有一个可变因 表明它在一定（ 范围内结晶。 素（T），表明它在一定（T）范围内结晶。 二元系三相平衡， 此时温度恒定， 成分不变， 二元系三相平衡 ， f= 2 － 3 ＋ 1=0， 此时温度恒定 ， 成分不变 ， 各因素恒定。 各因素恒定。
系中旧相 新相的转变过程称为相变。 新相的转变过程称为相变。 若转变前后均为固相 ， 则称为 固态相变 （ solid phase transformation ）。 从液相转变为固相的过程称为凝固 凝固( 从液相转变为固相的过程称为凝固(solidification)。若凝 ) 固后的产物为晶体称为结晶 结晶( 固后的产物为晶体称为结晶(crystallization)。 )
1 相图的基本知识
相律是检验、分析和使用相图的重要工具。 相律是检验、分析和使用相图的重要工具。利用它 可以分析和确定系统中可能存在的相数， 可以分析和确定系统中可能存在的相数，检验和研究 相图。 相图。 注意使用相律有一些限制： 注意使用相律有一些限制： 只适用于热力学平衡状态，各相温度相等（ （1）只适用于热力学平衡状态，各相温度相等（热量 平衡） 各相压力相等（机械平衡） 平衡）、各相压力相等（机械平衡）、各相化学势相 化学平衡） 等（化学平衡）。 只表示体系中组元和相的数目， （2）只表示体系中组元和相的数目，不能指明组元和 相的类型和含量。 相的类型和含量。 不能预告反应动力学（即反应速度问题） （3）不能预告反应动力学（即反应速度问题）。 （ 4 ） f ≧0
材料科学基础第六讲-相图
温度降到3点时，合金III全部转化为β固 溶体。
3-4点时，为单相固溶体，不发生变化。 4点以下，将从β相析出次生相αII
§4.4其它类型的二元合金相图
第五节 复杂相图
§5.1 二元合金相图的分析和使用
I 包晶反应：L+α β II 包晶反应：L+ β γ III 包晶反应：L+ ε η IV 共析反应： β α + γ V 共析反应： γ α + δ VI 共析反应： δ α + ε VII 共析反应： ζ δ + ε VIII 包析反应： γ + ε ζ IX 包析反应： γ + ζ δ X 熔晶反应： γ ε + L XI 共晶反应： L η + θ
相律：表示在平衡条件下，系统的自由度数、组元 数和相数之间的关系。它是检验、分析和使用相图 的重要工具。
F=C-P+2
F-平衡系统的自由度数 C-平衡系统的组元数 P-平衡系统的相数
当压力为常数时：F=C-P+1
J. Willard Gibbs
自由度：指平衡系统中可以独立改变的因素（如温度， 美国物理学家 压力，成分）等。纯金属的自由度最多一个，二元系 （1839-1903）
包晶转变区的特征是：反应相是液相和一个固相，其成分点位于水 平线的两端，所形成的固相位于水平线中间的下方。
典型合金的平衡结晶及组织
（一）含银量42.4%的铂银合金
当合金I自液态缓冷到1点时， 开始结晶出α相，与匀晶系 合金的结晶完全相同
当温度降到tD时，合金中 α 相的成分到P点，液相的成 分到C点。
应用相图时要注意的问题
连接线（等温线）：两个平衡相成分点之间的连线
第三节 一元系相图
3-4点时，为单相固溶体，不发生变化。 4点以下，将从β相析出次生相αII
§4.4其它类型的二元合金相图
第五节 复杂相图
§5.1 二元合金相图的分析和使用
I 包晶反应：L+α β II 包晶反应：L+ β γ III 包晶反应：L+ ε η IV 共析反应： β α + γ V 共析反应： γ α + δ VI 共析反应： δ α + ε VII 共析反应： ζ δ + ε VIII 包析反应： γ + ε ζ IX 包析反应： γ + ζ δ X 熔晶反应： γ ε + L XI 共晶反应： L η + θ
相律：表示在平衡条件下，系统的自由度数、组元 数和相数之间的关系。它是检验、分析和使用相图 的重要工具。
F=C-P+2
F-平衡系统的自由度数 C-平衡系统的组元数 P-平衡系统的相数
当压力为常数时：F=C-P+1
J. Willard Gibbs
自由度：指平衡系统中可以独立改变的因素（如温度， 美国物理学家 压力，成分）等。纯金属的自由度最多一个，二元系 （1839-1903）
包晶转变区的特征是：反应相是液相和一个固相，其成分点位于水 平线的两端，所形成的固相位于水平线中间的下方。
典型合金的平衡结晶及组织
（一）含银量42.4%的铂银合金
当合金I自液态缓冷到1点时， 开始结晶出α相，与匀晶系 合金的结晶完全相同
当温度降到tD时，合金中 α 相的成分到P点，液相的成 分到C点。
应用相图时要注意的问题
连接线（等温线）：两个平衡相成分点之间的连线
第三节 一元系相图
材料科学基础-第4章相图
第四章
材料的相结构与相图
PHASE STRUCTURE AND PHASE DIAGRAM OF MATERIALS
材料的相结构 二元相图及其类型 复杂相图分析 相图的热力学基础 三元相图及其类型
THE END
第一节
材料的相结构
PHASE STRUCTURE OF MATERIALS
相 — 体系中成分、结构、性能相同且与 其他部分有界面隔开的均匀部分或 连续变化的部分 合金中的相
(4) 晶内偏析及其有害影响 晶内偏析—固溶体晶粒内部成分不均匀的 现象，也称枝晶偏析．枝干富含高熔点 组元，枝间富含低熔点组元． 偏析倾向：取决于 L/S 相线垂直距离 偏析程度：取决于 L/S 相线水平距离 有害影响
⎧ ⎨ ⎩
降低强度、塑性、韧性 降低抗腐蚀性能 加热时过早熔化
(5) 均匀化退火—将有晶内偏析的材料加热至 固相线以下100～200℃长期保温
E AB E AB
1 = ( E AA + E BB ) 2 1 > ( E AA + E BB ) 2 1 < ( E AA + EBB ) 2
无序 偏聚 有序
2) 有序固溶体（超结构） 能量条件 形成条件
E AB 1 < ( E AA + EBB ) 2
成分条件 A、B成一定比例 温度条件 低于一定温度
5) 具有匀晶相图的陶瓷系统
Mg2SiO4→(Mg,Fe)2SiO4→(Fe,Mg)2SiO4→Fe2SiO4
Mg2SiO4-Fe2SiO4 相图
Mg[CO3]－Fe[CO3]， K[AlSi3O8]－Na[AlSi3O8] 其它： 菱镁矿 菱铁矿 钾长石 钠长石
2. 共晶相图及结晶分析 1) 相图分析
材料的相结构与相图
PHASE STRUCTURE AND PHASE DIAGRAM OF MATERIALS
材料的相结构 二元相图及其类型 复杂相图分析 相图的热力学基础 三元相图及其类型
THE END
第一节
材料的相结构
PHASE STRUCTURE OF MATERIALS
相 — 体系中成分、结构、性能相同且与 其他部分有界面隔开的均匀部分或 连续变化的部分 合金中的相
(4) 晶内偏析及其有害影响 晶内偏析—固溶体晶粒内部成分不均匀的 现象，也称枝晶偏析．枝干富含高熔点 组元，枝间富含低熔点组元． 偏析倾向：取决于 L/S 相线垂直距离 偏析程度：取决于 L/S 相线水平距离 有害影响
⎧ ⎨ ⎩
降低强度、塑性、韧性 降低抗腐蚀性能 加热时过早熔化
(5) 均匀化退火—将有晶内偏析的材料加热至 固相线以下100～200℃长期保温
E AB E AB
1 = ( E AA + E BB ) 2 1 > ( E AA + E BB ) 2 1 < ( E AA + EBB ) 2
无序 偏聚 有序
2) 有序固溶体（超结构） 能量条件 形成条件
E AB 1 < ( E AA + EBB ) 2
成分条件 A、B成一定比例 温度条件 低于一定温度
5) 具有匀晶相图的陶瓷系统
Mg2SiO4→(Mg,Fe)2SiO4→(Fe,Mg)2SiO4→Fe2SiO4
Mg2SiO4-Fe2SiO4 相图
Mg[CO3]－Fe[CO3]， K[AlSi3O8]－Na[AlSi3O8] 其它： 菱镁矿 菱铁矿 钾长石 钠长石
2. 共晶相图及结晶分析 1) 相图分析
材料科学基础(讲稿5章)
Cu-Ni合金的铸态组织 ×50 树枝状
39
3）特点 (ⅰ) 冷却速度较快. (ⅱ) 开始结晶温度低于液相线. (ⅲ) 结晶中，剩余液相特别是晶粒内部成分不 均匀，先结晶的部分含高熔点组元较多，后 结晶的部分含低熔点组元较多；固相平均成 分偏离固相线，液相平均成分是否偏离液相 线随冷却速度而异. (ⅳ) 结晶终了温度低于固相线. (ⅴ) 通常不能应用杠杆定律. (ⅵ) 室温铸态有晶内偏析，形成树枝状组织.
Zn 2+、Ga 3+、Ge 4+、As 5+在Cu+中的最大固溶度（摩尔分数） 分别为38%、20%、12%、7%
6
Zn 2+、Ga 3+、Ge 4+、As 5+在Cu+中达最大 固溶度时所对应的e/a≈1.4→极限电子浓度
超过极限电子浓度，固溶体就不稳定，会 形成新相。 计算电子浓度时，元素的原子价指的是： 原子平均贡献出的共有电子数，与该元素 在化学反应时的价数不完全一致。
不平衡共晶形成原因分析
56
3）离异共晶——合金中 先共晶相的量很多，共晶 体的量很少时，共晶体中 与先共晶相相同的相依附 于先共晶相生长，将共晶 体中的另一相孤立在先共 晶相的晶界处．这种共晶 体两相分离的组织称为离 异共晶.
57ቤተ መጻሕፍቲ ባይዱ
Pb-Sb共晶离异组织（铸态）×400 α 相依附初生晶α 析出，形成离异的 白色网状β
58
3、包晶相图及其结晶
（1）相图分析 液相线 单相区 两相区 固相线 三相区 固溶度曲线 （2）包晶反应 在一定温度下，由一固定成分的液相与一个固定成 分的固相作用，生成另一个成分固定的固相的反应， 称为包晶反应。
材料物理基础第4章相图与相变-4.1一元相图-20161107X
• 作某一成分合金的垂线，可以确定该合金状态随温度的变化过程（相变）。
• 横坐标为成分轴，通常下 横坐标为质量百分数，上 状态点
横坐标为原子百分数。
• 纵坐标为温度轴，相图两 端的纵坐标也代表合金系
的两个组元的位置。
7
• 将给定两组元配制成一系列不同成分的合金； • 将它们分别熔化后在缓慢冷却的条件下，分别测出它们的冷却曲线； • 找出各冷却曲线上的相变临界点（曲线上的转折点）； • 将各临界点注在温度——成分坐标中相应的合金成分线上； • 连接具有相同意义的各临界点，并作出相应的曲线； • 用相分析法测出相图中各相区（由上述曲线所围成的区间）所含的相，将它们的
D
J
L（液相）
C
-Fe A
F
H
I
G（气相 ）
T
-Fe 体心立方结构；-Fe 面心立方结构（高温相）
6
-Fe 密排六方结构（高压相）；-Fe 体心立方结构（高温相）
（3）二元相图的表示方法和测定 • 相图中任一点位置表示确某一成分的合金在某一温度下的平衡状态（组成 相类型、数量和各相的成分）。
• 熔化曲线随压力升高远离压力轴，固相的熔点随压力增大而升高。大
多数物质熔化时体积膨胀，统称为硫型物质。图中三相点O点代表液体
能够稳定存在的最低温度。 熔化时系统体积收缩
V液 V固
dP 0 dT 熔
• 熔化曲线随压力升高靠近压力轴，固相的熔点随压力增大而降低。冰， 铋，镓，锗等少数物质熔化时体积缩小，统称为水型物质。图中三相 点O点代表固体能够稳定存在的最高温度。
• 用图形的方式表明热力学平衡条件下物质系统的状态（组成相）与成份、 温度、压力之间的关系。 • 表示物质在热力学平衡条件下的情况，又称为平衡相图。 • 相图上的每一个点都对应着的某一个平衡状态，相图上的每一个点称为 状态点。 热分析法 显微组织法 X射线分析法 硬度法 电阻法 热膨胀法 磁性法
1 相图基本知识 一元相图
气体 液体 固体 同素异晶体
相与组元
材料的整体性能取决于
存在相的数目 它们的相对量 各相的成分与结构 相的尺寸和空间分布
材料的相依赖于
整体成分 温度和压力等变量
相与组元
组元
构成材料的最简单、最基本、可以独立存在的 物质 将既不分解也不发生化学反应的稳定化合物也 视为一种组元
学习
工作
重要的指导意义
材料科学 基础
报考材料学科的 研究生的专业课 -重要保障
考研
毕业
教学大纲
相平衡与相图
相图基本知识 合金相图，共晶相图 包晶相图，其他类型相图 铁碳相图 铁碳相图 三元相图
教学大纲
凝固
纯金属凝固，均匀形核 非均匀形核 固溶体结晶 溶质浓度分布，合金的成分过冷 主要凝固组织，共晶合金的凝固 共晶形成机制，非平衡凝固
晶界相可以是单质也可以是化合物同素异晶体11相与组元材料的整体性能取决于相的尺寸和空间分布材料的相依赖于温度和压力等变量12相与组元构成材料的最简单最基本可以独立存在的物质将既不分解也不发生化学反应的稳定化合物也视为一种组元一元系二元系三元系及多元系统13相与组元苏打水冰水冰苏打水一元系h两相气液一元系h两相液固二元系h14相平衡相平衡每一个组元在各相中的化学势相等是多相系统处于热力学平衡的必要条件也是其相平衡的必要条件证明过程略机械平衡热平衡化学平衡化学热力学平衡相平衡化学势化学势各组元15相平衡相平衡宏观上系统中参与相变过程的各相长时间不再互相转化指成分和相对量时所达到的平衡
化学平衡
相平衡
每一个组元在各相中的化学势相等是多相系统 处于热力学平衡的必要条件，也是其相平衡的 必要条件（证明过程略）
相与组元
材料的整体性能取决于
存在相的数目 它们的相对量 各相的成分与结构 相的尺寸和空间分布
材料的相依赖于
整体成分 温度和压力等变量
相与组元
组元
构成材料的最简单、最基本、可以独立存在的 物质 将既不分解也不发生化学反应的稳定化合物也 视为一种组元
学习
工作
重要的指导意义
材料科学 基础
报考材料学科的 研究生的专业课 -重要保障
考研
毕业
教学大纲
相平衡与相图
相图基本知识 合金相图，共晶相图 包晶相图，其他类型相图 铁碳相图 铁碳相图 三元相图
教学大纲
凝固
纯金属凝固，均匀形核 非均匀形核 固溶体结晶 溶质浓度分布，合金的成分过冷 主要凝固组织，共晶合金的凝固 共晶形成机制，非平衡凝固
晶界相可以是单质也可以是化合物同素异晶体11相与组元材料的整体性能取决于相的尺寸和空间分布材料的相依赖于温度和压力等变量12相与组元构成材料的最简单最基本可以独立存在的物质将既不分解也不发生化学反应的稳定化合物也视为一种组元一元系二元系三元系及多元系统13相与组元苏打水冰水冰苏打水一元系h两相气液一元系h两相液固二元系h14相平衡相平衡每一个组元在各相中的化学势相等是多相系统处于热力学平衡的必要条件也是其相平衡的必要条件证明过程略机械平衡热平衡化学平衡化学热力学平衡相平衡化学势化学势各组元15相平衡相平衡宏观上系统中参与相变过程的各相长时间不再互相转化指成分和相对量时所达到的平衡
化学平衡
相平衡
每一个组元在各相中的化学势相等是多相系统 处于热力学平衡的必要条件，也是其相平衡的 必要条件（证明过程略）
一元和二元体系相图-2
FBK:过冷晶型Ⅱ的介稳相区.
线:BG过热晶型Ⅰ的升华曲线;
CG:过冷液相的蒸发线; GH:过热晶型Ⅰ的熔融曲线
点:
G点:晶型Ⅰ的熔点.
4. 可逆和不可逆的多晶转变
低温相T—P关系
1）可逆转变
实线表示稳定态，虚线表示介稳态。
晶体1 晶体2 液相
1/
2/ L/
液相蒸汽 压—T关系
高温相T—P关系
L
2 1
E[sE，A＋(B)]
3）冷却析晶过程中各相含量的计算
成分为C的体系在T1温度 时处于液、固两相平衡 状态 a
L
m d WB E
WL WA W
b
B+L
WLCL WAC A WC
由以上两式可以得出
T1 c WA
T A+L
A+B
WL C C A cm WA CL C md
5. SiO2系统的相图
SiO2在自然界储量很大，以多种矿物的形态出现。如水晶、玛瑙、砂岩、蛋白石、 玉髓、燧石等。 在常压和有矿化剂存在的条件下，固态有7 种晶型，其转变温度如下：
熔体(1600℃) α－石英 870℃
熔体 (1670℃) α－鳞石英 163℃ β－鳞石英 117℃ γ－鳞石英 同 级 转 变(慢) 1470℃ α－方石英 1723℃ 熔融石英 急 冷 石英玻璃 同 类 转 (快) 变
升华 B
g 温度
其它金属或SiO2 , 低温相转变为高温相的过程，ΔV>0, 则斜率>0 。
对于有晶型转变的，由于ΔV很小，因而其界线几乎是垂直的。
3. 有多晶转变的一元体系相图
一元体系相图中各平衡相 名称 E 压 强
相平衡与相图一元系
水泥生产要求：在水泥熟料中希望C2S 是以 β晶型存在的，而且要防止介稳的β－C2S 向稳定的γ－C2S 转化。
原因：
β－C2S具有胶凝性质，而γ－C2S 没有胶 凝性。 β－C2S向γ－C2S转化时，发生体积膨胀 （约增大9％）使C2S 晶体粉碎，水泥熟料 粉化，水泥质量下降。
措施：急冷工艺，使β－C2S来不及转变为 γ－C2S ，以β－C2S 型过冷的介稳状态存 在下来. 也可以采用加人少量稳定剂（如：P205、 Cr203、V2O5、BaO、Mn2O3等）的方法。稳定 剂能溶入β－C2S 的晶格内，与β－C2S形 成固溶体，使其晶格稳定，防止β－C2S 转 变成γ－C2S ，并在常温下长期存在。
dp fus H m dT T fusV
vap H m 0
fus H m 0
斜率为正。 斜率为正。
fus H 0, fusV 0
斜率为负。
1、一般分析
2、亚稳态分析 单组分体系相图的共同特征点： 点：三相共存；f=0 线：二相共存；f=1 面：一相；f=2
三、SiO2系统相图
七种晶相
冷却速度影响晶相
1、SiO2相图的一般内容
①一级变体间的转变：指变体间结构转变较 大，转变时形成新的结构。
特点：转变速度非常缓慢，转变常常是 从外部向内部转变的。因此，只有长时 间的恒定温度下，才能实现这种转变。
-石英→ - 鳞石灰 -石英→ -方石英 -石英→ - 石英玻璃 石英玻璃→ -方石英
Si02多晶转变时的体积变化可知,在各 SiO2 变体的高低温型的转变中，方石英之间 的体积变化最为剧烈，石英次之，而鳞石英之 间的体积变化最微弱。 因此，为了获得稳定的致密硅砖制品，就 希望硅砖中含有尽可能多的鳞石英，而方石英 晶体越少越好。这也就是硅砖烧成过程的实质 所在。
相图基础上课课件
高能物理
在高能物理中，相图用于描述高能粒子在不同能量和密度条件下的 状态和行为，如重核衰变、高能碰撞等过程。
04
相图分析技巧
观察法
通过直接观察相图，理解相变过程和相变温度。
观察法是最基本的相图分析技巧，通过观察不同温度和压力下的物质状态，可以 大致判断出相变温度和相变过程。这种方法简单易行，但精度较低，需要多次重 复实验以提高准确性。
THANKS
感谢观看
根据相图的结果，可以应用于材料科学、 化学工程、冶金等领域，为相关领域的研 究和应用提供基础数据和理论支持。
06
相图发展前景与展望
相图研究现状
相图在材料科学领域的应用
相图是材料科学领域中重要的研究工具，用于描述不同成分和温度下材料的相态变化。目 前，相图的研究已经广泛应用于合金、陶瓷、高分子等材料体系，为材料设计和制备提供 了基础数据和指导。
计算机模拟法是近年来发展迅速的一种方法，通过计算机模拟实验，可以模拟不同温度和压力下的物质状态，从而得到相图 。这种方法精度高，且可以模拟复杂体系的相变过程，但对计算机技术和实验数据要求较高。
05
相图实验操作
实验准备
01
02
03
04
实验材料
需要准备实验所需的材料，如 金属、玻璃、塑料等。
实验设备
相图发展趋势
01
相图数据的整合与共享
随着大数据时代的到来，相图数据的整合与共享成为发展趋势。通过建
立相图数据库和共享平台，可以方便地查询和获取各种材料的相图数据
，促进学术交流和合作。
02
相图研究的跨学科融合
相图研究涉及到物理、化学、材料科学等多个学科领域，因此跨学科的
融合是未来发展的重要趋势。通过不同学科领域的交叉合作，可以开拓
在高能物理中，相图用于描述高能粒子在不同能量和密度条件下的 状态和行为，如重核衰变、高能碰撞等过程。
04
相图分析技巧
观察法
通过直接观察相图，理解相变过程和相变温度。
观察法是最基本的相图分析技巧，通过观察不同温度和压力下的物质状态，可以 大致判断出相变温度和相变过程。这种方法简单易行，但精度较低，需要多次重 复实验以提高准确性。
THANKS
感谢观看
根据相图的结果，可以应用于材料科学、 化学工程、冶金等领域，为相关领域的研 究和应用提供基础数据和理论支持。
06
相图发展前景与展望
相图研究现状
相图在材料科学领域的应用
相图是材料科学领域中重要的研究工具，用于描述不同成分和温度下材料的相态变化。目 前，相图的研究已经广泛应用于合金、陶瓷、高分子等材料体系，为材料设计和制备提供 了基础数据和指导。
计算机模拟法是近年来发展迅速的一种方法，通过计算机模拟实验，可以模拟不同温度和压力下的物质状态，从而得到相图 。这种方法精度高，且可以模拟复杂体系的相变过程，但对计算机技术和实验数据要求较高。
05
相图实验操作
实验准备
01
02
03
04
实验材料
需要准备实验所需的材料，如 金属、玻璃、塑料等。
实验设备
相图发展趋势
01
相图数据的整合与共享
随着大数据时代的到来，相图数据的整合与共享成为发展趋势。通过建
立相图数据库和共享平台，可以方便地查询和获取各种材料的相图数据
，促进学术交流和合作。
02
相图研究的跨学科融合
相图研究涉及到物理、化学、材料科学等多个学科领域，因此跨学科的
融合是未来发展的重要趋势。通过不同学科领域的交叉合作，可以开拓
相关主题
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
自由度与相律
纯金属（恒压下）：
当只有单相存在时：f = 1 - 1 + 1 = 1，其自由 度数为1，即温度是可以独立改变的； 当自由度 f = 0 时：0 = 1 - p + 1 即 p = 2，纯 金属可以（液－固）两相平衡共存，此时为恒 温状态。
自由度与相律
二元系金属（恒压下）：
材料科学基础
秦文静 60215746 qq:78976819 E-mail：q次不到取消考试资格
作业
作为平时成绩的参考
考试
无划重点
课堂纪律
请尽量不要迟到早退，课堂上不许喧哗
课代表
-材料学科的基础 -课程的重中之重
c
B
6
背景知识
宏观性能取决于微观结构
背景知识
材料的性能决定于内部的组织结构
C 石墨 无定形碳
金刚石
相与组元
组元
构成材料的最简单、最基本、可以独立存在的 物质 将既不分解也不发生化学反应的稳定化合物也 视为一种组元
• 元素（Fe，Si，C……） • 计量化合物（NaCl，Li2O，Si3N4……）
即可以是一种物质，也可以是混合体
气体 液体 固体 同素异晶体
相与组元
材料的整体性能取决于
存在相的数目 它们的相对量 各相的成分与结构 相的尺寸和空间分布
材料的相依赖于
整体成分 温度和压力等变量
相与组元
水 一元系 H2O 单相 液
苏打水
二元系 H2O CO2 两相 气 液
宏观上系统中参与相变过程的各相长时间不再 互相转化（指成分和相对量）时所达到的平衡。 相平衡属于动态平衡，微观上组元不停地通过 各相界面进行迁移的速度相等。
相变：一个相转变为其它相的过程。
自由度与相律
自由度
在平衡系统中独立可变的因素
• 温度、压力、相的成分
自由度数 f：自由度的最大数目
教学大纲
固态相变
固态相变形核与长大 过饱和固溶体分解 共析转变 马氏体转变 贝氏体转变
教学大纲
材料的变形与再结晶
单晶体的塑性变形 多晶体的塑性变形 材料的加工硬化 冷变形金属的回复与再结晶
本节大纲
相图基本知识
1 2 3 4 5
背景知识 相与组元 相平衡 自由度与相律 单元系相图 相图的建立
组元数 c = 2
f=c-p+2=4–p p ≥ 1，f ≤ 3 （组元浓度）
压力的影响甚小 f = c - p + 1 = 3 – p
p = 1 f = 2; p = 2 f = 1; p = 3 f = 0
温度——成分图
相图的建立
二元相图测定方法
二元相图的测定是根据各种成分材料的临界点 绘制。 临界点：是表示物质结构状态发生本质变化的 临界相变点
一元系、二元系、三元系及多元系统
相与组元
材料由基本的相所组成
相是在一个体系中，结构相同，成分和性能均 一，并以界面相互分开的均匀部分。 不同相之间必有界面分开（相界面），在相界 面处的物质的性能发生突变。（晶界）
相可以是单质，也可以是化合物
Au, Ag, Fe, SiO2, H2O
两相平衡：f = 2 - 2 + 1 = 1，其自由度数为1， 说明有一个可变因素，表明它在一定温度范围 内稳定存在； 三相平衡：f = 2 - 3 + 1 = 0，此时温度恒定， 三相成分恒定不变，各因素恒定。
单元系相图
单元系 组元数 c = 1
f=c-p+2=3-p p = 1 f = 2; p = 2 f = 1; p = 3 f = 0
学习
工作
重要的指导意义
材料科学 基础
报考材料学科的 研究生的专业课 -重要保障
考研
毕业
教学大纲
相平衡与相图
相图基本知识 合金相图，共晶相图 包晶相图，其他类型相图 铁碳相图 铁碳相图 三元相图
教学大纲
凝固
纯金属凝固，均匀形核 非均匀形核 固溶体结晶 溶质浓度分布，合金的成分过冷 共晶合金的凝固 非平衡凝固
α
潜热
时间
Cu Cu-Ni相图
30
50 70 wNi(%)
Ni
相图的建立
液相线
液相区
两相共存区 TA
L
L+α
TB 固相线
α
固相区
A
二元匀晶相图
B
相图的建立
从相图中得到的信息
材料发生相变的温度和相变的类型 得到某一温度下两相的成分 得到某一温度下两相的相对含量
L L+α
TB
TA
α
A
水的相图
单元系相图
纯铁的相图（同素异晶转变）
图中有4个特性点：
• α-Fe ←→γ-Fe ←→δ-Fe ←→ L相
单元系相图
课堂练习——SiO2的相图
相图的建立
二元系
Cu-Ni Zr-Ti Pb-Sn Pt-Ag Mg-Cu Fe-C …… CaO-MnO MgO-NiO FeO-MnO……
水：
• 温度、压力 • f=2
自由度与相律
相律
表示在平衡条件下，系统的自由度数、组元数 和相数之间的关系，是系统的平衡条件的数学 表达式。
相律数学表达式： f=c-p+n
p：平衡相数 ； c ：体系的组元数； f ：体系自由度数 ； n：温度和压力等因素
注：平衡状态下f≥0； p≥1 若 f＜0 系统处于非平衡状态
测定材料临界点有两种方法类型：
动态法：热分析法、膨胀法、电阻法 静态法：金相法、X-ray衍射分析法 通常配合使用
相图的建立
热分析法：
热分析装置示意图
相图的建立
L
温度
L+S 凝固开始 凝固终了 S
时间
热分析法
相图的建立
50% Ni 70% Ni Ni 30% Cu Ni
L
温度
冰水 一元系 H2O 两相 液 固
冰苏打水 二元系 H2O CO2 三相 气 液 固
相平衡
机械平衡 热平衡 化学热力学平衡 各相 各组元 化学势 相平衡
化学平衡
相平衡
每一个组元在各相中的化学势相等是多相系统 处于热力学平衡的必要条件，也是其相平衡的 必要条件（证明过程略）
相平衡
相平衡