电路分析第六章习题答案
天津理工电路习题及答案-第六章--一阶电路..
第六章一阶电路——经典分析法（微分方程描述）——运算分析法（代数方程描述）见第十三章一、重点和难点1. 动态电路方程的建立和动态电路初始值的确定；2. 一阶电路时间常数、零输入响应、零状态响应、冲激响应、强制分量、自由分量、稳态分量和暂态分量的概念及求解；3. 求解一阶电路的三要素方法；电路初始条件的概念和确定方法；1.换路定理（换路规则）仅对动态元件（又称储能元件）的部分参数有效。
①电容元件：u C(0-) = u C(0+)；（即：q C(0-) = q C(0+)）；i C(0-) ≠i C(0+)。
②电感元件：i L(0-) = i L(0+)；（即：ΨL(0-) = ΨL(0+)）；u C(0-) ≠u C(0+)。
③电阻元件：u R(0-) ≠u R(0+)；i R(0-) ≠i R(0+)。
因此，又称电容的电压、电感的电流为状态变量。
电容的电流、电感的电压、电阻的电压和电流为非状态变量。
如非状态变量的数值变化前后出现相等的情况则视为一种巧合，并非是一种规则。
2.画t=0+时刻的等效电路画t=0+时刻等效电路的规则：①对电容元件，如u C(0-) = 0，则把电容元件短路；如u C(0-) ≠ 0，则用理想电压源（其数值为u C(0-)）替代电容元件。
②对电感元件，如i L(0-) = 0，则把电感元件开路；如i L(0-) ≠ 0，则用理想电流源（其数值为i L(0-)）替代电感元件。
画t=0+时刻等效电路的应用：一般情况下，求解电路换路后非状态变量的初始值，然后利用三要素法求解非状态变量的过渡过程。
3. 时间常数τ①物理意义：衡量过渡过程快慢的技术指标(即等于一阶微分方程的特征方程的特征根)。
仅取决于电路的结构和元件的参数。
②几何意义：状态变量变化曲线中时间坐标轴上任意一点次切距的长度（即曲线上任意一点，如果以该点的斜率为固定变化率衰减，则经过τ时间后为零值）。
③单位：m(秒)、ms(毫秒)。
电路分析(中国石油大学(华东))智慧树知到课后章节答案2023年下中国石油大学(华东)
电路分析（中国石油大学（华东））智慧树知到课后章节答案2023年下中国石油大学（华东）中国石油大学（华东）绪论单元测试1.学好《电路》课的意义（）答案:《电路》是电类专业（自动化、电气工程、电子与信息工程、通信等专业）的第一门专业基础课，有着非常重要的地位。
;《电路》课程的掌握程度对于后续专业课程的学习，有着举足轻重的作用。
;《电路》也是多数电类专业研究生入学考试课。
第一章测试1.电流的参考方向为（）。
答案:沿电路任意选定的某一方向2.图示电路，求u：（）。
答案:-4V3.基尔霍夫电流定律应用于（）。
答案:节点4.在有n个节点，b条支路的连通电路中，可以列出独立KCL方程的个数为（）。
答案:n-15.图示电路中，直流电压表和电流表的读数分别为4V及1A,则电阻R为（）。
答案:76.图示电路中电压U为（）。
答案:2V7.图示电路中电压U AB为（）。
答案:-16V8.电路中b、c两点间的电压U bc为（）。
答案:2V9.图示为某电路中的一个回路，其KCL方程为（）。
答案:R1I1-R2I2-R3I3+R4I4=U S1+U S2-U S3-U S410.图示电路中电压U S为（）。
答案:4V第二章测试1.图示电路中的I为（）。
答案:2A2.电路如图所示，短路线中的电流I为（）。
答案:10A3.图示直流电路中，已知a点电位为5V，则参考点为（）。
答案:c点4.图示电路中的电流I为（）。
答案:0A5.图示电阻串联电路中，U=U1-U2+U3，再根据欧姆定律，可求出等效电阻R为（）。
答案:R1+R2+R36.在下列各图中，与图(N)所示伏安特性相对应的电路是（）。
答案:（B）7.图示电路的开路电压Uoc为（）。
答案:-2V8.图示电路中电位VA为（）。
答案:4V9.如图所示电路中I1为（）。
答案:2A10.图示电路的电压U与电流I的关系为（）。
答案:U=-1-3I第三章测试1.各点电位的高低是（）的，而两点之间的电压值是（）的。
数字电路与系统分析第六章习题答案
解：1）分析电路结构：该电路是由七个与非门及一个JKFF组成，且CP下降沿触发，属于米勒电路，输入信号X1，X2，输出信号Z。
2）求触发器激励函数：J=X1X2，K =X 1X2触发器次态方程：Q n+1=X1X 2Q n +X 1X2Q n=X1X 2Q n+(X1+X2)Q n电路输出方程：Z = X 1X2Q n+X 1X 2Q n +X1X 2Q n+X1X2Q n3)状态转移表：表6.3.1输入X1X2S(t)Q nN(t)Q n+1输出Z0 0 0 0 0 10 11 0 1 0 1 1 1 101111111111114)X1X2Q n为低位来的进位，Q n+1表示向高位的进位。
且电路每来一个CP，实现一次加法运算，Z为本位和，Q 在本时钟周期表示向高位的进位，在下一个时钟周期表示从低位来的进位。
例如X1=110110，X2=110100，则运算如下表所示：LSB MSB表6.3.2节拍脉冲CP CP1 CP2 CP3 CP4 CP5 CP6 CP7被加数X10 1 1 0 1 1 0加数X20 0 1 0 1 1 0低位进位Q n0 0 0 1 0 1 16.2 试作出101序列检测器的状态图，该同步电路由一根输入线X，一根输出线Z，对应与输入序列的101的最后一个“1”，输出Z=1。
其余情况下输出为“0”。
（1）101序列可以重叠，例如：X：010101101 Z：000101001（2）101序列不可以重叠，如：X：010******* Z：0001000010解：1）S0：起始状态，或收到101序列后重新检测。
S1：收到序列“1”。
S2：连续收到序列“10”。
0/01/0X/Z0/011…100…S2S1S1/00/01/12）0/01/0X/Z0/011…100…S2S1S1/00/01/1解：（1）列隐含表：A B CDCB×A B CDCB×ADBC××(a)(b)进行关联比较得到所有的等价类为：AD，BC。
电子电路第六章习题及参考答案
习题六6-1 什么是本征半导体？什么是杂质半导体？各有什么特征？答：所谓本征半导体就是指完全纯净的、结构完整的半导体。
在本征半导体中掺入杂质后的半导体称为杂质半导体。
本征的半导体中的自由电子数量和空穴的数量是相等的，而杂质半导体中根据掺杂的元素不同可分为N 型半导体和P 型半导体，在N 型半导体中电子的浓度远远大于空穴的浓度，而P 型半导体恰恰相反。
6-2 掺杂半导体中多数载流子和少数载流子是如何产生的？答：在本征半导体中，由于半导体最外层有四个电子，它与周边原子的外层电子组成共价键结构，价电子不仅受到本身原子核的约束，而且受到相邻原子核的约束，不易摆脱形成自由电子。
但是，在掺杂的半导体中，杂质与周边的半导体的外层电子组成共价键，由于杂质半导体的外层电子或多（5价元素）或少（3价元素），必然有除形成共价键外多余的电子或不足的空穴，这些电子或空穴，或者由于受到原子核的约束较少容易摆脱，或者容易被其它的电子填充，就形成了容易导电的多数载流子。
而少数载流子是相对于多数载流子而言的另一种载流子，它是由于温度、电场等因素的影响，获得更多的能量而摆脱约束形成的。
6-3，黑表笔插入COM ，红表笔插入V/Ω（红笔的极性为“+”），将表笔连接在二极管，其读数为二极管正向压降的近似值。
用模拟万用表测量二极管时，万用表内的电池正极与黑色表笔相连；负极与红表笔相连。
测试二极管时，将万用表拨至R ×1k 档，将两表笔连接在二极管两端，然后再调换方向，若一个是高阻，一个是低阻，则证明二极管是好的。
当确定了二极管是好的以后就非常容易确定极性，在低阻时，与黑表笔连接的就是二极管正极。
6-4 什么是PN 结的击穿现象，击穿有哪两种。
击穿是否意味着PN 结坏了？为什么？ 答：当PN 结加反向电压（P 极接电源负极，N 极接电源正极）超过一定的时候，反向电流突然急剧增加，这种现象叫做PN 结的反向击穿。
击穿分为齐纳击穿和雪崩击穿两种，齐纳击穿是由于PN 结中的掺杂浓度过高引起的，而雪崩击穿则是由于强电场引起的。
电路分析基础第四版课后习题第四章第五章第六章答案
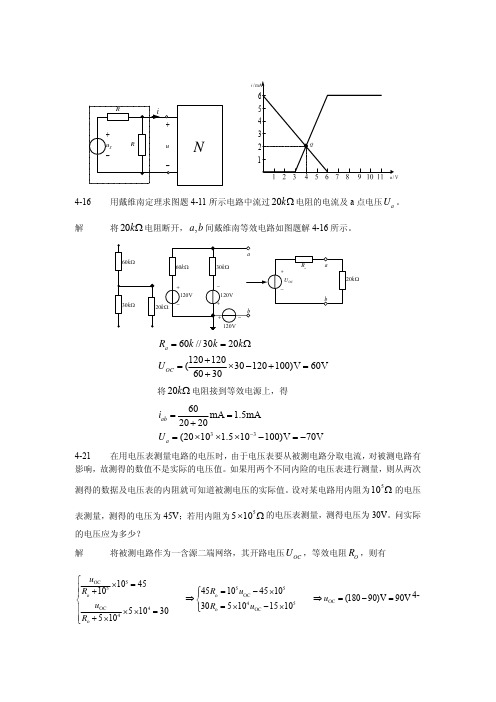
/i4-16 用戴维南定理求图题4-11所示电路中流过20k Ω电阻的电流及a 点电压。
a U 解将电阻断开，间戴维南等效电路如图题解4-16所示。
20k Ω,a bk Ω60//3020120120(30120100)V 60V6030a OCR k k k U ==Ω+=×−+=+ 将电阻接到等效电源上，得20k Ω3360mA 1.5mA2020(2010 1.510100)V 70V ab a i U −==+=×××−=− 4-21 在用电压表测量电路的电压时，由于电压表要从被测电路分取电流，对被测电路有影响，故测得的数值不是实际的电压值。
如果用两个不同内险的电压表进行测量，则从两次测得的数据及电压表的内阻就可知道被测电压的实际值。
设对某电路用内阻为的电压表测量，测得的电压为45V ；若用内阻为510Ω5510×Ω的电压表测量，测得电压为30V 。
问实际的电压应为多少？ 解将被测电路作为一含源二端网络，其开路电压，等效电阻OC U O R ，则有5OC 555o o OC OC 454OCo OC 4o 10451045104510(18090)V 90V 30510151051030510u R R u u u R u R ⎧×=⎪⎧+=−×⎪⎪⇒⇒=⎨⎨=×−×⎪⎪⎩××=⎪+×⎩−=4-28 求图题4-20所示电路的诺顿等效电路。
已知：12315,5,10,R R R =Ω=Ω=Ω。
10V,1A S S u i ==解对图题4-20所示电路，画出求短路电流和等效内阻的电路，如下图所示SC i对左图，因ab 间短路，故0,0i i α==，10A 0.5A 155SC i ==+ 对右图，由外加电源法，106ab R α=Ω− 4-30 电路如图题4-22所示。
第六章 三相交流电路习题册答案
第六章 三相交流电路§6-1 三相交流电源一、填空题1．三相交流电源是三个大小相等、频率相同而相位互差120°的单相交流电源按一定方式的组合。
2．由三根相线和一根中性线所组成的供电线路，称为三相四线制电网。
三相电动势到达最大值的先后次序称为相序。
3．三相四线制供电系统可输出两种电压供用户选择，即线电压和相电压。
这两种电压的数U 线超前U 相30°。
4．如果对称三相交流电源的U 相电动势e u =E m sin (314t+π6)V ，那么其余两相电动势分别为ev= E m sin (314t-90°)V ，ew =E m sin (314t+150°) V 。
二、判断题1．一个三相四线制供电线路中，若相电压为220 V ，则电路线电压为311 V 。
( × )2．三相负载越接近对称，中线电流就越小。
( √ )3．两根相线之间的电压叫相电压。
( × )4．三相交流电源是由频率、有效值、相位都相同的三个单个交流电源按一定方式组合起来的。
( × )三、选择题 1．某三相对称电源电压为380 V ，则其线电压的最大值为( A )V 。
A ．380 2B ．380 3 c ．380 6 D ．380232．已知在对称三相电压中，V 相电压为u v =220 2 sin(314t+π)V ，则U 相和W 相电压为(B )V 。
A. U u =220 2 sin (314t+π3) u w =220 2 sin (314t-π3) B ．u u =220 2 sin (314t-π3) u w =220 2 sin (314t+π3) C.u u =220 2 sin (314t+2π3) uw=220 2 sin (314t-2π3) 3．三相交流电相序U-V-W-U 属( A )。
A ．正序B ．负序C ．零序4．在如图6-1所示三相四线制电源中，用电压表测量电源线的电压以确定零线，测量结果U 12=380 V ，U 23 =220 V ，则( B )。
第六章 时序逻辑电路的分析与设计典型例题
解：解题步骤如下： （ 1） 求 激 励 输 入 议 程 ：
⎧ J 3 = Q2 , ⎨ ⎩K 3 = Q2 ⎧ J 2 = Q1 , ⎨ ⎩ K 2 = Q1 ⎧ J 1 = Q3 ⊕Q1 ⎨ ⎩K1 = J 1
因 为 将 J 3 = Q 2 ， K 3 = Q2 代 入 J - K 触 发 器 次 态 方 程 ， 有
3
n +1 励 方 程 D3、 D2、 D1中 ， 然 后 根 据 D触 发 器 次 态 方 程 Q = D ， 可 知 所 有 的 非 工
作 状 态 都 能 进 入 工 作 状 态 ， 即 101→ 001； 110→ 101→ 001； 111→ 001。 因 此 电路可以自启动。 （ 6） 画 完 整 状 态 转 换 图 如 下 图 所 示 。
J 1 = Q3 Q1 + Q3 Q1 + Q2 Q1 = Q3 ⊕ Q1 + Q2 Q1
修改后，具有自启动功能的电路如下图所示。
修改后的可自启动电路
5
Q1n +1 0 0 1 1 0
D3
0 1 0 0 0
D2
1 0 0 1 0
D1
0 0 1 1 0
0 1 0 0 0
1 0 0 1 0
（ 3） 求 激 励 输 入 方 程 组 。 首 先 要 根 据 状 态 转 换 真 值 表 ， 画 D3、 D2、 D1的 卡 诺 图 ， 然 后 通 过 卡 诺 图 化 简 得 到 激 励 输 入 方 程 。 D3、 D2、 D1的 卡 诺 图 如 下 图所示。
S0— — 为 初 始 状 态 以 及 不 属 于 以 下 定 义 的 状 态 ； S1— — 收 到 首 个 1； S2— — 收 1 后 再 收 1； S3— — 收 11 后 再 收 0； S4— — 收 110 后 再 收 1。
第6章 时序逻辑电路-习题答案
第六章 时序逻辑电路6-1 分析题图6-1所示的同步时序电路，画出状态图。
题图6-1解： 11221211n n n n J K Q T Q Z Q Q ====，，，，11111111212n n n n nn n nQ J Q K Q Q Q Q Q Q +=+=+=+122212n n n n Q T Q Q Q +=⊕=⊕，状态表入答案表6-1所示，状态图如图答案图6-1所示。
答案表6-1答案图6-16-2 分析题图6-2所示的同步时序电路，画出状态图。
题图6-2 解：按照题意，写出各触发器的状态方程入下：11J K A ==，21n J Q =，21K =，1212n n nQ Q Q +=，111n n Q A Q +=⊕状态表入答案表6-2所示，状态图如图答案图6-2所示。
答案表6-2答案图6-2Q 2n Q 1n Q 2n+1 Q 1n+1 Z0 0 0 1 1 0 1 1 0 1 1 1 1 1 0 0 0 0 0 1A Q 2n Q 1n Q 2n+1 Q 1n+1 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 0 0 1 1 0 0 0 1 0 1 1 0 0 1 0 0CLK D 1D 2D 3Q 3Q 2Q 1Q 2Q 3Q 1Q 1Q 2Q 3&6-3分析题图6-3所示的同步时序电路，画出状态图。
题图6-3解：按照题意，写出各触发器的状态方程入下：1112213232131n n n nn J K T J K Q Q T J Q Q K Q ========1，，， 133********n n n n n n n nQ J Q K Q Q Q Q Q Q +=+=+ 1222132n n n n nQ T Q Q Q Q +=⊕=⊕ 1111111n n n n Q T Q Q Q +=⊕=⊕=答案表6-3答案图6-36-4 在题图6-4所示的电路中，已知寄存器的初始状态Q 1Q 2Q 3=111。
电路分析基础第六章(李瀚荪)
t
t0
t U S uC 1 解二： iC [U S U S (1 e )] R R t US e , t0 R
二、RL电路的零状态响应 t=0
iR
R IS
iL
L
+ uL _
已知：iL(0_ ) = 0，求 iL(t) , uL(t) , t 0 解：１. 定性分析
1. 定性分析
① t＜ 0 —充电 ② t = 0 —换路
③ t≥0 —放电
2. 定量分析
建立图(b)电路的一阶微分方程
u R uC 0
齐次方程通解： 根据初始条件 其解为：
duC RC uC 0 dt
uC (t ) Ke
uC (0 ) Ke
t RC
st
1 S=－ RC
= 18e- 2500tV 18e- 2500t 6 ? 4 9
(t ? 0) 3e- 2500t A(t > 0)
uC (t ) 6 i1 (t ) = ? R 3+ 6
例3： 已知i (0 +) = 2A 求：i(t) , u(t) , t ≥ 0 3
i
0.5u
1
4H
+ u
_
u 3i (0.5u i) 1
t
6e 20 t V
( t 0)
duC U 0 t 6 20 t iC ( t ) C e e dt R 10 103 0.6e 20 t m A ( t 0)
电阻中的电流iR(t)可以用与iC(t)同样数值的电
流源代替电容，用电阻并联的分流公式求得 iR(t)
引例：求图示电路的一阶微分方程。
《电路分析》第六章 非线性电路
如图所示的含有小信号的非线性电阻电路
据KVL得：US us (t) R0i u(t)
①当只有直流电源作用时，根据前述的方法
（解析法、图解法、折线法）求得静态工作
点Q（ UQ，IQ ）
二分R、析0 小法信号
～ u_s (t)
i(t) u(t) R
US
_
②当直流电源和小信号共同作用时，由于us
u
D
u 0,i 0 i u 0,i 0
u
u
i
u
Di
u 0,i 0 u 0,i 0
u
i
D
u 0,i 0 i u 0,i 0
u
u
例：试绘出各电路的U~I关系曲线（D为理想二极管）。
I
D
U
5V
I 100 I
+
D U
15V
0
5V U
-
I
U
D
U 5V 0通，即UD UD U 5V<0止
解法可求得响应的波形。 i
i
i
u
N
0
u
0
t
ui
u2 uo
t
②TC图法：输入与输出是不同端口的电压、电流，其关系曲线 称为转移特性（transmission character ）TC曲线。已知TC曲 线和激励波形，通过图解法可求得响应的波形。见P170
四、非线性电阻电路的折线法： 用解析法分析非线性电阻电路，需要将元件的伏安关系用确切
是其两端电压的单值函数。q f (u)
②荷控型电容（QCC）：电容两端的电压是其
q
i
上聚集的电荷的单值函数。u h(q)
u
江西师范大学电路分析第六章答案
江西师范大学电路分析第六章答案1、问题:电路模型是实际的电路元件。
选项：A:正确B:错误答案: 【错误】2、问题:电路图中所标示的电压、电流方向默认均为参考方向。
电压电流实际方向可能与参考方向相同，也可能相反。
根据电压电流参考方向和电压电流数值的正负，即可确定电压电流的实际方向。
选项：A:正确B:错误答案: 【正确】3、问题:无论电阻的电压、电流是关联参考方向还是非关联参考方向，其电压电流关系都是。
选项：A:正确B:错误答案: 【错误】4、问题:电压源不能断路，电流源不能短路。
选项：A:正确答案: 【错误】5、问题:受控电源是由实际元件或电路抽象出来的一类电路模型，不同的实际元件或电路的电路模型可能对应不同类型的受控源。
选项：A:正确B:错误答案: 【正确】6、问题:如果电路中某条支路的电压为2V，电流为-3A，电压电流为非关联参考方向，则该支路实际吸收功率6W。
选项：A:正确B:错误答案: 【正确】7、问题:图1所示电路的电流 i 等于（）。
图1选项：A:1AB:2AC:3A答案: 【2A】8、问题:一只100、1W的电阻器，使用时电阻上的电压不得超过__V选项：A:5B:8C:10D:20答案: 【10】9、问题:电路分析的基本依据是______和基尔霍夫电压定律。
答案: 【基尔霍夫电流定律】第二周电路模型和电路定律（2） KCL和KVL测验题1、问题:求图示电路中的。
A:2AB:1AC:3AD:4A答案: 【2A】2、问题:求图示电路中电流源的电压。
选项：A:1.2VB:0.6VC:2.4VD:4.8V答案: 【1.2V】3、问题:求图示电路的。
选项：A:-6VB:-2VC:-4VD:-8V答案: 【-6V】4、问题:只有对闭合回路，才可以列写KVL方程。
选项：A:正确B:错误答案: 【错误】5、问题:对于一个结点来说，“流入电流等于流出电流”和“所有支路电流的代数和等于零”这两种说法是等价的。
《电路分析》_卢小芬 主编_课后答案_第六章 正弦稳态电路的分析-答案01
=7
并且
I = U1 = 8 = 2 A
R1 4
故阻抗 Z 吸收的功率为
P = U2I cosθ = 7 × 2 = 14 W
6-11 如 题 6-11 图 所 示电路， U&S = 100∠0o V , 电 路吸收的功率 P = 300 W ， 功率因数
λ = cosϕ = 1 。求 IC 。
+ U& S
间关系为
I = IG2 + IB2 由于 I&C 与 I&L 的相位相差 180°， 故 IB = IC − IL = 9 − 6 = 3 A，因此
IG = I 2 − IB2 = 52 − 32 = 4 A
类似于 RLC 串联电路和 GCL 并联电路， 对于 n 个元件串联组成的电路， 等效阻抗 Z 为
+
jωC6
+ Y3 ⎞⎟U&C ⎠
−
1 jω L4
U&
a
−
jωC6 U&b
= U& sY3
从本例可知， 电阻电路的节点分析法乃至一般分析方法可以直接推广到相量法中。
6-6 电路如题 6-6 图所示，虚线框内是一电感线圈的电感和电阻，已知 r=200 Ω， L1 =0.8H，
U1 =190 V，电源电压U =220 V，频率 f =50Hz，求其串联的电感 L。
L
1L
Q C
=
I
2 2
X
C
= 12
12 = 12 Var
Q = Q - Q = 32 -12 = 20 Var
C
L
C
S = P2 + Q2 = 24 + 16 = 40 VA
电路(巨辉)第6章作业+参考答案
第6章 正弦稳态电路分析——作业参考解答一、P6-14电路如图所示，当s rad 50ω/=时，求in Z 。
解：相量模型如图所示，则：Ω)41j 43()]Z Z //(Z [Z Z C 1R 1R L in +=++=二、P6-19电路如图所示，当s rad 10ω4/=时，求in Z ，并画出串联、并联等效模型及等效元件参数。
.（a ） （b ） （c ） 解：（1）求串联模型及元件参数设电压和电流，则相量模型如图解 (a):Ω20j 10210j L ωj Z 34L =⨯⨯== ， Ω100j 10110j 1C ωj 1Z 64C -=⨯⨯==- 由KVL 得：()•••+-+=U 2I 100j 20j 50U 11， 控制量：1I 50U ••= 可得：()11I 80j 150U ••-=， 则等效阻抗：()Ω80j 150I U Z 11eq -==••等效元件参数：Ω150R =，且：C 101j C ω1j 80j 4-=-=- 求得：uF 25.1C =串联等效元件参数模型如图解 (b)所示； （2）()S 0028.0j 0052.0Z 1Y eqeq +==Ω3.192G1R S 102.5G 3==→⨯=-，uF 28.0C C 10j C ωj 0028.0j 4=⇒==并联等效元件参数模型如解 (c)所示。
三、P6-25用节点分析法求图所示电路电压0u 。
..U .o解： V 025U s ︒∠=•Ω10j 101010j L ωj Z 33L =⨯⨯== ，Ω20j 105010j 1C ωj 1Z 63C -=⨯⨯==- 设参考节点、各独立节点，得相量模型如图所示：⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧⨯+==-=⎪⎪⎭⎫ ⎝⎛++-+--︒∠=--⎪⎪⎭⎫ ⎝⎛-++•••••••••201002121U 10j 3030U 20U I I 4U 10j 30120j 1U 20j 120025U 20j 1U 20j 1201201 可求得：φU U 00∠=•则：V )φt 10cos(2U u 300+=四、P6-32利用网孔分析法求图所示电路的电流0I •。
电路分析知到章节答案智慧树2023年上海电力大学
电路分析知到章节测试答案智慧树2023年最新上海电力大学第一章测试1.图示电路中,节点A和B之间的电压ＵAB为（）V。
参考答案:-162.图示电路中Ｉ= 0 时,电位ＵA=（）V。
参考答案:603.通常所说负载增加，是指负载（）增加。
参考答案:功率4.图示电路中Ｓ断开时Ｉ1= 0A,Ｉ=2A。
Ｓ闭合时Ｉ1=( )A,Ｉ=( )A。
（）参考答案:0;65.图示电路中,当ＩS=10A 时,电压Ｕ为（）V,当ＩS=8A时电压Ｕ为（）V。
（）参考答案:12;166.电路理论分析的对象是电路模型而不是实际电路。
（）参考答案:对7.欧姆定律可表示成U=RI,也可表示成U=-RI,这与采用的参考方向有关。
（）参考答案:对8.在节点处各支路电流的方向不能均设为流向节点，否则将只有流入节点的电流而无流出节点的电流。
（）参考答案:错9.在电压近似不变的供电系统中，负载增加相当于负载电阻减少。
（）参考答案:对10.理想电压源的端电压是由它本身确定的，与外电路无关，因此流过它的电流则是一定的，也与外电路无关。
（）参考答案:错第二章测试1.图示电路ＡＢ间的等效电阻为（）。
参考答案:14Ω2.电路如图所示，Ａ、Ｂ端的等效电阻Ｒ＝（）。
参考答案:4Ω3.电路如图所示，可化简为（）参考答案:3Ω电阻4.如图所示电路中，当电阻Ｒ2增加时电流Ｉ将（）。
参考答案:增加5.图示电路中，就其外特性而言，（）。
参考答案:ｂ、ｃ等效6.两只额定电压为110V的电灯泡串联起来总可以接到220V的电压源上使用。
（）参考答案:错7.电流相等的两个元件必属串联,电压相等的两个元件必属并联。
（）参考答案:错8.一个不含独立源的电阻性线性二端网络（可以含受控源）总可以等效为一个线性电阻。
（）参考答案:对9.一个含独立源的电阻性线性二端网络（可以含受控源）总可以等效为一个电压源与一个电阻串联或一个电流源与一个电阻并联。
（）参考答案:对10.已知图示电路中Ａ、Ｂ两点电位相等，则ＡＢ支路中必然电流为零。
电路分析第六章习题解答
=
6A
开关断开后，电路等效为
3Ω
2Ω
L
i
L = 1+ 1 = 5H 1+ 1 5 20
由 KVL 及换路定则得
⎪⎧5 di + 5i = 0 ⎨ dt ⎪⎩i(0+ ) = i(0− ) = 6 解得： i(t) = 6e−t A (t ≥ 0)
换路后无电源，故是零输入响应。
8． 如图题 6-8 所示，开关接在 a 点为时已久，t = 0 时开关接至 b 点，试求 t ≥ 0 时的
2Ω
ia
i1
+
2A
4Ω
u
+ 2i1 −
−
b
求得该二端电路的端口 VAR，便可得其等效电路。
设端电压 u 和端电流 i 的参考方向如上图所示，设 i 已知，则有
⎧u ⎩⎨i1
= =
2i + 4i1 2+i
+
2
i1
解得：
u = 12 + 8i
即该二端电路
uoc = 12V Req = 8Ω
开关动作后的电路可简化为
将电流源置零，从电感两端看进去的等效电阻为
R = 50 + 100 ×100 = 100Ω 100 + 100
τ = L = 0.1 = 1 s R 100 1000
由三要素公式，得
iL (t) = 0.05 + (0 − 0.05) e−1000t = (0.05 − 0.05e−1000 t ) A (t ≥ 0)
12Ω
+
40 V
−
t =0 +
8Ω u
−
+ 20nF uc
电路分析基础第6章习题答案
u(V)
30
i(t) ＋ R
τ=1ms
u(t) C －
o （b） t(ms)
（d）
由图(a)、(b)可知，N1的可能结构图如图(d)所示
u() Ri(t) 15 103 R 30
R 2 k
C
R
103 2 103
0.5 μF
6-11 图题6-10(a)所示电路中，N1原无贮能，在t＝0时电流i(t) ＝15mA开始作用于电路。
（2）利用化简后的电路列出图中所注明输出量u或i的微分方 程。
i1 R1
R2
＋
Cu
－
i1 R1
R2 ＋ uOC
－
Ro
＋
＋C u
－uOC －
（b）
uOC R1i1 100i1
uOC
RoC
du dt
u
Ro R1 R2 300
100i1
3 104
du dt
u
6-2 对图题6-2两电路，重复上题要求。
6-9 电路如图题6-8所示，电压源于 t =0 时开始作用于电路，试 求i (t)，t≥0。
－10i1(t)＋
4A 4 2H i1(t) i(t)
－10i1(t)＋
4A
＋
4
uOC
i1(t)
－
把除电感元件以外的电路进行戴维南变换
uOC 10i1 4i1 14i1 14 4 56 V u 10i1 4i1 14i1
由图(b)可得 i(0 ) 10 mA
开关闭合后瞬间 Ri(0 ) U 0
U 16.5 (10) 165 V
6-11 图题6-10(a)所示电路中，N1原无贮能，在t＝0时电流i(t) ＝15mA开始作用于电路。
电路分析基础(第四版)张永瑞答案第6章
29
第6 章
电路频率响应
题6.6图
30
第6 章
电路频率响应
解 并接Yx前电路处于谐振， 电容上电压应是电源电
压Q倍， 所以
U C 10 Q 100 U s 0.1
r 1 Q0C 1 20 6 12 100 2 3.14 10 80 10
31
第6 章
电路频率响应
H (j )
1 1 2 2
解得
c
R12 R2 2 2 R1 R2 rad/ s R1 R2C
28
第6 章
电路频率响应
6.6 在图示的rLC串联谐振电路中， 电源频率为1 MHz， 电源有效值Us=0.1 V， 当可变电容器调到C=80 pF时， 电路达 谐振。 此时， ab端的电压有效值UC=10 V。 然后， 在ab端之 间接一未知的导纳Yx， 并重新调节C使电路谐振， 此时电容 值为60 pF， 且UC=8 V。 试求所并接Yx中的电导Gx、 电容Cx， 电路中电感L和并接Yx前、 后的电路通频带BW。
10
第6 章
电路频率响应
题解6.2图
11
第6 章
电路频率响应
所以欲满足上述条件， 必须使
R RL 2 ( ) 1 cCRRL
则该网络的截止角频率
R RL c rad/ s RRLC
（3）
12
第6 章
电路频率响应
将式（3）代入H(jω)式中， 得
H (j )
c 1 j( )
电路频率响应
6.11 某电视接收机输入电路的次级为并联谐振电路，
如题6.11图所示。 已知电容C=10 pF， 回路的谐振频率f0=
电路分析基础知到章节答案智慧树2023年桂林电子科技大学
电路分析基础知到章节测试答案智慧树2023年最新桂林电子科技大学绪论单元测试1.同一型号的灯泡，单个灯泡接220V电源与两个灯泡串联接220V电源，灯泡的亮度有什么变化？（）参考答案:变暗第一章测试1.下图为连接甲乙两地的输电线路，若甲地工作于800kV，电流为1.8kA，则功率由( )地输送至( )地，其值为 ( )MW。
参考答案:甲，乙，14402.电压电流参考方向如图中所标，有关A、B两部分电路电压电流参考方向是否关联描述正确的是（）。
参考答案:A部分电压、电流参考方向非关联；B部分电压、电流参考方向关联。
3.电路如图所示, 其中电阻的值应分别为( ) Ω。
参考答案:100 , 1004.在集总假设条件下，对实际电路元件加以理想化，只能用一个表征该元件主要性质的模型来表示该元件。
参考答案:错5.在非关联的参考方向下，欧姆定律可以写成u=-iR。
其中R表示电阻，u为电阻两端的电压，i为流过电阻两端的电流。
参考答案:对6.电流和电压的参考方向可任意选定，选定后，在电路的分析和计算过程中也能改变。
参考答案:错7.对于集总参数电路中的任一节点，在任一瞬间，流向该节点的电流的代数和恒等于零。
参考答案:对8.独立电源可能产生功率，也可能吸收功率。
参考答案:对9.理想电压源的端电压u与外接电路有关。
参考答案:错10.理想电流源的端电压u由外电路确定。
参考答案:对11.实验中可以把电压源短路。
参考答案:错12.受控源是描述电子器件中某一支路对另一支路控制作用的理想模型，本身不直接起“激励”作用。
参考答案:对13.图示电路中，i1=i2。
参考答案:对14.图中所示电路中电流I等于_____A。
参考答案:null15.试求图中U AC为_____V。
参考答案:null16.图中 R1=500Ω，R3=200Ω， R2为500Ω的电位器。
输入电压为U1=12V , 输出电压U2的变化范围为{ }V～{ }V。
参考答案:null17.电路如图所示，电压ＵＳ等于_____V 。