有限元作业
有限元大作业
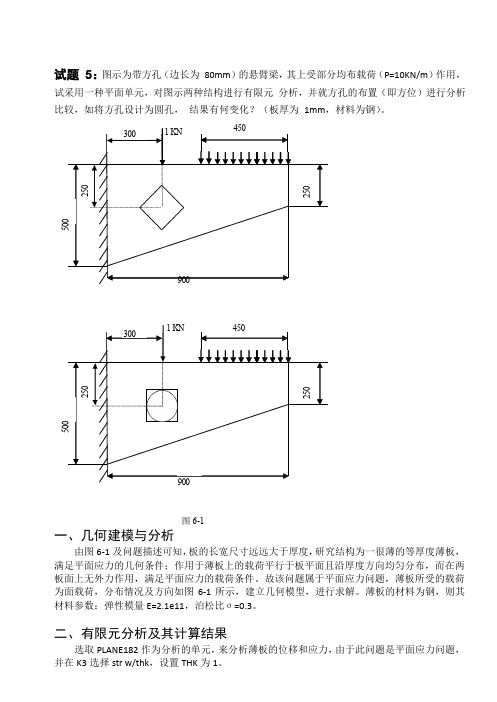
250250试题 5:图示为带方孔(边长为 80mm )的悬臂梁,其上受部分均布载荷(P=10KN/m )作用,试采用一种平面单元,对图示两种结构进行有限元分析,并就方孔的布置(即方位)进行分析比较,如将方孔设计为圆孔,结果有何变化?(板厚为 1mm ,材料为钢)。
3001KN9003001KN图6-1一、几何建模与分析由图6-1及问题描述可知,板的长宽尺寸远远大于厚度,研究结构为一很薄的等厚度薄板,满足平面应力的几何条件;作用于薄板上的载荷平行于板平面且沿厚度方向均匀分布,而在两板面上无外力作用,满足平面应力的载荷条件。
故该问题属于平面应力问题,薄板所受的载荷为面载荷,分布情况及方向如图6-1所示,建立几何模型,进行求解。
薄板的材料为钢,则其材料参数:弹性模量E=2.1e11,泊松比σ=0.3。
二、有限元分析及其计算结果选取PLANE182作为分析的单元,来分析薄板的位移和应力,由于此问题是平面应力问题,并在K3选择str w/thk ,设置THK 为1。
1)方孔竖直制,划分方式采用自由方式,划分后网格的模型如图6-2所示。
计算得到的位移和应力分布如图6-3所示。
图6-2 方孔竖直的网格划分图6-3 位移及应力分布云图2)方孔正直制,划分方式采用自由方式,划分后网格的模型如图6-4所示。
计算得到的位移和应力分布如图6-5所示。
图6-4 方孔正直的网格划分图6-5 位移及应力分布云图3)圆孔按图6-1所示模型进行建模。
并用PLANE182单元进行划分网格,网格大小采用全局网格控制,划分方式采用自由方式,划分后网格的模型如图6-6所示。
计算得到的位移和应力分布如图6-7所示。
图6-4 方孔正直的网格划分图6-5 位移及应力分布云图根据以上的模型分析的位移和应力图,可以得出方孔竖直、方孔正直、圆孔的最大最小位移应力的分布如表6-1所示。
三、比较与分析1)方孔竖直与方孔正直的比较,发现方孔正直的位移变形较小,应力相差不大2)圆孔与方孔比较,发现圆孔的位移变性最小,应力也最小,故可以得出圆孔的布置结构对整体布置的效果最好。
有限元作业—三梁平面框架结构的有限元分析

三梁平面框架结构的有限元分析针对如图1所示的框架结构,其顶端受均布力作用,用有限元方法分析该结构的位移。
结构中各个截面的参数都为:E=3.0 10 Pa,I =6.5 10〃m,2A =6.8 10 m,生成相应的有限元分析模型。
在ANSY平台上,完成相应的力学分析。
416~N nt3000N② ③144mI ------------------------------------------------------------------------------------------ |图1框架结构受一均布力作用ANSYS军答:对该问题进行有限元分析的过程如下。
(1)进入ANSYS设定工作目录和工作文件)程序—An sys —ANSYS In teractive —Worki ng directory (设置工作目录)—Initial jobname(设置工作文件名):beam3 —Run —OK(2)设置计算类型ANSYS Main Menu: Preferences , —Structural —OK(3)选择单元类型ANSYS Main Me nu: Preprocessor —Eleme nt Type —Add/Edit/Delete , —Add, —beam 2node188 —OK (返回到Element Types 窗口)—CloseCross-sectional area:6.8e-4 (梁的横截面积)—OK —Close八 Library of Element Types Library of Element TypesElement type referenc ■亡 number(4)定义材料参数ANSYS Mai n Me nu: Preprocessor — Material Props — Material Models —Structural — Lin ear — Elastic — Isotropic: EX:3e11 ( 弹性模量)—OKANSYS Main Menu: Preprocessor — Real Constants , — Add/Edit/Delete —Add — Type 1 Beam3 — OK — Real Constant Set No: 1 ( 第 1 号实常数),Ry finite 戟『気2 node 1882 node 188Canttl—鼠标点击该窗口右上角的“ ”来关闭该窗口。
现代设计方法(关于有限元)作业

《现代设计方法》作业关于有限元法的研究学院:机械工程学院专业:机械制造及其自动化0.有限元法有限元法分析起源于50年代初杆系结构矩阵的分析。
随后,Clough于1960年第一次提出了“有限元法”的概念。
其基本思想是利用结构离散化的概念,将连续介质体或复杂结构体划分成许多有限大小的子区域的集合体,每一个子区域称为单元(或元素),单元的集合称为网格,实际的连续介质体(或结构体)可以看成是这些单元在它们的节点上相互连接而组成的等效集合体;通过对每个单元力学特性的分析,再将各个单元的特性矩阵组集成可以建立整体结构的力学方程式,即力学计算模型;按照所选用计算程序的要求,输入所需的数据和信息,运用计算机进行求解。
当前,有限元方法/理论已经发展的相当成熟和完善,而计算机技术的不断革新,又在很大程度上推进了有限元法分析在工程技术领域的应用。
然而,如此快速地推广和应用使得人们很容易忽视一个前提,即有限元分析软件提供的计算结果是否可靠、满足使用精度的前提,是合理地使用软件和专业的工程分析。
有限元法分析一般包括四个步骤:物理模型的简化、数学模型的程序化、计算模型的数值化和计算结果的分析。
每一个步骤在操作过程中都或多或少地引入了误差,这些误差的累积最终可能会对计算结果造成灾难性的影响,进而蒙蔽我们的认识和判断。
1.受内压空心圆筒的轴对称有限元分析例图1.1所示为一无限长的受内压的轴对称圆筒,该圆筒置于内径为120mm的刚性圆孔中,试求圆筒内径处的位移。
结构的材料参数为:200=,0.3E GPaμ=。
图1 结构图对该问题进行有限元分析的过程如下。
(1)结构的离散化与编号由于该圆筒为无限长,取出中间一段(20mm高),采用两个三角形轴对称单元,如图1.2所示。
对该系统进行离散,单元编号及结点编号如图1.3所示,有关结点和单元的信息见表1.1。
图1.2 有限元模型图1.3 节点位移编号及单元编号表1.1 单元编号及结点编号单元编号结 点 编 号 ①②1 2 3 2 3 4结构的结点位移列阵为11223344[]T r r r r u w u w u w u w δ= (1.1) 结构的结点外载列阵12[000000]T r r F F F = (1.2)1r F 和2r F 为由内压作用而等效在结点1和结点2上的载荷,其大小为1122240202//502622r r r h p F N F N ππ-⨯⨯⨯==== (1. 3) 约束的支反力矩阵123344[00T z z r z r z R R R R R R R = ] (1.4)其中1z R 和2z R 为结点1和结点2在Z 方向的约束支反力,(3r R ,3z R )和(4r R ,4z R )为结点3和结点4在r 方向和Z 方向的约束支反力。
有限元大作业

1.推导有限元计算格式,理解有限元原理:建立图示受拉直杆在自重(设单位长度重度为q ,截面积为A )和外力P 作用下的拉伸问题的微分方程,并分别利用不同的原理(变分求极值(最小势能或虚功原理)、加权残值法)推导有限元计算格式(取两个单元)。
手工求出端点的位移(自己给定参数值)。
设杆长为L ,截面面积为A(x),弹性模数为E,单位长重量q ,受拉杆x 处的位移为u(x)。
取微元dx 的力平衡,建立受拉杆位移所满足的微分方程()du x dx ε=,()du x E E dxσε== dx 上下截面内力与微元自重相等得()*()()*()A x dx x dx A x x dx qdx σσ++-+=-(()())dA x x q dxσ∴=- (())d duEA x q dx dx=- 0x L << ()0u x = 0x =()duEA x p dx= x L = 得解析解:2()2q x P u Lx x EA EA=-+将其分为两个单元,节点为1,2,3,得22382qL PL u EA EA=+232qL PL u EA EA=+有限元法:1)位移函数01u α= 2111u u l α-=得1211(1)x x u u u l l =-+ 令11(1)x N l =-21x N l = 11122122u u N u N u N N u⎧⎫⎪⎪⎡⎤=+=⎨⎬⎣⎦⎪⎪⎩⎭{}1u N d ⎡⎤=⎣⎦ 2)应变、应力表达{}{}111211du dN d d dx dx l l ε⎡⎤⎡⎤===-⎢⎥⎣⎦⎣⎦{}1B d ε⎡⎤=⎣⎦ {}1E E B d σε⎡⎤==⎣⎦ {}1S d σ⎡⎤=⎣⎦3)势能表示{}{}(){}{}(){}{}{}{}{}1111''112211''121112210111111111111111121221222T V ll T T T T T U W D dV F u F u qdx u u d B E d Adx F u F u ql EA EA ql l l d d d F d EA EA ql l l εε⎡⎤=-=-+-⎣⎦+⎡⎤=-+-⎣⎦⎡⎤⎡⎤-⎢⎥⎢⎥⎢⎥⎢⎥=--⎢⎥⎢⎥⎢⎥-⎢⎥⎣⎦⎢⎥⎣⎦∏⎰⎰⎰4)单元平衡方程 a)最小势能原理110u ∂=∂∏120u ∂=∂∏111111212112112ql F u AE l u ql F ⎧⎫-⎪⎪⎧⎫⎡⎤-⎪⎪⎪⎪=⎨⎬⎨⎬⎢⎥-⎣⎦⎪⎪⎪⎪⎩⎭+⎪⎪⎩⎭b)虚位移原理{}(){}(){}TeTdd F qdx d δδδεσΩ+=Ω⎰⎰{}{}1B d σεδ⎡⎤=⎣⎦ {}1E E B d σεδ⎡⎤==⎣⎦{}(){}{}(){}111111TTT l d F d B E B d Adxδδ⎡⎤=⎣⎦⎰ 由虚位移任意性得,{}{}1111T lF B E B Adxd ⎡⎤=⎣⎦⎰ 积分得111111212112112ql F u AE l u ql F ⎧⎫-⎪⎪⎧⎫⎡⎤-⎪⎪⎪⎪=⎨⎬⎨⎬⎢⎥-⎣⎦⎪⎪⎪⎪⎩⎭+⎪⎪⎩⎭ 记为{}{}111k d F ⎡⎤=⎣⎦ 同理222212323112112ql F u AE l u ql F ⎧⎫-⎪⎪⎧⎫⎡⎤-⎪⎪⎪⎪=⎨⎬⎨⎬⎢⎥-⎣⎦⎪⎪⎪⎪⎩⎭+⎪⎪⎩⎭{}{}222k d F ⎡⎤=⎣⎦ {}{}ei i eF R =∑ 12220F F += 23F P =11111112211223222022202EAEAql F l l u ql ql EA EA EA EA u l l l l u ql EAEA P l l ⎡⎤⎧⎫-⎢⎥+⎪⎪⎢⎥⎧⎫⎪⎪⎢⎥⎪⎪⎪⎪⎢-+-⎥=+⎨⎬⎨⎬⎢⎥⎪⎪⎪⎪⎢⎥⎩⎭⎪⎪+⎢⎥⎪⎪--⎢⎥⎩⎭⎣⎦可得:22382qL PLu EA EA=+232qL PL u EA EA=+与解析解结果一致。
有限元作业整理版
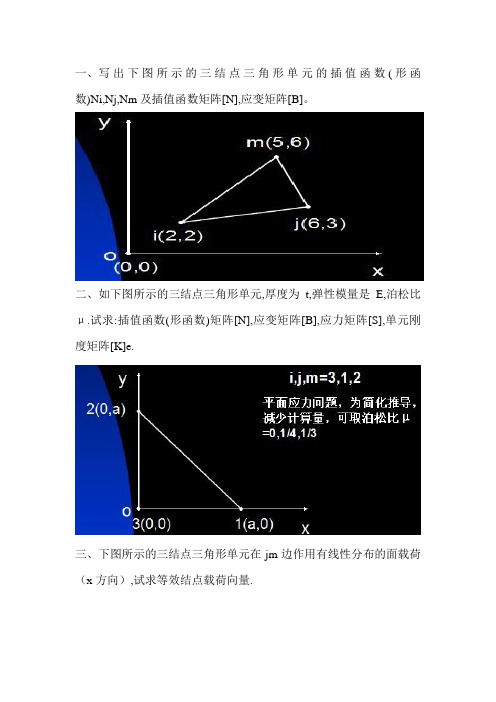
一、写出下图所示的三结点三角形单元的插值函数(形函数)Ni,Nj,Nm及插值函数矩阵[N],应变矩阵[B]。
二、如下图所示的三结点三角形单元,厚度为t,弹性模量是E,泊松比μ.试求:插值函数(形函数)矩阵[N],应变矩阵[B],应力矩阵[S],单元刚度矩阵[K]e.
三、下图所示的三结点三角形单元在jm边作用有线性分布的面载荷(x方向),试求等效结点载荷向量.
四、如下图所示,一正方形平板,厚度为t,边长为a,弹性模量E,泊松比μ.划分为两个三角形单元.求:1,3点的位移.
五、下图所示矩形板,分成四个三结点三角形单元.要求:
(1)写出由单元刚度矩阵组装总体刚度矩阵的表达式;
(2)如1234就是一个矩形单元,试求此单元的单元刚度矩阵.。
有限元分析大作业

有限元大作业一题目要求:图1所示为一悬臂梁,在端部承受载荷,材料弹性模量为E,泊松比为1/3,悬臂梁的厚度(板厚)为t,若该粱被划分为两个单元,单元和节点编号如图所示,试按平面应力问题计算各个节点位移计支反力。
一、单元划分1.计算简图及单元划分如下所示:2.进行节点及单元编号节点i j m单元① 2 3 4② 3 2 13.节点坐标值节点号1 2 3 4坐标值X 2 2 0 0Y 1 0 1 0二、计算单元刚度矩阵1、计算每个单元面积△以及i b ,i c (m j i i ,,=) ①②单元的面积相等,即12121=⨯⨯=∆ 单元①的i b ,i c⎩⎨⎧=--==-=0)(1m j i m j i y x c y y b ⎩⎨⎧=--==-=2)(0i m ji m j x x c y y b ⎩⎨⎧-=--=-=-=2)(1j i mj i m y x c y y b 对平面应力问题,其表达式为[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+-+-+-+∆-=s r s r sr s r s r s r s r s r b b uc c cb u b uc b c u c ub c c u b b u Et Krs 21212121)1(42 然后对单元①求解单元刚度子矩阵2==i r 2==i s []⎥⎦⎤⎢⎣⎡=3/1001329)1(22Et K 2==i r 3==j s []⎥⎦⎤⎢⎣⎡=03/23/20329)1(23Et K2==i r 4==m s []⎥⎦⎤⎢⎣⎡----=3/13/23/21329)1(24Et K 3==j r 3==j s []⎥⎦⎤⎢⎣⎡=4003/4329)1(33Et K 3==j r 2==i s []⎥⎦⎤⎢⎣⎡=03/23/20329)1(32Et K 3==j r 4==m s []⎥⎦⎤⎢⎣⎡----=43/23/23/4329)1(34Et K 4==m r 4==m s []⎥⎦⎤⎢⎣⎡=3/133/43/43/7329)1(44Et K 4==m r 2==i s []⎥⎦⎤⎢⎣⎡----=3/13/23/21329)1(42Et K 4==m r 3==j s []⎥⎦⎤⎢⎣⎡----=43/23/23/4329)1(43Et K由子矩阵[]e rs K 合成单元刚度矩阵[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡----------------=3/133/443/23/13/23/43/73/23/43/2143/24003/23/23/403/43/203/13/203/23/103/213/2001329)1(Et K将单元①的单元刚度矩阵补零升阶变为单元刚度矩阵,其在总体刚度矩阵中的位置为:节点号→单元②的i b ,i c⎩⎨⎧=--=-=-=0)(1m j im j i y x c y y b ⎩⎨⎧-=--==-=2)(0i m ji m j x x c y y b ⎩⎨⎧=--==-=2)(1j i mj i m y x c y y b 然后对单元 求解单元刚度子矩阵:3==i r 3==i s []⎥⎦⎤⎢⎣⎡=3/1001329)2(33Et K 3==i r 2==j s []⎥⎦⎤⎢⎣⎡=03/23/20329)2(32Et K 3==i r 1==m s []⎥⎦⎤⎢⎣⎡----=3/13/23/21329)2(31Et K 1 2 3 412[])1(22K[])1(23K[])1(24K3[])1(32K[])1(33K[])1(34K4[])1(42K[])1(43K[])1(44K2==j r 2==j s []⎥⎦⎤⎢⎣⎡=4003/4329)2(22Et K 2==j r 3==i s []⎥⎦⎤⎢⎣⎡=03/23/20329)2(23Et K 2==j r 1==m s []⎥⎦⎤⎢⎣⎡----=43/23/23/4329)2(21Et K 1==m r 1==m s []⎥⎦⎤⎢⎣⎡=3/133/43/43/7329)2(11Et K 1==m r 3==i s []⎥⎦⎤⎢⎣⎡----=3/13/23/21329)2(13Et K 1==m r 2==j s []⎥⎦⎤⎢⎣⎡----=43/23/23/4329)2(12Et K 由子矩阵[]e rs K 合成单元刚度矩阵[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡----------------=3/133/443/23/13/23/43/73/23/43/2143/24003/23/23/403/43/203/13/203/23/103/213/2001329)2(Et K将单元②的单元刚度矩阵补零升阶变为单元贡献矩阵,其在总体刚度矩阵中的位置为:节点号→1 2 3 41 [])2(11K[])2(12K[])2(13K2 [])2(21K[])2(22K[])2(23K3 [])2(31K [])2(32K [])2(33K 4三、计算总体刚度矩阵总体刚度矩阵是由各单元的贡献矩阵迭加而成)2()1(][][][][K K K K e +==∑四、进行节点约束处理根据节点约束情况,在总刚矩阵中可采用划行划列处理约束的方法,由题目易知,节点3和4的已知水平位移和垂直位移都为零,划去其相对应的行和列,则总刚矩阵由8阶变为4阶,矩阵如下:⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧--=⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--------2/02/03/13043/203/73/23/443/23/133/43/23/43/43/73292211p p v u v u Et329][Et K =1 2 3 413/133/43/43/743/23/23/4----3/13/23/21----000243/23/23/4----3/13003/73/43/403/13/23/21----33/13/23/21----3/43/403/13003/743/23/23/4----40003/13/23/21----43/23/23/4----3/133/43/43/7化简⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧--=⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--------Et p Et p v u v u 3/1603/160130122072412213424472211 五、求解线性方程组方法:采用LU 分解法 1.求解矩阵[]U 各元素⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-----⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡------⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--------75/10775/640075/6475/353007/767/27/7502447~7/877/87/7607/87/337/207/767/27/7502447~13012207241221342447⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----353/44900075/6475/353007/767/27/7502447~ 得到的[]U 矩阵如下:[]⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----=353/44900075/6475/353007/767/27/7502447U 2.求解矩阵[]L 各元素⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--------=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----13012207241221342447353/44900075/6475/353007/767/27/75024471353/6475/767/20175/27/40017/40001 得到的[]L 矩阵如下:[]⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--------=13012207241221342447L3.进行求解⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧---=⇒⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧--=Et p Et p Et p y Et p Et p Ly 79425/850800225/323/1603/1603/160⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧---=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----⇒=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡Et p Et p Et p v u v u y v u v u U 79425/850800225/323/160353/44900075/6475/353007/7675/27/750244722112211 解得Et p v /422.82-= Et p u /497.12-= Et p v /028.91-= Et p u /897.11=于是求得各节点的位移为:⎩⎨⎧-==Etp v Etp u /028.9/897.111 ⎩⎨⎧-=-=Etp v Etp u /422.8/497.122 ⎩⎨⎧==033v u ⎩⎨⎧==044v u 六、求解相应的支反力(运用静力学的平衡方程进行求解)3号节点和4号节点的支反力如下图所示:。
有限元作业

有限元作业一、名称:平面结构的静力学分析二、问题描述如图所示不规则板,板厚0.5,孔直径为1,倒角半径为0.4。
约束条件:在左边的孔约束全部自由度,载荷施加在右边圆的下半部分,两端施加最小值(50)逐渐均匀变大到底部的最大值(500)。
三、过程:1.选择单元格类型:新建材料类型Main Menu> Preprocessor > Material Props> Material Models> Structural > Linear > Elastic >Isotropic.并设置属性四、建立模型1.运行Main Menu> Preprocessor> Modeling> Create> Areas> Rectangle> By Dimensions分别输入:X1 = 0 X2 = 6 Y1 = -1 Y2 = 1X1 = 4 X2 = 6 Y1 = -1 Y2 = -3(1)在两个矩形的基础上依次建立两个圆形1运行Utility Menu> PlotCtrls> Pan, Zoom, Rotate2单击small dot3运行Utility Menu> WorkPlane> Display Working Plane4运行Utility Menu> WorkPlane> WP Settings点Polar .Grid. Triad5运行Main Menu> Preprocessor> Modeling> Create> Areas> Circle> Solid Circle6输入WP X = 0 WP Y = 07建立半径为1的圆.8同样的方法建立第二个圆(2)进行布尔运算运行Main Menu> Preprocessor> Modeling> Operate> Booleans> Add>Areas(3)倒圆角1.运行Utility Menu> PlotCtrls> Numbering点line numbering.2.运行Utility Menu> WorkPlane> Display Working Plane Main Menu>Preprocessor> Modeling> Create> Lines> Line Fillet选择17 和 8.3.输入半径0.44.运行Utility Menu> Plot> Lines5.运行Utility Menu> PlotCtrls> Pan, Zoom, Rotate点Zoom button.放大该区域6.运行Main Menu> Preprocessor> Modeling> Create> Areas> Arbitrary> ByLines选线4.5和17.运行Utility Menu> Plot> Areas分别建立两个孔1.运行Utility Menu> WorkPlane> Display Working Plane2.运行Main Menu> Preprocessor> Modeling> Create> Areas> Circle> SolidCircle输入WP X = 0WP Y = 03.建立半径为0.4的孔4.运行Utility Menu> WorkPlane> Offset WP to> Global Origin5.运行Main Menu> Preprocessor> Modeling> Create> Areas> Circle> SolidCircle选取点WP X = 0WP Y = 0建立第二个孔6.运行Utility Menu> WorkPlane> Display Working Plane7.运行Utility Menu> Plot> Replot和Utility Menu> Plot> Lines进行布尔运算运行Main Menu> Preprocessor> Modeling> Operate> Booleans> Add> Areas【一】设置材料属性运行Main Menu> Preprocessor> Material Props> Material Models如下图设置【二】定义实常数运行Main Menu> Preprocessor> Real Constants> Add/Edit/Delete输入【三】划分网格1.运行Main Menu> Preprocessor> Meshing> Mesh Tool Set Global Sizecontrol. 输入0.5。
国科大有限元作业1
作业1
1.叙述弹性力学中三维空间问题的平衡方程、几何方程、物理方程、力边界条
件和位移边界条件,并写出矩阵形式的表示式。
2.分别写出平面应力问题和平面应变问题的平衡方程、几何方程、物理方程、
力边界条件和变形协调方程,请以矩阵形式表示。
3.叙述最小势能原理,并写出其数学表示式。
4.试用流程图的形式概括有限单元法的分析过程。
5.用Galerkin加权余量法求解受均布外载荷简支梁的变形。
已知梁的横向位移
满足控制方程
4
4
w
d
EI q
dx
-=,其边界条件为
2
2
0(0)
d w
w x x l
dx
====
和。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
有限元作业答卷一、问题解答1、解:令221()()2()2dy p x q x y f x y dx ⎡⎤⎛⎫=+-⎢⎥ ⎪⎝⎭⎢⎥⎣⎦π则可以得到()()y q x y f x π=-,()y dy p x dx 'π=,()y d d dy p x dx dx dx '⎛⎫π= ⎪⎝⎭又有其Euler 方程公式为:0u u d dx'ππ-= 综上得到原泛函问题的Euler 方程及其边界条件为:()()(),[,](1().1.1),()a b d dy p x q x y f x x a b dx dx y a y y b y ⎧⎪⎨⎛⎫-+=∈ ⎪⎝⎭==⎪⎩2、(1)解:引入Sobolev 空间0V H ()∞=Ω,任取V v ∈乘以方程两端积分: (((,))(,))(,)k x y u q x y u vdxdy f x y vdxdy ΩΩ-∇∙∇+=⎰⎰⎰⎰再利用格林公式得到:((,)(,))(,)(,)uk x y u v q x y uv dxdy k x y vds f x y vdxdy n ΩΓΩ∂∙∇∇+-=∂⎰⎰⎰⎰⎰ 由边界条件得到:(,)((,)(,))(,)(,)g x y k x y u v q x y uv dxdy f x y vdxdy k x y vds nΩΩΓ∂∙∇∇+=+∂⎰⎰⎰⎰⎰ 令 A(,)((,)(,))(,)F()(,)(,)u v k x y u v q x y uv dxdy g x y v f x y vdxdy k x y vdsn ΩΩΓ⎧=∙∇∇+⎪⎪⎨∂⎪=+∂⎪⎩⎰⎰⎰⎰⎰ 得变分方程A(,)F(),(1.2.1)u v v v V=∈其解0u H ()∞∈Ω便为椭圆型方程第一边值问题的Galerkin 意义广义解。
(2)证:下面用Lax-Milgram 定理证明广义解的存在唯一性。
首先,由Hilbert 空间的Schwarz 不等式得到1(,)V f v f v f v v ≤≤∀∈又有1(,)()(,)g x y f v k x y v d s n Γ∂=∂⎰有界 于是11F(v)(,)(,)f v f f v f =+≤+,即F(v)在V 上是有界的。
其次,A (,)((,)(,))u v k x y u v q x y u v d x d y Ω=∙∇∇+⎰⎰中,A(,)u v 对称是显然的。
并且有:12((,)(,))(,)(,)K (,)Q (,)M ,V(),A ,k x y u v q x y uv dxdyk x y u vdxdy q x y uvdxdy u v u v uv u u v v ΩΩΩ∇∇+∇∇+≤∇∇=+≤≤∈⎰⎰⎰⎰⎰⎰说明A (,)u v 在V 上是有界的。
再证A (,)u v 正定,因为对于u V H ()∞∈=Ω, ()()()()222222222221((,)(,))(,)(,)(,)(,)(,)(,)A(,)x y x yk x y u q x y u dxdyk x y u dxdy q x y u dxdy k x y u u dxdy q x y uk x y u u q x y uu u u ΩΩΩΩ∇+=∇+=++=++≤α=⎰⎰⎰⎰⎰⎰⎰⎰根据Lax-Milgram 定理可知变分方程存在唯一解0u H ()∞∈Ω。
它是边值问题的Galerkin 广义解。
3、解:将第一边值条件齐次化,令b a u v x b ab aβ-αα-β=++--得,(,)(1.3.1)()()0d dv b a p q v x f x a b dx dx b a b a v a v b ⎧β-αα-β⎛⎫⎛⎫-+++=∈⎪ ⎪ ⎪--⎝⎭⎝⎭⎨⎪==⎩取广义解空间}{120V H [,],,()()0T a b v v v L v a v b ==∈==,再进行变分求广义解。
任取V v ∈,用它乘以式(1.3.1)中第一式的两边,并在区间I=[a,b]上积分:V bb a a d du b a p q u x vdx fvdx v dx dx b a b a ⎡β-αα-β⎤⎛⎫⎛⎫-+++=∀∈ ⎪ ⎪⎢⎥--⎝⎭⎝⎭⎣⎦⎰⎰对左端分部积分,bb b a a a du du dv b a p v p q u x v dx fvdx dx dx dxb a b a ⎡β-αα-β⎤⎛⎫-++++= ⎪⎢⎥--⎝⎭⎣⎦⎰⎰, 利用()()0v a v b ==,左端第一项为0,带入上式得()()()()V(1.3.2)bb a a b a pu x v x q u x x v x dx fvdx v b a b a ⎡β-αα-β⎤⎛⎫''+++=∀∈ ⎪⎢⎥--⎝⎭⎣⎦⎰⎰如前所述,满足(3.2)式的解V u ∈称为原两点边值问题Galerkin意义的广义解。
引入空间V 上的双线性泛函A(,)()()()()(1.3.3)ba b a u v pu x v x q u x x v x dx b a b a ⎡β-αα-β⎤⎛⎫''=+++ ⎪⎢⎥--⎝⎭⎣⎦⎰和线性泛函()()()(1.3.baF v f x v x d x=⎰于是原问题的Galerkin 广义解V u ∈可以表示为:A(,)(),V(1.3.5)u v F v v =∀∈下面用等距节点线性元推导有限元方程。
从(1.3.3)式可以得出,A(,)u v 不对称,下面采用Galerkin 法建立有限元方程。
可以知道变分方程为(1.3.5)式,求V u ∈使得(1.3.5)式成立。
下面构造V 的有限维子空间V h12V {(),(),...,()}h n span x x x =ϕϕϕ使得子空间V h 的形成按以下步骤进行:1)剖分区间I =[a ,b ] 011......i i n a x x x x x b-=<<<<<<= 由于是等距节点剖分,则有单元长度1()/i i h x x b a n -=-=-,于是()/i x a i b a n =+-,称小区间1e [,]i i i x x -=为单元。
2)线性函数的构造 取1,()0,e 1,2,...,i i i x i x x x hn--⎧∈⎪ϕ=⎨=⎪⎩其它可以得到12V {(),(),...,()}V h n span x x x =ϕϕϕ⊂。
假设在i x 处()u x 的值i u (未知),则在V h 中V u ∈的近似解为:nh i i i 1u (x)u (x)(1.3.6)==ϕ∑从而得到近似变分方程:求()V h h u x ∈使得A(,)(),V (1.3.7)h h u v F v v =∀∈将(1.3.6)带入(1.3.7)并取(x ),1,2,...,j v j n=ϕ=得到: ()()()()()()()()()()()()()n i i j j i 1i j j 11j 12j 2j j 112111222212A u ,F(),j 1,2,...,n A ,F(),j 1,2,...,nA ,A ,...A ,F(),j 1,2,...,nA ,A ,...A ,A ,A ,...A ,............A ,A ,...A ,ni i n n n n n n n n u u u u ==⎛⎫ϕϕ=ϕ= ⎪⎝⎭⇒ϕϕ=ϕ=⇒ϕϕ+ϕϕ++ϕϕ=ϕ=⎡ϕϕϕϕϕϕ⎢ϕϕϕϕϕϕ⎢⇒⎢⎢ϕϕϕϕϕϕ⎣∑∑1122F()F()......F()n n u u u ϕ⎤⎡⎤⎡⎤⎥⎢⎥⎢⎥ϕ⎥⎢⎥⎢⎥=⎥⎢⎥⎢⎥⎥⎢⎥⎢⎥ϕ⎣⎦⎣⎦⎦(1.3.8)Ku F⇒=要求解此方程组,首先需要计算出系数矩阵K 和常数向量F ,而根据12(),(),...,()n x x x ϕϕϕ的结构可知,()i j (),()0,x x i j ϕϕ≡≠。
这时方程组(1.3.8)的系数矩阵:()()()1122A ,0...00A ,...............00...A ,n n K ⎡ϕϕ⎤⎢⎥ϕϕ⎢⎥=⎢⎥⎢⎥ϕϕ⎣⎦作仿射变换 1,i i x x x e h --ξ=∈可将11,,...,n e e e 变成标准单元[0,1]e =。
引入函数011,[0,1],[0,1]()()0,0,N x N x -ξξ∈ξξ∈⎧⎧==⎨⎨⎩⎩其它其它111e (0),,(),i i i i x x x x x N hhx ---⎧∈⎪ϕ-ξξ===⎨⎪⎩其它由1i x x h -=+ξ得,()111111120A ,1()()()1,2,()()()()...,i i x i i i i i i x i i i dx x h x h N x h N d h b a p x q x x b a b a b a b b a np a i q ----⎡β-αα-β⎤⎛⎫+++ ⎪⎢⎥--⎝⎭⎣⎦⎡β-αα-β⎤⎛⎫+++ ⎪⎢⎥--⎝⎭⎣⎦''ϕϕ=ϕϕϕϕ=+ξ+ξξ+ξξξ=⎰⎰111()()(())bi i ai F f x x h N h f d dx-+ϕξξ==ξϕ⎰⎰带入(1.3.8)式得到相应方程组K u F= 则 ()(),u =A 1,2,...,(1.3.9,/)i i i i F i nϕ=ϕϕ这就是我们需要求的线性代数方程组——有限元方程。
4、解:取广义解空间}{120V H [0,1],,(0)0T v v v L v ==∈=,再进行变分求广义解。
任取V v ∈,用它乘以式4题中第一式的两边,并在区间I=[0,1]上积分:211200V d u u vdx vdx v dx ⎡⎤-+=∀∈⎢⎥⎣⎦⎰⎰对左端分部积分,111000du du dv v uv dx vdx dx dx dx ⎡⎤-++=⎢⎥⎣⎦⎰⎰利用(0)0v =以及边界条件(0)0u '=,再加之4题中第一式可以推出,左端第一项为0,带入上式得:[]11()()()()()(1.4.1)u x v x u x v x dx v x dx''+=⎰⎰于是原问题的Galerkin 广义解V u ∈可以表示为:A(,)(),V(1.4.2)u v F v v =∀∈其中: []1A(,)()()()()(1.4.3)u v u x vx u x v x dx''=+⎰1()()(1.4.4)F v v x dx=⎰剖分区间I =[0,1] 0110 (1)i i n x x x x x -=<<<<<<= 单元长度11/i i i h x x n h -=-==,称小区间1e [,]i i i x x -=为单元。
