空间与几何(新)
新高考数学-空间向量与立体几何-第2课时教案

新教材同步学案 数学 选择性必修第一册
2.在两个向量共线的充要条件中,为何要求 b≠0? 答:当 b=0 时,若 a≠0,仍有 a∥b,但不存在 λ∈R,使得 a=λb.
第6页
新教材同步学案 数学 选择性必修第一册
3.空间中的任意两个向量是否共面?为什么? 答:共面,任意两个向量都可以平移到同一个平面内,因此空间中向量的加 减运算与平面中一致.
课时学案
第9页
新教材同步学案 数学 选择性必修第一册
题型一 向量的共线问题 例 1 (1)已知 A,B,C 三点共线,O 为直线外任意一点,若O→C=mO→A+nO→B, 则 m+n=____1____. 【解析】 由于 A,B,C 三点共线,所以存在实数 λ,使得A→C=λA→B,即O→C -O→A=λ(O→B-O→A),所以O→C=(1-λ)O→A+λO→B,所以 m=1-λ,n=λ,所以 m+ n=1.
的直线互相____平__行__或__重_合_______
平行于同一个平面的向量
充要 条件
对于空间任意两个向量 a,b(b≠0),若两个向量 a,b 不共线,则向量 p
a∥b 的充要条件是存在实数 λ,使 a 与 a,b 共面的充要条件是存在唯一的
=λb
有序实数对(x,y),使 p=xa+yb
第3页
新教材同步学案 数学 选择性必修第一册
第15页
新教材同步学案 数学 选择性必修第一册
A→1F=25A→1C=25(A→C-A→A1) =25(A→B+A→D-A→A1)=25a+25b-25c. 所以E→F=A→1F-A→1E=25a-145b-25c=25(a-23b-c), 又E→B=E→A1+A→1A+A→B=-23b-c+a=a-23b-c, 所以E→F=25E→B,且有公共点 E,所以 E,F,B 三点共线.
专题37 空间几何体(知识梳理)(新高考地区专用)(解析版)

专题37 空间几何体(知识梳理)一、空间几何体1、空间几何体的基本定义如果只考虑一个物体占有空间部分的形状和大小,而不考虑其它因素,则这个空间部分就是一个几何体。
围成体的各个平面图形叫做体的面;相邻两个面的公共边叫做体的棱;棱和棱的公共点叫做体的顶点。
几何体不是实实在在的物体。
平面的特性:无限延展、处处平直、没有其他性质(如厚度、大小、面积、体积、重量等)。
例1-1.下列是几何体的是( )。
A 、方砖B 、足球C 、圆锥D 、魔方【答案】C【解析】几何体不是实实在在的物体,故选C 。
例1-2.判断下列说法是否正确:(1)平静的湖面是一个平面。
(×)(2)一个平面长3cm ,宽4cm 。
(×)(3)三个平面重叠在一起,比一个平面厚。
(×)(4)书桌面是平面。
(×)(5)通过改变直线的位置,可以把直线放在某个平面内。
(√)【解析】平面可以看成是直线平行移动形成的,所以直线通过改变其位置,可以放在某个平面内。
(6)平行四边形是一个平面。
(×)(7)长方体是由六个平面围成的几何体。
(×)(8)任何一个平面图形都是一个平面。
(×)(9)长方体一个面上任一点到对面的距离相等。
(√)(10)空间图形中先画的线是实线,后画的线是虚线。
(×)(11)平面是绝对平的,无厚度,可以无限延展的抽象的数学概念。
(√) 例1-3.下列说法正确的是 。
①长方体是由六个平面围成的几何体;②长方体可以看作一个矩形ABCD 上各点沿铅垂线向上移动相同距离到矩形D C B A ''''所围成的几何体;③长方体一个面上的任一点到对面的距离相等。
【答案】②③【解析】①错,因长方体由6个矩形(包括它的内部)围成,注意“平面”与“矩形”的本质区别;②正确;③正确。
[多选]例1-4.下列说法正确的是( )。
A 、任何一个几何体都必须有顶点、棱和面B 、一个几何体可以没有顶点C 、一个几何体可以没有棱D 、一个几何体可以没有面【答案】BC【解析】球只有一个曲面围成,故A 错、B 对、C 对,由于几何体是空间图形,故一定有面,D 错,故选BC 。
第三章_第一节 空间解析几何,李养成(新版),

它们的图像都是一条直线,z轴!
x y z a , 例3.1.4 讨论方程组 a 的图像. x y ax
x y z a 解:方程组的图像是球面 a a 与母线平行于z轴的圆柱面 x y 的交线
F x, y, z , G x, y, z
称为空间曲线的一般方程 注: (1)表示同一条曲线的方程不唯一。 (2)曲线上点的坐标都满足方程,
z
S1 S2
o
C
y
满足方程的点都在曲线上, x试考察方程
第3章 常见的曲面
本章在初步介绍空间图形与方程之间的一般关系 后,对柱面、锥面、旋转曲面以及二次曲面(包括椭球 面、单叶双曲面、双叶双曲面、椭圆抛物面和双曲抛 物面)进行讨论.
对于前三种曲面具有明显的几何特征,我们着重从 这些曲面的几何特性来建立它们的方程.
对于五种二次曲面,我们则从曲面的标准方程出 发来讨论它们的几何性质, 描述它们的几何形状.
z
点P 在该圆锥面上
L
cos OP, k cos
OP k OP k
cos
y
x
x y tan z , 整理得二次齐次方程
圆锥面的坐标式方程
习题8(1) 已知圆锥面的顶点为P0 (1, 2,3),轴垂直于 平面 x y z ,半顶角为 ,求这圆锥面的 方程. 解 圆锥面的轴过点 P0 , 方向向量 v 2,2, 1.
特别地,当 C0 是原点时,球面方程为
x2 y2 z 2 R2
表示上(下)球面 .
C0
2020_2021年新教材高中数学11.1空间几何体11.1.5旋转体ppt课件新人教B版必修第四册

知识点二 球
[填一填] (1)球面可以看成___一__个__半__圆_____绕着它的直径所在的直线 旋转一周所形成的曲面;球面围成的几何体,称为 ____球__.________ (2)形成球面的半圆的圆心称为球的_____球__心_______,连接 球面上一点和球心的线段称为球的____半__径________,连接球面上 两点且通过球心的线段称为球的_____直__径__._____ (3)由球面的形成过程可看出,球面可以看成空间中到一个 定点的距离等于定长的点的集合.
[解析] 根据球的定义可知 A 正确.由圆锥的定义知 B 正 确.只有当平面与圆锥的底面平行时底面与截面之间的部分为圆 台,故 C 错误.由圆柱的定义知 D 正确.
1.判断简单旋转体结构特征的方法 1明确由哪个平面图形旋转而成. 2明确旋转轴是哪条直线. 2.简单旋转体的轴截面及其应用 1简单旋转体的轴截面中有底面半径、母线、高等体现简单 旋转体结构特征的关键量. 2在轴截面中解决简单旋转体问题体现了化空间图形为平面 图形的转化思想.
(6)若球的半径为 R,则球的表面积为 S=___4_π_R_2________.
[答一答] 2.在平面几何中,你学习了直线与圆的位置关系,那么平 面与球的位置关系如何?
提示:类比平面上直线与圆的位置关系,平面与球有以下 几种位置关系:相离、相切、相交,其中相离是平面与球无公 共点,相切是平面与球有且只有一个公共点,相交则是平面与 球有无数多个公共点.
[变式训练 1] 判断下列各命题是否正确. (1)圆柱上底面圆上任一点与下底面圆上任一点的连线都是圆 柱的母线; (2)一直角梯形绕下底所在直线旋转一周,所形成的曲面围成 的几何体是圆台; (3)圆锥的轴截面是等腰三角形,圆台的轴截面是等腰梯形; (4)到定点的距离等于定长的点的集合是球.
2023版新教材高中数学第一章空间向量与立体几何1
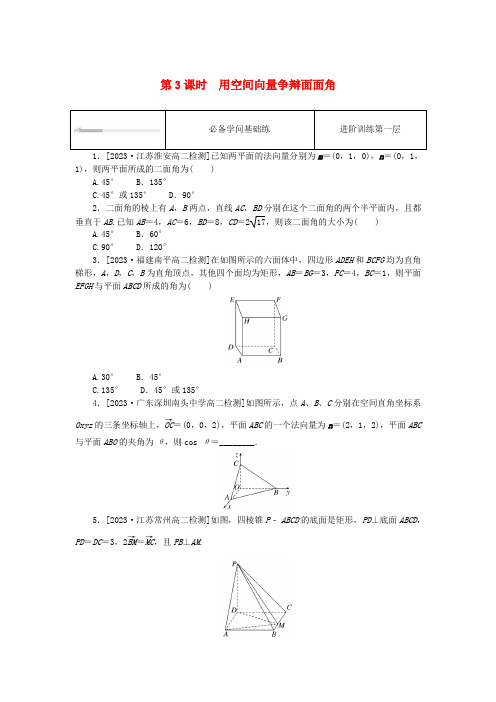
第3课时用空间向量争辩面面角必备学问基础练进阶训练第一层1.[2023·江苏淮安高二检测]已知两平面的法向量分别为m=(0,1,0),n=(0,1,1),则两平面所成的二面角为( )A.45° B.135°C.45°或135° D.90°2.二面角的棱上有A,B两点,直线AC,BD分别在这个二面角的两个半平面内,且都垂直于AB.已知AB=4,AC=6,BD=8,CD=217,则该二面角的大小为( )A.45° B.60°C.90° D.120°3.[2023·福建南平高二检测]在如图所示的六面体中,四边形ADEH和BCFG均为直角梯形,A,D,C,B为直角顶点,其他四个面均为矩形,AB=BG=3,FC=4,BC=1,则平面EFGH与平面ABCD所成的角为( )A.30° B.45°C.135° D.45°或135°4.[2023·广东深圳南头中学高二检测]如图所示,点A、B、C分别在空间直角坐标系Oxyz的三条坐标轴上,OC→=(0,0,2),平面ABC的一个法向量为n=(2,1,2),平面ABC 与平面ABO的夹角为θ,则cos θ=________.5.[2023·江苏常州高二检测]如图,四棱锥P ABCD的底面是矩形,PD⊥底面ABCD,PD=DC=3,2BM→=MC→,且PB⊥AM.(1)求AD的长;(2)求二面角P AM D的正弦值.6.如图,在三棱柱ABC A1B1C1中,四边形AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.(1)求证:AA1⊥平面ABC;(2)求平面A1C1B与平面B1C1B夹角的余弦值.关键力量综合练进阶训练其次层1.在四棱锥P ABCD中,PA⊥平面ABCD,ABCD是矩形,且AB=3,AD=4,PA=435,则平面ABD与平面PBD的夹角为( )A.30° B.45°C.60° D.75°2.[2023·湖南武冈高二检测]已知在菱形ABCD中,∠ABC=60°,沿对角线AC折叠之后,使得平面BAC ⊥平面DAC ,则二面角B CD A 的余弦值为( )A.2 B .12C.33 D .553.如图所示的多面体是由底面为ABCD 的正方体被截面EFGH 所截而得到的,其中AB =BC =4,AE =1,CG =4,BF =2.则二面角H BC A 的余弦值为( )A.255 B .45C.35 D .554.已知正三棱柱ABC A 1B 1C 1的棱长均为a ,D 是侧棱CC 1的中点,则平面ABC 与平面AB 1D 的夹角的余弦值为( )A.12 B .22 C .32D .0 5.[2023·福建漳州八中高二检测]已知正方形的边长为4,E ,F 分别为AD ,BC 的中点,以EF 为棱将正方形ABCD 折成如图所示的60°的二面角,点M 在线段AB 上.直线DE 与平面EMC 所成的角为60°,则平面MCE 与平面CEF 夹角的余弦值为________.6.[2023·江苏常州高二检测]把边长为2的正方形ABCD 沿对角线BD 折成两个垂直平面,O ,E 分别为BD ,DC 中点,以O 为原点,OC →方向,OD →方向,OA →方向分别为x 轴,y 轴,z 轴正方向建立空间直角坐标系.(1)求证:AE ⊥DC ;(2)求二面角A DC B 的余弦值.7.[2023·广东深圳高二测试]如图,直三棱柱ABC A 1B 1C 1中,底面是边长为2的等边三角形,D 为棱AC 中点.(1)证明:AB 1∥平面BC 1D ;(2)若面B 1BC 1与面BC 1D 的夹角余弦值为34,求CC 1.8.[2023·山东省试验中学高二检测]如图,在四棱锥P ABCD 中,四边形ABCD 为矩形,PD ⊥平面ABCD ,PD =CD =1,PA 与平面ABCD 所成角为30°,M 为PB 上一点且CM ⊥PA .(1)证明:PA ⊥DM ;(2)设平面PAD 与平面PBC 的交线为l ,在l 上取点N 使PN →=DA →,Q 为线段PN 上一动点,求平面ACQ 与平面PDC 夹角的正弦值的最小值.核心素养升级练进阶训练第三层1.[2023·广东广州高二检测]“堑堵”“阳马”和“鳖臑”是我国古代对一些特殊几何体的称谓.《九章算术·商功》中描述:“斜解立方,得两堑堵,斜解堑堵,其一为阳马,其一为鳖臑.”一个长方体ABCD A 1B 1C 1D 1沿对角面斜解(图1),得到两个一模一样的堑堵(图2),再沿一个堑堵的一个顶点和相对的棱斜解(图2),得到一个四棱锥,称为阳马(图3),一个三棱锥称为鳖臑(图4).若鳖臑的体积为4,AB =4,BC =3,则在鳖臑中,平面BCD 1与平面BC 1D 1夹角的余弦值为( )A.6565 B .66565 C.6513 D .265652.[2023·山东青岛高二检测]如图,在四棱锥P ABCD 中,底面ABCD 为直角梯形,CD ∥AB ,∠ABC =90°,AB =2BC =2CD =4,侧面PAD ⊥面ABCD ,PA =PD =2.(1)求证:PA ⊥BD ;(2)设平面PAD 与平面PBC 的交线为l ,在l 上是否存在点N ,使得平面PCD 和平面NCD 的夹角的余弦值为539?若存在,请确定N 点的位置;若不存在,请说明理由.第3课时 用空间向量争辩面面角必备学问基础练1.答案:C解析:cos 〈m ,n 〉=m ·n |m |·|n |=11·2=22,即〈m ,n 〉=45°.∴两平面所成二面角为45°或180°-45°=135°.故选C.2.答案:B 解析:由条件,知AC →·AB →=0,AB →·BD →=0,CD →=-AC →+AB →+BD →.∴|CD →|2=|AC →|2+|AB →|2+|BD →|2-2AC →·AB →+2AB →·BD →-2AC →·BD →,即62+42+82-2×6×8cos 〈AC →,BD →〉=(217)2,∴cos 〈AC →,BD →〉=12,即〈AC →,BD →〉=60°,所以二面角的大小为60°.故选B.3.答案:B 解析:由于四边形ADEH 和BCFG 均为直角梯形,A ,D ,C ,B 为直角顶点,其他四个面均为矩形,所以这个六面体是四棱柱,由题意可知DA ,DC ,DE 两两垂直,以点D 为原点建系如图,则E (0,0,4),G (1,3,3),C (0,3,0),H (1,0,3),则EH →=(1,0,-1),HG →=(0,3,0),依据题意可知DE ⊥平面ABCD ,所以DE →=(0,0,4),即为平面ABCD 的一个法向量,设n =(x ,y ,z )为平面EFGH 的法向量,则⎩⎪⎨⎪⎧n ·EH →=x -z =0,n ·HG →=3y =0取x =1,则z =1,y =0,则n=(1,0,1)为平面EFGH 的一个法向量,则cos 〈n ,DE →〉=n ·DE →|n ||DE →|=42×4=22,所以平面EFGH 与平面ABCD 所成的角为45°.故选B.4.答案:23解析:由题意可知,平面ABO 的一个法向量为OC →=(0,0,2),所以cos θ=|OC →·n ||OC →|·|n |=42×3=23. 5.解析:(1)∵PD ⊥平面ABCD ,四边形ABCD 为矩形,∴不妨以{DA →,DC →,DP →}为一组基底,建立如图所示的空间直角坐标系D xyz . 设BC =3a ,则B (3a ,3,0),P (0,0,3),M (2a ,3,0),A (3a ,0,0), 则PB →=(3a ,3,-3),AM →=(-a ,3,0), ∵PB ⊥AM ,则PB →·AM →=-3a 2+9=0,解得a =3, 故AD =3a =3 3.(2)AM →=(-3,3,0),AP →=(-33,0,3), 设平面PAM 的法向量为m =(x 1,y 1,z 1),则⎩⎪⎨⎪⎧m ·AM →=-3x 1+3y 1=0m ·AP →=-33x 1+3z 1=0,取x 1=3,可得m =(3,1,3),∵PD ⊥平面AMD ,∴可设平面AMD 的法向量为n =(0,0,1),cos 〈m ,n 〉=m ·n |m |·|n |=313×1=31313,因此二面角P AM D 的正弦值为1-⎝ ⎛⎭⎪⎫313132=21313.6.解析:(1)证明:∵四边形AA 1C 1C 是正方形, ∴AA 1⊥AC .又∵平面ABC ⊥平面AA 1C 1C ,平面ABC ∩平面AA 1C 1C =AC , 且AA 1⊂平面AA 1C 1C , ∴AA 1⊥平面ABC .(2)由AC =4,BC =5,AB =3,得AC 2+AB 2=BC 2, ∴AB ⊥AC .建立如图所示的空间直角坐标系,则A 1(0,0,4),B (0,3,0),B 1(0,3,4),C 1(4,0,4), ∴=(4,-3,4),=(0,-3,4),=(0,0,4).设平面A 1C 1B 的一个法向量为n 1=(x 1,y 1,z 1),平面B 1C 1B 的一个法向量为n 2=(x 2,y 2,z 2).令x 2=3,则y 2=4,∴n 2=(3,4,0), ∴|cos 〈n 1,n 2〉|=|n 1·n 2||n 1||n 2|=165×5=1625.∴平面A 1C 1B 与平面B 1C 1B 夹角的余弦值为1625.关键力量综合练1.答案:A解析:由于PA ⊥平面ABCD ,ABCD 是矩形,所以AB ,AD ,AP 两两垂直,故以A 为坐标原点,AB ,AD ,AP 为x 轴,y 轴,z 轴建立空间直角坐标系, 又AB =3,AD =4,PA =435,所以A (0,0,0),B (3,0,0),D (0,4,0),P (0,0,435),由于PA ⊥平面ABCD ,所以平面ABD 的一个法向量为n =(0,0,1), 而PB →=(3,0,-435),BD →=(-3,4,0),设平面PBD 的法向量为m =(x ,y ,z ), 则⎩⎨⎧m ·PB →=3x -435z =0m ·BD →=-3x +4y =0,取x =4,则平面PBD 的法向量为m =(4,3,53),cos 〈n ,m 〉=n ·m |n |·|m |=0×4+0×3+1×531×42+32+(53)2=32,所以〈n ,m 〉=30°,由图可知平面ABD 与平面PBD 的夹角为锐角,所以平面ABD 与平面PBD 的夹角为30°,故选A.2.答案:D 解析:由于平面BAC ⊥平面DAC ,设AC 的中点为O ,BO ⊥AC ,则BO ⊥平面DAC ,DO ⊥AC ,故以OC 方向为x 轴,OD 方向为y 轴,OB 方向为z 轴,建立空间直角坐标系,设菱形边长为2,则C (1,0,0),D (0,3,0),B (0,0,3),CD →=(-1,3,0),CB →=(-1,0,3),OB →=(0,0,3),明显OB →=(0,0,3)是平面DAC 的一个法向量,设平面BCD 的法向量为n =(x ,y ,z ),则满足⎩⎪⎨⎪⎧n ·CD →=0n ·CB →=0,即⎩⎨⎧x -3y =0x -3z =0,令x =3,可得y =z =1,故n =(3,1,1),则cos 〈OB →,n 〉=33·5=55,即二面角B CD A 的余弦值为55.故选D. 3.答案:B解析:由题可得以D 为原点,以DA ,DC ,DH 为x ,y ,z 轴建立空间直角坐标系,如图:则D (0,0,0),B (4,4,0),C (0,4,0),E (4,0,1),F (4,4,2),G (0,4,4), 设H (0,0,h ),由E ,F ,G ,H 共面可得存在实数λ,μ使得GH →=λEF →+μFG →, 所以(0,-4,h -4)=λ(0,4,1)+μ(-4,0,2)=(-4μ,4λ,λ+2μ), 则⎩⎪⎨⎪⎧0=-4μ-4=4λh -4=λ+2μ,解得h =3,所以H (0,0,3). 又DH ⊥平面ABCD ,所以DH →=(0,0,3)是平面ABCD 的一个法向量.设平面HBC 的法向量为n =(x ,y ,z ),又BC →=(-4,0,0),HC →=(0,4,-3), 所以⎩⎪⎨⎪⎧BC →·n =0HC →·n =0⇒⎩⎪⎨⎪⎧-4x =04y -3z =0,令z =4,则n =(0,3,4),所以cos 〈DH →,n 〉=DH →·n |DH →|·|n |=123×32+42=45,由图可知二面角H BC A 为锐角,所以二面角H BC A 的余弦值为45.故选B.4.答案:B 解析:以点A 为坐标原点,以垂直于AC 的直线为x 轴,以AC 所在直线为y 轴,以AA 1所在直线为z 轴,建立空间直角坐标系如图所示,由于ABC A 1B 1C 1是各棱长均等于a 的正三棱柱,D 是侧棱CC 1的中点,所以A (0,0,0),B 1(32a ,a 2,a ),D (0,a ,a2),C 1(0,a ,a ),故=(32a ,a 2,a ),AD →=(0,a ,a 2),=(0,0,a2),设平面AB 1D 的法向量为n =(x ,y ,z ),则⎩⎨⎧n ·AB 1=0n ·AD →=0,即⎩⎪⎨⎪⎧3a 2x +a 2y +az =0ay +a 2z =0,令y =1,则z =-2,x =3,故n =(3,1,-2),又平面ABC 的一个法向量为m =(0,0,1), 所以|cos 〈m ,n 〉|=|m ·n ||m ||n |=23+1+4×1=22,所以平面ABC 与平面AB 1D 所成的锐二面角的余弦值为22.故选B. 5.答案:14解析:由已知得,EF ⊥AE ,EF ⊥DE , ∴EF ⊥平面ADE ,又EF ⊂平面ABFE , ∴平面ABFE ⊥平面ADE .取AE 的中点H 为坐标原点,建立如图所示的空间直角坐标系,∴E (-1,0,0),D (0,0,3),C (0,4,3),F (-1,4,0),则ED →=(1,0,3),EC →=(1,4,3),设M (1,t ,0)(0≤t ≤4),则EM →=(2,t ,0),若平面EMC 的法向量为m =(x ,y ,z ),则⎩⎪⎨⎪⎧m ·EM →=0m ·EC →=0,即⎩⎨⎧2x +ty =0x +4y +3z =0,取y =-2,则m =(t ,-2,8-t3).由DE 与平面EMC 所成的角为60°,则82t 2+4+(8-t )23=32, ∴t 2-4t +3=0,解得t =1或t =3,均有直线DE 与平面EMC 所成的角为60°.取ED 的中点Q ,则Q ⎝ ⎛⎭⎪⎫-12,0,32,QA →=⎝ ⎛⎭⎪⎫32,0,-32, 又EC →=(1,4,3),EF →=(0,4,0), QA →·EC →=32-32=0,QA →·EF →=0,则QA →为平面CEF 的法向量, 设平面MCE 与平面CEF 夹角为θ. ∴|cos θ|=|QA →·m ||QA→|×|m |=|2t -4|3×t 2+4+(8-t 3)2=|t -2|t 2-4t +19.当t =1时,cos θ=14;当t =3时,cos θ=14.∴平面MCE 与平面CEF 夹角的余弦值为14.6.解析:(1)证明:由于正方形ABCD 的边长为2, 所以可得A (0,0,2),E (22,22,0),D (0,2,0),C (2,0,0),B (0,-2,0),AE →=(22,22,-2),DC →=(2,-2,0), 由于AE →·DC →=22×2-22×2=0,所以AE →⊥DC →⇒AE ⊥DC .(2)设平面ADC 的法向量为n =(x ,y ,z ), AD →=(0,2,-2),AC →=(2,0,-2),所以有⎩⎪⎨⎪⎧n ·AD →=0n ·AC →=0⇒⎩⎨⎧2y -2z =02x -2z =0⇒n =(1,1,1),由于ABCD 是正方形,所以AB =AD ,由于O 为BD 的中点,所以AO ⊥BD ,由于平面ABD ⊥平面BDC ,平面ABD ∩平面BDC =BD ,AO ⊂平面ABD , 所以AO ⊥平面BDC ,因此向量OA →=(0,0,2)是平面BDC 的法向量,所以二面角A DC B 的余弦值为OA →·n |OA →|·|n |=1×22×3=33.7.解析:(1)证明:如图,连接B 1C ,使B 1C ∩BC 1=E ,连接DE ,由直三棱柱知四边形B 1BCC 1为矩形,所以E 为B 1C 的中点, ∵在△AB 1C 中,D 、E 分别为AC 和B 1C 的中点,∴DE ∥AB 1, 又因平面AB 1C ∩平面BDC 1=DE ,DE ⊂平面BDC 1,AB 1⊄平面BDC 1, ∴AB 1∥平面BDC 1.(2)设CC 1=a ,以D 为坐标原点建系,则B 1(3,0,a ),B (3,0,0),C 1(0,1,a ),D (0,0,0),所以=(0,0,a ),=(-3,1,a ),DB →=(3,0,0),设平面BB 1C 1的法向量为m =(x 1,y 1,z 1),故可取n =(0,a ,-1),由于平面B 1BC 1与平面BC 1D 的夹角的余弦值为34,所以|m ·n ||m |·|n |=34,即34=3a 2×a 2+1,解得a =3,∴CC 1= 3.8.解析:(1)∵四边形ABCD 为矩形,则AD ⊥CD , 又∵PD ⊥平面ABCD ,CD ⊂平面ABCD ,∴PD ⊥CD ,AD ∩PD =D ,AD ,PD ⊂平面PAD , ∴CD ⊥平面PAD ,PA ⊂平面PAD ,则PA ⊥CD , ∵CM ⊥PA ,且CM ∩CD =C ,CM ,CD ⊂平面CMD , ∴PA ⊥平面CMD ,DM ⊂平面CMD ,则PA ⊥DM .(2)∵PD ⊥平面ABCD ,则∠PAD 为PA 与平面ABCD 所成的角,∴∠PAD =30°,又∵PD =1,则AD =3,以D 为原点,DA 为x 轴,DC 为y 轴,DP 为z 轴,建立空间直角坐标系,则D (0,0,0),A (3,0,0),C (0,1,0), ∵AD =3,且PN →=DA →,∴PN =3,令PQ =λ(0≤λ≤3),则Q (λ,0,1), ∴AC →=(-3,1,0),CQ →=(λ,-1,1),设n =(x ,y ,z )是平面ACQ 的一个法向量,则⎩⎪⎨⎪⎧n ·AC →=-3x +y =0n ·CQ →=λx -y +z =0,取x =1,则y =3,z =3-λ,即n =(1,3,3-λ),平面PDC 的一个法向量为m =(1,0,0), ∴cos 〈m ,n 〉=m ·n |m |·|n |=14+(3-λ)2, ∵0≤λ≤3,则当λ=3时,cos 〈m ,n 〉的最大值为12,即平面ACQ 与平面PDC 夹角的余弦值的最大值为12,∴平面ACQ 与平面PDC 夹角的正弦值的最小值为32.核心素养升级练1.答案:B解析:由切割过程可知:BC ⊥平面CC 1D 1,∵VB CC 1D 1=13S △CC 1D 1·BC =13×12×CC 1×4×3=4,∴CC 1=2;在长方体ABCD A 1B 1C 1D 1中,以D 为坐标原点,DA →,DC →,正方向为x ,y ,z 轴建立如图所示空间直角坐标系,则B (3,4,0),C (0,4,0),D 1(0,0,2),C 1(0,4,2), ∴BC →=(-3,0,0),=(-3,-4,2),=(0,4,0),设平面BCD 1的法向量为n =(x ,y ,z ),令a =2,解得b =0,c =3,∴m =(2,0,3); ∴|cos 〈m ,n 〉|=|m ·n ||m |·|n |=65×13=66565,即平面BCD 1和平面BC 1D 1夹角的余弦值为66565.故选B.2.解析:(1)证明:由于CD ∥AB ,∠ABC =90°, 所以∠BCD =90°,由于BC =CD =2,所以BD =BC 2+CD 2=22,∠CBD =45°,从而∠ABD =45°,由于AB =4,所以AD 2=AB 2+BD 2-2AB ·BD cos ∠ABD =8,所以AD 2+BD 2=AB 2,从而BD ⊥AD ,由于侧面PAD ⊥平面ABCD ,侧面PAD ∩平面ABCD =AD ,BD ⊂平面ABCD ,所以BD ⊥平面PAD ,又由于PA ⊂平面PAD ,所以PA ⊥BD .(2)延长AD 和BC 交于点M ,连接PM ,则l 就是直线PM ,CD 为△ABM 的中位线, 以B 为原点,建立空间直角坐标系B xyz ,如图所示,则P (1,3,2),D (2,2,0),M (4,0,0),C (2,0,0), 所以CD →=(0,2,0),PD →=(1,-1,-2), 设平面PCD 的法向量为n 1=(x 1,y 1,z 1), 则⎩⎪⎨⎪⎧n 1·CD →=0n 1·PD →=0,即⎩⎨⎧2y 1=0x 1-y 1-2z 1=0,令z 1=1,则x 1=2,y 1=0,取n 1=(2,0,1), 设在l 上存在点N ,满足PN →=λPM →(λ∈R ),则CN →=CP →+PN →=CP →+λPM →=(-1,3,2)+λ(3,-3,-2)=(3λ-1,3(1-λ),2(1-λ)).设平面NCD 的法向量为n 2=(x 2,y 2,z 2), 则⎩⎪⎨⎪⎧n 2·CD →=0n 2·CN →=0,即⎩⎨⎧2y 2=0(3λ-1)x 2+3(1-λ)y 2+2(1-λ)z 2=0, 令z 2=3λ-1,则x 2=-2(1-λ),y 2=0,取n 2=(-2(1-λ),0,3λ-1), 设平面PCD 和平面NCD 的夹角为θ, 则cos θ=|cos 〈n 1,n 2〉|=|n 1·n 2||n 1|·|n 2|=|5λ-3|3×11λ2-10λ+3=539,解得λ=15或λ=-35, 所以在l 上存在点N ,N 在线段PM 上,PN =15PM ,或者N 在线段PM 的反向延长线上,PN=35PM .。
2021_2022学年新教材高中数学第一章空间向量与立体几何数学文化课件新人教A版选择性必修第一册

1
2
40
AB.若这个刍甍的体积为3
,求异面直线AB与CF所成角的
解 (方法1)取CD,AB的中点M,N,连接FM,FN,
则多面体分割为棱柱与棱锥两个部分,设E到平面ABCD的距离为h,
1
1
40
则 ×4×h×2+ ×4×2×h= ,
2
3
3
解得 h=2.
∵CN= 16 + 4=2 5,
∴CF= 5 + 4=3.
称其上下底,以“正从”称其高,如图,在“邪田”ABCD中,E,F分别在“正从”和
“下头”上,沿EF,FD,DE将图形翻折起来,使A,B,C重合为一点O.
(1)求证:OE⊥DF;
(2)若在“邪田”ABCD中,“正从”AB=4,“上头”AD=5,试求平面ODF与平面
EFD的夹角的余弦值.
(1)证明 依题意E,F分别为AB,BC的中点,
∵CD∥AB,∴∠FCD 为异面直线 AB 与 CF 所成角.在△FCM
中,FM=FC=3,CM=2,
∴cos
9+4-9
∠FCD=
2×3×2
=
1
.
3
(方法2)取CD,AB的中点M,N,连接FM,FN,
则多面体分割为棱柱与棱锥两个部分,
设E到平面ABCD的距离为h,
1
1
40
则 ×4×h×2+ ×4×2×h= ,解得
2021
第一章
数学文化
1.中国古代数学名著《九章算术》中记载:“刍甍者,下有袤有广,而上有袤
无广.刍,草也.甍,屋盖也.”翻译为“底面有长有宽为矩形,顶部只有长没有宽
为一条棱.刍甍字面意思为茅草屋顶.”现有一个刍甍如图所示,四边形
空间几何的体积与表面积 高考数学一轮复习(提升版)(新高考地区专用)
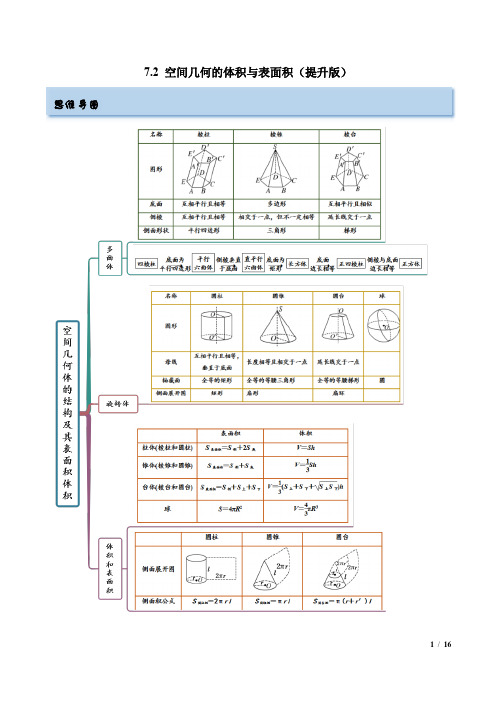
7.2 空间几何的体积与表面积(提升版)思维导图考点一柱锥台表面积【例1-1】(2022·青海)以边长为4的正方形的一边所在直线为旋转轴,将该正方形旋转一周,所得圆柱的侧面积为()A.32πB.16πC.32D.16【答案】A【解析】以边长为4的正方形的一边所在直线为旋转轴,旋转一周得到的旋转体为圆柱,其底面半径4r=,高4h=,故其侧面积224432S r hπππ=⋅=⨯⨯=.故选:A【例1-2】(2022·天津·南开中学模拟预测)已知圆锥PO的母线长与底面直径都等于2,一个圆柱内接于这个圆锥,即圆柱的上底面是圆锥的一个截面,下底面在圆锥的底面内,则圆柱侧面积的最大值为()A.3π2B.3πC.()633π-D.3【答案】A【解析】如图,1AB=,2BE=,3AE=,则30AEB∠=,设DC r=,01r<<,则2EC r=,3DE r=,则33AD AE DE r=-=-,考点呈现例题剖析∴圆柱侧面积为:)()221132π2π3323π23π22S r AD r r r r ⎡⎤⎛⎫=⋅=⋅=-+≤-+=⎢⎥ ⎪⎝⎭⎢⎥⎣⎦,当12r =时取等号.故选:A . 【一隅三反】1.(2023·全国·高三专题练习)《几何原本》是古希腊数学家欧几里得的一部不朽之作,其第十一卷中称轴截面为等腰直角三角形的圆锥为直角圆锥,若某直角圆锥内接于一球(圆锥的顶点和底面上各点均在该球面上),求此圆锥侧面积和球表面积之比( ) A .24B 22C 2D .24π【答案】A【解析】设直角圆锥底面半径为r 2r , ()222rr r -=,所以底面圆的圆心即为外接球的球心,所以外接球半径为r , 所以22224S rl r S r πππ==圆锥侧球故选:A. 2.(2022·福建三明·模拟预测)如图所示的建筑物是号称“神州第一圆楼”的福建土楼——二宜楼,其外形是圆柱形,圆楼直径为73.4m ,忽略二宜楼顶部的屋檐,若二宜楼的外层圆柱墙面的侧面积略小于底面直径为40m ,高为77的圆锥的侧面积的23,则二宜楼外层圆柱墙面的高度可能为( )A .16mB .17mC .18mD .19m【答案】A【解析】底面直径为40m ,高为77m ()2210772090m +=,所以该圆锥的侧面积为220901800cm ππ⋅⋅=,设二宜楼外层圆柱墙面的高度为h ,则由36.72h π⨯1200π=,解得16.3h ≈因为二宜楼的外层圆柱墙面的侧面积略小于底面直径为40m ,高为77的圆锥的侧面积的23, 所以二宜楼外层圆柱墙面的高度可能为16m , 故选:A3.(2022·江苏·阜宁县东沟中学模拟预测)民间娱乐健身工具陀螺起源于我国,最早出土的石制陀螺是在山西夏县发现的新石器时代遗址.如图所示的是一个陀螺的立体结构图.已知.底面圆的直径16cm AB =,圆柱体部分的高8cm BC =,圆锥体部分的高6cm CD =,则这个陀螺的表面积是( )A .2192m c πB .2252m c πC .2272m c πD .2336m c π【答案】C【解析】由题意可得圆锥体的母线长为226810l =+=, 所以圆锥体的侧面积为10880ππ⨯=,圆柱体的侧面积为168128ππ⨯=,圆柱的底面面积为2864ππ⨯=, 所以此陀螺的表面积为8012864272ππππ++=(2cm ),故选:C考点二 柱锥台的体积【例2-1】(2022·全国·高三专题练习)已知三棱锥S ABC -的所有顶点都在球O 的球面上,ABC 是边长为2的正三角形,SC 为球O 的直径,且4SC =,则此棱锥的体积为( )A 42B 43C 82D .42【答案】A【解析】解:因为ABC 是边长为2的正三角形,所以ABC 外接圆的半径12232sin 60r =⋅=︒所以点O 到平面ABC 的距离2226d R r -SC 为球O 的直径,点S 到平面ABC 的距离为462d =此棱锥的体积为2111464222sin 60332ABCV S d =⨯=⨯⨯,故选:A .【例2-2】(2022·天津·高考真题)如图,“十字歇山”是由两个直三棱柱重叠后的景象,重叠后的底面为正方形,直三棱柱的底面是顶角为120︒,腰为3的等腰三角形,则该几何体的体积为( )A .23B .24C .26D .27【答案】D【解析】该几何体由直三棱柱AFD BHC -及直三棱柱DGC AEB -组成,作HM CB ⊥于M ,如图, 因为3,120CH BH CHB ==∠=,所以3332CM BM HM ==, 因为重叠后的底面为正方形,所以33AB BC ==, 在直棱柱AFD BHC -中,AB ⊥平面BHC ,则AB HM ⊥, 由AB BC B ⋂=可得HM ⊥平面ADCB , 设重叠后的EG 与FH 交点为,I则132713813333,=3333=322224I BCDA AFD BHC V V --=⨯=⨯⨯则该几何体的体积为8127222742AFD BHC I BCDA V V V --=-=⨯-=.故选:D. 【例2-3】(2022·湖北·高三阶段练习)已知四面体D ABC -中,1AC BC AD BD ====,则D ABC -体积的最大值为( ) A 42B 32C 23D 3【答案】C【解析】设M 为CD 的中点,连接AM,BM , 设四面体A -BCD 的高为h ,则h AM ≤,由于1AC BC AD BD ====,故ACD BCD ≌ , 则ACD BCD ∠=∠,设π,(0,)2BCD ACD αα∈∠=∠=,则sin sin ,22cos 2cos AM BM BC CD CM BC αααα======, 所以1136D ABC A DBC BCDV V Sh CD BM AM --==⋅≤⋅⋅222222231112cos sin sin cos sin 2cos sin sin ()333232αααααααα++==⋅⋅23, 当且仅当平面ACD 与平面BCD 垂直且sin 2αα=即arctan 2α=时取等号,故选:C 【一隅三反】1.(2022·江苏)甲、乙两个圆锥的母线长相等,侧面展开图的圆心角之和为2π,侧面积分别为S 甲和S 乙,体积分别为V 甲和V 乙.若=2S S 甲乙,则=VV 甲乙( ) A 5B .22C 10D 510【答案】C【解析】设母线长为l ,甲圆锥底面半径为1r ,乙圆锥底面圆半径为2r ,则11222S rl rS r l r ππ===甲乙,所以122r r =,又12222r r l l πππ+=,则121r r l +=,所以1221,33r l r l ==,所以甲圆锥的高221459h l l =-=,乙圆锥的高2221229h l l =-=,所以221122221453931011223r h l V V r h l l ππ==⨯甲乙故选:C. 2.(2022·广西桂林)一个三棱锥S -ABC 的侧棱上各有一个小洞D ,E ,F ,且SD :DA =SE :EB =CF :FS =3:1,则这个容器最多可盛放原来容器的( ) A .89B .49C .5564D .23【答案】C【解析】由题意,这个容器最多可盛放原来容器的比例为DEF ABC S ABC S DEFS ABC S ABC V V V V V ------=,设C 到平面SAB 的距离为h ,则13S ABC C ABS SAB V V Sh --==.又91991646464S DEF F SDE SABSAB C ABS V V S h S h V ---==⨯=⨯=,故915564164DEF ABC S ABC S DEFS ABC S ABCV V V V V -------=== 故选:C3.(2023·全国·高三专题练习)足球起源于中国古代的蹴鞠游戏.“蹴”有用脚蹴、踢的含义,“鞠”最早系外包皮革、内饰米糠的球,因而“蹴鞠”就是指古人以脚蹴、踢皮球的活动,如图所示.已知某“鞠”的表面上有四个点,,,P A B C,满足1,PA PA =⊥面ABC ,AC BC ⊥,若23P ABC V -=,则该“鞠”的体积的最小值为( )A .256π B .9πC .92πD .98π【答案】C【解析】取AB 中点为D ,过D 作//OD PA ,且11==22OD PA ,因为PA ⊥平面ABC,所以OD ⊥平面ABC .由于AC BC ⊥,故DA DB DC ==,进而可知OA OB OC OP ===,所以O 是球心,OA 为球的半径.由112==4323P ABC V AC CB PA AC CB -=⨯⋅⋅⇒⋅,又2222=8AB AC BC AC BC =+≥⋅,当且仅当2AC BC ==,等号成立,故此时22AB =所以球半径()2222113+2222R OA OD AB ⎛⎫⎛⎫==+≥ ⎪ ⎪⎝⎭⎝⎭,故min 3=2R ,体积最小值为334439πππ3322R ⎛⎫== ⎪⎝⎭故选:C4.(2023·全国·高三专题练习)已知正四棱锥的侧棱长为l ,其各顶点都在同一球面上.若该球的体积为36π,且333l ≤≤ ) A .8118,4⎡⎤⎢⎥⎣⎦B .2781,44⎡⎤⎢⎥⎣⎦C .2764,43⎡⎤⎢⎥⎣⎦D .[18,27]【答案】C【解析】∴ 球的体积为36π,所以球的半径3R =,设正四棱锥的底面边长为2a ,高为h ,则2222l a h =+,22232(3)a h =+-,所以26h l =,2222a l h =-所以正四棱锥的体积42622411214()=333366936l l l V Sh a h l l ⎛⎫==⨯⨯=⨯-⨯- ⎪⎝⎭,所以5233112449696l l V l l ⎛⎫⎛⎫-'=-= ⎪ ⎪⎝⎭⎝⎭,当326l ≤≤0V '>,当2633l ≤0V '<, 所以当26l =时,正四棱锥的体积V 取最大值,最大值为643, 又3l =时,274V =,33l =814V =,所以正四棱锥的体积V 的最小值为274, 所以该正四棱锥体积的取值范围是276443⎡⎤⎢⎥⎣⎦,.故选:C.考点三 球的体积与表面积【例3】(2022·甘肃省武威第一中学)如图,半径为4的球O 中有一内接圆柱,当圆柱的侧面积最大时,球的表面积与圆柱的表面积之差为( )A .64πB .48πC .32πD .16π【答案】D 【解析】如图.设圆柱底面半径为r ,球的半径与圆柱底面夹角为OMN α∠=,则cos 4cos MN r R αα==⋅=,sin 4sin ON R αα=⋅=,∴圆柱的高8sin h α=,∴圆柱的侧面积为232sin2S r h ππα=⋅⋅=⋅,当且仅当4πα=时,sin21α=,圆柱的侧面积最大,为32π, 球的表面积与圆柱的表面积之差为22422(22)64321616R rh πππππππ--⨯=--=.故选:D . 【一隅三反】1.(2022·全国·赣州市第三中学)已知某正三棱锥S ABC -的内切球与外接球的球心恰好重合,如果其内切球的半径为1,其外接球的体积为36π,那么这个三棱锥的表面积为( ) A .24 B .243C .48D .483【答案】B【解析】由题意可知,点S 在底面ABC 内的射影点D 为等边ABC 的中心,取线段BC 的中点E ,连接AE ,则2AD DE =,易知三棱锥S ABC -的外接球球心O 在线段SD 上,设正三棱锥S ABC -的外接球半径为R ,则34363R ππ=,解得3R =,设正三棱锥S ABC -的内切球的半径为r ,则1r =,故314SD R r =+=+=,SD ⊥平面ABC ,AD ⊂平面ABC ,SD AD ∴⊥,易知3OA R ==,则222222AD OA OD R r --=所以,122DE AD ==32AE =26sin 3AEAB π== 由勾股定理可得2226SA SD AD =+=所以,正三棱锥S ABC -是边长为6 因此,正三棱锥S ABC -的表面积为(23426=243故选:B.2.(2022·天津·耀华中学二模)一个圆锥的侧面展开图是一个半圆,则该圆锥的内切球的表面积和圆锥的侧面积的比为( ) A .2:3 B .3:2 C .1:2 D .3:4【答案】A【解析】设圆锥的底面半径为r ,母线长为l ,圆锥的高为h ,内切球的半径为R ,其轴截面如图所示,设O 为内切球球心,因为圆锥的侧面展开图是一个半圆, 所以2l r ππ=,得2l r =,即2PA PB r ==, 所以222243PD PB BD r r r =--, 所以3PO PD OD r R =-=-, 因为POE △∴PBD △,所以PO OEPB BD=, 3r R Rr -=,得3R =, 所以圆锥的内切球的表面积和圆锥的侧面积的比为 22214:4:22:33R rl r r ππππ=⋅=,故选:A3.(2022·山东青岛·二模)《九章算术》中记录的“羡除”是算学和建筑学术语,指的是一段类似隧道形状的几何体,如图,羡除ABCDEF 中,底面ABCD 是正方形,EF ∥平面ABCD ,2EF =,其余棱长都为1,则这个几何体的外接球的体积为( )A 2B .4π3C 82D .4π【答案】B【解析】连接AC ,BD 交于点M ,取EF 的中点O ,则OM ⊥平面ABCD ,,取BC 的中点G ,连接FG ,作GH EF ⊥,垂足为H ,如图所示由题意可知,13,2HF FG ==222HG FG HF =- 所以2OM HG ==2AM =所以221OA OM AM +=,又1OE =, 所以1OA OB OC OD OE OF ======,即这个几何体的外接球的球心为O ,半径为1, 所以这个几何体的外接球的体积为33444ππ1π333V R ==⨯⨯=.故选:B.考点四 空间几何的截面【例4-1】(2022·全国·高三专题练习)已知圆锥的母线长为2,侧面积为23π,则过顶点的截面面积的最大值等于( ) A 3B 2C .3 D .2【答案】D【解析】由圆锥的母线长为2,侧面积为3π,假设底面圆周长为l ,因此12232l π⨯⨯=,故底面圆周长为23π3由于轴截面为腰长为2,底边长为底面圆直径32π3.故当截面为顶角是π2的等腰三角形时面积最大,此时1π22sin 222S =⋅⋅⋅=.故选:D【例4-2】.(2022·湖南·长沙一中模拟预测)(多选)传说古希腊数学家阿基米德的墓碑上刻着一个圆柱,圆柱内有一个内切球,这个球的直径恰好与圆柱的高相等.“圆柱容球”是阿基米德最为得意的发现;如图是一个圆柱容球,12O O ,为圆柱上下底面的圆心,O 为球心,EF 为底面圆1O 的一条直径,若球的半径2r =,则( )A .球与圆柱的表面积之比为12:B .平面DEF 截得球的截面面积最小值为165π C .四面体CDEF 的体积的取值范围为3203⎛⎤⎥⎝⎦,D .若P 为球面和圆柱侧面的交线上一点,则PE PF +的取值范围为22543⎡+⎣,【答案】BCD【解析】由球的半径为r ,可知圆柱的底面半径为r ,圆柱的高为2r ,则球表面积 为24r π,圆柱的表面积222226r r r r πππ+⋅=, 所以球与圆柱的表面积之比为23,故A 错误;过O 作1OG DO ⊥于G ,则由题可得125225OG ==设O 到平面DEF 的距离为1d ,平面DEF 截得球的截面圆的半径为1r ,则1d OG ≤,22221114164455r r d d =-=-≥-=, 所以平面DEF 截得球的截面面积最小值为165π,故B 正确; 由题可知四面体CDEF 的体积等于12E DCO V -,点E 到平面1DCO 的距离(0,4]d ∈, 又114482DCO S=⨯⨯=,所以123228(0,]33E DCO V d -=⨯∈,故C 正确;由题可知点P 在过球心与圆柱的底面平行的截面圆上,设P 在底面的射影为P ',则2222222,2,2,16PP PE P E PF P F P E P F '''''==+++=,设2t P E '=,则20,4t ⎡⎤∈⎣⎦,222216PE PF t t +++-所以()222222216241680PE PF t tt t +=++-=+-++()224281442485,48t ⎡⎤=+--++⎣⎦,所以225,43PE PF ⎡+∈+⎣,故D 正确.故选:BCD.【一隅三反】1.(2022·江西鹰潭·二模)《算数术》竹简于上世纪八十年代出土,这是我国现存最早的有系统的数学典籍,其中记载有求“囷盖”的术:“置如其周,令相乘也,叉以高乘之,三十六成一."该术相当于给出了由圆锥的底面周长L 与高h ,计算其体积V 的近似公式2136V L h ≈.它实际上是将圆锥体积公式中的圆周率π近似取为3.现有一圆锥底面周长为563,侧面面积为1123,其体积的近似公式为23112V L h ≈,用此π的近似取值(用分数表示)计算过该圆锥顶点的截面面积的最大值为( ) A .15 B .37C .8821D .8【答案】D【解析】若圆锥母线长为l ,底面半径为r ,则156112233l ⨯=,故4l,又5623r π=,故283r π=, 而22133112V r h L h π=≈,则2228356()()31123ππ⨯≈⨯,可得289π=, 所以3r =,若截面顶角θ,当截面为轴截面时2221cos 108r l θ=-=-<,此时2πθπ<<,又截面面积为21sin 8sin 2l θθ=,故当2πθ=时截面面积的最大值为8.故选:D2.(2022·河南·方城第一高级中学)某中学开展劳动实习,学生对圆台体木块进行平面切割,已知圆台的上底面半径为1,下底面半径为2,要求切割面经过圆台的两条母线且使得切割面的面积最大.3则切割面的面积为______3______. 【答案】 2 33【解析】解法一:如图,将圆台1O O 补成圆锥PO ,设圆台1O O 的上、下底面半径分别为r ,R ,高和母线长分别为h ,l ,则()222l h R r =+-.因为等腰梯形ABCD 为过两条母线的截面,设PC x =.APB θ∠=,则r x R x l=+,得rl x R r=-,则()()2221sin sin 22PAB PCD ABCD R r S S S x l x l R r θθ+⎡⎤=-=+-=⎣⎦-△△梯形.∴若33h ,则23l =,0120θ︒<≤︒,当90θ=︒时,切割面的面积最大,最大面积2S =;∴若3h =2l =,060θ︒<︒≤,当60θ=︒时,切割面的面积最大,最大面积33S =解法二:如图,设圆台上底面圆心为1O ,下底面圆心为O ,过两条母线的截面为四边形11ABB A ,可得四边形11ABB A 为等腰梯形.设111AO B AOB θ∠=∠=,圆台的高1O O h =,取11A B ,AB 的中点分别为1C ,D ,连接11O C ,1C D ,OD ,则四边形11O C DO 为直角梯形,过1C 作11C C O O ∥交OD 于点C.因为111O B =,2OB =,所以11cos2O C θ=,111122sin2A B B C θ==,2cos2OD θ=,24sin 2AB BD θ==,所以11cos 2CD OD O C θ=-=,所以221cos 2DC h θ=+则()11221111cos 222ABB A S S AB A B DC h θθ==+⋅=+梯形令sin 2t θ=,因为(]0,θπ∈,所以(]0,1t ∈,则2231S t h =-+(]0,1t ∈.∴当3h 时,2222244333232t t S t t ⎛⎫+- ⎪⎛⎫=-≤= ⎪ ⎪⎝⎭ ⎪⎝⎭,当且仅当2243t t =-,即6t =max 2S =.∴当3h =()22423434S t t t t =--+令2t x =,则(]0,1x ∈,()24224424t t x x x -+=-+=--+,当1x =时,取最大值3.此时max 33S =故答案为:2;333.(2022·青海·海东市第一中学)已知圆锥的底面直径为2323则该圆锥的体积为________. 5π【解析】由题意知:圆锥的底面半径3r =设圆锥的母线长为l ,则2213sin 2323l π⋅==22l =∴圆锥的高22835h l r =--=∴圆锥的体积2153V r h ππ=⋅=.5π.。
空间解析几何习题答案解析(最新整理)

一、计算题与证明题1.已知, , , 并且. 计算.1||=a 4||=b 5||=c 0=++c b a a c c b b a ⨯+⨯+⨯解:因为, , , 并且1||=a 4||=b 5||=c 0=++c b a 所以与同向,且与反向a b b a +c 因此,,0=⨯b a 0=⨯c b 0=⨯a c 所以0=⨯+⨯+⨯a c c b b a 2.已知, , 求.3||=⋅b a 4||=⨯b a ||||b a ⋅解:(1)3cos ||=⋅=⋅θb a b a(2)4sin ||=⋅=⨯θb a b a 得()222)1(+()252=⋅b a 所以5=⋅b a 4.已知向量与共线, 且满足, 求向量的坐标.x )2,5,1(,-a 3=⋅x ax 解:设的坐标为,又x ()z y x ,,()2,5,1-=a 则 (1)325=-+=⋅z y x x a 又与共线,则x a 0=⨯a x 即()()()05252512125251=-+++--=+---=-k y x j x z i z y kyx j y x i z y z y x kj i 所以()()()05252222=-+++--y x x z z y 即 (2)010*********22=-++++xy xz yz z y x 又与共线,与夹角为或x a x a 0π()30325110cos 222222222⋅++=-++⋅++⋅==z y x z y x ax 整理得(3)103222=++z y x 联立解出向量的坐标为()()()321、、x ⎪⎭⎫⎝⎛-51,21,1016.已知点, 求线段的中垂面的方程.)7,8,3(A )3,2,1(--B AB 解:因为,()7,8,3A )3,2,1(--B 中垂面上的点到的距离相等,设动点坐标为,则由得AB B A 、()z y x M ,,MB MA =()()()()()()222222321783++-++=-+-+-z y x z y x 化简得027532=-++z y x 这就是线段的中垂面的方程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
概念形成的学习过程,大致有下列几个阶段。
(1)辨别 (2)归类 (3)抽象概括 (4)强化
注*这是一般顺序,有时两个可以同时进行,甚至交叉进行。
讨论交流:二年级《轴对称图形》。
教学目标: 1、通过观察、动手操作交流初步感知轴对称图形基 本特征.。 2、通过判断,验证进一步加深对轴对称图形的认识 和理解,认识对称轴,根据特征会找和画一个轴对称 图形的对称轴。 3、培养学生观察、动手操作、思辩和语言表达能力, 发展学生的空间观念。 感知——分类
平行线的认识
1、概念的形成是在不断的强化中逐步完善的。 2、操作技能教学
教师预设自问: (1)学生现在在哪里?(关注学生的最近发展区) (2)学生不教行吗? (3) 学生不行,问题在哪里? (4)怎样实施无痕教育,让学生自己发现问题? (5)学生能找到问题的关键吗? (6)有学生找到问题关键,其他同学会引起关注吗? 课堂教师行为: (1)师问:画平行线会吗? (2)试一试。 (3)典型案例板演。 (4)师问:向上平移二点点、三点 点行吗? (5)倾听学生反应。 ( 6 )师:你的设想很好,如果尺不 晃动那该多好啊!(评价针对)
本文案例
注重学生自主建构知识的过程 和体验,注重情感态度价值观、 知识技能、过程与方法三维目 标统一。
作业:
结合概念教学和几何教学中的操作技能教学剖析,设计一节课, 人教版四年级(上)p:64—67“垂直与平行”中”平行线”的认识。 说明: 教材调整:4教时调整为3教时。 顺序:垂线——平行线——综合运用。 教学内容:平行线的概念;平行线的画法;平行线之间的距离处处相等。 要求:突出概念教学和画法教学(操作技能教学)。
把“空间与图形”教学划分为三个部分: 1、概念教学
2、几何教学中的操作技能教学
3、规则教学
一、概念教学
(一)概念学习的基本方式:概念的形成和概念的同化。 1.概念的形成 就人类而言,概念的形成是一种发现过程,也就是在对 事物感知和分析、比较、抽象的基础上,概括一类事物的本 质属性不断的提出假设和验证假设的过程。在教学条件下, 是指从一定的具体例子出发,以学生的感性经验为基础,形 成表象,进而以归纳方式抽象概括出事物本质属性,获得数 学概念的过程。
掌握了本质的非预பைடு நூலகம்生成
三、几何教学中的规则教学。
规则教学是以概念学习为基础的,它的复杂性和学习 层次,高于概念学习。小学几何教学中的规则教学主 要内容是形体求积。(包括平面图形的周长和面积计 算;立体图形的表面积和体积计算。) (注*规则教学是以概念学习为基础的。案例:长、正 方形的周长教学。)
在教学形体的求积的计算公式时,除圆锥体积计算 公式外,一般可根据形体之间的相互联系,通过割 补、剪拼的方法导出计算公式。
以平面图形的面积计算为例,形体求积的教学过程大致如下: (1)面积概念的建立。 (2)面积单位的引入。 (3)长方形面积的直接度量和面积公式的导出。(案例) (4)教学中一般由长方形面积(包括正方形面积)—— 平行四 边形面积——三角形面积——梯形面积——圆的面积——扇形的面 积的顺序出现,中间参杂组合图形面积。(举例)
怎样确定教学思路
1、新授内容中,有哪些是新的成分?(即新课“新”在何处)
2、(A)这些“新”的成分,学生有可能运用已有知识自己学会吗 (B)如果不行,学生的困难何在?如何创设情境、提 供信息、启发思维“——让学生在教师创设的教学情境 中,通过启发,帮助学生克服困难? 3、在上述基础上考虑:如何根据新课程改革的理念组织教学。
几何教学中的两个注意点:
(1)改进几何教学,重视培养空间观念。 (2)处理好直观形象与抽象概括的关系。(生活与数学的关系)
2.概念的同化
所谓概念的同化,就是利用学习者认知结构中原有的概
念,以定义或描述的方式直接向学习者揭示新概念的本质属性,
进而使学习者获得概念的过程。也就是以间接经验为基础,利用 已掌握的概念去学习新的概念的过程。
概念的同化的学习过程,大致有下列几个阶段。
(1)定义或描述
(2)同化
(3)强化
二、几何教学中的操作技能教学
该案例与传统教例的差异性 (1)
教学方式 传统教 例 本文案 例 以传授为主 思维种类 记忆 思维水平 按记忆程序操作(浅 层次思维)。 发展对数学概念和数 学思想方法的更深层 次理解(深层次思 维)。
传授、协商、 交流、释疑
想象、理解、 判断、推理、 记忆
该案例与传统教例的差异性 (2)
目标定位 传统教例 认识量角器的构造, 正确掌握用量角器度 量角的操作步骤。培 养学生动手操作实践 能力 理解量角器的构造, 能运用重叠的思想, 自主建构用量角器度 量角的方法,解决度 量角的问题,并从中 获得成功的体验。 课堂价值取向 注重学生掌握度量角的相关知 识和技能获得。
传统教学:一般是模仿练习法和程序练习法。
定向 —————— 分解 —————— 整合 ———— 熟练
了解操作的步 骤
分解操作步骤, 逐一模仿练习
形成一体化 的操作系统。
操作过程高度完 善化和自动化。
操作技能教学新的教学思路:
角的度量
操作技能教学新的教学思路:
1.着眼于让学生体会“为何如此操作”来确定教学思路,设计教学。 2、创设协商、交流与解释的时机,扩展学生积极思维的空间。 3、创设促使迁移发生的条件,扩展学生主动建构的空间。 4、给予展现“矛盾”的机会,扩展学生主动探究的空间。
强化
轴对称图形概念建构:
(1)比赛引入——辨别(感知阶段),聚焦轴对称图形的基本特征。 (2)学生争议中主动归类。 (3)学生演示中抽象概括。 (4)通过变式判断、辨析强化概念
小结:
概念教学:既要遵循规律又要实践创新。
注意的几个问题: 情景引入:揭示本质;排除干扰;激发兴趣; 概念揭示:尽可能自然生成。 强化:一般先具体——再抽象;先正例——再反例;先干扰少 的——再干扰多的;强化到概念的每个关键字的理解,每 一题都有目的性。 立足过程;关注能力。
