向心加速度公式的几种推导
向心加速度公式的推导

a BA
r
向心加速度公式的推导
创新微课
小结
1 、科学方法:
(1)发现物理规律的基本方法:以观察实验为基础,分析、综合的方法; (2)实验方法:研究物理问题的重要方法之一——控制因素(变量)法。
2、 知识整合:
圆
周 匀速圆
运 动
周运动
向心加速度
圆 匀速圆 周
运 周运动 动
同学,下节再见
B RB RC C
向心加速度公式的推导
创新微课
练习、如图所示,A、B两物体作匀速圆周运动时的向心加速
度随半径变化的关系图线,其中B图线为双曲线,可得出
( B)
A、A物体运动时的线速度大小保持不变 B、A物体运动时的角速度大小保持不变 C、B物体运动时的角速度保持不变 D、B物体运动的线速度随r而改变
V = △ L /△t
思考:从公式a=v2/r看
,向心加速度与圆周运
an
v2 r
r 2
动的半径成反比;从公 式a=rw2看,向心加速 度与半径成正比,这两
个结论是否矛盾?
向心加速度公式的推导
向心加速度的公式
v不变时,an与r 成反比
an =
v2 r
an = rω2
ω不变时,an与r 成正比
创新微课
创新微课 现在开始
向心加速度公式的推导
向心加速度公式的推导
向心加速度的公式推导
①由△OAB与△BVAVB相似有
v AB v R
创新微课
O
VB
② 当Δt很小很小时, AB /Δt表
示何物理量?
r
向心加速度公式的推导
创新微课
向心加速度的公式推导
圆周运动向心加速度公式推导(向心加速度公式的推导方法ppt)

圆周运动向心加速度公式推导(向心加速度公式的推导方法
ppt)
1、我没法画图,口述一下,你可以自己画了看看:在圆周上,取一小段圆弧AB,圆心为O,假设在A点速度为v1,在B 点速度为v2,那么v1,v2分别垂直于OA,OB,|v1|=|v2|=v。
2、把v2平移到跟v1起点相同的地方比较,可以发现v1跟
v2,以及v1,v2的差构成一个等腰三角形,顶角=角AOB,那么不难看出,当角AOB很小的时候,底边无限接近垂直于
v1,所以加速度也垂直于v1。
3、至于加速度大小,还是从这个等腰三角形中看,底边大小=2*v*sin(1/2角AOB),角AOB无限小就成了2*v*1/2*角
AOB=v*角AOB,从A到B时间为r*角AOB/v,所以加速度为速度的改变乘以时间=v1-v2/t=v^2/r。
4、推导中用到了正弦函数一个性质: x很小的时候,sin(x)越等于x。
5、在x越接近于0的时候,sin(x)/x越接近1。
这篇文章已经分享到这里了,希望对大家有帮助。
向心加速度的6个公式

向⼼加速度的6个公式
向⼼加速度的公式:an=Fn/m=4π²R/T²=4π²f²R=v²/R=ω²R=vω。
向⼼加速度公式
an=Fn/m
=4π²R/T²=4π²f²R
=v²/R=ω²R=vω
上式中,an表⽰向⼼加速度,Fn表⽰向⼼⼒,m表⽰物体质量,v表⽰物体圆周运动的线速度(切向速度),ω表⽰物体圆周运动的⾓速度,T表⽰物体圆周运动的周期,f表⽰物体圆周运动的频率,R表⽰物体圆周运动的半径。
(ω=2π/T)
由⽜顿第⼆定律,⼒的作⽤会使物体产⽣⼀个加速度。
合外⼒提供向⼼⼒,向⼼⼒产⽣的加速度就是向⼼加速度。
可能是实际加速度,也可能是物体实际加速度的⼀个分加速度。
法向加速度
法向加速度⼜称向⼼加速度,在匀速圆周运动中,法向加速度⼤⼩不变,⽅向可⽤右⼿螺旋定则确定。
质点作曲线运动时,所具有的沿轨道法线⽅向的加速度叫做法向加速度。
数值上等于速度v的平⽅除曲率半径r,即v²/r;或⾓速度的平⽅与半径r的乘积,即ω²r。
其作⽤只改变物体速度的⽅向,但不改变速度的⼤⼩。
向心加速度公式的推导两法

(于凤刚 推导整理) 向心加速度公式的推导两法
方法一:
加速度公式的推导关键注意:课本P 21“做一做”③如图5.5-4当角θ用弧度表示时,弧长QP 可以表示为。
当θ很小很小时(物理上定义为5o ),弧长与弦长没什么区别,所以此式也可以表示弦长。
这个关系也可以来计算矢量△v 的长度。
根据上述知识结合右图
设A B ==v v v
得: θ∆=v v (与QP=r θ同理) 根据a t ∆=∆v 及t
θω∆=∆ 得:
a t
θω∆=
=∆v v 又因为r ω=v 所以2a r ω=
方法二:
根据数学知识:当θ很小很小时(物理上定义为5o
),sin θθ≈(θ以弧度为单位的数值)。
在上图A B ∆、、v v v 矢量组成的三角形是等腰三角形,根据几何知识有, 2sin 2
θ∆∆=v v (设A B ==v v v ) 因为△θ很小很小,所以
sin
22
θθ∆∆= 故, θ∆=∆v v
根据a t ∆=∆v 及t
θω∆=∆ 得:
a t
θω∆=
=∆v v 又因为r ω=v 所以
2
a r ω=。
高中物理公式推导(匀速圆周运动向心加速度、向心力)
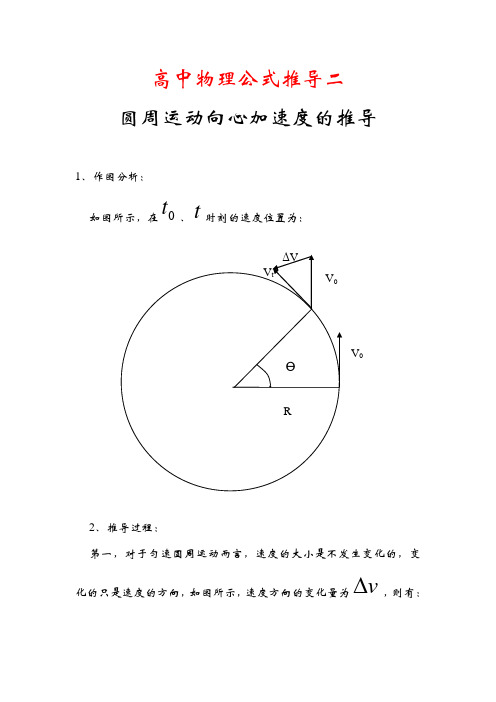
V tΔV 高中物理公式推导二 圆周运动向心加速度的推导1、作图分析: 如图所示,在0t、t 时刻的速度位置为:2、推导过程:第一,对于匀速圆周运动而言,速度的大小是不发生变化的,变化的只是速度的方向,如图所示,速度方向的变化量为v ,则有:RƟV 0V 0θθ∆=∆≈∆t v v v 0第二,根据加速度的定义:tv a ∆∆=则有:t v t v a n ∆∆=∆∆=θ0第三,根据圆周运动的相关关系知:Rv t =∆∆=θω是故,圆周运动的向心加速度为:Rv a n 2=第四,圆周运动的向心力的大小为:Rvmm a F n 2==3、意外收获:第一,对于圆周运动,我们应该理解速度、角速度、周期之间的关系。
具体为:R v =ωT πω2=vR πω2=第二,我们应该掌握极限的相关知识,合理利用极限来解决相关问题。
第三,如果我们谈论的不是匀速圆周运动,我们同样可以利用此方法进行谈论。
对于非匀速圆周运动(或者叫做曲线运动),不仅速度的方向发生了变化,而且速度的大小也发生了变化,所以, 不仅有向心加速度之外,应该也有使物体速度大小变化的加速度。
但是,在这种情况下,我们的向心加速度,叫做径向加速度,速度大小变化的加速度,叫做切向加速度。
故有:(1)向心加速度为:R v a n 2=(2)切向加速度为:t v a t ∆∆=(注意:这里的v∆是指切向速度方向速度的变化量,并不是指图上的v∆。
)4、注意事项:对于匀速圆周运动而言,需要掌握的知识点并不是很多,我们只要能够理解一些物理量之间的基本关系即可。
本篇的讨论只为学有余力的高中学生推荐,不过,物理推导讲究的是方法,并不是死记硬背公式,掌握了这一知识点的推导过程对以后了解其他物理知识会有很大的帮助。
向心加速度公式的几种推导

向心加速度公式的几种推导一、运用速度增量法推导如图,表示速度(率)v 作匀速圆周运动的物体,在时间Δt 内由A 点运动到B 点。
在这运动过程中,由于Δt 非常小,可以看成是过A 点切线方向速度为v 的匀速直线运动和在AO 方向初速度为零的匀加速直线运动的合运动。
物体过A 点沿切线方向的速度为v ,在AO 方向上的初速度v 0=0,当经过很短时间Δt 内,物体由A 点运动到B 点,线速度大小仍是v ,但方向改变了,由于方向的改变,使物体在AO 方向获得了分速度vt=vsin θ。
这时物体在AO 方向速度的增量应是:ΔV =V t-v0=vsin θ。
在这段时间内,物体沿切线方向匀速运动走过的距离可看成是由E 到B ,即EB=V ·Δt由此得到:v vθRsin EB t ==∆又根据加速度的定义式可得:Rv vv v 2/Rsin sin ta ===∆∆θθ二、运用位移合成法推导1、如图(1)表示以速率v 作匀速圆周运动的物体经过很短时间Δt ,由A 点运动到B 点,于是有错误!未指定书签。
AB=V Δt当Δt 小到某种程度,即AB 弦与AB 弧几乎重合,则有:AB 弦=AB 弧=v Δt ②如果物体位于A 点时,力的作用消失,则物体将沿切线方向作匀速运动,在Δt 时间内经过位移v Δt 。
但实际上物体在Δt 时间内沿圆周运动到了B 点,这是由于物体还受到向心力的作用,加速离开了切线,其位移为AF ,它和过A 点切线方向的位移v Δt 合成起来,使物体由A 移动到B 。
由于时间Δt 很短,向心力可近似看成在过A 点的半径方向,从图中可以看出:由于: ΔABC ∽ΔABF所以 AC AB ABAF=于是ACAB AF 2=将②式代入此式并注意AC=2R所以222t AF RV∆= 上式中v 、R 都是常量,此时表明位移AF 与时间Δt 的平方成正比,符合匀加速直线运动的规律。
与初速度为零的匀加速直线运动的位移公式221at S =相比较,可得出匀速圆周运动的向心加速度公式为:R v a 2=2、图(2)表示物体以速率v 作匀速圆周运动的情形,在很短时间Δt 内由A 点运动到B 点,与上题思考方法不同的是,现在把该运动过程看成是同时参与两个分运动的合运动。
向心加速度公式的推导方法

向心加速度公式的推导方法首先,我们假设一个物体在平面上做匀速圆周运动,其质量为m,速度为v。
这个物体受到一个向心力Fc的作用,该力指向物体所绕的圆心。
根据牛顿第二定律,物体所受的合力等于质量乘以加速度,即F = ma。
将合力拆分成两个分力:向心力Fc和切向力Ft。
1.向心力Fc:向心力Fc的方向指向物体所绕的圆心,大小为Fc = m•ac,其中ac为物体的向心加速度。
2.切向力Ft:切向力Ft的方向垂直于速度矢量v,大小为Ft = m•at,其中at为物体的切向加速度。
由于物体作匀速圆周运动,速度大小保持不变,所以at = 0。
根据向量加法,合力F等于向心力Fc和切向力Ft的矢量和。
由于切向力Ft为零,所以F=Fc。
现在我们来推导向心加速度公式。
根据牛顿第三定律,任何两个物体之间的作用力和反作用力大小相等、方向相反。
在这个圆周运动的例子中,物体对圆心施加向心力Fc,圆心对物体同样施加一个反向的力-Fc。
这个反向力-Fc实际上是质量为m的物体受到的合力F,即-Fc = F = ma。
根据向量的减法,力-Fc可以表示为-Fc = (-m•ac)。
再根据牛顿第二定律F = ma,我们有(-m•ac) = ma。
将方程两边除以-m,得到ac = a,即物体的向心加速度等于物体的加速度。
由于物体作匀速圆周运动,其速度方向始终垂直于加速度方向。
因此,速度v和加速度a的关系可以用速度的模长(大小)来表示,即v=,v,a=,a。
当物体作圆周运动时,其加速度a可以通过速度v的变化来计算。
由物体速度v的定义可知,v = ds/dt,其中ds表示质点在t时刻的位移矢量。
速度的变化可表示为dv = dv/dt。
将速度表示为位移的导数,我们有:dv/dt = d(ds/dt) / dt = d²s/dt²。
由于物体作匀速圆周运动,其速度大小,v,保持不变。
因此,dv/dt = 0,即加速度的时间变化率为零。
匀速圆周运动向心加速度公式推导方法

三 、利用开普勒第三定律 、万有 引力定 律和牛顿第二定律推导 向心加速度
质量 为 。的人造地球 卫星 以速 率 在 半
径 为 厂的近 圆轨道 上绕地球 运 行 , 运 行 周 期
为 乙 地球质量为 从
根据开普勒第三定律 尹 尸
为常
量
根据万有 引力 定律 户 改姚才广
对于 圆周运动 的物体有 介 二
湖南中学物理
”
年第 期
匀速 圆周运 动 向心加速度公式推导方法
张智 庄浪县紫荆 中学 , 甘肃 平凉
质 点做匀速 圆周运动 , 受力方 向与运动 方 向垂直 , 有 向心加速度 。为 了加深对 向心 加速度 概念 的理解 , 掌握 向心加速度 的大小 与质点运 动速度大小和运动半径 的关系 , 现 用三种方法推 导 向心加速度 的计算 公式
根据 牛顿第 二 定律
二
由以上各式可知 酬光丫 二’·沪 厂
即 二萨厂 。
设在很短 的时间 内 , 小球沿 圆周从 到 可分解为沿切线 方 向的匀速直线运 动和沿 方 向初速度 为零 的匀加速直线运 动 如图 一
故有 『尹 模型
设在很短 的时间 内 , 小球沿 圆周从 运动到 可分解 为沿 切线 方 向的匀速直 线运动和沿 方 向的初速 度 为零 的匀加速 直线运动 如 图
,·
张 智 匀速 圆周运动向心加速度公 式推导方法
一 厂 山个
声 挤生。、
由于 时 间 “ 良短 , 即 趋近 于
, 所以
由 △ 。 △ 可知
△阵
当 趋近于零时 , 由匀速 圆周运 动 定义和加速度 定义可 知
工了、趋近于 。。
故有 沪
二屁
△刁
故有 萨 尸
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
向心加速度公式的几种推导
向心加速度公式的几种推导
向心加速度是物体在做匀速圆周运动时所受到的加速度,它与物
体的速度和半径有关。
向心加速度的公式可以通过不同的推导方法得出。
本文将介绍几种常见的推导方法,解释向心加速度的概念和公式。
第一种推导方法是通过定义力的方向来推导。
在物体做匀速圆周
运动时,它受到一个向心力的作用,该力的方向指向圆心。
根据牛顿
第二定律,物体的加速度与受力成正比。
因此,我们可以得到向心加
速度的方向是指向圆心的。
根据定义,向心加速度的大小等于速度的
平方除以半径,表示为a = v^2 / r,其中a是向心加速度,v是速度,r是半径。
第二种推导方法是利用速度的变化率来推导。
在匀速圆周运动中,物体的速度大小是恒定的,但其方向在不断变化。
为了描述速度的变
化率,我们引入一个新的物理量,即角速度。
角速度表示单位时间内
物体在圆周运动中所转过的角度。
根据等速圆周运动的性质,角速度
与速度的大小之间存在一定的关系。
我们可以将速度的大小表示为v = ωr,其中v是速度,ω是角速度,r是半径。
由于角速度的单位是弧
度/秒,所以速度的单位是米/秒。
然后,我们对速度对时间求导,得
到加速度的大小。
根据导数的链式法则,加速度大小的推导公式为a = d(v)/dt = d(ωr)/dt = r(dω/dt)。
因为匀速圆周运动中角速度不变,所以dω/dt = 0,即加速度的大小为零。
但由于速度的方向在不断变化,所以加速度的方向是向心方向。
第三种推导方法是使用几何关系来推导。
考虑一个物体在半径为
r的圆周上运动,它在1秒内沿圆周运动一周。
我们知道圆周的周长等于2πr,所以物体运动的距离为2πr。
另外,我们知道速度的定义为
单位时间内所运动的距离。
所以,速度的大小等于运动的距离除以时间,即v = 2πr / 1 = 2πr。
根据速度的定义和向心加速度的定义,我们可以得到a = v^2 / r = (2πr)^2 / r = 4π^2r。
所以,物体在
匀速圆周运动时的向心加速度的大小为4π^2r,方向向心。
通过以上三种推导方法,我们得到了向心加速度的公式a = v^2 / r,其中a是向心加速度,v是速度,r是半径。
这个公式告诉我们,在匀速圆周运动中,物体受到的向心力会使它产生向心加速度。
向心
加速度的大小与速度的平方成正比,与半径成反比。
这个公式也可以
用来解决其他与向心加速度相关的物理问题。
总之,向心加速度是物体在做匀速圆周运动时所受到的加速度。
通过不同的推导方法,我们可以得到向心加速度的公式a = v^2 / r。
这个公式揭示了向心加速度与速度和半径之间的关系。
它让我们能够
理解和解决与向心加速度相关的物理问题,帮助我们更好地理解匀速
圆周运动的特性。
