2020年武汉市九年级元月调考试题答案
2020年-武汉市元月调考语文试卷(含答案)
2019-2020 学年度武汉市部分学校九年级质量检测语文试卷第 I 卷( 选择题共 30 分)一、( 共 9 分，每小题 3 分)1. 依次填人下面横线处的词语，恰当．．的一组是（）在双方难分伯仲的实力较量中，若能赢得竞争固然是一件 _ 的事情，然而更 的是, 贏得友谊和尊重——赢得对手的心，贏得世人的 ，赢在“灵魂的卓越”。
A. 激动人心 重要 感动B. 大快人心 关键 感动C. 大快人心 重要 感激D. 激动人心 关键 感激2. 下列各句中有．语．病．的一项是（）A. 不少市民特意购买首发车票，目的是第一时间感受汉十高铁带来的速度与便利。
B. 全年减税降费的政策红利，让企业不但可以轻装上阵，也点燃了投资者的热情。
C. 中国支持世贸组织进行改革，希望它在扩大开放、促进发展方面发挥更大作用。
D. 面对百年未有之大变局 , 我们应顺应时代潮流，在追求发展的道路上矢志不移。
3. 下列各句标点符号使．．的一项是（） A 不同国家、地区、民族，不同历史、宗教、习俗彼此交相辉映、相因相生 , 共同擘画出这个精彩纷呈的世界。
B. 故事一定要贯穿节目的每一个环节 : 从标题、片子开场，到主持人、评论员的每一个问题 , 都要跟这个故事配套。
C. 灿烂的阳光一扫冬日的阴霾，天空顿时湛蓝如洗。
山川河流早已解冻 , 泥土中散 发出草芽萌发的新鲜气息。
D. 无数黑骑在远处来回驰骋，长河上 , 一轮浑圆的血色落日挂在天际；孤城中 , 狼烟直直刺向昏黄的天空。
二、( 共 9 分，每小题 3 分) 阅读下面的文章，完成 4— 6 题。
小说的语言①我初学写作时喜欢把人物的对话写得很漂亮 , 有诗意，有哲理 , 有时甚至很“玄”。
沈从文先生对我说 : “你这是两个聪明脑壳打架 ! ”他的意思是说这不像真人说的话。
托尔斯泰说过 : “人是不能用警句交谈的。
②张岱写两个老者去逛一处园林 , 一老者说 : “真是蓬莱仙境了也 ! ”另一个老 者说: “个边哪有这样 ! ”生动之至，而且一听就是绍兴话。
湖北省武汉市市新观察2020年九年级数学元月调考复习交流卷(一) (解析版)
武汉市市新观察2020年九年级数学元月调考复习交流卷(一) 一、选择题（本大题共小10题，每小题3分，共30分）1．（3分）方程x2＝4x的根是（）A．x＝4 B．x＝0 C．x1＝0，x2＝4 D．x1＝0，x2＝﹣4 2．（3分）下列汽车标志中，既是轴对称图形又是中心对称图形的是（）A．B．C．D．3．（3分）将抛物线y＝（x﹣3）2﹣2向左平移（）个单位后经过点A（2，2）A．1 B．2 C．3 D．44．（3分）不透明的袋子中只有4个黑球和2个白球，这些球除颜色外无其他差别，随机从袋子中一次摸出3个球，下列事件是不可能事件的是（）A．3个球都是黑球B．3个球都是白球C．3个球中有黑球D．3个球中有白球5．（3分）如图，以点A为中心，把△ABC逆时针旋转120°，得到△AB'C′（点B、C的对应点分别为点B′、C′），连接BB'，若AC'∥BB'，则∠CAB'的度数为（）A．45°B．60°C．70°D．90°6．（3分）已知M、N是线段AB上的两点，AM＝MN＝2，NB＝1，以点A为圆心，AN长为半径画弧；再以点B为圆心，BM长为半径画弧，两弧交于点C，连接AC，BC，则△ABC一定是（）A．锐角三角形B．直角三角形C．钝角三角形D．等腰三角形7．（3分）从甲、乙、丙三人中任选两人参加“武汉军运会志愿者”活动，甲被选中的概率为（）A．B．C．D．8．（3分）如图，点A在⊙O上，BC为⊙O的直径，AB＝4，AC＝3，D是的中点，CD与AB相交于点P，则CP的长为（）A．B．C．D．9．（3分）已知抛物线y＝﹣x2+bx+4经过（﹣2，n）和（4，n）两点，则n的值为（）A．﹣2 B．﹣4 C．2 D．410．（3分）如图，已知P是⊙O外一点，Q是⊙O上的动点，线段PQ的中点为M，连接OP，OM．若⊙O的半径为2，OP＝4，则线段OM的最小值是（）A．0 B．1 C．2 D．3二、填空题（本大题共6小题，每小题3分，共18分）11．（3分）关于x的一元二次方程x2+2x+a＝0的一个根为1，则方程的另一根为．12．（3分）已知点A（2，a）、点B（b，﹣3）关于原点对称，则a+b的值为．13．（3分）在围棋盒中有x颗白色棋子和y颗黑色棋子，从盒中随机取出一颗棋子，取得白色棋子的概率是．如果再往盒中放进6颗黑色棋子，取得白色棋子的概率是，则原来盒中有白色棋子颗．14．（3分）如图，有一张矩形纸片，长10cm，宽6cm，在它的四角各剪去一个同样的小正方形，然后将四周突出部分折起，就能制作一个无盖的方盒，若方盒的底面积（图中阴影部分）是32cm2，则剪去的小正方形的边长为cm．15．（3分）如图，AB是半圆O的直径，且AB＝8，点C为半圆上的一点．将此半圆沿BC所在的直线折叠，若圆弧BC恰好过圆心O，则图中阴影部分的面积是．（结果保留π）16．（3分）如图，在平面直角坐标系中，点O是边长为2的正方形ABCD的中心．函数y＝（x﹣h）2的图象与正方形ABCD有公共点，则h的取值范围是．三、解答题（本大题共8小题，共72分）17．（8分）解方程：x2﹣4x﹣7＝0．18．（8分）如图，AB、CD是⊙O的直径，DF、BE是弦，且DF＝BE，求证：∠D＝∠B．19．（8分）小明有两双不同的运动鞋放在一起，上学时间到了，他准备穿鞋上学．（1）他随手拿出一只，恰好是右脚鞋的概率为；（2）他随手拿出两只，请用画树状图或列表法求恰好为一双的概率．20．（8分）如图，△ABC中，AB＝BC，点O为高AD上一点，以OD为半径的⊙O与AB相切于点E．（1）求证：点O在直线CE上；（2）若AE：EB＝2：3，AC＝，求⊙O的半径．21．（8分）如图，在由边长为1个单位长度的小正方形组成的网格中，建立平面直角坐标系A（﹣1，7），B（﹣6，3），C（﹣2，3）．（1）将△ABC绕格点P（1，1）顺时针旋转90°，得到△A'B'C'，画出△A'B'C'，并写出下列各点坐标：A'（，），B'（，），C'（，）；（2）找格点M，连CM，使CM⊥AB，则点M的坐标为（，）；（3）找格点N，连BN，使BN⊥AC，则点N的坐标为（，）．22．（10分）某商店分别花20000元和30000元先后两次以相同的进价购进某种商品，且第二次的数量比第一次多500千克．（1）该商店第一次购进多少千克这种商品？（2）已知该商品每天的销售量y（千克）与销售单价x（元/千克）之间的函数关系式为：y＝﹣10x+500，且每千克的利润不低于10元且不高于18元．①请直接写出自变量x的取值范围；②求该商店某天的最大利润．23．（10分）如图所示，已知正△ABC中射线CM⊥AB于F，射线BA绕B顺时针旋转，旋转后的射线记作a，同时线段AB所在直线绕A顺时针旋转，旋转后的直线记作直线l，当直线l旋转的角度是射线a旋转角度的4倍时，直线l于射线CM相交于E，与射线a相交于D，且∠D＝30°．（1）求射线a的旋转角是多少度；（2）求证：DE＝AB；（3）探索：线段DE，EF，DB的数量关系．24．（12分）如图1，平面直角坐标系xOy中，已知抛物线y＝ax2+4x与x轴交于O、A两点．直线y＝kx+m经过抛物线的顶点B及另一点D（D与A不重合），交y轴于点C．（1）当OA＝4，∠ABC＝90°时．①求该抛物线解析式；②求BC的解析式；（2）如图2，过点D作DE⊥x轴于点E，当a为任意负数时，试探究CO与OE的数量关系？参考答案与试题解析一、选择题（本大题共小10题，每小题3分，共30分）1．（3分）方程x2＝4x的根是（）A．x＝4 B．x＝0 C．x1＝0，x2＝4 D．x1＝0，x2＝﹣4 【分析】原式利用因式分解法求出解即可．【解答】解：方程整理得：x（x﹣4）＝0，可得x＝0或x﹣4＝0，解得：x1＝0，x2＝4，故选：C．2．（3分）下列汽车标志中，既是轴对称图形又是中心对称图形的是（）A．B．C．D．【分析】根据轴对称图形与中心对称图形的概念求解．【解答】解：A、是轴对称图形，不是中心对称图形，故本选项错误；B、既不是中心对称图形，也不是轴对称图形，故本选项错误；C、不是轴对称图形，是中心对称图形，故本选项错误；D、是中心对称图形，也是轴对称图形，故本选项正确．故选：D．3．（3分）将抛物线y＝（x﹣3）2﹣2向左平移（）个单位后经过点A（2，2）A．1 B．2 C．3 D．4【分析】直接利用二次函数平移规律结合二次函数图象上点的坐标特点得出答案．【解答】解：∵将抛物线y＝（x﹣3）2﹣2向左平移后经过点A（2，2），∴设向左平移a个单位，故y＝（x﹣3+a）2﹣2，则2＝（2﹣3+a）2﹣2，解得：a1＝﹣1（不合题意舍去），a2＝3，即将抛物线y＝（x﹣3）2﹣2向左平移3个单位后经过点A（2，2）．故选：C．4．（3分）不透明的袋子中只有4个黑球和2个白球，这些球除颜色外无其他差别，随机从袋子中一次摸出3个球，下列事件是不可能事件的是（）A．3个球都是黑球B．3个球都是白球C．3个球中有黑球D．3个球中有白球【分析】根据事件发生的可能性大小判断相应事件的类型．【解答】解：A、3个球都是黑球是随机事件；B、3个球都是白球是不可能事件；C、3个球中有黑球是必然事件；D、3个球中有白球是随机事件；故选：B．5．（3分）如图，以点A为中心，把△ABC逆时针旋转120°，得到△AB'C′（点B、C的对应点分别为点B′、C′），连接BB'，若AC'∥BB'，则∠CAB'的度数为（）A．45°B．60°C．70°D．90°【分析】先根据旋转的性质得到∠BAB′＝∠CAC′＝120°，AB＝AB′，根据等腰三角形的性质易得∠AB′B＝30°，再根据平行线的性质由AC′∥BB′得∠C′AB′＝∠AB′B ＝30°，然后利用∠CAB′＝∠CAC′﹣∠C′AB′进行计算．【解答】解：∵以点A为中心，把△ABC逆时针旋转120°，得到△AB'C′，∴∠BAB′＝∠CAC′＝120°，AB＝AB′，∴∠AB′B＝（180°﹣120°）＝30°，∵AC′∥BB′，∴∠C′AB′＝∠AB′B＝30°，∴∠CAB′＝∠CAC′﹣∠C′AB′＝120°﹣30°＝90°．故选：D．6．（3分）已知M、N是线段AB上的两点，AM＝MN＝2，NB＝1，以点A为圆心，AN长为半径画弧；再以点B为圆心，BM长为半径画弧，两弧交于点C，连接AC，BC，则△ABC一定是（）A．锐角三角形B．直角三角形C．钝角三角形D．等腰三角形【分析】依据作图即可得到AC＝AN＝4，BC＝BM＝3，AB＝2+2+1＝5，进而得到AC2+BC2＝AB2，即可得出△ABC是直角三角形．【解答】解：如图所示，AC＝AN＝4，BC＝BM＝3，AB＝2+2+1＝5，∴AC2+BC2＝AB2，∴△ABC是直角三角形，且∠ACB＝90°，故选：B．7．（3分）从甲、乙、丙三人中任选两人参加“武汉军运会志愿者”活动，甲被选中的概率为（）A．B．C．D．【分析】画出树状图，共有6个等可能的结果，1其中甲被选中的结果有4个，由概率公式即可得出结果．【解答】解：树状图如图所示：共有6个等可能的结果，其中甲被选中的结果有4个，则甲被选中的概率为＝；故选：A．8．（3分）如图，点A在⊙O上，BC为⊙O的直径，AB＝4，AC＝3，D是的中点，CD与AB相交于点P，则CP的长为（）A．B．C．D．【分析】如图作PH⊥BC于H．首先证明AP＝PH，设PA＝PH＝x，根据勾股定理构建方程即可解决问题；【解答】解：如图作PH⊥BC于H．∵＝，∴∠ACD＝∠BCD，∵BC是直径，∴∠BAC＝90°，∴PA⊥AC，∵PH⊥BC，∴PA＝PH，设PA＝PH＝x，∵PC＝PC，∴Rt△PCA≌Rt△PCH，∴AC＝CH＝3，∵BC＝＝5，∴BH＝2，在Rt△PBH中，∵PB2＝PH2+BH2，∴（4﹣x）2＝x2+22，解得x＝，∴PC＝＝，故选：D．9．（3分）已知抛物线y＝﹣x2+bx+4经过（﹣2，n）和（4，n）两点，则n的值为（）A．﹣2 B．﹣4 C．2 D．4【分析】根据（﹣2，n）和（4，n）可以确定函数的对称轴x＝1，再由对称轴的x＝即可求解；【解答】解：抛物线y＝﹣x2+bx+4经过（﹣2，n）和（4，n）两点，可知函数的对称轴x＝1，∴＝1，∴b＝2；∴y＝﹣x2+2x+4，将点（﹣2，n）代入函数解析式，可得n＝﹣4；故选：B．10．（3分）如图，已知P是⊙O外一点，Q是⊙O上的动点，线段PQ的中点为M，连接OP，OM．若⊙O的半径为2，OP＝4，则线段OM的最小值是（）A．0 B．1 C．2 D．3【分析】取OP的中点N，连结MN，OQ，如图可判断MN为△POQ的中位线，则MN＝OQ ＝1，则点M在以N为圆心，1为半径的圆上，当点M在ON上时，OM最小，最小值为1．【解答】解：设OP与⊙O交于点N，连结MN，OQ，如图，∵OP＝4，ON＝2，∴N是OP的中点，∵M为PQ的中点，∴MN为△POQ的中位线，∴MN＝OQ＝×2＝1，∴点M在以N为圆心，1为半径的圆上，当点M在ON上时，OM最小，最小值为1，∴线段OM的最小值为1．故选：B．二、填空题（本大题共6小题，每小题3分，共18分）11．（3分）关于x的一元二次方程x2+2x+a＝0的一个根为1，则方程的另一根为﹣3 ．【分析】设方程的另一个根为x2，根据韦达定理即可得到结论．【解答】解：设方程的另一个根为x2，根据题意得x2+1＝﹣2，解得：x2＝﹣3．故方程的另一个根为﹣3．故答案为：﹣3．12．（3分）已知点A（2，a）、点B（b，﹣3）关于原点对称，则a+b的值为 1 ．【分析】直接利用关于原点对称点的性质得出a，b的值进而得出答案．【解答】解：∵点A（2，a）、点B（b，﹣3）关于原点对称，∴b＝﹣2，a＝3，则a+b的值为：1．故答案为：1．13．（3分）在围棋盒中有x颗白色棋子和y颗黑色棋子，从盒中随机取出一颗棋子，取得白色棋子的概率是．如果再往盒中放进6颗黑色棋子，取得白色棋子的概率是，则原来盒中有白色棋子 4 颗．【分析】首先根据题意得方程组：，解此方程组即可求得答案．【解答】解：根据题意得：，解得：，∴原来盒中有白色棋子4颗．故答案为：4．14．（3分）如图，有一张矩形纸片，长10cm，宽6cm，在它的四角各剪去一个同样的小正方形，然后将四周突出部分折起，就能制作一个无盖的方盒，若方盒的底面积（图中阴影部分）是32cm2，则剪去的小正方形的边长为 1 cm．【分析】设剪去的小正方形的边长为xcm，根据矩形的面积公式结合方盒的底面积（图中阴影部分）是32cm2，即可得出关于x的一元二次方程，解之取其较小值即可得出结论．【解答】解：设剪去的小正方形的边长为xcm，依题意，得：（10﹣2x）（6﹣2x）＝32，整理，得：x2﹣8x+7＝0，解得：x1＝1，x2＝7（不合题意，舍去）．故答案为：1．15．（3分）如图，AB是半圆O的直径，且AB＝8，点C为半圆上的一点．将此半圆沿BC所在的直线折叠，若圆弧BC恰好过圆心O，则图中阴影部分的面积是．（结果保留π）【分析】过点O作OD⊥BC于点D，交于点E，则可判断点O是的中点，由折叠的性质可得OD＝OE＝R＝2，在Rt△OBD中求出∠OBD＝30°，继而得出∠AOC，求出扇形AOC的面积即可得出阴影部分的面积．【解答】解：过点O作OD⊥BC于点D，交于点E，连接OC，则点E是的中点，由折叠的性质可得点O为的中点，∴S弓形BO＝S弓形CO，在Rt△BOD中，OD＝DE＝R＝2，OB＝R＝4，∴∠OBD＝30°，∴∠AOC＝60°，∴S阴影＝S扇形AOC＝＝．故答案为：．16．（3分）如图，在平面直角坐标系中，点O是边长为2的正方形ABCD的中心．函数y＝（x﹣h）2的图象与正方形ABCD有公共点，则h的取值范围是﹣2≤h≤2 ．【分析】由于函数y＝（x﹣h）2的图象为开口向上，顶点在x轴上的抛物线，故可先分别得出点A和点B的坐标，因为这两个点为抛物线与与正方形ABCD有公共点的临界点，求出即可得解．【解答】解：∵点O是边长为2的正方形ABCD的中心，∴点A和点B坐标分别为（1，1）和（﹣1，1），∵函数y＝（x﹣h）2的图象为开口向上，顶点在x轴上的抛物线，∴其图象与正方形ABCD有公共点的临界点为点A和点B，把点B坐标代入y＝（x﹣h）2，得1＝（﹣1﹣h）2∴h＝0（舍）或h＝﹣2；把点A坐标代入y＝（x﹣h）2，得1＝（1﹣h）2∴h＝0（舍）或h＝2．函数y＝（x﹣h）2的图象与正方形ABCD有公共点，则h的取值范围是﹣2≤h≤2．故答案为：﹣2≤h≤2．三、解答题（本大题共8小题，共72分）17．（8分）解方程：x2﹣4x﹣7＝0．【分析】移项后配方得出x2﹣4x+4＝7+4，推出（x﹣2）2＝11，开方后得出方程x﹣2＝±，求出方程的解即可．【解答】解：移项得：x2﹣4x＝7，配方得：x2﹣4x+4＝7+4，即（x﹣2）2＝11，开方得：x﹣2＝±，∴原方程的解是：x1＝2+，x2＝2﹣．18．（8分）如图，AB、CD是⊙O的直径，DF、BE是弦，且DF＝BE，求证：∠D＝∠B．【分析】根据在同圆中等弦对的弧相等，AB、CD是⊙O的直径，则弧CFD＝弧AEB，由FD＝EB，得，弧FD＝弧EB，由等量减去等量仍是等量得：弧CFD﹣弧FD＝弧AEB﹣弧EB，即弧FC＝弧AE，由等弧对的圆周角相等，得∠D＝∠B．【解答】方法（一）证明：∵AB、CD是⊙O的直径，∴弧CFD＝弧AEB．∵FD＝EB，∴弧FD＝弧EB．∴弧CFD﹣弧FD＝弧AEB﹣弧EB．即弧FC＝弧AE．∴∠D＝∠B．方法（二）证明：如图，连接CF，AE．∵AB、CD是⊙O的直径，∴∠F＝∠E＝90°（直径所对的圆周角是直角）．∵AB＝CD，DF＝BE，∴Rt△DFC≌Rt△BEA（HL）．∴∠D＝∠B．19．（8分）小明有两双不同的运动鞋放在一起，上学时间到了，他准备穿鞋上学．（1）他随手拿出一只，恰好是右脚鞋的概率为；（2）他随手拿出两只，请用画树状图或列表法求恰好为一双的概率．【分析】（1）根据四只鞋子中右脚鞋有2只，即可得到随手拿出一只恰好是右脚鞋的概率；（2）依据树状图即可得到共有12种等可能的结果，其中两只恰好为一双的情况有4种，进而得出恰好为一双的概率．【解答】解：（1）∵四只鞋子中右脚鞋有2只，∴随手拿出一只，恰好是右脚鞋的概率为＝，故答案为：；（2）画树状图如下：共有12种等可能的结果，其中两只恰好为一双的情况有4种，∴拿出两只，恰好为一双的概率为＝．20．（8分）如图，△ABC中，AB＝BC，点O为高AD上一点，以OD为半径的⊙O与AB相切于点E．（1）求证：点O在直线CE上；（2）若AE：EB＝2：3，AC＝，求⊙O的半径．【分析】（1）连接CE，证明△BEC≌△BDA（SAS），得∠BEC＝∠BDA＝90°，根据圆的切线垂直于过切点的半径，可得点O在直线CE上；（2）设AE＝2x，BE＝3x，则AB＝BC＝5x，根据勾股定理得：AD2＝AB2﹣BD2＝AC2﹣CD2，列方程可得x的值，设⊙O的半径为r，则AO＝8﹣r，由勾股定理列方程可得半径的值．【解答】（1）证明：连接CE，∵AD⊥BC，AD过点O，∴BC为⊙O的切线，∵AB是⊙O的切线，∴BD＝BE，在△BEC和△BDA中，∵，∴△BEC≌△BDA（SAS），∴∠BEC＝∠BDA＝90°，∴CE⊥AB，∴点O在直线CE上；（2）解：设AE＝2x，BE＝3x，则AB＝BC＝5x，∴BD＝BE＝3x，CD＝2x，由勾股定理得：AD2＝AB2﹣BD2＝AC2﹣CD2，，x＝2，∴AD＝4x＝8，设⊙O的半径为r，则AO＝8﹣r，在Rt△AEO中，AE2+OE2＝AO2，42+r2＝（8﹣r）2，r＝3，则⊙O的半径是3．21．（8分）如图，在由边长为1个单位长度的小正方形组成的网格中，建立平面直角坐标系A（﹣1，7），B（﹣6，3），C（﹣2，3）．（1）将△ABC绕格点P（1，1）顺时针旋转90°，得到△A'B'C'，画出△A'B'C'，并写出下列各点坐标：A'（7 ， 3 ），B'（ 3 ，8 ），C'（ 3 ， 4 ）；（2）找格点M，连CM，使CM⊥AB，则点M的坐标为（﹣6 ，8 ）；（3）找格点N，连BN，使BN⊥AC，则点N的坐标为（﹣2 ， 2 ）．【分析】（1）依据△ABC绕格点P（1，1）顺时针旋转90°，即可得到△A'B'C'；（2）依据AB的方向和格点C的位置，即可得到格点M的位置；（3）依据AC的方向和格点B的位置，即可得到格点N的位置．【解答】解：（1）如图所示，△A'B'C'即为所求，A'（7，3），B'（3，8），C'（3，4）；故答案为：7，3，3，8，3，4；（2）如图所示，M（﹣6，8）；故答案为：﹣6，8；（3）如图所示，N（﹣2，2）．故答案为：﹣2，2．22．（10分）某商店分别花20000元和30000元先后两次以相同的进价购进某种商品，且第二次的数量比第一次多500千克．（1）该商店第一次购进多少千克这种商品？（2）已知该商品每天的销售量y（千克）与销售单价x（元/千克）之间的函数关系式为：y＝﹣10x+500，且每千克的利润不低于10元且不高于18元．①请直接写出自变量x的取值范围；②求该商店某天的最大利润．【分析】（1）根据“商店分别花20000元和30000元先后两次以相同的进价购进某种商品，且第二次的数量比第一次多500千克”列出分式方程求解即可；（2）列出函数关系式根据每千克的利润不低于10元且不高于18元得到自变量的取值范围，然后配方后确定最值即可．【解答】（1）设第一次购进m千克，则＝，∴m＝1000，经检验，当m＝1000时，m（m+500）≠0，m＝1000是原方程的解，∴第一次购进1000千克．（2）①该商品的原价为20000÷1000＝20元/千克，∵每千克的利润不低于10元且不高于18元，∴10≤x﹣20≤18，∴自变量x的取值范围：30≤x≤38；②设每天的利润为W元，则W＝（x﹣20）（﹣10x+500）＝﹣10（x﹣35）2+2250，当x＝35时，W max＝2250．23．（10分）如图所示，已知正△ABC中射线CM⊥AB于F，射线BA绕B顺时针旋转，旋转后的射线记作a，同时线段AB所在直线绕A顺时针旋转，旋转后的直线记作直线l，当直线l旋转的角度是射线a旋转角度的4倍时，直线l于射线CM相交于E，与射线a相交于D，且∠D＝30°．（1）求射线a的旋转角是多少度；（2）求证：DE＝AB；（3）探索：线段DE，EF，DB的数量关系．【分析】（1）根据三角形的一个外角等于与它不相邻的两内角的和，直线a，l的旋转角的关系建立方程4α＝30°+α即可；（2）先判断出∠BEC＝∠DBE，得出OE＝OB，进而判断出△DOE≌△COB（AAS），得出DE ＝BC，即可得出结论；（3）判断出△BDE≌△ECA，再代换即可．【解答】解：（1）设直线l旋转角为α，∴∠ABD＝α∵射线l旋转的角度是射线a旋转角度的4倍，∴∠BAE＝4α，∵∠BAE＝∠ABD+∠D，∴4α＝α+30°，∴α＝10°，射线a的旋转角是10°；（2）连接BE，BD与CM的交点记作点O，∵△ABC是正三角形，CM⊥AB，∴CM是AB的垂直平分线，∴AF＝BF，EA＝EB，∴∠EBA＝∠BAE＝40°，∴∠BEC＝∠AEB＝（180°﹣2∠BAE）＝50°，∠DBE＝∠AEB+∠ABD＝40°+10°＝50°，∴∠BEC＝∠DBE，∴OE＝OB，∵∠D＝∠BCO＝30°，∠DOE＝∠COB，∴△DOE≌△COB（AAS），∴DE＝BC，∵BC＝AB，∴DE＝AB，（3）∵∠BAE＝40°，∴∠AEC＝50°，∵∠ABE＝40°，∠ABD＝10°，∴∠EBD＝∠AEC＝50°∵∠BDE＝∠ACE＝30°，DE＝AC，∴△BDE≌△ECA，∴BD＝EC＝EF+FC＝EF+AB＝EF+DE．24．（12分）如图1，平面直角坐标系xOy中，已知抛物线y＝ax2+4x与x轴交于O、A两点．直线y＝kx+m经过抛物线的顶点B及另一点D（D与A不重合），交y轴于点C．（1）当OA＝4，∠ABC＝90°时．①求该抛物线解析式；②求BC的解析式；（2）如图2，过点D作DE⊥x轴于点E，当a为任意负数时，试探究CO与OE的数量关系？【分析】（1）①点A（4，0），则抛物线的表达式为：y＝ax（x﹣4），则顶点B的坐标为：（﹣，﹣），而函数的对称轴为：x＝2，即﹣＝2，解得：a＝﹣1，即可求解；②函数的对称轴为x＝2，故：B（2，4），设C（0，t），∠ABC＝∠AOC＝90°，则AC2＝BC2+AB2＝OC2+AO2，即：42+t2＝（2﹣4）2+（4﹣0）2+22+（4﹣t）2，即可求解；（2）由y＝ax2+4x＝0得x1＝0，x2＝﹣，则A（﹣，0），又y＝ax2+4x＝a（x+）2﹣，顶点B的坐标为（﹣，﹣），将B（﹣，﹣）代入y＝kx+m，得：﹣+m ＝﹣，解得m＝，点C（0，），即OC＝，由得x＝﹣或x＝，故E（，0），即可求解．【解答】解：（1）①点A（4，0），则抛物线的表达式为：y＝ax（x﹣4），则顶点B的坐标为：（﹣，﹣），而函数的对称轴为：x＝2，即﹣＝2，解得：a＝﹣1，故抛物线的表达式为：y＝﹣x2+4x；②函数的对称轴为x＝2，故：B（2，4），设C（0，t），∵∠ABC＝∠AOC＝90°，∴AC2＝BC2+AB2＝OC2+AO2，∴42+t2＝（2﹣4）2+（4﹣0）2+22+（4﹣t）2，∴t＝3，∴OC＝3，C（0，3），∴BC的解析式为y＝x+3；（2）由y＝ax2+4x＝0得x1＝0，x2＝﹣，则A（﹣，0），又y＝ax2+4x＝a（x+）2﹣，∴顶点B的坐标为（﹣，﹣），将B（﹣，﹣）代入y＝kx+m，得：﹣+m＝﹣，解得m＝，∴点C（0，），即OC＝，由得x＝﹣或x＝，∴E（，0），∴OE＝，∴OC：OE＝＝2，∴OC＝2OE．。
2020年湖北省武汉市硚口区九年级元月调考数学模拟试卷及答案解析
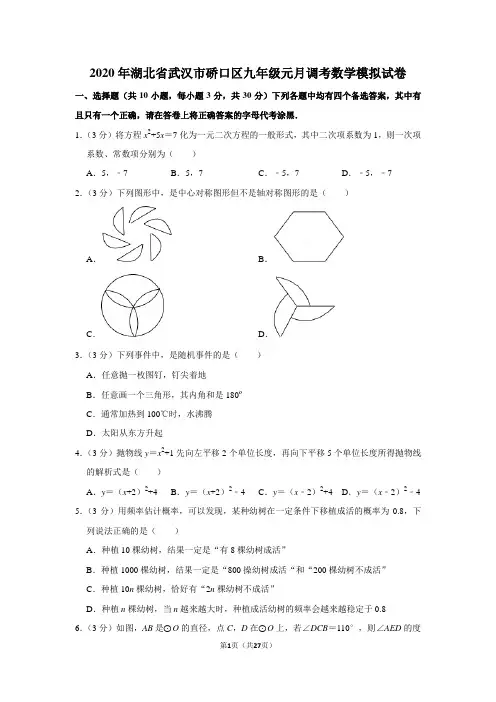
2020年湖北省武汉市硚口区九年级元月调考数学模拟试卷一、选择题（共10小题，每小题3分，共30分）下列各题中均有四个备选答案，其中有且只有一个正确，请在答卷上将正确答案的字母代考涂黑．1．（3分）将方程x2+5x＝7化为一元二次方程的一般形式，其中二次项系数为1，则一次项系数、常数项分别为（）A．5，﹣7B．5，7C．﹣5，7D．﹣5，﹣7 2．（3分）下列图形中，是中心对称图形但不是轴对称图形的是（）A．B．C．D．3．（3分）下列事件中，是随机事件的是（）A．任意抛一枚图钉，钉尖着地B．任意画一个三角形，其内角和是180oC．通常加热到100℃时，水沸腾D．太阳从东方升起4．（3分）抛物线y＝x2+1先向左平移2个单位长度，再向下平移5个单位长度所得抛物线的解析式是（）A．y＝（x+2）2+4B．y＝（x+2）2﹣4C．y＝（x﹣2）2+4D．y＝（x﹣2）2﹣4 5．（3分）用频率估计概率，可以发现，某种幼树在一定条件下移植成活的概率为0.8，下列说法正确的是（）A．种植10棵幼树，结果一定是“有8棵幼树成活”B．种植1000棵幼树，结果一定是“800操幼树成活“和“200棵幼树不成活”C．种植10n棵幼树，恰好有“2n棵幼树不成活”D．种植n棵幼树，当n越来越大时，种植成活幼树的频率会越来越稳定于0.86．（3分）如图，AB是⊙O的直径，点C，D在⊙O上，若∠DCB＝110°，则∠AED的度数为（）A．15°B．20°C．25°D．30°7．（3分）平面直角坐标系中，M点坐标为（﹣2，3），以2为半径画⊙M，则以下结论正确的是（）A．⊙M与x轴相交，与y轴相切B．⊙M与x轴相切，与y轴相离C．⊙M与x轴相离，与y轴相交D．⊙M与x轴相离，与y轴相切8．（3分）如图，将△ABC绕顶点C旋转得到△DEC，点A对应点D，点B对应点E，且点B刚好落在DE边上，∠A＝24°，∠BCD＝48°，则∠ABD等于（）A．30°B．38°C．36°D．45°9．（3分）如图，在€O中，＝，BC＝6．AC＝3，I是△ABC的内心，则线段OI 的值为（）A．1B．﹣3C．5﹣D．10．（3分）二次函数y＝x2+bx的对称轴为直线x＝1，若关于x的方程x2+bx﹣t＝0（t为实。
2020年湖北省武汉市九年级元月调考数学模拟试卷(包含答案)
2020年湖北省武汉市九年级元月调考数学模拟试卷一．选择题（满分27分，每小题3分）1．一元二次方程2x2+5x＝6的二次项系数、一次项系数、常数项分别是（）A．2，5，6 B．5，2，6 C．2，5，﹣6 D．5，2，﹣62．如图，△ABC与△A′B′C′关于点O成中心对称，则下列结论不成立的是（）A．点A与点A′是对称点B．BO＝B′OC．AB∥A′B′D．∠ACB＝∠C′A′B′3．二次函数y＝x2﹣1的图象的顶点坐标为（）A．（0，0）B．（0，﹣1）C．（﹣，﹣1）D．（﹣，1）4．下列说法正确的是（）A．调查某班学生的身高情况，适宜采用全面调查B．篮球队员在罚球线上投篮两次都未投中，这是不可能事件C．天气预报说明天的降水概率为95%，意味着明天一定下雨D．小南抛掷两次硬币都是正面向上，说明抛掷硬币正面向上的概率是15．下列方程中，有两个不相等的实数根的是（）A．5x2﹣4x＝﹣2 B．（x﹣1）（5x﹣1）＝5x2C．4x2﹣5x+1＝0 D．（x﹣4）2＝06．已知⊙O的半径为3，A为线段PO的中点，则当OP＝5时，点A与⊙O的位置关系为（）A．点在圆内B．点在圆上C．点在圆外D．不能确定7．要组织一次排球邀请赛，参赛的每个队之间都要比赛一场，根据场地和时间等条件，赛程计划7天，每天安排4场比赛．设比赛组织者应邀请x个队参赛，则x满足的关系式为（）A．B．C．x（x﹣1）＝28 D．x（x+1）＝288．如图，将矩形ABCD 绕点A 顺时针旋转到矩形AB ′C ′D ′的位置，旋转角为α（0°＜α＜90°）．若∠1＝112°，则∠α的大小是（ ）A ．68°B ．20°C ．28°D ．22°9．已知抛物线y ＝ax 2+bx +c （a ＜0）的对称轴为x ＝﹣1，与x 轴的一个交点为（2，0）．若于x 的一元二次方程ax 2+bx +c ＝p （p ＞0）有整数根，则p 的值有（ ） A ．2个B ．3个C ．4个D ．5个二．填空题（满分18分，每小题3分）10．已知A （m ，n ），B （m +8，n ）是抛物线y ＝﹣（x ﹣h ）2+2036上两点，则n ＝ ． 11．如图，小圆O 的半径为1，△A 1B 1C 1，△A 2B 2C 2，△A 3B 3C 3，…，△A n B n ∁n 依次为同心圆O 的内接正三角形和外切正三角形，由弦A 1C 1和弧A 1C 1围成的弓形面积记为S 1，由弦A 2C 2和弧A 2C 2围成的弓形面积记为S 2，…，以此下去，由弦A n ∁n 和弧A n ∁n 围成的弓形面积记为S n ，其中S 2020的面积为 ．12．《九章算术》作为古代中国乃至东方的第一部自成体系的数学专著，与古希腊的《几何原本》并称现代数学的两大源泉．在《九章算术》中记载有一问题“今有圆材埋在壁中，不知大小．以锯锯之，深一寸，锯道长一尺，问径几何？”小辉同学根据原文题意，画出圆材截面图如图所示，已知：锯口深为1寸，锯道AB ＝1尺（1尺＝10寸），则该圆材的直径为 寸．13．已知圆锥的底面半径为3，母线长为7，则圆锥的侧面积是．14．若抛物线y＝x2﹣4x+c的顶点在x轴上，则c的值是．15．一块等边三角形木板，边长为1，现将木板沿水平线翻滚，如图所示，若翻滚了40次，则B点所经过的路径长度为．三．解答题（共8小题，满分72分）16．（8分）解方程：x2+4x﹣3＝0．17．（8分）如图，在⊙O中，AB是弦，OC⊥AB于C，OA＝6，AB＝8，求OC的长．18．（8分）如图所示，有一张“太阳”和两张“小花”样式的精美卡片（共三张），它们除花形外，其余都一样．（1）小明认为：闭上眼从中任意抽取一张，抽出“太阳”卡片与“小花”卡片是等可能的，因为只有这两种卡片．小明的说法正确吗？为什么；（2）混合后，从中一次抽出两张卡片，请通过列表或画树状图的方法求出两张卡片都是“小花”的概率；（3）混合后，如果从中任意抽出一张卡片，使得抽出“太阳”卡片的概率为，那么应添加多少张“太阳”卡片？请说明理由．19．（8分）如图，等腰直角△ABC的斜边AB上有两点M、N，且满足MN2＝BN2+AM2，将△ABC绕着C点顺时针旋转90°后，点M、N的对应点分别为T、S．（1）请画出旋转后的图形，并证明△MCN≌△MCS；（2）求∠MCN的度数．20．（8分）如图，AE平分∠BAC，交BC于点D，AE⊥BE，垂足为E，过点E作EF∥AC，交AB于点F．求证：点F是AB的中点．21．（10分）某水果批发商销售每箱进价为40元的苹果，市场调查发现，若每箱以50元的价格调查，平均每天销售90箱，价格每提高1元，平均每天少销售3箱．（1）求平均每天销售量y（箱）与销售价x（元/箱）之间的函数关系式．（2）求该批发商平均每天的销售利润w（元）与销售价x（元/箱）之间的函数关系式．（3）当每箱苹果的销售价为多少元时，可以获得最大利润？最大利润是多少？22．（10分）如图，△ABC是等边三角形，AB＝2cm．动点P从点C出发，以lcm/s的速度在边BC的延长线上运动．以CP为边作等边三角形CPQ，点A、Q在直线BC同侧．连结AP、BQ 相交于点E．设点P的运动时间为t（s）（t＞0）．（1）当t＝s时，△ABC≌△QCP．（2）求证：△ACP≌△BCQ．（3）求∠BEP的度数．（4）设AP与CQ交于点F，BQ与AC交于点G，连结FG，当点G将边AC分成1：2的两部分时，直接写出△CFG的周长．23．（12分）如图，抛物线y＝ax2+2x+c（a＜0）与x轴交于点A和点B（点A在原点的左侧，点B在原点的右侧），与y轴交于点C，OB＝OC＝3．（1）求该抛物线的函数解析式；（2）如图1，连接BC，点D是直线BC上方抛物线上的点，连接OD，CD，OD交BC于点F，当S△COF ：S△CDF＝3：2时，求点D的坐标．（3）如图2，点E的坐标为（0，），在抛物线上是否存在点P，使∠OBP＝2∠OBE？若存在，请直接写出符合条件的点P的坐标；若不存在，请说明理由．参考答案一．选择题1．解：方程整理得：2x2+5x﹣6＝0，则方程的二次项系数、一次项系数、常数项分别是2，5，﹣6，故选：C．2．解：观察图形可知，A、点A与点A′是对称点，故本选项正确；B、BO＝B′O，故本选项正确；C、AB∥A′B′，故本选项正确；D、∠ACB＝∠A′C′B′，故本选项错误．故选：D．3．解：∵二次函数y＝x2﹣1，∴该函数图象的顶点坐标为（0，﹣1），故选：B．4．解：A、调查某班学生的身高情况，适宜采用全面调查，此选项正确；B、篮球队员在罚球线上投篮两次都未投中，这是随机事件，此选项错误；C、天气预报说明天的降水概率为95%，意味着明天下雨可能性较大，此选项错误；D、小南抛掷两次硬币都是正面向上，并不能说明每次抛出硬币一定向上，即抛掷硬币正面向上的概率不是1，此选项错误；故选：A．5．解：A、原方程可变形为5x2﹣4x+2＝0，∵△＝（﹣4）2﹣4×5×2＝﹣24＜0，∴方程5x2﹣4x＝﹣2无实数根；B、原方程可变形为6x﹣1＝0，∴方程（x﹣1）（5x﹣1）＝5x2只有一个实数根；C、∵△＝（﹣5）2﹣4×4×1＝9＞0，∴方程4x2﹣5x+1＝0有两个不相等的实数根；D、∵（x﹣4）2＝0，∴x1＝x2＝4，∴方程（x﹣4）2＝0有两个相等的实数根．故选：C．6．解：∵OA＝OP＝2.5，⊙O的半径为3，∴OA＜⊙O半径，∴点A与⊙O的位置关系为：点在圆内．故选：A．7．解：设比赛组织者应邀请x个队参赛，依题意，得： x（x﹣1）＝28．故选：A．8．解：∵四边形ABCD为矩形，∴∠BAD＝∠ABC＝∠ADC＝90°，∵矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置，旋转角为α，∴∠BAB′＝α，∠B′AD′＝∠BAD＝90°，∠AD′C′＝∠ADC＝90°，∵∠2＝∠1＝112°，而∠ABC＝∠D′＝90°，∴∠3＝180°﹣∠2＝68°，∴∠BAB′＝90°﹣68°＝22°，即∠α＝22°．故选：D．9．解：∵抛物线y＝ax2+bx+c（a＜0）的对称轴为x＝﹣1∴﹣＝﹣1，解得b＝2a．又∵抛物线y＝ax2+bx+c（a＜0）与x轴的一个交点为（2，0）．把（2，0）代入y＝ax2+bx+c得，0＝4a+4a+c解得，c＝﹣8a．∴y＝ax2+2ax﹣8a（a＜0）对称轴h＝﹣1，最大值k＝＝﹣9a如图所示，顶点坐标为（﹣1，﹣9a）令ax2+2ax﹣8a＝0即x2+2x﹣8＝0解得x＝﹣4或x＝2∴当a＜0时，抛物线始终与x轴交于（﹣4，0）与（2，0）∴ax2+bx+c＝p即常函数直线y＝p，由p＞0∴0＜y≤﹣9a由图象得当0＜y≤﹣9a时，﹣4＜x＜2，其中x为整数时，x＝﹣3，﹣2，﹣1，0，1 ∴一元二次方程ax2+bx+c＝p（p＞0）的整数解有5个．又∵x＝﹣3与x＝1，x＝﹣2与x＝0关于直线x＝﹣1轴对称当x＝﹣1时，直线y＝p恰好过抛物线顶点．所以p值可以有3个．故选：B．二．填空题（共6小题，满分18分，每小题3分）10．解：∵A（m，n）、B（m+8，n）是抛物线y＝﹣（x﹣h）2+2036上两点，∴A（h﹣4， n），B（h+4，n），当x＝h+4时，n＝﹣（h+4﹣h）2+2036＝2020，故答案为2020．11．解：∵小圆O的半径为1，△A1B1C1，△A2B2C2，△A3B3C3，…，△A n B n∁n依次为同心圆O的内接正三角形和外切正三角形，∴S1＝S﹣S＝﹣××，S2＝﹣2×1S3＝﹣4×2…发现规律：Sn＝﹣×（2n﹣1）×2n﹣2＝×22n﹣2﹣22n﹣4×＝22n﹣4（﹣）∴S2020的面积为：24036（﹣）．故答案为：24036（﹣）．12．解：设⊙O的半径为r．在Rt△ADO中，AD＝5，OD＝r﹣1，OA＝r，则有r2＝52+（r﹣1）2，解得r＝13，∴⊙O的直径为26寸，故答案为：26．13．解：圆锥的侧面积＝×2π×3×7＝21π．故答案为21π．14．解：∵y＝x2﹣4x+c＝（x﹣2）2+c﹣4，∴其顶点坐标为（2，c﹣4），∵顶点在x轴上，∴c﹣4＝0，解得c＝4，故答案为：4．15．解：从图中发现：B点从开始至结束所走过的路径长度为两段弧长即第一段＝＝π，第二段＝＝π．故B点翻滚一周所走过的路径长度＝π+π＝π，三次一个循环，∵40÷3＝13……1，若翻滚了40次，则B点所经过的路径长度为13×π+π＝18π．故答案为：18π．三．解答题（共8小题，满分72分）16．解：原式可化为x2+4x+4﹣7＝0即（x+2）2＝7，开方得，x+2＝±，x＝﹣2+；1x＝﹣2﹣．217．解：∵AB是⊙O的弦，OC⊥AB于点C，AB＝8，∴AC＝BC＝4，∠ACO＝90°，由勾股定理得：OC＝＝＝2；18．解：（1）答：不正确，P（抽出“太阳”卡片）＝，P（抽出“小花”卡片）＝；（2）设“太阳”卡片与“小花”卡片分别为A，B，列表得：（A，B）（B，B）﹣﹣﹣（A，B）﹣﹣﹣﹣（B，B）﹣﹣﹣﹣﹣（B，A）（B，A）∴两张卡片都是“小花”的概率为＝；（3）设应添加x张“太阳”卡片，，解得x＝3．∴应添加3张“太阳”卡片．19．解：（1）画图形如右图所示：证明：由旋转的性质可得：CS＝CN，AS＝BN，又∵MN2＝BN2+AM2，∴MN2＝AS2+AM2＝MS2，∴MS＝MN，又∵CS＝CN，CM＝CM，∴△MCN≌△MCS（SSS）．（2）由（1）得：△MCN≌△MCS，∴∠NCM＝∠MCS＝45°．20．证明：∵AE平分∠BAC，∴∠BAD＝∠CAD，∵EF∥AC，∴∠FEA＝∠CAD，∴∠BAD＝∠FEA，∴FA＝FE，∵AE⊥BE，∴∠BEF+∠AEF＝90°，∵∠ABE+∠BAE＝90°，∴∠ABE＝∠BEF，∴FB＝FE，∴FB＝FA，即点F是AB的中点．21．解：（1）y＝90﹣3（x﹣50）即y＝﹣3x+240；（2）w＝（x﹣40）y＝（x﹣40）（﹣3x+240）＝﹣3x2+360x﹣9600；（3）w＝﹣3x2+360x﹣9600＝﹣3（x﹣60）2+1200∵a＝﹣3＜0，∴当销售价x＝60元时，利润w最大．最大利润为1200元．22．解：（1）∵△ABC，△CPQ都是等边三角形，∴当PC＝AB＝2时，△ABC≌△QCP．∴t＝2s，故答案为2．（2）∵△ABC是等边三角形，∴∠ACB＝60°，AC＝BC，∵△CPQ是等边三角形，∴∠PCQ＝60°，CP＝CQ，∴∠ACP＝∠BCQ＝120°，∴△ACP≌△BCQ（SAS）．（3）∵△ACP≌△BCQ，∴∠CAP＝∠CBQ，∵∠BEP＝∠ABE+∠BAE，∴∠BEP＝∠ABC+∠BAC，∵△ABC是等边三角形，∴∠ABC＝∠BAC＝60°，∴∠BEP＝120°．（4）如图1中，∵△ACP≌△BCQ，∴∠CAF＝∠CBG，∵CA＝CB，∠ACF＝∠BCG＝60°，∴△ACF≌△BCG（ASA），∴CF＝CG，∵∠GCF＝60°，∴△GCF是等边三角形，当AG＝2CG时，CG＝cm，∴△CFG的周长为2cm如图2中，当CG＝2AG时，CG＝cm，△FCG的周长为4cm．综上所述，△CFG的周长为2cm或4cm．23．解：（1）c＝3，点B（3，0），将点B的坐标代入抛物线表达式：y＝ax2+2x+3并解得：a＝﹣1，故抛物线的表达式为：y＝﹣x2+2x+3…①；（2）如图1，过点D作DH⊥x轴于点H，交AB于点M，S△COF ：S△CDF＝3：2，则OF：FD＝3：2，∵DH∥CO，故CO：DM＝3：2，则DM＝C O＝2，由B、C的坐标得：直线BC的表达式为：y＝﹣x+3，设点D（x，﹣x2+2x+3），则点M（x，﹣x+3），DM＝﹣x2+2x+3﹣（﹣x+3）＝2，解得：x＝1或2，故点D（1，4）或（2，3）；（3）①当点P在x轴上方时，取OG＝OE，连接BG，过点B作直线PB交抛物线于点P，交y轴于点M，使∠GBM＝∠GBO，则∠OBP＝2∠OBE，过点G作GH⊥BM，设MH＝x，则MG＝，则△OBM中，OB2+OM2＝MB2，即（+）2+9＝（x+3）2，解得：x＝2，故MG＝＝，则点M（0，4），将点B、M的坐标代入一次函数表达式并解得：直线BM的表达式为：y＝﹣x+4…②，联立①②并解得：x＝3（舍去）或，故点P（，）；②当点P在x轴下方时，同理可得：点P（﹣，﹣）；综上，点P的坐标（，）或（﹣，﹣）．。
2020武汉市九年级元月调考语文试题及答案分析
2020-2021学年度武汉市九年级元月调考语文试卷亲爱的同学，在你答题前，请认真阅读下面的注意事项：1. 本试卷由第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分组成，全卷共8面，七大题，满分120分，考试用时150分钟。
2. 答题前，请将你的姓名，准考证号写在“答题卡”相应位置，并在“答题卡”背面左上角填写姓名和座位号。
3. 答第Ⅰ卷（选择题）时，选出每小题生案后，用2B铅笔把“答题卡”上对应题目的答案标号涂黑。
如需改动，用橡皮擦干净后，再选涂其他答案。
不得答在“试卷”上。
4. 答第Ⅱ卷（非选择题）时，答案用0.5毫米黑色笔迹签字笔书写在“答题卡”上，答在“试卷”上无效。
5. 认真阅读答案卡上的注意事项。
预祝你取得优异成绩！第Ⅰ卷（选择题共30分）一、（共12分，每小题3分）1、下列各组词语中加点字的书写或注音有误的一项是【C（“绊”的正确读音应为“bàn”。
“荒谬绝纶”中的“纶”的正确写法应该是“伦”）】A.嗔视鹰隼（sǔn）嫡传（dí）不可思议B.颦蹙麾下（huī）膂力（lǚ）如释重负C.褶皱磕绊（pàn）沮丧（jǔ）荒谬绝纶D.葳蕤鞑靼（dá）褴褛（lǚ）巡幽揽胜2.依次填入下面横线处的词语，恰当的一组是【D】社会转型，道德趋于多元化。
一些人精神，价值观扭曲。
在扶起跌倒老人或许惹上官司、爱心捐赠恐被挪作他用的中，善行因利益的考量而。
一个经历着深刻转型的社会，有这样的道德可以理解，但应该主动正视、积极引导。
A.困惑迟疑迷茫疑虑B.迷茫迟疑迷茫困惑C.困惑疑虑迟疑疑虑D.迷茫疑虑迟疑困惑3.下列各句中有语病的一项是【3．B （句式杂糅，“这一结果靠的是三大运营商的共同努力取得的”应该是“这一结果靠的是三大运营商的共同努力”和“这一结果是三大运营商的共同努力取得的”的杂糅。
）】A.如果个人信息保护进入民法典，就为个人信息的商业使用划定了一个明确的法律边界。
B.全国取消长途话费和漫游费，这一结果靠的是三大运行商的共同努力取得的。
2020年武汉市九年级元月调考物理试卷(Word版有答案)
2019—2020学年度武汉市部分学校九年级调研测试物理试卷武汉市教育科学研究院命制2020、1、9一、选择题（本题包括12小题，每小题只有1个正确选项。
每小题3分，共36分）9．下表归纳了固、液、气三态物质的宏观特性和微观特性，分析表格所填写的信息可知，表格中①②处应分别填写( )物态微观特性宏观特性分子和距离分子间作用力有无形状有无体积固态很小①有固定形状有固定体积液态较大较大无固定形状②气态很大很小无固定形状无固定体积A．很小；有固定体积 B．很小；无固定体积C．很大；有固定体积 D．很大；无固定体积10．关于内能，下列说法正确的是( )A．质量越大的物体内能也越大B．内能越大的物体分子运动越剧烈C．发生扩散现象时，物质只能从内能大的物体进入内能小的物体D．热传递过程中，放出热量的物体的内能可能小于吸收热量的物体的内能11．如图所示，把图钉按在铅笔的一端，手握铅笔使图钉钉帽在粗糙的硬纸板上来回摩擦，然后用手轻触钉帽，感觉钉帽的温度明显升高了，甚至发烫。
关于该实验，下列说法正确的是( )A．图钉的温度升高，内能减小B．图钉的内能增加，纸板的内能也增加C．改变图钉内能的方式是热传递D．图钉内能的大小等于图钉克服摩擦力做功的多少12．如图所示是四冲程汽油机工作时某个冲程的示意图，下列说法正确的是( )A．该冲程是排气冲程B．该冲程汽缸内的物质只有空气C．该冲程中机械能转化为内能D．该冲程汽缸内物质的内能在减小13．如图所示，将与毛衣摩擦过的气球靠近细小的水流，水流被吸引发生弯曲的原因是( )A．气球带电吸引细小水流B．气球和水流带同种电荷C．气球和水流带异种电荷D．气球和水流分子间存在引力14．如右图所示，在武汉举行的第七届世界军人运动会击剑比赛中，中国女子重剑选手孙一文在最后决定胜负的一剑中击中对手，为中国队夺得击剑项目的第一枚金牌。
击剑比赛中，当甲方的剑击中乙方的导电服时，相当于闭合开关S甲，乙方的指示灯L乙就会亮；当乙方的剑击中甲方时，相当于闭合开关S乙，甲方的指示灯L甲就会亮。
武汉市部分学校2020-2021学年度九年级元月调研测试数学试卷答案
2020-2021学年湖北省武汉市部分学校九年级（上）期末数学试卷（元月调考）参考答案与试题解析一、选择题（共10小题，每小题3分，共30分）1．（3分）将一元二次方程2x2﹣1＝3x化成一般形式后，二次项系数和一次项系数分别是（）A．2，﹣1B．2，0C．2，3D．2，﹣3【分析】先化成一般形式，即可得出答案．【解答】解：将一元二次方程2x2﹣1＝3x化成一般形式是2x2﹣3x﹣1＝0，二次项的系数和一次项系数分别是2和﹣3，故选：D．【点评】本题考查了一元二次方程的一般形式，能化成一元二次方程的一般形式是解此题的关键，注意：说项的系数带着前面的符号．2．（3分）下列垃圾分类标识中，是中心对称图形的是（）A．B．C．D．【分析】利用中心对称图形的定义进行解答即可．【解答】解：A、不是中心对称图形，故此选项不合题意；B、是中心对称图形，故此选项符合题意；C、不是中心对称图形，故此选项不合题意；D、不是中心对称图形，故此选项不合题意；故选：B．【点评】此题主要考查了中心对称图形，关键是掌握把一个图形绕某一点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形就叫做中心对称图形．3．（3分）下列四个袋子中，都装有除颜色外无其他差别的10个小球，从这四个袋子中分别随机摸出一个球，摸到红球可能性最小的是（）A．B．C．D．【分析】要求可能性的大小，只需求出各自所占的比例大小即可．求比例时，应注意记清各自的数目．【解答】解：第一个袋子摸到红球的可能性＝；第二个袋子摸到红球的可能性＝＝；第三个袋子摸到红球的可能性＝＝；第四个袋子摸到红球的可能性＝＝．故选：A．【点评】本题主要考查了可能性大小的计算，用到的知识点为：可能性等于所求情况数与总情况数之比，难度适中．4．（3分）已知⊙O的半径等于3，圆心O到点P的距离为5，那么点P与⊙O的位置关系是（）A．点P在⊙O内B．点P在⊙O外C．点P在⊙O上D．无法确定【分析】根据①点P在圆外⇔d＞r．②点P在圆上⇔d＝r．③点P在圆内⇔d＜r，即可判断．【解答】解：∵r＝3，d＝5，∴d＞r，∴点P在⊙O外．故选：B．【点评】本题考查点与圆的位置关系，解题的关键是熟练掌握基本知识，属于中考基础题．5．（3分）一元二次方程x2﹣4x﹣1＝0配方后可化为（）A．（x+2）2＝3B．（x+2）2＝5C．（x﹣2）2＝3D．（x﹣2）2＝5【分析】移项，配方，即可得出选项．【解答】解：x2﹣4x﹣1＝0，x2﹣4x＝1，x2﹣4x+4＝1+4，（x﹣2）2＝5，故选：D．【点评】本题考查了解一元二次方程的应用，能正确配方是解此题的关键．6．（3分）在平面直角坐标系中，抛物线y＝（x+2）（x﹣4）经变换后得到抛物线y＝（x﹣2）（x+4），则下列变换正确的是（）A．向左平移6个单位B．向右平移6个单位C．向左平移2个单位D．向右平移2个单位【分析】根据变换前后的两抛物线的顶点坐标找变换规律．【解答】解：y＝（x+2）（x﹣4）＝（x﹣1）2﹣9，顶点坐标是（1，﹣9）．y＝（x﹣2）（x+4）＝（x+1）2﹣9，顶点坐标是（﹣1，﹣9）．所以将抛物线y＝（x+2）（x﹣4）向左平移2个单位长度得到抛物线y＝（x﹣2）（x+4），故选：C．【点评】此题主要考查了二次函数图象与几何变换，要求熟练掌握平移的规律：左加右减，上加下减．7．（3分）如图，将△ABC绕点C按逆时针方向旋转至△DEC，使点D落在BC的延长线上．已知∠A＝33°，∠B＝30°，则∠ACE的大小是（）A．63°B．58°C．54°D．52°【分析】先根据三角形外角的性质求出∠ACD＝63°，再由△ABC绕点C按逆时针方向旋转至△DEC，得到△ABC≌△DEC，证明∠BCE＝∠ACD，利用平角为180°即可解答．【解答】解：∵∠A＝33°，∠B＝30°，∴∠ACD＝∠A+∠B＝33°+30°＝63°，∵△ABC绕点C按逆时针方向旋转至△DEC，∴△ABC≌△DEC，∴∠ACB＝∠DCE，∴∠BCE＝∠ACD，∴∠BCE＝63°，∴∠ACE＝180°﹣∠ACD﹣∠BCE＝180°﹣63°﹣63°＝54°．故选：C．【点评】本题考查了旋转的性质，三角形外角的性质，解决本题的关键是由旋转得到△ABC≌△DEC．8．（3分）三个不透明的口袋中各有三个相同的乒乓球，将每个口袋中的三个乒乓球分别标号为1，2，3．从这三个口袋中分别摸出一个乒乓球，出现的数字正好是等腰三角形三边长的概率是（）A．B．C．D．【分析】首先根据题意画出树状图，然后由树状图求得所有等可能的结果与两次摸出的乒乓球标号相同，并且三个标号符合三角形三边关系的情况，再利用概率公式即可求得答案．【解答】解：画树状图得：∵共有27种等可能的结果，两次摸出的乒乓球标号相同，并且三个标号符合三角形三边关系的有15种结果，∴出现的数字正好是等腰三角形三边长的概率是＝．故选：B．【点评】本题考查的是用列表法或画树状图法求概率．列表法或画树状图法可以不重复不遗漏的列出所有可能的结果，列表法适合于两步完成的事件，树状图法适合两步或两步以上完成的事件．用到的知识点为：概率＝所求情况数与总情况数之比．9．（3分）如图，PM，PN分别与⊙O相切于A，B两点，C为⊙O上一点，连接AC，BC．若∠P＝60°，∠MAC＝75°，AC＝，则⊙O的半径是（）A．B．C．D．【分析】连接OA、OC，过A点作AH⊥OC于H，如图，设⊙O的半径为r，根据切线的性质得到∠OAM＝90°，则∠OAC＝15°，再计算出∠AOH＝30°，则可表示出AH ＝r，OH＝r，利用勾股定理得到（r）2+（r+r）2＝（+1）2，然后解方程即可．【解答】解：连接OA、OC，过A点作AH⊥OC于H，如图，设⊙O的半径为r，∵PM与⊙O相切于A点，∴OA⊥PM，∴∠OAM＝90°，∵∠MAC＝75°，∴∠OAC＝15°，∵OA＝OC，∴∠OAC＝∠OCA＝15°，∴∠AOH＝30°，在Rt△AOH中，AH＝OA＝r，OH＝AH＝r，在Rt△ACH中，（r）2+（r+r）2＝（+1）2，解得r＝，即⊙O的半径为．故选：A．【点评】本题考查了切线的性质：圆的切线垂直于经过切点的半径．也考查了解直角三角形．10．（3分）已知二次函数y＝2020x2+2021x+2022的图象上有两点A（x1，2023）和B（x2，2023），则当x＝x1+x2时，二次函数的值是（）A．2020B．2021C．2022D．2023【分析】根据题意得出x＝x1+x2＝﹣，代入函数的解析式即可求得二次函数的值．【解答】解：∵二次函数y＝2020x2+2021x+2022的图象上有两点A（x1，2023）和B（x2，2023），∴x1、x2是方程2020x2+2021x+2022＝2023的两个根，∴x1+x2＝﹣，∴当x＝x1+x2时，二次函数y＝2020x2+2021x+2022＝2020（﹣）2+2021•（﹣）+2022＝2022．故选：C．【点评】本题考查了一元二次方程根与系数的关系以及二次函数图象上点的坐标特征，图象上的点符合解析式．二、填空题（共6小题，每小题3分，共18分）11．（3分）在直角坐标系中，点（﹣1，2）关于原点对称点的坐标是（1，﹣2）．【分析】根据平面直角坐标系中任意一点P（x，y），关于原点的对称点是（﹣x，﹣y），可得答案．【解答】解：在直角坐标系中，点（﹣1，2）关于原点对称点的坐标是（1，﹣2），故答案为：（1，﹣2）．【点评】本题考查了关于原点对称的点的坐标，关于原点的对称点，横纵坐标都变成相反数．12．（3分）如图，平行四边形ABCD的对角线交于点O，过点O的直线EF分别交边AB，CD于E，F两点，在这个平行四边形上做随机投掷图钉试验，针头落在阴影区域内的概率是．【分析】用阴影部分的面积除以平行四边形的总面积即可求得答案．【解答】解：∵四边形是平行四边形，∴对角线把平行四边形分成面积相等的四部分，观察发现：图中阴影部分面积＝S四边形ABCD，∴点A落在阴影区域内的概率为，故答案为：．【点评】此题主要考查了几何概率，以及平行四边形的性质，用到的知识点为：概率＝相应的面积与总面积之比．13．（3分）国家实施“精准扶贫”政策以来，贫困地区经济快速发展，贫困人口大幅度减少．某地区2018年初有贫困人口4万人，通过社会各界的努力，2020年初贫困人口减少至1万人．则2018年初至2020年初该地区贫困人口的年平均下降率是50%．【分析】设2018年初至2020年初该地区贫困人口的年平均下降率为x，根据该地区2018年初及2020年初贫困人口的数量，即可得出关于x的一元二次方程，解之取其正值即可得出结论．【解答】解：设2018年初至2020年初该地区贫困人口的年平均下降率为x，依题意得：4（1﹣x）2＝1，解得：x1＝0.5＝50%，x2＝1.5（不合题意，舍去）．故答案为：50%．【点评】本题考查了一元二次方程的应用，找准等量关系，正确列出一元二次方程是解题的关键．14．（3分）已知O，I分别是△ABC的外心和内心，∠BOC＝140°，则∠BIC的大小是125°或145°．【分析】利用圆周角定理得到∠BAC＝70°或∠BAC＝110°，由于I是△ABC的内心，则∠BIC＝90°+∠BAC，然后把∠BAC的度数代入计算即可．【解答】解：∵O是△ABC的外心，∴∠BAC＝∠BOC＝×140°＝70°（如图1）或∠BAC＝180°﹣70°＝110°，（如图2）∵I是△ABC的内心，∴∠BIC＝90°+∠BAC，当∠BAC＝70°时，∠BIC＝90°+×70°＝125°；当∠BAC＝110°时，∠BIC＝90°+×110°＝145°；即∠BIC的度数为125°或145°．故答案为125°或145°．【点评】本题考查了三角形的内切圆与内心：三角形的内心到三角形三边的距离相等；三角形的内心与三角形顶点的连线平分这个内角．也考查了三角形的外心．15．（3分）如图，放置在直线l上的扇形OAB，由图①滚动（无滑动）到图②，再由图②滚动到图③，若半径OA＝1，∠AOB＝90°，则点O所经过的路径长是π．【分析】点O所经过的路径是三个圆周长．【解答】解：点O所经过的路径长＝3×＝π．故答案为：π．【点评】本题考查轨迹，弧长公式等知识，解题的关键是理解题意，灵活运用所学知识解决问题．16．（3分）下列关于二次函数y＝x2﹣2mx+1（m为常数）的结论：①该函数的图象与函数y＝﹣x2+2mx的图象的对称轴相同；②该函数的图象与x轴有交点时，m＞1；③该函数的图象的顶点在函数y＝﹣x2+1的图象上；④点A（x1，y1）与点B（x2，y2）在该函数的图象上．若x1＜x2，x1+x2＜2m，则y1＜y2．其中正确的结论是①③（填写序号）．【分析】利用二次函数的性质一一判断即可．【解答】解：①∵二次函数y＝x2﹣2mx+1的对称轴为直线x＝﹣＝m，二次函数y ＝﹣x2+2mx的对称轴为直线x＝﹣＝m，故结论①正确；②∵函数的图象与x轴有交点，则△＝（﹣2m）2﹣4×1×1＝4m2﹣4≥0，∴m≥1，故结论②错误；③∵y＝x2﹣2mx+1＝（x﹣m）2+1﹣m2，∴顶点为（m，﹣m2+1），∴该函数的图象的顶点在函数y＝﹣x2+1的图象上，故结论③正确；④∵x1+x2＜2m，∴＜m，∵二次函数y＝x2﹣2mx+1的对称轴为直线x＝m∴点A离对称轴的距离大于点B离对称轴的距离∵x1＜x2，且a＝1＞0∴y1＞y2故结论④错误；故答案为①③．【点评】本题考查抛物线与x轴的交点、二次函数的性质，二次函数图象上点的坐标特征，解题的关键是熟练掌握基本知识，属于中考常考题型．三、解答题（共8小题，共72分）17．（8分）若关于x的一元二次方程x2﹣bx+2＝0有一个根是x＝1，求b的值及方程的另一个根．【分析】把x＝1代入方程计算求出b的值，进而求出另一根即可．【解答】解：∵关于x的一元二次方程x2﹣bx+2＝0有一个根是x＝1，∴1﹣b+2＝0，解得：b＝3，把b＝3代入方程得：x2﹣3x+2＝0，设另一根为m，可得1+m＝3，解得：m＝2，则b的值为3，方程另一根为x＝2．【点评】此题考查了根与系数的关系，以及一元二次方程的解，熟练掌握根与系数的关系是解本题的关键．18．（8分）如图，将△ABC绕点C顺时针旋转得到△DEC，点D落在线段AB上．求证：DC平分∠ADE．【分析】利用全等三角形的性质以及等腰三角形的性质即可解决问题．【解答】证明：由旋转可知，△ABC≌△DEC，∴∠A＝∠CDE，AC＝DC，∴∠A＝∠ADC，∴∠ADC＝∠CDE，即DC平分∠ADE．【点评】本题考查旋转的性质，全等三角形的性质，等腰三角形的性质等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．19．（8分）小刚参加某网店的“翻牌抽奖”活动，如图，四张牌分别对应价值2，5，5，10（单位：元）的四件奖品．（1）如果随机翻一张牌，直接写出抽中5元奖品的概率；（2）如果同时随机翻两张牌，求所获奖品总值不低于10元的概率．【分析】（1）根据概率公式计算可得；（2）画树状图列出所有等可能结果，再从中确定所获奖品总值不低于10元的结果数，利用概率公式计算可得．【解答】解：（1）∵在价值为2，5，5，10（单位：元）的四件奖品，价值为5元的奖品有2张，∴抽中5元奖品的概率为＝；（2）画树状图如下：由树状图可知共有12种等可能结果，其中所获奖品总值不低于10元的有8种，∴所获奖品总值不低于10元的概率为＝．【点评】此题还考查了列举法与树状图法求概率，解答此类问题的关键在于列举出所有可能的结果，画出树形图是解题的关键．20．（8分）如图是由小正方形构成的6×6网格，每个小正方形的顶点叫做格点．⊙P经过A，B两个格点，仅用无刻度的直尺在给定网格中按要求画图（画图过程用虚线表示，画图结果用实线表示）．（1）在图（1）中，⊙P经过格点C，画圆心P，并画弦BD，使BD平分∠ABC；（2）在图（2）中，⊙P经过格点E，F是⊙P与网格线的交点，画圆心P，并画弦FG，使FG＝F A．【分析】（1）取格点T，连接AT交BC于点P，连接AC，取AC的中点W，作射线PW 交⊙P于点D，线段BD即为所求作．（2）取格点J，连接AB，AJ延长AJ交⊙P于Q，连接BQ可得圆心P，取格点R，⊙P 与格线的交点D，连接FR，DR，作DR交⊙P于G，连接FG，可证F A＝FR＝FG，线段FG即为所求作．【解答】解：（1）如图，点P，线段BD即为所求作．（2）如图，点P，线段FG即为所求作．【点评】本题考查作图﹣应用与设计垂径定理，圆周角定理，线段的垂直平分线的性质等知识，解题的关键是理解题意，灵活运用所学知识解决问题．21．（8分）如图，正方形ABCD内接于⊙O，E是的中点，连接AE，DE，CE．（1）求证：AE＝DE；（2）若CE＝1，求四边形AECD的面积．【分析】（1）欲证明AE＝DE，只要证明＝．（2）连接BD，过点D作DF⊥DE交EC的延长线于F．证明△ADE≌△CDF（AAS），推出AE＝CF，推出S△ADE＝S△CDF，推出S四边形AECD＝S△DEF，再利用等腰三角形的性质构建方程求出DE，即可解决问题．【解答】（1）证明：∵四边形ABCD是正方形，∴AB＝CD，∴＝，∵E是的中点，∴＝，∴+＝+，即＝，∴AE＝DE．（2）解：连接BD，AO，过点D作DF⊥DE交EC的延长线于F．∵四边形ABCD是正方形，∴∠DBC＝∠DEC＝45°，DA＝DC，∵∠EDF＝90°，∴∠F＝∠EDF﹣∠DEF＝90°﹣45°＝45°，∴DE＝DF，∵∠AED＝∠AOD＝45°，∴∠AED＝∠F＝45°，∵∠ADC＝∠EDF＝90°，∴∠ADE+∠EDC＝∠CDF+∠EDC＝90°，∴∠ADE＝∠CDF在△ADE和△CDF中，，∴△ADE≌△CDF（AAS），∴AE＝CF，∴S△ADE＝S△CDF，∴S四边形AECD＝S△DEF，∵EF＝DE＝EC+DE，EC＝1，∴1+DE＝DE，∴DE＝+1，∴S四边形AECD＝S△DEF＝DE2＝+．【点评】本题考查正多边形与圆，正方形的性质，全等三角形的判定和性质，等腰直角三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，属于中考常考题型．22．（10分）疫情期间，按照防疫要求，学生在进校时必须排队接受体温检测．某校统计了学生早晨到校情况，发现学生到校的累计人数y（单位：人）随时间x（单位：分钟）的变化情况如图所示，y可看作是x的二次函数，其图象经过原点，且顶点坐标为（30，900），其中0≤x≤30．校门口有一个体温检测棚，每分钟可检测40人．（1）求y与x之间的函数解析式；（2）校门口排队等待体温检测的学生人数最多时有多少人？（3）检测体温到第4分钟时，为减少排队等候时间，在校门口临时增设一个人工体温检测点．已知人工每分钟可检测12人，人工检测多长时间后，校门口不再出现排队等待的情况（直接写出结果）．【分析】（1）由顶点坐标为（30，900），可设y＝a（x﹣30）2+900，再将（0，0）代入，求得a的值，则可得y与x之间的函数解析式；（2）设第x分钟时的排队等待人数为w人，根据w＝y﹣40x及（1）中所得的y与x之间的函数解析式，可得w关于x的二次函数，将其写成顶点式，按照二次函数的性质可得答案；（3）设人工检测m分钟时间后，校门口不再出现排队等待的情况，由于检测体温到第4分钟时，在校门口临时增设一个人工体温检测点，则体温检测棚的检测时间为（m+4）分钟，则学生到校的累计人数与人工检测m分钟后两种检测方式的检测人数之和相等时，校门口不再出现排队等待的情况，据此可列出关于m的方程，求解并根据问题的实际意义作出取舍即可．【解答】解：（1）∵顶点坐标为（30，900），∴设y＝a（x﹣30）2+900，将（0，0）代入，得：900a+900＝0，解得a＝﹣1，∴y＝﹣（x﹣30）2+900；（2）设第x分钟时的排队等待人数为w人，由题意可得：w＝y﹣40x＝﹣（x﹣30）2+900﹣40x＝﹣x2+60x﹣900+900﹣40x＝﹣x2+20x＝﹣（x﹣10）2+100，∴当x＝10时，w的最大值为100，答：排队等待人数最多时是100人；（3）设人工检测m分钟时间后，校门口不再出现排队等待的情况，由题意得：﹣（4+m）2+60（4+m）﹣40×4﹣（40+12）m＝0，整理得：﹣m2+64＝0，解得：m1＝8，m2＝﹣8（舍）．答：人工检测8分钟时间后，校门口不再出现排队等待的情况．【点评】本题主要考查了二次函数在实际问题中的应用，熟练掌握待定系数法求二次函数的解析式及二次函数的性质是解题的关键．23．（10分）问题背景如图（1），△ABD，△AEC都是等边三角形，△ACD可以由△AEB通过旋转变换得到，请写出旋转中心、旋转方向及旋转角的大小．尝试应用如图（2），在Rt△ABC中，∠ACB＝90°，分别以AC，AB为边，作等边△ACD和等边△ABE，连接ED，并延长交BC于点F，连接BD．若BD⊥BC，求的值．拓展创新如图（3），在Rt△ABC中，∠ACB＝90°，AB＝2，将线段AC绕点A顺时针旋转90°得到线段AP，连接PB，直接写出PB的最大值．【分析】问题背景由等边三角形的性质得出∠BAD＝60°，∠CAE＝60°，AD＝AB，AC＝AE，证得△ACD ≌△AEB（SAS），由旋转的概念可得出答案；尝试应用证明△ADE≌△ACB（SAS），由全等三角形的性质得出∠ADE＝∠ACB＝90°，DE＝CB，得出∠BDF＝30°，由直角三角形的性质得出BF＝DF，则可得出答案；拓展创新过点A作AE⊥AB，且使AE＝AD，连接PE，BE，由直角三角形的性质求出BE，PE的长，则可得出答案．【解答】问题背景解：∵△ABD，△AEC都是等边三角形，∴∠BAD＝60°，∠CAE＝60°，AD＝AB，AC＝AE，∴∠BAD+∠BAC＝∠CAE+∠BAC，∴∠DAC＝∠BAE，∴△ACD≌△AEB（SAS），∴△ACD可以由△AEB绕点A顺时针旋转60°得到，即旋转中心是点A，旋转方向是顺时针，旋转角是60°；尝试应用∵△ACD和△ABE都是等边三角形，∴AC＝AD，AB＝AE，∠CAD＝∠BAE＝60°，∴∠CAB＝∠DAE，∴△ADE≌△ACB（SAS），∴∠ADE＝∠ACB＝90°，DE＝CB，∵∠ADE＝90°，∴∠ADF＝90°，∵∠ADC＝∠ACD＝60°，∴∠DCF＝∠CDF＝30°，∴CF＝DF，∵BD⊥BC，∴∠BDF＝30°，∴BF＝DF，设BF＝x，则CF＝DF＝2x，DE＝3x，∴；拓展创新∵∠ACB＝90°，∴点C在以AB为直径的圆上运动，取AB的中点D，连接CD，∴CD＝AB＝1，如图，过点A作AE⊥AB，且使AE＝AD，连接PE，BE，∵将线段AC绕点A顺时针旋转90°得到线段AP，∴∠P AC＝90°，P A＝AC，∵∠EAD＝90°，∴∠P AE＝∠CAD，∴△CAD≌△P AE（SAS），∴PE＝CD＝1，∵AB＝2，AE＝AD＝1，∴BE＝＝＝，∴BP≤BE+PE＝+1，当且仅当P、E、B三点共线时取等号，∴BP的最大值为+1．【点评】本题是几何变换综合题，考查了旋转的性质，等边三角形的性质，全等三角形的判定与性质，勾股定理，直角三角形的性质，熟练掌握旋转的性质是解题的关键．24．（12分）如图，经过定点A的直线y＝k（x﹣2）+1（k＜0）交抛物线y＝﹣x2+4x于B，C两点（点C在点B的右侧），D为抛物线的顶点．（1）直接写出点A的坐标；（2）如图（1），若△ACD的面积是△ABD面积的两倍，求k的值；（3）如图（2），以AC为直径作⊙E，若⊙E与直线y＝t所截的弦长恒为定值，求t的值．【分析】（1）由A为直线y＝k（x﹣2）+1上的定点，可得k的系数为0，从而求得x值，则点A的坐标可得；（2）先求得顶点D的坐标，可得AD⊥x轴．分别过点B，C作直线AD的垂线，垂足分别为M，N，设B，C的横坐标分别为x1，x2由△ACD的面积是△ABD面积的两倍得出2x1+x2＝6．将抛物线解析式与直线y＝k（x﹣2）+1解析式联立，得出关于x的一元二次方程，方法一可以直接解方程，再结合2x1+x2＝6求得答案；方法二可以用韦达定理及2x1+x2＝6求得答案；（3）设⊙E与直线y＝t交于点G，H，点C的坐标为（a，﹣a2+4a），用含a的式子表示出点E的坐标，再由勾股定理得出关于a的方程；分别过点E，A作x轴，y轴的平行线交于点F，过点E作PE⊥GH，垂足为P，连接EH，用含a的式子表示GH2，根据GH为定值，可得答案．【解答】解：（1）∵A为直线y＝k（x﹣2）+1上的定点，∴A的坐标与k无关，∴x﹣2＝0，∴x＝2，此时y＝1，∴点A的坐标为（2，1）；（2）∵y＝﹣x2+4x＝﹣（x﹣2）2+4，∴顶点D的坐标为（2，4），∵点A的坐标为（2，1），∴AD⊥x轴．如图（1），分别过点B，C作直线AD的垂线，垂足分别为M，N，设B，C的横坐标分别为x1，x2，∵△ACD的面积是△ABD面积的两倍，∴CN＝2BM，∴x2﹣2＝2（2﹣x1），∴2x1+x2＝6．联立，得x2+（k﹣4）x﹣2k+1＝0，①解得x1＝，x2＝，∴2×+＝6，化简得：＝﹣3k，解得k＝﹣．另解：接上解，由①得x1+x2＝4﹣k，又由2x1+x2＝6，得x1＝2+k．∴（2+k）2+（k﹣4）（2+k）﹣2k+1＝0，解得k＝±．∵k＜0，∴k＝﹣；（3）如图（2），设⊙E与直线y＝t交于点G，H，点C的坐标为（a，﹣a2+4a）．∵E是AC的中点，∴将线段AE沿AC方向平移与EC重合，∴x E﹣x A＝x C﹣x E，y E﹣y A＝y C﹣y E，∴x E＝（x A+x C），y E＝（y A+y C）．∴E（1+，）．分别过点E，A作x轴，y轴的平行线交于点F，在Rt△AEF中，由勾股定理得：EA2＝+＝+，过点E作PE⊥GH，垂足为P，连接EH，∴GH＝2PH，EP2＝，又∵AE＝EH，∴GH2＝4PH2＝4（EH2﹣EP2）＝4（EA2﹣EP2）＝4[+﹣]＝4[﹣a+1+﹣（﹣a2+4a+1）+1﹣+t（﹣a2+4a+1）﹣t2]＝4[（﹣t）a2+（4t﹣5）a+1+t﹣t2]．∵GH的长为定值，∴﹣t＝0，且4t﹣5＝0，∴t ＝．【点评】本题属于二次函数综合题，综合考查了一次函数、二次函数、一元二次方程、勾股定理及圆的性质等知识点，数形结合并熟练掌握相关性质定理是解题的关键．菁优网APP 菁优网公众号菁优网小程序第21页（共21页）。
武汉市2020年九年级元调试卷附答案
2019-2020学年度武汉市部分学校九年级质量检测语文试卷武汉市教育科学研究院命制 2020.1.8亲爱的同学,在你答题前，请认真阅读下面的注意事项:1.本试卷由第I卷(选择题)和第1卷(非选择题)两部分组成。
全卷共8页，七大题，满分120分。
考试用时150分钟。
2.答题前，请将你的姓名、准考证号填写在“答题卡”相应位置，并在“答题卡”背面左上角填写姓名和座位号。
3.答第I卷(选择题)时,选出每小题答案后，用2B铅笔把“答题卡”上对应题目的答案标号涂黑。
如需改动，用橡皮擦干净后，再选涂其他答案。
答在“试卷”上无效。
4.答第卷(非选择题)时，答案用0.5毫米黑色笔迹签字笔书写在“答题卡”上。
答在“试卷”上无效。
5.认真阅读答题卡上的注意事项。
预祝你取得优异成绩!第I卷(选择题共30分)一、(共9分,每小题3分)1.依次填人下面横线处的词语，恰当的一组是( )在双方难分伯仲的实力较量中，若能赢得竞争固然是一件的事情，然而更的是，赢得友谊和尊重一赢得对手的心，贏得世人的,贏在“灵魂的卓越”。
A.激动人心重要感动B.大快人心关键感动C.大快人心重要感激D.激动人心关键感激2.下列各句中有语病的一项是( )A.不少市民特意购买首发车票，目的是第一时间感受汉十高铁带来的速度与便利。
B.全年减税降费的政策红利，让企业不但可以轻装上阵，也点燃了投资者的热情。
C.中国支持世贸组织进行改革，希望它在扩大开放促进发展方面发挥更大作用。
D.面对百年未有之大变局，我们应顺应时代潮流，在追求发展的道路上矢志不移。
3.下列各向标点符号使用不规范的一项是( )A.不同国家地区、民族，不同历史宗教、习俗，彼此交相辉映，相因相生，共同擘画出这个精彩纷呈的世界。
B.故事一定要贯穿节目的每一个环节:从标题、片子开场，到主持人，评论员的每一个问题，都要跟这个故事配套。
C.灿烂的阳光一扫冬日的阴霾，天空顿时湛蓝如洗。
山川河流早已解冻，泥土中散发出草芽萌发的新鲜气息。
2020年湖北省武汉市九年级元月调考数学复习试卷(4)
2020年湖北省武汉市九年级元月调考数学复习试卷（4）一、选择题（本大题共8小题，共24.0分）1.将方程x2−8x=10化为一元二次方程的一般形式，其中二次项系数为1，一次项系数、常数项分别是()A. −8、−10B. −8、10C. 8、−10D. 8、102.如图汽车标志中不是中心对称图形的是()A. B. C. D.3.抛物线y=−3(x−1)2+2的对称轴是()A. x=1B. x=−1C. x=2D. x=−24.一个十字路口的交通信号灯每分钟红灯亮30秒，绿灯亮25秒，黄灯亮5秒．当你抬头看信号灯时，是绿灯的概率是()A. 112B. 13C. 512D. 125.如图，四边形ABCD为⊙O的内接四边形，已知∠BOD=100°，则∠BCD的度数为()A. 50°B. 80°C. 100°D. 130°6.圆的直径为10cm，如果点P到圆心O的距离是d，则()A. 当d=8cm时，点P在⊙O内B. 当d=10cm时，点P在⊙O上C. 当d=5cm时，点P在⊙O上D. 当d=6cm时，点P在⊙O内7.某种植物的主干长出若干数目的支干，每个支干又长出同样数目的小分支，主干、支干和小分支的总数是13，则每个支干长出()A. 2根小分支B. 3根小分支C. 4根小分支D. 5根小分支8.关于x的方程(m−2)x2+2x+1=0有实数根，则m的取值范围是()A. m≤3B. m≥3C. m≤3且m≠2D. m<3二、填空题（本大题共5小题，共15.0分）9.在平面直角坐标系中，点(−3,2)关于原点对称的点的坐标是______．10.如图，PA，PB分别与⊙O相切于A，B两点，∠P=70°，点C在劣弧AB上，则∠C=______．11.某村种的水稻前年平均每公顷产7 200kg，今年平均每公顷产8 450kg.设这两年该村水稻每公顷产量的年平均增长率为x，根据题意，所列方程为______．12.在直角坐标系中，将抛物线y=−x2−2x先向下平移一个单位，再向右平移一个单位，所得新抛物线的解析式为______．13.用一个半径为10cm半圆纸片围成一个圆锥的侧面(接缝忽略不计)，则该圆锥的高为______ ．三、计算题（本大题共1小题，共6.0分）14.已知3是一元二次方程x2−2x+a=0的一个根，求a的值和方程的另一根．四、解答题（本大题共4小题，共32.0分）15.有6张看上去无差别的卡片，上面分别写着1、2、3、4、5、6(1)一次性随机抽取2张卡片，用列表或画树状图的方法求出“两张卡片上的数都是偶数”的概率(2)随机摸取1张后，放回并混在一起，再随机抽取1张，直接写出“第二次取出的数字小于第一次取出的数字”的概率．16.如图，正方形ABCD和直角△ABE，∠AEB=90°，将△ABE绕点O旋转180°得到△CDF．(1)在图中画出点O和△CDF，并简要说明作图过程；(2)若AE=12，AB=13，求EF的长．17.如图，在平面直角坐标系中，点A的坐标为(−3,4)，点C与点A关于原点O对称．(1)直接写出点C的坐标；(2)若正方形ABCD的顶点B在y轴左侧．①在坐标系中画出正方形ABCD；②直接写出边AB与x轴交点M的坐标．18.如图，已知直线PA交⊙O于A、B两点，AE是⊙O的直径，点C为⊙O上一点，且AC平分∠PAE，过C作CD⊥PA，垂足为D．(1)求证：CD为⊙O的切线；(2)若DC+DA=6，⊙O的直径为10，求AB的长度．答案和解析1.【答案】A【解析】解：x2−8x=10，x2−8x−10=0，所以一次项系数、常数项分别为−8、−10，故选A．先化成一元二次方程的一般形式，再根据方程的特点得出一次项系数和常数项即可．本题考查了对一元二次方程的一般形式的应用，把方程换成一般形式是解此题的关键，注意：说各个项的系数带着前面的符号．2.【答案】B【解析】解：A、是中心对称图形．故错误；B、不是中心对称图形．故正确；C、是中心对称图形．故错误；D、是中心对称图形．故错误．故选：B．根据中心对称图形的概念求解．本题考查了中心对称图形的概念：中心对称图形是要寻找对称中心，旋转180度后与原图重合．3.【答案】A【解析】解：令x−1=0，则x=1．故选A．根据二次函数的顶点式直接进行解答即可．本题考查的是二次函数的性质，熟知二次函数的顶点式是解答此题的关键．4.【答案】C【解析】解：一共是60秒，绿的是25秒，所以绿灯的概率是2560=512．故选：C．让绿灯亮的时间除以时间总数60即为所求的概率．本题考查概率的基本计算，用到的知识点为：概率等于所求情况数与总情况数之比．5.【答案】D【解析】解：∵∠BOD=100°，∴∠BAD=100°÷2=50°，∴∠BCD=180°−∠BAD=180°−50°=130°故选：D．首先根据圆周角与圆心角的关系，求出∠BAD的度数；然后根据圆内接四边形的对角互补，用180°减去∠BAD的度数，求出∠BCD的度数是多少即可．此题主要考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半，此题还考查了圆内接四边形的性质：圆内接四边形的对角互补．6.【答案】C【解析】解：∵圆的直径为10cm，∴圆的半径为5cm，∴当d>5cm时，点P在⊙O外；当d=5cm时，点P在⊙O上；当d<5cm时，点P在⊙O内．故选：C．先得到圆的半径为5cm，根据点与圆的位置关系的判定方法得到当d>5cm时，点P在⊙O外；当d=5cm时，点P在⊙O上；当d<5cm时，点P在⊙O内，然后对各选项进行判断．本题考查了点与圆的位置关系：点的位置可以确定该点到圆心距离与半径的关系，反过来已知点到圆心距离与半径的关系可以确定该点与圆的位置关系．7.【答案】B【解析】解：设每个支干长出x个小分支，根据题意得1+x+x⋅x=13，整理得x2+x−12=0，解得x1=3，x2=−4(舍去)．答：每个支干长出3个小分支．故选：B．设每个支干长出x个小分支，利用主干、支干和小分支的总数是13列方程得到1+x+ x⋅x=13，整理得x2+x−12=0，再利用因式分解法解方程求出x，然后检验即可得到x的值．本题考查了一元二次方程的应用：列方程解决实际问题的一般步骤是：审清题意设未知数，列出方程，解所列方程求所列方程的解，检验和作答．8.【答案】A【解析】解：当m−2=0，即m=2时，方程变形为2x+1=0，解得x=−1；2当m−2≠0，则Δ=22−4(m−2)≥0，解得m≤3且m≠2，综上所述，m的范围为m≤3．故选：A．讨论：当m−2=0，方程变形为2x+1=0，此一元一次方程有解；当m−2≠0，方程为一元二次方程，利用判别式的意义得到则Δ=22−4(m−2)≥0，解得m≤3且m≠2，然后综合两种情况即可得到m的范围．本题考查了根的判别式：一元二次方程ax2+bx+c=0(a≠0)的根与Δ=b2−4ac有如下关系：当Δ>0时，方程有两个不相等的两个实数根；当Δ=0时，方程有两个相等的两个实数根；当Δ<0时，方程无实数根．9.【答案】(3,−2)【解析】解：根据平面直角坐标系内两点关于原点对称横纵坐标互为相反数，∴点(−3,2)关于原点对称的点的坐标是(3,−2)，故答案为(3,−2)．根据平面直角坐标系内两点关于原点对称横纵坐标互为相反数，即可得出答案．本题主要考查了平面直角坐标系内两点关于原点对称横纵坐标互为相反数，难度较小．10.【答案】125°【解析】解：连结OA、OB，∠ADB为弧AB所对的圆周角，如图，∵PA，PB分别与⊙O相切于A，B两点，∴OA⊥PA，OB⊥PB，∴∠OAP=∠OBP=90°，∴∠AOB+∠P=180°，∴∠AOB=180°−70°=110°，∴∠D=1∠AOB=55°，2∴∠ACB=180°−∠D=125°．故答案为：125°．连结OA、OB，∠ADB为弧AB所对的圆周角，如图，根据切线的性质得∠OAP=∠OBP= 90°，再利用四边形内角和可计算出∠AOB=110°，接着根据圆周角定理得到∠D=1∠AOB=55°，然后根据圆内接四边形的性质计算∠ACB的度数．2本题考查了切线的性质：圆的切线垂直于经过切点的半径．运用切线的性质来进行计算或论证，常通过作辅助线连接圆心和切点，利用垂直构造直角三角形解决有关问题．也考查了圆周角定理．11.【答案】7200(1+x)2=8450【解析】解：设这两年该村水稻每公顷产量的年平均增长率为x，根据题意得：7200(1+x)2=8450，故答案为：7200(1+x)2=8450．由题意得：第一年水稻产量7200(1+x)，第二年水稻产量：7200(1+x)(1+x)，进而可得方程7200(1+x)2=8450．此题主要考查了由实际问题抽象出一元二次方程，关键是掌握求平均变化率的方法．若设变化前的量为a，变化后的量为b，平均变化率为x，则经过两次变化后的数量关系为a(1±x)2=b．12.【答案】y=−x2【解析】解：抛物线y=−x2−2x=−(x+1)2+1，它的顶点坐标为(−1,1)，把点(−1,1)先向下平移一个单位，再向右平移一个单位得到对应点的坐标为(0,0)，所以新的抛物线解析式是y=−x2．故答案为y=−x2．先利用配方法得到抛物线y=−x2−2x的顶点坐标为(−1,1)，再根据点利用的规律得到点(−1,1)平移后所得对应点的坐标为(0,0)，然后根据顶点式写出平移后抛物线的解析式．本题考查了二次函数与几何变换：由于抛物线平移后的形状不变，故a不变，所以求平移后的抛物线解析式通常可利用两种方法：一是求出原抛物线上任意两点平移后的坐标，利用待定系数法求出解析式；二是只考虑平移后的顶点坐标，即可求出解析式．13.【答案】5√3【解析】解：圆锥的侧面展开图的弧长为2π×10÷2=10π(cm)，∴圆锥的底面半径为10π÷2π=5(cm)，∴圆锥的高为：√102−52=5√3(cm)．故答案是：5√3．易得圆锥的母线长为10cm，以及圆锥的侧面展开图的弧长，也就是圆锥的底面周长，除以2π即为圆锥的底面半径，进而利用勾股定理即可求得圆锥的高．本题考查了圆锥的计算．用到的知识点为：圆锥的弧长等于底面周长；圆锥的高，母线长，底面半径组成直角三角形．14.【答案】解：将x=3代入x2−2x+a=0中得32−6+a=0，解得a=−3，将a=−3代入x2−2x+a=0中得：x2−2x−3=0，解得x1=3，x2=−1，所以a=−3，方程的另一根为−1．【解析】根据一元二次方程的解的定义把x=3代入x2−2x+a=0可求出a的值，然后把a的值代入方程得到x2−2x−3=0，再利用因式分解法解方程即可得到方程的另一根．本题考查了一元二次方程的解：能使一元二次方程左右两边相等的未知数的值是一元二次方程的解．又因为只含有一个未知数的方程的解也叫做这个方程的根，所以，一元二次方程的解也称为一元二次方程的根．15.【答案】解：(1)依题意列表如下：12345612，13，14，15，16，121，23，24，25，26，231，32，34，35，36，341，42，43，45，46，451，52，53，54，56，561，62，63，64，65，6由上表可知，随机抽取2张卡片可能出现的结果有15个，它们出现的可能性相等，其中“两张卡片上的数都是偶数”的结果有3个，所以P(两张卡片上的数都是偶数)=15；(2)画树形图得：随机抽取2张卡片可能出现的结果有36个，第二次取出的数字小于第一次取出的数字有15种，所以其概率=1536=512．【解析】(1)用列表法举出所有情况，看两张卡片上的数都是偶数的情况占总情况的多少即可；(2)画出树形图即可求出第二次取出的数字小于第一次取出的数字的概率．此题考查的是用列表法或树状图法求概率．列表法可以不重复不遗漏的列出所有可能的结果，适合于两步完成的事件；树状图法适合两步或两步以上完成的事件；解题时要注意此题是放回实验还是不放回实验．用到的知识点为：概率=所求情况数与总情况数之比．16.【答案】解：(1)如图所示：连接AC，BD，交于点O.连接EO并延长到点F，使OF=OE，连接DF，CF，(2)如图所示：过点O作OG⊥OE与EB的延长线交于点G，∵四边形ABCD为正方形∴OA=OB，∠AOB=∠EOG=90°∴∠AOE=∠BOG在四边形AEBO中∠AEB=∠AOB=90°∴∠EAO+∠EBO=180°=∠EBO+∠GBO∴∠GBO=∠EAO，∴在△EAO和△GBO中，∵{∠EAO=∠GBO OA=OB∠AOE=∠BOG∴△EAO≌△GBO(ASA)，∴AE=BG，OE=OG．∴△GEO为等腰直角三角形，∴OE=√22EG=√22(EB+BG)=√22(EB+AE)=17√22∴EF=17√2．【解析】(1)利用旋转的性质分别得出对应点位置进而得出答案；(2)首先过点O作OG⊥OE与EB的延长线交于点G，利用正方形的性质结合全等三角形的判定方法得出△EAO≌△GBO(ASA)，得出△GEO为等腰直角三角形，进而得出答案．此题主要考查了旋转变换以及全等三角形的判定与性质以及等腰直角三角形的性质等知识，得出△GEO为等腰直角三角形是解题关键．17.【答案】解：(1)点C的坐标为(3,−4)；(2)①如图，正方形ABCD为所作；②设直线AB 的解析式为y =kx +b ，把A(−3,4)，B(−4,−3)代入得{−3k +b =4−4k +b =−3，解得{k =7b =25， 所以直线AB 的解析式为y =7x +25，当y =0时，7x +25=0，解得x =−257，所以M 点的坐标为(−257,0)．【解析】(1)利用关于原点对称的点的坐标特征写出C 点坐标；(2)①把A 点绕原点逆时针旋转90°得到点B ，再确定B 点关于原点的对称点D ，则四边形ABCD 为所作；②利用待定系数法求出AB 的解析式，然后利用x 轴上点的坐标特征求M 点的坐标． 本题考查了作图−旋转变换：根据旋转的性质可知，对应角都相等都等于旋转角，对应线段也相等，由此可以通过作相等的角，在角的边上截取相等的线段的方法，找到对应点，顺次连接得出旋转后的图形．也考查了正方形的性质． 18.【答案】(1)证明：连接OC ，∵OA =OC ，∴∠OCA =∠OAC ，∵AC 平分∠PAE ，∴∠DAC =∠CAO ，∴∠DAC =∠OCA ，∴PB//OC ，∵CD ⊥PA ，∴CD ⊥OC ，∵CO 为⊙O 半径，∴CD为⊙O的切线；(2)解：过O作OF⊥AB，垂足为F，∴∠OCD=∠CDA=∠OFD=90°，∴四边形DCOF为矩形，∴OC=FD，OF=CD．∵DC+DA=6，设AD=x，则OF=CD=6−x，∵⊙O的直径为10，∴DF=OC=5，∴AF=5−x，在Rt△AOF中，由勾股定理得AF2+OF2=OA2．即(5−x)2+(6−x)2=25，化简得x2−11x+18=0，解得x1=2，x2=9．∵CD=6−x大于0，故x=9舍去，∴x=2，从而AD=2，AF=5−2=3，∵OF⊥AB，由垂径定理知，F为AB的中点，∴AB=2AF=6．【解析】本题考查了切线的判定和性质、勾股定理、矩形的判定和性质以及垂径定理，是基础知识，要熟练掌握．(1)连接OC，根据题意可证得PB//OC，再根据平行线的性质，得∠DCO=90°，则CD 为⊙O的切线；(2)过O作OF⊥AB，则∠OCD=∠CDA=∠OFD=90°，得四边形OCDF为矩形，设AD= x，在Rt△AOF中，由勾股定理得(5−x)2+(6−x)2=25，从而求得x的值，由勾股定理得出AB的长．。
2020年湖北省武汉市硚口区九年级元月调考数学模拟考试试卷(解析版)
2020年湖北省武汉市硚口区九年级元月调考数学模拟试卷一．选择题（共10小题）1．将方程x2+5x＝7化为一元二次方程的一般形式，其中二次项系数为1，则一次项系数、常数项分别为（）A．5，﹣7B．5，7C．﹣5，7D．﹣5，﹣72．下列图形中，是中心对称图形但不是轴对称图形的是（）A．B．C．D．3．下列事件中，是随机事件的是（）A．任意抛一枚图钉，钉尖着地B．任意画一个三角形，其内角和是180oC．通常加热到100℃时，水沸腾D．太阳从东方升起4．抛物线y＝x2+1先向左平移2个单位长度，再向下平移5个单位长度所得抛物线的解析式是（）A．y＝（x+2）2+4B．y＝（x+2）2﹣4C．y＝（x﹣2）2+4D．y＝（x﹣2）2﹣4 5．用频率估计概率，可以发现，某种幼树在一定条件下移植成活的概率为0.8，下列说法正确的是（）A．种植10棵幼树，结果一定是“有8棵幼树成活”B．种植1000棵幼树，结果一定是“800操幼树成活“和“200棵幼树不成活”C．种植10n棵幼树，恰好有“2n棵幼树不成活”D．种植n棵幼树，当n越来越大时，种植成活幼树的频率会越来越稳定于0.86．如图，AB是⊙O的直径，点C，D在⊙O上，若∠DCB＝110°，则∠AED的度数为（）A．15°B．20°C．25°D．30°7．平面直角坐标系中，M点坐标为（﹣2，3），以2为半径画⊙M，则以下结论正确的是（）A．⊙M与x轴相交，与y轴相切B．⊙M与x轴相切，与y轴相离C．⊙M与x轴相离，与y轴相交D．⊙M与x轴相离，与y轴相切8．如图，将△ABC绕顶点C旋转得到△DEC，点A对应点D，点B对应点E，且点B刚好落在DE边上，∠A＝24°，∠BCD＝48°，则∠ABD等于（）A．30°B．38°C．36°D．45°9．如图，在€O中，＝，BC＝6．AC＝3，I是△ABC的内心，则线段OI的值为（）A．1B．﹣3C．5﹣D．10．二次函数y＝x2+bx的对称轴为直线x＝1，若关于x的方程x2+bx﹣t＝0（t为实数）在﹣1＜x＜4的范围内有实数解，则t的取值范围是（）A．t≥﹣1B．﹣1≤t＜3C．﹣1≤t＜8D．t＜3二．填空题（共6小题）11．方程x2﹣x﹣＝0的判别式的值等于．12．若点A（m，7）与点B（﹣4，n）关于原点成中心对称，则m+n＝．13．2019女排世界杯于9月14月至29日在日本举行，赛制为单循环比赛（即每两个队之间比赛一场），一共比赛66场，中国女排以全胜成绩卫冕世界杯冠军，为国庆70周年献上大礼，则中国队在本届世界杯比赛中连胜场．14．一个不透明的口袋中装有一红一白两个小球，它们除颜色外完全相同，从口袋中随机摸出1个小球，记下摸出小球的颜色后，放回口袋摇匀；再从口袋中随机摸出1个小球，记下摸出小球颜色后，放回口袋摇匀；第三次从口袋中随机摸出1个小球，则三次摸出的小球恰好颜色相同的概率为．15．如图，正六边形ABCDEF纸片中，AB＝6，分别以B、E为圆心，以6为半径画、．小欣把扇形BAC与扇形EDF剪下，并把它们粘贴为一个大扇形（B与E重合，F与A重合），她接着用这个大扇形作一个圆锥的侧面，则这个圆锥的高为．16．如图，△ABC中，AB＝10，AC＝6，BC＝14，D为AC边上一动点（D不与A、C重合），将线段BD绕D点顺时针旋转90°得到线段ED，连接CE，则△CDE面积的最大值为．三．解答题（共8小题）17．解方程：x2﹣x﹣3＝0．18．如图A、B是⊙O上的两点，∠AOB＝120°，C是弧的中点，求证四边形OACB是菱形．19．一个不透明的布袋里装有4个大小、质地均相同的乒乓球，球上分别标有数字1，2，3，4．（1）小萱随机从布袋中摸出一个乒乓球，记下数据后放回布袋里，摇匀后，再随机从布袋中摸出一个乒乓球，请用列表或画树状图的方式列出所有可能的结果，并求出“两个乒乓球上的数字之和不小于5“的概率．（2）随机从布袋中一次摸出两个乒乓球，直接写出“两个乒乓球上的数字至少有一个是偶数“的概率为．20．如图，已知点A（﹣2，﹣1）、B（﹣5，﹣5）、C（﹣2，﹣3），点P（﹣6，0）．（1）将△ABC绕点P逆时针旋转90°得△A1B1C1，画出△A1B1C1，并写出点C的对应点C1的坐标为；（2）画出△ABC关于原点成中心对称的图形△A2B2C2，并写出点A的对应点A2的坐标为；（3）把△A2B2C2向下平移6个单位长度得△A3B3C3，画出△A3B3C3，由图可知△A3B3C3可由△A1B1C1绕点Q逆时针旋转90°而得到，则点Q的坐标为；21．如图，AB为 ⊙€O的一条弦，PB切 ⊙€O于B，P A＝PB，直线PO交AB于E，交€⊙O于点C．（1）求证：P A是 ⊙€O的切线；（2）若CD∥P A，CD交直线AB于点D，交 ⊙O于另一点F．①求证：AD＝CD．②若AB＝8，BD＝2，求 ⊙€O的半径长．22．某网点销售一种儿童玩具，每件进价30元，规定单件销售利润不低于10元，且不高于31元，试销售期间发现，当销售单价定为40元时，每天可售出500件，销售单价每上涨1元，每天销售量减少10件，该网点决定提价销售，设销售单价为x元，每天销售量为y件．（1）请直接写出y与x之间的函数关系式及自变量x的取值范围；（2）当销售单价是多少元时，网店每天获利8960元？（3）网店决定每销售1件玩具，就捐赠a元（2＜a≤7）给希望工程，每天扣除捐赠后可获得最大利润为8120元，求a的值．23．如图1，△ABC和△DEC都是等边三角形，点E在AC上．（1）求证：AD＝BE；（2）如图2，当CD＝AC时，将△DEC绕点C顺时针旋转30°，连接BD交AC于点G，取AB的中点F，连接FG①求证：BE＝2FG；②若△AFG的周长为9，求BC的长．24．如图，抛物线y＝a（x2﹣2mx﹣3m2）（其中a，m为正的常数）与x轴交于点A，B，与y轴交于点C（0，﹣3），顶点为F，CD∥AB交抛物线于点D．（1）当a＝1时，求点D的坐标；（2）若点E是第一象限抛物线上的点，满足∠EAB＝∠ADC．①求点E的纵坐标；②试探究：在x轴上是否存在点P，使以PF、AD、AE为边长构成的三角形是以AE为斜边的直角三角形？如果存在，请用含m的代数式表示点P的横坐标；如果不存在，请说明理由．参考答案与试题解析一．选择题（共10小题）1．将方程x2+5x＝7化为一元二次方程的一般形式，其中二次项系数为1，则一次项系数、常数项分别为（）A．5，﹣7B．5，7C．﹣5，7D．﹣5，﹣7【分析】一元二次方程化为一般形式后，找出一次项系数与常数项即可．【解答】解：方程整理得：x2+5x﹣7＝0，则一次项系数、常数项分别为5，﹣7，故选：A．2．下列图形中，是中心对称图形但不是轴对称图形的是（）A．B．C．D．【分析】根据轴对称图形与中心对称图形的概念进行判断即可．【解答】解：A、是中心对称图形但不是轴对称图形，故正确；B、是中心对称图形，是轴对称图形，故错误；C、不是中心对称图形，是轴对称图形，故错误；D、不是中心对称图形，不是轴对称图形，故错误．故选：A．3．下列事件中，是随机事件的是（）A．任意抛一枚图钉，钉尖着地B．任意画一个三角形，其内角和是180oC．通常加热到100℃时，水沸腾D．太阳从东方升起【分析】根据事件发生的可能性大小判断相应事件的类型．【解答】解：A、任意抛一枚图钉，钉尖着地是随机事件；B、任意画一个三角形，其内角和是180°是必然事件；C、通常加热到100℃时，水沸腾是必然事件；D、太阳从东方升起是必然事件；故选：A．4．抛物线y＝x2+1先向左平移2个单位长度，再向下平移5个单位长度所得抛物线的解析式是（）A．y＝（x+2）2+4B．y＝（x+2）2﹣4C．y＝（x﹣2）2+4D．y＝（x﹣2）2﹣4【分析】根据向左平移横坐标减，向下平移纵坐标减求出新抛物线的顶点坐标，再利用顶点式解析式写出即可．【解答】解：∵抛物线y＝x2+1的顶点为（0，1），∴抛物线y＝x2+1先向左平移2个单位长度，再向下平移5个单位长度，所得新抛物线顶点坐标为（﹣2，﹣4），∴所得到的新的抛物线的解析式为y＝（x+2）2﹣4．故选：B．5．用频率估计概率，可以发现，某种幼树在一定条件下移植成活的概率为0.8，下列说法正确的是（）A．种植10棵幼树，结果一定是“有8棵幼树成活”B．种植1000棵幼树，结果一定是“800操幼树成活“和“200棵幼树不成活”C．种植10n棵幼树，恰好有“2n棵幼树不成活”D．种植n棵幼树，当n越来越大时，种植成活幼树的频率会越来越稳定于0.8【分析】根据用频率估计概率的意义即可确定正确的选项．【解答】解：用频率估计概率，可以发现，某种幼树在一定条件下移植成活的概率为0.8，是在大量重复实验中得到的概率的近似值，故A、B、C错误，D正确，故选：D．6．如图，AB是⊙O的直径，点C，D在⊙O上，若∠DCB＝110°，则∠AED的度数为（）A．15°B．20°C．25°D．30°【分析】连接AC，如图，利用圆周角定理的推论得到∠ACB＝90°，则∠ACD＝∠DCB ﹣∠ACB＝20°，然后再利用圆周角定理可得到∠AED的度数．【解答】解：连接AC，如图，∵AB为直径，∴∠ACB＝90°，∴∠ACD＝∠DCB﹣∠ACB＝110°﹣90°＝20°，∴∠AED＝∠ACD＝20°．故选：B．7．平面直角坐标系中，M点坐标为（﹣2，3），以2为半径画⊙M，则以下结论正确的是（）A．⊙M与x轴相交，与y轴相切B．⊙M与x轴相切，与y轴相离C．⊙M与x轴相离，与y轴相交D．⊙M与x轴相离，与y轴相切【分析】根据M点坐标为（﹣2，3），求得点M到x轴的距离为3，到y轴的距离为2，根据点与圆的位置关系即可得到结论．【解答】解：∵M点坐标为（﹣2，3），∴点M到x轴的距离为3，到y轴的距离为2，∵⊙P的半径为2，∴圆心M到x轴的距离大于半径，到y轴的距离等于半径，故⊙M与x轴相离，与y轴相切，故选：D．8．如图，将△ABC绕顶点C旋转得到△DEC，点A对应点D，点B对应点E，且点B刚好落在DE边上，∠A＝24°，∠BCD＝48°，则∠ABD等于（）A．30°B．38°C．36°D．45°【分析】根据旋转的性质和等腰三角形的性质即可得到结论．【解答】解：∵△ABC绕顶点C旋转得到△DEC，∴∠D＝∠A＝24°，∠ACB＝∠DCE，∵∠BCD＝48°，∴∠CBE＝48°+24°＝72°，∵CE＝CB，∴∠E＝∠CBE＝48°，∴∠ECB＝180°﹣48°﹣48°＝84°，∵∠CBA＝∠E＝48°，∴∠ABD＝180°﹣48°﹣48°﹣48°＝36°，故选：C．9．如图，在€O中，＝，BC＝6．AC＝3，I是△ABC的内心，则线段OI的值为（）A．1B．﹣3C．5﹣D．【分析】如图，连接AO，延长AO交BC于H，连接OB．想办法求出OH，IH即可解决问题．【解答】解：如图，连接AO，延长AO交BC于H，连接OB．∵＝，∴AB＝AC，AH⊥BC，∴BH＝CH＝3，∴AH＝＝＝9，设OA＝OB＝x，在Rt△BOH中，∵OB2＝OH2+BH2，∴x2＝（9﹣x）2+32，∴x＝5，∴OH＝AHAO＝9﹣5＝4，∵S△ABC＝•BC•AH＝•（AB+AC+BC）•IH，∴IH＝＝﹣1，∴OI＝OH﹣IH＝4﹣（﹣1）＝5﹣，故选：C．10．二次函数y＝x2+bx的对称轴为直线x＝1，若关于x的方程x2+bx﹣t＝0（t为实数）在﹣1＜x＜4的范围内有实数解，则t的取值范围是（）A．t≥﹣1B．﹣1≤t＜3C．﹣1≤t＜8D．t＜3【分析】二次函数的表达式为y＝x2﹣2x，顶点为：（1，﹣1），x＝﹣1时，y＝4，x＝4时，y＝8，即可求解．【解答】解：二次函数y＝x2+bx的对称轴为直线x＝1，则x＝﹣＝﹣＝1，解得：b＝﹣2，二次函数的表达式为y＝x2﹣2x，顶点为：（1，﹣1），x＝﹣1时，y＝4，x＝4时，y＝8，t的取值范围为顶点至y＝8之间的区域，即﹣1≤t＜8；故选：C．二．填空题（共6小题）11．方程x2﹣x﹣＝0的判别式的值等于4．【分析】写出a、b、c的值，再根据根的判别式△＝b2﹣4ac代入数进行计算即可．【解答】解：由题意得：a＝1，b＝﹣1，c＝﹣，△＝b2﹣4ac＝（﹣1）2﹣4×1×（﹣）＝4，故答案为：4．12．若点A（m，7）与点B（﹣4，n）关于原点成中心对称，则m+n＝﹣3．【分析】两个点关于原点对称时，它们的横坐标互为相反数，纵坐标也互为相反数，直接利用关于原点对称点的性质得出m，n的值，进而得出答案．【解答】解：∵点A（m，7）与点B（﹣4，n）关于原点成中心对称，∴m＝4，n＝﹣7，∴m+n＝﹣3．故答案为：﹣3．13．2019女排世界杯于9月14月至29日在日本举行，赛制为单循环比赛（即每两个队之间比赛一场），一共比赛66场，中国女排以全胜成绩卫冕世界杯冠军，为国庆70周年献上大礼，则中国队在本届世界杯比赛中连胜11场．【分析】设中国队在本届世界杯比赛中连胜x场，则共有（x+1）支队伍参加比赛，根据一共比赛66场，即可得出关于x的一元二次方程，解之取其正值即可得出结论．【解答】解：设中国队在本届世界杯比赛中连胜x场，则共有（x+1）支队伍参加比赛，依题意，得：x（x+1）＝66，整理，得：x2+x﹣132＝0，解得：x1＝11，x2＝﹣12（不合题意，舍去）．故答案为：11．14．一个不透明的口袋中装有一红一白两个小球，它们除颜色外完全相同，从口袋中随机摸出1个小球，记下摸出小球的颜色后，放回口袋摇匀；再从口袋中随机摸出1个小球，记下摸出小球颜色后，放回口袋摇匀；第三次从口袋中随机摸出1个小球，则三次摸出的小球恰好颜色相同的概率为．【分析】首先根据题意画出树状图，然后由树状图求得三次摸出的小球恰好颜色相同的情况，再利用概率公式即可求得答案．【解答】解：根据题意画出树状图：∵由树状图可知，共有8种等可能结果，三次摸出的小球恰好颜色相同的情况有2种情况，∴三次摸出的小球恰好颜色相同的概率为＝；故答案为：．15．如图，正六边形ABCDEF纸片中，AB＝6，分别以B、E为圆心，以6为半径画、．小欣把扇形BAC与扇形EDF剪下，并把它们粘贴为一个大扇形（B与E重合，F与A重合），她接着用这个大扇形作一个圆锥的侧面，则这个圆锥的高为2．【分析】根据正六边形的性质和弧长的公式即可得到结论．【解答】解：正六边形ABCDEF纸片中，∵∠B＝∠E＝120°，∵AB＝6，∴+的长＝×2＝8π，∴圆锥的底面半径＝＝4，∴圆锥的高＝＝2，故答案为：2．16．如图，△ABC中，AB＝10，AC＝6，BC＝14，D为AC边上一动点（D不与A、C重合），将线段BD绕D点顺时针旋转90°得到线段ED，连接CE，则△CDE面积的最大值为15．【分析】如图，过点E作EF⊥AC于F，作BH⊥AC于点H，由勾股定理可求可求AH ＝5，由旋转的性质可求BD＝DE，∠BDE＝90°，由AAS可证△BDH≌△DEF，可得EF＝DH，由三角形面积公式和二次函数的性质可求解．【解答】解：如图，过点E作EF⊥AC于F，作BH⊥AC于点H，∴∠EFD＝∠BHD＝90°，∵BH2＝BC2﹣CH2，BH2＝AB2﹣AH2，∴196﹣（6+AH）2＝100﹣AH2，∴AH＝5∵将线段BD绕D点顺时针旋转90°得到线段ED，∴BD＝DE，∠BDE＝90°，∴∠BDF+∠EDF＝90°，且∠EAF+∠AEF＝90°，∴∠AEF＝∠BDF，且∠EFD＝∠BHD＝90°，BD＝DE，∴△BDH≌△DEF（AAS）∴EF＝DH，∵△CDE面积＝CD×EF＝（6﹣AD）×（5+AD）＝﹣（AD﹣）2+15∴△CDE面积的最大值为15，故答案为15；三．解答题（共8小题）17．解方程：x2﹣x﹣3＝0．【分析】根据方程的特点可直接利用求根公式法比较简便．【解答】解：a＝1，b＝﹣1，c＝﹣3∴x＝＝∴，．18．如图A、B是⊙O上的两点，∠AOB＝120°，C是弧的中点，求证四边形OACB是菱形．【分析】连OC，由C是的中点，∠AOB＝l20°，根据在同圆或等圆中，相等的弧所对的圆心角相等得到∠AOC＝∠BOC＝60°，易得△OAC和△OBC都是等边三角形，则AC＝OA＝OB＝BC，根据菱形的判定方法即可得到结论．【解答】证明：连OC，如图，∵C是的中点，∠AOB＝l20°∴∠AOC＝∠BOC＝60°，又∵OA＝OC＝OB，∴△OAC和△OBC都是等边三角形，∴AC＝OA＝OB＝BC，∴四边形OACB是菱形．19．一个不透明的布袋里装有4个大小、质地均相同的乒乓球，球上分别标有数字1，2，3，4．（1）小萱随机从布袋中摸出一个乒乓球，记下数据后放回布袋里，摇匀后，再随机从布袋中摸出一个乒乓球，请用列表或画树状图的方式列出所有可能的结果，并求出“两个乒乓球上的数字之和不小于5“的概率．（2）随机从布袋中一次摸出两个乒乓球，直接写出“两个乒乓球上的数字至少有一个是偶数“的概率为．【分析】（1）画树状图展示所有16种等可能的结果数，再找出两个乒乓球上的数字之和不小于5的结果数，然后根据概率公式求解；（2）画树状图展示所有12种等可能的结果数，再找出两个乒乓球上的数字至少有一个是偶数的结果数，然后根据概率公式求解．【解答】解：（1）画树状图为：共有16种等可能的结果数，其中两个乒乓球上的数字之和不小于5的结果数为10，所以两个乒乓球上的数字之和不小于5的概率是：＝；（2）画树状图为：共有12种等可能的结果数，两个乒乓球上的数字至少有一个是偶数的结果数有10种，所以两个乒乓球上的数字至少有一个是偶数的概率是＝．故答案为：．20．如图，已知点A（﹣2，﹣1）、B（﹣5，﹣5）、C（﹣2，﹣3），点P（﹣6，0）．（1）将△ABC绕点P逆时针旋转90°得△A1B1C1，画出△A1B1C1，并写出点C的对应点C1的坐标为（﹣3，5）；（2）画出△ABC关于原点成中心对称的图形△A2B2C2，并写出点A的对应点A2的坐标为（1，1）；（3）把△A2B2C2向下平移6个单位长度得△A3B3C3，画出△A3B3C3，由图可知△A3B3C3可由△A1B1C1绕点Q逆时针旋转90°而得到，则点Q的坐标为（3，3）；【分析】（1）分别作出A，B，C的对应点A1，B1，C1即可．（2）分别作出A，B，C的对应点A2，B2，C2即可．（3）分别作出A1，B1，C1的对应点A3，B3，C3即可．对应点连线段的垂直平分线的交点即为所求的点Q．【解答】解：（1）如图△A1B1C1即为所求．点C的对应点C1的坐标为（﹣3，5）；故答案为（﹣3，5）．（2）如图△A2B2C2即为所求．点A的对应点A2的坐标为（1，1）；故答案为（1，1）．（3）如图△A3B3C3即为所求．由图可知△A3B3C3可由△A1B1C1绕点Q逆时针旋转90°而得到，则点Q的坐标为（3，3），故答案为（3，3）．21．如图，AB为 ⊙€O的一条弦，PB切 ⊙€O于B，P A＝PB，直线PO交AB于E，交€⊙O于点C．（1）求证：P A是 ⊙€O的切线；（2）若CD∥P A，CD交直线AB于点D，交 ⊙O于另一点F．①求证：AD＝CD．②若AB＝8，BD＝2，求 ⊙€O的半径长．【分析】（1）连接OA，OB．证明△P AO≌△PBO（SSS），推出∠P AO＝∠PBO＝90°即可解决问题．（2）①连接AC，想办法证明∠DAC＝∠DCA即可解决问题．②利用勾股定理求出EC，设OB＝OC＝r，在Rt△OBE中，利用勾股定理构建方程即可解决问题．【解答】（1）证明：连接OA，OB．∵PB是⊙O的切线，∴PB⊥OB，∴∠PBO＝90°，∵P A＝PB，PO＝PO，OA＝OB，∴△P AO≌△PBO（SSS），∴∠P AO＝∠PBO＝90°，∴P A⊥OA，∴P A是⊙O的切线．（2）①证明：连接AC．∵P A＝PB，OA＝OB，∴OP⊥AB，∴∠AEC＝90°，∵∠P AO＝90°，∴∠EAO+∠AOE＝90°，∠AOE+∠APO＝90°，∴∠EAO＝∠APO，∵AP∥CD，∴∠APO＝∠DCE，∴∠EAO＝∠DCE，∵OA＝OC，∴∠OAC＝∠OCA，∴∠EAO+∠OAC＝∠DCE+∠OCE，即∠DAC＝∠DCA，∴DA＝DC．②解：∵P A＝PB，OA＝OB，∴OP⊥AB，∴AE＝EB＝AB＝4，∵DC＝DA＝AB+BD＝10，DE＝BE+BD＝6，∠CED＝90°，∴EC＝＝＝8，设OB＝OC＝r，在Rt△OEB中，∵OB2＝EB2+OE2，∴r2＝42+（8﹣r）2，∴r＝5，∴⊙O的半径为5．22．某网点销售一种儿童玩具，每件进价30元，规定单件销售利润不低于10元，且不高于31元，试销售期间发现，当销售单价定为40元时，每天可售出500件，销售单价每上涨1元，每天销售量减少10件，该网点决定提价销售，设销售单价为x元，每天销售量为y件．（1）请直接写出y与x之间的函数关系式及自变量x的取值范围；（2）当销售单价是多少元时，网店每天获利8960元？（3）网店决定每销售1件玩具，就捐赠a元（2＜a≤7）给希望工程，每天扣除捐赠后可获得最大利润为8120元，求a的值．【分析】（1）根据原销售件数减去减少的件数即为所求；（2）根据销售利润等于单件利润乘以销售量即可求解；（3）根据单件利润减去捐赠数为最后单件利润，再根据销售利润等于单件利润乘以销售量即可求解．【解答】解：（1）由题意得，y＝500﹣10（x﹣40）＝﹣10x+900；即y与x之间的函数关系式为：y＝﹣10x+900（40≤x≤61）；（2）根据题意得，（﹣10x+900）（x﹣30）＝8960，解得：x1＝63，x2＝57，∵40≤x≤61，∴x＝57，答：当销售单价是57元时，网店每天获利8960元；（3）设每天扣除捐赠后可获得利润为W，根据题意得，W＝（﹣10x+900）（x﹣30﹣a）＝﹣10x2+（1200+10a）x﹣900（30+a）＝﹣10（x﹣）2+（a﹣60）2∵对称轴x＝60+a，40≤x≤61，2＜a≤7，∴61＜a+60≤63∴x＝61时，每天扣除捐赠后可获得最大利润为8120元，﹣10（x﹣）2+（a﹣60）2取得最大值8120∴（61﹣30﹣a）（900﹣10×61）＝8120，解得a＝3答：a的值为3．23．如图1，△ABC和△DEC都是等边三角形，点E在AC上．（1）求证：AD＝BE；（2）如图2，当CD＝AC时，将△DEC绕点C顺时针旋转30°，连接BD交AC于点G，取AB的中点F，连接FG①求证：BE＝2FG；②若△AFG的周长为9，求BC的长．【分析】（1）由“SAS”可证△ACD≌△BCE，可得AD＝BE；（2）①根据旋转角的定义，可以得到∠ACE＝30°，则∠GCD＝90°，则AC⊥BD，可证明△BTG≌△DCG，从而得到FG是△ABD的中位线，然后证明Rt△BCE≌Rt△ACD，利用三角形的中位线定理以及全等三角形的性质即可确定．②由等边三角形的性质和直角三角形性质可得AF＝AG＝×3TG＝TG，FG＝AF＝TG，由△AFG的周长为9，可求TG的长，即可求解．【解答】证明：（1）∵△ABC和△DEC都是等边三角形，∴AB＝AC＝BC，CD＝CE＝DE，∠ACB＝∠DCE＝60°，∴△ACD≌△BCE（SAS）∴AD＝BE；（2）过B作BT⊥AC于T，连AD，如图2，∵CE绕C顺时针旋转30°，∴∠ACE＝30°，∴∠GCD＝90°，由勾股定理可得BT＝AB，又∵CD＝CE＝AB，∴BT＝CD．在△BTG和△DCG中，，∴△BTG≌△DCG（AAS），∴BG＝DG，TG＝CG，∵F是AB的中点．∴FG∥AD，FG＝AD．则在Rt△BCE和Rt△ACD中，∴Rt△BCE≌Rt△ACD（SAS）．∴BE＝AD，∴BE＝2FG．②∵△ABC是等边三角形，BT⊥AC，∴AT＝CT＝AC，∵TG＝CG，∴AC＝4TG，AG＝3TG，∴CD＝AC＝2TG＝CE，∴BE＝＝2TG，∵Rt△BCE≌Rt△ACD，∴BG＝GD，AD＝BE＝2TG，又∵AF＝BF，∴FG∥AD，∴FG＝AD＝TG，∵△AFG的周长为9，∴AG+AF+FG＝3TG+2TG+TG＝9，∴TG＝，∴BC＝AC＝4TG＝10﹣2．24．如图，抛物线y＝a（x2﹣2mx﹣3m2）（其中a，m为正的常数）与x轴交于点A，B，与y轴交于点C（0，﹣3），顶点为F，CD∥AB交抛物线于点D．（1）当a＝1时，求点D的坐标；（2）若点E是第一象限抛物线上的点，满足∠EAB＝∠ADC．①求点E的纵坐标；②试探究：在x轴上是否存在点P，使以PF、AD、AE为边长构成的三角形是以AE为斜边的直角三角形？如果存在，请用含m的代数式表示点P的横坐标；如果不存在，请说明理由．【分析】（1）根据题意将a＝1，C（0，﹣3）代入y＝a（x2﹣2mx﹣3m2），进而求出m 的值，即可得出答案；（2）①表示D点坐标，得出∠EAB＝∠BAD，则x轴平分∠BAD，可得出点D关于x 轴的对称点一定在直线AE上，求出直线AE的解析式，联立直线AE和抛物线解析式可得出点E的坐标．②由①知E点的坐标，得出F（m，﹣4）、A（﹣m，0）、D（2m，﹣3），再利用PF，AD，AE的关系得出答案．【解答】解：（1）当a＝1时，y＝a（x2﹣2mx﹣3m2）＝x2﹣2mx﹣3m2，∵与y轴交于点C（0，﹣3），∴﹣3m2＝﹣3，解得：m＝±1，∵m＞0，∴m＝1，∴抛物线解析式为：y＝x2﹣2x﹣3＝（x﹣1）2﹣4，∵CD∥AB，∴C，D关于直线x＝1对称，∴D点坐标为：（2，﹣3）；（2）①对于y＝a（x2﹣2mx﹣3m2），当y＝0，则0＝a（x2﹣2mx﹣3m2），解得：x1＝﹣m，x2＝3m，当x＝0，y＝﹣3am2，可得：A（﹣m，0）、B（3m，0），C（0，﹣3am2），∵抛物线过点C，∴﹣3am2＝﹣3，则am2＝1，∵CD∥AB交抛物线于点D，∴∠ADC＝∠BAD，∴点D与点C关于抛物线的对称轴x＝m对称，∴D（2m，﹣3），∵∠EAB＝∠ADC，∴∠EAB＝∠BAD，∴x轴平分∠BAD，∴点D关于x轴的对称点D'（2m，3）一定在直线AE上，∴直线AD′的解析式为：y＝x+1，联立，整理得x2﹣3mx﹣4m2＝0，解得x1＝4m，x2＝﹣m（舍去），∴E点的横坐标为4m，∴y＝．∴点E的纵坐标为5．②存在，理由：当x＝m时，y＝a（m2﹣2m2﹣3m2）＝﹣4am2＝﹣4，∴F（m，﹣4），∵E（4m，5）、A（﹣m，0）、D（2m，﹣3），设P（b，0），∴PF2＝（m﹣b）2+16，AD2＝9m2+9，AE2＝25m2+25，∴（m﹣b）2+16+9m2+9＝25m2+25，解得：b1＝﹣3m，b2＝5m∴P（﹣3m，0）或（5m，0）．。
2020武汉元调数学试卷及答案(Word精校版)
第1页 / 共12页2019-2020学年度武汉市部分学校九年级元月调考数学试卷一、选择题(共10小题，每小题3分，共30分)1.将一元二次方程2514x x 化成一般形式后，二次项系数和一次项系数分别是( ) A ．5，-1 B ．5，4 C ．5，-4 D ．5，12.下列四张扑克牌的牌面，不是中心对称图形的是( )A ．B ．C ．D ．3.抛物线22y x 与22yx 相同的性质是( ) A ．开口向下 B ．对称轴是y 轴 C ．有最低点 D ．对称轴是x 轴4.一个不透明的袋子中只有4个黑球，2个白球，每个球除颜色外都相同，从中任意摸出3个球，下列事件为必然事件的是( )A ．至少有1个球是黑球B ．至少有1个球是白球C ．至少有2个球是黑球D ．至少有2个球是白球5.已知O 的半径等于3cm ，圆心O 到点P 的距离为5cm ，那么点P 与O 的位置关系是( ) A ．点P 在O 内 B ． 点P 在O 外 C ．点P 在O 上 D ．无法确定6.要将抛物线2y x 平移后得到抛物线223y x x ，下列平移方法正确的是( ) A ．向左平移1个单位，再向上平移2个单位 B ．向左平移1个单位，再向下平移2个单位 C ．向右平移1个单位，再向上平移2个单位 D ．向右平移1个单位，再向下平移2个单位7.如图，将△ABC 绕顶点C 逆时针旋转角度得到A B C ，且点B 刚好落在A B 上，若∠A =28°，BCA =43°，则等于( )A ．36°B ．37°C ．38°D ．39°8.小明上学要经过三个十字路口，每个路口遇到红灯、绿灯的可能性都相等，小明上学经过三个路口时，不全是红灯的概率是( )A ．38 B ． 12 C ． 58 D ． 789.如果m 、n 是一元二次方程24x x +=的两个实数根，那么多项式222n mn m --的值是( )A ．16B ．14C ．10D ．610.如图，△ABC 的两个顶点A ，B的O 上，∠A =60°，∠B =30°.若固定点A ，点B 在O 上运动，则OC 的最小值是( )A第2页 / 共12页A ．B ．C ．D ．二、填空题(本大题共6个小题，每小题3分，共18分)11.在平面直角坐标系中，点P (1，2)关于原点对称的点坐标是________. 12. 一个盒子中有10枚黑棋子和若干枚白棋子，这些棋子除颜色外无其他差别，从盒中随机取出一枚棋子，记下颜色，再放回盒子中，不断重复上述过程，一共取了300次，其中有100次取到黑棋子，由此估计盒中约有________枚白棋子.13.如图，四边形ABCD 是⊙O 的内接四边形，∠BOD =100°，∠BCD 的大小是 .14.为响应全民阅读活动，某校面向社会开放图书馆，自开放以来，进馆人次逐月增加，第一个月进馆200人次，前三个月累计进馆872人次，若进馆人次的月增长率相同，为求进馆人次的月增长率，设进馆人次的月增长率为x ，依题意可列方程为 .15.已知二次函数()20y ax bx c c =++<的图像开口向上，对称轴为直线1x =，下列结论中，一定正确的 是 (填序号即可).①0b <； ②420a b c ++<； ③a c b +>； ④()a b t at b +≤+(t 是一个常数).16.我国魏晋时期的数学家刘徽首创“割圆术”，利用圆的内接正多边形逐步逼近圆来近似计算圆的周长，进而确定圆周率，某圆半径为R ，其内接正十二边形的周长为C ． 若R ，则C = ，2CR≈ ，(结果精确到0.01 2.449≈ 1.414≈).三、解答题(共8题，共72分)17.(本题8分)若关于x 的一元二次方程x 2+2x +m =0有两个相等的实数根，求m 的值及此时方程的根.B第3页 / 共12页18. (本题8分)如图，A ．B ．C 三点在半径为1的O 上，四边形ABCD 是菱形，求的长.19. (本题8分)在5种同型号的产品中，有1件不合格品和4件合格品. (1)从这5件产品中随机选取1件，直接写出抽到合格品的概率； (2)从这5件产品中随机选取2件，求抽到都是合格品的概率.20.(本题8分)请仅用无刻度的直尺完成下列画图，不写画法，保留画图痕迹(用虚线表示画图过程，实线表示画图结果). (1)如图(1)，P 是平行四边形ABCD 边AD 上一点，过点P 画一条直线把这个四边形分成面积相等的两部分； (2)如图(2)，五边形ABCDE 是正五边形，画一条直线把这个五边形分成面积相等的两部分； (3)如图(3)，△ABC 的外接圆的圆心是点O ，D 是的中点，画一条直线把△ABC 分成面积相等的两部分.(1)(2)(3)AED CBAD21.(如图8分)如图，P A，PB 分别与O相切于A，B两点，AC 是O的直径，AC=AP，连接OP交AB于点D，连接PC 交O于点E，连接DE.(1)求证：△ABC≌△PDA；(2)求BDDE的值.22.(本题10分)某公司经过市场调查，整理出来某种商品在某个月的第x天的销售价与销售量的相关信息如(1)求y与x的函数关系式；(2)问销售该商品第几天时，日销售利润为2250元？(3)问在当月有多少天的日销售利润不低于2400元，请直接写出结果.第4页 / 共12页23.(本题10分)问题背景：如图(1)，在四边形ABCD中，若BC=CD，∠BAD=∠BCD=90°，则AC平分∠BAD，小明为了证明这个结论，将△ABC绕点C顺时针旋转90°，请帮助小明完成他的作图.迁移应用：如图(2)，在五边形ABCDE中，∠A=∠C=90°，AB=BC，AE+CD=DE，求证：BD平分∠CDE.联系拓展：如图(3)，在Rt△ABC中，AC=BC，若点D满足1013AD AB，BD=AB，点P是AD的中点，直接写出PCAB的值.(1) (2) (3)BB第5页 / 共12页24.(本题12分)如图，在平面直角坐标系中，圆心为P(x，y)的动圆经过点A(m，2m+4)(m＞-2)，且与x轴相切于点B．y与x之间存在一种确定的函数关系，其图象是一条常见的曲线，记做曲线F.(1)如图(1)，①当y=32时，直接写出P的半径；②当m=-1，x=-2时，直接写出P的半径.(2)求曲线F最低点的坐标(用含有m的式子表示)；(3)如图(2)，若曲线F最低点总在直线y=12x+3的下方，点C(-2，y1)，D(1，y2)都在曲线F上，试比较y1与y2的大小.3第6页 / 共12页第7页 / 共12页2019-2020学年度武汉市部分学校九年级元月调考数学试卷参考答案9.答案：B 解析：∵m ，n 为方程x ²+x =4的解∴m +n =-1；mn =-4，且代n 到原式，得n ²=4-n∴原式=2(4-n )-mn -2m =8-2n -2m -mn =8-2(m +n )-mn =8+2+4 =1410.答案：A 解析：延长BC 交圆O 与D ，连O D ．取AD 的中点E ，连OE ，连CE ∵ ∠B =30°，∴∠DOA =60°，∴△DAO 为等边三角形 ∵3OA ，∴3AD∵∠DCA =90°，∴点C 在以点E为半径的圆上运动∵OC OE CE ，∴3322OC ，故答案选A二、填空题(本大题共6个小题，每小题3分，共18分) 11. ()1,2-- 12.20 13.130°14.()()220020012001872x x ++++=15.①②④16.答案：24； 3.1116.解析：过C 作CD ⊥AB 于D ， 正十二边形中心角∠CAD =30°B第8页 / 共12页∴12CD AC ==AD ==，BD AB AD =- 在Rt △CDB中，2CB =，∴24C =， 3.112CR≈三、解答题(共8题，共72分) 17. m =1，方程的根为x 1=x 2=-118. 23π19.(1)45；(2)3520. (1)(2)(作法不唯一)(3)21. 证明：(1)∵P A 为O 切线，∴∠P AO =90° ∵AC 为O 直径，∴∠ABC =90°∴∠BAC +∠ACB =∠BAC +∠P AD ，∴ ∠ACB =∠P ADBE第9页 / 共12页∵P A ，PB 为O 切线，∴P A =PB∵OA =OB ，P A =PB ，∴OP ⊥AB ，∴∠ADP =90° 在△ABC 和△PDA 中 ∠=∠=⎧⎪⎨⎪⎩=∠∠ACB PAD AC PA ABC PDA ∴△ABC ≌△PDA (AAS )解:(2)连接AE ，连接BE 交DP 于点F ∵∠ADO =∠ABC =90°，∴OP ∥BC ，∴∠BCE =∠FPE ，∵AC 为直径，∴∠AEC =90°， ∵∠P AO =90°，AC =AP ，∴∠ACE =45°，CE =PE 在△CEB 和△PEF 中 ∠=∠=∠⎧⎪⎨⎩=∠⎪BCE FPE CE PECEB PEF ∴△CEB ≌△PEF (ASA ) ∴BE =FE∵∠ABE =∠ACE =45°，∠BDP =∠ADP =90°，∴BD =DF 在Rt △BDF 中，222+=BD DF BF ，∴222=BD BF ，∴BF∵BE =EF ，∴BDDE22. 解：(1)y =[(x +40)-20](100-2x ) ,∴y =-2x 2+60x +2000 (2)由(1)知y =-2x 2+60x +2000当日销售利润为2250元时，有-2x 2+60x +2000=2250 解得：x 1=5； x 2=25故该销售商品第5天或第25天时，日销售利润为2250元. (3)11天当销售利润为2400时，有-2x 2+60x +2000=2400 解得：x 1=10； x 2=20 由二次函数图像性质可知：共有11天(第10天到第20天)，销售利润不低于2400元.23. (1) 解：第10页 / 共12页(2) 证明：延长DC 至点F ，使CF =AE ，连接BE ，BF在△ABE 和△CBF 中 ==BCF =AB BC A AE CF ⎧⎪⎨⎪⎩∠∠ ∴△ABE ≌△CBF (SAS )，∴BE =BF 又∵DE =AE +CD 且AE =CF ，∴DE =DF 在△BDE 和△BDF 中 BE BF DE DF BD BD =⎧⎪=⎨⎪=⎩∴△BDE ≌△BDF (SSS )∴∠BDE =∠BDF ，∴BD 平分∠CDE (3)①当D 在AB 左侧时连接CP ，过点C 作CE ⊥CP ，交DA 的延长线于E 点∵AB =BD ，且P 是AD 的中点，∴BP ⊥AD ，即∠CBP =∠CAE∵AD =1013AB ，∴AP =12AD =513AB ，BP1213AB∵=ACE PCB ∠∠，在△BCP 和△ACE 中第11页 / 共12页CBP CAE BC ACBCP ACE =⎧⎪=⎨⎪=⎩∠∠∠∠ ∴△BCP ≌△ACE (ASA )∴AE =PB =1213AB ，PE =AP +AE =1713AB ∵PC =CE ，PC ⊥CE ，∴△PCE 为等腰直角三角形PCPE，即PC AB ②当D 在AB 右侧时连接CP ，过点C 作CQ ⊥CP 交BP 于点Q由①可知：∠APB =∠ACB =90°，AP =513AB ，PB =1213AB ∵PC ⊥CQ ，∴∠PCQ =∠ACB =90°，∴∠ACP =∠BCQ ∵∠APB =∠ACB ，∴∠CAP =∠CBQ在△ACP 和△BCQ 中CAP CBQ AC BCACP BCQ =⎧⎪=⎨⎪=⎩∠∠∠∠ ∴△ACP ≌△BCQ (ASA )∴BQ =AP =513AB PQ =BP -BQ =713AB ，PC =PQ ∵PC ⊥CQ ，∴△PCQ 为等腰直角三角形∴PCPQAB ，即PC = 综上所述：PC AB =24.解：(1)①32②54(2)依题意得：PB =P Ay = B D第12页 / 共12页 ()()22224y y m x m ---=-，∴()()21242y x m m m =-+++， 即顶点(m ，m +2)(3)方法一：顶点(m ，m +2)在直线y =x +2运动 又∵最低点一直在132y x =+下方，x +2＜132x +，即m ＜2，∴-2＜m ＜2 ∵C (-2，y 1)，D (1，y 2)，∴()()212242m y m m +=+++，()()221242m y m m =+++－ ()()()()()2212213214242m m m y y m m +--+-==++，令y 1=y 2，解得12m =- ①当-2＜m ＜12－时，()()32142m m ++＜0 ，即y 1-y 2＜0，故y 1＜y 2； ②当12m =-时，()()32142m m ++=0，y 1=y 2； ③当-12＜m ＜2时，()()32142m m ++＞0，y 1＞y 2. 综上①当-2＜m ＜12－时，y 1＜y 2；②当12m =-时，y 1=y 2；③当-12＜m ＜2时，y 1＞y 2. 方法二：(3)函数值的大小可以比较点到对称轴的距离当m =12－时，y 1=y 2 ；当-2＜m ＜12－时，y 1＜y 2 ；当-12＜m ＜2时，y 1＞y 2.。
湖北省武汉市新观察2020年九年级数学元月调考复习交流卷(四) (解析版)
湖北省武汉市新观察2020年九年级数学元月调考复习交流卷（四）一．选择题（共10小题）1．一元二次方程（3x﹣1）2＝5x化简成一般式后，二次项系数为9，其一次项系数为（）A．1 B．﹣1 C．﹣11 D．112．下列图形中，是中心对称图形的是（）A．B．C．D．3．若将抛物线y＝（2x﹣1）2先向右平移个单位长度，就得到抛物线（）A．y＝（2x﹣1）2﹣1 B．C．y＝4x2D．y＝4（x﹣1）24．军运会设计运动中，运动员每次射击击中靶的环数为1到10，不考虑脱靶的情况下，下列事件为随机事件的是（）A．某运动员两次射击总环数大于1B．某运动员两次射击总环数等于1C．某运动员两次射击总环数大于20D．某运动员两次涉及总环数等于205．直角△ABC，∠BAC＝90°，AB＝8，AC＝6，以A为圆心，4.8长度为半径的圆与直线BC 的公共点的个数为（）A．0 B．1 C．2 D．不能确定6．小名同学响应学习号召，在实际生活中发现问题，并利用所学的数学知识解决问题，他将汽车轮胎如图放置在地面台阶直角处，他测量了台阶高a为160mm，直角顶点到轮胎与底面接触点AB长为320mm，请帮小名计算轮胎的直径为（）mm．A．350 B．700 C．800 D．4007．某单行道路的路口，只能直行或右转，任意一辆车通过路口时直行或右转的概率相同．有3辆车通过路口．恰好有2辆车直行的概率是（）A．B．C．D．8．有5人患了流感，经过两轮传染后共有605人患流感，则第一轮后患流感的人数为（）A．10 B．50 C．55 D．459．如图，AB为半圆⊙O的直径，AB＝10，AC为⊙O的弦，AC＝8，D为的中点，DM⊥AC 于M，则DM的长为（）A．B．C．1 D．10．在平面直角坐标系中，已知m≠n，函数y＝x2+（m+n）x+mn的图象与x轴有a个交点，函数y＝mnx2+（m+n）x+1的图象与x轴有b个交点，则a与b的数量关系是（）A．a＝b B．a＝b﹣1 C．a＝b或a＝b+1 D．a＝b或a＝b﹣1 二．填空题（共6小题）11．已知1是一元二次方程x2﹣3x+p＝0的一个根，则p＝．12．在平面直角坐标系中，点P（4，1）关于点（2，0）中心对称的点的坐标是．13．用数字1、2、3随机组成一个三位数，那么组成的三位数是2的倍数的概率是．14．如图，正六边形ABCDEF，连接AE，CF，则＝．15．航天飞机从某个时间t秒开始，其飞行高度为h＝﹣10t2+700t+21000（单位：英尺），对人而言不低于31000英尺时会感觉到失重，则整个过程中能体会到失重感觉的时间为秒．16．如图，⊙O的半径为1，点D为优弧上一动点，AC⊥AB交直线BD于C，且∠B＝30°，当△ACD的面积最大时，∠BAD的度数为．三．解答题（共8小题）17．解方程：2x2﹣5x﹣3＝0．18．如图，已知AB＝AC，BD＝CD，点D在BC上，以A为圆心的圆恰好经过点D，求证：BC 为⊙A的切线．19．九年级某班联欢会上，节目组设计了一个即兴表演节目游戏，在一个不透明的盒子里，放有五个完全相同的乒乓球，乒乓球上分别标有数字1、2、3、4、5，游戏规则是参加联欢会的50名同学，每人同时从众里一次摸出两个乒乓球，若两球上的数字之和是偶数就给大家即兴表演一个节目；否则，下一个同学依次进行，直至50名同学都摸完．（1）若小朱是该班同学，用列表法或画树状图法求小朱同学表演即兴节目的概率；（2）若参加联欢会的同学每人都有一次摸球的机会，请估计本次联欢会上有多少个同学表演即兴节目？20．如图，在边长为1的正方形网格中，已知A（0，0），B（8，6），C（8，0），要求用无刻度直尺作图，画出△ABC的内心．（1）在AC上找一格点D，使得BD平分∠ABC，则D（，）；（2）在BD上找一格点I使得CI平分∠ACB，则I点即为△ABC的内心，I （，）；（3）直接写出△ABC内切圆半径为．21．点A，B在⊙O上，∠ABO的平分线交⊙O于点C．（1）如图1，连接CO，证明：CO∥AB；（2）如图2，过点C作CE⊥AO于E，若AE＝2，AB＝6，求CB的长．22．科幻小说《实验室的故事》中，有这样一个情节，科学家把一种珍奇的植物分别放在不同温度的环境中，经过一天后，测试出这种植物高度的增长情况（如表）：温度x/℃……﹣4 ﹣2 0 2 4 4.5 ……植物每天高度增长量y/mm……41 49 49 41 25 19.75 ……由这些数据，科学家推测出植物每天高度增长量y是温度x的函数，且这种函数是一次函数和二次函数中的一种．（1）请你选择一种适当的函数，求出它的函数关系式，并简要说明不选择另外一种函数的理由；（2）温度为多少时，这种植物每天高度的增长量最大？（3）如果实验室温度保持不变，在10天内要使该植物高度增长量的总和超过250mm，那么实验室的温度x应该在哪个范围内选择？请直接写出结果．23．已知△ACB和△ADE都是等腰直角三角形，∠ACB＝∠ADE＝90°，以CE、BC为边作平行四边形CEFB，连CD、CF．（1）如图1，当E、D分别在AC和AB上时，求证：CD＝CF；（2）如图2，△ADE绕点A旋转一定角度，判断（1）中CD与CF的数量关系是否依然成立，并加以证明；（3）如图3，AE＝，AB＝，将△ADE绕A点旋转一周，当四边形CEFB为菱形时，直接写出CF的长．24．已知，抛物线y＝m与y轴交于点C，与x轴交于点A和点B（其中点A在y轴左侧，点B在y轴右侧）．（1）若抛物线y＝m的对称轴为直线x＝1，求抛物线的解析式；（2）如图1，∠ACB＝90°，点P是抛物线y＝m上的一点，若S△BCP ＝，求点P的坐标；（3）如图2，过点A作AD∥BC交抛物线于点D，若点D的纵坐标为﹣m，求直线AD 的解析式．参考答案与试题解析一．选择题（共10小题）1．一元二次方程（3x﹣1）2＝5x化简成一般式后，二次项系数为9，其一次项系数为（）A．1 B．﹣1 C．﹣11 D．11【分析】一元二次方程ax2+bx+c＝0（a，b，c是常数且a≠0）的a、b、c分别是二次项系数、一次项系数、常数项．【解答】解：一元二次方程（3x﹣1）2＝5x的一般形式9x2﹣11x+1＝0，其中二次项系数9，一次项系数﹣11，常数项是1，故选：C．2．下列图形中，是中心对称图形的是（）A．B．C．D．【分析】根据中心对称图形的概念求解．【解答】解：A、不是中心对称图形，故此选项不符合题意；B、是中心对称图形，故此选项符合题意；C、不是中心对称图形，故此选项不符合题意；D、不是中心对称图形，故此选项不符合题意；故选：B．3．若将抛物线y＝（2x﹣1）2先向右平移个单位长度，就得到抛物线（）A．y＝（2x﹣1）2﹣1 B．C．y＝4x2D．y＝4（x﹣1）2【分析】先求出抛物线的顶点坐标，再根据向右平移横坐标加，向上平移纵坐标加求出平移后的抛物线的顶点坐标即可．【解答】解：抛物线y＝（2x﹣1）2＝4（x﹣）2的顶点坐标为（，0），∵向右平移个单位长度，∴平移后的抛物线的顶点坐标为（1，0）．∴平移后得到新抛物线的解析式是：y＝4（x﹣1）2故选：D．4．军运会设计运动中，运动员每次射击击中靶的环数为1到10，不考虑脱靶的情况下，下列事件为随机事件的是（）A．某运动员两次射击总环数大于1B．某运动员两次射击总环数等于1C．某运动员两次射击总环数大于20D．某运动员两次涉及总环数等于20【分析】直接利用随机事件以及必然事件的定义分别分析得出答案．【解答】解：A、某运动员两次射击总环数大于1，是必然事件，不合题意；B、某运动员两次射击总环数等于1，是不可能事件，不合题意；C、某运动员两次射击总环数大于20，是不可能事件，不合题意；D、某运动员两次涉及总环数等于20，是随机事件．故选：D．5．直角△ABC，∠BAC＝90°，AB＝8，AC＝6，以A为圆心，4.8长度为半径的圆与直线BC 的公共点的个数为（）A．0 B．1 C．2 D．不能确定【分析】根据直线和圆的位置关系与数量之间的联系进行判断．若d＜r，则直线与圆相交；若d＝r，则直线于圆相切；若d＞r，则直线与圆相离．【解答】解：∵∠BAC＝90°，AB＝8，AC＝6，∴BC＝10，∴斜边上的高为：＝4.8，∴d＝4.8cm＝r＝4.8cm，∴圆与该直线AB的位置关系是相切，交点个数为1，故选：B．6．小名同学响应学习号召，在实际生活中发现问题，并利用所学的数学知识解决问题，他将汽车轮胎如图放置在地面台阶直角处，他测量了台阶高a为160mm，直角顶点到轮胎与底面接触点AB长为320mm，请帮小名计算轮胎的直径为（）mm．A．350 B．700 C．800 D．400【分析】如图，连接OB，OC，作CD⊥OB于D．⊙O半径为xmm，在Rt△OCD中，由勾股定理得方程，（x﹣160）2+3202＝x2，求出x即可．【解答】解：如图，连接OB，OC，作CD⊥OB于D．设⊙O半径为xmm，在Rt△OCD中，由勾股定理得方程，（x﹣160）2+3202＝x2，解得，x＝400，∴2x＝800，答：车轱辘的直径为800mm．故选：C．7．某单行道路的路口，只能直行或右转，任意一辆车通过路口时直行或右转的概率相同．有3辆车通过路口．恰好有2辆车直行的概率是（）A．B．C．D．【分析】根据题意画出树状图得出所有等情况数和恰好有2辆车直行的情况数，再根据概率公式即可得出答案．【解答】解：根据题意画图如下：共有8种等情况数，其中恰好有2辆车直行的有3种，则恰好有2辆车直行的概率是；故选：B．8．有5人患了流感，经过两轮传染后共有605人患流感，则第一轮后患流感的人数为（）A．10 B．50 C．55 D．45【分析】设每轮传染中每人传染x人，根据经过两轮传染后共有605人患流感，即可得出关于x的一元二次方程，解之即可得出x的值，取其正值代入（5+5x）中即可求出结论．【解答】解：设每轮传染中每人传染x人，依题意，得：5+5x+x（5+5x）＝605，整理，得：x2+2x﹣120＝0，解得：x1＝10，x2＝﹣12（不合题意，舍去），∴5+5x＝55．故选：C．9．如图，AB为半圆⊙O的直径，AB＝10，AC为⊙O的弦，AC＝8，D为的中点，DM⊥AC 于M，则DM的长为（）A．B．C．1 D．【分析】如图，连接OD交AC于H，连接BC．利用勾股定理求出BC，再利用相似三角形的性质求出OH，AH，DH，证明△DMH∽△AOH，构建关系式即可解决问题．【解答】解：如图，连接OD交AC于H，连接BC．∵AB是直径，∴∠ACB＝90°，∴BC＝＝6，∵＝，∴OD⊥AB，∵∠OAH＝∠CAB，∠AOH＝∠ACB＝90°，∴△AOH∽△ACB，∴＝＝∴＝＝∴OH＝，AH＝，∵DH＝OD﹣OH＝5﹣＝，∵DM⊥AC，∵∠DMH＝∠AOH＝90°，∠DHM＝∠AHO，∴△DMH∽△AOH，∴＝，∴＝，∴DM＝1，故选：C．10．在平面直角坐标系中，已知m≠n，函数y＝x2+（m+n）x+mn的图象与x轴有a个交点，函数y＝mnx2+（m+n）x+1的图象与x轴有b个交点，则a与b的数量关系是（）A．a＝b B．a＝b﹣1 C．a＝b或a＝b+1 D．a＝b或a＝b﹣1 【分析】根据题意，利用分类讨论的方法可以求得a、b的值，从而可以得到a和b的关系，本题得以解决．【解答】解：∵函数y＝x2+（m+n）x+mn的图象与x轴有a个交点，m≠n，∴（m+n）2﹣4mn＝（m﹣n）2＞0，∴a＝2；∵函数y＝mnx2+（m+n）x+1的图象与x轴有b个交点，m≠n，∴当mn＝0时，该函数为y＝（m+n）x+1与x轴有一个交点，∴b＝1；当mn≠0时，（m+n）2﹣4mn＝（m﹣n）2＞0，∴b＝2；由上可得，a＝b+1或a＝b，故选：C．二．填空题（共6小题）11．已知1是一元二次方程x2﹣3x+p＝0的一个根，则p＝ 2 ．【分析】根据一元二次方程的解的定义把x＝1代入方程x2﹣3x+p＝0得到关于p的一元一次方程，然后解此方程即可．【解答】解：把x＝1代入方程x2﹣3x+p＝0，得1﹣3+p＝0，解得p＝2．故答案为：2．12．在平面直角坐标系中，点P（4，1）关于点（2，0）中心对称的点的坐标是（0，﹣1）．【分析】直接利用中心对称图形的性质结合平面直角坐标系得出答案．【解答】解：如图所示：点P（4，1）关于点（2，0）中心对称的点的坐标是：（0，﹣1）．故答案为：（0，﹣1）．13．用数字1、2、3随机组成一个三位数，那么组成的三位数是2的倍数的概率是．【分析】先得到用1、2、3三个数字组成一个三位数的所有情况数，再根据2的倍数的特征，得出组成的数是2的倍数的情况数，然后利用概率公式求解即可．【解答】解：用1，2，3三个数字组成一个三位数的所有情况是：123，132，213，231，312，321，其中组成的三位数是2的倍数的有132，312，共2种，所以组成的三位数是2的倍数的概率是＝．故答案为：．14．如图，正六边形ABCDEF，连接AE，CF，则＝．【分析】连接BD交CF于K．四边形ABDE是矩形，设FG＝CK＝a，则AF＝BC＝AB＝2a，推出CF＝4a，于是得到结论．【解答】解：连接BD交CF于K．∵六边形ABCDEF是正六边形，∴∠BAF＝∠AFE＝120°，FA＝FE，∴∠FAE＝30°，∴∠BAE＝90°，同理可证∠AED＝∠BDE＝90°，设FG＝CK＝a，则AF＝BC＝AB＝2a，∴CF＝4a，AE＝2AG＝2a，∴＝＝，故答案为：．15．航天飞机从某个时间t秒开始，其飞行高度为h＝﹣10t2+700t+21000（单位：英尺），对人而言不低于31000英尺时会感觉到失重，则整个过程中能体会到失重感觉的时间为30 秒．【分析】代入h＝31000可求出t值，两个t值做差后即可得出结论．【解答】解：依题意，得：﹣10t2+700t+21000＝31000，解得：t1＝20，t2＝50，∴整个过程中能体会到失重感觉的时间为50﹣20＝30（秒）．故答案为：30．16．如图，⊙O的半径为1，点D为优弧上一动点，AC⊥AB交直线BD于C，且∠B＝30°，当△ACD的面积最大时，∠BAD的度数为30°．【分析】连接OA、OD，如图，根据圆周角定理得到∠AOD＝2∠B＝60°，则△OAD为等边三角形，所以AD＝OA＝1，而∠C＝60°，利用圆周角定理可判断点C在AD为弦，圆周角为60°的弧上运动，根据三角形面积公式，当C在的中点时△ADC的面积最大，此时∠CAD＝60°，从而得到∠BAD＝30°．【解答】解：连接OA、OD，如图，∵∠B＝30°，∴∠AOD＝2∠B＝60°，∵OA＝OD，∴△OAD为等边三角形，∴AD＝OA＝1，∵BA⊥AC，∴∠BAC＝90°，∴∠C＝60°，∴点C在AD为弦，圆周角为60°的弧上运动，当C在的中点时点C到AD的距离最大，则△ADC的面积最大，此时△ADC为等边三角形，∠CAD＝60°，此时∠BAD＝30°．故答案为30°．三．解答题（共8小题）17．解方程：2x2﹣5x﹣3＝0．【分析】将方程左边的多项式利用十字相乘法分解因式，然后利用两数相乘积为0，两因式中至少有一个为0转化为两个一元一次方程，求出一次方程的解即可得到原方程的解．【解答】解：方程2x2﹣5x﹣3＝0，因式分解得：（2x+1）（x﹣3）＝0，可得：2x+1＝0或x﹣3＝0，解得：x1＝﹣，x2＝3．18．如图，已知AB＝AC，BD＝CD，点D在BC上，以A为圆心的圆恰好经过点D，求证：BC 为⊙A的切线．【分析】如图，连结AD，通过证明AD⊥BC得到BC为⊙A的切线．【解答】证明：如图，连结AD，∵AB＝AC，BD＝CD，∴AD⊥BC，又∵AD是⊙A的半径，∴BC为⊙A的切线．19．九年级某班联欢会上，节目组设计了一个即兴表演节目游戏，在一个不透明的盒子里，放有五个完全相同的乒乓球，乒乓球上分别标有数字1、2、3、4、5，游戏规则是参加联欢会的50名同学，每人同时从众里一次摸出两个乒乓球，若两球上的数字之和是偶数就给大家即兴表演一个节目；否则，下一个同学依次进行，直至50名同学都摸完．（1）若小朱是该班同学，用列表法或画树状图法求小朱同学表演即兴节目的概率；（2）若参加联欢会的同学每人都有一次摸球的机会，请估计本次联欢会上有多少个同学表演即兴节目？【分析】（1）根据画出的树状图得出所有等情况数和两个数字之和为偶数的结果数，然后根据概率公式即可得出答案；（2）表演即兴节目的同学数＝学生总数×相应概率．【解答】解：（1）根据题意画图如下：由表可知，共有20种等可能结果，其中两个数字之和为偶数的结果有8个，所以小朱同学表演即兴节目的概率＝．（2）根据题意得：50×＝20（名），答：估计本次联欢会上有20个同学表演即兴节目．20．如图，在边长为1的正方形网格中，已知A（0，0），B（8，6），C（8，0），要求用无刻度直尺作图，画出△ABC的内心．（1）在AC上找一格点D，使得BD平分∠ABC，则D（ 5 ，0 ）；（2）在BD上找一格点I使得CI平分∠ACB，则I点即为△ABC的内心，I（ 6 ， 2 ）；（3）直接写出△ABC内切圆半径为 2 ．【分析】（1）作BD平分∠ABC，即可找到点D；（2）作CI平分∠ACB，即I点为△ABC的内心，即可写出I的坐标；（3）根据作图过程即可写出△ABC内切圆半径．【解答】解：如图，（1）在AC上找一格点D，使得BD平分∠ABC，则D（5，0）；（2）在BD上找一格点I使得CI平分∠ACB，则I点即为△ABC的内心，I（6，2）；（3）∵I点为△ABC的内心，∴I到三角形三边的距离为△ABC内切圆半径，∴IE＝IF＝2，即为△ABC内切圆半径．故答案为：5，0；6，2；2．21．点A，B在⊙O上，∠ABO的平分线交⊙O于点C．（1）如图1，连接CO，证明：CO∥AB；（2）如图2，过点C作CE⊥AO于E，若AE＝2，AB＝6，求CB的长．【分析】（1）证明∠C＝∠ABC即可解决问题．（2）延长BO交⊙O于点D，作CF⊥OD于F，CG⊥BA延长线于G，连CD，CA，OC．利用全等三角形的性质求出BF，CF即可解决问题．【解答】解：（1）如图1中，∵OC＝OB，∴∠C＝∠OBC，∵BC平分∠OBA，则∠OBC＝∠CBA，∴∠C＝∠ABC，∴OC∥AB．（2）延长BO交⊙O于点D，作CF⊥OD于F，CG⊥BA延长线于G，连CD，CA，OC．∵CB平分∠ABD，CF⊥BD，CG⊥BG，∴CF＝CG，∵OA＝OB，∴∠OAB＝∠OBA，∵OC∥AB，∴∠COA＝∠OAB，∠DOC＝∠OBA，∴∠DOC＝∠COA，∵CF⊥OD，CE⊥OA，∴CF＝CE，∴CA平分∠OAG，则Rt△CAG≌Rt△CAE（HL），Rt△CEO≌Rt△CFO（HL），Rt△CGB≌Rt△CFB（HL），Rt△CEA≌Rt△CFD（HL），∴BG＝BF＝8，AE＝DF＝2，∴BD＝BF+DF＝10，∴OC＝5，OF＝3，∴CE＝CF＝＝＝4，在Rt△CFB中，CB＝＝＝4．22．科幻小说《实验室的故事》中，有这样一个情节，科学家把一种珍奇的植物分别放在不同温度的环境中，经过一天后，测试出这种植物高度的增长情况（如表）：温度x/℃……﹣4 ﹣2 0 2 4 4.5 ……植物每天高度增长量y/mm……41 49 49 41 25 19.75 ……由这些数据，科学家推测出植物每天高度增长量y是温度x的函数，且这种函数是一次函数和二次函数中的一种．（1）请你选择一种适当的函数，求出它的函数关系式，并简要说明不选择另外一种函数的理由；（2）温度为多少时，这种植物每天高度的增长量最大？（3）如果实验室温度保持不变，在10天内要使该植物高度增长量的总和超过250mm，那么实验室的温度x应该在哪个范围内选择？请直接写出结果．【分析】（1）选择二次函数，设y＝ax2+bx+c（a≠0），然后选择x＝﹣2、0、2三组数据，利用待定系数法求二次函数解析式即可，再根据反比例函数的自变量x不能为0，一次函数的特点排除另两种函数；（2）把二次函数解析式整理成顶点式形式，再根据二次函数的最值问题解答；（3）求出平均每天的高度增长量为25mm，然后根据y＝25求出x的值，再根据二次函数的性质写出x的取值范围．【解答】解：（1）选择二次函数，设y＝ax2+bx+c（a≠0），∵x＝﹣2时，y＝49，x＝0时，y＝49，x＝2时，y＝41，∴，解得，所以，y关于x的函数关系式为y＝﹣x2﹣2x+49；不选另外两个函数的理由：∵点（0，49）不可能在反比例函数图象上，∴y不是x的反比例函数；∵点（﹣4，41），（﹣2，49），（2，41）不在同一直线上，∴y不是x的一次函数；（2）由（1）得，y＝﹣x2﹣2x+49＝﹣（x+1）2+50，∵a＝﹣1＜0，∴当x＝﹣1时，y有最大值为50，即当温度为﹣1℃时，这种作物每天高度增长量最大；（3）∵10天内要使该植物高度增长量的总和超过250mm，∴平均每天该植物高度增长量超过25mm，当y＝25时，﹣x2﹣2x+49＝25，整理得，x2+2x﹣24＝0，解得x1＝﹣6，x2＝4，∴在10天内要使该植物高度增长量的总和超过250mm，实验室的温度应保持在﹣6℃＜x ＜4℃．23．已知△ACB和△ADE都是等腰直角三角形，∠ACB＝∠ADE＝90°，以CE、BC为边作平行四边形CEFB，连CD、CF．（1）如图1，当E、D分别在AC和AB上时，求证：CD＝CF；（2）如图2，△ADE绕点A旋转一定角度，判断（1）中CD与CF的数量关系是否依然成立，并加以证明；（3）如图3，AE＝，AB＝，将△ADE绕A点旋转一周，当四边形CEFB为菱形时，直接写出CF的长．【分析】（1）连接FD．证明△ADC≌△EDF（SAS）推出△DFC为等腰直角三角形即可解决问题．（2）成立．连接FD，证明△ADC≌△EDF（SAS）推出△DFC为等腰直角三角形即可解决问题．（3）分两种情形分别画出图形，利用（2）中结论求出CD即可解决问题．【解答】（1）证明：连接FD，∵AD＝ED，∠ADE＝90°，∴∠DAC＝∠DEF＝45°，∵四边形BCEF是平行四边形，∠BCE＝90°，∴四边形BCEF是矩形，∴∠CEF＝∠AEF＝90°，BC＝EF＝AC，∴∠DEF＝45°，∴∠A＝∠DEF，∴△ADC≌△EDF（SAS），∴DC＝DF，∠DCA＝∠DFE，∴∠FDC＝∠FEC＝90°，从而△DFC为等腰直角三角形，∴CD＝CF．（2）解：成立．理由：连接FD，∵AD⊥DE，EF⊥AC，∴∠DAC＝∠DEF，又AD＝ED，AC＝EF，∴△ADC≌△EDF（SAS），∴DC＝DF，∴∠FDC＝90°，从而△DFC为等腰直角三角形，∴CD＝CF．（3）解：如图3﹣1中，设AE与CD的交点为M，∵CE＝CA，DE＝DA，∴CD垂直平分AE，∴＝，DM＝，∴CD＝DM+CM＝3，∵CF＝CD∴CF＝6．如图3﹣2中，设AE与CD的交点为M，同法可得CD＝CM﹣DM＝﹣＝2，∴CF＝CD＝4，综上所述，满足条件的CF的值为6或4．24．已知，抛物线y＝m与y轴交于点C，与x轴交于点A和点B（其中点A在y轴左侧，点B在y轴右侧）．（1）若抛物线y＝m的对称轴为直线x＝1，求抛物线的解析式；（2）如图1，∠ACB＝90°，点P是抛物线y＝m上的一点，若S△BCP ＝，求点P的坐标；（3）如图2，过点A作AD∥BC交抛物线于点D，若点D的纵坐标为﹣m，求直线AD 的解析式．【分析】（1）由对称轴x＝1，可求解；（2）先求出点A，点B，点C坐标，由勾股定理可求m的值，即可求抛物线解析式，在y轴上选取点Q（0，3），则，过Q作PQ∥BC，则直线与抛物线的交点就是点P，可求PQ解析式，联立方程组，可求点P坐标；（3）由题意可得A（m，0），B（1，0），点C（0，m），可求出BC解析式，AD解析式，联立方程组，可求点D坐标，代入解析式可m的值，即可求解．【解答】解：（1）∵抛物线y＝m的对称轴为直线x＝1，∴对称轴直线为，∴m＝1，∴抛物线解析式为．（2）∵，∴当y＝0时，x1＝1，x2＝m，∴点A（m，0），点B（1，0），∴AB＝1﹣m，∵C点坐标为（0，），点A（m，0），点B（1，0），∴AB2＝（m﹣1）2，＝1+m2，∵∠ACB＝90°，∴AB2＝AC2+BC2，∴1+m2＝（m﹣1）2，∴m＝﹣4，∴抛物线解析式为，A（﹣4，0），B（1，0）C（0，﹣2），∴，如图1，在y轴上选取点Q（0，3），则，过Q作PQ∥BC，则直线与抛物线的交点就是点P，∵B（1，0）C（0，﹣2），∴直线BC解析式为：y＝2x﹣2，则直线PQ解析式为：y＝2x+3，∴，解得，，∴P坐标为（，）或（，）（3）由题意知＞0，∴m＜0，∴A（m，0），B（1，0），且点C（0，m），∴直线BC解析式为：y＝﹣mx+m，∴AD解析式为：，∴解得：x1＝1﹣m，x2＝m（舍，这是A点的横坐标），∴点D（1﹣m，﹣）∴，解得m＝，∴AD解析式为．。
湖北省武汉市2020年元调九年级学业考试英语试卷有答案
2020年武汉市元调初三学业考试英语试卷第I卷（选择题共85分）第一部分听力部分一、听力测试（共三节）第一节（共5小题，每小题1分，满分5分）听下面5个问题。
每个问题后有三个答语，从题中所给的A,B,C三个选项中选出最佳选项。
听完每个问题后，你都有5秒钟的时间来作答和阅读下一小题。
每个问题仅读一遍。
1. A. I like it. B. So late. C. By school bus.2. A. He's14. B. This Friday. C. A big cake.3. A. Clean the garden. B. With my father. C. To the East Lake.4. A. To make a plan. B. Mary's idea. C. It's a hard job.5. A. Very expensive. B. The blue one. C. On both sides.第二节(共7小题，每小题1分,满分7分)听下面7段对话。
每段对话后有一个小题，从题中所给的A,B,C三个选项中选出最佳选项。
听完每段对话后，你都有10秒钟的时间来作答有关小题和阅读下一小题。
每段对话仅读一遍。
6. Where are most probably the two speakers?A. At a swimming pool.B. ln a library.C. At a clothing store.7. What can we know about Bill?A. He got seriously hurt.B. He broke his feet.C. He tried to slip on the floor.8. What are they mainly talking about?A. A job.B. A person.C. A book.9. What does the woman mean?A. She will give a talk.B. Jackson is ready.C. Jackson is busy now.10. How is the woman now?A. Quite alright.B. A little better.C. Even worse.l1. When will the bus reach the town?A. In about 30 minutes.B. In about 40 minutes.C. In about 70 minutes.12. What will Tim do tonight?A. To go to a movie.B. To prepare for an exam.C. To borrow some materials.第三节（共13小题，每小题1分，满分13分）听下面4段对话或独白。
2020年湖北省武汉市硚口区九年级元月调考数学模拟试卷及答案解析
2020年湖北省武汉市硚口区九年级元月调考数学模拟试卷一、选择题（共10小题，每小题3分，共30分）下列各题中均有四个备选答案，其中有且只有一个正确，请在答卷上将正确答案的字母代考涂黑．1．（3分）将方程x2+5x＝7化为一元二次方程的一般形式，其中二次项系数为1，则一次项系数、常数项分别为（）A．5，﹣7B．5，7C．﹣5，7D．﹣5，﹣7 2．（3分）下列图形中，是中心对称图形但不是轴对称图形的是（）A．B．C．D．3．（3分）下列事件中，是随机事件的是（）A．任意抛一枚图钉，钉尖着地B．任意画一个三角形，其内角和是180oC．通常加热到100℃时，水沸腾D．太阳从东方升起4．（3分）抛物线y＝x2+1先向左平移2个单位长度，再向下平移5个单位长度所得抛物线的解析式是（）A．y＝（x+2）2+4B．y＝（x+2）2﹣4C．y＝（x﹣2）2+4D．y＝（x﹣2）2﹣4 5．（3分）用频率估计概率，可以发现，某种幼树在一定条件下移植成活的概率为0.8，下列说法正确的是（）A．种植10棵幼树，结果一定是“有8棵幼树成活”B．种植1000棵幼树，结果一定是“800操幼树成活“和“200棵幼树不成活”C．种植10n棵幼树，恰好有“2n棵幼树不成活”D．种植n棵幼树，当n越来越大时，种植成活幼树的频率会越来越稳定于0.86．（3分）如图，AB是⊙O的直径，点C，D在⊙O上，若∠DCB＝110°，则∠AED的度数为（）A．15°B．20°C．25°D．30°7．（3分）平面直角坐标系中，M点坐标为（﹣2，3），以2为半径画⊙M，则以下结论正确的是（）A．⊙M与x轴相交，与y轴相切B．⊙M与x轴相切，与y轴相离C．⊙M与x轴相离，与y轴相交D．⊙M与x轴相离，与y轴相切8．（3分）如图，将△ABC绕顶点C旋转得到△DEC，点A对应点D，点B对应点E，且点B刚好落在DE边上，∠A＝24°，∠BCD＝48°，则∠ABD等于（）A．30°B．38°C．36°D．45°9．（3分）如图，在€O中，＝，BC＝6．AC＝3，I是△ABC的内心，则线段OI 的值为（）A．1B．﹣3C．5﹣D．10．（3分）二次函数y＝x2+bx的对称轴为直线x＝1，若关于x的方程x2+bx﹣t＝0（t为实数）在﹣1＜x＜4的范围内有实数解，则t的取值范围是（）A．t≥﹣1B．﹣1≤t＜3C．﹣1≤t＜8D．t＜3二、填空题（每小题3分，共计18分）11．（3分）方程x2﹣x﹣＝0的判别式的值等于．12．（3分）若点A（m，7）与点B（﹣4，n）关于原点成中心对称，则m+n＝．13．（3分）2019女排世界杯于9月14月至29日在日本举行，赛制为单循环比赛（即每两个队之间比赛一场），一共比赛66场，中国女排以全胜成绩卫冕世界杯冠军，为国庆70周年献上大礼，则中国队在本届世界杯比赛中连胜场．14．（3分）一个不透明的口袋中装有一红一白两个小球，它们除颜色外完全相同，从口袋中随机摸出1个小球，记下摸出小球的颜色后，放回口袋摇匀；再从口袋中随机摸出1个小球，记下摸出小球颜色后，放回口袋摇匀；第三次从口袋中随机摸出1个小球，则三次摸出的小球恰好颜色相同的概率为．15．（3分）如图，正六边形ABCDEF纸片中，AB＝6，分别以B、E为圆心，以6为半径画、．小欣把扇形BAC与扇形EDF剪下，并把它们粘贴为一个大扇形（B与E重合，F与A重合），她接着用这个大扇形作一个圆锥的侧面，则这个圆锥的高为．16．（3分）如图，△ABC中，AB＝10，AC＝6，BC＝14，D为AC边上一动点（D不与A、C重合），将线段BD绕D点顺时针旋转90°得到线段ED，连接CE，则△CDE面积的最大值为．三.解答题（共8小题，共计72分）17．（8分）解方程：x2﹣x﹣3＝0．18．（6分）如图A、B是⊙O上的两点，∠AOB＝120°，C是弧的中点，求证四边形OACB是菱形．19．（8分）一个不透明的布袋里装有4个大小、质地均相同的乒乓球，球上分别标有数字1，2，3，4．（1）小萱随机从布袋中摸出一个乒乓球，记下数据后放回布袋里，摇匀后，再随机从布袋中摸出一个乒乓球，请用列表或画树状图的方式列出所有可能的结果，并求出“两个乒乓球上的数字之和不小于5“的概率．（2）随机从布袋中一次摸出两个乒乓球，直接写出“两个乒乓球上的数字至少有一个是偶数“的概率为．20．（8分）如图，已知点A（﹣2，﹣1）、B（﹣5，﹣5）、C（﹣2，﹣3），点P（﹣6，0）．（1）将△ABC绕点P逆时针旋转90°得△A1B1C1，画出△A1B1C1，并写出点C的对应点C1的坐标为；（2）画出△ABC关于原点成中心对称的图形△A2B2C2，并写出点A的对应点A2的坐标为；（3）把△A2B2C2向下平移6个单位长度得△A3B3C3，画出△A3B3C3，由图可知△A3B3C3可由△A1B1C1绕点Q逆时针旋转90°而得到，则点Q的坐标为；21．（8分）如图，AB为 ⊙€O的一条弦，PB切 ⊙€O于B，P A＝PB，直线PO交AB于E，交 ⊙O于点C．（1）求证：P A是 ⊙€O的切线；（2）若CD∥P A，CD交直线AB于点D，交 ⊙O于另一点F．①求证：AD＝CD．②若AB＝8，BD＝2，求 ⊙€O的半径长．22．（10分）某网点销售一种儿童玩具，每件进价30元，规定单件销售利润不低于10元，且不高于31元，试销售期间发现，当销售单价定为40元时，每天可售出500件，销售单价每上涨1元，每天销售量减少10件，该网点决定提价销售，设销售单价为x元，每天销售量为y件．（1）请直接写出y与x之间的函数关系式及自变量x的取值范围；（2）当销售单价是多少元时，网店每天获利8960元？（3）网店决定每销售1件玩具，就捐赠a元（2＜a≤7）给希望工程，每天扣除捐赠后可获得最大利润为8120元，求a的值．23．（12分）如图1，△ABC和△DEC都是等边三角形，点E在AC上．（1）求证：AD＝BE；（2）如图2，当CD＝AC时，将△DEC绕点C顺时针旋转30°，连接BD交AC于点G，取AB的中点F，连接FG①求证：BE＝2FG；②若△AFG的周长为9，求BC的长．24．（12分）如图，抛物线y＝a（x2﹣2mx﹣3m2）（其中a，m为正的常数）与x轴交于点A，B，与y轴交于点C（0，﹣3），顶点为F，CD∥AB交抛物线于点D．（1）当a＝1时，求点D的坐标；（2）若点E是第一象限抛物线上的点，满足∠EAB＝∠ADC．①求点E的纵坐标；②试探究：在x轴上是否存在点P，使以PF、AD、AE为边长构成的三角形是以AE为斜边的直角三角形？如果存在，请用含m的代数式表示点P的横坐标；如果不存在，请说明理由．2020年湖北省武汉市硚口区九年级元月调考数学模拟试卷参考答案与试题解析一、选择题（共10小题，每小题3分，共30分）下列各题中均有四个备选答案，其中有且只有一个正确，请在答卷上将正确答案的字母代考涂黑．1．（3分）将方程x2+5x＝7化为一元二次方程的一般形式，其中二次项系数为1，则一次项系数、常数项分别为（）A．5，﹣7B．5，7C．﹣5，7D．﹣5，﹣7【分析】一元二次方程化为一般形式后，找出一次项系数与常数项即可．【解答】解：方程整理得：x2+5x﹣7＝0，则一次项系数、常数项分别为5，﹣7，故选：A．【点评】此题考查了一元二次方程的一般形式，其一般形式为ax2+bx+c＝0（a≠0）．2．（3分）下列图形中，是中心对称图形但不是轴对称图形的是（）A．B．C．D．【分析】根据轴对称图形与中心对称图形的概念进行判断即可．【解答】解：A、是中心对称图形但不是轴对称图形，故正确；B、是中心对称图形，是轴对称图形，故错误；C、不是中心对称图形，是轴对称图形，故错误；D、不是中心对称图形，不是轴对称图形，故错误．故选：A．【点评】本题考查的是中心对称图形与轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后两部分重合．3．（3分）下列事件中，是随机事件的是（）A．任意抛一枚图钉，钉尖着地B．任意画一个三角形，其内角和是180oC．通常加热到100℃时，水沸腾D．太阳从东方升起【分析】根据事件发生的可能性大小判断相应事件的类型．【解答】解：A、任意抛一枚图钉，钉尖着地是随机事件；B、任意画一个三角形，其内角和是180°是必然事件；C、通常加热到100℃时，水沸腾是必然事件；D、太阳从东方升起是必然事件；故选：A．【点评】本题考查的是必然事件、不可能事件、随机事件的概念．必然事件指在一定条件下，一定发生的事件．不可能事件是指在一定条件下，一定不发生的事件，不确定事件即随机事件是指在一定条件下，可能发生也可能不发生的事件．4．（3分）抛物线y＝x2+1先向左平移2个单位长度，再向下平移5个单位长度所得抛物线的解析式是（）A．y＝（x+2）2+4B．y＝（x+2）2﹣4C．y＝（x﹣2）2+4D．y＝（x﹣2）2﹣4【分析】根据向左平移横坐标减，向下平移纵坐标减求出新抛物线的顶点坐标，再利用顶点式解析式写出即可．【解答】解：∵抛物线y＝x2+1的顶点为（0，1），∴抛物线y＝x2+1先向左平移2个单位长度，再向下平移5个单位长度，所得新抛物线顶点坐标为（﹣2，﹣4），∴所得到的新的抛物线的解析式为y＝（x+2）2﹣4．故选：B．【点评】本题考查了二次函数图象与几何变换，平移的规律：左加右减，上加下减，利用顶点的变化求解更简便．5．（3分）用频率估计概率，可以发现，某种幼树在一定条件下移植成活的概率为0.8，下列说法正确的是（）A．种植10棵幼树，结果一定是“有8棵幼树成活”B．种植1000棵幼树，结果一定是“800操幼树成活“和“200棵幼树不成活”C．种植10n棵幼树，恰好有“2n棵幼树不成活”D．种植n棵幼树，当n越来越大时，种植成活幼树的频率会越来越稳定于0.8【分析】根据用频率估计概率的意义即可确定正确的选项．【解答】解：用频率估计概率，可以发现，某种幼树在一定条件下移植成活的概率为0.8，是在大量重复实验中得到的概率的近似值，故A、B、C错误，D正确，故选：D．【点评】此题主要考查了利用频率估计概率，大量反复试验下频率稳定值即概率．用到的知识点为：频率＝所求情况数与总情况数之比．6．（3分）如图，AB是⊙O的直径，点C，D在⊙O上，若∠DCB＝110°，则∠AED的度数为（）A．15°B．20°C．25°D．30°【分析】连接AC，如图，利用圆周角定理的推论得到∠ACB＝90°，则∠ACD＝∠DCB ﹣∠ACB＝20°，然后再利用圆周角定理可得到∠AED的度数．【解答】解：连接AC，如图，∵AB为直径，∴∠ACB＝90°，∴∠ACD＝∠DCB﹣∠ACB＝110°﹣90°＝20°，∴∠AED＝∠ACD＝20°．故选：B．【点评】本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．推论：半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径．7．（3分）平面直角坐标系中，M点坐标为（﹣2，3），以2为半径画⊙M，则以下结论正确的是（）A．⊙M与x轴相交，与y轴相切B．⊙M与x轴相切，与y轴相离C．⊙M与x轴相离，与y轴相交D．⊙M与x轴相离，与y轴相切【分析】根据M点坐标为（﹣2，3），求得点M到x轴的距离为3，到y轴的距离为2，根据点与圆的位置关系即可得到结论．【解答】解：∵M点坐标为（﹣2，3），∴点M到x轴的距离为3，到y轴的距离为2，∵⊙P的半径为2，∴圆心M到x轴的距离大于半径，到y轴的距离等于半径，故⊙M与x轴相离，与y轴相切，故选：D．【点评】本题考查了直线与圆的位置关系，坐标与图形性质，正确的理解题意是解题的关键．8．（3分）如图，将△ABC绕顶点C旋转得到△DEC，点A对应点D，点B对应点E，且点B刚好落在DE边上，∠A＝24°，∠BCD＝48°，则∠ABD等于（）A．30°B．38°C．36°D．45°【分析】根据旋转的性质和等腰三角形的性质即可得到结论．【解答】解：∵△ABC绕顶点C旋转得到△DEC，∴∠D＝∠A＝24°，∠ACB＝∠DCE，∴∠CBE＝48°+24°＝72°，∵CE＝CB，∴∠E＝∠CBE＝72°，∴∠ECB＝180°﹣72°﹣72°＝36°，∵∠CBA＝∠E＝72°，∴∠ABD＝180°﹣72°﹣72°＝36°，故选：C．【点评】本题考查了旋转的性质，等腰三角形的性质，熟练掌握旋转的性质即可得到结论．9．（3分）如图，在€O中，＝，BC＝6．AC＝3，I是△ABC的内心，则线段OI 的值为（）A．1B．﹣3C．5﹣D．【分析】如图，连接AO，延长AO交BC于H，连接OB．想办法求出OH，IH即可解决问题．【解答】解：如图，连接AO，延长AO交BC于H，连接OB．∵＝，∴AB＝AC，AH⊥BC，∴AH＝＝＝9，设OA＝OB＝x，在Rt△BOH中，∵OB2＝OH2+BH2，∴x2＝（9﹣x）2+32，∴x＝5，∴OH＝AHAO＝9﹣5＝4，∵S△ABC＝•BC•AH＝•（AB+AC+BC）•IH，∴IH＝＝﹣1，∴OI＝OH﹣IH＝4﹣（﹣1）＝5﹣，故选：C．【点评】本题主要考查的是三角形的内心和外心、勾股定理等知识，掌握本题的辅助线的作法是解题的关键．10．（3分）二次函数y＝x2+bx的对称轴为直线x＝1，若关于x的方程x2+bx﹣t＝0（t为实数）在﹣1＜x＜4的范围内有实数解，则t的取值范围是（）A．t≥﹣1B．﹣1≤t＜3C．﹣1≤t＜8D．t＜3【分析】二次函数的表达式为y＝x2﹣2x，顶点为：（1，﹣1），x＝﹣1时，y＝4，x＝4时，y＝8，即可求解．【解答】解：二次函数y＝x2+bx的对称轴为直线x＝1，则x＝﹣＝﹣＝1，解得：b＝﹣2，二次函数的表达式为y＝x2﹣2x，顶点为：（1，﹣1），x＝﹣1时，y＝4，x＝4时，y＝8，t的取值范围为顶点至y＝8之间的区域，即﹣1≤t＜8；故选：C．【点评】本题考查的是抛物线与x轴的交点，主要考查函数图象上点的坐标特征，要求学生非常熟悉函数与坐标轴的交点、顶点等点坐标的求法，及这些点代表的意义及函数特征．二、填空题（每小题3分，共计18分）11．（3分）方程x2﹣x﹣＝0的判别式的值等于4．【分析】写出a、b、c的值，再根据根的判别式△＝b2﹣4ac代入数进行计算即可．【解答】解：由题意得：a＝1，b＝﹣1，c＝﹣，△＝b2﹣4ac＝（﹣1）2﹣4×1×（﹣）＝4，故答案为：4．【点评】此题主要考查了根的判别式，关键是掌握根的判别式的计算公式．12．（3分）若点A（m，7）与点B（﹣4，n）关于原点成中心对称，则m+n＝﹣3．【分析】两个点关于原点对称时，它们的横坐标互为相反数，纵坐标也互为相反数，直接利用关于原点对称点的性质得出m，n的值，进而得出答案．【解答】解：∵点A（m，7）与点B（﹣4，n）关于原点成中心对称，∴m＝4，n＝﹣7，∴m+n＝﹣3．故答案为：﹣3．【点评】此题主要考查了关于原点对称点的性质，解题时注意：点P（x，y）关于原点O 的对称点是P′（﹣x，﹣y）．13．（3分）2019女排世界杯于9月14月至29日在日本举行，赛制为单循环比赛（即每两个队之间比赛一场），一共比赛66场，中国女排以全胜成绩卫冕世界杯冠军，为国庆70周年献上大礼，则中国队在本届世界杯比赛中连胜11场．【分析】设中国队在本届世界杯比赛中连胜x场，则共有（x+1）支队伍参加比赛，根据一共比赛66场，即可得出关于x的一元二次方程，解之取其正值即可得出结论．【解答】解：设中国队在本届世界杯比赛中连胜x场，则共有（x+1）支队伍参加比赛，依题意，得：x（x+1）＝66，整理，得：x2+x﹣132＝0，解得：x1＝11，x2＝﹣12（不合题意，舍去）．故答案为：11．【点评】本题考查了一元二次方程的应用，找准等量关系，正确列出一元二次方程是解题的关键．14．（3分）一个不透明的口袋中装有一红一白两个小球，它们除颜色外完全相同，从口袋中随机摸出1个小球，记下摸出小球的颜色后，放回口袋摇匀；再从口袋中随机摸出1个小球，记下摸出小球颜色后，放回口袋摇匀；第三次从口袋中随机摸出1个小球，则三次摸出的小球恰好颜色相同的概率为．【分析】首先根据题意画出树状图，然后由树状图求得三次摸出的小球恰好颜色相同的情况，再利用概率公式即可求得答案．【解答】解：根据题意画出树状图：∵由树状图可知，共有8种等可能结果，三次摸出的小球恰好颜色相同的情况有2种情况，∴三次摸出的小球恰好颜色相同的概率为＝；故答案为：．【点评】此题考查了列表法或树状图法求概率．用到的知识点为：概率＝所求情况数与总情况数之比．15．（3分）如图，正六边形ABCDEF纸片中，AB＝6，分别以B、E为圆心，以6为半径画、．小欣把扇形BAC与扇形EDF剪下，并把它们粘贴为一个大扇形（B与E重合，F与A重合），她接着用这个大扇形作一个圆锥的侧面，则这个圆锥的高为2．【分析】根据正六边形的性质和弧长的公式即可得到结论．【解答】解：正六边形ABCDEF纸片中，∵∠B＝∠E＝120°，∵AB＝6，∴+的长＝×2＝8π，∴圆锥的底面半径＝＝4，∴圆锥的高＝＝2，故答案为：2．【点评】本题考查正多边形和圆，勾股定理，弧长的计算，正确的理解题意是解题的关键．16．（3分）如图，△ABC中，AB＝10，AC＝6，BC＝14，D为AC边上一动点（D不与A、C重合），将线段BD绕D点顺时针旋转90°得到线段ED，连接CE，则△CDE面积的最大值为15．【分析】如图，过点E作EF⊥AC于F，作BH⊥AC于点H，由勾股定理可求可求AH ＝5，由旋转的性质可求BD＝DE，∠BDE＝90°，由AAS可证△BDH≌△DEF，可得EF＝DH，由三角形面积公式和二次函数的性质可求解．【解答】解：如图，过点E作EF⊥AC于F，作BH⊥AC于点H，∴∠EFD＝∠BHD＝90°，∵BH2＝BC2﹣CH2，BH2＝AB2﹣AH2，∴196﹣（6+AH）2＝100﹣AH2，∴AH＝5∵将线段BD绕D点顺时针旋转90°得到线段ED，∴BD＝DE，∠BDE＝90°，∴∠BDF+∠EDF＝90°，且∠EAF+∠AEF＝90°，∴∠AEF＝∠BDF，且∠EFD＝∠BHD＝90°，BD＝DE，∴△BDH≌△DEF（AAS）∴EF＝DH，∵△CDE面积＝CD×EF＝（6﹣AD）×（5+AD）＝﹣（AD﹣）2+15∴△CDE面积的最大值为15，故答案为15；【点评】本题考查了旋转的性质，全等三角形的判定和性质，勾股定理，二次函数的性质等知识，添加恰当辅助线是本题的关键．三.解答题（共8小题，共计72分）17．（8分）解方程：x2﹣x﹣3＝0．【分析】根据方程的特点可直接利用求根公式法比较简便．【解答】解：a＝1，b＝﹣1，c＝﹣3∴x＝＝∴，．【点评】本题考查了解一元二次方程的方法，求根公式法适用于任何一元二次方程．方程ax2+bx+c＝0（a≠0，且a，b，c都是常数）的解为x＝（b2﹣4ac≥0）．18．（6分）如图A、B是⊙O上的两点，∠AOB＝120°，C是弧的中点，求证四边形OACB是菱形．【分析】连OC，由C是的中点，∠AOB＝l20°，根据在同圆或等圆中，相等的弧所对的圆心角相等得到∠AOC＝∠BOC＝60°，易得△OAC和△OBC都是等边三角形，则AC＝OA＝OB＝BC，根据菱形的判定方法即可得到结论．【解答】证明：连OC，如图，∵C是的中点，∠AOB＝l20°∴∠AOC＝∠BOC＝60°，又∵OA＝OC＝OB，∴△OAC和△OBC都是等边三角形，∴AC＝OA＝OB＝BC，∴四边形OACB是菱形．【点评】本题考查了圆心角、弧、弦的关系：在同圆或等圆中，相等的弧所对的圆心角相等．也考查了等边三角形的判定与性质以及菱形的判定．19．（8分）一个不透明的布袋里装有4个大小、质地均相同的乒乓球，球上分别标有数字1，2，3，4．（1）小萱随机从布袋中摸出一个乒乓球，记下数据后放回布袋里，摇匀后，再随机从布袋中摸出一个乒乓球，请用列表或画树状图的方式列出所有可能的结果，并求出“两个乒乓球上的数字之和不小于5“的概率．（2）随机从布袋中一次摸出两个乒乓球，直接写出“两个乒乓球上的数字至少有一个是偶数“的概率为．【分析】（1）画树状图展示所有16种等可能的结果数，再找出两个乒乓球上的数字之和不小于5的结果数，然后根据概率公式求解；（2）画树状图展示所有12种等可能的结果数，再找出两个乒乓球上的数字至少有一个是偶数的结果数，然后根据概率公式求解．【解答】解：（1）画树状图为：共有16种等可能的结果数，其中两个乒乓球上的数字之和不小于5的结果数为10，所以两个乒乓球上的数字之和不小于5的概率是：＝；（2）画树状图为：共有12种等可能的结果数，两个乒乓球上的数字至少有一个是偶数的结果数有10种，所以两个乒乓球上的数字至少有一个是偶数的概率是＝．故答案为：．【点评】此题考查的是用列表法或树状图法求概率；树状图法适合两步或两步以上完成的事件；解题时要注意此题是放回实验还是不放回实验．用到的知识点为：概率＝所求情况数与总情况数之比．20．（8分）如图，已知点A（﹣2，﹣1）、B（﹣5，﹣5）、C（﹣2，﹣3），点P（﹣6，0）．（1）将△ABC绕点P逆时针旋转90°得△A1B1C1，画出△A1B1C1，并写出点C的对应点C1的坐标为（﹣3，5）；（2）画出△ABC关于原点成中心对称的图形△A2B2C2，并写出点A的对应点A2的坐标为（1，1）；（3）把△A2B2C2向下平移6个单位长度得△A3B3C3，画出△A3B3C3，由图可知△A3B3C3可由△A1B1C1绕点Q逆时针旋转90°而得到，则点Q的坐标为（3，3）；【分析】（1）分别作出A，B，C的对应点A1，B1，C1即可．（2）分别作出A，B，C的对应点A2，B2，C2即可．（3）分别作出A1，B1，C1的对应点A3，B3，C3即可．对应点连线段的垂直平分线的交点即为所求的点Q．【解答】解：（1）如图△A1B1C1即为所求．点C的对应点C1的坐标为（﹣3，5）；故答案为（﹣3，5）．（2）如图△A2B2C2即为所求．点A的对应点A2的坐标为（1，1）；故答案为（1，1）．（3）如图△A3B3C3即为所求．由图可知△A3B3C3可由△A1B1C1绕点Q逆时针旋转90°而得到，则点Q的坐标为（3，3），故答案为（3，3）．【点评】本题考查作图﹣旋转变换，平移变换等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．21．（8分）如图，AB为 ⊙€O的一条弦，PB切 ⊙€O于B，P A＝PB，直线PO交AB 于E，交 ⊙O于点C．（1）求证：P A是 ⊙€O的切线；（2）若CD∥P A，CD交直线AB于点D，交 ⊙O于另一点F．①求证：AD＝CD．②若AB＝8，BD＝2，求 ⊙€O的半径长．【分析】（1）连接OA，OB．证明△P AO≌△PBO（SSS），推出∠P AO＝∠PBO＝90°即可解决问题．（2）①连接AC，想办法证明∠DAC＝∠DCA即可解决问题．②利用勾股定理求出EC，设OB＝OC＝r，在Rt△OBE中，利用勾股定理构建方程即可解决问题．【解答】（1）证明：连接OA，OB．∵PB是⊙O的切线，∴PB⊥OB，∴∠PBO＝90°，∵P A＝PB，PO＝PO，OA＝OB，∴△P AO≌△PBO（SSS），∴∠P AO＝∠PBO＝90°，∴P A⊥OA，∴P A是⊙O的切线．（2）①证明：连接AC．∵P A＝PB，OA＝OB，∴OP⊥AB，∴∠AEC＝90°，∵∠P AO＝90°，∴∠EAO+∠AOE＝90°，∠AOE+∠APO＝90°，∴∠EAO＝∠APO，∵AP∥CD，∴∠APO＝∠DCE，∴∠EAO＝∠DCE，∵OA＝OC，∴∠OAC＝∠OCA，∴∠EAO+∠OAC＝∠DCE+∠OCE，即∠DAC＝∠DCA，∴DA＝DC．②解：∵P A＝PB，OA＝OB，∴OP⊥AB，∴AE＝EB＝AB＝4，∵DC＝DA＝AB+BD＝10，DE＝BE+BD＝6，∠CED＝90°，∴EC＝＝＝8，设OB＝OC＝r，在Rt△OEB中，∵OB2＝EB2+OE2，∴r2＝42+（8﹣r）2，∴r＝5，∴⊙O的半径为5．【点评】本题属于圆综合题，考查了切线的判定和性质，全等三角形的判定和性质，解直角三角形，平行线的性质，等腰三角形的判定和性质等知识，解题的关键是正确寻找全等三角形解决问题，属于中考常考题型．22．（10分）某网点销售一种儿童玩具，每件进价30元，规定单件销售利润不低于10元，且不高于31元，试销售期间发现，当销售单价定为40元时，每天可售出500件，销售单价每上涨1元，每天销售量减少10件，该网点决定提价销售，设销售单价为x元，每天销售量为y件．（1）请直接写出y与x之间的函数关系式及自变量x的取值范围；（2）当销售单价是多少元时，网店每天获利8960元？（3）网店决定每销售1件玩具，就捐赠a元（2＜a≤7）给希望工程，每天扣除捐赠后可获得最大利润为8120元，求a的值．【分析】（1）根据原销售件数减去减少的件数即为所求；（2）根据销售利润等于单件利润乘以销售量即可求解；（3）根据单件利润减去捐赠数为最后单件利润，再根据销售利润等于单件利润乘以销售量即可求解．【解答】解：（1）由题意得，y＝500﹣10（x﹣40）＝﹣10x+900；即y与x之间的函数关系式为：y＝﹣10x+900（40≤x≤61）；（2）根据题意得，（﹣10x+900）（x﹣30）＝8960，解得：x1＝63，x2＝57，∵40≤x≤61，∴x＝57，答：当销售单价是57元时，网店每天获利8960元；（3）设每天扣除捐赠后可获得利润为W，根据题意得，W＝（﹣10x+900）（x﹣30﹣a）＝﹣10x2+（1200+10a）x﹣900（30+a）＝﹣10（x﹣）2+（a﹣60）2∵对称轴x＝60+a，40≤x≤61，2＜a≤7，∴61＜a+60≤63∴x＝61时，每天扣除捐赠后可获得最大利润为8120元，﹣10（x﹣）2+（a﹣60）2取得最大值8120∴（61﹣30﹣a）（900﹣10×61）＝8120，解得a＝3答：a的值为3．【点评】本题考查了二次函数的应用，难度较大，最大销售利润的问题常利用函数的增减性来解答．23．（12分）如图1，△ABC和△DEC都是等边三角形，点E在AC上．（1）求证：AD＝BE；（2）如图2，当CD＝AC时，将△DEC绕点C顺时针旋转30°，连接BD交AC于点G，取AB的中点F，连接FG①求证：BE＝2FG；②若△AFG的周长为9，求BC的长．【分析】（1）由“SAS”可证△ACD≌△BCE，可得AD＝BE；（2）①根据旋转角的定义，可以得到∠ACE＝30°，则∠GCD＝90°，则AC⊥BD，可证明△BTG≌△DCG，从而得到FG是△ABD的中位线，然后证明Rt△BCE≌Rt△ACD，利用三角形的中位线定理以及全等三角形的性质即可确定．②由等边三角形的性质和直角三角形性质可得AF＝AG＝×3TG＝TG，FG＝AF＝TG，由△AFG的周长为9，可求TG的长，即可求解．【解答】证明：（1）∵△ABC和△DEC都是等边三角形，∴AB＝AC＝BC，CD＝CE＝DE，∠ACB＝∠DCE＝60°，∴△ACD≌△BCE（SAS）∴AD＝BE；（2）过B作BT⊥AC于T，连AD，如图2，∵CE绕C顺时针旋转30°，∴∠ACE＝30°，∴∠GCD＝90°，由勾股定理可得BT＝AB，又∵CD＝CE＝AB，∴BT＝CD．在△BTG和△DCG中，，∴△BTG≌△DCG（AAS），∴BG＝DG，TG＝CG，∵F是AB的中点．∴FG∥AD，FG＝AD．则在Rt△BCE和Rt△ACD中，∴Rt△BCE≌Rt△ACD（SAS）．∴BE＝AD，∴BE＝2FG．②∵△ABC是等边三角形，BT⊥AC，∴AT＝CT＝AC，∵TG＝CG，∴AC＝4TG，AG＝3TG，∴CD＝AC＝2TG＝CE，∴BE＝＝2TG，∵Rt△BCE≌Rt△ACD，∴BG＝GD，AD＝BE＝2TG，又∵AF＝BF，∴FG∥AD，∴FG＝AD＝TG，∵△AFG的周长为9，∴AG+AF+FG＝3TG+2TG+TG＝9，∴TG＝，∴BC＝AC＝4TG＝10﹣2．【点评】本题是几何变换综合题，考查了全等三角形的判定和性质，直角三角形的性质，三角形中位线定理，等边三角形的性质等知识，添加恰当辅助线构造全等三角形是本题的关键．24．（12分）如图，抛物线y＝a（x2﹣2mx﹣3m2）（其中a，m为正的常数）与x轴交于点A，B，与y轴交于点C（0，﹣3），顶点为F，CD∥AB交抛物线于点D．（1）当a＝1时，求点D的坐标；（2）若点E是第一象限抛物线上的点，满足∠EAB＝∠ADC．①求点E的纵坐标；②试探究：在x轴上是否存在点P，使以PF、AD、AE为边长构成的三角形是以AE为斜边的直角三角形？如果存在，请用含m的代数式表示点P的横坐标；如果不存在，请说明理由．【分析】（1）根据题意将a＝1，C（0，﹣3）代入y＝a（x2﹣2mx﹣3m2），进而求出m的值，即可得出答案；（2）①表示D点坐标，得出∠EAB＝∠BAD，则x轴平分∠BAD，可得出点D关于x 轴的对称点一定在直线AE上，求出直线AE的解析式，联立直线AE和抛物线解析式可得出点E的坐标．②由①知E点的坐标，得出F（m，﹣4）、A（﹣m，0）、D（2m，﹣3），再利用PF，AD，AE的关系得出答案．【解答】解：（1）当a＝1时，y＝a（x2﹣2mx﹣3m2）＝x2﹣2mx﹣3m2，∵与y轴交于点C（0，﹣3），∴﹣3m2＝﹣3，解得：m＝±1，∵m＞0，∴m＝1，∴抛物线解析式为：y＝x2﹣2x﹣3＝（x﹣1）2﹣4，∵CD∥AB，∴C，D关于直线x＝1对称，∴D点坐标为：（2，﹣3）；（2）①对于y＝a（x2﹣2mx﹣3m2），当y＝0，则0＝a（x2﹣2mx﹣3m2），解得：x1＝﹣m，x2＝3m，当x＝0，y＝﹣3am2，可得：A（﹣m，0）、B（3m，0），C（0，﹣3am2），∵抛物线过点C，∴﹣3am2＝﹣3，则am2＝1，∵CD∥AB交抛物线于点D，∴∠ADC＝∠BAD，∴点D与点C关于抛物线的对称轴x＝m对称，∴D（2m，﹣3），∵∠EAB＝∠ADC，∴∠EAB＝∠BAD，∴x轴平分∠BAD，∴点D关于x轴的对称点D'（2m，3）一定在直线AE上，∴直线AD′的解析式为：y＝x+1，联立，整理得x2﹣3mx﹣4m2＝0，解得x1＝4m，x2＝﹣m（舍去），∴E点的横坐标为4m，∴y＝．∴点E的纵坐标为5．②存在，理由：当x＝m时，y＝a（m2﹣2m2﹣3m2）＝﹣4am2＝﹣4，∴F（m，﹣4），∵E（4m，5）、A（﹣m，0）、D（2m，﹣3），设P（b，0），∴PF2＝（m﹣b）2+16，AD2＝9m2+9，AE2＝25m2+25，∴（m﹣b）2+16+9m2+9＝25m2+25，解得：b1＝﹣3m，b2＝5m∴P（﹣3m，0）或（5m，0）．【点评】本题是二次函数综合题，考查了二次函数性质、两点间的距离公式、轴对称的性质及函数图象上点的坐标性质等知识，理解用好函数思想和方程思想得出E点坐标是解题关键．。
2020武汉元调数学试卷及答案(Word精校版)
第1页 / 共12页2019-2020学年度武汉市部分学校九年级元月调考数学试卷一、选择题(共10小题，每小题3分，共30分)1.将一元二次方程2514x x 化成一般形式后，二次项系数和一次项系数分别是( ) A ．5，-1 B ．5，4 C ．5，-4 D ．5，12.下列四张扑克牌的牌面，不是中心对称图形的是( )A ．B ．C ．D ．3.抛物线22y x 与22yx 相同的性质是( ) A ．开口向下 B ．对称轴是y 轴 C ．有最低点 D ．对称轴是x 轴4.一个不透明的袋子中只有4个黑球，2个白球，每个球除颜色外都相同，从中任意摸出3个球，下列事件为必然事件的是( )A ．至少有1个球是黑球B ．至少有1个球是白球C ．至少有2个球是黑球D ．至少有2个球是白球5.已知O 的半径等于3cm ，圆心O 到点P 的距离为5cm ，那么点P 与O 的位置关系是( ) A ．点P 在O 内 B ． 点P 在O 外 C ．点P 在O 上 D ．无法确定6.要将抛物线2y x 平移后得到抛物线223y x x ，下列平移方法正确的是( ) A ．向左平移1个单位，再向上平移2个单位 B ．向左平移1个单位，再向下平移2个单位 C ．向右平移1个单位，再向上平移2个单位 D ．向右平移1个单位，再向下平移2个单位7.如图，将△ABC 绕顶点C 逆时针旋转角度得到A B C ，且点B 刚好落在A B 上，若∠A =28°，BCA =43°，则等于( )A ．36°B ．37°C ．38°D ．39°8.小明上学要经过三个十字路口，每个路口遇到红灯、绿灯的可能性都相等，小明上学经过三个路口时，不全是红灯的概率是( )A ．38 B ． 12 C ． 58 D ． 789.如果m 、n 是一元二次方程24x x +=的两个实数根，那么多项式222n mn m --的值是( )A ．16B ．14C ．10D ．610.如图，△ABC 的两个顶点A ，B的O 上，∠A =60°，∠B =30°.若固定点A ，点B 在O 上运动，则OC 的最小值是( )A第2页 / 共12页A ．B ．C ．D ．二、填空题(本大题共6个小题，每小题3分，共18分)11.在平面直角坐标系中，点P (1，2)关于原点对称的点坐标是________. 12. 一个盒子中有10枚黑棋子和若干枚白棋子，这些棋子除颜色外无其他差别，从盒中随机取出一枚棋子，记下颜色，再放回盒子中，不断重复上述过程，一共取了300次，其中有100次取到黑棋子，由此估计盒中约有________枚白棋子.13.如图，四边形ABCD 是⊙O 的内接四边形，∠BOD =100°，∠BCD 的大小是 .14.为响应全民阅读活动，某校面向社会开放图书馆，自开放以来，进馆人次逐月增加，第一个月进馆200人次，前三个月累计进馆872人次，若进馆人次的月增长率相同，为求进馆人次的月增长率，设进馆人次的月增长率为x ，依题意可列方程为 .15.已知二次函数()20y ax bx c c =++<的图像开口向上，对称轴为直线1x =，下列结论中，一定正确的 是 (填序号即可).①0b <； ②420a b c ++<； ③a c b +>； ④()a b t at b +≤+(t 是一个常数).16.我国魏晋时期的数学家刘徽首创“割圆术”，利用圆的内接正多边形逐步逼近圆来近似计算圆的周长，进而确定圆周率，某圆半径为R ，其内接正十二边形的周长为C ． 若R ，则C = ，2CR≈ ，(结果精确到0.01 2.449≈ 1.414≈).三、解答题(共8题，共72分)17.(本题8分)若关于x 的一元二次方程x 2+2x +m =0有两个相等的实数根，求m 的值及此时方程的根.B第3页 / 共12页18. (本题8分)如图，A ．B ．C 三点在半径为1的O 上，四边形ABCD 是菱形，求的长.19. (本题8分)在5种同型号的产品中，有1件不合格品和4件合格品. (1)从这5件产品中随机选取1件，直接写出抽到合格品的概率； (2)从这5件产品中随机选取2件，求抽到都是合格品的概率.20.(本题8分)请仅用无刻度的直尺完成下列画图，不写画法，保留画图痕迹(用虚线表示画图过程，实线表示画图结果). (1)如图(1)，P 是平行四边形ABCD 边AD 上一点，过点P 画一条直线把这个四边形分成面积相等的两部分； (2)如图(2)，五边形ABCDE 是正五边形，画一条直线把这个五边形分成面积相等的两部分； (3)如图(3)，△ABC 的外接圆的圆心是点O ，D 是的中点，画一条直线把△ABC 分成面积相等的两部分.(1)(2)(3)AED CBAD21.(如图8分)如图，P A，PB 分别与O相切于A，B两点，AC 是O的直径，AC=AP，连接OP交AB于点D，连接PC 交O于点E，连接DE.(1)求证：△ABC≌△PDA；(2)求BDDE的值.22.(本题10分)某公司经过市场调查，整理出来某种商品在某个月的第x天的销售价与销售量的相关信息如(1)求y与x的函数关系式；(2)问销售该商品第几天时，日销售利润为2250元？(3)问在当月有多少天的日销售利润不低于2400元，请直接写出结果.第4页 / 共12页23.(本题10分)问题背景：如图(1)，在四边形ABCD中，若BC=CD，∠BAD=∠BCD=90°，则AC平分∠BAD，小明为了证明这个结论，将△ABC绕点C顺时针旋转90°，请帮助小明完成他的作图.迁移应用：如图(2)，在五边形ABCDE中，∠A=∠C=90°，AB=BC，AE+CD=DE，求证：BD平分∠CDE.联系拓展：如图(3)，在Rt△ABC中，AC=BC，若点D满足1013AD AB，BD=AB，点P是AD的中点，直接写出PCAB的值.(1) (2) (3)BB第5页 / 共12页24.(本题12分)如图，在平面直角坐标系中，圆心为P(x，y)的动圆经过点A(m，2m+4)(m＞-2)，且与x轴相切于点B．y与x之间存在一种确定的函数关系，其图象是一条常见的曲线，记做曲线F.(1)如图(1)，①当y=32时，直接写出P的半径；②当m=-1，x=-2时，直接写出P的半径.(2)求曲线F最低点的坐标(用含有m的式子表示)；(3)如图(2)，若曲线F最低点总在直线y=12x+3的下方，点C(-2，y1)，D(1，y2)都在曲线F上，试比较y1与y2的大小.3第6页 / 共12页第7页 / 共12页2019-2020学年度武汉市部分学校九年级元月调考数学试卷参考答案9.答案：B 解析：∵m ，n 为方程x ²+x =4的解∴m +n =-1；mn =-4，且代n 到原式，得n ²=4-n∴原式=2(4-n )-mn -2m =8-2n -2m -mn =8-2(m +n )-mn =8+2+4 =1410.答案：A 解析：延长BC 交圆O 与D ，连O D ．取AD 的中点E ，连OE ，连CE ∵ ∠B =30°，∴∠DOA =60°，∴△DAO 为等边三角形 ∵3OA ，∴3AD∵∠DCA =90°，∴点C 在以点E为半径的圆上运动∵OC OE CE ，∴3322OC ，故答案选A二、填空题(本大题共6个小题，每小题3分，共18分) 11. ()1,2-- 12.20 13.130°14.()()220020012001872x x ++++=15.①②④16.答案：24； 3.1116.解析：过C 作CD ⊥AB 于D ， 正十二边形中心角∠CAD =30°B第8页 / 共12页∴12CD AC ==AD ==，BD AB AD =- 在Rt △CDB中，2CB =，∴24C =， 3.112CR≈三、解答题(共8题，共72分) 17. m =1，方程的根为x 1=x 2=-118. 23π19.(1)45；(2)3520. (1)(2)(作法不唯一)(3)21. 证明：(1)∵P A 为O 切线，∴∠P AO =90° ∵AC 为O 直径，∴∠ABC =90°∴∠BAC +∠ACB =∠BAC +∠P AD ，∴ ∠ACB =∠P ADBE第9页 / 共12页∵P A ，PB 为O 切线，∴P A =PB∵OA =OB ，P A =PB ，∴OP ⊥AB ，∴∠ADP =90° 在△ABC 和△PDA 中 ∠=∠=⎧⎪⎨⎪⎩=∠∠ACB PAD AC PA ABC PDA ∴△ABC ≌△PDA (AAS )解:(2)连接AE ，连接BE 交DP 于点F ∵∠ADO =∠ABC =90°，∴OP ∥BC ，∴∠BCE =∠FPE ，∵AC 为直径，∴∠AEC =90°， ∵∠P AO =90°，AC =AP ，∴∠ACE =45°，CE =PE 在△CEB 和△PEF 中 ∠=∠=∠⎧⎪⎨⎩=∠⎪BCE FPE CE PECEB PEF ∴△CEB ≌△PEF (ASA ) ∴BE =FE∵∠ABE =∠ACE =45°，∠BDP =∠ADP =90°，∴BD =DF 在Rt △BDF 中，222+=BD DF BF ，∴222=BD BF ，∴BF∵BE =EF ，∴BDDE22. 解：(1)y =[(x +40)-20](100-2x ) ,∴y =-2x 2+60x +2000 (2)由(1)知y =-2x 2+60x +2000当日销售利润为2250元时，有-2x 2+60x +2000=2250 解得：x 1=5； x 2=25故该销售商品第5天或第25天时，日销售利润为2250元. (3)11天当销售利润为2400时，有-2x 2+60x +2000=2400 解得：x 1=10； x 2=20 由二次函数图像性质可知：共有11天(第10天到第20天)，销售利润不低于2400元.23. (1) 解：第10页 / 共12页(2) 证明：延长DC 至点F ，使CF =AE ，连接BE ，BF在△ABE 和△CBF 中 ==BCF =AB BC A AE CF ⎧⎪⎨⎪⎩∠∠ ∴△ABE ≌△CBF (SAS )，∴BE =BF 又∵DE =AE +CD 且AE =CF ，∴DE =DF 在△BDE 和△BDF 中 BE BF DE DF BD BD =⎧⎪=⎨⎪=⎩∴△BDE ≌△BDF (SSS )∴∠BDE =∠BDF ，∴BD 平分∠CDE (3)①当D 在AB 左侧时连接CP ，过点C 作CE ⊥CP ，交DA 的延长线于E 点∵AB =BD ，且P 是AD 的中点，∴BP ⊥AD ，即∠CBP =∠CAE∵AD =1013AB ，∴AP =12AD =513AB ，BP1213AB∵=ACE PCB ∠∠，在△BCP 和△ACE 中第11页 / 共12页CBP CAE BC ACBCP ACE =⎧⎪=⎨⎪=⎩∠∠∠∠ ∴△BCP ≌△ACE (ASA )∴AE =PB =1213AB ，PE =AP +AE =1713AB ∵PC =CE ，PC ⊥CE ，∴△PCE 为等腰直角三角形PCPE，即PC AB ②当D 在AB 右侧时连接CP ，过点C 作CQ ⊥CP 交BP 于点Q由①可知：∠APB =∠ACB =90°，AP =513AB ，PB =1213AB ∵PC ⊥CQ ，∴∠PCQ =∠ACB =90°，∴∠ACP =∠BCQ ∵∠APB =∠ACB ，∴∠CAP =∠CBQ在△ACP 和△BCQ 中CAP CBQ AC BCACP BCQ =⎧⎪=⎨⎪=⎩∠∠∠∠ ∴△ACP ≌△BCQ (ASA )∴BQ =AP =513AB PQ =BP -BQ =713AB ，PC =PQ ∵PC ⊥CQ ，∴△PCQ 为等腰直角三角形∴PCPQAB ，即PC = 综上所述：PC AB =24.解：(1)①32②54(2)依题意得：PB =P Ay = B D第12页 / 共12页 ()()22224y y m x m ---=-，∴()()21242y x m m m =-+++， 即顶点(m ，m +2)(3)方法一：顶点(m ，m +2)在直线y =x +2运动 又∵最低点一直在132y x =+下方，x +2＜132x +，即m ＜2，∴-2＜m ＜2 ∵C (-2，y 1)，D (1，y 2)，∴()()212242m y m m +=+++，()()221242m y m m =+++－ ()()()()()2212213214242m m m y y m m +--+-==++，令y 1=y 2，解得12m =- ①当-2＜m ＜12－时，()()32142m m ++＜0 ，即y 1-y 2＜0，故y 1＜y 2； ②当12m =-时，()()32142m m ++=0，y 1=y 2； ③当-12＜m ＜2时，()()32142m m ++＞0，y 1＞y 2. 综上①当-2＜m ＜12－时，y 1＜y 2；②当12m =-时，y 1=y 2；③当-12＜m ＜2时，y 1＞y 2. 方法二：(3)函数值的大小可以比较点到对称轴的距离当m =12－时，y 1=y 2 ；当-2＜m ＜12－时，y 1＜y 2 ；当-12＜m ＜2时，y 1＞y 2.。
2020武汉九年级元调英语试题及答案
2020武汉九年级元调英语试题及答案26、、 He might have read it、A、I don’t agreeB、 No problemC、You can’t do thatD、You’d better not27、Smith felt that he knew everybody’s duty better than they knew it 、A、 itselfB、 themselvesC、 oneselfD、 himself28、、A、 With pleasureB、I’m so happyC、 Pleased to meet youD、Oh, that’s very nice of you29、 Yes, I bought this watch here last Sunday, butit 、A、didn’t workB、won’t workC、doesn’t workD、hadn’t work30、 No, mine there behind the door、A、 is hangingB、 has hungC、 hangsD、 hung31、- Excuse me! Could you please move your bike a little? It’s the way、 How could she her body on one hand? We hope this book will act as a between doctor and patient、How was the concert last night? What’s wrong with you, Ellen? You don’t look fine、 Could I ask your neighbors for help, Tom? Can John and Jane speak French? Can you tell me at the party?-- his love for life was gone、I asked Dad to live with me on my small farm,hoping the fresh air could42 him、 Within a week after he moved in, I43 the invitation- he was unsatisfied with everything I did、One day, I read an article saying pet dogs would44 some difference、 So I drove to the animal shelter、As soon as I got there, a dog’ s45 caught my attention、A staff member sai d, “His name is up tomorrow, for we don’t have much46 for every unclaimed（无人认领的）dog、”“You mean you’re going to47 him?” I turned to the man, then I said, “I’ll take him、”I drove home with the dog、 I was helping it out of the car when Dad walked onto the front porch、“Look at what I got you!”I said excitedly、Dad’s face48 、“I don’t want it、” he said, turning back towards the49 、 Then, suddenly, the dog50 free from my grasp、 He sat down in front of Dad、Dad came to feel51 , and soon he was hugging the dog、This was the beginning of a warm52 、 Dad named the dog Alvin、 Together, they spent long hours walking down the woods and got53 on the banks of the river、Then, late one night two years later, I felt Alvin’s cold54 searching through my bed covers- he’d never com e into my bedroom before at night、So I quickly ran into Dad’s room, and just found that he had passed away、Two days later, my shock and sadness deepened when I discovered Alvin lying55 , beside Dad’s bed、 As I put him under the ground near their favorite river, I silently thanked the dog for rebuilding Dad’s peace of mind、41、A、 remainedB、 diedC、 continuedD、 appeared42、A、 feedB、 comfortC、 saveD、 help43、A、 regrettedB、 refusedC、 copiedD、 accepted44、A、 tellB、 solveC、 makeD、 change45、A、 ownerB、 eyesC、 bodyD、 house46、A、 roomB、 energyC、 knowledgeD、 information47、A、 keepB、 sellC、 killD、 return48、A、 shoneB、 cloudedC、 movedD、 ached49、A、 dogB、 carC、 riverD、 house50、A、 setC、 pulledD、 stayed51、A、 lonelyB、 healthyC、 disappointedD、 pleased52、A、 talkB、 welcomeC、 friendshipD、 day53、A、 frightenedB、 relaxedC、 boredD、 excited54、A、 noseB、 faceC、 head55、A、 illB、 aliveC、 deadD、 sad四、阅读理解A56、 According to the advertisement, the advantages of the four tour sights connect with 、A、 visits or callsB、 U、S、 dollarsC、 beach lifeD、 plane flights57、 If you want to have Grand Circle Island tour, you will 、A、 have to pay more moneyB、 have private airport transfersC、 enjoy dinner at BazaarD、 have to book flight tickets today58、25％ off food and beverages are offered at 、A、 Warwick FijiB、 Mantra on ViewC、 Centara Karon Resort PhuketD、 The Laylow Autograph Collection59、 How many airlines will cut down the prices of flight tickets for two people together?A、4B、3C、2D、160、 If you choose your next WORLD BEACH ESCAPE, you can have 、A、 all half pricesB、 lowest pricesC、 free dinnersD、 free additional resortsBA group of high school students from the United States has planted hope by cleaning up an empty lot in their neighborhood、The students are from Buchtel High School in Akron, Ohio、The empty lot, which is owned by a local bank, was filled with grass and poison ivy、 As a project for theschool’s biohealth（生物健康）class, eight students decided to turn the lot into a space that will improve the mental（心理的）and emotional health of people who live near it、They first came up with a design, didresearch and created3D models of their plan、 Ideas were then presented and judgers picked the winning plans、Finally, the students brought those plans to life、Now when walk onto the lot, you can see a wood walkway leading to a purple iron bench、 A few beautiful plants are already in the ground、 There is also a hopscotch（跳房子游戏）board that is painted bright blue、 A wall painting with the words “Love” and “Peace” has taken shape on a back fence, dotted with the students’ handprints、 The rest of the fence was painted grey to cover plain wood、The students said they painted the bench purple because they found that purple has a comforting effect on people、 They thought kids could go there and sit together, exchange ideas and stay out of trouble、As for the hopscotch board, it was set up for a group of8 to10 school – age kids who lived in the neighborhood but had no where to play、“It gives the neighborhood a little hope and a little beauty,” said Lyle Jenkins, a member of the Neighborhood Network、“A lot of people love the neighborhood and have great hopes for things getting better、”61、Before the students’ plans came true, they hadto 、A、 plant many kinds of plantsB、 present their plans to be judgedC、improve people’s health first、D、 build up a wood walkway62、 The students had their plans about the empty lot because of 、A、 a local bankB、 the neighborhoodC、 a particular projectD、 grass and poison ivy63、 The iron beach was painted purple for 、A、 people to have a comfortable placeB、 kids to play togetherC、 students themselves to exchange ideas、D、 the neighborhood to remember64、 From what Lyle Jenkins said, we learn that people of neighborhood were 、A、 upsetB、 seriousC、 helpfulD、 satisfied65、 The best title for the reading should be 、A、 Nice NeighborhoodB、 School ProjectC、 Love and HopeD、 Health and SuccessCWhenever I look at this photo, I think of an afternoon fishing with my grandfather、 My grandfather loves fishing、 My grandfather lovesfishing、When we were younger, he tried to get my brother and I excited about it、“It’s a wonderful way to spend the afternoon together,” he t old us、 Every Saturday he asked us to go with him、 At first we would, but fishing seemed so boring to us、 At last we told him that fishing wasn’t our thing、One Saturday afternoon not long ago, I changed my mind and decided to go with him、 I thought that maybe I would enjoy fishing more now that a few years have passed、 So down to the water we went、 We got in the water, threw the line, and waited、 And waited、After three hours all we had was a single tiny fish、“Grandpa, why do you like standing out here for hours like this?” I asked、“You’ve done nothing all afternoon!”“Well,” he said, “When I was a boy,fishing wasn’t ‘nothing’、 In fact, it was everything、I didn’t have TV, or video games, or smartphones、 So I fished、 Now, when I fish, I go back to being that boy、 It was a happy time、” This photo really changed how I see my grandfather、 He is the man who has seen many changes and has had many experiences、Looking at the photo also reminds me that opinion of fishing changed that afternoon、 Right after I took the picture, Grandpa felt a strong pull on his line、 In a few seconds the two of us were struggling to bring in the biggest fish I had ever seen! It was really exciting、From then on I went fishing with him whenever I could、66、 The writer decided to go fishing with his grandpa one day because 、A、 it was Saturday againB、his brother wouldn’t goC、he knew he’d catch a single tiny fishD、 he came up with a different idea67、For the writer’s grandpa, fishing is 、A、 a wonderful way to be with othersB、 part of his lifeC、 not much fun without the writerD、 meaningless without a smartphone68、 It is clear that 、A、 the writer used to live and fish with grandpaB、the writer’s brother had no interest in fishingC、 Grandpa likes thinking in the water for long hoursD、 Grandpa always shows his fishing skills to others69、The underlined words “that boy” refers to 、A、 the writerC、 Grandpa himselfB、the writer’s brotherD、 nobody70、 We can infer that the writer 、A、 always catches more fish than GrandpaB、 took a picture whenever he went fishingC、 became a good fishing partner of GrandpaD、 he himself would teach others how to fish六、阅读理解填词Many years ago Mrs、 Hill moved back to Australia and settled down in a small town near a big farm、On ahot Saturday afternoon when she did all the things around the house, Mrs、 Hill went to her small shop、 That was her small b 、 She opened the only window of the shop andlooked outside、 She p to see the green farm in front、There were many cows, horses and small a on the farm、 At this time she saw a kangaroo coming towards her and stopped under her window、 It was interesting to see that it was wearing an old jacket、 It looked so c 、 Mrs、Hill felt it strange that the kangaroo came to her shop、It was c to be hungry!Then Mrs、 Hill went to f some bread and water and gave then to it、 The kangaroo soon had them all、 Then it became happy and jumped away、Suddenly something dropped on the grass from the jacket pocket、 It was a w ! She picked it up, opened it and found there was ﹩300 and a photo in it、 That was a man’s photo with his name “Bob” on it、 Bob? She looked more carefully and r she had a brother many years ago、 His name was also Bob、“Is this man my l brother?” she thought、 She took the photo with her and began to look for the man、 She asked many people in the town for information, but there was no r 、Then she came to the farm and asked one farmer、 To her surprise, she found the man was her brother Bob、 They hugged each other and could not say a word、七、书面表达英语老师委托你组织一场“新年联欢会”，请用英语起草一则口头通知。
【2020精品中考数学提分卷】武汉市初三元调数学试卷-+答案
2020年武汉市元月调考数学试卷一.选择题(共10小题，每小题3分，共30分) 1.方程x (x -5)=0化成一般形式后，它的常数项是 A ．-5B ．5C ．0D ．12.二次函数y =2(x -3)2-6 A ．最小值为-6 B ．最大值为-6 C ．最小值为3D ．最大值为33.下列交通标志中，是中心对称图形的是A ．B ．C ．D ．4.事件①：射击运动员射击一次，命中靶心；事件②：购买一张彩票，没中奖，则 A ．事件①是必然事件，事件②是随机事件. B ．事件①是随机事件，事件②是必然事件. C ．事件①和②都是随机事件. D ．事件①和②都是必然事件.5.投掷一枚质地均匀的硬币，正面朝上的概率为0.5，下列说法正确的是 A ．连续投掷2次必有1次正面朝上. B ．连续投掷10次不可能都正面朝上. C ．大量反复投掷每100次出现正面朝上50次. D ．通过投掷硬币确定谁先发球的比赛规则是公平的.6.一元二次方程20x m ++=有两个不相等的实数根则A ．3m >B ．3m =C ．3m <D ．3m ≤7.圆的直径是13cm ，如果圆心与直线上某一点的距离是6.5cm ，那么直线和圆的位置关系是 A ．相离B ．相切C ．相交D ．相交或相切8.如图，等边△ABC 的边长为4，D ，E ，F 分别为边AB ，BC ，AC 的中点，分别以A ，B ，C 三点为圆心，以AD 长为半径作三条圆弧，则图中三条圆弧的弧长之和是 A ．πB ．2πC ．4πD ．6π9.如图，△ABC 的内切圆与三边分别相切于点D ，E ，F ，则下列等式：①∠EDF=∠B ，②2∠EDF=∠A+∠C ，③2∠A=∠FED+∠EDF ，④∠AED+∠BFE+∠CDF=180°，其中成立的个数是 A ．1个B ．2个C ．3个D ．4个10.二次函数y=-x2-2x+c 在32x -≤≤的范围内有最小值-5，则c 的值是 A ．-6 B ．-2 C ．2 D ．3二.填空题(共6小题，每小题3分，共18分)11.一元二次方程20x a -=的一个根是2，则a 的值是_____ .12.把抛物线22y x =先向下平移1个单位，再向左平移2个单位，得到的抛物线的解析式是______________.13.一个不透明的口袋中有四个完全相同的小球，把它们分别标记为1，2，3，4.随机摸取一个小球然后放回， 再随机摸出一个小球，两次取出的小球标号的和为5的概率是___________.14.设计人体雕像时，使雕像的上部(腰以上)与下部(腰以下)的高度比，等于下部与全部(全身)的比，可以增加视觉美感，按此比例，如果雕像的高为2m ，那么上部应设计为多高？设雕像的上部高为x m ，列方程，并化成一般形式为____________.15.如图，正六边形ABCDEF 中，P 是边ED 的中点，连接AP ，则APAB ＝___________BB16.在O 中，AB 所对的圆心角108AOB ∠=︒，点C 为O 上的动点，以AO ，AC 为边构造AODC ，当∠A= °时，线段BD 最长.三.解答题(共8小题，共72分)17. (本题8分)解方程230x x +-=18. (本题8分)如图在O 中，半径OA 与弦BD 垂直，点C 在O 上，∠AOB=80°. (1)若点C 在优弧BD 上，求∠ACD 的大小； (2)若点C 在劣弧BD 上，直接写出∠ACD 的大小.19.(本题8分)甲，乙，丙三个盒子中分别装有除颜色以外都相同的小球，甲盒中装有两个AA球，分别为一个红球和一个绿球，乙盒中装有三个球，分别为两个绿球和一个红球；丙盒中装有两个球，分别为一个红球和一个绿球，从三个盒子中各随机取出一个小球.(1)请画树状图，列举所有可能的结果；(2)请直接写出事件“取出至少一个红球”的概率.20. (本题8分)如图，在平面直角坐标系中有点A(-4，0)，B(0，3)，分别为C，D．(1)当a=-4时，①在图中画出线段CD，保留作图痕迹；②线段CD向下平移_______个单位时，四边形ABCD为菱形；(2)当a=______时，四边形ABCD为正方形.21. (本题8分)如图，点D在⊙O的直径AB的延长线上，CD切⊙O于点C，AE⊥CD于点E.(1)求证：AC 平分∠DAE. (2)若AB=6，BD=2，求CE 的长.22. (本题10分)投资1万元围一个矩形菜园(如图)，其中一边靠墙，另外三边选用不同材料建造.墙长24m ，平行于墙的边的费用为200元/m ，垂直于墙的边的费用为150元/m.设平行于墙的边长为xm.(1)设垂直于墙的一边长为y ，请直接写出y 与x 之间的函数关系式. (2)若菜园面积为384m2，求x 的值. (3)求菜园的最大面积.23. (本题10分)如图，点C 为线段AB 上一点，分别以AB ，AC ，CB 为底作顶角为120°的A等腰三角形，顶角顶点分别为D ，E ，F ，(点E ，F 在AB 的同侧，点D 在另一侧). (1)如图1，若点C 是AB 的中点，则∠AED=__________； (2)如图2，若点C 不是AB 的中点， ①求证：△DEF 为等边三角形；②连接CD ，若∠ADC=90°，AB=3，请直接写出EF 的长.24.(本题12分)已知抛物线22y ax x c =++与x 轴交于A(-1，0)，B(3，0)两点，一次函数y=kx+b 的图象l 经过抛物线上的点C(m ，n).AA(1)求抛物线的解析式；(2)若m=3，直线l与抛物线只有一个公共点，求k的值；(3)若k=-2m+2，直线l与抛物线的对称轴相交于点D，点P在对称轴上，当PD=PC时，求点P的坐标.2020年武汉市元月调考数学试卷解析一.选择题9.如图：①∵∠EOF=2∠EDF ，∠EOF+∠B=180°， ∴2∠EDF+∠B=180°所以①错误 ②∵∠EOF=2∠EDF ，∠EOF+∠B=180°， ∠A+∠B+∠C=180°，∴2∠EDF=∠A+∠C 所以②正确③∵∠EDF+∠DEF=2x+y+z=90°+x ，∵∠A+∠EOD=180°，∴∠A=180°-2(y+z)=2x ， ∴2(∠EDF+∠DEF)-180°=∠A 所以③错误④∠AED+∠BFE+∠CDF=90°-x+90°-y+90°-z =270°-(x+y+z)=270°-90°=180° 所以④正确二.填空题11. 4 12. 2287y x x =++13. 1414. 2-640x x +=15.16.27°16.延长AO 与O 交于点P ，连接DP ，如图，则 O CAO D P ∆∆≌ DP OC ∴=，即点D 的运动轨迹是以点P 为圆心，OC 长为半径的圆.如图所示，连接BP ，BP 与P 的交点记作'DPD’BOACBBD 最大值为'BD ，此时1'272A POD APB ∠=∠=∠=三.解答题17.1x，1x =18. (1)∵OA ⊥BD ， ∴AB =AD ，∴∠ACD=12∠AOB=40°(2)40°或140°19.(1)由题意可得如下树状图，由图可知共有12种等可能的情况.(2)5620. (1)如图所示 (2)2(3)72-21.(1)证明：连OC∵CD 与⊙O 切于点C ， ∴OC ⊥DE ，∠OCD=90°∵AE ⊥DE ， ∴∠E=90°，∴∠OCD=∠E=90°，∴OC//AE ， ∴∠1=∠2 ∵OC=OA ， ∴∠1=∠3， ∴∠2=∠3， ∴AC 平分∠DAE (2)解：作CH ⊥OD ∵AB=6， ∴AO=OB=OC=3∵AC 平分∠DAE ，CH ⊥OD ，CE ⊥AE ， ∴CE=CH∵∠OCD=90°， ∴∵OCD S ∆=12OC ·CD=12OD ·CH ， ∴CH=125， ∴CE=12522. (1)由题意可知： 200x+150⨯2y=10000化简得：210033y x =-+∴y 与x 之间的函数关系式210033y x =-+(024x ＜≤) (2)210038433x x ⎛⎫-+= ⎪⎝⎭整理得：()22549x -=解得：x1=18，x2=32 ∵024x ＜≤ ∴x=18即菜园面积为384m2，x 的值为18. (3)设菜园的面积SS=210033x x ⎛⎫-+ ⎪⎝⎭=()2212502533x --+∵203-＜，开口向下对称轴x=25∴当024x ＜≤时，y 随x 的增大而增大. ∴当x=24时，S 的最大值为416. 所以，菜园的最大面积为416 m2 23. (1)90°(2)①证明：延长AE 、BF 交于G ，连DG.易证四边形ADBG 为菱形，△ADG 为等边三角形，四边形EGFC 为平行四边形. 可证∠DAE=∠DGF=60°，AE=CE=GF. 在△ADE 和△GDF 中.DA DG DAE DGF AE GF =⎧⎪∠=∠⎨⎪=⎩∴△ADE ≌△GDF(SAS)∴DE=DF ，∠ADE=∠GDF∴∠EDF=∠EDG+∠GDF=∠EDG+∠ADE=∠ADG=60°∴△EDF 为等边三角形.②EF=24. (1)将A(-1，0)，B(3，0)代入22y ax x c =++中得： 02096a c a c =-+⎧⎨=++⎩解得：a ＝-1，c ＝3∴抛物线的解析式为223y x x =-++ (2)当m ＝3时，n ＝-9+6+3=0， ∴C(3，0)， 将点C 代入y ＝kx+b 中得： 0=3k+b ， ∴b=-3k ，∴l 的解析式为y ＝kx-3k联立：2323y kx k y x x =-⎧⎨=-++⎩得：()22330x k x k +---=∵l 与抛物线只有一个交点∴()()224330k k ∆=----=得：k=-4(3)当k ＝-2m+2时，y=(-2m+2)x+b 且m ≠1A将C(m ，n)代入y=(-2m+2)x+b 中得：n ＝(-2m+2)m+b∵223n m m =-++∴23b m =+，l 的解析式为()2223y m x m =-+++ ∵D 为l 与抛物线对称轴的交点∴1D x =， 当x ＝1时，225y m m =-+ ∴()21,25D m m -+，()2,23C m m m -++ 设()1,P a ， ∵PC ＝PD ，∴22PC PD =即()()()2222212325m m m a m m a -+-++-=-+- 解得：154a =， ∴P 的坐标为(1，154)。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2016-2017学年度武汉市部分学校九年级调研测试英语试卷武汉市教育科学研究院命制2017.1.13第I卷（选择题共85分）第一部分听力部分一、听力测试(共三节)第一节(共5小题,每小题1分, 满分5分)听下面5个问题。
每个问题后有三个答语,从题中所给的A、B、C三个选项中选出最佳选项。
听完每个问题后, 你都有5秒钟的时间来作答和阅读下一小题。
每个问题仅读一遍。
1. A. He’s my brother. B. He’s outgoing. C. He’s sixteen.2. A. A lovely toy. B. Quite cheap. C. It’s a blue one.3. A. Just a few. B. The new one. C. It’s for Brown.4. A. Very soon. B. With Mr. Black. C. On the wall.5. A. In the meeting hall. B. At two thirty. C. Half an hour.第二节(共7小题,每小题1分, 满分7分)听下面7段对话。
每段对话后有一个小题, 从题中所给的A、B、C三个选项中选出最佳选项。
听完每段对话后, 你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
6. When will the woman leave?A. At 7:15.B. At 7:30.C. At 7:45.7. What are they most probably doing?A. Planning a party.B. Having a party.C. Cleaning the room.8. What can we learn about the man?A. He sells flowers in winter.B. He likes his flowers a lot.C. He helps the woman plant flowers.9. Where was Bob yesterday afternoon?A. At home.B. At school.C. At the cinema.10. Who are most probably these two people?A. Husband and wife.B. Teacher and student.C. Boss and secretary.11. What is the woman looking for?A. Her keys.B. Her handbag.C. Both.12. Why is Smith so successful?A. He never makes any mistakes.B. He can quickly solve problems.C. He is always thinking of others.第三节(共13小题,每小题1分,满分13分)听下面4段对话或独白。
每段对话或独白后有几个小题, 从题中所给的A、B、C三个选项中选出最佳选项。
听每段对话或独白前,你将有时间阅读各个小题,每小题5秒钟；听完后,各小题将给出5秒钟的作答时间, 每段对话或独白读两遍。
听下面一段对话,回答13至15 三个小题。
13. When and where are they talking?A. After dinner in the garden.B. Before dinner at home.C. After lunch in the office.14. What’s the weather like today?A. Fine.B. Cold.C. Hot.15. What’s the weather like in Beijing?A. Much colder.B. much drier.C. Much hotter.听下面一段对话，回答16-18三个小题。
16. Why is Mrs. Green calling?A. To see if Mr. White have come back.B. To invite the Whites home for the party.C. To tell Mr. White his wife is at her home.17. What does Mr. White say to Mrs. Green?A. he will let her know whether they will go or not.B. They have no time next Friday evening.C. He will have a good time in Hong Kong.18. What do you know about Mr. White?A. He is polite and careful.B. He doesn’t care for his wife.C. He is always very busy.听下面一段对话，回答19-22四个小题。
19. What do you think the woman is?A. Paul’s mother.B. Paul’s classmate.C. Paul’s friend.20. What do we know about Paul?A. He is not clever enough to study.B. He can hardly find time to study.C. He is always too tired to study.21. When does Paul usually do his homework?A. In the morning.B. In the afternoon.C. At night.22. What does the woman suggest?A. Paul should stop playing soccer.B. Paul should give up the volunteer work.C. Paul should spend more time on his studies.听下面一段独白，回答23-25三个小题。
23. Why did the man buy a dog for her daughter?A. His daughter has few children to play with.B. His daughter is good at looking after a dog.C. A dog can eat food with her daughter.24. What can we know about the dog?A. It is clean but makes the girl dirty.B. It is easier to look after for the family.C. It doesn’t always eat up it’s food.25. What has happened to the man?A. He is tired of the dog.B. He doesn’t smoke any more.C. He will have to move again.第二部分笔试部分二、选择填空（共15小题，每小题1分；满分15分）从题中所给的A、B、C、D四个选项中，选出一个最佳答案。
26. — May I use your phone?— ________.A. Of course notB. You may, if you likeC. You do itD. No, I don’t mind27. — I wonder whether I will send Tom to do that?— Whom can you trust, if not ________?A. himselfB. heC. himD. his28. My dictionary ________, I have looked for it everywhere but still I ________ it.A. has lost; don’t findB. is missing; hadn’t foundC. had lost; didn’t findD. is missing; haven’t found29. — Can I get you a cup of coffee?— ________ .A. That’s very nice of youB. With pleasureC. You can, pleaseD. Thank you for your coffee30. Would you like some drink ________ shall we set down to business right away?A. andB. thenC. orD. so31. —Jenny’s voice was shaking when she made a speech today.— It was her first speech in public, so it was _______ to be nervous.A. unusualB. properC. naturalD. impossible32. — What did you do at the top of the mountain just now?— We _______ a train until it disappeared in the distance.A. sawB. watchedC. noticedD. found33. — When can I come for the photos? I need them tomorrow.—They _______ be ready by 12:00.A. canB. shouldC. mightD. need34. —What’s it on the board?—It’s a(n) ________ saying that the meeting has been put off.A. sentenceB. messageC. noticeD. poster35. I know you don’t like collecting things, but interest can be ________.A. achievedB. shownC. discoveredD. developed36. —What a nice house you’ve drawn!—_____. I’m glad you like it.A. No, noB. Not at allC. Thank youD. You’re welcome37.Nobody noticed the thief slip into the house because the lights happened to _______.A. be put upB. give inC. be turned onD. go out38.—Why can’t you ever take anything _______?—I can’t agree with you. I have my own way to do things.A. easilyB. seriouslyC. anxiouslyD. badly39.— Shall I sit at the end of the boat or the other end?— You can sit at ________ end if you keep still.A.anyB. eachC. neitherD. either40.—Do you know _________?— At 11:00 in this morning.A. what time does the train leaveB. what time the train leavesC. the train what time leavesD. the train leaves what time三、完形填空（共15分；每小题1分，满分15分）阅读下面短文，从短文后各题所给的四个选项A、B、C、D中、选出可以填入空白处的最佳答案。