正方体截面问题
正方体截面的探究 课件-高一下学期数学人教A版(2019)必修第二册
梯形
平行四边形
菱形
（图组3）
长方形
正方形
性质探究
正方体截面可能的形状（五边形、六边形）： 试说明：截出的五边形具备的特征（可以是正五边形吗？）.
五边形
六边形 （图组4）
正六边形
性质总结
（1）正方体截面为三角形时只能是：_锐__角__三__角__形_. （2）正方体截面为四边形一定是：梯__形__或__平__行__四__边_ 形 （3）正方体截面为五边形时一定不是__正__五__边___形__. （4）正方体截面为六边形时的特点是_每__组__对__边___互__相_.平行
GGB模拟实验检验并汇报： 实验1
三角形、四边形 五边形、六边形 思考：分别具有的性质是什么？
实物模型对比赏析！
性质探究
正方体截面可能的形状（三角形）： 试证明：截出的三角形一定是锐角三角形.
一般锐角三角形
等腰三角形 （图组2） 等边三角形
性质探究
正方体截面可能的形状（四边形）： 试说明：截出的四边形一定是梯形或平行四边形.
我们可以研究与截面相关 的什么最值问题？
最值探究
结合 指出最大面积的截面六边形形状和该六边形的面积； ② 当截面的内切圆最大时，截面形状及圆的半径.
答：正六边形
正六边形面积：3 3 ；内切圆半径： 6
4
4
截面应用
2023高考全国1卷第12题改编：
6
（1）当棱长为1的正方体截面内切圆最大时，直径为__2 _.
（2）底面直径为1.2m,高为00..011mm的圆柱体能被放进棱长为1m的正方体吗？
因为 6 1.2，高度相对较小， 2
所以能.
动图
几何体
截面
正方体的截面形状与训练含详解
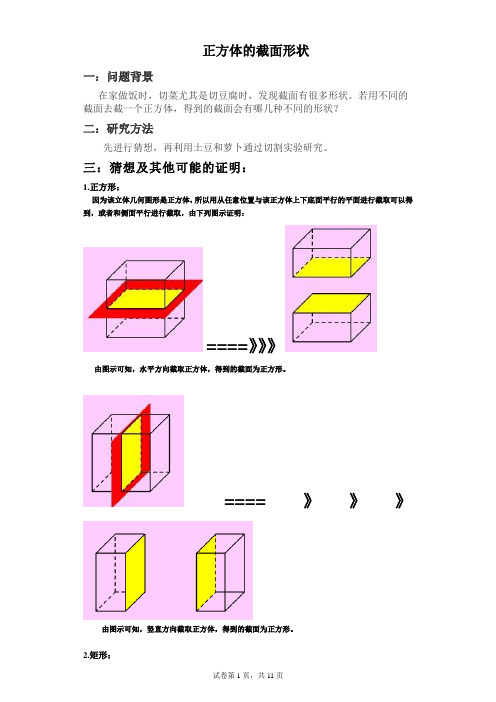
正方体的截面形状一：问题背景在家做饭时，切菜尤其是切豆腐时，发现截面有很多形状。
若用不同的截面去截一个正方体，得到的截面会有哪几种不同的形状？二：研究方法先进行猜想，再利用土豆和萝卜通过切割实验研究。
三：猜想及其他可能的证明：1.正方形：因为该立体几何图形是正方体，所以用从任意位置与该正方体上下底面平行的平面进行截取可以得到，或者和侧面平行进行截取，由下列图示证明：====》》》由图示可知，水平方向截取正方体，得到的截面为正方形。
====》》》由图示可知，竖直方向截取正方体，得到的截面为正方形。
2.矩形：因为正方形也属于矩形，所以对正方形的证明同适用于矩形。
其次，当长宽不等的矩形截面的图示如下：由上图所示可知，按不同角度截取正方体可以得到矩形。
例如，正方体的六个对角面都是矩形。
3.平行四边形：当平面与正方体的各面都不平行时，所得截面为平行四边形，图示如下：==》由上图所示可知，当截面不与正方体的各面平行时，所得截面可能为平行四边形。
4.三角形：根据一定角度过正方体的三条棱进行截取可以得到三角形的截面，图示如下:==》》》由上图可知，正方体可以截得三角形截面。
但一定是锐角三角形，包括等腰和等边三角形特别的，当截面刚好经过三个面的对角线时，所得的三角形截面为正三角形，图示如下：==》得到：正三棱锥5.猜想之外的截面形状：（1）菱形：如下图所示，当A,B为所在棱的中点时，该截面为菱形：（2）梯形：如图所示，当按一定角度使截面在正方体的上下底面上所存在的线段长短有异时，所得截面可能是梯形：==》》》（3）五边形：如图所示，可以截得五边形截面：=》通过实践及资料查询可知，无法得到正五边形。
（4）六边形：如图所示，可以截得六边形截面：=》特别的，当平面与正方体各棱的交点为中点时，截面为正六边形，如图所示：拓展探究：1.正方体最大面积的截面三角形2.正方体最大面积的截面四边形3.最大面积的截面形状4.截面五边形、六边形性质1.正方体最大面积的截面三角形：如该图所示可证明，由三角面对角线构成的三角形。
正方体的截面问题研究资料讲解
正方体的截面问题研究研究性学习报告——正方体的截面形状【课题】正方体的截面形状【作者】刘可歆岳新茹【摘要】探究正方体截面形状，通过实践和图示证明其结果，列举特例。
【研究方法】首先经过猜想，列举出猜想到的截面，其次进行画图和实践等方法证明猜想是否正确。
再通过网络查询资料，寻找未猜想到的情况。
【研究过程】探究1：当截面为三角形根据一定角度过正方体的三条棱进行截取可以得到三角形的截面，图示如下:====由上图可知，正方体可以截得三角形截面。
特别的，当截面刚好经过三个面的对角线时，所得的三角形截面为正三角形，图示如下：====》正三棱锥探究2：当截面是四边形1.正方形：因为该立体几何图形是正方体，所以用从任意位置与该正方体上下底面平行的平面进行截取可以得到，或者和侧面平行进行截取，由下列图示证明：====》》》由图示可知，水平方向截取正方体，得到的截面为正方形。
====》》》由图示可知，竖直方向截取正方体，得到的截面为正方形。
2.矩形：因为正方形也属于矩形，所以对正方形的证明同适用于矩形。
其次，当长宽不等的矩形截面的图示如下：由上图所示可知，按不同角度截取正方体可以得到矩形。
3.平行四边形：当平面与正方体的各面都不平行时，所得截面为平行四边形，图示如下：==》由上图所示可知，当截面不与正方体的各面平行时，所得截面可能为平行四边形。
4．菱形：如下图所示，当A,B为所在棱的中点时，该截面为菱形：5．梯形：如图所示，当按一定角度使截面在正方体的上下底面上所存在的线段长短有异时，所得截面可能是梯形：==》》》探究3：当截面是五边形6.五边形：如图所示，可以截得五边形截面：=》探究3：当截面是六边形7.六边形：如图所示，可以截得六边形截面：=》特别的，当平面与正方体各棱的交点为中点时，截面为正六边形，如图所示：【拓展探究】1. 正方体最大面积的截面三角形：如该图所示可证明，由三角面对角线构成的三角形。
2. 正方体最大面积的截面四边形:通过猜想及查询资料可知，正方体截面可能得到的四边形有：正方形、矩形、梯形、平行四边形。
(完整版)正方体的截面图形
正方体的截面问题
七年级数学教研组
一、截面是三角形
一、截面是三角形
常见的截图为三角形的图形 演 示
二、截面是四边形
二、截面是四边形
二、截面是四边形
常见的截图为四边形的图形
二、截面是四边形
演 示
三、截面是五边形
三、截面是五边形
四、截面是六边形
特 当平面与正方体 别 各棱的交点为中 注 点时，截面为正 意 六边形
四、截面是六边形
形状 三角形 四边形 五边形 六边形
特殊情形
等
等
腰
边
三
三
角
角
形
形
长
正
梯
四
方
方
形
边
形
形
形
向量法作正方体截面
向量法作正方体截面光山县第二高级中学陈宏天已知正方体棱上的三点（不在同一侧面内）作正方体的截面，是一个古老的话题，对有些同学来说也是一个难题。
正方体的截面问题分为两大类，一类是已知的三点中有两点在同一侧面的棱上，此类问题较易解决；另一类是已知的三点没有任何两点在同一侧面内，这一类截面问题的解决有“垂线法”和“向量法”两种，“垂线法”早有书籍介绍，但“向量法”却鲜为人知。
现将两种方法介绍如下：一、垂线法【问题】如图，在正方体ABCD－A1B1C1D1中，已知M、N、P分别是棱AB、CC1、D1A1上的点，求作过点M、N、P的正方体的截面。
【分析】此类问题的难点在于已知的三点没有任何两点在正方体的同一侧面内，解题的方向是把该问题转化为第一类问题，即在已知的点中有两点在正方体的同一侧面内。
设过点M、N、P的正方体的截面所在的平面为α，则平面α与平面AD1相交（公理3），我们有理由相信平面α与棱AA1相交于一点，不妨设该点为R，如果我们能确定R在棱AA1上的位置，问题就转化为第一类问题。
【作法】过点P作棱AD的垂线，记垂足为Q，连接QM、AC、PM，记QM ∩AC＝O，过点O作线段MQ的垂线，交线段PM于点O1，显然点O1∈平面α，又点O1∈平面ACC1A1，所以直线NO1与直线AA1共面且相交，其交点即为点R，余下过程略。
二、向量法如图建立空间直角坐标系，不妨设正方体的棱长为1，M(1,a,0)，N(0,1,b)，P (c ,0,1)，设R (1,0,r )是正方体截面与棱AA 1的交点，则四点MNPR 共面，即向量RM 、RN 、RP 共面，因为),,0(r a RM -=、),1,1(r b RN --=、)1,0,1(r c RP --=，根据平面向量基本定理知，存在实数对),(μλ，使得RN RM RP μλ+=，所以),1,1(),,0()1,0,1(r b r a r c --+-=--μλ，从而⎪⎩⎪⎨⎧-+-=-+=-=-r b r r a c μμλμλμ101，消去λ、μ得1)1(+-+-=c ac bc b a r ，即得R 在棱AA 1上的具体位置，同理可得正方体截面与其它棱的交点位置，但过程要比确定R 点的位置简单的多。
强基专题--立体几何中的截面问题
强基专题3 立体几何中的截面问题
[跟进训练]
1．(2021·重庆模拟)在三棱锥 P-ABC 中，PA，PB，PC 两两垂直，
PA＝3，PB＝4，PC＝5，点 E 为线段 PC 的中点，过点 E 作该三棱
锥外接球的截面，则所得截面圆的面积不可能为( )
A．6π
B．8π
C．10π
D．12π
1234 5
(2)当π2＜θ＜π时，0＜α＜θ＜π，此时sin θ＜1，sin α可以取到最 大值1，
此时过圆锥母线的截面面积最大，最大值为S＝12l2.
1234 5
强基专题3 立体几何中的截面问题
综上所述，过圆锥母线的截面面积的最大值与轴截面顶角θ的范 围有关，
当0＜θ≤π2时，轴截面面积最大，最大值为S＝12l2sin θ. 当π2＜θ＜π时，过圆锥母线的截面面积最大，最大值为S＝12l2.
同理 FG∥EH，所以四边形 EFGH 为平行四边形，又 AD⊥BC， 所以四边形 EFGH 为矩形．
1234 5
强基专题3 立体几何中的截面问题
由相似三角形的性质得BECF＝AACF，FACC＝AFDG， 所以BECF＋FAGD＝AACF＋FACC，BC＝AD＝2， 所以 EF＋FG＝2，所以四边形 EFGH 的周长为定值 4，S 四边形 EFGH ＝EF×FG≤EF＋2 FG2＝1， 所以四边形 EFGH 的面积有最大值 1.故选 B．]
1 2
l2sin θ.截面VCD的面积S′＝12l2sin α.在△V强基专题3 立体几何中的截面问题
(1)当0＜θ≤π2时，0＜α＜θ≤π2，sin α＜sin θ⇒S′＜S，此时过圆 锥母线的截面面积最大为轴截面面积S＝12l2sin θ.
截面形状及相应面积的求法 (1)结合线、面平行的判定定理与性质定理求截面问题； (2)结合线、面垂直的判定定理与性质定理求正方体中截面问题； (3)猜想法求最值问题：“要灵活运用一些特殊图形与几何体的 特征，“动中找静”，如正三角形、正六边形、正三棱锥等； (4)建立函数模型求最值问题：①设元；②建立二次函数模型； ③求最值．
正方体截面总结
结论如下：1、可能出现的：锐角三角型、等边、等腰三角形，正方形、矩形、非矩形的平行四边形、梯形、等腰梯形、五边形、六边形、正六边形2、不可能出现：钝角三角形、直角三角形、直角梯形、正五边形、七边形或更多边形正方体的截面形状一：问题背景在家做饭时，切菜尤其是切豆腐时，发现截面有很多形状。
若用不同的截面去截一个正方体，得到的截面会有哪几种不同的形状？二：研究方法先进行猜想，再利用土豆和萝卜通过切割实验研究。
三：猜想及其他可能的证明：1.正方形：因为该立体几何图形是正方体，所以用从任意位置与该正方体上下底面平行的平面进行截取可以得到，或者和侧面平行进行截取，由下列图示证明：====》》》由图示可知，水平方向截取正方体，得到的截面为正方形。
====》》》由图示可知，竖直方向截取正方体，得到的截面为正方形。
2.矩形：因为正方形也属于矩形，所以对正方形的证明同适用于矩形。
其次，当长宽不等的矩形截面的图示如下：由上图所示可知，按不同角度截取正方体可以得到矩形。
例如，正方体的六个对角面都是矩形。
3.平行四边形：当平面与正方体的各面都不平行时，所得截面为平行四边形，图示如下：==》由上图所示可知，当截面不与正方体的各面平行时，所得截面可能为平行四边形。
4.三角形：根据一定角度过正方体的三条棱进行截取可以得到三角形的截面，图示如下:==》》》由上图可知，正方体可以截得三角形截面。
但一定是锐角三角形，包括等腰和等边三角形特别的，当截面刚好经过三个面的对角线时，所得的三角形截面为正三角形，图示如下：==》得到：正三棱锥5.猜想之外的截面形状：（1）菱形：如下图所示，当A,B为所在棱的中点时，该截面为菱形：（2）梯形：如图所示，当按一定角度使截面在正方体的上下底面上所存在的线段长短有异时，所得截面可能是梯形：==》》》（3）五边形：如图所示，可以截得五边形截面：=》通过实践及资料查询可知，无法得到正五边形。
（4）六边形：如图所示，可以截得六边形截面：=》特别的，当平面与正方体各棱的交点为中点时，截面为正六边形，如图所示：拓展探究：1.正方体最大面积的截面三角形 2.正方体最大面积的截面四边形3.最大面积的截面形状4.截面五边形、六边形性质1.正方体最大面积的截面三角形：如该图所示可证明，由三角面对角线构成的三角形。
正方体的截面问题研究报告
正方体的截面问题研究报告研究报告：正方体的截面问题一、引言：正方体是一种具有六个面都是正方形的立体，它具有许多有趣的性质和特点。
其中一个问题是关于正方体的截面问题，即在不同位置和方式截取正方体，观察其截面形状和特征。
本研究报告将对正方体的截面问题进行研究和分析。
二、研究目的：1. 研究正方体的截面形状及特征。
2. 探索正方体的不同截面位置和方式对截面形状的影响。
3. 分析正方体的截面特性与其它几何形体的关系。
三、研究方法：通过数学分析与计算机模拟相结合的方式进行研究。
首先，研究者将正方体进行截面，观察并记录截面形状、面积和其他特征。
然后，通过数学模型和计算机模拟，研究者将确定各种截面形状的数学方程，并分析其特性和关系。
四、实验过程与结果：1. 实验过程：研究者首先在正方体的不同位置划定截面平面，包括水平截面、垂直截面和倾斜截面。
然后，使用切割工具在规定的截面平面上进行截取操作，获得正方体的截面。
最后，通过测量和计算，记录截面的形状、面积及其他特征。
2. 实验结果：不同位置和方式的截面形状各不相同。
水平截面和垂直截面一般为正方形，但大小和位置不同。
而倾斜截面则为一种四边形，具有奇特的形状。
截面的面积也因位置和方式的不同而有差异。
五、分析与讨论：1. 正方体的截面形状与其位置和方式密切相关。
对于水平和垂直截面，截面形状为正方形，且大小和位置相对稳定。
而倾斜截面则更具变化性，形状可能是一种特殊的四边形。
2. 正方体的截面特性与其他几何形体有一定的关系。
在特定的截面位置和方式下，正方体的截面形状可能与柱体、圆柱体等具有相似的形态。
3. 正方体的截面问题与数学几何有密切关系，通过研究正方体的截面形状和特性，可以深入理解几何形体的性质，丰富几何学科的研究。
六、结论：通过对正方体的截面问题进行研究和分析，我们发现正方体的截面形状与其位置和方式密切相关，同时也与其他几何形体具有一定的关系。
正方体的截面问题在数学几何研究中具有一定的重要性，对于深入理解几何形体的性质具有积极的作用。
正方体截面问题题型汇总
正方体截面问题题型汇总开高 张文伟2019.11.28答案：B分析：12题除了直观解题法之外，还有另一种解法:（1）正方体的十二条棱长度相等，与平面的夹角相等，必有在平面上投影的长度相等。
（2）一个封闭的平面图形中有十二条相等的线段，必然想到正六边形的顶点与其中心的连线。
（3）所以说，投影是一个正六边形。
分析：面D1B1C与各个棱所处角相等，面A1DB与各个棱所处角相等，所以两个面与已知的平面α平行。
根据正方体的特性，体对角线AC1与两个面垂直，交点分别是M、N，且M、N是体对角线的三等分点，所以，棱与面所成角的正弦值为：三分之根号三。
向平面做投影，本质是几何体的顶点向射影面做垂线。
所以，点C1D1B1C向平面α做垂线，得到的是△D1B1C，点AA1DB向平面α做垂线，得到的是△A1DB，两个三角形重叠到一个平面，得到的就是右图，再连接端点直线，就得到一个正六边形。
由题意可得B1D1的长为根号二，所以高B1E就是二分之根号六，所以半径就是三分之根号六，即正六变形的边长是三分之根号六。
总结：1. 三条面对角线构成等边三角形所在的平面与正方体的每一个棱所成角都相等，2.正方体在体对角线垂直于投影面上的投影是一个正六面形；3.体对角线垂直于投影面，三条面对角线构成等边三角形，投影面积是这个等边三角形面积的两倍。
12.【2018全国一卷12】已知正方体的棱长为1，每条棱所在直线与平面α所成的角相等，则α截此正方体所得截面面积的最大值为A B C D【答案】A【分析】最大是正六边形首先利用正方体的棱是3组每组有互相平行的4条棱，所以与12条棱所成角相等，只需与从同一个顶点出发的三条棱所成角相等即可，从而判断出面的位置，截正方体所得的截面为一个正六边形，且边长是面的对角线的一半，应用面积公式求得结果.【详解】根据相互平行的直线与平面所成的角是相等的，所以在正方体1111ABCD A B C D −中，平面11AB D 与线11111,,AA A B A D 所成的角是相等的，所以平面11AB D 与正方体的每条棱所在的直线所成角都是相等的，同理平面1C BD 也满足与正方体的每条棱所在的直线所成角都是相等， 要求截面面积最大，则截面的位置为夹在两个面11AB D 与1C BD 中间的，，所以其面积为26S ，故选A. 点睛：该题考查的是有关平面被正方体所截得的截面多边形的面积问题，首要任务是需要先确定截面的位置，之后需要从题的条件中找寻相关的字眼，从而得到其为过六条棱的中点的正六边形，利用六边形的面积的求法，应用相关的公式求得结果.8．在棱长为2的正方体ABCD －A 1B 1C 1D 1中，点P ，Q ，R 分别为棱AA 1，BC ，C 1D 1的中点，经过P ，Q ，R 三点的平面为α，平面α被此正方体所截得截面图形的周长为A B ． C D ．分析：【解析】 是正六边形 11.棱长为2的正方体1111ABCD A B C D −中，E 为棱AD 中点，过点1B ，且与平面1A BE 平行的正方体的截面面积为（ ）A. 5B.。
正方体中几种常见的截面作法
新教育·上旬刊正方体中几种常见的截面作法□海南师范大学附属中学廖云霞如果用一个平面去截几何体,那么该平面与这个几何体的各个面相交,由交线围成的平面图形叫几何体的截面。
打个比方,木匠用锯子将某个小木块锯成两块,“锯口”就是我们所说的截面。
本文将以正方体为载体,展开讨论关于截面的如下两个问题:一是过三点(均在棱上)作正方体的截面的做法;二是截面面积或周长的计算。
通过研究正方体的截面问题,我们能更好地揭示空间图形与平面图形之间的内在联系。
因为正方体的各个面都是平面,所以用平面去截它所得的截面必是多边形。
由于截面至少与正方体的三个面相交,至多与六个面相交,所以截面的形状只能是三角形、四边形、五边形、六边形四种。
截面与正方体每一个面的交线由两个公共点决定,所以只要找到截面与正方体某个面的两个公共点,就能做出截面与该面的交线。
公共点与交线的求得,主要依据为:1.公理1:如果一条直线上的两点在一个平面内,那么这条直线在此平面内。
2.公理2:过不在一条直线上的三点,有且只有一个平面,及公理2的三个推论。
3.公理3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线。
4.面面平行的性质定理:如果两个平行平面同时和第三个平面相交,那么它们的交线平行。
5.如果三个平面两两相交,那么所得三条交线平行或共点。
例1.已知正方体ABCD -A 1B 1C 1D 1的棱长为1,E 是棱AB 的中点,F 是棱CC 1的中点。
做过D 1、E 、F 三点的截面,并求截面图形的周长。
图1作法1(延长线法):如图1,分别延长D 1F 、DC 交于点P ;连接PE ,交BC 于点N ;延长PE ,交DA 的延长线于点S ;连接D 1S ,交AA 1于点M ,则五边形D 1MENF 即为所求作的截面图形。
由三角形相似可得A 1M=3MA,CN=2NB ,易得截面五边形D 1MENF 的周长为11213√+95√)。
正方体的截面问题
正方体的截面问题
正方体的截面问题
夏老师伴你学
我们知道正方体有六个面，用一个平面去解正方体至少要经过三个面，最多经过六个面. 所以出现的截面只可能是三角形、四边形、五边形和六边形.
一、截面是三角形
用一平面截正方体，当平面经过正方体的三个面时，所得的截面的形状为三角形.所得的三角形可能是锐角三角形、等腰三角形、等边三角形. 其中等边三角形三个顶点是正方形的顶点.
二、截面是四边形
用一平面截正方体，当平面经过正方体的四个面时，所得的截面的形状为正方形、长方形、梯形.
三、截面是五边形
用平面截正方体，当平面经过正方体的五个面时，所得截面是五边形
四、截面是六边形
用平面截正方体，当平面经过正方体的六个面时，所得截面是六边形。
拓展研究：
1.最大面积的截面三角形
2.最大面积的截面四边形：由两条平行的面对角线和两对平行棱构成的四边形
3.最大面积的截面形状：
正方体的截面可以分为：三角形、正方形、梯形、矩形、平行四边形、五边形、六边形、正六边形。
其中三角形还分为锐角三角型、等边、等腰三角形。
梯形分位非等腰梯形和等腰梯形。
首先比较三角形与五边形和六边形，所得这三种截面的情况有一共同特点：不能完整在该截面所在平面在正方体内所截的范围的最大值，有部分空间空出。
因此可以得到：最大面积一定是四边形。
所以最大面积的截面形状：即最大截面四边形（猜想）。
初步推断为如图所示的矩形：
4.截面五边形、六边形性质：
截面五边形：有两组边互相平行.
截面六边形：三组对边平行的六边形.用一个平面截正方体，由于正方体共有六个面，所以不可能截出7边形。
已阅读 (1939)。
有关正方体的截面问题
有关正方体的截面问题
①截面可以是三角形：等边三角形、等腰三角形、一般三角形；
②截面三角形是锐角三角形；截面三角形不能是直角三角形、钝角三角形；
③截面可以是四边形：平行四边形、矩形、菱形、正方形、梯形、等腰梯形；截面为四边形时，这个四边形中至少有一组对边平行；
④截面不能是直角梯形；
⑤截面可以是五边形；截面五边形必有两组分别平行的边，同时有两个角相等；截面五边形不可能是正五边形；
⑥截面可以是六边形；截面六边形必有分别平行的边，同时有两个角相等；
⑦截面六边形可以是等角(均为120°)的六边形，特别地可以是正六边形．
对应截面图形如下图中各图形所示．。
正方体截面总结(最全,适用于公务员图形推理)
M / * B结论如下：1可能出现的：锐角三角型、等边、等腰三角形，正方形、矩形、边形、梯形、等腰梯形、五边形、六边形、正六边形2、不可能出现：钝角三角形、直角三角形、直角梯形、正五边形、非矩形的平行四七边形或更多边正方体的截面形状一：问题背景在家做饭时，切菜尤其是切豆腐时，发现截面有很多形状。
若用不同的截面去截一个正方体，得到的截面会有哪几种不同的形状？二：研究方法先进行猜想，再利用土豆和萝卜通过切割实验研究。
三：猜想及其他可能的证明：1•正方形：因为该立体几何图形是正方体，所以用从任意位置与该正方体上下底面平行的平面进行截取可以得到，或者和侧面平行进行截取，由下列图示证明：由图示可知，水平方向截取正方体，得到的截面为正方形。
由图示可知，竖直方向截取正方体，得到的截面为正方形。
2矩形：因为正方形也属于矩形，所以对正方形的证明同适用于矩形。
其次，当长宽不等的矩形截面的图示如下: 由上图所示可知，按不同角度截取正方体可以得到矩形。
例如，正方体的六个对角面都是矩形。
3. 平行四边形：当平面与正方体的各面都不平行时，所得截面为平行四边形，图示如下:==》》》 ==》》》由上图所示可知，当截面不与正方体的各面平行时，所得截面可能为平行四边形。
4. 三角形：根据一定角度过正方体的三条棱进行截取可以得到三角形的截面，图示如下==》由上图可知，正方体可以截得三角形截面。
但一定是锐角三角形，包括等腰和等边三角形特别的，当截面刚好经过三个面的对角线时，所得的三角形截面为正三角形，图示如下:==》得到: 正三棱锥5. 猜想之外的截面形状：（1）菱形：如下图所示，当A,B 为所在棱的中点时，该截面为菱形:(2)梯形：如图所示，当按一定角度使截面在正方体的上下底面上所存在的线段长短有异时，所得截面可能是梯形：(3 )五边形:(4 )六边形：如图所示，可以截得六边形截面:==》》》如图所示，可以截得五边形截面:通过实践及资料查询可知，无法得到正五边形。
立体几何中截面问题
立体几何中截面问题（周长、面积、体积、长度）1．在正方体 ABCD - A 1B 1C 1D 1 中，E ，F 分别为棱 AB ，BC 的中点，过点 D 1 ，E ，F 作该正方体的截面，截面将正方体分成两部分，则较小部分与较大部分的体积的比值为 （ ）2．已知正方体 ABCD - A 1B 1C 1D 1 的棱长为 2 ，直线 AC 1 ⊥ 平面α ，平面α 截此正方体所得截面中，正确的说法是（ ）A ．截面形状可能为四边形B ．截面形状可能为五边形C ．截面面积最大值为32D ．截面面积最大值为 233 3．正方体 ABCD -- A 1B 1C 1D 1，E 、F 分别是 AA 1 、CC 1 的中点，P 是CC 1 上的动点（包括 端点），过 E 、D 、P 作正方体的截面，若截面为四边形，则 P 的轨迹是（ ）A ．线段C 1FB ．线段CFC ．线段CF 和一点C 1D ．线段C 1F 和一点 C4．已知圆锥的高为 1，母线长为 5 ，则过此圆锥顶点的截面面积的最大值（ ）5．如下图，正方体 ABCD - A 1B 1C 1D 1 的棱长为 1，E ，F ，G 分别为棱 AB ， A 1D 1，C 1D 1 的中点，经过 E ，F ，G 三点的平面被正方体所截，则截面图形的面积为（ ）6．如上图，在正方体 ABCD - A `B `C `D ` 中,平面 垂直于对角线 AC ,且平面 截得正方体的六个表面得到截面六边形,记此截面六边形的面积为 S ,周长为l ,则（ ）A ． S 为定值, l 不为定值B ． S 不为定值, l 为定值C ． S 与l 均为定值D ． S 与l 均不为定值7．已知正方体ABCD - A1B1C1D1 棱长为4，P 是AA1中点，过点D1作面α 满足CP ⊥ 平面α ，则平面α 与正方体ABCD - A1B1C1D1的截面周长为（）第7题第8题第9题8．如图，在直三棱柱ABC - A1B1C1中，AC = BC = CC1= 6，AC ⊥ BC ，E､F 分別为BB1，A1C1中点，过点A､E､F 作三棱柱的截面交B1C1于M，则EM =9．在长方体A B C D - A1 B1C1 D1 中，AB = AD = 4, AA2 = 2 ，过点A1作平面α 与A B, A D 分别交于M,N 两点，若AA1与平面α 所成的角为45︒ ，则截面A1MN 面积的最小值是（）10．已知圆锥SO1 的顶点和底面圆周均在球O 的球面上，且该圆锥的高为8. 母线SA =12 ，点B 在SA上，且SB = 2BA ，则过点B 的平面被该球O 截得的截面面积的最小值为（）11．在直三棱柱ABC - A1B1C1 中，M 是BB1 上的点，AB = 3 ，BC = 4，AC = 5，CC1= 7 ，过三点A、M 、C1作截面，当截面周长最小时，截面将三棱柱分成的两部分的体积比为（）．12．已知正方体ABCD - A1B1C1D1 的体积为8，点M 在线段BC 上（点M 异于B、C 两点），点N 为线段CC1的中点，若平面AMN 截正方体ABCD - A1B1C1D1所得的截面为五边形，则线段BM 长度的取值范围是______.13．已知正方体ABCD - A1B1C1D1的棱长为1，E ，F ，G 分别是棱AB ，BC ，CC1的中点，过E ，F ，G 三点作该正方体的截面，点M 为底面ABCD 内一动点.若MD1与该截面平行，则直线MD1与CC1所成角的余弦值的最大值为______.答案：1、47252、D3、C4、25 5、433 6、B 7、2654 8、13 9、24 10、32π 11、1110 12、（1,2） 13、36。
正方体的截面
正方体的截面引言截面是指一个物体被一个平面所切割后的形状。
正方体是一个具有六个相等的正方形面的立方体。
在本文中，我们将讨论正方体的截面形状和性质。
正方体的基本概念正方体是一种特殊的立方体，具有六个相等的正方形面。
它的每个面都与其他三个面相邻，形成直角相交。
正方体的边长被定义为所有正方形面的边长。
正方体的截面形状正方体的截面形状取决于截割平面的方向和位置。
根据截面与正方体边长的相对位置，可以将截面分为以下几种情况：1. 水平截面当截割平面与正方体的底面平行时，截面为一个正方形。
正方形的边长等于正方体的边长。
2. 垂直截面当截割平面与正方体的一个侧面平行时，截面为一个长方形。
长方形的边长等于正方体的边长，而宽度则取决于截割平面与正方体的相对位置。
3. 平面截面当截割平面与正方体的一个角相交时，截面为一个不规则多边形。
多边形的形状取决于截割平面的位置和角度。
4. 对角线截面当截割平面通过正方体的两个相对角点时，截面为一个菱形。
菱形的对角线为正方体的对角线。
5. 中心截面当截割平面通过正方体的中心点时，截面为一个正六边形。
正六边形的边长等于正方体的边长。
正方体截面的性质正方体的截面具有一些特殊的性质，这些性质可以用来解决一些几何问题。
以下是一些常见的性质：1. 截面面积正方体的截面面积取决于截割平面的形状和位置。
对于水平和垂直截面，其面积等于正方体的底面积。
对于其他类型的截面，其面积可以通过几何计算方法进行求解。
2. 截面形状对称性正方体的截面形状具有一定的对称性。
例如，水平和垂直截面是关于正方体的中心点对称的。
对称性可以帮助我们简化计算和分析截面的性质。
3. 截面相对位置正方体的截面相对位置可以用来确定截面之间的关系。
例如，两个水平截面之间的距离等于正方体的高度。
总结正方体的截面形状和性质是几何学中的重要概念。
通过研究截面，我们可以更好地理解正方体的结构和特性。
了解正方体截面的形状和性质对于解决几何问题和应用数学都具有重要的意义。
《数学探究活动(一)：正方体截面探究》
教师给出截面的概念,学生理解截面的边是平面和几何体各面的交线.
教师继续提出问题：正方体是立体几何中的一个重要模型,它是一种非常对称的几何体.
如果我们拿一个平面去截一个正方体,那么会得到什么形状的截面图呢？
学生分组,利用手中的橡皮泥（或萝卜）及小刀做实验,先用橡皮泥捏一个正方体（或用
萝卜切块）,再用小刀截手中的正方体,得到一个截面并观察,完成6个探究任务,得出答案.
北师大版同步教材精品课件
高中数学 GAOZHONGSHUXUE
《数学探究活动（一）： 正方体截面探究》
学而优 · 教有方
情景引入
高中数学 GAOZHONGSHUXUE
教学内容
按照习惯,我们是不吃西瓜皮,只吃西瓜瓤的.现在有一个外皮已经洗净的西瓜,设想一下,你 一般是如何吃到里面的瓢的呢？
师生互动
教师拿出一个西瓜,让学生抽象出它是哪一种空间图形. 学生回答,一致认为它应该是球体. 教师进一步提出左边的问题让学生抢答,并进一步要求学生思考：刀经过的面是一个什么 形状的图形呢？ 学生回答后,教师再请学生上台演示切西瓜,验证答案.
2.正方体截面
（1）锐角三角形、等边三角形、等腰三角形
（2）正方形、矩形、非矩形的平行四边形、菱形、梯形、等腰梯形 （3）五边形、六边形、正六边形 3.例 4.小结与作业
学而优 · 教有方
教学研讨
高中数学 GAOZHONGSHUXUE
教学设计中设计了一系列跨度很大的探究问题串,探究的难点是分类找出所有可能的截 面,并证明哪些形状的截面一定存在或者一定不存在.经历通过动手操作试验、猜想、验证 答案等活动,逐渐深入地探究观察,有利于培养学生发现问题、分类讨论、作图表达、推理 论证等能力.
探究5：能否截出正五边形？为什么？
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
正方体截面问题
课题:正方体截面问题
班级:高二(2)班
小组:数学兴趣小组
指导老师:王长喜
组员:崔云鹏、庹元杰、张成昊、杨浩、陈一峰、尚世伟、彭世宇
组长:张皓楠
课题目的:探索正方体可能的截面形状，通过实践和图示来证明其结果，列举特
例，拓展空间观念与全面考虑问题的能力。
探究方法:首先通过猜想，列举出预计猜想到的截面，其次进行画图和实践等方
法证明猜想得正确与否。
再通过网络的资料查询，寻找未猜想到的情况。
大题小做:
:什么叫几何板的截面, 问题1
答:一个几何和一个平面相交所得到的平面图形 (包含它的内部)，叫做几何体的截面。
问题2:截面的边是如何得到的,
答:截面的边是平面和几何体各面的交线。
问题3:正方体是立体几何中一个重要的模型，它是一种非常对称的几何体。
如果我们拿一个平面去截一个正方体那么会得到什么形状的截面图呢,截面图最多有几条边,
答:因为正方形只有六个面，所以它与平面最多有六条交线，即所截到得截面图最都有六条边。
所以截图可能是三角形，四边形，五边形，六边形。
探究1:截面图为三角形时，有几种情况, 1.是否可以截出等腰三角形:
(1)解析:
A’
a
C
c
B bA
如上图，一正方体被一平面所截后得到截面abc
若截面三角形abc是
以为bc底的等腰三角形，
那么只要三角形Aba全等于三角形Aca就可以截到。
所以，截到等腰三角形的情况存在。
(2)做法:
在一棱AA’上取a
在棱AB.AC上取Ab.等于Ac.
就可得到以bc为底的等腰三角abc。
(3)证明:因为角bAa等于角cAa， Aa边公用，
Ab等于Ac，
所以三角形全等于三角形。
所以ba等于ca,
所以三角形abc是以为bc底的等腰三角形。
2.是否可以截出等边三角形: (1)解析
A’
a
C
c
bBA
一正方体被一平面截后得到三角形abc，若三角形abc是等边三角形，
只要三角形aAb,aAc, bAc两两全等就可以得到。
所以，截到等边三角形的情况存在。
(2)做法:
在棱AA’,AB.AC上分别取Aa等于Ab等于Ac 就可以得到三角形abc为等边三角形。
(3)证明:
因为Aa等于Ab等于Ac，
角bAa等于角cAa,
所以，三角形bAa全等于三角形cAa。
所以ab等于ac。
同理可证ba等于bc,ca等于cb。
所以三角形是等边三角形。
3.是否可以截出直角三角形:
A’
a
C
c
B bA
解析:若一正方体被一平面截后角acb是直角，那么就有:ac2+cb2=ab2.
因为角adb是直角，所以ab2=db2+ad2; 因为角adc是直角，所以
ac2=ad2+cd2; 因为角bdc是直角，所以bc2=db2+cd2. 所以
ad2+cd2+db2+cd2=db2+ad2.
化简后得2cd2=0.
所以，这截得是普通三角形，不是直角三角形。
小结:用以平面去截正方体只能截到三边形: (1)等腰三角形，
(2)等边三角形，
(3)普通三角形;
(4)不能截出直角三角形。
探究2:如果，截面为四边形，那么，可以截出哪几类呢? 1.是否可以截出长方形:
分析:过一正方体的一棱有无数个矩形，只要长宽不等，就是长方形。
所以，存在这一情况。
a b
c
d 做法:
如上图;取正方体一棱，
过棱沿一个不与原表面重合的平面截下，就可以得到一个矩形。
证明:
设原棱长为a，
因为过棱沿一不与原表面重合的平面截下，所以bd大于ab，
因为过一正方体的一棱有无数个矩形，而截面不是正方形，
所以截面是矩形。
2.是否可以截出正方形:
分析:正方体六个表面都
是正方形只要用一垂直于
原表面的平面去截正方体，
就可以得到正方形。
做法:
用一垂直于原表面的平面去截
正方体，就可以得到正方形。
证明:因为垂直于原表面
的在正方体的截图都是正方形，所以截到得垂直于原表面的平面
就是正方形。
3.是否可以截出梯形:
分析:用一平面从一上正方体表面斜截下去交与底面，因为上下两底面平行，斜截下去截
距不等，所以可截到梯形。
C
A
B
F
D E
做法:
用一平面从一上正方体表面
斜截下去交与底面就可截到
梯形。
证明:
平面ABC平行于DEF,
所以AC平行于DE;
斜截下去截距不等，
所以AC不等于DE;
所以DECA是梯形。
小结:用以平面去截正方体只能截到四边形:
(1.)长方形;
(2.)正方形;
(3.)梯形。
探究3:截面多边形的边数最多有几条,
解析:
因为正方形只有六个面，所以它与平面最多有六条交线，
即所截到得截面图最都有六条边。
所以截图可能是三角
形，四边形，五边形,六边形。
探究4:截面可能是正多边形吗,可能有几种, 答:截面是正多边形有可能。
可能有正三角形，正方形，正五边形，
和正六边形。
(如下图)
探究5:如果截面可能是三角形，其面积最大是什么?
如下图:
解析:
截面为三角形，面积是底乘高。
底和高最大是连接正方体的三个顶点，所以这时三角形面积最大。
总结;
A.用以平面去截正方体只能截到三边形: (1)等腰三角形，
(2)三角形，
(3)普通三角形;
(4)不能截出直角三角形。
B.用以平面去截正方体只能截到四边形: (1.)长方形;
(2.)正方形;
(3.)梯形。
C. 用以平面去截正方体还能截到五边形,六边形。
课后反思:
1:截图有可能是等腰梯形吗,
2:截到五边形,六边形有哪几类, 3:从这个课题还可以延伸到什么, 探究启示: 创新所带给人的精神愉悦是
任何物质享受和感官享乐所无法比拟的，那是灿烂的生命之花最深沉、最辉煌、最恣意的绽放，从某种意义上说，创新是自我实现的最高表现形式，教育作为人道主义的事业，
理所当然应该关注个人生的提升。