工程制图-06-线面、面面相对位置
机械制图线面相对位置

1. 平面与直线平行
•若一直线平行于平面内的一直线,则该直线与平 若一直线平行于平面内的一直线, 若一直线平行于平面内的一直线 面平行。 面平行。
k’ b’
例1. 判断直线与平 面是否平行 a’ 不平行
a
d’ c’ e’
k
b
d e c
1. 平面与直线平行
•若一直线与平面平行,通过平面上的任一点必定 若一直线与平面平行, 若一直线与平面平行 能在该平面内作一直线平行于已知直线。 能在该平面内作一直线平行于已知直线。
例 过线段BC作平面平行于线段DE,再过点A 作铅垂面 平行于线段DE。
解: 1.过BC任一点B作BI//DE; 2.过A作铅垂面平行DE,正面投影有无数解。
5-5 已知线段MN =30 mm,点N 在点M 之后,且线段MN 与 ABC 平行,完成线段MN 和 ABC 的另一投影。
解: 1.用直角三角形法求MN的水平投影mn ; 2.在 ABC的水平投影上作c1//mn。 3.过1’作c’1’//m’n’确定c’,连接a’b’c’为 ABC正面投影。
s’ p’ r’
q
r
t
p p p s
⑴
b’ d’(e’)
⑵ a’
c’ b’ c d a(b)
d’
判 断 直 线 与 平 面 是 否 平 行
a’ c’ a c d b e
平行
平行
e’
e b’ c’ a’ d’ 不平行
⑶
d’ a’ b’ c’ c a b d
⑷
f’
平行
e’ e
e’
b e
p’
(1) (2) (3)
q
p
19.4判断直线ⅠⅡ与平面ABC的相对位置。
工程制图 平面的投影-线面相对位置解读
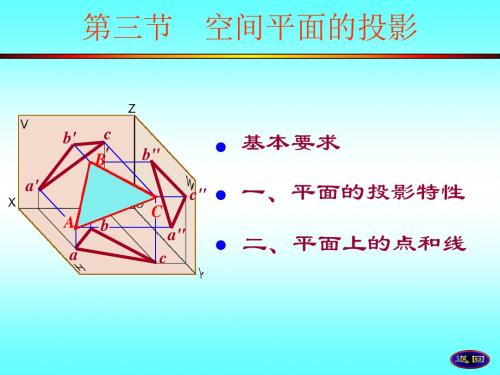
(一)投影面的垂直面
2.铅垂面:只垂直于H面,倾斜于V面和W面的平面
z p' p' p" O
P
p"
x
yW
p
p
yH
投影特性 :(1) H面投影积聚为一条线p
(2) p与x、 y轴的夹角反映β、角的真实大小 (3) p'、 p为平面P的类似形
b'
b' c'
z b"
c'
b" a' c" x O a"
c" yW
B
a'
A
a 投影特性:
C
b
c
b
a" a c yH
(1) 一般平面的三面投影既不反映实形也没有积聚性。 (2) 其三面投影均为空间平面的类似形,且面积缩小。
平面投影特性判断
正平面
铅垂面
侧平面
正平面
正垂面
侧平面
侧垂面
一般位置平面
二、平面上的点和线
C
D A B
A C F a
D
D A B a C K E B F b c(f) d(e)
K
F
E
d(e) a b
E
c(f)
c(f)
k
d(e)
k
b
一
二
三
一、平行问题
1.直线与平面平行
直线与平面平行具有下列几何关系: 若直线与平面平行<- ->该直线必平行于平面上的一条直线; 当平面垂直于投影面时<- ->该直线的投影必然与平面具有积聚性 的投影平行。
线面投影及位置(工程图学)
g c d
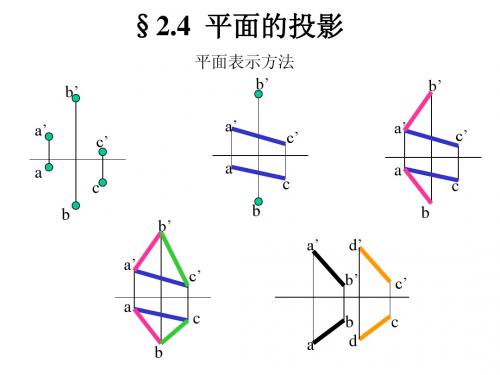
3、平面上的投影面平行线
平面上平行于投影面的直线称为平面上的投影面 平行线。有三类 : 面上水平线 、正平线、侧平线。
V
B
a’ A
图示水平线AB
b a PH
a’
e’
b’ d’
c’ a e
b d
c
分析水平线、正平线且在平面上
例3: 已知点E 在ABC平面上,且点E距离V 面10,距离H面15,试 求点E的投影。本三
EK正面投影可见
e
k
1
a c
a’ f’
作图步骤 1. 利用积聚性求出K点水平投 影k 2. 利用点在线上的投影特性求 出K点正面投影k ’ 3. 判别可见性 c’
b’
1’(2’)
k’ e’
b
f
2
y1>y2,即点Ⅰ在点Ⅱ前方,
EK正面投影可见
e
k
1
a c
1、利用积聚性求交点和交线
(1)一般位置直线与特殊位置平面相交
a′
Zab
x a
ΔZab
α
b′
b
重作
a
YH
3 . 一般位置平面
对三个投影面都处于倾斜位置的平面称为一般位置平面。
投影特性 1 、 △ abc、△abc、△abc 均为 ABC的类似形。 2 、 不反映 、、 的真实角度 。
二、平面上的点和直线
1、平面上的点
在给定平面上取点,可直接取自该平面上的已知直线
e d
据此特性可以解决以下问题:
(1) 作直线垂直平面或平面 垂直直线
(2) 判断线面是否垂直
例1:试过定点S作一平面垂直于已知直线EF。
n’
f’
工程制图全册复习要点

点和直线§1-1投影知识1, 中心投影法1、平行投影法(正投影法斜投影法)§1-2点的投影一个形体是由多个侧面所围成,各侧面又相交于多条侧棱,各侧棱又相交于多各顶点,则只要把这些点的投影画出来,再连成线就可作出一个形体的投影。
所以,点是形体的最基本元素。
且点的投影规律是线, 面, 体的投影基础。
一, 点在三投影面体系中的投影1, 点的直角坐标及三面投影的关系”’到W面的距离’”到V面的距离’”到H面的距离2, 三投影面体系中点的投影规律(1)a’a在同一条投影连线上,垂直于X轴。
这两个投影都反映A点的X 坐标。
a’a⊥X轴(2)a’a”在同一条投影连线上,垂直于Z轴。
这两个投影都反映A点的Z 坐标。
a’a”⊥Z轴(3)点的水平投影到X轴的距离等于侧面投影到Z轴的距离。
这两个投影都反映A点的Y坐标。
”二, 两点的相对位置1、对于两个点在空间就有相对位置的问题了。
(1)对V面投影时,靠近V面的为后,远离V面的为前。
H, W面投影可反映出其前后关系。
(2)对H面投影时,靠近H面的为下,远离H面的为上。
V, W面投影可反映出其上下关系。
(3)对W面投影时,靠近W面的为右,远离W面的为左。
V, H面投影可反映出其左右关系。
三, 重影点当空间两点处于特别位置,即两点恰好在同一条投影线上,此时两点在同一投影面上的投影重合,这时称两点为该投影面的重影点。
四, 投影轴和投影面上点的投影小结:1, 作空间一个点的投影①利用坐标值②利用点到投影面的距离③利用两点间的相对位置。
2, 点的投影方向:自上向下, 自前向后, 自左向右3, 推断重影点的可见性:前遮后, 上遮下, 左遮右§1-2直线的投影一, 直线的投影图从几何学知道,直线是无限长的。
直线的空间位置可由线上随意两点的位置确定,即两点定一线,在次要作直线投影只要作两个点的投影即可。
二, 各类直线的投影特性1, 投影面平行线特点:平行某一投影面,倾斜其他投影面。
机械制图 直线与平面 平面与平面的相对位置课件

求交线的方法
通过在每个平面上选择一组点, 并确定这些点在另一个平面上的 投影,可以找到交线。
平面与平面平行
平面与平面平行
求平行平面的方法
当两个平面在三维空间中没有重叠部 分时,它们平行。平行的平面永远不 会相交。
通过选择两个平面上对应的点并确保 它们之间的距离相等,可以找到平行 的平面。
平行的性质
交点
直线与平面的的投影。
直线与平面平行
直线的投影与平面的投影 平行,且无重影。
直线与平面内无数条直线 平行。
直线平行于平面,且与平 面无交点。
定义
投影特性 性质
直线与平面垂直
定义
直线垂直于平面,并与平面相交于一点。
性质
直线与平面内任意直线垂直。
机械制图 - 直线与平面、 平面与平面的相对位置
xx年xx月xx日
• 直线与平面的关系 • 平面与平面的相对位置 • 直线和平面、平面和平面相对位
置的应用 • 直线和平面、平面和平面相对位
置的作图技巧 • 直线和平面、平面和平面相对位
置的练习题和解析
目录
01
直线与平面的关系
直线与平面相交
定义
直线与平面在某一点交汇,除该点外,直线不在平面上。
平行线法
通过作平行线来帮助确定平面与平面的相对位置,如过一点作平面 的平行线,再判断该平行线与另一个平面的关系。
05
直线和平面、平面和平面 相对位置的练习题和解析
练习题一:直线与平面的关系
直线与平面关系的基本概念
•·
01
直线与平面平行:直线不在
平面内,且与平面无交点。
02
03
直线与平面相交:直线在平 面内,或有且仅有一个交点
7线面、面面相对位置

V c'
d' C c
D a'
b' B A
AB AB
CD EFG a' X a
d
PH a
b H b' O b
平行
b' c' e' e b c
g'
AB平行于P AB平行于P a' 平行于 X PH a
一、平行问题:1.直线与平面平行 平行问题:
C D
A B
P
(1)CD∥AB,且 AB∈P => CD∥P ) ∥ , ∈ ∥ (2)CD∥P => P 平面内一定存在一条直线 AB∥CD。 ) ∥ ∥ 。
例:求直线EF与三角形ABC的交点,并判断可见性。 求直线EF与三角形ABC的交点,并判断可见性。 EF与三角形ABC的交点
Pv b’ k’ c’ e’ a’ b a e c k f f’
1、求交点 采用辅助平面法 包含ef直线作垂直面P ef直线作垂直面 a) 包含ef直线作垂直面Pv b) 线面求交 c) 线线求交 2、判断可见性 利用重影法 注意: 注意: 对于一般情况相交, 对于一般情况相交,两面投影都 要判断可见性
目录
直线与平面、 直线与平面、两平面之间 的相对位置
平行问题 相交问题 垂直问题
直线与平面、 直线与平面、平面与平面的相对位置
目 录
相对位置包括平行、相交和垂直。 相对位置包括平行、相交和垂直。 平行
直线与平面平行 平面与平面平行 直线与平面相交 平面与平面相交 直线与平面垂直 平面与平面垂直
一、平行问题:1.直线与平面平行 平行问题:
A
特殊情况相交 2. 特殊线与一般面相交
求铅垂线AB与平面CDE的交点。 AB与平面CDE的交点 [例] 求铅垂线AB与平面CDE的交点。 因交点的H 因交点的H面投影与直线 AB的积聚投影重合 的积聚投影重合, AB的积聚投影重合,又因交 点也属于平面, 点也属于平面,故可用平面 内取点的方法,求交点的V 内取点的方法,求交点的V 面投影。 面投影。过a(b)作辅助线 df,并求出d f 与 b 的交点 。 的交点k df,并求出d’f’与a’b’的交点k’。 d' X 可见性判断: 可见性判断: 利用重影点M 来判断) (利用重影点M和N来判断) d 投影可看出, 在前, 从H投影可看出,m在前, 在后, 可见, k 与 n在后,故b’k’可见,a’k’与 k 可见 平面的重影部分为不可见。 平面的重影部分为不可见。 a' c' k' f'
工程制图第4章 直线与平面、平面与平面的相对位置

m
b k f n
c
l
a O
m
m
k b
f
a l
n
二、辅助平面法
A E
K 1
2
D
C
B 过AB作平面P垂直于H投影面
a
d
2
k 作题步骤: 1、 过AB作铅 垂平面P。 2、求P平面与 ΔCDE的交线 e ⅠⅡ。 O 3、求交线 ⅠⅡ与AB的交 e 点K。
c
1
X
PH
b
a
1
第一节
第二节
平行问题
相交问题
4.2 相交问题
第三节
第四节
垂直问题
综合问题分析及解法
第一节 平行问题
一、直线与平面平行
C P A
D
B
若平面外的一条直线与平面内的一条直线平行,则该直线 与该平面平行。
例1 试判断直线AB是否平行于平面 CDE。
c g d f
e
b
a
X
f d e
O
a
g c
e f d
a
b r
X
c
O
e s
SH
d
a c b
f
结论:两平面平行
r P H
第二节
相交问题
D B
交点与交线的性质
P K A
K
A
B
C
L
E
F
直线与平面、平面与平面不平行则必相交。直线与平面相交 有交点,交点既在直线上又在平面上,因而交点是直线与平面的 共有点。两平面的交线是直线,它是两个平面的共有线。求线与 面交点、面与面交线的实质是求共有点、共有线的投影。
X
m k b
画法几何及机械制图课件:第章直线、平面的相对位置 (一)

画法几何及机械制图课件:第章直线、平面
的相对位置 (一)
本文将从以下三个方面详细介绍《画法几何及机械制图课件》第一章内容,主要包括直线、平面基本概念、相互位置关系和解题技巧。
一、基本概念
直线:有无数个点组成,是长度无限的线段。
通常用一字母标记,如AB。
平面:是用无数个点组成的,长度和宽度均无限的平面。
通常用大写字母表示,如平面α。
向量:它由长度和方向两部分组成,通常用小写字母加无箭头表示,如a。
二、相互位置关系
相交:两条直线或直线与平面相交于一点。
平行:两条直线不相交,在平面外平移但方向不变。
垂直:两条直线相交,在相交点处互相垂直。
相交于无穷远处:两条平行直线或直线与平面,因长度无限,永远不相交。
但可借助扩展线找到两条直线的交点,如图1-5。
三、解题技巧
绘图法:根据问题条件用图示,找到几何实体的相对位置。
假设法:缺少某个条件时,可以先“假设”该条件成立,然后根据已知条件推出结论,并且判断假设条件是否合理。
巧用扩展线:有些相互位置关系,可能在图中表现不出来,可以利用扩展线把直线或平面延长,找到相应点的位置。
综上所述,《画法几何及机械制图课件》第一章介绍了直线、平面的基本概念和相互位置关系,以及解决几何问题的技巧。
这些基础内容是后续学习几何和机械制图必须掌握的知识点,希望同学们能够认真学习和练习,掌握相关技能,为更深入的学习打下坚实的基础。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
b’
(d’)
X
OX
O
a
(b)
QH
PH
d 交线是
正垂线 c
平面与平面相交 关键是求平面与平面的公有线——交线
一般面与投影面垂直面相交 可利用平面有积聚性的投影求出两平面的交线。
垂直面与一般面 相交
[例] 求铅垂面P与三角形的交线,并判断其投影的可见性。
分别过与p的交点m和与p 的交点n向上作垂线,与a’c’ 和b’c’分别相交于m’ 和n’;连接m’n’即为交 线从。H投影可知,在平 面p之前,所以V投影 a’m’n’b’ 为可见。m’c’n’ 与p’的重 影 部分为不可见。
直线与平面、平面与平面
目 录
的相对位置
直线与平面相交 平面与平面相交 直线与平面平行 平面与平面平行 直线与平面垂直 平面与平面垂直
直线与平面相交
利用平面有积聚性的投影求 线面的交点
[例] 求直线与铅垂面 的交点。
由AB与平面CDE的交点, 向上作垂线,与a b 交于k , 则点K(k,k)即为交点。
在投影图上作平面的垂线 时,可作出平面的水平线和正 平线作为面上的相交二直线。 此时所作垂线与水平线所夹的 直角,其H投影仍为直角;垂 线与正平线所夹的直角,其V 投影仍为直角。
M
P A1
C1
C
A DK
E D1
E1
H
线面垂直
MK AE MK CD MK 平面P
m'
c'
a' Xa
k' e'
d' b'
O
MK ABC
dk c e
mb
直线与平面垂直(续)
b' 线面垂直
a'
直线与投影面垂直面垂直
直线垂直于某投影面的 垂直面时,它必然是该投影 面的平行线。即与铅垂面垂
X
O
b
PH
a
是水平线
QV d'
c'
X
O
c
d
是正平线
直的直线必为水平线;与正 垂面垂直的直线必为正平线。 p' b' a'
d' a' e'
b'
b
直线与平面垂直(续)
垂直线与一 般面相交
[例] 求铅垂线与平面的交点。
因交点的H面投影与直线
的积聚投影重合,又因交
点也属于平面,故可用平面 内取点的方法,求交点的V
面投影。过a(b)作辅助线
,并求出d’f’与a’b’的交 点k’。
d'
可见性判断:
X
(利用重影点m’和n’来判断)
从H投影可看出在前,n在
d
后,故b’k’可见,a’k’与平面
d bc
O
e f
[例] 过点A作水平线AB平行于 CDE,AB长20mm.
例
在三角形内作一水平线(, d’f’),并过点a作
平行于,使长为20, 并求出a’b’。
a'
b' c'
d'
f'
e'
X
O
bc f
e
a
d
平行
平面与平面平行
面 面
平
行
几何条件:若平面内有两条相交直线与另一平面内的两条相
交直线对应平行,则这两平面平行。
当两个投影面垂直面相互平行时,它们的积聚投影也互相平
行。
a'
C P D Q b'
AB F E
X
f' e' c' d' O X
H
b
cd
QH
O PH
PQ
af
e
两平面的积聚投影平行
两平面平行
QP
例
平面与平面平行
[例] 判断 ABC与 DEF是 否平行。
过 DEF内的任意点 K的水平投影k作km ab, 作kn cb,并求出相应的 k’m’,k’n’;
由图中可看出,k’m’ a’b’, k’n’ c’b’, 所以 两三角形互相平行。
b'
e'
c' n'
m'
a' X
d' k'
f' O
a
c
k
f
dn
m
b
e
KM AB KN CB 两三角形平面互相平行
直线与平面垂直
直线与一般面垂直
几何条件:若一直线 (相交 或交叉)垂直于平面上的任意两 条相交直线,则此直线必垂直 于该平面。
B P
A
X pb
OXa
c' O
e
c d
Hb
a
a 是水平线
b 是正平线
直线与平面垂直(续)
[例] 过M点作一直线MN垂 直 1 在 于ABCA内BC任,作并水求平其线垂C足E 。
b' n’ e' k’
例
d'
c'
和正平线AD,并过m及m’点分 别作mn ce,m’n’ a’d’,则直
a'
m’
线MN ABC。
的重影部分为不可见。
a' c'
k' f' 重影点 e'
m(’ n’)
b'
O
n
e
(m)(k) a(b) f
C
平面与平面相交
关键是求平面与平面的公有线——交线 两投影面垂直面相交 交线是一条垂直于该投影面的垂直线。
二垂直面相 交
交线垂直 于H面
AQ P
H
QH B PH
a’ 交线是
RV S V
铅垂线
c’
不 可 见
p’ a’ m’
c’
n’
X
c
n
pH m a
可 见 b’
O b
平面与平面相交
[例] 求正六棱锥被正垂 面 截切后的截交线。
只需分别求出正垂面 与正六棱锥各棱面的交线。 为求交线,可求出 与各 条棱线的交点后依次连之。
注意应画出H 投影中仍 存在的棱线。 AB是PV与左前棱面的交线 BC是PV与前棱面的交线 CD是PV与右前棱面的交线 DE是PV与右后棱面的交线 EF是PV与后棱面的交线 FA是PV与左后棱面的交线
a'
X a
PH
b' g' d'
c'
f'
e' e bc
O f d
g
c dPH a 平行于P a'
b
H b'
X
O
PH
b
a
平行
[例] 判断直线AB与 CDE是否平行。
例
在三角形内作df平行于ab,求出d’f’,因d’f’不平行于a’b’,可
知AB与 CDE不平行。
不平行 b'
c'
f'
e'
a'
d'
X
平行 a
例
s'
PV
b' a'
(f')
c' d' (e')
fe
a sd
bc
直线与平面平行
线面平
行
几何条件:若直线平行于平面内一直线,则直线 与平面平
行若直。线与投影面垂直面平行,则该平面的投影面垂直面的积聚投
影与该直线的同面投影平行。
B AB CD
AB P A C
D
V d'
b'
D a' B
c'
C
A
AB CD AB EFG
X
O
2 求MN与 ABC的交点K, 并判断其投影的可见性。
bm
e
a
k
d
n
c
直线与平面垂直(续)
[例] 求点A到直线的距离。
距
离
实 长
m'
1. 过点A作水平线AB MN,
作正平线AC MN,则平面ABC
MN。
a'
2 求直线与平面的交点K。 X
3 用直角三角形法求的
a
实长。
m
例
c'
k' b'
n' nO c k
可见性判断:线面相交, 交点把直线AB分为AK和BK 两 段。由水平投影可看出,AK 在平面之前,所以a k 为可 见,b k 与平面重影部分为 不可见(用虚线画出)。
Vc
垂直
面与
a一般 线相交dbk'
C
eA E
K
BD
e
b d ck
aH
c'
a'
d'
k'
e'
X b'
O
b
e
ck a d
直线与平面相交
利用直线有积聚性的投影求线面交点
