第10 讲 MATLAB CUMCM 真题求解实例一:数据型
用matlab解析实际案例

Matlab大作业专业:东凌经济管理学院班级:小组成员:2012年5月1成员分工:**(组长):第一题模型一建立,文档编写***:第一题模型二建立,文档编写***:第二题模型建立2第一题某小型超市出售某一品牌八宝粥,其需求量与消费者平均收入和商品价格密切相关,根据近期几个月每一个月的消费记录以及消费者收入市场调查,统计如下表。
现在在一个地区新建一所同样的超市,出售同样一款八宝粥,该超市附近消费者平均收入为4000元,超市经理想知道八宝粥定价6元时,进多少货才会比较合适。
需求量100 75 80 70 50 65 90 100 110 60 收入4000 2400 4800 2000 1200 1600 5200 4400 5200 1200 价格 5 7 6 6 8 7 5 4 3 92.1 基本假设1)假设该品牌八宝粥的超市库存量与需求量一致,不存在多余库存。
2)假设超市每个月就进一次货。
3)假设超市之前调查的数据充分准确。
4)假设在新超市,人群收入以及商品价格对需求量的影响与之前规律类似。
5)假设该品牌八宝粥的需求量除了与消费者收入和商品价格有关,其他因素影响很小,可以忽略不计。
2.2 符号设定I(income):消费者收入向量。
P(price):商品价格向量。
Rrequiremen):商品需求向量。
(t2.3 模型建立2.3.1 模型分析:因为有商品价格P 和消费者收入I 两个参数对商品需求量R 产生影响,所以我们选择采用回归模型解决这个问题。
模型一:多元二项式回归模型222211210P I P I R βββββ++++=Matlab 程序:I=[4000 2400 4800 2000 1200 1600 5200 4400 5200 1200]; P=[5 7 6 6 8 7 5 4 3 9];R=[100 75 80 70 50 65 90 100 110 60]; f=[I' P'];rstool(f,R','purequadratic')程序运行结果以及图像:预测结果beta =110.53130.0366-26.5709-4.7229*10^(-6)1.8475rmse =4.5362residuals =5.2724-0.7162-4.5158-1.9390-3.33153.45663.4843-3.4452-0.09761.8320结果分析:由实验可得回归模型为:228475.1)6(^10*7229.4-5709.260366.05313.110P I P I R +--+=,因为剩余标准差为4.5362,说明此回归模型的显著性较好。
matlab程序设计例题及答案

matlab程序设计例题及答案1.编写程序:计算1/3+2/5+3/7+……+10/21法一: s=0;for i=1:10s=s+i/(2*i+1); end ss =法二:sum((1:10)./(3:2:21)) ans =2.编写程序:计算1~100中即能被3整除,又能被7整除的所有数之和。
s=0;for i=1:100if mod(i,3)==0&&mod(i,7)==0 s=s+i; end,end ss =2103.画出y=n!的图,阶乘的函数自己编写,禁用MATLAB 自带的阶乘函数。
x=1:10; for i=1:10try y(i)=y(i-1)*i; catch y(i)=1; end,end plot(x,y)106123456789104.一个数恰好等于它的因子之和,这个数就称为完数。
例如,6的因子为1,2,3,而6=1+2+3,因此6就是一个完数。
编程找出20XX以内的所有完数。
g=;for n=2:20XX s=0;for r=1:n-1if mod(n,r)==0 s=s+r; end endif s==ng=[g n]; end end gg =6 28 4965.编写一个函数,模拟numel函数的功能,函数中调用size函数。
function y=numelnumel(x) m=size(x); y=m(1)*m(2);numelnumel([1 2 3;4 5 6])ans =66. 编写一个函数,模拟length函数的功能,函数中调用size函数。
function y=lengthlength(x) m=size(x);y=max(m(1),m(2));lengthlength([1 2 3;4 5 6])ans =37.求矩阵rand的所有元素和及各行平均值,各列平均值。
s=rand(5);sum=sum(sum(s)) mean2=mean(s,2) mean1=mean(s)sum =mean2 =mean1 =8.编程判断1001,1003,1007,1009,1011为素数,若不是,输出其约数。
(完整word版)含答案《MATLAB实用教程》

第二章 MATLAB 语言及应用实验项目实验一 MATLAB 数值计算三、实验内容与步骤1.创建矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=987654321a(1(2)用(3)用(42.矩阵的运算(1)利用矩阵除法解线性方程组。
⎪⎪⎩⎪⎪⎨⎧=+++=-+-=+++=+-12224732258232432143214321421x x x x x x x x x x x x x x x 将方程表示为AX=B ,计算X=A\B 。
(2)利用矩阵的基本运算求解矩阵方程。
已知矩阵A 和B 满足关系式A -1BA=6A+BA ,计算矩阵B 。
其中⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=7/10004/10003/1A ,Ps: format rata=[1/3 0 0;0 1/4 0;0 0 1/7];b=inv(a)*inv(inv(a)-eye(3))*6*a(3)计算矩阵的特征值和特征向量。
已知矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=1104152021X ,计算其特征值和特征向量。
(4)Page:322利用数学函数进行矩阵运算。
已知传递函数G(s)=1/(2s+1),计算幅频特性Lw=-20lg(1)2(2w )和相频特性Fw=-arctan(2w),w 的范围为[0.01,10],按对数均匀分布。
3.多项式的运算(1)多项式的运算。
已知表达式G(x)=(x-4)(x+5)(x 2-6x+9),展开多项式形式,并计算当x 在[0,20]内变化时G(x)的值,计算出G(x)=0的根。
Page 324(2)多项式的拟合与插值。
将多项式G(x)=x 4-5x 3-17x 2+129x-180,当x 在[0,20]多项式的值上下加上随机数的偏差构成y1,对y1进行拟合。
对G(x)和y1分别进行插值,计算在5.5处的值。
Page 325 四、思考练习题1.使用logspace 函数创建0~4π的行向量,有20个元素,查看其元素分布情况。
Ps: logspace(log10(0),log10(4*pi),20) (2) sort(c,2) %顺序排列 3.1多项式1)f(x)=2x 2+3x+5x+8用向量表示该多项式,并计算f(10)值. 2)根据多项式的根[-0.5 -3+4i -3-4i]创建多项式。
高等应用数学问题的MATLAB求解_习题参考解答

【求解】 假设正三角形逆时针旋转 θ 度,则可以得出如图 2-2a 所示的示意图,三角形的三个 顶点为 (cos θ, sin θ), (cos(θ + 120◦ ), sin(θ + 120◦ )), (cos(θ + 240◦ ), sin(θ + 240◦ )),可以绘制出 其曲线,如图 2-2b 所示,试减小步距,如选择 ∆θ = 2, 1, 0.1,观察效果。 >> t=[0,120,240,0]*pi/180; xxx=[]; yyy=[]; for i=0:5:360 tt=i*pi/180; xxx=[xxx; cos(tt+t)]; yyy=[yyy; sin(tt+t)]; end
−1 −1
= A−1 − A−1 B C −1 + B T A−1 B
B T A−1
试根据上面的算法用 MATLAB 语句编写一个函数对矩阵 M 进行求逆,并通过一个小例子来 检验该程序,并和直接求逆方法进行精度上的比较。 【求解】 编写这个函数 function Minv=part_inv(A,B,C) Minv=inv(A)-inv(A)*B*inv(inv(C)+B’*inv(A)*B)*B’*inv(A);
>> M1=sym(M); iM0=inv(M1) >> norm(double(iM0)-iM) % 直接求解的误差范数 >> norm(double(iM0)-iM1) % 间接求解的误差范数 可见,用间接方法得出的逆矩阵误差更大,因为在这里新编写的函数中 inv() 函数使用 了多次,由此产生很大的传递误差。由此可以得出结论:如果某问题存在直接解,则尽量别 使用间接方法,以加大传递误差。 11 下面给出了一个迭代模型 xk+1 = 1 + yk − 1.4x2 k yk+1 = 0.3xk 写出求解该模型的 M-函数,如果取迭代初值为 x0 = 0,y0 = 0,那么请进行 30000 次迭代求出 一组 x 和 y 向量,然后在所有的 xk 和 yk 坐标处点亮一个点 (注意不要连线),最后绘制出所 需的图形。提示 这样绘制出的图形又称为 Henon 引力线图,它将迭代出来的随机点吸引到一 起,最后得出貌似连贯的引力线图。 【求解】 用循环形式解决此问题,可以得出如图 2-1 所示的 Henon 引力线图。 >> x=0; y=0; for i=1:29999 x(i+1)=1+y(i)-1.4*x(i)^2; y(i+1)=0.3*x(i); end plot(x,y,’.’) 上述的算法由于动态定义 x 和 y ,所以每循环一步需要重新定维,这样做是很消耗时间 的,所以为加快速度,可以考虑预先定义这两个变量,如给出 x=zeros(1,30000)。 12 用 MATLAB 语言的基本语句显然可以立即绘制一个正三角形,试结合循环结构,编写一个 小程序,在同一个坐标系下绘制出该正三角形绕其中心旋转后得出的一系列三角形,还可以 调整旋转步距观察效果。
MATLAB数值分析实例解析

2016-2017 第一学期数值分析上机实验报告姓名: xxx学号: 20162…….学院:土木工程学院导师:………..联系电话:…………..指导老师:………..目录第一题 (1)1.1题目要求 (1)1.2程序编写 (1)1.3计算结果及分析 (2)第二题 (4)2.1题目要求 (4)2.2程序编写 (4)2.3计算结果及分析 (6)第三题 (7)3.1题目要求 (7)3.2程序编写 (7)3.3计算结果及分析 (8)第四题 (9)4.1题目要求 (9)4.2程序编写 (9)4.3计算结果及分析 (10)第五题 (11)5.1题目要求 (11)5.2程序编写 (12)5.3计算结果及分析 (13)第六题 (17)6.1题目要求 (17)6.2程序编写 (17)6.3计算结果及分析 (18)6.4程序改进 (18)第一题选做的是第(1)小问。
1.1题目要求编出不动点迭代法求根的程序;把x3+4x2−10=0写成至少四种x=g(x)的形式,取初值x0=1.5,进行不动点迭代求根,并比较收敛性及收敛速度。
1.2程序编写1.3计算结果及分析① 第一种迭代公式:x =x 3+4x 2+x −10; matlab 计算结果如下: (以下为命令行窗口的内容)② 第二种迭代公式:x =√(10−x 3)/42; matlab 计算结果如下: (以下为命令窗口内容)③ 第三种迭代公式:x =√10(x +4)⁄2; matlab 计算结果如下:(以下为命令窗口内容)⁄;matlab计算结果如下:④第四种迭代公式:x=10(x2+4x)(以下为命令窗口内容)上述4种迭代公式,1、4两种由于在x真实值附近|g`(x)|>1,不满足迭代局部收敛条件,所以迭代序列不收敛。
对于2、3两种式子,由于在x真实值附近|g`(x)|<=L<1,满足迭代局部收敛条件,所以迭代序列收敛。
对于2、3两迭代公式,由于L3<L2,所以第3个迭代公式比第2个迭代公式收敛更快。
MATLAB考试复习题及例题

例、用一个简单命令求解线性系统3x1+ x2 - x3 = 3.6x1+2x2+4x3 = 2.1-x1+4x2+5x3 = -1.4对于线性系统有Ax=bA=[3 1 -1;1 2 4;-1 4 5];b=[3.6;2.1;-1.4];x=A\bx =1.4818-0.46060.3848例、用简短命令计算并绘制在0≤x≤6范围内的sin(2x)、sinx2、sin2x。
x=linspace(0,6)y1=sin(2*x),y2=sin(x.^2),y3=(sin(x)).^2;plot(x,y1,x, y2,x, y3)例1-1 绘制函数y=2sin(1+x)的图像,并计算当x=0.5 时的函数值。
x=(1:0.1:10); %给出自变量x 的定义域y=2*sin(1+x); %写出函数形式plot(x,y) %绘出函数图形y=2*sin(1+0.5) %求当x=0.5 时的y 值,其后不加分号,直接在窗口中给出结果y =1.9950 %输出y 的计算结果例1-2 绘制函数y=3x3-10x2+5x-8的图像for i=1:100x(i)=0.1*i;y(i)=3*x(i)^3-10*x(i)^2+5*x(i)-8;endplot(x,y)上机练习(1)(1)以两种方式打开MATLAB 工作窗口,进入MATLAB 6.0 的工作环境,并尝试用不同的方式退出。
(2)尝试、熟悉MATLAB 6.0 的各栏菜单以及各个工具栏的功能。
(3)重新启动MATLAB 6.0,进入MATLAB 工作窗口,用who 命令查看当前工作空间内有无变量及其值。
(4)绘制函数y=cos(5x+2)/sin(3x+1) 的图像,并求解当x=2 时的函数值。
(5)此时再次用who 命令查看工作空间内的变量名及其值,与(3)比较,同时用whos 命令查看变量,比较与who 命令的不同。
(6)熟练掌握MA TLAB 的通用命令。
Matlab考试试题库答案解析(2021年整理精品文档)

Matlab考试试题库答案解析编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(Matlab考试试题库答案解析)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为Matlab考试试题库答案解析的全部内容。
填空题1、标点符号;%—用来表示该行为注释行。
可以使命令行不显示运算结果,2、x为0~4pi,步长为0。
1pi的向量,使用命令 x=0:0.1*pi:4*pi创建。
3、输入矩阵A=,使用全下标方式用A(2,2)取出元素“-5”,使用单下标方式用A(5)取出元素“-5"。
4、符号表达式sin(2*a+t)+m中独立的符号变量为t。
5、M脚本文件和M函数文件的主要区别是M脚本文件没有函数定义和M函数文件有函数定义_______。
6。
设x是一维数组,x的倒数第3个元素表示为x(_end-2_)设y为二维数组,要删除y的第34行和48列,可使用命令y(34,:)=[];y(:,48)=[];7. 将变量x以Ascii文本格式存储到文件fname。
txt,应使用命令 save _x ;8。
在while 表达式, 语句体, End 循环语句中,表达式的值非零时表示循环条件为真,语句体将被执行,否则跳出该循环语句;9。
要从键盘读入一个字符串并赋值给变量x,且给出提示“Who is she?”,应使用命令x=input(‘Who is she?',’s’) ;10.设A=和B=和C=均为m*n矩阵,且存在于WorkSpace中,要产生矩阵D=,可用命令D=(A-C)/B.^C,计算可用命令det(inv(A’*B)11. 在MATLAB命令窗口中的“>>”标志为MATLAB的命令行提示符,“│”标志为输入提示符。
matLAB经典例题及答案
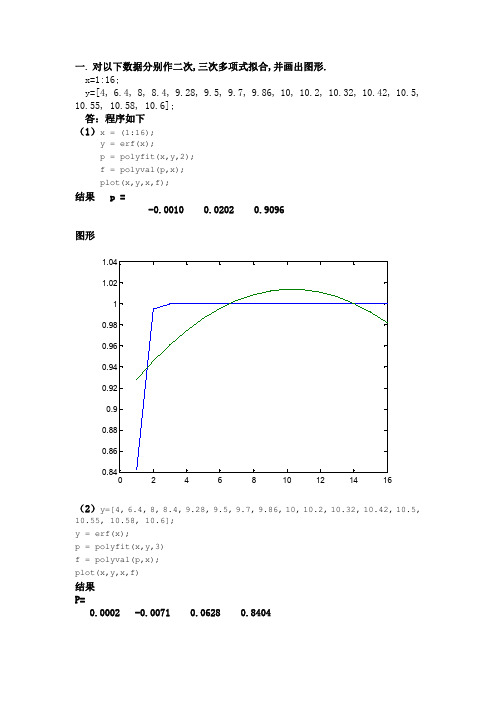
一.对以下数据分别作二次,三次多项式拟合,并画出图形.x=1:16;y=[4,6.4,8,8.4,9.28,9.5,9.7,9.86,10,10.2,10.32,10.42,10.5, 10.55,10.58,10.6];答:程序如下(1)x=(1:16);y=erf(x);p=polyfit(x,y,2);f=polyval(p,x);plot(x,y,x,f);结果p=-0.00100.02020.9096(2)y=[4,6.4,8,8.4,9.28,9.5,9.7,9.86,10,10.2,10.32,10.42,10.5, 10.55,10.58,10.6];y=erf(x);p=polyfit(x,y,3)f=polyval(p,x);plot(x,y,x,f)结果P=0.0002-0.00710.06280.8404二.在[0,4pi]画sin(x),cos(x)(在同一个图象中);其中cos(x)图象用红色小圆圈画.并在函数图上标注“y=sin(x)”,“y=cos(x)”,x轴,y轴,标题为“正弦余弦函数图象”.答:程序如下x=[0:720]*pi/180;plot(x,sin(x),x,cos(x),'ro');x=[2.5;7];y=[0;0];s=['y=sin(x)';'y=cos(x)'];text(x,y,s);xlabel('正弦余弦函数图象'),ylabel('正弦余弦函数图象')图形如下三.选择一个单自由度线性振动系统模型,自定质量、弹簧刚度、阻尼、激振力等一组参数,分别编程(m 文件)计算自由和强迫振动时的响应,并画出振动曲线图。
(要求画出该单自由度线性振动系统模型图)其中质量为m=1000kg,弹性刚度k=48020N/m,阻尼c=1960N.s/m,激振力f(t)=0.阻尼比ζ的程序p=1960/(2*sqrt(48020*1000))求得p=0.1414而p为阻尼比ζ强迫振动时的响应程序g =tf([-101],[48020048020*1.9848020]);bode(g)图形g =tf([001],[0001]);bode(g)振动曲线图程序:函数文件function dx =rigid(t,x)dx =zeros(2,1);dx(1)=x(2);dx(2)=(-48020*x(1)-1960*x(2))/1000;命令文件options =odeset('RelTol',1e-4,'AbsTol',[1e-41e-4]);[T,X]=ode45(@rigid,[012],[11],options);plot(T,X(:,1),'-')其图形如下024681012-6-5-4-3-2-11234单自由度线性强迫振动系统模型图其中质量为m=1000kg,弹性刚度k=48020N/m,阻尼c=1960N.s/m,f(t)=cos(3*pi*t)振动曲线图程序:函数文件function dx=rigid(t,x)dx=zeros(2,1);dx(1)=x(2);dx(2)=(-48020*x(1)-1960*x(2))/1000+cos(3*pi*t);命令文件options=odeset('RelTol',1e-4,'AbsTol',[1e-41e-4]);[T,X]=ode45(@rigid,[020],[11],options);plot(T,X(:,1),'-')力等一组参数,建立Simulink仿真模型框图进行仿真分析。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
红酒显著性检验结果
T检 验 值
6
T(0.05)值
T(0.01)值
4
2
T检 验 值
0
0
5
10
15
20
25
30
样品号
白酒显著性检验结果
T检 验 值 T(0.05)值
3
T(0.01)值
2
1
T检 验 值
0
0
5
10
15
20
25
30
样品号
图 1 每个样品的 T 检验值与参考值的比较
运行程序,得到每个样品的 T 检验结果(如图 1 所示)和平均 T 检验值:
t 检验分为单总体检验和双总体检验。单总体 t 检验时检验一个样本平均数与一个已知 的总体平均数的差异是否显著;双总体 t 检验是检验两个样本平均数与其各自所代表的 总体的差异是否显著。对于该问题,由于有两个样本,因此可以采用双总体 t 检验。
2.2 模型的建立和求解
2.2.1 差异显著性评判
由于 t 检验是比较成熟的方法,所以这里将不再对 t 检验的理论进行探讨,而是 直接应用该方法。
i=N
∑ T ∗ = Ti i=1
其中,T ∗ 为平均 T 检验值,i 为样品号, N 为样品总数,Ti 为两组品酒师对样品 i 的
T 检验值。 由于红酒和白酒品质差异比较大,所以我们将分别对红酒和白酒的评价结果进行显著性
分析,及对于红酒来说,N=27,对白酒来说,N=8。 至此就可以用 MATLAB 编写程序来求解该问题了,具体程序如下:
本讲针对的题型是数据型的建模问题, 2012 年的 A 题就是一道典型这类问题,接下 来将介绍这道题的 MATLAB 求解过程。
1 问题的提出
确定葡萄酒质量时一般是通过聘请一批有资质的评酒员进行品评。每个评酒员在对葡萄 酒进行品尝后对其分类指标打分,然后求和得到其总分,从而确定葡萄酒的质量。酿酒葡萄 的好坏与所酿葡萄酒的质量有直接的关系,葡萄酒和酿酒葡萄检测的理化指标会在一定程度 上反映葡萄酒和葡萄的质量。附件 1 给出了某一年份一些葡萄酒的评价结果,附件 2 和附 件 3 分别给出了该年份这些葡萄酒的和酿酒葡萄的成分数据。请尝试建立数学模型讨论下 列问题:
i=N
∑ V = (Si − u0 )2 i=1
其中,V 为样本对总体样本的方差,Si 为第 i 品酒师的给酒样的总分,u0 为总体样本
均值。 由于在计算 T 检验的过程中,已得到该表达式中的所有参数的值,所以可以很快得到每
组品酒师对每个样品的方差了。在上面程序的基础上,稍作修改,就可以编写出计算该方差 的程序如下:
第 10 讲 MATLAB CUMCM 真题求解实例一:数据型
作者:卓金武, MathWorks 中国
要想在建模比赛中取得好成绩, 光学不练是不行的, 真题的实训有助于积累实战经验, 对建模、编程、写论文技能的大幅提升非常有帮助。 从本讲开始, 将以历年国赛真题为实 例,介绍 MATLAB 在实际比赛中的具体应用过程。
%% 2012A_question1_T evaluation %------------------------------------------------------------------------%% 数据准备 % 清空环境变量 clear all clc
%导入数据 X1=xlsread('2012A_T1_processed.xls', 'T1_red_grape', 'D3:M272'); X2=xlsread('2012A_T1_processed.xls', 'T2_red_grape', 'D3:M272');
值与其比较,作出统计推断,推断依据如下所示。 表 1 T 检验推断依据表
T
P值
差异显著程度
T ≥ T(df)0.01
P ≤ 0.01
差异非常显著
T ≥ T(df)0.05
P ≤ 0.05
差异显著
T < T(df)0.05
P > 0.05
差异不显著
方法确定后,我们再来确定研究对象,即对哪个主体利用该方法,因为这个问题里面, 对于每个样品既有单项评分,又有总分,而从品酒员角度,每个品酒员又有评分。为此,我 们针对问题的目标,即评判两组评酒员的评价结果有无显著性差异,来确定最合适的研究对 象。
for j=1:n2 SX3(i,j)=sum(X3(10*i-9:10*i,j)); SX4(i,j)=sum(X4(10*i-9:10*i,j)); end end % 计算每组样品得分的均值 for i=1:K2 Mean3(i)=mean(SX3(i,:)); Mean4(i)=mean(SX4(i,:)); end % 计算检验值 for i=1:K2 S2(1,i)=(sum((SX3(i,:)-Mean3(i)).^2)+sum((SX4(i,:)Mean4(i)).^2))/(n2*(n2-1)); T2(1,i)=(Mean3(i)-Mean4(i))/(sqrt(S2(1,i))); end AT_W=abs(T2); M_AT_W=mean(AT_W); %% 结果显示与比较 a=2.102; % T(0.05,2,18)=2.101 b=2.878; % T(0.01,2,18)=2.878 set(gca,'linewidth',2) % 红酒结果 for i=1:K1 Ta1(i)=a; Tb1(i)=b; end t1=1:K1; subplot(2,1,1);
(1) 两组品酒师对红酒和白酒的评价结果差异都不显著; (2) 对白酒评价结果的差异小于对红酒的差异。
2.2.2 评价结果稳定性
基于上面的分析,我们可知,两组品酒师对酒样的评判结果差异不显著,即可以认为来 自于同个样本的数据。这样我们就可以用每组品酒师的得分对总体样本的方差来表示各组品 酒师评价结果的稳定性了,即:
% 白酒结果 for i=1:K2
Ta2(i)=a; Tb2(i)=b; end t2=1:K2; subplot(2,1,2); plot(t2,AT_W,'*k-',t2,Ta2,'r-',t2,Tb2,'-.b', 'LineWidth', 2) title('白酒显著性检验结果','fontsize',14) legend('T 检验值', 'T(0.05)值', 'T(0.01)值') xlabel('样品号'), ylabel('T 检验值') % 显示平均检验结果 disp(['两组品酒师对红酒的平均显著性 T 检验值:' num2str(M_AT_R)]); disp(['两组品酒师对白酒的平均显著性 T 检验值:' num2str(M_AT_W)]); %% end
Mean2(i)=mean(SX2(i,:)); end % 计算检验值 for i=1:K1
S1(1,i)=(sum((SX1(i,:)-Mean1(i)).^2)+sum((SX2(i,:)Mean2(i)).^2))/(n1*(n1-1));
T1(1,i)=(Mean1(i)-Mean2(i))/(sqrt(S1(1,i))); end AT_R=abs(T1); M_AT_R=mean(AT_R); %% 白葡萄酒 T 检验计算过程 [m2,n2]=size(X3); K2=28; % 计算每个样品的总得分 for i=1:K2
%% 红葡萄酒 T 检验计算过程 [m1,n1]=size(X1); K1=27; % 计算每个样品的总得分 for i=1:K1
for j=1:n1 SX1(i,j)=sum(X1(10*i-9:10*i,j)); SX2(i,j)=sum(X2(10*i-9:10*i,j)); end end % 计算每组样品得分的均值 for i=1:K1 Mean1(i)=mean(SX1(i,:));
(n1 − 1) + (n2 − 1)
n1
n 2
当 n1 = n2 = n 时,
Hale Waihona Puke ∑ ∑ S x1−x2 =(x1 − x1 )2 + (x2 − x2 )2 n(n − 1)
S x1−x2 为均数差异标准误, n1 、 n2 , x1 、 x2 分别为两样本含量、平均数。
(3)根据 df=(n1-1)+(n2-1),查临界 t 值: t0.05 、 t0.01 ,将计算所得 t 值的绝对
2 问题 1 模型的建立和求解
2.1 问题 1 的分析
问题 1 要求我们首先首先要确定两组评酒员的评价结果有无显著性差异,再评判哪组 结果更可信。既然是显著性差异,我们很容易就想到可以用统计学中的显著性检验方法来确 定该问题。
显著性检验(test of significance)又叫假设检验,是统计学中一个很重要的内容。显著 性检验的方法很多,常用的有 t 检验、F 检验和χ2 检验等。尽管这些检验方法的用途及使用 条件不同,但其检验的基本原理是相同的。根据本问题的场景,结合以上三个检验方法的特 点,该问题比较适合用 t 检验方法。
在该问题中,每个样品的品质可以认为是固定的,所以对每个样品,不同组品酒员的总 分应用 T 检验最合适,也最能反应两组品酒员的评价结果。
为此,在利用 T 检验之前,需要对原始数据进行一些预处理,主要处理内容包括: (1) 数据质量检查与清洗,即查看数据是否有缺失,如果有缺失,则需要进行填充。通 过检查数据质量发现,的确存在数据缺失现象,为此对于缺失的值,用同组的平均值来进行 填充。 (2) 对各个 sheet 中的数据按照样品编号进行重新排列,以便利用程序进行比较。 经过这样的处理,就可以用程序来计算这些样品的 T 检验值了, 这样就可以用每组检 验值的平均值来表示每组品酒师对红酒和白酒的显著性差异,即:
