四线电阻触摸屏校准算法小结

合集下载

电阻式触摸屏校准算法分析

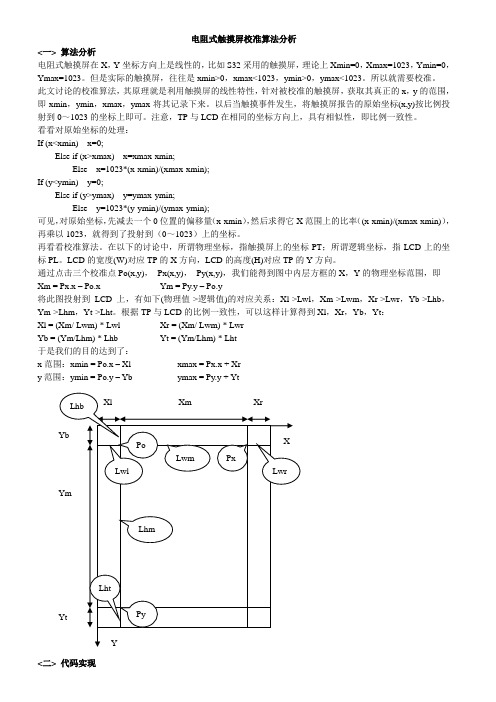
电阻式触摸屏校准算法分析<一> 算法分析电阻式触摸屏在X，Y坐标方向上是线性的，比如S32采用的触摸屏，理论上Xmin=0，Xmax=1023，Ymin=0，Ymax=1023。

但是实际的触摸屏，往往是xmin>0，xmax<1023，ymin>0，ymax<1023。

所以就需要校准。

此文讨论的校准算法，其原理就是利用触摸屏的线性特性，针对被校准的触摸屏，获取其真正的x，y的范围，即xmin，ymin，xmax，ymax将其记录下来。

以后当触摸事件发生，将触摸屏报告的原始坐标(x,y)按比例投射到0～1023的坐标上即可。

注意，TP与LCD在相同的坐标方向上，具有相似性，即比例一致性。

看看对原始坐标的处理：If (x<xmin) x=0;Else if (x>xmax) x=xmax-xmin;Else x=1023*(x-xmin)/(xmax-xmin);If (y<ymin) y=0;Else if (y>ymax) y=ymax-ymin;Else y=1023*(y-ymin)/(ymax-ymin);可见，对原始坐标，先减去一个0位置的偏移量（x-xmin），然后求得它X范围上的比率（(x-xmin)/(xmax-xmin)），再乘以1023，就得到了投射到（0～1023）上的坐标。

再看看校准算法。

在以下的讨论中，所谓物理坐标，指触摸屏上的坐标PT；所谓逻辑坐标，指LCD上的坐标PL。

LCD的宽度(W)对应TP的X方向，LCD的高度(H)对应TP的Y方向。

通过点击三个校准点Po(x,y)，Px(x,y)，Py(x,y)，我们能得到图中内层方框的X，Y的物理坐标范围，即Xm = Px.x – Po.x Ym = Py.y – Po.y将此图投射到LCD上，有如下(物理值->逻辑值)的对应关系：Xl->Lwl，Xm->Lwm，Xr->Lwr，Yb->Lhb，Ym->Lhm，Yt->Lht。

电阻触摸屏三点校准法

三点校准法三点校准法较之前面介绍的二点校准法更为精确。

当触摸屏与液晶屏间的角度差很小时，经过推理可以假设触摸屏与液晶显示器各点之间的对应关系为（假设液晶显示器的坐标为（XD, YD），触摸屏的坐标为（X,Y））：XD = AX + BY + CYD =DX + EY + F因为要取三个点进行校准，所以存在六个变量，即要通过六个方程式求出液晶显示器的坐标。

此处要求三个点尽量分散，最好为左上角、中间、右下角三点。

得：XD0 = AX0 + BY0 + CXD1 = AX1 + BY1 + CXD2 = AX2 + BY2 + CYD0 = DX0 + EY0 + FYD1 = DX1 + EY1 + FYD2 = DX2 + EY2 + F可求出 A、B、C、D、E、F的值，一旦这些参数值定下来，便可利用上面的方程组，通过触摸屏上的原始数据计算出它在LCD显示器上的对应点。

推导得出将K作为各方程式的公分母，便可得出未知量：K ＝ (X0－X2)(Y1－Y2)－(X1－X2)(Y0－Y2)A ＝ ((XD0－XD2)(Y1－Y2)－(XD1－XD2)(Y0－Y2))／KB ＝ ((X0－X2)(XD1－XD2)－(XD0－XD2)(X1－X2))／KC ＝ (Y0(X2XD1－X1XD2) + Y1(X0XD2－X2XD0) + Y2(X1XD0－X0XD1))／KD ＝ ((YD0－YD2)(Y1－Y2)－(YD1－YD2)(Y0－Y2))／KE ＝ ((X0－X2)(YD1－YD2)－(YD0－YD2)(X1－X2))／KF ＝ (Y0(X2YD1－X1YD2) + Y1(X0YD2－X2YD0) + Y2(X1YD0－X0YD1))／K。

屏幕4点校准算法

屏幕4点校准算法介绍屏幕4点校准算法是一种用于校准触摸屏幕的方法。

通过测量用户点击屏幕时的坐标，并与屏幕上实际显示的坐标进行比较，可以计算出触摸屏幕的误差，并进行校准，从而提高触摸屏幕的准确性和灵敏度。

本文将详细介绍屏幕4点校准算法的原理、步骤和应用。

原理屏幕4点校准算法的原理基于触摸屏幕在不同位置的响应误差是不一样的。

通常情况下，由于制造过程中的一些偏差和材料差异，触摸屏幕在边缘和角落的响应误差较大，而在中心位置的响应误差较小。

因此，通过在触摸屏幕的四个角落进行校准，可以得到一个精确的校准参数，从而减小触摸屏幕的误差。

步骤屏幕4点校准算法的步骤如下：步骤1：选择参考点首先，需要选择四个参考点，一般选取屏幕的四个角落。

这四个参考点的坐标需要事先确定，并且要尽可能分布在屏幕的不同位置。

步骤2：用户操作用户需要按照指示在屏幕上分别点击四个参考点位置。

系统会记录下用户点击时的坐标。

步骤3：计算校准参数根据用户点击时的坐标和事先确定的参考点坐标，可以计算出校准参数。

校准参数可以通过线性插值或者其他数学模型得到，具体的计算方法要根据具体情况而定。

步骤4：应用校准参数最后，将计算出的校准参数应用到触摸屏幕上，以校正触摸屏幕的误差。

校准参数可以通过软件或者硬件的方式进行应用。

应用屏幕4点校准算法广泛应用于各类触摸屏设备，例如智能手机、平板电脑、工控机等。

通过校准触摸屏幕，可以提高用户的触控体验，减少误操作，并且可以精确地控制光标的位置。

总结屏幕4点校准算法是一种用于校准触摸屏幕的方法，通过选择参考点、用户操作、计算校准参数和应用校准参数等步骤，可以提高触摸屏幕的准确性和灵敏度。

该算法广泛应用于各类触摸屏设备，可以改善用户的触摸体验。

电阻技术触摸屏的校正算法及应用编程设计

式２３ —
ＹＢ＝ＹＡ４Ｋ（ＢＹＬＬＹＹ — Ａ）－
由式２２我们可以推出计算Ｋ系数的公式 —
Ｋ＝ＸＢ— Ａ） × — Ａ）Ｘ（ＬＸＬ／ＢＸ（
Ｋ＝ＹＢ— Ａ）Ｙ — Ａ）Ｙ（ＬＹＬ／ＢＹ（
３触摸屏应用的编程思路
维普资讯
２１穰述，窳薪周知，基于电阻技术触摸屏分为四线电阻触摸
屏、线电阻触摸屏或更多线电阻触摸屏，薹但无论哪一类
电阻触摸屏都有一个最大共性．电压成线性均匀分布正
圉２１ —
２２２逻辑坐标的计算．由于电阻式触摸屏的电压成线性均匀分布，那么～Ｄ转换后的坐标也成线性。假如我们将液晶最左下角点２２１物理坐标和逻辑坐标．对应的触撞屏上的点定为物理坐标原点Ａ其物理坐标记
式２ —１
Ｋ＝｛Ｌ —ＹＣ）Ｙ —Ｙ＋ＹＢＬ／ＢＤ）Ｙ（ＡＬ／ＡＣ）（Ｌ —ＹＤ）Ｙ —ＹＪＹ（（／２（将Ｃ点逻辑坐标作为基坐标，据式２２触摸屏６）根 — 则上任意一点Ｆ逻辑坐标与基坐标的关系为：ＸＦ＝ＸＣ４Ｋ（Ｆ—Ｘ）ＬＬＸＸ－ＣＹＦ＝ＹＣ４Ｋ（Ｆ—Ｙ）ＬＬＹＹ－Ｃ式２４ —
Ｂｔｎ的矩形区域内。ｕｔｏ如果液晶上有若干个Ｂｔｎ区域，么我们将每个ｕｔｏ那
（）１首先在ＡＣＥ对应的位置逐步用尖状物触摸，到ＢＤ得

四线电阻式触摸屏控制与校准

Bottom film with transparent conductor on top side
YX+ Insulating material (usually glass)
Conductive bar
2008 年 12 月 17 日
文件编号 001-50412 版本 **
1
[+] Feedback
触摸屏结构
四线触摸屏的结构如图 1 所示，由两个透明层构成，透明层的内表面均涂了薄薄一层导电材料。当触摸屏表面受到的压力（如通过触笔或手指进行按压）足够大时，顶层与底层之间会产生接触，从而使电阻层发生接触。
图 1. 四线触摸屏结构
Top film with transparent conductor on bottom side Y+ X-
前言
电阻式触摸屏广泛用于各种类型的设计中。其结构简单，成本低，且使用方法易于被用户掌握。虽然操作简单，但触摸屏器件几乎都要求进行校准，以便将触摸屏坐标转换成实际屏幕坐标（LCD 或其它）。
第一种测量方法
触摸可以由三个参数界定。第一和第二参数分别是 X 触摸点位置和 Y 触摸点位置。第三参数即为“触摸压力”，可使触摸屏区分手指接触和触笔接触。图 2 说明的是被触摸和未被触摸的屏幕的等效电路。每个测量周期均采用不同的电压组合。在本项目中，触摸屏接 Vdd 是指切换 PSoC® 端口驱动模式为 “strong” 并把逻辑值设为 “high”。接地是指将端口驱动模式设为 “strong” 并把逻辑值设为 “low” 。 PSoC® 输出级漏电阻较低，其感应也小。校准算法可以对这种差异进行补偿。
R g (U t − U x ) ; Rt = ext U cc − U y

电阻式触摸屏数据校准的一种补偿算法

桎梏，ＬＤ和触摸屏的坐标变换入手，出了一种可行的补偿算法。从Ｃ给
【关键词】触摸屏；Ｃ坐标；：ＬＤ；补偿；算法
ｌ引言、
Ｐ＝ＫＸＯＹＸ＇、＋＋Ｔｏ［．－￣＋ｌｅＸＫＹＹ】ＴＫ
即：
Ｐ＝ＫＲｏＯＯＲｉＯＸ，ｓ０ｅｃｓ＋ＴＤ【ｃｓ－Ｋｓ＋ＴＫｉ＋ＫＲｏＯＹ］ｎｎ
根据式１得：．
ＸＩＡＸｌＢＹｌＣ）ｌ＝＋＋ＸｍＡＸ２ＢＹ＋＝＋！Ｃ
Ｙｍ＝ＤＸＥＹｏ＋Ｆ
Ｙｍ＝ＤＸＩＥ＋＋ＹＩＦ
Ｙｍ＝ＤＸ＋ＥＹ２＋Ｆ
由上面的方程得到：
Ｋ（０ｘ（－Ｙ）（－Ｙ— １＝）一＿Ｙ－２ＸｒＸ（ｏＹ【９－ｊ
【陈文智．２】嵌入式系统开发原理与实践．北京：清华大学出版社，０５２０：
２０５
［林晓飞，３】林兵，张辉．于ＡＲ嵌入式Ｌｎｘ应用开发与实例教程．基Ｍｉｕ清
华大学出版社．０：２ — ３２７２４２２０
Ａ：—
（Ｄ－ｋｚＹ－：－ｘ（ｏ．），Ｙ）（ｍ－ｘ：Ｙ－：ｘ％（ｏ）ｏＹ）（）
—
Ｂ：—
ｉ，．，（－）（ｏ－ｏ（－ｘ：ｆ，－￣０ｘｏｘ：－ｘｏｘＯｘ，ｘ，））
—
，、一
ｆｏＸＪＸ，ｖ）ＩＸ：Ｙ（￣一Ｘ：＋Ｙ（ｏ一Ｘ：ｚ）：Ｘ０Ｘｏｏ）Ｘ：，ＸｏＸ￣＋Ｙ（ｏ一ＸＯｏＸｔ（Ｙ，ＹＯＹ－２－（ｏ－ｍ）ｏＹ）（ｏ－ｏ（，Ｙ）Ｙ，Ｙ（－：）Ｙ）

四线电阻触摸屏校准算法小结

3 + 1得xoff = [(X2 + X1)-xfac(x2 + x1)]/2; //得到x轴方向的偏移量
4 -2得yfac = (Y2 -Y1)/(y2 -y1); //得到y轴方向的比例因子
4 + 2得yoff = [(Y2 + Y1)-yfac(y2 + y1)]/2; //得到y轴方向的偏移量
有如下方程组：
X1 = xfac * x1 + xoff; // 1
Y1 = yfac * y1 + yoff; // 2
X2 = xfac * x2 + xoff; // 3
Y2 = yfac * y2 + yoff; // 4
解得：
3 -1得xfac = (X2 -X1)/(x2 -x1); //得到x轴方向的比例因子
OK!所谓的三点触摸校准，四点触摸校准只不过是加了可靠的滤波算法，因为触摸笔和屏
的接触不是很准确的！而像素点是很小的，所以通常都用四点校准，而且经验证这此算法是
必须加的，否则很不准,参见STM32学习笔记相关实验实验例程，已验证通过理论知识:
*触摸屏实际是在普通的lcd上贴了一个触摸膜,没有原生的触摸屏
B=(Xt[0]-Xt[2])*(Xd1-Xd2)-(Xd0-Xd2)*(Xt[1]-Xt[2]);
C=Yt[0]*(Xt[2]*Xd1-Xt[1]*Xd2)+Yt[1]*(Xt[0]*Xd2-Xt[2]*Xd0)+Yt[2]*(Xt[1]*Xd0-Xt[0]*Xd1);
D=(Yd0 -Yd2)*(Yt[1] -Yt[2]) -(Yd1 -Yd2)*(Yt[0] -Yt[2]);
有3个未知数abc,显然需要3个方程

触摸屏校准常用算法分析_许荣斌

/#0!, 1!. 20’- 1’. 210!- 1!. 20’, 1’. 2 $#00!", 1!". 20’- 1’. 210!"- 1!". 20’, 1’. 22 3 / &#00!, 1!. 20!"- 1!". 210!", 1!". 20!- 1!. 22 3 / (#0’, 0!. !"- 1!- !". 2%’- 0!, !". 1!. !", 2%’. 0!- !", 1!, !"- 22 3 / )#00’", 1’". 20’- 1’. 210’"- 1’". 20’, 1’. 22 3 / *#00!, 1!. 20’"- 1’". 210’", 1’". 20!- 1!. 22 3 / +#0’, 0!. ’"- 1!- ’". 2%’- 0!, ’". 1!. ’", 2%’. 0!- ’", 1!, ’"- 22 3 /
.4-&)VQ] .&9I-5)--)NVa/3‘--)JV_ : ]FAB_ ； .4-&)WQ] .&9I-5)--)NWa /3‘--)JW_ : ]ARB_ ；
计算触摸屏中此按钮的左上角坐标 ]5O--)’V@， R） 5O--)’W@_ 和右下角坐标 ]5O--)’VA， 5O--)’WA_：
3..VQ+ONVXXR 3..WQ+ONWXXR
触摸屏校准常用算法分析关系，进行校准。
!
触摸屏的校准举例假设液晶屏 ]FAB^ARB_ 中有一个实心矩形作为按钮，此实

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

有如下方程组：
X1 = xfac * x1 + xoff; // 1
Y1 = yfac * y1 + yoff; // 2
X2 = xfac * x2 + xoff; // 3
Y2 = yfac * y2 + yoff; // 4
解得：
3 -1得xfac = (X2 -X1)/(x2 -x1); //得到x轴方向的比例因子
OK!所谓的三点触摸校准，四点触摸校准只不过是加了可靠的滤波算法，因为触摸笔和屏
的接触不是很准确的！而像素点是很小的，所以通常都用四点校准，而且经验证这此算法是
必须加的，否则很不准,参见STM32学习笔记相关实验实验例程，已验证通过理论知识:
*触摸屏实际是在普通的lcd上贴了一个触摸膜,没有原生的触摸屏
E=(Xt[0] -Xt[2])*(Yd1 -Yd2) -(Yd0 -Yd2)*(Xt[1] -Xt[2]);
F=Yt[0]*(Xt[2]*Yd1 -Xt[1]*Yd2) + Yt[1]*(Xt[0]*Yd2 -Xt[2]*Yd0) + Yt[2]*(Xt[1]*Yd0 -Xt[0]*Yd1);
2012-8-源代码中给M[0]~M[2]赋值,然后x[0]等是
从驱动读数,最后解方程即可
最后abc表达式,
F= (Xt[0] -Xt[2])*(Yt[1] -Yt[2]) -(Xt[1] -Xt[2])*(Yt[0] -Yt[2]);
//计算参数
A=(Xd0-Xd2)*(Yt[1]-Yt[2])-(Xd1-Xd2)*(Yt[0]-Yt[2]);
四线电阻触摸屏校准算法的实现
(一)
四线电阻屏的触摸板坐标和屏坐标有如下关系：
X0 = xfac * X + xoff;
Y0 = yfac * Y + yoff;
其中X0,Y0是屏的物理坐标，xfac,yfac为x,y方向的比例因子，xoff,yoff为x,y方向的偏移
量.
既然说到了校准，那么这四个量肯定是不变的，所以我们可以用至少两个屏的物理坐标点就
可算出这四个量,也即是两点校准法，由于按下屏后读出的是X,Y值，而校准时用的X0,Y0
也是已知的，那么就是解四元一次方程组了,算法如下：
(X1,Y1)和（X2,Y2）是用于校准时屏上显示的两个点，这两个点的坐标必须不一样，
是已知的;
(x1,y1)和(x2,y2)是校准时读取的被按下的两点的触摸板坐标值;
有3个未知数abc,显然需要3个方程
M[0] = A * x[0] + B * y[0] + C
M[1] = A * x[1] + B * y[1] + C
M[2] = A * x[2] + B * y[2] + C
M[0]~M[2]代表lcd的坐标, x[0]~x[2], y[0]~y[2]是触摸膜坐标
这里a = 640 / 1024 = 0.625
再说c
由于安装的机械问题,可能有水平的平移,这里就是c
最后说b
一开始还以为公式错了,为什么x的东西还有y的事,原理还是安装机械的问题,若膜和lcd
安装有一定的倾斜角度y就不是0了
计算abcdef参数
对应abc和def来说是独立的,类似的,下面以计算abc为例
校准公式
X液晶= ax + by + c x,y是触摸屏
Y液晶= dx + ey + d
公式原理
X,Y的公司类似,这里就已X液晶的公式为例
先说a
首先,液晶和触摸膜的分辨率通常是不一样的,如液晶分辨率640*480,触摸膜分辨率
1024 * 768,
则这时就需要把触摸膜的分辨率乘一个系数才和液晶分辨率对应,这里就是ax中的a,
3 + 1得xoff = [(X2 + X1)-xfac(x2 + x1)]/2; //得到x轴方向的偏移量
4 -2得yfac = (Y2 -Y1)/(y2 -y1); //得到y轴方向的比例因子
4 + 2得yoff = [(Y2 + Y1)-yfac(y2 + y1)]/2; //得到y轴方向的偏移量
B=(Xt[0]-Xt[2])*(Xd1-Xd2)-(Xd0-Xd2)*(Xt[1]-Xt[2]);
C=Yt[0]*(Xt[2]*Xd1-Xt[1]*Xd2)+Yt[1]*(Xt[0]*Xd2-Xt[2]*Xd0)+Yt[2]*(Xt[1]*Xd0-Xt[0]*Xd1);
D=(Yd0 -Yd2)*(Yt[1] -Yt[2]) -(Yd1 -Yd2)*(Yt[0] -Yt[2]);