大学物理A静电场中的导体和电介质习题答案及解法201064
静电场中的导体和电介质习题解答

第十章 静电场中的导体和电介质一选择题 1.半径为R 的导体球原不带电, 则导体球的电势为 () q B.羊 4 n o a 今在距球心为 a 处放一点电荷q ( a >R 。
设无限远处的电势为零, qa D . 4 n o (a R )解:导体球处于静电平衡,球心处的电势即为导体球电势,感应电荷 C.4 n o (a R) q 分布在导体球表面上,且 q ( q ) 0 ,它们在球心处的电势 1 V 乩q 4 n o R点电荷q 在球心处的电势为 47^ q dq V J 据电势叠加原理,球心处的电势 4 n o aV o V Vq 。
4 n o a 所以选(A ) 2.已知厚度为d 的无限大带电导体平板, 则板外两侧的电场强度的大小为 ( 2 A. E B. E 2 o o两表面上电荷均匀分布, 电荷面密度均为 ,如图所示,d C. E 二一 D. E=—— ⑰ 2匂解:在导体平板两表面外侧取两对称平面, 做侧面垂直平板 的高斯面,根据高斯定理,考虑到两对称平面电场强度相等,且高斯面内电荷为2 S ,可得E —。
0选择题2图 所以选(C ) 3.如图,一个未带电的空腔导体球壳,内半径为 量为+q 的点电荷。
() R,在腔内离球心的距离为 用导线把球壳接地后,再把地线撤去,选无穷远处为电势零点,则球心 d 处(d<R ,固定一电o 处的电势为A. C.B. 4 n o d q 1 D. (—4 n 0 d 解:球壳内表面上的感应电荷为 q _q 4n o d 4n o R 选择题3图 1R ) -q,球壳外表面上的电 (+q . j 荷为零,所以有V o 所以选(D ) 4.半径分别为 在忽略导线的影响下,A . R/r B. R 2 / r 2 C. r 2 / R 解:两球相连,当静电平衡时,两球带电量分别为 分布,且两球电势相等,取无穷远为电势零点,则 QR 和r 的两个金属球,相距很远,用一根细长导线将两球连接在一起并使它们带电, 两球表面的电荷面密度之比 R / r 为() B. R 2 / r 2 C. r 2 / R 2 D. r / R Q q ,因两球相距很远,所以电荷在两球上均匀 所以选(D )R Q/4 R 2r q /4 r 2「的均匀电介质,若测得导体表面附近场强为 E,则导体球面的自由电荷面密度 为() 上D S S ,即 所以选(B )6. 一空气平行板电容器,充电后测得板间电场强度为 煤油,待稳定后,煤油中的极化强度的大小应是(£ A . —E g £ £(£ 1 )匸 B . E 0£不管是否注入电介(£ 1) C. E 。
《物理学基本教程》课后答案第九章静电场中的导体和电介质精品资料

第九章静电场中的导体和电介质9-1把一厚度为d的无限大金属板置于电场强度为 E 0的匀强电场中, E 0与板面垂直,试求金属板两表面的电荷面密度.- σ’+ σ’分析对于有导体存在的静电场问题,首先由静电-+平衡条件分析放入静电场后导体上电荷的重新分布情-+况,再计算空间电场和电势的分布.-+E0本题中,将金属板放入均匀电场后,由于静电感应,-+平板两面带上等值异号感应电荷.忽略边缘效应,两带-+电面可视为平行的无限大均匀带电平面.解设平板两表面的感应电荷面密度分别为和,如图 9-1 所示.由例题 8-7 结果知,带感应电荷图 9-1的两表面视为带等量异号电荷的无限大平行平面,在导体中产生的场强为E,方向与E0相反,由场强叠加原理,平板中任一点的总场强为E E0E E0根据静电平衡条件,金属板中场强E0 ,代入上式得E00则E0 0,E0 0结果与板的厚度无关.9-2一金属球壳的内外半径分别为R1和 R2,在球壳内距球心为 d 处有一电荷量为 q 的点电荷,(1 )试描述此时电荷分布情况及球心O 处电势;(2 )将球壳接地后,以上问题的答案; (3 )如原来球壳所带电荷量为Q ,(1)、(2)的答案如何改变.分析 当导体内达到静电平衡后, 应用高斯定理可以确定导体上电荷重新分布的情况,然后用电势叠加原理求电势.解( 1 )按照静电平衡条件,导体内部E 0 ,在球壳内外表面间作同心高斯球面, 应用高斯定理,可知球壳内表面上应有 q 的感应电荷,为非均匀分布,如图 9-2 所示.根据电荷守恒定律和高斯定理,球壳外表面上有 + q 的感应电++ – +– d R 1+ q + –q ·+- q – R 2+– ++荷,且均匀分布.点电荷 q 在 O 点产生的电势为V 1图 9-2q4 d球壳内外表面上的感应电荷q 和 + q 无论分布情况如何,到球心距离分别为R 1 和 R 2 ,电势叠加原理表达式为标量求和,所以在O 点产生的电势分别为q V 3q V 2R 14R 24O 点电势为VV 1V 2 V 3q qq 4d4 R 1 4R 2q ( 11 1 )4dR 1R 2(2 )将球壳接地后,外球面上的感应电荷消失,球面上电荷分布不变,得V V 1V 2 q (11 )4dR 1(3 )如果原来球壳带电量为 Q ,达静电平衡后外球面上电荷 Q+ q 均匀分布,内球面上电荷分布不变,得V V1V2V3q( 1 1 1 )Q4 d R1R2 4 R2球壳接地后,结果与( 2)相同.9-3一无限长圆柱形导体半径为R a,单位长度带有电荷量λ1,其外有一共轴的无限长导体圆筒,内外半径为分为R b和 R c,单位长度带有电荷量λ2,求(1)圆筒内外表面上每单位长度的电荷量;(2)r R a, R c r R b, R b r R c,r R c四个区域的电场强度.分析静电平衡条件下,在圆筒导体内场强为零,用高斯定理和电荷守恒定律可求出感应电荷的分布.解( 1)如图 9-3所示,在圆筒形导体内作半径为r ,高为单位长的同轴圆柱形高斯面 S,设导体圆筒内外表面单位长的感应电荷分别为和,由静电平衡条件知导体内E 0,故有- λ1λ1R aE d S1q 1(1)0Rb0012λ+λ即得半径为 R b的圆筒内表面单位长上的感S r R c应电荷为 -λ1.由电荷守恒定律知,半径为 R c的圆筒外表面上单位长的感应电荷应为λ1,加上原有电荷量图 9-3λ2,单位长上总带电量为21.(2 )电荷重新分布的结果形成三个同轴的无限长带电圆柱面如图9-3 ,由于电荷分布具有轴对称性的,产生的电场也是轴对称的,用高斯定理可求出r R a时,E0R a r R b时,E12rR b r R c时,E0r R c时,E1220r9-4证明:两平行放置的无限大带电的平行平面金属板 A 和 B 相向的两面上电荷面密度大小相等,符号相反,相背的两面上电荷面密度大小相等,符号相同,如果两金属板的面积同为 100cm 2,电荷量分别为Q A 6 10 8C和Q B410 8 C ,略去边缘效应,求两个板的四个表面上的电荷面密度.分析根据静电平衡条件,一切净电荷都分布在导体表面,本题中的电场空间可视为四个无限大均匀带电平行平面产生的电场的叠加,金属板 A 、 B 内任意点场强为零.由电荷守恒定律可以建立各表面的电荷面密度与两金属板的总电荷量之间的关系.A Bσ1σ2σ3σ4解设 A、B 两板的四个表面上的电荷面密度(先假定为正)分别为σ1、σ2、σ3和σ4,如图9-4所示.设向右为正向,由无限大均匀带电平面的场强公式和场强叠加原理,考虑到金属板 A 、B 内任意点场强为零,得图 9-4金属板 A内123422220金属板 B内1234222200 0解得23,又由电荷守恒定律得S()Q A,S(34)QB联立解得Q A Q B 5 106C/ 2 mS2Q A1110 6 C/m 2S31106 C/m 29-5 三个平行金属板 A 、B 和 C,面积都是 200cm2,A、B 相距 4.0mm ,A、C 相距 2.0mm ,B、C 两板都接地,如图 9-5 所示,如果 A 板带正电3.010 7C,略去边缘效应,(1)求 B 板和 C 板上感应电荷各为多少?(2 )以地为电势零点,求 A 板的电势.分析由静电平衡条件, A 、B、C 板内各点的场强均为零, A 板上电荷分布在两个表面上,因B、C 两板均接地,感应电荷应分布在内侧表面上.解(1)设 A板 1 、2 两面上带电量分别为 q 1和 q 2,B、C 两板与 A 相对的两内侧表面 3 、 4上的感应电荷分别为 q 1’和 q 2’,如图 9-5所示.作侧面与平板垂直的高斯面 S1,两端面处E=0,忽略d1- d2 -边缘效应,侧面无电场线穿过,由高斯定理B A C31 2 411q1S q1S) 0S SE d S q(S0SS得q1q1S1q 1’q 2’同理可得 q2q2.AB板间和AC板间为匀强电场,场强分别为q1q 2q1E q2E12SS图 9-5又已知 V AB V AC,即E1d1E2d 2因q 1 q 2q 3.0 10 7 C由以上各式,得 B 、C 两板上的感应电荷分别为q 1q 1q 1.0 10 7C3q 2 q 22q 12.0 10 7C(2 )取地电势为零, A 板电势即为 A 、 B 间电势差V AVABE 1 d 1q 1d 12.3 103 VS9-6 半径为 R 11.0cm 的导体球所带电荷量为 q 1.0 10 10 C ,球外有一个内外半径分别为 R 23.0cm 和 R 34.0cm 的同心导体球壳,壳上带有电荷量Q 11 11 10 C ,求:( 1)两球的电势;(2)用导线把两球连接起来时两球的电势;( 3)外球接地时,两球电势各为多少?(以地为电势零点. )分析 根据静电平衡条件可以确定感应电荷的分布,用导线连接的导体电势相等,外球接地后电势为零.解 ( 1)根据静电平衡条件,导体球壳内表面感应电荷为-q ,外表面感应电荷为 q ,原有电荷量 Q .由电势叠加原理,导体球电势为V 1qq q Q 1 ( qq q Q) 3.3 10 2 VR 14 R 2 4R 34R 1R 2R 3导体球壳的电势为V 2q q Q q Q q 2.7 102 V4R34 R 34 R 34 R 3(2 )球壳和球用导线相连后成为等势体, 电势等于半径为 R 3 带电量为 Q+ q的均匀带电球面的电势,以无穷远为电势零点,得V 2Q q 2.7 102 V4 R 3(3 )外球接地后,只乘下内表面的电荷 -q ,由电势叠加原理内球电势为qq V 1460V4 R 1R 2外球壳接地与地等势,即V 2 0另外,求 V 1 ’时还可以用内球产生的电场的线积分计算,即R 2qdr q (11) 60VV 2r 2 R 144R 1 R 29-7 半径为 R 的金属球离地面很远,并用细导线与地相连,在与球心的距离为 D 3R 处有一点电荷q ,试求金属球上的感应电荷.R q ’ q分析 由于导体球接地, 其表面上的感应正电荷通过导线与地球内负电荷中和, 只剩下负感应电荷在金属球表面不均匀地分布, 如图 9-7 所示.接地后,导体球上各点电势均为零,球心OOD图 9-7点的电势应等于点电荷在该点电势与金属球表面感应负电荷在该点电势的代数和.解 设金属球上感应电荷为 q ,在金属球表面不均匀地分布,但这些电荷到O 点距离相等,电势叠加后得V 2qR4点电荷 q 在 O 点的电势为V 1q3R4V V 1q qV 243R4R得感应电量为qq3由此可以推证,当 D nR 时,qqn9-8 如图 9-8 所示,三个“无限长”的同轴导体圆柱面 A 、B 和 C ,半径分别为 R A 、 R B 、 R C ,圆柱面 B 上带电荷, A 和 C 都接地,求: B 的内表面单位长度电荷量 1 ,外表面单位长度电荷量2之比值 1/ 2.分析本题与题 9-5 的解题思路相似.解 在导体 B 内作单位长圆柱面形高斯面, 可以说明 A 面单位长度上感应电荷为 1 .同理,可说明 C 面单位长度上感应电荷为 2 .由高斯定理可知场强分布为R ArR B 时, E 1,方向沿径向由 B 指向 A .rR BrR C 时, E 2 2,方向沿径向由 B 指向 C .rRR AdrR BV BA RA1 1lnBA 间电势差E 2 d rR BB2r2R ABC 间电势差V BC2ln R C- λ22R BR B λ1 λ2B 为等势体, A 、C 接地, V BAV BC ,从而CARR1 ln( R C / R B )A B C- λ12ln( R B / R A )9-9 半径分别为 R 1 和 R 2 ( R 2 R 1 ) 的两个同心导体薄球壳,电荷量分别为 Q 1和Q 2 ,今将内球壳图 9-8用细导线与远处的半径为 r 的导体球相联,导体球原来不带电,并假设导线上无电荷分布,试求相连后,导体球所带电荷量q .分析 带电的内球壳与导体球用导线相连后, 一部分电荷通过导线转移到导体球表面上.两者相距甚远,可以认为两球壳与球的电场互不影响,已假设导线上无电荷分布,利用内球壳与远处导体球电势相等建立方程求解.解因两球壳与球的电场互不影响,导体球电势为V1q4r2假设导线上无电荷分布,则内球壳上电荷量变为Q1q ,由电势叠加原理,内球壳的电势为Q1q Q 2V2R1 4R2Q24Q1- q q 内球壳与远处导体球电势相等,即R1R rV1V22qQ1q Q24 r 4 R1 4 R2图 9-9解得q r ( R1Q2R2Q1 ) R2 (R1r )9-10地球表面的电场强度为150N/C ,方向垂直指向地面,若把地球视为导体,试求地球表面的电荷面密度和地球带的总电荷量.分析由于地球表面的电场强度方向垂直指向地面,可知地球带负电,将地球视为导体,在静电平衡状态下,电荷分布在表面上.解设地球表面的电荷面密度为,表面附近的场强E,则E 0(150 8.85 10 12 )C/m 2 1.33 10 9 C/m 2地球半径 R 6.3710 6 m ,地球带的总电荷量为q 4 R 1.33 10 942C 6.8 10 5 C680kC9-11设有一孤立导体球,半径为R.,(1 )试求其在真空中的电容表示式;(2)若把地球视为R 6.37 106m的导体球,它的电容量多大?( 3)欲使地球的电势改变 1V ,需使其所带电荷量改变多少?解(1 )将孤立导体球视为与无穷远处的同心导体球面组成的球形电容器,利用球形电容器电容表达式,(9-4 )式给出孤立导体球的电容Q4 R .CV(2)地球电容C4 6.37 106 F 710 4F(3)欲使地球电势改变 1 伏特,需使地球电量的改变为Q CV 7104 1 7 104C这个值很大,所以地球带电量的日常变化不会引起地球电势发生明显的改变,这就是通常可以选取地球作为电势零点的原因.9-12已知空气的击穿电场强度为 3 106 V/m ,求处于空气中一个半径为1m 的导体球最多能带多少电荷及能达到的最高电势.分析在带电导体球周围的空气形成一种绝缘介质包围着导体球,当导体球产生的电场足够强时,会使其周围的空气发生电离而成为导体,致使带电导体球放电,通常称为空气被击穿.因均匀带电导体球面的电场强度和电势与带电量成正比,为了不击穿周围的空气,带电导体球所带电量要受到限制.解由题意击穿电场强度Emax3106 V/m而E mQ m a x a xR2 4Qmax Emax4R 2310648.8510 1212C 3.3 10 4C最高电势为Q max E max 4R26 Vmax C4R RE max 310 V或Qmax 3.310 4V6 V maxR43 10V419-13收音机里的可变电容器如图9-13 (a)所示,其中共有 n 块金属片,相邻两片的距离均为 d ,奇数片联在一起固定不动(叫定片),偶数片联在一起可一同转动(叫动片),每片的形状如图9-13 ( b )所示,求当动片转到使两组片重叠部分的角度为时,电容器的电容.分析除了最外侧的两片外,每块金属片的两个表面分别与相邻的金属片表面构成一个电容器,如图 9-13(c)所示,所以 n 块金属片如此连接等效于( n 1 )个平行板电容器并联.当两组片重叠部分的角度为时,每个电容器有效极板面积为 S( ) ,因此电容器的等效电容是的函数.收音机调频的电容器就是根据这个原理设计的.r 2r 1(a)(b)(c)图 9-13解当两组片重叠部分的角度为时,每个电容器有效极板面积为S( r12r2 )360( n-1 )个极板面积为S,板间距为 d 的平行板电容并联时的等效电容为C(n 1) 0S (n 1)r22r12 d360 d式中以度计.9-14半径都为 a 的两根平行长直导线相距为 d (d a) .(1)设两导线每单位长度上分别带电和,求两导线的电势差;(2)求此导线组每单位长度的电容.分析因 d a ,可设两导线的电场互不影响,由场强叠加原理可求出两导线间的场强分布,d再用场强与电势的积分关系求两导线间电势差,rO P由电容器电容的定义即可求出单位长导线组的等2 a效电容.图 9-14解作两导线组合的截面图,以带正电导线轴心为原点建立坐标系如图9-14 所示.不难看出,正负电荷在P 点的场强均沿r 轴正向,矢量叠加简化为标量和E E E(d r )(11 )2 r r d - r 两导线间电势差为d a d a E d ra2a (11)dr lnd a r d r a由电容器电容的定义,导线单位长电容为Cd aVlna9-15有两个半径分别为 R1和 R2的导体球放在真空中,两球表面相距为d,已知 d R1和 d R2,试求两导体构成的电容器的电容.+Q- QOR1P R2d r图 9-15分析按题意d R2,可认为当两导体球分别带电Q 和Q 时,彼此电场互不影响,即各球面上电荷分布仍是均匀的,由场强叠加原理可求出两球球心连线上任一点的场,用与上题相似的方法可以求出两球电势差和两球构成的电容器电容.解以大球球心为原点,建立如图9-15 所示的坐标系,在坐标为r 处的 P 点(在连心线上),两球产生的电场均沿r 轴正向,得Q QE E E24( R1 R2 d r ) 24 r 两带电导体球间电势差为V R1 dE d rQ R1 d[11]dr R14R1r2( R1R2 d r )2Q1111)4(R2 d R1 d R2R1考虑到 d R1, d R2,可将电势近似表示为V Q ( 11 2 )4R1R2d此两导体球构成的电容器电容为Q4C12VR1 R2d9-16 两只电容器C18 F,C2 2 F ,分别把它们充电到1000V ,然后将它们反接,如图9-16 所示,求此时两极间电势差.分析并联电容极板间电压相同,因两电容器电容不等,则反接前两电容器带的电量必定不等.反接后,相连的极板上正负电荷中和,可以计算出中和后电荷量的代数和及并联电容器的等效电容C,从而求出电势差.解反接前,设 C1和 C 2带电量分别为 Q1和 Q2,充电电压 U 01000 V ,则Q1C1U 0Q2C2U 0+-反接后,正负电荷中和,中和后总电量为C1C2-+Q Q1 Q2,并联等效电容 C C1 C2,则并联电容器两板间电势差为图 9-16Q(C1C2)U0(810 62106 )1000 UC1C28 106210 6V 600VC9-17 如图 9-17所示, C110F, C2 5.0F,C3 5.0 F ,求:(1)AB间的电容;(2)在 AB 间加上 100V 电压时,求每一个电容器上的电荷量和电压;( 3)如果 C1被击穿,问 C3上的电荷量和电压各是多少?分析并联电容器极板电势相等,串联电容器极板上电荷量相等,总电压等于各电容器上电压之和.当C1上电压超过 C1的额定电压, C1将被击穿, C1支路即短路,全部电压就加在 C 3上,如超过 C3的额定电压, C 3将被击穿,A、B间就发生短路.所以,在设计电容器组合电路时,除应计算等效电容外,还应考虑分配到每个电容器上的电压是否超过所选电容器的额定电压.解(1)C1和C2并联电容为C C1 C 2,再与 C 3串联后,等效电容为C C 33.75 FCC C 3(2 )等效电容所带电量为Q CU ,串联的电容所带电量相等Q3Q CU 3.75 10 4 CAU 3Q375VC 3C C12U 1 U2Q Q1Q225V CC C1 C 23B又因Q1Q 2Q10 4C 图 9-17可解得Q1 2.5Q2 1.2510 4C(3)如果 C1被击穿, AB 间电压就加在 C3上,即U 3 U100V则Q3 C3U 3 5 104C9-18平板电容器,两极间距离为 1.5cm ,外加电压 39kV ,若空气的击穿电场强度为 30kV/cm,问此时电容器是否会被击穿?现将一厚度为0.3cm 的玻璃插入电容器并与两板平行,若玻璃的相对电容率为7 ,击穿电场强度为100kV/cm,问此时电容器是否会被击穿?结果与玻璃片的位置有无关系?分析加玻璃片后,电场被分成两部分,应分别计算出空气和玻璃中的电场强度,再判断是否有哪种介质中的场强超过了其击穿场强.可以证明结果与玻璃板的位置无关.解未加玻璃前平板电容器内场强为E U39 V/cm26kV/cm30kV/cm d 1.5因其量值小于空气的击穿电场强度,电容器不会被击穿.加玻璃后,设电容器极板的电荷面密度为,平行板电容器中电位移 D.设玻璃和空气中场强分别为E 1 和 E 2 ,则有DDE 1E 20 r00U玻璃厚为 d 1 ,则空气层厚为 d - d 1,得E 1d 1 E 2 (d d 1 ) U图 9-18由以上各式得E 1U4.48kV/cm( d d 1d 1 ) rU r31.4kV/cm 30kV/cmE 2d 1 ) d 1 (dr即空气部分首先被击穿,然后全部电压加在玻璃板上,致使玻璃中场强为U 39 E 1130kV/cm 100kV/cmd 10.3玻璃部分也会被击穿.9-19一平板电容器极板面积为 S ,两板间距离为 d ,其间充以相对电容率分别为r1、r2的两种均匀介质, 每种介质各占一半体积, 若忽略边缘效应,(1 )与两种不同介质相对的两部分极板所带电荷面密度是否相等?如果不相等,求:1 /2 = ?( 2)试证此电容器的电容为CS r1r 2d2分析忽略边缘效应,电容器中的电场可视为无限大平行平面间的电场,从而可以确定两种不同介质中场强与极板电势差的关系, 以及与两部分极板上的电荷面密度的关系, 从而可知极板上的总电荷量. 另一种思路是将充入两种介质后的电容器视为由两个电容器并联而成,直接应用并联电容器的计算公式.解 1(1)设电容器端电压为U ,两种介质中场强分别为E1和 E2,由充满均匀介质的平行板电容器的场强与电压的关系可得E1 E2U( 1)d设1、2分别为两种不同介质对应部分极板上的电荷面密度,忽略边缘效应,电容器中的电场可视为无限大平行平面间的电场,则有12(2 )E1E20 r10 r2S代入 (1) 式可得1r1εr1εr2d2r2即两部分极板所带电荷面密度不相等.由( 1 )和( 2)式可得极板上的总电荷量为图 9-19Q S0SU r1r2)(12)d(22由电容器定义得Q0S(r 1r 2) Cd2U解 2由并联电容器公式求总电容C C1S S0S(r 1r 2) C 20 r10 r 22 2d2d d可见第二种方法计算简单,用第一种方法可对物理过程、电场电荷分布有更明确的概念.另外在第一种方法中亦可用介质中的高斯定理求解.9-20一球形电容器,在外球壳的半径R 和内外导体间的电势差U 维持恒定的条件下,内球半径R 为多大时才能使内球表面附近的电场强度最小?并求这个最小电场强度的值.分析导体表面附近的场强与电荷面密度成正比,而当极板间电势差恒定时,极板所带电荷量取决于电容 C ,电容器的电容由电介质性质和几何因素决定,根据这些关系可以确定内球半径对内球表面附近电场强度的影响.解 球形电容器电容为4 RR CR R极板上带电量为4 RRU q CUR R当外球壳的半径 R 和极板间电势差 U 恒定时, q 是内球半径 R 的函数.内球表面附近的场强大小为qRU E2R(R R)4 R即也是 R 的函数.欲求场强的最小值,令dE2R R] 0RU [ R 2 ( R R ) 2 dR得RR2并有 RR时,d 2 E0 ,即 RR时,场强有极小值,且2dR 224U E minR9-21 图 9-21 为水蒸气分子 H 2O 中氧氢原子核及核外电子云示意图. 由于分子的正负电荷中心不重合,故其为有极分子,电矩p 6.2 10 30 C m .( 1)水分子有 10 个正电荷及 10 个负电荷,试求正负电荷中心之距 d= ?(2)如将水蒸气置于 E1.5 10 4 N/C 的匀强电场中,求其可能受到的最大力矩?( 3)欲使电矩与外场平行反向的水分子转到外场方向(转向极化),问电场力作功多少?3kT 的多少分之一?在室温 这功的大小为室温( 300K )水分子的平均平动动能2下实现水分子的转向极化,外加电场强度应该多大?分析由电矩 pqd 及已知的水分子电量可计算正负电荷中心之距d .由电偶极子在外场中受的力矩Mp E, MpE sin,可知,当 p 与 E 正交时力矩最大 .当电矩与外场平行反向(180 ) 时,电场力的力矩作功将使减小,最后0 ,注意到在此过程中 d0.如果这个功与室温下水分子的平均平动动能3k T 相比较是微不足道的,那么要使水分子在常温下实现极化,外电场作的功2至少要等于平均平动动能才能克服热运动的干扰,这就要求外电场足够强. 本题的目的在于启发在实际问题中综合各种物理因素的分析方法和数量级分析的方法.解 ( 1)由题意,水分子正负电荷中心不重合,形成一个电偶极子,电量q 10e , 电矩大小 p qd (10e)d30正负电荷中心之距dp 6.2 1019 3.9 10 12 m 10e 10 1.6 10题9-21图中, OH键距为 0.958 1010 m , d 为这个距离的4%.(2 )由电场力作用于电偶极子的力矩Mp E,力矩大小为MPE sin ,90 ,M达极大 .M maxPE6.2 10301.5 1049.3 1026 N m(3 )力矩作功为 W Md ,本题中,当转向极化进行时,力矩作正功但dWPE sin d2PE1.9 10 25Jθ180E而 T=300K 时,水分子的平均平动动能pk3kT3 1.38 10 23 300 6.2 10 21J22图 9-21k32630W可见在这样大小的外电场中,水分子的转向极化将被分子的热运动干扰,要实现转向极化,使180 的水分子也转到外电场的方向上,电场力作的功至少要等于分子热运动的平均平动动能k ,从而外场场强值至少要达到E W k 6.2 10 21 5 108 N/C2 p 2 p 2 6.210 309-22 平板电容器两级板相距 3.0cm ,其间平行地放置一层r 2.0 的介质,其位置和厚度如图 9-22(a) 所示,已知 A 板带负电、 B 板带正电,极板上电荷面密度为0 8.85 10 10 C/m 3,略去边缘效应,求:(1)极板间各区域的D、E;(2 )极板间距 A 极 1cm 、 2cm 、 3cm 处的电势(设 A 板电势为零);( 3)绘出 D x 、 E x 、 U x 曲线;(4)介质表面的极化电荷面密度.解( 1)作如图9-22(a) 所示的高斯面S1和S2,由介质中的高斯定理可以证明各区域 D 相等,得D08.8510 10 c/m 2介质外场强D10V 0/m E0介质内场强E D50 V / mr(2 )以 A 板电势为零,则x1cm 处A S2B V1E0 x11000.011Vx2cm 处V2V1E( x2x1 )S1 1.5Vx1cm 处V3V2E0 ( x3x2 ) 2.5V0 1 2 3x /cmD/ (C/m)E/ (V/m)V/ V100(a)σ025010 1 2 3x0 1 2 3x0 1 23(b)图 9-22(3) D x , E x , V x 曲线如图 9.22(b)所示.(4 )介质表面的极化电荷面密度为(1 1) 4.42510 10 C/m r9-23平板电容器两极间充满某种介质,板间距d2mm ,电压 600V ,如果断开电源后抽出介质,则电压升高到1800V ,求:(1 )介质的相对电容率;( 2)介质上的极化电荷面密度;(3 )极化电荷产生的电场强度.分析断开电源后抽出介质意味着极板上的自由电荷电量保持不变,电位移D也不变,但是电场强度改变,电压也会改变.在计算有均匀各向同性电介质的平行板电容器之间的电场时,电场强度可以表示为E E0E0,即自由电荷的电场和极化电荷产生的附加电场的00叠加,其中电介质对电场的影响以极化电荷面密度的形式表现出来,反映了空间电场是自由电荷和极化电荷共同产生的;介质中的电场强度也可以直接表示为 E0,其中电介质对电场的影响以相对电容率r 的形式表现出来,也反映0 r了空间的电场是自由电荷和极化电荷共同产生的.这两种表现形式是等效的.解(1)由 E0U 0, EU,得相对电容率为d dE0U 01800rU3E600(2 )在平行板电容器两极板间充满均匀电介质时,忽略边缘效应,得(1 1 )(11) E0 0 5.31 10 6 C/mr r(3 )极化电荷的分布形成等量异号带电板,忽略边缘效应,得E 6 10 5 V/m9-24 盖革计数器可用来测量电离辐射,它的正极是半径为R1的金属丝,负极是半径为 R2的同轴圆柱面,当管内充以低压惰性气体,并使两极间建立起强电场,若有辐射粒子进入器壁时将使气体电离,在电子向正极运动的过程中,又会与其他气体原子产生碰撞电离,这样将有更多的电子到达正极并产生一个信号,记录下该辐射,假设 R125 10 6 m , R2 1.4 10 2 m ,管长 L 1610 2 m ,两级间电势差 U 6000V ,低压惰性气体的相对电容率r 1 ,试计算此时阳极上的电荷量和电荷数.分析由于 L R2 , L R1,忽略边缘效应,可以把盖革计数器视为带等量异号电荷的无限长同轴圆柱面电容器.解 两级间场强为 E,方向沿径向指向阴极.电势差为2 0rUR 2drR 2r2ln2 0R 1R 1则Uln R 2R 1阳极上电荷量为2 0UL 2600016 10 2 10 9CqLR 2 ln(1.4 10 2/ 2510 6)8.4 lnR 1q 8.4 10 相应的电荷数为Ne 1.6 109195.25 10109-25圆柱形电容器是由半径为 R 1 的导体圆柱和与它同轴的导体圆筒构成 的,圆筒的半径为 R 2 ,电容器的长为 L ,其间充满相对电容率为 r 的介质,设沿轴线单位长度上圆柱带电荷量为,圆筒单位长带电荷量为,忽略边缘效应,求:(1)介质中的电位移和电场强度; (2 )介质表面的极化电荷面密度; (3)两极之间的电势差 U ,从而求电容器电容.分析 已知电荷分布,由介质中的高斯定理可知介质中的 D 和 E ,由场强叠加原理可求出极R 2εrεR 1rLλ化电荷的面密度 .–λ解 (1)由于电场具有轴对称性,以半径为r 作高为 L 的同轴高斯面,介质中的高斯定理得2 rL D L图 9-25DrD( 1)Er 2rr (2 )设介质内外表面单位长上的极化电荷分别为和,在介质内,其内表面极化电荷产生的附加电场的场强为E2 0 r根据场强叠加原理,在介质内电场是导体圆柱表面的自由电荷产生的电场和介质内表面极化电荷产生的附加电场的叠加,即E E0E( 2)2 0 r 2 0 r由( 1)和( 2)式解得(1 1 )r介质内外表面单位长的面积分别为 2 R2, 2 R1,则极化电荷面密度分别为2 R1(1)(1)2 R1r2R2 2R2r(3 )电容器两极板电势差为U E d rR2dr ln R2R2R1R120 r r0rR1电容为Q L20rL CR2R2 U ln ln2R1R10 r9-26在半径为 R 的金属球外有一层外半径为R 的均匀介质层,设电介质的相对电容率为r ,金属球带电量为Q,求:(1 )介质层内外的电场强度;(2 )介质层内外的电势;( 3)金属球的电势.分析本题为球对称场,已知电荷分布由介质中的高斯定理可求出D、E 分布.以无穷远电势为零由场强与电势的积分关系或电势叠加原理可求电势分布.解( 1)如图 9-26,作半径为 r的球面为高斯面,由有介质的高斯定理得4 r 2 D QDQ4r 2R在介质内, R r RD Q R’r E14r r20r0εr在介质外,r RD Q E24r 2(2 )介质内任一点的电势为图 9-26V1RE1dr E2 dr Q1(1 1)1( 1)4r r R Rr R介质外任一点电势为V2Q rE2 dr4 0 r(3 )金属球的电势可由( 1)式中令 r R 得到,即V0Q1111 4 0R R Rr9-27球形电容器由半径为R1的导体球和与它同心的导体球壳组成,球壳内半径为 R3,其间有两层均匀电介质,分界面半径为R2,相对电容率分别为r1和r2 ,如图9-27所示,求:(1)当内球所带电荷量为Q 时,电场强度的分布;( 2)各介质表面上的束缚电荷面密度;(3 )电容器电容.分析本题电场为球对称的,已知电荷分布,可由介质中的高斯定理先求 D ,再求 E 的分布.束缚电荷分布在内外两层介质的四个表面上,因为各表面的曲率。
第十章 静电场中的导体和电介质习题解答
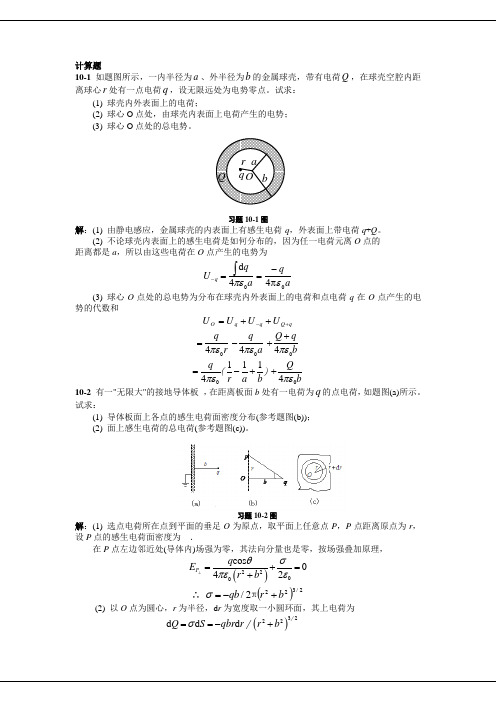
10-1 如题图所示,一内半径为a 、外半径为b 的金属球壳,带有电荷Q ,在球壳空腔内距离球心r 处有一点电荷q ,设无限远处为电势零点。
试求: (1) 球壳内外表面上的电荷;(2) 球心O 点处,由球壳内表面上电荷产生的电势;(3) 球心O 点处的总电势。
习题10-1图解:(1) 由静电感应,金属球壳的内表面上有感生电荷-q ,外表面上带电荷q +Q 。
(2) 不论球壳内表面上的感生电荷是如何分布的,因为任一电荷元离O 点的 距离都是a ,所以由这些电荷在O 点产生的电势为0d 4q qU aπε-=⎰aq04επ-=(3) 球心O 点处的总电势为分布在球壳内外表面上的电荷和点电荷q 在O 点产生的电势的代数和q Q q q O U U U U +-++=04qr πε=04qa πε-04Q qb πε++01114()q r a bπε=-+04Q bπε+ 10-2 有一"无限大"的接地导体板 ,在距离板面b 处有一电荷为q 的点电荷,如题图(a)所示。
试求:(1) 导体板面上各点的感生电荷面密度分布(参考题图(b)); (2) 面上感生电荷的总电荷(参考题图(c))。
习题10-2图解:(1) 选点电荷所在点到平面的垂足O 为原点,取平面上任意点P ,P 点距离原点为r ,设P 点的感生电荷面密度为.在P 点左边邻近处(导体内)场强为零,其法向分量也是零,按场强叠加原理,()220cos 024P q E r b θσεπε⊥=+=+ ∴ ()2/3222/b r qb +-=πσ (2) 以O 点为圆心,r 为半径,d r 为宽度取一小圆环面,其上电荷为 ()3222d d d //Q S qbr r r bσ==-+q Q a bO r()q brrr qb S Q S-=+-==⎰⎰∞2322d d /σ10-3 如题图所示,中性金属球A ,半径为R ,它离地球很远.在与球心O 相距分别为a 与b 的B 、C 两点,分别放上电荷为A q 和B q 的点电荷,达到静电平衡后,问: (1) 金属球A 内及其表面有电荷分布吗?(2) 金属球A 中的P 点处电势为多大?(选无穷远处为电势零点)B C R AP Oq A q Bba习题10-3图解:(1) 静电平衡后,金属球A 内无电荷,其表面有正、负电荷分布,净电荷为零. (2) 金属球为等势体,设金属球表面电荷面密度为. ()()000d 4=4////AP A B S U U S R q a q a σπεπε==⋅+⎰⎰∵d 0AS S σ⋅=⎰⎰∴ ()()04///P A B U q a q a πε=+10-4 三个电容器如题图联接,其中C 1 = 10×10-6 F ,C 2 = 5×10-6 F ,C 3 = 4×10-6 F ,当A 、B 间电压U =100 V 时,试求:(1) A 、B 之间的电容;(2) 当C 3被击穿时,在电容C 1上的电荷和电压各变为多少?ABC 1C 2 C 3U习题10-4图解:(1) =+++=321321)(C C C C C C C 3.16×10-6 F(2) C 1上电压升到U = 100 V ,电荷增加到==U C Q 111×10-3 C10-5 一个可变电容器,由于某种原因所有动片相对定片都产生了一个相对位移,使得两个相邻的极板间隔之比为2:1,问电容器的电容与原来的电容相比改变了多少?(a) (b)习题10-5图解:如图所示,设可变电容器的静片数为n ,定片数为1-n ,标准情况下,极板间的距离为d (图a ),极板相对面积为S 。
大学物理第7章静电场中的导体和电介质课后习题及答案

大学物理第7章静电场中的导体和电介质课后习题及答案-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN第7章 静电场中的导体和电介质 习题及答案1. 半径分别为R 和r 的两个导体球,相距甚远。
用细导线连接两球并使它带电,电荷面密度分别为1σ和2σ。
忽略两个导体球的静电相互作用和细导线上电荷对导体球上电荷分布的影响。
试证明:Rr=21σσ 。
证明:因为两球相距甚远,半径为R 的导体球在半径为r 的导体球上产生的电势忽略不计,半径为r 的导体球在半径为R 的导体球上产生的电势忽略不计,所以半径为R 的导体球的电势为R R V 0211π4επσ=14εσR= 半径为r 的导体球的电势为r r V 0222π4επσ=24εσr= 用细导线连接两球,有21V V =,所以R r =21σσ 2. 证明:对于两个无限大的平行平面带电导体板来说,(1)相向的两面上,电荷的面密度总是大小相等而符号相反;(2)相背的两面上,电荷的面密度总是大小相等而符号相同。
证明: 如图所示,设两导体A 、B 的四个平面均匀带电的电荷面密度依次为1σ,2σ,3σ,4σ(1)取与平面垂直且底面分别在A 、B 内部的闭合圆柱面为高斯面,由高斯定理得S S d E S ∆+==⋅⎰)(10320σσε 故 +2σ03=σ上式说明相向两面上电荷面密度大小相等、符号相反。
(2)在A 内部任取一点P ,则其场强为零,并且它是由四个均匀带电平面产生的场强叠加而成的,即0222204030201=---εσεσεσεσ 又 +2σ03=σ 故 1σ4σ=3. 半径为R 的金属球离地面很远,并用导线与地相联,在与球心相距为R d 3=处有一点电荷+q ,试求:金属球上的感应电荷的电量。
解:如图所示,设金属球表面感应电荷为q ',金属球接地时电势0=V由电势叠加原理,球心电势为=O V R qdq R 3π4π4100εε+⎰03π4π400=+'=Rq R q εε故 -='q 3q 4.半径为1R 的导体球,带有电量q ,球外有内外半径分别为2R 、3R 的同心导体球壳,球壳带有电量Q 。
静电场中的导体与电介质一章习题解答讲解

静电场中的导体与电介质一章习题解答习题8—1 A 、B 为两个导体大平板,面积均为S ,平行放置,如图所示。
A 板带电+Q 1,B 板带电+Q 2,如果使B 板接地,则AB 间电场强度的大小E 为:[ ] (A)S Q 012ε (B) SQ Q 0212ε- (C) SQ01ε (D) S Q Q 0212ε+解:B 板接地后,A 、B 两板外侧均无电荷,两板内侧带等值异号电荷,数值分别为+Q 1和-Q 1,这时AB 间的场应是两板内侧面产生场的叠加,即SQS Q S Q E 01010122εεε=+=板间 所以,应该选择答案(C)。
习题8—2 C 1和C 2两个电容器,其上分别标明200pF(电容量),500V(耐压值)和300pF ,900V 。
把它们串联起来在两端加上1000V 的电压,则[ ](A) C 1被击穿,C 2不被击穿 (B) C 2被击穿,C 1不被击穿 (C) 两者都被击穿 (D) 两者都不被击穿 答:两个电容器串联起来,它们各自承受的电压与它们的电容量成反比,设C 1承受的电压为V 1,C 2承受的电压为V 2,则有231221==C C V V ①100021=+V V ②联立①、②可得V 6001=V , V 4002=V可见,C 1承受的电压600V 已经超过其耐压值500V ,因此,C 1先被击穿,继而1000V 电压全部加在C 2上,也超过了其耐压值900V ,紧接着C 2也被击穿。
所以,应该选择答案(C)。
习题8—3 三个电容器联接如图。
已知电容C 1=C 2=C 3,而C 1、C 2、C 3的耐压值分别为100V 、200V 、300V 。
则此电容器组的耐压值为[ ](A) 500V (B) 400V (C) 300V (D) 150V (E) 600V解:设此电容器组的两端所加的电压为u ,并且用C 1∥C 2表示C 1、C 2两电容器的并联组合,这时该电容器组就成为C 1∥C 2与C 3的串联。
《大学物理学》习题解答(第12章 静电场中的导体和电介质)(1)

(2)两输电线的电势差为 U
xR
E dl
R
Ed x
d R ln 0 R
(3)输电线单位长度的电容 C
U
0 / ln
d R d 0 / ln 4.86 1012 F R R
【12.9】半径为 R1 的导体球被围在内半径为 R2 、外半径为 R3 、相对电容率为 r 的介质球壳内,它们是同 球心的。若导体带电为 Q ,则导体内球表面上的电势为多少? 【12.9 解】先求各区域电场 (1)
Q 4 0 R3
( R3 r )
B 球壳为等势体,其电势为
V
R3
E dr
Q 4 0
R3
r
dr
2
【12.2】一导体球半径为 R1,外罩一半径为 R2 的同心薄导体球壳,外球壳所带总电荷为 Q,而内球的电势为 V0.求此系统的电势和电场分布。 【12.2 解】已知内球电势为 V0 ,外球壳带电 Q 。 (1)先求各区域的电场强度:设内球带电荷 q 。由高斯定理,有
E
U
z
2R
( 1 )一根带电 的输电线在两线之间、距其轴心 x 处 p 点的场强为
x
dx
p
E i 2 0 x
另一根带电 的输电线在 p 点产生的电场强度为
x
E
2 0 ( d x )
i
p 点的总电场强度为
E E E
d R
1 1 ( )i 2 0 x d x
E1 0
(r R1 ) ( R1 r R2 ) 4 r 2 D Q , D 0 r E3
题解-静电场中的导体和电介质

q1 '
R1
q2 ' R2
(2) :U q1 ' q2 '
40R1 40R2
q1'q2 ' q1 q2
C
q1'q2 U
'
4
0
(R1
R2 )
(3) 1 R2 ; E E1 R2
2 R1
0 E2 R1
15、
C
εrC0;W
q2 2C
q2
2 r C0
W0 εr
16、
C1
C
C1
C2
U2
U
q C
减小
E2
W2
1 2
0E2
减小
17、
W
1 2
0
r
E
2
1 2
ε
0εr
(
U12 d
)2
18、
W0
q2 2C0
d
20S
q2;
W
q2 2C'
d
20r S
q2;W
1 εr
W0
W0
1 2
C0U
2
0S
2d
U
2;
W
1 2
C'U 2
0r S
2d
U
2;W
εr W0
0 E02S
(d
y
y
r
)
r 1 W ' W0,且与x无关
22、C 23、B
24、A
W0
q2 2C0
d
20S
q2;
W q2 d q2;
2C' 20r S
W0
1 2
C0U
(整理)静电场中的导体和电介质习题详解

习题二一、选择题1.如图所示,一均匀带电球体,总电量为+Q ,其外部同心地罩一内、外半径分别为1r 和2r 的金属球壳。
设无穷远处为电势零点,则球壳内半径为r 的P 点处的场强和电势为[ ] (A )200, 44Q QE U r rεε==ππ; (B )010, 4QE U r ε==π;(C )00, 4QE U rε==π;(D )020, 4QE U r ε==π。
答案:D解:由静电平衡条件得金属壳内0=E ;外球壳内、外表面分别带电为Q -和Q +,根据电势叠加原理得000202Q Q Q QU r r r r εεεε-=++=4π4π4π4π2.半径为R 的金属球与地连接,在与球心O 相距2d R =处有一电量为q 的点电荷,如图所示。
设地的电势为零,则球上的感应电荷q '为[ ](A )0; (B )2q ; (C )2q-; (D )q -。
答案:C解:导体球接地,球心处电势为零,即000044q q U dRπεπε'=+=(球面上所有感应电荷到球心的距离相等,均为R ),由此解得2R qq q d '=-=-。
3.如图,在一带电量为Q 的导体球外,同心地包有一各向同性均匀电介质球壳,其相对电容率为r ε,壳外是真空,则在壳外P 点处(OP r =)的场强和电位移的大小分别为[ ] (A )2200,44r Q Q E D rr εεε==ππ; (B )22,44r Q QE D r r ε==ππ; (C )220,44Q Q E D r r ε==ππ; (D )2200,44Q QE D r r εε==ππ。
答案:C解:由高斯定理得电位移 24QD r =π,而 2004D QE r εε==π。
4.一大平行板电容器水平放置,两极板间的一半空间充有各向同性均匀电介质,另一半为空气,如图所示。
当两极板带上恒定的等量异号电荷时,有一个质量为m 、带电量为+q 的质点,在极板间的空气区域中处于平衡。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
静电场中的导体和电解质习题、答案及解法一.选择题1.一个不带电的空腔导体球壳,内半径为R 。
在腔内离球心的距离为a 处放一点电荷q +,如图1所示。
用导线把球壳接地后,再把地线撤去。
选无穷远处为电势零点,则球心O 处的电势为 [ D ] (A )aq 02πε; (B )0 ;(C )Rq 04πε-; (D )⎪⎭⎫ ⎝⎛-R a q 1140πε。
参考答案:)11(4)11(440020Ra q a R q dl Rq Edl V RaRa-=--===⎰⎰πεπεπε 2.三块互相平行的导体板之间的距离21d d 和比板面积线度小得多,如果122d d =外面二板用导线连接,中间板上带电。
设左右两面上电荷面密度分别为21σσ和,如图2所示,则21σσ为(A )1 ; (B )2 ; (C )3 ;(D )4 。
[ B ]解:相连的两个导体板电势相等2211d E d E =,所以202101d d εσεσ= 1221d d =σσ3.一均匀带电球体如图所示,总电荷为Q +,其外部同心地罩一内、外半径分别为1r ,2r 的金属球壳。
设无穷远处为电势零点,则在球壳内半径为r 的P 点处的场强和电势分别为[ B ] (A )204r q πε,0 ; (B )0,204r q πε ;(C )0,rq 04πε ; (D )0,0 。
参考答案:⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛-∞-==•+•=•=⎰⎰⎰⎰∞∞∞2020201411441222r Q rQdr r Q ld E l d E ld E U r r r rpp πεπεπε4.带电导体达到静电平衡时,其正确结论是 [ D ] (A ) 导体表面上曲率半径小处电荷密度较小; (B ) 表面曲率较小处电势较高; (C ) 导体内部任一点电势都为零;(D ) 导体内任一点与其表面上任一点的电势差等于零。
参考答案:带电导体达到静电平衡时,导体是一个等势体,其外表面是一个等势面。
5.两个同心薄金属球壳,半径分别为)(和2121R R R R <,若内球壳带上电荷Q ,则两者的电势分别为22114R 4R Q V Q V πεπε==和,(选无穷远处为电势零点)。
现用导线将两球壳相连接,则它们的电势为 [ D ](A )1V (B )()2121V V + (C )21V V + (D )2V参考答案:带电导体达到静电平衡时,导体是一个等势体,其外表面是一个等势面。
6.当平行板电容器充电后,去掉电源,在两极板间充满电介质,其正确的结果是[ C ](A ) 极板上自由电荷减少 (B ) 两极板间电势差变大 (C ) 两极板间电场强度变小 (D ) 两极板间电场强度不变参考答案:UQC =d S C r εε0= S Q E r εε0= S Qd Ed U r εε0==7.一个大平行板电容器水平放置,两极板间的一半空间充有各向同性均匀电介质,另一半为空气,如图4所示。
当两极板带上恒定的等量异号电荷时,其正确的结果是 [ A ] (A ) 极板左半边电荷面密度大 (B ) 左半边电介质内电场强度大 (C ) 极板右半边电荷面密度大 (D ) 左半边电介质内电场强度小 参考答案:dSC r 20εε=左 dSC 20ε=右dU r 00εεσ=左 dU 00εσ=右 d U E 0=左 dUE 0=右 8.一个平行板电容器,充电后断开电源,使电容器两极板间距离变小,则两极板间的电势差12U ,电场强度的大小E ,电场能量W 将发生如下变化 [ D ] (A) U 12 减小, E 减小,W 减小 ; (B)U 12 增大, E 增大,W 增大 ; (C) U 12 增大, E 不变,W 增大 ; (D)U 12 减小, E 不变,W 减小 。
参考答案:UQC =d S C r εε0= Ed Q d S r =εε0d S QEd U r εε0== S QE r εε0= d SE C Q CU W r 2022212121εε=== 9、两空气电容器1C 和2C ,串联起来接上电源充电。
充满后将电源断开,再把一电介质板插入1C 中,如图5所示,则[ D ](A)1C 极板上电荷增加,2C 极板上电荷减少 (B)1C 极板上电荷减少,2C 极板上电荷增加(C)1C 极板上电荷增加,2C 极板上电荷增加Q-(D)1C 极板上电荷不变,2C 极板上电荷不变 参考答案:111U Q C =充满后将电源断开,电量不变 10. 1C 和2C 两空气电容器并联以后接电源充电,在电源保持连接的情况下,在1C 中插入一电介质板,如图6所示,则(A)1C 极板上电荷不变,2C 极板上电荷减少 (B)1C 极板上电荷不变,2C 极板上电荷增加 (C)1C 极板上电荷增加,2C 极板上电荷不变 (D)1C 极板上电荷减少,2C 极板上电荷不变 [ C ] 参考答案:U Q C 11=dS C r εε0= 11,有两只电容器,F C F C μμ2,821==,分别把它们充电到2000V ,然后将它们反接(如图所示),此时1C 两极板间的电势差为 [ D ](A )600V ; (B )200V ; (C )0V ; (D )1200V 。
参考答案:011U Q C =22U QC = ()21021Q Q U C C -=- ()()V 1200210211=+-='C C U C C U二、填空题1、如图8所示,两块很大的导体平板平行放置,面积都是S ,有一定厚度,带电荷分别为1Q ,2Q ,如不计边缘效应,则A ,B , C , D 4个表面上的电荷面密度分别为1C 2C ++--参考答案:()()⎪⎪⎩⎪⎪⎨⎧=+=+-==21Q S Q S D C B A CB D A σσσσσσσσ ⎪⎪⎩⎪⎪⎨⎧-=-=+==∴S Q Q S Q Q C B D A 222121σσσσ2一金属球壳的内外半径分别为21,R R 带电荷为Q ,在球心处有一电荷为q 的点参考答案:2214R Qq Sqni iπσ+==∑= 3、如果地球表面附近的电场强度为1C N 200-⋅,把地球看做半径为m 104.66⨯的导体球,则地球表面的电荷Q=()/C m N 109412290•⨯=πε参考答案:02041r r Q E πε=()592620101.9109104.62004⨯=⨯⨯⨯==地ER Q πε4、如图9所示,在静电场中有一立方形均匀导体,边长为a ,已知立方体中心O 处的电势为0V ,则立方体顶点A 的电参考答案:导体是一个等势体5、分子的正负电荷中心重合的电介质叫做 参考答案:无极分子;电偶极子6、在相对电容率为r ε的各向同性的电介质中,电位移矢量D 与场强E 之间的关系是E D rεε0=参考答案:E D rεε0=7、一平行电容器,充电后与电源保持连接,然后使两极板间充满相对电容率为rεA的各向同性均匀电介质,这时两极板上的电荷是原来的 r ε 倍,电场强度是原来是的 1 倍。
电场能量是原来的 r ε 倍参考答案:0C C r ε= 00Q CU Q r ε== S Q d U E 000ε==SQdEd U r εε0== 0200202121W U C CU W r r εε===8、一平行板电容器,两板间充满各向同性均匀电介质,已知相对电容率为r ε。
若极板上的自由电荷面密度为σ,则介质中电位移的大小D= σ ,电场强度的大小参考答案: ⎰∑==•Sn i i q S d D 1 σ=D r r D E εεσεε00== 9、一平行板电容器充电后切断电源,若使两电极板距离增加。
则两极板间电势差将 增大,电容将减小(填增大或减小或不变)参考答案:d S Q Ed U 0ε== UQC = d S C 0ε= 三、计算题1、图10为一半径为a 、带有正电荷Q 的导体球,球外有一内半径为b ,外半径为c势零点,试求内球和外壳的电势。
解:球壳内表面将出现负的感生电荷-Q ,外表面为正的感生电荷Q .按电势叠加原理(也可由高斯定理求场强,用场强的线积分计算)导体球的电势为⎪⎭⎫ ⎝⎛+-=⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛-=+⋅+=•+•+•=•=⎰⎰⎰⎰⎰⎰⎰∞∞∞c b a Q c Q b a Q dr r Qdr dr r Q ld E l d E l d E ld E U c c b ba cc bb aa1114141144104100020203211εεεπεπεπππ球壳电势 c Qdr r Q l d E U cc 0202441επεπ==•=⎰⎰∞∞2、一空气平行板电容器,两极板面积均为S ,板间距离为d (d 远小于极板线度),在两极板间平行地插入一面积也是S ,厚度为t ()d t 〈的金属片,如图所示。
试求; (1)电容C 的值;(2)金属片放在两极板间的位置对电容值有无影响?解:设极板上分别带电荷+q 和-q ;金属片与A 板距离为d 1,与B 板距离为d 2;金属片与A 板间场强为 SqE 01ε=金属板与B 板间场强为 Sq E 02ε=金属片内部场强为 0='E 则两极板间的电势差为)()(02102211t d S qd d S q d E d E l d E U U ABB A -=+=+=⋅=-⎰εε由此得 td SU U q C B A -=-=0ε 因C 值仅与d 、t 有关,与d 1、d 2无关,故金属片的安放位置对电容值无影响.3、3个电容器如图所示,其实F 101061-⨯=C , F 10562-⨯=C ,F 10463-⨯=C 当A ,B 间电压V 100=U 时,试求:2C(1)A ,B 之间的电容;(2)当3C 被击穿时,在电容3C 上的电荷和电压各变为多少?解:(1) ()F 1016.3)(6321321-⨯=+++=C C C C C C C(2) 1C 上电压升到V 100=U ,电荷增加到()C 101511-⨯==U C Q4、一平行板电容器,其极板面积为S ,两极的距离为d(d<<S ),中间充有两种各向同性的均匀电介质,其界面与极板平行,相对电容率分别为21,r r εε厚度分别为1d 和2d ,且d d d =+21如图所示,设两极板上所带电荷分别为Q +和Q -,求 (1)电容器的电容; (2)电容器储存的能量.解:(1) 两极板间电位移的大小为 SQ D ==σ 在介质中的场强大小分别为S QD E r r r 1010101εεεεσεε=== SQD E r r r 2020202εεεεσεε=== 两板间电势差⎪⎪⎭⎫⎝⎛+=+=⋅=⎰22110221112r r Ld d S Q d E d E l d E U εεε 电容 122121012r r r r d d S U Q C εεεεε+== (2) 电场能量 ()SQ d d CU W r r r r 21021221212221εεεεε+==。
