二元一次方程组的解法经典练习题教程文件
二元一次方程组解法练习题精选含答案(供参考)
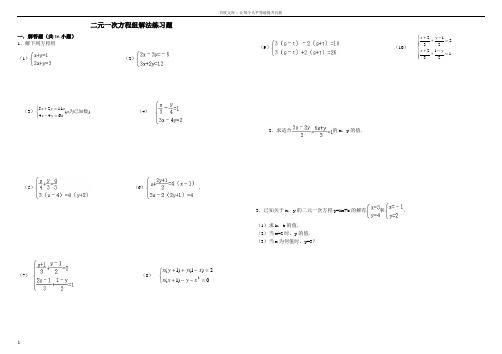
1二元一次方程组解法练习题一.解答题(共16小题) 1.解下列方程组 (1)(2)(3))(6441125为已知数a a y x a y x ⎩⎨⎧=-=+ (4)(5)(6).(7)(8)⎩⎨⎧=--+=-++0)1(2)1()1(2x y x x x y y x(9)(10) ⎪⎪⎩⎪⎪⎨⎧=-++=-++1213222132y x y x2.求适合的x ,y 的值.3.已知关于x ,y 的二元一次方程y=kx+b 的解有和.(1)求k ,b 的值.(2)当x=2时,y 的值. (3)当x 为何值时,y=3?1.解下列方程组(1)(2);(3);(4)(5).(6)(7)(8)(9)(10);2.在解方程组时,由于粗心,甲看错了方程组中的a,而得解为,乙看错了方程组中的b,而得解为.(1)甲把a看成了什么,乙把b看成了什么?(2)求出原方程组的正确解.2二元一次方程组解法练习题精选参考答案与试题解析一.解答题(共16小题)1.求适合的x,y的值.考点:解二元一次方程组.分析:先把两方程变形(去分母),得到一组新的方程,然后在用加减消元法消去未知数x,求出y的值,继而求出x的值.解答:解:由题意得:,由(1)×2得:3x﹣2y=2(3),由(2)×3得:6x+y=3(4),(3)×2得:6x﹣4y=4(5),(5)﹣(4)得:y=﹣,把y的值代入(3)得:x=,∴.点评:本题考查了二元一次方程组的解法,主要运用了加减消元法和代入法.2.解下列方程组(1)(2)(3)(4).考点:解二元一次方程组.分析:(1)(2)用代入消元法或加减消元法均可;(3)(4)应先去分母、去括号化简方程组,再进一步采用适宜的方法求解.解答:解:(1)①﹣②得,﹣x=﹣2,解得x=2,把x=2代入①得,2+y=1,解得y=﹣1.故原方程组的解为.(2)①×3﹣②×2得,﹣13y=﹣39,解得,y=3,把y=3代入①得,2x﹣3×3=﹣5,解得x=2.故原方程组的解为.(3)原方程组可化为,①+②得,6x=36,x=6,①﹣②得,8y=﹣4,y=﹣.所以原方程组的解为.(4)原方程组可化为:,①×2+②得,x=,把x=代入②得,3×﹣4y=6,y=﹣.所以原方程组的解为.点评:利用消元法解方程组,要根据未知数的系数特点选择代入法还是加减法:①相同未知数的系数相同或互为相反数时,宜用加减法;②其中一个未知数的系数为1时,宜用代入法.3.解方程组:考解二元一次方程组.3:专题:计算题.分析:先化简方程组,再进一步根据方程组的特点选用相应的方法:用加减法.解答:解:原方程组可化为,①×4﹣②×3,得7x=42,解得x=6.把x=6代入①,得y=4.所以方程组的解为.点评:;二元一次方程组无论多复杂,解二元一次方程组的基本思想都是消元.消元的方法有代入法和加减法.4.解方程组:考点:解二元一次方程组.专题:计算题.分析:把原方程组化简后,观察形式,选用合适的解法,此题用加减法求解比较简单.解答:解:(1)原方程组化为,①+②得:6x=18,∴x=3.代入①得:y=.所以原方程组的解为.点评:要注意:两个二元一次方程中同一未知数的系数相反或相等时,把这两个方程的两边相加或相减,就能消去这个未知数,得到一个一元一次方程,这种方法叫做加减消元法.本题适合用此法.5.解方程组:考点:解二元一次方程组.专题:计算题;换元法.分析:本题用加减消元法即可或运用换元法求解.解答:解:,①﹣②,得s+t=4,①+②,得s﹣t=6,即,解得.所以方程组的解为.点评:此题较简单,要熟练解方程组的基本方法:代入消元法和加减消元法.6.已知关于x,y的二元一次方程y=kx+b的解有和.(1)求k,b的值.(2)当x=2时,y的值.(3)当x为何值时,y=3?考点:解二元一次方程组.专题:计算题.分析:(1)将两组x,y的值代入方程得出关于k、b的二元一次方程组,再运用加减消元法求出k、b的值.(2)将(1)中的k、b 代入,再把x=2代入化简即可得出y的值.(3)将(1)中的k、b和y=3代入方程化简即可得出x的值.解答:解:(1)依题意得:①﹣②得:2=4k,所以k=,所以b=.4(2)由y=x+,把x=2代入,得y=.(3)由y=x+把y=3代入,得x=1.点评:本题考查的是二元一次方程的代入消元法和加减消元法,通过已知条件的代入,可得出要求的数.7.解方程组:(1);(2).考点:解二元一次方程组.分析:根据各方程组的特点选用相应的方法:(1)先去分母再用加减法,(2)先去括号,再转化为整式方程解答.解答:解:(1)原方程组可化为,①×2﹣②得:y=﹣1,将y=﹣1代入①得:x=1.∴方程组的解为;(2)原方程可化为,即,①×2+②得:17x=51,x=3,将x=3代入x﹣4y=3中得:y=0.∴方程组的解为.点评:这类题目的解题关键是理解解方程组的基本思想是消元,掌握消元的方法有:加减消元法和代入消元法.根据未知数系数的特点,选择合适的方法.8.解方程组:考点:解二元一次方程组.专题:计算题.分析:本题应把方程组化简后,观察方程的形式,选用合适的方法求解.解答:解:原方程组可化为,①+②,得10x=30,x=3,代入①,得15+3y=15,y=0.则原方程组的解为.点评:解答此题应根据各方程组的特点,有括号的去括号,有分母的去分母,然后再用代入法或加减消元法解方程组.9.解方程组:考点:解二元一次方程组.专题:计算题.分析:本题为了计算方便,可先把(2)去分母,然后运用加减消元法解本题.解答:解:原方程变形为:,两个方程相加,得4x=12,x=3.把x=3代入第一个方程,得4y=11,5y=.解之得.点评:本题考查的是二元一次方程组的解法,方程中含有分母的要先化去分母,再对方程进行化简、消元,即可解出此类题目.10.解下列方程组:(1)(2)考点:解二元一次方程组.专题:计算题.分析:此题根据观察可知:(1)运用代入法,把①代入②,可得出x,y的值;(2)先将方程组化为整系数方程组,再利用加减消元法求解.解答:解:(1),由①,得x=4+y③,代入②,得4(4+y)+2y=﹣1,所以y=﹣,把y=﹣代入③,得x=4﹣=.所以原方程组的解为.(2)原方程组整理为,③×2﹣④×3,得y=﹣24,把y=﹣24代入④,得x=60,所以原方程组的解为.点评:此题考查的是对二元一次方程组的解法的运用和理解,学生可以通过题目的训练达到对知识的强化和运用.11.解方程组:(1)(2)考点:解二元一次方程组.专题:计算题;换元法.分析:方程组(1)需要先化简,再根据方程组的特点选择解法;方程组(2)采用换元法较简单,设x+y=a,x﹣y=b,然后解新方程组即可求解.解答:解:(1)原方程组可化简为,解得.(2)设x+y=a,x﹣y=b,∴原方程组可化为,解得,∴∴原方程组的解为.点评:此题考查了学生的计算能力,解题时要细心.12.解二元一次方程组:6(1);(2).考点:解二元一次方程组.专题:计算题.分析:(1)运用加减消元的方法,可求出x、y的值;(2)先将方程组化简,然后运用加减消元的方法可求出x、y的值.解答:解:(1)将①×2﹣②,得15x=30,x=2,把x=2代入第一个方程,得y=1.则方程组的解是;(2)此方程组通过化简可得:,①﹣②得:y=7,把y=7代入第一个方程,得x=5.则方程组的解是.点评:此题考查的是对二元一次方程组的解法的运用和理解,学生可以通过题目的训练达到对知识的强化和运用.13.在解方程组时,由于粗心,甲看错了方程组中的a,而得解为,乙看错了方程组中的b,而得解为.(1)甲把a看成了什么,乙把b看成了什么?(2)求出原方程组的正确解.考点:解二元一次方程组.专题:计算题.分析:(1)把甲乙求得方程组的解分别代入原方程组即可;(2)把甲乙所求的解分别代入方程②和①,求出正确的a 、b,然后用适当的方法解方程组.解答:解:(1)把代入方程组,得,解得:.把代入方程组,得,解得:.∴甲把a看成﹣5;乙把b看成6;(2)∵正确的a是﹣2,b是8,∴方程组为,解得:x=15,y=8.则原方程组的解是.点评:此题难度较大,需同学们仔细阅读,弄清题意再解答.14.考点:解二元一次方程组.分析:先将原方程组中的两个方程分别去掉分母,然后用加减消元法求解即可.解答:解:由原方程组,得,由(1)+(2),并解得x=(3),把(3)代入(1),解得7y=∴原方程组的解为.点评:用加减法解二元一次方程组的一般步骤:1.方程组的两个方程中,如果同一个未知数的系数既不互为相反数又不相等,就用适当的数去乘方程的两边,使一个未知数的系数互为相反数或相等;2.把两个方程的两边分别相加或相减,消去一个未知数,得到一个一元一次方程;3.解这个一元一次方程;4.将求出的未知数的值代入原方程组的任意一个方程中,求出另一个未知数,从而得到方程组的解.15.解下列方程组:(1);(2).考点:解二元一次方程组.分析:将两个方程先化简,再选择正确的方法进行消元.解答:解:(1)化简整理为,①×3,得3x+3y=1500③,②﹣③,得x=350.把x=350代入①,得350+y=500,∴y=150.故原方程组的解为.(2)化简整理为,①×5,得10x+15y=75③,②×2,得10x﹣14y=46④,③﹣④,得29y=29,∴y=1.把y=1代入①,得2x+3×1=15,∴x=6.故原方程组的解为.点评:方程组中的方程不是最简方程的,最好先化成最简方程,再选择合适的方法解方程.16.解下列方程组:(1)(2)考点:解二元一次方程组.分析:观察方程组中各方程的特点,用相应的方法求解.解答:解:(1)①×2﹣②得:x=1,将x=1代入①得:2+y=4,y=2.∴原方程组的解为;(2)原方程组可化为,①×2﹣②得:﹣y=﹣3,y=3.将y=3代入①得:x=﹣2.∴原方程组的解为.点评:解此类题目要注意观察方程组中各方程的特点,采用加减法或代入法求解.8。
二元一次方程组解法练习题精选(含答案)

二元一次方程组解法练习题精选(含答案)【1】一.解答题(共16小题)1.求适合的x,y的值.2.解下列方程组(1)(2)(3)(4).3.解方程组:4.解方程组:5.解方程组:6.已知关于x,y的二元一次方程y=kx+b的解有和.(1)求k,b的值.(2)当x=2时,y的值.(3)当x为何值时,y=3?7.解方程组:(1);(2).8.解方程组:9.解方程组:10.解下列方程组:(1)(2)11.解方程组:(1)(2)12.解二元一次方程组:(1);(2).13.在解方程组时,由于粗心,甲看错了方程组中的a,而得解为,乙看错了方程组中的b,而得解为.(1)甲把a看成了什么,乙把b看成了什么?(2)求出原方程组的正确解.14.15.解下列方程组:(1);(2).16.解下列方程组:(1)(2)17.方程组的解是否满足2x-y=8?满足2x-y=8的一对x,y的值是否是方程组的解?二元一次方程组解法练习题精选(含答案)参考答案与试题解析一.解答题(共16小题)1.求适合的x,y的值.考点:解二元一次方程组.分析:先把两方程变形(去分母),得到一组新的方程,然后在用加减消元法消去未知数x,求出y 的值,继而求出x的值.解答:解:由题意得:,由(1)×2得:3x﹣2y=2(3),由(2)×3得:6x+y=3(4),(3)×2得:6x﹣4y=4(5),(5)﹣(4)得:y=﹣,把y的值代入(3)得:x=,∴.点评:本题考查了二元一次方程组的解法,主要运用了加减消元法和代入法.2.解下列方程组(1)(2)(3)(4).考点:解二元一次方程组.分析:(1)(2)用代入消元法或加减消元法均可;(3)(4)应先去分母、去括号化简方程组,再进一步采用适宜的方法求解.解答:解:(1)①﹣②得,﹣x=﹣2,解得x=2,把x=2代入①得,2+y=1,解得y=﹣1.故原方程组的解为.(2)①×3﹣②×2得,﹣13y=﹣39,解得,y=3,把y=3代入①得,2x﹣3×3=﹣5,解得x=2.故原方程组的解为.(3)原方程组可化为,①+②得,6x=36,x=6,①﹣②得,8y=﹣4,y=﹣.所以原方程组的解为.(4)原方程组可化为:,①×2+②得,x=,把x=代入②得,3×﹣4y=6,y=﹣.所以原方程组的解为.点评:利用消元法解方程组,要根据未知数的系数特点选择代入法还是加减法:①相同未知数的系数相同或互为相反数时,宜用加减法;②其中一个未知数的系数为1时,宜用代入法.3.解方程组:考点:解二元一次方程组.专题:计算题.分析:先化简方程组,再进一步根据方程组的特点选用相应的方法:用加减法.解答:解:原方程组可化为,①×4﹣②×3,得7x=42,解得x=6.把x=6代入①,得y=4.所以方程组的解为.点评:注意:二元一次方程组无论多复杂,解二元一次方程组的基本思想都是消元.消元的方法有代入法和加减法.4.解方程组:考点:解二元一次方程组.专题:计算题.分析:把原方程组化简后,观察形式,选用合适的解法,此题用加减法求解比较简单.解答:解:(1)原方程组化为,①+②得:6x=18,∴x=3.代入①得:y=.所以原方程组的解为.点评:要注意:两个二元一次方程中同一未知数的系数相反或相等时,把这两个方程的两边相加或相减,就能消去这个未知数,得到一个一元一次方程,这种方法叫做加减消元法.本题适合用此法.5.解方程组:考点:解二元一次方程组.专题:计算题;换元法.分析:本题用加减消元法即可或运用换元法求解.解答:解:,①﹣②,得s+t=4,①+②,得s﹣t=6,即,解得.所以方程组的解为.点评:此题较简单,要熟练解方程组的基本方法:代入消元法和加减消元法.6.已知关于x,y的二元一次方程y=kx+b的解有和.(1)求k,b的值.(2)当x=2时,y的值.(3)当x为何值时,y=3?考点:解二元一次方程组.专题:计算题.分析:(1)将两组x,y的值代入方程得出关于k、b的二元一次方程组,再运用加减消元法求出k、b的值.(2)将(1)中的k、b代入,再把x=2代入化简即可得出y的值.(3)将(1)中的k、b和y=3代入方程化简即可得出x的值.解答:解:(1)依题意得:①﹣②得:2=4k,所以k=,所以b=.(2)由y=x+,把x=2代入,得y=.(3)由y=x+把y=3代入,得x=1.点评:本题考查的是二元一次方程的代入消元法和加减消元法,通过已知条件的代入,可得出要求的数.7.解方程组:(1);(2).考点:解二元一次方程组.分析:根据各方程组的特点选用相应的方法:(1)先去分母再用加减法,(2)先去括号,再转化为整式方程解答.解答:解:(1)原方程组可化为,①×2﹣②得:y=﹣1,将y=﹣1代入①得:x=1.∴方程组的解为;(2)原方程可化为,即,①×2+②得:17x=51,x=3,将x=3代入x﹣4y=3中得:y=0.∴方程组的解为.点评:这类题目的解题关键是理解解方程组的基本思想是消元,掌握消元的方法有:加减消元法和代入消元法.根据未知数系数的特点,选择合适的方法.8.解方程组:考点:解二元一次方程组.专题:计算题.分析:本题应把方程组化简后,观察方程的形式,选用合适的方法求解.解答:解:原方程组可化为,①+②,得10x=30,x=3,代入①,得15+3y=15,y=0.则原方程组的解为.点评:解答此题应根据各方程组的特点,有括号的去括号,有分母的去分母,然后再用代入法或加减消元法解方程组.9.解方程组:考点:解二元一次方程组.专题:计算题.分析:本题为了计算方便,可先把(2)去分母,然后运用加减消元法解本题.解答:解:原方程变形为:,两个方程相加,得4x=12,x=3.把x=3代入第一个方程,得4y=11,y=.解之得.点评:本题考查的是二元一次方程组的解法,方程中含有分母的要先化去分母,再对方程进行化简、消元,即可解出此类题目.10.解下列方程组:(1)(2)考点:解二元一次方程组.专题:计算题.分析:此题根据观察可知:(1)运用代入法,把①代入②,可得出x,y的值;(2)先将方程组化为整系数方程组,再利用加减消元法求解.解答:解:(1),由①,得x=4+y③,代入②,得4(4+y)+2y=﹣1,所以y=﹣,把y=﹣代入③,得x=4﹣=.所以原方程组的解为.(2)原方程组整理为,③×2﹣④×3,得y=﹣24,把y=﹣24代入④,得x=60,所以原方程组的解为.点评:此题考查的是对二元一次方程组的解法的运用和理解,学生可以通过题目的训练达到对知识的强化和运用.11.解方程组:(1)(2)考点:解二元一次方程组.专题:计算题;换元法.分析:方程组(1)需要先化简,再根据方程组的特点选择解法;方程组(2)采用换元法较简单,设x+y=a,x﹣y=b,然后解新方程组即可求解.解答:解:(1)原方程组可化简为,解得.(2)设x+y=a,x﹣y=b,∴原方程组可化为,解得,∴∴原方程组的解为.点评:此题考查了学生的计算能力,解题时要细心.12.解二元一次方程组:(1);(2).考点:解二元一次方程组.专题:计算题.分析:(1)运用加减消元的方法,可求出x、y的值;(2)先将方程组化简,然后运用加减消元的方法可求出x、y的值.解答:解:(1)将①×2﹣②,得15x=30,x=2,把x=2代入第一个方程,得y=1.则方程组的解是;(2)此方程组通过化简可得:,①﹣②得:y=7,把y=7代入第一个方程,得x=5.则方程组的解是.点评:此题考查的是对二元一次方程组的解法的运用和理解,学生可以通过题目的训练达到对知识的强化和运用.13.在解方程组时,由于粗心,甲看错了方程组中的a,而得解为,乙看错了方程组中的b,而得解为.(1)甲把a看成了什么,乙把b看成了什么?(2)求出原方程组的正确解.考点:解二元一次方程组.专题:计算题.分析:(1)把甲乙求得方程组的解分别代入原方程组即可;(2)把甲乙所求的解分别代入方程②和①,求出正确的a、b,然后用适当的方法解方程组.解答:解:(1)把代入方程组,得,解得:.把代入方程组,得,解得:.∴甲把a看成﹣5;乙把b看成6;(2)∵正确的a是﹣2,b是8,∴方程组为,解得:x=15,y=8.则原方程组的解是.点评:此题难度较大,需同学们仔细阅读,弄清题意再解答.14.考点:解二元一次方程组.分析:先将原方程组中的两个方程分别去掉分母,然后用加减消元法求解即可.解答:解:由原方程组,得,由(1)+(2),并解得x=(3),把(3)代入(1),解得y=,∴原方程组的解为.点评:用加减法解二元一次方程组的一般步骤:1.方程组的两个方程中,如果同一个未知数的系数既不互为相反数又不相等,就用适当的数去乘方程的两边,使一个未知数的系数互为相反数或相等;2.把两个方程的两边分别相加或相减,消去一个未知数,得到一个一元一次方程;3.解这个一元一次方程;4.将求出的未知数的值代入原方程组的任意一个方程中,求出另一个未知数,从而得到方程组的解.15.解下列方程组:(1);(2).考点:解二元一次方程组.分析:将两个方程先化简,再选择正确的方法进行消元.解答:解:(1)化简整理为,①×3,得3x+3y=1500③,②﹣③,得x=350.把x=350代入①,得350+y=500,∴y=150.故原方程组的解为.(2)化简整理为,①×5,得10x+15y=75③,②×2,得10x﹣14y=46④,③﹣④,得29y=29,∴y=1.把y=1代入①,得2x+3×1=15,∴x=6.故原方程组的解为.点评:方程组中的方程不是最简方程的,最好先化成最简方程,再选择合适的方法解方程.16.解下列方程组:(1)(2)考点:解二元一次方程组.分析:观察方程组中各方程的特点,用相应的方法求解.解答:解:(1)①×2﹣②得:x=1,将x=1代入①得:2+y=4,y=2.∴原方程组的解为;(2)原方程组可化为,①×2﹣②得:﹣y=﹣3,y=3.将y=3代入①得:x=﹣2.∴原方程组的解为.点评:解此类题目要注意观察方程组中各方程的特点,采用加减法或代入法求解.2022年3月23日;第11页共10页。
二元一次方程组的解法练习题参考.doc

二元一次方程组的解法练习题一. 选择题(共6小题)I •二元-次方程组愿4的解为()2. 已知x, y 满足方程组J X+6y "12 ,贝】Jx+y 的值为()I3x — A. 9 B. 7 C. 5 D. 33. 若二元一次联立方程式1° 的解为x 二a, y=b,贝Ua+b 之值为何?()I - 3x+2y=21 A. 1^. B. — C. 7 D. 132 24. 若关于x, y 的二元一次方程组j X+y= 5k的解也是二元一次方程2x+3y=6的解,则k 的 x 一 y=9kA ・ 1 B. 2 C. 3 D. 4 6. 己知方程组fx+yh,贝|J % - y 值是( )[x+2y=8A. 5B. - 1C. 0 D- 1二. 填空题(共5小题)7. 已知(沪2是二元一次方程组严+by=7的解,贝|ja-b 二 _______ .,y=l |^ax - by=l 8. 写出一个解为(X=1的二元一次方程组—.ly=29. 已知卩弍是二元一次方程组P x+ny=2的解,则m+3n 的值为,y=l |^nx - iny=l 10. 当沪—时,方程组的解为X 二y.(x+2y 二2aA. ・3B . 3C. 2D.4 135.4x+3y=lax - (a~ l)y=3的解x 与y 互为相反数,则a 的值等于(值为( ) 若方程组11. 若关于X 、y 的二元一次方程组j 2x+y=3a ~ 1的解满足x+y=l,则a 的值为二2 三. 解答题(共3小题)12. 己知关于x, y 的二元一次方程组的解互为相反数,求k 的值.x+2y=-113. 已知二元一次方程2x+y=3(1)若y 的值是负数,求x 的取值范围;的值.(2)已知关于x, y 的方程组|X "y=a 的解x,^x+2y=b y 满足二元一次方程2x+y=3,求a 2+2ab+b 214.解方程(组)、不等式(组): ①寺[汀吉&-1)+1]-|(汀1)② 3+0. 2x ^0-20. 2+0, 3x0. 01uO.75③ Jx+1 二 5(y+2) U[3(2x-5)=5+4(3y+l )④3x+2y=5y+12x 二・ 3⑤矿萨73x - y+z 二14①X2 -②得,7x=7, x=l,代入①中得,2+y=14,二元一次方程组的解法练习题参考答案与试题解析一. 选择题(共6小题)1.二元一次方程组(X+y=5的解为()[2x - y=4A.卩二1B.卩二2 c. (x 二3 D . (x 二4l 尸4 l 尸3 l 尸2 l 尸1 【解答】解:(x+尸5①2x -尸4② ① +②,得3x=9, 解得x=3, 把x=3代入①, 得 3+y=5,y=2,所以原方程组的解为(X=3.1尸2 故选C.2•己知"满足方程组{豊爲,则泊的值为()A. 9B. 7C. 5D. 3 【解答】解: ①+②得:4x+4y=20, 则 x+y=5, 故选C3. 若二元一次联立方程式Q2x+y=14一 3x+2y=21的解为x=a, y=b,则a+b 之值为何? A •葺 B •号 C.7 D ,13【解答】解:J2x+y=14①[-3x+2y=21 ②解得y=12,则 a+b=l+12=13, 故选D.4.若关于x, y 的二元一次方程组X+y=5k的解也是二元一次方程2x+3y=6的解,则k 的 x 一 y=9k值为( )A.・丄B.丄 C ・2 D.4 4 3 3①+②得:2x=14k,即 x=7k,将 x=7k 代入①得:7k+y=5k,即 y= - 2k,将 x=7k, y= - 2k 代入 2x+3y=6 得:14k - 6k=6, 解得:k 」.4故选B.5. 若方程组(4x+3享1 的解x 与y 互为相反数,则a 的值等于( )ax -(8 - 1)尸3 A. I B. 2 C. 3 D. 4【解答】解:Tx, y 的值互为相反数, •I x+y=O,则4x+3y=l 可以变形为4x - 3x=l,解得x=l, 则 y= - 1,把 x=l, y= - 1 代入 ax - (a - 1) y=3,可得 a+ (a - 1) =3, 解得a=2.故选B.3y=9, y=3,把尸3代入②得:6.己知方程组< 值是(A. 5B.-1 C ・ 0D. 1【解答】解:方法-:{:爲 ②X2 -①得: ① ②'【解答】解:(x+y= 5k®[x - y=9k ②x=2, ••产,1尸3贝ij x - y=2 - 3= - 1,方法二:①■②得到:x - y= - 1, 故选:B. 二. 填空题(共5小题) 7.已知(尸2是二元一次方程组J ax+by=?的解,贝IJ a - b= - 1 y=lI ax - by=l【解答】解:把产2代入二元-次方程组严比尸7得:[y=l |^ax - by=l(2s+b 二7[2a-b=f 解得:(吧lb 二 3 a - b=2 - 3= - 1, 故答案为:~ 1.【解答】解:由1+2=3, 1・2二・1・列出方程组得 故答案为:J x+y=3・(答案不唯一).x - y 二一19.已知产2是二元一次方程组严+2=2的解,则m+3n 的值为3 ,y=l nx 一 iny=l①+②得m+3n=3, 故答案为:3.10.当a= - 3 时,方程组I'* 尸* 1的解为x 二y. ^x+2y=2a 【解答】解:Tx 二y, ・(x=a+l l3x=2a 解得a= - 3,8.写出一个解为“I 二的二元-次方程组x+y=3・(答案不唯一) x _ y= _ 1x+y=3x _ y= _ 1x=2y=l代入mx+ny=2 nx 一 iny=l 2irrl-n=2 2n 一 ITF I①②'【解答】解:故答案为:・3・11若关升、y 的二元一次方程组{蔦囂“的解满足5则a 的值为代入 x+y=l 中得:a+-^=l, 解得:a=-2,3 故答案为:23三. 解答题(共3小题)12. 已知关于x, y 的二元一次方程组的解互为相反数,求k 的值.[x+2y= - 1 【解答】解:『x+尸k ① x+2y 二-1②K - 1①+②得:3 (x+y ) =k- 1,即 x+y 二一, L- 一 1由题意得:x+y=O,即丄^二0,•j解得:k=l.13. 已知二元一次方程2x+y=3(1)若y 的值是负数,求x 的取值范围;{X — V —a的解x, y 满足二元一次方程2x+y=3,求x+2y=b的值.【解答】解:(1)方程整理得:y=3-2x, 由y 为负数,得到3 - 2x<0, 解得:x>1.5;(2)(m ①,[x+2y=b ② ①+②,得 2x+y 二a+b,【解答】解:"2x+y 二 3n- 1 ①\x+2y=2②①+②得:3 (x+y) =3a+l,即 x+y=a+丄,32+2ab+b 2T2x+y=3, •I a+b=3,a 2+2ab+b 2= (a+b) 2=9-14. 解方程(组)、不等式(组):① 专[x -y(x - l)+l]=y(x - 1) 心3+0・ 2x 0. 2+0. 3x 八 卄 ②…-―_ 0. 75③ Jx+1 二 5(y+2) °〔3(2x-5)二 5+4(3y+l) ④ 3x+2y=5y+12x 二・ 3 ⑤ 寿亍7.3x 一 y+z=14【解答】解:①去括号得:丄x -丄(x ・1) +丄=2 (x- 1),2 4 2 3去分母得:6x - 3 (x - 1) +6=8 (x - 1), 去括号得:6x - 3x+3+6=8x - 8, 移项合并得:5x=17, 解得:x=3.4;② 方程组整理得:15+x ・ 20 - 30x=0.75, 移项合并得:29x=・ 5.75, 解得:x=・旦;116②-①得:3y= - 5,即 y=-—,3把y=・5代入②得:X-2,3 3,_2x=3~则方程组的解为彳 -;①X4 -②得:3y= - 9,即尸・3, JC y= - 3代入①得:x=l, 则方程组的解为―③方程组整理得:鼻-5尸9①x - 2尸4②④整理得:3x+2y=- 3①12x+5尸- 3②r3x- 2尸。
(完整版)二元一次方程解法大全.,推荐文档

二元一次方程解法大全 1、直接开平方法: 直接开平方法就是用直接开平方求解二元一次方程的方法。
用直接开平方法解形如(x-m)2=n(n≥0)的方程,其解为x=±根号下n+m. 例1.解方程(1)(3x+1)2=7(2)9x2-24x+16=11 分析:(1)此方程显然用直接开平方法好做,(2)方程左边是完全平方式(3x-4)2,右边=11>0,所以此方程也可用直接开平方法解。
(1)解:(3x+1)2=7× ∴(3x+1)2=5 ∴3x+1=±(注意不要丢解) ∴x= ∴原方程的解为x1=,x2= (2)解:9x2-24x+16=11 ∴(3x-4)2=11 ∴3x-4=± ∴x= ∴原方程的解为x1=,x2= 2.配方法:用配方法解方程ax2+bx+c=0(a≠0) 先将常数c移到方程右边:ax2+bx=-c 将二次项系数化为1:x2+x=- 方程两边分别加上一次项系数的一半的平方:x2+x+()2=-+()2 方程左边成为一个完全平方式:(x+)2= 当b^2-4ac≥0时,x+=± ∴x=(这就是求根公式) 例2.用配方法解方程3x^2-4x-2=0(注:X^2是X的平方) 解:将常数项移到方程右边3x^2-4x=2 将二次项系数化为1:x2-x= 方程两边都加上一次项系数一半的平方:x2-x+()2=+()2 配方:(x-)2= 直接开平方得:x-=± ∴x= ∴原方程的解为x1=,x2=. 3.公式法:把一元二次方程化成一般形式,然后计算判别式△=b2-4ac的值,当b2-4ac≥0时,把各项系数a,b,c的值代入求根公式x=[-b±(b^2-4ac)^(1/2)]/(2a),(b^2-4ac≥0)就可得到方程的根。
例3.用公式法解方程2x2-8x=-5 解:将方程化为一般形式:2x2-8x+5=0 ∴a=2,b=-8,c=5 b^2-4ac=(-8)2-4×2×5=64-40=24>0 ∴x=[(-b±(b^2-4ac)^(1/2)]/(2a) ∴原方程的解为x1=,x2=. 4.因式分解法:把方程变形为一边是零,把另一边的二次三项式分解成两个一次因式的积的形式,让两个一次因式分别等于零,得到两个一元一次方程,解这两个一元一次方程所得到的根,就是原方程的两个根。
二元一次方程练习题有过程带答案

二元一次方程练习题有过程带答案8.1二元一次方程组一、填空题1、二元一次方程4x-3y=12,当x=0,1,2,3时,y=____2、在x+3y=3中,若用x表示y,则y表示x,则x=3、已知方程x2+x+y=k+2,当k=______时,方程为一元一次方程;当k=______时,方程为二元一次方程。
4、对二元一次方程2-3=10,当x=0时,则y=____;当y=0时,则x=____。
5、方程2x+y=5的正整数解是______。
6、若2+|2y+1|=0,则?x?2?x?y?a7、方程组?的一个解为?,那么这个方程组的另一个解是。
y?3xy?b??8、若x?1时,关于x、y的二元一次方程组2?ax?2y?1的解互为倒数,则??x?by?2a?2b?二、选择题1、方程2x-3y=5,xy=3,x?二元一次方程的有个。
A、1B、2C、3D、42、方程2x+y=9在正整数范围内的解有A、1个B、2个C、3个D、4个3、与已知二元一次方程5x-y=2组成的方程组有无数多个解的方程是A、10x+2y=B、4x-y=C、20x-4y=D、15x-3y=64、若是5x2ym与4xn?m?1y2n?2同类项,则m2?n的值为A、1B、-1C、-D、以上答案都不对5、在方程x2+x+y+3k=0中,若此方程为二元一次方程,则k值为?3,3x-y+2z=0,x2?y?6中是yA、2B、-C、2或-D、以上答案都不对.6、若??x?2是二元一次方程组的解,则这个方程组是 ?y??1?x?3y?5?y?x?3?2x?y?5?x?2yA、? B、? C、?D、?x?y?5y?2x?5x?y?1x?3y?17、在方程2?3?3中,用含x的代数式表示y,则A、y?5x?B、y??x?C、y?5x?D、y??5x?38、已知x=3-k,y=k+2,则y与x的关系是A、x+y=5B、x+y=1C、x-y=1D、y=x-19、下列说法正确的是A、二元一次方程只有一个解B、二元一次方程组有无数个解C、二元一次方程组的解必是它所含的二元一次方程的解D、三元一次方程组一定由三个三元一次方程组成?3x?5y?610、若方程组? 的解也是方程3x+ky=10的解,则k的值是x?15y?16?A、k=6= B、k=10C、k=9D、k=三、解答题1、解关于x的方程x?a?22、已知方程组?1 10?x?y?7,试确定a、c的值,使方程组:?ax?2y?c有一个解;有无数解;没有解3、关于x、y的方程3kx?2y?6k?3,对于任何k的值都有相同的解,试求它的解。
二元一次方程组解法及应用___知识要点+典型例题+配套练习

七下数学--第八章 二元一次方程组要点一:二元一次方程组的解法 【知识要点】1.二元一次方程:含有两个未知数,且未知项的次数为1,这样的方程叫二元一次方程。
①二元一次方程左右两边的代数式必须是整式;(不是整式的化成整式) ②二元一次方程必须含有两个未知数;③二元一次方程中的“一次”是指含有未知数的项的次数,而不是某个未知数的次数。
2.二元一次方程的解:能使二元一次方程左右两边的值相等的一对未知数的值叫做二元一次方程的解任何一个二元一次方程都有无数解。
3.二元一次方程组:①由两个或两个以上的整式方程组成,常用“ ”把这些方程联合在一起; ②整个方程组中含有两个不同的未知数,且方程组中同一未知数代表同一数量; ③方程组中每个方程经过整理后都是一次方程, 4.二元一次方程组的解:注意:方程组的解满足方程组中的每个方程,而每个方程的解不一定是方程组的解。
5.会检验一对数值是不是一个二元一次方程组的解6.二元一次方程组的解法:(1) 代入消元法 (2)加减消元法 三、理解解二元一次方程组的思想转化消元一元一次方程二元一次方程组四、解二元一次方程组的一般步骤(一)、代入法一般步骤:变形——代入——求解——回代——写解 (二)、加减法一般步骤:变形——加减——求解——代入——写解 【典型例题】 一、选择题1、(2009·福州中考)二元一次方程组2,0x y x y +=⎧⎨-=⎩的解是 ( C )A .0,2.x y =⎧⎨=⎩B .2,0.x y =⎧⎨=⎩C .1,1.x y =⎧⎨=⎩D .1,1.x y =-⎧⎨=-⎩2、(2009·百色中考)已知21x y =⎧⎨=⎩是二元一次方程组71ax by ax by +=⎧⎨-=⎩的解, 则a b -的值为( B ).A .1B .-1C . 2D .33、(2009·内江中考)若关于x ,y 的方程组⎩⎨⎧=+=-n my x m y x 2的解是⎩⎨⎧==12y x ,则n m -为( D )A .1B .3C .5D .24、(2009·日照中考)若关于x ,y 的二元一次方程组⎩⎨⎧=-=+ky x k y x 9,5的解也是二元一次方程632=+y x 的解,则k 的值为 (B. )(A )43- (B )43 (C )34 (D )34-5、(2009·绵阳中考)小明在解关于x 、y 的二元一次方程组⎩⎨⎧=⊗-=⊗+133,y x y x 时得到了正确结果⎩⎨⎧=⊕=.1,y x 后来发现“⊗”“ ⊕”处被墨水污损了,请你帮他找出⊗、⊕ 处的值分别是( B ) A .⊗ = 1,⊕ = 1 B .⊗ = 2,⊕ = 1 C .⊗ = 1,⊕ = 2 D .⊗ = 2,⊕ = 26、(2009·青海中考)已知代数式133m x y --与52n m n x y +是同类项,那么m n 、的值分别是(C )A .21m n =⎧⎨=-⎩B .21m n =-⎧⎨=-⎩C .21m n =⎧⎨=⎩D .21m n =-⎧⎨=⎩7、(2007·丽水中考)方程组5210x y x y +=⎧⎨+=⎩ ,由②-①,得正确的方程是( B )(A )310x = (B ) 5x = (C )35x =- (D )5x =- 8、若5x -6y =0,且xy ≠0,则yx yx 3545--的值等于( )(A )32(B )23(C )1 (D )-1二、填空题9、(2009·定西中考)方程组25211x y x y -=-⎧⎨+=⎩,的解是 .34x y =⎧⎨=⎩,10、(2008·临沂中考)已知x 、y 满足方程组⎩⎨⎧=+=+,42,52y x y x 则x -y 的值为___1_____.11、(2009·呼和浩特中考)如果|21||25|0x y x y -++--=,则x y +的值为 6 三、解答题12、 (2009·湘西中考)解方程:2725x y x y -=⎧⎨+=⎩①②【解析】①+② 得 4x =12,即 x =3 代入① 有6-y =7,即 y =-1所以原方程的解是:⎩⎨⎧-==13y x13、(2007·青岛中考)解方程组:2536x y x y +=-=⎧⎨⎩,.【解析】25,3 6.x y x y +=-=⎧⎨⎩①×3,得 6x +3y =15. ③ ②+③,得 7x =21,x =3. 把x =3代入①,得2×3+y =5,y =-1.14、如果(a -2)x+(b+1)y=13是关于x ,y 的二元一次方程,则a ,b 满足什么条件?15、二元一次方程组437(1)3x y kx k y +=⎧⎨+-=⎩的解x ,y 的值相等,求k .16、方程组2528x y x y +=⎧⎨-=⎩的解是否满足2x -y=8?满足2x -y=8的一对x ,y 的值是否是方程组① ②2528x y x y +=⎧⎨-=⎩的解? 【配套练习】1.判断下列方程是不是二元一次方程4).1(22=+y x 222).2(x y x x =-+ 6).3(=-y xyy x =).4( 6).5(2=++z y x 811).6(=+yx2.在下列每个二元一次方程组的后面给出了x 与y 的一对值,判断这对值是不是前面方程组的解?(1)⎩⎨⎧=+=-)2(7032)1(53y x y x ⎩⎨⎧==12y x (2)⎩⎨⎧=+=-)2(1147)1(123y x y x ⎩⎨⎧==11y x3.判断(1)由两个二元一次方程组成方程组一定是二元一次方程组( )(2)方程组⎩⎨⎧=+=-3513y x y x 的解是方程x +5y =3的解,反过来方程x +5y =3的解也是方程组⎩⎨⎧=+=-3513y x y x 的解 ………( ) 4.在方程4x -3y =7里,如果用x 的代数式表示y ,则437yx +=( ) 5.任何一个二元一次方程都有( ) (A )一个解;(B )两个解; (C )三个解;(D )无数多个解;6. 关于x 、y 的方程组⎩⎨⎧=-=+m y x my x 932的解是方程3x +2y =34的一组解,那么m 的值是( )(A )2;(B )-1;(C )1;(D )-2;7. 与已知二元一次方程5x -y =2组成的方程组有无数多个解的方程是( ) (A )15x -3y =6 (B )4x -y =7(C )10x +2y =4(D )20x -4y =38. 下列方程组中,是二元一次方程组的是( )(A )⎪⎩⎪⎨⎧=+=+9114y x y x(B )⎩⎨⎧=+=+75z y y x (C )⎩⎨⎧=-=6231y x x(D )⎩⎨⎧=-=-1y x xyy x9. 已知方程组⎩⎨⎧-=+=-135b y ax y x 有无数多个解,则a 、b 的值等于( )(A )a =-3,b =-14(B )a =3,b =-7 (C )a =-1,b =9(D )a =-3,b =1410. 若x 、y 均为非负数,则方程6x =-7y 的解的情况是( ) (A )无解(B )有唯一一个解 (C )有无数多个解(D )不能确定11. 若|3x +y +5|+|2x -2y -2|=0,则2x 2-3xy 的值是( ) (A )14 (B )-4 (C )-12 (D )1212. .已知⎩⎨⎧-==24y x 与⎩⎨⎧-=-=52y x 都是方程y =kx +b 的解,则k 与b 的值为( )(A )21=k ,b =-4 (B )21-=k ,b =4 (C )21=k ,b =4(D )21-=k ,b =-413. 如果0.4x -0.5y =1.2,那么用含有y 的代数式表示的代数式是_____________;14已知方程组⎩⎨⎧-=+=+m y x ay x 26432有无数多解,则a =______,m =______;15. 若4x +3y +5=0,则3(8y -x )-5(x +6y -2)的值等于_________;16.若x +y =a ,x -y =1同时成立,且x 、y 都是正整数,则a 的值为________;17.从方程组)0(030334≠⎩⎨⎧=+-=--xyz z y x z y x 中可以知道,x :z =_______;y :z =________;18.解方程组(1)⎪⎪⎩⎪⎪⎨⎧=-=-1332343n m nm (2))(6441125为已知数a a y x a y x ⎩⎨⎧=-=+(3)⎪⎪⎩⎪⎪⎨⎧=++=+125432y x yx y x (4)⎩⎨⎧=--+=-++0)1(2)1()1(2x y x x x y y x(5)⎪⎩⎪⎨⎧=-+-=-+=-+3113y x z x z y z y x (6)⎪⎩⎪⎨⎧=+-==30325:3:7:4:z y x z x y x19. m 取什么整数值时,方程组⎩⎨⎧=-=+0242y x my x 的解:(1)是正数;(2)是正整数?并求它的所有正整数解。
二元一次方程组解法练习题精选(含答案)

二元一次方程组解法练习题一.解答题 1.解下列方程组 (1)(2)(3))(6441125为已知数a a y x ay x ⎩⎨⎧=-=+(4)(5)(6).(7)(8)⎩⎨⎧=--+=-++0)1(2)1()1(2x y x x x y y x(9)(10) ⎪⎪⎩⎪⎪⎨⎧=-++=-++1213222132y x y x2.求适合的x ,y 的值.3.已知关于x,y的二元一次方程y=kx+b 的解有和.(1)求k,b的值.(2)当x=2时,y的值.(3)当x为何值时,y=3?1.解下列方程组(1)(2);(3);(4)(5).(6)(7)(8)(9)(10);2.在解方程组时,由于粗心,甲看错了方程组中的a ,而得解为,乙看错了方程组中的b ,而得解为.(1)甲把a看成了什么,乙把b看成了什么?(2)求出原方程组的正确解.二元一次方程组解法练习题精选参考答案与试题解析一.解答题(共16小题)1.求适合的x,y的值.考点:解二元一次方程组.分析:先把两方程变形(去分母),得到一组新的方程,然后在用加减消元法消去未知数x,求出y的值,继而求出x的值.解答:解:由题意得:,由(1)×2得:3x﹣2y=2(3),由(2)×3得:6x+y=3(4),(3)×2得:6x﹣4y=4(5),(5)﹣(4)得:y=﹣,把y的值代入(3)得:x=,∴.点评:本题考查了二元一次方程组的解法,主要运用了加减消元法和代入法.2.解下列方程组(1)(2)(3)(4).考点:解二元一次方程组.分析:(1)(2)用代入消元法或加减消元法均可;(3)(4)应先去分母、去括号化简方程组,再进一步采用适宜的方法求解.解答:解:(1)①﹣②得,﹣x=﹣2,解得x=2,把x=2代入①得,2+y=1,解得y=﹣1.故原方程组的解为.(2)①×3﹣②×2得,﹣13y=﹣39,解得,y=3,把y=3代入①得,2x﹣3×3=﹣5,解得x=2.故原方程组的解为.(3)原方程组可化为,①+②得,6x=36,x=6,①﹣②得,8y=﹣4,y=﹣.所以原方程组的解为.(4)原方程组可化为:,①×2+②得,x=,把x=代入②得,3×﹣4y=6,y=﹣.所以原方程组的解为.点评:利用消元法解方程组,要根据未知数的系数特点选择代入法还是加减法:①相同未知数的系数相同或互为相反数时,宜用加减法;②其中一个未知数的系数为1时,宜用代入法.3.解方程组:解二元一次方程组.考点:计算题.专题:先化简方程组,再进一步根据方程组的特点选用相应的方法:用加减法.分析:解答:解:原方程组可化为,①×4﹣②×3,得7x=42,解得x=6.把x=6代入①,得y=4.所以方程组的解为.点;二元一次方程组无论多复杂,解二元一次方程组的基本思想都是消元.消元的方法有代入法和加减法.评:4.解方程组:考点:解二元一次方程组.专题:计算题.分析:把原方程组化简后,观察形式,选用合适的解法,此题用加减法求解比较简单.解答:解:(1)原方程组化为,①+②得:6x=18,∴x=3.代入①得:y=.所以原方程组的解为.点评:要注意:两个二元一次方程中同一未知数的系数相反或相等时,把这两个方程的两边相加或相减,就能消去这个未知数,得到一个一元一次方程,这种方法叫做加减消元法.本题适合用此法.5.解方程组:考点:解二元一次方程组.专题:计算题;换元法.分析:本题用加减消元法即可或运用换元法求解.解答:解:,①﹣②,得s+t=4,①+②,得s﹣t=6,即,解得.所以方程组的解为.点评:此题较简单,要熟练解方程组的基本方法:代入消元法和加减消元法.6.已知关于x,y的二元一次方程y=kx+b的解有和.(1)求k,b的值.(2)当x=2时,y的值.(3)当x为何值时,y=3?考点:解二元一次方程组.专题:计算题.分析:(1)将两组x,y的值代入方程得出关于k、b的二元一次方程组,再运用加减消元法求出k、b的值.(2)将(1)中的k、b代入,再把x=2代入化简即可得出y的值.(3)将(1)中的k、b和y=3代入方程化简即可得出x的值.解答:解:(1)依题意得:①﹣②得:2=4k,所以k=,所以b=.(2)由y=x+,把x=2代入,得y=.(3)由y=x+把y=3代入,得x=1.点评:本题考查的是二元一次方程的代入消元法和加减消元法,通过已知条件的代入,可得出要求的数.7.解方程组:(1);(2).考点:解二元一次方程组.分析:根据各方程组的特点选用相应的方法:(1)先去分母再用加减法,(2)先去括号,再转化为整式方程解答.解答:解:(1)原方程组可化为,①×2﹣②得:y=﹣1,将y=﹣1代入①得:x=1.∴方程组的解为;(2)原方程可化为,即,①×2+②得:17x=51,x=3,将x=3代入x﹣4y=3中得:y=0.∴方程组的解为.点评:这类题目的解题关键是理解解方程组的基本思想是消元,掌握消元的方法有:加减消元法和代入消元法.根据未知数系数的特点,选择合适的方法.8.解方程组:考点:解二元一次方程组.专题:计算题.分析:本题应把方程组化简后,观察方程的形式,选用合适的方法求解.解答:解:原方程组可化为,①+②,得10x=30,x=3,代入①,得15+3y=15,y=0.则原方程组的解为.点评:解答此题应根据各方程组的特点,有括号的去括号,有分母的去分母,然后再用代入法或加减消元法解方程组.9.解方程组:考点:解二元一次方程组.专题:计算题.分析:本题为了计算方便,可先把(2)去分母,然后运用加减消元法解本题.解答:解:原方程变形为:,两个方程相加,得4x=12,x=3.把x=3代入第一个方程,得4y=11,y=.解之得.点评:本题考查的是二元一次方程组的解法,方程中含有分母的要先化去分母,再对方程进行化简、消元,即可解出此类题目.10.解下列方程组:(1)(2)考点:解二元一次方程组.专题:计算题.分析:此题根据观察可知:(1)运用代入法,把①代入②,可得出x,y的值;(2)先将方程组化为整系数方程组,再利用加减消元法求解.解答:解:(1),由①,得x=4+y③,代入②,得4(4+y)+2y=﹣1,所以y=﹣,把y=﹣代入③,得x=4﹣=.所以原方程组的解为.(2)原方程组整理为,③×2﹣④×3,得y=﹣24,把y=﹣24代入④,得x=60,所以原方程组的解为.点评:此题考查的是对二元一次方程组的解法的运用和理解,学生可以通过题目的训练达到对知识的强化和运用.11.解方程组:(1)(2)考点:解二元一次方程组.专题:计算题;换元法.分析:方程组(1)需要先化简,再根据方程组的特点选择解法;方程组(2)采用换元法较简单,设x+y=a,x﹣y=b,然后解新方程组即可求解.解答:解:(1)原方程组可化简为,解得.(2)设x+y=a,x﹣y=b,∴原方程组可化为,解得,∴∴原方程组的解为.点评:此题考查了学生的计算能力,解题时要细心.12.解二元一次方程组:(1);(2).考点:解二元一次方程组.专题:计算题.分析:(1)运用加减消元的方法,可求出x、y的值;(2)先将方程组化简,然后运用加减消元的方法可求出x、y的值.解答:解:(1)将①×2﹣②,得15x=30,x=2,把x=2代入第一个方程,得y=1.则方程组的解是;(2)此方程组通过化简可得:,①﹣②得:y=7,把y=7代入第一个方程,得x=5.则方程组的解是.点评:此题考查的是对二元一次方程组的解法的运用和理解,学生可以通过题目的训练达到对知识的强化和运用.13.在解方程组时,由于粗心,甲看错了方程组中的a,而得解为,乙看错了方程组中的b,而得解为.(1)甲把a看成了什么,乙把b看成了什么?(2)求出原方程组的正确解.考点:解二元一次方程组.专题:计算题.分析:(1)把甲乙求得方程组的解分别代入原方程组即可;(2)把甲乙所求的解分别代入方程②和①,求出正确的a、b,然后用适当的方法解方程组.解答:解:(1)把代入方程组,得,解得:.把代入方程组,得,解得:.∴甲把a看成﹣5;乙把b看成6;(2)∵正确的a是﹣2,b是8,∴方程组为,解得:x=15,y=8.则原方程组的解是.点评:此题难度较大,需同学们仔细阅读,弄清题意再解答.14.考点:解二元一次方程组.分析:先将原方程组中的两个方程分别去掉分母,然后用加减消元法求解即可.解答:解:由原方程组,得,由(1)+(2),并解得x=(3),把(3)代入(1),解得y=∴原方程组的解为.点评:用加减法解二元一次方程组的一般步骤:1.方程组的两个方程中,如果同一个未知数的系数既不互为相反数又不相等,就用适当的数去乘方程的两边,使一个未知数的系数互为相反数或相等;2.把两个方程的两边分别相加或相减,消去一个未知数,得到一个一元一次方程;3.解这个一元一次方程;4.将求出的未知数的值代入原方程组的任意一个方程中,求出另一个未知数,从而得到方程组的解.15.解下列方程组:(1);(2).考点:解二元一次方程组.分析:将两个方程先化简,再选择正确的方法进行消元.解答:解:(1)化简整理为,①×3,得3x+3y=1500③,②﹣③,得x=350.把x=350代入①,得350+y=500,∴y=150.故原方程组的解为.(2)化简整理为,①×5,得10x+15y=75③,②×2,得10x﹣14y=46 ④,③﹣④,得29y=29,∴y=1.把y=1代入①,得2x+3×1=15,∴x=6.故原方程组的解为.点评:方程组中的方程不是最简方程的,最好先化成最简方程,再选择合适的方法解方程.16.解下列方程组:(1)(2)考点:解二元一次方程组.分析:观察方程组中各方程的特点,用相应的方法求解.解答:解:(1)①×2﹣②得:x=1,将x=1代入①得:2+y=4,y=2.∴原方程组的解为;(2)原方程组可化为,①×2﹣②得:﹣y=﹣3,y=3.将y=3代入①得:x=﹣2.∴原方程组的解为.。
完整版二元一次方程组解法练习题精选含答案

二元一次方程组解法练习题精选(含答案)一.解答题(共16小题).求适合的值.y,1x的.解下列方程组2(1))2((3).)4(3.解方程组:4.解方程组:5.解方程组:y=kx+by.已知关于x,的二元一次方程的解有.和6 的值.,)求(1kb 时,x=2)当(2y的值.)当(3y=3为何值时,x?7.解方程组:);(1.(2 ).解方程组:89.解方程组:.解下列方程组:10(1))2 (11.解方程组:)(1)2 (.解二元一次方程组:12;)1(.).(2而得解为,,由于粗心,13.在解方程组甲看错了方程组中的a 时,,而得解为.乙看错了方程组中的b(1)甲把a看成了什么,乙把b看成了什么?(2)求出原方程组的正确解..1415.解下列方程组:);1().2()2 )((16.解下列方程组:1x?y?25?的解是否满足2x-y=8?满足方程组17.2x-y=8的一对x,的值是否是方程y?8y??x2?25?x?y?组的解??8?y?x2?二元一次方程组解法练习题精选(含答案)参考答案与试题解析一.解答题(共16小题).求适合的x,y的值.1考解二元一次方程组.809625点:分,然后在用加减消,得到一组新的方程先把两方程变形(去分母)析:的值.的值,继而求出,求出yx元法消去未知数x解,解:由题意得:答:3),2y=22由(1)×得:3x﹣(6x+y=3)由(2×3得:(4),),54y=46x)(3×2得:﹣(,)得:4y=﹣)﹣((5的值代入(把y3,)得:x=∴.本题考查了二元一次方程组的解法,主要运用了加减消元法和代入法.点评:.解下列方程组2.)(12)((3).)4 (解二元一次方程组.809625 考点:(1)(2)用代入消元法或加减消元法均可;分析:(3)(4)应先去分母、去括号化简方程组,再进一步采用适宜的方法求解.解解:(1)①﹣②得,﹣x=﹣2,答:解得x=2,把x=2代入①得,2+y=1,解得y=﹣1.故原方程组的解为.39,得,﹣﹣②×213y=﹣3(2)①×y=3,解得,5,﹣﹣代入y=3①得,2x3×3=把.解得x=2故原方程组的解为.,)原方程组可化为3(.①+②得,6x=36,x=6,①﹣②得,8y=﹣4,﹣.y=所以原方程组的解为.)原方程组可化为:(4,,得,x=①×2+②4y=6得,x=代入②3,×﹣把y=.﹣.所以原方程组的解为利用消元法解方程组,要根据未知数的系数特点选择代入法还是加减法:点评:①相同未知数的系数相同或互为相反数时,宜用加减法;②其中一个未知数的系数为1时,宜用代入法..解方程组:3809625 解二元一次方程组.考:点计算题.专:题先化简方程组,再进一步根据方程组的特点选用相应的方法:用加减法.分.析:解解:原方程组可化为,答:3,得①×4﹣②×7x=42,.解得x=6 .x=6代入①,得y=4把.所以方程组的解为注意:二元一次方程组无论多复杂,解二元一次方程组的基本思想都是消点评:元.消元的方法有代入法和加减法..解方程组:4809625 考解二元一次方程组.:点计算题.专:题把原方程组化简后,观察形式,选用合适的解法,此题用加减法求解比较分析:简单.解,)原方程组化为1(解:答:得:6x=18,②①+ x=3∴..y=得:①代入.所以原方程组的解为.要注意:两个二元一次方程中同一未知数的系数相反或相等时,把这两个点评:方程的两边相加或相减,就能消去这个未知数,得到一个一元一次方程,这种方法叫做加减消元法.本题适合用此法..解方程组:5考解二元一次方程组.809625点:专计算题;换元法.题:分本题用加减消元法即可或运用换元法求解.析:解解:,答:s+t=4,,得①﹣②,s,得﹣t=6①+②,即解得..所以方程组的解为点此题较简单,要熟练解方程组的基本方法:代入消元法和加减消元法.评:和.的解有,y的二元一次方程y=kx+b 6.已知关于x 的值.1)求k,b(的值.)当x=2时,y(2 y=3)当x为何值时,?(3 考解二元一次方程组.809625:点计算题.专题:的二元一次方程组b,的值代入方程得出关于k、(1)将两组x,y分析:再运用加减消元法求出k、b的值.(2)将(1)中的k、b代入,再把x=2代入化简即可得出y的值.(3)将(1)中的k、b和y=3代入方程化简即可得出x的值.解解:)依题意得:(1 答:①﹣②得:2=4k,k=,所以b=.所以x+,2)由y=(y=.代入,得x=2把x+)由y=3(.x=1代入,得y=3把点本题考查的是二元一次方程的代入消元法和加减消元法,通过已知条件的评:代入,可得出要求的数.7.解方程组:);(1).2 (考解二元一次方程组.809625点:分根据各方程组的特点选用相应的方法:(()先2)先去分母再用加减法,1 去括号,再转化为整式方程解答.析:解解:(1)原方程组可化为,答:①×2②得:﹣,y=﹣1 ①得:1将y=﹣代入.x=1方程组的解为;∴2()原方程可化为,,即①×得:②2+ ,17x=51.x=3,将x=3代入x﹣4y=3中得:y=0.方程组的解为.∴这类题目的解题关键是理解解方程组的基本思想是消元,掌握消元的方法点评:有:加减消元法和代入消元法.根据未知数系数的特点,选择合适的方法..解方程组:8考解二元一次方程组.809625点:专计算题.题:分本题应把方程组化简后,观察方程的形式,选用合适的方法求解.析:解解:原方程组可化为,答:①+②,得10x=30,x=3,代入①,得15+3y=15,y=0.则原方程组的解为.解答此题应根据各方程组的特点,有括号的去括号,有分母的去分母,然点.评:后再用代入法或加减消元法解方程组..解方程组:9解二元一次方程组.809625 考:点计算题.专题:分本题为了计算方便,可先把(2)去分母,然后运用加减消元法解本题.析:解解:原方程变形为:,答:两个方程相加,得4x=12,x=3.把x=3代入第一个方程,得,4y=11.y=解之得.本题考查的是二元一次方程组的解法,方程中含有分母的要先化去分母,点评:再对方程进行化简、消元,即可解出此类题目..解下列方程组:10.)1()2 (解二元一次方程组.809625 考:点计算题.专:题此题根据观察可知:分析:(1)运用代入法,把①代入②,可得出x,y的值;(2)先将方程组化为整系数方程组,再利用加减消元法求解.解,)1(解:答:③,①由,得x=4+y ,,得代入②4(4+y)+2y=﹣1﹣y=,所以﹣.=把y=代入﹣③,得x=4所以原方程组的解为.,(2)原方程组整理为24,﹣,得④×2③×﹣3y= 把y=,,得④代入﹣24x=60.所以原方程组的解为点此题考查的是对二元一次方程组的解法的运用和理解,学生可以通过题目评:的训练达到对知识的强化和运用.11.解方程组:)(1)(2解二元一次方程组.809625 考:点计算题;换元法.专:题方程组(1分)需要先化简,再根据方程组的特点选择解法;析:方程组(2)采用换元法较简单,设x+y=a,x﹣y=b,然后解新方程组即可求解.解)原方程组可化简为,(解:1答:解得.﹣,)设(2x+y=axy=b,,∴原方程组可化为,解得.∴原方程组的解为∴.点此题考查了学生的计算能力,解题时要细心.评:12.解二元一次方程组:);(1.)(2解二元一次方程组.考809625点:计算题.专:题(1)运用加减消元的方法,可求出x、y分的值;析:(2)先将方程组化简,然后运用加减消元的方法可求出x、y的值.解解:(1)将①×2﹣②,得答:15x=30,x=2,把x=2代入第一个方程,得y=1.则方程组的解是;,)此方程组通过化简可得:2(.①﹣②得:y=7,把y=7代入第一个方程,得x=5.则方程组的解是.此题考查的是对二元一次方程组的解法的运用和理解,学生可以通过题目点评:的训练达到对知识的强化和运用.而得解为,a,.在解方程组时,由于粗心,甲看错了方程组中的13,而得解为b乙看错了方程组中的.(1)甲把a看成了什么,乙把b看成了什么?(2)求出原方程组的正确解.考解二元一次方程组.809625点:专计算题.题:分(1)把甲乙求得方程组的解分别代入原方程组即可;析:(2)把甲乙所求的解分别代入方程②和①,求出正确的a、b,然后用适当的方法解方程组.解代入方程组,(解:1)把答:,得.解得:代入方程组,把得,解得:.∴甲把a看成﹣5;乙把b看成6;(2)∵正确的a是﹣2,b是8,方程组为,∴.解得:x=15,y=8.则原方程组的解是点此题难度较大,需同学们仔细阅读,弄清题意再解答.评:.14考809625 解二元一次方程组.点:先将原方程组中的两个方程分别去掉分母,然后用加减消元法求解即可.分析:解解:由原方程组,得答:,1由()2(+),并解得,)3(x=把(3)代入(1),解得y=,原方程组的解为.∴用加减法解二元一次方程组的一般步骤:点评:1.方程组的两个方程中,如果同一个未知数的系数既不互为相反数又不相等,就用适当的数去乘方程的两边,使一个未知数的系数互为相反数或相等;2.把两个方程的两边分别相加或相减,消去一个未知数,得到一个一元一次方程;3.解这个一元一次方程;4.将求出的未知数的值代入原方程组的任意一个方程中,求出另一个未知数,从而得到方程组的解.15.解下列方程组:);(1)(2.809625 考解二元一次方程组.点:分将两个方程先化简,再选择正确的方法进行消元.析:1解:()化简整理为,解,③3x+3y=1500,得3①×答:②﹣③,得x=350.把x=350代入①,得350+y=500,∴y=150.故原方程组的解为.)化简整理为,(2①×5,得10x+15y=75③,②×2,得10x﹣14y=46④,③﹣④,得29y=29,∴y=1.把y=1代入①,得2x+3×1=15,∴x=6.故原方程组的解为.点方程组中的方程不是最简方程的,最好先化成最简方程,再选择合适的方评:法解方程.)(216.解下列方程组:(1)考解二元一次方程组.809625点:分观察方程组中各方程的特点,用相应的方法求解.析:解解:(1)①×2﹣②得:x=1,得:①代入x=1将答:2+y=4,y=2.原方程组的解为;∴)原方程组可化为,(2①×2﹣②得:﹣y=﹣3,y=3.将y=3代入①得:x=﹣2.原方程组的解为.∴点解此类题目要注意观察方程组中各方程的特点,采用加减法或代入法求解.评:。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二元一次方程组的解法
代入法解二元一次方程组
一、初步练习
1、将方程5x-6y=12变形:若用y 的式子表示x ,则x=______,当y=-2时,x=_______;若用含x 的式子表示y ,则y=______,当x=0时,y=________ 。
2、在方程2x+6y-5=0中,当3y=-4时,2x= ____________。
3、若⎩⎨⎧-=-=+⎩⎨⎧-==1by ax 7
by ax 2y 1x 是方程组的解,则a=______,
b=_______。
4、若方程y=1-x 的解也是方程3x+2y=5的解,则x=____,y=____。
5、用代人法解方程组 ①
⎩⎨⎧=+-=7y 3x 23x y ②, 把____代人____,可以消去未知数______。
6、已知方程组⎩⎨⎧=-=-1y 7x 45y x 3的解也是方程组⎩⎨⎧==-5by -x 34
y 2ax 的解,
则a=_______,b=________ ,3a+2b=___________。
7、已知x=1和x=2都满足关于x 的方程x 2
+px+q=0,则p=_____,q=________ 。
8、当k=______时,方程组⎩⎨⎧=-+=+3y 1k kx 1y 3x 4)(的解中x 与y 的值相等。
9、用代入法解下列方程组:
⑴⎩⎨⎧=+=5x y 3
x ⑵⎩⎨⎧==+y 3x 2y 32x ⑶⎩⎨⎧=-=+8y 2x 57y x 3
二、训练
1、方程组
{1y 2x 11
y -x 2+==的解是( )
A.⎩⎨
⎧==0y 0
x B.⎩⎨⎧==37y x C.⎩⎨⎧==73y x D.⎩⎨⎧-===37y x
2、已知二元一次方程3x+4y=6,当x 、y 互为相反数时,x=_____,
y=______;当x 、y 相等时,x=______,y= _______ 。
3、若2a y+5b 3x 与-4a 2x b 2-4y 是同类项,则a=______,b=_______。
4、对于关于x 、y 的方程y=kx+b ,k 比b 大1,且当x=21
时,
y=21
,则k 、b 的值分别是( )
A.32,31-
B.2,1
C.-2,1
D.-1,0
5、用代入法解下列方程组
⑴⎪⎩⎪⎨⎧
=+=228232y y xx x
⑵
⎩⎨
⎧=-=+3
45
32y x y x ⑶⎩⎨⎧=-+=-0133553y x y x
⑷⎩⎨⎧=++=++08540238y x y x ⑸⎩⎨⎧-=+-=+1)(258y x x y x ⑹⎪⎩⎪⎨⎧+=+=-32
4
1132x y y x
6、如果(5a-7b+3)2
+5
3+-b a =0,求a 与b 的值。
7、已知2x 2m-3n-7
-3y
m+3n+6
=8是关于x,y 的二元一次方程,求n
2m
8、若方程组⎩⎨⎧-=+=-15x 4by ax y 与⎩⎨⎧=-=+184393by ax y x 有公共的解,求a ,
b.
加减法解二元一次方程组
一、初步练习
1、 方程组⎩⎨⎧-=+=-252132y x y x 中,x 的系数特点是______;方程组
⎩⎨
⎧=-=+4378
35y x y x 中,y 的系数特点是________.这两个方程组用
______法解比较方便。
2、 用加减法解方程组⎩⎨⎧-=-=-382532y x y x 时,①-②得___________.
3、 解二元一次方程组⎩⎨⎧=+=-12464y x y x 有以下四种消元的方法:
⑴由①+②得2x=18; ⑵由①-②得-8y=-6; ⑶由①得x==6-4y ③,将③代人②得6-4y+4y=12; ⑷由②得x=12-4y ④,将④代人①得,12-4y-4y=6.其中正确的是_______________。
4、 已知⎩⎨⎧=-=+31y x y x ,则2xy 的值是__________.
5、 在等式y=kx+b 中,当x=0时,y=2;当x=3时,y=3;则k=______,b=_______.
6、 已知⎩⎨⎧=+=+8272y x y x ,则y x y x +-=_________.
7、 用加减法解下列方程组:
⑴⎩⎨⎧=-=+33263y x y x ⑵⎩⎨⎧=--=+47587y x y x ⑶⎩
⎨⎧+=+-=-)1(24)
2(31x y x y ⑷⎩⎨⎧=-=-525232b a b a ⑸⎩⎨⎧=-=+93513
23y x y x ⑹⎪⎪⎩⎪⎪⎨⎧-=-=+13
2
143y
x y
x
一、 训练
1、 若3a+2b=4,2a-b=5,则5a+b=__________.
2、 已知⎩⎨⎧=+=+8272y x y x ,那么x-y 的值是___________.
3、 若(3x-2y+1)2
+333--y x =0,则x=______,y=______.
4、 已知方程mx+ny=10
有两个解,分别是⎩
⎨⎧-==⎩⎨⎧=-=12
21y x y x 和,则m=________,n=__________.
5、 关于x 、y 的二元一次方程⎩⎨⎧=-=+k y x k y x 4233的解为_________.
6、 已知⎩
⎨⎧=-=+a y x a
y x 22,a ≠0,则y x
=__________.
7、 如果二元一次方程组⎩⎨⎧=-=+a y x a y x 4的解是二元一次方程
3x-5y-28=a 的一个解,那么a 的值是_________.
8、 若2a+3b=4和3a-b=-5能同时成立,则a=_____,b=______ 9、 用加减消元法解下列方程组:
⑴⎩⎨⎧=-=+121132x y y x ⑵⎪⎪⎩⎪⎪⎨⎧
=-=-62
392y x y x ⑶⎩⎨⎧=-=+67381953y x y x
⑷⎩⎨⎧=---=-+-82)(3)3(287)2(4)2(3y x y x y x y x ⑸⎪⎪⎩⎪⎪⎨⎧-=--+=-++132
532y x y x y
x y x
10若关于x 、y 的二元一次方程组⎩⎨⎧-=+=+1532m y x m y x 的解x 与y
的差是7,求m 的值。
