《传热学》实验:平板导热系数测定实验
稳态双平板法测定非金属材料的导热系数

稳态双平板法测定非金属材料的导热系数一、实验内容应用传热学知识,根据实际情况对实验进行简化,进而利用一维稳态导热相关知识求解非金属材料的导热系数。
二、实验原理双平板法是以无限大平板的导热规律为基础的。
设有一块厚度为δ,导热系数为λ = A + Bt 的无限大平板,一侧以恒定流密度q (W/㎡)加热,平板两表面的温度分别保持恒等于t 1和t 2 。
如图10-6所示。
根据付立叶定律,描写板内温度场的导热微分方程式为 dxdtBt A dx dt q )(+-=-=λ(10-1) 相应的边界条件为:x = 0处,t = t 1x =δ处,t = t 2 (10-2)12122t t t t q A B δ+-⎡⎤=+⋅⎢⎥⎣⎦ (10-3)令 m m Bt A t t B A +=++=221λ (10-4) 即在平均温度t m =(t 1+t 2)/2的条件下,板材的导热系数等于在 t 1和t 2间材料的平均导热系数λm 。
(10-10)式则写为δλ)(21t t q m -= (10-5)如果是为了确定板材的导热系数,则需在热稳定时,测出加热(或冷却)平板一侧的恒热流密度q (W/m 2)和温度t 1、t 2,依据(10-11)式便可得板材的平均导热系数: 21t t q m -=δλ (10-6)三、实验设备及参数 1、设备介绍如图10-7所示,它包括NK Ⅲ-200型双试件导热率测定装置、双路直流稳压电源、恒温水浴和测试系统。
NK Ⅲ-200型双试件导热率测定装置为对称的双平板结构,它的中央为圆形主加热器,其周围为环形辅助加热器,它们均为薄片型加热器,由电阻带均匀绕成。
二者共平面,其之间有一小的环形隔缝。
在主、辅加热器上,各放置由导热系数较大的黄铜做的圆形均热板。
主、辅均热板也是同厚度共平面,二者之间有1㎜的环形隔缝。
实验时将两块直径均等于环形辅助加热器均热板外径相等厚度的同种试件分别置于两侧的均热板上。
《传热学》实验:平板导热系数测定实验

《传热学》实验一:准稳态平板导热系数测定实验一、 实验目的1.快速测量绝热材料(不良导体)的导热系数和比热,掌握其测试原理和方法。
2.掌握使用热电偶测量温差的方法。
二、 实验原理本实验是根据第二类边界条件,无限大平板的导热问题来设计的。
设平板厚度为δ2,初始温度为0t ,平板两面受恒定的热流密度c q 均匀加热(见图1)。
求任何瞬间沿平板厚度方向的温度分布()τ,x t 。
导热微分方程、初始条件和第二类边界条件如下:()()22,,xx t a x t ∂∂=∂∂τττ()00,t x t =(),0c t q x δτλ∂+=∂()0,0=∂∂x t τ方程的解为:()()()()2212002132,1cos exp 6n c n n n n q x x t x t F ατδτδμμλδδμδ∞+=⎡⎤-⎛⎫-=-+--⎢⎥ ⎪⎝⎭⎣⎦∑ (1) 式中:τ——时间;λ——平板的导热系数;α——平板的导温系数;123n n n μβδ==,,,,; 02a F τδ=——傅里叶准则; 0t ——初始温度;c q ——沿x 方向从端面向平板加热的恒定热流密度。
随着时间τ的延长,0F 数变大,式(1)中级数和项愈小。
当5.00>F 时,级数和项变得很小,可以忽略,式(1)变成:图1()20221,26c q x t x t δαττλδδ⎛⎫-=+- ⎪⎝⎭(2) 由此可见,当5.00>F 后,平板各处温度和时间成线性关系,温度随时间变化的速率是常数,并且到处相同。
这种状态称为准稳态。
在准稳态时,平板中心面0=x 处的温度为:()0210,6c q t t δαττλδ⎛⎫-=- ⎪⎝⎭平板加热面x δ=处为:()⎪⎭⎫ ⎝⎛+=-31,20δτλδτδa q t t c 此两面的温差为:()()λδττδc q t t t ⋅=-=∆21,0, (3) 如已知c q 和δ,再测出t ∆,就可以由式(3)求出导热系数:tq c ∆=2δλ (4) 实际上,无限大平板是无法实现的,实验中是用有限尺寸的试件。
导热系数测量实验报告.doc

导热系数测量实验报告篇一:导热系数实验报告实验2.8 用稳态平板法测定不良导体的导热系数实验报告一、实验目的.(1)用稳态平板法测定不良导体的导热系数. (2)利用物体的散热速率求传热速率. 二、实验器材.实验装置、红外灯、调压器、杜瓦瓶、数字式电压表. 三、实验原理.导热是物体相互接触时,由高温部分向低温部分传播热量的过程.当温度的变化只是沿着一个方向(设z方向)进行时,热传导的基本公式可写为dTdQ=?λ ?????????---------------------------------------------(2.8.1)它表示在dt时间内通过dS面积的热量dQλ为导热系数,它的大小由物体????dT本身的物理性质决定,单位为W????1????1,它是表征物质导热性能大小的物理量,式中符号表示热量传递向着温度降低的方向进行.在图中,B为待测物,它的上下表面分别和上下铜、铝盘接触,热量由高温铝盘通过待测物B向低温铜盘传递.若B 很薄,则通过B侧面向周围环境的散热量可以忽略不计,视热量只沿着垂直待测板B的方向传递.那么在稳定导热(即温度场中各点的温度不随时间而变)的情况下,在?t时间内,通过面积为S、厚度为L的匀质圆板的热量为????????? ---------------------------------------------(2.8.2)式中,???为匀质圆板两板面的恒定温差,若把(2.8.2)式写成?Q=?λ??????=?λ?? ---------------------------------------------(2.8.3)的形式,那么???便为待测物的导热速率,只要知道了导热速率,由(2.8.3)式即可求出λ. 实验中,使上铝盘A和下铜盘P分别达到恒定温度??1、??2,并设??1??2,即热量由上而下传递,通过下铜盘P向周围散热.因为??1和??2不变,所以,通过B的热量就等于C向周围散发的热量,即B 的导热速率等于C的散热速率.因此,只要求出了C在温度??2时的散热速率,就求出了B的导热速率???.因为P的上表面和B的下表面接触,所以C的散热面积只有下表面面积和侧面积之和,设为????,而实验中冷却曲线是C全部裸露于空气中测出来的,即在P的上下表面和侧面积都散热的情况下记录的.设其全部表面积为??全,根据散热速率与散热面积成正比的关系可得??? ????????????部全=??部全---------------------------------------------(2.8.4)式中,???为??部面积的散热速率,???为??全面积的散热速率.而散热速率???就部全部?????????等于(2.8.3)式中的导热速率,这样(2.8.3)式便可写作????????? =?λ?? 部---------------------------------------------(2.8.5)设下铜盘直径为D,厚度为δ,那么有??部??全??2=?? +????????2=2?? +??????---------------------------------------------(2.8.6)???由比热容的基本定义c=Δ????Δ??‘,得ΔQ=cmΔ??’,故???cmΔ??’= 全---------------------------------------------(2.8.7)将(2.8.6)式、(2.8.7)式代入(2.8.4)式得?????+4?? =?????? 部---------------------------------------------(2.8.8)将(2.8.8)式代入(2.8.5)式得λ=?????????????/2---------------------------------------------(2.8.9)式中,m为下铜盘的质量,c为下铜盘的比热容. 四、实验内容.(1)用游标卡尺多次测量下铜盘的直径D、厚度δ和待测物厚度L,然后取其平均值.下铜盘质量m由天平测出,其比热容c=3.850×102??? kg?℃?1.(2)实验时,先将待测样品放在散热盘P上面,然后将发热铝盘A放在样品盘P上方,再调节三个螺栓,使样品盘的上下两个表面与发热铝盘A和散热铜盘P紧密接触.(3)将集成温度传感器插入散热盘P侧面的小孔中,并将集成温度传感器接线连接到仪器面板的传感器插座.用专用导线将仪器机箱后部插座与加热组件圆铝盘上的插座加以连接.为了保证温度测量的准确性,采用同一个温度传感器测温,在需要测量发热盘A和散热盘P温度时,采用手动操作,变换温度传感器的测温对象.(4)接通电源,在“温度控制”仪表上设置加温的上限温度.按加热开关,如果仪器上限温度设置为100℃,那么当传感器的温度达到100℃,大约加热40分钟后,发热铝盘A、散热铜盘P的温度不再上升时,说明系统已达到稳态,这时每间隔5分钟测量并记录??1和??2的值.(5)测量散热盘在稳态值??2附近的散热速率.移开发热铝盘A,取下待测盘,并将发热铝盘A的底面和铜盘P直接接触,当P盘的温度上升到高于稳态值??2值若干度(例如5℃左右)后,再将发热铝盘A移开,让散热铜盘P自然冷却.这时候,每隔30s记录此时的??2值并记录.五、实验数据记录与处理.表一下铜盘直径、厚度,待测物厚度实验结果记录表下铜盘质量为m=655 g.取平均值,稳态时,??1=102.3℃、??2=79.2℃.表三测下铜盘散热速率实验结果记录表利用作图法求下铜盘的散热速率得下铜盘散热速率为K=0.02976T????1. 由(2.。
传热学实验指导书---实验一(本部)
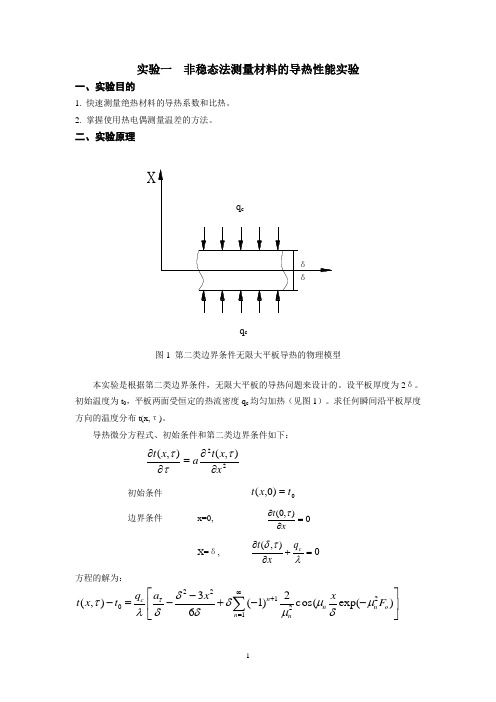
实验一 非稳态法测量材料的导热性能实验一、实验目的1. 快速测量绝热材料的导热系数和比热。
2. 掌握使用热电偶测量温差的方法。
二、实验原理X图1 第二类边界条件无限大平板导热的物理模型本实验是根据第二类边界条件,无限大平板的导热问题来设计的。
设平板厚度为2δ。
初始温度为t 0,平板两面受恒定的热流密度q c 均匀加热(见图1)。
求任何瞬间沿平板厚度方向的温度分布t(x,τ)。
导热微分方程式、初始条件和第二类边界条件如下:22),(),(x x t a x t ∂∂=∂∂τττ初始条件 0)0,(t x t =边界条件x=0,0),0(=∂∂xt τX=δ,0),(=+∂∂λτδcq x t 方程的解为:⎥⎦⎤⎢⎣⎡--+--=-∑∞=+1221220)exp(cos(2)1(63),(n o n n n n c F x x a q t x t μδμμδδδδλττq c式中: t —温度; τ—时间; t 0 — 初始温度;ɑ — 平板的导温系数; μn — n π n=1,2,3,……2δτa Fo =— 傅立叶准则; q c— 沿方向从端面向平板加热的恒热流密度;随着时间t 的延长,Fo 数变大,上式中级数和项愈小。
当Fo>0.5时,级数和项变得很小,可以忽略,上式变成:)612(),(220-+-=-δτδτλδτa a q t x t c 由此可见,当Fo>0.5后,平板各处温度和时间成线性关系,温度随时间变化的速率是常数,并且到处相同。
这种状态称为准稳态。
在准稳态时,平板中心面x=0处的温度为:)61(),0(20-=-δτλδτa q t t c 平板加热面X=δ处为:)31(),(20+-=-δτλδτδa q t t c 此两面的温差为:λδττδcq t t t 21),0(),(=-=∆如已知q c 和δ,再测出t ∆,就可以由上式求出导热系数:tq c∆=2δλ式中,λ—平板的导热系数,oW /(m C)⋅ cq —沿x 方向给平板加热的恒定热流密度,2W /mδ—平板的厚度,mt ∆—平板中心面x=0处和平板加热面x=δ处两面的温差,o C又,根据热平衡原理,在准稳态有下列关系:式中,F —平板的横截面积ρ—试件材料的密度C —试件材料的比热—准稳态时的温升速率由上式可求得比热为:实验时, 以试件中心处为准。
传热学实验报告

传热学实验报告班级:安全工程(单)0901班姓名:***学号:01第一节稳态平板法测定绝热材料导热系数实验一、实验目的1.巩固和深化稳定导热过程的基本理论,学习用平板法测定绝热材料导热系数的试验方法和技能。
2.测定试验材料的导热系数。
3.确定试验材料导热系数与温度的关系。
二、实验原理导热系数是表征材料导热能力的物理量。
对于不同的材料,导热系数是各不相同的,对同一材料,导热系数还会随着温度、压力、湿度、物质的结构和重度等因素而变异。
各种材料的导热系数都用试验方法来测定,如果要分别考虑不同因素的影响,就需要针对各种因素加以试验,往往不能只在一种实验设备上进行。
稳态平板法是一种应用一维稳态导热过程的基本原理来测定材料导热系数的方法,可以用来进行导热系数的测定试验,测定材料的导热系数及其和温度的关系。
实验设备是根据在一维稳态情况下通过平板的到热量Q 和平板两面的温差t ∆成正比,和平板的厚度h 成反比,以及和导热系数λ成反比的关系来设计的。
我们知道,通过薄壁平板(壁厚小于十分之一壁长和壁宽)的稳定导热量为:S t hQ *∆*=λ(1)其中:Q 为传到平板的热量,w ;λ为导热系数,w/m ℃;h 为平板厚度,m ; t ∆为平板两面温差,℃; S 为平板表面积;m 2;测试时,如果将平板两面温差t ∆、平板厚度h 、垂直热流力向的导热面积S 和通过平板的热流量Q 测定后,就可以根据下式得出导热系数:St hQ *∆*=λ (2) 其中:d u T -T t =∆,T u 为平板上测温度,T d 为平板下侧温度,℃;这里,公式2所得出的导热系数是在当时的平均温度下材料的导热系数值,此平均温度为:()d u T T 21t +=(3) 在不同的温度和温差条件下测出相应的λ值,然后按λ值标在λ-t 坐标图内,就可以得出()t f =λ的关系曲线。
三、实验装置及测试仪器稳态平板法测定绝热材料的导热系数的电器连接图和实验装置如图1和图2所示。
《传热学》课程教学大纲-蔡琦琳

《传热学》课程教学大纲一、课程基本信息二、课程目标(-)总体目标:《传热学》是研究由温差引起的热能传递规律的科学,是建筑环境与能源应用工程专业的一门基础课程和学位课程。
在制冷、热能动力、机械制造、航空航天、化工、材料加工、冶金、电子与电气和建筑工程等生产技术领域中存在大量的传热问题,课程旨在使学生掌握传热的基本概念、基本原理和计算方法,使学生对热量传递这一普遍存在的现象有理性的认识,并能熟练运用基础知识来思考、分析和解决实际传热问题。
(二)课程目标:本课程旨在使学生掌握热量传递的三种基本方式及其物理机制,掌握传热基础理论与计算方法;掌握传热学的基本实验,具备分析工程传热问题的能力,能够解决增强传热、削弱传热和温度控制等工程传热问题;了解传热学的前沿知识及其在科学技术领域的应用,培养学生分析问题和解决问题的能力,以及团队合作意识。
课程目标1:系统深入学习,掌握传热基础理论与计算方法。
1.1 掌握传热的基本概念、理论、机理及影响因素;1.2 掌握热传导、热对流和热辐射三种传热模式的基本公式,能够进行各种工况下传热量的计算,并能对工程传热问题进行描述和分析。
课程目标2:掌握传热实验,应用传热学知识,解决工程传热问题。
2.1 掌握传热学中的实验研究方法,使学生对热量传递这一普遍存在的现象有理性的认识。
2.2 根据所学传热理论和实验知识,熟练掌握增强或削弱热能传递过程的方法,能够在工程应用中对热能有效利用、热力设备效率的提高、节能降耗技术等问题从传热学角度进行思考、分析和解决问题。
课程目标3:培养学生的自主学习意识、团队合作能力、口头和书面表达能力,探索传热学前沿科学知识。
3.1 通过课堂分组讨论等方式培养团队合作意识、沟通交流能力和对工程问题进行清清晰表达的能力;3.2 通过课外文献调研并撰写课程报告,提升文献查阅能力和书面表达能力。
(H)课程目标与毕业要求、课程内容的对应关系三、教学内容第一章结论1 .教学目标(1)了解传热的定义;了解传热学的研究内容及其在生活和工程中的应用;(2)掌握热量传递的三种基本方式及其物理机理;(3)掌握傅里叶定律、牛顿冷却定律及斯忒藩定律,并能应用这三个定律分析基础传热问题;(4)了解传热过程的特点以及电.热模拟的作用和意义;(5)掌握热流密度、热阻和综合传热系数的计算方法。
南昌大学传热学实验指导书1

1.实验目的、原理、步骤、数据整理; 2.作出直线,写出准则方程式; 3.误差分析.
七、思考题
1.怎样才能使本实验管的加热条件成为常壁温? 2.管子表面的热电偶应沿长度和圆周均匀分布,目的何在? 3.如果室内空气温度不平静,会导致什么后果? 4.本实验的 范围有多大,是否可达到紊流状态?
实验二 自由对流横管管外放热系数的测
定
一、实验目的和要求
1. 了解空气沿管表面自由放热的实验方法,巩固课堂上学过的知识; 2. 测定单管的自由运动放热系数;
3. 根据对自由运动放热的相似分析,整理出准则方程式。
二、实验原理
对铜管进行电加热,热量应是以对流和辐射两种方式来散发的,所以对 换热量为总热量与辐射换热量之差,即:
t3(或t4)。进行实验时,可以通过热电偶t1(或t3)和t2(或t4)测量出 一个试件的两个表面的中心温度。如图1-2所示。
温度是利用温度数显表和转换开关来测量的。主加热器的电功率是 数字电压表指示值与主加热器阻值乘积计算(该加热器冷阻和热阻一 致),即P=Q=U2/R(W),R为主加热器阻值。 [附]实验台的主要参数 1.试验材料 2.试件外型尺寸:260×260 mm2 3.导热计算面积F:200 ×200 mm2(即主加热器面积) 4.试件厚度δ:20mm 5.主加热器电阻值:100Ω 6.辅加热器(每个)电阻值:50Ω 7.热电偶材料:镍铬-镍硅 8.试件最高加热温度:≤80℃
3.整理数据; 根据所测热电势算出平均值查出对应的温度,计算加热器的热量 a、 求对流放热系数 b、 查出物性参数 定性温度取空气边界层平均温度,在书的附录中查得空气的导热系 数、 热膨胀系数、运动粘度 导温系数、和普朗特数。 c、 用标准公式计算对流换热系数Nu和。
实验三 空气纵掠平板时局部换热系数的测定
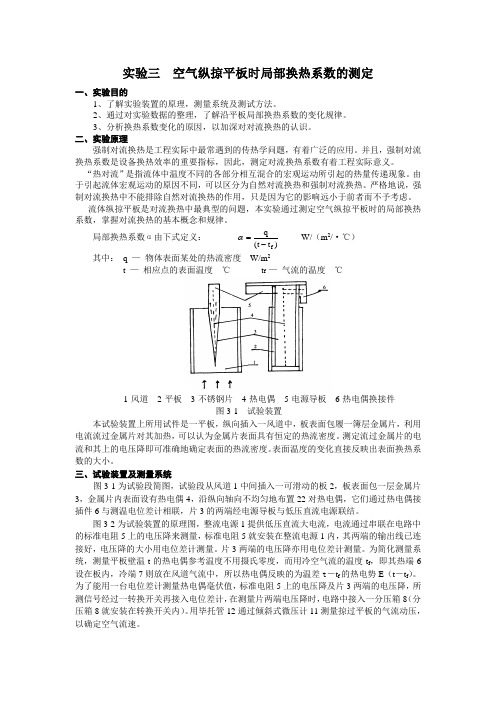
实验三 空气纵掠平板时局部换热系数的测定一、实验目的1、了解实验装置的原理,测量系统及测试方法。
2、通过对实验数据的整理,了解沿平板局部换热系数的变化规律。
3、分析换热系数变化的原因,以加深对对流换热的认识。
二、实验原理强制对流换热是工程实际中最常遇到的传热学问题,有着广泛的应用。
并且,强制对流换热系数是设备换热效率的重要指标,因此,测定对流换热系数有着工程实际意义。
“热对流”是指流体中温度不同的各部分相互混合的宏观运动所引起的热量传递现象。
由于引起流体宏观运动的原因不同,可以区分为自然对流换热和强制对流换热。
严格地说,强制对流换热中不能排除自然对流换热的作用,只是因为它的影响远小于前者而不予考虑。
流体纵掠平板是对流换热中最典型的问题,本实验通过测定空气纵掠平板时的局部换热系数,掌握对流换热的基本概念和规律。
局部换热系数α由下式定义: )t (t q f -=α W/(m 2/·℃) 其中: q — 物体表面某处的热流密度 W/m 2t — 相应点的表面温度 ℃ t f — 气流的温度 ℃1-风道 2-平板 3-不锈钢片 4-热电偶 5-电源导板 6-热电偶换接件图3-1 试验装置本试验装置上所用试件是一平板,纵向插入一风道中,板表面包履一簿层金属片,利用电流流过金属片对其加热,可以认为金属片表面具有恒定的热流密度。
测定流过金属片的电流和其上的电压降即可准确地确定表面的热流密度。
表面温度的变化直接反映出表面换热系数的大小。
三、试验装置及测量系统图3-1为试验段简图,试验段从风道1中间插入一可滑动的板2,板表面包一层金属片3,金属片内表面设有热电偶4,沿纵向轴向不均匀地布置22对热电偶,它们通过热电偶接插件6与测温电位差计相联,片3的两端经电源导板与低压直流电源联结。
图3-2为试验装置的原理图,整流电源1提供低压直流大电流,电流通过串联在电路中的标准电阻5上的电压降来测量,标准电阻5就安装在整流电源1内,其两端的输出线已连接好,电压降的大小用电位差计测量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《传热学》实验一:
准稳态平板导热系数测定实验
一、 实验目的
1.快速测量绝热材料(不良导体)的导热系数和比热,掌握其测试原理和方法。
2.掌握使用热电偶测量温差的方法。
二、 实验原理
本实验是根据第二类边界条件,无限大平板的导热问题来设计的。
设平板厚度为δ2,初始温度为0t ,平板两面受恒定的热流密度c q 均匀加热(见图1)。
求任何瞬间沿平板厚度方向的温度分布()τ,x t 。
导热微分方程、初始条件和第二类边界条件如下:
()()22,,x
x t a x t ∂∂=∂∂τττ
()00,t x t =
(),0c t q x δτλ
∂+=∂
()0,0=∂∂x t τ
方程的解为:
()()()()2212002132,1cos exp 6n c n n n n q x x t x t F ατδτδμμλδδμδ∞+=⎡⎤-⎛⎫-=-+--⎢⎥ ⎪⎝⎭⎣⎦
∑ (1) 式中:
τ——时间;
λ——平板的导热系数;
α——平板的导温系数;123n n n μβδ==,,,,
; 02a F τδ
=——傅里叶准则; 0t ——初始温度;
c q ——沿x 方向从端面向平板加热的恒定热流密度。
随着时间τ的延长,0F 数变大,式(1)中级数和项愈小。
当5.00>F 时,级数和项变得很小,可以忽略,式(1)变成:
图1
()20221,26c q x t x t δαττλδδ⎛⎫-=+- ⎪⎝⎭
(2) 由此可见,当5.00>F 后,平板各处温度和时间成线性关系,温度随时间变化的速率是常数,并且到处相同。
这种状态称为准稳态。
在准稳态时,平板中心面0=x 处的温度为:
()0210,6c q t t δαττλδ⎛⎫-=- ⎪⎝⎭
平板加热面x δ=处为:
()⎪⎭
⎫ ⎝⎛+=-31,20δτλδτδa q t t c 此两面的温差为:
()()λ
δττδc q t t t ⋅=-=∆21,0, (3) 如已知c q 和δ,再测出t ∆,就可以由式(3)求出导热系数:
t
q c ∆=2δλ (4) 实际上,无限大平板是无法实现的,实验中是用有限尺寸的试件。
一般可以认为,试件的横向尺寸是厚度的6倍以上时,两侧散热对试件中心的温度影响可以忽略不计。
试件两端面中心处的温度差就是无限大平板时两端面的温度差。
根据热平衡原理,在准稳态时,有下列关系:
τ
δρd dt F c F q c ⋅⋅⋅⋅=⋅ (5) 式中:
F ——试件的横截面积;
c ——试件的比热;
ρ——其密度; τd dt ——准稳态时的温升速率。
实验时,τ
d dt 以试件中心处为准。
由式(5)可得比热:
τ
δρd dt q c c ⋅⋅= 按定义,材料的导温系数可表示为
2()()2c c c t t c q t λδλδδδαρττ
===∆∆∆ m 2/s 综上所述,应用恒热流准稳态平板法测试材料热物性时,在一个实验上可同时测出材料的三个重要热物性:导热系数、比热容和导温系数。
三、 实验装置
非(准)稳态法热物性测定仪内,实验本体由四块厚度均为δ、面积均为F 的被测试材重叠在一起组成。
在第一块与第二块试件之间夹着一个薄型的片状电加热器,在第三块和第四
块试件之间也夹着一个相同的电加热器;在第二块与第三块试件交界面中心,一个电加热器中心各安置一对热电偶;这四块重叠在一起试件的顶面和底面各加上一块具有良好保温特性的绝热层,并用机械的方法把它们均匀地压紧。
电加热器由直流稳压电源供电,两对热电偶所测量到的温度由巡检仪进行采集处理。
1、试件及夹具:试件分为四块,采用的是200×200毫米的有机玻璃块,厚度为8毫米,重量400g 。
2、测量系统:采用高精度的测温铂电阻测量仪表,用以显示加热功率的高精度直流电压、电流表,以及宽范围的直流稳压源,热传感器采用镍铬-镍硅热电偶(K 型)。
3、加热部分为200×200毫米的金属薄膜加热器,阻值标称为100Ω左右,配以0-60V ,5A 的直流稳压一台。
图2 实验设备系统图
四、 实验步骤
1﹑按原理图接好线路(加热系统、测温系统);
2、测试件Ⅱ上下表面的初温,即()0,0t 和(),0t x ,并记录;
3、开始加热。
调节加热电流或电压,并维持加热功率为一恒定值。
4、实验测试。
从开始加热时计时,即开始加热的同时启动秒表,并按每分钟的间隔时间,记录一组试件Ⅱ上下表面的温度,即()00,t τ及(),x t x τ,测温同时计算相对应的上下表面温差,直到出现连续6~8组相同的温差时,结束实验测试;
5、功率测量,因是恒定功率加热,故不受时间限制,记录加热电流和电压;
6、实验结束,调节加热电流或电压为0,关闭电源。
五、 热流密度q c 的计算
这里我们虽然用薄片状电加热器加热,但它毕竟有一定的热容量,在加热过程中,加热器本身要吸收热量,且先于试件。
因此试件实际所吸收的热量必需从电功率中扣除电加热器吸收的热量。
根据实验原理,我们仅研究电加热器对中间两块试件加热时的温度变化就可
以了,但为了避免因电加热器向外难以估计的散热给q c 的计算带来困难,所以在两加热器外侧各补上一块相同厚度的试件并加以保温,这样,电加热器将同等地加热其两侧的每块试材,每块试件内的温度场对于电加热器是对称的。
两个同样的电加热器是并联(或串联)供电的。
基于以上分析,试件表面实验所吸收的热量应为:
()42h c h C U I t q F δτ
⋅=-∆ W/m 2
式中:
U ——加热器的电压V ;
I ——加热器的电流A ;
F ——加热器(即试件)面积,m 2;
h C =0.079J/(m 2•℃)——加热器单位面积的比热容;
()()()h w c t t t δδδτττ
==∆∆∆——加热器(也是试件加热面)的温度变化率。
六、 实验要求
1.预习实验指导书,弄懂实验原理和实验方法。
2.细心装配试材,电加热器和热电偶,避免损坏。
3.根据实验数据,绘出温度变化曲线,计算出试件的导热系数、比热容和导温系数。
七、实验数据记录
试件名称:;试件厚度: mm;试件重量: g;
加热电流:A;加热电压:V:试件面积:mm2。
