物理化学知识点总结(热力学第一定律)
物理化学上热力学第一定律知识框架图总结
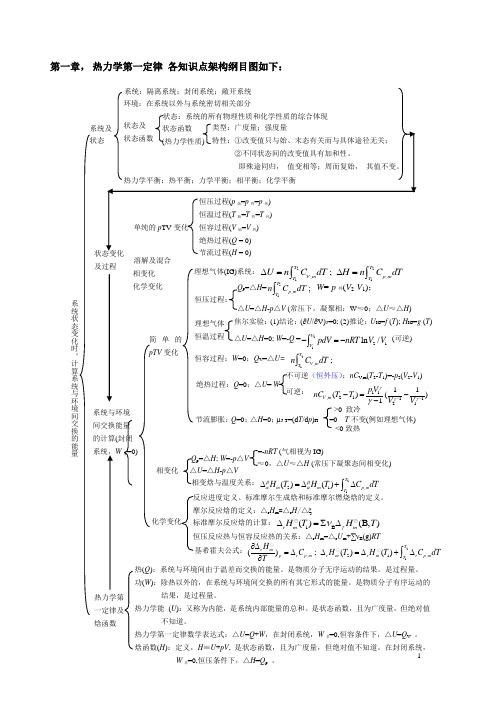
1第一章, 热力学第一定律 各知识点架构纲目图如下:及过程 溶解及混合 化学变化 相变化 热(Q ):系统与环境间由于温差而交换的能量。
是物质分子无序运动的结果。
是过程量。
功(W ):除热以外的,在系统与环境间交换的所有其它形式的能量。
是物质分子有序运动的结果,是过程量。
热力学能 (U ):又称为内能,是系统内部能量的总和。
是状态函数,且为广度量,但绝对值不知道。
热力学第一定律数学表达式:△U =Q +W ,在封闭系统,W 非=0,恒容条件下,△U =Q V 。
焓函数(H ):定义,H ≡U +pV , 是状态函数,且为广度量,但绝对值不知道。
在封闭系统,W 非=0,恒压条件下,△H =Q p 。
热力学第一定律及 焓函数系统与环境间交换能量 的计算(封闭 系统,W 非=0)简单的pTV 变化 理想气体(IG)系统:2211,,;T TV m p mT T U n C dT H n C dT ∆=∆=⎰⎰ 理想气体 恒温过程 焦尔实验:(1)结论:(∂U /∂V)T =0; (2)推论:U IG =f (T ); H IG =g (T ) △U =△H =0; W =-Q =2121ln /VVpdV nRT V V -=-⎰ (可逆)恒容过程:W =0;Q V =△U= 21,;TV mT n C dT ⎰绝热过程:Q =0;△U = W 不可逆(恒外压):nC V ,m (T 2-T 1)=-p 2(V 2-V 1) 可逆: 11,21112111()()1V m p V nC T T V V γγγγ---=-- Q p =△H =21,;T p m T n C dT ⎰W =-p 外(V 2-V 1); △U =△H -p △V (常压下,凝聚相:W ≈0;△U ≈△H )恒压过程: 节流膨胀:Q =0;△H =0;μJ-T =(d T /d p )H =0 T 不变(例如理想气体) <0致热 >0 致冷 相变化 △U =△H -p △VQ p =△H ; W =-p △V≈0,△U ≈△H (常压下凝聚态间相变化)=-nRT (气相视为IG) 相变焓与温度关系:2121,()()Tm m p mT H T H T C dT ββαα∆=∆+∆⎰化学变化 摩尔反应焓的定义:△r H m =△r H /△ξ 恒压反应热与恒容反应热的关系:△r H m =△r U m +∑νB (g)RT标准摩尔反应焓的计算:1B ()(B,)r m f mH T H T ν∆=∑∆反应进度定义、标准摩尔生成焓和标准摩尔燃烧焓的定义。
物理化学知识点(全)
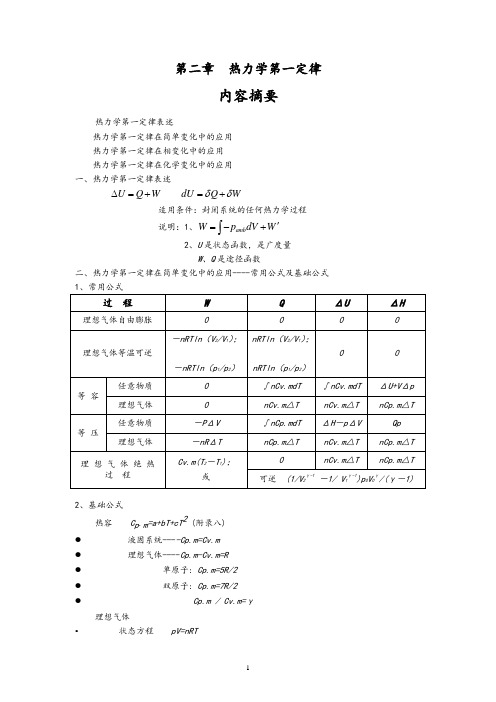
第二章热力学第一定律内容摘要热力学第一定律表述热力学第一定律在简单变化中的应用 热力学第一定律在相变化中的应用 热力学第一定律在化学变化中的应用 一、热力学第一定律表述U Q W ∆=+ dU Q W δδ=+适用条件:封闭系统的任何热力学过程 说明:1、amb W p dV W '=-+⎰2、U 是状态函数,是广度量W 、Q 是途径函数 二、热力学第一定律在简单变化中的应用----常用公式及基础公式 过 程WQΔUΔH理想气体自由膨胀理想气体等温可逆-nRTln (V 2/V 1); -nRTln (p 1/p 2) nRTln (V 2/V 1);nRTln (p 1/p 2)0 0等 容任意物质0 ∫nCv.mdT ∫nCv.mdT ΔU+V Δp 理想气体 0 nCv.m △T nCv.m △T nCp.m △T 等 压任意物质-P ΔV ∫nCp.mdT ΔH -p ΔV Qp 理想气体-nR ΔT nCp.m △TnCv.m △T nCp.m △T 理 想 气 体 绝 热过 程 Cv.m(T 2-T 1);或nCv.m △TnCp.m △T可逆 (1/V 2γ-1-1/ V 1γ-1)p 0V 0γ/(γ-1)2、基础公式热容 C p .m =a+bT+cT 2 (附录八) ● 液固系统----Cp.m=Cv.m ● 理想气体----Cp.m-Cv.m=R ● 单原子: Cp.m=5R/2 ● 双原子: Cp.m=7R/2 ● Cp.m / Cv.m=γ理想气体• 状态方程 pV=nRT• 过程方程 恒温:1122p V p V = • 恒压: 1122//V T V T = • 恒容: 1122/ / p T p T =• 绝热可逆: 1122 p V p V γγ= 111122 T p T p γγγγ--=111122 TV T V γγ--= 三、热力学第一定律在相变化中的应用----可逆相变化与不可逆相变化过程1、 可逆相变化 Q p =n Δ相变H m W = -p ΔV无气体存在: W = 0有气体相,只需考虑气体,且视为理想气体ΔU = n Δ相变H m - p ΔV2、相变焓基础数据及相互关系 Δ冷凝H m (T) = -Δ蒸发H m (T)Δ凝固H m (T) = -Δ熔化H m (T) Δ凝华H m (T) = -Δ升华H m (T)(有关手册提供的通常为可逆相变焓)3、不可逆相变化 Δ相变H m (T 2) = Δ相变H m (T 1) +∫Σ(νB C p.m )dT 解题要点: 1.判断过程是否可逆;2.过程设计,必须包含能获得摩尔相变焓的可逆相变化步骤;3.除可逆相变化,其余步骤均为简单变化计算.4.逐步计算后加和。
《物理化学》知识点汇总

《物理化学》知识点汇总热力学系统:热力学系统是指热力学研究的对象,是物质或物质的集合体。
状态:状态是指热力学系统中物质的宏观性质及其变化的状态。
热力学第一定律:能量守恒定律在热力学中的表现形式,它说明能量不能被创造或消失,只能从一种形式转化为另一种形式。
能量守恒:能量既不能被创造也不能被消失,它只能从一种形式转化为另一种形式。
热力学第二定律:热力学中描述自然过程方向性的定律,它表明,在一个封闭系统中,自发过程总是向熵增加的方向进行。
熵增:在封闭系统中,自发过程总是向熵增加的方向进行,也就是说,系统总是朝着更大的混乱状态发展。
相平衡:在热力学中,相平衡是指不同物相之间达到的平衡状态。
化学平衡:在化学反应中,反应物和生成物之间达到的平衡状态。
化学动力学:研究化学反应速率以及反应机制的科学。
表面化学:研究表面吸附、表面反应等表面现象的化学分支。
胶体分散系:由一种或多种物质在另一种物质中分散而成的系统。
以上是《物理化学》中的一些重要知识点,这些知识点是理解物理化学概念和应用的基础。
在学习过程中,需要不断巩固和深化对这些知识点的理解,以更好地掌握物理化学这门学科。
《经济法基础》是会计专业技术资格考试中的一门科目,主要考察考生对经济法相关知识的掌握程度和应用能力。
考试内容涉及广泛,包括经济法的基本概念、市场主体、市场秩序、宏观调控、劳动法等。
考试形式为闭卷、笔试,考试时间为90分钟。
经济法的基本概念:经济法的定义、特征、原则等。
市场主体:各类企业、个体工商户、农村承包经营户等市场主体的设立、变更和终止的相关法律规定。
市场秩序:市场竞争、市场准入、市场退出等方面的法律规定。
宏观调控:产业政策、财税政策、货币政策等宏观调控手段的法律规定。
劳动法:劳动者的权利和义务,劳动合同的签订和履行,劳动安全卫生、社会保险等方面的法律规定。
经济法涉及的法律法规众多,需要考生具备较为扎实的法律基础。
考试内容涉及面广,考生需要全面掌握各个方面的知识。
物理化学知识点总结(热力学第一定律)

热力学第一定律一、基本概念1.系统与环境敞开系统:与环境既有能量交换又有物质交换的系统。
封闭系统:与环境只有能量交换而无物质交换的系统。
(经典热力学主要研究的系统)孤立系统:不能以任何方式与环境发生相互作用的系统。
2.状态函数:用于宏观描述热力学系统的宏观参量,例如物质的量n、温度T、压强p、体积V等。
根据状态函数的特点,我们把状态函数分成:广度性质和强度性质两大类。
广度性质:广度性质的值与系统中所含物质的量成正比,如体积、质量、熵、热容等,这种性质的函数具有加和性,是数学函数中的一次函数,即物质的量扩大a倍,则相应的广度函数便扩大a倍。
强度性质:强度性质的值只与系统自身的特点有关,与物质的量无关,如温度,压力,密度,摩尔体积等。
注:状态函数仅取决于系统所处的平衡状态,而与此状态的历史过程无关,一旦系统的状态确定,其所有的状态函数便都有唯一确定的值。
二、热力学第一定律热力学第一定律的数学表达式:对于一个微小的变化状态为:dU=公式说明:dU表示微小过程的内能变化,而δQ和δW则分别为微小过程的热和功。
它们之所以采用不同的符号,是为了区别dU是全微分,而δQ和δW不是微分。
或者说dU与过程无关而δQ和δW却与过程有关。
这里的W既包括体积功也包括非体积功。
以上两个式子便是热力学第一定律的数学表达式。
它们只能适用在非敞开系统,因为敞开系统与环境可以交换物质,物质的进出和外出必然会伴随着能量的增减,我们说热和功是能量的两种传递形式,显然这种说法对于敞开系统没有意义。
三、体积功的计算1.如果系统与环境之间有界面,系统的体积变化时,便克服外力做功。
将一定量的气体装入一个带有理想活塞的容器中,活塞上部施加外压。
当气体膨胀微小体积为dV时,活塞便向上移动微小距离dl,此微小过程中气体克服外力所做的功等于作用在活塞上推力F与活塞上移距离dl的乘积因为我们假设活塞没有质量和摩擦,所以此活塞实际上只代表系统与环境之间可以自由移动的界面。
物理化学热力学第一定律总结

物理化学热力学第一定律总结热力学第一定律是热力学中最基本的定律之一,并且与能量守恒原理密切相关。
它陈述了一个闭合系统内部的能量转换过程。
根据热力学第一定律,能量是不能从真空中产生的,也不能消失,它只能在系统内部进行转化。
该定律可以用以下公式表达:ΔU=Q-W其中,ΔU表示系统内部能量的变化,Q表示系统吸收的热量,W表示系统对外界做的功。
这个公式说明了能量的守恒,即系统吸收的热量和对外界做的功之和等于系统内部能量的变化。
当系统从外界吸收热量时,其内部能量会增加,而当系统对外界做功时,其内部能量会减少。
这种能量的转化是一个相互依存的过程,可以通过热力学第一定律进行描述。
热力学第一定律的应用十分广泛,并且在实际问题中具有重要的意义。
以下是热力学第一定律在不同领域的应用:1.在化学反应中,热力学第一定律可以用来计算反应的焓变。
通过测量反应前后系统吸收或释放的热量,可以计算出反应的焓变,从而了解反应的能量转化和方向。
2.在工程领域,热力学第一定律常用于能量转换设备的设计和优化中。
例如,蒸汽轮机、内燃机和制冷机等能量转换系统的效率可以通过热力学第一定律进行评估和计算。
3.在生物学领域,热力学第一定律可以用于研究生物体内的能量转化过程。
例如,通过测量生物体吸收的热量和对外界做的功,可以计算出生物代谢的能量转换效率。
热力学第一定律的重要性在于揭示了能量守恒的基本原理,为能量转化和能量利用提供了基础理论支持。
它对于研究和解决实际问题具有重要指导意义。
热力学第一定律的应用可以帮助我们评估能量转换过程的效率,优化能量利用方式,并促进可持续发展。
总之,物理化学热力学第一定律表述了能量守恒的原则,描述了能量转化和能量守恒的过程。
它在化学、工程、生物等领域具有广泛的应用,并对能量转换和利用提供了理论支持。
热力学第一定律的理解和应用可以帮助我们更好地理解能量转换过程,优化能量利用方式,并实现可持续发展的目标。
物理化学 热力学一定律、二定律复习

H nC p,m dT
T1
T2
H Qp
此式适用于W′=0、dp=0的封闭系统所进行的一切过程
理想气体恒温pVT 变化:
U 0
H 0
4. 化学反应热效应
由生成焓求反应焓 r H m B f H m B 由燃烧焓求反应焓 r H m B c H m B
2. 单纯pVT变化过程的熵变
V2 T2 S nR ln nCV ,m ln V1 T1 p1 T2 S nR ln nC p ,m ln p2 T1
将C p ,m、CV ,m看成定值
p2 V2 S nCV ,m ln nC p ,m R ln p1 V1
3. 相变化过程的熵变
U QV 适用于W ' 0, dV 0的封闭系统所进行的一切过程。
H U ( pV ),式中:( pV ) p2V2 pV1 1
此式适用于封闭系统的一切过程。
此式适用于n、Cp,m恒定的理想气体单纯pVT变化的一切过程; 或n、Cp,m恒定的任意单相纯物质的恒压变温过程。
熵判据
不可逆 自发 隔离系统:S 0 或 dS 0 可逆 平衡 自发 S隔离 S系统 S环境 0 平衡
V2 p1 nR ln 理想气体的恒温可逆和不可逆过程:T S nR ln V1 p2
纯物质的恒压变温可逆和不可逆过程: p S nC p ,m ln T2 T1 纯物质的恒容变温可逆和不可逆过程:V S nCV ,m ln T2 T1 理想气体pVT都变的可逆过程:
5. 理想气体的绝热可逆方程:
T2
T1
Cv ,m
物理化学知识点总结

第一章 热力学第一定律一、基本概念系统与环境,状态与状态函数,广度性质与强度性质,过程与途径,热与功,内能与焓。
二、基本定律热力学第一定律:ΔU =Q +W 。
焦耳实验:ΔU =f (T ) ; ΔH =f (T ) 三、基本关系式1、体积功的计算 δW = -p e d V恒外压过程:W = -p e ΔV可逆过程:1221ln ln p p nRT V V nRT W ==2、热效应、焓等容热:Q V =ΔU (封闭系统不作其他功) 等压热:Q p =ΔH (封闭系统不作其他功) 焓的定义:H =U +pV ; d H =d U +d(pV )焓与温度的关系:ΔH =⎰21d p T T T C3、等压热容与等容热容热容定义:V V )(T U C ∂∂=;p p )(T H C ∂∂=定压热容与定容热容的关系:nR C C =-V p 热容与温度的关系:C p =a +bT +c’T 2 四、第一定律的应用1、理想气体状态变化等温过程:ΔU =0 ; ΔH =0 ; W =-Q =⎰-p e d V 等容过程:W =0 ; Q =ΔU =⎰T C d V ; ΔH =⎰T C d p 等压过程:W =-p e ΔV ; Q =ΔH =⎰T C d p ; ΔU =⎰T C d V 可逆绝热过程:Q =0 ; 利用p 1V 1γ=p 2V 2γ求出T 2,W =ΔU =⎰T C d V ;ΔH =⎰T C d p不可逆绝热过程:Q =0 ; 利用C V (T 2-T 1)=-p e (V 2-V 1)求出T 2,W =ΔU =⎰T C d V ;ΔH =⎰T C d p2、相变化可逆相变化:ΔH =Q =n Δ_H ;W=-p (V 2-V 1)=-pV g =-nRT ; ΔU =Q +W3、热化学物质的标准态;热化学方程式;盖斯定律;标准摩尔生成焓。
摩尔反应热的求算:)298,()298(B H H m f B m r θθν∆=∆∑反应热与温度的关系—基尔霍夫定律:)(])([,p B C T H m p BB m r ∑=∂∆∂ν。
物理化学基本知识点与公式总结

3、气体组分的化学势
RT lnp/p
B
B
RT
ln p B /p
RT lnp/p
B
B
RT lnpBB/p
化学平衡总结
化学平衡总结
1、标准平衡常数
K 0 ( pBeq p0 )B
Qp
H
T2 T1
nC
p,m
dT
n,
C
为常数
p,m
nCp,m (T2 T1)
Cp,m-CV,m=R(理想气体) 单原子理想气体: CV,m=3/2 R
双原子理想气体:CV,m=5/2 R
多原子理想气体:CV,m=3R
可逆相变
Q2 相变过程的热力学计算
不可逆相变
状态函数法
Q3
热力学第一定律
可不 逆可 相逆
热力 学
第三 定律
PVT
程程 程过 程 程程
程
变相 变
热力学基本方程
Maxwell关系式
过程判据
S判据
0 dS隔离 0
0
不可逆,自发 可逆, 平衡 不可能
不可逆 dSiso dSsys dSamb 0 可逆
A判据 A 0
A=U-TS
自发进行
nC p ,m
ln
T2 T1
nR
ln
p1 p2
S
nCV ,m
ln
p2 p1
nC p ,m
ln
V2 V1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
热力学第一定律
一、基本概念
1.系统与环境
敞开系统:与环境既有能量交换又有物质交换的系统。
封闭系统:与环境只有能量交换而无物质交换的系统。
(经典热力学主要研究的系统)
孤立系统:不能以任何方式与环境发生相互作用的系统。
2.状态函数:用于宏观描述热力学系统的宏观参量,例如物质的量n、温度T、压强p、
体积V等。
根据状态函数的特点,我们把状态函数分成:广度性质和强度性质两大类。
广度性质:广度性质的值与系统中所含物质的量成正
比,如体积、质量、熵、热容等,这种性质的函数具有加
和性,是数学函数中的一次函数,即物质的量扩大a倍,
则相应的广度函数便扩大a倍。
强度性质:强度性质的值只与系统自身的特点有关,
与物质的量无关,如温度,压力,密度,摩尔体积等。
注:状态函数仅取决于系统所处的平衡状态,而与此状态的历史过程无关,一旦系统的状态确定,其所有的状态函数便都有唯一确定的值。
二、热力学第一定律
热力学第一定律的数学表达式:
∆U=Q+W
对于一个微小的变化状态为:
dU=δQ+δW
公式说明:dU表示微小过程的内能变化,而δQ和δW则分别为微小过程的热和功。
它们之所以采用不同的符号,是为了区别dU是全微分,而δQ和δW不是微分。
或者说dU与过程无关
而δQ和δW却与过程有关。
这里的W既包括体积功也包括非体积功。
以上两个式子便是热力学第一定律的数学表达式。
它们只能适用在非敞开系统,因为敞开系统与环境可以交换物质,物质的进出和外出必然会伴随着能量的增减,我们说热和功是能量的两种传递形式,显然这种说法对于敞开系统没有意义。
三、体积功的计算
1.如果系统与环境之间有界面,系统的体积变化时,便克服外力做功。
将一定量的气体装
入一个带有理想活塞的容器中,活塞上部施加外压p
外。
当气体膨胀微小体积为dV时,活塞便向上移动微小距离dl,此微小过程中气体克服外力所做的功等于作用在活塞上推力F与活塞上移距离dl的乘积δW=−Fdl
因为我们假设活塞没有质量和摩擦,所以此活塞实际上只代表系统与环境
之间可以自由移动的界面。
因此推力F实际上是作用于环境,而由p
外
产生的外力则作用于系统,两者属于作用力与反作用力,若A代表活塞的体积,则δW=
−p
外Adl=−p
外
dV,积分得到
2
1
外
d
V
V
W p V
=-⎰
2.如果系统体积膨胀对环境做功,则W<0。
环境对系统做功体积压缩,则W>0。
3.若膨胀过程分为无穷多步完成,其中每一步都可以看成是一个平衡态,则可逆膨胀做功计算公式为:
W=−∫pdV=
V2
V1−∫
nRT
V
dV=−nRT ln
V2
V1 V2
V1
由上可知,功与变化的途径有关。
可逆膨胀,系统对环境做功最多;可逆压缩,环境对系统做的功最小。
热力学的一个过程,其中每一个步骤都可以在相反方向进行而不在环境中引起其他变化,我们称这样的过程叫可逆过程。
思考:有人说可逆过程可以理解成可以逆向进行的过程? 为什么热力学中计算体积功时不用内压用外压?
四、热的计算
1.等容热效应,由热力学第一定律∆U =Q +W 可知,若系统不做非体积功,且等容条件下(体积功为0),则:
∆U =Q V ,
此结果表明,等容且不做非体积功过程的内能变化热效应等于系统等压热效应。
2.等压热效应,由热力学第一定律∆U =Q +W 可知,系统在等压条件下,则:
δQ =dU +pdV =d (U +pV )
由于等压过程中p 是常数,即dp=0我们定义H=U+pV ,即
δQ p =dH 。
对整个过程积分则得到:
∆H =Q p
此结果表明,等压且不做非体积功过程的热效应等于系统焓值的变化。
3.热容及简单的变温过程热的计算 在物理学中,热容的定义是
C =δQ dT
其意义是在没有非体积功的情况下,将系统的温度升高1K 时所吸收的热量,由于热量δQ 与过程有关,所以在不同的过程中有不同的热容,我们需要掌握的是等容热容和等压热容。
等容热容代表在等容条件下,系统升高1K 时所吸收的热量,记作
C V =
δQ V
dT
在没有非体积功的条件下δQ =dU ,于是
C V =(ðU )V
由此可知,对于微小的等容简单变温过程有
dU =C V dT
若系统的温度由T 1变成T 2,则此式两端积分,得到
∆U =∫C V dT T 1
T 2
类似地,等压热容,在没有非体积功的条件下δQ =dH ,于是
C p =(ðH ðT )p
由此可知,对于微小的等压简单变温过程有
dH =C p dT 若系统的温度由T 1变成T 2,则此式两端积分,得到
∆H =∫C p dT T 1
T 2
我们知道热容是具有广度性质的函数,除以物质的量n 之后,相应的热容就成为了摩尔等容热
容
C V,m和摩尔等压热容C p,m,这两个物理量则具有强度性质。
5.等容热容与等压热容的关系
6.理想气体的热容
由于理想气体的U和H只与温度有关,故(ðU
ðV )
T
=0,(ðH
ðp
)
T
=0
故对于理想气体,有
7.理想气体的绝热过程,我们需要掌握理想气体的绝热、可逆、且不做非体积功的三个过程方程,这部分大家去翻一翻教材吧。
五、实际气体的内能和焓
对于一定量的任意气体
H =f (T,p )
所以
dH =C p dT +(ðH
ðp )T
dp
则实际气体任意过程的焓变要通过下式计算
dH =∫C p dT T 2
T 1+∫(ðH
ðp )T dp p 2
p 1
Similarly, 对于一定量的任意气体
U =f (T,V )
所以
dU =C V dT +(ðU
ðV )T
dV
则实际气体任意过程的内能变化要通过下式计算
dU =∫C V dT T 2
T 1+∫(ðU
ðV )T
dV V 2
V 1
以上内容就是热力学第一定律的主要部分剌,希望能给大家一些帮助。
(注:文档可能无法思考全面,请浏览后下载,供参考。
可复制、编制,期待你的好评与关注!)。
