CORDIC算法在QR分解中应用解析
(完整版)QR分解及其应用

《矩阵分析与应用》专题报告――QR分解及应用学生姓名:卢楠、胡河群、朱浩2015年11月25日目录1 引言 (3)2 QR 分解 (4)2.1QR分解的性质 (4)2.2 QR分解算法 (5)2.2.1 采用修正Gram-Schmidt法的QR分解 (5)2.2.2 Householder QR 分解 (6)2.2.3 采用Give ns旋转的QR分解 (8)3 QR分解在参数估计中的应用 (9)3.1 基于QR 分解的参数估计问题 (9)3. 2 基于Householder 变换的快速时变参数估计 (12)3. 3基于Give ns旋转的时变参数估计 (14)4 QR分解在通信系统中的应用 (16)4.1基于QR分解的稳健干扰对齐算法 (16)4.2基于QR分解的MIMO置信传播检测器 (19)总结 (21)参考文献 (22)1 引言矩阵分解是指将一个矩阵表示为结构简单或具有特殊性质的若干矩阵之积或之和,大体上可以分为满秩分解、QR 分解和奇异值分解。
矩阵分解在矩阵分析中占有很重要的地位,常用来解决各种复杂的问题。
而QR分解是工程中应用最为广泛的一类矩阵分解。
QF分解是目前求一般矩阵全部特征值的最有效并广泛应用的方法,一般矩阵先经过正交相似变换成为Hessenberg 矩阵,然后再应用QF分解求特征值和特征向量。
它是将矩阵分解成一个正交矩阵Q与上三角矩阵R, 所以称为QR分解。
参数估计是在已知系统模型结构时,用系统的输入与输出数据计算系统模型参数的过程。
它在系统辨识和无线通信领域有着广泛的应用。
18 世纪末德国数学家C.F. 高斯首先提出参数估计的方法,他用最小二乘法计算天体运行的轨道。
20 世纪60 年代,随着电子计算机的普及,参数估计有了迅猛的发展。
参数估计有很多方法,如矩估计、极大似然法、一致最小方差无偏估计、最小风险估计、同变估计、最小二乘法、贝叶斯估计、极小极大熵法等。
其中最基本的是最小二乘法和极大似然法。
CORDIC算法及其硬件实现

CORDIC算法及其硬件实现
季中恒;宋博
【期刊名称】《弹箭与制导学报》
【年(卷),期】2005(025)003
【摘要】详细阐述了CORDIC算法的原理、应用、硬件结构和实现.并通过基于FPGA的CORDIC算法实现和实际应用统计结果,进一步验证了使用硬件来实现CORDIC算法所具有的快速、精确和经济的特点.同时也为CORDIC算法的ASIC 实现提供了依据.
【总页数】3页(P609-610,627)
【作者】季中恒;宋博
【作者单位】信息工程大学国家数字交换系统工程技术研究中心(NDSC),郑州,450002;信息工程大学国家数字交换系统工程技术研究中心(NDSC),郑
州,450002
【正文语种】中文
【中图分类】TN914
【相关文献】
1.CORDIC算法硬件实现的误差分析 [J], 郑辛星
2.CORDIC算法硬件电路实现及改进 [J], 李庆锋
3.CORDIC算法的优化及硬件实现 [J], 梁杰;孙未
4.CORDIC算法研究及其硬件实现 [J], 丁晓红
5.基于改进CORDIC算法的QR码快速检测硬件实现方法 [J], 陈荣军;于永兴;钟秀媚;谢舜道;赵慧民;谭洪舟
因版权原因,仅展示原文概要,查看原文内容请购买。
WLAN MIMO-OFDM系统DSAP设计与实现

WLAN MIMO-OFDM系统DSAP设计与实现朱勇旭;易芝玲;吴斌;周玉梅【摘要】针对无线局域网(WLAN)多输入多输出和正交频分复用(MIMO-OFDM)系统中矩阵的QR分解预处理的延时问题,提出一种分布式脉动阵列处理器(DSAP)进行QR分解预处理。
该处理器通过脉动阵列边界单元和内部单元中流水线CORDIC计算,实现子载波信道矩阵的QR分解分布式处理,不同子载波QR分解分布于脉动阵列边界单元和内部单元中CORDIC流水线计算的不同级。
与串行脉动阵列处理器(SSAP)相比,在复杂度几乎没有增加情况下,DSAP结构充分利用时钟周期,分解延时约为SSAP结构的8%。
在SMIC 0.18μm CMOS工艺下,该分布式脉动阵列结构应用于2发2收MIMO-OFDM数模混合芯片中,芯片测试验证结果表明,数据处理延时能有效减少。
%To reduce the delay of QR-decomposition in WLAN (wireless local area network) MIMO-OFDM (multiple input multiple output and orthogonal frequency division multiplexing) systems, a distributed systolic array processor (DSAP) is proposed. The structure uses the coordinate rotation digital computer (CORDIC) in the boundary and internal cells of systolic array, and distributes the QR-decomposition of different sub-carriers into the different stages of the pipelining operation of CORDIC in systolic array. Compared with serial systolic array processor (SSAP), the clock periods can be put to great use in the DSAP, and the delay is reduced by 92%with the same complexity. In SMIC 0.18 μm CMOS technology, a ×22 analog -digital mixed MIMO-OFDM chip with DSAP has been implemented, andthe test results show that it can reduce the delay of data processing effectively.【期刊名称】《电子科技大学学报》【年(卷),期】2014(000)003【总页数】6页(P353-358)【关键词】分布式脉动阵列处理;低延时;MIMO-OFDM;QR分解【作者】朱勇旭;易芝玲;吴斌;周玉梅【作者单位】中国移动研究院北京西城区 100053;中国移动研究院北京西城区100053;中国科学院微电子研究所北京朝阳区 100029;中国科学院微电子研究所北京朝阳区 100029【正文语种】中文【中图分类】TN911M IMO检测器是多输入多输出和正交频分复用(M IMO-OFDM)系统中最为核心的模块。
数字中频与FPGA
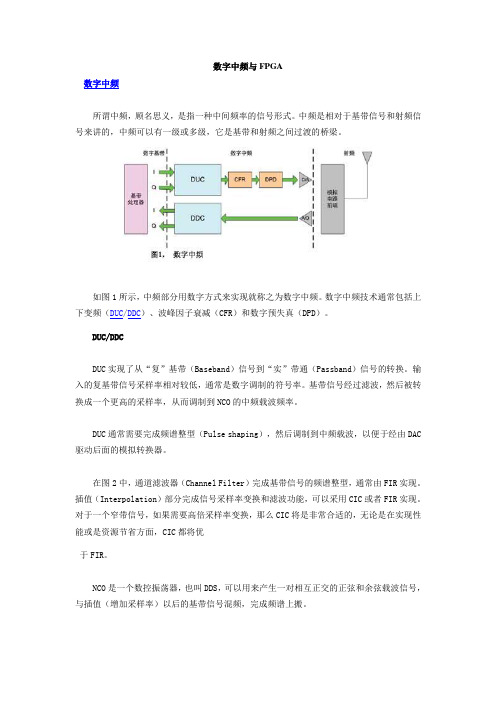
数字中频与FPGA数字中频所谓中频,顾名思义,是指一种中间频率的信号形式。
中频是相对于基带信号和射频信号来讲的,中频可以有一级或多级,它是基带和射频之间过渡的桥梁。
如图1所示,中频部分用数字方式来实现就称之为数字中频。
数字中频技术通常包括上下变频(DUC/DDC)、波峰因子衰减(CFR)和数字预失真(DPD)。
DUC/DDCDUC实现了从“复”基带(Baseband)信号到“实”带通(Passband)信号的转换。
输入的复基带信号采样率相对较低,通常是数字调制的符号率。
基带信号经过滤波,然后被转换成一个更高的采样率,从而调制到NCO的中频载波频率。
DUC通常需要完成频谱整型(Pulse shaping),然后调制到中频载波,以便于经由DAC 驱动后面的模拟转换器。
在图2中,通道滤波器(Channel Filter)完成基带信号的频谱整型,通常由FIR实现。
插值(Interpolation)部分完成信号采样率变换和滤波功能,可以采用CIC或者FIR实现。
对于一个窄带信号,如果需要高倍采样率变换,那么CIC将是非常合适的,无论是在实现性能或是资源节省方面,CIC都将优于FIR。
NCO是一个数控振荡器,也叫DDS,可以用来产生一对相互正交的正弦和余弦载波信号,与插值(增加采样率)以后的基带信号混频,完成频谱上搬。
与DUC相反,DDC基本上完成了以下几个工作:1. 频谱下搬:将ADC送来的数字信号有用频谱,从中频搬移到基带2. 采样率降低:将频谱搬移后的数据从ADC的高速采样率降低到一个合适的采样速率水平,通过抽取(Decimation)实现。
3. 通道滤波:在将I/Q信号送入基带处理以前,需要再对其进行滤波实际上,数字上下变频技术应用非常广泛,其在无线通信、有线电视网络(Cable Modem)、数字电视广播(DVB)、医学成像设备(超声),以及军事领域当中,都是不可或缺的功能。
CFR目前许多无线通信系统,如WCDMA、WiMAX,其中频信号通常由多个独立的基带信号相加而成。
基于CORDIC的精确快速幅相解算方法

基于CORDIC的精确快速幅相解算方法孙悦;王传伟;康龙飞;叶超;张信【期刊名称】《电子学报》【年(卷),期】2018(046)012【摘要】针对传统CORDIC算法进行高精度幅度相位解算时迭代次数过多、时延较长、相位收敛较慢等局限,提出了一种基于最佳一致逼近方法的幅度与相位补偿算法,即利用传统CORDIC算法迭代一定次数后得到的向量信息,采用最佳一致逼近方法对幅度和相位分区间进行一阶多项式补偿,有效提高了计算精度.仿真及实测结果表明,对传统CORDIC算法4次迭代后的结果进行补偿,幅度相对误差可达到10-5量级、相位绝对误差可达到10-5度量级,最大输出时延不大于100ns.在使用部分专用乘法器的条件下,寄存器消耗降低了42.5%,查找表消耗降低了15.5%.采用该补偿算法,每多一次CORDIC迭代其相位精度可提高约一个数量级.因此,本文提出的补偿CORDIC算法在迭代次数、计算精度等方面优于传统CORDIC算法,适合于高精度计算的场合.【总页数】7页(P2978-2984)【作者】孙悦;王传伟;康龙飞;叶超;张信【作者单位】中国工程物理研究院流体物理研究所,四川绵阳621999;中国工程物理研究院流体物理研究所,四川绵阳621999;中国工程物理研究院流体物理研究所,四川绵阳621999;中国工程物理研究院流体物理研究所,四川绵阳621999;中国工程物理研究院流体物理研究所,四川绵阳621999【正文语种】中文【中图分类】TN741【相关文献】1.转子动不平衡信号幅相特征的精确提取方法 [J], 耿慧2.转子振动幅相特征精确的提取方法 [J], 于军;李济顺3.基于时空域混合法利用Kaula正则化精确和快速解算GOCE地球重力场 [J], 郑伟;许厚泽;钟敏;员美娟;周旭华4.一种基于普通分布目标的极化SAR幅相不平衡快速评价方法 [J], 蒋莎;仇晓兰;韩冰;胡文龙;卢晓军5.一种基于普通分布目标的极化SAR幅相不平衡快速评价方法 [J], 蒋莎;仇晓兰;韩冰;胡文龙;卢晓军;;因版权原因,仅展示原文概要,查看原文内容请购买。
qr分解的应用场景

qr分解的应用场景QR分解是一种数学方法,用于将一个复杂的矩阵分解成两个简单的矩阵的乘积。
它在许多应用场景中都有广泛的应用,本文将介绍其中几个重要的应用场景。
1. 矩阵计算QR分解在矩阵计算中起到了重要的作用。
通过QR分解,我们可以将一个复杂的矩阵分解成一个正交矩阵和一个上三角矩阵的乘积。
这种分解可以简化矩阵的计算,使得计算更加高效。
在线性代数、最小二乘问题等领域中,QR分解被广泛应用。
2. 最小二乘问题在最小二乘问题中,我们需要找到一个最优解来最小化误差的平方和。
QR分解可以帮助我们求解最小二乘问题。
通过将系数矩阵进行QR分解,可以将最小二乘问题转化为一个更简单的问题,从而得到最优解。
3. 特征值计算特征值计算是在分析矩阵的性质时非常重要的一部分。
通过QR分解,我们可以将一个矩阵分解成一个正交矩阵和一个上三角矩阵的乘积。
这种分解可以帮助我们计算矩阵的特征值和特征向量,进而了解矩阵的性质。
4. 图像压缩QR分解在图像压缩中也有重要的应用。
图像可以表示为一个矩阵,通过QR分解,我们可以将图像矩阵分解成一个正交矩阵和一个上三角矩阵的乘积。
由于正交矩阵具有良好的特性,可以用更少的数据表示图像,从而实现图像的压缩。
5. 信号处理在信号处理中,我们经常需要对信号进行分析和处理。
QR分解可以帮助我们分解信号矩阵,从而得到信号的特征和结构信息。
这对于信号的降噪、频谱分析等都有重要的意义。
6. 数据降维在大数据时代,数据处理变得越来越重要。
QR分解可以帮助我们对数据进行降维处理。
通过将数据矩阵进行QR分解,可以得到一个正交矩阵和一个上三角矩阵的乘积,从而减少数据的维度,提高数据处理的效率。
7. 机器学习在机器学习中,QR分解也有广泛的应用。
通过QR分解,可以将复杂的矩阵分解成两个简单的矩阵的乘积,从而简化机器学习算法的计算过程。
在特征选择、参数估计等方面,QR分解都可以发挥重要作用。
QR分解作为一种重要的数学方法,在许多领域中都有广泛的应用。
数字预失真技术设计及实现

数字预失真技术设计及实现赵毅峰;姚彦;曹新容【摘要】预失真技术是克服功率放大器非线性失真的一种很有效的方法.采用最小二乘法(LS)算法的预失真技术可以获得很好的功率放大器线性化性能,但是其中的矩阵求逆运算在硬件上实现比较困难.论文采用坐标旋转数字计算算法(CORDIC)实现QR分解,并应用在预失真技术中,获得了较好的放大器线性化性能.通过在可编程逻辑阵列(FPGA)硬件平台上的仿真,验证了方法的可行性和有效性.【期刊名称】《厦门大学学报(自然科学版)》【年(卷),期】2010(049)004【总页数】4页(P501-504)【关键词】数字预失真技术;QR分解;线性化【作者】赵毅峰;姚彦;曹新容【作者单位】厦门大学信息科学与技术学院,福建,厦门,361005;厦门大学信息科学与技术学院,福建,厦门,361005;厦门大学信息科学与技术学院,福建,厦门,361005【正文语种】中文【中图分类】TN911现代通信系统中,具有较大峰均比和带宽的线性调制信号经过大功率放大器会产生非线性失真和记忆效应[1].预失真技术则是补偿功率放大器非线性失真最好的方法之一.预失真技术是在功率放大器输入端增加一个具有功率放大器逆特性的非线性模块,用于抵消功率放大器的非线性失真.此技术的线性化性能较好,适应性强,可以提供足够的带宽,效率高,实现成本较低,是一种适合于未来通信系统发展的线性化技术.预失真技术可以在模拟域(基带、中频、射频)实现,也可以在数字域(基带)实现.射频预失真技术具有电源效率高、成本低等优点,但这种方法需要使用射频非线性有源器件,它们的控制和调整是一个不易处理的过程[2-3].数字基带预失真技术不涉及难度大的射频信号处理,只在低频部分对基带信号进行补偿处理,因此便于采用现代数字信号处理技术[4-5].本文针对具有记忆效应的功率放大器,采用基带预失真技术,结合QR分解,实现了记忆型非线性放大器的预失真,并完成系统设计及仿真.识别放大器的逆特性,是求解预失真器系数的一个关键.可通过采样功率放大器的输入、输出数据来获得放大器的逆特性[1].最小二乘法(LS)就是一种很实用的方法,可以从测得的数据中直接寻求变量之间的依赖关系,获得满足放大器逆特性的预失真器.假设放大器的输入信号u,输出信号y.直接求解功率放大器的逆特性,就需要令y作为预失真器模型的输入,u作为输出,采用非线性抽头延时多项式模型[6-7],有假设一组采样数据u的个数为N,多项式函数模型的奇次阶数为K,记忆深度为Q,则需要求解系数c的因子个数为K×Q.u为放大器N个输入数据构成的N×1向量,Y 为放大器的输出数据按照模型形式构成的矩阵,有因此,可以将式(1)写成矩阵形式,即系数c的求解过程,利用LS算法求解[8]:求得的系数c变换形式,得到K×Q的矩阵.整个模型直接反映功率放大器的逆特性,可以代入预失真器,实现功率放大器的线性化.LS算法具有线性化效果好的优点,同时也存在硬件实现复杂的缺点.LS算法求解的关键是矩阵求逆.为了达到一定的准确度,算法建立的矩阵Y是比较庞大的,如何在硬件上很好地实现矩阵求逆,成为研究中的一个难点.LS算法,实际上就是建立式(2),利用式(3)估算预失真器模型系数c.但当式(2)的Y矩阵近似列相关时,将导致YTY接近病态,此时较难从式(3)中估算出预失真模型系数.同时,在硬件实现时,对矩阵的求逆运算也较为困难.而QR分解,是解决此问题的一种比较简便的方法.QR分解是指将矩阵Y分解为正交矩阵Q左乘上三角矩阵R的形式.即:Y=QR.将上式代入式(2),可得u=QRc,然后两边同乘以Q-1,从而得到Q-1u=Q-1QRc.由于矩阵Q是正交矩阵,Q-1=QT,Q-1Q=E,得到:Rc=QTu=u′.其中R是一个上三角矩阵,由式(4)可以方便地求出系数c.其中,i=N-1,N-2, (1)QR分解的最终目标是使矩阵Y=Q×R.Q是正交阵,R是三角阵,且有QTY=R,其中,Q矩阵则是由N次旋转后得到Q=Q0Q1…QN-1.整个过程中,每步的旋转都可以通过坐标旋转数字计算方法(CORDIC)实现.这样就可以在FPGA上较方便地实现QR算法.LS算法中的待分解的矩阵Y是N×M的,它的QR分解,可以由多次2×M的矩阵旋转求得.在最后的系数求解中,根据等式Rc=QTz=z′,并不需要求出完整的矩阵Q,而只需要QT与向量z的乘积z′,可以看成矩阵u与Y进行了相同的旋转.所以,建立矩阵[Y,z],用CORDIC旋转进行QR分解时,同时获得需要的矩阵z′.整体采用心脏收缩的方法,每次都只把一行向量中第一个数据点变为0.经过N次收缩之后就变成一个三角矩阵,且对角值均为实数.如图1所示,纵向传递信号的实部和虚部,横向传递行内的旋转角度.在FPGA上用Verilog HDL语言编程实现这个结构[9],根据多项式阶数和记忆深度确定矩阵的大小.将采样数据经过一定处理后送入此结构进行QR分解,获得需要的预失真器系数.采样数据需要一定的冗余,以保证计算的准确程度.最后得到的矩阵对角值均为实数,就可以方便地利用式(1)求出所需系数.基带预失真放大器系统的设计是结合FPGA硬件平台和Matlab软件平台的优点实现的.实际的基带预失真放大器系统包括:振荡器,正交调制器,上、下变频器,滤波器,数模转换器和功率放大器等部件[10].在实验室的研究中,假设变频及正交调制解调等模块都是理想的,基带预失真放大器系统简化如图2所示.在FPGA上主要完成了基带预失真器以及预失真系数更新算法的实现,但基于硬件条件的限制和为了调试方便,功率放大器模块可根据实际的功率放大器进行建模,并通过Matlab软件仿真实现.同时假设上、下变频及正交调制解调模块为理想模块,根据图2可验证整体基带预失真设计系统的可行性和预失真算法的有效性.在完成软件仿真后,可直接在硬件上进行调试.QR分解可以看成是由多个PE(Processing element)进行功能实现的,而每个PE 都是由3个CORDIC模块组合而成,如图3所示.约定行内旋转角度Φ为把复数信号变成实数信号所旋转的角度,行间旋转角度θ为把两行中的某一个点变为0时旋转的角度.图4是反馈回路中QR分解的功能仿真结果.其中I_in和Q_in为采样到的数据流,经调整后,转换为矩阵形式A_I和A_Q.数据进入QR分解结构,经过多次旋转运算之后得到复数形式的上三角矩阵R,图中R_I为R矩阵的实部数据,R_Q为R矩阵的虚数部分.由图4可知,在硬件上实现QR分解需要较大的运算资源以及较长的运算时间,若进行实时更新预失真器系数,则系统的设计难度较大.但是,功率放大器的线性化性能具有短期的平稳性,因此,在实际系统中,可以在图2中增加一个误差比较单元,比较基带传输信号和反馈信号之间的差异,若两者差异较大,即功率放大器线性化性能发生了较大劣化,可使反馈回路运行预失真算法,实现预失真器的系数更新.图5是在Matlab上得到的功率放大器功率频谱比较图.仿真中使用数据源为3载波WCDMA宽带信号的一部分,模拟功率放大器采用并行Weiner模型[8],预失真器采用记忆多项式模型[6].从图5中可以看出,记忆型功率放大器的非线性会引起严重的邻道干扰,而本系统设计实现的预失真器是可以较好地抑制传输信号的邻信道干扰.同时表1给出了3载波WCDMA宽带信号经过本系统设计的预失真器的误差矢量幅度(EVM)和邻道功率比(ACPR)的改善情况.其中,“EVM”表征带内失真情况,“ACPR”表征带外失真情况.实验证明,在硬件平台上采用CORDIC实现QR分解,并应用到预失真技术的硬件实现上,可以提高功率放大器系统的性能,获得良好的线性化效果.另外,在硬件设计中还要考虑数据采样匹配,数据量化等各方面的问题.只有解决好这些问题,才能在实际应用中更好地提升功率放大器的线性化效果.【相关文献】[1] Montoro G,Gilabert P L,Bertran E,et al.A new digital predictive predistorter for behavioral power amplifier linearization[J].IEEE Microwave and Wireless Components Letters,2007,17(6):448-450.[2] Clark C,Chrisikos GJ,Muha M S,et al.Time-domain envelope measurement technique with application to wideb and power amplifier modeling[J].IEEE Trans on Microwave Theory and Techniques,1998,46(12):2531-2540.[3] Cox D C.Linear amplification with nonlinear components[J].IEEE Trans on Communications,1974,22(12):1942-1945.[4] Marsalek R,Jardin P,Baudoin G.From post-distortion to predistortion for power amplifiers linearization[J].IEEE Communications Letters,2003,7(7):308-310.[5] Gilabert P L,Montoro G,Cesari A.A recursive digital predistorter for linearizing RF power amplifiers with memory effects[C]//Microwave Conference.Yokohama:APMC,2006:1043-1047.[6] Raich R,Qian H,Zhou G T.Digital baseband predistortion of nonlinear power amplifiers using orthogonal polynomials[C]//2003 IEEE International Conference on A-coustics,Speech,and Signal Processing.NewYork:IEEE,2003:689-692.[7] 钱业青,刘富强.Wiener功率放大器的简化预失真方法[J].通信学报,2007,28(10):55-59.[8] Lei D,Zhou G T,Morgan D R,et al.Memory polynomial predistorter based on the indirect learning architecture[C]//Global TelecommunicationsConference.Bamako:IEEE,2002:967-971.[9] Kenington P B.Linearized transmitters:an enabling technology for software defined radio[J].IEEE Communication Magazine,2002,40(2):156-162.[10] 夏宇闻.Verilog数字系统设计教程[M].北京:北京航空航天大学出版社,2003.。
改进型CORDIC算法的研究及发展趋势

2010 年第 4 期 (总第 128 期)大 众 科 技DA ZHONG KE JINo.4, 2010 (Cumulatively No.128)改进型 CORDIC 算法的研究及发展趋势朱文瑾(桂林电子科技大学,广西 桂林 541004)【摘 要】CORDIC 算法虽然在运算速度上并不占优势,但其硬件实现简单的特点,使之在现代通信、计算机等领域得到 了广泛应用。
目前的 CORDIC 算法改进趋势是充分发挥其高速、 低耗的硬件实现潜力, 因此, 研究国内外具有代表性的 CORDIC 算法的改进趋势具有重要的意义。
【关键词】CORDIC 算法;分解;旋转;迭代 【中图分类号】TP301.6 【文献标识码】A 【文章编号】1008-1151(2010)04-0017-02(一)引言CORDIC 算法的全称是 Coordinate Rotation Digital Computer,即坐标旋转数字计算机算法,最早由 Jack E. Volder 于 1959 年提出。
历经 50 余年的发展, CORDIC 算法得 到了极大改进, 应用领域也愈加广泛。
1971 年, John Walther 提出了统一的 CORDIC 算法,可用于估算包括乘、除、正弦、 余弦、正切、反正切、双曲正弦、双曲余弦、双曲正切、反 双曲正切、自然对数和平方根在内的初等函数。
该算法的提 出, 极大地拓宽了 CORDIC 算法在工程应用领域的前景, 同时, 统一的 CORDIC 算法意味着能够在保持高速运算的同时能够进 一步降低硬件功耗。
统一的 CORDIC 算法,迭代方程如下:X n +1 = X n − mσ n Yn • 2 − n Yn +1 = Yn + mσ n X n • 2 − n Z n +1 = Z n − σ nθ nCORDIC 算法是一种运算顺序固定的算法,这使其发展遇 到了两个难题:一是对于任意一级的迭代,必须等到前一级 迭代完成后,产生一个中间向量,才能在此基础上执行本级 迭代中的旋转;二是只有在完成了第 i 级旋转之后才能确定 第(i+1)级旋转的方向。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.介绍QR分解算法之一——Givens分解法 2.cordic算法实现Givens分解
GIVENS分解
• GIVENS矩阵旋转表示为如下形式的矩阵
•
ii
• i,k分别表示矩阵
• 其中i、k代表某次迭代矩阵的元素下标
• 其中s和c形式分别如下:
令A=
GIVENS算法求上三角形矩阵的思想是: GIVENS矩阵G(1,1, )与A矩阵相乘得矩阵B1, 再将B1矩阵乘以对应的GIVENS矩阵,直到 第一列除最上面元素外全为零为止。此时对 得到的矩阵除第一行和第一列外进行相同的 运算,然后开始第二次迭代。
• 第K次迭代后矩阵形式为:
举例:对矩阵A=[-12 3 3;3 1 -2;3 -2 7] 第一次迭代:吉文斯矩阵G1= B1=G1*A= 再对B1进行吉文斯变换:G2=
• B2=G2*B1=
• 第二次迭代:对B2的部分 GIVENS变换
进行
• 所以G=
,
• G*
=
• 综上两次迭代:上三角形矩阵为
其中 x[0] = ai,l y[0] = aj,l
,
z[0]初始角度。
•
是第j次迭代的旋转方向。每
次迭代会产生一个比例因子
• 迭代完成后总比例因子为常数:
FPGA处理单元的结构
• function [Q,R]=qrgv(A)
• n=size(A,1);
• R=A;
• Q=eye(n);
• for i=1:n-1
a
' j.l
cos(i,k ) * a j,l
sin(i,k ) * ai,l
其中:k l n
由知,吉文斯方法产生上三角形矩阵的过 程涉及到大量的乘法、除法、开根方等运算, 在计算硬件中运算效率较低。CORDIC算法 能用于角度计算旋转操作,可以方便地计算 出的结果,从而使得QR分解变得更有效率。
CORDIC算法原理:
将需要旋转的角度分解成一系列预先设定的 基本旋转角度的加权和,使得角度旋转可以通 过一系列的移位和加法来实现,避免了复杂的 乘法器,从而降低了硬件实现成本。
CORDIC 基本算法
将角度旋转关系式 x1 = x cos a - y sin a y1 = x sina + y cos a
= y(i) + x(i) tana(i)
只考虑角度旋转,不考虑 幅度变化
ai = arctan 2-i
i ai(弧度) ai(度)
0 /4
45
1 0.4637 26.6
2 0.2450 14
3 0.1244 7.1
4 0.0624 3.6
5 0.0312 1.8
6 0.0156 0.9
7 0.0078 0.4
) •乘积,
1
Ki
1 22i
•为常数取决于迭代的次数和角度
cordic可以分解为2步
(1)伪旋转
R(i+1)= R(i) (1+tan2 a(i))1/2 x(i+1)= R(i+1) cos(+a(i))
= x(i)– y(i) tana(i) y(i+1)= R(i+1)sin(+a(i))
• R=
• (-2.7192e-016和-3.5111e-016约为零)
• 在吉文斯矩阵G与矩阵相乘中反复出现
•
G * = i, j
A' i,k
A' j,k
c - s
* = s
c
A' i,k
A' j,k
a0i',k
a' i,k 1
a' j,k 1
a' i,k 2
a' j,k 2
ai',n
•
for j=2:n-i+1
•
x=R(i:n,i);
•
rt=givens(x,1,j);
•
r=blkdiag(eye(i-1),rt);
•
Q=Q*r';
•
R=r*R;
•
end
• end
• function [R,y]=givens(x,i,j)
• xi=x(i);
• xj=x(j);
• r=sqrt(xi^2+xj^2);
a
' j,n
• 其中 Gi, j 表示迭代过程中的吉文斯矩阵,i、
j表示行数,1 第i,j两行,i
i j k
n; n;
A' i,k
A' j,k
分别表示矩阵的
设ai,k 式:
a
j,k
分别是
A' i,k
A' j,k
两行的元素,展开上
ai',l cos(i,k ) * ai,l sin(i,k ) * a j,l
8 0.0039 0.2
9 0.0019 0.1
例:将某矢量进行30度的伪旋转
(2)Scaling operation is used to maintain the “norm” of the original vector
• P常数,可以优化
QR Decomposition by CORDIC
作如下变换 x1 = cos a • ( x - y tan a ) y1 = cos a • ( y + x tan a )
分解 aa1+a2+ …+ am 选择am ,使得am = tan-1 2-m 或 tan am = 2-m •方程中乘以 tan am 变成简单的移位操作
•第 步,从 计算 可改写为 ith
(xi, yi)
(xi+1, yi+1)
:
xi+1 = Ki ( xi - yi di 2-i ) yi+1 = Ki ( yi + xi di 2-i )
残余的角度为:zi+1 = zi - di tan-1(2-i )
式中
Ki cos(tan1 2i )
1 1 22i
di=sign(zi)
• cost=xi/r;
• sint=xj/r;
• R=eye(length(x));
• R(i,i)=cost;
• R(i,j)=sint;
• R(j,i)=-sint;
• R(j,j)=cost;
• y=x(:);
• y([i,j])=[r,0];
仿真程序
