简单的线性规划问题.ppt
合集下载
福建省福鼎市第二中学人教A版高中数学必修五《3-3 简单的线性规划问题》课件(共18张PPT)

设获得的利润为z,则有
2
4
z 2x 3y
6
8
x -4y≤ - 3
例1、画出不等式组 3x+5y≤ 25 表示的平面区域
x≥1
x-4y≤-3
在该平面区域上
3x+5y≤25 x≥1
y x=1
问题 1:x有无最大(小)值? 问题2:y有无最大(小)值? 问题3:2x+y有无最大(小)值?
C 设z=2x+y
y x≥1 2x-y=0
当z=0时,设直线 l0:2x-y=0 3x+5y=25
平移:l0, 当l0经过可行域上点A时,
C (1,4.4)
-z 最小,即z最大。
x-4y=-3
平移l0 ,当l0经过可行域上点C时,
o
-z最大,即z最小。
B
x=1
A
(5,2)
x
由
x-4y=-3 3x+5y=25得A点坐标__(5_,_2_);由
4
N
作日出满生约足产束条件所表8示的平面区1域6,如图所1示2
应用举例
【引例】:
某工厂用A、B两种配件生 产甲、乙两种产品,每生 产一件甲产品使用4个A配 件并耗时1h,每生产一件 乙产品使用4个B配件并耗 时2h,该厂每天最多可从 配件厂获得16个A配件和 12个B配件,按每天工作 8h计算,该厂所有可能的 日生产安排是什么?
y
或 最小值 的可 行 解。
C
设Z=2x+y,式中变量x、y
x-4y≤-3
满足下列条件 3x+5y≤25 ,
B
x≥1
o
x-4y=-3
A
3x+5y=25
人教版高中数学必修5第三章不等式《3.3.2 简单的线性规划问题》教学PPT

在线性约束条件下,求目标函数最小值.
思考5:作可行域,使目标函数取最小
值的最优解是什么?目标函数的最小值
为多少? 28x+21y=0
7x+14y=6
y
A最最优小解值1(671.,
4 7
),
7x 7 x
7y 5 14 y 6
14x 7 y 6
x 0, y 0
x=4
思考3:图中阴影区域内任意一点的坐
标都代表一种生产安排吗?
y
x 2y 8
0 x 4 0 y 3 x N , y N O
y=3 x
x+2y=8 x=4
阴影区域内的整点(坐标为整数的点) 代表所有可能的日生产安排.
思考4:若生产一件甲产品获利2万元, 生产一件乙产品获利3万元,设生产甲、 乙两种产品的总利润为z元,那么z与x、 y的关系是什么?
3.3.2 简单的线性规划问题
第一课时
问题提出
1.“直线定界,特殊点定域”是画二元 一次不等式表示的平面区域的操作要点, 怎样画二元一次不等式组表示的平面区 域?
2.在现实生产、生活中,经常会遇到资 源利用、人力调配、生产安排等问题, 如何利用数学知识、方法解决这些问题, 是我们需要研究的课题.
探究(一):线性规划的实例分析 t
5730
【背景材料】某工厂用A、B两种配件 生产甲、乙两种产品,每生产一件甲 产品使用4个A配件耗时1h;每生产一 件乙产品使用4个B配件耗时2h.该厂每 天最多可从配件厂获得16个A配件和12 个B配件,每天工作时间按8h计算.
思考1:设每天分别生产甲、乙两种产 品x、y件,则该厂所有可能的日生产 安排应满足的基本条件是什么?
2x y 15
思考5:作可行域,使目标函数取最小
值的最优解是什么?目标函数的最小值
为多少? 28x+21y=0
7x+14y=6
y
A最最优小解值1(671.,
4 7
),
7x 7 x
7y 5 14 y 6
14x 7 y 6
x 0, y 0
x=4
思考3:图中阴影区域内任意一点的坐
标都代表一种生产安排吗?
y
x 2y 8
0 x 4 0 y 3 x N , y N O
y=3 x
x+2y=8 x=4
阴影区域内的整点(坐标为整数的点) 代表所有可能的日生产安排.
思考4:若生产一件甲产品获利2万元, 生产一件乙产品获利3万元,设生产甲、 乙两种产品的总利润为z元,那么z与x、 y的关系是什么?
3.3.2 简单的线性规划问题
第一课时
问题提出
1.“直线定界,特殊点定域”是画二元 一次不等式表示的平面区域的操作要点, 怎样画二元一次不等式组表示的平面区 域?
2.在现实生产、生活中,经常会遇到资 源利用、人力调配、生产安排等问题, 如何利用数学知识、方法解决这些问题, 是我们需要研究的课题.
探究(一):线性规划的实例分析 t
5730
【背景材料】某工厂用A、B两种配件 生产甲、乙两种产品,每生产一件甲 产品使用4个A配件耗时1h;每生产一 件乙产品使用4个B配件耗时2h.该厂每 天最多可从配件厂获得16个A配件和12 个B配件,每天工作时间按8h计算.
思考1:设每天分别生产甲、乙两种产 品x、y件,则该厂所有可能的日生产 安排应满足的基本条件是什么?
2x y 15
高二数学必修5简单的线性规划问题-PPT

问题 1:x有无最大(小)值? 问题2:y有无最大(小)值? 问题3:2x+y有无最大(小)值?
C 设z=2x+y
y=-2x+ z
2x+y=0
o
问题4:z几何意义是:
斜率为-2的直线在y轴上的截距
x-4y=-3
A
3x+5y=25
x B 当直线过点 B(1,1)时,z 最小,即zmin=3 当直线过点A(5,2)时,z最大,即zmax= 2×5+2=12
产安排是什么?
应用举例
【引例】:
某工厂用A、B两种配件生 产甲、乙两种产品,每生 产一件甲产品使用4个A配 件并耗时1h,每生产一件 乙产品使用4个B配件并耗 时2h,该厂每天最多可从 配件厂获得16个A配件和 12个B配件,按每天工作 8h计算,该厂所有可能的 日生产安排是什么?
4 2
2
4
6
8
应用举例
【优化条件】: 若生产一件甲产 品获利2万元,生 产一件乙产品获 利3万元,采用哪 种生产安排获得 利润最大?
4
M(4,2 )
2
2
4
6
8
z y2x2x3yz
33
x -4y≤ - 3
例1、画出不等式组 3x+5y≤ 25 表示的平面区域
x≥1
x-4y≤-3
在该平面区域上
3x+5y≤25 x≥1
y x=1
3
故有四个整点可行解.
2
1
x +4y=11
0 1 2 3 4 5x
3x +2y=10
应用举例
练习5: 某工厂计划生产甲、乙两种产品,这两种产品都需要两
3.3.2简单的线性规划问题(1).ppt1
3.3.2简单的线性规划问题(1)
y
o
x
1.课题导入
在现实生产、生活中,经常会遇到资源利用、人力调配、 生产安排等问题。 1、下面我们就来看有关与生产安排的一个问题:
某工厂用A、B两种配件生产甲、乙两种产品,每 生产一件甲产品使用4个A配件耗时1h,每生产一件乙 产品使用4个B配件耗时2h,该厂每天最多可从配件厂 获得16个A配件和12个B配件,按每天工作8h计算,该 厂所有可能的日生产安排是什么? 按甲、乙两种产品分别生产x、y件,由 已知条件可得二元一次不等式组
5 x+3 y 1 5 1 y x+ x-5 y 3
1.解:作出平面区域
y
A
o x C
y x x+y 1 y - 1
z=2x+y
B
作出直线y=-2x+z的 图像,可知z要求最大值, 即直线经过C点时。 求得C点坐标为(2,-1), 则Zmax=2x+y=3
把z=2x+3y变形为
由上图可以看出,当实现直线x=4与直线x+2y-8=0的交点M z 14 (4,2)时,截距的值最大 ,最大值为 , 3 3
这时 2x+3y=14. 所以,每天生产甲产品 4 件,乙产品 2 件时, 工厂可获得最大利润14万元。
二、基本概念
Hale Waihona Puke 一组关于变量x、y的一次不等式,称为线性约束 条件。 把求最大值或求最小值的的函数称为目标函数,因 为它是关于变量x、y的一次解析式,又称线性目标函数。 在线性约束条件下求线性目标函数的最大值或最小值 y 问题,统称为线性规划问题。 4 可行域 最优解 满足线性约束的解
3
(x,y)叫做可行解。 由所有可行解组成 可行解 的集合叫做可行域。
y
o
x
1.课题导入
在现实生产、生活中,经常会遇到资源利用、人力调配、 生产安排等问题。 1、下面我们就来看有关与生产安排的一个问题:
某工厂用A、B两种配件生产甲、乙两种产品,每 生产一件甲产品使用4个A配件耗时1h,每生产一件乙 产品使用4个B配件耗时2h,该厂每天最多可从配件厂 获得16个A配件和12个B配件,按每天工作8h计算,该 厂所有可能的日生产安排是什么? 按甲、乙两种产品分别生产x、y件,由 已知条件可得二元一次不等式组
5 x+3 y 1 5 1 y x+ x-5 y 3
1.解:作出平面区域
y
A
o x C
y x x+y 1 y - 1
z=2x+y
B
作出直线y=-2x+z的 图像,可知z要求最大值, 即直线经过C点时。 求得C点坐标为(2,-1), 则Zmax=2x+y=3
把z=2x+3y变形为
由上图可以看出,当实现直线x=4与直线x+2y-8=0的交点M z 14 (4,2)时,截距的值最大 ,最大值为 , 3 3
这时 2x+3y=14. 所以,每天生产甲产品 4 件,乙产品 2 件时, 工厂可获得最大利润14万元。
二、基本概念
Hale Waihona Puke 一组关于变量x、y的一次不等式,称为线性约束 条件。 把求最大值或求最小值的的函数称为目标函数,因 为它是关于变量x、y的一次解析式,又称线性目标函数。 在线性约束条件下求线性目标函数的最大值或最小值 y 问题,统称为线性规划问题。 4 可行域 最优解 满足线性约束的解
3
(x,y)叫做可行解。 由所有可行解组成 可行解 的集合叫做可行域。
简单的线性规划问题课件
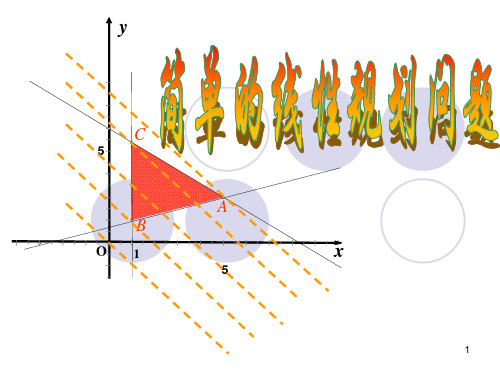
y
y 2x 12
y 2x 3
C(1, 4.4)
y 2x 5
x 4 y 3 这 纵是 截3xx斜距1率为5为zy的-2直,2线5
B(1, 1)
O1
x=1
x-4y+3=0 求z=2x+y的最大
A(5, 2)
值和最小值。
所以z最大值12
5
x
3x+5y-25=0
z最小值为3
【解析】
由z 2x y y 2x z
A
3, 2
5 2
,
zmax
17
B 2, 1, zmax 11
5x+3y≤15 y≤ x+1 x-5y≤3
【解析】
5x 3y 15 0
x y1 0
A
练习 B
x 5y 3 0
7
解线性规划问题的步骤:
(1)画:画出线性约束条件所表示的可行域,
和直线 ax by 不0(全a,b为 目标0函,数为
y
C
5
A B
O1
x
5
1
复习: vv二元一次不等式Ax+By+C>0在平面直角 坐标系中表示直线Ax+By+C=0某一侧所有 点组成的平面区域。
确定方法:
方法1:直线定界,特殊点定域;
若C≠0,则直线定界,原点定域;
方法2:如:x-y+1<0
x<y-1
表示直线x-y+1=0左侧的区域。
注意:若不等式中是严格不等号,则边界
【解析】
由z 2x y y 2x z
A(5,2) C(1, 22)
5
zmin
21
22 5
3.3《简单的线性规划问题3》课件(苏教版必修5).

{
2x+y≥15, x+2y≥18, x+3y≥27, x≥0 y≥0
目标函数为 z=x+y
作出可行域(如图) 作出可行域(如图)
例题分析
{
2x+y≥15, x+2y≥18, x+3y≥27, x≥0, x∈N ∈ y≥0 y∈N ∈
y 15
调整优值法
作出一组平行直线z=x+y, , 作出一组平行直线
甲产品 消耗量 产品 (1 杯) 资源 奶粉( 奶粉(g) 咖啡(g) 咖啡(g) 糖(g) 利润( 利润(元) 乙产品(1 乙产品 杯) 资源限额( ) 资源限额(g)
9 4 3 0.7
4 5 10 1.2
3600 2000 3000
ቤተ መጻሕፍቲ ባይዱ
设每天应配制甲种饮料x 设每天应配制甲种饮料x杯,乙种饮料y杯,则 乙种饮料y
y
x-y=0 1 x 1
(2,-1)
z=2x+y 叫做
线性目标函数 ;
都叫做可行解 满足 线性约束条件 的解(x,y)都叫做可行解; 都叫做可行解; 取得最大值 使z=2x+y取得最大值的可行解为 (2,-1) 取得最大值的可行解为 且最大值为 3 ; ,
0
(-1,-1)
y=-1
2x+y=0
取得最小值 使z=2x+y取得最小值的可行解 (-1,-1) , 取得最小值的可行解 且最小值为
应 用
简单的线性规划
可行解 可行域
求解方法: 求解方法:画、 移、求、答
最优解
练习巩固
1.某家具厂有方木材 某家具厂有方木材90m3 , 木工板 木工板600m3 , 准备加工成 某家具厂有方木材 书桌和书橱出售, 已知生产每张书桌需要方木料0.1m3 、 书桌和书橱出售 , 已知生产每张书桌需要方木料 木工板2m 生产每个书橱需要方木料0.2m3 , 木工板 木工板 3 ; 生产每个书橱需要方木料 1m3 , 出售一张书桌可以获利 元 , 出售一张书橱可以 出售一张书桌可以获利80元 获利120元; 获利 元 (1)怎样安排生产可以获利最大? )怎样安排生产可以获利最大? (2)若只生产书桌可以获利多少? )若只生产书桌可以获利多少? (3)若只生产书橱可以获利多少? )若只生产书橱可以获利多少?
人教A版高中数学必修五课件3.3.2简单的线性规划问题2.pptx

5.已知线性目标函数 z=3x+2y,在线性约束条件
x+y-3≥0 2x-y≤0 y≤a
下取得最大值时的最优解只有一个,则实数 a
的取值范围是________.
x+y-3≥0
解析: 作出线性约束条件2x-y≤0
y≤a
表示的平面
区域,
如图中阴影部分所示.
• 因为取得最大值时的最优解只有一个,所以目 标函数对应的直线与平面区域的边界线不平行, 根据图形及直线的斜率,可得实数a的取值范 围是[2,+∞).
元.该企业在一个生产周期内消耗A原料不超过 13吨、B原料不超过18吨,那么该企业可获得最 大利润是( )
• A.12万元
B.20万元
• C.25万元D.27万元
解析: 设该企业在一个生产周期内各生产甲、乙产品
x、y 吨,获得利润 z 万元,根据题意,得
3x+y≤13
2x+3y≤18 x≥0
• (3)求:解方程组求最优解,进而求出目标函数的 最大值和最小值.
• [注意] 画可行域时,要特别注意可行域各边 的斜率与目标函数直线的斜率的大小关系,以 便准确判断最优解.
• 2.最优解的确定
• 最优解的确定可有两种方法:
• (1)将目标函数的直线平行移动,最先通过或 最后通过的顶点便是最优解.
交点 A(4,5)时,目标函数 z=200x+300y 取到最小值为 2 300
元,故所需租赁费最少为 2 300 元.
• 答案: 2300
• 2.某企业生产甲、乙两种产品,已知生产每吨 甲产品要用A原料3吨、B原料2吨;生产每吨乙产
品要用A原料1吨、B原料3吨.销售每吨甲产品可 获得利润5万元、每吨乙产品可获得利润3万
规格类型 钢板类型
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
产生最大利润,最大利润为3万元。
练习:P91 T2
小结:
线性规划求最优整数解的一般方法:
1.平移找解法: 即先打网格,描出可行域内的
整点,平移直线,最先经过或最后经过的整点 坐标即为最优整解.
2.调整优解法:即先求非整数条件下的最优解,
调整Z的值使不定方程Ax+By=Z存在最大(小) 的整点值,最后筛选出整点最优解.
解:设x、y分别为计划生产甲、乙两种混合 肥料的车皮数,于是满足以下条件: y
4 x+y 10
18x+15y
x
0
66 ,
x,
y
N
y 0
x
o
解:设生产甲种肥料x车皮、乙种肥料y车皮,能够产 生利润Z万元。目标函数为Z=x+0.5y,可行域如图:
把Z=x+0.5y变形为y=-2x+2z,它表示斜率为 -2,在y轴上的截距为2z的一组直线系。
3
y
由图可以看出,当直 30 线Z=7.2x+10.8y经过
可行域上的点M时,截
距最大,即Z最大。
20
M
易求得M(20,10),则
Zmax= 7.2x+10.8y =252 o
20
30
40 x
故开设20个初中班和10个高中班,收取的学费最
多,为252万元。
巩固练习一
咖啡馆配制两种饮料.甲种饮料每杯含奶粉9g 、咖啡4g、糖 3g,乙种饮料每杯含奶粉4g 、咖啡5g、糖10g.已知每天原料 的使用限额为奶粉3600g ,咖啡2000g 糖3000g,如果甲种饮 料每杯能获利0.7元,乙种饮料每杯能获利1.2元,每天在原料 的使用限额内饮料能全部售出,每天应配制两种饮料各多少
下面我们就来看看线性规划在实际中的一些应用:
二、例题
例5、营养学家指出,成人良好的日常饮食应该至少 提供0.075kg的碳水化合物,0.06kg的蛋白质, 0.06kg的脂肪,1kg食物A含有0.105kg碳水化合物, 0.07kg蛋白质,0.14kg脂肪,花费28元;而1kg食物 B含有0.105kg碳水化合物,0.14kg蛋白质,0.07kg 脂肪,花费21元。为了满足营养专家指出的日常饮食 要求,同时使花费最低,需要同时食用食物A和食物B 多少kg?
7 x 7 y 5
14x 7 y 6
x
1 7
得M点的坐标为:
y
4 7
所以zmin=28x+21y=16
5、答
由此可知,每天食用食物A143g,食物B约 571g,能够满足日常饮食要求,又使花费最低, 最低成本为16元。
解线性规划问题的步骤:
1、找 找出线性约束条件、目标函数;
得到
20 x+y 30 30
x+2y
40
x
0
20
y 0
o
20
30
40 x
设收取的学费总额为Z万元,则目标函数
Z=0.16×45x+0.27×40y=7.2x+10.8y。
Z=7.2x+10.8y变形为 y 2 x 5z
它表示斜率为
2
3 54
的直线系,Z与这条直线的截距有关。
行直线系, z 4
4 是
直线在Y轴上的
y
x2y 8
x4
截距,当 z 最大时,z取得最大
4 值。所以直线
y1x
N
4
M
y 3 与可行域相交且在Y轴上的截距
最大时,目标函数取得最大值。
由图可见,当 直线 z x 4y
o
4
8
x
经过可行域上的N点时
大,即 z 最大。
z 4
最
y1x 4
{2x+y≥15, x+2y≥18, x+3y≥27, x≥0, x∈N* y≥0 y∈N*
目标函数t = x+y
y 15
B(3,9)
9
C(4,8)
A(18/5,39/5)
打网格线法
x+y =0
2 1 0 12
作出一组平行直线t = x+y,
78
2x+y=15
x
18
27
x+2y=18 x+3y=27
规格类型 钢板类型
A规格
B规格 C规格
第一种钢板
2
1
1
第二种钢板
1
2
3
某顾客需要A,B,C三种规格的成品分别为15,18,27块,若你是
经理,问各截这两种钢板多少张既能满足顾客要求又使所用钢板张
数最少。
分 析
解:设需截第一种钢板x张,第二种钢板y张,
2x+y≥15,
钢板总张数为Z则,
问
x+2y≥18,
0 2 4 6 8 12 18
平移L找交点及交点坐标
2x+y=15 x+y=12 x+2y=18
x
27
x+3y=27
当直线L经过点A时z=x+y=11.4, 但它不是最优整数解. 作直线x+y=12
解得交点B,C的坐标B(3,9)和C(4,8) 直线x+y=12经过的整点是B(3,9)和C(4,8),它们是最优解.
o
4
8x
使目标函数取得最大值或最小值的可行解叫做
这个问题的最优解。
解:按甲、乙两种产品分别生产x、y件,目标函数为Z,那么:
约束条件为
x 2y
x y
4 3
x 0
y 0
作出上述约束条件所表示的
可行域如下:
8 目标函数为 z x 4 y
1z
这将是z 斜 x率为4变y形1为,随zy变 化 4的x平 4
甲种饮料 x 乙种饮料 y
9
4
4
5
33
1.2
0.7
1.2
原 料限 额 3600 2000 3000
解:设每天应配制甲种饮料x杯,乙种饮料y杯,则
9x 4 y 3600
34xx
(1)2、画: 画出线性约束条件所表示的可行域;
(2)3、移: 在线性目标函数所表示的一组平行线中,
利用平移的方法找出与可行域有公共点 且纵截距最大或最小的直线; (3)4、求:通过解方程组求出最优解;
(4)5、答:作出答案。
12
例题6 某工厂现有两种大小不同规格的钢板可截成A、B、C三种规格, 每张钢板可同时截得三种规示 :格的小钢板的块数如下表所
题
x+3y≥27, x≥0
:
y≥0
标目函数: z=x+y (x,y N)
约束条件:
{ 2x+y≥15, x+2y≥18, x+3y≥27, x≥0,
y 15
调整优解法
y≥0
目标函数:z=(xx,y+y N) 10
8
画可行域 x+y
=0
6
4
B(3,9)
C(4,8)
A(3.6,7.8)
作出直线L:x+y=0,2
由图可以看出,当直线经过可行域上的点M时, 截距2z最大,即z最大。
y
容易求得M点的坐标为 (2,2),则Zmin=3
故生产甲种、乙种肥料各 2车皮,能够产生最大利润, 最大利润为3万元。
M x
o
例7 在上一节例4(P85)中,若生产1车皮甲种肥料,产生的 利润为10000元;生产1车皮乙种肥料,产生的利润为5000元, 那么分别生产甲、乙两种肥料各多少车皮,能够产生最大利润?
y y
0.06 0.06
174xx174
y y
6 6
x
0
x
0
y 0
y 0
目标函数为:z=28x+21y
1、找
作出二元一次不等式组所表示的平面区域,即可行域
把目标函数z=28x+21y 变形为 y 4 x z
2、画
它表示斜率为
杯能获利最大? 解:将已知数据列为下表:
设每天应配制甲种饮料x杯,乙种饮料y杯,则 目标函数为:z =0.7x +1.2y
9x 4 y 3600原
34xx
料
5y 2000 10y 30奶00粉(g)
x 0
咖啡(g)
y 0
糖(g)
利 润(元)
每配制1杯饮料消耗的原料
元,高中每人每年可收学费2700元。那么开设初中
班和高中班多少个?每年收费的学费总额最多?
解:设开设初中班x个,高中班y个。因办学规模以 20~30个班为宜,所以, 20≤x+y≤30
而由于资金限制,26x+54y+2×y2x+2×3y≤1200
另外,开设的班级不能为负,则x≥0,y≥0。
把上面四个不等式合在一起,
一组关于变量x、y的一次不等式,称为线性约束条
件。
把求最大值或求最小值的的函数称为目标函数,因为
它是关于变量x、y的一次解析式,又称线性目标函数。
在线性约束条件下求线性目标函数的最大值或最小值
问题,统称为线性规划问题。y
满足线性约可束行的域解
4
3
最优解
(x,y)叫做可行解。
由所有可可行行解解组成的
集合叫做可行域。
分析:将已知数据列成表格
食物/kg 碳水化合物/kg
A
0.105
B
0.105
蛋白质/kg
