4–4剪力方程和弯矩方程·剪力图和弯矩图
《材料力学》课程讲解课件第四章弯曲内力

x
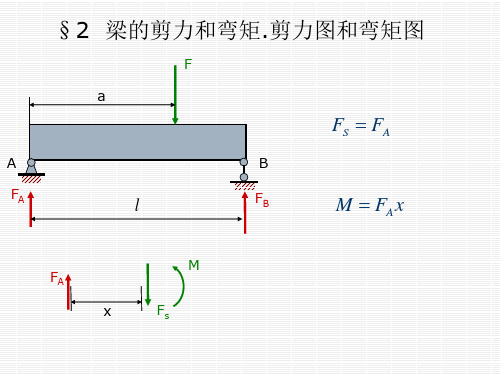
∴ 弯曲构件内力:Fs -剪力,M -弯矩。
若研究对象取m - m 截面的右段:
Y 0, Fs F FBY 0.
mC 0,
FBY
FBY (l x) F(a x) M 0.
Fs
F (l a) l
,
M F (l a) x 18 l
1. 弯矩:M 构件受弯时,横截面上
存在垂直于截面的内力偶矩 (弯矩)。
由 Fy 0, 得到:
A
FAy
a
Mc
C FSc
FAy q 2a FSc 0
FSc FAy q 2a qa
(剪力FS 的实际方向与假设方
向相反,为负剪力)
由 MC 0, 得到:
MC FAy 2a 2qa a M1 0
MC FAy 2a 2qa a M1 2qa2
F
M (x) FAY x M A
F(x L) (0 x l)
x
③根据方程画内力图
FL
x
41
§4-4 剪力方程和弯矩方程 剪力图和弯矩图
q
例题4-2
悬臂梁受均布载荷作用。
x
试写出剪力和弯矩方程,并
q
l
x
FS
M x
FS x
画出剪力图和弯矩图。
解:任选一截面x ,写出
剪力和弯矩方程
ql FS x=qx
变形特点——杆轴线由直线变为一条平面的曲线。
P
主要产生弯曲变形的杆--- 梁。
q
M
二、平面弯曲的概念:
RA
NB
3
F1
q
F2
M
纵向对称面
平面弯曲 受力特点——作用于杆件上的外力都垂直于杆的轴线,且都在
剪力图和弯矩图(最全面)-剪刀图弯矩图特征 PPT

P q
Pa 2
qa2 2
A
BM
x x
+ P
=
=+
A
B M1
Pa 2
+
+
q
qa 2
A
B M2
2 +
x
三、对称性与反对称性的应用: 对称结构在对称载荷作用下,Q图反对称,M图对称;对称
结构在反对称载荷作用下,Q图对称,M图反对称。
[例8] 作下列图示梁的内力图。
P
PL
Q
x
0L 0.5P L 0.5P L
q AB
RA qa Q qa/2
+ – qa/2
qa2 CD
RD
– qa/2
M
qa2/2
+
–
3qa2/8 qa2/2
qa2/2
解:求支反力 RAq2a; RDq2a
左端点A:
Q qa; M 0 2
x
B点左: Qqa;M1qa2
2
2
B点右: Q qa;M1qa2
2
2
C点左: Qqa;M1qa2
M
– N图
P1a
M图 P1a+ P2 l
二、曲杆:轴线为曲线的杆件。 内力情况及绘制方法与平面刚架相同。
[例11] 已知:如图所示,P及R 。试绘制Q、M、N 图。
解:建立极坐标,O为极点,OB
R
P
极轴,q表示截面m–m的位置。
A
q
B
O
x
q q qq M ( ) P P ( R x R c ) o P ( 1 c s R ) ( o 0 s )
q q q Q () P 1 P si( n 0)
试写出下列各梁的剪力方程和弯矩方程,并作剪力图和弯...

4-2 试写出下列各梁的剪力方程和弯矩方程,并作剪力图和弯矩图。
4-3 试利用载荷集度、剪力和弯矩间的微分关系作下列各梁的剪力图和弯矩图。
4-4 试作下列具有中间铰的剪力图和弯矩图。
4-14 一根搁在地基上的梁承受载荷如图所示。
假设地基的反力按直线规律
连续变化。
试求反力在两端A点和B点处的集度q A和q B,并作梁的剪力图和弯矩图。
4-15 试作图示刚架的剪力图、弯矩图和轴力图。
4-22 厚度为h=1.5mm的钢带,卷成直径为D=3m的圆环,试求钢带横截面上的最大正应力。
已知钢的弹性模量E=210GPa。
4-25 矩形截面的悬臂梁受集中力和集中力力偶作用,如图所示。
试求截面m-m和固定端截面n-n上A、B、C、D四点处的正应力。
4-32 简支梁的荷载情况及尺寸如图所示,试求梁的下边缘的总伸长。
4-39 一矩形截面简支梁由圆柱形木料锯成。
已知F =5kN ,a =1.5m ,[σ]=10MPa 。
试确定弯曲截面系数为最大时矩形截面的高宽比h /b ,以及梁所需木料的最小直径d 。
4-48 一矩形截面木梁,其截面尺寸及载荷如图,q =1.3kN/m 。
已知[σ]=10MPa ,[τ]=2MPa 。
试校核梁的正应力和切应力强度。
4-52 图示木梁受一可移动的载荷F =40kN 作用。
已知[σ]=10MPa ,[τ]=
3MPa 。
木梁的横截面为矩形,其高宽比23=b h 。
试选择梁的截面尺寸。
剪力、弯矩方程与剪力、弯矩图

截面位置对剪力和弯矩的影响
总结词
截面位置对剪力和弯矩具有显著影响。不同的截面位置会导致剪力和弯矩的大小和方向发生变化。
详细描述
在结构分析中,截面位置是影响剪力和弯矩的重要因素之一。不同的截面位置会导致剪力和弯矩的大小和方向发 生变化,从而影响结构的整体受力性能。例如,在梁中选取不同的截面位置进行支撑或固定,会对梁的剪力和弯 矩产生显著影响。
05 剪力、弯矩与材料力学性 能的关系
材料弹性对剪力和弯矩的影响
弹性材料在剪力和弯矩作用下会发生弹性变形,变形量与外力成正比,当外力去 除后,材料能够恢复原状。
弹性材料的剪切模量和弯曲刚度决定了剪力和弯矩的大小,剪切模量越大,材料 抵抗剪切变形的能力越强;弯曲刚度越大,材料抵抗弯曲变形的能力越强。
根据绕顺时针方向观察确定,使上侧 纤维受拉时为正。
02 剪力方程与弯矩方程
剪力图与弯矩图的绘制
1
剪力图和弯矩图是表示梁上剪力和弯矩随截面位 置变化的图形。
2
这些图的绘制基于剪力方程和弯矩方程的计算结 果,通过将计算得到的剪力和弯矩值标在图中相 应的位置上,并连接成线。
3
剪力图和弯矩图的绘制有助于直观地了解梁在不 同截面位置的受力状态和应力分布情况。
弯矩
在梁或结构中,由于弯曲而产生 的力矩,表示弯曲变形的大小。
剪力与弯矩在力学中的作用
剪力
主要影响结构的剪切变形,对梁的剪切承载能力有重要影响 。
弯矩
主要影响结构的弯曲变形,对梁的弯曲承载能力有重要影响 。
剪力与弯矩的符号规定
剪力正方向
根据右手定则确定,从杆件的受压一 侧指向受拉一侧。
弯矩正方向
02
材料强度越高,抵抗剪力和弯矩等外力的能力越强, 所能承受的剪力和弯矩越大。
梁的剪力和弯矩.剪力图和弯矩图
突变,顺下逆上,大小与M 同,FS图不发生变化。
例题
4.9
作图示梁的内力图
3kN 4.5kN m
2kN m
D
A
C
B
FA 10kN
1m 2m
2m
7
3
x 1.56 2
3
2
2.44 2
E FB 2kN 1m
kN
kNm
例题
4.10
4kN m
6kN
1m
1m
4.5
kN
FL
0 xL 0x L
kNm
例题 4.6
图示外伸梁,,试作剪力图和弯矩图.
20kN 40kN m
X1 A 1m 35kN
15
20
kN
20
10kN m
4m
2.5
FS x1 20kN
X2
B
0 x1 1
25kN
M x1 20x1
0 x1 1
FS x2 25 10x2
2Fl
lC
l
FCs
l
C MC
2Fl
FCs
MC
C
l
F
B D
FCs F FCs F
MC Fl MC Fl
MC 2Fl Fl 0
F
B
D
FDs
MD
F
DB
FDs F MD 0
截开后取左边为示力对象:
❖向上的外力引起正剪力,向下的外力引起负剪力; ❖向上的外力引起正弯矩,向下的外力引起负弯矩; ❖顺时针引起正弯矩,逆时针引起负弯矩。
剪力图是斜直线. 弯矩图是二次抛物线.
剪力图和弯矩图
2 括号里的不等式说明对应的内力方程所使用的区段。
FS(x)qx (0xl) M(x)1qx2 (0xl)
2 剪力图为一斜直线
FS(0) 0 FS(l) ql
弯矩图为二次抛物线
M (0) 0 M ( l 2 ) 1 ql 2
8 M ( l ) 1 ql 2
绘剪力图和弯矩图的基本方法:首先分别写出梁 的剪力方程和弯矩方程,然后根据它们作图。
Fs(x)
o
x
o
x
Fs 图的坐标系
M(x) M 图的坐标系
不论在截面的 左侧 或 右侧 向上的外力均将引起 正值 的弯矩,而向下 的外力则引起 负值 的弯矩。
例题:图示简支梁 ,在全梁上受集度为 q 的均布荷载作用。 试作此梁的剪力图和弯矩图。
FS 称为 剪力
y
FA
m
C
A
xm
FS x
由平衡方程
a
P
m
m C0
MFAx0
A
B
m
可得 M = FAx
x
内力偶 M 称为 弯矩
y
FA
m FS
C
x
A
xm
M
结论
a
P
m
梁在弯曲变形时,
横截面上的内力有
A
B
两个,即,
m x
剪力 FS 弯矩 M
y
FA
m FS
C
x
A
xm
M
取右段梁为研究对象。
y
FA
m FS
-
FS FS
dx
(2)弯矩符号 横截面上的弯矩使考虑的脱离体下边受拉,上边受压时为 正 。
剪力图和弯矩图(史上最全面)解析

三、 叠加原理: 多个载荷同时作用于结构而引起的内力等于每个载荷单
独作用于结构而引起的内力的代数和。
Q(P1P2 Pn) Q1(P1) Q2(P2) Qn(Pn)
M(P1P2 Pn) M1(P1) M2(P2) Mn(Pn)
M (P1P2 Pn) M1(P1) M2(P2) Mn(Pn)
适用条件:所求参数(内力、应力、位移)必然与荷载满 足线性关系。即在弹性限度内满足虎克定律。
27
二、材料力学构件小变形、线性范围内必遵守此原理 ——叠加方法
步骤: ①分别作出各项荷载单独作用下梁的弯矩图; ②将其相应的纵坐标叠加即可(注意:不是图形的简单
四、对称性与反对称性的应用: 对称结构在对称载荷作用下,Q图反对称,M图对称;对称
结构在反对称载荷作用下,Q图对称,M图反对称。
M 的驻点: Q 0 ; M 3 qa2 2
x
右端点: Q 0; M 3 qa2 2
22
[例5] 用简易作图法画下列各图示梁的内力图。AB=BC=CD=a
q AB
RA qa Q qa/2
+ – qa/2
qa2 CD
RD
– qa/2
M
qa2/2
+
–
3qa2/8 qa2/2
qa2/2
RB
Pa l
Y
0,
YA
P(l a) l
XA A YA
P B
P B
RB
11
②求内力——截面法
Y
0,
Q YA
P(l a) l
mC 0 , M YA x
m XA A
剪力图和弯矩图(基础)

轴,。
以表(a)(c)(1)(2) (3)≤ (4) 以剪力图是平行于轴的直线。
段的剪力为正,故剪力图在轴上方;段剪力为负,故剪力图在轴之下,如图8-12(b )所示。
由式(2)与式(4)可知,弯矩都是的一次方程,所以弯矩图是两段斜直线。
根据式(2)、(4)确定三点,, ,由这三点分别作出段与段的弯矩图,如图8-12(c )。
例8-4 简支梁受集度为的均布载荷作用,如图8-13(a )所示,作此梁的剪力图和弯矩图。
图8-13解 (1)求支反力 由载荷与支反力的对称性可知两个支反力相.即(2)列出剪力方程和弯矩方程 以梁左端为坐标原点,选取坐标系如图所示。
距原点为的任意横截面上的剪力和弯矩分别为x C l x AC x BC x x 0=x 0)(=x M a x =l Fabx M =)(l x =0)(=x M AC BC AB q A x解 (1)求支反力 由静力平衡方程,得(2)列剪力方程和弯矩方程 由于集中力作用在处,全梁内力不能用一个方程来表示,故以为界,分两段列出内力方程段0<≤ (1)0≤< (2)段 ≤< (3)≤≤(4) (3) 画剪力图和弯矩图 由式(1)、(3)画出剪力图,见图8-14(b );由式(2)(4)画出弯矩图,见图8-14(c )。
二、弯矩、剪力与分布载荷集度之间的微分关系在例8-4中,若将的表达式对取导数,就得到剪力。
若再将的∑=0)(x M A ∑=0)(x M B m C C AC l mF x F A Q ==)(x a xl m x F x M A ==)(x a BC l mF x F A Q ==)(a x l mx l mm x F x M A -=-=)(a x l )(x M x )(x F Q )(x F Q表达式对取导数,则得到载荷集度。
这里所得到的结果,并不是偶然的。
实际上,在载荷集度、剪力和弯矩之间存在着普遍的微分关系。
现从一般情况出发加以论证。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例题4.4,4.5(课本P120)
例题 : 一简支梁受移动荷载 F 的作用如图所示。试求梁的 最大弯矩为极大时荷载 F 的位置。
F
A
B
F
RA
RB
A
B
C
x
l
解:先设 F 在距左支座A 为 x 的任意位置。求此情况下梁的 最大弯矩为极大。 荷载在任意位置时,支反力为:
RA
F(l l
x)
RB
Fx l
RB
b
A
B
两侧横截面上的弯矩值(图)
C
l
发生突变,其突变值等于集
FS
m l
中力偶矩的数值。此处剪力
图没有变化。
ma
M
l
x
x
mb l
梁上集中力作用处左、右两侧横截面上,剪力值 (图)有突变,其突变值等于集中力的数值。在此处弯矩图 则形成一个尖角。
梁上集中力偶作用处左、右两侧横截面上的弯矩值 (图)也有突变,其突变值等于集中力偶矩的数值。但在 此处剪力图没有变化。
当荷载 F 在距左支座为 x
F RA
RB
的任意位置 C 时,梁的弯
A
B
矩值为 :
C
x
MC
RA x
F (l l
x)
x
l
令
dM C 0
dx
F (l 2x) 0 l
x
l 2
此结果说明:当移动荷载 F 在简支梁的跨中时,
梁的最大弯矩为极大。
将
x
l 2
代入式
MC
RA x
F (l l
x)
x
得最大弯矩值
(2) (3)
CB段 : x=a , x= l ,
mb M C右 l
M=0
m
RA a
RB
b
A
B
C
x
x l
AC段 :
m
RA a
RB
b
x=0,
M=0
A
B
x=a,
ma M C左 l
C
x
CB段 : x=a , x=l ,
M
C右
mb l
M=0
x l
ma
M
l
x
绘出梁的弯矩图
mb l
m
梁上集中力偶作用处左、右 RA a
由(2),(4)式可知,AC, CB 两段梁的弯矩图各是一 条斜直线
RA a
A
x
F b
c
x
l
M
RB
B
Fba l
x
在集中荷载作用处的左,右 两
RA a
Fb
RB
A
B
侧截面上剪力值(图)有突变 。
c
突变 值等于集中荷载F。弯矩
x x
l
图形成尖角,该处弯矩值最大 ,
FS
Fb l
+MFra bibliotekxFa l
Fba l
x
例题5:图示的简支梁在 C点处受矩为m的集中力偶作用。 试作此梁的的剪力图和弯矩图。
M (x) m (l x) l
(0 x a)
(a x l)
(2) (3)
AC,CB 两梁段的弯矩图各是一条倾斜直线。
AC段 : x=0, x=a,
M=0
M
C左
ma l
m
RA a
RB
b
A
B
C
x
l
M (x) m x l
M (x) m (l x) l
(0 x a)
(a x l)
M
max
1 4
Fl
习题4.4 i),j)(课本P129)
m
RA a
RB
b
A
B
C
解: 求梁的支反力
l
RA
m l
RB
m l
将坐标原点取在梁的左端。 因为梁上没有横向外力,所以 全梁只有一个剪力方程
m
RA a
RB
b
A
B
C
Fs(x) m (0 x l) (1)
l
l
AC 段和 BC 段的弯矩方程不同
m
RA a
RB
b
AC段 :
A
B
C
M(X) mx l
(0 x a)
(2) x
x
CB段 :
l
M (x) m x m m (l x)
l
l
(a x l)
(3)
m
Fs(x) m (0 x l)
(1)
l
RA a
RB
b
A
B
由(1)式可见,整个梁的剪力
C
图是一条平行于 x 轴的直线。梁
的任一横截面上的剪力为 Fs m l
绘出梁的剪力图
l
m
FS
l
+
x
M (x) m x l
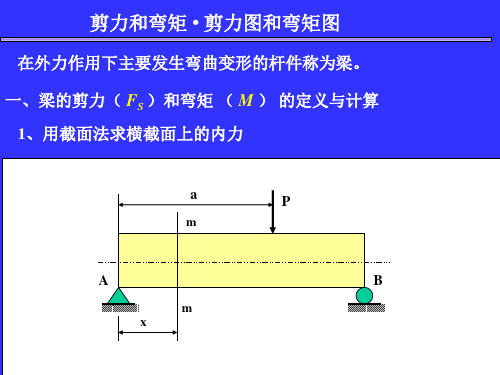
§4–4 剪力方程和弯矩方程 ·剪力图和弯矩图 一、剪力方程和弯矩方程 用函数关系表示沿梁轴线各横截面上剪力和弯矩的变化规律,分 别称作剪力方程和弯矩方程 。
1、剪力方程 Fs = Fs (x )
2、弯矩方程 M = M(x)
M (x) Fb x (0 x a)
(2)
l
M (x) Fa (l x) (a x l) (4) l
